The Science of Doom

When I wrote Do Trenberth and Kiehl understand the First Law of Thermodynamics? I imagined that (almost) no one would have a problem with the model created. Instead, I thought perhaps some might question its relevance to climate.

It was a deliberate choice to use conduction to demonstrate the point – the reason is that radiation is less familiar to most people, while conduction is more straightforward and easier to understand.

Here is the model from that article – a heat source in a hollow PVC sphere, located in the depths of space:

Many people have experienced a lagged hot water pipe. The more lagging (insulation), the higher the temperature rises. It seems straightforward.

However, the conceptual barrier that some people have is so large that anything – literally – will be put forward to make the model fit their conceptual idea. In case the case of one blog, claiming that energy can be destroyed in an effort to get the “right” result. A delicious irony that the first law of thermodynamics is cast aside to protect.. the first law of thermodynamics.

The reason this PVC sphere model appears so wrong to many people is for similar reasons that the famous Kiehl & Trenberth diagram seems wrong – the radiation “internally” (earth surface) is higher than the external radiation to space. (Note that the radiation values in the K&T diagram can be measured).

Explaining How the Result is Calculated

..in simple terms.

Solving the maths for the model above is straightforward (refer to the first article for the actual maths). Here is the solution in simple terms:

For the steady state condition the energy radiated from the outer surface must equal the energy source in the center (30,000 W). Otherwise the system will keep accumulating energy.

Given the surface area and the stated emissivity the outer surface temperature (T2) must be 133K (to radiate 30,000 W).

The only way that heat can be transferred from the inner surface to the outer surface is through conduction. This means 30,000 W is conducted through the PVC.

Given the (low) thermal conductivity of PVC and the dimensions, the temperature difference must be 290K, making T1 = 423K.

If the temperature differential is any lower then less than 30,000W will be conducted through the wall. And if that was the case then heat would be accumulated at the inner surface – increasing its temperature until eventually 30,000W did flow through.

Conversely, if the temperature was higher than 423K then more than 30,000W would be conducted through the sphere. This would start to reduce the temperature until only 30,000W was conducted.

Simple really. However, when the result doesn’t seem right, people begin their mental gyrations to get the “right” result.

This article is not written to convince people who have their minds made up. It’s written to help those who are asking the legitimate question:

Haven’t you just created energy? And can’t I use that to run a small power station?

Good question.

This article is not about proving what has already been demonstrated, it’s about helping with mental models.

The equations of heat transfer have already been clearly explained in Part One. So far, the arguments against that have been put forward consist of:

• the argument from incredulity
• 3m of PVC can transmit radiation straight through (no it can’t)
• energy disappears under the right circumstances (that was just the first of many flaws in that person’s argument..)

Of course, if someone comes up with yet another alternative calculation of the heat transfer I will be happy to look at it.

In the meantime, let’s create a mental model..

The Power Station

A few people have jubilantly claimed that the model I created, if correct, can run a power station of 1.8 MW, from a source of only 30,000 W.

That’s what it might seem like on the surface. But strangely, the model results were derived by conserving energy. That is, no energy was created or destroyed..

In the steady state condition:

• 30,000 W is produced from the internal source
• 30,000 W is conducted through the PVC “wall”
• 30,000 W is radiated from the outer surface

Energy is not being created or destroyed. Where is the energy accumulation in this model? Where is the usable energy being stockpiled?

• If you want to understand the subject, this point is the one to focus on and think about
• If you don’t want to understand the subject say “he’s created 1.8 MW of energy from 30,000W – ridiculous”, and move on (it sounds good)

The inner surface of the sphere has an area of 1,257 m² (4πr²). Consider one square meter of internal surface, we’ll call it “A” – these kind of models always have catchy names for different components of the model.

• Each second, A receives 23.9 W/m² from the internal heat source (30,000W / 1,257 m²).
• Each second, A conducts 23.9 W/m² through the wall.
• Each second, A absorbs 1,452 W/m² radiated from the rest of the inner wall.
• Each second, A re-radiates 1,452 W/m².

This is another way of saying that no energy is being created or destroyed. Where is the energy to run this power station?

All that happens if we start drawing power out of this system is the temperature internally reduces very quickly.

How Does the Sphere Heat Up?

In my efforts to understand the conceptual problems people have, I believe that this might help. I can’t be certain – this article is about mental models.

Let’s picture the scene when the PVC sphere is “started up”.

Outside it is 0K. Inside it is 0K. Chilly. Very chilly.

Now the 30,000 W heat source is fired up. 30,000 J every second gets radiated out from this source. Every second, 80% of this 30,000 J gets absorbed by the inner surface (with 20% reflected).

At this stage almost no energy is conducted through the PVC sphere. It can’t – because the temperature differential is not nearly high enough. Conduction requires a heat differential. So instead, the energy goes into heating up the inner surface of the sphere.

As the inner surface heats up it begins to conduct heat through to the outer surface – but most of the energy still goes into heating the inner surface.

A necessary consequence of the inner surface being heated up is that it radiates. All of this radiation is absorbed by the rest of the inner surface AND THEN re-radiated. Energy is not being created. This energy can’t be “tapped off” to do anything useful.

A small supply of energy is simply being “bounced around” (not really “bounced” but it might be a useful way to think about it)

This energy is simply the energy that has been accumulated by the inner surface during the initial heating process. It keeps being accumulated until finally the temperature is high enough to conduct the full 30,000 W through to the outer surface.

Now we have reached equilibrium! On our journey to equilibrium, while the inner surface was heating up, it accumulated heat, and this accumulated heat is now radiated, absorbed, re-radiated, absorbed…

You can connect it to a power station and very quickly you will draw down this accumulation of energy. The maximum you can draw out long term will be 30,000 W.

Conclusion

This article is all about mental models – explaining why the actual results for this model don’t violate the First Law of Thermodynamics. The results were calculated from the very simple and standard heat transfer equations.

Analysis of this model, with the results that I have presented (in part one), demonstrates that energy is conserved.

At first glance it might not seem like it to many people – because the inner surface radiation is so high. But the energy is just re-radiated from the energy absorbed. It’s like a small stockpile of energy that is being “bounced around” from wall to wall.

There is only one (legitimate) way to solve the heat transfer equations for this model. Other approaches invent /destroy physics in an attempt to get a low enough value for the radiation emitted from the inner wall.

Read Full Post »

With apologies to my many patient readers who want to cover more challenging subjects.

Many people trying to understand climate science have a conceptual problem.

I have written (too) many articles about the second law of thermodynamics – the real and the imaginary version. Resulting comments on this blog and elsewhere about those articles frequently contain comments of this form:

So if we take bucket A full of water at 80°C and bucket B full of water at 10°C, Science of Doom is saying that bucket A will heat up because of bucket B? Right! That’s ridiculous and climate science is absurd!

Yes, if anyone was saying that it would be ridiculous. I agree. To take one example from many, in The Real Second Law of Thermodynamics I said:

Put a hold and cold body together and they tend to come to the same temperature, not move apart in temperature.

Of course, it could be that I am inconsistent in my application of this principle.

One observation on the many contrary claims resulting from my articles – not a single person has provided a mathematical summary to demonstrate that the examples provided contradict the first or second law of thermodynamics.

It should be so easy to do – after all if one of the many systems I have outlined contravenes one of these laws, surely someone can write down the equations for energy conservation (1st law of thermodynamics) or for change in entropy (2nd law of thermodynamics) and prove me wrong. We aren’t talking complex maths here with double integrals or partial differentiation. Just equations of the form a + b = 0.

And here’s the reason why – the problem that people have is conceptual. It seems wrong so they keep explaining why it seems wrong.

Conceptual problems are the hardest to get around. At least, that’s what I have always found. Until a subject “clicks”, all the mathematical proof in the world is just a jumble of letters.

So with that introduction, I offer a conceptual model to help those many people who don’t understand how a cold atmosphere can lead to a warmer surface than would occur without the cold atmosphere.

And if you are one of those people in the “firmly convinced” camp, let me suggest this reason for making the effort to understand this conceptual model. If you understand why others are wrong you can help explain it to them. But if you just don’t understand the argument of people on “the other side” you can’t offer them any useful assistance.

Model 2 – Two bodies – The Boring One that Everyone Really Does Agree With

Very quickly, to “warm everyone up”, and to once again state the basics – if we have two bodies in a closed system, and body A is at temperature 80°C and body B is at 10°C, then over a period of time both will end up at the same temperature somewhere between 10°C and 80°C. It is impossible, for example, for body A to end up at 100°C and body B at 0°C.

Everyone is in agreement on this point.

Note that the “period of time” might be anything between seconds and many times the age of the universe – dependent upon the circumstances of the two bodies.

Model 3A – Three Bodies with the Third Body Being Quite Cold

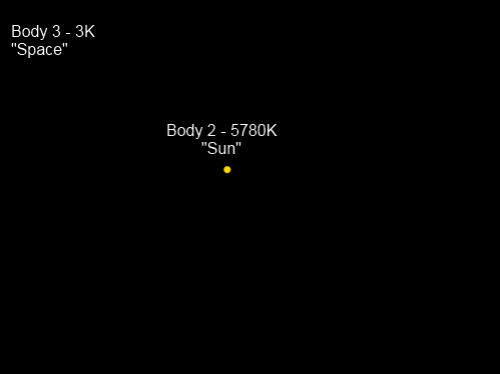
Where’s Body 1? This picture is the view from Body 1, also known as “Chilly Earth”, which is a spherical solid planet.

To make the problem much easier to solve we will state that the heat capacities of Body 2 and Body 3 are extremely high. This means that whether they gain or lose energy, their temperature will stay almost exactly the same. Body 1, “Chilly Earth”, has a much lower heat capacity and will therefore adjust quickly to a temperature which balances the absorption and emission of radiation.

“Chilly Earth” doesn’t have an atmosphere.

However, for the purposes of helping the conceptual model, “Chilly Earth” reflects 30% of shortwave radiation from the Sun but at longer wavelengths absorbs 100% (reflects 0%). This means its emissivity at longwave is also 100%.

“Chilly Earth” has a very high conductivity for heat, and therefore the whole planet is at the same surface temperature. (See note 1).

“Sun” is 150M km away from “Chilly Earth”, and “Chilly Earth” has a radius of 1,000 km (a little different from the planet we call home).

Let’s calculate the approximate equilibrium temperature of “Chilly Earth”, T₁

How do we do this? By calculating the energy absorbed from Body 2 and from Body 3, and calculating the temperature of a surface that will radiate that same energy back out.

The method is simple – see below.

Energy Absorbed from Body 2, “Sun”

Radiation from “Sun” at 5780K = 6.3 x 10⁷ W/m² – near the surface of the sun. By the time the sun’s radiation reaches earth, because of the inverse square law (the radiation has “spread out”), it is reduced to 1,369 W/m². Remember that 30% is reflected, so the absorbed radiation = 958 W/m².

The surface area that “captures” this radiation = πr² = 3.14 x 10⁶ m².

Energy absorbed from body 2, E_r2 = 958 x 3.14 x 10⁶ = 3.01 x 10⁹ W.

Energy Absorbed from Body 3, “Space”

Radiation from “Space” at 3K = 4.59 x 10^-6 W/m². Apart from the very tiny angle in the sky for “Sun”, the entire rest of the sky is radiating towards the earth from all directions in the sky.

The surface area that “captures” this radiation = 4πr² = 1.26 x 10⁷ m².

Energy absorbed from body 3, E_r3 = 4.59 x 10^-6 x 1.26 x 10⁷ = 57.7W.

So energy from body 3 can be neglected which is not really surprising.

Energy Radiated from Body 1, “Chilly Earth”

For thermal equilibrium (energy in = energy out), “Chilly Earth” must radiate out 3.01 x 10⁹ W, from its entire surface area of 1.26 x 10⁷ m².

This equates to 239 W/m², which for a body with an emissivity of 1 (a blackbody) means T₁ = -18°C.

So we have calculated the equilibrium temperature of “Chilly Earth”.

Now, if we change the model conditions – the reflected portion of solar radiation, the emissivity of the earth at longwave, or the conductivity of the planet’s surface – any of these factors would affect the result. They wouldn’t invalidate the analysis, they would simply lead to a different number, one that was slightly more difficult to work out.

But hopefully everyone can agree that with these conditions there is nothing wrong with the method. (I realize that a few people will not agree..)

Model 3B – Three Bodies with the Third Body Being Somewhat Warmer

So now we are going to perform the same analysis with our new Body 1, “Warmer Earth” (a wild stab at an appropriate name).

The only thing that has really changed about the environment is that Body 3, “Crazy Background Radiation”, is now at 250K instead of 3K.

Note that the temperature of Body 3 is higher than before but lower than the equilibrium temperature of 255K calculated for “Chilly Earth” in the last model. As before, body 3 has an emissivity of 1 for longer wavelengths.

Body 1, “Warmer Earth”, still reflects 30% of solar radiation and is the same in every way as “Chilly Earth”.

What are we going to find?

We will do the same analysis as last time. Repeated in full to help those unfamiliar with this kind of problem.

Energy Absorbed from Body 2, “Sun”

Radiation from “Sun” at 5780K = 6.3 x 10⁷ W/m² – near the surface of the sun. By the time the sun’s radiation reaches earth, because of the inverse square law (the radiation has “spread out”), it is reduced to 1,369 W/m². Remember that 30% is reflected, so the absorbed radiation = 958 W/m².

The surface area that “captures” this radiation = πr² = 3.14 x 10⁶ m².

Energy absorbed from body 2, E_r2 = 958 x 3.14 x 10⁶ = 3.01 x 10⁹ W.

Energy Absorbed from Body 3, “Crazy Background Radiation”

Radiation from “Crazy Background Radiation” at 250K = 221 W/m². Apart from the very tiny angle in the sky for “Sun”, the entire rest of the sky is radiating towards the earth from all directions in the sky.

The surface area that “captures” this radiation = 4πr² = 1.26 x 10⁷ m². (See note 2).

Energy absorbed from body 3, E_r3 = 221 x 1.26 x 10⁷ = 2.78 x 10⁹ W.

In this case, energy from body 3 is comparable with body 2.

Energy Radiated from Body 1, “Warmer Earth”

Body 1 absorbs E_tot= E_r2 + E_r3 = 5.79 x 10⁹ W

For thermal equilibrium (energy in = energy out). “Warmer Earth” must radiate out 5.79 x 10⁹ W, from its entire surface area of 1.26 x 10⁷ m².

This equates to 460 W/m², which for a body with an emissivity of 1 (a blackbody) means T₁ = +27°C.

Discussion

Our two cases have revealed something very interesting.

A very very cold sky led to a surface temperature on our slightly different earth of -18°C, while a cold sky (colder than the original experiment’s planetary surface temperature) led to a surface temperature of 27°C.

Well, and here’s the thing, strictly speaking the temperature is actually caused primarily by the bright object in the middle of the picture, “Sun”. The energy absorbed from the sky just changes the outcome a little.

In both cases we calculated the equilibrium temperature by using the first law of thermodynamics (energy in = energy out).

If we do the calculation of entropy change we will find something interesting.. but first, let’s consider the conceptual model and what exactly is going on.

It’s very simple.

In a 3-body problem the temperature of the coldest body still has an effect on the equilibrium temperature of the body being heated by a hotter body.

I could make it more catchy, more media-friendly, but that would go against everything I stand for. I will call this Doom’s Law.

Entropy

The second law of thermodynamics says that entropy can’t reduce. The many cries of anguish that will now arise will claim that Model 3B has broken the Second Law of Thermodynamics. But it hasn’t.

See The Real Second Law of Thermodynamics for more on how to do this calculation. And even clearer, the article by Nick Stokes:

Change in entropy, δS = δQ / T

where δQ = change in energy, T = temperature

We will consider both models over 1 second.

Model 3A

Body 2, “Sun”, δS₂ = -3.85 x 10²⁶ / 5780 = -6.66 x 10²² J/K

Body 3, “Space”, δS₃ = 3.85 x 10²⁶ / 3 = +1.28 x 10²⁶ J/K

And finally, Body 1, “Chilly Earth”, δS₁ = 0 / 255 = 0 J/K

Total Entropy Change = δS₁ + δS₂ + δS₃ = +1.28 x 10²⁶ J/K  :a net increase in entropy.

Model 3B

Body 2, “Sun”, δS₂ = -3.85 x 10²⁶ / 5780 = -6.66 x 10²² J/K

Body 3, “Crazy Background Radiation”, δS₃ = 3.85 x 10²⁶ / 250 = +1.54 x 10²⁴ J/K

And finally, Body 1, “Warmer Earth”, δS₁ = 0 / 255 = 0 J/K

Total Entropy Change = δS₁ + δS₂ + δS₃ = +1.47 x 10²⁴ J/K   :a net increase in entropy.

Important points to note about the entropy calculation

Both scenarios increase entropy – by transferring heat from a high temperature source, “Sun”, to a low temperature source, “Space” in 3A, and “Crazy Background Radiation” in 3B (which is really also Space at a higher temperature).

The earth-like planet is sitting in the middle and doesn’t have a significant effect on the entropy of the universe.

In both cases the entropy of the system increases, so both are in accordance with the second law of thermodynamics.

The earth cools to space, but just at a slower rate when the background temperature of “space” is higher.

If we replaced “crazy background radiation” by an atmosphere that was mostly transparent to solar radiation, the analysis would be a little more complex but the result wouldn’t be much different.

Reasons Why It Might be Wrong

Just to be clear, these aren’t true..

1. The hotter body can’t absorb radiation from the colder body

a) see Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics for six textbooks on heat transfer which all say, yes it does. Actually, seven textbooks, thanks to commenter Bryan identifying his “non-cherrypicked” textbook by “real physicists” which also agreed.

b) see The Amazing Case of “Back Radiation” – Part Three which includes the EBEX experiment as well as a brief explanation of fundamental physics

c) see Absorption of Radiation from Different Temperature Sources – clearing up a few misconceptions on this idea

2. It’s not a real situation because the atmosphere isn’t a black body

It is true that the atmosphere is not a blackbody. But look back at model 3B. It doesn’t matter. Body 3 in this model could be a 250K body with an emissivity of 0.1 and the temperature would still increase over model 3A.

In fact, if the claim is that a colder body can never increase the temperature of a warmer body – all we need is one counter-example to falsify this theory. Now, if you want to modify your theory to something different we can examine this new theory instead.

Reasons Why It Has to be Right

1. The First Law of Thermodynamics. This neglected little jewel is quite important. Energy can’t disappear (or be created) or be quarantined into a mental box.

There is a reason why all the people disputing these basic analyses never explain where the energy goes (if it “can’t” go into changing the temperature of the hotter body that might have absorbed it). The reason – they don’t know.

2. The Second Law of Thermodynamics. This law says that in a closed system entropy cannot decrease. Despite angry claims about “no such thing as a closed system” – that’s what the second law says. Entropy is often simple to calculate.

If a solution uses simple radiation of energy (Stefan-Boltzmann’s law) and satisfies the first and second law of thermodynamics, and some people don’t like it, it suggests that the problem is with their conceptual model.

Conclusion

This is a conceptual model that is very simple.

The sun warms up the earth, and the earth cools to space. The colder “space” is, the faster the rate of net heat transfer. The warmer “space” is, the slower the rate of net heat transfer. And because the sun “pumps in” heat at the same rate, if you slow the rate of heat loss the equilibrium temperature has to increase.

The first law of thermodynamics is the key to understanding this problem. It is simple to verify that model 3A & 3B both satisfy the first law of thermodynamics. In fact, more importantly, a different result would contradict the first law of thermodynamics.

It is also easy to verify that in both 3A & 3B entropy increases.

Just to be clear on a tedious point, the earth and space do not have to radiate as a blackbody to have these conclusions. They just make the model simpler to explain, and the maths easier to understand. We could easily change the emissivity of the planet to 0.9 and the emissivity of space to 0.5 in both models and we would still find that Model 3B had a warmer planetary surface than Model 3A.

Many people will be unhappy, but this blog is not about bringing happiness. Clarity is the objective.

One more hopeless note of despair – this article uses simple theory to prove a point, which is actually a very valuable exercise. Next, some will say – “I don’t want that pointless over-theoretical theory, these people need to prove it with some experiments“.

And so I offer the series, The Amazing Case of “Back Radiation” as proof, especially Part Three. Result of Part Three was – “well, that can’t happen because it goes against theory“..

And so the circle is complete.

Notes

Note 1 – These strange conditions that don’t relate to the real world are to make the conceptual model simpler (and the maths easy). This is the staple of physics (and other sciences) – compare simple models first, then make them more complex and more realistic. If you can prove a theory with a simple model you have saved a lot of work and more people can understand it.

Note 2 – Solar radiation is from a tiny “angle” in the sky, and so the radiation is effectively “captured” by the earth as a flat disk in space. This area is the area of a disk = πr². By contrast, radiation from the sky is from all around the planet, and so the radiation is effectively captured by the surface area of the sphere. This area = 4πr². See The Earth’s Energy Budget – Part One for more explanation of this.

Read Full Post »