A long and interesting discussion followed Venusian Mysteries. One commenter posed an excellent thought experiment:
Consider Venus with its existing atmosphere, and put a totally opaque enclosure (to incoming Solar radiation) around the entire planet at the average location of present outgoing long wave radiation. Use a surface with the same albedo as present Venus for the enclosure.
What would happen to the planetary surface temperature over a reasonably long time?
For this case, NO Solar incoming radiation reaches the surface. I contend that the surface temperature will be about the same as present.
Now assume the gas temperature and distribution are initially different from present levels, but no gases are condensed other than those that form the present clouds. I contend the temperature will go to about the present distribution and level. The only reason for this not to not match exactly the same as the actual atmosphere would be due to the fact that for the atmosphere, outgoing radiation actually leaves from a finite gas thickness, but the present version is a surface.
With further clarification:
Assume the surface has a black body emissivity for the long wave outgoing radiation. Also assume it is a thin but good conducting material.
And also answered that the opaque enclosure radiates in both directions (both outgoing to space and to the surface of the planet).
The First Simple Model
Here’s a very simple radiative balance below. The “opaque enclosure” is E, and the surface is S. This has one layer of opaque atmosphere,1, to get us started: 
The gaps in the diagram are simply to enable us to see the radiation values from each layer more easily – they don’t represent any kind of physical discontinuity.
I started with a many layer model of the atmosphere – as described a little in Venusian Mysteries.
As a result of the solution to the equations, it made sense to explain a one layer model of the atmosphere first. I started by assuming that the initial conditions were that the enclosure and surface were initially very cold to see what happens.
Because E is a “thin but good conducting layer” we assume that E is “isothermal” – all at the same temperature. And because it is thin we assume that it heats up quickly when irradiated by solar energy – i.e., its heat capacity is low so it doesn’t take long to reach equilibrium.
Because gases have very low conductivity, and because radiation from the inside surface of the “opaque layer” is taking place, we assume that radiation to the surface is “much greater” than conductivity.
In this simple (unrealistic) one layer model, we also assume that the atmosphere is isothermal (all at one temperature). This is just to get us started. We can add a many layer model later, where each layer is isothermal, but each layer is at a different temperature from the ones above and below.
A Little Maths
Reviewing the diagram above, assuming that radiation is the only heat transfer mechanism, and assuming that the solar radiation is equally spread (note 1 at end):
TSI + R1 = 2RE [1]
2R1 = RS + RE [2]
RS = R1 [3]
So:
[3] -> [2] 2RS = RS + RE, or RS = RE [4]
[4], [3] -> [1] TSI + RS = 2RS, or TSI = RS
And so, in equilibrium (after every layer has heated up to steady state):
RS = R1 = RE = TSI
That is, each layer radiates the same as every other, and at the same value as the solar irradiance of 158 W/m2 (absorbed solar radiation).
Which means that the enclosure layer will reach an equilibrium temperature of 229K – and this will also be the equilibrium planetary surface temperature.
If these are the equilibrium temperatures what will drive conduction or convection of heat? Nothing. With the surface, the atmosphere and the “enclosure layer” of our thought experiment, all at the same temperature there will be no convection or conduction.
The Many Layer Model
The example above can be extended to many layers of opaque atmosphere. I checked out a 3-atmospheric layer model and the same results are obtained. (It’s tedious writing down the 5 equations and showing the substitutions to solve, especially as wordpress doesn’t do subscripts easily).
But the more realistic many-layer models solve exactly the same way. So with an outer atmospheric layer absorbing the solar radiation and then heating up and radiating in to the surface (and out to space), we find that the surface is no hotter than the outer atmospheric layer.
Compare this with the many layer model in the original article (under How Can the Surface Get so Hot? An Over-Simplified Climate Model), where, because the surface was heated by solar irradiance, the surface could become much hotter due to “backradiation” from the many layers above.
Then, in that model, as a result of the high surface temperatures, convection was initiated which moderated the high temperatures.
In this model, radiation can’t create those conditions – at least from a cold starting condition.
[Note added, 25th June – This model is aimed at demonstrating that radiative effects through an opaque atmosphere are totally different when the solar radiation is received at the outer layer of the atmosphere compared with at the surface. The “isothermal” model of the atmosphere (=the atmosphere all at the same temperature) is just for the purposes of constructing this radiation model – and as Leonard Weinstein points out, his thought experiment explicitly stated that the atmospheric temperature varies. In a “many layer” model with low conductivity (as found in gases) the radiation model would still be valid, even though the temperature varies from night to day and at different latitudes. Therefore, another mechanism of significant heat transfer is required to get the surface temperature of “thought experiment Venus” (TEV) to the temperature of actual Venus.
So in normal Venus we have a mechanism – radiation – for driving the temperature so high. But in TEV we need another mechanism.]
What about the Real World Effects?
In practice, one half of the atmosphere is heated during the day while the other half cools, and vice-versa for the night. This doesn’t affect conduction which has a tiny effect.
Does this create a stronger heating through to the surface and initiate some convective activities? How about if we started with a hot surface (from volcanic activity), would we reach a different equilibrium effect?
In both of these cases, there is no explanation for why any convective lapse rate would be maintained – unless a high source of internal heat from something like volcanic activity was maintained.
If we started with a hot initial condition (but no ongoing source of heat) instead of a cold initial condition, convection would simply move heat up to the top of the atmosphere until the same steady state condition was reached – where each layer was at the same temperature.
Convection is the bulk movement of heat as gases or liquids carry heat from one location to another. But something needs to drive convection. In the case of the earth’s atmosphere it is the relatively high surface temperature (from radiation) heating gases which expand and so are less dense. Gases that are less dense rise – and so heat is moved more effectively from the surface than can be achieved by radiation.
When heating the atmosphere from the top – with the vacuum of space above – there is no explanation for high temperatures in layers below.
In the case of the real Venus we at least saw what a totally opaque atmosphere could achieve. In the case of this thought experiment we see a totally different result.
Perhaps someone can produce a more comprehensive model which shows how the surface could radiate at 16,000 W/m2 in this thought experiment. I doubt that it can be done.
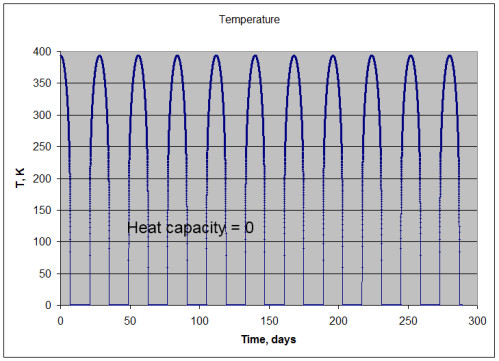
Note 1: If we assume that the solar radiation is equally spread across all surface elements, we get the result in the 1-layer or many-layer model. Strictly speaking this is not the case – as the solar radiation only heats one side of the planet at any one time, and that somewhat unequally. Is this a good approximation? Yes, if the heat capacity of the atmosphere is sufficiently high.
If the heat capacity is lower we simply get a relatively hotter surface temperature during “the day” and a relatively colder surface temperature during “the night”. No mechanism for Venusian surface temperatures.
Update – New article – Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion