Basic Science | The Science of Doom

Archive for the ‘Basic Science’ Category

Simple Atmospheric Models – Part Two

Posted in Basic Science on April 7, 2011| 18 Comments »

In Part One we saw how a very simple energy balance model with some very basic assumptions provided some insight into how the surface and atmospheric temperatures are determined.

We assumed that the atmosphere was transparent to solar radiation (radiation less than 4 μm), that the atmosphere was totally opaque to terrestrial radiation (greater than 4 μm), and that the atmosphere was isothermal (all at one temperature).

All of these assumptions are incorrect.

We derived an average surface temperature of 303K – instead of the realistic 288K – from this simple energy balance model.

In this article we will look at a very basic model to estimate the temperature of the stratosphere. If you aren’t clear about the troposphere/stratosphere, take a look at Tropospheric Basics. For caveats and explanations about simple models, and about radiation and emissivity, please check Part One.

In the troposphere, heat transfer is dominated by convection. The atmosphere transitions to what we call the stratosphere when convection ceases because radiation becomes more effective for moving energy. The atmosphere progressively thins out the higher we go – and as a necessary consequence it becomes optically thinner (note 1). This also implies that the temperature in the stratosphere will not vary significantly with height because radiation can transfer energy across large distances.

In practice, absorption of solar radiation by ozone means that the stratospheric temperature increases with height. However, in this simple model we want to make huge assumptions just to see what results we get, and in this model we continue to assume (incorrectly) that the atmosphere is totally transparent to solar radiation.

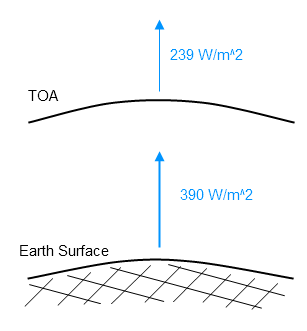
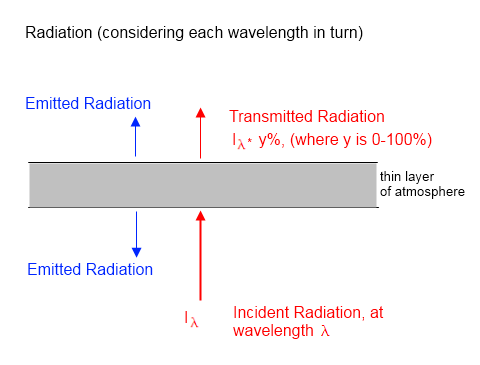
Here is an extract from Elementary Climate Physics by Prof. F.W. Taylor.

It is another very simple model:

Figure 1

Note there there is a correction (in red) to the diagram (his fig 3.5). Even Professors of Physics make mistakes (or their editors do).

If you followed the method of calculation in Part One then this won’t be too difficult.

We know that the earth/troposphere emits to space at an “effective radiating temperature” of 255K. This term effective radiating temperature causes a lot of confusion. It is convenient shorthand for the temperature at which a blackbody would be to radiate that flux. It doesn’t mean that blackbodies exist – perish the thought. And it doesn’t mean that anyone is assuming that the atmosphere is radiating as a blackbody.

What it means is that the earth/atmosphere emits 239 W/m² to space. We call that an “effective radiating temperature” of 255K. It’s not meant to upset anyone. If we wanted we could just call it 239 W/m². We will do that later just to see the effect.

And following Part One, with the assumption of an optically thick surface/troposphere (read about “optically thick” in that article), we have the emission of surface radiation:

E = σT_E⁴

where T_E is the average emitting temperature of the surface/troposphere (as if it was a blackbody)

And if we make some assumptions about the optical properties of the stratosphere we might find some approximate answers that are interesting.

We assume (incorrectly) that the stratosphere is an isothermal layer at temperature, T_s. We assume that the stratosphere is optically thin so that the emission from the surface/troposphere is approximately equal to the emission to space.

The stratosphere has an emissivity, ε, which is very small.

From Kirchhoff’s law, emissivity = absorptivity for the same wavelength ranges. We will come back to review this assumption a little later, but for now note that if the surface/troposphere and the stratosphere are at similar temperatures then this assumption:

absorptivity of stratosphere for surface/troposphere radiation = emissivity of stratosphere

– is approximately correct.

Therefore, from energy balance considerations, the energy absorbed by the stratosphere must be the energy emitted by the stratosphere. So, from figure 1:

εσT_E⁴ = 2εσT_s⁴

therefore:

T_s = T_E / 2^1/4 = 215 K

Now, surprisingly enough for such simple assumptions, this is a reasonable value for the temperature at the bottom of the stratosphere.

Without “Effective Radiating Temperatures”

Let’s redo the calculations – this time using the actual flux to space from the surface/troposphere instead of the “effective radiating temperature”.

The surface/troposphere radiates (globally annually averaged) 239 W/m². The stratosphere absorbs a small fraction of this, determined by absorptivity = emissivity = ε:

ε x 239 = 2εσT_s⁴

therefore:

T_s = (239/σ)^1/4 / 2^1/4 = 215 K

The value is the same as previously calculated, no surprise to anyone who has got to grips with this subject.

Using Kirchhoff

Earlier we used the fact that absorptivity = emissivity for the stratosphere, because of Kirchhoff’s law.

It is very important to understand how to use this law correctly. An excellent example of how not to use it was done by Martin Herztberg in his paper, Earth’s Radiative Equilibrium in the Solar Irradiance, Energy & Environment (2009).

Let me paint a picture with some graphs.

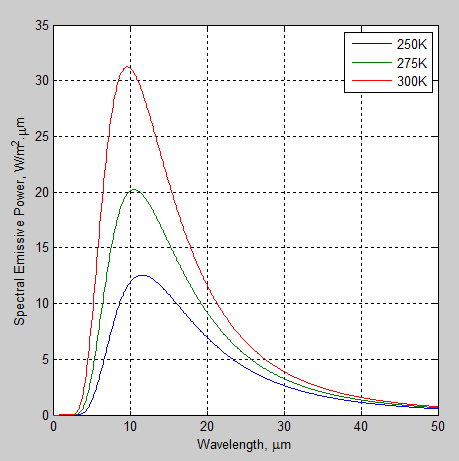
First, the wavelength dependence of blackbody radiation for three different temperatures. Remember that blackbody radiation is just a “perfect emitter”, or the “gold standard” of radiation. Real bodies cannot radiate at a higher intensity at any wavelength, although many come close.

The solar radiation has been normalized to the value at the earth’s surface (because it’s a long way from the sun to the earth – check out The Sun and Max Planck Agree – Part Two):

Figure 2

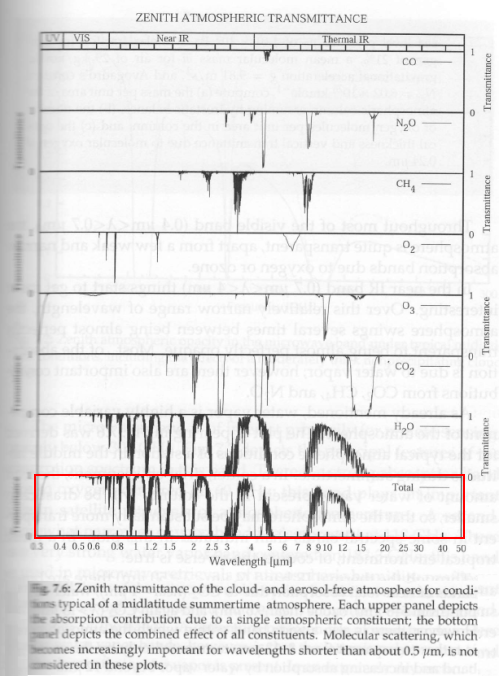
Now, the transmittance for the atmosphere as a function of wavelength. For 4μm and longer wavelengths, absorptance = 1 – transmittance. For shorter wavelengths, especially below 0.5 μm, scattering becomes significant, which means that absorptance = 1 – transmittance – reflectance.

In any case, what should be clear is that absorptance is a strong function of wavelength. See the red marked graph at the bottom:

From Petty (2006)

Figure 3

At any given wavelength, absorptance = emissivity.

So let’s consider the case of a 255 K atmosphere absorbing solar radiation.

The solar radiation is the blue curve in figure 2 – so to calculate how the atmosphere/surface absorbs this radiation we can use the absorptivity (≈ 1 – transmissivity) between 0-5 μm.

The surface/troposphere radiates according to the green curve. We need to multiply this curve by the emissivity = absorptivity at these wavelengths.

So although absorptivity (at a given wavelength) = emissivity (at a given wavelength), it isn’t much use if the source of the incident radiation is at very different wavelengths from the emission. Which is why Martin Herztberg hasn’t passed the competency test in this field. A “rookie mistake”.

You should be able to see from figure 2 that although the surface/troposphere and stratosphere are at different temperatures, an average absorptivity value for absorbing radiation at 255 K will be quite similar to the emissivity value for emitting radiation at 215K.

If we wanted accurate results we would need to use the absorptivity at the relevant wavelength and the emissivity at the relevant wavelength. We also would not assume that the stratosphere was isothermal, or that it was perfectly transparent to solar radiation.

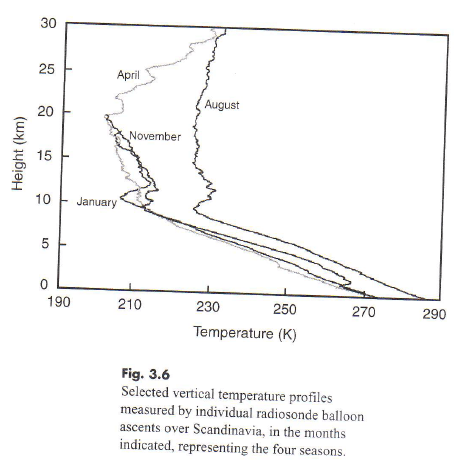
By the way, here are some temperature measurements of the stratosphere in one location:

Figure 4

Conclusion

Calculating the temperature of the stratosphere is a difficult problem. However, as in many fields of scientific endeavor, we can make a very simple model and see how the results compare with reality (and the results of more complex models).

In the example here we make some very simple assumptions and find a result for the stratospheric temperature which is not too far off the mark. However, the only reason for producing (reproducing) this model was to help newcomers to the field gain a conceptual feel for the basics of energy balance and radiative transfer.

By the way, as explained in Part One, no one in climate science believes that the assumptions for this model are correct. Everyone knows that the atmosphere is not a blackbody (perfectly opaque) for all wavelengths greater than 4 μm, and is not perfectly transparent for all wavelengths less than 4 μm.

Notes

Note 1: Optical thickness is proportional to the number of absorbers (molecules that absorb radiation) in the path. So as the atmosphere thins out the density reduces and, therefore, the optical thickness must also reduce. You can read more about the equations of optical thickness in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations

Read Full Post »

Simple Atmospheric Models – Part One

Posted in Basic Science on April 5, 2011| 42 Comments »

Most good textbooks introduce simple models to help the student gain a conceptual understanding.

In Elementary Climate Physics, Prof. F.W. Taylor does the same.

Now the atmosphere is mostly transparent to solar radiation (shortwave) which is centered around 0.5 μm, and quite opaque to terrestrial radiation (longwave) which is centered around 10 μm. Note that absorptivity is very wavelength dependent, especially for radiatively-active gases.

So in this first model, which is very common in introductory books on atmospheric physics, three things are assumed – and none of them are true:

the atmosphere is isothermal – a slab of atmosphere all at the same temperature
the atmosphere is completely transparent to solar radiation
the atmosphere is completely opaque to terrestrial radiation

From Elementary Climate Physics, F.W. Taylor

Figure 1

As many people know, climate scientists introduce things that are not true in climate science books because either they have no idea what they are talking about, or because they are trying to deceive their readers.

Surprisingly, despite the incompetence and mendacity of these awful people the model is quite illuminating.

How do we calculate the surface temperature?

With apologies for the lengthy explanation that follows – necessary because of the confusion frequently spread on this subject. To grasp the essence of the simple model you don’t need to follow every point here.

When a body is a perfect absorber of radiation it is also a perfect emitter. If this is true at all wavelengths, the body is called a blackbody. In practice, no real bodies, or bodies of gases, are blackbodies but many come close. Especially, many come very close at certain wavelengths or bands of wavelengths.

If a layer of atmosphere has an optical thickness = 10 across a band, then its emissivity in that band = 1.0000.

This means, in this band it is.. still not actually a blackbody because its emissivity has not really reached 1, it is actually = 0.9999546. And if the optical thickness = 20 across a band, then its emissivity in that band = 0.9999999979 – still not a blackbody. For all practical purposes we can say it is a blackbody at these wavelengths because within the limits of accuracy we need, emissivity = 0.9999546 is the same as saying emissivity = 1. Nothing special or magical happens in the equations of heat transfer when we transition from 0.99 to 1.00. And assuming 0.9999546 = 1 introduces a 0.005% error.

The equation for the emission of thermal radiation is Planck’s law which describes how the intensity varies with wavelength for a perfect emitter (i.e., a blackbody), e.g.:

Figure 2

For any real surface (or body of gas) this Planck curve is multiplied by the emissivity curve (vs wavelength) to get the actual thermal emission vs wavelength.

To calculate the flux (W/m²) we can instead use the Stefan-Boltzmann equation (which is just the integral of the Planck curve over all wavelengths):

E = εσT⁴

where E = energy emitted in W/m², ε = emissivity, σ = 5.67 x 10^-8, T = surface temperature

Because ε is a function of wavelength, and because increasing temperatures shift the emission to shorter wavelengths we need to use the value of emissivity for the temperature in question.

Notice, in figure 2, that the emission is very low below 4 μm.

Now, for our incorrect assumption that the atmosphere is completely opaque for all wavelengths greater than 4 μm (longwave) then the equation for emission from the atmosphere will be:

E = εσT⁴, and as ε=1 at these wavelengths,

E = σT⁴

Now we have that out of the way..

Energy Balance

The (incorrectly assumed) optically thick atmosphere emits radiation to the surface at σT_a⁴ and out to space at σT_a⁴ (where T_a is the temperature of the atmosphere). The radiation from the earth’s surface is (incorrectly assumed) completely absorbed by the atmosphere.

In equilibrium, as the general rule:

E_in = E_out

Therefore, the absorbed solar radiation = energy emitted to space from the atmosphere.

Absorbed solar radiation = (1-0.3) x S/4, where S = solar constant of 1367 W/m². The “0.3” is the reflected radiation due to the albedo of the earth and climate system. So only 70% of solar radiation is actually absorbed on average. The term 1/4 appears because solar radiation is not directly overhead all points on the globe at all times. For the detailed explanation see The Earth’s Energy Budget – Part One.

Therefore, for the energy balance of the whole climate system:

(1-0.3) x S/4 = σT_a⁴ [1]

And for the surface energy balance, where T_s= surface temperature (and refer to figure 1):

(1-0.3) x S/4 + σT_a⁴ = σT_s⁴ [2]

So, [1] -> [2]

2σT_a⁴ = σT_s⁴

Re-arranging, we get: T_s = 2^1/4.T_a [3]

And from [1], T_a = (239/5.67 x 10^-8)^1/4 = 255 K

Therefore, T_s = 303 K

So we have a solution to the problem for our simple model with three totally incorrect assumptions. Compare the calculated value with the observed 288 K average surface temperature.

Conclusion

As Taylor says:

This calculated greenhouse enhancement of 48 K is rather larger than the observed 33 K, not surprisingly in the light of the simplicity of the model.

This model helps us see how temperature of the atmosphere and the surface are related under the simplest of assumptions.

In practice, the atmosphere is not completely opaque to terrestrial radiation and therefore, does not emit like a blackbody. The atmosphere is not completely transparent to solar radiation, and therefore, the atmosphere is also warmed directly by the sun. The atmosphere is not isothermal and, therefore, emits differently to the surface compared with its emission to space.

And everyone in climate science knows this. Real climate models are slightly more sophisticated.

When you read examples like this and like the “multiple shell” model, they are for illumination and education. Simple models teach beginners more than complex models. Who can understand a GCM if they can’t understand this model?

When you read people writing that climate science assumes the atmosphere radiates as a blackbody you know they didn’t make much progress in their elementary climate science textbook. That is if they even picked one up.

Further reading:

Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations – the actual equations of radiative transfer (no blackbodies or Stefan-Boltzmann equations to be seen)

CO2 – An Insignificant Trace Gas? Part Five – the radiative-convective model with a couple of solutions

The Amazing Case of “Back Radiation” -Part One – for measurements of radiation from the atmosphere

Read Full Post »

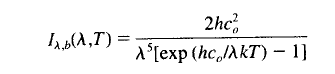
Find Stuff Out and Book Reviews

Posted in Basic Science, Commentary on February 26, 2011| 200 Comments »

Reading one good text book on climate science can save 100’s of hours of reading rubbish on the internet. And there is a lot (of rubbish). Well-meaning people without the baggage of any knowledge of the subject writing rubbish, then repeated by other well-meaning people.

Text books cost money. But depending on which country you live in and whether you have an income, the “payback” means that not buying it is like working for $1/hr. That assumes reading rubbish isn’t a hobby for you..

And depending on where you live you can often join a university library as an “outsider” for anything ranging from $100/year up – and borrow as many books as you like.

Learning can be like a drug. In which case, other justifications aren’t necessary, you have to feed the habit regardless. So pawn family jewelery, sell your furniture, etc. Well, as an addict you already know the drill..

Just some ideas.

Global Physical Climatology – by Dennis Hartmann

Academic Press (1994)

Amazon for $88 (reduced from $118, the price at the normally amazing bookdepository.co.uk).

Why am I recommending such an old book? This covers the basics very thoroughly. When someone covers a lot of subjects there is inevitably a compromise. To cover each of the subjects “properly” would be 4,000 pages or 40,000 pages – not 400 pages. What I like about Hartmann:

a) very readable

b) very thorough

c) enough detail to feel like you understand the basics without drowning in maths or detail.

Maths is the language of science, and inevitably there is some maths. But without any maths you can still learn a lot.

Now, a few samples..

From Chapter 4:

From chapter 11:

As you can see, there is some maths, but if you are maths averse you can mostly “punch through” and still get 80% instead of the full 100%.

Elementary Climate Physics by Prof. F.W. Taylor

Oxford University Press (2005)

bookdepository.co.uk for $44 with FREE shipping lots of places in the world, unbelievable but true.

Amazon has it for $60 plus shipping.

This is an excellent book with more radiative physics than Hartmann, but also more maths generally. For example, in the derivation of the lapse rate there is some assumed knowledge. That’s par for the course with textbooks. They are written with an audience in mind. The audience in mind here is people who already have a decent knowledge of physics, but not of climate.

However, even with a tenuous grasp of physics you will get a lot out of this book. Here’s the downside though – quite some maths:

Well, he is teaching physics.

A First Course in Atmospheric Radiation – Grant Petty

Sundog Publishing 2006

Amazon from $48

Thanks to DeWitt Payne for recommending this book, which is excellent. This is the best place to start understanding radiation in the atmosphere. Goody & Yung 1989 is comprehensive and detailed – but not the right starting point.

Radiative physics is no walk in the park. There is no way to make it astoundingly simple. But Petty does a great job of making it five times easier than it should be:

Now onto “not climate science”:

An Introduction to Thermal Physics – Daniel Schroeder

Published by different companies in different countries.

Amazon from $45 plus shipping and Bookdepository for $56 free shipping.

A book that is nothing to do with climate science, but quite brilliant in explaining very hard stuff – heat and statistical thermodynamics – so it sounds really easy. Not many people can explain hard subjects so they sound easy. Most textbooks writers make slightly difficult stuff sound incomprehensible until after you understand it – at which point you don’t need the textbook.

It wasn’t until I read this book that I realized that Statistical Thermodynamics was actually interesting and useful.

The Inerrancy of Textbooks?

Are textbooks without error and without flaw?

No

So what’s the point then?

The people who write textbooks usually have 20+ years of study in that field behind them. And until such time as E&E start a line of textbooks, the publishers of textbooks, with their own reputation to protect, only ask people who have a solid background in that field to write a textbook.

So even if you are intent on demonstrating that climate science has no idea about basic physics – how are you going to do this?

You could follow the path of many other brave bloggers and commenters who write about the “paltry understanding” of climate science without actually knowing anything about climate science.

But if you choose to do it the old-fashioned way then you should at least find out what climate science says.

Read Full Post »

Heat Transfer Basics – Convection – Part One

Posted in Atmospheric Physics, Basic Science on January 2, 2011| 44 Comments »

A while ago we looked at some basics in Heat Transfer Basics – Part Zero.

Equations aren’t popular but a few were included.

As a recap, there are three main mechanisms of heat transfer:

conduction
convection
radiation

In the climate system, conduction is generally negligible because gases and liquids like water don’t conduct heat well at all. (See note 2).

Convection is the transfer of heat by bulk motion of a fluid. Motion of fluids is very complex, which makes convection a difficult subject.

If the motion of the fluid arises from an external agent, for instance, a fan, a blower, the wind, or the motion of a heated object itself, which imparts the pressure to drive the flow, the process is termed forced convection.

If, on the other hand, no such externally induced flow exists and the flow arises “naturally” from the effect of a density difference, resulting from a temperature or concentration difference in a body force field such as gravity, the process is termed natural convection. The density difference gives rise to buoyancy forces due to which the flow is generated..

The main difference between natural and forced convection lies in the mechanism by which flow is generated.

From Heat Transfer Handbook: Volume 1, by Bejan & Kraus (2003).

The Boundary Layer

The first key to understanding heat transfer by convection is the boundary layer. A typical example is a fluid (e.g. air, water) forced over a flat plate:

From Incropera & DeWitt (2007)

This first graphic shows the velocity of the fluid. The parameter u_∞ is the velocity (u) at infinity (∞) – or in layman’s terms, the velocity of the fluid “a long way” from the surface of the plate.

Another way to think about u_∞ – it is the free flowing fluid velocity before the fluid comes into contact with the plate.

Take a look at the velocity profile:

At the plate the velocity is zero. This is because the fluid particles make contact with the surface. In the “next layer” the particles are slowed up by the boundary layer particles. As you go further and further out this effect of the stationary plate is more and more reduced, until finally there is no slowing down of the fluid.

The thick black curve, δ, is the boundary layer thickness. In practice this is usually taken to be the point where the velocity is 99% of its free flowing value. You can see that just at the point where the fluid starts to flow over the plate – the boundary layer is zero. Then the plate starts to slow the fluid down and so progressively the boundary layer thickens.

Here is the resulting temperature profile:

From Incropera & DeWitt (2007)

In this graphic T_∞ is the temperature of the “free flowing fluid” and T_s is the temperature of the flat plat which (in this case) is higher than the free flowing fluid temperature. Therefore, heat will transfer from the plate to the fluid.

The thermal boundary layer, δ_t, is defined in a similar way to the velocity boundary layer, but using temperature instead.

How does heat transfer from the plate to the fluid? At the surface the velocity of the fluid is zero and so there is no fluid motion.

At the surface, energy transfer only takes place by conduction (note 1).

In some cases we also expect to see mass transfer – for example, air over a water surface where water evaporates and water vapor gets carried away. (But not with air over a steel plate).

From Incropera & DeWitt (2007)

So a concentration boundary layer develops.

Newton’s Law of Cooling

Many people have come across this equation:

q” = h(T_s – T_∞)

where q” = heat flux in W/m², h is the convection coefficient, and the two temperatures were defined above

The problem is determining the value of h.

It depends on a number of fluid properties:

density
viscosity
thermal conductivity
specific heat capacity

But also on:

surface geometry
flow conditions

Turbulence

The earlier examples showed laminar flow. However, turbulent flow often develops:

Flow in the turbulent region is chaotic and characterized by random, three-dimensional motion of relatively large parcels of fluid.

Check out this very short video showing the transition from laminar to turbulent flow.

What determines whether flow is laminar or turbulent and how does flow become turbulent?

The transition from laminar to turbulent flow is ultimately due to triggering mechanisms, such as the interaction of unsteady flow structures that develop naturally within the fluid or small disturbances that exist within many typical boundary layers. These disturbances may originate from fluctuations in the free stream, or they may be induced by surface roughness or minute surface vibrations

from Incropera & DeWitt (2007).

Imagine treacle (=molasses) flowing over a plate. It’s hard to picture the flow becoming turbulent. That’s because treacle is very viscous. Viscosity is a measure of how much resistance there is to different speeds within the fluid – how much “internal resistance”.

Now picture water moving very slowly over a plate. Again it’s hard to picture the flow becoming turbulent. The reason in this case is because inertial forces are low. Inertial force is the force applied on other parts of the fluid by virtue of the fluid motion.

The higher the inertial forces the more likely fluid flow is to become turbulent. The higher the viscosity of the fluid the less likely the fluid flow is to become turbulent – because this viscosity damps out the random motion.

The ratio between the two is the important parameter. This is known as the Reynolds number.

Re = ρu_∞x / μ

where ρ = density, u_∞ = free stream velocity, x is the distance from the leading edge of the surface and μ = dynamic viscosity

Once Re goes above around 5 x 10⁵ (500,000) flow becomes turbulent.

For air at 15°C and sea level, ρ=1.2kg/m³ and μ=1.8 x 10^-5 kg/m.s

Solving this equation for these conditions, gives a threshold value of u_∞x > 7.5 for turbulence.. This means that if the wind speed (in m/s) x the length of surface over which the wind flows (in m) is greater than 7.5 we will get turbulent flow.

For example, a slow wind speed of 1 m/s (2.2 miles / hour) over 7.5 meters of surface will produce turbulent flow. When you consider the wind blowing over many miles of open ocean you can see that the air flow will almost always be turbulent.

The great physicist and Nobel Laureate Richard Feynman called turbulence the most important unsolved problem of classical physics.

In a nutshell, it’s a little tricky. So how do we determine convection coefficients?

Empirical Measurements & Dimensionless Ratios

Calculation of the convection heat transfer coefficient, h, in the equation we saw earlier can only be done empirically. This means measurement.

However, there are a whole suite of similarity parameters which allow results from one situation to be used in “similar circumstances”.

It’s not an easy subject to understand “intuitively” because the demonstration of these similarity parameters (e.g., Reynolds, Prandtl, Nusselt and Sherwood numbers) relies upon first seeing the differential equations governing fluid flow and heat & mass transfer – and then the transformation of these equations into a dimensionless form.

As the simplest example, the Reynolds number tells us when flow becomes turbulent regardless of whether we are considering air, water or treacle.

And a result for one geometry can be re-used in a different scenario with similar geometries.

Therefore, many tables and standard empirical equations exist for standard geometries – e.g. fluid flow over cylinders, banks of pipes.

Here are some results for air flow over a flat isothermal plate (isothermal = all at the same temperature) – calculated using empirically-derived equations:

Click for a larger view

The 1st graph shows that the critical Reynolds number of 5×10⁵ is reached at 1.3m. The 2nd graph shows how the boundary layer grows under first laminar flow, then second under turbulent flow – see how it jumps up as turbulent flow starts. The 4th graph shows the local convection coefficient as a function of distance from the leading edge – as well as the average value across the 2m of flat plate.

Conclusion

Not much of a conclusion yet, but this article is already long enough. In the next article we will look at the experimental results of heat transfer from the ocean to the atmosphere.

Notes

Note 1 – Heat transfer by radiation might also take place depending on the materials in question.

Note 2 – Of course, as explained in the detailed section on convection, heat cannot be transferred across a boundary between a surface and a fluid by convection. Conduction is therefore important at the boundary between the earth’s surface and atmosphere.

Read Full Post »

Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part One

Posted in Atmospheric Physics, Basic Science on December 23, 2010| 114 Comments »

This first part considers some elementary points. In the next part we will consider more advanced aspects of this subject.

Since 1978 we have had satellites continuously measuring:

incoming solar radiation
reflected solar radiation
outgoing terrestrial radiation

To see how we can differentiate the solar and terrestrial radiation, take a look at The Sun and Max Planck Agree – Part Two.

Top of Atmosphere Satellite Measurements

The top of atmosphere (TOA) radiation from the climate system is usually known as outgoing longwave radiation, or OLR. “Longwave” is a climate convention for wavelength >4μm.

Here’s what the OLR looks like to the satellites. I thought it might be interesting for some people to see how the values change each month:

All of this data comes from CERES – Clouds and the Earth’s Radiant Energy System. You can review this data for yourself here. How accurate is the data?

The uncertainty of an individual top-of-atmosphere OLR measurement is 5 W/m², while the uncertainty of average OLR over a 1°-latitude x 1°-longitude box, which contains many viewing angles, is ≈1.5 W/m²

from Dessler et al (2007) writing about the CERES data.

If we summarize this data into monthly global averages:

The average for 2009 is 239 W/m². This average includes days, nights and weekends. The average can be converted to the total energy emitted from the climate system over a year like this:

Total energy radiated by the climate system into space in one year = 239 x number of seconds in a year x area of the earth in meters squared

= 239 x 60 x 60 x 24 x 365 x 4 x 3.14 x (6.37 x 10⁶ )²

= 239 x 3.15 x 10⁷ x 5.10 x 10¹⁴

E_TOA= 3.8 x 10²⁴ J

The reason for calculating the total energy in 2009 is because many people have realized that there is a problem with average temperatures and imagine that this problem is carried over to average radiation. Not true. We can take average radiation and convert it into total energy with no problem.

What about the radiation from the surface?

Surface Radiation

What do the satellite measurements say about surface radiation?

Nothing.

Well strictly speaking – they say a lot, but only once certain theories of radiative transfer are embraced.

To be more accurate, what satellite measurements OF surface radiation do we have?

None.

That’s because the atmosphere interacts with the radiation emitted from the surface. So any top-of-atmosphere measurements by satellite are not “unsullied surface measurements”.

There are temperature stations all around the world – not enough for some people, and not as well-located as they could be – but what about stations for measuring radiation upwards from the earth (and ocean) surface?

Thin on the ground, extremely thin.

Luckily, there is a very simple formula for radiation emitted from the surface of the earth:

E = εσT⁴

where σ is a constant = 5.67 x 10^-8, ε = emissivity, a property of surface material, and T = temperature in K (absolute temperature)

This equation is called the Stefan-Boltzmann equation. More about it in Planck, Stefan-Boltzmann, Kirchhoff and LTE. It is a well-proven equation with 150 years of evidence behind it – and from all areas of engineering and physics. It is used in calculations for heat-exchangers and boilers, for example.

Still, many people when they find out that the radiation from the surface of the earth is calculated not measured are very suspicious. It’s good to be skeptical. Ask questions. But don’t assume it’s made up just because it’s calculated. Why trust thermometers? They actually rely on material properties as well..

Anyway, back to the emission of radiation from the surface. What about this parameter emissivity, ε?

Emissivity is a function of wavelength. This means it varies as the wavelength of radiation varies. Some examples, not all of them materials from the surface of the earth:

Reflectivity vs wavelength for various surfaces, Incropera (2007)

Note that reflectivity = 1 – emissivity in the graph above.

Without going into a lot of detail, all it means is that the measurement of emissivity needs to be for the appropriate temperature. See note 1.

If we measure emissivity of water one day, we find it is the same the next day and also in 589 days time. It is a material property which means that once measured, the only questions we have are:

a) what is the temperature of the surface
b) what is the material of the surface (so we can look up the measured emissivity for this temperature)

Generally the emissivity of the earth’s surface is very close to 1 (for “longwave” measurements).

Oceans, which cover 71% of the earth’s surface, have an emissivity of about 0.98 – 0.99.

The average temperature of the earth’s surface (including days, nights and all locations) is around 15°C (288K). Average temperature is a problematic value because radiation is not linearly dependent on temperature – it is dependent on the 4th power of temperature. See The Dull Case of Emissivity and Average Temperatures for an example of the problems in using “average temperature”.

Here is an example of measurement of upward surface radiation:

Upward and downward radiation measurements, EBEX 2000, Kohsiek (2007)

The line with the x’s is the measured surface upward radiation.

Here is the actual temperature:

Temperature for 14 August 2000, from Wim Kohsiek, private communication

And calculated emitted radiation:

Calculated (theoretical) upward radiation, 14 August 2000

Note how it matches the measured value. You can see this in more detail in The Amazing Case of “Back Radiation” – Part Three.

The theory about emitted radiation

E = εσT⁴

– is a solid theory, backed up over the last 150 years.

If we calculate the average radiation from the surface, globally annually averaged, we get a value around 390 W/m².

If we calculate the total surface radiation over one year, we get E_surf = 6.2 x 10²⁴ J.

The Inappropriately-Named “Greenhouse” Effect

The surface radiates around 390 W/m². The climate system radiates around 239 W/m² to space:

How does this happen?

As I found with previous articles, many people’s instinctive response is “you’ve made a mistake”.

Usually those that just aren’t happy with this diagram solve the “dissonance” by concluding that there is something wrong with the averaging, or Stefan-Boltzmann’s law, or the measurement of emissivity around the planet.

Here’s the total energy for one year radiated from top of atmosphere and from the surface:

Remember that the top of atmosphere number is measured. Remember that the surface radiation is calculated, and relies on measurements of temperature, the material property called emissivity and an equation backed up by 150 years of experimental work across many fields.

This effect which we see has come, inappropriately, to be called the “greenhouse” effect. We could convert the effect to a temperature but there are more important things to move onto.

Before examining how this amazing effect takes place and what happens to all this energy – “Does it just pile up and eventually explode, no – so obviously you made a mistake”, and so on – I’ll leave one thought for interested students..

We have looked at the average radiation from surface and top of atmosphere (and also totaled that up).

Instead, we could take a look at some individual ocean locations where the temperature is well known. We have the CERES monthly averages on a 1° x 1° grid above.

Take a few ocean locations and find the average temperatures for each month.

Then calculate the surface radiation using the known emissivity of 0.99. Compare that to the top of atmosphere radiation from the CERES charts at the start of the article. Also calculate what value of ocean emissivity would actually be needed for surface radiation to equal the top of atmosphere radiation (so as to make the “greenhouse” effect disappear). Please report back in the comments.

The reason I chose the ocean for this exercise is because the emissivity is well known and measured so many times, because ocean surfaces don’t change temperature very much from day to night (because of the high heat capacity of water) and because oceans cover 71% of the earth’s surface. If ocean data verifies the “greenhouse” effect to you, then it’s pretty hard to find emissivity values of other surface types that would make the “greenhouse” effect disappear.

Interaction of Matter with a Radiation Field

Huh? Let’s choose a different heading..

What Happens to Radiation as it Travels Through the Atmosphere

If longwave radiation (remember this is the radiation emitted by the earth and climate system) was transparent to the various gases in the atmosphere the surface radiation would not change on its journey to the top of atmosphere. See The Hoover Incident for more on this and the consequences.

Instead at each height in the atmosphere there is absorption of some radiation. The detail gets pretty complicated because each gas absorbs at very selective wavelengths (see note 2).

The very fact that radiation can be absorbed by gases shows that you shouldn’t expect the radiation going into a layer of atmosphere to be the same value when it emerges the other side. Here’s a simple diagram (which also can be found in Theory and Experiment – Atmospheric Radiation):

If a proportion of the upward radiation is absorbed by the atmosphere so that less radiation emerged than entered (the red text and arrows) then isn’t this a first law of thermodynamics problem?

Well, being specific:

Energy In – Energy Out = Energy Retained in Heating the Layer

So if the temperature of that layer was not increasing or decreasing then:

Energy in = Energy out.

So surely, absorption of radiation with no continuous heating is a problem for the first law of thermodynamics?

Of course, energy transfer can also take place via convection. So it is theoretically possible that energy could be absorbed as radiation and leave via convection. But that isn’t really possible all through the climate as convection would need to transfer energy from high up in the atmosphere to the surface, whereas in general, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.

So what happens and how does the first law of thermodynamics stay intact?

Very simple – every layer of atmosphere also radiates energy. This is shown as blue text and arrows in the diagram.

Each layer in the atmosphere does obey the first law of thermodynamics. But by the time we reach the top of atmosphere the upwards radiation has been significantly reduced – on average from 390 W/m² to 239 W/m².

Each layer in the atmosphere absorbs radiation from below (and above). The gases that absorb the energy share this energy via collisions with other gases (thermalization), so that all of the different gases are at the same temperature.

And the radiately-active gases (like water vapor and CO2) then radiate energy in all directions.

This last point is the key point. If the radiation was (somehow magically) only upwards then the “greenhouse” effect would not occur.

Digression – Up & Down or All Around?

You will often see explanations with “the layer then radiates both up and down” – and I think I have used this expression myself. Some people then respond:

Doesn’t it radiate in all directions? Looks like another climate science over-simplication..

This is a good point. Radiation from the atmosphere does go in all directions not just up and down.

In the radiative transfer equations this is taken into account. The simplified explanation just makes for an easier to understand point for beginners. See Vanishing Nets under Diffusivity Approximation for more about the calculation.

End of digression.

Radiation Through the Atmosphere

Solar radiation is mostly absorbed by the earth’s surface (because the atmosphere is mostly transparent to solar radiation). This heats the surface, which radiates upward. The typical radiation from the earth’s surface at 15°C measured just above it looks something like this:

The atmosphere absorbs this longwave radiation and consequently radiates in all directions. This is why, when we view the spectrum of the upward radiation at the top of atmosphere we see something like this:

From Atmospheric Radiation, Goody (1989)

Note the reversal of the x-axis direction.

The “missing bits” in the curve are the wavelengths where the radiatively active gases have absorbed and re-radiated. Some of the radiation is downward, which explains where the “missing radiation” goes.

At the surface we can measure this downward radiation from the atmosphere. See The Amazing Case of “Back Radiation” -Part One and the following two parts for more discussion of this.

But – as already stated – at each height in the atmosphere, energy fluxes are balanced:

Energy in = Energy out

Or – the difference between energy in and energy out results in increasing or decreasing temperature.

If you like, think of the atmosphere as a partial mirror reflecting a proportion of the radiation at a number of layers up through the atmosphere. It’s a mental picture that might help even though what actually happens is somewhat different.

Convection

No explanation of radiation would be complete without people saying that this argument is falsified by the fact that convection hasn’t been discussed. Just to forestall that: Convection moves heat from the surface up into the atmosphere very effectively and cools the surface compared with the case if convection didn’t occur.

But – emission and absorption of radiation still takes place. Convection doesn’t change the absorption of radiation (unless it changes the concentration of various gases). But convection, by changing the temperature profile, does change emission.

As we will see in Part Two, absorption is a function of concentration of each gas; while emission is a function of concentration of each gas plus the temperature of that portion of the atmosphere.

Conclusion

The atmosphere interacts with the radiation from the surface and that’s why the surface radiation has been reduced by the time it leaves the climate system.

The satellites measure the value at the top of atmosphere very comprehensively.

For those convinced that there is no “greenhouse” effect, I recommend focusing on the emissivity measurements used in the calculation of emission from the surface.

The ocean has been measured at 0.98-0.99 and covers 71% of the surface of the earth but perhaps the average surface emissivity at terrestrial temperatures is only 0.61.. A measurement snafu..

In the next part we will consider in more detail how the different effects cause changes in the OLR.

Other articles:

Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only

Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.

Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.

Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”

Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies

Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking

And Also –

Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.

References

An analysis of the dependence of clear-sky top-of-atmosphere outgoing longwave radiation on atmospheric temperature and water vapor, Dessler et al, Journal of Geophysical Research (2008).

Notes

Note 1: Radiation from a surface at 15°C (288K) will have a peak radiation at 10μm with radiation following the Planck curve. The average emissivity for 288K needs to be the wavelength-dependent emissivity weighted appropriately for the corresponding Planck curve. This will be very similar for the emissivity for the same surface type at 300K or 270K but is likely be totally different for the emissivity for the surface at 3000K – not a situation we find on earth.

Note 2: The most common gases in the atmosphere, Nitrogen and Oxygen, don’t interact with longwave radiation. They don’t absorb or emit – at least, any interaction is many orders of magnitude lower than the various trace gases like water vapor, CO2, methane, NO2, etc. This is after taking into account their much higher concentration. See CO2 – An Insignificant Trace Gas? Part Two

Read Full Post »

Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three and a Half – The Creation of Energy?

Posted in Basic Science, Debunking Flawed "Science" on December 4, 2010| 12 Comments »

I’m in the process of writing a couple more in-depth articles but have been much distracted by “First Life” in recent weeks.. sad and unfortunate, because writing Science of Doom articles is much more interesting..

While writing a new article – What’s the Palaver? – Kiehl and Trenberth 1997 – I thought that I should separately explain a few things which related to the earlier article: Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three.

I know that many readers already get the point. But clearly some people find the model – and real life – so controversial that they will find many ways to claim “real life” wrong. Stefan-Boltzmann, who was he? Pyrgeometers– clearly a fake product that should be investigated by the Justice Department? And so on.

One of the problems is that radiant heat transfer is not something in accord with everyday life and so – as we all do – people draw on their own experience. But people also draw on confused ideas about the First Law of Thermodynamics to make their case.

In this article, two ideas.

First, is the Atmosphere Made of PVC?

In the original article – Do Trenberth and Kiehl understand the First Law of Thermodynamics? – I used a simple heat conduction problem to demonstrate that temperatures can be much higher inside a system than outside a system, when the system is heated from within.

One commenter explained the link between this and the atmosphere, although perhaps my attempts at humor had slightly back-fired. I had disclaimed any relationship between PVC spheres and the atmosphere..

Well, I confirm the atmosphere is not made of PVC, and that conduction is not important for heat transfer through the atmosphere.

But there is relevance for the atmosphere. Where is the relevance?

Solar radiation heats the climate system “from within”. The atmosphere is mostly transparent to solar radiation so the solar energy initially heats the surface of the earth. Then the surface of the earth heats the atmosphere. Finally the atmosphere radiates energy back out to space.

If it were true that the first law of thermodynamics – the conservation of energy – was violated by a simple “lagged pipe” model – well, that would be the end of an important branch of thermodynamics.

The model showed that the temperature of an inner surface can be higher than an outer surface – and, therefore, radiation from an inner surfaces can be higher than the radiation to space from the outer surface.

The reason for providing the model of the PVC sphere – much simpler than the atmosphere – was to demonstrate that simple point.

Second, What if the Radiation from an Inner Surface CANNOT be Higher than from an Outer Surface

Many people write entertainingly inaccurate articles about this subject (see Interesting Refutation of Some Basics for one example). Apparently, if the radiation from the atmosphere/surface into space is 239 W/m² then the radiation from the inner surface itself cannot be more than 239 W/m². A confusion about the First Law of Thermodynamics.

To be specific, the actual claim from the believers in the Imaginary First Law of Thermodynamics (IFTL) is that the total radiation from the earth’s surface cannot be higher than the total radiation from the climate system into space.

This, according to the IFLT, is not allowed.

Let’s consider the consequences and calculate the results. All we need to connect the two values – when we have the W/m² for both surfaces – is the ratio of surface areas.

If E₁ is the radiation in W/m² from inner surface A₁, and E₂ is the radiation from the outer surface, of area A₂:

E₁A₁ = E₂A₂

The area of a sphere is proportional to its radius squared (A = 4πr²), so the above equation becomes:

E₁r₁² = E₂r₂²

a) The Earth and Climate System

In the case of the Earth and climate system, the radius of the earth and the radius of the “climate system” are almost identical..

The radius of the earth, r₁ = 6,380 km or 6.38 x 10⁶ m.

The radiation to space takes place from an average height of around 6km from the surface, so the radius of “the climate system”, r₂ = 6.39 x 10⁶ m (at most).

The total radiation to space, E₂ = 239 W/m² (measured by satellite).

If the IFTL believers are correct then E₁r₁² = E₂r₂²

Therefore, E₁ = 239 x (6.39 x 10⁶)² / (6.38 x 10⁶)² = 240 W/m²

Unsurprisingly, this surface radiation value is almost the same as the radiation into space because the two areas are almost identical.

The Stefan-Boltzmann law says that radiation from a surface, E = εσT⁴

The “currently believed” average value from the earth’s surface is 396 W/m². This is due to the emissivity of the earth’s surface being very close to 1.

So there are three simple choices for why the “believed value” of 396 W/m² is so much higher than the believers in the IFLT appear to claim:

The Stefan-Boltzmann law is wrong
The emissivity of the earth’s surface, for the wavelengths under question, is an average of 0.61
The surface temperature has been massively over-estimated and the “average” temperature of the earth’s surface is actually around -18°C (see note 1).

The 3rd choice should not be ruled out. Perhaps Antartica is a lot larger than measured, or a lot colder. How many temperature stations are there on Antarctica anyway? Maybe there is some cartographical error in estimating the area of this continent from when planes have flown over Antarctica and satellites have crossed the poles.

Perhaps the Gobi desert is a lot colder than people think. No one really makes an effort to measure this stuff, climate scientists just take it all for granted, sitting in their nice warm comfortable offices looking over the results of supercomputer climate models. No one does any field research.

Quite plausible really. It’s not too hard to make the case that the average temperature of the earth is much much much colder than is generally claimed.

b) The PVC Sphere

Let’s review the very simple hollow PVC sphere model. In the original article, the inner radius was 10m and the outer radius was 13m.

Let’s look at what happens as the inner radius is increased up to 10,000m while the wall thickness stays at 3m.

Instead of keeping the internal energy source of 30,000W constant, we will keep the internal energy source per unit area of inner surface constant. In the original example, this value was 23.9 W/m².

Real First Law

With the equations provided in the maths section of Part One, and an energy source of 23.9W/m², here is the temperature difference from inner to outer surface as the inner radius increases:

Note that the x-axis is a log scale. The initial value, 10¹ (=10) was the value from the original example, and the temperature difference was 290K.

As the sphere becomes much larger (and the wall thickness stays constant) the temperature difference tends towards 377K.

Now that is a very interesting number that we can check.

When the wall thickness becomes very thin in comparison to the sphere it is really approximating a planar wall. The equation for heat conduction (per unit area) through a planar wall is:

q = k . ΔT/Δx

where q = W/m², k = conductivity (0.19 W/m.K), ΔT = temperature difference, Δx = wall thickness, m

So for a 3m thick planar PVC wall conducting 23.9 W/m², let’s re-arrange and plug the numbers into the equation:

ΔT = 23.9 x 3 / 0.19 = 377 K

Correct.

So this is a very simple test. There is no other way to link heat conduction and temperature difference. The simple equations that anyone can check support the PVC sphere model results.

Imaginary First Law

Let’s find out what happens under the imaginary first law. It will be quite surprising for the supporters of the theory.

I couldn’t check the imaginary first law in any textbooks, because it’s.. anyway, as far as I can determine, here are the steps:

1. The radiation from the inner surface must be 23.9 W/m². This means (for an emissivity, ε = 0.8 that has already been prescribed for this model) that the inner surface temperature, T₁ = 151.5K (E = εσT⁴)

2. The inner and outer surface radiation values are related by the equations provided earlier:

E₁r₁² = E₂r₂²

3. Therefore, we can calculate the outer surface temperature and therefore the temperature difference.

Here is the graph of temperature difference as the radius increases:

Note the important point that as the radius increases the temperature difference reduces to almost nothing – this is the inevitable consequence of the (flawed) argument that inner surface radiation has to equal outer surface radiation.

Because when r1=10,000m, r2=10,003m, therefore, the areas are almost identical.

Therefore, the radiation values are almost identical, therefore the temperatures are almost identical.

Ouch. This means that somehow 23.9 W/m² is driven by heat conduction across 3m of PVC with no temperature difference.

How can this happen? Well – it can’t. To get 23.9 W/m² across a planar PVC wall 3m thick requires a temperature difference of 377 K.

When r1 = 10,000 m, ΔT = 0.02 K according to my IFTL calculations – and so the conducted heat per unit area, q = 0.0013 W/m². The heat can’t get out, which means the temperature inside increases.. and keeps increasing until the temperature differential is high enough to drive 23.9 W/m² though the wall.

Hopefully, this makes it clear to anyone who hasn’t already made a total nana of themselves that the imaginary first law of thermodynamics, is .. imaginary.

Notes

Note 1 – The concept of an average temperature is not really needed to actually do this calculation. Averaging temperatures across different surface materials like oceans, rocks, deserts clearly has some problems – see for example, Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored.

All that is really required is to calculate the average radiation value instead. Just find the temperature at each location and calculate the emitted radiation. Then average up all the numbers (area-weighted).

As a note to the note.. To get 240 W/m² with an emissivity close to 1, the “average temperature” can be at most -18°C. With a wider day/night and seasonal variation than we actually experience on earth the “average temperature” would then be lower than -18°C.

Read Full Post »

Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three – The Creation of Energy?

Posted in Basic Science, Debunking Flawed "Science" on November 14, 2010| 123 Comments »

When I wrote Do Trenberth and Kiehl understand the First Law of Thermodynamics? I imagined that (almost) no one would have a problem with the model created. Instead, I thought perhaps some might question its relevance to climate.

It was a deliberate choice to use conduction to demonstrate the point – the reason is that radiation is less familiar to most people, while conduction is more straightforward and easier to understand.

Here is the model from that article – a heat source in a hollow PVC sphere, located in the depths of space:

Many people have experienced a lagged hot water pipe. The more lagging (insulation), the higher the temperature rises. It seems straightforward.

However, the conceptual barrier that some people have is so large that anything – literally – will be put forward to make the model fit their conceptual idea. In case the case of one blog, claiming that energy can be destroyed in an effort to get the “right” result. A delicious irony that the first law of thermodynamics is cast aside to protect.. the first law of thermodynamics.

The reason this PVC sphere model appears so wrong to many people is for similar reasons that the famous Kiehl & Trenberth diagram seems wrong – the radiation “internally” (earth surface) is higher than the external radiation to space. (Note that the radiation values in the K&T diagram can be measured).

Explaining How the Result is Calculated

..in simple terms.

Solving the maths for the model above is straightforward (refer to the first article for the actual maths). Here is the solution in simple terms:

For the steady state condition the energy radiated from the outer surface must equal the energy source in the center (30,000 W). Otherwise the system will keep accumulating energy.

Given the surface area and the stated emissivity the outer surface temperature (T2) must be 133K (to radiate 30,000 W).

The only way that heat can be transferred from the inner surface to the outer surface is through conduction. This means 30,000 W is conducted through the PVC.

Given the (low) thermal conductivity of PVC and the dimensions, the temperature difference must be 290K, making T1 = 423K.

If the temperature differential is any lower then less than 30,000W will be conducted through the wall. And if that was the case then heat would be accumulated at the inner surface – increasing its temperature until eventually 30,000W did flow through.

Conversely, if the temperature was higher than 423K then more than 30,000W would be conducted through the sphere. This would start to reduce the temperature until only 30,000W was conducted.

Simple really. However, when the result doesn’t seem right, people begin their mental gyrations to get the “right” result.

This article is not written to convince people who have their minds made up. It’s written to help those who are asking the legitimate question:

Haven’t you just created energy? And can’t I use that to run a small power station?

Good question.

This article is not about proving what has already been demonstrated, it’s about helping with mental models.

The equations of heat transfer have already been clearly explained in Part One. So far, the arguments against that have been put forward consist of:

the argument from incredulity
3m of PVC can transmit radiation straight through (no it can’t)
energy disappears under the right circumstances (that was just the first of many flaws in that person’s argument..)

Of course, if someone comes up with yet another alternative calculation of the heat transfer I will be happy to look at it.

In the meantime, let’s create a mental model..

The Power Station

A few people have jubilantly claimed that the model I created, if correct, can run a power station of 1.8 MW, from a source of only 30,000 W.

That’s what it might seem like on the surface. But strangely, the model results were derived by conserving energy. That is, no energy was created or destroyed..

In the steady state condition:

30,000 W is produced from the internal source
30,000 W is conducted through the PVC “wall”
30,000 W is radiated from the outer surface

Energy is not being created or destroyed. Where is the energy accumulation in this model? Where is the usable energy being stockpiled?

If you want to understand the subject, this point is the one to focus on and think about
If you don’t want to understand the subject say “he’s created 1.8 MW of energy from 30,000W – ridiculous”, and move on (it sounds good)

The inner surface of the sphere has an area of 1,257 m² (4πr²). Consider one square meter of internal surface, we’ll call it “A” – these kind of models always have catchy names for different components of the model.

Each second, A receives 23.9 W/m² from the internal heat source (30,000W / 1,257 m²).
Each second, A conducts 23.9 W/m² through the wall.
Each second, A absorbs 1,452 W/m² radiated from the rest of the inner wall.
Each second, A re-radiates 1,452 W/m².

This is another way of saying that no energy is being created or destroyed. Where is the energy to run this power station?

All that happens if we start drawing power out of this system is the temperature internally reduces very quickly.

How Does the Sphere Heat Up?

In my efforts to understand the conceptual problems people have, I believe that this might help. I can’t be certain – this article is about mental models.

Let’s picture the scene when the PVC sphere is “started up”.

Outside it is 0K. Inside it is 0K. Chilly. Very chilly.

Now the 30,000 W heat source is fired up. 30,000 J every second gets radiated out from this source. Every second, 80% of this 30,000 J gets absorbed by the inner surface (with 20% reflected).

At this stage almost no energy is conducted through the PVC sphere. It can’t – because the temperature differential is not nearly high enough. Conduction requires a heat differential. So instead, the energy goes into heating up the inner surface of the sphere.

As the inner surface heats up it begins to conduct heat through to the outer surface – but most of the energy still goes into heating the inner surface.

A necessary consequence of the inner surface being heated up is that it radiates. All of this radiation is absorbed by the rest of the inner surface AND THEN re-radiated. Energy is not being created. This energy can’t be “tapped off” to do anything useful.

A small supply of energy is simply being “bounced around” (not really “bounced” but it might be a useful way to think about it)

This energy is simply the energy that has been accumulated by the inner surface during the initial heating process. It keeps being accumulated until finally the temperature is high enough to conduct the full 30,000 W through to the outer surface.

Now we have reached equilibrium! On our journey to equilibrium, while the inner surface was heating up, it accumulated heat, and this accumulated heat is now radiated, absorbed, re-radiated, absorbed…

You can connect it to a power station and very quickly you will draw down this accumulation of energy. The maximum you can draw out long term will be 30,000 W.

Conclusion

This article is all about mental models – explaining why the actual results for this model don’t violate the First Law of Thermodynamics. The results were calculated from the very simple and standard heat transfer equations.

Analysis of this model, with the results that I have presented (in part one), demonstrates that energy is conserved.

At first glance it might not seem like it to many people – because the inner surface radiation is so high. But the energy is just re-radiated from the energy absorbed. It’s like a small stockpile of energy that is being “bounced around” from wall to wall.

There is only one (legitimate) way to solve the heat transfer equations for this model. Other approaches invent /destroy physics in an attempt to get a low enough value for the radiation emitted from the inner wall.

Read Full Post »

Interesting Refutation of Some Basics

Posted in Basic Science, Commentary on November 12, 2010| 16 Comments »

I while ago I wrote an article – Do Trenberth and Kiehl understand the First Law of Thermodynamics?

It could have been very short. “Yes”.

However, I did produce an extremely basic model to demonstrate that simple systems with heating “from within” can lead to outcomes that – for many people – are unexpected.

A huge admirer of this blog has written an embarrassingly pro-Science of Doom post entitled:

Why ‘Science of Doom’ Doesn’t Understand the 1st Law of Thermodynamics

So I thought I would return the favor by sending readers to take a look. At the very least, the blog writer will have the comfort of a small lift in visits as well as the welcome opportunity to explain their unique point of view. I just hope that my readers realize that their gushing praise for this blog does not involve any payments whatsoever.

And with apologies to the mysterious Dr. Philips who has had no part (ever) in the writing of this blog.

And on a less important note, if anyone is wondering how a PVC hollow sphere, heated from the inside and sitting in space has anything to do with the planet Earth – I can only hang my head in shame as it clearly has nothing whatsoever to do with our amazing planet.

A PVC sphere is nothing like the earth. The atmosphere is not made out of PVC. Conduction is not an important mechanism in climate physics. What was I thinking?

In any case, I fully expect the author of the laudatory blog article to change the title to something like “Why ‘Science of Doom’ Doesn’t Understand that the Atmosphere Isn’t Made out of PVC”.

And on a small technical note, let’s hope that the article writer fixes up the tiny technical mistakes in their article. If PVC can’t “transmit” radiation then conduction will be required, and.. ouch..

Read Full Post »

The Three Body Problem

Posted in Basic Science, Debunking Flawed "Science" on November 5, 2010| 174 Comments »

With apologies to my many patient readers who want to cover more challenging subjects.

Many people trying to understand climate science have a conceptual problem.

I have written (too) many articles about the second law of thermodynamics – the real and the imaginary version. Resulting comments on this blog and elsewhere about those articles frequently contain comments of this form:

So if we take bucket A full of water at 80°C and bucket B full of water at 10°C, Science of Doom is saying that bucket A will heat up because of bucket B? Right! That’s ridiculous and climate science is absurd!

Yes, if anyone was saying that it would be ridiculous. I agree. To take one example from many, in The Real Second Law of Thermodynamics I said:

Put a hold and cold body together and they tend to come to the same temperature, not move apart in temperature.

Of course, it could be that I am inconsistent in my application of this principle.

One observation on the many contrary claims resulting from my articles – not a single person has provided a mathematical summary to demonstrate that the examples provided contradict the first or second law of thermodynamics.

It should be so easy to do – after all if one of the many systems I have outlined contravenes one of these laws, surely someone can write down the equations for energy conservation (1st law of thermodynamics) or for change in entropy (2nd law of thermodynamics) and prove me wrong. We aren’t talking complex maths here with double integrals or partial differentiation. Just equations of the form a + b = 0.

And here’s the reason why – the problem that people have is conceptual. It seems wrong so they keep explaining why it seems wrong.

Conceptual problems are the hardest to get around. At least, that’s what I have always found. Until a subject “clicks”, all the mathematical proof in the world is just a jumble of letters.

So with that introduction, I offer a conceptual model to help those many people who don’t understand how a cold atmosphere can lead to a warmer surface than would occur without the cold atmosphere.

And if you are one of those people in the “firmly convinced” camp, let me suggest this reason for making the effort to understand this conceptual model. If you understand why others are wrong you can help explain it to them. But if you just don’t understand the argument of people on “the other side” you can’t offer them any useful assistance.

Model 2 – Two bodies – The Boring One that Everyone Really Does Agree With

Very quickly, to “warm everyone up”, and to once again state the basics – if we have two bodies in a closed system, and body A is at temperature 80°C and body B is at 10°C, then over a period of time both will end up at the same temperature somewhere between 10°C and 80°C. It is impossible, for example, for body A to end up at 100°C and body B at 0°C.

Everyone is in agreement on this point.

Note that the “period of time” might be anything between seconds and many times the age of the universe – dependent upon the circumstances of the two bodies.

Model 3A – Three Bodies with the Third Body Being Quite Cold

Where’s Body 1? This picture is the view from Body 1, also known as “Chilly Earth”, which is a spherical solid planet.

To make the problem much easier to solve we will state that the heat capacities of Body 2 and Body 3 are extremely high. This means that whether they gain or lose energy, their temperature will stay almost exactly the same. Body 1, “Chilly Earth”, has a much lower heat capacity and will therefore adjust quickly to a temperature which balances the absorption and emission of radiation.

“Chilly Earth” doesn’t have an atmosphere.

However, for the purposes of helping the conceptual model, “Chilly Earth” reflects 30% of shortwave radiation from the Sun but at longer wavelengths absorbs 100% (reflects 0%). This means its emissivity at longwave is also 100%.

“Chilly Earth” has a very high conductivity for heat, and therefore the whole planet is at the same surface temperature. (See note 1).

“Sun” is 150M km away from “Chilly Earth”, and “Chilly Earth” has a radius of 1,000 km (a little different from the planet we call home).

Let’s calculate the approximate equilibrium temperature of “Chilly Earth”, T₁

How do we do this? By calculating the energy absorbed from Body 2 and from Body 3, and calculating the temperature of a surface that will radiate that same energy back out.

The method is simple – see below.

Energy Absorbed from Body 2, “Sun”

Radiation from “Sun” at 5780K = 6.3 x 10⁷ W/m² – near the surface of the sun. By the time the sun’s radiation reaches earth, because of the inverse square law (the radiation has “spread out”), it is reduced to 1,369 W/m². Remember that 30% is reflected, so the absorbed radiation = 958 W/m².

The surface area that “captures” this radiation = πr² = 3.14 x 10⁶ m².

Energy absorbed from body 2, E_r2 = 958 x 3.14 x 10⁶ = 3.01 x 10⁹ W.

Energy Absorbed from Body 3, “Space”

Radiation from “Space” at 3K = 4.59 x 10^-6 W/m². Apart from the very tiny angle in the sky for “Sun”, the entire rest of the sky is radiating towards the earth from all directions in the sky.

The surface area that “captures” this radiation = 4πr² = 1.26 x 10⁷ m².

Energy absorbed from body 3, E_r3 = 4.59 x 10^-6 x 1.26 x 10⁷ = 57.7W.

So energy from body 3 can be neglected which is not really surprising.

Energy Radiated from Body 1, “Chilly Earth”

For thermal equilibrium (energy in = energy out), “Chilly Earth” must radiate out 3.01 x 10⁹ W, from its entire surface area of 1.26 x 10⁷ m².

This equates to 239 W/m², which for a body with an emissivity of 1 (a blackbody) means T₁ = -18°C.

So we have calculated the equilibrium temperature of “Chilly Earth”.

Now, if we change the model conditions – the reflected portion of solar radiation, the emissivity of the earth at longwave, or the conductivity of the planet’s surface – any of these factors would affect the result. They wouldn’t invalidate the analysis, they would simply lead to a different number, one that was slightly more difficult to work out.

But hopefully everyone can agree that with these conditions there is nothing wrong with the method. (I realize that a few people will not agree..)

Model 3B – Three Bodies with the Third Body Being Somewhat Warmer

So now we are going to perform the same analysis with our new Body 1, “Warmer Earth” (a wild stab at an appropriate name).

The only thing that has really changed about the environment is that Body 3, “Crazy Background Radiation”, is now at 250K instead of 3K.

Note that the temperature of Body 3 is higher than before but lower than the equilibrium temperature of 255K calculated for “Chilly Earth” in the last model. As before, body 3 has an emissivity of 1 for longer wavelengths.

Body 1, “Warmer Earth”, still reflects 30% of solar radiation and is the same in every way as “Chilly Earth”.

What are we going to find?

We will do the same analysis as last time. Repeated in full to help those unfamiliar with this kind of problem.

Energy Absorbed from Body 2, “Sun”

The surface area that “captures” this radiation = πr² = 3.14 x 10⁶ m².

Energy absorbed from body 2, E_r2 = 958 x 3.14 x 10⁶ = 3.01 x 10⁹ W.

Energy Absorbed from Body 3, “Crazy Background Radiation”

Radiation from “Crazy Background Radiation” at 250K = 221 W/m². Apart from the very tiny angle in the sky for “Sun”, the entire rest of the sky is radiating towards the earth from all directions in the sky.

The surface area that “captures” this radiation = 4πr² = 1.26 x 10⁷ m². (See note 2).

Energy absorbed from body 3, E_r3 = 221 x 1.26 x 10⁷ = 2.78 x 10⁹ W.

In this case, energy from body 3 is comparable with body 2.

Energy Radiated from Body 1, “Warmer Earth”

Body 1 absorbs E_tot= E_r2 + E_r3 = 5.79 x 10⁹ W

For thermal equilibrium (energy in = energy out). “Warmer Earth” must radiate out 5.79 x 10⁹ W, from its entire surface area of 1.26 x 10⁷ m².

This equates to 460 W/m², which for a body with an emissivity of 1 (a blackbody) means T₁ = +27°C.

Discussion

Our two cases have revealed something very interesting.

A very very cold sky led to a surface temperature on our slightly different earth of -18°C, while a cold sky (colder than the original experiment’s planetary surface temperature) led to a surface temperature of 27°C.

Well, and here’s the thing, strictly speaking the temperature is actually caused primarily by the bright object in the middle of the picture, “Sun”. The energy absorbed from the sky just changes the outcome a little.

In both cases we calculated the equilibrium temperature by using the first law of thermodynamics (energy in = energy out).

If we do the calculation of entropy change we will find something interesting.. but first, let’s consider the conceptual model and what exactly is going on.

It’s very simple.

In a 3-body problem the temperature of the coldest body still has an effect on the equilibrium temperature of the body being heated by a hotter body.

I could make it more catchy, more media-friendly, but that would go against everything I stand for. I will call this Doom’s Law.

Entropy

The second law of thermodynamics says that entropy can’t reduce. The many cries of anguish that will now arise will claim that Model 3B has broken the Second Law of Thermodynamics. But it hasn’t.

See The Real Second Law of Thermodynamics for more on how to do this calculation. And even clearer, the article by Nick Stokes:

Change in entropy, δS = δQ / T

where δQ = change in energy, T = temperature

We will consider both models over 1 second.

Model 3A

Body 2, “Sun”, δS₂ = -3.85 x 10²⁶ / 5780 = -6.66 x 10²² J/K

Body 3, “Space”, δS₃ = 3.85 x 10²⁶ / 3 = +1.28 x 10²⁶ J/K

And finally, Body 1, “Chilly Earth”, δS₁ = 0 / 255 = 0 J/K

Total Entropy Change = δS₁ + δS₂ + δS₃ = +1.28 x 10²⁶ J/K :a net increase in entropy.

Model 3B

Body 2, “Sun”, δS₂ = -3.85 x 10²⁶ / 5780 = -6.66 x 10²² J/K

Body 3, “Crazy Background Radiation”, δS₃ = 3.85 x 10²⁶ / 250 = +1.54 x 10²⁴ J/K

And finally, Body 1, “Warmer Earth”, δS₁ = 0 / 255 = 0 J/K

Total Entropy Change = δS₁ + δS₂ + δS₃ = +1.47 x 10²⁴ J/K :a net increase in entropy.

Important points to note about the entropy calculation

Both scenarios increase entropy – by transferring heat from a high temperature source, “Sun”, to a low temperature source, “Space” in 3A, and “Crazy Background Radiation” in 3B (which is really also Space at a higher temperature).

The earth-like planet is sitting in the middle and doesn’t have a significant effect on the entropy of the universe.

In both cases the entropy of the system increases, so both are in accordance with the second law of thermodynamics.

The earth cools to space, but just at a slower rate when the background temperature of “space” is higher.

If we replaced “crazy background radiation” by an atmosphere that was mostly transparent to solar radiation, the analysis would be a little more complex but the result wouldn’t be much different.

Reasons Why It Might be Wrong

Just to be clear, these aren’t true..

1. The hotter body can’t absorb radiation from the colder body

a) see Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics for six textbooks on heat transfer which all say, yes it does. Actually, seven textbooks, thanks to commenter Bryan identifying his “non-cherrypicked” textbook by “real physicists” which also agreed.

b) see The Amazing Case of “Back Radiation” – Part Three which includes the EBEX experiment as well as a brief explanation of fundamental physics

c) see Absorption of Radiation from Different Temperature Sources – clearing up a few misconceptions on this idea

2. It’s not a real situation because the atmosphere isn’t a black body

It is true that the atmosphere is not a blackbody. But look back at model 3B. It doesn’t matter. Body 3 in this model could be a 250K body with an emissivity of 0.1 and the temperature would still increase over model 3A.

In fact, if the claim is that a colder body can never increase the temperature of a warmer body – all we need is one counter-example to falsify this theory. Now, if you want to modify your theory to something different we can examine this new theory instead.

Reasons Why It Has to be Right

1. The First Law of Thermodynamics. This neglected little jewel is quite important. Energy can’t disappear (or be created) or be quarantined into a mental box.

There is a reason why all the people disputing these basic analyses never explain where the energy goes (if it “can’t” go into changing the temperature of the hotter body that might have absorbed it). The reason – they don’t know.

2. The Second Law of Thermodynamics. This law says that in a closed system entropy cannot decrease. Despite angry claims about “no such thing as a closed system” – that’s what the second law says. Entropy is often simple to calculate.

If a solution uses simple radiation of energy (Stefan-Boltzmann’s law) and satisfies the first and second law of thermodynamics, and some people don’t like it, it suggests that the problem is with their conceptual model.

Conclusion

This is a conceptual model that is very simple.

The sun warms up the earth, and the earth cools to space. The colder “space” is, the faster the rate of net heat transfer. The warmer “space” is, the slower the rate of net heat transfer. And because the sun “pumps in” heat at the same rate, if you slow the rate of heat loss the equilibrium temperature has to increase.

The first law of thermodynamics is the key to understanding this problem. It is simple to verify that model 3A & 3B both satisfy the first law of thermodynamics. In fact, more importantly, a different result would contradict the first law of thermodynamics.

It is also easy to verify that in both 3A & 3B entropy increases.

Just to be clear on a tedious point, the earth and space do not have to radiate as a blackbody to have these conclusions. They just make the model simpler to explain, and the maths easier to understand. We could easily change the emissivity of the planet to 0.9 and the emissivity of space to 0.5 in both models and we would still find that Model 3B had a warmer planetary surface than Model 3A.

Many people will be unhappy, but this blog is not about bringing happiness. Clarity is the objective.

One more hopeless note of despair – this article uses simple theory to prove a point, which is actually a very valuable exercise. Next, some will say – “I don’t want that pointless over-theoretical theory, these people need to prove it with some experiments“.

And so I offer the series, The Amazing Case of “Back Radiation” as proof, especially Part Three. Result of Part Three was – “well, that can’t happen because it goes against theory“..

And so the circle is complete.

Notes

Note 1 – These strange conditions that don’t relate to the real world are to make the conceptual model simpler (and the maths easy). This is the staple of physics (and other sciences) – compare simple models first, then make them more complex and more realistic. If you can prove a theory with a simple model you have saved a lot of work and more people can understand it.

Note 2 – Solar radiation is from a tiny “angle” in the sky, and so the radiation is effectively “captured” by the earth as a flat disk in space. This area is the area of a disk = πr². By contrast, radiation from the sky is from all around the planet, and so the radiation is effectively captured by the surface area of the sphere. This area = 4πr². See The Earth’s Energy Budget – Part One for more explanation of this.

Read Full Post »

Planck, Stefan-Boltzmann, Kirchhoff and LTE

Posted in Atmospheric Physics, Basic Science on October 24, 2010| 67 Comments »

This post covers some foundations which are often misunderstood.

Radiation emitted from a surface (or a gas) can go in all directions and also varies with wavelength, and so we start with a concept called spectral intensity.

This value has units of W/m².sr.μm, which in plainer language means Watts (energy per unit time) per square meter per solid angle per unit of wavelength. (“sr” in the units stands for “steradian“).

Most people are familiar with W/m² – and spectral intensity simply “narrows it down” further to the amount of energy in a direction and in a small bandwidth.

We’ll consider a planar opaque surface emitting radiation, as in the diagram below.

Hemispherical Radiation, Incropera and DeWitt (2007)

The total hemispherical emissive power, E, is the rate at which radiation is emitted per unit area at all possible wavelengths and in all possible directions. E has the more familiar units of W/m².

Most non-metals are “diffuse emitters” which means that the intensity doesn’t vary with the direction.

For a planar diffuse surface – if we integrate the spectral intensity over all directions we find that emissive power per μm is equal to π (pi) times the spectral intensity.

This result relies only on simple geometry, but doesn’t seem very useful until we can find out the value of spectral intensity. For that, we need Max Planck..

Planck

Most people have heard of Max Planck, Nobel prize winner in 1918. He derived the following equation (which looks a little daunting) for the spectral intensity of a blackbody:

where T = absolute temperature (K); λ = wavelength; h = Planck’s constant = 6.626 x 10^-34 J.s; k = Boltzmann’s constant = 1.381 x 10^-23 J/K; c₀ = the speed of light in a vacuum = 2.998 x 10⁸ m/s.

What this means is that radiation emitted is a function only of the temperature of the body and varies with wavelength. For example:

Note the rapid increase in radiation as temperature increases.

What is a blackbody?

A blackbody:

absorbs all incident radiation, regardless of wavelength and direction
emits the maximum energy for any wavelength and temperature (i.e., a perfect emitter)
emits independently of direction

Think of the blackbody as simply “the reference point” with which other emitters/absorbers can be compared.

Stefan-Boltzmann

The Stefan-Boltzmann equation (for total emissive power) is “easily” derived by integrating the Planck equation across all wavelengths and using the geometrical relationship explained at the start (E=πI). The result is quite well known:

E = σT⁴

where σ=5.67 x 10^-8 and T is absolute temperature of the body.

The result above is for a blackbody. The material properties of a given body can be measured to calculate its emissivity, which is a value between 0 and 1, where 1 is a blackbody.

So a real body emits radiation according to the following formula:

E = εσT⁴

where ε is the emissivity. (See later section on emissivity and note 1).

Note that so long as the Planck equation is true, the Stefan-Boltzmann relationship inevitably follows. It is simply a calculation of the total energy radiated, as implied by the Planck equation.

The Smallprint

The Planck law is true for radiant intensity into a vacuum and for a body in Local Thermodynamic Equilibrium (LTE).

So that means it can never be used in the real world

Or so many people who comment on blogs seem to think. Let’s take a closer look.

The Vacuum

The speed of light in a vacuum, c₀ = 2.998 x 10⁸ m/s. This value appears in the Planck equation and so we need to cater for it when the emission of radiation is into air. The speed of light in air, c_air = c₀/n, where n is the refractive index of air = 1.0008.

Here’s a comparison of the Planck curves at 300K into air and a vacuum:

Not easy to separate. If we expand one part of the graph:

We can see that at the peak intensity the difference is around 0.3%.

The total emissive power into air:

E = n²σT⁴, where n is the refractive index of air

So the total energy radiated from a blackbody into air = 1.0016 x the total energy into a vacuum.

This is why it’s a perfectly valid assumption not to bother with this adjustment for radiation into air. In glass it’s a different proposition..

Local Thermodynamic Equilibrium

The meaning, and requirement, of LTE (local thermodynamic equilibrium) is often misunderstood.

It does not mean that a body is at the same temperature as its surroundings. Or that a body is all at the same temperature (isothermal).

An explanation which might help illuminate the subject – from Thermal Radiation Heat Transfer, by Siegel & Howell, McGraw Hill (1981):

In a gas, the redistribution of absorbed energy occurs by various types of collisions between the atoms, molecules, electrons and ions that comprise the gas. Under most engineering conditions, this redistribution occurs quite rapidly, and the energy states of the gas will be populated in equilibrium distributions at any given locality. When this is true, the Planck spectral distribution correctly describes the emission from a blackbody..

Another definition, which might help some (and be obscure to others) is from Radiation and Climate, by Vardavas and Taylor, Oxford University Press (2007):

When collisions control the populations of the energy levels in a particular part of an atmosphere we have only local thermodynamic equilibrium, LTE, as the system is open to radiation loss. When collisions become infrequent then there is a decoupling between the radiation field and the thermodynamic state of the atmosphere and emission is determined by the radiation field itself, and we have no local thermodynamic equilibrium.

And an explanation about where LTE does not apply might help illuminate the subject, from Siegel & Howell:

Cases in which the LTE assumption breaks down are occasionally encountered.

Examples are in very rarefied gases, where the rate and/or effectiveness of interparticle collisions in redistributing absorbed radiant energy is low; when rapid transients exist so that the populations of energy states of the particles cannot adjust to new conditions during the transient; where very sharp gradients occur so that local conditions depend on particles that arrive from adjacent localities at widely different conditions and may emit before reaching equilibrium and where extremely large radiative fluxes exists, so that absorption of energy and therefore populations of higher energy states occur so strongly that collisional processes cannot repopulate the lower states to an equilibrium density.

Now these LTE explanations are far removed from most people’s perceptions of what equilibrium means.

LTE is all about, in the vernacular:

Molecules banging into each other a lot so that normal energy states apply

And once this condition is met – which is almost always in the lower atmosphere – the Planck equation holds true. In the upper atmosphere this doesn’t hold true, because the density is so low. A subject for another time..

So much for Planck and Stefan-Boltzmann. But for real world surfaces (and gases) we need to know something about emissivity and absorptivity.

Emissivity, Absorptivity and Kirchhoff

There is an important relationship which is often derived. This relationship, Kirchhoff’s law, is that emissivity is equal to absorptivity, but comes with important provisos.

First, let’s explain what these two terms mean:

absorptivity is the proportion of incident radiation absorbed, and is a function of wavelength and direction; a blackbody has an absorptivity of 1 across all wavelengths and directions
emissivity is the proportion of radiation emitted compared with a blackbody, and is also a function of wavelength and direction

The provisos for Kirchhoff’s law are that the emissivity and absorptivity are equal only for a given wavelength and direction. Or in the case of diffuse surfaces, are true for wavelength only.

Now Kirchhoff’s law is easy to prove under very restrictive conditions. These conditions are:

thermodynamic equilibrium
isothermal enclosure

That is, the “thought experiment” which demonstrates the truth of Kirchhoff’s law is only true when there is a closed system with a body in equilibrium with its surroundings. Everything is at the same temperature and there is no heat exchanged with the outside world.

That’s quite a restrictive law! After all, it corresponds to no real world problem..

Here is how to think about Kirchhoff’s law.

The simple thought experiment demonstrates completely and absolutely that (under these restrictive conditions) emissivity = absorptivity (at a given wavelength and direction).

However, from experimental evidence we know that emissivity of a body is not affected by the incident radiation, or by any conditions of imbalance that occur between the body and its environment.

From experimental evidence we know that the absorptivity of a body is not affected by the amount of incident radiation, or by any imbalance between the body and its environment.

These results have been confirmed over 150 years.

As Siegel and Howell explain:

Thus the extension of Kirchhoff’s law to non-equilibrium systems is not a result of simple thermodynamic considerations. Rather it results from the physics of materials which allows them in most instances to maintain themselves in LTE and this have their properties not depend on the surrounding radiation field.

The important point is that thermodynamics considerations allow us to see that absorptivity = emissivity (both as a function of wavelength), and experimental considerations allow us to extend the results to non-equilibrium conditions.

This is why Kirchhoff’s law is accepted in thermodynamics.

Operatic Considerations

The hilarious paper by Gerlich and Tscheuschner poured fuel on the confused world of the blogosphere by pointing out just a few pieces of the puzzle (and not the rest) to the uninformed.

They explained some restrictive considerations for Planck’s law, the Stefan-Boltzmann equation, and for Kirchhoff’s law, and implied that as a result – well, who knows? Nothing is true? Not much is true?Nothing can be true? I had another look at the paper today but really can’t disentangle their various claims.

For example, they claim that because the Stefan-Boltzmann equation is the integral of the Planck equation over all wavelengths and directions:

Many pseudo-explanations in the context of global climatology are already falsified by these three fundamental observations of mathematical physics.

Except they don’t explain which ones. So no one can falsify their claim. And also, people without the necessary background who read their paper would easily reach the conclusion that the Stefan-Boltzmann equation had some serious flaws.

All part of their entertaining approach to physics.

I mention their papertainment because many claims in the blog world have probably arisen through uninformed people reading bits of their paper and reproducing them.

Conclusion

The fundamentals of radiation are well-known and backed up by a century and a half of experiments. There is nothing controversial about Planck’s law, Stefan-Boltzmann’s law or Kirchhoff’s law.

Everyone working in the field of atmospheric physics understands the applicability and limits of their use (e.g., the upper atmosphere).

This is not cutting edge stuff, instead it is the staple of every textbook in the field of radiation and radiant heat transfer.

Notes

Note 1 – Because emissivity is a function of wavelength, and because emission of radiation at any given wavelength varies with temperature, average emissivity is only valid for a given temperature.

For example, at 6000K most of the radiation from a blackbody has a wavelength of less than 4μm; while at 200K most of the radiation from a blackbody has a wavelength greater than 4μm.

Clearly the emissivity for 6000K will not be valid for the emissivity of the same material at a temperature of 200K.

Read Full Post »

« Newer Posts - Older Posts »

	pjmacha on Extreme Weather #17 – Mo…
	E. Schaffer on Clouds & Water Vapor – Par…
	E. Schaffer on Clouds & Water Vapor – Par…
	Rok Adamlje on Clouds and Water Vapor –…
	Everything You Need… on Sensible Heat, Latent Heat and…
	Philip Schmidt on The “Greenhouse” E…
	Philip Schmidt on The Real Second Law of Th…
	Barton Paul Levenson on Opinions and Perspectives…
	Your Guide to Gambli… on Natural Variability and Chaos…
	Mane Oliva on The Amazing Case of “Bac…
	Tucker C on Heat Transfer Basics – P…
	Alll Teens Relate on Stratospheric Cooling
	DeWitt Payne on Clouds & Water Vapor – Par…
	DeWitt Payne on The Imaginary Second Law of…
	Ivan on The Imaginary Second Law of…

Evaluating and Explaining Climate Science

Archive for the ‘Basic Science’ Category

Without “Effective Radiating Temperatures”

Using Kirchhoff

Conclusion

Energy Balance

Conclusion

Global Physical Climatology – by Dennis Hartmann

Elementary Climate Physics by Prof. F.W. Taylor

A First Course in Atmospheric Radiation – Grant Petty

An Introduction to Thermal Physics – Daniel Schroeder

The Inerrancy of Textbooks?

The Boundary Layer

Newton’s Law of Cooling

Turbulence

Empirical Measurements & Dimensionless Ratios

Conclusion

Notes

Top of Atmosphere Satellite Measurements

Surface Radiation

The Inappropriately-Named “Greenhouse” Effect

Interaction of Matter with a Radiation Field

What Happens to Radiation as it Travels Through the Atmosphere

Digression – Up & Down or All Around?

Radiation Through the Atmosphere

Convection

Conclusion

References

Notes

First, is the Atmosphere Made of PVC?

Second, What if the Radiation from an Inner Surface CANNOT be Higher than from an Outer Surface

a) The Earth and Climate System

b) The PVC Sphere

Notes

Explaining How the Result is Calculated

The Power Station

How Does the Sphere Heat Up?

Conclusion

Model 2 – Two bodies – The Boring One that Everyone Really Does Agree With

Model 3A – Three Bodies with the Third Body Being Quite Cold

Model 3B – Three Bodies with the Third Body Being Somewhat Warmer

Discussion

Entropy

Reasons Why It Might be Wrong

Reasons Why It Has to be Right

Conclusion

Notes

Planck

Stefan-Boltzmann

The Smallprint

The Vacuum

Local Thermodynamic Equilibrium

Emissivity, Absorptivity and Kirchhoff

Operatic Considerations

Conclusion

Notes

Pages

Recent Posts

Recent Comments

Categories

Climate Websites

Science of Doom Key Pages

Subscribe by RSS

Subscribe by Email

Archives

Meta