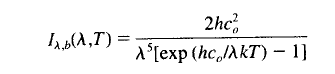The Science of Doom

In Radiation Basics and the Imaginary Second Law of Thermodynamics I covered a fair amount of ground because it started in answer to another question/point from a commenter.

We all agree that the net effect of radiation between hot and colder bodies is that heat flows from the hotter to the colder body, but many people have become convinced that this means radiation from a colder body has no effect on a hotter body.

After explaining a few basics about emission and absorption, I concluded:

Therefore, there is no room in this theory for the crazy idea that colder bodies have no effect on hotter bodies. To demonstrate the opposite, the interested student would have to find a flaw in one of the two basic elements of thermodynamics described above.

And just a note, there’s no point reciting a mantra (e.g., “The second law says this doesn’t happen”) upon reading this.

Instead, be constructive. Explain what happens to the emitting body and the absorbing body with reference to these elementary thermodynamics theories.

One of our regular commenters has finally explained what happens.

This was a great day of joy because in three other articles on this blog (The Imaginary Second Law of Thermodynamics, How Much Work Can One Molecule Do? and On the Miseducation of the Uninformed by Gerlich and Tscheuschner (2009)) and one on another blog the subject has been much discussed.

I have asked many many times:

What happens to radiation from the colder body when it “reaches” the hotter body?

But I had never been given an answer – until now. (Note: the general consensus from the imaginary second law advocates – as much as I can determine – is that the colder body does emit radiation so at least there is agreement on the first step).

Finally, the answer is revealed:

Back to thermodynamics and electromagnetic radiation.

Scienceofdoom and others think that the hot surface has no option but to absorb a photon from the cold surface.

I think a lot of this radiation is in fact scattered from the hot surface and is not absorbed.

“A Lot” is Not Absorbed?

Before we dive into the fascinating topic of absorptivity and absorption, I hope people don’t think I am being pedantic for drawing attention to the fact that one of our most prominent advocates of the theory (the Imaginary Second Law) has actually failed to support it.

Science is about detail.

If no radiation from the colder body is absorbed by the hotter body then the imaginary second law stands. That is, if any radiation emitted by a colder body “reaches” the hotter body and is absorbed by the hotter body then the colder body has transferred energy to the hotter body.

The colder body has had “an effect”.

It’s hard to be certain about the imaginary second law of thermodynamics because I can’t find it in a text book. In fact, on another note, it has been a day of double joy, because another imaginary second law advocate stepped up to the plate when presented with this from a thermodynamics textbook:

 

 

And said:

It is absolutely in error.

Which was wonderful to hear because up until now everyone else had simply ignored the question as to whether Incropera and DeWitt didn’t understand the basics of radiation (for reasons that are all too easy to imagine).

But I digress.

I can’t be 100% certain what the imaginary second law of thermodynamics teaches but it has appeared up until now – from the comments by many advocates – that colder bodies have no effect on hotter bodies.

How can it be that the first time someone explains what happens to the incident radiation they agree, at least in principle, with the rest of the world? We (the rest of the world) all think that cold bodies have an effect on hotter bodies.

Perhaps more advocates can comment and vote on this idea..

[Stop press – after writing this a newer entrant to the field has promoted a new idea but this one can wait until another day]

Absorptivity and Absorption

There are a few basic concepts in traditional thermodynamics that are worth explaining, even though they might appear a little tedious.

I was already thinking about writing an article on this after I had earlier explained:

According to Kirchoff’s law, emissivity = absorptivity for a given substance at the same wavelength (and for some surfaces direction needs to be defined also).

And the same commenter responded:

You have a particularly naive view of heat transfer.

When a green plant absorbs some em radiation to make starch does it simultaneously emit the same radiation?

You have not grasped the fact that if the absorption of 4um radiation was exactly balanced by the emission of 4um radiation the net effect would be zero.

Which would shoot a massive hole in the case for AGW.

I prefer to think of my understanding of physics as traditional rather than naive. So, a few basics need explaining so that readers can judge for themselves.

Just a comment, as well, for new people looking into this subject. The basics often seem a little dull, but hopefully I can persuade a few to dig deep and work hard to get the very basics clear. I can promise unrelenting joy down the track as you realize that you understand more than most other people who had jumped ahead and are now writing confused comments.. (assuming this will give you unrelenting joy).

Let’s look at snow in sunlight and use it to “shed light” on a dull subject.

First of all, there are two important factors involved in the absorption of radiation:

• the radiation incident on the snow (i.e., the radiation value as a function of wavelength)
• the absorptivity – the property of the snow (as a function of wavelength) which determines how much radiation is absorbed and how much is reflected

We will focus on the snow being heated by sunlight and ignore terrestrial radiation – even though the material will also be heated by terrestrial radiation. This is because we aren’t trying to work out a complete energy balance for this particular material, just illustrating the important points.

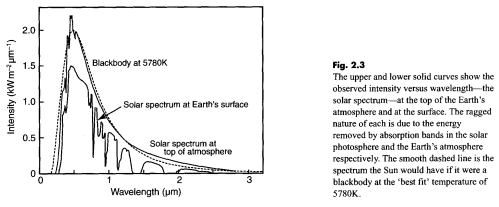
Solar radiation has a spectrum which looks something like this:

 

 

This shows how the radiation incident on the snow varies with wavelength. The actual amplitude is dependent on the time of day, the latitude, the amount of clouds, and so on.

The important point is that radiation from the sun peaks at a wavelength of around 0.5μm and above 2μm is much reduced (91% of solar radiation is below 2μm). Therefore, to find out how much radiation the material actually absorbs we need to know the absorptivity at these wavelengths.

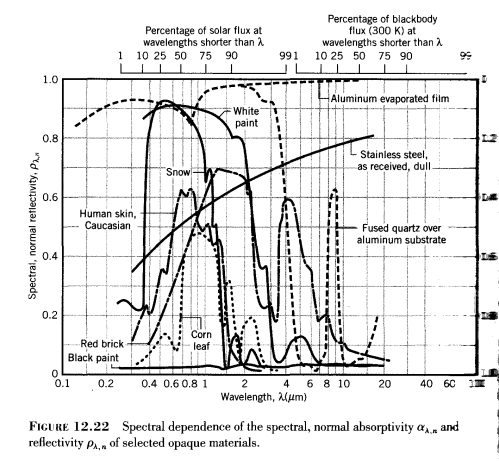
Here are some examples of reflectivity and absorptivity of various materials across quite a wide spectral range:

 

 

The scale on the left is reflectivity and on the right (harder to see) is absorptivity from 1.0 at the bottom up to 0.0 at the top.  Absorptivity = 1-reflectivity.

Absorptivity is a function of wavelength and is the proportion of incident radiation at that wavelength which is absorbed.

Absorptivity is an inherent property of that material

Let’s take snow as an example. Sunlight on snow will be mostly reflected and not absorbed. That’s because the incident sunlight is mostly between 0.2μm to 2μm – and if you check the reflectivity/absorptivity graph above you will see that the absorptivity is quite low (and reflectivity quite high).

Snow has a high albedo for sunlight – around 60% – 80% is reflected, meaning only 20%-40% is absorbed.

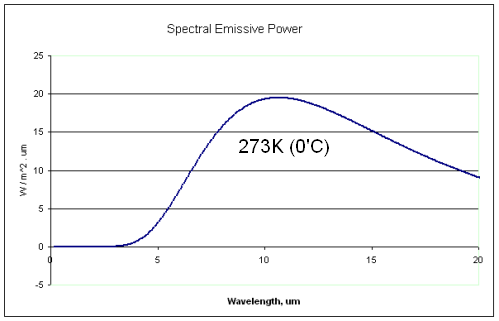
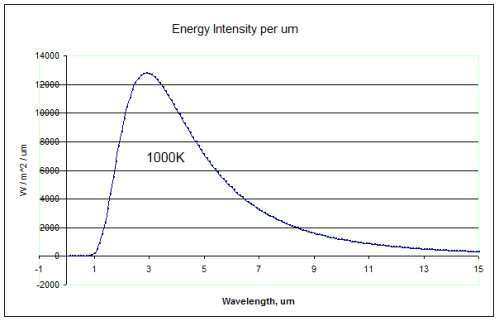
Now let’s consider the snow at a temperature of 0°C (273K). How much thermal radiation does it emit?

If it was a blackbody, it would emit radiation as the Planck function at 273K:

 

 

The first thing you notice is that the snow is radiating at completely different wavelengths to the solar radiation. The solar radiation is mostly between 0.2μm to 2.0μm, while the snow is radiating between 5μm and 50μm.

So we need to know the emissivity between these wavelengths to work out the actual emission of radiation from the snow. Emissivity is a value between 0 and 1 which says how close to a blackbody the material is at that wavelength. Emissivity is equal to absorptivity – see the next section – so we can just look up the absorptivity instead.

In the graph from Incropera the absorptivity of snow at higher wavelengths is not shown. But it’s clear that it has changed a lot (and in fact absorptivity is very high – and reflectivity very low – at these higher wavelengths, which climate scientists call “longwave”).

Kirchhoff’s Law

Kirchoff’s law says that emissivity = absorptivity as a function of wavelength – and sometimes direction. That is, these two intrinsic properties of any material have the same value at any wavelength. (The derivation of this formula isn’t something that will be discussed here).

Kirchoff didn’t say that emission = absorption

That’s because emissivity is not the same as emission. And absorptivity is not the same as absorption.

Of course, if a body is only gaining and losing energy by radiation (i.e., no conduction or convection), and the body is not heating up or cooling down then absorption will equal emission. This is due to the first law of thermodynamics or conservation of energy.

But if absorption increases, the body will heat up until the new value of emission balances the increase in absorption. However, the absorption might be in one wavelength range and the emission in a totally different one.

It’s not so difficult to understand, but it does require that you grasp hold of the basics.

So (digressing) back to our commenter, it’s clear that his “reasons” for ditching Kirchhoff’s law weren’t because Kirchhoff was wrong..

And Kirchhoff’s law is very strong. It would need a monumental effort to overturn this part of thermodynamics basics. Reasonable people might expect that if over-turning Kirchhoff’s law is necessary to support the imaginary second law of thermodynamics, then this might imply that the imaginary law is, well, imaginary..

However, even stranger concepts are necessary to support the imaginary second law.

Would Sir like to Absorb this Radiation? No? Very Good Sir, I’ll take it Back.

Now that we have covered a few basics, perhaps some points might start to make sense.

And perhaps this comment might seem a little flawed:

Back to thermodynamics and electromagnetic radiation.

Scienceofdoom and others think that the hot surface has no option but to absorb a photon from the cold surface.

I think a lot of this radiation is in fact scattered from the hot surface and is not absorbed.

Let’s examine the idea that radiation from the cold surface is “not absorbed”, and see it in its comedic glory.

Consider a surface of 0°C (273K).

And now consider one body at 10°C radiating towards this 0°C surface. According to the imaginary second law advocates the radiation from the 10°C body is accepted.

Now consider a similar scenario but the 10°C body has been replaced with a
-10°C body. According to the imaginary second law advocates the radiation from the colder -10°C body is not accepted. And according to its strongest advocate, “it is scattered and not absorbed“.

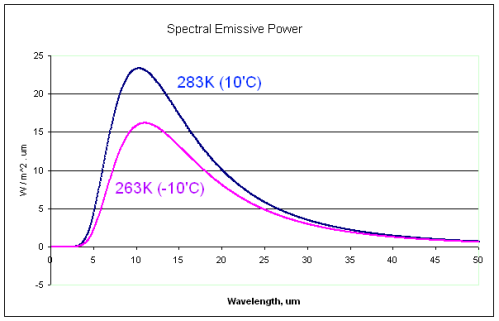
Here is the comparison spectrum for the two radiating bodies:

 

 

Notice the very similar radiation curves.

And remember that absorptivity is simply a function of the material receiving the radiation.

And ask yourself, how can the 0°C surface reflect the 10μm radiation from the colder -10°C body, and yet absorb 10μm radiation from the hotter +10°C body?

If the absorptivity at 10μm is 0.9 then it will accept 90% of the radiation at this wavelength from a +10°C body and 90% of the radiation at this wavelength from a -10°C body. It can’t check the menu and “send it back”.

Likewise for each wavelength in question.

[By the way, the fact that the body at -10°C emits radiation that is absorbed by the 0°C surface doesn’t mean that the real second law of thermodynamics is violated. Simple, the 0°C surface is also radiating, and at a higher intensity than the -10°C surface. The net is from the hotter to the colder.]

Conclusion

It took many many requests to finally hear the explanation as to why radiation from a colder body has no effect on a hotter body.

It’s not an explanation that will stand the test of time – except for the wrong reasons. It requires the advocate to believe amazing things about materials. Perhaps that’s why it took so long to get the answer.

Yet more ridiculous ideas have recently been proposed. All in the cause of supporting the imaginary second law of thermodynamics. (These need considering in another post).

Just a digression on the perpetual motion machine (because I don’t want to write a whole post on it). For some reason, perhaps the Gerlich and Tscheuschner miseducation, many confused people think that the absorption and re-emission of longwave radiation by the atmosphere constitutes a perpetual motion machine – and therefore this proves the inappropriately-named “greenhouse” effect can’t exist! Well, we all agree that there is no perpetual motion machine.

But why would the atmosphere radiating towards the earth constitute “perpetual motion”?

Think for a minute before answering, if you claim this.

Right now the earth is around the same temperature it was 100 years ago and also 1000 years ago. Is that a perpetual motion machine – a machine that can’t exist? No. The sun warms the earth. And the sun is powered by internal reactions.

Ok. So if the sun turns off what happens? The earth cools down.

For people who think that the earth’s surface is radiating towards the colder atmosphere, and the colder atmosphere is radiating less energy back towards the earth, and the earth is absorbing this radiation.. we expect the same thing to happen when the sun turns off. The earth will cool down. Just a little slower.

No perpetual motion machine.

Well, the second law of thermodynamics is quite a basic one but misunderstood by many who think they are supporting it.

For newcomers to this debate the approach I have taken is to take a specific example and ask the advocates of their theory how specific well-understood physical properties can possibly support their argument. Mostly I get no response.

I have finally had two answers. One is considered here and it’s hard to understand how anyone can believe it.

See the followup article – The First Law of Thermodynamics Meets the Imaginary Second Law

And the later article – The Real Second Law of Thermodynamics

Read Full Post »

This post will suffer from the unfortunate effect of too much maths – something I try to avoid in most posts and certainly did in The Imaginary Second Law of Thermodynamics. It’s especially unfortunate as the blog has recent new found interest thanks to the very kind and unexpected words of Steve McIntyre of Climate Audit.

However, a little maths seems essential. Why?

Some of the questions and triumphant points some commentators have made can only be properly answered by a real example, with real equations.

It’s something I commented on in American Thinker Smoking Gun – Gary Thompson’s comments examined, where I explained that a particular theory is not usually a generalized statement about effects but rather a theory is usually a set of mathematical equations to be applied under certain well-defined circumstances.

In The Imaginary Second Law of Thermodynamics the example was of a sun radiating into the nothingness of space, when a new star was brought into the picture. And the new star was hotter. So the question was, would the radiation from the colder star actually have an effect on the hotter star.

Some Gerlich and Tscheuschner apostles thoughtfully spent some time trying to enforce some discipline about terminology of heat vs energy and whether radiation was a vector – but forgot to answer the actual question.

Recently a commentator suggested that the real answer lay in considering two stars of equal temperature which were brought into proximity.

As for the sun and the other star, only the sun at T10,000 will go up in T if you insert another T11,000 star, never mind how hard one thinks about it. Maybe this becomes obvious once you make the sun and the new star equally hot at T10,000 . They don’t become both hotter, which is what is predicted in the thought experiment. If the sun heats up the newly inserted star it should not matter really if that new star is at T11,000 or T10,000 does it?

And I said:

Unless all of the radiation is reflected it will increase the surface temperature. It might be 0.1K, 1K, 0.0001K – it all depends on the W/m^2 at that point – and the absorptivity at the wavelengths of the incident radiation.

If that isn’t the case, then you have a situation where incident radiation is absorbed but has zero effect.

And our commentator responded:

Congratulations on sticking with it! I think you just discovered the endless source of energy we are all so desperately looking for. When you expect two equally hot bodies to keep heating each other, where is the limit? and could we not syphon off some off that excess heat.

Which bring us to here. Many people gets confused around these basic points, which is why we need a post with some maths. The maths can prove the point, unlike “talk”.

Conceptual understanding is what everyone seeks. I hope that this article brings some conceptual understanding even though it has a core maths section.

Some Unfortunate but Necessary Maths

Let’s first of all consider one “star” out in the nothingness of space.

The star has a radius of 1000m (1km) and a temperature of 1000k (727°C). This temperature is identical all over the surface and is powered from internal stellar processes. This internal heat generation is constant and not dependent on any changes in surface temperature. We will also assume – only necessary for the second part of the experiment – that the thermal conductivity of this star is extremely high. This means that any radiation absorbed on one part of the surface will conduct rapidly around the surface of the star – to avoid any localized heating.

We also assume that its emissivity is 1 – it is a blackbody across all wavelengths.

A few derived facts about this star, which we will give, in true mathematical style, the exotic name of “1”.

Surface area:

A₁ = 4πr² = 1.256×10⁷m²

Flux from the surface of star 1, from the Stefan-Boltzmann equation:

F₁ = εσT⁴ = 1 x 5.67×10^-8 x 1000⁴ = 56,700 W/m²

How the radiation emission varies with wavelength:

Total thermal energy radiated:

E₁ = A₁. F₁ = 7.12 x 10¹¹W

If this is the thermal energy radiated, and star 1 is at equilibrium, then the heat generated within the star must also be this value. After all, if the heat generated was higher then the star’s surface temperature would keep increasing until steady state was reached.

For example, if the internal energy source increased its output (for some reason) to 8 x 10¹¹W then the output of the star would eventually reach this value. So F₁(new) = 8 x 10¹¹/A₁ = 6.37 x 10⁴ W/m²

And from the Stefan-Boltzmann equation, T = 1,030K. Just an example, for illustration.

And now, two stars brought into some proximity

So what happens when two identical stars are brought into some proximity? According to our commentator, nothing happens. After all, if “something” happens, it can only be thermal runaway.

The only way we can find out is to use the maths of basic thermodynamics. For people who go into “fight or flight” response when presented with some maths, the conclusion – to relieve your stress – is that the system doesn’t go into thermal runaway, but both stars end up at a slightly higher temperature. Deep breaths. See a later section for “conceptual” understanding.

We define E₁ = the energy from star 1 before star 2 (an identical star) appears on the scene.
And E₁‘ = the energy from star 1 after star 2 appears on the scene.

The distance between the two stars = d

The radius of each star (the same) = r = 1000m

Consider star 2, radiating thermal energy. Some proportion of star 2’s thermal radiation is incident on star 1, which has an absorptivity (= emissivity) of 1.

To calculate how much of star 2’s thermal radiation is incident on star 2, we use the very simple but accurate idea of a large sphere at radius d from star 2. This large sphere has a surface area of 4πd².

On this large sphere we have a small 2-d disk of area πr², which is the area projected by the other star on this very large sphere. And so the proportion of radiation from star 2 which is incident on star 1:

b = πr² / 4πd² = r² / 4d² [equation 1]

This value, b, will be a constant for given values of r and d.

So, our big question, when star 2 and star 1 are “wheeled in” closer to each other, at a distance d from each other – what happens?

Well, some of star 2’s radiation is incident on star 1. And some of star 1’s radiation is incident on star 2.

Will this – according to the crazy theories I have been promoting – lead to thermal runaway? Star 1 heats up star 2, which heats up star 1, which heats up star 2.. thermal runaway! The end of all things?

Thermal Runaway? Or a Slight Temperature Increase of Both Stars?

To work out the answer, it’s all about the maths. Not that the subject can’t be understood conceptually. It can be. But for those who are convinced this is wrong, “conceptual” just leads to “talk”. Whereas maths has to be disputed by specifics.

When our two stars were an infinite distance from each other in the vastness of space, E₁ = E₂ – with the values calculated above.

Now that the two stars are only a distance, d, from each other, a new source of thermal energy is added.

Consider star 1. If this star absorbs thermal radiation from elsewhere, it must emit more radiation or its temperature will rise. If its temperature rises then it will emit more radiation. (See note 1 at end).

So:

E₁‘ = E1 + E₂‘ b   [equation 2]

E₂‘ = E2 + E₁‘ b   [equation 3]

This is simply showing mathematically what I have already expressed in words.

And because the stars are identical:

E₁ = E₂ [equation 4],  and

E₁‘ = E₂‘   [equation 5]

So, from [2] and [4],  E₁‘ = E₁ + E₁‘ b, or (rearranging):

E₁ = E₁‘(1-b), so E₁‘ = E₁ / (1-b)   [equation 6]

So once new equilibrium is reached, we can calculate the new radiation value, and from the Stefen-Boltzmann equation, we can calculate the new temperature.

These equations don’t tell us how long it takes to reach equilibrium, as we don’t know the heat capacity of the stars.

Let’s put some numbers in and see what the results are:

Let d=1000km = 1,000,000m or 1×10⁶m

Therefore, from [1]:

b =1000²/4x(1×10⁶)²

b = 2.5×10^-7

And, from [6]:

E₁‘ = E₁/0.99999975 = 1.00000025 E₁

Do we even want to work out the change in temperature required to increase the radiation from the star by this tiny amount? Just for interest, the new surface temperature = 1000.00006 K

But this is the new equilibrium for both stars.

Note that there is no thermal runaway.

The approach can now be subject to criticism. (So far no one has checked my maths, so it’s quite likely to have a mistake which changes the numerical result). I can’t see how there can be a mistake which would change the main result that no thermal runaway occurs. Or that would change the result so that no change in temperature occurs.

For more interest, suppose the stars were only 10km or 10,000m apart. Strictly speaking, while the distance between the stars is “much greater” than the radius of the stars we can use my equations above. The mathematical expression for this “much greater” is, d>>r. Once the stars are close enough together the maths gets super-complicated. This is because the distance from one point on one star to one point on another star is no longer “d”. For example, as a minimum it will be d-2r (the two closest points)

No one wants to see this kind of “integral” (as the required maths is called). Least of all, me, I might add.

Well, we’ll ignore the complexities and how it might change the result, just to get a sense of roughly what the values are.

If d=10,000, b=0.0025 and so E₁‘ = E₁ / 0.9975 =  1.0025 E₁

Consequently the change in surface temperature to increase the temperature by this amount, T=1000.6K

Not very exciting, and still no thermal runaway.

Conceptual Understanding and Some Radiation Theory

Understanding this conceptually for most people won’t be too difficult. If you add energy to a body it will warm up. And it will emit more radiation. There will be a new equilibrium.

Two bodies doing this to each other will also just reach a new equilibrium – they can’t go into thermal runaway. Of course, no one believes that thermal runaway will result, least of all the person who made the original comment – that was their whole point. They just didn’t realize that a new equilibrium could exist. The only way I can prove it is mathematically.

Conceptual thinking is very valuable. Maths is very tedious. But because Gerlich and Tscheuschner have made such a huge contribution to the misunderstanding of basic thermodynamics it needs some extended explanation, including some maths.

Many people have got confused about the subject because

Heat flows from the hotter body to the colder body

We all agree.

Many people have taken the statement about heat flow and imagined that thermal radiation from a colder body cannot have any effect on a hotter body. This is where they go wrong.

A body with a temperature above absolute zero will radiate according to its emissivity (and according to the 4th power of temperature). This property is dependent on wavelength and sometimes on direction. The emissivity of a body is also equal to the absorptivity at these same wavelengths and directions.

The wavelength dependence of emissivity and absorptivity is very striking:

 

 

Absorptivity is the scale on the right from 1 at the bottom to zero at the top and is 1-reflectivity. (See note 2).

Here you can see that snow is highly reflective at solar wavelengths (shortwave) and absorbs little radiation, whereas it has a high absorptivity at longer wavelengths (and therefore does not reflect much longwave radiation).

The same goes for white paint. It reflects sunlight but absorbs terrestrial radiation.

The equation for how much radiation is emitted by a body – εσT⁴ – does not include any terms for where the radiation might end up. So whether this radiation will be incident on a colder or hotter body, it has no effect on the radiation from the source. (See note 3).

Similarly, when radiation is incident on a body the only factor which affects how much radiation is absorbed and how much radiation is reflected is the absorptivity of the body at that direction and wavelength. The body cannot put out traffic cones because the incident radiation has been emitted by a colder body.

This is elementary thermodynamics. Emissivity and temperature determine the radiation from a body. Absorptivity determines how much incident radiation is absorbed.

Therefore, elementary thermodynamics shows that a cold body can radiate onto the surface of a hotter body. And the hotter body will absorb the radiation – assuming it has absorptivity at that wavelength and direction.

And once thermal radiation is absorbed it must heat the body, or slow down a loss of heat which is taking place. It cannot have no effect. This would be contrary to the first law of thermodynamics.

Two bodies at different temperatures in proximity both radiate towards each other. Heat flow is determined by the net effect. As standard textbooks indicate:

 

 

Why the Original Misconception?

I think that the original comment about two bodies with the same temperature being unable to heat each other is an easy misconception for two reasons:

First, the most likely mental image immediately conjured up is of two pots of water at say 50ºC. When these two pots of water are mixed together the temperature is obviously still at 50ºC.

Second, the two stars are probably pictured as already in equilibrium at the original temperature. Well, if that’s the case then nothing will change. The change only occurs when they are brought closer together and so the mutual radiation from each has a slight increase on the temperature of the other.

It’s just my guess. But what actually happens in the thought experiment probably isn’t intuitively obvious.

Conclusion

When two bodies have an energy source which has created a constant surface temperature and they are subsequently brought into proximity with each other, there will be an increase in each other’s temperature. But no thermal runaway takes place, they just reach a new equilibrium.

Basic thermodynamics explains that bodies emit thermal radiation according to temperature (to the fourth power) and according to emissivity. Not according to the temperature of a different body that might happen to absorb this radiation.

And basic thermodynamics also explains that bodies absorb thermal radiation according to their absorptivity at the wavelengths (and directions) of the incident radiation. Not according to the temperature (or any other properties) of the originating body.

Therefore, there is no room in this theory for the crazy idea that colder bodies have no effect on hotter bodies. To demonstrate the opposite, the interested student would have to find a flaw in one of the two basic elements of thermodynamics described above. And just a note, there’s no point reciting a mantra (e.g., “The second law says this doesn’t happen”) upon reading this. Instead, be constructive. Explain what happens to the emitting body and the absorbing body with reference to these elementary thermodynamics theories.

Update – now that one advocate has given some explanation, a new article: Intelligent Materials and the Imaginary Second Law of Thermodynamics

Notes

1. I said earlier: “If this star absorbs thermal radiation from elsewhere, it must emit more radiation or its temperature will rise. If its temperature rises then it will radiate more energy.” Strictly speaking when radiation is absorbed it might go into other forms of energy. For example, if ice receives incident radiation it may melt, and all of the heat is absorbed into changing the state of the ice to water, not to increasing the temperature.

2. Incident radiation can also be transmitted, e.g. through a thin layer of glass, or through a given concentration of CO2, but this won’t be the case with radiation into a body like a star. The total of reflected energy plus absorbed energy plus transmitted energy has to equal the value of the incident radiation.

3. The Stefan-Boltzmann equation is the integral of the Planck function across all wavelengths and directions:

 

 

Where h, c₀ and k are constants, T is temperature and λ is the wavelength.

The Planck function describes how spectral intensity changes with wavelength (or frequency) for a blackbody. If the emissivity as a function of wavelength is known it can be used in conjunction with the Planck function to determine the actual flux.

Read Full Post »