The Science of Doom

A long time ago I wrote the article The Dull Case of Emissivity and Average Temperatures and expected that would be the end of the interest in emissivity. But it is a gift that keeps on giving, with various people concerned that no one has really been interested in measuring surface emissivity properly.

Background

All solid and liquid surfaces emit thermal radiation according to the Stefan-Boltzmann formula:

E = εσT⁴

where ε=emissivity, a material property; σ = 5.67×10^-8 ; T = temperature in Kelvin (absolute temperature)

and E is the flux in W/m²

More about this formula and background on the material properties in Planck, Stefan-Boltzmann, Kirchhoff and LTE.

The parameter called emissivity is the focus of this article. It is of special interest because to calculate the radiation from the earth’s surface we need to know only temperature and emissivity.

Emissivity is a value between 0 and 1. And is also depends on the wavelength of radiation (and in some surfaces like metals, also the direction). Because the wavelengths of radiation depend on temperature, emissivity also depends on temperature.

When emissivity = 1, the body is called a “blackbody”. It’s just the theoretical maximum that can be radiated. Some surfaces are very close to a blackbody and others are a long way off.

Note: I have seen many articles by keen budding science writers who have some strange ideas about “blackbodies”. The only difference between a blackbody and a non-blackbody is that the emissivity of a blackbody = 1, and the emissivity of a non-blackbody is less than 1. That’s it. Nothing else.

The wavelength dependence of emissivity is very important. If we take snow for example, it is highly reflective to solar (shortwave) radiation with as much as 80% of solar radiation being reflected. Solar radiation is centered around a wavelength of 0.5μm.

Yet snow is highly absorbing to terrestrial (longwave) radiation, which is centered around a wavelength of 10μm. The absorptivity and emissivity around freezing point is 0.99 – meaning that only 1% of incident longwave radiation would be reflected.

Let’s take a look at the Planck curve – the blackbody radiation curve – for surfaces at a few slightly different temperatures:

The emissivity (as a function of wavelength) simply modifies these curves.

Suppose, for example, that the emissivity of a surface was 0.99 across this entire wavelength range. In that case, a surface at 30°C would radiate like the light blue curve but at 99% of the values shown. If the emissivity varies across the wavelength range then you simply multiply the emissivity by the intensity at each wavelength to get the expected radiation.

Sometimes emissivity is quoted as an average for a given temperature – this takes into account the shape of the Planck curve shown in the graphs above.

Often, when emissivity is quoted as an overall value, the total flux has been measured for a given temperature and the emissivity is simply:

ε =  actual radiation measured / blackbody theoretical radiation at that temperature

[Fixed, thanks to DeWitt Payne for pointing out the mistake]

In practice the calculation is slightly more involved, see note 1.

It turns out that the emissivity of water and of the ocean surface is an involved subject.

And because of the importance of calculating the sea surface temperature from satellite measurements, the emissivity of the ocean in the “atmospheric window” (8-14 μm) has been the subject of many 100’s of papers (perhaps 1000’s). These somewhat overwhelm the papers on the less important subject of “general ocean emissivity”.

Measurements

Aside from climate, water itself is an obvious subject of study for spectroscopy.

For example, 29 years ago Miriam Sidran writing Broadband reflectance and emissivity of specular and rough water surfaces, begins:

The optical constants of water have been extensively studied because of their importance in science and technology. Applications include a) remote sensing of natural water surfaces, b) radiant energy transfer by atmospheric water droplets, and c) optical properties of diverse materials containing water, such as soils, leaves and aqueous solutions.

In this study, values of the complex index of refraction from six recent articles were averaged by visual inspection of the graphs, and the most representative values in the wavelength range of 0.200 μm to 5 cm were determined. These were used to find the directional polarized reflectance and emissivity of a specular surface and the Brewster or pseudo-Brewster angle as functions of wavelength.

The directional polarized reflectance and emissivity of wind-generated water waves were studied using the facet slope distribution function for a rough sea due to Cox and Munk [1954].

Applications to remote sensing of sea surface temperature and wave state are discussed, including effects of salinity.

Emphasis added. She also comments in her paper:

For any wavelength, the total emissivity, ε, is constant for all θ [angles] < 45° [from vertical]; this follows from Fig. 8 and Eq. (6a). It is important in remote sensing of thermal radiation from space, as discussed later..

The polarized emissivities are independent of surface roughness for θ < 25°, while for θ > 25°, the thermal radiation is partly depolarized by the roughness.

This means that when you look at the emission radiation from directly above (and close to directly above) the sea surface roughness doesn’t have an effect.

I thought some other comments might also be interesting:

The 8-14-μm spectral band is chosen for discussion here because (a) it is used in remote sensing and (b) the atmospheric transmittance, τ, in this band is a fairly well-known function of atmospheric moisture content. Water vapor is the chief radiation absorber in this band.

In Eqs. (2)-(4), n and k (and therefore A and B) are functions of salinity. However, the emissivity value, ε, computed for pure water differs from that of seawater by <0.5%.

When used in Eqs. (10), it causes an error of <0.20°C in retrieved Ts [surface temperature]. Since ε in this band lies between 0.96 and 0.995, approximation ε= 1 is routinely used in sea surface temperature retrieval. However, this has been shown to cause an error of -0.5 to -1.0°C for very dry atmospheres. For very moist atmospheres, the error is only ≈0.2°C.

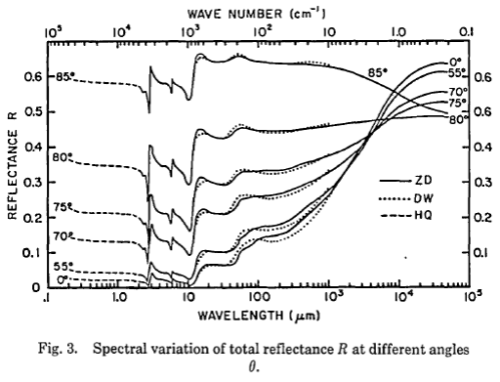
One of the important graphs from her paper:

Click to view a larger image

Emissivity = 1 – Reflectance. The graph shows Reflectance vs Wavelength vs Angle of measurement.

I took the graph (coarse as it is) and extracted the emissivity vs wavelength function (using numerical techniques). I then calculated the blackbody radiation for a 15°C surface and the radiation from a water surface using the emissivity from the graph above for the same 15°C surface. Both were calculated from 1 μm to 100 μm:

The “unofficial” result, calculating the average emissivity from the ratio: ε = 0.96.

This result is valid for 0-30°C. But I suspect the actual value will be modified slightly by the solid angle calculations. That is, the total flux from the surface (the Stefan-Boltzmann equation) is the spectral intensity integrated over all wavelengths, and integrated over all solid angles. So the reduced emissivity closer to the horizon will affect this measurement.

Niclòs et al – 2005

One of the most interesting recent papers is In situ angular measurements of thermal infrared sea surface emissivity—validation of models, Niclòs et al (2005). Here is the abstract:

In this paper, sea surface emissivity (SSE) measurements obtained from thermal infrared radiance data are presented. These measurements were carried out from a fixed oilrig under open sea conditions in the Mediterranean Sea during the WInd and Salinity Experiment 2000 (WISE 2000).

The SSE retrieval methodology uses quasi-simultaneous measurements of the radiance coming from the sea surface and the downwelling sky radiance, in addition to the sea surface temperature (SST). The radiometric data were acquired by a CIMEL ELECTRONIQUE CE 312 radiometer, with four channels placed in the 8–14 μm region. The sea temperature was measured with high-precision thermal probes located on oceanographic buoys, which is not exactly equal to the required SST. A study of the skin effect during the radiometric measurements used in this work showed that a constant bulk–skin temperature difference of 0.05±0.06 K was present for wind speeds larger than 5 m/s. Our study is limited to these conditions.

Thus, SST used as a reference for SSE retrieval was obtained as the temperature measured by the contact thermometers placed on the buoys at 20-cm depth minus this bulk–skin temperature difference.

SSE was obtained under several observation angles and surface wind speed conditions, allowing us to study both the angular and the sea surface roughness dependence. Our results were compared with SSE models..

The introduction explains why specifically they are studying the dependence of emissivity on the angle of measurement – for reasons of accurate calculation of sea surface temperature:

The requirement of a maximum uncertainty of ±0.3 K in sea surface temperature (SST) as input to climate models and the use of high observation angles in the current space missions, such as the 55° for the forward view of the Advanced Along Track Scanning Radiometer (AATSR) (Llewellyn-Jones et al., 2001) on board ENVISAT, need a precise and reliable determination of sea surface emissivity (SSE) in the thermal infrared region (TIR), as well as analyses of its angular and spectral dependences.

The emission of a rough sea surface has been studied over the last years due to the importance of the SSE for accurate SST retrieval. A reference work for many subsequent studies has been the paper written by Cox and Munk (1954)..

The experimental setup:

The results (compared with one important model from Masuda et al 1988):

Click on the image for a larger graphic

This paper also goes on to compare the results with the model of Wu & Smith (1997) and indicates the Wu & Smith’s model is a little better.

The tabulated results, note that you can avoid the “eye chart effect” by clicking on the table:

Click on the image for a larger view

Note that the emissivities are in the 8-14μm range.

You can see that the emissivity when measured from close to vertical is 0.98 – 0.99 at two different wind speeds.

Konda et al – 1994

A slightly older paper which is not concerned with angular dependence of sea surface emissivity is by Konda, Imasato, Nishi and Toda (1994).

They comment on a few older papers:

Buettner and Kern (1965) estimated the sea surface emissivity to be 0.993 from an experiment using an emissivity box, but they disregarded the temperature difference across the cool skin.

Saunders (1967b, 1968) observed the plane sea surface irradiance from an  airplane and determined the reflectance. By determining the reflectance as the ratio of the differences in energy between the clear and the cloudy sky at different places, he calculated the emissivity to be 0.986. The process of separating the reflection from the surface irradiance, however, is not precise.

Mikhaylov and Zolotarev (1970) calculated the emissivity from the optical constant of the water and found the average in the infrared region was 0.9875.

The observation of Davies et al. (1971) was performed on Lake Ontario with a wave height less than 25 cm. They measured the surface emission isolated from sky radiation by an aluminum cone, and estimated the emissivity to be 0.972. The aluminum was assumed to act as a mirror in infrared region. In fact,aluminum does not work as a perfect mirror.

Masuda et al. (1988) computed the surface emissivity as a function of the zenith angle of observed radiation and wind speed. They computed the emissivity from the reflectance of a model sea surface consisting of many facets, and changed their slopes according to Gaussian distribution with respect to surface wind. The computed emissivity in 11 μm was 0.992 under no wind.

Each of these studies in trying to determine the value of emissivity, failed to distinguish surface emission from reflection and to evaluate the temperature difference across the cool skin. The summary of these studies are tabulated in Table 1.

The table summarizing some earlier work:

Konda and his co-workers took measurements over a one year period from a tower in Tanabe Bay, Japan.

They calculated from their results that the ocean emissivity was 0.984±0.004.

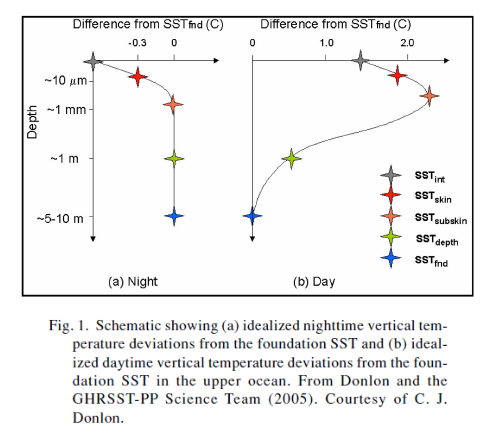
One of the challenges for Konda’s research and for Niclòs is the issue of sea surface temperature measurement itself. Here is a temperature profile which was shown in the comments of Does Back Radiation “Heat” the Ocean? – Part Three:

The point is the actual surface from which the radiation is emitted will usually be at a slightly different temperature from the bulk temperature (note the logarithmic scale of depth). This is the “cool skin” effect. This surface temperature effect is also moderated by winds and is very difficult to measure accurately in field conditions.

Smith et al – 1996

Another excellent paper which measured the emissivity of the ocean is by Smith et al (1996):

An important objective in satellite remote sensing is the global determination of sea surface temperature (SST). For such measurements to be useful to global climate research, an accuracy of ±0.3K or better over a length of 100km and a timescale of days to weeks must be attained. This criterion is determined by the size of the SST anomalies (≈1K) that can cause significant disturbance to the global atmospheric circulation patterns and the anticipated size of SST perturbations resulting from global climate change. This level of uncertainty is close to the theoretical limits of the atmospheric corrections..

It is also a challenge to demonstrate that such accuracies are being achieved, and conventional approaches, which compare the SST derived from drifting or moored buoys, generally produce results with a scatter of ±0.5 to 0.7K. This scatter cannot be explained solely by uncertainties in the buoy thermometers or the noise equivalent temperature difference of the AVHRR, as these are both on the order of 0.2K or less but are likely to be surface emissivity/reflectivity uncertainties, residual atmospheric effects, or result from the methods of comparison

Note that the primary focus of this research was to have accurate SST measurements from satellites.

The experimental work on the research vessel Pelican included a high spectral resolution Atmospheric Emitted Radiance Interferometer (AERI) which was configured to make spectral observations of the sea surface radiance at several view angles. Any measurement from the surface of course, is the sum of the emitted radiance from the surface as well as the reflected sky radiance.

Also measured:

• ocean salinity
• intake water temperature
• surface air temperature
• humidity
• wind velocity
• SST within the top 15cm of depth

There was also independent measurement of the radiative temperature of the sea surface at 10μm with a Heimann broadband radiation thermometer “window” radiometer. And radiosondes were launched from the ship roughly every 3 hours.

Additionally, various other instruments took measurements from a flight altitude of 20km. Satellite readings were also compared.

The AERI measured the spectral distribution of radiance from 3.3μm to 20μm at 4 angles. Upwards at 11.5° from zenith, and downwards at 36.5°, 56.5° and 73.5°.

There’s a lot of interesting discussion of the calculations in their paper. Remember that the primary aim is to enable satellite measurements to have the most accurate measurements of SST and satellites can only really “see” the surface through the “atmospheric window” from 8-12μm.

Here are the wavelength dependent emissivity results shown for the 3 viewing angles. You can see that at the lowest viewing angle of 36.5° the emissivity is 0.98 – 0.99 in the 8-12μm range.

Note that the wind speed doesn’t have any effect on emissivity at the more direct angle, but as the viewing angle moves to 73.5° the emissivity has dropped and high wind speeds change the emissivity considerably.

Henderson et al – 2003

Henderson et al (2003) is one of the many papers which consider the theoretical basis of how viewing angles change the emissivity and derive a model.

Just as an introduction, here is the theoretical variation in emissivity with measurement angle, versus “refractive index” as computed by the Fresnel equations:

The legend is refractive index from 1.20 to 1.35. Water, at visible wavelengths, has a refractive index of 1.33. This shows how the emissivity reduces once the viewing angle increases above 50° from the vertical.

The essence of the problem of sea surface roughness for large viewing angles is shown in the diagram below, where multiple reflections take place:

Henderson and his co-workers compare their results with the measured results of Smith et al (1996) and also comment that at zenith viewing angles the emissivity does not depend on the wind speed, but at larger angles from vertical it does.

A quick summary of their model:

We have developed a Monte Carlo ray-tracing model to compute the emissivity of computer-rendered, wind-roughened sea surfaces. The use of a ray-tracing method allows us to include both the reflected emission and shadowing and, furthermore, permits us to examine more closely how these processes control the radiative properties of the surface. The intensity of the radiation along a given ray path is quantified using Stokes vectors, and thus, polarization is explicitly included in the calculations as well.

Their model results compare well with the experimental results. Note that the approach of generating a mathematical model to calculate how emissivity changes with wind speed and, therefore, wave shape is not at all new.

Water retains its inherent properties of emissivity regardless of how it is moving or what shape it is. The theoretical challenge is handling the multiple reflections, absorptions, re-emissions that take place when the radiance from the water is measured at some angle from the vertical.

Conclusion

The best up to date measurements of ocean emissivity in the 8-14 μm range are 0.98 – 0.99. The 8-14 μm range is well-known because of the intense focus on sea surface temperature measurements from satellite.

From quite ancient data, the average emissivity of water across a very wide broadband range (1-100 μm) is 0.96 for water temperatures from 0-30°C.

The values from the ocean when measured close to the vertical are independent of wind speed and sea surface roughness. As the angle of measurement moves from the vertical around to the horizon the measured emissivity drops and the wind speed affects the measurement significantly.

These values have been extensively researched because the calculation of sea surface temperature from satellite measurements in the 8-14μm “atmospheric window” relies on the accurate knowledge of emissivity and any factors which affect it.

For climate models – I haven’t checked what values they use. I assume they use the best experimental values from the field. That’s an assumption. I’ve already read enough on ocean emissivity.

For energy balance models, like the Trenberth and Kiehl update, an emissivity of 1 doesn’t really affect their calculations. The reason, stated simply, is that the upwards surface radiation and the downward atmospheric radiation are quite close in magnitude. For example, the globally annually averaged values of both are 396 W/m² (upward surface) vs 340 W/m² (downward atmospheric).

Suppose the emissivity drops from 0.98 to 0.97 – what is the effect on upwards radiation through the atmosphere?

The upwards radiation has dropped by 4W/m², but the reflected atmospheric radiation has increased by 3.4W/m². The net upwards radiation through the atmosphere has reduced by only 0.6 W/m².

One of our commenters asked what value the IPCC uses. The answer is they don’t use a value at all because they summarize research from papers in the field.

Whether they do it well or badly is a subject of much controversy, but what is most important to understand is that the IPCC does not write papers, or perform GCM model runs, or do experiments – and that is why you see almost no equations in their many 1000’s of pages of discussion on climate science.

For those who don’t believe the “greenhouse” effect exists, take a look at Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part One in the light of all the measured results for ocean emissivity.

On Another Note

It’s common to find claims on various blogs and in comments on blogs that climate science doesn’t do much actual research.

I haven’t found that to be true. I have found the opposite.

Whenever I have gone digging for a particular subject, whether it is the diurnal temperature variation in the sea surface, diapycnal & isopycnal eddy diffusivity, ocean emissivity, or the possible direction and magnitude of water vapor feedback, I have found a huge swathe of original research, of research building on other research, of research challenging other research, and detailed accounts of experimental methods, results and comparison with theory and models.

Just as an example, in the case of emissivity of sea surface, at the end of the article you can see the first 30 or so results pulled up from one journal – Remote Sensing of the Environment for the search phrase “emissivity sea surface”. The journal search engine found 348 articles (of course, not every one of them is actually about ocean emissivity measurements).

Perhaps it might turn out to be the best journal for this subject, but it’s still just one journal.

References

Broadband reflectance and emissivity of specular and rough water surfaces, Sidran, Applied Optics (1981)

In situ angular measurements of thermal infrared sea surface emissivity—validation of models, Niclòs, Valor, Caselles, Coll & Sànchez, Remote Sensing of Environment (2005)

Measurement of the Sea Surface Emissivity, Konda, Imasato, Nishi and Toda, Journal of Oceanography (1994)

Observations of the Infrared Radiative Properties of the Ocean—Implications for the Measurement of Sea Surface Temperature via Satellite Remote Sensing, Smith, Knuteson, Revercomb, Feltz, Nalli, Howell, Menzel, Brown, Brown, Minnett & McKeown, Bulletin of the American Meteorological Society (1996)

The polarized emissivity of a wind-roughened sea surface: A Monte Carlo model, Henderson, Theiler & Villeneuve, Remote Sensing of Environment (2003)

Notes

Note 1: The upward radiation from the surface is the sum of three contributions: (i) direct emission of the sea surface, which is attenuated by the absorption of the atmospheric layer between the sea surface and the instrument; (ii) reflection of the downwelling sky radiance on the sea, attenuated by the atmosphere; and (iii) the upwelling atmospheric radiance emitted in the observing direction.

So the measured radiance can be expressed as:

where the three terms on the right are each of the three contributions noted in the same order.

Note 2: 1/10th of the search results returned from one journal for the search term “emissivity sea surface”: