A while ago we looked at some basics in Heat Transfer Basics – Part Zero.
Equations aren’t popular but a few were included.
As a recap, there are three main mechanisms of heat transfer:
- conduction
- convection
- radiation
In the climate system, conduction is generally negligible because gases and liquids like water don’t conduct heat well at all. (See note 2).
Convection is the transfer of heat by bulk motion of a fluid. Motion of fluids is very complex, which makes convection a difficult subject.
If the motion of the fluid arises from an external agent, for instance, a fan, a blower, the wind, or the motion of a heated object itself, which imparts the pressure to drive the flow, the process is termed forced convection.
If, on the other hand, no such externally induced flow exists and the flow arises “naturally” from the effect of a density difference, resulting from a temperature or concentration difference in a body force field such as gravity, the process is termed natural convection. The density difference gives rise to buoyancy forces due to which the flow is generated..
The main difference between natural and forced convection lies in the mechanism by which flow is generated.
From Heat Transfer Handbook: Volume 1, by Bejan & Kraus (2003).
The Boundary Layer
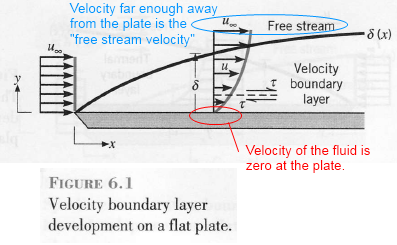
The first key to understanding heat transfer by convection is the boundary layer. A typical example is a fluid (e.g. air, water) forced over a flat plate:
This first graphic shows the velocity of the fluid. The parameter u∞ is the velocity (u) at infinity (∞) – or in layman’s terms, the velocity of the fluid “a long way” from the surface of the plate.
Another way to think about u∞ – it is the free flowing fluid velocity before the fluid comes into contact with the plate.
Take a look at the velocity profile:
At the plate the velocity is zero. This is because the fluid particles make contact with the surface. In the “next layer” the particles are slowed up by the boundary layer particles. As you go further and further out this effect of the stationary plate is more and more reduced, until finally there is no slowing down of the fluid.
The thick black curve, δ, is the boundary layer thickness. In practice this is usually taken to be the point where the velocity is 99% of its free flowing value. You can see that just at the point where the fluid starts to flow over the plate – the boundary layer is zero. Then the plate starts to slow the fluid down and so progressively the boundary layer thickens.
Here is the resulting temperature profile:
In this graphic T∞ is the temperature of the “free flowing fluid” and Ts is the temperature of the flat plat which (in this case) is higher than the free flowing fluid temperature. Therefore, heat will transfer from the plate to the fluid.
The thermal boundary layer, δt, is defined in a similar way to the velocity boundary layer, but using temperature instead.
How does heat transfer from the plate to the fluid? At the surface the velocity of the fluid is zero and so there is no fluid motion.
At the surface, energy transfer only takes place by conduction (note 1).
In some cases we also expect to see mass transfer – for example, air over a water surface where water evaporates and water vapor gets carried away. (But not with air over a steel plate).
So a concentration boundary layer develops.
Newton’s Law of Cooling
Many people have come across this equation:
q” = h(Ts – T∞)
where q” = heat flux in W/m², h is the convection coefficient, and the two temperatures were defined above
The problem is determining the value of h.
It depends on a number of fluid properties:
- density
- viscosity
- thermal conductivity
- specific heat capacity
But also on:
- surface geometry
- flow conditions
Turbulence
The earlier examples showed laminar flow. However, turbulent flow often develops:
Flow in the turbulent region is chaotic and characterized by random, three-dimensional motion of relatively large parcels of fluid.
Check out this very short video showing the transition from laminar to turbulent flow.
What determines whether flow is laminar or turbulent and how does flow become turbulent?
The transition from laminar to turbulent flow is ultimately due to triggering mechanisms, such as the interaction of unsteady flow structures that develop naturally within the fluid or small disturbances that exist within many typical boundary layers. These disturbances may originate from fluctuations in the free stream, or they may be induced by surface roughness or minute surface vibrations
from Incropera & DeWitt (2007).
Imagine treacle (=molasses) flowing over a plate. It’s hard to picture the flow becoming turbulent. That’s because treacle is very viscous. Viscosity is a measure of how much resistance there is to different speeds within the fluid – how much “internal resistance”.
Now picture water moving very slowly over a plate. Again it’s hard to picture the flow becoming turbulent. The reason in this case is because inertial forces are low. Inertial force is the force applied on other parts of the fluid by virtue of the fluid motion.
The higher the inertial forces the more likely fluid flow is to become turbulent. The higher the viscosity of the fluid the less likely the fluid flow is to become turbulent – because this viscosity damps out the random motion.
The ratio between the two is the important parameter. This is known as the Reynolds number.
Re = ρu∞x / μ
where ρ = density, u∞ = free stream velocity, x is the distance from the leading edge of the surface and μ = dynamic viscosity
Once Re goes above around 5 x 105 (500,000) flow becomes turbulent.
For air at 15°C and sea level, ρ=1.2kg/m³ and μ=1.8 x 10-5 kg/m.s
Solving this equation for these conditions, gives a threshold value of u∞x > 7.5 for turbulence.. This means that if the wind speed (in m/s) x the length of surface over which the wind flows (in m) is greater than 7.5 we will get turbulent flow.
For example, a slow wind speed of 1 m/s (2.2 miles / hour) over 7.5 meters of surface will produce turbulent flow. When you consider the wind blowing over many miles of open ocean you can see that the air flow will almost always be turbulent.
The great physicist and Nobel Laureate Richard Feynman called turbulence the most important unsolved problem of classical physics.
In a nutshell, it’s a little tricky. So how do we determine convection coefficients?
Empirical Measurements & Dimensionless Ratios
Calculation of the convection heat transfer coefficient, h, in the equation we saw earlier can only be done empirically. This means measurement.
However, there are a whole suite of similarity parameters which allow results from one situation to be used in “similar circumstances”.
It’s not an easy subject to understand “intuitively” because the demonstration of these similarity parameters (e.g., Reynolds, Prandtl, Nusselt and Sherwood numbers) relies upon first seeing the differential equations governing fluid flow and heat & mass transfer – and then the transformation of these equations into a dimensionless form.
As the simplest example, the Reynolds number tells us when flow becomes turbulent regardless of whether we are considering air, water or treacle.
And a result for one geometry can be re-used in a different scenario with similar geometries.
Therefore, many tables and standard empirical equations exist for standard geometries – e.g. fluid flow over cylinders, banks of pipes.
Here are some results for air flow over a flat isothermal plate (isothermal = all at the same temperature) – calculated using empirically-derived equations:
Click for a larger view
The 1st graph shows that the critical Reynolds number of 5×105 is reached at 1.3m. The 2nd graph shows how the boundary layer grows under first laminar flow, then second under turbulent flow – see how it jumps up as turbulent flow starts. The 4th graph shows the local convection coefficient as a function of distance from the leading edge – as well as the average value across the 2m of flat plate.
Conclusion
Not much of a conclusion yet, but this article is already long enough. In the next article we will look at the experimental results of heat transfer from the ocean to the atmosphere.
Notes
Note 1 – Heat transfer by radiation might also take place depending on the materials in question.
Note 2 – Of course, as explained in the detailed section on convection, heat cannot be transferred across a boundary between a surface and a fluid by convection. Conduction is therefore important at the boundary between the earth’s surface and atmosphere.







Treacle = molasses for those outside the UK. Think viscous and sticky.
Thanks, I added a translation.
G&T point out that conduction cannot be ignored in any climate model.
The air particles hitting the warmer Earth surface leave with a temperature characteristic of the surface due to conduction.
In the air the conductive transfer is very small apart from the thermalisation of the absorbed IR radiation.
This process which many people describe as part of the greenhouse effect causes local temperature increase best described as conductive transfer between the ‘energised’ CO2 and H2O and N2 and O2 molecules.
In line with your recent emphasis on accuracy then conduction cannot be ignored even though the mathematical treatment is very difficult.
And your evidence that climate models ignore conduction is???
They then show that it is very small compared to radiation and convection but pretend that they have done something significant.
Eli Rabett
Since surface conduction gives rise to convection it must have a significantly similar magnitude.
Further the thermalisation caused by the IR active gases seems to be ignored.
Bryan,
I think you are omitting the radiative transfer from surface to atmosphere; depending on how much is conducted versus how much is absorbed, the magnitude of that transferred by conduction does not have to be that similar to that redistributed via convection. That omission would be inconsistent with the ‘atmosphere is saturated’ crowd.
But then, I’m not following your claim that the thermalisation of the energy absorbed is ignored. It isn’t ignored, and if conductive transfere were the principle driver of convection, that would mean that radiative transfer was minor in comparison.
Chris G
Right at the boundary layer the incident air molecules leave with the characteristic temperature of the surface.
Heat transfer by conduction.
I don’t think there is much dispute that at the surface boundary this is the major form of heat transfer.
This rapidly produces convection.
Radiation at the boundary will play a small part in the overall net transfer of heat at this stage.
However in general the radiatively active gases do contribute to heat transfer as the 15um “bite” out of the outgoing Earth radiation shows.
What I cant make out is the treatment of the thermalised radiation.
How much of this conductive transfer (or % transfer) is then convected or radiated away at longer wavelengths.
Or how any of this is then reflected in the lapse rate.
DeWitt Payne
…..”And your evidence that climate models ignore conduction is???”…….
I thought that this was a generally accepted fact!
However if you can point to a model that explicitly includes conductive transfer in the atmosphere I will certainly revise my understanding.
Then it should be easy for you to cite a reference or three with quantitative estimates of the error from failure to include conduction somewhere.
Meteorologists do indeed ignore conduction in the atmosphere to a first approximation.
To quote you:
So what was it that G&T pointed out precisely?
DeWitt Payne
Most comment now on climate change seems to have switched from a direct bulk effect of CO2 IR absorption to a feedback forcing amplified effect.
This indicates that a small effect is scaled up to have any significance.
This implies that errors previously introduced by ignoring real properties might have significance.
Most explanations of IPCC climate change atmospheric interactions skip conduction or say it only matters at the Earth surface/air boundary.
G&T point out that unless a climate model includes conductive transfer in the atmosphere it is bound to fail.
Bryan:
As many people might miss the italicized indented key point in the body of the article:
At the surface, energy transfer only takes place by conduction (note 1).
– I added note 2 in the introduction.
Bryan,
A nice chain of hand waving and assertion with absolutely no supporting evidence. I’m still waiting for your evidence that climate models do, in fact, ignore thermal conductivity in the atmosphere and that it causes a significant error. As I said above, if this is common knowledge then you should be able to easily find a multitude of references. [sound of crickets]
The whole subject brings this Shakespeare quote to mind:
Henry IV, part 1, Act III
Glendower: I can call spirits from the vasty deep.
Hotspur: Why, so can I, or so can any man; But will they come when you do call for them?
DeWitt Payne
What evidence are you looking for?
You seem to be well aware of the point I was making yourself;
……”Meteorologists do indeed ignore conduction in the atmosphere to a first approximation.”………..
This seems to be a typical model where conduction of heat only seems to be included at air/Earth surface boundary.
http://www.giss.nasa.gov/tools/modelii/
What about the thermalisation caused by the IR active gases?
I think a bit more care in what we we regard as negligible is required!
Howe else are we going to help Trenbirth find the “missing heat”
Every GCM has an energy equation. This incorporates a spatial term for vertical conduction, and one for convection. The term for conduction is necessary, and can’t be omitted. The reason is, as SoD said, that conduction is the mechanism for heat transfer at the boundary. This has to be reflected in the maths, otherwise the boundary condition won’t work.
In CAM3, the heat part is Eq 3.66.
GCM’s omit horizontal conduction because there are no barriers in the horizontal direction, and so no boundary conditions.
Thanks Nick and Frank.
It will take some time to identify the process of atmospheric conduction through the troposphere from your leads.
The result of IR thermalisation and implied onward conductive transfer is hard to identify.
This must be a significant part of heat transfer in the troposphere in the IPCC narrative?
This is where the doubling of CO2 concern must enter the story.
Every GCM has an energy equation. This incorporates a spatial term for vertical conduction, and one for convection. The term for conduction is necessary, and can’t be omitted. The reason is, as SoD said, that conduction is the mechanism for heat transfer at the boundary. This has to be reflected in the maths, otherwise the boundary condition won’t work.
In CAM3, the heat part is Eq 3.66.
GCM’s omit horizontal conduction because there are no barriers in the horizontal direction, and so no boundary conditions. Horizontal conduction is always negligible relative to advection.
Nick and Bryan: I couldn’t make much sense out of Eqn 3.66, but did find Section 4.10 (Surface Exchange Formulations) containing Eqn 4.408, which describes sensible heat flux between the surface and the lowest model layer of atmosphere. This equation resembles “Newton’s Equation of Cooling” cited above by SOD. Perhaps Bryan will find this section somewhat clearer. http://www.cesm.ucar.edu/models/atm-cam/docs/description/node24.html
It seems as if conduction from the surface to the atmosphere heats up only a very thin layer of atmosphere near the surface and that buoyancy-driven vertical convection begins in this thin layer. Am I correct in assuming that the lowest layer in a typical model is orders of magnitude thicker than thin layer directly heated by conduction? Is sensible heat conducted from the surface assumed to spread vertically though out the lowest layer of the model atmosphere?
Looking backward at Equations (3.3) through (3.13), Equation (3.5) is the the equation of interest. The text following Equation (3.13) says: ” . . . while and represent sources attributable to horizontal diffusion of temperature and a contribution from frictional heating (see sections on horizontal diffusion and horizontal diffusion correction).”
“Horizontal diffusion of temperature” means heat conduction within the fluid in the horizontal plane.
These equations become Equation (3.23) through (3.32) and Equation (3.5) becomes Equation (3.25). Then in Section 3.1.3, these equations become Equation (3.33) through (3.42), and now Equation (3.35) is the equation of interest.
However, in Section 3.1.5. just prior to Equation (3.66), the text says: “We now turn to the internal energy equation, obtained by combining the thermodynamic equation (3.36), without the , , and terms, and the continuity equation (3.59):”
The reference to Equation (3.36) in that text is incorrect; it should be a reference to Equation (3.35). The terms stated to be omitted from the subject equation don’t appear in Equation (3.36), they appear in Equation (3.35).
Note that the horizontal diffusion of temperature, i. e. conduction, is among the terms that have been dropped.
There is no conduction term in Equation (3.66), as far as I can determine.
It is not necessary to include an accounting of conduction in the energy equation for the fluid. Many engineering problems that involve energy exchange between a fluid and a surface at a different temperature are formulated without the conduction terms in the energy equation for the fluid. It is only a matter of the magnitude of the conduction within the fluid relative to the transport of energy by the fluid. And that usually boils down to the magnitude of the conductivity of the fluid; liquid metals having much larger values than gases. I can provide many textbook citations if anyone insists.
It is required, of course, to have an accounting of the energy exchange between the fluid and the adjacent surface when that energy exchange is considered important within the context of situation of interest. The so-called Newton’s Law of Cooling usually provides that connection. For the case of coupled convection-conduction problems, the general energy conservation equation when applied to the solid becomes the conduction equation.
Math symbols got dropped in a couple of places when I converted to text. See the online document for the symbols.
“GCM’s omit horizontal conduction because there are no barriers in the horizontal direction, and so no boundary conditions. Horizontal conduction is always negligible relative to advection.”
There’s a discussion of horizontal temperature diffusion, conduction, in Section 3.1.6 Horizontal diffusion.
SOD: Above, you discuss a boundary layer for laminar or turbulent flow which is <1 m in your graphs. Elsewhere, people discuss a well-mixed "boundary layer" of the atmosphere (up to 500 mb? 5 km?). Could you explain the relationship (if any) between these two boundary layers?
You showed that wind near the surface of the earth will be turbulent if it persists over many kilometers. Does the same conclusion apply to ocean currents?
Frank:
For steady stream air forced over a flat surface the boundary layer, δ, grows according to this equation:
δ = 0.37.x.Re^(-1/5) : once the flow has become turbulent
where the Reynolds number, Re is as defined above and x is the distance over the surface over which the air flows.
This would indicate that a 10m/s wind blowing over 500-600km of totally flat surface would create a boundary layer of over 900m height.
The atmospheric boundary layer generally ranges from a few hundred meters to 1-2 km above the surface of the earth.
This turbulent layer occurs because the earth’s surface is very complex (geometrically) over land – hills, valleys, houses, trees, etc. – not flat, and the wind speed higher up is faster and because the air blows over a very “long” surface.
1. Boundary layers are important in convection, but not the sort you introduce here. Here you have the standard fluid dynamics boundary layer with a fluid approaching a flat plate with some speed u∞ – this is a different sort of boundary layer, and introducing it here is just confusing. The thermal boundary layer has nothing to do with any u∞. The thermal boundary layer is – as Frank says – a thin layer where heat is transferred by conduction, before convection takes over.
2. Newton’s law of cooling does not hold for convective heat transfer. The heat flux is proportional to some power of the temperature difference, usually about 4/3.
3. Dimensionless Ratios are important, but you have not even mentioned the one that matters for convection! The important ratio in convection is called the Rayleigh number, Ra. This is the ratio of destabilising effect of the temperature difference and gravity to the stabilising effects of thermal diffusion and fluid viscosity.
If Ra is fairly small (in fact up to a thousand or so) then there is no convection and you get a linear (conduction) temperature profile. If Ra is bigger, you get laminar overturning convection cells. If Ra is very big, you get unsteady turbulent convection and a thin boundary layer. In nature, Ra is usually very large.
PaulM:
It’s the flow of air at the earth’s surface which slows it down and creates a turbulent boundary layer of velocity changes and heat transfer.
The flat plate is just the simplest possible version of our real world.
Here’s what Roland Stull says in Boundary Layer Meteorology (1988):
(Emphasis his).
Click for a larger view
ScienceOfDoom,
Not really questioning the accuracy of your description of laminar versus turbulent flow of air over a surface, (if jives well with what I remember from my days as an aeronautical student), but I think PaulM has a valid point. For instance. in the text above, I would have interpreted the reference to “turbulence” as the the turbulence resulting from air masses moving past each other, including convective currents, rather than as strictly surface-air interactions.
PaulM:
Re: equation for heat transfer, here’s another specific example of heat transfer from a climate science textbook rather than a thermodynamics textbook.
From Grant Bigg, The Oceans and Climate (2003):
Here is an extract from the paper, A note on bulk aerodynamic coefficients for sensible heat and moisture fluxes by Pond, Fissel & Paulson (1974). It was published by the journal Boundary Layer Meteorology.
For formulae derived from empirical measurements it is likely that there are many different possible arrangements.
Do you have the reference handy so we can take a look at the complete equation, the other parameters and the conditions under which it is believed valid?
These formulas can’t be right in all circumstances, since with no wind, U=0, there would be no convective heat flux! I prefer to think about the simpler case of ‘free convection’ where there is no driving wind. Of course in this case the surface ground/water heats up from the sun leading to warm thermals rising in the atmosphere.
A discussion and reference for this case, mentioning the 4/3 power, can be found here. You seem to have access to a lot of textbooks – can you find that one by A F Mills?
PaulM:
The equations which govern heat transfer from the surface to the wind – forced convection, are of course, different from those that govern buoyancy driven convection (free convection).
The graph in the article for the turbulent convection coefficient was calculated from the standard formula:
Nu = h.x/k = 0.0296.Re^(4/5).Pr^(1/3)
where Nu is the Nusselt number, h is the convection coefficient, x is the distance from the leading edge of the surface, k is the conductivity in air, Re is the Reynolds number and Pr is the Prandl number.
The Prandtl number is the ratio of viscous diffusion to thermal diffusion (kinematic viscosity/thermal diffusivity). It is around 0.7-0.8 for air in the atmosphere.
These types of equations help to calculate the convection coefficient for air flow over a surface.
The Rayleigh number, Ra = Prandtl number x Grashof number.
The Grashof number is the ratio of buoyancy to viscous forces.
Considering it’s form, I’m not sure how you would use it for natural convection from the earth’s surface (it seems to be used a lot for convection caused by heated vertical plates and pipes). What value would you choose for the length parameter (L in the equation below)??
Using the standard values for air around 300K I calculate that the Grashof number, Gr = 1.3×10^8 (Ts-T∞).L^3
– but that’s using the vertical plate form of the equation, as I can’t find a horizontal surface form.
Good question – what if there is no meaningful lengthscale? This had me stumped for a while until I looked at the book Dan helpfully provided which reminded me of the rather nice answer (see page 422):
If the Nusselt number is proportional to the Rayleigh (or Grashof) number to the power of 1/3, then L cancels out, in other words the convective heat flux does not depend on L so it doesnt matter what you choose. Recall that Nu = convective heat flux / conductive heat flux. Now the conductive heat flux is proportional to dT/L, so
convective heat flux = (dT/L) Nu = (dT/L) (…dt L^3)^(1/3)
which is proportional to dT^(4/3) and independent of L.
In fact, this is often used as a theoretical argument to support the 4/3 scaling I mentioned originally.
If you go back and put all the units in you end up with something like
convective heat flux = (g alpha dT^4 K)^1/3 rho Cp
multiplied by an arbitrary constant and an arbitrary function of the Prandtl number. Here alpha is the expansion coefficient and K is thermal diffusivity.
Alternatively of course we could have said that there is no lengthscale in the problem and used dimensional analysis to come up with something that has the right units for heat flux out of relevant things like dT and g which would lead to a similar formula (though I think we’d have one undetermined power).
Science of Doom,
I see that you frequently reproduce pages from heat transfer textbooks in your posts. There’s a free online text available from: http://web.mit.edu/lienhard/www/ahtt.html . The pdf version can be downloaded, too.
There are physical phenomena and processes for which investigations into the effects of conduction within the fluid are important. For these cases, conduction heat transfer within the fluid alters the temperature distribution in such a way that important different responses, compared to results without conduction heat transfer, are obtained. Conduction heat transfer within the fluid, for example, can introduce inflection points into the temperature distribution. Additionally, if the fluid transport, and thermodynamic state, properties are strong functions of the temperature, these can feed into changes in the velocity distribution. Inflection points, and temperature dependency on fluid properties, are frequently related to issues associated with stability of the flow. The response of thermo-syphons and the stability of flows in parallel channels, especially at lower velocity, are two examples. The temperature-density behavior of water near its maximum density state is another. And all flows that involve thermodynamic states near / at the critical point are another.
Dan Hughes:
Thanks very much. I have downloaded it and had a read of a few sections – looks excellent.
And it’s accessible to everyone which is amazing.
PaulM (January 6, 2011 at 1:10 pm):
Thanks, I’ll take a longer look at this section in the light of your comments.
Although your model is useful, an important part of the thermal mixing process is that the surface of the ocean is not smooth. Indeed, interaction of the atmosphere and the ocean surface on a small scale at the marine boundary layer drive the process
[…] some basic background over related terms, check out Heat Transfer Basics – Convection – Part One, with some examples of fluid flowing over flat plates, boundary layers, laminar flow and turbulent […]
腕時計 ロレックス サブマリーナ http://www.pr1x.comrolexロレックス-4u-2.html/
Fluid being the same, why do we have more heat transfer in turbulent flow than laminar flow despite of the fact that turbulent boundary layers are thicker? As you said conduction is the only phenomena of heat transfer in thermal boundary layers, I see no variable in fouriers law of heat transfer that simply explains this.
The term ‘boundary layer’ has several meanings. For thermal conductivity, it’s the stagnant layer attached to a surface. With turbulent flow, this layer is thinner, not thicker, hence more rapid heat transfer. The atmospheric boundary layer is something else entirely. For one thing, it isn’t stagnant.
@DeWitt Payne and @scienceofdoom: Thanks for your reply. I am still not clear about the ‘several meanings of bounday layers’ that you mentioned. For the case of air flow over a flat plate, my understanding is that both thermal and velocity boundary layers are thicker for the turbulent flow than the laminar flow. Thermal conductivity of air is very low and conduction being the only phenomena taking place in the boundary layers, heat transfer in turbulent flow should be less than the laminar flow. I still do not understand the concept of more heat transfer in turbulent air flow over a hot plate than laminar flow. I might be in the middle of a silly thing, will appreciaite your understanding.
PS: I am ignoring the radiation effect.
My training is in mass transfer rather than heat transfer, but the fundamental equations are the same. Convective mass transfer with laminar or turbulent flow is faster than diffusion. One can think of diffusion only occurring in a thin layer attached to the surface. Increasing the rate of forced convection makes this layer thinner and increases the rate of mass transfer for a given concentration difference between the surface and the bulk solution. See, for example, a rotating disk electrode, RDE.
If the Reynolds number of an RDE is increased to the point of turbulence and beyond, the rate of mass transfer continues to increase, i.e. the diffusion layer continues to get thinner, not thicker. But the math gets too complicated to make this useful for electrochemical analysis,
As far as the velocity boundary layer getting thicker, this is more than compensated for by the turbulent mixing in the velocity boundary layer causing the concentration(temperature) gradient at the surface to increase drastically, resulting in the big jump in the convection coefficient at a flat plate at the point where the flow becomes turbulent (lower right graph here.)
Sharma,
With reference to this diagram (from the main article):
The original question you posed relates to the red circle – that is, actually on the boundary (not the whole boundary layer) the velocity of molecules is zero. A “few molecules away” from the boundary, there is some motion. A little further, more motion.
The question you posed first was to query whether it really was conduction that transferred heat across this boundary, given the issue of laminar vs turbulent flow.
The boundary layer is the layer from the boundary to the point where the flow has reached the free stream velocity of the fluid.
Hope this helps.
Sharma,
It’s an interesting question. The way to think of the problem is how does any heat get transferred during convection over a surface? Say for example, a fluid forced over a hot surface. What mechanism makes the fluid obtain heat from the surface? It’s not convection because convection of heat is simply (in this case) the movement of hot fluid. How does the heat pass to the fluid? It has to be conduction (also radiation is possible).
The reason for different heat transfers across the plate to the fluid during convection is due to the different profiles of the viscous boundary layer.
[…] continuemos con nuestro planeta imaginario. La superficie calentada por el sol calienta a su vez el nitrógeno adyacente por conducción y empieza a actuar la convección. En ese momento, bolsas de nitrógeno más calientes que su entorno empiezan a elevarse y lo hacen […]