In Atmospheric Circulation – Part One we saw how the higher temperatures in the tropics vs the poles (due to higher solar insolation in the tropics) led to a greater “geopotential height”. This means simply that the height of a given atmospheric pressure (e.g. 500mbar) is greater in the tropics, and so the geopotential surfaces slope down from the tropics to the poles.
And in Atmospheric Circulation – Part Two – Thermal Wind we saw how that effect, due to the Coriolis force, causes a W-E wind (“zonal wind”) that increases with height. This culminates in the sub-tropical jets (see figure 5) that are a maximum around 30°.
The question arise – why don’t the zonal winds just keep increasing in the poleward direction? Why the peak value at the sub-tropics?
Conservation of Angular Momentum
The angular momentum of a parcel of air is conserved if there is no net torque acting on that parcel.
So let’s consider a parcel of air at the equator at rest with respect to the surface of the earth. Now let’s push that parcel of air out towards the north pole and let’s calculate the resulting net W-E velocity of that parcel.
The angular momentum at the equator is significant because the earth is rotating. At the parcel of air moves north, the radius around the axis of rotation continually reduces (at the pole the radius around the axis of rotation = 0):
Figure 1
– and so for conservation of angular momentum the W-E velocity of the air with respect to the ground must increase.
The maths is simple to calculate, here is a calculation of the resulting W-E velocity if angular momentum is conserved:
Figure 2
If we refer back to figure 5 in Part Two we see that the annual average maximum of the zonal winds is around 30 m/s.
It’s clear what is going on – as parcels of air move towards the pole they speed up (due to conservation of annual momentum) to the point where the large scale atmospheric motions break down and eddies take over. A lab example of this effect was shown in the previous article:
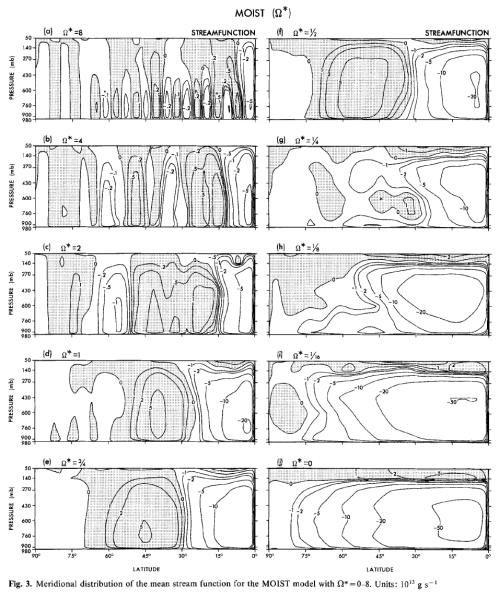
Figure 3
The rotational speed of the earth is a critical factor.
Here are some fascinating GCM results from Williams (1988), first the zonal (W-E) winds as the planetary rotation is increased from zero to 8x the Earth’s rotation:
Figure 4 – Click for a larger image
And second, the meridional winds (N-S winds):
Figure 5 – Click for a larger image
And finally the average temperature distribution in the N-S direction:
Figure 6 – Click for a larger image
We see that the effect of increasing rotation is to create more and more “cells” – like the Hadley cell, the tropical to sub-tropical cell, which was shown in figure 4 of Part One – and to create a stronger differential temperature from equator to pole. The faster the earth rotates the “harder” it is for warmer air to move poleward and so the differential solar heating does not get “smeared out” poleward.
This paper by Williams is quite fascinating. It has a number of simplifications like no variation in longitudinal effects, a “swamp” ocean and some factors that are fixed at the current earth’s rotation value (note 1). Isaac Held recently wrote a post, The “Fruit Fly” of Climate Models which highlights many issues around simplifying climate models to illustrate the important principles underlying climate dynamics. This post is well worth reading as well as exploring the referenced papers.
Prof. Isaac Held is one of the gurus of climate dynamics and has been writing influential papers on this (and other) topics since the mid 1970s. For example, Nonlinear axially symmetric circulations in a nearly inviscid atmosphere, Held & Hou, Journal of the Atmospheric Sciences (1980). Many scientists have contributes to this topic, including the well-known Prof. Richard. S. Lindzen with Axially symmetric steady-state models of the basic state for instability and climate studies. Part I. Linearized calculations, EK Schneider & RS Lindzen, Journal of the Atmospheric Sciences (1977).
In the next article we will look at how eddy motions transport heat to the poles outside of the Hadley cell.
References
The dynamical range of global circulations I, Gareth Williams, Climate Dynamics (1988) – behind paywall
Notes
Note 1 – Extract from the Introduction of Williams (1988):
In this paper (to be published in two parts), we generate a comprehensive set of circulations by varying some of the fundamental external parameters and primary internal factors that control the dynamics of a terrestrial global circulation model (GCM). The solutions are developed for two purposes: (1) to study basic circulation dynamics; and (2), to define the parametric variability of circulations.
By altering the size, strength, and mix of the eddies, jets, and cells in a variety of flow forms, we hope to develop further insight into how they arise and interact. By developing a wide range of circulations, we hope to gain perspective on the parametric circumstance of Earth’s climate and to broaden the data base from which we extrapolate in theorizing about other planets and other climates (Hunt 1979a, b, 1982).
To generate as complete a circulation set as possible, we evaluate moist, dry, axisymmetric, oblique, and diurnal model atmospheres over a wide range of rotation rates: Ω* = 0-8, where Ω*= Ω/ΩE is normalized by the terrestrial value.
For the set to be meaningful, the GCM must be valid at all parameter values. We believe this to be so, although we cannot prove it. The GCM has some known limitations, such as the non-universal boundary-layer and radiation formulations, but these do not affect the fundamental structure of the flows. We also assume, in presenting the solutions, the hypothesis that circulation variability is limited to the mix of a few elementary components that can be understood in terms of regular quasi-geostrophic (QG) and Hadley theories. The interpretation of the solutions in terms of these theories is essentially qualitative — just as it is for the terrestrial (Ω* = 1) case (Held and Hoskins 1985).
The modern view of the terrestrial circulation is still based on the explanation summarized by Lorenz (1967, 1969): that in low latitudes, the time-averaged flow is mainly the product of thermal forcing (as suggested by Palm6n) and described by quasi-Hadley (QH) theories; that in mid-latitudes, the time- and zonal-averaged flow is essentially the product of forcing by the large-scale eddies (as suggested by Eady, Rossby and Starr) and described by QG theories; and that the two flows and regions interact extensively.
In the Northern Hemisphere, strong orographically driven standing waves complicate this view (Wallace and Lau 1985), but we ignore surface inhomogeneities in this paper. The outstanding circulation issue posed by Lorenz in 1969 concerned the role of the eddies in forming and maintaining the angular-momentum characteristics: why is the eddy-momentum transport mainly poleward; what is the basic state with which the eddies interact; what form does the idealized symmetric-Hadley (SH) state take and how does it relate to the natural state? Some of these questions have been resolved and new ones have emerged..
And from Section 2.5, Non-universal model features:
As a representation of Earth’s atmosphere, the GCM has significant deficiencies. For example, it omits land surfaces and ocean transports, it does not forecast the cloud, carbon dioxide and ozone distributions, and it has no snowcover or ice-albedo feedbacks. The imposed distributions of the minor gases, clouds, and albedo in the radiation calculation relate only to the Ω*= 1 state and at other Ω* produce only a relative forcing and circulation. But for our purposes any reasonable thermodynamical forcing suffices and the strong tuning of the radiative heating to conditions at Ω*=1 at least provides a realistic reference state.
A more troublesome non-universality having a more direct dynamical impact lies in the PBL formulation. In the GCM, the PBL is assumed to be neutrally stable so that only mechanical mixing occurs and the associated Prandtl- and Ekman layer depths are fixed at empirical values.
This prescription provides a reasonable first approximation for Ω*= 1 studies. Although a formulation with ze ~ Ω-1 would be more appropriate for an Ω*-varying GCM, even it fails at low Ω*. Given such limitations, we decided not to make the PBL formulation a function of Ω*. Thus the PBL parameters, like the radiation ones, are fixed at their Ω*= 1 values. This is not a satisfying compromise to make but it does eliminate the great inconvenience of having to make the vertical grid spacing a function of Ω*. We believe that these PBL limitations mainly affect the surface winds and do not significantly influence circulation structure.







SoD,
Thanks for a very illuminating post. As before I have just some nitpicking on what I feel as a more natural way of discussing the same phenomena.
You write
and further down
That’s true for the angular momentum around the Earth axis, but a parcel of air is a local concept not strongly linked to the global scale. On local scale the parcel follows the Newtonian equations of motion for a body, i.e. it’s velocity vector is changed by the forces that act on the body. The only forces taken into account in the above situation are the vertical forces (gravity and pressure gradient) that keep the parcel at constant altitude, but do not alter its horizontal speed. Going towards higher latitudes means that the surface moves slower leading to the fact that a parcel that keeps the earlier velocity from lower latitude starts to move relative to the surface. It does not speed up, the point of reference (the surface) is switched to a slower one.
As I said this is nitpicking but as a physicist I feel that the way angular momentum is used in the argument is not really a good one. Angular momentum is conserved by the Earth as a whole, it’s not as a good concept in the discussion of an individual parcel, not even in cases where the conclusions are correct.
(I know that it’s not an accident that the conclusions are correct and the mathematics is valid but even so I dislike the approach.)
Pekka,
Just to be clear, do you mean that:
a. conservation of angular momentum of a parcel of air is not true
b. conservation of angular momentum can be applied to a parcel of air and this means that a northwards moving parcel from the equator keeps the same angular speed which means that its speed relative to the surface of the earth increases in the W-E direction (i.e., you think the English description was too loose)
The way I read your comment both seem implied but angular momentum is definitely applicable to a parcel of air, as of course, momentum can be applied to a parcel of air.
SoD,
Conservation of angular momentum around the Earth axis is true, but it’s not the natural variable to consider for a parcel of air which has dimensions that are very much smaller than the radius of the Earth.
The parcel of air is influenced by local forces. It’s not moving freely around the Earth as are satellites. For satellites the angular momentum is a truly conserved quantity while any parcel of air is influenced strongly by other forces (pressure gradients and wind share) that make all more realistic calculations so local that the angular momentum around the Earth axis is not a natural quantity to consider.
I don’t disagree with your physics, my comments are only on what is the most natural way of describing that physics. That’s related to the question of whether some particular description is a good starting point for more detailed analysis of the system.
Pekka
You are right that there are two ways of looking at this and they both give the same answer. Either you say speed stays the same, but the distance the packet needs to travel to cover one radian goes down, so the angular velocity goes up, or you say that the angular momentum stays the same but the parcel has moved closer to the axis so the angular velocity goes up. And if you replace the sentence above with the appropriate equations then you will see that you come to the same answer. Both result in an increase in speed relative to the solid surface of exactly the same amount.
All this is hardly surprising because conservation of angular momentum and conservation of momentum are both trivial implications of Newton’s laws.
For my money conservation of angular momentum is a more physical idea that conservation of speed. Note you can’t say that (linear) momentum is conserved because it isn’t – centripetal acceleration sees to that.
Some further thoughts on the issue. (I was sloppy when I made my earlier comments. I should have made a stronger comment.)
The conservation of angular momentum leads actually to a different result for a parcel of air from the conservation of linear momentum or velocity when it is moved to a higher latitude. Both result to a change in speed relative to the Earth surface at the corresponding latitude, but the change is larger if the angular momentum is conserved as that would require that the velocity is increased, not only kept unchanged.
This means that the argument based on the conservation of angular momentum is actually wrong as no natural mechanism is given that could increase the velocity and energy of the parcel when it’s moved to a higher latitude. The total angular momentum of the Earth must be conserved but a parcel of air does not conserve it’s angular momentum around the Earth axis when it is moved to a higher latitude unless it is forced to a higher speed and such forcing is not a natural part of the change in latitude.
Two more short points.
1. As long as we haven’t defined what “moving to a higher latitude” means we may have different ideas about that and its concequences.
2. The Coriolis effect is derived looking at linear momentum or velocity, not cosidering angular momentum with respect to the Earth axis. This is clear support for my way of looking at the situation.
Pekka,
Angular momentum is like the black sheep of the family. No one is sure how to deal with them, and many start to wonder if they are from the family at all.
I have had my confusion about the relationship between momentum and angular momentum and even more about the relationship between angular momentum and the Coriolis force. This questioning was inspired in part by Edward Lorenz, The Nature and Theory of the General Circulation of the Atmosphere, WMO (1967) saying:
However, this now makes complete sense and perhaps it is worth an article explaining how all of these different ‘forces’ are related – how all roads lead to Rome..
I dare to doubt what Lorenz is saying there.
The derivation of the Coriolis force does not refer to angular momentum and we have the Coriolis effect also on motion that goes along latitudes where the angular momentum does not change.
Pekka,
Of course we should dare to doubt. I wrote his comment out in my notebook when I found it along with a big question mark.
James R Holton cleared up the mystery for me and I hope to prove it to you.
Await the next article: Coriolis, Angular Momentum, Apparent Forces, Rotating Frames of Reference and All Roads Lead to Rome.
Or I might go for a long title.
But here again the answer is not unique before all factors are stated fully. No changes just happen without some cause and some influencing mechanism and what that is influences the outcome.
And to continue on that. The Coriolis effect can transform a force to an acceleration perpendicular to that. I think that what you are referring goes along those lines. That was already discussed in part two and I wrote a comment on explaining that effect.
But here we come back to what all is assumed about the situation.
And to continue further. My view of the setup was significantly determined by your choice of discussing a parcel of air, i.e. a local concept. If we consider a belt at constant latitude the point of view is different. Then we may have a persistent pressure gradient that makes work when it forces air to higher latitudes which leads to increasing velocity and does that, indeed, in a way where the angular momentum does not change as the pressure gradient is purely in North South direction.
Perhaps I do understand Lorenz after all.
I try to explain a little better where my use the concepts differs. I’m used to that a finite body, and a parcel of gas, is influnced by forces that affect its velocity according to Newtons law and by a torque that inflences its rotation around an axis that goes throudh the center of mass of the body. All finite bodies are formed from parts and the torque affecting the whole body can be determined summing the moments that influnce those parts.
In this approach discussing the forces affecting the parcel in terms of torque with respect to the Earth axis is very strange, although mathematically well defined.
The words have connotations that go beyond their mathematical definitions and switching from one field of application to another leads typically to the result that the hidden assumptions differ and that concise expressions may get very different meaning. Every now and then I notice that my background in other fields of physics and in engineering leads to misunderstanding statements of atmospheric scientists. The sentenses seem familiar and I feel that I understand them fully but it turns out that they are supposed to be read differently.
As my comments can be seen as confusing I add the description of a simple experiment that shows acceleration of a body when its distance from the axis of circular motion is decreased.
Fix a vertical tube with a smooth upper end so that there’s free space around the tube.
Fix a weight in a string and pull the string through the pipe so that the weight is hanging from the top.
Throw the weight so that it starts to circulate around the tube.
Pull from the string so that the radius of the circular motion is decreased.
Now the speed of the weight is increased to maintain the angular momentum around the vertical tube. The extra kinetic energy is supplied from the work done in pulling the string.
Releasing some string will correspondingly reduce the speed of the weight as kinetic energy does work when it pulls more string out of the tube.
The role of the string is here in a similar role with the North-South pressure gradients in case of atmosphere.
I add one more to my own comments where I try to make clearer the relationship between to ways (local based only on forces and global based also on angular momentum or related concepts) of approaching the acceleration of a parcel of air.
The the speed of the parcel can be increased only by a force that has a component along the velocity of the of the parcel. When the parcel is forced closer to the axis of Earth rotation it’s velocity has a component towards the axis (otherwise it would not move closer). For this reason a force that’s directed towards the axis has a small component along the velocity of the parcel. That’s the explanation of the increase of the velocity when expressed in terms of forces acting locally to the parcel.
Picking nits but there’s a tiny typo:
“how that effect, due to the Coriois force, causes”
Enlightening post as always. Thank You!
Fixed, thanks.
I see that climate models doesn`t get circulation right either. Decreasing winds, perhaps as a result of higher latitude warming. I suppose that this will pick up less moisture, and decrease transport of sensible and potential heat. Goes into the discussion of effects of changing water vapor.
Abstract
“Using an observed dataset, we study the changes of surface wind speeds from 1979 to 2016 over the Northern Hemisphere and their impacts on wind power potential. The results show that surface wind speeds were decreasing in the past four decades over most regions in the Northern Hemisphere, including North America, Europe and Asia. In conjunction with decreasing surface wind speeds, the wind power potential at the typical height of a commercial wind turbine was also declining over the past decades for most regions in the Northern Hemisphere. Approximately 30%, 50% and 80% of the stations lost over 30% of the wind power potential since 1979 in North America, Europe and Asia, respectively. In addition, the evaluation of climate models shows their relatively poor ability to simulate long-term temporal trends of surface winds, indicating the need for enhancing the process that can improve the reliability of climate models for wind energy assessments.”
Observed and global climate model based changes in wind power potential over the Northern Hemisphere during 1979–2016
Authors: QunTian, GangHuang, KaimingHu, DevNiyogi, preprint 2018