This post tries to help visualizing, or understanding better, the greenhouse effect.
By the way, if you are new to this subject and think CO2 is an insignificant trace gas, then at least take a look at Part One.
I tried to think of a good analogy, something to bring it to life. But this is why the effect of these invisible trace gases is so difficult to visualize and so counter-intuitive.
The most challenging part is that energy flowing in – shortwave radiation from the sun – passes through these “greenhouse” gases like they don’t exist (although strictly speaking there is a small effect from CO2 in absorption of solar radiation). That’s because solar radiation is almost all in the 0.1-4μm band (see The Sun and Max Planck Agree – Part Two).
But energy flowing out from the earth’s surface is absorbed and re-radiated by these gases because the earth’s radiation is in the >4μm band. Again, you can see these effects more clearly if you take another look at part one.
If we try and find an analogy in everyday life nothing really fits this strange arrangement.
Upwards Longwave Radiation
So let’s try and look at it again and see if starts to make sense. Here is the earth’s longwave energy budget – considering first the energy radiated up:
Of course, the earth’s radiation from the surface depends on the actual temperature. This is the average upwards flux. And it also depends slightly on the factor called “emissivity” but that doesn’t have a big effect.
The value at the top of atmosphere (TOA) is what we measure by satellite – again that is the average for a clear sky. Cloudy skies produce a different (lower) number.
These values alone should be enough to tell us that something significant is happening to the longwave radiation. Where is it going? It is being absorbed and re-radiated. Some upwards – so it continues on its journey to the top of the atmosphere and out into space – and some back downwards to the earth’s surface. This downwards component adds to the shortwave radiation from the sun and helps to increase the surface temperature.
As a result the longwave radiation upwards from the earth’s surface is higher than the upwards value at the top of the atmosphere.
Here’s the measured values by satellite averaged over the whole of June 2009.
Of course, the hotter parts of the globe radiate out more longwave energy.
Downwards Longwave Radiation
But what does it look like at the earth’s surface to an observer looking up – ie the downwards longwave radiation? If there was no greenhouse effect we should, of course, see zero longwave radiation.
Here are some recent measurements:
Note that the wavelengths have been added under “Wavenumber” (that convention of spectrum people) and so the graph runs from longer to shorter wavelength.
This is for a winter atmosphere in Canada.
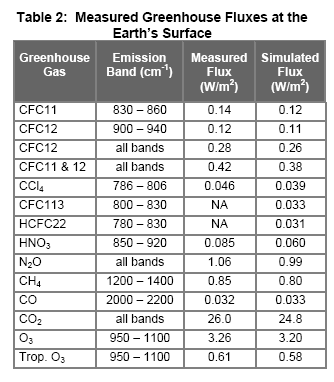
Now what the scientists did was to run a detailed simulation of the expected downwards longwave radiation using the temperature, relative humidity and pressure profiles from radiosondes, as well as a detailed model of the absorption spectra of the various greenhouse gases:
What is interesting is seeing the actual values of longwave radiation at the earth’s surface and the comparison 1-d simulations for that particular profile. (See Part Five for a little more about 1-d simulations of the “radiative transfer equations”). The data and the mathematical model matches very well.
Is that surprising?
It shouldn’t be if you have worked your way through all the posts in this series. Calculating the radiative forcing from CO2 or any other gas is mathematically demanding but well-understood science. (That is a whole different challenge compared with modeling the whole climate 1 year or 10 years from now).
They did the same for a summer profile and reported in that case on the water vapor component:
As an interesting aside, it’s a lot harder to get the data for the downwards flux at the earth’s surface than it is for upwards flux at the top of atmosphere (OLR). Why?
Because a few satellites racing around can measure most of the radiation coming out from the earth. But to get the same coverage of the downwards radiation at the earth’s surface you would need thousands or millions of expensive measuring stations..
Conclusion
Measurements of longwave radiation at the earth’s surface help to visualize the “greenhouse” effect. For people doubting its existence this measured radiation might also help to convince them that it is a real effect!
If there was no “greenhouse” effect, there would be no longwave radiation downwards at the earth’s surface.
Calculations of the longwave radiation due to each gas match quite closely with the measured values. This won’t be surprising to people who have followed through this series. The physics of absorption and re-emission is a subject which has been extremely thoroughly studied for many decades, in fact back into the 19th century.
How climate responds to the “extra radiation” (radiative forcing is the standard term) from increases in some “greenhouse” gases is whole different story.
More in this series –
Part Seven – The Boring Numbers – the values of “radiative forcing” from CO2 for current levels and doubling of CO2.
Part Eight – Saturation – explaining “saturation” in more detail
CO2 Can’t have that Effect Because.. – common “problems” or responses to the theory and evidence presented
AND much more about the downward radiation from the atmosphere – The Amazing Case of “Back-Radiation”, Part Two, and Part Three
Reference
Measurements of the Radiative Surface Forcing of Climate, W.J.F. Evans & E. Puckrin, American Meteorological Society, 18th Conference on Climate Variability and Change (2006)






[…] – Part Six is now published – Visualizing the greenhouse […]
[…] on February 11, 2010 at 8:46 pm | Reply CO2 – An Insignificant Trace Gas? Part Six – Visualization « The Science of Doom […]
Combustion engineers routinely do radiation calculations involving CO2 and H2O. As you say, it’s well worth distinguishing proper science, used in all manner of non-climate contexts, and based on ample experimental measurement performed in labs with no incentive to bias the results, from do-it-yourself tripe, concocted to “explain” climate-specific phenomena. I have in mind particularly the do-it-yourself statistical methods that the tree-ring chumps have used, and the idiocies involved in manipulation of some of the surface temperature measurements.
Is the above Figure 3 implying that water vapor emits longwave rad across a broad spectrum?
Follow up question: how does one measure and attribute radiation from specific elements? Is it purely theoretical or is there real data stating, for example, CFC11 emits at this wavelength?
Fred Nieuwenhuis:
Figure 3 surprised me as well. If you look at the Hitrans plot which you can see at http://spectralcalc.com/spectral_browser – and do a linear plot of H2O between 5-20um there’s just the 5-7um band and then a few lines start to show up from around 15um.
But if you do a log plot you can see that water vapor lines exist all through the longwave range.
Try this URL – I just created the graphic and uploaded it but didn’t place it inside any posts.
So if the water vapor concentration is high you would get absorption at lots of lines through the longwave spectrum. Well, obviously you do because we can see it here..
Fred Nieuwenhuis:
On your follow up question – measurement. Take a gas in a tube, shine radiation through it and measure the absorption at each wavelength. Expensive equipment.
The absorption lines do match the theoretical values as calculated from quantum mechanics.
Measuring absorption of radiation is a very detailed and involved process but reality is further complicated by other effects.
In Part Two I commented:
Fred,
Since I am one of those “spectrum” people, yes, there are extensive wavelength atlases available, for nearly all ranges of the spectrum. They normally list only the major absorption/emission wavelengths, however, as the number of possible lines is practically infinite. They can also be calculated to a degree. However, I am going to point out that the absorption lines ARE the emission lines for any given atom OR molecule. For instance, an SiO2 molecule at the surface WILL NOT absorb at the same lines that CO2, or any other gas for that matter, radiate at. I am afraid that a lot of sincere people have fallen into the trap of believing that all infrared is equivalent, which is the view from a thermodynamics standpoint, but in my line of work it simply isn’t true. The TSI portion of solar spectral irradiance is produced by plasma composed of nearly totally ionised atoms, and the free electrons are capable of radiating a continuous range of wavelengths. Atoms and molecules don’t have this property, or spectroscopy would not be possible.
BTW, ~50% of solar TSI output is in the infrared. I don’t hear any of the IPCC or AGW people ever mentioning this little factoid. This means that you CANNOT tell where any particular range of wavelengths originated, i.e., solar vs. earth. Because of the rescaling used on the graphs those people supply, the relative amount of IR radiation supplied by the sun is obscured.
And those “windows” they are so afraid will become “saturated” don’t really exist, either. They are artifacts of the low resolution of the spectrometers used for IR and the close spacing of molecular absorption lines (compared to atomic A/E lines). So an SiO2 molecules emission from the surface cannot be absorbed by any of the gasses in the atmosphere, either.
And yes, water (liquid, vapor, ice) has many hundreds of thousands, and possibly millions, of absorption/emission lines (not all, but many, are in the IR region).
It’s all a scam.
Have a nice day.
It is not the individual discrete lines that broaden, it is the line profile that broadens, as more discrete lines with lower intensities to the sides of the primary absorption/emission line, which can be produced by either resonance or foreign gas broadening, sometimes referred to as collision induced absorption.
Either way, it can’t heat the surface.
One easy point to pick up from UncertaintyRunAmok:
Nicely misleading via the word “infrared”. Infrared means light with a longer wavelength than the visible spectrum, i.e. greater than 0.7um.
Of course, generally when we talk about solar and the earth’s radiation we use the terms “shortwave” (solar) and “longwave” (terrestrial). They aren’t technical definitions and most textbooks of course make that clear – they are really just shorthand definitions.
And the general loose definition is that shortwave is that radiation less than 4um in wavelength and longwave is that which is greater than 4um in wavelength.
So let’s look at what proportion of solar radiation is “infrared” which is of course a red herring– and how much has a wavelength >4um.
The Sun at 5780K surface temperature emits a total radiance = 2.01E+07 W/m2/sr (20,100,000 W/m2/sr)
Of that, what proportion is infrared?
And what proportion is above 4um?
Infrared; greater than 0.7um = 1.03E+07W/m2/sr or 51% of the total. Our poster is correct, although misleading..
Greater than 4um = 195,840 W/m2/sr or 0.97%, let’s call it 1%
So only 1% of solar radiation is greater than 4um.
What about terrestrial radiation? There are a lot of different surface temperatures, let’s take the average of 15’C or 288K – (which actually is not actually the best average, a subject for another day).
Earth emits a total radiance = 124 W/m2/sr
What proportion of this radiation is below 4um?
Less than 4um = 0.18 W/m2/sr or 0.014%.
So 0.14% of terrestrial radiation is less than 4um.
Hopefully everyone can see that the overlap between terrestrial and solar radiation – longwave and shortwave radiation – is very small.
One commenter on another post asked about the absolute values – because the sun’s radiation is so much greater than the earth, but that’s when measured at the source.
At the earth’s surface the absolute value of solar and terrestrial radiation are similar.
So when radiation is measured as >4um we can be 99% certain it originated from the earth. And when it is less than 4um we can be 99% certain it originated from the sun.
[Footnote for people who like definitions..
The units might be confusing to some people. When the radiation has units of Watts per square meter per “steradian” you multiply by pi (3.14) to turn it into Watts per square meter. Steradian is solid angle]
Interesting ideas.
“When the radiation has units of Watts per square meter per “steradian” you multiply by pi (3.14) to turn it into Watts per square meter. Steradian is solid angle]”
I don’t think so… Basically, a surface differential area in spherical coordinates is given by
dA = r^2*cos(theta)*dtheta*dphi
where r is the radius of the sphere, theta is latitudinal angle in the range [-pi/2,pi/2], and phi is longitudinal angle in the range [-pi,pi]. The term r^2 has units of meters^2, obviously, and dtheta*dphi has units of steradians (square units of angle).
Thus, if you have a value X in W/m^2/steradian, and you want to get the total Wattage, you would integrate X*dA, which would have units of Watts. If you want to look at a small area which is locally flat, you shouldn’t scale the value by anything at all, just drop the “steradian” nomenclature.
Bart
Thanks for the comment. Hopefully you can save me from digging out the books on volume integrals, stuff I would rather forget.
But every book on atmospheric physics that digs deep shows this relationship. It’s also there, unexplained on spectralcalc.com – a number I was just looking up:
Radiant emmittance: 477.962 W/m2
Radiance: 152.14 W/m2/sr
Can you shed any light on it, or do I need to dig some more books out?
Very strange. I would at least expect a value of 4*pi since, if X is a constant, the total wattage would be X*4*pi*r^2. The units of X*4*pi would be W/m^2, but it would be meters of radius at the surface element squared rather than area meters squared.
That’s one small point to make: If 390 is the average wattage density over the Earth’s surface going up, at the top of the atmosphere, then without any absorption along the way, I would expect to see 390*(Re/(Re+h))^2 W/m^2 where “Re” is the Earth’s radius and “h” is the altitude at which the outgoing radiation is measured. So, if h is, say, 200 km and Re = 6378 km, I would expect to see 367 W/m^2. At about 1300 km, I would expect 267 W/m^2, but I assume that is way higher than what is meant by “top of the atmosphere.”
This is why I prefaced my comment with a vague “don’t think so…” Because they may be using a convention with which I am not familiar.
Maybe it’s meters of diameter? That is, X*4*pi*r^2 = X*4*pi*(D/2)^2 = X*pi*D^2? It would seem an odd way to do things.
I’m just looking at it again, here the wikipedia explanation at http://en.wikipedia.org/wiki/Stefan-Boltzmann_law
“The quantity [equation I can’t paste] is the power radiated by a surface of area A through a solid angle dΩ in the frequency range v->v+dv .”
“To derive the Stefan–Boltzmann law, we must integrate Ω over the half-sphere and integrate ν from 0 to ∞. Furthermore, because black bodies are Lambertian (i.e. they obey Lambert’s cosine law), the intensity observed along the sphere will be the actual intensity times the cosine of the zenith angle φ, and in spherical coordinates, dΩ = sin(φ) dφ dθ.”
So in the end, paraphrasing, P/A is pi x the original thing.
Does that make sense (need to review link of course) for a volume integral result?
Emm… Well, I did go to Wikipedia to look up the difference between radiant emittance and radiance, and got directed to this page. Of “radiance”, it says
So, I have a feeling that may be the answer. All these quantities are normalized to a diameter of the Earth squared (projected source area, the projection being to the surface of the Earth), with all the scaling for different distances from the center of the Earth already accounted for. So, 390 W/m^2 means that, if you multiply that by the diameter of the Earth squared, you will get the total output in Watts.
I don’t know if this is it, but it seems plausible, if a little convoluted.
Not being a volume integral kind of person I’m glad I don’t have to work through many hours of maths to make sure it’s correct.
It vaguely – but not rigorously mathematically – makes sense to me. Intensity in W/m^2/sr should be lower than W/m^2 because you’ve got to integrate over a solid angle. But it can’t be as much as 4.pi.r^2 because it comes up only from the surface of the earth not radiated in all directions.
[…] The background is the series CO2 – An Insignificant Trace Gas? and especially the last post – which maybe should have come earlier! – CO2 – An Insignificant Trace Gas? Part 6 – Visualization […]
“But it can’t be as much as 4.pi.r^2 because it comes up only from the surface of the earth not radiated in all directions.”
But, it is radiated in all directions if you integrate about the entire Earth. My explanation of why it is pi instead of 4*pi is, I think, because the convention is to use diameter of the Earth instead of radius, so you get 4*pi*r^2=pi*D^2, and the values are normalized to D^2.
Science,
“At the earth’s surface the absolute value of solar and terrestrial radiation are similar.”
I take this to mean that the > 4um radiation at the surface of the earth are about the same between earth and solar?
If so, then,
“So when radiation is measured as >4um we can be 99% certain it originated from the earth. And when it is less than 4um we can be 99% certain it originated from the sun.”
= Uh? Percentages would have nothing to do with it. If the solar LW (> 4um) radiation at the top of the atmosphere is of the same order of magnitude as the earths LW emissions, then any measurement of radiation emissions (looking either up or down) is going to be ambiguous as to source.
(reposting the comment, a second time because some characters were missing first time.. and the second time I typed too fast and didn’t read..)
Kevoka:
Maybe I didn’t explain it very well.
Solar Radiation has 99% of its total energy less than 4um
Terrestrial Radiation has 99.9% of its total energy greater than 4um
The total energy (across ALL wavelengths) of solar and terrestrial is similar.
Therefore, total solar energy greater than 4um is around 1% of the value of the terrestrial radiation.
So if we measure radiation of greater than 4um we can be 99% sure it was not radiated from the sun.
(Or course, as one commenter on another blog kept reminding me as though it changed the situation – the “original” source of all energy is the sun).
Does this clear things up?
You can also see the graphic posted in: https://scienceofdoom.com/2010/02/15/co2-cant-have-that-effect-because/
This shows graphically how little overlap there is between solar and terrestrial radiation.
The problem with the graphic you referenced and is posted a gazillion other places, is the scale factor applied to the solar radiation. So it appears to be very misleading – we lose the true magnitude of the LW tail (greater than 4 um) that solar radiation has.
From Uncertaintyrunamok:
“Because of the rescaling used on the graphs those people supply, the relative amount of IR radiation supplied by the sun is obscured.”
Let me try to rephrase what you are saying (to make sure I am getting it) when using percentages:
~1% of the solar radiation received at the earths surface is LW greater than 4um. The total average solar energy reaching the earths surface is 342 W/m2, so 1% of 342 W/m2 is 3.42 W/m2.
Therefore, when measuring LW > 4um, looking up from the earths surface, 3.42 W/m2 will be from the sun and the remaining 321.58 W/m2 (324 W/m2 – 3.42 W/m2) is from GHG’s. Or 99% will be from GHG’s.
Correction the 342 W/m2 should be at the at the TOA, not the earths surface (according to Kiehl and Trenberth)
Hi Kevoka,
I’m glad to see you working through the maths to make sense of it.
Your analysis (of what I am explaining) is in the right direction.
The first point above “it appears to be misleading..” – not really because the sun – at source – has a much higher total energy than the earth. But at the earth the energy received from the sun is comparable to the energy radiated from the earth (of course, otherwise the earth would heat up very rapidly!).
Anyhow, I think you have already seen that from your maths analysis.
And you spotted that 342W/m^2 is TOA.
The average solar radiation absorbed by the atmosphere and the earth’s surface is 239W/m^2.
So – without getting into more detail (but we will later) at the earth’s surface we can reasonably say that around 2-3W/m^2 of downward radiation greater than 4um is solar.
And everything else we measure of downward radiation greater than 4um is re-emitted radiation from the atmosphere – from gases like CO2, methane, O3. (Or you need a theory to explain where it comes from).
And if we want to look at radiation greater than 13um (for the important CO2 band) then 0.03% of solar radiation is greater than 13um.
So if we find downward radiation greater than 13um we could say that perhaps 0.07W/m^2 was from the sun.
At this point we would also note that this tiny portion of solar radiation would have experienced some CO2 absorption and re-emission on the way in.
However, you can see that those numbers are really very low, and not really measurable.
Kevoka
I promised some more detail..
The average solar radiation is 342W/m^2 at TOA.
The average solar radiation absorbed by the earth’s climate system is 239W/m^2.
The average absorbed by the atmosphere is about 67W/m^2 and by the ground about 168W/m^2. (How much absorbed by the atmosphere is a subject of debate, see note at end)
Now if we think about averages we get a sense of proportion and this is very useful – in fact, it is the starting point.
Now if we look at one specific time in one specific location we will get quite different numbers.
Solar radiation incoming at night – zero
Solar radiation on a clear day when the sun is directly overhead – not certain.. but’s let’s do a quick calculation.
The maximum possible is 1367W/m^2 – but usually just under 30% is reflected by clouds, aerosols and the atmosphere. This leaves 950-1,000 W/m^2. Then around 30% is absorbed by the atmosphere so that leaves 660 – 700 W/m^2.
That’s with the sun directly overhead.
Of course, on a winter day in Canada this would not be the case. It’s “simple” trigonometry to work it out..
As you can see the numbers vary but still, at most we might see 7W/m^2 greater than 4um in wavelength, and 0.21 W/m^2 greater than 13um.
Note on atmospheric absorption – From Kiehl & Trenberth (1997) on atmospheric absorption: “Until these discrepancies are resolved, we should remain open to the possibility that the atmospheric absorption may be greater than the traditional estimates.”
[…] downwards radiation, which we can measure – see Part Six – Visualization, is what increases the surface […]
[…] those who want to see a better experiment that compared real and modeled conditions, take a look at Part Six – Visualization where actual measurements of humidity and temperature through the atmosphere were taken, the […]
[…] in CO2 – An Insignificant Trace Gas? Part Six – Visualization I said: I tried to think of a good analogy, something to bring it to […]
[…] is a lot greater than that leaving through the top of atmosphere. For more on this take a look at CO2 – An Insignificant Trace Gas? – Part Six – Visualization and the followup CO2 Can’t Have That Effect Because.. as well as the start of the series on […]
Here is the famous paper that confirms to me that CO2 is cooling the atmosphere by re-radiating sunshine (12 hours per day).
http://www.iop.org/EJ/article/0004-637X/644/1/551/64090.web.pdf?request-id=76e1a830-4451-4c80-aa58-4728c1d646ec
Note that they measured this radiation as it bounced back to earth from the moon. Follow the green line in fig. 6, bottom . Note that it already starts at 1.2 um, then one peak at 1.4 um, then various peaks at 1.6 um and 3 big peaks at 2 um.
This paper here shows that there is absorption of CO2 at between 0.21 and 0.19 um (close to 202 nm) (UV):
Click to access DUV-CO2.pdf
There are other papers that I can look for again that will show that there are also absorptions of CO2 at between 0.18 and 0.135 um and between 0.125 and 0.12 um.
We already know from normal IR that CO2 has big absorption between 4 and 5 um.
So, to sum it up, we know that CO2 has absorption in the 14-15 um range causing some warming (by re-radiating earthshine, 24 hours per day) but as shown and proved above it also has a number of absorptions in the 0-5 um range causing cooling (by re-radiating sunshine). This cooling happens at all levels where the sunshine hits on the carbon dioxide same as the earthshine. The way from the bottom to the top is the same as from top to the bottom. So, my question is: how much cooling and how much warming is caused by the CO2? How was the experiment done to determine this and where are the test results? If it has not been done, why don’t we just sue the oil companies to do this research? (I am afraid that simple heat retention testing will not work here, we have to use real sunshine and real earthshine to determine the effect in W/m3 [0.04%]CO2/m2/24hours)
I am going to state it here quite categorically that if no one has got these results then how do we know for sure that CO2 is a greenhouse gas?, i.e that the net effect of CO2 is warming rather than cooling?
henry Pool:
It’s a good question. I have seen some papers which discuss the absorption by CO2 of solar radiation – but not the paper you linked. I will have a read. Watch this space for comment.
[…] effect. See the CO2 – An Insignificant Trace Gas? series, and especially Part Six – Visualization and CO2 Can’t Have that Effect Because.. if you don’t understand or agree with these […]
I get a lot of blah ,blah, blah, but no results of tests.
I am sorry, but where are the results of the tests?
How much cooling and how much warming is caused by the CO2?
henry Pool:
And yet there are results of tests here.
Downward longwave radiation from CO2, expressed as W/m^2.
The downward longwave radiation would be the warming. But how much cooling is caused by the CO2 ?
henry Pool:
CO2 absorbs at 2.7 and 4.3um. There is also absorption by CH4 and NO2. The line strengths are not so strong here.
Looking at the graphs in W.D.Collins et al, Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the IPCC AR4 (2006) the effect of CO2 absorbing solar radiation is less by more than a factor of 10 compared with CO2 absorbing longwave radiation.
The other important point to consider is that solar radiation absorbed by the atmosphere rather than the surface is also contributing energy to the climate system, albeit from a different place.
In due course I will post an article with these graphs.
You ignore my initial posting (March 17). There are many more absorptions; as shown, most recently they also discovered there are absorptions of CO2 in the UV region.
We need some test results from actual experiments, not estimates (where they only look at the conventional wisdom of CO2 only absorbing in the 2 and 4 um region.)
The other point you make is simply not true and/or also not proven. There is only so much energy that can be taken up by a molecule. My theory is that at the absorption places in the spectra the molecule sort of acts as a mirror, after it accepts one or more photons. Hence the fact that ozone blocks so much UV and the fact that we are able to measure the radiation from CO2 as it bounces back from the moon. Which proves that CO2 must be cooling the atmosphere – and it appears from your documents that nobody really knows how much – true or not true?
henry Pool
You can see response on some of these questions at:
CO2 in the Solar Spectrum
Feel free to comment there, and I will separately post on your other comment (hopefully in the next week or so) on How much work can one molecule do?
Science of doom, you say:
“For example, the solar radiation between 2 – 4μm is only 5% of the solar radiation, so any absorption by CO2 will be quite limited”.
According to various sources that I consulted the amount of energy coming onto earth is 46-47% from the infra red region of the sun. So this presentation is flawed from the beginning.
For example, when I stand here in the African sun, in the summer, I can only allow my skin a few minutes exposure, then I have to look for cover. The radiation on my skin gets too hot. But, if during the same day, the humidity rises, that same direct heat from the skin becomes less. You can feel this. This is the reason why the temperature on the coast (where humidity is higher) is always a few degrees less than more inland. So carbon dioxide, like water vapor does exactly the same thing….. it cools the atmosphere. My question was and is: by how much?
There is also no mention in your graphs of all the absorptions of CO2 including those in the UV region which have only been discovered lately.
You also say : “We are only eyeballing the two graphs anyway”.
When there is so much at stake here.?
You cannot do that.You have to come with an experiment and with actual test results. in W/m3 (0.04%-0.06% CO2)/m2/24 hours cooling and warming. We know that Svante Arhenius formula was wrong, so where is the right formula? Don’t come with stories that really is only a believe system. We have to have formulas like Newton made, real science that everyone can test and rely on.
No eyeballing.
Sigh! This site has the data that shows the key problem with one dimensional atmospheric models. (Figures 1 and 3) But then goes on to totally ignore the information there.
Near the poles, CO2 is the primary greenhouse gas (GHG). More CO2 means more solar radiation trapped above the Arctic and Anarctic Circles. But most solar radiation hitting Earth is in the lower latitudes, where water is the dominant GHG. So now you need a model which includes water vapor. Worse, since water evaporates (and sublimates directly from snow and ice), then condenses and freezes in the atmosphere, your model has to get this right. (Water condensing in the atmosphere releases heat which was absorbed at the Earth’s surface during evaporation. So some of the long wave radiation (LWR) from the water vapor bypasses the lower atmosphere.
Worse, in clouds atmospheric CO2 is absorbed into water droplets–not a big effect on the total energy and GHG budget. But it reduces the rate of evaporation within clouds. In other words, atmospheric CO2 results in more net rainfall, thereby reducing the amount of water vapor acting as a GHG. Not to mention the effects of clouds on the whole energy budget. (High albedo so lots of sunlight gets reflected into space, and also radiation from the Earth gets reflected back downwards.) This is why clear nights result in rapid cooling in the temperate zones, while fog and clouds can reduce the nighttime cooling to almost zero. (I won’t go into the effects of rainfall within the clouds, but just point out, that even when it is not raining at the Earth’s surface, condensation and evaporation within the clouds maintains a huge temperature difference between the cloud tops and bottoms.)
So what is the net effect of all this? I don’t know. At the poles, CO2 causes warming. At the Equator, it causes cooling. At about 40 degrees North or South, the two effects cancel out. But a good three dimensional model of the entire atmosphere is supercomputer territory. The various weather services run these models every day–but they are chaotic and running a decent model for a week of simulated time takes several hours of real time. Running one model for 100 simulated years would give one answer on global warming, running the same model starting with the next day’s weather will give you a (very) different answer on global temperatures a hundred years from now.
So what is missing? Very good question. Climate does not vary wildly on a century to century basis, but local temperatures do vary wildly–sometimes more than 100 degrees (Fahrenheit) in a day. There must be some additional (slow) contributors to climate that act to moderate temperature swings. (I’m not ignoring the heat stored in the oceans and land masses. That is already built into the weather models.)
By the way, I think that CO2 levels should be lowered. They are not high when you look at climate over millions of years. But they are now higher than they have ever been since humans evolved. We are not designed to handle these CO2 levels even if the Earth is and many other species are.
What’s the point of this post? This post tries to help visualizing, or understanding better, the greenhouse effect.
That’s because many people read through the other posts which explain the science and some of the maths and have conceptual difficulties.
Take a look at Part One through to Part Seven
Then, if it’s not too tiresome for you – i.e., if you have a contribution to make or a question to ask, go right ahead.
A point at the center of a sphere sees 2*pi steradians of solid angle. A point on a plane only sees a hemisphere so one multiplies by pi not 2 pi. The same applies when observing as long as the altitude is not so high that spherical geometry starts to make a significant difference.
For emission, the maximum emission intensity is set by the Planck equation. At 250 K, the intensity at 2.7 and 4.3 micrometers is a lot less than at 15 micrometers. I have my spreadsheet set to calculate in wavenumbers rather than wavelength so it will be W m-2 cm-1
3704 cm-1 (2.7 um) 1.06 E-06
2326 cm-1 (4.3 um) 7.27 E-04
668 cm-1 (14.97 um) 2.44 E-01
Shorter wavelengths will be even less intense. A lower temperature will be even worse in terms of relative intensity and 220 K is probably a more relevant temperature for CO2 emission. So radiative cooling to space by CO2 at 4.3 and 2.7 um is not significant.
Henry@DeWittPayne
You cannot accept such results unless you did some experiments. In any case, the question was: what is the net effect of the radiative cooling and warming of CO2?
See my post at March 17.
Henry@DeWittPAyne
We have the same problem (of no test results) also with ozone.
Here is a post of mine on that issue:
I was a bit out and I guess I lost you guys on the main argument but I just wanted to make a final point.
a) we know ozone increased, due to the elimination of CFC’s. If we cannot use the antarctic data then perhaps this one?
http://cordis.europa.eu/fetch?CALLER=EN_NEWS&ACTION=D&SESSION=&RCN=31685
That is a 14% rise from 1995 to 2008
b) we know that CO2 rose by 70 ppm or 0.007% during the past 50 years, that is about 6% over the same period 1995 to 2008
These are two gases that would trap radiation from earthshine between 13 and 15 um, causing warming, bottum up.
Both gases have spectra showing absorptions in the 0-5 um range meaning it also causes cooling by deflecting radiation from the sun. Said cooling would probably be more noticable from the top.
Unfortunately we have no test results that would tell us what the net effect is of the radiative cooling and warming of each gas. My best guess on that would be that the ozone is cooling slightly more than warming and that CO2 is slightly warming more than cooling. Taken together that would mean that the net effect of the increase in these trace gases could be close to to zero.
I admit that this is just a rough estimate – but what do you expect from me if no one did any testing?
That brings us back to where we were. with the climate, ie. the sun, the cloud formation and what drives continuing overcast conditions.
[…] just very computationally expensive, so big computers and plenty of time are required. See Part Six for an example of theory matched up with […]
I have some technical questions. 1) In Figure 3, I can begin to see the outline of a blackbody emission spectrum that would have its peak about 400-600 cm-1 which is about where the max emission would be for 220-260 degK. Am I correct in assuming that the graph shows a series of discrete emission lines that correspond to lines in the absorption spectrum? So, is it correct to assume that gases in the atmosphere emit only at the wavelengths where they absorb and that the intensity of the radiation at that wavelength is given by Boltzmann’s Law? I don’t see how the atmosphere can have a high emissivity (near 1) under these circumstances? 2) What are the units on the vertical axis of Figure 3 and do they somehow translate into W/m^2? 3) When I look at the Figure from Kiehl and Trenberth, how any I supposed to interpret 265 W/m^2 outgoing? Is this the total OLR measured by a detector of a spacecraft? Since this isn’t blackbody radiation, why do I think I see many people converting 265 W/m^2 to an effective blackbody temperature?
Frank:
To the first section – the answer is yes and almost yes. The Stefan-Boltzmann law is the integral of the Planck function across all wavelengths. The Planck function is what you are thinking of, which expresses the intensity of radiation at a given wavelength.
I think I see the question.. well, if each spectral line is represented by the Planck function for the temperature of that gas then we will see an effective blackbody for the average radiating temperature in each wavelength.
Imagine a satellite measurement in an atmosphere where a few narrow spectral lines are the only absorbers for the radiation from the earth’s surface. What we would measure would be the effective radiation of the earth’s surface and yet at a few wavelengths we would measure the effective radiation from the atmosphere. If the atmosphere was colder we would measure a lower radiation intensity at these wavelengths. As more and more spectral lines absorb the radiation from the earth’s surface we are only measuring (out in space) the radiation from each spectral line in the atmosphere – each line at it’s effective temperature.
Take a look at The Earth’s Energy Budget – Part Three
The units are W/(cm^2.sr.cm^-1).
This is the spectral intensity, which is per unit solid angle per unit wavelength. Solid angle, sr = steradians, with the wavelength being expressed in cm^-1 instead of um.
Whereas W/(m^2.um) (or W/(cm^2.um) is the spectral hemispherical emissive power – i.e., the spectral intensity integrated over all directions.
And W/m^2 is the total emissive power = total intensity, which is the spectral hemispherical emissive power integrated over all wavelengths.
The conversion from per unit solid angle to hemispherical power is just to multiply by pi (assuming a diffuse emitter).
So to work out the W/m^2 – for example for the CO2 band – you can visually integrate to get W/m^2 (or print out and get a ruler, divide up, multiply and sum) by taking the average value per cm^-1 and multiply by the approx 150cm^-1 in the CO2 band, this gives you the value expressed per solid angle per cm^2 and then multiply by pi to get the hemispherical power and then by 10,000 (100^2) to get m^2.
Painful and tedious, but such is the world of units.
Yes it is the total OLR measured by satellite, like ERBE or CERES.
And in this case, it is the measured value averaged globally annually in the case of clear sky. The same value across all skies – cloudy and clear – is around 240W/m^2.
It’s an average. The surface of the earth emits quite close to a blackbody (see The Dull Case of Emissivity and Average Temperatures ), while, as you commented earlier, the various gases radiate as a blackbody at their various spectral lines.
See the post The Earth’s Energy Budget – Part Three
Is my confusion with emissivity ended? Looking down from space, an observer either sees: 1) emissions from atmospheric GHG’s – at the wavelengths they absorb/emit and with intensity calculated from oT^4, OR 2) the ground which is effectively a blackbody emitter with an average temperature of 288 degK. Therefore the emissivity of the earth/atmosphere combination is high because one or the other emits at all wavelengths. On the other hand, looking up from the ground at clear sky at night, one sees (in the infrared ignoring the stars) only emission from GHG’s at the wavelengths they absorb. Therefore the emissivity of the atmosphere alone can be very low and will vary with the amount of water vapor. How low is low?
In both cases, the temperature controlling the emission intensity of GHG’s will depend on the concentration/optical depth of the emitter/absorber. In regions where CO2 absorbs strongly, the emission intensity observed from space will be determined by temperature very high in the atmosphere (perhaps even from the warmer altitudes above the tropopause) and the intensity observed from earth will be determined by air temperature near the surface of the earth. For trace GHG’s or weak emission lines, the intensity of emission will be determined by temperature at many altitudes. (Perhaps someday you’ll blog about what fraction of the atmosphere long wavelength radiation can pass through before half of the photons have been absorbed by potent GHG’s.)
This leaves only clouds. Do they radiate like blackbodies?
Frank:
I think you’ve covered it pretty well.
Clouds are a difficult subject, I am just writing the first article on clouds at the moment – Clouds and Water Vapor – watch out for it.
There is a lot of variability depending on the cloud type and thickness. Low thick cloud – almost blackbodies. But many clouds are very thin..
[…] surface of the earth receives more energy than it would without these gases and so it is hotter. See CO2 – An Insignificant Trace Gas? Part Six – Visualization for some more insight into […]
I appreciate the clarification this website provides on the short wave radiation of the sun versus the long wave radiation of earth’s heat and the way that they DON’T overlap. For some reason I had assumed that there was considerable overlap. In fact I think I assumed that Planck’s curve of earth’s radiation completely fit within the sun’s curve.
“If we try and find an analogy in everyday life nothing really fits this strange arrangement.”
I think of it as an electric blanket under a comforter. In the atmosphere energy penetrates through clear skies to the bottom of the atmosphere. In an electric blanket energy penetrates via the electrical cord to the bottom of the comforter. Once beneath the comforter (or at the bottom of the atmosphere) the energy must “work” its way out as heat normally does.
A question that occurs to me. If one works the difference between theoretical temp of -18 and a measured surface temperature of 15, you get 33. If one takes that 33 and plugs it back in to Stefan Boltzman (or some other relevant formula) do you get a figure which helps you calculate sensitivity? How does that work? Is it explored somewhere in on this website? You’ve got 33 degrees to play with and yet I think I’ve read that sensitivity for a doubling of CO2 is less than 1 degree C.
Hank! Study my report
http://www.letterdash.com/HenryP/more-carbon-dioxide-is-ok-ok
HankHenry:
For a more complete explanation of terrestrial vs solar radiation, see The Sun and Max Planck Agree – Part Two
The calculation has to be done using a more comprehensive calculation – “line by line” or using “band models”. See Part Seven
And the method of calculating the “no feedback” temperature change from the “radiative forcing” of more CO2 is by comparing the 2 scenarios and assuming all other things remain equal. And in this case, what increase in surface temperature will cause the outgoing radiation to match the absorbed solar radiation.
scienceofdoom:
Thank you for the feedback. I’ll take time to read and digest. My aim is to understand how CO2 sensitivity is reckoned.
I enjoy your website.
Recently came across your excellent blog site. The graphs comparing CO2 and water vapor are quite revealing, as I did not fully appreciate that water vapor dwarfs CO2 in its effects on long wave radiation absorption. I further understand now how clouds can greatly hinder the escape of heat from the surface of the earth.
Chad says
Henry says
Try to understand that you cannot calculate that which has never been measured first…
http://blogs.24.com/henryp/2011/08/11/the-greenhouse-effect-and-the-principle-of-re-radiation-11-Aug-2011/
Very good blog post. I certainly appreciate this site.
Keep writing!
You write that there should be no downward IR radiation in the absence of greenhouse gases. The sun does however emit in the IR band. Am I correct that you are assuming that all incoming solar IR radiation is absorbed by greenhouse gases so that none reaches the surface?
Ignoring scatter, there would indeed be effectively no downward IR unless you were looking directly at the sun or moon when either or both were above the horizon. When both the sun and moon are below the horizon, there would indeed be nearly zero downward IR. There would a very small contribution from collision induced emission from nitrogen and oxygen at very long wavelength. So strictly speaking, no downward IR is not correct, but it is correct for all practical purposes.
Most of incident solar energy, > 95% or so, is at wavelengths shorter than 5 μm, which is outside the thermal IR band. Most of the energy emitted by a 300K blackbody is at wavelengths longer than 5μm.
Thank you for the replies.
This is a very good series of explanations.
From the author of a blog:
“That’s all there is too it. The peak of the outgoing radiation lands almost perfectly on top of a CO2 spike. Incoming light goes right through the CO2, outgoing light get’s absorbed and re-emitted.”
There are many examples of simplifications. If only 0,1% of suns radiation is in the IR range it is still a lot of energy. Together with short wave radiation (including ultra violet range) it will heat the atmosphere from above. I think it is worth considering, so I understand your question Philip.
nobodysknowledge,
For clear sky conditions, most of the light from the sun does go through to the surface. Short wavelength UV is absorbed in the stratosphere, causing it to warm with altitude. But that doesn’t have much effect on the surface temperature. Clouds, on the other hand, reflect a significant fraction of incident sun light and absorb strongly at wavelengths longer than 700nm, a substantial fraction of the total incident flux. As a result, only about 166 W/m² of the 342 W/m² (averaged over time and area) of incident sunlight reaches the surface. And some of that is reflected rather than absorbed.
nobodysknowledge,
It’s a super-simple article, trying to convey an idea for people who struggle with the concept.
For more, you could read The ‘Greenhouse’ Effect Explained in Simple Terms
And as I say in that article “One of the challenges of writing a short simple explanation is it opens you up to the criticism of having omitted important technical details that you left out in order to keep it short..”
Or the series: Visualizing Atmospheric Radiation
Philip:
The article says something a little different:
By convention, shortwave radiation is radiation less than 4μm and longwave radiation is radiation greater than 4μm.
In other articles I’ve explained why this is a good crossover point for solar vs terrestrial radiation, e.g. The Sun and Max Planck Agree – Part Two.
The sun emits plenty of IR, which by convention is outside the visible range – greater than about 800nm.
Hope this helps clarify things.