We cover some basics in this post. The subject was inspired by one commenter on the blog.
- When we look at a “radiative forcing” what does it mean?
- What immediate and long-term impact does it have on temperature?
- What is the new equilibrium temperature?
Radiative Forcing
The IPCC, drawing on the work of many physicists over the years, states that the radiative forcing from the increase in CO2 to about 380ppm is 1.7 W/m2. You can see how this is all worked out in the series CO2 – An Insignificant Trace Gas.
What is “radiative forcing”? At the top of atmosphere (TOA) there is an effective downward increase in radiation. So more energy reaches the surface than before..
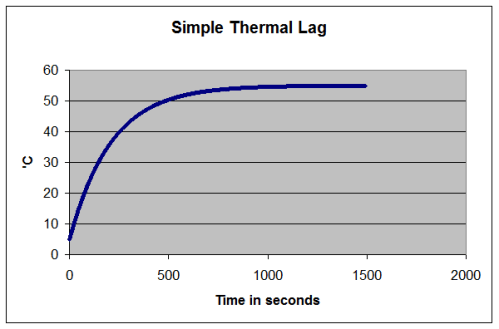
Thermal Lag
If you put very cold water in a pot and heat it on a stove, what happens? Let’s think about the situation if the water doesn’t boil because we don’t apply so much heat..
I used simple concepts here.
T= water temperature and the starting temperature of the water, T (t=0) = 5°C
Air temperature, T1 = 5°C
Energy in per second = constant (=1000W in this example)
Energy out per second = h x (T – T1), where h is just a constant (h=20 in this example)
And the equation for temperature increase is:
Energy per second, Q = mc.ΔT
m = mass, and c= specific heat capacity (how much heat is required to raise 1kg of that material by 1’C) – for water this is 4,200 J kg-1 K-1. I used 1kg.
ΔT is change in temperature (and because we have energy per second the result is change in temperature per second)
The simple and obvious points that we all know are:
- the liquid doesn’t immediately jump to its final temperature
- as the liquid gets closer to its final temperature the rate of temperature rise slows down
- as the temperature of the liquid increases it radiates or conducts or convects more energy out, so there will be a new equilibrium temperature reached
In this case, the heat calculation is by some kind of simple conduction process. And is linearly proportional to the temperature difference between the water and the air.
It’s not a real world case but is fairly close – as always, simplifying helps us focus on the key points.
What might be less obvious until attention is drawn to it (then it is obvious) – the final temperature doesn’t depend on the heat capacity of the liquid. That only affects how long it takes to reach its equilibrium – whatever that equilibrium happens to be.
Heating the World
Suppose we take the radiative forcing of 1.7W/m2 and heat the oceans. The oceans are the major store of the climate system’s heat, around 1000x more energy stored than in the atmosphere. We’ll ignore the melting of ice which is a significant absorber of energy.
Ocean mean depth = 4km (4000m) – the average around the world
Only 70% of the earth’s surface is covered by ocean and we are going to assume that all of the energy goes into the oceans so we need to “scale up” – energy into the oceans = 1.7/0.7 = 2.4 W/m2 going into the oceans.
The density of ocean water is approximately 1000 kg/m3 (it’s actually a little more because of salinity and pressure..)
Each square meter of ocean has a volume of 4000 m3 (thinking about a big vertical column of water), and therefore a mass of 4×106 kg.
Q = mc x dT
Q is energy, m is mass, c is specific heat capacity = 4.2 kJ kg-1 K-1,
dT = change in temperature
We have energy per second (W/m2), so change in temperature per second, dT = Q/mc
dT per second = 2.4 / (4×106 x 4.2×103)
= 1.4 x10-10 °C/second
dT per year = 0.004 °C/yr
That’s really small! It would take 250 years to heat the oceans by 1°C..
Let’s suppose – more realistically – that only the top “well-mixed” 100m of ocean receives this heat, so we would get (just scaling by 4000m/100m):
dT per year = 0.18 ‘C per year.
An interesting result, which of course, ignores the increase in heat lost due to increased radiation, and ignores the heat lost to the lower part of the ocean through conduction.
If we took this result and plotted it on a graph the temperatures would just keep going up!
Calculating the new Equilibrium Temperature
The climate is slightly complicated. How do we work out the new equilibrium temperature?
Do we think about the heat lost from the surface of the oceans into the atmosphere through conduction, convection and radiation? Then what happens to it in the atmosphere? Sounds tricky..
Fortunately, we can take a very simple view of planet earth and say energy in = energy out. This is the “billiard ball” model of the climate, and you can see it explained in CO2 – An Insignificant Trace Gas – Part One and subsequent posts.
What this great and simple model lets us do is compare energy in and out at the top of atmosphere (TOA). Which is why “radiative forcing” from CO2 is “published” at TOA. It helps us get the big picture.
Energy radiated from a body per unit area per second is proportional to T4, where T is temperature in Kelvin (absolute temperature). Energy radiated from the earth has to be balanced by energy we absorb from the sun.
This lets us do a quick comparison, using some approximate numbers.
Energy absorbed from the sun, averaged over the surface of the earth, we’ll call it Pold = 239 W/m2.
Surface temperature, we’ll call it Told = 15°C = 288K
If we add 1.7W/m2 at TOA what does this do to temperature? Well, we can simply divide the old and new values, making the equation slightly easier..
(Tnew/Told)4 =Pnew/Pold
So Tnew=288 x (239+1.7/239)1/4
Therefore, Tnew = 288.5K or 15.5°C – a rise of 0.5°C
I don’t want to claim this represents some kind of complete answer, but just for some element of completeness, if we redo the calculation with the radiative forcing for all of the “greenhouse” gases, excluding water vapor, we have a radiative forcing of 2.4W/m2.
Tnew = 288.7 or 15.7°C – a rise of 0.7°C.
(Note for the purists, I believe the only way to actually calculate the old and new surface temperature is using the complete radiative transfer equations, but the results aren’t so different)
Conclusion
The aim of this post is to clarify a few basics, and in the process we looked at how quickly the oceans might warm as a result of increased radiative forcing from CO2.
It does demonstrate that depending on how well-mixed the oceans are, the warming can be extremely slow (250 years for 1°C rise) or very quick (5 years for 1°C rise).
So from the information presented so far, temperatures we currently experience at the surface might be the new equilibrium from increased CO2, or a long way from it – this post doesn’t address that huge question! Or any feedbacks.
What we ignored in the calculation of temperature rise was the increased energy lost as the temperature rose – which would slow the rise down (like the heated water in the graph). But at least it’s possible to get a starting point.
We can also see a rudimentary calculation of the final increase in temperature – the new equilibrium – as a result of this forcing (we are ignoring any negative or positive feedbacks).
And the new equilibrium doesn’t depend on the thermal lag of the oceans.
Of course, calculations of feedback effects in the real climate might find thermal lag parameters to be extremely important.


Thanks for the post, Steve.
You mentioned the melting ice as a significant heat absorber. What would happen if it were all (or mostly) gone? I suppose the warming would be accelerated somewhat.
I never found this subject in the projections. Would you recommend some paper for further reading?
I assume I am right in saying that the ocean does not delay the temperature rise with respect to energy input?
– when energy increases ocean temp will immediately begin to increase. And vice versa.
So if increase in TSI is the source then the ocean will increase in temperature until TSI begins to fall when the increase in ocean temp will cease immediately. i.e. the ocean temp is not a delayed and smoothed copy of TSI.
Another though. The 1st few metres of ocean respond within a few weeks to increase in solar radiation. Winter sea temps are lower than summer. How deep does this change go? How well does the sea mix these suface layers with lower ones?
“The 1st few metres of ocean respond within a few weeks to increase in solar radiation. Winter sea temps are lower than summer. How deep does this change go? How well does the sea mix these suface layers with lower ones?”
This pdf from NOAA has a graph showing model results for ocean temps over the decades. The depth profile gives you some idea of the slow mixing that occurs.
http://www.gfdl.noaa.gov/cms-filesystem-action/user_files/kd/pdf/gfdlhighlight_vol1n4.pdf
Alexandre:
That’s an interesting question. The main result if all the ice goes is that the albedo is reduced.
Albedo of fresh snow is 0.8 and of ice is around 0.5-0.7.
That means 50-80% of solar energy is reflected.
If it’s ocean the albedo is 0.03 with the sun directly overhead through to 0.09 with the sun close to the horizon. So less than 10% of solar energy is reflected.
So the change in energy absorbed by the climate system would be significant.
If we talk about melting sea ice compared with heating the oceans we are still talking about absorbing energy into the climate system.
But it doesn’t immediately raise the temperature while the ice is melting. However, once there is no sea ice the energy absorbed would go into increasing the water temperature.
(Sea ice also prevents heat being radiated out from that portion of the ocean underneath (because it is a good insulator) – but I’m not sure how much different that really makes because the ice and the water underneath are at similar temperatures and the ice will still radiate).
I don’t know of any papers – although there will be 100s about the various Arctic measurements and projections.
It will be incorporated into all the GCMs as it’s straightforward.
The subject of ice melt process though is a lot more complex and subject to lots of uncertainties.
thefordprefect:
Correct.
Almost. If TSI begins to fall then you can easily have the situation where the new TSI value will still have a heating effect. Why?
Let’s suppose ocean temp is 15’C and TSI increases X%. The ultimate equilibrium temperature would be 16’C. After 1 year the ocean is still at 15.1’C (because of thermal lag) and TSI starts decreasing over 10 years to return to its old value.
For some time ocean temperatures will still increase. Until the time when the equilibrium temperature is below the actual temperature and at that time it will start to fall.
Thinking only about this as a simple system is just like many control processes in engineering where the output is a damped and lagged version of the input or source.
It is the top few meters, mostly mixed due to the wind and waves. Below this the next 100m then has a steady drop in temperature down to the rest of the ocean which has a fairly constant temperature with depth.
Because higher temperature waters are less dense, they float to the top so the oceans are mostly quite well “stratified”. Unlike the atmosphere where the heating of the lower atmosphere by the sun causes it to expand and rise, causing convective turbulence.
The actual ocean currents are very complex. Take a look at the article on the thermohaline currents – Predictability? With a pinch of salt please..
Hi new to your blog came over from WUWT from you answer to my question on the article in American Thinker.
Thank you for your answer it was most informative and congratulations on a most enjoyable and enlightening blog.
As a very unscientific layperson it is nice to see in depth articles and also well informed comments.
Common sense seemed to tell me that the little CO2 put in the atmosphere by man could not have the catastrophic affect attributed to it. But my common sense has not always been correct in my own field of commerce, where the variables enabled by circumstances and human input has made it just an educated guess.
scienceofdoom,
What is the impact of the low angels of sunlight hitting the polar regions in the summer period?
If I recall, the angel of incidence greatly influences the ability of the light to penertrate water. The lower the angel, the less effectively the light penetrates.
Is this correct?
scienceofdoom,
Please excuse my redundant question. I see your answer.
sorry about that.
Peter Whale … this …
has always puzzled me, because common sense then would lead one to believe that a tiny amount of sarin in the atmosphere couldn’t be harmful, or that a small amount of LSD in your body couldn’t have a profound affect on you.
Yet, people don’t make common sense arguments of this sort. People accept that poisons or drugs can be extremely effective in small quantities.
Also, man puts HUGE amounts of CO2 in the air. It is only the *concentration* that is low.
28,431,741,000 metric tons of CO2 emissions per year doesn’t seem like a small number to me.
HI dhogaza, Thanks for the reply, as I said I am a lay person in scientific terms. When I looked at the amount of C02 put in the air by natural means and the amount put in by human activity it seemed too small to cause the catastrophic climate change attributed to it. When I look at the potential for C02 to be put in the atmosphere by natural climate change such as a return to the MWP surely the natural process would be able to cope with it once again.
But then people who understand the different principles involved know the difference.
Oh, wait, we must panic, there is an order of magnitude (or there abouts) more H2O in the atmosphere than CO2, and the human produced proportion of CO2 in the atmosphere is only a fraction of the total CO2 in the atmosphere, and it doesn’t sound small to you, by which I assume you mean it is bad and panic worthy.
PANIC.
Well, maybe I won’t. Instead I will try to understand the interactions and the atmospheric transport mechanisms and how the planet must have coped in the past with atmospheric CO2 levels quite a number of doublings larger than they are currently.
dhogaza:
Sorry, recovered your comment from the spam queue. You’re not blacklisted, the spam filter is just over-eager. In this case it knows that many spam machines promote “drugs”..
Richard Sharpe:
Apologies on behalf of my over-eager spam filter. Again the word “drug” attracts it..
I think it’s a little more complicated than you suggest. (As is usual in climate science!)
Here’s some data.
http://www.cefas.co.uk/data/sea-temperature-and-salinity-trends/presentation-of-results/station-26-newlyn.aspx
The surface of the sea can change temperature relatively quickly. And it is the very top layer that interacts most directly with the atmosphere (and any greenhouse changes), what with water being pretty opaque to IR. The lag in the peak is about two months after the solar peak.
The longer-term lag is not due to thermal inertia as such, but I think to slow mixing processes between the surface and deeper layers that operate on a range of time-scales, that have even been reported to be affected by things like jellyfish swimming up and down and stirring the layers up. There are lots of confounding factors that could also lead to trends.
Some more discussion on the exchange of heat between ocean and atmosphere would be interesting. Visible light penetrates deeply, but IR back-radiation from the sky penetrates only the sub-millimetre thick skin. Evaporation is presumably important, and I am curious about the varying effects of conduction, diffusion, wave action, convection, equatorial-polar currents, and salinity on the flow of heat below the surface.
(And while it’s a bit off-topic for this post, some of the commenters above may be interested in knowing about the solubility pump.)
Excellent blog! Cheers.
Nullius in Verba
It’s a basic post to help people understand the basics, which is what it says at the start. Most times we don’t cover the complete theory of everything in one post.
That is thermal inertia.
If you add energy to a system with tiny heat capacity it heats up in very short time period. If you add energy to a system with very large heat capacity – like the oceans – then it takes a long time to heat up.
Q = mc x dT
I think it may be a question of identifying the essential, dominant factor at play.
The heat capacity of solid rock is not that much less than that of water, and there’s a lot more of it, and hence the thermal inertia of land is surely no less than that of the oceans?
The difference between sea and land is not that the oceans have more thermal inertia, it is something else. Not to do with the capacity but with the flow.
The bottom of your pan of water is alternately warmed and cooled, above and below it’s current temperature. The temperature changes, with a relatively short time lag. Is it obvious that if the warm and cool points are increased slightly, by an amount far less than their range, that it will take a much longer time than the above-mentioned lag for it to settle to the new conditions?
And how much faster or slower is land?
But I’m pleased to hear that this is not your last word on the subject. I have met all too many people who seem to believe that this simple explanation is all there is to it.
Hi,
Is Newton’s Law of Cooling a good representation of how SST’s respond to a forcing. I know this model works well in small scale experiments, but does it scale up to oceanic surface sizes? Note that, if possible, I’m interested in the two dimensional surface and not the 3D volume.
The reason I ask is because I’m developing my own sniff test for the temperature commitment (aka, “heat in the pipeline”, “unrealized temperature increase”) question. In Newton’s law, the term “e^(rt)” (where r<0), is the unrealized change factor. My challenge was to estimate "r". I choose to do so using seasonal lags in SST using the methods described here:
http://www.math.montana.edu/frankw//ccp/cases/newton/overview.htm
My method was to calculate the seasonal lag in mid-latitude (40-50 degrees lat. N and S) SST's in both hemispheres. The maximum lag I could find was less than 80 days. At 80 days, r = -1.23 on a yearly basis and e^r = .29. This means that given a forcing, about 70% is recognized in the first year, 70% of what remains is recognized the following year, and so on. By year 4, over 99% of the forcing is recognized. Here's my spreadsheet:
https://spreadsheets.google.com/ccc?key=0AiP3g3LokjjZdDg3UDNPR21QRk9TUmVZZWlORU5uU3c&hl=en&authkey=CL-ow8wM
I chose mid-latitude SST's because daily clear-sky solar irradiance at 45 degrees follows an almost perfect sinusoidal yearly cycle, whereas the tropics and polar regions do not. Here's a spreadsheet of daily irradiance at 45N and 45S vs. a sine wave:
https://spreadsheets.google.com/ccc?key=0AiP3g3LokjjZdFo3Mk9TWnV0ejVJbHZpR2hoajIyV1E&hl=en&authkey=CJ6XwOwF
I also calculated the lags for a number of mid-latitude locations and summarized the results here:
https://spreadsheets.google.com/ccc?key=0AiP3g3LokjjZdG8zdW5aZ2xTbWN5Zmd4ZWdMU0ZJM3c&hl=en&authkey=CM-G48cI
It was clear from this exercise that the lags were shortest for those locations furthest downwind from a major body of water. Given that there are ocean effects that lengthen land lags, it might also be reasonable to assume that land effects shorten ocean lags. Also note that the ratio between the actual temperature amplitude and model amplitude was increased for the inland locations. I will speculate, amongst other factors, that real sky irradiance dampened maritime amplitudes.
To compensate for land effects on SST's, I assumed that the amplitudes were correct for all locations but the actual/model amplitude ratio was only correct for the city with the shortest lag. From this, I adjusted the relative amplitudes and calculated new lags and r values. The maximum lag calculated in this exercise was ~87 days with r=-0.44 and 10.4 years to realize 99% of the forcing. I'm not sure of the merits of this technique, but I'm guessing that if anything, it over compensates for land effects on SST's.
So, in summary, I would like to know if Newton's Law is a good approximation of SST response to a forcing? Is there any merit to my methods? I realize that this posting is old and that the chances I will get a response can be described as a limit approaching zero ;), but any feedback would be great.
Cheers,
AJ
AJ:
It seems unlikely, but maybe someone has demonstrated that it somehow is a good empirical model of the oceans.
Terms to consider:
1. Direct solar heating via radiation, generally proportional to cosine of the zenith angle, plus some model for the absorbers of solar radiation in that path.
2. Radiative heating from the atmosphere. See The Amazing Case of Back Radiation.
2. Radiative cooling = 5.67×10^-8 x T^4.
3. Convective cooling (Newton’s law of cooling I think) which is generally of the form Q=h(Ta-Ts), where Ta is the air temp, Ts is the sea team and h is just about anything depending on wind speed and other factors (convection is a tough one).
4. Latent heat removal via evaporation. This depends on the relative humidity of the air that finds itself above the ocean surface, along with the actual air temp and the non-linear Clausius-Clapeyron function – see Clouds and Water Vapor – Part Two.
Thanks SoD!
If I were attempting to refute Newton’s model, I would simply take the values I calculated for the yearly cycle and apply them to a daily cycle. So take r=-1.23 on a yearly basis and divide by 365 to get the daily equivalent of r=-0.0034. Given this low value, I suspect the model would predict a lag approaching 6hrs and a temperature amplitude of next to zero. I would be surprised if this were the case.
On this basis I would agree that, over time, conduction becomes more significant relative to radiation.
It might be interesting to examine seasonal lags and amplitude changes at different ocean depths. Argo data might be able to provide this data and it could be useful in GCM verification.
It might also be interesting to examine lags and amplitudes over longer periods such as solar cycles and glacial cycles, but I doubt if a reliable signal could be detected out of the noise.
Thanks again,
AJ
“What is “radiative forcing”? At the top of atmosphere (TOA) ths ere is an effective downward increase in radiation. So more energy reaches the surface than before..”
I have been trying to find an answer to what a “forcing” is. Who better to answer it than the communicator of climate science physics.
From my standpoint, in physics you either have a force or you don´t have a force. A force requires energy and it either acts on a system or the system acts on its surroundings. The energy has to be accounted for, it will be part of the total energy in the process.
Now to the question, a “forcing” increase the energy inside the system, it acts like a force. Where does that energy come from?
How can energy in the system increase by a “forcing” when the “forcing” is not work or added energy?
I might have missed something, but this “forcing” seems like another exclusive greenhouse concept. From my very dry and realistic viewpoint I am reluctant to use theories that are built on new and unique concepts of unmeasurable forces, like for example dark matter, because they explain things by using made up, unproven physics that is nothing more than guessing or fantasy.
Are there any proven theories confirmed by experimental and/or observational evidence beside the greenhouse that use the “forcing”? Or is it another of the unique and comfortable processes that we find in the “special” physics of the greenhouse without windowpanes?