This post covers a dull subject. If you are new to Science of Doom, the subject matter here will quite possibly be the least interesting in the entire blog. At least, up until now. It’s possible that new questions will be asked in future which will compel me to write posts that climb to new heights of breath-taking dullness.
So commenters take note – you have a duty as well. And new readers, quickly jump to another post..
Recap
In an earlier post – Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored – we looked at the many problems of trying to measure the surface of the earth by measuring the air temperature a few feet off the ground. And also the problems encountered in calculating the average temperature by an arithmetic mean. (An arithmetic mean for those not familiar with the subject is the “usual” and traditional averaging where you add up all the numbers and divide by how many values you had).
We looked at an example where the average temperature increased, but the amount of energy radiated went down. Energy radiated out would seem to be a more useful measure of “real temperature” so clearly arithmetic averages of temperature have issues. This is how GMST is calculated – well not exactly, as the values are area-weighted, but there is no factoring in of how surface temperature affects energy radiated.
But in the discussion someone brought up emissivity and what effect it has on the calculation of energy radiated. So in the interests of completeness we arrive here.
Emissivity of the Earth’s Surface
Our commenter asked:
So what are the non-black body corrections required for the initial calculation 396W/sqm? And what are the corrections for the equivalent temperature calculation? And do they cancel out (I think not due to the non-linearity issue) ?
What’s this about? (Of course, read the earlier post if you haven’t already).
Energy radiated from a body, E=εσT4
where T is absolute temperature (in K), σ=5.67×10-8 and ε is the emissivity.
ε is a value between 0 and 1, and 1 is the “blackbody”. The value – very important to note – is dependent on wavelength.
So the calculations I showed (in the thought experiment) where temperature went up but energy radiated went down need adjustment for this non-blackbody emissivity.
How Emissivity Changes
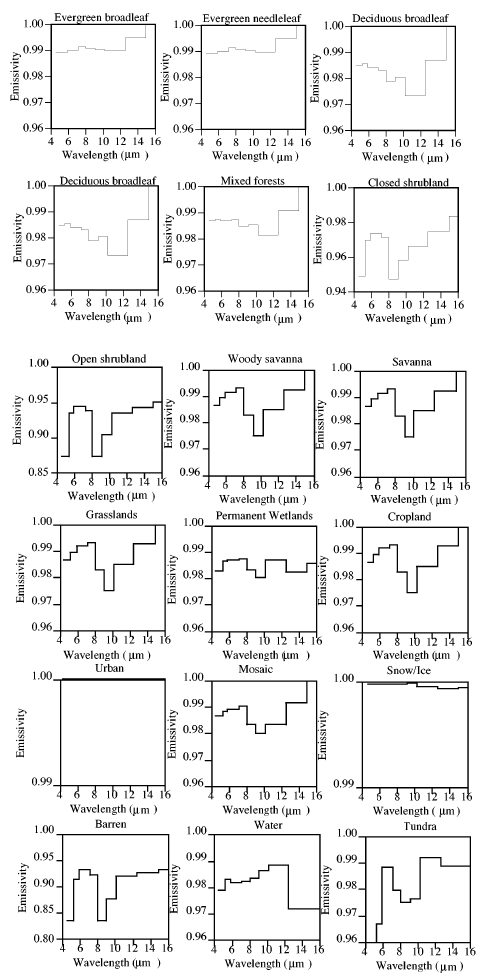
Here we consult the “page-turner”, Surface Emissivity Maps for use in Satellite Retrievals of Longwave Radiation by Wilber (1999).
And yet more graphs at the end of the post – spreading out the excitement..
Note the key point, in the wavelengths of interest emissivity is close to 1 – close to a blackbody.
For beginners to the subject, who somehow find this interesting and are therefore still reading, the wavelengths in question: 4-30μm are the wavelengths where most of the longwave radiation takes place from the earth’s surface. Check out CO2 – An Insignificant Trace Gas? for more on this.
I did wonder why the measurements weren’t carried on to 30μm and as far as I can determine it is less interesting for satellite measurements – because satellites can see the surface the best in the “atmospheric window” of 8-14μm.
So with the data we have we see that generally the value is close to unity – the earth’s surface is very close to a “blackbody”. Energy radiated in 4-16μm wavelengths only account for 50-60% of the typical energy radiated from the earth’s surface, so we don’t have the full answer. Still with my excitement already at fever pitch on this topic I think others should take on the task of tracking down emissivity of representative earth surface types at >16μm and report back.
So we have some ideas of emissivities, they are not 1, but generally very close. How does this affect the calculation of energy radiated?
Mostly Harmless
Not much effect.
I took the original example with 7 equal areas at particular temperatures for 1999 and show emissivities (these are arbitrarily chosen to see what happens):
- Equatorial region: 30°C ; ε = 0.99
- Sub-tropics: 22°C, 22°C ; ε = 0.99
- Mid-latitude regions: 12°C, 12°C ; ε = 0.80
- Polar regions: 0°C, 0°C ; ε = 0.80
The average temperature, or “global mean surface temperature” = 14°C.
And in 2009 (same temperatures as in the previous article):
- Equatorial region: 26°C ; ε = 0.99
- Sub-tropics: 20°C, 20°C ; ε = 0.99
- Mid-latitude regions: 12°C, 12°C ; ε = 0.80
- Polar regions: 5°C, 5°C ; ε = 0.80
The average temperature, or “global mean surface temperature” = 14.3°C.
The calculation of the energy radiated is done by simply taking each temperature and applying the equation above – E=εσT4
Because we are calculating the total energy we are simply adding up the energy value from each area. All the emissivity does is weight the energy from each location.
- With the emissivity values as shown, the 1999 energy = 2426 W/ arbitrary area
- With the emissivity values as shown, the 2009 energy = 2416 W/ same arbitrary area
So once again the energy radiated has gone down, even though the GMST has increased.
If we change around the emissivities, so that ε=0.8 for Equatorial & Sub-Tropics, while ε=0.99 for Mid-Latitude and Polar regions, the GMST values are the same.
- With the new emissivity values, the 1999 energy = 2434 W/ arbitrary area
- With the emissivity values as shown, the 2009 energy = 2442 W/ same arbitrary area
So the temperature has gone up and the energy radiated has also gone up.
Therefore, emissivity does change the situation a little. I chose more extreme values of emissivity than are typically found to see what the effect was.
The result is not complex or non-linear because emissivity simple “weights” the value of energy making it more or less important as the emissivity is higher or lower.
In the second example above, if the magnitude of temperature changes was slightly greater in the polar and equatorial regions this would be enough to still show a decrease in energy while “GMST” was increasing.
More Emissivity Graphs
Conclusion
Emissivity in the wavelengths of interest for the earth’s radiation is generally very close to 1. Assuming “blackbody” radiation is a reasonable assumption for most calculations of interest – as other unknowns are typically a higher source of error.
Because the earth’s surface has been mapped out and linked to the emissivities, if a particular calculation does need high level accuracy the emissivities can be used.
In the terms of how emissivity changes the “surprising” result that temperature can increase while energy radiated decreases – the answer is “not much”.



As the OP who instigated this article – first thank you – I enjoyed reading it. I hope others will not be put off by your modest and self-deprecating introduction.
Second, absorption/emissivity is actually a very important topic in radiative transfers – as anyone living on planet earth knows, it is one of the most important factors in human comfort The colour of your roof or your car is vitally important – white is much cooler than black as most people in the Mediterranean know. People wear metallic sunshades to reflect much of the light
Third – is the title a subtle joke on surface texture? Shiny surfaces have low absorption and low emissivity while dull surfaces perform a lot better. So is ‘dull’ and in-joke?
Finally, I asked elsewhere for a coherent explanation of why we get radiative cooling at night on quite a massive scale – hence inversions and even ice forming in the desert on clear nights. The issue of emissivity is very important here – both for the ground emissivity and spectrum as well as the atmospheric emissivity. I look forward to a good explanation of this as it is directly relevant to human experience and is quite probably a significant driver of local weather.
“white is much cooler than black as most people in the Mediterranean know”
I’m not sure if that’s what you’re suggesting, but emissivity is not something directly related to the color of the body.
Notice that the snow & ice graph shows a nearly perfect “black body” (meaning the physical concept).
And at solar wavelengths snow and ice are highly reflective, not good absorbers.
I recently saw Prof. Howard Hayden on Youtube and it got me interested in the Stefan-Bolzmann Law / equation. Being an Australian I have had many opportunities to test emissivity’s with my feet in summer!! This led me to thinking of the endothermic cooling effect of forests (greater concentration of photosynthesis). They have a low albedo and it is taken they have an emissivity the same as apshalt! It takes often tens to hundreds of millennia for a forest to give off most of its longwave radiation. The sheer size of the earth most probably makes up for this, but perhaps not. In the meantime it coolly fuels an abundance of life forms.. Using a S-B calculator I found that with an emissivity of 0.888 and using 1970s 14C global temperature I got a pretty accurate figure of 342.3, but if you 0.98 it jacks the radiation up to 377.8, making a mockery out of the IPCC’s 2.2 Watts per square metre of warming. I got the emissivity of 0.888 through inputting known averages for radiation and temperature in the S-B Calculator.
That’s another bit I learned. I thought emissivity was something related to the whole spectrum of the Planck’s curve. Something like the emissivity of that body on that temperature. Apparently, it’s related to each specific frequency, that probably can be averaged to the black body spectrum afterwards.
Here’s an interesting graph from Fundamentals of Heat and Mass Transfer by Incropera (2007).
It shows reflectivity vs wavelength (absorptivity = 1-reflectivity for an opaque material).
You can see that white paint is not reflective at all once into “longwave”.
(Absorptivity is on the right-hand axis, not quite visible from the scan, but goes from 0 at the top to 1 at the bottom).
I guess the dull stainless steel curve is showing the effect of wavelength dependence on surface roughness?
I.e. at visible frequencies the steel is reasonably dull because the surface texture is larger than the wavelengths. At long wavelengths the roughness is smaller in relation so it becomes ‘shinier’.
And the reason for the curve rather than a step-jump is because the SS roughness has a statistical distribution covering a wide range of wavelengths.
[…] is very close to a blackbody (the emissivity is close to 1) for longwave radiation – see The Dull Case of Emissivity and Average Temperatures. The atmosphere is not even close to being a blackbody. Atmospheric gases absorb and emit radiation […]
I wonder about your assertion that the earth without an atmosphere would be very similar to a blackbody.
Some folks are claiming to disprove greenhouse gas theory, as it is normally understood, in a novel way. They say GGT begins with the premise that without greenhouse gasses, the earth would be a perfect blackbody. The difference in temps between this hypothetical blackbody and actual temps is credited to greenhouse gasses. However, the moon has no atmosphere and it does not act like a perfect blackbody. It averages 40 degrees warmer than a hypothetical blackbody, with no greenhouse gasses. Therefore, if this is correct, the baseline for calculating the effect of greenhouse gasses on earth is way, way off.
Click to access Greenhouse_Effect_on_the_Moon.pdf
The writers of the article you cite don’t really understand the subject.
Nice balloon picture, but not particularly useful to understand emissivity.
In fact, the many graphs above, in the body of this article, are measurements of various surface types. They are not assumptions.
The emissivity of most of the earth’s surface (in the wavelengths the earth radiates at) is close to 1.
I haven’t looked at any studies on the moon, but reading the first part of the article it’s not the inappropriately-named “greenhouse” theory they are casting doubt on but basic thermodynamics.
One day I will write an article about the moon..
[…] with a longwave emissivity close to 1 for most of the earth’s surface, this would be a temperature of […]
So far as I can see, the above material is based on the currently dominant school of thought exemplified by B. Hapke’s 1993 book, “Theory of Reflectance and Emittance Spectroscopy”, Cambridge University Press, New York. The idea of this school of thought is to ignore the basic physics of propagation of electromagnetic radiation, including the infrared, at an interface between two media, and to use the term “””emissivity””” in a newly defined sense that ignores or forgets the sense in which the term is usually defined for atmospheric radiation studies. The effect of the influence of this school of thought is hard to assess, because it is followed by many of today’s experts, who value time-saving speed and efficiency above scientific accuracy.
In 1858, two years before Kirchhoff’s celebrated 1860 paper which earned him the reputation of originating his law of radiation, Balfour Stewart explained the correct physics which is ignored by the currently dominant school of thought. The correct physics was noted by Rayleigh in 1900 and is also used by Planck in his 1906/1914 book on heat radiation, and is also noted in Born and Wolf’s “Principles of Optics”, 7th edition, 1999, at page 423, but not even these sources have reached the quick and efficient currently dominant school. The correct physics is reviewed by R.J. Potton (2004), ‘Reciprocity in Optics’, “Rep. Prog. Phys.” 67: 717-754.
In 1858, Stewart explained that each medium has its own intrinsic material emissivity, in the sense of emissivity used in atmospheric studies today. But at the interface between two media, there occurs reflection, because of the discontinuity of the optical properties at the interface. The reflectivity is a specific property of the interface, not of either of the media separately, and this property needs to be specifically considered in an account of propagation of light (including IR) at the interface. It was discovered by Stokes in 1849 and later by Helmholtz that there is a principle that the reflectivity is the same whichever is the sense of propagation of light in a given direction across the interface. This is explained in some detail in J. Lekner’s 1987 book “Theory of Reflection of Electromagnetic and Particle Waves”, Martinus Nijhoff Publishers, Dordrecht.
The principle here has nothing to do with emissivity and absorptivity of molecules that is the concern of quantum mechanics and of atmospheric radiation studies. This principle is about macroscopic interfaces considered purely in terms of classical physics. It states that when a beam of light hits an interface, the energy that penetrates the interface plus the energy that is reflected from the interface is equal to the total energy of the incident beam, and that for a given interface, there is a specific property of the interface, its reflectivity, which is the ratio of reflected to incident energy, and that in a given direction, the reflectivity is the same for a beam incident in either sense, for example from the condensed matter medium to the gaseous medium, or from the gaseous medium to the condensed matter medium.
Thus for example if the reflectivity of the sea surface / atmosphere interface has the value r, the material emissivity of the sea has value ε at temperature T, and σ denotes the Stefan-Boltzmann constant, and by Sd we denote the IR radiation that proceeds from the sea surface down into the sea, and by Su we denote the IR radiation that proceeds from the sea surface up into the atmosphere, and by Ed we denote the IR radiation that hits the sea surface having originated in the atmosphere, then (ignoring the IR content of solar radiation) we have
Sd = (1 − r) Ed + r εσ T^4
and Su = r Ed + (1 − r) εσ T^4.
So far as I can see, the above blog entries are made according to the currently dominant time saving quick and efficient school of thought that neglects this simple, basic, and long established physics. r and ε are apparently not separately measured, which they ought to be.
Christopher Game:
I’m not sure I understand what you are saying.
α(λ) + τ(λ) + r(λ) = 1
Absorptivity + transmissivity + reflectivity = 1, where each is a function of wavelength.
From Kirchoff’s law, ε(λ) = α(λ) for a diffuse surface.
And for the surface of the earth, transmittance = 0, therefore
ε(λ) = 1 – r(λ)
So measure reflectance at each wavelength and you know the emissivity.
When I read your extracted comment it sounds like you agree but in other parts of your comment you don’t agree, for reasons that aren’t clear.
replying to scienceofdoom’s post of 2010 Jul 19 7:06 am.
The formulae you quote are quick and efficient but are not good physics. I was just writing about the interface, which can allow fractions of the beam to penetrate or be reflected; that’s all it knows about; it doesn’t know what will happen to the penetrating fraction. The transmission that appears in your quick and efficient formula does not refer to the interface, but to to the layer of material behind the interface, about which the interface does not know. The physics for an interface is as I wrote. I just made a slight slip, in that I wrote of “the direction” of the beam. What I should have written was of ‘the path’ of the beam, which is refracted at the interface. I suggest you read Planck 1906/1914 to get the right physics, if what I wrote is not clear to you. The other references I gave are also valid.
Christopher Game
That’s a strong claim.
I don’t have a copy of Planck 1906/1914 – why don’t you explain in your own words what is actually wrong with the formula.
Absorption + reflection = 100% – how should this be improved?
Absorptivity = emissivity – how should this be improved?
replying to scienceofdoom’s post of 2010 Jul 19 12:23 pm.
The formulae absorption + reflection = 100% and absorptivity = emissivity are not exactly the formulae that you quoted in your previous post. You have been quick and efficient in translating between the formulae.
At this level, the proper formula for the interface is penetration + reflection = incidence. This is conservation of energy.
The interface does not know what will happen to the three terms of this formula when they are propagating apart from it. It does however sustain a relation between penetration and reflection, a coefficient of reflectivity. The ‘reversion-reciprocity’ principle requires that the coefficient of reflectivity for each ray is the same in either sense, from condensed medium to gaseous medium or from gaseous medium to condensed medium. The reflection is determined by the discontinuity between the two media, and is not a property of either alone. It needs direct measurement, distinct from measurements or calculations of absorption and emission.
The interface is a notional geometrical two-dimensional surface of discontinuity of material properties, and has itself no volume and material mass, and so can neither absorb nor emit radiation of itself. It can only see propagation of radiation to and from elsewhere.
The radiations within the separate media are their respective private businesses, not to do with each other; this refers to propagation beyond, not at, the interface; within the respective separate media we mean that there is no discontinuity of properties to require reflection. Propagation within the respective media is governed by laws of absorption and emission, because it refers to respective three dimensional material media, with their respective mass densities and other material properties.
The formula you quote here, absorption + reflection = 100% mixes up what happens at the interface with what happens within the respective media. It fails to recognise ‘reversion-reciprocity’ of reflection at the interface.
As for the formula absorptivity = emissivity, it comes with careful definitions and conditions for its applicability; it is possible to mistake those definitions and conditions. I will not right here discuss this point, but will just say, let’s get the previous formula right first before moving on to this one.
It is regrettable that some textbooks, that should know better, do not bother to get this right.
[…] is 275K or 2°C. The surface of the earth emits radiation very close to the blackbody shape (see The Dull Case of Emissivity and Average Temperatures) but by the time the radiation leaves the earth’s atmosphere that isn’t what we […]
[…] Emissivity is a value between 0 and 1, where 1 is a “blackbody” or perfect radiator. The surface of the earth has an emissivity very close to 1. See The Dull Case of Emissivity and Average Temperatures. […]
[…] not linearly dependent on temperature – it is dependent on the 4th power of temperature. See The Dull Case of Emissivity and Average Temperatures for an example of the problems in using “average […]
[…] long time ago I wrote the article The Dull Case of Emissivity and Average Temperatures and expected that would be the end of the interest in emissivity. But it is a gift that keeps on […]