Checkout the more comprehensive: The Sun and Max Planck Agree – Part Two
For regular readers of this blog, this post adds nothing new. Think of it as placeholder – a link to send people to when they ask about this basic subject.
A very handy aspect of climate science is that we can easily differentiate between solar (from the sun) radiation and terrestrial (from the earth) radiation. We can do this because emission of radiation changes with wavelength and depends on the temperature of the body radiating:
Picture the scene, if you will.
The climate science enthusiast explains that the sun heats the atmosphere and the surface of the earth – both land and sea. And everyone agrees. Of course some solar radiation is reflected and no one disputes it.
The climate science enthusiast explains that the earth, when heated up by the sun, emits thermal radiation which is upward radiation (of course). And everyone agrees.
The climate science enthusiast explains that the atmosphere absorbs some terrestrial radiation, heats up and emits thermal radiation in all directions – some of it downward. Many are not so sure.
You are mixing up solar radiation with this ‘back-radiation’ from the atmosphere. Please provide data from night-time only.
This has been a theme on many other blogs and in many comments on Science of Doom so it’s worth pulling together the basics.
Max Planck and Blackbody Radiation
Max Planck was awarded the Nobel Prize in 1918 for his contributions to science, including this gem about radiation:
This equation describes the spectral intensity of a “blackbody” as a function of temperature (absolute temperature) and wavelength.
The values of h, k and c0 are constants. T is absolute temperature and λ is wavelength.
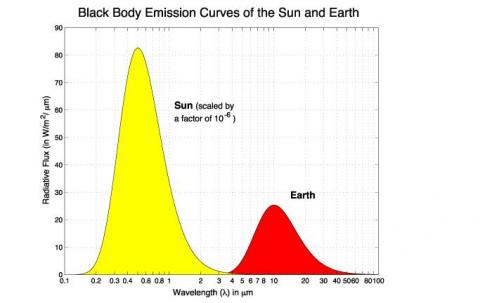
If we plot the result of this equation for a temperature of 5780K – the sun – we get a graph which looks remarkably like the radiation we actually measure from the sun outside the atmosphere.
That’s a good thing, and Max won’t have to hand back his Nobel prize:
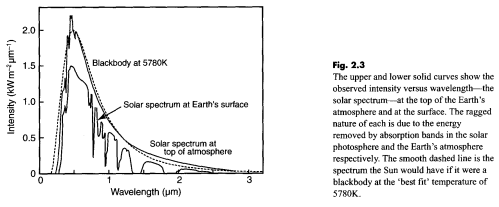
This is from Incropera and DeWitt – for those suspicious of everything produced by climate science, a work untouched by climate scientists – which goes by the enthralling name of Fundamentals of Heat and Mass Transfer and is now in its sixth edition.
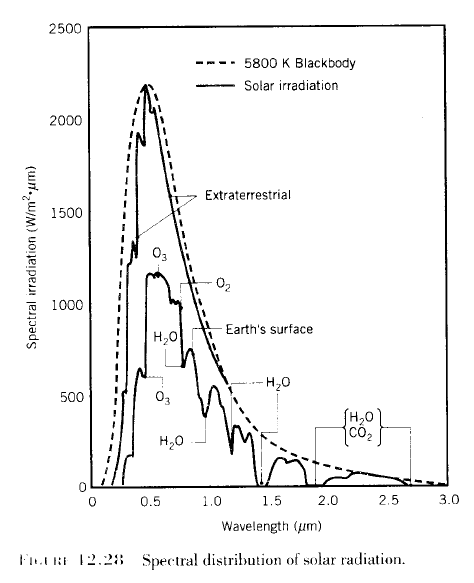
From climate science itself, from Professor F.W. Taylor of Oxford University, from Elementary Climate Physics (2005):
Much the same. And it gives us confidence that Max Planck was right. In which case we can calculate some key parameters about the radiation from the sun and from the earth.
Solar vs Terrestrial Radiation
Solar radiation at 5780K has a few interesting properties which are easily calculated using the equation above. You can put the equation into excel and work it out for yourself.
Or you can use spectralcalc.com to do the heavy lifting. With spectralcalc just select a temperature and at the bottom select an “Upper limit” and “Lower limit” of wavelength. This will calculate the spectral intensity between these two wavelengths using Planck’s equation. Don’t forget to make sure you divide this Band Radiance by the Radiance, and not the Radiant emittance (check the units to make sure you are comparing like with like).
Some important results from Max and from the sun..
As a proportion of total solar irradiance:
- Total energy from 0 – 0.75μm 54% – all energy up to infra-red
- Total energy from 0.39μm – 0.75μm 43% – visible light only
- Total energy from 0 – 4μm 99% – all “shortwave”
- Total energy from 4-infinity 1% – all “longwave”
- Total energy from 13μm-infinity 0.03% – major 15μm CO2 band and above
Terminology:
- >0.75μm is infra-red (slightly different conventions exist about the maximum value for visible light, but nothing substantial)
- 0-4μm is “shortwave” – a climate science convention referring to solar radiation
- 4μm-infinity is “longwave“- a climate science convention referring to terrestrial radiation
For various temperatures of the earth’s surface, the proportion of its radiation which is in the “longwave” band (4μm and above):
- 15°C (288K) – 99.9%
- -50°C (223K) – 99.99%
- 50°C (323K) – 99.6%
The last important point to consider is that sometimes people get confused about the relative magnitude of solar and terrestrial radiation – for example, with the first graph in the post the solar radiation is much higher than the terrestrial radiation. But this is because the solar radiation in that example is the value close to the surface of the sun. But the earth only receives about one two-billionth of the solar radiation due to its distance from the sun.
Overall, and on average, the solar energy into the atmosphere is of a similar magnitude to the terrestrial radiation out of the atmosphere. (Otherwise the earth would heat up or cool down very quickly).
But in any one location on any given day it is possible for the solar radiation to vary from zero (night-time) to potentially over 1000 W/m2 (sun overhead on a cloudless sky). The absolute maximum is the total solar irradiance of 1367 W/m2 – this would be the case if the sun was directly overhead and the atmosphere reflected or absorbed nothing, which is never the case, but let’s consider this condition to get an idea of the maximum possible solar radiation in the longwave.
With the sun directly overhead and no atmospheric reflection or absorption we would have:
- 13.7 W/m2 > 4μm
- 4.1 W/m2 > 6μm
- 0.4 W/m2 > 13μm
- 0.25 W/m2 in the CO2 band of 13μm – 17μm
Conclusion
Well, hopefully everyone can see that even though the radiation spectrum by wavelength for any radiating body extends to infinity, the amount of solar radiation which is >4μm is 1% and the amount of terrestrial, or longwave, radiation which is <4μm is much less than 1%.
- This means, if we measure radiation with a wavelength of >4μm it is not from the sun, even if it is daytime (to a 96 – 99% accuracy).
- And if we measure radiation with a wavelength of >13μm it is not from the sun, even if it is daytime (to greater than 99.9% accuracy).
That is, unless Max Planck and the sun are wrong.
If you think this explanation or conclusions are wrong in any way then stay on this post and ask questions or explain what is wrong with it. Because if this basic element is confusing it will be difficult to make any progress in understanding climate science.
Update – followup article – The Sun and Max Planck Agree – Part Two
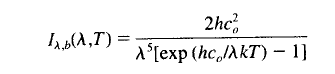


Thank you for a very informative post.
Only one point I wanted to clarify is in the conclusion.
You state that: ‘the amount of solar radiation which is >4μm is 1%.’
Then you state that: ‘this means, if we measure radiation with a wavelength of >4μm it is not from the sun, even if it is daytime (to a 96 – 99% accuracy).’
I am no expert on mathematics but just to get my head around this are you saying that although 1% of the solar radiation is >4μm then the probability of the radiation within this category being from the sun is 1-4%? Therefore it is possibly entirely from other sources i.e. terrestrial sources and back radiation as stated in the early part of your posting?
I know it sounds like a really dumb question but like I say I am no expert on mathematics so I want to get it straight in my head before I argue the point with the idiots who won’t accept the truth about climate change.
Many thanks for your time.
Kev C
Kev Coleman:
You ask a good question that I should have clarified better.
The proportion of solar radiation above 4um is 1%.
But solar radiation at it’s peak instantaneous value (sun directly overhead) can be up to 4x the magnitude of the terrestrial radiation, so when we actually measure radiation greater than 4um, up to 4% of the measured value could be from solar radiation.
So if, for example, solar radiation was 100x the magnitude of the terrestrial radiation this 1% of 4um and above would be of a similar magnitude to the terrestrial radiation and we wouldn’t easily be able to distinguish between terrestrial and solar.
Does this clarify things?
Hello again,
Yes that does clarify the basic premise of the 1% value although I still had to read it a few times to get it clear in my mind. Got it in the end.
Many thanks.
Kev C
The deviations from the blackbody spectrum of the sun:
I have heard that they are due to radiative flux through the star, from the inner core through the outer layers. A blackbody, on the other hand, assumes that it absorbs all of its internal energy and re-radiates it out of the surface. Is that correct? Or are there other reasons for deviation from a blackbody?
Notice the difference in approach between the climate scientist (Taylor), the physicist (Incropera), and the climate blogger. The climate scientist (who wants to increase public confidence in GW theory) picks the sun’s temperature by doing a best-fit between observation and theory. He ignores the spike in emission at about 0.5 um that is about 7% (?) higher than theory would predict. (If this spike was caused by random experimental error a best-fit would be appropriate, but the spike shows up in both graphs.) The physicist knows that no real object radiates exactly like a perfect blackbody, so he picks the sun’s surface temperature so that the highest points on the curve agree with theory. The substantially larger deviations between theory and observation occur at wavelengths where the emissivity is lower than 100%, or where gases or particles in the sun’s “outer atmosphere” absorb energy. Most climate science bloggers show only the theoretical curves in yellow and red and don’t tell us what a “blackbody” really is – a hypothetical object which absorbs 100% of all wavelengths of light that strike it. Planck’s equation tells us the MAXIMUM amount of energy an object at a given temperature CAN emit. We need to know how much it absorbs at each wavelength – and possibly other factors – to calculate how much it WILL emit. With thousands of absorption lines these are difficult calculations.
The dirty secret is that most components of the atmosphere – all of the nitrogen oxygen, argon, and other inert gases – do not absorb or EMIT long wavelength radiation. So the atmosphere is not a blackbody in the infrared.
A simple thought experiment suggests that Planck’s Law doesn’t apply to all situations. If we allow gas molecules to expand until we have relatively few molecules in a cubic meter rather than the usual 10^20 or so molecules, the radiation in W/m^2 leaving a region is unlikely to remain constant. At some point, there simply isn’t enough kinetic energy in the molecules to support the theoretical outflow of energy.
Speaking of the sun’s “outer atmosphere”, the temperature of the corona is millions of degrees. Given that total emission varies with the fourth power of temperature and that wavelength varies with the reciprocal of temperature, Planck’s law would suggest that the earth receives 10^12 times more energy at wavelengths around 0.001 um (hard UV and X-rays) than it does around 1 um. (This radiation is mostly absorbed by the thermosphere and is responsible for the relative warmth of this section of the atmosphere. However, some people think this radiation could influence cloud formation.) Unfortunately, there is so little material in the corona (and the thermosphere) that they are not in a state of thermal equilibrium – another undisclosed requirement for objects emitting blackbody radiation. Since laboratory studies on blackbody radiation are usually performed in cavities lined with solid black materials, some physicists are concerned whether Planck’s Law and related laws apply to liquids, gases, or plasmas. Scientists are having difficulty explaining the sun’s structure and behavior using these laws. (See http://www.thermalphysics.org). In an earlier post, Science of Doom did a great service by posting some experimental evidence that long-wavelength radiation returning to the earth’s surface does follow Kirchkoff’s Law. A post about coronal emission of hard UV deserves equal time.
Skeptical readers of Science of Doom might be better served by ignoring oversold theories and simply looking at the observed radiation reaching the earth (1365-6 W/m^2 in the visible according to satellites; ? W/m^2 in the far UV from the sun’s corona – which needs different detectors) and at the observed radiation reaching the earth’s surface (both in clear and cloudy locations). These are facts. The facts are superficially consistent with theory, but we haven’t taken a thermometer to the sun’s surface to test that theory.
Frank:
What makes you think that Prof FW Taylor is trying to fit the solar spectrum into any kind of preconceived agenda? Have you read his book?
I’ve taken one extract here without any accompanying text because this post is about one simple subject. From memory he touches on the solar radiation but it’s not the focus of the book.
Taylor is a professor of physics at Oxford University. I’m not sure what kind of preconceived ideas you have but I recommend you read his book – only $40 from bookdepository.co.uk. You might be surprised.
The legend for Taylor’s graph says that a “best-fit temperature of 5780 degK” was used to generate the theoretical curve. Given that known mechanisms (absorption, <100% emissivity) reduce the intensity of emission, isn't a best-fit to the data inferior to Incropera's "envelop fit"? For that matter, can't a temperature of 7000 degK or even 10,000 degK combined with emissivity <100% and/or absorption theoretically produce the observed distribution of intensity vs. wavelength?
Does the earth receive radiation from the sun corona? Does the same simple application of Planck's Law explain the wavelength and intensity of this radiation?
I looked at the accessible sections of Taylor's book online (Googlebooks) and the great price and ordered a copy. He is candid about the limitations of models and bluntly honest about aspects others avoid. For example: "Although water vapor is the single most important absorber of those that produce the greenhouse effect, in our simple model, the effect of increasing water vapor is negligible provided the increase is confined to the troposphere. The physical reason is that the lower atmosphere is already optically thick, and the vertical transfer of energy is dominated not by radiation but by convection." (p 116)
Jormundgard:
“I have heard that they are due to radiative flux through the star, from the inner core through the outer layers. A blackbody, on the other hand, assumes that it absorbs all of its internal energy and re-radiates it out of the surface. Is that correct?”
The internal temperature of the Sun is in the millions of degrees – the surface temperature is on the order of thousands of degrees.
When the Sun is viewed from a sufficient distance such that the surface is well defined, we don’t care about the internal temperature of the Sun – just it’s surface temperature.
The assumption of a black body implies the absorption of radiation is equal to its emission on the surface in question – which requires that the temperature of the surface remain constant.
For the Sun, the assumption of a constant temperature surface is a reasonable assumption.
However, when you attempt to estimate the temperature of planets based the Sun’s radiation, then you need to be careful since the planets are tilted on their axis, rotate and absorb and store radiation as heat and in general can’t be modeled as constant temperature surfaces.
Note, the Stefan-Boltzmann law can be derived from the Carnot cycle. If you should ever falsify the second law of thermodynamics then the Stefan-Boltzmann law dies with it.
DrAgile,
I think my question was not clear. The incoming solar radiation spectrum is very close to, but not exactly equal to, the theoretical blackbody spectrum. For example, there is a very modest shift of energy from small to large wavelengths. This deviation is not very important to radiative balance of the Earth, and is therefore probably outside the scope of this blog, but I’d still be interested to know what causes it.
One explanation I have heard in passing is that the internal nuclear processes closer to the core release more radiation than is absorbed by the outer layers. In other words, some of the internal energy passes through the outer layers and reaches the earth. (This is what I was referring to in my previous post.)
In any case, there are no perfect blackbody radiators, even if it is difficult to find strong deviations, and I was asking what particular non-blackbody quirks were contributing to the sun’s deviations from a perfect blackbody curve.
Again, just to be clear, I know this is a very small effect, as demonstrated by the plot on this page, and hardly matters to terrestrial climate.
Some of my questions are answered on this page:
http://www.ccpo.odu.edu/SEES/ozone/class/Chap_4/4_3.htm
I should have checked things out on my own first!
[…] centered around 0.5μm and radiates out with wavelengths centered on 10μm. See, for example, The Sun and Max Planck Agree. So there is no reason to expect that absorptivity = emissivity (because we are considering the […]
[…] without an atmosphere that absorbs longwave radiation there is no way that the radiation from the surface can be greater than the radiation from the top […]
This article is a nice diversion, but when are you going to get to the meat of the issues. CO2 drives global warming because it has a positive feedback, or water vapor offsets the warming effect of the reflected long wave radiation absorption and CO2 has only minimal effect on global temperatures.
Are you a man or mouse? Get to the meat of the issue.
[…] Regular readers of this blog will be clear about the difference between solar and “terrestrial” radiation. Solar radiation has its peak value around 0.5μm, while radiation from the surface of the earth or from the atmosphere has its peak value around 10μm and there is very little crossover. For more details on this basic topic, see The Sun and Max Planck Agree […]
You say 2-billionths of the sun’s energy at source reaches the earth. I think the proportion should be 2-one hundred thousandths. Either way, why scale the graphic by 10^-6?
The almost complete separation of the solar and terrestrial curves is at odds with the typical explanatory graphic of the phenomenon which shows nested curves, those for colder temperatures enveloped by those for warmer ones. Unlike your graphic they are also asymmetric with an extended long-wave tail. Why these differences?
John Millett:
You are right depending on what we take as the source, so I haven’t been specific enough. If we take the total radiated solar energy then the correct value is 1 in 2-billion.
If we take the solar flux (W/m^2) then the correct value will be rsun^2/distance^2 = 2.2×10^-5
= (696×10^6/150×10^9)^2.
Both come to the same value.
If you take a set of nested curves and then divide the top one by a factor of 100,000 what do you think you will see?
Will the curve that is now divided by a factor of 100,000 still be above the other curves at all points?
Yes. The effective radiating temperature of the solar flux at TOA is 394K, higher than the surface’s 288 which in turn exceeds the atmosphere’s 255 or so. Curves for these three temperatures are nested (one of your posts shows two such nested, long-tailed curves). This means that the atmosphere interacts with infra-red radiation from both TOA and surface. The IPCC’s global mean energy budget confirms this. showing a quarter of incoming radiation absorbed in the atmosphere. This has the uncomfortable implication, for the AGW hypothesis, that surface warming could result from the atmosphere absorbing less incoming radiation or more of the outgoing variety, rendering the cause of global warming moot.
John Millett:
What the satellites measure for incoming solar radiation at TOA is 1367W/m^2.
When averaged over the surface of the earth this is 342 W/m^2 (=1367/4).
And the measured reflected solar radiation is 103 W/m^2 (global annual average).
This means that 239 W/m^2 is absorbed by the climate system.
These are the measured values.
Outgoing longwave radiation (OLR) measurements also get this value. Instrument error means that there is an uncertainty of around 5W/m^2.
If you convert 239 W/m^2 to an effective radiating temperature it is 255K.
Check out Earth’s Energy Budget
[…] July 25, 2010 by scienceofdoom I didn’t think that a Part Two would be needed after the initial installment – The Sun and Max Planck Agree […]
[…] of solar radiation is <4μm – see The Sun and Max Planck Agree. Solar and longwave radiation are of a similar magnitude (at the top of atmosphere) therefore when […]
[…] out The Sun and Max Planck Agree and The Sun and Max Planck Agree – Part Two for more on this […]
As a measure of the esteem I attach to Scienceofdoom, I am devoting the first month of 2011 to a systematic review of articles, beginning with CO2. I was soon directed to the Sun and Max Planck Agree in which you conclude :
“the amount of solar radiation which is >4μm is 1% and the amount of terrestrial, or longwave, radiation which is <4μm is much less than 1%”.
Question: Given that GHGs in the atmosphere absorb only wavelengths greater than 4 microns and that, according to K&T, the atmosphere absorbs up to 26% of solar radiation, most of it presumably in the band 0.75 microns to 4 microns, which molecules in the atmosphere are responsible for the absorption?
The question arose only obliquely in our original conversation in Part two.
John Millett:
Thankyou for the kind words.
The GHGs absorb at many wavelengths between 0-4μm.
Compare the top of atmosphere solar spectrum with that measured at the ground.
Water vapor, ozone, CO2 are absorbers. And for the high energy ultraviolet, oxygen (O2) is an “absorber” – which is where ozone (O3) comes from.
And so that is why saying the atmosphere is “transparent” to solar radiation is not quite right.
“Mostly transparent” is a better description.
So, GHGs are dual-purpose components of the climate system: they cool the surface by absorbing solar radiation in particular wavelengths; and they warm it by radiating to the surface at different wavelengths.
Would it be correct to think that GHGs absorb higher average intensity solar radiation than they emit terrestrial radiation, implying a net cooling of the surface?
Hi there–
I’ve been puzzling over solar irradiance and thought you might be able to help. There was a 2010 paper by Haigh et al. showing a variability in solar spectrum irradiance that wasn’t predicted by existing models. Apparently, for a 3-yr period during the down slope of the most recent solar cycle, UV-range irradiance dropped much more steeply, and visible-range irradiance increased more dramatically, than expected.
This got me thinking: if the sun is pretty much considered a black body, why would spectral irradiance change in any way not predicted by the black body spectrum? Or are such measured changes small enough to conform to the black body model? What are all the variables that determine such differential changes in spectral irradiance?
Thanks.
While you can calculate the effective black body temperature of solar radiation, the sun itself is not a black body. It has structure and parts like the photosphere, chromosphere and corona. And even the apparent surface, the photosphere, isn’t at a uniform temperature.
I would like to calculate the sun’s radiance in the 8-14 micron range both at ground level and TOA, is there a site to do that online?
Not that I am aware of.
At TOA it is a pretty simple exercise.
Although the radiation from the sun is not a perfect blackbody of 5780K, the spectral intensity is pretty close to that.
So use the Planck formula for a blackbody of 5780K integrated across 8-14um, then use the inverse square law for the distance to the earth.
(And of course there are lots of measurements of spectral intensity of solar radiation at TOA).
If you are considering the angle of incidence then the value is multiplied by cos (angle of incidence).
At the surface it is a much more difficult exercise.
In fact, the proportion of solar radiation absorbed by the atmosphere is one of the atmospheric values with the most uncertainty, due to the sparcity of high quality groundstations and the variability in solar absorption/reflection from clouds, aerosols and the varying proportions of gases like ozone and water vapor.
I would like to follow up my last question, as you pointed out calculating the radiation at the surface is more difficult, is there a reasonably priced instrument that can make this measurement. I have not found a radiometer specifically for this application but I am interested in one.
It depends on your definition of reasonable. I doubt you could make the measurement you want without using a spectrophotometer. An FT-IR spectrophotometer configured to make high resolution emission measurements would be on the order of $50,000, I think. It would get more expensive to configure the device to measure direct normal solar radiation in that wavelength region. I suspect you would need a low pass interference filter to screen out UV, visible and near IR wavelengths like those used on pyrgeometers, among other things.
what if the pyranometer is recording the value of 1450 w/m2.
Thanks very happy to see the details in the historical science, Maxwell Planck, Spectral Intensity as it relates to climate change. On the Shoulder of Giants. Of course I’m very warry when I see the opinion and conclusion before the discussion. First off, a single equation, 100 years old will not do as a complete analysis, of even the basics. There have been considerable advances. Hundreds of detailed Climate Simulations, by professional experts in many fields working together. Second yours is very shallow approach without any professional pier review, is incomplete at best. Please provide your professional details, and Linkedin. Third there are numerous gapes in your logic.
Please be careful, the risk is high, I hope that will remove your blog.
Rick,
Your post is incoherent and incompetent. Peer (note spelling) review is no guarantee of correctness. The NEJM and Lancet papers on hydroxychloroquine were peer reviewed. They were completely fabricated with no actual data.
Climate simulations are just that, simulations. They are not reality. Sometimes not even close. ‘Professional experts’ is pretty close to being an oxymoron. And what’s your evidence that they are from many fields.
Gaps in logic? Cite please. Unsupported assertions are meaningless.
Shakespeare, Henry IV Part 1, Act 3 Scene 1
Credentials are also no guarantee of correctness.
Rick: Perhaps you should think before you write and check your logic. You write:
“Of course I’m very warry [sic] when I see the opinion and conclusion before the discussion.”
A scientific paper will have a title and abstract that presents a conclusion (or opinion if you insist) before the discussion. In non-scientific writing, an introduction with a thesis statement is recommended practice, so readers knows where the article is attempting to lead. In the case of this post, the thesis statement is:
“A very handy aspect of climate science is that we can easily differentiate between solar (from the sun) radiation and terrestrial (from the earth) radiation.”
Then our host presents a good, albeit not perfect, justification for this claim. (If one wants to be picky, not all photons important to climate science are emitted by materials that emit like blackbodies. Gases in the atmosphere don’t emit like blackbodies. Fortunately, Planck’s function is also found in the equations governing the emission from a layer of atmosphere (Schwarzschild’s equation for radiation transfer), so our host’s thesis is correct for our climate system.
As for “pier” review and credentials, this blog has been peer reviewed far more carefully any scientific article written by the greatest climate scientist. Peer review occurs in the comments below each article. It was immediately obvious to me when I came here to learn, that some very intelligent people (including a few climate science professors) read this blog and comment – both supporters and skeptics of the consensus. There are few places where people on both sides of an issue discuss the subject respectful. And their comments were/are taken into account. This article was prompted by a comment from the reader of an earlier post:
“You are mixing up solar radiation with this ‘back-radiation’ from the atmosphere. Please provide data from night-time only.”
This post was a rely to that comment. Comments about this post prompted the writing of a second post “The Sun and Max Planck Agree – Part Two”, and the reader is alerted at the top of this post, to look for additional information. And you will find posts about Schwarschild’s equation and the observed spectrum of downward long wavelength radiation emitted by the atmosphere. (Many people argue about what theory predicts; few present evidence from observations.).
Rick writes: “First off, a single equation, 100 years old will not do as a complete analysis, of even the basics. There have been considerable advances.”
The usual strategy: Create a straw man argument and then dismiss information that makes you uncomfortable. An ideal strategy for ensuring that a reader never confronts and assimilates information that contradicts what he already believes.
If you want to benefit from your reading about climate science, I can tell you from personal experience that this is a great place to read from beginning to end – the embarrassingly-hostile, decade-old comments above from “Frank” are from me – once angry and confused because the consensus has over-simplified the subject and grossly failed to deal with the problems and doubts they created. This blog confronts those issues fairly.
Finally, although climate models are based on fundamental physics and chemistry, they deal with many critical phenomena that can’t be modeled with today’s computers using PARAMETERS that must be TUNED, so that the model produces a reasonable version of today’s climate. Tuning parameters one-by-one or with ensembles of parameters doesn’t lead to an optimum solution. If you were to look closely, you’d see that models seriously disagree about many things, including things as fundamental as the amount of energy solar radiation delivers to the surface. Most climate scientists don’t want to discuss the limitations of models, because policymakers are desperate for reliable information about what rising GHGs will do to our climate. Their very imperfect models are the only tools available for providing answers. Every projection from the IPCC should begin with: “If our climate models are correct, then …”
Thanks, very helpful.
Can you do a comparison of
1. Total energy of the solar radiation which is absorbed or blocked by UV on the way in
2. Total energy of the terrestrial radiation which is absorbed or trapped by CO2 on the way out
Thanks in advance.
markwadsworth,
Those aren’t trivial questions. The upper limit on solar radiation absorbed in the stratosphere is the total amount of solar radiation absorbed by the atmosphere, ~80W/m². But that’s likely way too high. If you look at the total IR energy emitted by the stratosphere and above using the Archer MODTRAN page, with the 1976 US Standard Atmosphere at 11km (the height of the beginning of the stratopause) looking up, you get ~25W/m². At 20km (the top of the stratopause) it’s ~10W/m²That would be assuming that all the energy emitted comes from absorbed solar radiation, which should be approximately true, especially above 20km.
The amount of surface radiation absorbed by CO2 can also be estimated from using MODTRAN. Using the US Standard Atmosphere again, at 400ppmv CO2 and 100km looking down, 267.8W/m² is emitted. Setting CO2 to zero, 295.9W/m² is emitted for a difference of 28.1W/m². But that’s not completely correct because you have CO2 emission in the stratosphere. At 20km looking down, the difference is 30W/m².
However, the US Standard Atmosphere is only an approximation of the average composition of the atmosphere because there are substantial variations in water vapor by latitude. So these numbers are only approximate.
My first reply got swallowed, so try again…
“Thanks for taking the time to look this up.
1. Your first figure of 80 W/m2 (during daytime) looks about right to me. 20 W/m2 must be understated.
Let’s look at total thermal energy in Joules per m3 of surface.
Stratosphere – warmed from top down by UV-B and UV-C interacting with oxygen and ozone
= 2,000 kg x 1,000 J/kg/K x 240K avg temp = 480 million Joules
Troposphere plus top 1m of ocean (warmed from bottom up by solar hitting the surface)
= 7,500 kg air x 1,000 J/kg/C x 255 avg temp = 1,912 million J
Plus 1,000 kg water x 4,000 J/kg/K x 255 avg temp = 1,020 million J
Sub-total = 2,932 million J
Grand total = 3,392 million J
480 ÷ 3,392 = 14%
Solar in = 685 W/m2 avg during daytime less 30% reflected = 480 W/m2
480 W/m2 x 14% = 67 W/m2
Adjust for lower heat capacity of land v water = call it 80 W/m2 (day time)
2. IR emitted by effective surface =
One third land/ocean @ 288K = 390 W/m2
Two thirds cloud cover, 6 km altitude at top of clouds @ 250 K x 75% emissivity = 166 W/m2
Weighted average (by day or night) = 240 W/m2, which is what is actually emitted = overall effective temp 255K as viewed from space.
So I don’t see much trapped or blocked radiation going out. Certainly not 30 W/m2 (I’ve not seen this number before).
markwadsworth,
You said terrestrial radiation which I read as surface radiation. 30W/m² is for cloud free atmosphere. Clouds are completely opaque to surface radiation, so cut that back to 10W/m². Now if you want to consider clouds as a higher surface, then 400ppmv atmospheric CO2 absorbs about 13W/m² of the radiation emitted by the cloud tops corrected for partial coverage. So it’s either 10 or 23W/m² depending on how you define the surface.
You’re ignoring the substantial absorption of solar near IR radiation by clouds. 80W/m² is way too high for the absorption by oxygen and ozone in the stratosphere. Also, I’m using the 24 hour and average, not just daytime. The stratosphere would be a lot hotter and emit more radiation to space if it absorbed 80W/m², even for just 12 hours. Total energy is irrelevant. Dividing incoming radiation intensity by total energy does not tell you anything.
I used MODTRAN to see how much radiation the stratosphere emitted downward, which would be about the same as it emitted upward. That’s where I get 10-20W/m². Come to think about it, I need to multiply by 2 to include upward and downward emission. That would make it 20-40W/m², still a far cry from 80W/m². And that’s an upper limit because it doesn’t include absorption of upward IR by ozone or any other form of heat transfer from the lower atmosphere.
If you want to see how to do an energy balance, I refer you to Trenberth, Kiehl and Fasullo, 2009.
Mark: Whenever you do calculations with radiation (W/m2) and heat capacity (J/m3/K), you encounter problems with dimensional analysis. Watts are J/s. So, you end up with an answer with units of K/m/s. If you decide on the depth (m) of the material being heated through its surface area (you appear to have arbitrarily chosen the top one meter of the ocean), your answer is still a rate of temperature change (K/s). Such calculations are useful if you want to know how much the mixed layer of the ocean and atmosphere will warm in response to an instantaneous forcing of 1 W/m2. (Answer: 0.2 K/yr for a 50 m mixed layer). Although I don’t understand your calculation, my guess is that your approach is doomed to failure for this reason.
The solution to this dilemma in climate change is that we usually integrate imbalances over time until we reach a 0 W/m2 radiative imbalance and reach a new steady state temperature. After 1 year of a 1 W/m2 forcing, an hypothetical 0.2 K warmer planet would be radiating more heat to space and the radiative imbalance at the TOA would now be less than 1 W/m2. (Some of the imbalance is also penetrating below the mixed layer.) If ECS were 3.6 or 1.8 K/doubling, the planet would be emitting 1.0 or 2.0 W/m2 more for every degK the surface warmed.
DeWitt’s approach avoids this problem by relying on radiative transfer calculations based on a steady-state model of temperature in the atmosphere (and at the surface). When we specify the temperature and composition of the atmosphere at all altitudes, radiative transfer calculations such as Modtran can tell us how the upward flux of LWR changes from the surface (where it averages about 390 W/m2) to space (where it averages 240 W/m2) and how DLR increased from 0 to 333 W/m2 traveling in the opposite direction. (We ignore the horizontal components of flux.) We don’t need to worry about the role of SWR, because the temperatures in the model (including in the stratosphere) are a consequence of all heat fluxes (absorption, emission and convection) through the atmosphere, including the absorption of UV by ozone and oxygen).
When I use Modtran with a cloudless tropical atmosphere (tropopause at 17 km 195 K; stratosphere max at 50 km and 270 K from absorbed UV), I get upward and downward fluxes of LWR at 70 km of 298.52 and 0.05 W/m2. At the tropopause, these fluxes are 299.40 and 9.66 W/m2. So the upward flux is reduced by net absorption+emission by 0.88 W/m2 as LWR travels upward through the stratosphere and increased 9.56 W/m2 by net absorption+emission as it travels downward through the stratosphere. Therefore the tropical stratosphere emits 10.5 W/m2 more LWR than it absorbs – power which it must obtain by absorbing UV. So I get basically the same answer as DeWitt does using radiative transfer calculations for the US Standard Atmosphere.
The problem with Modtran is that the answers you get vary with the region of the planet (tropic, temperate, polar), season (winter or summer, except in the tropics), and the altitude of clouds (if any). Unfortunately, Modtran doesn’t perform a composite calculation for the entire planet. With cumulus cloud tops at 2.7 km in a tropical atmosphere, upward LWR is 269.57 and 269.82 W/m2 at 17 and 70 km, a difference of 0.25 (instead of 0.88) W/m2.
DWP, re my question 2, I refer you to the first diagram in your post <a href=https://scienceofdoom.com/2010/02/11/co2-%E2%80%93-an-insignificant-trace-gas-part-six-visualization/here.
It shows 390 W/m2 up from ground and 265 W/m2 going into space. means that 1125 W/m2 is reflected-trapped-absorbed by the atmosphere. If we assume it’s only CO2 doing the trapping, that seems pretty conclusive evidence of GHG theory, until you remember clouds.
I agree that clouds appear to block-reflect-absorb all IR coming up from the land/ocean. And when I said “terrestrial” I meant upwards IR from clouds as well. Perhaps I should have mentioned that expressly. So we can ignore IR emitted by land/oceans under cloud cover and start again with IR emitted from upper surface of clouds.
I used your approach and did the more complicated calculation with a weighted average IR emitted by land/oceans and clouds, you get upward radiation 240 W/m2, which is what goes to space. So there’s no obvious “missing” or “trapped” IR.
DWP re 1, you say “80W/m² is way too high for the absorption by oxygen and ozone in the stratosphere. Also, I’m using the 24 hour and average, not just daytime”
Well, facts are facts. Energy comes in as radiation and is converted to mainly thermal energy, plus chemical energy (in plants) or electric energy (by solar panels).
Frank, the stratosphere is on average only 4% or so cooler than the troposphere, so multiply up mass x specific heat capacity x temperature and you find that the thermal energy in the stratosphere is about 14% of the thermal energy in the troposphere plus top bit of ocean (my top one metre is just an estimate for the amount that is the same temperature as the air above it).
Therefore, we must assume that the stratosphere and the ozone in it convert about 14% of incoming radiation energy to thermal energy. Solar radiation is the only source of energy that it has. There is no significant exchange of thermal energy between stratosphere and troposphere, or else there would not be this temperature minimum at the tropopause.
There’s no need to average incoming solar between day and night in this context, 14% is 14%.
“Therefore the tropical stratosphere emits 10.5 W/m2 more LWR than it absorbs”
That is working backwards from the wrong end. The amount is IR an object emits bears no relation to radiation it has absorbed to reach its temperature.
I could warm up two identical objects to 50C. I have warmed, one by putting it in warm water and the other by putting it in front of a three-bar electric fire. The first hasn’t absorbed any radiation whatsoever, the second one clearly has. But the two objects will be emitting the same amount of IR.
Also, I thought that only GHGs can absorb and emit IR. If the stratosphere is just N2, O2 and O3, and can’t absorb IR, how can it emit any?
Mark wrote: “That is working backwards from the wrong end. The amount is IR an object emits bears no relation to radiation it has absorbed to reach its temperature.”
Applying conservation of energy to a problem often allows one to deduce the equilibrium or steady state for a problem without worrying about transient details. If the stratosphere has a stable temperature, the power being absorbed by the stratosphere must be equal to the power being emitted by the stratosphere. Assuming we know the temperature and composition of the stratosphere and troposphere, radiative transfer calculation allow us to calculate the upward and downward LWR fluxes into and out of the stratosphere. Conservation of energy allows us to deduce how much power is delivered to the stratosphere by SWR; the net flux must be zero.
The amount of IR an object emits is a function of its temperature and emissivity, BUT emissivity and absorptivity are equal (Kirckhoff’s Law). The temperature of the stratosphere depends on absorption and emission of LWR as well as absorption of UV. For optically thin layers like the stratosphere, emissivity and absorptivity are proportional to the concentration of GHGs and their absorption cross-sections. Radiative transfer calculations are great for summing up absorption by and emission from many optically thin layers of stratosphere. (If they handled SWR as well as LWR, they would directly calculate absorbed UV for you, but the only software accessible to me only deals with SWR.)
Mark wrote: “There is no significant exchange of thermal energy between stratosphere and troposphere, or else there would not be this temperature minimum at the tropopause.”
Yes, but there is significant exchange of LWR energy between the troposphere and the stratosphere. Stratospheric ozone is involved in both absorption of UV and absorption and emission of LWR. The temperature of the stratosphere is very sensitive the the amount of CO2 and is predicted to drop about 10 K when CO2 doubles (from increased radiative cooling by CO2).
Mark asked: “Also, I thought that only GHGs can absorb and emit IR. If the stratosphere is just N2, O2 and O3, and can’t absorb IR, how can it emit any?”
Today’s stratosphere is 400+ ppm CO2 and 1.8 ppm methane, just like the troposphere. Water vapor is about 3 ppm, the mixing ratio at the tropopause. To be more precise, some of the methane is oxidized to CO2, increasing the water vapor modestly. However, we don’t need to worry about all of these details, since programs like Modtran have been loaded with the best mixing ratio and temperature data available at the time. However, we do need to worry that the appropriate temperature and mixing ratio data are used and these values vary different regions of the planet.
I think that your calculation is based on the hypothesis that the internal energy of the stratosphere (heat capacity * temperature) is related to the internal energy of troposphere and 1 m of ocean lying below it. Equipartition of energy is important in some situations, but it isn’t clear why this should be the case in this situation. And the assumption of 1 m of ocean appears somewhat arbitrary. The mixed layer of the ocean about (about 50 m) is stirred by winds.
That is not an answer.
My answers – feel free to dismiss them as ‘opinions’ if yours differ – are
1. About 14%
2. About 0%
What are your answers?
Getting a straight answer here is about as difficult as getting a Creationist to explain away the existence of ancient fossils.
I have one quick question, when you plot Max Planck’s distribution for the sun and use Wein’s displacment law to find the peak, that peak is approx 15% higher than the Stefan-Boltzmann law predicts for total area under the curve. My question is which is the worst case? which should be used to identify worst case output?
I think you’re mixing units. The units of the Planck distribution for wavelength is W/m²/μm. The units for the Stefan-Boltzmann equation are W/m². There is no conflict between the two.
The units are different. There is no conflict. Both numbers, assuming they were calculated correctly are right.
but that is the W/m^2 per the wave length, I get 8.3 W/m^2 at 0.504 micrometers wavelength peak, which is much higher that the total area under the graph which is stefan-Boltzmann
Nope. It’s 8.3 W/m²/μ on the graph or from the Planck equation for wavelength adjusted for distance. If the peak of a Planck curve is 8, than the area under the curve is going to be a lot higher than 8. Your problem seems to be using the S-B equation. The total area is on the order of 1,000 W/m² at the Earth’s surface for ~6,000K minus the atmospheric absorption and the 1/r² loss from the distance between the surface of sun and the Earth’s orbit. At the top of the atmosphere it’s 1380W/m² plus or minus a couple of watts depending on where the Earth is in it’s orbit around the sun.
Johnathan: Units of radiant energy transfer were quite confusing to me until I (hopefully) mastered them. The sun’s peak output is about 500 nm (0.5 um). However, a negligible fraction of photons will be emitted with a wavelength of exactly 500.0000 nm. We can talk about how much power is emitted between 499.9995 and 500.0005 nm: 26.882 W/m2/sr. Or we can talk about the power emitted between 499.5 and 500.5 nm: 26,882 W/m2/sr. However, since Planck’s function doesn’t change appreciably over either wavelength range, both measurement are the same when reported in units of W/m2/sr PER NM: 26,882 W/m2/sr/nm. This is often called “spectral intensity”, the intensity at a particular wavelength. However, Planck’s function does vary modestly over the range 400-600 nm, so dividing the total power emitted over this wavelength range by 200 nm gives a lower, misleading value
In other words, to get the power delivered over a range of wavelengths where the Planck function varies, you need to integrate the “spectral intensity” over that range to get the “intensity” of the radiation in W/m2/sr. And you need to numerically integrate in wavelength increments small enough that Planck’s function is effectively constant. When you integrate over all wavelengths, there is a definite integral available – the Stefan-Boltzmann equation for a blackbody (W = oT^4). For non-ideal emitters or “gray bodies, we add an emissivity fudge factor (W = eoT^4).
Spectral intensity can also be reported in units of W/m2/sr/cm-1 or W/m2/sr/Hz.
Planck’s Law is for the intensity of radiation emitted in all directions – over a sphere of 4Pi steradians, which is why “sr” present in W/m2/sr/um. This is appropriate for emission by GHG molecules in the atmosphere. For radiation emitted by the surface of the earth, radiative cooling to space (OLR), or DLR or SWR arriving at the surface of our planet, we usually think in terms of the “flux” of radiation perpendicular to a surface in units of W/m2 or possibly the “spectral flux” (W/m2/um). We talk about fluxes perpendicular to a surface because “viewing angle” is critical to radiative transfer of power (Lambert’s cosine law). When you convert the intensity (W/m2/sr) emitted from a point on a surface over a hemisphere (2Pi steradians) into the flux emitted perpendicular to the surface, you pick up factor of Pi. 1 W/m2/sr becomes 3.14159 W/m2 radiated perpendicular to the surface. When considering GHGs emitting in all directions in the atmosphere, 2 W/m2/sr becomes 3.14159 W/m2 traveling upward (OLR), 3.14159 W/m2 traveling downward (OLR) and horizontal fluxes that cancel. The is called the “two-stream” approximation. Climate science usually deals with incoming or outgoing flux (W/m2) perpendicular to the surface, not intensity (W/m2/sr).
The maximum spectral intensity of thermal IR at 288 degK is at 10 um and 8.1 W/m2/sr/um. The maximum spectral flux is about 25 W/m2/um. This is the spectral flux reported by Modtran.
http://climatemodels.uchicago.edu/modtran/
Contrast it with the spectral intensity (8.1 W/m2/sr/um) reported by this online Planck calculator:
https://ncc.nesdis.noaa.gov/data/planck.html
Thanks for the nice illustration. Regarding to the first figure, why is the solar radiation scaled by 10^-6?
Because the sun is 93,000,000 miles away. A factor of 10^-6 is approximately the decrease in intensity from the r^-2 factor. The figure gives the approximate intensity with wavelength of solar radiation at the top of the Earth’s atmosphere.
Thanks, [1] If the distance between the sun and the Earth is approximately 10^8 miles, then the factor r^-2 should be 10^16. Am I missing something?
[2] The second figure shows that the intensity of the solar radiation reaches 2200 w/m2 at nearly 0.5 um, which is different from what is shown in the first figure. Thanks
The diameter of the sun is not zero. The reduction factor is the ratio of the surface area of the sun to the surface area of a sphere with a radius of 93,960,000 miles, or the square of the ratio of the sun’s radius, 432,690 miles, to the distance of the surface of the sun to the earth, 92,527,000 miles or a factor of 45,728. So more like 10^-5 than -6. But close enough.
Thanks, now, if the solar radiation depicted in the first figure refers to the radiation at the top of the atmosphere of Earth, then it would be better to remove the scaling statement mentioned over the figure. The scaling statement means that the readers must read the number on the left axis as “num X 10^6”, which is incorrect. When discussing how those calculations have been conducted, a scaling statement may be mentioned. Lastly, I am not sure why the numbers of w/m2 are in ten whereas the subsequent figures are in thousands.
Picky, picky. I’m not the author of the article and I can’t read his mind so I can’t explain all of his editorial decisions.