On a couple of unrelated articles on this blog, people have been asking questions about the moon. This is because a lot of people have read an article called A Greenhouse Effect on the Moon from www.ilovemycarbondioxide.com that makes some confused claims.
The article starts:
We’ve been told that the earth’s surface is quite a bit warmer than calculations predict. Theory has it that heat-trapping “greenhouse gases” account for a 33° Celsius disparity. But it turns out that our airless moon is also quite a bit warmer than predicted.
And finishes with:
The Earth is not “unusually” warm. It is the application of the predictive equation that is faulty. The ability of common substances to store heat makes a mockery of blackbody estimates. The belief that radiating trace gases explain why earth’s surface temperature deviates from a simple mathematical formula is based on deeply erroneous assumptions about theoretical vs. real bodies.
A long time ago a friend told me that the way the Bank of England trains people to spot counterfeit notes is to give them real notes to spend time getting used to the feel, texture, weight and so on. They don’t give them lots of counterfeits because it’s not as effective.
I have no idea if the story is true but I always thought that it was a useful concept for approaching any subject. Best to spend the time helping people understand the real theory – as all scientific “facts” are called – rather than spend 5% of the time on the real theory and introduce them to 19 flawed theories.
Therefore, most of this article will focus on building understanding of the basics rather than pointing out the many flaws in the article. We will look at the temperature of a moon-like body by way of very simple models.
These models are in Excel because it’s quick and easy.
The Model
The concept is very simple. This is an idealized moon-like surface for illustration.
For my moon-like body, we will consider one square meter of surface. This is because lateral heat flow within the surface will be extremely low and so we don’t want or need to build a GCM to solve this problem.
Solar radiation is absorbed by this surface and heats up. The surface has a definite heat capacity which we vary in the model to see how the results change.
The sun moves slowly through the sky so the amount of solar radiation incident on the surface varies over the course of the lunar “day”. The surface has an “absorptivity” for solar radiation – the proportion of solar radiation absorbed vs the proportion reflected.
When the sun is directly overhead the solar radiation incident is 1367 W/m2 and when the sun is on the horizon the solar radiation is zero – then for the whole “night” the radiation stays zero. Therefore, I’m considering the “equator”.
For reasons of laziness I set the lunar day to be 28 days, but the exact value doesn’t matter.
And the absorptivity was set to 0.9 (which means 90% of incident solar radiation is absorbed and 10% is reflected). Also the emissivity was set to the same value, but in this example it could be different. With different values similar results would occur but with different equilibrium temperatures. See Note 1.
The simple maths for the model is at the end of the post as many people don’t like seeing equations.
The Results
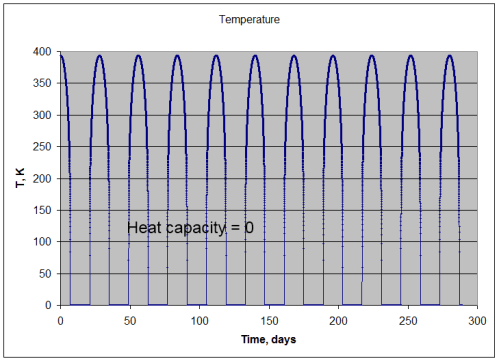
Now, if the surface had no heat capacity (or as mathematicians might say, “as the heat capacity tends to zero”) then the surface would instantaneously heat up until the radiation emitted matched the absorbed radiation.
So in that unrealistic case, the temperature would follow this curve:
Moon-like surface, zero heat capacity
So during the moon-like night, the surface drops immediately to absolute zero, and during the “day” the emission of radiation exactly matches the absorption. (For mathematically inclined readers this follows a cos θ relationship – see maths section at end).
Note that this isn’t like the earth or any real body. It’s just a useful thought experiment to show what would happen if the surface had no heat capacity.
Under this condition:
- absorption of solar radiation = 391.7 W/m2 (averaged over many cycles)
- emission of lunar radiation = 391.7 W/m2 (averaged over many cycles)
- mean temperature = 169.3K
- min temperature = 0K
- max temperature = 394K
Energy in = energy out – so no surprises there.
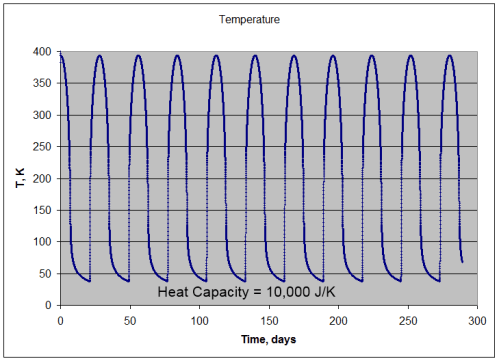
Let’s start increasing the heat capacity and see what happens – per m2, 10,000J/K heat capacity:
Moon-like surface with 10,000 J/K heat capacity per m^2
- absorption of solar radiation = 391.7 W/m2 (averaged over many cycles)
- emission of lunar radiation = 391.7 W/m2 (averaged over many cycles)
- mean temperature = 195.3K
- min temperature = 38K
- max temperature = 397K
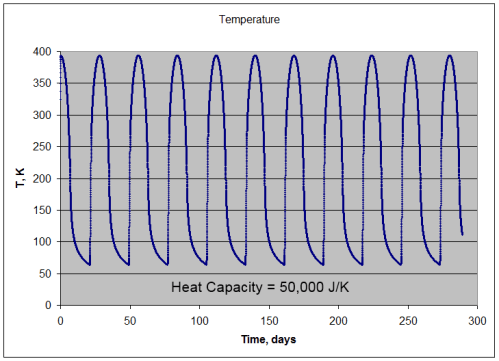
Per m2, 50,000J/K heat capacity:
Moon-like surface with 50,000 J/K heat capacity per m^2
- absorption of solar radiation = 391.7 W/m2 (averaged over many cycles)
- emission of lunar radiation = 391.5 W/m2 (averaged over many cycles)
- mean temperature = 211.3K
- min temperature = 64K
- max temperature = 394K
Per m2, 500,000J/K heat capacity:
Moon-like surface with 500,000 J/K heat capacity per m^2
- absorption of solar radiation = 391.7 W/m2 (averaged over many cycles)
- emission of lunar radiation = 390.0 W/m2 (averaged over many cycles)
- mean temperature = 247.7K
- min temperature = 133K
- max temperature = 393K
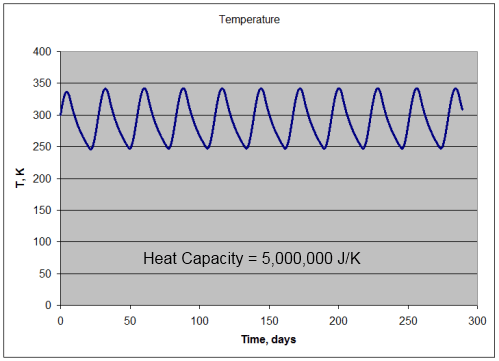
Per m2, 5,000,000J/K heat capacity:
Moon-like surface, 5,000,000 J/K per m^2
- absorption of solar radiation = 391.7 W/m2 (averaged over many cycles)
- emission of lunar radiation = 391.7 W/m2 (averaged over many cycles)
- mean temperature = 290.9K
- min temperature = 247K
- max temperature = 342K
Hopefully, for most people, the fact that the temperature range is reducing as heat capacity increases is reasonably intuitive. If you want to heat up a cupful of water it takes less time than heating a swimming pool. If you want to cool down both through the same surface area it will take longer for the swimming pool to cool down.
Summary of Results
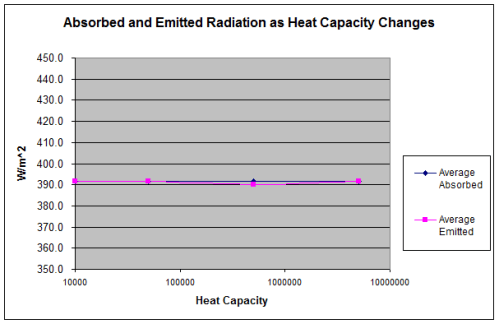
Notice that in each case the average value of absorption = emission – to within 1%.
The 1% is just a result of imperfect starting conditions. If the chosen simulation starting temperature was exactly right, or there were enough “spin up” cycles to get into the steady state before the averaging was done then the absorption = emission exactly.
It’s probably not surprising to anyone that absorption = emission over a set number of cycles because otherwise the overall trend in temperature would be increasing or decreasing.
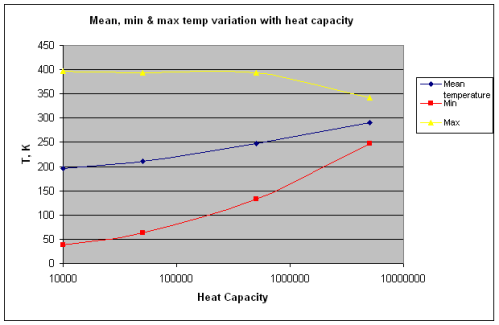
Next a plot of mean, min and max temperature as the heat capacity increases, note the log axis for heat capacity:
The reason for plotting the heat capacity on a “log” or logarithmic axis was because the heat capacity is increased by a an order of magnitude each time. Linear plots make the results of this kind of simulation less clear.
The mean temperature is simply the arithmetic average of temperature over every single time step. (All the numbers added up and divided by the number of results).
So the mean temperature does increase when the surface has an increased heat capacity!
It looks like the ilovemyco2 writers were correct and the whole greenhouse effect was just a result of heat capacity of the oceans and land.
Time for me to pack my bags and head off into the sunset..
But wait, hold on a minute..
There’s something very strange going on. The temperature is increasing, but the average emission of radiation has stayed exactly the same:
How can temperature increase without the radiation increasing? Radiation is emitted in proportion to the 4th power of temperature – for a blackbody (ε=1), E = σ . T4, where σ = 5.67×10-8
If the temperature goes up, radiation must go up as well. Is there something wrong with the model?
No. And for those who’ve read Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored this example won’t be surprising.
Take 3 “temperatures”: 1, 10, 100.
Now we average them -> average = 111/3 = 37K
And calculate the energy radiated, E = 37 4 x 5.67×10-8 = 1,874,161 x 5.67×10-8 = 0.11 W/m2
Alright, let’s do it the other way. Let’s calculate the energy radiated for each temperature:
- 14 x 5.67×10-8 = 1 x 5.67×10-8 = 5.67×10-8
- 104 x 5.67×10-8 = 10,000 x 5.67×10-8 = 5.67×10-4
- 1004 x 5.67×10-8 =100,000,000 x 5.67×10-8 = 5.67
And now average the energy radiated -> average = (5.6705670567/3) = 1.89 W/m2
One method gives 18x the other method – how can this be and which one is right?
Just for the many people would prefer to see the calculation without the Stefan-Boltzmann constant of 5.67×10^8 everywhere – in that case we compare 374 = 1,874,161 with the alternative method of (14 + 104 + 1004)/3 = 100,010,001/3= 33,336,667
Also (of course) a factor of 18 between the two methods of calculating the “average”.
There’s nothing surprising about this – average a series of numbers and raising the average to the 4th power will almost always give a different answer to first calculating the 4th power for each of a series of numbers and averaging the results.
Now the moon has some extreme temperature ranges in the examples shown and, therefore, the “mean” temperature changes significantly.
The earth by contrast, with less extreme temperatures has this result –
- the “average” temperature = 15°C, and converting that to the “average” radiation = 390 W/m2
- calculated the correct and painful way, the individually calculated values of radiation from each and every surface temperature around the globe every few hours over a year.. then averaged = 396 W/m2
Conclusion
So the reason that the moon – with a surface with a real heat capacity – appears to have a warmer climate “than predicted” is just a mathematical error. A trap for the unwary.
The right way to calculate a planet’s average radiation is to calculate it for each and every location and average the results. The wrong way is to calculate the average temperature and then convert that to a radiation. In the case of the earth’s surface, it’s not such a noticeable problem.
In the case of the moon, because of the wide variation in temperature, the incorrect method produces a large error.
So there’s no “lunar explanation” for the inappropriately-named “greenhouse” effect.
In the case of the earth there is anyway a huge difference from the moon. The solar radiation absorbed at the top of the earth’s atmosphere – about 240W/m2 is approximately balanced by the outgoing longwave radiation of the same amount. But the radiation from the surface of the earth of 396W/m2 is much larger than this top of atmosphere value of 240W/m2.
That’s the greenhouse effect.
But ilovemyco2 – hats off to you for enthralling and exciting so many people with a simple mathematical puzzle.
Maths in the Model
Ein = S . cosθ . α – for -90° < θ < 90°
Ein = 0 otherwise
where Ein = energy absorbed by the surface in J/s, S = the solar irradiance in W/m2, θ = angle of the sun from the zenith, α = absorptivity of the surface at the solar radiation wavelengths.
Eout = ε . σ . T4
where Eout = energy radiated by the surface in J/s, ε = emissivity of the surface at the wavelengths it is radiating at, σ = 5.67 x 10-8, and T is the temperature in K (absolute temperature). This is the Stefan-Boltzmann equation.
and for each time step, Δt:
ΔT = (Ein – Eout)/C
where C = heat capacity of a 1m2 surface in J/K and ΔT is the change in temperature.
For people who like even more detail:
The assumption is that the conductivity of heat into the surface is very high with some kind of insulating layer below the “heat capacity” layer. This makes the calculation slightly easier to understand than using thermal diffusivity.
And the conductivity of heat laterally is very low to avoid considering thermal equalization between adjacent surfaces.
Neither of these assumptions has any significant effect on the “experiment”, or on the principles that it demonstrates.
Note 1
Emissivity and absorptivity are inherent properties of the material in question and are wavelength dependent. In the case of a surface like the earth, the surface receives solar radiation centered around 0.5μm and radiates out with wavelengths centered on 10μm. See, for example, The Sun and Max Planck Agree. So there is no reason to expect that absorptivity = emissivity (because we are considering the properties at different wavelengths).
Just so; and after reading your post on a GMST is it time to relook at McKitrick’s paper?
Click to access GlobTemp.JNET.pdf
Doesn’t this mean that all the blackbody calculations from solar flux to average Temperature are wrong as well (like in, for example, Earth Energy Budget – Part three 🙂 )? I’m fairly certain it is actually even more complicated than taking account heat capacity. The solid and liquid part of the earth seem to be oversimplied rather often in the conversation.
S.o.D.
Why not stick to the same value of e?
“And the absorptivity was set to 0.9 (which means 90% of incident solar radiation is absorbed and 10% is reflected). Also the emissivity was set to the same value, but in this example it could be different. With different values similar results would occur but with different equilibrium temperatures. See Note 1.”
“How can temperature increase without the radiation increasing? Radiation is emitted in proportion to the 4th power of temperature – for a blackbody (ε=1), E = σ . T4, where σ = 5.67×10-8”
Remember also that the raw data for the Moons temperature was supplied by NASA.
Its not clear how you can explain a “greenhouse effect” from the Moon with no atmosphere!
Bryan:
Can you clarify your point, because I don’t understand it.
The Stefan Boltzmann equation doesn’t even give the maximum Lunar temperature accurately.
Planck’s Equation, Kirchoff’s Law, Stefan Boltzmann equation are interrelated and all rest on on conclusions relating to a hollow cavity.
If these constraints are ignored we get a picture of events that reality does not recognise.
If different values of emissivity and absorbency are used we can get a “cold earth” or a “hot earth” outcome.
Extract from link below.
COMPLEXITIES IN DETERMINING THE ABSORPTIVITY TO
EMISSIVITY RATIO OF THE EARTH.
The problem of obtaining a realistic value for the absorptivity to emissivity ratio for
all the entities at Earth’s surface, and in its atmosphere, that participate in the radiative
balance is a formidable task. The first and most difficult part of the problem is simply
to locate the “surface” involved in the radiative-equilibrium process. Upon closer
examination, one finds that the “surface” on which the incident solar irradiance is
absorbed, and from which Earth radiates outward into Space , is not a simple surface
at all. Most of Earth’s albedo is caused by reflection of the incident solar flux from
several surfaces: from the tops of clouds, from the surface of the oceans, from the
surfaces of continents, and from the surfaces of dust particles in the atmosphere. There
is also a scattering component to the albedo: from homogeneous gases and
heterogeneous particulates in the atmosphere. Furthermore, the absorbed fraction of
the solar flux is not only absorbed heterogeneously at those same surfaces, but also
homogeneously by the gaseous components: water vapor mainly, with smaller
contributions from other gases. That same distribution of homogeneous and
heterogeneous absorbers emits the flux that is radiated from Earth to Space.
Click to access EE20-1_Hertzberg.pdf
Bryan:
You have pasted in some text from a paper that says that earth has a variable emissivity due to its changing surface, oceans, icecaps and due to its atmosphere, which is subject to fluctuations in aerosols and water vapor.
That’s all wonderful but what does that have to do with the moon? And what does it have to do with the moon-like surface which is developed here?
Please identify the inaccuracy. Please be specific.
I know that since you read an item in the madness of Gerlich and Tscheuschner about Kirchhoff and Stefan-Boltzmann being subject to something vague you pull out this kind of comment. But probably don’t understand it.
You need to actually state a scientific point of view and it needs to be something you understand.
The Stefan-Boltzmann equation is the integration of the Planck function over all wavelengths.
Can you explain where the Stefan-Boltzmann equation applies? And what its limitations are? Can you identify the flaw in the Planck formula?
Do you think that the Stefan-Boltmann relationship is correct for a surface with a measured emissivity?
Occasionally correct? Just wrong? Can you state the conditions under which it is true?
This is foundational thermodynamics and what you may not realize is that Gerlich and Tscheuschner simply commented on some dull points that are well-known to atmospheric physics and general physics.
It has the same “full on, knock you out” impact as their ground-breaking statement: “a larger portion of the incoming sunlight lies in the infrared range than in the visible range“. Quite fascinating and well-known to everyone but just wonderful that they have written a paper about it. Their students must be so proud!
So to make a contribution to this post, other than to demonstrate that you jump on any idea which may possibly cast doubt on the “greenhouse” theory, please make a specific point that you can explain about the examples given in the article.
The Stefan Boltzmann equation doesn’t even give the maximum Lunar temperature accurately.
Look at the predicted value of SB and see that it is never reached
Click to access Greenhouse_Effect_on_the_Moon.pdf
You are on again with impertinent remarks like
……”the madness of Gerlich and Tscheuschner ”
Yet you have yet to prove them wrong in one item.
I have challenged you and also sylas in (CRN) to substantiate or withdraw the statement that they claim that “radiation from a colder surface cannot fall on a warmer surface”
This formed the major part of the Halpern group comment on G&T.
My background is in Physics.
The last thing a physicist would do is to grab hold of an equation and use it out of context.
Some people use an equation like a crutch.
They don’t understand the background from which the equation was derived but are happy to use it anyway.
This has now become much worse with computer programmes that will solve equations for those who would find it impossible to do it manually.
Like the pupil who doesn’t know arithmetic but has a calculator.
To divide 12 by 3 he gets 36 and doesn’t know the difference.
A physicist will look at the experimental evidence to determine how to proceed
The original “greenhouse glasshouse theory” was falsified by a simple experiment by Woods.
It now looks like the IPCC “greenhouse theory” and the assumption behind the use of SB equation are facing a challenge from the Moon.
S.O.D.:
???. You are still missing the whole point, I think. The iloveco2 article was not “calculating radiation,” as you are saying. It was comparing actual temperatures with calculated TEMPERATURES. It was calculating temperatures from radiation, in the same way (well almost) that the “warmers” calculate what the temperature of the Earth “should be” without a greenhouse effect. The “actual” temperature values given for the moon are MEASURED values, which are not the same as the values calculated from radiation, alone.
Do you really think Sidons et. al. are this dumb?
The original NASA model doesn’t go to zero at night because the Apollo landing site always sees radiation from the Earth. A minimum temperature of 35 K only radiates 0.085 W/m2. That seems reasonable for the amount of radiation received from a body with a brightness temperature of 255 K at a distance of 240,000 miles. Other than that, it’s clear that the original model still has a surface heat capacity of zero. Since no physical body has a heat capacity of zero, it’s clear that the original model was not meant to be exact, but to give a ballpark estimate. Which it did.
The measured temperature shows all the characteristics of a surface with finite heat capacity and a diffusive surface, including a phase lag of the temperature compared to the incoming radiation. Just like the surface temperature at any point on the Earth peaks several hours after local noon.
The NASA paper also doesn’t say whether they corrected the incoming solar radiation for local albedo. If they didn’t, that would explain the discrepancy between the calculated and measured peak temperature. If you look up lunar characteristics, the peak surface temperature is listed as 123 C or 396 K, which matches the calculation for an albedo of 0.1 for solar radiation at the lunar equator.
Radiative transfer physics are not falsified by the temperature behavior of the moon. Quite the opposite. Radiative transfer physics were used to determine the properties of the regolith by how the actual temperature was perturbed from that for a toy model.
The calculation of 33 K for the approximate value for greenhouse warming also uses a trivial model of a superconducting gray body for comparison. It’s wrong too, but not by very much. F=ma assuming mass is constant isn’t completely correct either, but for most situations it’s good enough.
Bryan,
I’d be interested in your response to any of SoD’s questions from 11:23, exempli gratiae:
The Stefan-Boltzmann equation is the integration of the Planck function over all wavelengths.
Can you explain where the Stefan-Boltzmann equation applies? And what its limitations are? Can you identify the flaw in the Planck formula?
Do you think that the Stefan-Boltmann relationship is correct for a surface with a measured emissivity?
Occasionally correct? Just wrong? Can you state the conditions under which it is true?
These seem like trivial questions for one with a “background… in Physics” to answer.
Viz your assertion: “radiation from a colder surface cannot fall on a warmer surface,” have you read https://scienceofdoom.com/2010/05/21/intelligent-materials-and-the-imaginary-second-law-of-thermodynamics/ ? Is it incorrect, and if so in what particular?
I agree with you that it’s shameful when people “don’t understand the background from which the equation was derived but are happy to use it anyway.” Hopefully you can clear up which equations are being so misused.
PDA:
Good grief, man. Read Bryan’s statement again, carefully. HE is not saying that radiation from a colder surface cannot fall on a warmer surface. He is evidently challenging someone who has said that G&T said that.
Hmmm. It seems DeWitt is doing a lot of guessing about what NASA did, how much radiation is transferred to Moon from Earth, etc. Is that arm-waving?
DeWitt Payne
…….”The original NASA model doesn’t go to zero at night because the Apollo landing site always sees radiation from the Earth. “………
This appears to be already factored in .
See comment at bottom of diagram labelled (6)
PDA
Gerlich and Tscheuscher’s paper pointed out that errors would follow if care was not applied when using the Stefan Boltzmann Equation(pg 19,20) and Kirchhoff’s Law (pg 48,49)
This peer reviewed paper from outside the climate science area shows how limited Kirchhoff’s Law is;
Planck’s equation and Stefan-Boltzmann equation (the integration of the Planck function over all wavelengths) rely on Kirchhoff’s Law.
Click to access PP-19-01.PDF
This paper has experimental evidence to back it up.
Can you be more specific?
Jae,
The NASA graph of calculated temperature shows a flat bottom at ~35K. You only get a flat bottom if the heat capacity is zero. The S-B calculation for a BB at 35 K is 0.085 W/m2. That was eyeballing the curve. A more exact calculation is luminosity of the earth divided by 4*pi*r^2 where r is the distance from the moon to the earth. Luminosity is the surface area of the Earth times 240 W/m2. That turns out to be 0.0662 W/m2 or a temperature of 32.9 K. So my eyeball estimate was indeed in the ballpark.
Bryan,
The point was to show the reason why SoD’s graph at zero heat capacity was different from the graph in the NASA article. To be even more precise, I should have added the contribution from the CMB at 2.7 K, but that only changes the received flux from 0.066209 to 0.066212.
SOD,
You are correct as far as you went. However there is an issue with the Earth that complicates the issue more. The radiation into space is not directly based on location on the Earth. Both wind and ocean currents transport energy large distances, so the final surface temperature and storage are smeared from the direct input locations, and the temperature at the edge of the atmosphere has inputs from many locations. The result is that even if you had exact surface temperatures for all times, using radiation out and convection straight up would not give a correct average, even if you used T^4 before averaging. The entire concept of an average temperature is limited beyond a first order approximation of outgoing levels.
The horizontal thermal conductivity of the atmosphere and oceans also contributes to why an isothermal body is a good approximation for calculating the magnitude of the greenhouse effect.
JAE:
Do you see that average temperature, (T1+T2)/2, can be different in two cases yet the same average radiation can be emitted?
Leonard Weinstein:
I’m not sure I’m understanding you.
Are you saying that radiation from the ocean surface at 0’N, 0’E and emitted directly up which is not absorbed doesn’t leave the earth directly above this point an infinitesimal time later? (I’m sure you’re not)
Just jumping ahead if you’re not – the radiation emitted from the earth’s surface computed from the Stefan-Boltzmann equation is exactly that – the radiation emitted from the earth’s surface.
The atmosphere absorbs lots of this and moves it around.
But I don’t see why that doesn’t mean we can’t accurately calculate the radiation emitted from the surface of the earth.
It’s obviously not the same as the radiation from the earth’s climate system into space.
Probably I’m missing what you are getting at..
My reading is that Leonard is saying that while the total flux upward at the TOA is related to the flux upward at the surface, it’s not one to one everywhere. The relationship is different at the poles than at the equator. The extreme example is 0.69 for a Tropical atmosphere and 0.84 for Subarctic Winter (MODTRAN not corrected for the tails of the spectrum).
The claim that _the_ Moon is “warmer than expected” rests on the wrong interpretation of NASA’s measurements as a long term ‘global’ temperature. The best I can find in terms of these are from an astronomy web site, which gives the average day and night temperatures as 107C and -153C respectively (I am not entirely confident using these, since I don’t know how they got them, but it’s the best I can find). This works out to an average of 250K. Just found the same figure somewhere else. But maybe someone has a reference to a proper source.
This is about 20K cooler than the theoretical black body temperature of 270K (which you can find on NASA’s planet facts web site or calculate yourself like Cthulhu did on another thread).
So where’s the problem?
As an aside: all those oh-so-skeptical people seem to be prepared to take the temperature data at face value when even the NASA says that there are lots of problems with the measurements which were only meant to be trial-runs.
D.
Bryan,
“Planck’s equation and Stefan-Boltzmann equation (the integration of the Planck function over all wavelengths) rely on Kirchhoff’s Law.
http://www.ptep-online.com/index_files/2009/PP-19-01.PDF“
Your continued citation of a paper that applies only to the special case of a cavity with perfectly reflecting walls at microwave frequencies as a proof that Kirchhoff’s Law is invalid at all times and in all places is getting old. While it’s called a Law, there are lots of cases where it doesn’t apply. The lower atmosphere and planetary surfaces do not fall into any of those special cases the vast majority of the time. There are non-thermal events like lightning in the atmosphere but they have an insignificant effect on the overall behavior.
Science of Doom,
I highly value your “Bank-of-England-approach”.
Thanks.
S.O.D.
“Do you see that average temperature, (T1+T2)/2, can be different in two cases yet the same average radiation can be emitted?”
Yes, but that proves nothing.
“There’s something very strange going on. The temperature is increasing, but the average emission of radiation has stayed exactly the same:”
Yeah, I think we have a pea-under-the-thimble game here, which is exposed by the idea of “average.” It isn’t the “average emission” that is critical, it’s the total heat in vs heat out. Pack your bags.
I’m not writing this to convince Bryan of anything, but new people visit the blog all the time and some might think, because of the confidence with which he speaks and the technical terms used, that perhaps he has shown some issues that need to be addressed.
The Planck equation for emission of thermal radiation – see for example The Sun and Max Planck Agree is one of the most solid and established laws in thermodynamics.
If you know the temperature of a body and you know its emissivity (a fundamental property of the material) you can be certain that you will know the emission of radiation from that body.
This is why Planck’s law is so widely used and so foundational – because it is always found to be true.
Planck’s law tells you the spectral intensity (how much energy at each wavelength in each direction per unit solid angle) and so Stefan-Boltzmann’s equation is simply the integration of this across all wavelengths and all directions.
You can see this equation in the maths section at the end of the article, also in the main section.
Bryan doesn’t appear to understand the particular reference that G&T make to this equation -instead mixed it up with ideas about Kirchhoff’s law. But it’s simply the fact that the Stefan-Boltzmann equation is the “hemispherical emissive power” – which if you picture a planar surface is the radiation not just up, but also “off to the sides” and “down to the horizon”.
There’s no confusion in reality about how much radiation is emitted from a 200K surface, or a 100K surface, or the surface at any temperature. So long as the emissivity is known. And emissivity isn’t a random property that has any uncertainty attached. People produce measurements of emissivities of surfaces and materials and gases and other people use them to make furnaces, aircraft, boilers and just about everything else that requires, or deals, with heat.
JAE:
JAE, total heat out is average emission x time x surface area.
(Where average emission is measured in W/m^2)
It’s not average temperature x anything.
How will you work out “heat out” from average temperature?
Write down the equation and let’s have a look at it.
S.O.D.
Yes, that’s one way to express the total heat, but it is NOT the way heat flows in the real world, because you are artifically constraining time. Your model is screwy, because it assumes constant power. You need to look at total HEAT (joules), not power (watts–joules/sec). I can input 1,000,000 w/m-2 for an hour and then output 41,666 w/m-2 over 24 hours. I still have radiative balance, which seems to me to be the real the point here.
Oops, probably a math error there, but the point stands.
JAE:
So your argument is that my power output will change over time – in fact it does.
So total heat (J) = “integral sign” emission(t). area . dt
This means that we integrate emission (which is a function of time) x area over the time period.
Well that’s why I calculated average emission.
Average emission = total heat radiated / time
I took the average of all of my radiated power values for each time step instead of summing the energy at each time step.
I could have shown that figure instead but it’s just a little harder for people to digest as it is a large number.
Total heat = average emitted power x time x area.
Let’s see the units on both sides of the equations:
On the left side = J
On the right side = W/m^2 x s x m^2 = J/(s.m^2) x s x m^2 = J
(I added this because you said I was dealing with power, not heat)
Radiative balance is the real point. That’s why there is a graph showing how absorbed energy and radiated energy “change” (don’t change) as we vary the heat capacity.
They don’t, because energy in = energy out. And yet the fictional idea of “average” temperature changes.
There’s no “pea under the thimble” stuff going on. There’s no trickery. This is just basic physics.
Roger Pielke Sr has made a point about this for some years – average temperature is a fairly useless and arbitrary construct. If we want to do any kind of averaging we should be averaging T^4 as it provides a measure of radiated power.
If you think I’m wrong, just go ahead and write down your formula using your average temperature.
It’s a serious comment – it’s when you try to write down an equation that you have the first opportunity to see whether your ideas are correct.
(Note: my model uses 1 m^2 surface area for simplicity, which is why I was able to drop “area” out of some of the equations above – for readability – just in case anyone thinks the maths is wrong).
tomorrow, if I can figure it out. 🙂
Dr Doom,
Just to make sure I’ve understood you correctly – you agree that if earth had 100% nitrogene atmosphere (a non greenhouse gas), the “average” temperature of earth would be different (I’m not entirely sure it wouldn’t be lower) from the 255 K blackbody radiation would suggest.
I have a feeling that some of the blog readers have somehow made a leap from the explanation of concepts to real world applications. A bit like explaining that airplanes are a proof that gravity doesn’t exist. Or, maybe a more appropriate example, the fact that two objects weighing the same amount can fall at different speeds, means that F=mg is not correct (I think someone made that point a few posts back already). I’m sure that they are trying to actually argue that you can’t find out the rate at which an object falls on earth using F=mg (only), while noone has actually made a claim that you can.
I guess I should have been more specific about F=ma. If you’re measuring to enough significant figures, even if the velocity isn’t all that high, you have to start thinking about relativistic corrections to mass and acceleration. The clocks in the GPS satellites have to be corrected for both velocity and the strength of the gravitational field if measuring position to military precision (on the order of cm).
Mait:
[Now I’ve reread the question I’m not sure I read it right]
(?) Correct (if I understood what you asked..). The average temperature of earth would be 255K
Where “average temperature” is defined via the equivalent average radiation of 239W/m^2.
After all, with nothing to absorb longwave radiation, if the earth surface radiated at its current 396W/m^2 the OLR would also be 396W/m^2 and the planet would cool down.
And once it dropped below 239W/m^2 the planet would heat up.
How the energy would be redistributed about the planet is a totally different question.
Of course, many people struggle with the idea but it’s just radiation 101 and the 1st law of thermodynamics.
Readers may be interested in just what the limitations of applicability of Planck’s equation, Stefan-Boltzmann equation (the integration of the Planck function over all wavelengths) and how they are related to Kirchhoff’s Law.
The reference below takes the reader through first principles and by a step by step approach reaches the conclusion that great care must be exercised in the use of these three equations.
They are not universal.
Click to access PP-11-06.PDF
DeWitt Payne
I wonder if you are the DeWitt D. P. cited in ref 17 below of the article in my post above?
17. DeWitt D. P. and Nutter G. D. Theory and practice of radiation
thermometry. John Wiley and Sons Inc., New York, NY, 1988.
For interest, the absorption vs radiation graphs for the last 3 cases:
You can see the lag that develops between absorbing and emitting radiation.
scienceofdoom
Out of interest, redo the absorption vs radiation graphs for the last 3 cases, this time using emissivity (e) having a value of unity.
And by popular demand, the absorption vs radiation graphs for the last 3 cases but with emissivity and absorptivity changed to 1.0:
Note that the starting conditions are not quite right so the first cycle is different from subsequent cycles, which also means that if I calculated the averages across all cycles there would be a larger spread of average emitted radiation.
scienceofdoom
……”Note that the starting conditions are not quite right so the first cycle is different from subsequent cycles,”…..
Why not use the correct starting conditions?
I guess because the correct starting conditions are only known after you’ve generated the graph and it’s rather pointless to bother when it doesn’t change the result. It would be little different than just omitting the first cycle from the graph.
I think most people are missing the significance of SoD’s analysis here; as has been shown before this statistical interpretation of Stefan-Boltzman really cuts the legs from underneath the AGW based nexus between radiative imbalance and increases in GMST, the base paramenter of AGW. Lubos looked at it here:
http://motls.blogspot.com/2008/05/average-temperature-vs-average.html
The Pielke paper is here:
Click to access r-321.pdf
And the final word is here from Lucia after eli had a shot at the Pielke paper:
http://rankexploits.com/musings/2008/spatial-variations-in-gmst-eli-rabbett-vs-dr-pielke-sr/
The Alan Siddons paper I think raises a good point about regolith heating and subsequent release of heat; on the Moon, without an atmosphere, this effect can be lag adjusted without impugning the applicability of SB; on Earth with an atmosphere maligned Nahle raises an interesting point about induced emission;
http://biocab.org/Induced_Emission.html
Nahle argues that night-time induced emission by released heat from the regolith prevails over the backradiation which is a product of spontaneous emission.
re the answer to Mait:
The popular belief in the greenhouse effect of some 33 degC
is based on outgoing radiation 240W/m2 , average, radiated from a surface at 255K
assuming an emissitivity of 1,0.
The outgoing radiation 240 W/m2 can also be explained as coming from a surface at 288K, with an emissivity of 0,62.
In such a case, no greenhouse effect have to be explained.
SOD,
DeWitt got my point.
scienceofdoom
Why not compare like with like?
You spent a great deal of effort showing that the emissivity values are very nearly unity.
Redo the temperature time graph with e=1 and then compare it to the ilovemycarbondioxide graph.
After all that’s what this thread is all about.
SoD
I think you read my question the wrong way around. I’m fairly certain the average temperature wouldn’t be 255 K, which would radiate at the absorbed rate (I had assumed for simplicy that the absortion of earth without to be 239 W/m2, which wasn’t probably a very good idea).
I’ll take a few steps back to illustrate what I’m trying to say. I’m going to take a very extreme example, but I hope you’ll manage to extract my point from it without dwelling of the impossibilty of it.
Let’s assume a earth model that absorbs in the solar spectrum as a black body (albedo is 0). In this case, we get the total energy absorbed by earth of 1,74 x 10^17 W, which makes 342 W/m2 (from earlier blogposts). And the corresponding blackbody temperature would be about 279 K (from sperctralcalc.com) Now let’s assume that we have a magical earth with a 10000 km2 area of earth (10^10 m2) which we’ll call “Latvia”. Now Latvia has surface temperature of 2353,6 K and hence radiates
1,74 x 10^6 W/m2 (Latvia is a very black place) and the total “radiative power” of Latvia is
1,74 x 10^6 x 10^10 = 1,74 x 10^17 W
Which means that the rest of the earth should have a temperature of 0 K in order to maintain radiative balance. Now to calculate the average temperature of earth we multiply the temperature of Latvia with the relation of area of Latvia to area of earth we get:
2353,6 K * 10^10 m2 / (5,1 x 10^14 m2) = 0,46149 K
Which is noticably different from the 279 K I would say.
This is ofcourse insanly over the top example, but it should demonstrate that you can’t calculate the average temperature of the surface like this as long as the temperature isn’t uniform across the body, which it can’t be for a earth sized object powered by the sun due to laws of physics and our understanding of geometry (I don’t think it’s even theoretically possible with current theories). This is ofcourse due to the power of 4 in the equation. I’m fairly certain you wrote a blogpost about why the average surface temperature is not a very meaningful thing which uses somewhat similar concepts in my opinion.
———————————————————
“Where “average temperature” is defined via the equivalent average radiation of 239W/m^2.”
———————————————————
I don’t think this definition makes any sense unfortunately.
Mait:
Well explained, and as I’ve been describing everything that’s wrong with averages I should have been much more careful in my explanation.
After writing a very long comment I decided to turn it into a post.. out shortly.
Here’s the measured temperature on the moon.
http://diviner.ucla.edu/science.html
You will note that the bottom of the curve is fairly flat and the corner sharp, not showing the smooth transition to exponential decay of SoD’s curves, nor is the decay clearly tending to zero. The flat bottom is around 70-100 K, at any latitude. The peak varies from about 270 to 400 K, pole to equator. (The graph annoyingly uses a false origin, starting at 50 K.)
I suspect the reason for the difference is that the thermal behaviour is not that of a simple heat reservoir with a well-defined heat capacity. The rock a short distance beneath the regolith remains at a constant temperature, constituting a heat reservoir with a huge capacity. (I’ve discussed this issue before in the debate on whether the oceans have more thermal capacity than the land.) Although the ground has a very large thermal capacity (infinite for all practical purposes), it is isolated from the surface by a layer with a large thermal resistance. (So the effective heat capacity is frequency-dependant.) The temperature below the surface settles to a long-term average determined by the (integrated) average of the heat conducted in and out – which is linear in the temperature difference, not a fourth power as with radiation.
At sunset the temperature change is initially sharp, as the sudden change in insolation is “high-frequency” and therefore corresponds to a small thermal capacity, but the overall day/night cycle is a much lower frequency and therefore has access to a much greater thermal capacity.
So we have the underground temperature determined by a linear average of the subsurface heat flow, and the surface temperature determined by the non-linear response to the sum of the heat coming from the sun and the subsurface. The surface must on average radiate the same amount of heat as it absorbs from the sun during the day. But the temperature at any given time is a more complicated affair.
This is a very nice article for showing what is wrong with the very odd unpublished paper at “ilovemycarbondioxide”. It has been raised as a topic at other blog articles, and by providing a place where this paper is the main topic, you provide a useful service for those who would like to discuss it. Thank you!
The difficulty with the “ilovemycarbondioxide” paper is, as you show, a superficial application of Stephan Boltzman relations with no consideration of other properties of the surface to which it is being applied. This is, of course, no criticism at all of NASA or the IPCC or other working Lunar physicists who apply well established physical relations more appropriately.
I would like to underline, however, that there is more than only heat capacity involved in estimating surface temperatures. In particular; although the Moon is far less geologically active than the Earth, it does have considerable internal heat and there is a small flux of heat going up towards the surface. The upper layers of regolith are a very effective insulator, but not a perfect insulator. On average, there there is a small flux of heat of around 25 or so mW / m^2 up from the interior to the surface. Different estimates of this value exist in the literature, but the basic fact is well established and it also bears somewhat upon the nature of surface temperature; particularly at night.
The temperatures a little below the surface are almost constant, with a short and sharp gradient to the surface over the last few centimeters that swings around from positive to negative with the day night cycle.
Hi Bryan. I am too busy with other matters to take up this subject at this time; but since you had an interest I thought I would drop in this one comment here and wish you well as you all discuss this topic. It is a good topic for understanding more about applications of thermodynamics to a planetary surface in a particularly simple case where there is no atmosphere; which simplifies the whole matter enormously.
Cheers all — sylas
Mait and Nullius are right but to my thinking are still in agreement with what SoD has written. The Alan Siddon’s article showed how a NASA assumption of what the Moon’s temperature should be based on incident radiation, reflectivity and the application of Stefan-Boltzmann based on what was assumed to be emissions from the surface was incorrect.
The problem which Siddons high-lighted was regolith absorption and storage of heat which when gradually or suddenly released would confound an assumed surface temperature based on an assumed emissivity. But as SoD has noted that stored heat could be normalised and the surface temperature calculated in a way consistent with Nullius’s view of how the stored heat is released.
The second, more profound problem [which Alan missed] is that a particular location where emissivity based on insolation and regolith release is calculated cannot be used to determine an average temperature for the whole Moon. I have given a number of links above to where this issue has been debated before and it is summed up by this: The AGW GMST is incorrect because it does not allow for this effect, that is: (A + B)^4 > A^4 + B^4; as Mait shows you can have an average temperature which does not reflect the radiative balance of the Moon and vice-versa.
This second point applies to Earth despite the fact that Earth has backradiation which the Moon does not have; so any point on Earth will have incident solar, reflectivity, regolith absorption and back radiation confounding any application of SB to calculate temperature at that site. But Colin Davidson on another thread puts backradiation in its proper perspective:
“The NET fluxes from the Surface are:
a. Direct Radiation “through the window” to Space. According to Kiehl&Trenberth this is 40W/m^2.
b. Fluxes into the Atmosphere:
(1) Evaporated Water Vapour, 78W/m^2
(2) NET Radiation, 26W/m^2
(3) Conduction, 24W/m^2
[Numbers are from Kiehl &Trenberth, 1997. See IPCC, AR4, WG1, Chapter 1.]
Note that the items at b are all converted to sensible heat, at various heights in the atmosphere, and are ALL then convected. For Conduction, we know this is at the bottom of the column. For Radiation, this is also very close to the ground, probably the majority of radiation is absorbed by 25m altitude (if you doubt this, check out the absorption tables for CO2). For Evaporated water vapour the injection of heat into the atmosphere is more spread out, and probably most of this heat enters the atmosphere literally in the clouds.”
So AGW fails in 2 respects; firstly, the idea of a GMST is fatally flawed because it does not reflect the Nexus between ERB or MoonRB and any Tave. Secondly, backradiation, which is essential for the greenhouse effect, is insignificant compared to the other methods of heat transfer.
Well, I still think there is some hockus-pokus, shell-game, or smoke-and-mirrors going on (maybe all three 🙂 ).
We should not be comparing a series of planetoids that differ only in their heat capacity. I thought we were looking at a comparison of what the temperature “should be,” according to only the SB equation vs. what it actually is. That is what the iloveco2 paper is about.
Through the eons, the moon (and Earth) have basked in the sunshine long enough to reach a rough thermal equilibrium. That equilibrium includes a LOT of stored heat in the oceans, atmosphere, etc. The SB calcs do not include that, and that is the issue, it seems to me.
The “average insolation over a disk that has the radius of the planet” is WAY simplistic and is not instructive.
In short, I still don’t see how the current exercise has anything to do with the iloveco2 thesis. Do I need Dr. Phil?
Nonsense. Backradiation is very large and this is DATA. It is MEASURED.
The largest single energy flux at the surface of the Earth is the upwards thermal IR radiation. The backradiation is the second largest. These two are both much larger than any of the other energy fluxes. In particular, the energy absorbed at the surface from incoming solar radiation is about half of what is absorbed from downwards backradiation. OK?
Reference: Stern, S.C., and F. Schwartzmann (1954) “An Infrared Detector For Measurement Of The Back Radiation From The Sky”. J. Atmos. Sci., 11, 121–129. This obtained values in Maryland, and they were in the range 314 to 405 W/m^2 (daytime) and from 206 to 312 W/m^2(nighttime), limited to clear sky conditions.
Modern measurements give the same magnitudes and much more spectral detail. The spectral characteristics of backradiation show the greenhouse effect very directly, as the energy is from emission in the bands where greenhouse gases are able to interact with thermal radiation.
Note that greenhouse effects are critical on Earth, but play no part for the much simpler case of the Moon, which is the proper topic here. Sorry for adding to the divergence into greenhouse, but I felt this assertion needed correcting.
Back to the Moon, folks…. enjoy! Cheers — sylas
sylas: The measurements you cite do not prove cause-effect of any sort. Of course the amount of IR corresponds to the temperature of the air. It has to. But that means absolutely nothing, relative to temperature, as shown by the following exercise:
Please provide me with some measurements, at night, showing the difference in backradiation between Phoenix and Atlanta on a nice July day (these cities are at almost the same latitude and elevation). Please consider the fact that the amount of “greenhouse gases” in Atlanta is about 4 times that in Phoenix. Where is the “greenhouse effect,” since is is MUCH hotter at midnight in Phoenix in July than it is in Atlanta?
I’m looking for some empirical evidence of the “greenhouse effect,” and I have found none in about 3 years.
[…] 5, 2010 by scienceofdoom On Lunar Madness and Physics Basics, one commenter asked a very good question in response to a badly phrased answer from […]
Mait:
The overly-long “response” is at The Hoover Incident and I would be interested in your comments – and anyone else’s of course.
JAE:
You asked that question a while ago and I said:
The whole point is there are many regional and local climate effects. Equally many locations at the same latitude that receive exactly the same solar radiation and have the same humidity are at quite different temperatures. But no one is claiming the sun’s radiation has no effect.
If we measure 300 W/m^2 of downward longwave radiation at the surface it has exactly the same effect as 300W/m^2 of solar radiation at that spot (once we allow for the fact that there will be more reflection of the solar radiation).
This is just thermodynamics basics.
Claiming it’s not the case because two cities at the same latitude should have exactly the same temperature (without “greenhouse” downward longwave radiation) is amazing.
Pair up different cities around the world at the same latitude and compare the temperatures!
I’m sorry Sylas, I thought it was plain that I was quoting Colin in respect of NET fluxes:
“The NET fluxes from the Surface are:
a. Direct Radiation “through the window” to Space. According to Kiehl&Trenberth this is 40W/m^2.
b. Fluxes into the Atmosphere:
(1) Evaporated Water Vapour, 78W/m^2
(2) NET Radiation, 26W/m^2
(3) Conduction, 24W/m^2
[Numbers are from Kiehl &Trenberth, 1997. See IPCC, AR4, WG1, Chapter 1.]”
The 2008 K&T cartoon gives a NET upward radiation flux from the surface of 33w/m2 with a downward adjustment to water vapour to 76w/m2 and conduction to 16w/m2 but the point holds; that point is more net heat is leaving the surface through methods other than radiation, particularly water; that to me means 2 things; water is a dominant mover of heat compared to CO2 and the sun’s 168/166 w/m2 is a far more dominant heater than CO2 backradiation.
sylas
No, thanks for adding it.
I’m continually amazed that so many people believe 300W/m^2 doesn’t have any effect on the earth’s surface temperature.
It’s a thermodynamic revolution.
cohenite:
I’m still amazed – even with the explanation.
Consider a surface with an upward radiation of 350W/m^2 and downward longwave radiation (due to the “greenhouse” effect) of 340W/m^2.
The net radiation is 10W/m^2 so we can just ignore the “back-radiation” effect – after all it’s not really significant compared with other climate effects.
Currently the surface is at 280K (7’C) – (from the Stefan-Boltzmann equation with longwave emissivity = 1).
So we remove the “backradiation” of 340W/m^2 because it’s insignificant right?
So the surface temperature will continue to be about 7’C?
Is that what you are saying?
Ok, so let’s consider this at a highish latitude in winter where the average solar radiation during the day is around 340W/m^2.
Let’s remove the sun.
Clearly nothing will happen and the temperature of this surface will stay around 7’C.
After all, you can take away 340W/m^2 and nothing significant happens.
What’s wrong with this picture?
JAE:
Energy out > Energy in – the planet cools down
Energy in < Energy out – the planet warms up
(Energy in can include sources of energy like nuclear or geothermal as Sylas points out)
That’s why I demonstrated the points that I did in the article. It doesn’t matter how much heat capacity a planet has or how much heat is already stored there.
All that happens when you start off with a very cold or a very hot “radiating temperature” relative to the incoming radiation is that the planet heats up or cools down until it reaches its equilibrium.
And all that happens why you increase a planet’s heat capacity is that it takes longer to change temperature.
Thermodynamics basics. It’s very simple. Not simplistic.
If you don’t grasp the basics it will always seem like “smoke and mirrors” even though you can’t explain what’s wrong with it.
“All that happens when you start off with a very cold or a very hot “radiating temperature” relative to the incoming radiation is that the planet heats up or cools down until it reaches its equilibrium.”
Yes. That is all I said.
Sheesh! Without backradiation the Earth’s GMST is 255C, with backradiation 288C.
Just following on, noting that radiated energy increases with the 4th power of temperature so backradiation is in addition to the first temperature effect of the insolation:
166w/m2/255C; is that correct?
“Pair up different cities around the world at the same latitude and compare the temperatures!”
I did that for the USA, not the world, and it is the same story.
THERE IS ABSOLUTELY NO EMPIRICAL PROOF OF A GREENHOUSE EFFECT. PERIOD. IF YOU HAVE SUCH PROOF, I WOULD REALLY LIKE TO SEE IT. YOU HAVE ONLY A WEAK HYPOTHESIS. ADMIT IT.
No, of course 166w/m2/255C can’t be correct; it must be 341w/m2/255K
JAE:
If the hypothesis is that “greenhouse” radiation alone explains local temperature at each and every place around the world then you have falsified the theory.
But it’s not the theory that I’ve read or the one that I try to explain here.
There’s an average of about 300W/m^2 downward longwave radiation from the atmosphere absorbed by the earth’s surface.
I find this very convincing. I don’t know which bit you don’t understand or believe even though you have tried to explain it before.
cohenite:
I’m not sure I understand the question.
In case I’m roughly right.. if you had only 168W/m^2 absorbed by the surface the temperature would be 233K (-40’C).
Why isn’t it 255K?
Because the atmosphere absorbs some of the solar radiation and this is added to the climate system.
So when the atmosphere is radiating to the earth, some of that is because of solar heating. The atmosphere absorbs around 70W/m^2 of solar radiation.
Then if you add the average “backradiation” from the atmosphere of 324W/m^2 you get a total of 492W/m^2 absorbed by the surface – so these radiation values just get added.
492W/m^2 = 305K (32’C) but that’s not actually what happens because over 100W/m^2 is moved from the surface into the atmosphere by convection and conduction.
So the actual radiation from the surface is around 390W/m^2 (15’C)
These are global annual average values, which means lateral heat movement gets netted out.
At any one location on any one day the numbers might be quite different – some examples in Sensible Heat, Latent Heat and Radiation .
Some of the numbers are estimates, calculated as the missing bits via an energy balance equation. Some values are still uncertain to within 20W/m^2 especially the solar absorption in the atmosphere.
Well, I hope I understood the question..
I have trouble marrying a GMST, which you and others have invalidated, and the need for a GMST to measure the greenhouse effect. The greenhouse effect seems to have a certain logic which doesn’t explain what is happening, or what should be happening with an increase in a major greenhouse component. Take Arthur Smith’s opus:
Click to access 0802.4324v1.pdf
Smith notes this:
“Planet solar constant albedo solar day Teff Tave Difference
(W/m2) (Earth days) (K) (K) (K)
Mercury 9127 0.12 176 434 ? ? 11
Venus 2615 0.75 117 232 737 505 0.7
Earth 1367 0.306 1 255 288 33 0.04
Moon 1367 0.11 29.53 270 253 -17 20
Mars 589 0.25 1.03 210 210 0 0.2”
Look at the Moon; the average temperature is less than the effective temperature; but none of the planets conform to Smith’s dictum that: “thanks to Holder’s inequality, this average temperature Tave(t) is always less than or equal to the effective thermal radiation temperature Teff (t), so T 4 ave is less than or equal to T 4 eff”; not even Mercury which has no atmosphere and Mars which has a thin but CO2 dominated atmosphere.
That aside Earth and Venus have a higher Tave than Teff supposedly because of the greenhouse effect. The greenhouse effect on Earth is 33C which is produced by 323w/m2 of backradiation according to AGW theory. According to Lindzen, if there were only radiative transfer of heat, that 323w/m2 of backradiation would create a greenhouse effect of 77C instead of 15C [288K]; the greenhouse effect is only working at less than 25% of its potential. I made the suggestion that the NET radiative flux should be compared with other heat transfer processes; you think otherwise. What is your solution to the underperforming greenhouse?
cohenite:
You don’t need a GMST to measure it. You can simply work with the radiation number instead, it’s just a convention to turn it into an “effective temperature” – check out The Hoover Incident.
On your other early points I will try and get a chance to check the paper and comment in the next day or so.
If radiative transfer of heat was the only mechanism for moving heat from the surface through the atmosphere, the temperature at the surface would be much higher, as Lindzen rightly points out. Uncontroversial in climate science.
Convection moves heat through the lower atmosphere and effectively moderates the surface temperature.
You can name it an “underperforming” greenhouse if you like, it doesn’t really matter.
If you do the maths as to the surface temperature without the greenhouse effect it’s much colder.
It’s interesting to compare the net radiative flux with other processes but it doesn’t tell you the effect of removing one side of the process. The surface will always radiate according to the Stefan-Boltzmann law, so take away 320W/m^2 incoming and you will have a colder temperature.
Surely another interesting question is what would happen if CO2 did not radiate/absorb in the infra red.
If we remove any effects on plants/animals that this would involve.
The thermal properties of the atmosphere would be virtually unchanged.
The Lunar example shows that even without an atmosphere the temperature profile is smoothed out.
If we add;
1. An insulating atmosphere.
2. The ability of water to moderate temperature by changing its state(ice,liquid water and water vapour).
3. The high value of waters specific heat capacity and the extent of the Oceans gives a vast storage system to moderate temperature change.
4. The effect of gravity in producing tidal flows and rivers means that Earths water will be well mixed.
5. The Earth is considerably more geothermally active than the Moon
I think that this is why a growing number of people are very sceptical of the notion that the so called trace gas CO2 “greenhouse effect” exists.
“There’s an average of about 300W/m^2 downward longwave radiation from the atmosphere absorbed by the earth’s surface.”
Yes. But the question was about the greenhouse effect, and there’s a logical step missing between this statement, and the one you’re trying to prove.
Simple example, I have a pan of water on the stove. 700 W are going into the bottom, and the temperature at the bottom of the water in the pan is 100 C. I turn up the gas to increase the heat entering to 1000 W. We have an additional 300 W entering the water. So, by how much does the temperature of the water rise?
You see, you cannot jump from “300 W/m^2 more heat flow” to “therefore surface temperature rises in a ‘greenhouse’ effect” without some additional discussion of the other mechanisms involved. One statement does not logically follow from the other. That doesn’t mean the gap can’t be filled in, but if you don’t even recognise that there is a gap there, readers who think there is are always going to struggle.
Yes, the stove emits the extra 300 W. Yes, the pan absorbs it. The stove is far hotter than the pan, and heat flows spontaneously from one to the other. It does not magically bypass or bounce off the pan when it gets to 100 C. If you draw a Kiehl-Trenberth type of diagram, the initial state has 700 W going in the bottom of the pan, and 700 W coming out of the top. If you scratch out that lower 700 W and draw in 1000 W, there is a net “forcing” of 300 W that tends to increase the heat in the pan. None of this is in doubt. But you can’t use any of these statements to logically deduce that the temperature of the water will increase. There is no “stoval warming”.
It’s off topic for this post, but you might like to think about doing another post to fill in that logical gap, sometime.
Bryan says:
Name something that they are right on (that is original to them). As for things they are wrong on, let’s start with this sentence in their reply to our comment: “The correct question is, whether the colder body that radiates less intensively than the warmer body warms up the warmer one. The answer is: It does not.” We gave multiple examples of how in fact the presence of a colder body does warm up a warmer body relative to the temperature that it would have in its absence. That is a pretty basic thing to be wrong about.
cohenite says:
I think it looks just about as bad the second time as it did the first. The main problems with that paper are:
(1) It makes an irrelevant point. A metric such as global temperature (or, better, global temperature anomaly) is a metric or figure of merit. The fact that it is not rigorously definable thermodynamic quantity is irrelevant. In fact, temperature in any system not in equilibrium is not rigorously definable thermodynamic quantity and no systems are truly in equilibrium and yet we still find temperature to be a useful metric.
(2) Its only real attempt to show relevance (at the end where they see how different kinds of definitions of the average temperature can lead to different temperature trends) just demonstrates that if you define the metric stupidly enough, it isn’t very useful, hardly exciting news. In particular, they take the average of the temperature to ridiculously large positive and negative powers so that their “average” essentially just picks out the lowest or highest temperature in each month. The solution to the problem is simply not to do this. (And, the fact that they have only a fairly small number of different stations but have ones that span a large range of the earth’s temperatures probably exaggerates the effect on the trend relative to what would occur with a more realistic network of stations, even if they did use such ridiculous averages.)
” we still find temperature to be a useful metric.” “We” are costing a lot of people a lot of money on the basis of supposed increases in GMST being the main indicator of AGW. This thread and the follow up one, “The Hoover Incident”, show that a GMST can badly misrepresent Earth’s energy budget conditions. The fact is the use of the GMST has been abused because the obvious caveats that the McKitrick paper raises have not been applied.
Joel Shore
It’s just that Bryan thinks they are right on this. And even though painfully and slowly on this blog we have worked through to the logical conclusion that a colder body can increase the temperature of a hotter body – in The First Law of Thermodynamics Meets the Imaginary Second Law – Bryan has failed to reach a conclusion.
First, appears to support it
Second, appears to claim it’s irrelevant for the earth
Third, says we need to have “scale” defined before we can draw any conclusions
Fourth, claims formulas not correctly applied:
And implied (but not demonstrated) that the Stefan Boltzmann equation was not used correctly – but simply refers to G&T who note the exciting fact that the Stefan-Boltzmann equation is the total hemispherical power from a surface. Which is how I have used the formula.
And finally, admitted the truth:
However, nothing can break his unshakeable faith in the imaginary second law.
cohenite:
…Which really gets to the crux of the matter: Namely, if you sufficiently dislike a policy, then you can find reasons (poor though they may be, as McKitrick et al.’s are) to not accept the science.
And yet, noone has presented any actual evidence that the use of global temperature anomalies in any way misrepresents the temperature changes that are occurring. McKitrick et al.’s attempt to show that they might is misguided for the reasons that I explained.
“And yet, noone has presented any actual evidence that the use of global temperature anomalies in any way misrepresents the temperature changes that are occurring.” Well, that’s not quite right:
http://pielkeclimatesci.wordpress.com/2010/03/19/an-example-of-why-a-global-average-temperature-anomaly-is-not-an-effective-metric-of-climate/
Click to access r-321.pdf
In any event, this thread and The Hoover Incident should give you pause about the use of a GMST to support unequivocally AGW.
Joel Shore says
…We gave multiple examples of how in fact the presence of a colder body does warm up a warmer body relative to the temperature that it would have in its absence. ….
scienceofdoom goes even further
…It’s just that Bryan thinks they are right on this. And even though painfully and slowly on this blog we have worked through to the logical conclusion that a colder body can increase the temperature of a hotter body…..
What emerged from an earlier discussion at SoD was that a colder object cannot “heat” another object higher than its own temperature.
In other words the radiation coming from -20c atmosphere cannot “heat” Earth surface to more than -20c.
I think it was Nick Stokes and Alexander Harvey who pointed that out.
This shows the limited influence of backradiation.
Now if you are talking about the atmosphere as an insulator i.e. reducing the rate at which the hotter object loses internal energy then that all right.
However radiation makes the same contribution as say conduction in that regard.
If however you imply that HEAT travels from a colder substance to a warmer substance without a heat pump then you are completly wrong.
Joel will perhaps take this opportunity to apologize for the Halpern Group statement that G&T said that ‘radiation cannot flow from a colder body to a hotter body’
Alternatively give a page number from the G&T paper to back up this false claim.
scienceofdoom
Have you noticed that the nice graphs produced earlier in the thread are almost exactly analogous to a diode and capacitor circuit rectifying AC current.
With a bigger and bigger capacitor the current gets smoother and smoother.
The Earths Oceans are analogously a very large capacitor.
Bryan, can you please give a reference of where Halpern et al say that G&T said that ‘radiation cannot flow from a colder body to a hotter body’.
I can not find this. As far as I can tell Halpern et al talk about radiative heat transfer, e.g. in the abstract: “They claim that radiative heat transfer from a colder atmosphere to a warmer surface is forbidden[…]”
D.
Bryan:
What emerged from The First Law of Thermodynamics Meets the Imaginary Second Law was that a colder object can increase the temperature of a hotter object.
Bryan has yet to explain which particular step is wrong, or which formula is wrongly applied.
But Bryan can’t find a fault with the example, other than that he doesn’t like the conclusion.
scienceofdoom
I believe if you check back you will find that this is an accurate quote.
…..”In other words the radiation coming from -20c atmosphere cannot “heat” Earth surface to more than -20c.
I think it was Nick Stokes and Alexander Harvey who pointed that out.
This shows the limited influence of backradiation.”……
Bryan:
It was your quote Bryan. Well done for citing yourself. That obviously proves it.
Newcomers and more skeptical folk might be interested in your analysis of The First Law of Thermodynamics Meets the Imaginary Second Law and your demonstration of exactly where it goes wrong.
diessoli
From Rabetts G&T 11
In GT09 there seems to be confusion about whether the Clausius statement applies to net heat flow or simply any flows of heat. Qualitatively one can make a simple argument about interchange of thermal energy between two bodies. Consider two perfectly absorbing disks in a vacuum at temperatures TA and TB, with TA > TB. If B is isolated, it will emit thermal energy at a rate given by the Stefan-Boltzmann Law. If the Clausius statement referred to any flow of heat when the two disks were placed opposite each other, B would have to stop radiating towards A because if it did not, heat would be transferred from a body at lower temperature to a body at higher temperature. This is obviously absurd. The ability of either disk to radiate does not depend on the presence of another disk that absorbs the emitted radiation. …..
In several blogs where Rabett and friends opine they seem to have convinced themselves that the G&T paper implied that G&T were saying that radiation from cold surfaces cannot move to warmer surfaces.
Indeed you will find heavy hints of this in SoDs threads here.
However SoD has been careful about being explicit on this point.
Bryan:
Exactly right.
Until I had my first encounter with Bryan (search April 11th, 2010 at 3:29 am) I imagined that the only way that someone could avoid the obvious conclusion was to claim that the radiation from the atmosphere didn’t “reach” the surface.
The other choices are:
– the surface doesn’t accept the incident radiation (absurd)
– the absorbed radiation doesn’t “have any effect” (violates the first law of thermodynamics)
For some reason I thought that the first idea – the radiation doesn’t exist – was more likely for “imaginary second law” believers.
Bryan put me right on that one, with an interesting diversion into first claiming that the downward longwave radiation (DLR) at the earth’s surface was Rayleigh scattering.
But after I asked why the spectrum of the DLR was heavily weighted towards CO2, O3, CH4 as well as water vapor wavelengths, dropped that one.
Then just didn’t answer my question, which I asked in very similar versions on that blog and many Science of Doom blogs, e.g.:
After many exchanges.. on Radiation Basics.. Bryan finally said:
As a result, I wrote Intelligent Materials and the Imaginary Second Law of Thermodynamics which pointed out that 10um radiation from a +10’C body would be absorbed in exactly the same way as 10um radiation from a -10’C body.
Bryan didn’t comment on this key point until pressed at great length (search “Bryan” in that post for the many “not quite answering the question” answers) but finally said:
So now that the radiation “reaches” the surface, and the surface “absorbs” the radiation, I wrote The First Law of Thermodynamics Meets the Imaginary Second Law
This point is very simple. If the surface absorbs this energy, the surface must heat up (if it was cooling, it must cool down slower, but if it was already at equilibrium it must heat up).
At this point, as already predicted, Bryan found this one difficult, and (as noted earlier on this post ) never actually pointed out the flaw.
This is because there isn’t one.
And this is why anyone who is dealing with “imaginary second law” advocates has such a challenge. One (or more) of three impossible claims need to be believed:
– the radiation emitted by the colder atmosphere doesn’t reach the surface
– the radiation isn’t absorbed
– the absorbed radiation just does nothing, in violation of the first law of thermodynamics
And so far – incredibly – Bryan has been the most forthcoming of this movement, and yet to get each specific question specifically answered has been like getting blood out of a stone. As you can see by simply following these earlier links and searching for my questions of Bryan and his non-answers.
Not surprising for the rest of the world because once you have agreed with normal science for the first two points you are left with either claiming the first law of thermodynamics “doesn’t apply” or rejecting your faith.
Not pleasant. But amusing for everyone else.
Bryan
You seem to forget that neither the surface of earth nor atmosphere are isolated objects from the rest of the world. In fact they both have the same energy source which is the sun. Now it is probably somewhat misleading (not necessarily wrong though) to claim that atmosphere is “heating” up the earth. In my opinion it is better to say, that it keeps the surface warmer (it loses less energy).
To illustrate the concept, let’s take a human sized object at human temperatures, remove all it’s clothes and send it out in the winter (let’s say it’s -10 C outside). Let it stroll about a few minutes or so (just so that it wouldn’t freeze to death), and then come back inside where we immediately measure it’s surface temperature. Now once it’s temperature has been restored to normal operating levels, we give it a warm coat (which is let’s say cooled down to 5 C). We send the human sized object out again and let it do the same things before for the same time. Let it come in again where we measure it’s surface temperature (under the coat).
Now a few questions to Bryan:
1. Do you think that the surface temperature of the human size object is higher in the second scenario?
2. If so, then why, considering the only difference is a coat which was at a lower temperature than the human sized object?
PS. I’m aware that this example has almost nothing to do with thermal radiation.
Mait
Perhaps you didn’t see my earlier post.
The atmosphere insulates the Earth.
The four mechanisms of heat transfer(including phase change) all play their part.
…”Surely another interesting question is what would happen if CO2 did not radiate/absorb in the infra red.
If we remove any effects on plants/animals that this would involve.
The thermal properties of the atmosphere would be virtually unchanged.
The Lunar example shows that even without an atmosphere the temperature profile is smoothed out.
If we add;
1. An insulating atmosphere.
2. The ability of water to moderate temperature by changing its state(ice,liquid water and water vapour).
3. The high value of waters specific heat capacity and the extent of the Oceans gives a vast storage system to moderate temperature change.
4. The effect of gravity in producing tidal flows and rivers means that Earths water will be well mixed.
5. The Earth is considerably more geothermally active than the Moon
I think that this is why a growing number of people are very sceptical of the notion that the so called trace gas CO2 “greenhouse effect” exists.”…….
Nullius in Verba made a very helpful comment
……”You see, you cannot jump from “300 W/m^2 more heat flow” to “therefore surface temperature rises in a ‘greenhouse’ effect” without some additional discussion of the other mechanisms involved. One statement does not logically follow from the other. That doesn’t mean the gap can’t be filled in, but if you don’t even recognise that there is a gap there, readers who think there is are always going to struggle.”…………
scienceofdoom
Given the figure of 300W/m2 backradiation one would think something dramatic could be shown that would be decisive in coming to a conclusion about the topic.
Gords “solar oven” pointed to the cold night sky can actually freeze water.
This came as a surprise to me, it was fairly dramatic.
You do not seem to have any physical effect to demonstrate this large magnitude of backradiation.
A cold object can radiate to a warmer object we are all agreed.
When the radiation gets to the surface it can ;
1. Be scattered or reflected
2. Be absorbed
3. Pass through
We will ignore 3 in this case.
The exact % split between 1 and 2 is where I am looking for some evidence and it obviously depends on the surface.
Simply saying Kirchoff’s Law says……. is not evidence.
In fact at the moment I am trying to find any experimental evidence to support Kirchhoff’s Law.
If you know of some experiments please let me know.
Phrases such as the colder surface “Warms up” or “heats up” or causes the “temperature to rise” implies a violation of the second law of thermodynamics.
You can just go back to The First Law of Thermodynamics Meets the Imaginary Second Law and demonstrate the problem with the examples.
Because I did not even use Kirchhoff’s law to demonstrate anything. You kept waving around possible irrelevant problems with Kirchhoff’s law as your green card.
But you finally agreed:
Therefore, although it took some time, you have accepted that radiation is absorbed into this hotter body from the colder body.
Now you have the problem that you have to throw out the first law of thermodynamics or the “imaginary second law”.
So you don’t need Kirchhoff’s law accepted or rejected. You need to come up with a reason why radiation from the colder body when absorbed by a hotter body can’t have any effect.
And decide whether to stick the knife in the first law or the imaginary second law.
No wonder you said: “I don’t know”.
End of the road.
Sure, except that backradiation is NOT a net flux. It is one part (the negative part, in fact) of the net radiative heat flow from the surface to the atmosphere. And its contribution is simply enormous! Certainly larger than any of the net flows.
Hence it is very significant indeed!
If there was no backradiation, the thermal radiative heat flow would be approaching 400 W/m^2 up from the surface, given the high temperatures we enjoy. Because we have a greenhouse effect, there is another 333 W/m^2 or so backradiation to include, which brings the NET heat flow to something around 60 to 70 W/m^2; which includes 40 W/m^2 or so escaping direct to space and rest being part of the flow of heat into the atmosphere. If our atmosphere disappeared, then the surface would drop rapidly in temperature, and ALL the emitted surface radiation would just end up going to space, and that would also be the net heat flow to space.
WITH the atmosphere, the surface radiates nearly 400 W/m^2, of which 356 W/m^2 is absorbed in the atmosphere (using figures in the updated 2009 paper of Trenberth et al), and then you SUBTRACT 333 W/m^2 of backradiation to get a net that is small; only about 20 to 30 W/m^2. This is SMALL, because backradiation is enormous, almost as much comes back as is absorbed from the surface in the atmosphere.
The Moon is a simple case because there is no atmosphere. If there was an atmosphere, but one made up of, say, nitrogen only with no greenhouse effect, then the Moon STILL be simple, with a small additional damping effect, and no additional warming overall.
JAE: my apologies, but I do not have a great deal of time, and explaining the observational evidence for the greenhouse effect here is a low priority for me. This article is about the Moon, which is much much simpler because it has no greenhouse effect. I am just pointing out that the magnitude of backradiation is LARGE in the very references cohenite is using — and any comparison of backradiation with net flows or with other individual energy fluxes confirms that it is enormously significant. If do not accept the validity of cohenite’s numbers and sources, then go in peace; I cannot help you. I will stick to emphasizing that the sources cohenite is using give numbers for backradiation which are very significant indeed, especially when compared with net heat flow.
Cheers — sylas
Bryan,
Just to make sure – you agree that surface temperature on earth would be lower if it didn’t have an insulator (atmoshpere) around it? Meaning the atmosphere keeps the surface warmer?
I don’t dispute an atmospheric effect – I don’t like the term greenhouse for reasons G&T correctly describe – and I don’t dispute backradiation. The issues are, how much does CO2 contribute to Tave [ OK, there is no better term, greenhouse] and how much will increases in CO2 contribute to an increase in the greenhouse: the answers: little and less.
Mait
Just to make sure…….
The effect of the atmosphere is to reduce the heat flow from the hotter object.
Heat only flows one way.
From a higher temperature object to a lower temperature object.
Unless or coarse a heat pump or such like forces it to go the other way
Bryan,
I’m not still following your thought pattern here I’m afraid.
Doesn’t reducing the heatflow out mean that it would need to become hotter, if the heatflow in remains the same (the sun still emits at the same temperature and the absorbtion by earth shouldn’t change either). Otherwise, where would all that heat go? Whatever heat is.
Bryan says:
You are welcome to your interpretation of what G&T are saying but if they are just saying what Nick Stokes and Alexander Harvey say then why did G&T write their paper? Was it to point out that something irrelevant to the greenhouse effect can’t occur?
(And, by the way, how much conduction of heat is there between the earth & its atmosphere and space?)
cohenite says:
Maybe I should have been a little clearer in my statement. It is quite true that a metric consisting of one number necessarily loses detail relative to looking at the entire distribution of temperature changes. And, one can argue about how well surface temperature changes are measured and how representative they are of atmospheric changes as a whole.
However, what McKitrick et al. tried to show is that the global temperature metric is meaningless and tried to imply that you could find just about any trend you wanted (including negative trend) depending on how you decided to take the average. This is the argument for which support is lacking, at least for any reasonable definition of the metric “average temperature” [be it, say, or ()^(1/4)] and any real-earth temperature distribution.
It just shows that you have to be intelligent in your analysis of data…particularly if you are dealing with a body, like the moon, where the heat capacity is small enough that the temperature changes between day and night or different locations are quite extreme.
Mait
Imagine its nightime and you had a magic switch that could make the atmosphere disappear and appear.
You plot a graph of temperature against time for 10 hours of one hour duration;
switch on, followed by one hour switch off.
During the switch on period the temperature drop would have a small value
During the switch off period the temperature drop would have a larger value.
Never will you see the temperature rise.
Phrases such as the colder surface “Warms up” or “heats up” or causes the “temperature to rise” in the Earth surface imply a violation of the second law of thermodynamics.
Joel Shore you say
…….”(And, by the way, how much conduction of heat is there between the earth & its atmosphere and space?)”…….
I would not be so dismissive of conduction.
The air particles on hitting the Earth Surface leave with a temperature characteristic of the surface.
The air particles speed up, in other words their temperature increases, the hotter air is less dense than colder air above and hence moves up (convection).
So convection in the atmosphere is caused mainly by conduction at the surface, so they must have approximately the same magnetude.
scienceofdoom:
“And even though painfully and slowly on this blog we have worked through to the logical conclusion that a colder body can increase the temperature of a hotter body”
As long as the ice in my lemonade at room temperature melts and the lemonade cools, the only thing you’ve demonstrated is your inability to model nature.
Bryan,
I agree that using the phrase “heat up” is somewhat misleading, but that’s pretty much all it is (poor choice of words at worst). As you demonstrated yourself, the surface without atmosphere has a lower temperature than the one with atmosphere. Vacuum is a very “cold” thing.
DrAgile
No one disagrees that if you mix two substances together they will end up at the same temperature.
Why not take a look at The First Law of Thermodynamics Meets the Imaginary Second Law and point out the errors.
The four examples are quite simple.
Example 2 is closest to your lemonade where 2 bodies in proximity and no sun to heat them simply cool down while getting closer together in temperature.
Example 4 is the one of interest where the first body has reached an equilibrium temperature with the sun and then a second body with a slightly lower temperature is moved into proximity.
In example 4 radiation from this colder body is incident on the first body and this energy is absorbed.
Pretty simple really but they can’t work like ice in lemonade because the 2 bodies aren’t mixed together. However, if you take a look at this example you will see that the two bodies do become closer together in temperature.
I see that you have already made a comment on that article which I answered, but feel free to point out the errors. So far, no one else has explained what they are.
Bryan says:
But, if you did the same thing during the daytime (i.e., turned back on the greenhouse effect after having turned it off), you could indeed see the temperature rise. So, is G&T’s argument that the sun is a necessary part of the system to discuss the greenhouse effect? Who has argued otherwise? And what does it have to do with the greenhouse effect being “fictitious”?
“It just shows that you have to be intelligent in your analysis of data…particularly if you are dealing with a body, like the moon”
Speaking of the Moon Joel, your co-author Arthur in his famous rebuttal to G&T provides this table on the Moon and planets:
Planet solar constant albedo solar day Teff Tave Difference
(W/m2) (Earth days) (K) (K) (K)
Mercury 9127 0.12 176 434 ? ? 11
Venus 2615 0.75 117 232 737 505 0.7
Earth 1367 0.306 1 255 288 33 0.04
Moon 1367 0.11 29.53 270 253 -17 20
Mars 589 0.25 1.03 210 210 0 0.2″
Arthur also notes: “thanks to Holder’s inequality, this average temperature Tave(t) is always less than or equal to the effective thermal radiation temperature Teff (t), so T 4 ave is less than or equal to T 4 eff”; that is, for bodies without an atmosphere and which do not receive insolation over their whole surface similtaneously such as the Moon; but Tave for the Moon is much less than Teff; any ideas as to why that is?
cohenite says:
As Arthur notes, Holder’s Inequality dictates that T_ave must always be less than or equal to T_eff (for a body that does not have a greenhouse effect or internally generate its own heat sufficiently to influence the temperature). Equality would be obtained for the case where the temperature is uniform. The more non-uniform the temperature is, the larger is T_eff-T_ave. The moon has a fairly non-uniform temperature distribution and hence it is not surprising that T_eff is larger than T_ave.
There are many terms in science which we seem to be stuck with despite unfortunate connotations. “Big Bang” is my favourite example.
As you say, we are stuck with the term “greenhouse”. It’s been used for well over a hundred years and that isn’t going to change anytime soon. The difference between a glass greenhouse and an atmospheric greenhouse is well known and usually a part of any introduction to the subject. This is not in any dispute.
The term “greenhouse” is not all bad. Both a glass greenhouse and an atmospheric greenhouse lead to higher surface temperatures by blocking a flow of heat upwards, while having much less effect on the heat flow downwards. In the case of a glass greenhouse; it is mainly by blocking convection. In the case of an atmospheric greenhouse is it by blocking thermal radiation. Like any other analogy, this has limits, but there is also a basis for similarity.
In this case, the similarity is that the flow of heat downwards from the Sun is not much impacted, but the shedding of that heat from the surface is limited, which drives surface temperatures up until an energy balance is found again.
You have given no basis for your answers “little” and “less”. In fact, a straight observation of the thermal emissions from the atmosphere show that carbon dioxide plays a substantial role in the Earth’s natural greenhouse effect. Water is the most important contributor, with carbon dioxide an easy second, and smaller contributions observable in the measured spectrum of the atmosphere from methane, ozone (particularly tropospheric ozone) and nitrous oxide.
So the first answer is not “little”, but that carbon dioxide is observably a significant part of the total natural greenhouse effect.
As for the effect of changes to carbon dioxide, the major result of increasing concentrations is to increase the width of the main carbon dioxide absorption band for which the optical depth becomes large. That is, with more carbon dioxide there are additional frequencies along the skirts of the absorption band for which the atmosphere becomes opaque.
The contribution is known to good accuracy, to be about 5.35 W/m^2 additional forcing per natural logarithm of carbon dioxide concentrations. Forget subjective terms like “little” or “a lot”. We can quantify the impact on radiation balance quite effectively.
Cheers — sylas
OK sylas let’s get specific about the role of CO2 in the original greenhouse before AGW reared its ugly head; is this graph wrong:
As for additional CO2 maintaining a major role in increasing the greenhouse; the ‘wing’s argument; isn’t it the case for those wing frequencies to be engaged requires pressure and temperature increases which have never been seen on Earth?
Without any context I have no idea about that graph.
And no, it is most definitely NOT the case that you require anything special in temperature and pressure increases. No changes in temperature or pressure are required; only more CO2, and nothing else.
This is mindbogglingly simple. At some frequencies the atmosphere is mostly transparent. At others it is most opaque. In between are frequencies at which the optical depth is around unity.
As concentrations of carbon dioxide increase, the atmosphere becomes “more opaque” to thermal radiation in those bands where CO2 is absorbing most strongly. For a frequency at which the atmosphere is already opaque (absorbing most of the radiation) then for that frequency it makes little difference to add more CO2. For a frequency at which the atmosphere is mostly transparent, then adding more CO2 will make it a little bit less transparent, but not by much. The frequencies which are most affected are those around the transition between opaque and transparent, and this is by far the major cause of the addition absorption as CO2 concentrations increase. The major CO2 absorption band is around 14 to 15 microns, and because of the factors I describe above, the width of the band for which the atmosphere is mostly opaque will increase as CO2 concentrations increase.
I don’t have any expectation that you will be convinced of that, and that is your prerogative. But for people who would like more technical detail, “Principles of Planetary Climate” by Ray Pierrehumbert is excellent and is coming out in December this year; and many other textbooks cover this as well. This basic result is not in any credible doubt, and it is the main basis for the known logarithmic relation of about 5.35 W/m^2 forcing per natural log CO2 at any conceivable conditions we are likely to see on Earth this millennium.
5.35 W/m^2 forcing per natural log CO2 is as specific as all get out, and you still have to catch up with that levels of specificity, with any kind of specific objection. Note that this relation is used without any particular qualm by more capable “skeptics” like Lindzen, or Christy, or others with a level of scientific understanding of what they are doing.
Cheers — sylas
And I’ll just add for cohenite that you can see the effect of doubling CO2 (vs pre-industrial values) via modeled line by line calculations of CO2 in CO2 – An Insignificant Trace Gas? – Part Eight – Saturation.
This is calculated using the well-known absorption characteristics of CO2 at the relevant temperature and pressure for each altitude in the model.
sylas, I picked up the idea that extra [terrestrial] temperature and pressure were necessary for line broadening of CO2 from here:
http://rabett.blogspot.com/2007/07/temperature-anonymice-gave-eli-new.html
The graph I included was the original graph showing the logarithmic decline in temperature response to increases in CO2; I thought you knew of it. Here is another more recent one based on Modtran;
However, the ‘log’ decline effect of increasing CO2 is in itself arguable and best put by Steve Short:
“Over time I have begun to suspect that there is something dubious about the tendency of modern climate science to shy away from absolute temperature as the dependent variable – or indeed other absolute parameters such as rainfall, sea level etc., and to treat most dependent variables, other than the assumed pCO2 ‘independent variable’ in terms of arbitrarily defined ‘anomalies’.
The acme of what particularly annoys me about this approach is IPCCs insistence on the effect of carbon dioxide being roughly logarithmic. IPCC assumes that every time time CO2 (or some other greenhouse gas) is doubled, the increase in temperature is the same as the previous increase.
If I may paraphrase Jeffrey Glassmann’s excellent summation their (IPCC’s) description is simply wrong.
Jeffrey rightly points out that the relationship between pCO2 and any dependent variable is a decaying exponential, not a logarithmic curve. So, for example, if y is the % of Radiation Remaining and C is the CO2 Concentration, then the curve is y = e^-kC, where k is a positive constant.
All empirical scientists know very well that this equation is a physical necessity to make any sort of filter work logically and correctly. I know this from my catchment model fits to flow recessions (and yes I do measure the Nash-Sutcliffe). I am positive Jan too knows this from his process control circuits.
For example, Radiative Forcing (RF) is the amount of radiation absorbed, not remaining, that is, not the amount transmitted forward. So the normalized RF = 1 – y = 1 – e^-kC. The fact that the equation can be turned around to C = -ln(y)/k is immaterial.
IPCC makes the reasonable approximation that the temperature and radiative forcing are proportional, ΔTs = λRF, where λ, is the climate sensitivity parameter refer AR4, Para 2.2, p. 133. So ΔTs = λ(1 – e^-kC), and Ts = To + λ(1 – e^-kC).
Doubling the pCO2 concentration squares the proportion of radiation absorbed, y. However, temperature change does not follow a logarithmic curve, but instead is the complement of a decaying exponential.
Since the logarithmic curve and this complement function are convex in the same sense (“convex down”), sure the logarithmic curve can make a pretty good fit to most any (discrete) region but in extremis it extrapolates to impossible results (far too hot).
For an increasing independent variable, the complement of the exponential has a horizontal asymptote, while the logarithm has none. On the contrary, the flawed IPCC model goes to infinity.
This in effect means that worse than no saturation, CO2 (and H2O) are each ‘capable’ (according to IPCC) of exceeding their own share of the LW IR band! The Beer-Lambert Law by definition correctly expresses saturation in each and every IR band.
IPCC really needed to determine whether, and under what conditions the Beer-Lambert Law was valid, and then to find where the atmosphere was on the saturation curve described by the complement of a decaying exponential. Instead IPCC simply brushed that problem under the carpet and thus making the climate e.g. surface temperature, too sensitive to CO2 overall.
They have repeated this type of flawed approach again and again.”
SoD, this is a long post so I’ll finish with this thought: why is radiative flux equated with heat transfer as the backradiation appears to be?
Then you misunderstood it completely, because what you SAID previously is this:
Line broadening is a completely different thing from absorption in the wings of a spectral band.
The answer to your question above is an emphatic and unambiguous NO. There’s no wriggle room here, you definitely don’t need ANY change in pressures and temperatures to get the wing frequencies taken up as concentrations of CO2 increase; and this is the major part of the additional forcing from increased CO2 concentrations.
As for line broadening — a different matter entirely from increased wing absorption — this IS considered as well in forcing computations, and even THAT certainly does not require conditions never before seen on Earth. We are moving into conditions which have probably not existed for over a hundred thousand years (though this isn’t certain).. but only by a few degrees, if things carry on as they are. Climatically significant, of course; but physically no big surprising in atmospheric absorptions given a few more degrees. There is no special problem at all with the calculations in this regard.
The forcing of 5.35 W/m^2 per natural log CO2 is on solid grounds and your arguments trying to disparage this merely show that you are confused on the physics involved. At this elementary level, basic textbooks can are really your best friend, and you are simply wrong to say that there’s any great missing problem at the kind of fundamental level you are dealing with.
Joel Shore
……”But, if you did the same thing during the daytime (i.e., turned back on the greenhouse effect after having turned it off)”………
During Sunlight hours the temperature would rise.
Both the sceptic and the AGW believer would have their ‘world view’ satisfied.
During night hours with atmosphere the temperature would fall at a low rate.
Some AGW backers believe that the “Greenhouse Effect” would come fully into prominence some even believe that the temperature of the Earth would rise.
An interpretation of your post could be that at nightime the greenhouse effect is switched off.
I don’t think you believe that so I wont take that any further.
At night with no atmosphere (hence no greenhouse) the temperature would fall at a higher rate than before.
But interestingly as the Lunar example shows there would be a substantial “pseudo greenhouse effect”.
………”what does it have to do with the greenhouse effect being “fictitious”?”……….
The behavior of the atmosphere can be explained without reference to the “fictitious greenhouse effect” and in particular the attempts to single out CO2 as being almost a dangerous pollutant.
This “fictitious co2 greenhouse effect” is causing a major dislocation of the world economy and as usual the poorest people on the planet will pay the price.
scienceofdoom:
“Pretty simple really but they can’t work like ice in lemonade because the 2 bodies aren’t mixed together. ”
That’s complete nonsense. They all involve heat flow.
In all cases the entropy of the system is increasing.
“I see that you have already made a comment on that article which I answered, but feel free to point out the errors. So far, no one else has explained what they are.”
.
The errors have been already been pointed out – you just ignore them. It’s a waste of time.
DrAgile:
I don’t think it’s a waste of time because many people watch and observe the way that question and answers are handled.
You say “it’s a waste of time” after only providing an analogy of mixing lemonade and ice and a vague reference to increasing entropy.
And “the errors have already been pointed out” without being specific. Did you mean the “errors” you pointed out ?
These were responded to with no comment or acknowledgement from you.
For the many people who watch and observe, if you feel that a specific comment, question or claim has not been responded to – feel free to ask for clarification.
Of course, many people feel that there is something wrong with the examples provided in The First Law of Thermodynamics Meets the Imaginary Second Law.
But feelings aren’t science. Vague claims aren’t science.
If there was a real problem with the examples in the article you would expect someone to have explained what they were.
It should be easy. Even our most passionate “imaginary second law” believer said “I don’t know” in response to those examples.
scienceofdoom
…..”Even our most passionate “imaginary second law” believer said “I don’t know” in response to those examples.”…
You have created your own” IMAGINARY imaginary second law” perhaps based on misreading of the Gerlich and Tscheuschner paper.
The mistake you made was to confuse infra red radiation and heat.
You perhaps thought that because G&T said no heat moved from a colder body to a hotter body that meant no radiation moved from a colder to a hotter body.
Now that this misunderstanding on your part and others has been cleared up its time to move on.
Find any real mistakes in the paper instead of making up your own version and blaming G&T.
SOD – nicely done here, once again!
I notice your discussion of heat capacity effects seems to echo what I felt was perhaps one original point in my article, which I believe you’re aware of, and several people have referred to already in this comment thread –
http://arxiv.org/abs/0802.4324
There (starting with section III B – “Model 2”) I used a “thermal inertia coefficient” rather than a fixed heat capacity – that allows a coupling of both capacity and thermal diffusivity/conductivity effects at once for a more realistic treatment of heat flow below-ground (or ocean). Note the relationship between average, maximum, minimum, and “effective radiative” temperatures shown in figure 2 as a function of the one main parameter (“roughly … the
ratio of the quantity of incoming energy absorbed in a day to the total heat content of the surface … at the effective radiative temperature”). Anyway, of course the temperature curves resemble yours here. Just thought I should point it out…
Arthur Smith:
Thanks.
Nice work. It looks like I copied you..
Ah, here’s Arthur; a good paper which considers the Moon’s radiative budget and temperature profile is here:
Click to access Huang08ASR.pdf
cohenite: (from June 8, 2010 at 11:23 am
I’d describe it as a confused jumble of ideas from a well-meaning person who doesn’t understand the subject.
The subject has been well-studied for over 40 years and is described in any basic atmospheric physics text book and of course 100’s of papers.
The question of absorption and re-emission of terrestrial radiation is solved using the fundamental radiative transfer equations – see the whole series on CO2 – An Insignificant Trace Gas?, sorry I can’t condense it to a handy sound-bite. For a guide, see the Roadmap which at least outlines what each of the eight sections is about.
As one sample from your quote:
I find it hard to know where to start. None of these words represent anything real.
Instead, a series of papers from Manabe and Wetherald (1967) through Ramanathan and Coakley (1978) followed by a whole legion of others, dissected and calculated the effect of current concentrations and future concentrations of CO2 on the climate (pre-feedback). These values are calculated at the tropopause, the surface, and everywhere in between in minute detail. And of course, people like RM Goody studied the radiative properties of atmospheric trace gases and produced massive tomes of analysis and data.
And many actual measurements of OLR and surface downward longwave radiation back up the current values to a high level of accuracy.
They wouldn’t do this if the idea was a vague jumble of IPCC nonsense – to paraphrase your writer.
The subject of feedback is a much more challenging one, but the subject of CO2 in the atmosphere is one which is technically and mathematically challenging, but, like the motions of the planets, well-understood.
Here’s my sound-bite guide – when you read one of the many thousands who write about the problems in calculating the (pre-feedback) effect of CO2 on climate – if they don’t mention the radiative transfer equations – and what’s wrong with the radiative transfer equations – they haven’t got past first base.
Like reading a commentator on the origins of the second world war who doesn’t mention the first world war and Versailles.
Better to spend a few hours trying to understand a good text book than many years reading people who haven’t read a text book. Just my tip for the day.
OK, my final suggestion on the issue of ‘log’ decline and backradiation is this paper by Mike Hammer:
http://jennifermarohasy.com/blog/2009/03/radical-new-hypothesis-on-the-effect-of-greenhouse-gases/#comment-87115
Bryan,
“I wonder if you are the DeWitt D. P. cited in ref 17 below of the article in my post above?
17. DeWitt D. P. and Nutter G. D. Theory and practice of radiation
thermometry. John Wiley and Sons Inc., New York, NY, 1988.”
No.
cohenite,
“Nahle argues that night-time induced emission by released heat from the regolith prevails over the backradiation which is a product of spontaneous emission.”
The problem with trying to invoke induced vs. spontaneous emission is that line-by-line radiative transfer programs actually use the Einstein A (spontaneous) and B (induced) coefficients in the calculations. They’re in the HITRAN database.
Sorry, but I’m still struggling to understand how this back-radiation thing works in real-life…
How can we compare the blackbody radiation which obviously has well defined direction of radiation, to atmospheric radiation which is totally scattered. Back-radiation has no direction and probably can not heat anything, as almost every radiated photon has counterpart radiated in opposite direction, so the sum over some arbitrary volume must be very close to zero, right?
Please, can anybody explain to me where am I getting this wrong, because I find it hard to believe that nobody has thought about this, so there must be some kind of explanation….
TIA!
Allan Kiik:
You are confusing a few different ideas.
Atmospheric radiation is emitted in all direction. So is radiation from a blackbody. (See note at end).
The direction and the intensity are two different attributes.
If you take some measurements at the earth’s surface, the backradiation might be around 300W/m^2. The value varies of course, dependent on many factors including clouds, the temperature of the atmosphere and the amount of water vapor. You can see some example measurements over the course of a day in Sensible Heat, Latent Heat and Radiation.
But let’s say that at a particular time we do measure 300W/m^2 of longwave radiation from the atmosphere at the earth’s surface.
This has exactly the same heating effect as 300W/m^2 that came from the sun. (Well, strictly speaking a little more solar radiation might be reflected so we need to compare absorbed radiation).
Does this clear things up?
If not is the question about whether the measured values of back-radiation are wrong?
Or whether we can measure a value of incident radiation but this is somehow not able to affect the surface?
Or something else?
[Adding the note that I forgot when I posted the comment originally]
Note: Radiation from a planar surface will be usually emitted in all directions, so long as it is a “diffuse” surface. However, from a planar surface the radiation directly above (normal direction to the surface) will be higher than the radiation close to “the horizon”. So the radiation intensity varies in proportion to cos (x), where x is the angle from the normal. Radiation from a sphere will be equal in all directions, again assuming a diffuse surface. And so radiation from the atmosphere will be equal in all directions.
Thanks, SoD, but this is the standard explanation I have been reading here and elsewhere for long time, but I’m still confused.
I do not dispute measured values, but I can’t understand where it comes – is it the infinitesimal layer near the sensor? Or some volume, say, from first 100 meters, or 1000 meters?
For having some flux there must be directed radiation through some area, radiating earth can do this, of course, but how is it possible for zillions of microscopic “blackbodys” who each radiate to every direction, mostly against each other, and so large part of the flux must cancel out. There is only one preferred direction and this goes from earth to space. As we know from basic quantum mechanics, bosons like a company (as opposed to fermions who obey Pauli exclusion principle) and this means, probably, that there is slightly higher probability for new photon from GHG-s to be radiated upwards (btw I asked this question some 5 years ago at Realclimate, and real climate scientists told me that this should be negligible, I tend to agree). This is small effect, of course, but there’s no other preferred direction and we all know how to sum vectors…
I am a complete layman in climate, as you all have already understood, but I have studied radio engineering (long time ago) and have used physics for engineering tasks for most of my life, and I find it kind of painful not to be able to get “simple” textbook level atmospheric physics.
Allan Kiik:
This is the first step – if we can measure something there must be a physical reason..
Clearly they don’t, otherwise we wouldn’t measure any of this downward longwave radiation at the earth’s surface.
If a photon is absorbed one of two things can happen.
1. It is re-emitted immediately. This changes its direction but keeps its wavelength – because it is the same energy.
2. More likely in the lower atmosphere.. it increases the local temperature via collisions with other gas molecules and that region of gas emits radiation according to its temperature. This changes the wavelength but the radiation is isotropic (equal in all directions).
If a photon isn’t absorbed then no “cancellation” will take place with photons moving in the other direction. A photon will keep zipping through the atmosphere until finally it is absorbed by somewhere in the atmosphere or the surface (or it disappears off into space).
Perhaps this is the way to think about it – Picture lots of layers of the atmosphere. Within each layer there is “horizontal” radiation, so that won’t affect the surface. From each layer there will also be radiation upwards and downwards.
The downwards component will either heat up the layer of the atmosphere below – OR – pass through the layer of the atmosphere below. Probably some proportion will do the first – be absorbed – and the balance will do the second – be transmitted.
From each “layer” of the atmosphere, the proportion that is transmitted will finally be incident on the earth’s surface and most of that will be absorbed by the surface.
From each “layer” of the atmosphere, the proportion that is absorbed will just change the temperature (or hold it constant) and – in equilibrium – that layer will re-emit radiation according to the temperature of that layer.
This is how radiation arrives at the earth’s surface and heats it up (or prevents it cooling).
The main point is that we can measure this downward radiation – so there must be a reason for it.
LOL. As usual, beautiful “logic,” but no cigar when empirical evidence is included. Where oh where is some evidence for this neat radiation balance? Could there be some other “variable” like convection that screws this theory? But it IS a nice theory, though.
I’m curious, folks. According to the AGW gospel, we have an average of 324 wm-2 backradiation for the whole planet, according to K&T, 1997. Can someone in the Church of AGW please tell me what the average backradiation is in Atlanta on July 4?
If you can’t, your theory has absolutely no credibility!
“The main point is that we can measure this downward radiation – so there must be a reason for it.”
LOL. Just what does this “conclusion” mean? Of course you can measure it and of course there is a “reason for it.” It is a frigging basic property of the warmed air molecules. I keep wondering just why this PARAMETER is proof of “something.” Just because it is radiating doesn’t mean anything, folks. The CONCEPT that backradiation “slows” the release of heat to outer space is still a HYPOTHESIS, until these self-annointed “experts” prove otherwise.
We have a basic cause-effect dilemna!
Thanks, SoD, but:
“2. More likely in the lower atmosphere.. it increases the local temperature via collisions with other gas molecules and that region of gas emits radiation according to its temperature. ”
What does this fact tell us about emissivity of CO2 in real atmosphere? We know that absorbtivity is rather high, because spectrum measurements show us almost complete absorbtion at characteristic wavelengths after small distances, and we also know that far more likely than re-emitting the energy, CO2 molecule increases local air temperature by collisions.
So I tried to find some example how to calculate CO2 emissivity in real atmospheric conditions and found this writing from Nasif Nahle:
Click to access ECO2.pdf
“The appropriate formula for obtaining the total emissivity of carbon dioxide is as follows:
ECO2 = 1- (a-1* 1-PE / a+b-1+ PE) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0 (Modest. 2003. Pp. 339-346) (3)
PE = effective pressure of the absorbent gas (p + 0.28 pa) / p.
p = Total pressure of the mixed gases (1 bar for the atmosphere at sea level).
pa = Partial pressure of the absorbent gas.
(paL) m = Partial pressure of the absorbent gas (a) modified by Planck’s function.
(paL)0 = partial pressure of the absorbent gas (a) at L = 0.
paL = Partial pressure of the absorbent gas (a) at L = 0.1 m.
a, b, c = Proportionality constants.
(ЄCO2)0 = Emissivity of the CO2 at (L = 0, p = 1 bar m, T = 300.15 K) = 0.001 [Hottel (1954), Leckner (1972), Pitts & Sissom (1998), Modest (2003), Manrique (2002)]”
And after inserting appropriate values, he gets this:
ECO2 = [1- (-0.099965 / -0.303)] [exp. (-3.315)] * 0.156 = [(0.67) (0.008)] * 0.156 = 0.00084
Is this correct (or at least plausible) result? If not, can you point out the errors in calculations or numbers?
If Nahle is even close to be right, CO2-s part of the measured backradiation is in the range of 100’s of milliwatts and we still have an unanswered question – where does this ~300W/m² come from? Water vapour? Or something else ?
SoD wrote:
“…that region of gas emits radiation according to its temperature. ”
I notice that unlike some others in their comments, you are not adding ” at characteristic wavelengths” to above sentence. Do you mean that mixture of gases at given temperature can radiate on non-characteristic wavelengths too, or you are just omitting the obvious?
We all know that colliding particles can lose energy and radiate photons (or even hadrons when there’s enough energy) with this lost amount of energy, why then we think that gases are different? Is there some known cut-off energy level for this process?
Allan Kiik:
According to Kirchhoff’s law, absorptivity = emissivity. This equality is at each wavelength. So just a technical note – if a gas absorbs from one spectrum (e.g. solar) and emits at another (according to its temperature of course) then the ratios don’t need to be the same.
But if we take the 15um band, for example, we find that CO2 is a very strong absorber and a very strong emitter.
Not correct. The obvious error is simply by inspection of the downward longwave radiation at the earth’s surface:
You can see CO2 is the strong 15um emitter. Here is a comment by DeWitt Payne on Nahle which might be of interest.
Just omitting the obvious.
According to Kirchhoff’s law, absorptivity = emissivity. This equality is at each wavelength. So just a technical note – if a gas absorbs from one spectrum (e.g. solar) and emits at another (according to its temperature of course) then the ratios don’t need to be the same.
But if we take the 15um band, for example, we find that CO2 is a very strong absorber and a very strong emitter.
Is this [Nahle] correct (or at least plausible) result? If not, can you point out the errors in calculations or numbers?
Not correct. The obvious error is simply by inspection of the downward longwave radiation at the earth’s surface:
No matter what absorptive-radiative band you take; the emissivity and absorptivity of the carbon dioxide doesn’t change.
It’s precisely an example taken from observation in nature and experimentation.
Consequently, your assertion on “if we take the 15um band, for example, we find that CO2 is a very strong absorber and a very strong emitter” doesn’t change the real thermal property given that it is all bands available for carbon dioxide which were taken into account in both the experiment and the observation of nature.
I suppose you’re tuned in to the connotation of Total Emissivity, which implies THE SUM of ALL BAND ABSORPTANCIES considering the mass of the absorbent gas in a given medium.
On the other hand, the value 0.001 was taken from both Hottel’s and Leckner’s experiments, which has been corroborated by many modern investigators, and the algorithm that I applied corroborates quite well the magnitude of the total emissivity of the carbon dioxide, i.e. the theoretical results match quite well the experimental results.
Under these real circumstances, the deduction is that the carbon dioxide, far from being a “greenhouse” gas, is a coolant gas.
Allan Kiik
I think your question to SoD deserves a clear answer rather than a reference to another post.
Round and round in circles.
If SoD and others do not agree with Nahle on the emissivity of CO2 in the atmosphere, what value would give for the emissivity.
If they cannot give a value perhaps they could explain why not!
Bryan and Allan,
Calculating an average emissivity for an atmospheric column 100 km high with a temperature that varies with altitude and a pressure that decreases exponentially with altitude is not trivial. It’s made even more difficult because the emissivity of CO2 varies with wavelength. But we can make an estimate of (ЄCO2)0 using the Hottel data correctly. CO2 is ~380 ppmv at present and the height of the atmosphere if it were at constant pressure at all altitudes (take the column and make it parallel to the Earth’s surface at sea level instead of vertical) is about 8 km so CO2 has a path length at 1 atm of 3.04 m or 3.04 atm m. In this graph ( http://i165.photobucket.com/albums/u43/gplracerx/CO2emissivity.jpg ) of Hottel’s data, the maximum CO2 path is 0.61 atm m. But it’s a logarithmic scale and we can compare the data for 0.12 and 0.61 to get an estimate for 3.04 atm m. 0.12 is about .15 and 0.61 is about 0.18 so 3.04 is probably on the order of 0.21 uncorrected for water vapor overlap, not 0.001. Btw, the temperature scale is Rankine, which is Fahrenheit degrees starting at absolute zero rather than the 0 F, or temperature in F + 459.8 so 500 R is 277.8 K or 40.2 F. Nahle’s error is using an atmospheric column length of 1 m instead of 8 km.
I pointed this out to him some time ago but he claimed that my graph of Hottel’s data wasn’t really Hottel’s data. Since I didn’t have access to the book he was using, and he refused to post a copy of his table, I was not able to make further progress.
As far as the equation goes, I see many problems. To name just one, “(paL) m = Partial pressure of the absorbent gas (a) modified by Planck’s function.” Planck’s function at what wavelength and temperature and justify your choice. CO2 absorbs and emits over a range of wavelengths, not to mention temperature, not to mention that Planck’s function doesn’t have the dimensions of pressure.
In this graph ( http://i165.photobucket.com/albums/u43/gplracerx/CO2emissivity.jpg ) of Hottel’s data, the maximum CO2 path is 0.61 atm m. But it’s a logarithmic scale and we can compare the data for 0.12 and 0.61 to get an estimate for 3.04 atm m. 0.12 is about .15 and 0.61 is about 0.18 so 3.04 is probably on the order of 0.21 uncorrected for water vapor overlap, not 0.001. Btw, the temperature scale is Rankine, which is Fahrenheit degrees starting at absolute zero rather than the 0 F, or temperature in F + 459.8 so 500 R is 277.8 K or 40.2 F. Nahle’s error is using an atmospheric column length of 1 m instead of 8 km.
That’s not an error because I considered the partial pressure of the carbon dioxide, which implies the mass of the absorbent gas, carbon dioxide for this case, in the atmosphere. As the concentration of the absorbent gas diminishes, its mass and partial pressure diminish also giving a lower and lower total emissivity. Remember that I took into account the partial pressure of the carbon dioxide and considered the instantaneous temperature for the conversion to mass fraction of the carbon dioxide in the atmosphere.
If you like the algorithm, try it by introducing different backed up mass fractions of the carbon dioxide at different temperatures. The results you’ll find will surprise you because the thermal properties of the carbon dioxide have been exaggeratedly magnified for obtaining the desired results, not the real effects.
On the other hand, the magnitude given by Hottel and Leckner was adapted by other authors like Modest and Manrique to degrees Celsius. Other authors adapted it to atm feet and other to degrees Fahrenheit. Thus, you can find that kind of graphs adapted to almost all the known scales and units of pressure, i.e. bar m, bar cm, atm feet, atm m, and atm cm. That doesn’t change the outcome because the whole formula must be developed using the same units.
SoD wrote:
“According to Kirchhoff’s law, absorptivity = emissivity.”
Yes, of course, but as we all know, this is just another way to describe energy conservation in thermodynamic equilibrium, very similar to Kirchhoff’s circuit laws about conservation of charge. So in this particular case, when we all agree about CO2 habit to give energy away to surrounding air with collisions, there’s no problem with energy conservation and this “law” does not hold.
SoD: “Just omitting the obvious.”
For me, this is the most counter-intuitive part of this controversy, it can still be true, but it’s really hard to imagine a hot substance, say N2 or O2, without any thermal radiation…. When heated up and there’s no conduction, it will stay hot forever, right?
Allan Kiik:
I don’t think you understand what emissivity vs emission means, and maybe this is the heart of the problem.
Emissivity is the proportion of radiation emitted, compared with the Planck function, at a given wavelength. And absorptivity is the proportion of radiation absorbed (vs reflected), at a given wavelength.
These parameters range from 0.0 to 1.0, as in this graph:
This is totally different from emission and absorption.
The first pair are proportions, the second pair are energy radiated in W/m^2 – or, W/m^2.um
So if you want to know what proportion of energy is reflected vs absorbed you need to know “absorptivity”. And likewise if you want to know what proportion of energy is actually emitted vs a blackbody, you need to know “emissivity”.
But if you want to know how much energy is emitted you need to know the temperature and the emissivity. If you want to know how much energy is absorbed you need to know the amount of incident radiation AND the absorptivity.
Therefore, a hot body with little incident radiation will cool down. And a cold body with lots of incident radiation will heat up.
All that emissivity and absorptivity tell you is the proportions of emitted radiation or the proportions of absorbed radiation at a given wavelength.
Do you see the difference?
DeWitt Payne
Thanks for going to the trouble of supplying a rough estimate of emissivity for CO2 at stp.
Maybe my interpretation of your post is inaccurate but I think you were implying an upper limit of 0.2 for a composite e value for that temperature and pressure, falling as temperature and pressure drops.
Lets accept the upper limit value and think that water vapour might be something similar.
If we then use this information and notice that only about 1% of air molecules radiate in the IR it is hard to see how the backradiation has such a high value!
The value for backradiation of 324W/m2 is almost as high as the surface radiation 390W/m2 from a sold/liquid high emissivity Earth Surface.
SoD has hinted that he might deal with this in his next theme.
Bryan
DeWitt Payne
Thanks for going to the trouble of supplying a rough estimate of emissivity for CO2 at stp.
Maybe my interpretation of your post is inaccurate but I think you were implying an upper limit of 0.2 for a composite e value for that temperature and pressure, falling as temperature and pressure drops.
Lets accept the upper limit value and think that water vapour might be something similar.
If we then use this information and notice that only about 1% of air molecules radiate in the IR it is hard to see how the backradiation has such a high value!
The value for backradiation of 324W/m2 is almost as high as the surface radiation 390W/m2 from a sold/liquid high emissivity Earth Surface.
SoD has hinted that he might deal with this in his next theme.
An emissivity of 0.2 for carbon dioxide implies a mass fraction of 5% of the CO2 in the atmosphere and a temperature of 1000 K, which is absolutely unreal.
You continue to misunderstand the meaning of the unit ‘atm-m’ in the Hottel data as it relates to atmospheric column density. Here’s a discussion of atm-cm, which is, of course, atm-m times 100 (link: http://mc-computing.com/qs/Global_Warming/Atmospheric_Analysis.html )
atm-cm
The total amount of a gas in a column of air is sometimes expressed in
atm-cm at STP
Given a column of gas at STP, this is the length in centimeters.
Note: STP – Standard temperature and pressure – zero degrees C and one atmosphere pressure
When discussing ozone, Dobson Units (DU) are used, partly because Dobson was the first person to study atmospheric ozone and partly because there is very little ozone in the air.
1 DU = 1 milli-atm-cm (also shown as 1 m atm-cm)
ozone concentration = 0.3 atm-cm = 300 m atm-cm = 300 DU
This means that all the ozone in a column of air, when placed in a single layer at 0 degrees C and one atmosphere, would produce a layer of gas only 3mm thick.
Without correcting for temperature and pressure, the following are approximate values for CO2 (based on the table above). Corrected values should be about 9% less (because the temperature would be lower).
350ppm 9.76 ft -> 297 atm-cm The value found in some references
380ppm 10.59 ft -> 323 atm-cm Current value
450ppm 12.55 ft -> 383 atm-cm Reasonable expected maximum after ALL oil is burned
700ppm 19.52 ft -> 595 atm-cm Burning coal can provide a higher value
1000ppm 27.88 ft -> 850 atm-cm IPCC projects values higher than this
9.76 ft at 1 atm * 12 in/ft * 2.54 cm/in = 297 atm-cm (when rounded to 3 significant figures)
The column of air referred to is the entire atmosphere above a unit area which has a column density of 8500 atm-m.
It should be constant pressure path length not column density. Nasif’s calculation would be correct if the atmosphere had a pressure path length of 1 atm-m. But it doesn’t. It’s 8500 atm-m.
DeWitt Payne…
As far as the equation goes, I see many problems. To name just one, “(paL) m = Partial pressure of the absorbent gas (a) modified by Planck’s function.” Planck’s function at what wavelength and temperature and justify your choice. CO2 absorbs and emits over a range of wavelengths, not to mention temperature, not to mention that Planck’s function doesn’t have the dimensions of pressure.
The answer is : To all wavelenghts. Planck’s function can be used at particular wavelenghts, but it describes the emission of radiative energy at all wavelenghts.
By the way, I don’t know why you insist in a particular wavelenght or spectral apsorption band when the physics concepts I managed in my article include the whole radiation at all wavelenghts. Don’t forget that the total emissivity is crucial for knowing how much energy a body radiates. Carbon dioxide is not a “strong” radiator.
You must change your arguments to the ocean surface, land surface, land’s subsurface materials, and water vapor, sincerely.
Regarding your second assertion, “Planck’s constant doesn’t have the dimensions of pressure”, you’re correct, but Planck’s function has been applied here as a modifier (blackbody spectral radiance intensity of the energy flux in the normal direction at a given T) of the partial pressure of carbon dioxide. The procedure gives a magnitude of 0.225 bar cm.
SoD:
“This is totally different from emission and absorption.”
Is it correct to describe this difference as similar with max possible potential for something and realized the same something? If yes, then I guess I have understood emissivity correctly – this is theoretical limit for emission at given wavelength.
Of course, in real life, it will depend on various other things, like partial pressure of emitting gas, total pressure and temperature, microphysical processes etc, so it’s not at all unreasonable to try to calculate real-life emissivity, as Nahle did.
So, we have measured 300W from dark, clear sky and we want to know how large part of this is possibly from CO2, how can we calculate this?
Eye-balling the image (a spectrum of the greenhouse radiation…) few comments back, it looks like most of the energy comes from CO2, at least 60% of it, or ~180W/m².
But I don’t see H2O in this spectrum and everybody has experienced the very different cooling rates after sunset with humid and dry air, so water vapour must be an important factor. I guess, the energy under this curve is much less than 300W, because it is measured in a location where there’s virtually no H2O in the air…
Allan Kiik
So, we have measured 300W from dark, clear sky and we want to know how large part of this is possibly from CO2, how can we calculate this?
Use the same procedure explained in my article, but introducing the instantaneous temperatures in Kelvin. For example, if the air temperature is the temperature we had last night, you have to introduce 296 K to the fourth power:
I = ECO2 (σ) (T)4 / π
I = 0.001 (5.6697 W/m^2 K^4) (296 K)^4 / 3.1415…
This gives a total normal intensity of radiative thermal energy flux by the carbon dioxide in the atmosphere of 0.14 W/m^2 sr.
The total normal intensity of the emitted energy by the carbon dioxide alone is extremely low. In the same moment, the total normal intensity of the energy emitted by the surface was 104 W/m^2 sr (290 K, Es = 0.82), so the energy emitted by the surface overwhelms the energy emitted by the carbon dioxide and the second law of thermodynamics and the induced emission come into action together with the spontaneous emission, but the latter outdone by the induced emission caused by the energy flux from the surface.
Sometimes we think that the carbon dioxide makes the job alone, but no. Every mass in the universe is capable of absorbing and emitting energy. Nitrogen and oxygen are good absorbers and emitters of radiant energy.
Nasif Nahle:
What do you make of the measured spectrum of downwards radiation in the comment above?
I do nothing… It continues like spontaneous emission, although the downward radiation doesn’t warm up the surface due to induced emission. You can corroborate this observation making some measurements during nighttime.
The example I gave in that post was taken from real nature. The air was at 296 K and the surface (soil) was at 290 K, i.e. 6 K lower that the temperature of the air.
The difference is that the surface emitts more energy than the carbon dioxide in the atmosphere if the temperature of the latter is homogeneous and constant during at least one minute, because the surface has a strong total absorptivity (e.g. 0.9 for dry clay combined containing organic matter).
Isn’t measured backradiation mostly just the radiation emitted by the first tens of meters of the atmosphere (depending on the optical density). Meaning that if we magically cooled down the first 25 meter of air by 100 Kelvins, backradiation would drastically as all the radiation from above would be absorbed before it reaches the surface.
Mait
Isn’t measured backradiation mostly just the radiation emitted by the first tens of meters of the atmosphere (depending on the optical density). Meaning that if we magically cooled down the first 25 meter of air by 100 Kelvins, backradiation would drastically, as all the radiation from above, would be absorbed before it reaches the surface.
You’re correct.
Of course. But then what? You’d have to keep refrigerating that first 25 m of air to remove the heat from radiation and conduction from the rest of the atmosphere as well as from the surface. If you magically removed that 25 m and replaced it with a vacuum, the radiation measured at the surface from above wouldn’t change much at all.
To use Hottel correctly also requires correcting the emissivity of CO2 for the water vapor overlap. So 0.2 by itself is somewhat too large. I don’t have the data to do the calculation correctly, but I can estimate the emissivity using MODTRAN. For 375 ppmv CO2 at 296 K surface temperature, 0 km, looking up, 1976 standard atmosphere, the total radiant flux is 282.443 W/m2. Changing nothing else but setting CO2 to zero, the flux is 249.599 W/m2. That’s a difference of 32.844. Plugging that into the equation gives an emissivity of 0.075. That’s a lot closer to 0.2 than to 0.001.
MODTRAN has been validated against observation many times. The calculated spectra agree quite well with those measured with a Fourier Transform- Infrared Spectrophotometer.
I followed the commands step by step… :), including the corrected emissivity of CO2 in the presence of water vapor which, by the way, doesn’t change any, and I obtained always the same result, i.e. 0.00088… I mean, there is not any error in the procedure.
The total emissivity of 0.2 for carbon dioxide corresponds to a concentration of 10% of carbon dioxide (I had said 5%, but I was wrong) and a temperature of 1000 K, which is absolutely unreal. I dare correcting your cipher; the total emissivity of carbon dioxide under those conditions is 0.156, not 0.2.
On the other hand, the actual “correction” factor to which you made a mention is 0.072, which correspond to the band overlap. We must to deduct that magnitude from the sum of the total emissivity of water vapor plus the total emissivity of carbon dioxide.
Anyway, the total emissivity of the carbon dioxide remains the same. The nature of the molecule doesn’t change by the presence of water vapor or other gases in the mixture of air. What really changes is the total emissivity of the mixture of air, but the contribution of the carbon dioxide in the mixture is quite insignificant. In fact, the water vapor does the core part of the effect because it has a total emissivity higher than 0.5.
Nasif Nahle
It seems as though you attempting to calculate downward radiation at the surface from the atmospheric CO2.
And the measurements are very much higher than your calculation. That’s why I asked the question.
We can come to the “effects” of downward radiation later, but what about the discrepancy between your calculations and one sample measured spectrum?
I’m not doing that; I’m calculating the Total Emissivity of the atmospheric carbon dioxide using real data.
Perhaps, those measurements are the bulk energy emitted by the mixed air, not by the carbon dioxide alone. Then those measurements must include the emissivity of 3% – 5% of water vapor in the atmosphere.
There is no discrepancy between my calculations and the results of experimentation. That’s why I said that the observation and experimentation corroborate the theory.
A question for those in the know:
Induced emission has been mentioned a few times and I tried in vain to find something about it happening in the atmosphere.
If the figures I have found about the energies required to get CO2 into an excited state are correct, they are in the ultra-violet part of the spectrum.
So how much induced emission -if any- does actually happen in the atmosphere (for CO2 or other gases)?
D.
The induced emission changes vastly because the intensity of the solar photon stream (and also the electron and proton stream) and the intensity of the surface photon stream fluctuate according to other conditions; exempli gratia, when the cloudiness is dense, the solar photon stream during daytime diminishes considerably. You can feel it daily.
On the other hand, during nighttime, the surface photon stream can diminish if it encounters liquid water or water vapor immediately above it. The solar photon stream changes with latitude and responds also to the solar activity.
Nevertheless, in general terms, the induced emission during daytime, towards the surface, reaches almost 23%, and during nighttime, leaving the surface, is around 15%.
Given that the spontaneous emission of the carbon dioxide is extremely low, the induced emission by the solar photon stream and the induced emission by the surface photon stream always overwhelm the spontaneous emission of the carbon dioxide. The induced emission takes always the directionality of the photon stream (or electron, or proton stream), i.e. towards the upper atmosphere during nighttime and towards the surface during daytime. It occurs because the surface absorbs enormous quantities of energy during daytime, which is liberated mostly during nighttime.
You can calculate the intensity of the radiative heat transfer from the atmosphere to other systems through the following formula:
Iav = h 1/4π [(Aul / Bul) / (gl *Blu / gu * Bul) e^hν/kT – 1
Where Iav is for the radiative intensity from the atmosphere, h is for the Planck constant (it has the value 6.626 x 10^-34 J s), π is ≈ 3.1416, Aul is for the Einstein coefficient for spontaneous emission, Bul is for the Einstein coefficient for induced emission from high energy states to low energy states, Blu is for the Einstein coefficient for induced emission from low energy states to high energy states, gl denotes degeneracies from low energy states to high energy states, gu denotes degeneracies from high energy states to low energy states, hv is the energy of a photon, k is the absorption coefficient variable, and T is for temperature.
In the case of our atmosphere, which is a mixture of gases, the water vapor spontaneous emission takes the advantage over the induced emission during nighttime. That’s why I recommended that DeWitt Payne should change his discourse to water vapor, on which nobody would say the opposite.
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6VSV-40SFK77-11&_user=10&_coverDate=11%2F30%2F1995&_rdoc=1&_fmt=high&_orig=search&_sort=d&_docanchor=&view=c&_searchStrId=1372210762&_rerunOrigin=google&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=6324ed5f818c3600da1b8adefb94e98d
Addendum on the next paragraph:
“On the other hand, during nighttime, the surface photon stream can diminish if it encounters liquid water or water vapor immediately above it. The solar photon stream changes with latitude and responds also to the solar activity.”
It should have said:
“On the other hand, during nighttime, the surface photon stream can diminish if it encounters liquid water, water vapor, OR OTHER MASSIVE BODIES immediately above it. The solar photon stream changes with latitude and responds also to the solar activity.”
For example, my molecules interfere with the surface photon stream during nightime and with the solar photon stream during daytime. Those photons collide and are absorbed by my molecules… I hate heat. 🙂
Thanks for the answer, but it does not really help me.
Maybe you have better access to that information than I have, so can you tell me what the required energies are to excite CO2 into a state where induced emission can happen? Even the lowest that I can find requires UV light and I don’t see how we can get any induced emission, in particular not at nighttime (except maybe for special situations as described in the paper you link to).
D.
And you’re welcome, diessoli. My source (the best in my opinion) on this issue is the Journal of Quantitative Spectroscopy and Radiative Transfer.
First of all, there must be an energy density gradient with an energy difference between two upper and lower limit states of energy = hv.
As you know, the spontaneous emission is random, i.e. the spontaneous emission of photons by an excited molecule is isotropic, so it is modified by the induced negative absorption, which depends more on the frequency and the intensity of the photons in the stream than on the degree of excitation of the molecules.
By this mechanism, the unpredictability of the spontaneous emission is modified by the photon stream, no matter the degree of excitation of the molecule “under fire”. Thus, the photon stream induces the molecule to emit in the straight direction of the photon stream and the isotropy of the spontaneous emission diminishes to values lower than the directional emission. That’s the point.
There are some good NASA’s pictures of the emission of energy from the surface during nighttime. I have not the links for now, but I will look for them so you can see the phenomenon quantitatively. Something very interesting is that the intensity of the energy emitted during nighttime is by far higher from populated areas than from uninhabited land.
DeWitt Payne,
The point of using magic was to demonstrate, that the backradiation is directly dependant on the temperature of the air close to the surface. As you well know yourself, the temperature of that layer depends on more factors than just radiative properties of the atmosphere, which makes the backradiation a somewhat useless value in my opinion. I have a feeling, that in a perfectly opaqe atmosphere, mathematically the backradiation would have to equal emitted radiation if measured at the same height.
And that’s the reason by which the planetary boundary layer remains colder than the free atmosphere during nighttime, and continues cooling despite the higher temperature of the air.
I guess, diessoli is talking about energy needed for total population inversion, but there can still be amount of induced radiation even without population inversion. This was theoretically predicted by Einstein in 1916, long before invention of laser in the sixties.
Nasif Nahle:
These are the measurements in the 15um band.
When we look at the outgoing spectrum at TOA we see the absorption of the 15um band and it’s very significant.
When we look at the surface downward spectrum we see the emission of the 15um band and it’s very significant.
(No suprise given Kirchhoff’s law that absorptivity equals emissivity).
I’m not sure what you are claiming – that because you believe your calculations are correct other gases are strong emitters in the 15um band?
Which would mean that these other gases were also strong absorbers in the 15um band. And yet we don’t find that in the HITRANS database.
Total Emissivity includes all absorption bands, so the 15um is included also.
That doesn’t change the total emissivity of carbon dioxide, i.e. 0.001, which is modified by the partial pressure and the temperature of the gas.
My calculations are correct and it is not what I think, but what nature shows.
Thanks, Nasif, for your clarifications.
You wrote:
“Every mass in the universe is capable of absorbing and emitting energy. Nitrogen and oxygen are good absorbers and emitters of radiant energy.”
This was really helpful – it’s a kind of painful to think about the hot balls of N2 or O2 in the space sustaining their temperature forever without any source of energy.
There are many bright and knowledgeable people around (even Roy Spencer had an essay some months ago based on this idea) who seem to think that gases can radiate only strictly on characteristic wavelengths and when there is no IR radiating molecules in the mixture, there will be no radiation at all.
Allan Kiik Nasif Nahle
……“Every mass in the universe is capable of absorbing and emitting energy. Nitrogen and oxygen are good absorbers and emitters of radiant energy.”…….
N2 and O2 do not have any significant radiation in the IR region.
As a look at their spectra will confirm
N2and O2 can lose or gain energy by collision with other air molecules some of which like co2 and water vapour can radiate in this region.
Bryan, do you remember the excitement of physics community when COBE satellite sent down almost perfect Planck curve?
http://en.wikipedia.org/wiki/COBE
So, there’s no low-energy limit (if temp is higher than 0K) for Planck curve and every heated body has this according to it’s temperature. Specific spectrum lines are on the top of it, and I guess, when we want to study the line spectrums, this flat Planck curve is probably subtracted from raw signal, as “contamination” from environmental temperature.
This is just a speculation, but when you put your sensor on the ice (CO2 ice is even better), you will probably see flat Planck curve and specific line spectrum on the top of it. I’ve seen spectrum images looking like this, recorded in Antarctica, but can’t find the images now.
Allan Kiik
Many bright and knowledgeable people say it because it is basic science and extremely well-established.
If you visit SpectralCalc you can check for yourself the absorption of the various gases.
Just for reference, here is a comparison of water vapor, CO2, O2 and N2 from the HITRANS database:
This is on a logarithmic graph, so as you can see O2 and N2 are fully 1,000,000,000 times less intense absorbers at their peak, and these peaks are in very narrow bands. Whereas water vapor and CO2 absorb across the whole spectrum.
This is why bright and knowledgeable people say that O2 and N2 are insignificant absorbers and emitters of terrestrial radiation – because it’s true.
And people who claim that O2 and N2 are significant absorbers and emitters of terrestrial radiation have failed radiation 101.
Thanks, SoD, but what do you think of this atmospheric radiation spectrum, recorded by Nimbus 4 spacecraft? Do you see blackbody-like background radiation?
@scienceof doom…
And people who claim that O2 and N2 are significant absorbers and emitters of terrestrial radiation have failed radiation 101.
You had to elaborate your answer by saying that gases with non polar molecule symmetry do not absorb or emit energy within the temperature parameters with any application in engineering, e.g. O2, N2, H2…, while gases with polar molecule symmetries are significant absorbers and emitters of radiative energy, e.g. H2O, CO2, SO3… for engineering applications, depending of their density, temperature and pressure in a given environment.
However, from those significant radiative gases, the best is water vapor, followed by NO2, N2O, SO2, SO3. In reality, as I have demonstrated, the carbon dioxide is not a significant radiative gas.
Experimentation, observation and theory shows the inhability of the carbon dioxide to produce any significant effect in the atmopheric temperature.
I would like you show me a single calculation which demonstrates that the total emissivity of the carbon dioxide at its current mass fraction in the atmosphere is not 0.001.
I am sure you won’t find it because it is basic knowledge that the propaganda machine sees convenient to be hidden.
However, I give you a clue: find Hottel’s and Leckner’s charts on the total emissivity of the carbon dioxide; look for the total emissivity of the latter at 290 K, a partial pressure of 0.00034 m atm, and a total pressure of 1 m atm. You’ll find that Hottel’s and Leckner’s experiments gave the same results than theory, that is, 0.001 at all absorption bands, no more.
Nasif Nahle
You seem to have access to sources not generally available to the public.
Do you have similar figures for water vapour.
Have you done a similar calculation for water vapour.
If so what would be composite emissivity for an atmospheric temperature of around say 10C.
This might lead us to a physical basis for so called “backradiation”.
My sources are quite common and of public domain. Most of my sources are recent editions of text books and articles from scientific journals.
APS’ journals have been especially helpful because they offer updated data and peer reviewed information.
Regarding water vapor, yes, I have made the calculations at different temperatures starting from 100 °C down to room temperatures and partial pressures according to the mass fraction of the water vapor in the atmosphere.
The lesser the temperature considered in the calculation, the lesser the total emissivity of the water vapor is. It happens this way because, as the temperature diminishes below 100 °C the water vapor is converted gradually to liquid water.
Inside out, when the temperature increases, the water vapor reacts with other substances in the environment and its partial pressure in the atmosphere diminishes also. This is the reason by which many researchers negligently prefer to not include the water vapor as the main actor of the movie (flawed models and calculations), unless they have a completely controlled environment. The last only occurs in models by computer, not in real life.
As water vapor in the atmosphere is converted to liquid water, its partial pressure decreases gradually and, subsequently, the water vapor total emissivity diminishes also. The point here is that the partial pressure of the absorbent gas and the temperature has a large impact on their total emissivity.
At a concentration of 5% in the atmosphere and a temperature of 35 °C, water vapor has a total emissivity of 0.04, which matches almost perfectly with the experimental data. In this particular case, the liquid water has a total emissivity 12.7 times higher than the water vapor with 70% of Nitrogen, and the water vapor has a total emissivity 40 times higher than the carbon dioxide. Let me tell you that I am considering real physical conditions in the environment.
Nasif Nahle:
I said earlier:
You keep telling me that nature backs up your calculations, but haven’t actually explained why the downward surface measured 15um band (=nature) is 1000x times your calculation.
You seemed to imply it was other gases. Is that correct? If so, which ones?
Because you’re confounded, scienceofdoom… The carbon dioxide has a total emissivity of 0.001 at all bands, including that 15 um that you mention. If you have a temperature of, let’s say, 1000 K and a partial pressure of carbon dioxide of 10% (0.1) in an atmosphere at 5 m atm, the total emissivity of the carbon dioxide would be barely 0.156; nonetheless, those are not real physical conditions on the Earth.
The direct problems of heat transfer are well impersonated, so they match with reality more than with our desires; it’s very simple. I cannot do the carbon dioxide does what I wish it to do. Show me a single experiment where the total emissivity of carbon dioxide at a partial pressure = 0.00034 m atm and temperature = 300 K is 0.2.
From where you deduce that I am implying other gases? I am talking about the total emissivity of the carbon dioxide. If you wish to know the total emissivities of other gases, just ask me for them. I will tell you the true values.
@ scienceofdoom…
Why you are confounded?
1. You are talking about a photon stream corresponding to the band 15 μm, as if it was exclusively emitted by the carbon dioxide. Your argument is erroneous and absurd.
2. You are not specifying if that famous measurement was made during daytime, nighttime or thru 24 hours.
3. You are erroneously assuming that the incident energy on the surface is emitted by the carbon dioxide.
4. You’re deducting an emissivity for the carbon dioxide starting from ill-posed inverse heat transfer problems which are only applicable on the construction of machines and thermal devices, not in natural processes.
5. You are dismissing the concept of spontaneous emission.
6. You are dismissing the concept of induced emission.
7. You are not specifying the layer of the atmosphere at which that “measurement” was made.
8. You are not specifying the authors of that experiment, neither the location where the experiment was performed.
9. The value you are running (0.2) for the emissivity of the carbon dioxide in the atmosphere is absolutely unreal because the physical conditions for it to take place require a temperature of 1000 K, a partial pressure of the carbon dioxide of 0.1 m atm and a total pressure of 5 m atm; those values are good for blackbodies. From here your second confusion:
10. You think that the carbon dioxide behaves almost like a blackbody, which is unreal because all the gray bodies behave almost like a blackbody; some almost 0.03 for 1, some almost 0.3 for 1, etc. The problem here is that usually the word almost eliminated and considered the carbon dioxide like a blackbody.
11. The actual amount of energy absorbed by the carbon dioxide in the famous absorbing band of 15 μm is 0.1% (or 0.001 if you prefer), not 100%. I repeat, carbon dioxide is not a blackbody and that is the reason by which we must introduce the magnitude of the TOTAL EMISSIVITY in any algorithm meant to obtain the load of energy emitted by any radiative surface.
12. The carbon dioxide emits at other infrared wavelength bands, depending on diverse factors.
Nasif,
I’ll try this one more time for the edification of those who think you might actually be correct:
“However, I give you a clue: find Hottel’s and Leckner’s charts on the total emissivity of the carbon dioxide; look for the total emissivity of the latter at 290 K, a partial pressure of 0.00034 m atm, and a total pressure of 1 m atm. You’ll find that Hottel’s and Leckner’s experiments gave the same results than theory, that is, 0.001 at all absorption bands, no more.”
The partial pressure of CO2 is 0.00038 atm not atm-m or m-atm. The total pressure is 1 atm, not m-atm. For a path length of 1 m of air, the constant pressure path length of CO2 in air is 0.00038 atm-m. But of course, the path length is not 1 m. For the full atmosphere, you have 10,329 kg of air/m2 (101,325/9.81 or F/a where a is actually the acceleration due to gravity or g). The density of air at STP (0C and 101,325 Pa or 1 atm) is 1.293 kg/m3 so the constant pressure path length of the air column at STP is 7988 atm-m not 1 atm-m. At a partial pressure of 0.00038 atm, the constant pressure path length of CO2 is then 3.04 atm-m. Instead of looking up the emissivity at 290 K and 0.00034, you should be looking at 290 K and 3.04. My graph doesn’t go that high and I’m not at all sure it’s for the same geometry as yours.
The closest I’ve been able to find so far on line is Figure 2 in this document: http://www.fire.nist.gov/bfrlpubs/fire93/PDF/f93096.pdf
The curve in Figure 2 is for a CO2 partial pressure of 0.505 kPa and a path length of 36.58m or 0.18 atm-m (0.505*36.58/101.3). The emissivity at ~ 300K, as close as I can eyeball it, is 0.12 for their data and 0.14 for Hottel (1954). Note: the graph says emittance, but it has to be emissivity or Figure 1 is very wrong as it has emittance going down with temperature where, if it were really emittance, it would be going up with the fourth power of the temperature.
I found a spreadsheet on line ( ronney.usc.edu/spreadsheets/PlanckMeanAndLeckner.xls ) that calculates CO2 and water vapor emissivity based on Leckner, Combust. Flame, 19,33 (1972). For a partial pressure of CO2 of 0.00038 atm and a path length of 8,000 m, eCO2 was 0.14. As a cross check, for a partial pressure of 0.005 atm (0.505 kPa) and a path length of 36.58 m eCO2 is 0.105, or pretty close to my eyeball estimate of 0.12 from the graph.
Has the horse been reduced to a bloody pulp yet?
The URL didn’t come across as a link so I’ll try again:
ronney.usc.edu/spreadsheets/PlanckMeanAndLeckner.xls
Or the html: click on this
But it is unreal because it is at an air temperature of 5000 K.
I made the calculation introducing the partial pressure that you suggested and the total emissivity of the carbon dioxide at 3.04 atm m (an unreal magnitude) obtained is insignificant.
The Effective Pressure of the carbon dioxide in the atmosphere is p + 0.28 pCO2 / p, no more.
You say:
The partial pressure of CO2 is 0.00038 atm not atm-m or m-atm. The total pressure is 1 atm, not m-atm.
Given that those are common units in radiative heat transfer, I recommend you to learn a little more about units. Anyway, you use the same units than I, and the authors of the article, from your link, do so.
You say:
But of course, the path length is not 1 m. For the full atmosphere, you have 10,329 kg of air/m2 (101,325/9.81 or F/a where a is actually the acceleration due to gravity or g). The density of air at STP (0C and 101,325 Pa or 1 atm) is 1.293 kg/m3 so the constant pressure path length of the air column at STP is 7988 atm-m not 1 atm-m. At a partial pressure of 0.00038 atm, the constant pressure path length of CO2 is then 3.04 atm-m. Instead of looking up the emissivity at 290 K and 0.00034, you should be looking at 290 K and 3.04. My graph doesn’t go that high and I’m not at all sure it’s for the same geometry as yours.
Next the reasons by which I affirm that yours is pseudoscience:
First of all the pressure is not constant in the column of air. Second, the procedure is wrong because it is not taking into account the mass fraction of the absorbent gas. Third, you are including that “odious” meter in the expression “3.01 atm m”, so the question is: Does the calculation introduce one meter or not? It seems you’re falling into your own criticism. Fourth, have you made the calculation through the algorithm from my article? I think you’re plenty wrong because the calculation taking into account the value you give for the partial pressure of the carbon dioxide, and you suggested I had to introduce in the algorithm instead 0.00034 atm m, gives a total emissivity of 0.000000082.
I’d like you to make a conversion from 3.04 atm m to mass fraction for you can perceive the wrongness of the model that you proposed.
DeWitt Payne
Has the horse been reduced to a bloody pulp yet?
I don’t know what the meaning of the phrase above is, but… I will teach you how to convert partial pressures to mass fractions:
First step, convert the partial pressure that you suggested, i.e. 3.04 atm m, to a percentage.
Second, convert the percentage to mass fraction.
Third and final step, tell me the result and what you think about it.
Here the data for the carbon dioxide from your link to an Excel worksheet (the author’s magnitudes are in cursive. My comments in bold):
Partial P CO2 = 0.05 atm m
Not true because the partial pressure of the carbon dioxide in the atmosphere is 0.00034 atm m (or 0.00038 atm, if you wish)
Notice that the author of the worksheet is using the same units of pressure than I applied in my algorithm.
a = 1.06
Not true because the constant of proportionality a for the carbon dioxide is 1+0.1/t^1.45
b = 0.23
Check! And it is the sole correct magnitude
The real proportionality constant c is 1.47, but it has been ignored by the author
Consequently, the rest of your tale is wrong, especially the final conclusion:
eCO2 (p=0) = 0.0189
Introducing the exaggerated partial pressure of the carbon dioxide from the author’s Excel worksheet, the total emissivity of the carbon dioxide is 0.01, not 0.2 as you said.
You know, 0.05 atm m are equivalent to 5% of carbon dioxide in the atmosphere, which is unreal at present.
Nasif,
It’s a spreadsheet. Have you never used one? Apparently you didn’t notice that you can put any number you want in the spreadsheet for atmospheric pressure, gas temperature, ambient temperature, path length, mole fraction of H2O, CO2, CO, NH3, CH4, N2O and SF6. You did notice that the CO2 was 0.05, but you completely missed that the gas temperature was 1500 K, not 290 K and the path length was 0.05 m, not 1 m. The units for pressure is atm, not atm-m, btw. Hottel/Leckner was mostly used to calculate heat transfer in things like boilers with high flame temperatures and high ambient CO2 and water vapor as combustion products so it’s not surprising that the example data was not close to atmospheric conditions. When I put in a gas temperature of 290 K, a mole fraction of 0.00034 for CO2 and a path length of 1 m I get eCO2 = 0.00386127. a is then 1.60 and b remains 0.23. I didn’t write the spreadsheet so you would need to discuss with Paul Ronney why there is no value for c listed.
If you really want to compare apples with apples, what do you get for CO2 emissivity for 1500 K and 0.0025 atm-m? I’ll be very surprised if it’s not real close to 0.0189. Pick some other numbers and plug them into the spreadsheet and compare them with your table or calculation. 1000K and 0.003 atm-m is 0.0331, 2000 K and 0.012 atm-m is 0.0266 and 500 K and 0.00091 is 0.0140. Just be sure to set the temperature (cell B10) to what you want and the path length (cell D10) to 1 m in the spreadsheet then set the mole fraction of CO2 (cell B12) to what you want so that the pressure-path length will be the same as what you use to look up or calculate the result.
I didn’t say it was 290 K, in the first place. I’m pointing out the errors from that spreadsheet or whatever it is. I found more errors; e.g. deltaE, which is not 0.666.
Another error is that he is using a mixture of gases, so he is obtaining the sum of the total emissivities of each gas in the mixture, which includes water vapor, not of the carbon dioxide alone.
The total emissivity of any absorbent gas depends on the temperature and its density; that’s why it is not constant. You think it is constant.
I made the calculations using thos absurd 3.04 m atm and the result has been infinitesimal.
What you say about the introduction of 23500 m from the whole column of air, I want to tell you that it is introduced when calculating the CHANGE OF EMISSIVITY, not to obtain the TOTAL EMISSIVITY.
I had noticed your mistake since your first intervention, but I was expecting you would correct it after my explanations. But no, you insist in the same mistake.
Again… I am calculating the TOTAL EMISSIVITY of the carbon dioxide in the real nature, not in a model introducing fabulous magnitudes like 1000 K, 500 K, 3.04 m atm, etc.
My work is simple and straight, and it shows very clearly that the carbon dioxide doesn’t influence in the climate of the Earth. If you have any doubt, revise the literature at the end of my article.
By the way, you have not answered my question and it is very important you answer it because it will show you how you are confounded and how is it that you are in the mistake:
I’d like you to make a conversion from 3.04 atm m to mass fraction for you can perceive the wrongness of the model that you proposed.
Nasif Nahle from June 18, 2010 at 12:12 am:
The paper is:
Measurements of the Radiative Surface Forcing of Climate, W.J.F. Evans & E. Puckrin, American Meteorological Society, 18th Conference on Climate Variability and Change (2006)
And you can see some data from this paper at CO2 – An Insignificant Trace Gas? Part Six – Visualization
For this measured spectrum of downward longwave radiation at the surface by an FTIR, the theoretical values were also calculated.
The theoretical calculations were done by solving the radiative transfer equations and with the most accurate method of using the line by line spectra. The temperature and humidity in the atmosphere at that location were measured by radiosonde for the calculation.
These theoretical values match the measured values quite closely.
This – along with thousands of other similar experiments – is why atmospheric physicists use the radiative transfer equations.
You are convinced that your values are correct, of course.
For others reading, it should be clear that the calculations by Nasif Nahle for the atmospheric emission don’t match what we observe in practice.
The thorough way to do the calculations is by using the radiative transfer equations, as outlined in the CO2 series or in any atmospheric physics text book.
This method calculates the absorption and emission of each layer in the atmosphere. It uses the temperature and concentration of each trace gas at each layer in the atmosphere with either a band model or using line by line calculations. (This latter method is the most accurate but values within 10% can be obtained using band models).
The simpler approach to calculating the downward radiation from a given gas by the total concentration across say 10km of atmosphere is going to give a very approximate answer – this is because the absorption lines change their width with pressure and temperature. And from the top of the troposphere to the surface the pressure changes by a factor of 5 and the temperature by around 0.75.
However, the answer from this method shouldn’t be producing mW/m^2 when the correct theoretical method produces many W/m^2.
This indicates that the calculation has an error – this is what DeWitt Payne has been explaining (I haven’t reviewed his calculations).
Without an alternative source for emission of radiation in the 15um band, the obvious conclusion is that Nasif Nahle’s calculations must be in error.
As Nasif Nahle says:
I am assuming this – as other gases have an absorptivity and emissivity many orders of magnitude lower than CO2 in this band. See the spectra from HITRANS given above.
However, the subject of radiation transfer and molecular spectroscopy will be revolutionized if a new source of such strong 15um absorption and emission can be located. And if someone can explain why the radiative transfer equations using the HITRANS database give theoretical values that match observed values.
Nasif,
I’m tired of repeating myself and I’m sure everyone else is bored to tears. So for the last time in the simplest terms I know.
If you take a cubic meter box of dry air at STP and separated the component gases into boxes with dimensions 1 by 1 by x meters, the boxes would have different lengths (x) summing to 1 meter. Nitrogen would have x= 0.7808 m , Oxygen 0.2095 m, Argon 0.0093 m, CO2 0.00038 m, Neon 0.00001818 m, etc. Suppose you then took 2 of these boxes and stacked them on top of each other. Then the total height of each component would be twice the height of a 1 m box. However, instead of putting them one on top of each other, put them side by side so the pressure on each box is 1 atm. Keep doing that until you have 7998 boxes. The total mass of those boxes will be 10,342.7 kg, equal to the mass of the atmosphere above one square meter of the Earth/s surface at sea level (101325 kg/(m sec2)/9.81 m/sec2). So the constant pressure path length of the entire vertical column of the atmosphere at a pressure of 1 atm is 7998 atm-m (1 atm * 10342.7 kg/m2/ 1.293 kg/m3). The total constant pressure path length of CO2 for the vertical column of the atmosphere is then 0.00038*7998 or 3.04 atm-m.
The temperatures and atm-m values I gave you are not absurd in the context of a gas fired boiler or an open fire, which is the sort of thing that Hottel researched. Extending Hottel to the atmosphere is the real stretch.
“Hoyt Clarke Hottel (1903-1998) was a professor in the department of Chemical Engineering at MIT. He was an expert on fuels, combustion, radiant heat transfer and fire.”
[my emphasis]
link: http://en.wikipedia.org/wiki/Hoyt_C._Hottel
To show that the spread sheet calculates emissivity from pressure times path length let’s enter the following data assuming ideality for the CO2, which isn’t too far off for a pressure of 1 atm, and a gas temperature of 290 K:
path length (m) mole (volume) fraction CO2 eCO2
100.0 0.000004 0.004389933
10.00 0.000040 0.004389935
1.000 0.000400 0.004466133
0.100 0.004000 0.004390123
0.010 0.040000 0.004391829
0.001 0.400000 0.004407909
So when using Hottel or Hottel/Leckner, one must multiply the volume fraction of CO2 by the path length of interest and the path length for the vertical column of the atmosphere is nearly four orders of magnitude larger than 1 m. One could argue that the entire atmosphere doesn’t contribute, only 80%. So the pressure path length is 2.432 atm m for an emissivity of 0.140862914 compared to 0.140023437 for 7998 atm m. Even for a path length of 1 km, or only 1/8 of the atmosphere ( an altitude corresponding to 886 hPa or only slightly greater than 1 km for the 1976 standard atmosphere eCO2 is still 0.121996958.
And that’s it for me on this subject.
@ scienceofdoom and DeWitt Payne…
I didn’t invent the formula. It is the fundamental formula for calculating the Total Emissivity of any absorbent gas. Don’t you have books on radiative heat transfer? Buy this:
Leckner, B. The Spectral and Total Emissivity of Water Vapor and Carbon Dioxide. Combustion and Flame. Volume 17; Issue 1; August 1971, Pages 37-44.
There you would learn how to calculate the total emissivity of the carbon dioxide and the water vapor at any density and temperature.
The remainder of your tales is pseudoscience.
@ DeWitt Payne…
Again, you are absolutely confounded because what you are calculating is not the Total Emissivity of the carbon dioxide, but the band overlaps, which is absolutely different to Total Emissivity. The formula you are applying is as follows:
ΔE = [[ζ / (10.7 + 101 ζ)] – 0.0089 ζ^10.4] (log10 [(pH2O + pCO2) L] / (paL) 0)^2.76
And the real result, with data taken from the nature, is 0.003, not 0.2 as you say.
Besides, your calculations are wrong.
On the other hand, the formula for calculating the Total Emissivity of the carbon dioxide is as follows:
ECO2 = 1- (a-1* 1-PE / a+b-1+ PE) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0 (Modest. 2003. Pp. 339-346)
If you read the reference, you will find that the partial pressure of the carbon dioxide in the atmosphere is 0.00034 atm m, no more.
Again… For knowing why you are confounded, convert 3.04 atm m to mass fraction; or your new number, 2.432 atm, to mass fraction. Tell me your results.
@ ScienceofDoom
Again, those are not my calculations, but the development of a quite common algorithm from 101 science of radiative heat transfer.
Let’s talk like scientists. Don’t send me to a link of a conference. Just show me your algorithm, numbers and deductions. If you find a single algorithm through which you obtained a total emissivity of the carbon dioxide higher than 0.001, show it to me. That’s simple.
@ ScienceofDoom…
You say:
For others reading, it should be clear that the calculations by Nasif Nahle for the atmospheric emission don’t match what we observe in practice.
And what are you observing, specifically? Go straight in your answer, please.
@ DeWitt Payne…
You say:
So when using Hottel or Hottel/Leckner, one must multiply the volume fraction of CO2 by the path length of interest and the path length for the vertical column of the atmosphere is nearly four orders of magnitude larger than 1 m.
Show me a reference, from scientific sources, to the bolded assertion.
Dimensional Analysis
link: http://en.wikipedia.org/wiki/Dimensional_analysis
The unit of pressure in this case is atmospheres or atm for short.
The unit of length is meters, m.
Therefore a unit defined as atm m is the product of pressure times length.
Cite a reference other than yourself where the CO2 partial pressure is given 0.00038 atm m rather than just atm.
Total column ozone, which is what matters for solar UV absorption, just like total column CO2 is what matters for CO2 emissivity, is often expressed in Dobson Units. A Dobson unit is defined as 0.00001 atm m. The peak ozone partial pressure in the stratosphere is on the order of 0.02 Pa. So is the total column path length of ozone 0.0000002 atm m? No. It’s 300 Dobson units or 0.003 atm m. See here for example: http://jwocky.gsfc.nasa.gov/teacher/basics/dobson.html
I asked for a scientific source… Please?
Regarding some sources which say how to obtain the partial pressures of any gas in a mixture of gases:
You’ll find that the procedure is quite elemental, my dear DeWitts:
For calculation of the pO2 in the atmosphere (notice that the procedure applies to any gas in the air):
Robert H. Perry and Don W. Green. Perry’s Chemical Engineers’ Handbook-7th Edition, 1997. McGraw-Hill
In Physics applied to physiology:
Click to access ppPhysics.pdf
“…The partial pressure of a gas is determined by the concentration of the gas and the ambient pressure, eg, the concentration of O2 in air is about 21%, and the partial pressure of O2 in air at surface (1 atm abs) is about 0.21 atm. The concentration of O2 in air remains the same at depth, but the partial pressure reflects the increasing pressure and compression of the gas. At 2 atm abs, the number of O2 molecules per unit volume is twice what it is at the surface, and the partial pressure is double.”
In Climate science:
http://www.engr.colostate.edu/~ramirez/ce_old/classes/ce422_ramirez/CE422_Web/WaterVapor/water_vapor_CE322.htm
(Nasif’s Note: partial pressure = volume mixing ratio)
A bit more complicated, but understandable. Notice that 1 atm = 760 torr, Ok? (Read the example at the end of the page):
http://www.mikeblaber.org/oldwine/chm1045/notes/Gases/Mixtures/Gases06.htm
Quite simple, Uh?
Nasif Nahle:
This, as already explained several times:
scienceofdoom
Whats happened to the water vapour in Figure 1 above?
@SoD
No, no, no… You said you had evidence of the total emissivity of the carbon dioxide = 0.2. Where is it that evidence?
Besides, the author or authors from whom you probabily have taken that unreal information are ignoring three physical phenomena, i.e. buoyancy, enthalpy and latent heat which, by the way, are processes that cool, not warm, the surface, during nighttime and during daytime. (Peixoto&Oort. 1992. Page 14).
By the way, the number in your graph says 0.000008 W/(cm^2 sr/cm), which is not absorptivity, but irradiance.
I can’t seem to leave well enough alone. A short aside: When a telemarketer calls, I tell them I don’t accept telephone solicitations and hang up. My technician at work, before I retired, had a different philosophy. He would try to keep them talking as long as possible. Having them hang up on him was considered a win for him. Since I have nothing but time now…
This discussion has been useful to me. I didn’t really understand what Dobson Units were and how they were measured, mostly because I hadn’t looked into it. Dobson Units are a quantity of ozone as opposed to a concentration. Ozone is measured by absorption spectrophotometry using the sun as the light source. In a laboratory you make measurements using a cell and a single wavelength. In a single beam instrument, you zero the instrument with an empty cell and then measure the reduction in transmission (I/Io) with the material to be measured in the cell. The reduction in transmission is proportional to the total quantity of material in the cell. This is expressed as a concentration times the path length of the cell. You get the same reduction in transmission for a cell with a length of 1 unit and a concentration of 1 unit as for a cell with a length of 10 units and a concentration of 0.1 units. See, concentration times path length again.
But for ozone in the atmosphere, you don’t have a cell. The spectrophotometer just looks at the sun. But there are wavelengths where ozone absorbs and wavelengths where it doesn’t absorb and the ratio of the intensities of these wavelengths in the solar spectrum is constant. So one can calibrate the instrument in the lab by shining light at the selected wavelengths through a cell containing a known quantity of ozone. By measuring the ratios of the absorbing and non-absorbing wavelengths with different quantities of ozone, one gets a calibration curve. Then when the instrument is pointed at the sun, the ratios are compared to the calibration curve and the total amount of ozone between the sun and the instrument can be calculated without knowing the path length. One can then report this quantity in a variety of ways. Dobson chose to use the path length of pure ozone at STP that would produce the same transmission ratio. Pure ozone is quite unstable, so I’m betting that calibration was actually done with diluted ozone.
Emission spectrophotometry follows many of the same rules as absorption spectrophotometry except you don’t measure a ratio, you measure the absolute emission intensity. But it still involves a quantity, not a concentration and the product of path length and concentration define the quantity.
I used spectracalc.com to calculate the transmission spectra for different path lengths for CO2 from 617 to 717 cm-1 at a volumetric mixing ratio of 0.00038, a total pressure of 1013.25 mbar and a temperature of 296 K at 0.01, 0.1, 1.0, 10.0, 100, 1000 and 7998 m path length. The emission spectra would look very similar except they would be inverted, with emission increasing to the Planck limit with path length. Total flux would be the area under the curve. I’d calculate the emission spectra over a wider range, but Spectracalc wants money for that and I’m cheap.
Link: http://i165.photobucket.com/albums/u43/gplracerx/CO2transmittancevspathlength.png
Note the y axis scale change for 1000 and 7998 m path lengths.
Another example of how a constant pressure path length represents a quantity.
How much CO2 is in the atmosphere, not the concentration, but the total mass. The sea level partial pressure doesn’t really tell us much without knowing the mass and density of the rest of the atmosphere. But the the surface area of the Earth, the constant pressure path length of CO2 and the ideal gas law does. At STP, 1 mole or 44 grams of CO2 has a volume of 22.4 liters. There are 1000 liters in a cubic meter. So a constant pressure (STP) path length of 3.04 m is 3.04 cubic meters of CO2/m2 of surface area. 44*3.04/0.0224 = 5.971 kg CO2/m2. Using 6371 km as the radius of the earth, the surface area is 510E12 m2 and the total amount of CO2 is 3.046E15 kg, which matches other estimates.
Bryan:
It was measured in winter in Canada so it was quite dry. You can see the summer spectrum with the water vapor lines at CO2 – An Insignificant Trace Gas? Part Six – Visualization.
scienceofdoom
Yet this study from deep midwinter in Antarctica still found water vapour radiation to be 2.6 times that of CO2.
So where does that leave the interested observer.
A clash of graphs?
They cant both be right
Click to access TownEtAl_2005.pdf
Bryan:
What do you mean? They are both measured spectra of downward longwave radiation.
Why can’t they both be right? Do you think the FTIR measurement is flawed? Be specific. Explain the flaw in measurements or theory.
And if you “believe” the Antartic measurement, perhaps you can explain to Nasif Nahle that the CO2 measurements are 1000x times his theoretical calculation.
Considering that Nasif ignores the presence of 99.9875% of the CO2 in the atmosphere (100*(1-0.00038/3.04)) a factor of 1000 error is about right.
scienceofdoom
…..”Why can’t they both be right? Do you think the FTIR measurement is flawed? Be specific. Explain the flaw in measurements or theory”……..
Your graph shows absolutely no presence of water vapour.
The reason you gave is, it is a winter reading.
Yet I supplied a source from winter in Antarctica that says the water vapour radiation at 15um is still mostly from water vapour.
That means that they cant both be right.
Bryan,
The contribution from water vapor isn’t highlighted on the graph, but it’s there. All the absorption in the short wavelength tail of the spectrum between 1400 and 2000 cm-1 is from water vapor. the major water vapor features are at longer wavelength or lower wavenumber than shown on the graph. The spectrum stops at 600 cm-1. Here are MODTRAN calculated spectra with 375 ppmv CO2 but most of the water vapor removed, with both CO2 and water vapor and with water vapor but without CO2.
Under these conditions, the contribution of water vapor at 667 cm-1 or 15 micrometers is small. In the high humidity tropical atmosphere, the overlap is much greater when viewed from the surface, but the effect on the emission to space is larger.
DeWitt Payne
Thanks for the graphs.
Have a look at Fig 2 page 4238
Click to access TownEtAl_2005.pdf
The authors maintain that H2O/CO2 flux ratio is in excess of 2 even for deep winter in Antarctica.
@DeWitt Payne
You say:
How much CO2 is in the atmosphere, not the concentration, but the total mass. The sea level partial pressure doesn’t really tell us much without knowing the mass and density of the rest of the atmosphere. But the the surface area of the Earth, the constant pressure path length of CO2 and the ideal gas law does. At STP, 1 mole or 44 grams of CO2 has a volume of 22.4 liters. There are 1000 liters in a cubic meter. So a constant pressure (STP) path length of 3.04 m is 3.04 cubic meters of CO2/m2 of surface area. 44*3.04/0.0224 = 5.971 kg CO2/m2. Using 6371 km as the radius of the earth, the surface area is 510E12 m2 and the total amount of CO2 is 3.046E15 kg, which matches other estimates.
DeWitt… The total pressure of the whole column of the air, 23.5 km in height, is 1 atm on the surface. You cannot introduce in any formula a value like 3.04 atm m as the partial pressure of any gas because it would imply that partial pressure of the gas is 300%, which is unreal.
Since you don’t want to convert those 3.04 atm m to mass fraction, I’ll do it for you:
3.04 atm m, the magnitude that you suggest as the partial pressure of the carbon dioxide to be introduced in my algorithm, represents 3,000,000 ppmV of carbon dioxide in the atmosphere… What’s this, DeWitt? It’s imaginary because 1,000,000 kg of air cannot contain 3,000,000 kg of carbon dioxide. It’s against any known physical law and against Archimedes’ discovery some 2200 years ago.
Please, examine your numbers in your new post, because they are wrong also. You’ll find they are unreal, but I don’t want to tell you what the errors are until you find them by yourself.
@DeWitt Payne…
You say:
Considering that Nasif ignores the presence of 99.9875% of the CO2 in the atmosphere (100*(1-0.00038/3.04)) a factor of 1000 error is about right.
DeWitt… again failing in your own words… 0.00034 atm m is the partial pressure of the carbon dioxide, not the percentage of carbon dioxide in the atmosphere. Besides, your numbers are wrong because you ignore the algorithm that I applied, which is used by all physicists, all climate physicists, all biophysicists, all ecologists, all etc.:
0.00038 atm m * 100 gives 0.038%… It’s a factor of 100, not 1000. Besides, 3.04 atm is imaginary. I have told you why in my previous post addressed to you.
Holy cows! It seems you don’t know what the partial pressure is.
Correction:
I wrote:
“0.00038 atm m * 100 gives 0.038%… It’s a factor of 100, not 1000. Besides, 3.04 atm is imaginary. I have told you why in my previous post addressed to you.”
It should have said:
“(0.00038 atm m / 1 atm m [p]) * 100 gives 0.038%… It’s a factor of 100, not 1000. Besides, 3.04 atm is imaginary. I have told you why in my previous post addressed to you.”
@Bryan
DeWitt Payne
Thanks for the graphs.
Have a look at Fig 2 page 4238
Click to access TownEtAl_2005.pdf
The authors maintain that H2O/CO2 flux ratio is in excess of 2 even for deep winter in Antarctica.
Thank you for the link, Bryan!
Had you noticed the graph shows units in milliWatts?
The radiance of the carbon dioxide is 80 (mW/m^2 sr)/cm, which are 0.08 (W/m^2 sr)/cm on its best wavelength. According to my calculations the total normal intensity of the energy radiated by the carbon dioxide at 308 K is 0.16 W/m^2 sr; it cannot be otherwise because the total emissivity of the carbon dioxide is 0.001.
Nasif Nahle:
So previously I asked about the measurements at the surface of downward radiation in the 15um CO2 band.
Then again, and again.
I still don’t know what you think because originally you implied the measurements were irrelevant, then, that other gases were somehow strong emitters in the 15um band.
Now in this statement it seems that you think this graph is agreeing with your CO2 emissivity calculations because of the measurements in the 15um band.
Can you confirm what you believe about measurements of downward surface radiation in the 15um band.
Is it from CO2?
If you can make a simple answer we can move to the next stage of trying to determine whether your theory matches the reality.
If you can’t make a simple answer then readers will be able to draw their own conclusions.
@ScienceofDoom…
So previously I asked about the measurements at the surface of downward radiation in the 15um CO2 band.
Then again, and again.
And again… It doesn’t invalidate the results of the basic algorithm for obtaining the total emissivity of the carbon dioxide, which is 0.001.
I still don’t know what you think because originally you implied the measurements were irrelevant, then, that other gases were somehow strong emitters in the 15um band.
And I sustain what I said because what I calculated is the total emissivity of the carbon dioxide, which includes all emission bands. Remember?
Now in this statement it seems that you think this graph is agreeing with your CO2 emissivity calculations because of the measurements in the 15um band.
It cannot be otherwise because my algorithm is correct. The result of my calculation is that the total emissivity of the carbon dioxide is 0.001, BUT… the total normal intensity by the carbon dioxide coincides with your graph, multyplied by 2. 🙂
My result for the total normal intensity is 0.16 W/m^2 sr, while the graph shows 0.08 W/m^2 sr. 0.16 is 0.08 * 0.16.
Can you confirm what you believe about measurements of downward surface radiation in the 15um band.
Is it from CO2?
No, I confirm the graph shows several radiance values for several absorbers-emitters. The problem is that you think it is a measurement of a ghostly “downward” radiation, while the authors of the graph are showing the spectral bands of several constituents of the atmosphere, not any measurement of any downward radiation.
If you can make a simple answer we can move to the next stage of trying to determine whether your theory matches the reality.
If you can’t make a simple answer then readers will be able to draw their own conclusions.
What my theory says?
scienceofdoom
Graph, Fig 2 page 4238 shows water vapour as the major contributor at this wavelenght
Click to access TownEtAl_2005.pdf
……”I still don’t know what you think because originally you implied the measurements were irrelevant, then, that other gases were somehow strong emitters in the 15um band.”…..
This study is quite revealing.
CO2 is well mixed over the surface of the planet .
Water vapour on the other hand is strongly dependent on temperature.
Humidity readings against temperature confirm this.
It would therefore seem logical that midwinter Antarctic would give the smallest H2O/CO2 flux ratio for the planet.
Yet the study shows it is in excess of 2.
Logic would further imply that as we move closer to the equator, daylight and temperature rising, will also increase humidity.
There does not seem to be a physical mechanism for the emissivity of CO2 to rise significantly.
This would indicate that H2O/CO2 flux ratio would increase significantly.
It seems to me therefor, that the obsession of some people in reducing CO2 is misplaced.
Bryan:
This is wonderful news.
Does this mean that you accept the results of the line-by-line radiative transfer model?
After all, this is how the values in the study were calculated?
Correction:
I said:
“My result for the total normal intensity is 0.16 W/m^2 sr, while the graph shows 0.08 W/m^2 sr. 0.16 is 0.08 * 0.16.”
It should have said:
“My result for the total normal intensity is 0.16 W/m^2 sr, while the graph shows 0.08 W/m^2 sr. 0.16 is 0.08 * 2.”
scienceofdoom
Bryan:
This study is quite revealing.
CO2 is well mixed over the surface of the planet .
Water vapour on the other hand is strongly dependent on temperature. Humidity readings against temperature confirm this.
It would therefore seem logical that midwinter Antarctic would give the smallest H2O/CO2 flux ratio for the planet. Yet the study shows it is in excess of 2.
This is wonderful news.
Does this mean that you accept the results of the line-by-line radiative transfer model?
After all, this is how the values in the study were calculated?
The model doesn’t work for real conditions, according to Peixoto&Oort and other authors.
scienceofdoom
…..”This is wonderful news.
Does this mean that you accept the results of the line-by-line radiative transfer model?
After all, this is how the values in the study were calculated?”…..
There is unfortuately no simple “yes or no” to this question.
(See Nasif Nahle above.)
However some interesting indications follow from the study.
The study indicated that only 23W/m2 could be attributed to CO2 in midwinter Antarctica.
So if we now consider the planet average KT diagram.
Let the CO2 increase by a generous 20% to account for the increased temperature, making its contribution 27.6W/m2.
However the total backradiation according to KT is 324W/m2.
This means that CO2 only contributes
8.5% of the backradiation!
Why disrupt the economy of the planet for such a small effect?
Bryan,
“The authors maintain that H2O/CO2 flux ratio is in excess of 2 even for deep winter in Antarctica.”
Integrated over the entire spectrum, I’m sure that ‘s true. But it wouldn’t be true at precisely 15 micrometers.
Nasif,
The surface pressure of the entire atmosphere is 101325 Pa at STP. The mass of the atmosphere above 1 m2 of the surface is 101325Pa/9.81m/s2 or 10329 kg. The volume at STP of the entire atmospheric column above 1 m2 of the surface, ignoring water vapor, is 10329kg /1.293kg/m3 or 7988 m3 So the constant pressure path length of the atmosphere is 7988 atm m, not 1. Of that 10,329 kg, 5.971 kg is CO2 or 578 ppm on a w/w basis (578*29/44 or 381 ppm on a volume basis). At STP, the volume of 5.971 kg of CO2 is 3.04 m3 (.0224 m3/mole *5.971kg/0.044kg/mole). So the constant pressure path length of CO2 is indeed 3.04 atm m and that does not represent 3,000,000 ppmv.
The mistake is on your part by thinking that atm and atm m have the same meaning. They don’t.
On the MODTRAN page,
http://geoflop.uchicago.edu/forecast/docs/Projects/modtran.orig.htmlhttp://geoflop.uchicago.edu/forecast/docs/Projects/modtran.orig.html ,
if you opt to save the full text and then access it by clicking on the link below the graphs, there are many table. In the third one down from the top, there are atmospheric profiles of various gases in the atmosphere in units of atm cm/km. For 375 ppmv CO2, the value for CO2 is 3.55E+01 at a pressure of 1013 mbar and a temperature of 288.2 K. Correcting to 273.2 K, that’s 37.45 atm cm/km or 0.3745 atm m/km. Divide by 1000 to convert km to m and cancel the units and you get 0.0003745 atm. 0.3745 atm m/km*7.988 km gives 2.99 atm m. Oxygen is 1.98E+04 atm cm/km or 198 atm m/km. Correcting to STP makes that 208.87 atm m/km or 0.2089 atm. That’s within rounding error of the standard value of 0.2095 atm. So according to you, Professor Archer and the authors of the MODTRAN program are wrong by many orders of magnitude too.
Really? It’s quite obvious because the pressure at STP is 1 atm abs, which is equal to 101.325 kPa.
Are you saying that a partial pressure of carbon dioxide of 3.04 atm m is not equivalent to 3000000 ppmV?
3.04 atm m is equivalent to ~3000000 ppmV here and everywhere in the known universe, and I have shown you how to calculate it, but you disregard real science and insist in your unreal models…
You say:
The mistake is on your part by thinking that atm and atm m have the same meaning. They don’t.
Wow! Now you know what I am thinking…
It seems that you don’t know the units that we have to use in the algorithm for obtaining the partial pressure of the absorbent gases.
The partial pressure of the carbon dioxide in the atmosphere at 1 atm m is 0.00034 atm m, which is equal to 34.4505 Pa m, which is equal to 0.2584 Torr m, which is equal to 0.2584 mm-Hg-m, which is equal to 34.4505 N / m; got it?
You must use those units in the algorithm for calculating the total emissivity of the absorbent gases.
By the way, the definition of atmosphere meter, or atm m or m atm is as follows:
“The depth of an equivalent atmosphere of a given gas, in meter-atmospheres, is equal to the depth in meters that the atmosphere would have if it were composed entirely of the gas in question and in the same amount as exists in the actual atmosphere, and had a uniform temperature and pressure of 0°C and 1 standard atmosphere. Abbreviated m-atm. Also known as atm-meter. ”
Source: http://www.answers.com/topic/meter-atmosphere
These are the units we must introduce in the algorithm for obtaining the total emissivity of the carbon dioxide in the atmosphere.
So your arguments about the introduction of the path length into an algorithm, just because it doesn’t give the numbers that you wish, are null.
Saying that I have to multiply the partial pressure of the absorbent gas by the path length of the column of air is unreal given that I am considering the depth in meters of an atmosphere made absolutely by the actual mass fraction of the carbon dioxide in the atmosphere which, by the way, it’s not 3000000 ppmV, but just 383 ppmV.
I have calculated the total emissivity of the carbon dioxide using your unreal ciphers which you erroneously have deduced through MODTRAN and the result, following the correct algorithm step by step (which you can learn from my article and from the references that I have provided there) is a very unreal number: 8.714 x 10^-8… This is ~0.0000001 for the total emissivity of the carbon dioxide by introducing your unreal ciphers in the correct algorithm.
Read Peixoto’s & Oort’s textbook on The Physics of Climate, page 114, Section 6.6, third paragraph and stop trying to mislead your readers into pseudoscientific arguments (bolds are mine):
“The maintenance of a steady state in the atmosphere is only possible through the transfer of sensible heat… and latent heat… from the Earth’s surface to the atmosphere.”
Fourth paragraph (bolds are mine):
“In general, in clear and calm nights the long-wave radiative flux increases with height, leading to a flux divergence and a cooling of the atmosphere.”
So don’t insist on introducing unreal values from a model trying to change a well-developed algorithm deduced and established by physicists from experimentation and observation, who have dedicated their lives to the study of the actual radiative heat transfer.
Now, show me your formulas… 🙂
Nasif,
I do know what you’re thinking and you continue to be wrong. 1 atm m is not equal to 1 atm.
The unit atm m in SI units has the dimension m only (a Dobson Unit is 0.00001 atm m so 300 Dobson units is 0.003 m), which is a little confusing I admit. It took me a while to figure that out. It’s the mass of gas per unit area divided by the density of the gas at 1 atm. So then the mass of gas/m2 is atm m times the density. One atm m of a gas with the density of dry air at STP (1 atm, 273.2 K) has a mass of 1.293 kg/m2. 1 atm in SI units has the dimensions kg m-1 sec-2. As you should be able to see, they’re really quite different. 3.04 atm m of CO2 then has a mass of 5.971 kg. 7988 atm m of dry air has a mass of 10,328 kg/m2 or the mass/m2 of the atmosphere (101,325 Pa/9.81 m/2(g)). So again, 3.04 atm m of CO2 is not 3,000,000 ppmv, it’s 3.04/7988 or 0.00038 ppmv.
One can also have kPa m, which would then be the mass of gas/m2 divided by the density of the gas at 1 kPa pressure. Or in English units, atm foot, which would be the mass in pounds of gas/square foot divided by the density at STP in pounds/cubic foot. Once you understand that atm m is a length, it’s all very simple. And it is a length.
For an optically thin emission source, doubling the path length doubles the emission. By saying that CO2 in the entire vertical column of the atmosphere is 0.00038 atm m, you’re really saying that the atmosphere is only 1 m thick.
@DeWitt Payne…
I think I have found your problems:
1. You don’t know a reliable formula for obtaining the total emissivity of an absorbent gas in the atmosphere.
2. You mix things pertaining to one concept with other unrelated things, for example, DU with carbon dioxide.
3. You don’t know the real meaning of the units atm m because you say that 0.00038 atm m is equal to one meter thick. You’re absolutely wrong. 0.00034 atm m, not 0.00038 atm m, is the thickness that the atmosphere would have if it were composed exclusively by carbon dioxide at its current density, which would be 0.34 millimeters. It couldn’t be otherwise because the density of the carbon dioxide in the Earth’s atmosphere is 0.00062 Kg/m^3, and its mass fraction is barely 383 ppmV. But you say it is 3.04 atm m, which is equivalent to 3,000,000 ppmV, which is equivalent to 5.81300 kg / m^3. 🙂
4. You don’t know how to obtain partial pressures because you said that 3.04 atm is the partial pressure of the carbon dioxide in the atmosphere. See what you said:
“DeWitt Payne
Another example of how a constant pressure path length represents a quantity.
How much CO2 is in the atmosphere, not the concentration, but the total mass. The sea level partial pressure doesn’t really tell us much without knowing the mass and density of the rest of the atmosphere. But the the surface area of the Earth, the constant pressure path length of CO2 and the ideal gas law does. At STP, 1 mole or 44 grams of CO2 has a volume of 22.4 liters. There are 1000 liters in a cubic meter. So a constant pressure (STP) path length of 3.04 m is 3.04 cubic meters of CO2/m2 of surface area. 44*3.04/0.0224 = 5.971 kg CO2/m2. Using 6371 km as the radius of the earth, the surface area is 510E12 m2 and the total amount of CO2 is 3.046E15 kg, which matches other estimates.”
I’ve never seen more confusing erroneous arguments.
Nasif,
“I’ve never seen more confusing erroneous arguments.”
Erroneous how. Be specific. If you can’t follow my reasoning, what do you think is the total mass of CO2 in the atmosphere or the mass/m2?
Dobson units are relevant because they are the same as atm m (@STP) except for a scale factor of 100,000.
I don’t say 0.00038 atm m is 1 m. Quite the opposite. 0.00038 atm m = 0.00038 m (@ STP in SI units). and 1 atm m = 1 m (@STP in SI units). atm m, as I said has the dimension meters. What you continue to miss is that the vertical column of the atmosphere of the Earth at STP is 7988 atm m, not 1 atm m.
Physics is not complicated. If the mass fraction of carbon dioxide is 383 ppmV per each cubic meter, at an altitude of one meter a P = 1 atm abs, and a temperature of 308 K, the density of that cubic meter of air is 0.00067 Kg/m^3.
I am introducing real magnitudes, so it is what we observe in nature.
Those 0.00067 Kg/m^3 of carbon dioxide represent 0.038% of the total mixture of gases comprising the air, which is equivalent to 0.038% of the absolute pressure at the sea level, which is the absolute pressure applied by the whole column of the mixture of air, i.e. 1 atm.
Consequently, the partial pressure of the carbon dioxide in the atmosphere, at the sea level, is 0.038% / 100 % * 1 atm at every meter of the air column, assuming that the mixture of gases in the atmosphere is homogeneous in temperature and density at any altitude below 23500 m.
We know this is not real because the temperature, the composition, the density and the pressure of the air decrease with altitude. You are dismissing this fact, assuming that the partial pressure of the carbon dioxide has to be multiplied by the height of the column of air. This practice gives always false data.
Conclusion, the pressure of the carbon dioxide in the Earth’s atmosphere is 0.00038 atm at any altitude. The latter means that, assuming that the mixture of gases in the Earth’s atmosphere is the same in composition, pressure and temperature at any altitude, the partial pressure of the carbon dioxide is 0.00038 atm at any altitude, let’s say, meter by meter (which you are ignoring since the beginning).
However, as the total pressure changes as the altitude changes, and the density of the gases decreases with altitude, the partial pressure of the carbon dioxide decreases also and consequently, its total emissivity because it is absolutely dependant of pressure and temperature.
The partial pressure of the carbon dioxide decreases also when the temperature of the atmosphere decreases. Given that the temperature of the carbon dioxide and its density decreases with altitude, its total emissivity decreases also.
No scientists will add up, or multiply the number of meters of the height of the atmosphere for calculating the partial pressure of its gaseous components because it is misleading, i.e. pseudoscience.
Instead, the partial pressure of the gaseous components of the atmosphere is calculated at the seal level, on where the absolute pressure acquires its maximum value.
Consequently, physicists calculate the total emissivity of the carbon dioxide using the next formula:
ECO2 = 1- (a-1* 1-PE / a + b – (1+ PE)) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
Now, introduce your ciphers in this formula, DeWitt Payne, and tell us about your results.
You didn’t answer the question. The question is still: what’s the mass/m2 of CO2 in the atmosphere? You can’t correctly calculate emission of CO2 from a path length of just one meter. You obviously have a poor understanding of emission and absorption spectroscopy if you think that partial pressure is all that matters for calculating emission or absorption.
Beer’s Law, for example, (see: http://en.wikipedia.org/wiki/Beer%E2%80%93Lambert_law ) is
T = I/Io = exp(-sigma*l*N)
where sigma is the cross section of light absorption by a single molecule, l is the path length and N is the number of molecules in a unit volume. N is of course proportional to the partial pressure. You can’t calculate the transmission, or emission for that matter, from just the partial pressure and the cross section, you need the path length as well. The path length of interest for CO2 emission at the surface is the entire column of atmosphere above the surface, not just the first meter.
Sorry, that should have been:
You can’t correctly calculate emission of CO2 from the whole atmosphere from a path length of just one meter.
DeWitt Payne
Nasif,
“I’ve never seen more confusing erroneous arguments.”
Erroneous how. Be specific. If you can’t follow my reasoning, what do you think is the total mass of CO2 in the atmosphere or the mass/m2?
Dobson units are relevant because they are the same as atm m (@STP) except for a scale factor of 100,000.
I don’t say 0.00038 atm m is 1 m. Quite the opposite. 0.00038 atm m = 0.00038 m (@ STP in SI units). and 1 atm m = 1 m (@STP in SI units). atm m, as I said has the dimension meters. What you continue to miss is that the vertical column of the atmosphere of the Earth at STP is 7988 atm m, not 1 atm m.
You’re more confused than I thought before. Dobson Units definition (bolds are mine):
“Dobson unit (DU) A unit to measure the total amount of ozone in a vertical column above the Earth’s surface (total column ozone). The number of Dobson units is the thickness in units of 10–5 m that the ozone column would occupy if compressed into a layer of uniform density at a pressure of 1,013 hPa and a temperature of 0°C. One DU corresponds to a column of ozone containing 2.69 × 1,020 molecules per square metre. A typical value for the amount of ozone in a column of the Earth’s atmosphere, although very variable, is 300 DU.”
Source: The IPCC!!! http://www.ipcc.ch/publications_and_data/ar4/wg1/en/annex1sglossary-a-d.html
And you wrote (bolds are mine):
It’s the mass of gas per unit area divided by the density of the gas at 1 atm. So then the mass of gas/m2 is atm m times the density. One atm m of a gas with the density of dry air at STP (1 atm, 273.2 K) has a mass of 1.293 kg/m2.
First of all, see how you have a wrong concept of Dobson Units. Second, haven’t you said some posts above that atm m didn’t imply pressure, mass, etc.? The circle is set in motion again… 3.04 atm m, according to your paragraph above, implies mass, so it implies pressure, density, etc. And the conclusion is exactly as I have said in my question to you: 3.04 atm m is 3,000,000 ppmV.
Why your calculations are wrong? See only one example. You wrote:
7988 atm m of dry air has a mass of 10,328 kg/m2 or the mass/m2 of the atmosphere (101,325 Pa/9.81 m/2(g)). So again, 3.04 atm m of CO2 is not 3,000,000 ppmv, it’s 3.04/7988 or 0.00038 ppmv.
Let’s take your last “formula”:
… it’s 3.04/7988 = 0.00038 ppmb
Let’s introduce units in your formula:
3.04 atm m / 7988 m
Eliminating units:
3.04 atm x / 7988 x = 0.00038 atm…
What did you write? You wrote: “3.04 atm m of CO2 is not 3,000,000 ppmv, it’s 0.00038 ppmv
The result of your formula indicates very clearly that the final units are atm, which is a unit of pressure, partial pressure of the carbon dioxide in the atmosphere for this case. And it is what I have been managing all through this useless discussion.
See why I said that I have never seen more confusing erroneous arguments before, regarding your arguments?
The IPCC definition is, of course, correct. It’s also what I said. 300 DU corresponds to a layer of ozone at STP that is 3 mm or 0.003 m thick. So atm m has the dimension of m only. You jump on trivial errors of nomenclature where I wasn’t as precise as I should have been. The atmosphere is 7998 atm m at STP, CO2 is 3.04 atm m at STP so the ratio of CO2 to the atmosphere is 0.00038, and because the reference pressure is one atmosphere, the partial pressure of CO2 is 0.00038 atm.
Units are trivial for you?
Nasif,
“Consequently, physicists calculate the total emissivity of the carbon dioxide using the next formula:
ECO2 = 1- (a-1* 1-PE / a + b – (1+ PE)) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0”
What was the publication date of the book or paper from which you extracted that formula? I’m betting no later than 1980 and probably earlier. Because that’s Stone Age technology.. If anyone even bothers to calculate a total emissivity, which isn’t necessary or even terribly meaningful, They use line-by-line or band models to calculate emissivity at each wavelength or frequency and temperature and pressure and then integrate under the calculated curve. MODTRAN, for example, uses a medium resolution band model. But why integrate first. For calculating emission, it’s more accurate to multiply the emissivity at each point by the Planck function at that point and sum over all wavelengths to get the total emission.
Still, the result should be in the ballpark if you used the correct parameters. The problem is that your value of (ECO2)0 is orders of magnitude too low.
2003
DeWitt said:
“I’m betting no later than 1980 and probably earlier. Because that’s Stone Age technology.”
But this was golden age of science (when compared to current times), Feynman was still alive and maybe acted like kind of adult supervisor for physicists… If you don’t want to become famous as actor in some of his immortal jokes, you will not speak nonsense 🙂
Nasif said in one early comment that stimulated emission is possible and significant in atmospheric conditions (Gavin Schmidt answered at RealClimate “it should be negligible”) and see what I have just found:
8. M. J. Mumma, D. Buhl, G. Chin, D. Deming, F. Espenak, T. Kostiuk, D. Zipoy, Discovery of natural gain
amplification in the 10-micrometer carbon dioxide laser bands on Mars – A natural laser, Science 212, 45–49,
1981.
9. D. Deming, F. Espenak, D. Jennings, T. Kostiuk, M. Mumma, D. Zipoy, Observations of the 10-micron natural
laser emission from the mesospheres of Mars and Venus, Icarus 55, 347–355, 1983.
So, it has been detected using “Stone Age technology” in the very different atmospheres of Mars and Venus, and it’s obvious that to some extent it must happen here too, but most famous climate scientists in the world don’t know about such fenomenon.
“If anyone even bothers to calculate a total emissivity, which isn’t necessary or even terribly meaningful”
It is meaningful if we want to know how big part can play CO2 (and other) resonant lines in radiative cooling of the planet. Spectrometers show us peaks elevated over background quantum noise but it’s still difficult to measure how much energy is emitted at resonant wavelengths when compared to wide band “noise.”
LTE doesn’t apply in the mesosphere ( if it did, you couldn’t get a population inversion and lasing) because the pressure is too low, so the example isn’t relevant to the bulk of the atmosphere where the GHE occurs. Line by line radiative models include the Einstein spontaneous and stimulated emission coefficients (A and B) in the calculations. The data are in the HITRAN database.
See:
Click to access TransmissionCalculation.pdf
and
here
(hope that actually works)
I was afraid of that. The full URL probably won’t work either but here it is.
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TVR-4GXVDVS-2&_user=10&_coverDate=03%2F31%2F2006&_rdoc=14&_fmt=high&_orig=browse&_srch=doc-info%28%23toc%235541%232006%23999019998%23612144%23FLA%23display%23Volume%29&_cdi=5541&_sort=d&_docanchor=&view=c&_ct=14&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=dc877df56e0ec9c0828b43d0e6d9f94c
something to do with cookies probably. Beside it’s money-walled for non-subscribers. Anyway, the title of the article is:
Einstein A-coefficients and statistical weights for molecular absorption transitions in the HITRAN database
Journal of Quantitative Spectroscopy and Radiative Transfer
Volume 98, Issue 1, March 2006, Pages 130-155
You don’t need the emittance to compare the relative importance if you have the total flux, which is what comes from MODTRAN.
Nasif,
You still haven’t told me your value for kg/m2 of CO2 in the atmosphere or why it isn’t 5.971 kg/m2. You can’t correctly calculate the absorption or emission of a column of gas unless you specify both the concentration and the path length. If you use just the concentration (partial pressure, whatever) then if you’re using SI units, the path length will be 1 m. They put path length as an input in the gas cell calculator module at Spectracalc for a reason. If the concentration is in kg/m3 then the product of concentration in kg/m3 and path length in meters is kg/m2. Kg/m2 can also be converted to the length of a column with a surface area of 1 m2 where the gas is at STP. One does that by dividing by the density at STP. This is the same way one calculates the column length of the atmosphere as a whole. The density of CO2 at STP is 0.044 kg/mole/0.0224 m3/mole or 1.9643 kg/m3. 5.971/1.9643 is 3.04 m. The density of dry air at STP is 1.293 kg/m3 and the mass/m2 is 10,328.7 kg so the column length is 7988 m. 0.00038 ppm by volume * 7988 m = 3.036 m. The numbers all add up.
I posted a link to show how the transmittance of CO2 at a volume mixing ratio of 0.00038 (or 0.00038 atm at 1 atm) varied by path length in my comment above here:
https://scienceofdoom.com/2010/06/03/lunar-madness-and-physics-basics/#comment-3140
You can nitpick my sometimes less than careful syntax all you want, but you still can’t avoid the fact that your value for ECO2(0) is too low because you ignore the path length when you calculate it. Since all your further calculations depend on the value of ECO2(0), they are all wrong whether the rest of the parameters in your equation are correct or not.
Why don’t you use 3.04 atm m to calculate ECO2(0) and plug it into your equation and calculate total emission even if you don’t think it’s correct.
DeWitt Payne
LTE doesn’t apply in the mesosphere ( if it did, you couldn’t get a population inversion and lasing) because the pressure is too low, so the example isn’t relevant to the bulk of the atmosphere where the GHE occurs.
What are you referring to with LTE? Let me guess… Are you referring to Total Emissivity? Sorry for disappointing you but total emissivity is relevant everywhere in the universe wherever you have matter.
You cannot deny that you base your whole idea of the GHE on the heat transfer process by radiation, and that you send away the importance of the processes of conduction and convection for being, as you usually say on things that contradict your ideas, “negligible”. However, for you have a process of radiation of energy, you need an absorber (of energy) – emitter (of energy).
For you assure that the carbon dioxide “warms up” the surface, something that is not feasible in the real world, you need the carbon dioxide has an emissive power, that is, a physical characteristic known as emissivity. Then you need to know the total normal intensity of the energy radiated by the carbon dioxide, and here is where you cannot dismiss the total emissivity of the carbon dioxide.
Then you need to know the load of solar energy absorbed by the surface, consequently, you need to know the absorptive power of the surface. Alas, you need to know how much energy is emitted by the surface to the atmosphere, and again, you need to know what the emissivity of the surface is.
The problem is that you disregard those concepts and facts that contradict your ideas. This way of thinking is the way of pseudoscience.
Now that I’ve told you that the source of the formula was a book published in 2003 (the first edition), proceed to introduce your ciphers in the algorithm and tell me your results.
You guessed wrong. LTE means Local Thermal Equilibrium which is defined to mean that collisions are the principal means of energy transfer and the distribution of kinetic energy is the Boltzmann distribution. It’s very difficult, impossible for most processes, to achieve a population inversion, a majority of molecules in a higher energy level that is normally a minority of the molecules. You can’t have a laser without a population inversion.
http://en.wikipedia.org/wiki/Population_inversion
“You cannot deny that you base your whole idea of the GHE on the heat transfer process by radiation, and that you send away the importance of the processes of conduction and convection for being, as you usually say on things that contradict your ideas, “negligible”. However, for you have a process of radiation of energy, you need an absorber (of energy) – emitter (of energy).
Where do I say that convection is negligible? This is a classic straw man argument. You claim that I’m wrong about something I never said. I have many comments where I point out that radiation drives convection and that without convective heat transfer from the surface of the Earth, it would be considerably hotter.
That “you” was not addressed to you exclusively.
Now, go on the formula introducing your ciphers.
@DeWitt Payne…
You say:
You can nitpick my sometimes less than careful syntax all you want,
I’m not doing that, your whole idea is wrong and I have demonstrated it through the whole blog.
but you still can’t avoid the fact that your value for ECO2(0) is too low because you ignore the path length when you calculate it.
I’m not avoiding anything. The total emissivity of the atmospheric carbon dioxide is its real total emissivity, according with the physics of heat transfer. I invite you again to introduce your ciphers in the formula provided and show your results.
Since all your further calculations depend on the value of ECO2(0), they are all wrong whether the rest of the parameters in your equation are correct or not.
Again, it’s not my further calculations; it’s the procedure followed by all physicists and engineers. You cannot calculate the total normal intensity of the radiation by any gas in the atmosphere if you don’t know its total emissivity. Here the formula for the total normal intensity goes again:
I = ECO2 (σ) (T)4 / π
Do you see that ECO2? Well it is for Total Emissivity of the carbon dioxide.
Now, if you prefer the formula deduced from Stefan-Boltzmann principle, you’ll find that odious total emissivity again, and again, and again:
q = e (σ) (A) [(Ts) ^4 – (Ta) ^4]
The small e means… Emissivity.
Why don’t you use 3.04 atm m to calculate ECO2(0) and plug it into your equation and calculate total emission even if you don’t think it’s correct.
Because I have already done it, but you don’t read what I write in my posts. Besides, I let my pupils to learn from their own errors through examining the issues by themselves.
Again, do it yourself and tell me your results.
Nasif,
I = ECO2 (σ) (T)4 / π
More or less. But ECO2 is 0.0733 for the total column of the atmosphere at the surface looking up using the 1976 standard atmosphere with a surface temperature of 288.2 K so I = 9.13 W m-2 ster-1.
Nope, ECO2 is 0.001, no more.
@DeWitt Payne…
You say:
You still haven’t told me your value for kg/m2 of CO2 in the atmosphere or why it isn’t 5.971 kg/m2. You can’t correctly calculate the absorption or emission of a column of gas unless you specify both the concentration and the path length.
Because I never said it wasn’t. The problem is that you don’t know that the partial pressures of the components of the atmosphere are the results of their total mass fraction in the atmosphere.
On the other hand, I expected you corrected your mistake, but I see you are not prone to do it. You say that I dismiss the path length of the radiation of energy; however, if you take a brief look to the formula for obtaining the Total Emissivity, you’ll find this term: paL. You know what is it for? Thanks!
So… I don’t know why you say that I am not considering the mass of the carbon dioxide in the atmosphere.
By the way, emittancy and emissivity are not the same thing.
Oops! Sorry! I forgot to give you a reference for the difference between emittance and emissivity, here it goes:
http://en.wikipedia.org/wiki/Thermal_emittance
PaL is the partial pressure, Pa, multiplied by the path length, L.
Note the ‘multiplied by the path length’ part.
See example 6.22 in Heat Transfer by Anthony F. Mills starting on page 564.
Begin quote:
Example 6.22 Total Properties of a Hydrocarbon Fuel Combustion Products
Exhaust gas from a combustor burning a hydrocarbon fuel is at 1600 K and 3 atm pressure. The composition can be approximated as 10% CO2, 10% H2O and 80% N2, by volume. Calculate the total emissivity for a path length of 0.34 m and the total absorptivity for radiation from a black wall at 800 K.
[snip]
We first calculate PaL’ from Eq. (6.99b), where for the CO2-H20 mixture, Pe is replaced by the total pressure, P.
PaL’ = PaLP^m
Pa = (0.1)(3) = 0.3 atm; PaL = (0.3)(0.34) = 0.102 atm m. From Fig. 6.26b, m = 0.26
PaL’ = (0.102)(3)^0.26 = 0.136 atm m
From Eq. (6.99a) and Fig. 6.36a
Eg = Eg(Tg, PaL’) = Eg(1600, 0.136) = 0.19
End quote.
Not that the gas mixture is at constant pressure and isothermal. The atmosphere isn’t. So applying this to the atmosphere is a stretch.
Again, Pa is the volume fraction times the pressure, (0.1)(3) = 0.3. PaL is Pa times the path length. So PaL is (0.3)(0.34) or 0.102, not 0.3. Pa for CO2 is (0.00038)(1) = 0.00038. The path length for CO2 in the atmosphere is thousands of meters, not one meter so PaL for CO2 for calculating total emissivity =/= 0.00038.
The link for google books for the page in question is:
http://books.google.com/books?id=IVzSHjZ2LeEC&pg=PA565&lpg=PA565&dq=paL+unit+heat+transfer&source=bl&ots=x9iSd-whvJ&sig=O9bkwmoVvfJpnFgHCIpO-COaMyI&hl=en&ei=DVUhTNnbFsKqlAeAoJgd&sa=X&oi=book_result&ct=result&resnum=4&ved=0CCkQ6AEwAw#v=onepage&q&f=false
@DeWitt Payne…
From Mills’ example, 0.1 is 10%/100, i.e. the partial pressure of the gas at its whole fraction in the mixture of gases. The same applies to the carbon dioxide in the atmosphere and there is no need of multiplying the result by the total length of the column since the atm abs is 1 atm.
Now, let’s calculate the partial pressure of the carbon dioxide at 1 atm abs, which is the pressure applied by the whole column of air from 0 m up to 23500 m above the sea level.
1 atm abs is 100% of the mixture of gases of the air exerted by the whole column of air upon the surface of the Earth. 0.034% corresponds to carbon dioxide, 78% to N2 and 20% to O2 in the whole column of air from the surface up to 23500 m of altitude, not of 1 meter above the surface, as you have erroneously interpreted.
Consequently, the partial pressure of the carbon dioxide in the whole column of air (given that 1 atm abs is the pressure of the whole mass of air above the sea level) is (0.034%/100) * 1 atm = 0.00034 atm.
If we multiply 0.00034 atm by the total altitude of the column of air studied, 23500 m in this case, we will have a false magnitude because 0.00034 atm is the partial pressure exerted by the whole column of carbon dioxide over heads and we will be mislead to a terrible false result (7.99 atm, which is absolutely false because the carbon dioxide alone cannot apply a partial pressure upon the surface of the Earth 7 times higher than the Pabs).
At this point, I think we have to consider the difference between state functions of thermodynamic systems and process functions. Pressure and temperature are state functions of thermodynamic systems considered between both endpoints of a path. In the case of the atmospheric pressure or of the partial pressure of any of the components of the atmosphere, it is from 0 m to 23500 m. In short, it is not the pressure that the air exerts by each meter of length, but the pressure exerted by the whole column of air. Otherwise, you should multiply the Pabs by 23500 m, which will give you an atrocious false result, i.e. a Pabs of 23500 atm.
Now, we find the temperature of the air in the first meter above the sea level is 308 K. We look the total emissivity of the carbon dioxide at Hottel’s and Leckner’s tables at that particular temperature and at Pabs of 1 atm at I cm above the surface (Leckner’s table is more precise than Hottel’s results) but we have not to multiply the temperature by 23500 m, because it is the temperature at 1 cm above the surface. If you do that, then you’ll obtain a terrible false result, i.e. 7,238,000 K.
Thus, we have to get real.
Now, we want to know the PE of the carbon dioxide, what to do? We use the following formula:
p + 0.28(pa) / p0
I assume you’re a chemist, so you can calculate the PE of the carbon dioxide in the atmosphere. Go on…
If there was no reason to multiply by the path length, then why did Mills do it?
It’s simple algebra. If a*b = a, then b = 1. Do you really think the path length in the atmosphere is 1 m? Apparently you do, and of course, that’s your problem.
Because he was considering a limited box containing a mixture of gases which was homogeneous. You won’t find an atmosphere with 1 atm of Pabs at 7 kilometers of altitude, so your results are biased. I invite you again to introduce your figures in the formula and see the UNREAL results you will obtain:
ECO2 = 1- (a-1* 1-PE / a + b – (1+ PE)) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
I have done it, now it’s your turn for verifying what I’m telling you. Show your readers your results.
I’d like to finish this dialogue with the formula that DeWitt Payne has been trying to apply, which generated his set of confusions. The formula is as follows:
(ΔIη) abs = – κη * Iη * Δs
Where the negative sign is introduced because the intensity decreases through the path lenght, ΔIη is the attenuation by absorption and scattering, κη is for the linear absorption coefficient Iη is the radiative intensity in vacuum, and Δs is the path (or distance) the beam travels through the medium.
As you can see, this formula is not for calculating emissivity or total emissivity of absorbent gases, but to know the decrease of the intensity of radiation by absorption and scattering.
By the way, the absorption coefficient (κη) of the carbon dioxide in the atmosphere is really, really low.
Nasif,
I had other things to do yesterday. If you give up now, I win.
At local thermal equilibrium, (LTE), Kirchhoff’s Law applies and emissivity = absorptivity. Absorptivity, in the absence of reflectivity, is the complement of transmissivity, a = 1 – t. If you know the transmissivity at a wavelength, you also know the absorptivity and the emissivity. Then emission = B(f,T)* (1-exp(-sigma*l*N), where B(f,T) is the Planck function for frequency f and temperature T.
As far as plugging my numbers into your equation, you won’t give me the numbers I need. If I use your numbers, I’ll get the same answer as you, but that’s begging the question. I’m not going to look them up elsewhere and have you say that they aren’t correct. To use your equation I need the coefficients for a temperature of 296, a pressure of 1 atm, a volume mixing ratio of 0.00038 and a path length of 7988 m (PaL = 3.04 atm m). I don’t care if you think they’re absurd. I need them so I can compare the result with Spectralcalc, a line-by-line radiative transfer model. You’ve inspired me to spend the $25 to subscribe for a month so I can calculate emission spectra not just transmission and atmospheric paths, not just constant pressure, isotropic paths.
One of your problems seems to be that you think your equation is the only way to calculate emissivity. That’s wrong. There are a variety of ways. If they are all correct then you should get about the same answer whichever method you choose. The fact that your method gives a result orders of magnitude less than MODTRAN is convincing to me that you are doing something wrong, since your method, if applied correctly, should be in the ballpark.
The absorption coefficient of carbon dioxide at 15 micrometers in the atmosphere is actually quite high. At a partial pressure of 0.00038 atm, transmittance at 15 micrometers for a path length of 1 m is very close to zero. But of course, if you calculate absorptivity the same way you calculate emissivity, you would come to the conclusion that the absorption coefficient is low.
Now off to Spectralcalc to spend some time and money.
Uh! Oh! Is that the purpose of your arguments? To win? Win what? That your pseudoscience is superior to real science? Please… That’s not a scientific argument.
If you don’t calculate the Total Emissivity of the carbon dioxide introducing your ciphers in the formula:
ECO2 = 1- (a-1* 1-PE / a + b – (1+ PE)) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
Then, it’s obvious you know you’re wrong and I’m right.
I can’t unless you give me (ECO2)0 (or ECO2(0)) for 3.04 atm m CO2 as well as the rest of the coefficients for those conditions. Then there’s the problem of how the value of PaL can be anything other than zero for L=0. Do you really mean the limit of PaL/L as L goes to zero? Then there’s the (PaL)m. If I had the book in question, I might be able to do it, but I don’t. If I spring for the Modest book, does that have everything I would need? It’s $74.10 from Amazon. Of course there’s still the problem that you think that bar and bar m are interchangeable when they’re not. So it probably wouldn’t help even if I had the book.
“Then, it’s obvious you know you’re wrong and I’m right.”
I could just as well say that your failure to calculate Total Emissivity assuming PaL is not the same as Pa means that you know you’re wrong and I’m right.
Spectralcalc results for 1 atm total pressure (1013.25 mbar), 296 K, 1 m path length and volume mixing ratio of 0.00038 gives an emission intensity of 0.85 W m-2 sr-1. That’s pretty close to the value of 0.14 that Nasif posted above.
The emission spectrum looks like this:
But of course, the path length through the atmosphere is much longer than one meter. If we use a horizontal, isotropic, isothermal path that contains the same mass/unit area as the atmosphere, then we get an emission intensity of 28.912 W m-2 sr-1 with a spectrum that looks like this:
But the atmosphere isn’t isothermal and isotropic so we’ll look at an atmospheric path from the ground straight up. Spectralcalc won’t let me put the background source at 1 m so I used 1 km and a CO2 scale factor of 0.001. Emission is 0.65 W m-2 sr-1 and the spectrum looks like this:
For the full atmosphere vertical path with the US 1976 standard atmosphere, the total emission is 20.95 W m-2 sr-1. I couldn’t calculate the spectra in one pass. I can copy and post the pieces if anyone is really interested. I also forgot that the US standard atmosphere has a surface temperature of 288.2. Recalculating the horizontal path at 288.2 K gives a total emission of 26.0073 W m-2 sr-1
More apples and oranges. The US standard atmosphere in Spectralcalc has a VMR for CO2 of 0.000330. Spectralcalc takes too long to do atmospheric paths for 0.000330 CO2, MODTRAN gives 18.85 W m-2 sr-1 and Spectralcalc horizontal path is 25.45 W m-2 sr-1. As expected, the horizontal path is the highest and MODTRAN and Spectralcalc differ by about 10%.
The emissivity of 0.07 I calculated above was too low. I divided by pi when I didn’t need to. Or I didn’t divide the S-B calculated emission by pi. S-B is W m-2, not W m-2 sr-1. So for T = 288.2 and CO2 = 0.00033, the emissivity for the full atmospheric column is 0.151 for MODTRAN, 0.168 for Spectralcalc and 0.204 for Spectralcalc horizontal path. 0.204 is pretty close to the 0.21 I estimated from the Hottel emissivity graph for 3.04 atm m of CO2 at 300 K.
Three independent calculations of emissivity are in the same ballpark and 2 orders of magnitude higher than Nasif’s estimate.
Again… What you are calculating is the intensity decreases through the path lenght, not the total emissivity of the carbon dioxide.
And finally, use the correct formula introducing your numbers and see the result… Isn’t it quite simple, DeWitt?
Nasif,
Absorption increases with path length. Emissivity = absorptivity, so emission also increases with path length.
To all the readers of this blog:
The formula that I applied for the calculation of the Total Emissivity of the carbon dioxide is the most complete and the generally applied by scientists for making the calculations. Perhaps, you can find other “formulas” from other books labeled by DeWitt like “stone-age” texts which differ from the formula that I provided, but the formula that I applied is the top formula on this issue until now.
My source is nothing less than Michael Modest in his book titled “Radiative Heat Transfer”, published in 2003, Pp. 339-346.
Instead of accepting my invitation for calculating the total emissivity of the carbon dioxide applying the formula and introducing his unreal ciphers, DeWitt Payne has spent space and time with evasive arguments and flawed calculations.
Why is DeWitt afraid of accepting my invitation?
Thanks for reading my posts.
Nasif Nahle
Why are you afraid of accepting my invitation?
The formula Nasif uses is useful for calculating thermal emission and heat transfer in combustion gases that are isotropic and isothermal with a short path length. The atmosphere is none of those things so using that equation is going to give a ballpark estimate at best. The more fundamental problem is that Nasif uses the equation incorrectly, equating PaL to Pa, so his calculation isn’t even in the ballpark.
Read the book, DeWitt… Read the book… Then find what is the formula applied for. After you have read the book, introduce your ciphers in the formula and tell me your results… 🙂
By the way, PaL is defined as the partial pressure of the absorbent gas at L, which is the same that I wrote in my article. Consequently, PaL implies Pa, and without Pa, there would be no PaL.
What is it pseudoscience is considering that the concentration of the carbon dioxide in the atmosphere is the same at any altitude. That’s the most absurd argument I have known in the last years.
Again… Is the Pabs of the air 1 atm at 7 km altitude?
DeWitt Payne
Nasif,
Absorption increases with path length. Emissivity = absorptivity, so emission also increases with path length.
Absurd, your argument is plainly absurd. Get real… Calculate the absorptivity of the carbon dioxide at 7 km of height and the total emissivity of the cd at 7 km of height and show us your results.
For total emissivity, use the formula that I have provided, and for absorptivity, use the next formula:
Αλ = 1 – e ^ (-κλχ)
Obvioulsy, you’re confused again.
Nasif,
“Absurd, your argument is plainly absurd. Get real”
I’m reminded of The Princess Bride and the character Vizzini. The relevant quote is:
[Vizzini has just cut the rope The Dread Pirate Roberts is climbing up]
Vizzini: HE DIDN’T FALL? INCONCEIVABLE.
Inigo Montoya: You keep using that word. I do not think it means what you think it means.
Substitute absurd for inconceivable.
I did emission spectrometry for a living before I retired. Emission is indeed a function of concentration and path length. In inductively coupled plasma emission spectrometry, the source is optically thin so emission is linear with concentration over up to six orders of magnitude. In flame emission, however, the source is inches long and the emission is only linear over a narrow range.
Sorry to say it, but you have a wrong idea on what the total emissivity depends on. All physicists say it depends on density and temperature of the gas in question.
I think I’ve found what I need from using the search book function on Amazon.
This link may get you to the book:
http://www.amazon.com/Radiative-Transfer-Second-Michael-Modest/dp/0125031637/ref=cm_cr_pr_product_top
If it doesn’t go to amazon.com and search heat transfer modest 2003. That should get you the link for Radiative Heat Transfer, 2nd Edition (Hardcover). On that page use the look inside search feature for: PaL. That should give you a link to page 340 and sufficient following pages to find what I found.
Page 343 table 10.4
PE = (p + 0.28pa)/p0
p is the actual pressure and p0 is the reference pressure = 1 bar
pa is the partial pressure of CO2
For p = 1 bar and pa = 0.00038 bar, that makes
PE = (1 + 0.28*0.00038)/1 = 1.0001
a = 1 + 0.1/t^1.45
t is T/To where T is the actual temperature and To is the reference temperature = 1000 K.
a = 1 + 0.1/(0.3)^1.45 = 1.57
b = 0.23
c = 1.47
(paL)m/(paL)0 = 0.054/t^2 = 0.6
(paL)0 = 1 bar cm or 0.01 bar m or atm m
(paL)m = 0.006 atm m
ECO2/ECO2(0) = 1-(((a-1)*(1-PE))/(a + b – 1 + PE))*exp(-c*(log10((paL)m/paL))^2)
So the equation as given by Allan Kiik and Nasif has a couple of parentheses missing.
= 1-(((0.57)*(-0.0001))/(1.57 + 0.23 -1 + 1.0001))* exp(-1.47*(log10(0.006/3.04))^2)
= 1 -(-0.000032)*(0.000021) = 1
ECO2=ECO2(0) = ECO2 (304 bar cm,1bar,300 K) ~ 0.2 (Figure 10.25 only goes to 100 bar cm, but the lines are pretty close together at that point. Note that the table is not as L approaches zero, but for infinite dilution, i.e. as pa goes to zero and L becomes very large but pa * L is constant. The value of a property at infinite dilution is a concept that is familiar to most chemists. But it illustrates that both the partial pressure and the path length are important.
http://www.ehow.com/about_5459313_definition-infinite-dilution.html
This result should not be surprising since the correction factor is for pressure different from 1 atm and it isn’t.
So your calculations say that the cd has a total emissivity of 1, i.e. the total emissivity of a blackbody, higher than the total emissivity of any material on the Earth… Do you think it is correct?
First of all, the value you used for (PaL)m/(PaL)0 was 0.54/t^2, which is a constant applied when t than 0.7 m because we are considering the altitude of 1 meter.
Second, the magnitude of the proportionality constant a is 1+0.1/t^1.45. You calculated 1 + 0.1/(0.3)^1.45 = 1.57, which is wrong. Make it again.
Third, your final calculations are wrong; you wrote (in cursive, bolds are mine):
ECO2/ECO2(0) = 1-(((0.57)*(-0.0001))/(1.57 + 0.23 -1 + 1.0001))* exp(-1.47*(log10(0.006/3.04))^2)
= 1 – (-0.000032)*(0.000021) = 1
(Bolded parentheses don’t exist in the original formula).
Which is not correct because 1-(-0.000032) is 1.000032, which multiplied by 0.000021 is 0.000021000672. Notice that there are a sign of multiplication which separates the right side from the left side, so the “1-” corresponds to the left side alone.
Again, in the original formula those parentheses you added don’t exist:
There are not parentheses inclosing the multiplication, i.e. you don’t have 1 – [(-0.000032)*(0.000021)], but 1 – (-0.000032) * 0.000021, that is,
Now, (ECO2)0 at 1000 K and 1 atm (from your calculation), in the expression ECO2/ECO2(0), is 0.156; so you must multiply the result by (ECO2)0, i.e. 0.156, which gives a total emissivity for the carbon dioxide equal to 0.000003276104832.
The reference T that I used was 300 K from Leckner tables, not 1000 K; therefore, (Pal)m = 0.225*t^2.
Now, you’d like to know where the parentheses must be placed; well, from Modest book:
ECO2 = 1- (a-1* 1-PE / a+b-1+ PE) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
Left side, 1- (a-1* 1-PE / a+b-1+ PE)
Right side, exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
scienceofdoom,
this is going to be long. I hope you don’t mind.
Nasif,
Let’s look at your calculation of ECO2 for your paper:
Click to access ECO2.pdf
I’ll italicize quotes from your paper:
Known Magnitudes
ECO2o at T = 1000 K and pp 5.04 bar cm = 0.156
Wrong. On page 343 of Modest it clearly states that for a path length of 1 m, a mixing ratio of 0.1 and a pressure of 5 bar, Pco2L = 50 bar cm. If you go to Figure 10-25 on page 342, 50 bar cm at 1000 K is between 0.1 and 0.2 while 5 bar cm is between 0.05 and 0.1
a = 1.1
True for T = 1000 K, not true for 300 K
From Table 10.5 on page 344, a = 1 + 0.1/(t)^1.45, t = T/To = 300/1000 = 0.3 so a = 1.57 not 1.1
b = 0.23
c = 1.47
Pco2 = 0.1 * 0.00034
Wrong. It would be correct if the atmospheric pressure were 0.1 bar, but it’s not. Pco2 = 1 * 0.00034 = 0.00034 bar, not bar m.
P = 0.00034 bar m
Wrong. P is the total pressure. In the example it was 5 bar. For the atmosphere it’s 1 bar and again, not bar m.
Po = 1 bar m
PE = P + [0.28(Pco2)]/Po = 0.00035 bar m
Wrong and wrong again. Po = 1 bar, not bar m and since you calculated P incorrectly, the effective pressure is wrong too.
PE = [1 + 0.28(0.00034)]/Po = 1.0000952
(Pco2L)m = 0.225 (thickness = 1 m greater than 0.7 cm)
Wrong. t is not thickness, it’s a temperature ratio. In the line at the bottom of table 10.5 t =T/To where T is the gas temperature and To is the reference temperature = 1000 K. If T = 300 K, then t = 300/1000 = 0.3, which is less than 0.7 ( a ratio which has no units) so (PaL)m/(PaL)o = 0.054/(t)^2 = 0.6. It also specifies that (PaL)o = 1 bar cm. Then (PaL)m = 0.6 bar cm.
Pco2L = 0.0034 bar cm
Wrong again. Pco2L = 0.00034 * 798800 cm = 271.6 bar cm.
Ts = 330 K
Ta = 308 K
Mass of CO2 = 0.00069 kg
CpCO2 = 871 J/kg K
Emissivity of carbon dioxide at it’s current concentration in the atmosphere:
Eco2 = [1 – (a -1 * 1 – PE/a + b – 1 + PE)]exp.(-c(log10(pal)m/pal)^2 * Eo
The temperatures, mass of CO2 and heat capacity are irrelevant for this calculation. Your parentheses don’t balance in the equation and you really needed a few more to make the calculation a bit easier to follow.
Introducing magnitudes:
Eco2 = [ 1-1.1 * 1 – 0.00035/1.1 + 0.23 -1 + 0.00035) exp. (-1.47(log10 (0.225/0.0034 bar cm)^2] * 0.156
Eco2 = [ 1- (-0.099965/-0.303][ exp. (-3.315)] * 0.156 = [(0.67)(0.008)] * 0.156 = 0.00084; rounding up the cipher, Eco2 = 0.001
Even using your own numbers you get it wrong. It’s
Eco2 = [ 1 – ((x) * exp(y))] * 0.156, so using your numbers:
Eco2 = [1 – (0.33)*(0.008)] * 0.156 = 0.99736 * 0.156 = 0.1555886; rounding to 0.156.
But your numbers are wrong too and the equation doesn’t do what you think it does. It’s corrects for pressure only. The temperature factor is for emissivities taken from the Figure at temperatures other than 1000 K, and even then you only use the equation if the pressure is different from 1 atm. Ignoring the fact that your (Eco2)0 is for 50 bar cm an 1000 degrees, the correction factor is:
f = [1 – ((1.57-1)*(1 – 1.0000952)/(1.57 + 0.23 -1 + 1.0000952))* exp (-1.47 * (log10 (0.6/271))^2]
f = [1 – ((0.57)*(0.0000952)/(1.8000952)) * exp (-10.36)]
f = 1 – (0.00003015) * (0.000031654) = 1 to a very good approximation.
I should really proofread this carefully, but I think I have it right and I surely haven’t made as many mistakes as in the original.
Those parentheses you added to the formula don’t exist in the original.
You say:
Even using your own numbers you get it wrong. It’s
Eco2 = [ 1 – ((x) * exp(y))] * 0.156, so using your numbers:
Eco2 = [1 – (0.33)*(0.008)] * 0.156 = 0.99736 * 0.156 = 0.1555886; rounding to 0.156.
The original formula is as follows (read the book, please):
ECO2 = 1- (a-1* 1-PE / a+b-1+ PE) * exp. [-c [Log10 (paL) m / (paL)] 2] * (ECO2)0
Read my post above this one, so you can see how you have made wrong calculations.
You have changed a formula for sustaining your pseudoscience.
Nasif,
You should read the book. That isn’t the original equation.
The original equation is in this image:
In a form as close as I can do by text it’s
ECO2/ECO2(0) = 1 – term 1 * term 2
term 1 = numerator /denominator
numerator = (a – 1)(1-PE)
denominator = a + b -1 + PE
term 2 = exp{-c[log10(paL)m/paL]^2}
When you multiplied through by ECO2(0) you didn’t multiply the 1.
When multiplied through the equation would look like this:
ECO2 = ECO2(0) -term1 * term 2 * ECO2(0)
Apparently, you can’t do simple algebra.
DeWitt… Another very serious mistake in your calculations:
You obtained an erroneous ECO2 of 1, but you forgot to multiply by your reference ECO2 at 1000 K and 10% of carbon dioxide, i.e. 0.156. So, according with your wrong calculations and additions of parentheses that don’t exist in the original formula, the total emissivity of the carbon dioxide would be 0.156, that is, the same total emissivity of the carbon dioxide at a density of 207,655 mg/cubic meter?
Do you know that the current density of the carbon dioxide in the atmosphere is 690 mg/cubic meter?
Now think rationally… Is the temperature of the atmosphere 1000 K and the mass fraction of the carbon dioxide in the atmosphere is 112,647 ppmV?
No. I did not obtain an erroneous ECO2 of 1. As in the original text, I calculated the pressure correction factor, which equals 1. It’s you that chose the wrong emissivity. As stated in the book 0.157 is the emissivity for 50 bar cm of CO2 or a path length of 50 cm at 1 atmosphere for pure CO2 and 1000 K. Do you want a screen shot of that?
The pressure specified in the problem in the book is 5 atmospheres and the temperature is 1000 K. Do you want a screen shot of that too? 1 cubic meter at 1000 K and 5 atmospheres would be 1.37 cubic meters at STP assuming ideality. The composition is 20% water vapor, 10 % CO2 and 70 % nitrogen by volume. At STP, the density of water vapor is 0.018 kg/0.0224 m3 = 0.804, N2 is 0.028/0.0224 = 1.25 kg/m3 and CO2 is 0.044/0.0224 = 1.96 kg/m3. That makes the total mass of CO2 in 1 cubic meter at 5 bar and 1000 K = 1.96 * 0.1 * 1.37 = 0.27 kg. That would be 0.196 kg/m3 at STP or fairly close to your 207,655 mg/m3. Ideality probably breaks down somewhat at that temperature and pressure. N2 = 1.25 * 0.7 *1.37 = 1.20 kg and water vapor = 0.804 * 0.2 * 1.37 = 0.22. Total mass = 1.69 kg for a density at STP of 1.24 kg/m3. The denser CO2 doesn’t quite make up for the less dense water vapor when comparing the density at STP to dry air.
You’re the one who used the wrong emissivity, not me. Your lack of algebra skills isn’t my problem either. The correct emissivity for Pco2L = 0.034 bar cm at 300 K is not on the chart, but for 0.05 bar cm, it’s between 0.007 and 0.01, depending on whether you believe that the x axis is C as listed or K. K would make the vertical line at 1000 make more sense. But of course, Pco2L for the full vertical column of the atmosphere is over three orders of magnitude larger, on the order of 100 bar cm.
Revise the formula in the next link and tell me where those parentheses you added are found:
http://www.amazon.com/reader/0125031637?_encoding=UTF8&query=total%20emissivity#reader_0125031637
Here your medicine on applying your fantasious parentheses:
(ЄCO2)0 at T = 373 K and p = 1 bar = 0.001 (Please, consult Leckner’s tables and notice that T was given in °C).
t = 0.82 (308/373 = 0.82, which is > 0.7).
T0 = 373 K
a = 1.5
b = 0.23
c = 1.47
pCO2 = 0.00034 bar
pabs = 1 bar
p0 (absolute pressure at length 100 cm) = 1 bar cm
PE = pabs + [0.28 (pCO2)] / p0 = 1 bar + [0.28 (0.00034 bar) / 1 = 1.0001 bar
(PCO2L) m / (PCO2L)0 = 0.225 * t2 (if t > 0.7) = 0.151
PCO2L = 0.00034 bar (0.00034 bar at L 100 cm = 0.034 bar cm)
T = 308 K
Introducing magnitudes:
ECO2 = [1- (1.5-1 * 1-1.0001 bar / (1.5 + 0.23) – (1 + 1.0001 bar cm) * [exp. [-1.47 (Log10 (0.151 bar cm /0.034 bar cm) 2]] * 0.001
ECO2 = 1- [(0.47 * -0.0001 bar / (1.73) – (2.0001 bar) * [exp. [-1.47 (Log10 (0.151 bar cm /0.034 bar cm) 2]] * 0.001
ECO2 = 1- [(-0.000047 bar / -0.2701 bar) * [exp. [-1.47 (Log10 (0.151 bar cm /0.034 bar cm) 2]] * 0.001
ECO2 = [1 – [(0.00017)(0.54)]] * 0.001 = 0.001
With this scholar demonstration, I put the final point to DeWitt’s nonsense.
Thanks a lot, ScienceofDoom, for allowing me to post in your blog. Physics is easy. 🙂
308 K? Isn’t 35 C a little above average? Now that the algebra is cleaned up, we get back to the principle argument. Pco2L is only 0.034 bar cm if the path length is 100 cm at a CO2 volume fraction of 0.00034. The atmosphere is a lot higher than that and 0.035 bar cm is optically thin. There will be a contribution from the next 100 cm and the next one after that. Off to Spectralcalc again:
I calculated emissivities using Spectralcalc at 35 C and 400 C at bar cm values corresponding to the lines in Figure 10-25 in Modest. Using a screen shot of the the figure, I then overlaid a plot of the calculated emissivity at the two temperatures. The agreement is quite good. I also calculated the emissivity for 50 bar cm and 1000 K. It was 0.152 compared to 0.157 in Modest. The graph is here:
The Spectralcalc emissivity value for 0.034 bar cm is 0.0059, by the way. [ self-snip gloating]
Let’s introduce your ciphers and your imaginary parentheses and see what happens:
(ЄCO2)0 = Emissivity of the CO2 at (L = 0, p = 1 bar, T = 373 K) = 0.0077 [Hottel (1954), Leckner (1972), Pitts & Sissom (1998), Modest (2003), Manrique (2002)]
(PaL)m = 105,700 bar cm (altitude 700,000 cm, or 7 Km)
PCO2L = 238 (altitude 700,000cm, or 7 Km).
ECO2 = [1- (1.5-1 * 1-1.0001 bar / (1.5 + 0.23) – (1 + 1.0001 bar) * [exp. [-1.47 (Log10 (105,700 bar cm /238 bar cm) 2]] * 0.0077
ECO2 = 1- [(0.47 * -0.0001 bar / (1.73) – (2.0001) * [exp. [-1.47 (Log10 (105,700 bar cm /0.034 bar cm) 2]] * 0.0077
ECO2 = 1- [(-0.000047 bar / -0.2701 bar) * [exp. [-1.47 (Log10 (105,700 bar cm /238 bar cm) 2]] * 0.008
ECO2 = 1 – [0.00017)] [0.0000335] * 0.0077 = 0.0076
What happened?
The answer is very simple. You followed the example of the book and took ECO2 at 1000 K and 50 bar cm, when the correct procedure is to find the ECO2 at 0.05 bar cm and 373 K, which are the magnitudes near to the reality. That’s a big difference. 🙂
If you graph the results at different partial pressures of the carbon dioxide, you’ll find that the total emissivity of the carbon dioxide is inversely proportional to its partial pressure.
Graph the results.
Nope, 35 °C (308 K) is a real temperature.
I forgot to mention that the for the Spectralcalc calculations at constant temperature, only path length was changed. The partial pressure of CO2 was held constant at 0.00034 bar. The 0.034 bar cm emissivity was calculated at 308 K.
I would also like to thank scienceofdoom for letting us do this. It was actually more interesting than frustrating and I did learn a few things. After doing the emissivity calculations on Spectralcalc, it does make sense to just do them once and then put the data in tabular or graphical form and fit some sort of empirical function to the data for interpolation. That’s especially true if you do it right and extrapolate to zero partial pressure. That means several calculations at each temperature and pressure-path length. For 11 curves covering 0-2000 C, you’re looking at something on the order of 1,000 individual calculations. That’s a lot of hours, since it takes several minutes for each calculation, and that’s if you don’t have to split the range.
And that’s just for CO2. You also have to do water vapor and CO2-water vapor mixtures because there’s overlap.
DeWitt… You continue immersed in the error. Look at the tables, especially Leckner tables. The Total Emissivity of the carbon dioxide, obtained by experimentation, i.e. the real world, at 0.034 bar cm is 0.001. Through the calculation, your results must coincide with the results obtained by experimentation and observation.
For the algorithm gives you the real total emissivity of the carbon dioxide at 308 K and 0.00034 atm of p CO2, you must to take off your imaginary parentheses.
I have given a link to the Modest’s book, from which you would verify that those parentheses don’t exist. From Leckner’s tables, find the partial pressure 0.001 atm feet (equivalent to 0.034 bar cm in the table), and find the total emissivity of the carbon dioxide at 278 K (500 R). Which is the ECO2 at those conditions? 0.001. Hence, your calculations must to coincide with the observed and experimental data.
It will only be possible if you take off those imaginary parentheses.
I bought a copy of Leckner, 1972. There are no tables of emissivity data in that paper, only graphs. I used the coefficients for CO2 emissivity (M=3,N=4) in the paper for Eq 17 to calculate the emissivity for CO2 from 0-2200 C even though Leckner says the fit is only good to 400 C. For 300 K, or 26.8 C, the total emissivity of CO2 at 0.034 bar cm is 0.004 Comparing the fitted curve to the dashed lines in Fig. 9, the fitted data is too low at low temperature.
But Leckner’s work was done in 1971. His data was calculated using the best available radiative transfer model at the time, a band model with resolution 5-25 cm-1. Now we have high resolution line-by-line programs to calculate emission and total emissivity with a resolution of 0.1 cm-1. Spectralcalc is such a program. The program uses the most up-to-date database of molecular emission lines, HITRAN 2008. The total emissivity for CO2 at 308 K and 0.034 bar cm calculated by Spectralcalc is 0.0059. That’s not bad agreement with 0.004.
But that doesn’t really matter all that much. Actual measurements with all sorts of instruments from precision infra-red radiometers ( http://www.eppleylab.com/FrmInstrumentation.htm ) to FT-IR spectrometers show that emission from the atmosphere to the surface is orders of magnitude higher than you claim and that radiative transfer models calculate total emission and spectra that are in very good agreement with observation.
You’re the one ignoring the observations, not me.
I’ve spent all the money I’m going to on this project. If you want me to look at the emissivity data you claim proves your point, then post a copy on line. 0.001 atm feet is 0.030 bar cm, not 0.034. If it’s Hottel’s original work, then it’s wrong. Leckner wrote his paper to correct Hottel and the reasons why Hottel’s observations were biased are detailed in Leckner’s paper.
As far as extra parentheses, have you never used a spreadsheet or written a computer program? Parentheses are needed to make sure the program calculates things in the correct order, which you didn’t until I pointed out your rather basic algebra error.
Well… Those are good news because you have admited that my formula does exist. Remember that you and SoD were doubting about my formula.
Regarding the value for (ECO2)0, derived from Leckner’s database, not from the graph, you have to use another formula. Learn the formula here (it is F. 3):
http://biocab.org/Total_Emisivity_CO2.html
Regarding my basic algebra error, I repeat, there are not such parentheses in the original formula from Modest book. Read it and you’ll see no parentheses. It is an error induced by the text, not because I lack of knowledge on algebra.
On the other hand, I pointed on your real basic physics and algebra ignorance in my previous posts.
The total emissivity of the carbon dioxide is 0.001. I invite you to read my peer reviewed article at:
http://biocab.org/Total_Emisivity_CO2.html
Heh! I’m almost sure you won’t like my article because it is pure physics and mathematics, and it contradicts your ideology.
It will take me many re-readings to reach any understanding of De Witt’s and Nasif’s debate; one point about the 15u part of the backradiation spectrum; these 2 papers suggest it is due to water:
http://ams.confex.com/ams/Madison2006/techprogram/paper_113279.htm
Click to access acpd-3-5099-2003-print.pdf
And I want to ask De Witt, whose contributions I value this; if backradiation were as AGW theory and SoD claim, where is the THS, which would seem to be a logical result?
Dear Cohenite… The debate is all about the total emissivity of the carbon dioxide; it is deeply examined in the article linked in my previous post:
http://biocab.org/Total_Emisivity_CO2.html
Regarding your question, I have the answer, but you asked DeWitt first. 🙂
All the best,
Nasif
Well Nasif, you’re a bit of a tease; and you don’t mind an argument; from your link;
“Something valuable to emphasize is that the total emissivity of the carbon dioxide decreases as the density of the gas in the atmosphere increases, as long as the temperature remains constant; as well, when increasing the temperature of the atmosphere, the emissivity of the carbon dioxide decreases logarithmically”
So extra CO2 cools; this puts a twist on pressure broadening; the AGW view is that this shows CO2 will increase temp at higher temps and pressure and concentration; you seem to be saying the opposite; so I suppose you would be saying that an increase in CO2 mitigates the THS?
In respect of CO2 sensitvity to climate change, which is not quite the same thing you are saying, what do you think of the Franks paper?
http://www.nature.com/nature/journal/v463/n7280/abs/nature08769.html
I’m sorry for giving the impression that I’m a bit of a tease; perhaps, it obeys to my English, which is not my mother’s language.
Regarding your first question, yes, I am assuring it because experimentation has shown those results. Graphing the databases of Leckner and Hottel, which we can read from almost all books on heat transfer, we can see this phenomenon. Far from increasing the energy that the carbon dioxide absorbs and emits, the increases of its density lowers its total emissivity and, therefore, the temperature of the mixture of gases decreases. Thus, the carbon dioxide acts like a coolant, not like a warmer.
Truly, I don’t know why most models resolve the equations on the opposite way. The data is quite clear and all the equations derived from those experiments give the same results.
The explanation could be very simple: as more molecules of carbon dioxide are added in the atmosphere more available microstates toward which the energy emitted by the surface could be dispersed would be there, so the amount of energy absorbed by a sole molecule of carbon dioxide gets limited by the whole mass of the gas in a given medium. On the other hand, if the density of the carbon dioxide remains relatively constant and the temperature of the medium increases, then the total emissivity of the carbon dioxide would also decrease.
Another explanation could be the expansion of the gas by the increasing temperature. As the gas warms up it expands and its mass fraction decreases; therefore, its total absorptivity and emissivity also decrease.
Regarding your second question, the paper of Frank et al agrees with my paper in many points, except for the argument on the global warming caused by emissions of carbon dioxide through human activities. It is relevant this phrase taken from their conclusions:
“Our results are incompatibly lower (P < 0.05) than recent pre-industrial empirical estimates of ~40 p.p.m.v. CO2 per °C (refs 6, 7), and correspondingly suggest ~80% less potential amplification of ongoing global warming."
Actually, their data seems to have been taken from an ambient out of this Earth with temperatures near to the 833 K and densities of carbon dioxide of almost 1 Kg/cubic meter.
Nasif, Chilingar beat you to the punch with the idea that CO2 increase leads to cooling, albeit for different reasons!
http://www.informaworld.com/smpp/content~db=all?content=10.1080/15567030701568727
Oh, no! Actually, Chillingar et all are rising my hand; the only difference is that they attribute the cooling power of the carbon dioxide to the adiabatic effect; while I attribute it to more sensible additional statistical causes. One way or another, the adiabatic effect has more to do with energy states than with peripheral operators.
The observations, including Chillingar’s one, is that the carbon dioxide behaves like a coolant as its density increases in the atmosphere.
The explanation could be much uncomplicated, on condition that we apply physics properly.
cohenite,
The two papers you linked above are for total downwelling longwave radiation, not specifically the 15 micrometer band of CO2. Since the majority of downwelling longwave radiation is from water vapor (clear sky) and liquid water (cloudy sky), the part of the algorithm dealing with clouds and water vapor is obviously important.
THS???
De Witt, are you saying “THS???” because you don’t know it stands for tropical hot spot [which I can’t believe] or because you don’t get the connection between backradiation and a THS, which I understood to be the case because the Troposphere would warm faster than the surface since it is being heated by a warmer surface, to wit, the surface of the planet which is getting warmed by the aforesaid backradiation; and in addition to but not withstanding that the troposphere whould also rise which would be another aspect of the THS, with the final characteristic being that said THS would occur in the tropics where the warming effect of extra water would be most pronounced, also as a consequence of backradiation?
Tropical Hot Spot wasn’t one of the alternatives listed for the acronym THS and I’ve had total this and that on my mind so I couldn’t think of anything corresponding to Total HS.
As to the Tropical Hot Spot, that’s really a function of water vapor feedback, not a first order forcing. You don’t see it in MODTRAN as implemented on line, for example. A surface temperature offset entered in MODTRAN only affects the temperature up through 10 km and it’s constant. You get the THS only if the lapse rate decreases as temperature goes up because the moist lapse rate gets lower as specific humidity goes up (higher energy content/kg). A decreasing lapse rate is actually a negative feedback, but the increased radiation from increased water vapor is supposed to more than make up for that.
Say the lapse rate is 6.5 K/km and the surface temperature is 300 K. Then the temperature at 10 km would be 235 K (300-6.5*10). Now let’s raise the surface temperature by 10 K and lower the lapse rate to 6 K/km. Now the surface temperature is 310 K and the temperature at 10 km is 250 K (310-6*10). So the surface has warmed by 10 K and the 10 km temperature has gone up by 15 K. That’s the source, but with smaller numbers, of the THS.
Exactly right, at least for the theory which is depicted at Fig 9.1, page 675 of AR4; the AGW position is probably summed up by Santer’s ‘fact sheet’:
Click to access santer_etal_IJoC_08_fact_sheet.pdf
And the PR paper is:
http://www.gfdl.noaa.gov/reference/bibliography/forthcoming/bds0801_man.html
The problem is the THS doesn’t appear to be there.
Nasif,
Leckner’s database? You keep moving the goalposts. Do you have a link or citation for that? It’s hard to believe that the database gives a different result than the graph derived from the database. In your link, you say 0.0015 is from F.3, not from Leckner’s database, wherever that is. Since your F.2 is wrong, your derivation of F.3 is also suspect. Not to mention the circularity of calculating Eco2(0) from an equation derived from an equation that was meant to calculate a correction to Eco2(0).
Here’s your F.2:
(E/ E0)CO2 = [1- ((a-1) (1-PE)/ (a+b) – (1+ PE))]) e [-c (Log10 (paL) m/paL)^2]] (F. 2)
Here’s the correct formula direct from Modest, 2003:
As anyone with seventh grade algebra skills can see, the first left bracket in your F.2 should be after the 1 – , not before, not to mention the other parenthesis errors that would cause Excel, for example, to evaluate the formula incorrectly.
Let’s go way back to your comment:
https://scienceofdoom.com/2010/06/03/lunar-madness-and-physics-basics/#comment-3339
“Absorption increases with path length. Emissivity = absorptivity, so emission also increases with path length.
Absurd, your argument is plainly absurd. Get real… Calculate the absorptivity of the carbon dioxide at 7 km of height and the total emissivity of the cd at 7 km of height and show us your results.”
You might want to read this:
http://www.barrettbellamyclimate.com/page45.htm
Chapter 8 in Grant W. Petty, A First Course in Atmospheric Radiation ( http://www.sundogpublishing.com/AtmosRad/index.html ), or Atmospheric Radiation: Theoretical Basis, Goody, R.M. and Y.L. Yung ( http://www.amazon.com/Atmospheric-Radiation-Theoretical-R-Goody/dp/0195102916/ref=sr_1_1?ie=UTF8&s=books&qid=1277819889&sr=8-1 ) has more detail. If you use the ‘Search Inside This Book’ function and use ‘schwarzschild’, then page 205 in Petty and page 22 in Goody and Yung will give you the derivation of Schwarzschild’s equation.
So it’s not at all absurd that emission increases with path length, it’s basic physics.
The way Leckner calculated total emissivity was to calculate the emission spectrum for a given path length, temperature and partial pressure using a band model, integrate to obtain the total emission and divide by the Stefan-Boltzmann black body emission for that temperature. Here’s a screen shot of the text of interest:
We can do a better job today using a line-by-line rather than a band model. A total emissivity of 0.0015 corresponds to an emission intensity at 308 K of 0.243 W m-2 sr-1. Using Spectralcalc with T = 308 K, P = 1.01325 bar and Pco2 = 0.00034 bar, the path length for that emission intensity is 19.4 cm. Spectrum here:
That corresponds to a pressure path length of 0.0066 bar cm, not 0.034 bar cm.
To reiterate for the umpteenth time: Ignoring the algebra errors, your principal error is to assume that path length doesn’t matter or is somehow constant and equal to 1 m or 100 cm. If you used a path length that was closer to the actual path length in the atmosphere, your calculation would be close rather than orders of magnitude low. It would be different because the method assumes that temperature and pressure are constant over the path length and they’re not in the atmosphere.
If we use a temperature of 308 K, a partial pressure of 0.00034 bar for CO2 and a path length of 798800 cm, the emissivity from the equations in Leckner is 0.1448. The total emission is then 23.5 W m-2 sr-1. Plugging the same numbers into Spectralcalc gives 34.0 W m-2 sr-1 ( http://i165.photobucket.com/albums/u43/gplracerx/CO2308K000034bar798800cm.png ). But that’s not surprising because the Leckner equations don’t claim validity below 400 C and inspection of the graphs shows the emissivity increases at low temperature rather than decrease as the empirical polynomial equation does. Still, it’s less than a factor of two different. For an atmospheric path using MODTRAN (I have to break up the spectra into pieces for SpectralCalc which takes too long) at 340 ppmv and 0 ppmv CO2 for a surface temperature of 308 K and the 1976 US Standard atmosphere, the CO2 emission intensity from the surface looking up is 24.8 W m-2 sr-1 ( http://i165.photobucket.com/albums/u43/gplracerx/MODTRAN340.gif with CO2 and W m-2 so divide the scale on the y axis by pi).
23.5, 34.0, 24.8. That’s three independent methods that give similar answers for the same problem stated correctly. Note that the emission spectrum from SpectralCalc looks quite a bit like the MODTRAN spectrum, ignoring the bumps and wiggles from the N2O and water vapor in the stratosphere that I can’t remove, as well as the atmospheric emission spectrum in SoD’s comment here: https://scienceofdoom.com/2010/06/03/lunar-madness-and-physics-basics/#comment-3018
Oh! DeWitt Payne cannot find Leckner’s database… It seems you’re desperate before the truth. The link you provide is not the formula that you can read from Modest’s book. Here again the link to the page to the formula in Modest’s book. Tell me where your parentheses are:
http://www.amazon.com/reader/0125031637?_encoding=UTF8&query=total%20emissivity#reader_0125031637
Besides, You can test my results with the formula with parentheses, but using the correct parameters. You’ll see that my calculations are correct and the total emissivity of the carbon dioxide, at its current concentration, is 0.001.
Even using your spurious partial pressure of 0.0066 bar cm, which is not a value for partial pressure but a concept invented by yourself, the result is the same: 0.0017. No more.
The problem with you is that you have not yet understood that the absolute pressure of 1 atm is the sum of all partial pressures of all components of the atmosphere, at the sea level, of course.
As you can see, it is basic physics. Show me your algorithms in the same way I show my algorithms in my articles.
Just for giving an example, when you say that the value of 0.066 bar cm is the partial pressure of the carbon dioxide in the column of air, you are saying that the proportion of the carbon dioxide in the atmosphere at 1 cm above the surface is 6.6%, which is a blatant lie. Isn’t it to twist the science to the extreme for filling an ideology?
Introduce your numbers to the formula and you’ll see the truth about the carbon dioxide.
Again… The same happened with Modest’s formula; you were saying it had been invented by me. Now you are suggesting that the F. 3 from my article and the database of Leckner are invented. Before I show you real physics, spend some money for finding the sources. Spend some money looking for the source of the formula F. 3 and demonstrate it is not a reliable formula. 🙂
Sorry, that PR paper by Santer is here:
http://www3.interscience.wiley.com/journal/121433727/abstract?CRETRY=1&SRETRY=0
Correction:
I said:
“Just for giving an example, when you say that the value of 0.066 bar cm is the partial pressure of the carbon dioxide in the column of air, you are saying that the proportion of the carbon dioxide in the atmosphere at 1 cm above the surface is 6.6%, which is a blatant lie. Isn’t it to twist the science to the extreme for filling an ideology?”
It should have said:
“Just for giving an example, when you say that the value of 0.0066 bar cm is the partial pressure of the carbon dioxide in the column of air, you are saying that the proportion of the carbon dioxide in the atmosphere at 1 cm above the surface is 0.66%, which is a blatant lie. Isn’t it to twist the science to the extreme for filling an ideology?”
The link provided by Cohenite doesn’t work. Here the link to the article:
http://www3.interscience.wiley.com/journal/121433727/abstract
And the paper that Santer et al’s paper is rebutting [sic] is this one:
@DeWitt…
You say:
To reiterate for the umpteenth time: Ignoring the algebra errors, your principal error is to assume that path length doesn’t matter or is somehow constant and equal to 1 m or 100 cm. If you used a path length that was closer to the actual path length in the atmosphere, your calculation would be close rather than orders of magnitude low. It would be different because the method assumes that temperature and pressure are constant over the path length and they’re not in the atmosphere.
Show me one single algebraic error in my paper.
Make the calculations by yourself and tell me… Where the algebraic error is?
Ask Modest why he didn’t write the parentheses in his formula; that’s the correct procedure.
You say:
To reiterate for the umpteenth time: Ignoring the algebra errors, your principal error is to assume that path length doesn’t matter or is somehow constant and equal to 1 m or 100 cm.
And I sustain it. You’re absolutely wrong when thinking that the partial pressure at 7.7 Km of altitude is the same than the partial pressure of the carbon dioxide at 1 m of altitude above the seal level.
When you measure the pressure of the air at 1 cm of altitude you are meassuring the pressure of the whole column of air which, by the way, it is 1 atm, not 7700 atm as you are assuring.
I know you don’t know how to obtain the partial pressure of the carbon dioxide in a mixture of gases. Here it goes:
The carbon dioxide constitutes ~383 ppmV of the whole volume of air.
This does 2.3e+20 molecules in one mole of air molecules:
6e+17 * 383 = 2.3e+20 molecules.
Therefore, the mole fraction of the carbon dioxide is 2.3e+20 molecules divided by 6.02e+23 moles:
Then, the mole fraction of the carbon dioxide is:
Mole Fraction of the CO2 = 2.3e+20/6.02.e+23 = 0.000382
From here, the partial pressure of the carbon dioxide is:
pCO2 = MF * pabs
pCO2 = 0.000382 * 1 atm = 0.000382 atm
Conclusion, the partial pressure of the carbon dioxide is 0.000382 atm at any L at which you can verify that the mass fraction of the carbon dioxide is 383 ppmV and its mole fraction is 0.000382. Point.
I think your problem is that you don’t understand the meanings of mass fraction, mole fraction, absolute pressure, partial pressure, etc. Or perhaps you don’t want to understand.
Nasif, it’s been a while but you said this to SoD some time ago in response to his question:
SoD:”Can you confirm what you believe about measurements of downward surface radiation in the 15um band.
Is it from CO2?”
Nasif replies: “No, I confirm the graph shows several radiance values for several absorbers-emitters. The problem is that you think it is a measurement of a ghostly “downward” radiation, while the authors of the graph are showing the spectral bands of several constituents of the atmosphere, not any measurement of any downward radiation.”
Nasif, can you elaborate that please?
Yes, I will. The graph provided by SoD is a graph on the hypothetical irradiance of several gases which could be forming part of the atmospheric mixture of gases; nonetheless, the graph was made by simulators, and were not the results of real measurements of the irradiance of the gases taken individually, as the authors of the graph clearly pointed out (bolds are mine):
“In order to extract the greenhouse flux from individual gases, the background emission of the atmosphere was simulated using the radiative transfer code, FASCOD3 (Clough et al., 1988). The simulations incorporated the temperature, relative humidity and pressure profiles from radiosonde measurements obtained at Maniwaki, Quebec, a location 280 km distant from Peterborough.”
So the graph is a ghostly graph because those ciphers were not obtained by direct measurements with radiometers; they were simulated. Nothing real, Cohenite. Besides, the hemispherical radiance attributed to the carbon dioxide barely makes 0.000008 W/m^2 sr at its maximum value in the spectral band. The total irradiance of the carbon dioxide in the atmosphere simulated by Evans and Puckrin not even reaches the magnitude that I deduced through the appropriate algorithms. In other words, the total emissivity of the carbon dioxide in the atmosphere, according to Evans and Puckrin, is by far smaller than 0.001.
Besides, the authors didn’t graphed the total irradiance of water vapor. I have a copy of Evan’s article.
Thanks Nasif; I think I’ll need to have a yarn with my mate Jan Pompe to make heads and tails of this.
What is your impression SoD?
I’ve sent an email to Dr. Leckner at Chalmers University in Sweden asking if he will comment.
Do keep us up to date, im sure its not just me thats been trying to follow this discussion. 😉
Nasif Nahle:
Says:
But this is not the case and Nasif Nahle is confused.
The graph is a measurement by an FT-IR. The authors of the paper say:
So the graph is reality.
Then they use the well-known radiative transfer equations to see what the theory says and whether it matches the measurement.
The graph is what we measure. The simulations, using the radiative transfer equations, tell us whether the theory and the measurements match.
Earlier in the comments for this article Nasif Nahle was quite positive about these measurements because he thought it backed up his claims.
So because of his joy, I asked yet again if he could confirm whether these measurements in the 15um band were from CO2. And I concluded my question:
But no answer was forthcoming, until now.
Well, strictly speaking, Nasif Nahle hasn’t actually answered because he doesn’t realize that Fig 1 is a measurement, but he does say:
Ooops.
Units and details of calculations are not an exciting subject. But because of the confidence with which Nasif Nahle writes – after dodging the question for so long – it is worth examining these units and I hope the newcomers and non-mathematical types can stay with me..
Unit Conversion 101
The units for the graph are:
And the peak value in these units measured in the 15um band (wavenumber = 667 cm^-1) is 8 x 10^-6 (see the graph).
Now let’s deconstruct the units – or convert them to W/m^2.
1. W/cm^2 compared with W/m^2
There are 100 cm in a meter, so there are 10,000 cm^2 in 1 m^2. Or we could equally write: 1×10^4 cm^2 in 1 m^2.
So if we look at the peak value per m^2, it is 8 x 10 ^-2 W/(m^2 sr cm-1) = 0.08 W/(m^2 sr cm-1)
-We have just converted the radiation received in one very small surface area (cm^2), into the amount of radiation received in a much larger surface area (m^2).
2. per cm^-1 (or per 1/cm) – what does this mean? When the measurement is in 1/cm, it is in wavenumber.
For most non-specialists, it is much easier to think in terms of wavelength, or um. Converting from wavenumber to um is done like this:
Wavenumber in cm^-1 = 10,000 / wavelength in um.
So if wavelength = 15um, wavenumber = 10,000/15 = 667 cm^-1
The easiest way to understand how to convert the values in the graph is to look back at the graph.
The total radiation can be calculated by multiplying the radiance per (cm^-1) by the amount of (cm^-1) – to work out the area under the graph.
Between 600cm-1 and 740cm-1 the value on the graph is around 7×10^-6 W/(cm2 sr cm-1) or 0.07 W/(m^2 sr cm-1).
So to work out the W/(cm^2 sr) we have to multiply this value of 0.07 W/(m^2 sr cm-1) x 150 cm^-1 = 10.5 W/(m^2 sr).
Note that this value is quite approximate because to do it properly would require a more detailed measurement of “area under the curve”. However, this quick calculation gives us a very approximate estimate.
3. What about “sr”? Sr is steradians which is solid angle. When measuring radiation which goes in all directions it is commonly measured per “steradian”.
This is the case here. Converting this value to the total radiation in all direction means multiplying the value per each 1 steradian by pi (3.14).
So 10.5 W/(m^2 sr) = 33 W/m^2.
Well, in the paper, the actual value, properly integrated, comes out at 26 W/m^2.
Conclusion
Converting units is very turgid. But sometimes necessary to explain the results in units that people are used to.
We can see that 8 x 10^-6 (0.000008) W/(cm^2 sr cm^-1) over 150 cm^-1 is actually around 33 W/m^2.
Nasif Nahle was very happy to see this low number of 0.000008 because he felt it vindicated his low calculation.
However, the measured value of 15um radiation converted into W/m^2 is around 1000x higher than he calculates for CO2.
And CO2 is the dominant emitter in the 15um band. This is why I asked him to confirm that these measurements in the 15um band were from CO2.
He was very happy because he thought the values appeared low and vindicated his theory.
Except the measured values are actually much higher, as a simple units comparison can confirm.
Therefore, we will now see the claim that either:
a) this radiation is not from CO2 but some other unspecified gas
b) the unit conversion is wrong
Because option c) would be “Nasif Nahle’s calculations of CO2 emission in the atmosphere are out by a factor of 1000”
And clearly that is a ridiculous option..
Your graph, the graph you insert in your post, is a simulation. The authors clarify the point.
@SoD…
You say,
Therefore, we will now see the claim that either:
a) this radiation is not from CO2 but some other unspecified gas
b) the unit conversion is wrong
Because option c) would be “Nasif Nahle’s calculations of CO2 emission in the atmosphere are out by a factor of 1000”
And clearly that is a ridiculous option..
My calculations are correct. DeWitt Payne found the same results, but he won’t admit it, not even introducing his numbers in the formula, which, by the way, he has found it exists.
The sole probability is that Evans et al “adjusted” the measurements and made a bad simulation, because my calculations coincide with the graphs on total emissivity made through experimentation by Hottel, Edwards, Leckner, etc.
Oh! I forgot to comment over your tortured conversions.
You have, effectively, 0.000008 W/(cm^2 sr 1/m). You’ll see your errors if you answer four simple questions:
1. How many centimeters are in 1 meter?
2. How do you express 1 cm in meters?
3. How do you express 1/m in cm?
4. If you divide 1 cm^2 sr by 100 cm, which the units of the final result are?
Introduce your results in the expression W/(cm^2 sr) / cm and tell me your results.
Nasif Nahle says:
Your graph, the graph you insert in your post, is a simulation. The authors clarify the point..
The authors in their own words in the paper:
This has been an interesting discussion, and I had particular value for the math details and formulas.
As SoD has brought the thread back to the ‘back radiation’, I wanted to comment on data from two of his references.
*SoD on June 18, 2010 at 10:03 pm, reference to Measurements of the Radiative Surface Forcing of Climate, W.J.F. Evans & E. Puckrin, American Meteorological Society, 18th Conference on Climate Variability and Change (2006)
my percentages using data from Evans and Puckrin:
Figure 1 shows the strong CO2 peak (Winter measurement) as noted by SoD in earlier comments,
and in corresponding Table 2,
we see that CO2 accounts for about 80% of the back radiation on a water free basis.
Then in Table 3a: Measured Winter Downward Surface Fluxes which includes H20,
the Water is 70 to 75% of the back radiation, and CO2 contribution is 20 to 25% (WINTER).
The CO2 back radiation value didn’t change, but we can now compare it to the H2O back radiation.
In Table 3b: Measured Summer Downward Surface Fluxes
The H20 contribution is even more dominant, at around 94%, and the CO2 contribution is about 4% (SUMMER).
Their energy back radiation values are as follows (Evans and Puckrin, tables 3a and 3b):
Winter
H20 94 to 125 W m-2
CO2 31 to 35 W m-2
Summer
H20 178 to 256 W m-2
CO2 10.5 W m-2
Not only did the relative CO2 contribution drop in Summer, but the back radiation value decreased from about 30 Winter to about 10 W m-2 Summer.
*How do these Evans and Puckrin (2006) values compare with and confirm the energy estimates in Kiehl & Trenberth, 1997?
The back radiation shown in the K & T chart is 324 W m-2.
Data from Evans and Puckrin suggests that CO2 accounts for at most 10% of K&T, and in Summer, CO2 is only about 3% of the K&T back radiation.
To get close to the K&T back radiation values, there apparently needs to be a LOT of H2O in the atmosphere.
I don’t believe I can be of assistance to Nasif Nahle.
But if anyone else is confused about the conversion of the radiance measurements in the measurement to total W/m^2 for CO2, please ask and I will be happy to explain it from another perspective.
@SoD…
Now you’re torturing the text. The authors say with respecto to the graph you introduced in your post:
“In order to extract the greenhouse flux from individual gases, the background emission of the atmosphere was simulated using the radiative transfer code, FASCOD3 (Clough et al., 1988). The simulations incorporated the temperature, relative humidity and pressure profiles from radiosonde measurements obtained at Maniwaki, Quebec, a location 280 km distant from Peterborough.”
You see? the attribution of x total irradiance for the carbon dioxide is a simulation, that is, imaginary.
@SoD…
I’ve waiting for your answer to my questions, but you are evading them resourcing to insults to my person, like this one:
“I don’t believe I can be of assistance to Nasif Nahle.”
and,
“Because option c) would be “Nasif Nahle’s calculations of CO2 emission in the atmosphere are out by a factor of 1000”
And clearly that is a ridiculous option.”
Which clearly is an unscientific practice.
I have to leave now and will come back until tomorrow night. Let’s examine this portion of your discourse:
“We can see that 8 x 10^-6 (0.000008) W/(cm^2 sr cm^-1) over 150 cm^-1 is actually around 33 W/m^2.”
In other words, you’re saying that W/(cm^2 sr/cm) = to W/cm sr. You forgot eliminating units:
0.000008 W/((cm^2 sr) * 1/100 cm) [because one meter is 100 cm, not 150 cm).
Which would be 0.0008 W/cm sr, or 0.08 W/meter sr.
Therefore, your first mistake is having forgotten the elimination of units.
Now tell me, what the units W/m sr are for?
Your second error is that you multiplied 0.08 by 3.1416, that is, by π; however, you should not multiply by π, but to divide by 4π, given that you’re considering the whole sphere (deducted from your discourse). This gives a very small quantity: 0.006 W/m:
0.08 W/ (m * 12.6) = 0.08 W/12.6 m = 0.006 W/m.
Now tell me, what the units W/m are for?
Dave in Delaware
Good questions.
I would like to do an article on the subject of back-radiation as many questions have been asked through different articles.
This might take a little while but I will get to it.
Yes, thanks Dave from Delaware; my understanding of the spectrum is primitive but what has been confusing me is that if the backradiation is correct and the majority is at ~ 15um, isn’t that wavelength dominated by H2O?
http://www.nov55.com/atmo.html
cohenite
CO2 is the dominant absorber and emitter at 15um.
H2O has an influence throughout the longwave spectrum, including some effect at 15um but it is a few orders of magnitude less.
See the extracts from spectralcalc above in this post.
Also, the particular spectrum shown from the Evans paper is one measurement at one time in one location. In that example, winter time in Canada, the water vapor effect is quite small.
“it is a few orders of magnitude less”; do you have a reference for that; I thought because H2O has a permanent dipole that it would dominate CO2 in overlaping wavelengths because CO2 does not have a permanent dipole.
cohenite:
A reference?
Ok..; [in an attempt to inject humour into the debate];
But seriously a paper by Barrett, which even Nick thinks is a good paper [for E&E] calculates that the greenhouse temp contribution of CO2 is 6.7K [page 8]; Table 1 shows this:
GHG % Absorption Absorption relative
To water vapour = 1
Water vapour 68.2 1.000
CO2 (285 ppmv) 17.0 0.249
CO2 (570 ppmv) 18.5 0.271
CH4 1.2 0.018
N2O 0.5 0.007
Total [water, CO2 (285 ppmv), CH4, N2O] 86.9
Combination with 285 ppmv CO2 72.9 1.069
Combination with 570 ppmv CO2 73.4 1.076
So even 2xCO2 only increases CO2 absorption to 18.5% of what H2O absorbs. Your graphs show CO2 dominating at 15um but if H2O absorbs much more than than CO2 why do you say CO2 dominates backradiation? Wien distribution?
cohenite:
Water vapor dominates backradiation on a global annual average. CO2 comes in second place.
Clearly the ratio will vary with time and place as water vapor concentration has a large variation with latitude, season and time. Whereas CO2 is “well-mixed” and therefore usually around 380ppm.
CO2 is a much stronger absorber than water vapor at 15um.
re cohenite
There is no H2O in Figure 1 from Evans and Puckrin, because they left it out. That figure is re-assembled from the individual ‘measurements’. Admittedly, the H2O was left out so that it was easier to see the contributions of the other dozen GHGs. The H2O is included in their Table 3, so it was there, just not shown in Fig1.
To get the individual profiles, they took the ‘full’ spectrum, and subtracted out ‘everything else’. They give this example (with Figure 2) on how this was done. Note that H2O peaks are shown in their Fig 2, and listed in their description as one of the things they had to sort out to get the other components.
From Evans and Puckrin (2006) Figure 2 example
“The extraction of the thermal emission
band of CFC-12 from the measured atmospheric
emission spectrum (curve A). Curve B represents
the simulated background thermal emission in the
absence of CFC-12. The subtraction of curve B
from curve A shows the thermal radiation
associated with CFC-12 (curve C). Curve A in
Figure 2 shows the measured downward
thermal emission for January, 1994. Besides
the emission from CFC-12 in the 900-940 cm-
1 region, other gases including nitric acid,
water vapour and carbon dioxide have
emission bands that overlap with those of
CFC-12, as noted in the figure. The simulated
emission of these other gases is represented
by curve B in Figure 2. Subtracting the
simulated background thermal emission from
the measured emission yields the measured
downward greenhouse radiation at the
surface that is associated with atmospheric
CFC-12 (curve C). The downward radiation
fluxes at the surface for all greenhouse gases
measured up to 1996 are summarized in
Table 2.”
They determined the ‘everything else’ using a computer model –
“In order to extract the greenhouse flux
from individual gases, the background
emission of the atmosphere was simulated
using the radiative transfer code, FASCOD3
(Clough et al., 1988).”
Thanks Dave; do you have a link to that Evans and Puckrin text?
SoD has given the reference earlier in this thread, or perhaps on another SoD article. Here it is again. The paper is:
Measurements of the Radiative Surface Forcing of Climate, W.J.F. Evans & E. Puckrin, American Meteorological Society, 18th Conference on Climate Variability and Change (2006)
I think this link will take you to the abstract and the PDF from that conference.
http://ams.confex.com/ams/Annual2006/techprogram/programexpanded_313.htm
Their entry was P1.7 in the 2:30 to 4 pm Monday list. I was able to access the PDF from there.
Thanks Dave; I find the Evans and Puckrin paper very puzzling. You may find the Barrett paper which I referred to earlier interesting:
Click to access barrett_ee05.pdf
Just a note: If you look at Nassif’s other “work” you’ll see him calculate that the cosmic flux measured by the Pioneer probes (IIRC) correlates with the temperature record and this “proves” that GCR is the cause of current warming.
However, these GCRs are high energy particles, going at the speed of light. This means that these particles take a few hours to go from the pioneer craft to the earth.
But to make the correlation, he has to delay the GCR intensity by (agan IIRC) weeks.
No mechanism for how these GCRs are slowed down yet kept coherent.
Nassif asserts his complete expertise in astronomy and astrophysics.
How he thinks anyone can be taken in by this (except by those who have a vested interest in believing anything that “disproves” AGW) remains a mystery.
Rather like the slowdown of the GCRs.
Oh, dear Mark… Ignorance is the worst enemy of AGW idea. Are you assuring that protons and electrons are traveling at c? Have you read the article or your making assumptions a priori?
It won’t take you too much time… Read my whole article at:
http://biocab.org/Cosmic_Rays_Graph.html
Thanks… 😀
Nassif.
Data ends ~2004. Why? cf “TGGWS” which stopped showing solar and temperature data after 1995 because the solar output went down and temperatures went up.
And those graphs show NOTHING about the correlation between GCRs and temperature. This is why you keep them separate.
Look at july 2004. Slump in temps. Nothing looking like that in the He figures… In fact that entire graph looks as though it’s proving the lack of correlation.
as to this:
“Are you assuring that protons and electrons are traveling at c”
What are the energies of GCRs? What is the velocity (if it’s low compared to c, you can ignore relativistic effects)
proton mass: 10^-27
1MeV: 10^-16J
1Mev would make a proton move at
v=sqrt(10^-11) m/s ~ 3×10^5 m/s covering 100AU in 17 days, rather than your 13.6 months…
What are YOUR a priori assertions on the energy of the cosmic rays your measures are of?
I really do wonder at how someone can seem so certain of their theory all the time. What sort of delusion makes someone like Nassif think he’s found “the answer” when he so obviously has not.
I mean, not even a correlation, never mind a causation (CLOUD has shown that there’s no discernable effect of cosmic rays on cloud formation). But the 76% correlation between temperature and CO2 measurements since 1890 to him doesn’t exist and have to be explained away.
Mark… The graphs are on ICR, not SCR. The database is from the Vikings, so the information ends in 2004 and there is not any “special” reason for this limit.
You’re conjecturing about my “motivations”, but there is nothing like that. It is simply that NASA released the data only for the graphed date. Besides, the article was written on November 2005. I will update it when I have more information from the Vikings.
Regarding you other “observations”, read the paper and you’ll find the amount of energy of the ICR reaching the Earth.
Unfortunately for you, it is information released by NASA and I’m not assuming anything:
http://science.nasa.gov/science-news/science-at-nasa/2009/23dec_voyager/
I hope real science takes you out from that pseudoscientific pit.
BTW, I have more bad news to you:
http://biocab.org/Downwelling_Energy_and_Radiation_Pressure.html
Oh! I forgot to mention that the speed of H and He protons is from 26 to 400 Km/s. They have mass, Mark.
Have you forgotten that nothing can travel at c? It’s elementary RP. 🙂
http://helios.gsfc.nasa.gov/RTSWdata.html
Read it well, please. 🙂
Mark…
Your calculations are pure nonsense…
You say:
1Mev would make a proton move at
v=sqrt(10^-11) m/s ~ 3×10^5 m/s covering 100AU in 17 days, rather than your 13.6 months…
Well… 3 x 10^5 m/s = 300 km/s, which is the media of the speed that I reported in my graphs.
The distance from the Sun to the Bow Shock Zone is 100 AU, which are 14,959,787,070 Km.
Therefore, the protons take some 49,865,956.9 s for crossing the space from the BS to the Sun, traveling at a speed of 300 km/s, as you say.
There are 2,629,743.83 s in one month. Consequently, the protons take 19 months to reach the Earth. Simple mathematics, uh?
I am not here to teach you basic mathematics. Ok? 😡
Uh, if it’s moving at 300kps, then that’s only 1MeV.
GCRs are 1000x more energetic.
Why so slow?
Now, what is your causation? CLOUD shows that upper air clouds don’t happen more because of GCRs (any increase in cloud nuclei is countered by there being less moisture around any one nuclei to create a cloud). The cloud would have to be extra high to cause a cooling, and the observations of cloud do not show a correlation with the temperature rises OR with the GCR figure you’ve used.
So there’s no mechanism.
Cloud cover changes that HAVE been observed show a minor increase, but <10% of the temperature change can be attributed to that.
Where's the other 90% coming from?
Now as well as explaining your causation, you have to explain away the CO2 causation.
Why is CO2 not having the effect that physics asserts? After all, we know that Venus' effect shows that there's no problem with CO2 saturation even when you're 98% CO2. So your causation has to explain away 76% correlation.
So much to do, so little attempt to do it…
Mark… You say:
Uh, if it’s moving at 300kps, then that’s only 1MeV.
GCRs are 1000x more energetic.
Why so slow?
I don’t know… Ask protons why so slow. You’ve verified that the speed you’re handling is the media of the speeds that I reported in my article.
You say:
So there’s no mechanism.
Of course, there is a mechanism. The problem is that you don’t know it.
You say:
Cloud cover changes that HAVE been observed show a minor increase, but <10% of the temperature change can be attributed to that.
Where's the other 90% coming from?
From the Sun is the answer.
You say:
Now as well as explaining your causation, you have to explain away the CO2 causation.
Why is CO2 not having the effect that physics asserts? After all, we know that Venus’ effect shows that there’s no problem with CO2 saturation even when you’re 98% CO2. So your causation has to explain away 76% correlation.
So much to do, so little attempt to do it…
I’ve done it, but you don’t want to accept real physics. Sorry. I cannot do anything to help you to get rid of your dogma if you don’t want to see the truth.
“Mark… The graphs are on ICR, not SCR.”
And ICR is intergalactic.
So in the main, since there’s much more time to accellerate in a charged particle, of higher energy than Solar.
“Have you forgotten that nothing can travel at c? It’s elementary RP.”
Have you forgotten that photons can? So can neutrinos. GCRs from outside the solar system (ICR) such as muons that decay in atmosphere in 10^-6 seconds (therefore travelling less than 10cm at c) manage to reach the surface, 10km lower than it should? This is caused by time dilation as you get close to c.
And you can get arbitrarily close to c.
Which GCR/ICR can.
That you thought you had a zinger there yet failed at even A-level physics understanding to reach that conclusion shows that you have been unable to determine your own competence in elementary (as in simple) particle physics.
PS Nassif, although you REALLY NEED remedial physics training, I’m not here to give it to you.
😛
Heh… Well, I don’t like your physics; you know, your assertion that an AU = 100 km and other “physics” from you.
Also how can changes in the solar output affect GCRs that passed poineer 100AU further away from the Sun when those GCRs travel toward the earth from 100AU away from the Sun to the earth?
Is the Sun a source of Tachyons?
Are GCRs so powerful they can read the future? Or maybe, once they’ve been hit by the solar wind, they travel back in time so that it all ends up in the right place?
I mean, your phenomenology is all backward. It only works if the GCRs are only affected when they pass pioneer once and then never again by the solar wind.
Which would be odd indeed.
“Unfortunately for you, it is information released by NASA and I’m not assuming anything:
http://science.nasa.gov/science-news/science-at-nasa/2009/23dec_voyager/”
Problem: that link has nothing to do with your data or your assumption.
“Voyager passes through heliopause” has nothing to do with your theology. It’s a discovery. And you’re assuming that it does, but leaving how out of the picture.
Please, read the other article that I provided:
http://helios.gsfc.nasa.gov/RTSWdata.html
It’s evident you don’t read the articles I recommend.
I do Nassif. They don’t make any sense and do not bolster your case. Like that one on the heliopause. This has nothing to do with your theology.
That link talks about SCR not ICR, and I refer you to your earlier statement:
“The graphs are on ICR, not SCR”
And that link has nothing (yet again) about your theology you’re trying to spread here.
Is your mind really damaged and you honestly believe you’re pointing to proof of your work here?
“Why so slow?
I don’t know… Ask protons why so slow.”
So you don’t know why your He GCRs are going 1000x slower, but you say they are anyway.
You’ve just admitted you have no clue about physics you’re using here.
“Where’s the other 90% coming from?
From the Sun is the answer.”
Except the sun has not been tracking the temperature graphs. Also, here again you’re admitting that GCR effects on clouds are less than 10% of the effect, therefore you have not shown that the IPCC are wrong. Yet you still continue as if you have broken new ground here.
“Why is CO2 not having the effect that physics asserts? After all, we know that Venus’ effect shows that there’s no problem with CO2 saturation even when you’re 98% CO2. So your causation has to explain away 76% correlation.
So much to do, so little attempt to do it…
I’ve done it, but you don’t want to accept real physics.”
But you’re merely SAYING you’ve done it. Nothing in any link nor anything here has answered that query.
You have never done it.
Prove me wrong. Explain why CO2 isn’t having the effect that physics asserts. Explain the 76% correlation with temperature. Especially now you’ve accepted that less than 10% is from clouds and that is accepted as a forcing by you.
Prove me wrong and show why.
@ Mark…
I do Nassif. They don’t make any sense and do not bolster your case. Like that one on the heliopause. This has nothing to do with your theology.
Is science a theology? It seems you have not read the article; otherwise, you would have learn what the properties of nucleons are, including their speed.
You are making massive particles with charge travel at c, which is a blatant lie and shows ignorance about elemental physics.
That link talks about SCR not ICR, and I refer you to your earlier statement:
“The graphs are on ICR, not SCR”
And that link has nothing (yet again) about your theology you’re trying to spread here.
What link? Perhaps you don’t know what’s the difference between ICR and SCR. Do you?
Is your mind really damaged and you honestly believe you’re pointing to proof of your work here?
“Why so slow?
I don’t know… Ask protons why so slow.”
So you don’t know why your He GCRs are going 1000x slower, but you say they are anyway.
Your question: “Why so slow?” is wrongly elaborated. Make a scientific question and I will respond it appropriately.
You’ve just admitted you have no clue about physics you’re using here.
Really? How is it that I haven’t said anything related to admit that I have no clue?
“Where’s the other 90% coming from?
From the Sun is the answer.”
Except the sun has not been tracking the temperature graphs. Also, here again you’re admitting that GCR effects on clouds are less than 10% of the effect, therefore you have not shown that the IPCC are wrong. Yet you still continue as if you have broken new ground here.
Again, I’m not admitting anything wrong. Isn’t the Sun the main source of energy for the whole planetary system?
“Why is CO2 not having the effect that physics asserts? After all, we know that Venus’ effect shows that there’s no problem with CO2 saturation even when you’re 98% CO2. So your causation has to explain away 76% correlation.
One more “why”, and I will send you out from the classroom.
For Venus, use the following formulas and you’ll find an answer to your question on Venus:
GPL = QSUN / 4π (POR)^2
EMPR = U / c
So much to do, so little attempt to do it…
I’ve done it, but you don’t want to accept real physics.”
But you’re merely SAYING you’ve done it. Nothing in any link nor anything here has answered that query.
You have never done it.
Read all my posts along this thread, and you’ll find my answer is true. I have done it, but you were absent from my cathedrae.
Prove me wrong. Explain why CO2 isn’t having the effect that physics asserts. Explain the 76% correlation with temperature. Especially now you’ve accepted that less than 10% is from clouds and that is accepted as a forcing by you.
Prove me wrong and show why.
I’ve told you, one more “why”, and you’ll be expulsed from the classroom.
Anyway, I’ll try to answer your “question”:
The CO2 surely have the effect that physics asserts; the problem is that you have not the correct physics of the carbon dioxide.
That 76% correlation exists only in your mind and I have not accepted that the carbon dioxide is the cause of any warming. The carbon dixode is not a primary source of heat. Point.
“The carbon dixode is not a primary source of heat. ”
So when I heat CO2 up to 1000C it isn’t going to be a source of heat when I release it into your room???
I take it you don’t bother wearing clothes either, since they are no source of heat and therefore there’s no point wearing anything in colder weather you wouldn’t wear in the high summer heat? After all, a wolly jumper is not a primary source of heat.
Laughable.
Can I put a point toward “insanity” as your problem Nassif?
PS GCRs are not a primary source of heat. Yet you purport their effects cause warming on the earth. How can you hold mutually contradictory stances? Or is that another tick on the insanity checklist..?
“And that link has nothing (yet again) about your theology you’re trying to spread here.
What link? ”
The one to http://helios.gsfc.nasa.gov/RTSWdata.html.
It talks about the heliopause. Nothing about GCRs. Other links have talked about solar wind speeds, but you assert you’re talking about ICR, not SCR, so again is not supporting your theology here.
““Why is CO2 not having the effect that physics asserts? After all, we know that Venus’ effect shows that there’s no problem with CO2 saturation even when you’re 98% CO2. So your causation has to explain away 76% correlation.
One more “why”, and I will send you out from the classroom.
For Venus, use the following formulas and you’ll find an answer to your question on Venus:
GPL = QSUN / 4π (POR)^2
EMPR = U / c”
You would need to enter the classroom, Nassif. For the first time.
That doesn’t explain temperatures hot enough to melt lead on Venus. And you didn’t explain the units because Venus isn’t getting enough solar radiation at it’s mildly closer distance to manage that.
This is because Venus has a runaway greenhouse effect, caused by 98% of its atmosphere being CO2 which traps IR radiation but is transparent to the visible range the sun peak output is at. And that greenhouse effect is higher than earth’s because Venus has more CO2 than earth. Therefore CO2 can’t be saturated at Earth-like concentrations because otherwise Venus would not be as hot as it is.
Do you know anything about physics? Or can you just regurgitate misapplied formulae, selected by you specifically so that they make an answer you WISH to be true.
Come on, WHY isn’t CO2 having the effect physics demands. WHY.
You haven’t managed that yet.
“The CO2 surely have the effect that physics asserts; the problem is that you have not the correct physics of the carbon dioxide.”
That is not the why because I (or the IPCC and supporting papers) are (unlike you) using the RIGHT physics for CO2.
Here’s one:
Plass, G.N. (1956b). “The Influence of the 15 Band on the Atmospheric Infra-Red Cooling Rate.” Quarterly J. Royal Meteorological Society 82: 310-29.
I notice you have NOTHING about the “correct physics of the carbon dioxide” [sic]. What do YOU think the correct physics is?
Come on, prove me wrong.
“That 76% correlation exists only in your mind”
Actually, it’s in the data.
http://bartonpaullevenson.com/Correlation.html
(of course, you’ve never actually done any proper correlation testing, have you)
What exists only in your mind is that there’s a link from GCRs and temperature that does away with greenhouse gasses like CO2.
Mark
You seem to have information proving the importance of CO2 compared with H2Os radiative effects.
“Prove me wrong. Explain why CO2 isn’t having the effect that physics asserts. Explain the 76% correlation with temperature. Especially now you’ve accepted that less than 10% is from clouds and that is accepted as a forcing by you.”
This study from deep midwinter in Antarctica still found water vapour radiation to be 2.6 times that of CO2.
Now CO2 is well mixed throughout the atmosphere.
In contrast water vapour is not.
Click to access TownEtAl_2005.pdf
This should be the lowest H2O/CO2 ratio on the planet as these conditions give minimum humidity.
As we move towards average values, it is easy to see why H2O could have a significantly more contribution.
It can increase to almost 5% of the atmosphere under certain conditions.
Its ability to be solid/liquid or a vapour in the atmosphere further enhances its radiative and heat carrying potential.
For example in August total backradiation 66 W/m2
CO2 contribution must have been around 25 W/m2
This at atmospheric temperatures around 223K
At average backradition 324 W/m2 at temperature of 250K what contribution would CO2 make?
Well if CO2s absorption rises in line with temperature we would expect a contribution of 28 W/m2
Thus CO2 contributes less than 9% of the backradiation and H2O more than 90%.
As far as I can see this analysis stays within the bounds of “consensus” climate science.
There must be some other physical mechanism for all the IPCC dread of increased levels of CO2.
Perhaps you could enlighten me!
@ Mark…
You say:
Mark
“The carbon dixode is not a primary source of heat. ”
So when I heat CO2 up to 1000C it isn’t going to be a source of heat when I release it into your room???
I take it you don’t bother wearing clothes either, since they are no source of heat and therefore there’s no point wearing anything in colder weather you wouldn’t wear in the high summer heat? After all, a wolly jumper is not a primary source of heat.
Laughable.
Laguhable is what you are arguing. If you heat up a given volume of CO2 up to 1000 °C, you are using an external source of heat, not the CO2 itself.
All the authors on radiative heat transfer states that the carbon dioxide emissivity at 1000 °C is not more than 0.157; so where is the physical property of the carbon dioxide that enables it to have an emissivity ten times higher than that of a blackbody? I have the answer:
Just in your mind.
Regarding the formulas I provided, show me the numbers you have obtained after introducing the variables. That would be a good opportunity to you for demonstrating your knowledge.
I’ll stay waiting for your numbers… if you can… Heh! 🙂
@Mark…
You say:
But you’re merely SAYING you’ve done it. Nothing in any link nor anything here has answered that query.
You have never done it.
Read the posts from this thread. Haven’t you read them? Well, a good teacher should be tolerant with his pupils, so read it from this article (Oh! Don’t forget to read the references at the end of the article… scroll down the page to find them):
Click to access ECO2.pdf
Anyway, you’ll find it here, in this thread.
@Bryan…
Indeed. The EMRP by CO2 is 8.23 × 10^-13 atm, while the EMRP by the total backradiation is 1.07 × 10^-11 atm. Therefore, the EMRP by CO2 is only 7% of the total backradiation.
As we know, the EMPR force coerces the photons to stream from denser regions to lesser dense regions, so the carbon dioxide cannot warm the surface by any physical means and, what is more important, cannot be the source of the back-radiated energy.
“But you’re merely SAYING you’ve done it. Nothing in any link nor anything here has answered that query.
You have never done it.
Read the posts from this thread. Haven’t you read them? ”
Yes.
They say you’ve done it but nothing to prove you actually did it.
Did you read your OWN posts from this thread???
Your pdf is absolutely hilarious!
Please, explain how Venus gets to 400C and how the earth gets above 270C if greenhouse gasses do not have an effect, the major one being CO2 (since in the “Goldilocks zone” H2O tends to fall out as rain rather easily to be a driver of temperature, and therefore is relegated to a role of amplifier feedback on others.
Either you’re saying that the feedback ratio is VERY high, or you’re completely incompetent.
Your abuse of Beers Law (which is about the transmission through an isothermal gas volume which the atmosphere on earth IS NOT) also indicates your inability to do anything other than parrot equations with no sense of actual understanding getting in the way.
Go read that PROPER paper, peer reviewed, by Gilbert Plass. In there you will find that you have to take layers that are at least quasi-isothermic and sum the effect of each layer in conjunction with the others.
There is another problem you have in your lack of understanding. Despite proclaiming giant stature in astrophysics, if your abuse of Beers Law were correct, it would be impossible for Stellar Astrophysicists to ascertain how much of an element a star has in its atmosphere, since the photon production comes from deep within the star interior, where Beers Law would have 100% absorption for all absorptive elements long before reaching the optical surface.
Either you’re wrong or every single astrophysicist has been making up the stellar observations since the days of the telescope and the prism.
So please explain, if your PDF is correct, how can you find out the proportion of metals in a star from the stellar spectrum?
Because YOU are WRONG, but I’m not closed-minded like you, I’m willing to give you a chance of proving your theology correct.
So go ahead.
Explain the stellar spectra.
“Laguhable is what you are arguing. If you heat up a given volume of CO2 up to 1000 °C, you are using an external source of heat, not the CO2 itself.”
Is it, or is it not, a source of heat if it’s at 1000C?
You never said anything about temperature when you baldly lied with “co2 is not a temperature source”.
Now, you’re saying it is?
So, here’s how it goes (let me know when I’ve gone too fast for you):
IR comes from the earth and is intercepted by a CO2 molecule which absorbs it.
Because this CO2 molecule now has more energy than it had before, it is a source of energy itself. Energy which is expressed as heat when transported through to the other constituent molecules of the gaseous atmosphere.
This energy in the atmosphere can go back down to the earth and cause that to have more energy than it would otherwise have had if that CO2 molecule had not absorbed that IR photon.
This is expressed as temperature. Heating of the earth.
CO2 is a source of heating.
Or do you disagree with the laws of thermodynamics?
Your numbers from the formulas I provided, please?
I’m not saying that the carbon dioxide is a primary source of energy, but the opposite. Show me where I did say that.
You are who disregard the laws of thermodynamics, in particular the first and the second laws of thermodynamics. You’re making that the carbon dioxide creates energy from nothing (against the first law) and that the energy flows from lesser dense systems (the carbon dioxide) to the denser systems (against the second law which states that the energy always flows from the systems with lesser available microstates to the systems with more available microstates.
One thing is clear. Your model of energy transfer has nothing of real science.
Besides, you resort to insult people and it is a clear sign of scientific illiteracy.
I’m still waiting for your numbers from the formulas I provided… zzzz! 🙂
Uh, “the opposite”?
Among your astounding lists of incapabilities are such diverse topics as
1) elementary particle physics
2) astronomy
3) maths
4) stellar physics
5) thermodynamics
Truly the dunning of all krugers is Nassif.
So you DO disagree with the laws of thermodynamics!
CO2 is a source of heating for the atmosphere and the earth at the surface because the laws of thermodynamics states that extra energy is partitioned out and randomised to be expressed as temperature.
Nassif insists that CO2 is not a source of heating for anything, therefore he disavows all the laws of thermodynamics.
“Indeed. The EMRP by CO2 is 8.23 × 10^-13 atm, while the EMRP by the total backradiation is 1.07 × 10^-11 atm.”
Backradiation is not measured in atmospheres. It’s measured in watts per square meter (if planar radiation).
Is there no limit to your ignorance?
Hah!!!! You made me laugh!!! Thank you, Mark. I needed this long, long smile.
EMRP… Don’t you know what is it? Hah!
Don’t you know what backradiation is measured in?!?!?!? ROFLMAO!!!
http://en.wikipedia.org/wiki/Effective_radiated_power
“In radio telecommunications, effective radiated power or equivalent radiated power (ERP) is a standardized theoretical measurement of radio frequency (RF) energy using the SI unit watts,”
Note several other problems with your stupidities so brazenly on show:
1) RF != IR
2) Atmosphere != dipole radar
“This study from deep midwinter in Antarctica still found water vapour radiation to be 2.6 times that of CO2.”
Uh, deep midwinter there’s no sun.
So what are you measuring and what does it mean?
And most of the world is not midwinter antartica, so why bring that up in a discussion about global climate and energy balance globally?
“Thus CO2 contributes less than 9% of the backradiation and H2O more than 90%.”
Really? Then how is this true:
“For example in August total backradiation 66 W/m2
CO2 contribution must have been around 25 W/m2”
Which is deep midwinter nowhere…
“At average backradition 324 W/m2 at temperature of 250K what contribution would CO2 make?”
Uh, what? You’re managing that old math lie of proving 1+1=0.
If you’re really having trouble, go here:
http://www.aip.org/history/climate
There’s plenty there, including the measurements you ask for. With references which I am unable to supply rigorously.
Plus also numerous other information on this very site.
Try reading this site, you may find answers, but only if you’re willing to listen.
Yes, you ARE sleepy Nassif. You fell asleep when I showed you the source of the equations:
Plass, G.N. (1956b). “The Influence of the 15 Band on the Atmospheric Infra-Red Cooling Rate.” Quarterly J. Royal Meteorological Society 82: 310-29.
Go ahead, feel free to read it.
Or are you going to do a Nelson and see no ships?
@Mark…
You say:
“Indeed. The EMRP by CO2 is 8.23 × 10^-13 atm, while the EMRP by the total backradiation is 1.07 × 10^-11 atm.”
Backradiation is not measured in atmospheres. It’s measured in watts per square meter (if planar radiation).
Is there no limit to your ignorance?
I answered:
Hah!!!! You made me laugh!!! Thank you, Mark. I needed this long, long smile.
EMRP… Don’t you know what is it? Hah! 😀
No, you don’t know what it is.
But projection is a common element when someone is as deep into DK territory as you.
And still waiting to find out how SCR’s going at 400kps and 100AU away from earth and getting further away means that ICR’s going at 100’s of times faster in the other direction are therefore moving at 400kps AND NEVER AGAIN AFFECTED BY THE SOLAR WIND.
Still waiting to find out how the Stellar Astrophysicist knows the chemical components of the sun (let alone any other star).
Still nothing? Nassif, please don’t let your Opus Mangum fall to the wayside because you never considered Stellar Astrophysics!!!
@Mark…
It seems you’ve not read the articles at http://www.aip.org/history/climate/
which you provided. Have you read how the scientists in the epoch of Arrhenius discharged his calculations?
Besides, few years after, Hottel, Leckner, Smith, and many, many other scientists made experiments and observations on real life, and demonstrated that Arrhenius, your prophet, was plainly wrong.
Still waiting for your results using the formulas I provided. If you have lost them, here they are again:
GPL = QSUN / 4π (POR)^2
EMPR = U / c”
Except you are incorrect. Solutions of those equations result in a Venus and Earth far far colder than they are measured with actual thermometers.
But maybe you’re plugging in the wrong numbers.
Lets see.
Can’t cite papers properly?
Lilo, Sitch and Kraken have shown your “scientists” are charlatans and were falsifying evidence to achieve notoriety by falsifying Arrhenius’ work.
Still waiting for how you calculate the earth’s temperature from those equations because they produce an earth far too cold and a venus EXTREMELY below the temperature read by actual thermometers.
Or maybe Nassif managed to find someone who told him you could use this and “disprove” AGW and, because he knows nothing about science, merely regurgitates what he’s seen, never actually applied it himself.
Still waiting for his mechanism for He atoms at the heliopause to cause warming and cooling at the earth.
@ Mark…
You say:
And still waiting to find out how SCR’s going at 400kps and 100AU away from earth and getting further away means that ICR’s going at 100′s of times faster in the other direction are therefore moving at 400kps AND NEVER AGAIN AFFECTED BY THE SOLAR WIND.
I have provided the article where you can learn it from. If you have not read it, it’s not my fault. Here again:
http://helios.gsfc.nasa.gov/RTSWdata.html
Nope, It doesn’t tell me anything about the speed of ICRs that your graph was about.
It tells me about the SOLAR WIND that is SCR, not ICR and was not what your theology espouses as the cause of earth’s temperature changes.
That page doesn’t answer my question and never will no matter how many times you put a link to it. You have to explain it or find a link to something that does.
That link doesn’t.
@ Mark…
Except you are incorrect. Solutions of those equations result in a Venus and Earth far far colder than they are measured with actual thermometers.
But maybe you’re plugging in the wrong numbers.
Lets see.
Wow! You have the numbers! Tell the tale! Tell us what those results are! 🙂
Ah, so you solved them incorrectly! After all, EVERY schoolboy knows you should show your workings.
Go on, you claim that those equations show that CO2 doesn’t have to have an effect to explain Venus and Earth temperatures.
To do that, you have to be misapplying them. However, I don’t know how you misapplied them, so I can’t show your working and where you’ve gone wrong.
When you show me your workings, I will be able to show you where you went wrong.
Mark
Sorry to have disturbed you.
From your reply I do not think you are capable of answereing my question.
Well, you have to ask a question first, Bri. You didn’t.
You made several *claims* but no questions. E.g. “given that… therefore it must be…”.
These are not questions.
So try to be clear and stop with the “if heffalumps exist, then how heavy are they?”.
Though I must say it looks like you don’t want to learn.
Still waiting on how the solar wind makes faster moving galactic cosmic rays move 400kps…
Still waiting to find out why radiation is measured in pressure…
Bryan, if you’re wanting to learn, why are you asking Nassif why his radiation is measured in pressure and why he gets 1/13 when you get 1/10th?
Is it because you don’t think Nassif knows what he’s on about either?
Still waiting for Nassif to tell us how he gets the temperature of the earth at its correct temperature with his equation.
Every time I try, it comes out ~30C too cold for earth and over 400C too cold for Venus.
Mark
I will have another go
I said at the end of my last post
…..”There must be some other physical mechanism for all the IPCC dread of increased levels of CO2.
Perhaps you could enlighten me!”…….
That’s a question!
Midwinter Antarctic will give the lowest backradiation figures for both CO2 and particularly H2O.
I carefully explained the reasons why we should expect to get a much bigger contribution from H2O as we move to planetary average conditions. Humidity,clouds rain all increase.
H2O is not well mixed. CO2 is well mixed
Here is the question again rephrased
What physical mechanism will enable CO2 to contribute more than 9% of the average backradiation?
”There must be some other physical mechanism for all the IPCC dread of increased levels of CO2. Perhaps you could enlighten me!”
Consider instead: why, since the IPCC and many highly educated specialists in the field feel such dread, why do YOUR calculations show nothing to fear?
Which is more likely:
1) your calcuations are incorrect
2) they are scaredy-cats
?
Personally, my money would NOT be on #2.
Yours?
http://en.wikipedia.org/wiki/File:The_green_house_effect.svg
Go have a look there.
Look later in that wiki entry.
The highest level of forcing is from CO2. 1.4W/m2 Other GHG’s add another ~0.7W/m2.
Water is ignored because it rains. Something else has to increase the temperature before it can hold more water as vapour.
This also means that reducing CO2 reduces water vapour AT THE SAME TIME.
This is why the IPCC are so concerned about CO2.
”There must be some other physical mechanism for all the IPCC dread of increased levels of CO2. Perhaps you could enlighten me!”
http://en.wikipedia.org/wiki/File:The_green_house_effect.svg
Go have a look there.
Look later in that wiki entry.
The highest level of forcing is from CO2. 1.4W/m2 Other GHG’s add another ~0.7W/m2.
Water is ignored because it rains. Something else has to increase the temperature before it can hold more water as vapour.
This also means that reducing CO2 reduces water vapour AT THE SAME TIME.
This is why the IPCC are so concerned about CO2.
Mark, Mark… It seems that knowing the truth has distressed you a little.
All the information you ask for and need is in my articles and in the links I have provided to other authors. I apologize for having stressed you.
You say that my PDF is hilarious… As you’re assuring that my article is hilarious, you’ve gotten the compromise of demonstrating, step by step, where and how it is that my PDF is hilarious. Otherwise, I will assume you’re writing that argument just because you have a typewriting before you. 😀
On the other hand, you have to explain how you meet the criteria for you qualify my profession as astrophysics. 🙂
Again, no the links you give do not explain my questions.
Yes, that article IS hilarious. I’ve already given several reasons why it is so.
Your use Beers Law is incorrect, since it only concerns transparency through an isothermal layer which the atmosphere is not
If your use WERE correct, you would be unable to determine the chemical composition of the stars from their emission spectra
How do I meet the criteria for being knowledgeable in astrophysics? I know about optical depth and how you can ascertain the composition of stellar atmospheres.
You don’t know, therefore you do not meet the requirements.
That’s because you’ve not read them.
You’re evading to answer my questions straightforward.
The whole algorithm applied in my calculations is in Modest’s book on radiative heat transfer. It seems you are following the same tactics than DeWitt Payne, who was saying that the algorithm didn’t exist, until he verified by himself that it exists and that my calculations were correct.
For more references, read this thread. Heh! 🙂
If you found that I don’t qualify for being an astrophysicist, then how is it that you insist in calling me an astrophysicist?
Take the formulas from my articles. Introduce your numbers and get the results. Demonstrate, scientifically, not by bla, bla, bla, that the physics contained in my articles is wrong. That’s the way you must follow.
By the way, your response to Bryan is incorrect. The link you provided to Wikipedia is not talking about any cause that makes the CO2 to have an absorptiviy and emissivity higher than 0.001 at its current concentration and temperature in the atmosphere. 😀
Mark
…”Water is ignored because it rains. Something else has to increase the temperature before it can hold more water as vapour.
This also means that reducing CO2 reduces water vapour AT THE SAME TIME.
This is why the IPCC are so concerned about CO2.”
Increased water vapour => clouds => net cooling effect as we all know.
The clouds absorb and reflect more of the incident Solar radiation, particularly the IR bands.
Hence the IPCC concern over CO2 is misplaced.
“Increased water vapour => clouds => net cooling effect as we all know.”
We do?
Which is colder: a clear night or nights with cloud?
The feedback from clouds is small, but positive.
If the clouds are high up, they reflect more radiation than they trap.
If the clouds are low, then they retain more heat from the earth than they lose to space.
And increasing moisture will tend to cause clouds to appear lower and lower. The heights depend on the instability in the atmosphere, not the moisture content, so is not as likely to cause cloudtops to rise as quickly as the cloudbase falls.
The effect is close, but tends toward the positive.
Hence your dismissal of the IPCC is misplaced
Yes, I did read them Nassif.
You used Beers Law.
It doesn’t apply to the atmosphere as was known back in the 1920’s, though only concretely proven so in 1956.
“If you found that I don’t qualify for being an astrophysicist, then how is it that you insist in calling me an astrophysicist?”
Every link that isn’t your own site is to NASA. Space agency. And GCRs and the solar wind are astronomical features.
Since you do not know about astrophysics, see if your “work” in that PDF is correct by using the completely NOT climate-change based science of Stellar Astrophysics.
You will find that it is not in accord.
Your workings are incorrect.
“Demonstrate, scientifically, not by bla, bla, bla, that the physics contained in my articles is wrong. ”
Yes, Beer’s Law is for transmission through an isothermal medium.
This has nothing to do with radiative loss from the earth because that doesn’t demand transmission from the earth’s surface alone.
It also has nothing to do with radiative loss from the earth because the atmosphere is not isothermal.
This is the science.
You can’t use Beer’s Law in that manner in the same way you can’t use Newton’s third law and show that you can’t move something.
Sticking your fingers in your ears and going “I can’t hear you!” isn’t changing it.
“It seems you are following the same tactics than DeWitt Payne, who was saying that the algorithm didn’t exist,”
Oh, I’m saying they DO exist.
But applying them gets a temperature far too low to account for Earth and ASTOUNDINGLY too cold for Venus.
But you don’t know how to apply them. Which is why you hide your mathematics.
“The link you provided to Wikipedia is not talking about any cause that makes the CO2 to have an absorptiviy and emissivity higher than 0.001 at its current concentration and temperature in the atmosphere.”
Absorptivity doesn’t depend on concentration.
I guess we have to add
6) radiation physics.
@Mark…
That doesn’t make the carbon dioxide emits more than 25 W/m^2 towards all directions, so its EMRP is ridiculous.
Take the water vapor alone and see what’s the power of the energy emitted by the water vapor alone. That’s the answer to Bryan’s question, not the CO2.
The flux of thermal energy emitted by the water vapor alone is 256 W/m^2 in all directions, while the flux of thermal energy emitted by the carbon dioxide in all directions could be 26 W/m^2 (although this quantity has been taken from models because it is not possible to separate individual measurements from the bulk measurements of the energy emitted by a mixture of gases, excluding the water vapor). Therefore:
(26 W/m^2 * 100) / 256 W/m^2 = 10.16%.
That means that the carbon dioxide isotropic emission of energy is only the 10.2% of the isotropic emission of energy by the water vapor.
The bulk flux of energy from the atmosphere towards all directions is 357 W/m^2. Hence, the assumed flux of energy emitted by the carbon dioxide in all directions is 7.3%.
Now tell me, if Evans et al recorded some 270 W/m^2 radiated from the whole mixture of gases… Where the remainder 87 W/m^2 come from? 🙂
What is ridiculous is measuring radiation in units of pressure.
@Mark…
I’m not hidding any mathematics… They are all explained in my articles. See an example taken from my peer reviewed article on Total Emissivity of the Carbon Dioxide:
FORMULA:
ECO2 = 1-[(a-1 * 1-PE / (a + b) – (1+ PE)) * e [-c (Log10 (paL) m / paL)2]] * (ECO2)0 (Formula 2)
Introducing magnitudes:
ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) – (1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]] * 0.0016
ECO2 = 1- [(0.45 * -0.0001 bar / (1.68) – (2.0001)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]] * 0.0016
ECO2 = 1- [(-0.000045 bar / -0.3201 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm) 2)]] * 0.0016
ECO2 = 1 – [(0.00014 * 0.3712)] * 0.0.0016 = (0.999948) (0.0016) = 0.0017
What am I hidding? Heh! 😀
Units.
That’s what you’re hiding.
“example taken from my peer reviewed article ”
Peer reviewed by who? Your dad?
Come on, if you had it peer reviewed, then you’ll have a proper cite, like Plass did.
So you have emissivity in bar cm?
bar is pressure. mass per square metre.
So emissivity is in kg/m?
http://en.wikipedia.org/wiki/Emissivity
“Emissivity is a dimensionless quantity, so it does not have units.”
This would indicate you have the wrong equation.
Still waiting to see how Nassif gets a warm Earth from his equation.
Still waiting to see how Astronomers can find the proportion of elements in a stellar atmosphere.
Still waiting to see how GCR’s travelling at near c travel at the speed of the solar wind that’s going in the other direction…
Bryan:
On June 20, 2010 at 12:43 pm I asked:
And you said:
Now on July 14, 2010 at 4:27 pm you said:
So I’ll ask again, does this mean you accept the results of the radiative transfer equations which were used to calculate these numbers?
Do you think they calculate the right values?
Or are out by a factor of 10 or 100 or 1000?
Because the answer to your question is easy – but I see little point in giving it to you until you commit yourself to a position.
After all, you have embraced everyone and every position that might cause some question to the role of CO2 in climate without any critical thinking. Once it doesn’t help your position you move on to the next flimsy argument.
Personally I like this, because it helps readers to see that they are flimsy positions.
Anyway, if you’d like to explain your position on why the results match the calculations in this paper about the South Pole then I would be happy to give you the answer to your question.
Maybe Bryan doesn’t believe his own numbers about how CO2 is not a problem…
On your “peer reviewed” (maybe Monckton reviewed it…) paper your “Further reading” on Emissivity has two links to
1) a document about how you can find baseline temperatures to compare against in the climate record
nothing to do with emissivity
2) a document about climate sensitvity and how it’s changed over the years
which is about how CO2 changes are the cause of climate shifts of the strength seen.
The rest of your cites are similarly unrewarding as to discovering what your theology is talking about.
Oh! Your discharging the work of Hottel, Leckner, Andrews, Modest, Pott, etc… Wow! Who’s your priest?
Hmmm.
So you don’t know why your equation as you used it has units when you’re calling it emissivity and emissivity has no units.
Which priest told you that was the correct incantation?
Your problems here are indicative of the ones where your other equations when misapplied by you produce your errant beliefs.
@Mark…
You say:
Yes, Beer’s Law is for transmission through an isothermal medium.
This has nothing to do with radiative loss from the earth because that doesn’t demand transmission from the earth’s surface alone.
It seems you are confused… I’m not talking about absorptivity neither transmissivity, but of Total Emissivity, which depends on temperature and concentration.
Total emissivity is crucial for knowing the radiative loss of energy from the Earth. 🙂
Nope, it’s definitely YOU are the confused one.
Total Emissivity?
Click to access z088-089.pdf
Which is unitless.
Note, they have the temperature too!
Total emissivity is crucial and the fact that you don’t understand it explains why you fail to understand the radiative losses from earth.
If you mean total emissions (radiative emissions) then that’s measured in watts and depends on temperature to the fourth power, for a product in thermal equilibrium.
Poor Mark… You’re talking nonsense. Here my references are:
1. Hottel, H. C. Radiant Heat Transmission-3rd Edition. 1954. McGraw-Hill, NY.
2. Leckner, B. The Spectral and Total Emissivity of Water Vapor and Carbon Dioxide. Combustion and Flame. Volume 17; Issue 1; August 1971, Pages 37-44.
3. Manrique, José Ángel V. Transferencia de Calor. 2002. Oxford University Press. England.
4. Modest, Michael F. Radiative Heat Transfer-Second Edition. 2003. Elsevier Science, USA and Academic Press, UK.
5. Pitts, Donald and Sissom, Leighton. Heat Transfer. 1998. McGraw-Hill, NY.
6. Chilingar; G. V., Khilyuk, L. F.; Sorokhtin, O. G.. Cooling of Atmosphere Due to CO2 Emission. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects; Volume 30, Issue: 1 January 2008; pages 1 – 9.
It’s easy for you to say lies.
What lies?
And to your cites:
1. And? He doesn’t get emissivity (total or otherwise ) in bar cm.
2. Volume 17 of what?
3. What paper?
4. Same as #1
5. ditto
6. volume 30 of what?
It’s easy for you to claim lies when you’re neck deep in them. You have nothing to lose in the accusation when the lies are so obvious and pointed out for all to see.
Now you’re playing the idiot. Wher I did add units to Total Emissivity? The results of the calculations is ECO2 = 0.0017. Where the units are? Hahaha!!! 😀
Here: “ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]]”
That makes the result have units.
@Mark…
You say:
What lies?
And to your cites:
1. And? He doesn’t get emissivity (total or otherwise ) in bar cm.
2. Volume 17 of what?
3. What paper?
4. Same as #1
5. ditto
6. volume 30 of what?
It’s easy for you to claim lies when you’re neck deep in them. You have nothing to lose in the accusation when the lies are so obvious and pointed out for all to see.
Hahaha! You don’t know how to read and follow bibliographic references!!! 😀
I know how to read bibliographic references.
You don’t know how to write them.
That you have to dodge using this method speaks volumes about this: you know you’re wrong. You’re struggling on the line.
Now, if you’re saying that total emittance is 0.0017, you’re getting closer. Still quite wrong, but closer. Will you see it? Tense!
But you’re still trying to point at Newton’s third law of motion and say “this PROVES you can’t push a cart!”.
We still have a long way to go.
And we haven’t even gotten to the 12 other problems you have.
@Mark…
You say:
Here: “ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]]”
That makes the result have units.
Hahaha! You don’t know either how to eliminate units!!!
No indeed you don’t!
@Mark…
You say:
What lies? And to your cites: 1. And? He doesn’t get emissivity (total or otherwise ) in bar cm. 2. Volume 17 of what? 3. What paper? 4. Same as #1 5. ditto 6. volume 30 of what? It’s easy for you to claim lies when you’re neck deep in them. You […]
I know how to read bibliographic references.
You don’t know how to write them.
That you have to dodge using this method speaks volumes about this: you know you’re wrong. You’re struggling on the line.
All is explained in my articles. Your looking for the three feet of the cat knowing it has four feet.
You’re saying that no author knows how to write references!!!
If you know how to eliminate units, then the result of
ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm / 0.034 bar cm))2]]
is unitless.
And if you substitute 10001000Pa in there, you get WHAT answer?
A different one.
One that depends on the units used in the equation.
Unitless values do not do this.
@Mark…
Now, if you’re saying that total emittance is 0.0017, you’re getting closer. Still quite wrong, but closer. Will you see it? Tense!
But you’re still trying to point at Newton’s third law of motion and say “this PROVES you can’t push a cart!”.
We still have a long way to go.
And we haven’t even gotten to the 12 other problems you have.
You’re trolling… but giving me the reason. Indeed, real physics PROVES that the the carbon dioxide cant push a cart.
And… What your numbers are? 😀
My numbers are 30C too cold for Earth and over 400C too cold for Venus.
Because the PROPER use of those equations are proof that CO2’s effect is real and significant.
As stellar physics will tell you too.
The value of total emissivity does nothing to prove CO2 has no effect. The shape of the spectral emissivity however is both relevant and necessary.
Now, stop asking teacher to do your homework.
I don’t want to jump into the middle of this, but for any readers staying with it and not involved, I did point out earlier on July 2, 2010 at 10:32 that Nasif Nahle didn’t seem to understand how to do a simple conversion from:
– Radiance in W/(cm^2 sr cm-1) to
– Total flux in W/m^2
He also insists that the results of the particular paper under discussion were simulations when the authors explain in great detail about their FT-IR measurements. The fact that they did a simulation as well to match to their measurements seems proof that everything was a simulation.
As I commented at the time I can't be assistance to Nasif Nahle but I would suggest that if you have made it this far (you must be interested) and are wondering if he has something to offer, the answer is "unlikely“.
Units conversion is pretty fundamental, and so is reading a paper describing an experiment and not claiming it’s a simulation.
If anyone else wants to see the units conversion explained in more detail just ask. I will be happy to take the time.
Sorry, SoD, but you’re confused also. What I’m reporting in my article is the total normal intensity of the radiation, which you can verify from Modest’s and other authors’ books. You’re referring to other units which I never reported in my article. It’s quite evident you are trolling and don’t know a cent about Heat Transfer physics.
Total normal intensity? But you just called it in atmospheres, not watts.
Units: your sloppy practices (that may be getting accepted by the unscientific like Monckton) is causing your errors to be extremely obvious.
That you cannot and will not see is extreme DKing.
@Mark…
And if you substitute 10001000Pa in there, you get WHAT answer?
A different one.
One that depends on the units used in the equation.
Unitless values do not do this.
Yes, you’re trolling… I cannot substitute that Pa because the Pa I introduced is the real Pa, and if I substitute it by other unreal Pa it would be quite evident that it would be pseudoscience.
Your numbers? 😀
No, Pa is a measure of pressure.
I refer you to the equations YOU referred by author earlier and show that pressure is needed.
You’re using it incorrectly and therefore your equations are incorrect.
That you don’t see this and are sloppy in your workings (not to say evasive!) is why your theology is incorrect but you can’t (won’t) see it.
You are not capable in this field of physics.
Your sloppiness is proof.
Wrong! What’s the real Pa of the atmosphere today? Hahaha!!! Sorry… I have no time for dealing with ignorant people who thinks that the units for Total Normal Intensity are W/cm^2 sr cm^-1 and people who thinks that massive charged particles travel at c, and that an astronomical unit is 203 meters.
Still waiting to see how a solar wind 100AU beyond earth travelling at 400kps has anything to do with slowing galactic cosmic rays to less than 300kps.
And how these energetic but incomprehensibly (even to the author of this theology) slow particles cause temperature changes on earth, much more at daytimes than at night, too, when the difference in the amount of sky in those two times is practically identical…
@ Mark…
Still not read the articles? What a lazy person you are!!! 😀 Ciao! I have to work
Still claiming that links answer questions when they don’t?
Or is your ICR graph about SCR after all? In which case, the particles have a 4 hour trip to earth, not 14 months.
The real Pa today? About 10^5.
Given you don’t know even this, shows that we have
7) Meteorology
Hahaha! You don’t know what the term Pa is for… Hahaha! Waste of time with you.
Yes, *I* do.
Do you?
No.
All you can do is laugh at someone who doesn’t understand your misunderstanding.
Mark
….“Increased water vapour => clouds => net cooling effect as we all know.”
We do?
Which is colder: a clear night or nights with cloud?.”……
Here in Scotland a cloudy day always means lower than average temperatures.
So if the solar IR doesn’t even get to the Earth surface its overall cooler on a 24 hour basis.
It is conceivable that at night following the cloudy day some of the clouds absorbed radiation is re emitted downwards.
“Here in Scotland a cloudy day always means lower than average temperatures.”
So extra vapour disappears at night? That some heavy rainfall over the world!!!
No, it doesn’t do that, does it.
You get cloudy nights in Scotland too.
“So if the solar IR doesn’t even get to the Earth surface its overall cooler on a 24 hour basis.”
So where does the solar Vis go? How about solar UVa and UVb?
Where is the peak output of the sun?
In the visible.
http://en.wikipedia.org/wiki/Black_body
PS you didn’t answer the question, did you. Even though you took the effort to quote it.
“It is conceivable that at night following the cloudy day some of the clouds absorbed radiation is re emitted downwards.”
Bryan, if you wanted answers, why did you ignore them?
https://scienceofdoom.com/2010/06/03/lunar-madness-and-physics-basics/#comment-4051
I quote:
The feedback from clouds is small, but positive.
If the clouds are high up, they reflect more radiation than they trap.
If the clouds are low, then they retain more heat from the earth than they lose to space.
And increasing moisture will tend to cause clouds to appear lower and lower. The heights depend on the instability in the atmosphere, not the moisture content, so is not as likely to cause cloudtops to rise as quickly as the cloudbase falls.
The effect is close, but tends toward the positive.
Oh, and how about a clear day followed by a cloudy night?
Warm and wet nights. Very uncomfortable.
Strangely, the next morning is warmer than it would have been too. And *that’s* part of the day too!
Then as the air warms, the cloud dissipates and the midday sun shines through!
Compare to one where there was no cloud.
Wasn’t it cold that night? Wasn’t it chilly that morning. Lovely sun, though. Took hours to warm the air, didn’t it!
More cloud.
But warmer.
You DO know that people have worked on this? And I don’t just mean stood outside their front door.
Still waiting to hear how astronomers find the chemical composition of the stars if Nassif is right. Either they’ve been colluding so that some time in the future the IPCC will be born (and if they can predict THAT, they can certainly predict the climate 100s of years ahead!) or Nassif is wrong.
Maybe Nassif hasn’t thought of that and thinks you can know something and never have to check the consequences of that knowledge against reality.
SoD
……”Does this mean that you accept the results of the line-by-line radiative transfer model?
After all, this is how the values in the study were calculated?”…….
I am unsure of these equations and I am keeping an open mind on the issue.
Over on the other thread
Venusian Mysteries – Part Two
I noticed you were doing the same.
There is nothing wrong with this approach.
Many people are afraid to express doubt and claim to know for certain things that they have little or no evidence for.
There is also nothing wrong with accepting the equations as a working hypothesis.
Then applying some logic to show that the conclusions of the theory are in conflict with its own building blocks.
You’re unsure of the line models.
But you USE their results.
???
If you’re unsure of the models, you can’t use their results in any form of proof.
I’ll accept the models
I’ll not use their data
Pick one.
Note: all science is provisional. It’s a path to truth, not truth itself.
“Then applying some logic to show that the conclusions of the theory are in conflict with its own building blocks.”
Practice what you preach:
“Increased water vapour => clouds => net cooling effect as we all know.”
Which is colder: a clear night or nights with cloud?
The answer to which rhetorical question is: without.
Now, given that your hypothesis “Increased water vapour => clouds => net cooling effect” is in conflict with its own building blocks “cloudless nights are colder”, maybe you ought to reconsider.
Mark
……”Where is the peak output of the sun?
In the visible”………….
However there is more IR solar energy than visible!
Uh, no there isn’t.
Did you not read the black body curve?
Or, if you want to be picky, there’s more energy NOT in IR than in IR from the sun.
But that’s peanuts to Bryan’s strawmanning away with answering “where is the peak output of the sun” with something that doesn’t have a damn thing to do with clouds.
Bryan, you’re also “conveniently” (for you) “forgetting” that CO2 is opaque to IR and is available nearly exclusively above the tropopause where H2O is notoriously absent. Since the IR comes DOWN, any absorbed by the CO2 (or other greenhouse gases) isn’t going to get much of a chance being absorbed by H2O in the cloud layer.
Mark
What planet are you living on!
If we have a month of cloudy weather the average temperature for that month will go down rather than up as you seem to imply.
Earth.
Which one you living on?
But here on earth, we have places that are NOT Scotland.
You should try visiting our planet. It’s much larger than yours. Plenty room.
@Mark…
You say:
Still waiting to hear how astronomers find the chemical composition of the stars if Nassif is right. Either they’ve been colluding so that some time in the future the IPCC will be born (and if they can predict THAT, they can certainly predict the climate 100s of years ahead!) or Nassif is wrong.
Maybe Nassif hasn’t thought of that and thinks you can know something and never have to check the consequences of that knowledge against reality.
First of all, for taking you off your confusion:
What I am or am not right on? Please, tell me what’s the issue you’re referring to when saying “if Nasif is right”.
Second… I don’t know too much about fantasyland, where you live, but only on the real world that you’re confunding on your dreamsland; thus, you’re correct when saying that I don’t know your religion… Oops! sorry, your reality.
You really don’t read what you write, do you, Nassif.
biocab.org/ECO2.pdf
All explained here (again):
https://scienceofdoom.com/2010/06/03/lunar-madness-and-physics-basics/#comment-4009
Please try to keep up, I can’t hold your hand all the time you know.
Of course, Nassif is just trying his “oh, where did I put my glasses” routine to hide the fact that his religious fervour to consider CO2 which is produced by fossil fuel combustion is blameless in any wrongdoing.
“What I am or am not right on? ”
Darn near everything.
That Nassif has to forget what he’s said and what I’ve asked for a score of times is just him trying to avoid answering the question which will forever seal his fate:
Answer truthfully and own up to being wrong
Lie his head off and be proven a liar.
Mark
I said
However there is more IR solar energy than visible!
You said
“Uh, no there isn’t.”
What G&T say and SoD has the table.
Visible 44.8%
IR 45.2%
Uh, an hour ago: UVa and UVb ring a bell?
Mark says……
Bryan, you’re also “conveniently” (for you) “forgetting” that CO2 is opaque to IR and is available nearly exclusively above the tropopause where H2O is notoriously absent. Since the IR comes DOWN, any absorbed by the CO2 (or other greenhouse gases) isn’t going to get much of a chance being absorbed by H2O in the cloud layer.
I say …..
However if CO2 is absorbing all this IR above the troposphere it too will have a net cooling effect will it not?
Uh, what does that have to do with increasing water vapour causes a cooling effect? It’s CO2. Not H2O.
Maybe the planet Bryan is on has CO2 clouds.
Do you, Bryan?
Anyway, I can see where Bryan wants to “learn” from. G&T. The place that fails Junior School Science.
You don’t want to learn, do you?
Sorry to have disturbed you.
@Mark
You say:
Bryan, you’re also “conveniently” (for you) “forgetting” that CO2 is opaque to IR and is available nearly exclusively above the tropopause where H2O is notoriously absent. Since the IR comes DOWN, any absorbed by the CO2 (or other greenhouse gases) isn’t going to get much of a chance being absorbed by H2O in the cloud layer.
Mark, the carbon dioxide is not a blackbody, and this is something that you cannot understand.
Just answer the following questions:
1. For how much the carbon dioxide is opaque to IR?
2. What kind of IR the carbon dioxide does absorb?
3. What’s the composition of the layer “above the tropopause”?
4. What’s the absorptivity of the carbon dioxide in its current density in the atmosphere?
5. How long is the free cross path of a photon in the surface photon stream?
If you answer these easy questions straightly, you’ll find that you and the IPCC are wrong and completely against scientific knowledge.
Nassif, the earth is not a black body either.
It’s also spherical.
Unless you’re a flat-earther…
1: http://en.wikipedia.org/wiki/File:Atmospheric_Transmission.png
2. IR. (see above).
3. http://en.wikipedia.org/wiki/Stratosphere
http://www.newton.dep.anl.gov/askasci/wea00/wea00081.htm
4. http://en.wikipedia.org/wiki/File:Atmospheric_Transmission.png
5. ??? Photons do not interact. MFP in a photon stream: infinity.
If you answer these questions correctly, you get this:
http://www.ipcc-wg1.unibe.ch/
Though since the last question makes no sense, you don’t actually have to answer #5.
Of course, if you answer them INCORRECTLY, you will find out that the IPCC is wrong.
@Mark…
You say:
Of course, Nassif is just trying his “oh, where did I put my glasses” routine to hide the fact that his religious fervour to consider CO2 which is produced by fossil fuel combustion is blameless in any wrongdoing.
“What I am or am not right on? ”
Darn near everything.
That Nassif has to forget what he’s said and what I’ve asked for a score of times is just him trying to avoid answering the question which will forever seal his fate:
Answer truthfully and own up to being wrong
Lie his head off and be proven a liar.
Hahaha! Science is a lie for ignorants, did you know that?
Why should I accept your fantasies about the CO2, if scientists specialized on radiative heat transfer say the same thing that I’m saying? It would be the same than saying that Hottel, Leckner, Edwards, Pitts, Modest, Chillingar, Evans, etc. are saying lies.
Find any error in my calculations and concepts, considering serious academic and scientific books on heat transfer, and after show them here or in any scientific magazine.
Now I see the cause why you found my article “hilarious”:
YOU know nothing of physics. Hahaha! 😀
“Find any error in my calculations and concepts”
I have: you used Beer’s Law inappropriately.
However, this gives you an answer you can’t use to “prove” CO2 is not a problem.
You have used GPL=QSUN…. incorrectly. Actually, you know this because you refuse to display your working.
Here’s a hint: the earth is a sphere, not a flat disk.
You don’t know what you don’t know and assume that everyone else doesn’t know squat because they know you’re wrong.
Classic Dunning-Kruger.
Mark
I said
There is also nothing wrong with accepting the equations (or statements) as a working hypothesis.
Then applying some logic to show that the conclusions of the theory are in conflict with its own building blocks.
You said
“Bryan, you’re also “conveniently” (for you) “forgetting” that CO2 is opaque to IR and is available nearly exclusively above the tropopause where H2O is notoriously absent. Since the IR comes DOWN, any absorbed by the CO2 (or other greenhouse gases) isn’t going to get much of a chance being absorbed by H2O in the cloud layer.”
I say that your conclusion that CO2 absorbs most of the solar radiation above the troposphere undermines your belief in increased levels of CO2 leading to global warming.
Correction
I say that your conclusion that CO2 absorbs most of the solar radiation
Should read
I say that your conclusion that CO2 absorbs most of the solar radiations Infra Red
Where was that my conclusion?
Still waiting for how the solar wind going at 400kps makes the GCRs going in the other direction move at less than 400kps…
Still waiting for how stellar physicists can get their chemical compositions from absorption lines if Nassif’s theology is correct.
Still waiting for how cosmic rays cause temperature changes on the earth.
Still waiting for how he calculates the earth’s temperature with GPL=…
Mark
I said
… that your conclusion that CO2 absorbs most of the solar radiation above the troposphere undermines your belief in increased levels of CO2 leading to global warming…..
You said
……..”Where was that my conclusion?”…….
I was making the assumption from other comments that you believed in AGW caused by increased levels of CO2.
If this is not the case then my assumption was incorrect.
Then you are a fellow sceptic.
“I was making the assumption from other comments that you believed in AGW caused by increased levels of CO2.”
a) No, not belief. Physics precludes belief, the only belief science as is: there is a universe that can be understood
b) So you’re admitting you made it up
AGW is caused by increased levels of anthropogenic sources of greenhouse gasses (among other human effects on the atmosphere) the greatest effect of which is CO2.
This follows on from the climate science that includes CO2’s effects in past climate changes.
The only way this is “AGW” is that this time, the CO2 is human produced.
So stop making up words I say and say ones yourself.
Still waiting for how CO2 has no effect despite absorbing IR radiation from the earth and how CO2 is not a source of heat, despite having temperature.
Still waiting for how total emissivity is used to calculate the temperature of the earth.
Still waiting for many other things, but all Nassif can manage is “lol! you don’t know any physics!!!” rather than explain how he knows physics.
Mark you said
Still waiting for how CO2 has no effect despite absorbing IR radiation from the earth and how CO2 is not a source of heat, despite having temperature.
I say
Is a cold cup of coffee in a centrally heated lounge a source of heat?
Does it heat the room?
A cup of coffee is not the atmosphere.
Now, if you heat the coffee by a hand-held waveguide emitting microwaves, it will be a source of heat. This is because the water is opaque to microwaves (like CO2 is opaque to IR) and the air in the room is transparent to them (like the air is transparent to visible).
Or is microwaving a cup of coffee not a source of heat?
Why bother with a microwave emitter?
When the coffee was hotter than the room it was a source of heat.
So a cold cup of coffee has no temperature, Bryan? Or does it have a temperature and therefore a source of heat?
Seems like Bryan has an equivalent lack of knowledge of thermodynamics to Nassif’s. So lacking, there’s not even knowledge of how nonexistent it is.
Maybe that’s why he’s tag-teaming him.
Mark you said
“So a cold cup of coffee has no temperature, Bryan? Or does it have a temperature and therefore a source of heat?”
I say it has a temperature which is lower than the room.
It is not therefore a source of heat as heat only flows spontaneously from a higher to a lower temperature.
Uh, no, a cold cup of coffee will be at the same temperature as the room (again displaying how lacking your knowledge is). It may *feel* colder because your body temp is still higher and the coffee is a better conductor than the air.
Now why haven’t you answered the microwave question?
Because you can’t mentally or because you daren’t?
“It is not therefore a source of heat as heat only flows spontaneously from a higher to a lower temperature.”
It is a source of heat. Heat is not temperature.
This is why we have such terms in the science of Thermodynamics as The Specific Heat Capacity.
Another example of why you know nothing and begging the question: why do you think you do?
Especially odd when you proclaim there’s plenty of information leading you to consider *me* needing a foundational course.
Mark
Unfortunately there is a audit trail here and anyone who has a passing knowledge of thermodynamics knows you are in sore need of a foundational level course.
cf “a cold cup of coffee is colder than the room” issue.
Thermodynamics fail.
You’re letting PERCEPTION of temperature become the MEASURE of temperature. Just like you did with “it’s cloudy and cold toDAY therefore clouds make it colder”.
Uh, only someone whose completely lack of knowledge leads them to a DK effect.
YOU *believe* so because the alternative is you’re wrong.
Mark
Leave out the personal attacks Mark.
Reread the sites etiquette policy.
Yes, why don’t you leave out the personal attacks, Bryan?
And while you’re not doing that, you’ll have time to actually answer questions rather than gish gallop past them.
“Why bother with a microwave emitter?”
Because otherwise you don’t have an analogue in your analogy of the coffee cup in the room.
Without that analogue, all you have is “y”.
I explained, but you didn’t want to listen:
Now, if you heat the coffee by a hand-held waveguide emitting microwaves, it will be a source of heat. This is because the water is opaque to microwaves (like CO2 is opaque to IR) and the air in the room is transparent to them (like the air is transparent to visible).
But do you want to continue a PROPER analogy, or make stuff up to hide behind?
@Mark…
You talk pure nonsense because you don’t want to accept and grasp real science.
Science is there… Take it or leave it, but you should be conscious that if you leave it, it would be under your own risk of being in a ridiculous situation. Instead of looking for faults of truthful and honest scientists, who knows what they are doing, look for the damage that you are inflicting to the true scientific knowledge with all those twisted imaginary arguments invented without experimental or observational basis.
As for me, I am always based on the scientific task of honest scientists, who have a great academic value from any scope. The thing is as simple as to take each one of my references and to verify that all the data and results in my articles are accurate and adhered to the scientific methodology. Another thing is that you do not like them because you remain thinking that the world must be as you wish; but don’t, the universe is and behaves as it is and you cannot change it with simple ideas from your imagination.
Take a book, just as DeWitt Payne did it, and demonstrate through its pages that I am wrong. Do not look failures on my five sensorial organs, that if I use eyeglasses or not, but on the scientific data and show me what is wrong. It is simple.
But not, what you do is to look for a way to denigrate the person, not to criticize his work scientifically. Yours is not the way of science, but of pseudo-politics.
Coming from you, “real science” is misapplied science and no wonder I do not wish to embrace it.
I prefer the truth.
“As for me, I am always based on the scientific task of honest scientists,”
Self delusion and self aggrandisement.
You fail SO HARD.
Two posts, both failing to answer any questions set. Because those questions cannot be answered and keep your house of cards standing.
“but on the scientific data and show me what is wrong. ”
You don’t have to have scientific data wrong if you don’t apply the principles correctly.
Ask Steve McIntyre, he’s still complaining that Mann et al used the wrong PCA analysis on the scientific data. His contention is Mann is wrong not on the scientific data, but the use of the analysis tools.
You’re wrong to use Beer’s Law in the method you do to “prove” CO2 could not have that effect as was known in the 1920’s.
You may want to check G N Plass’ paper where he does the scientific calculations. IF you can find the error he makes, then say so and prove why.
But you don’t do that, do you, because you know he’s right and you are no scientist and do not wish to work scientifically if that leads you away from your theology.
You have not even pseudo-science. It is anti-science.
@Bryan…
It’s a waste of time and liver talking with this people, who looks the way for denigrating honest scientists.
They cannot prove any of their arguments because nature contradicts them.
Mark says that I lack of knowledge on thermodynamics, but he doesn’t show a single calculation made by himself. This is because he is only trolling and knows nothing on science. For example, he assured that an astronomical unit was 203 meters, and that the nucleons of H and He speed was 299909 km/s. Is it worth to discuss with this… Mark, who doesn’t know, the same as SoD, how to eliminate units?
You have shown only that you do not understand anything.
Your use of that GPL=QSUN… graph ignores that the earth and venus (in fact all the planets) are spheres.
You have never managed to answer any questions put to you. Any of them.
And your continued lying is extremely obvious. Previously you accused me of a 100km AU. Now 203m?
But you have nothing to add except mistaken and misapplied science and bask in the adulation of those who desire to be told “There’s No Problem”.
And still you fail to answer questions, determining that only attacks are possible.
Pathetic.
“but he doesn’t show a single calculation made by himself.”
So why am I still waiting to see how you arrive at the temperature of the earth and venus from your two equations that you state will do so?
Still waiting for (among other things)
how total emissivity is used to calculate the temperature of the earth.
how CO2 has no effect despite absorbing IR radiation from the earth and how CO2 is not a source of heat, despite having temperature.
how he calculates the earth’s temperature with GPL=…
how cosmic rays cause temperature changes on the earth.
how stellar physicists can get their chemical compositions from absorption lines if Nassif’s theology is correct.
how the solar wind going at 400kps makes the GCRs going in the other direction move at less than 400kps.
But all he can manage is “he doesn’t know!!!!”.
Also waiting for the explanation of how warm clothes work, them not being a source of heat and all. And additionally, being COLDER than the body they are warming…
@Mark…
“but he doesn’t show a single calculation made by himself.”
So why am I still waiting to see how you arrive at the temperature of the earth and venus from your two equations that you state will do so?
Besides an ignorant, you’re blind and deaf.
You’re talking about yourself, who thinks that the astronomical unit is 203 meters.
Read my articles and you’ll find there hundreds of calculations and all my algorithms are well known algorithms by all physicists in this world. You’re just trolling because you don’t know a cent of physics, Mark. Hah! 😀
“who thinks that the astronomical unit is 203 meters.”
Again the lies slip from your lips.
Earlier you said
“Nasif Nahle July 13, 2010 at 9:19 pm
Heh… Well, I don’t like your physics; you know, your assertion that an AU = 100 km and other “physics” from you.”
Note: you said then 100km.
Then you said 203m.
Now you’re saying another lie: that you have never said 100km.
The lies catch you up
Mark…
You say:
Still waiting for (among other things)
how total emissivity is used to calculate the temperature of the earth.
You see? You know nothing of physics. Total emissivity is crucial for calculating the load of energy emitted by any thermodynamic system. That’s basic knowledge that you don’t have. Red books, Mark. If you don’t know how much energy a thermodynamic system emits, you would never know the temperature that a given thermodynamic system can cause or can get.
how CO2 has no effect despite absorbing IR radiation from the earth and how CO2 is not a source of heat, despite having temperature.
Again… You know nothing of heat transfer science.
The amount of energy that the carbon dioxide has an insignificant effect on the temperature of the Earth. It is not a primary source of heat because heat is a process function, not a state function.
Have you seen the CO2 burning? 😀
how he calculates the earth’s temperature with GPL=…
how cosmic rays cause temperature changes on the earth.
1. You ignore what’s the meaning of the term Gpl. Tell us what it is for… Heh!
2. In the same way the solar cosmic rays cause changes of temperature on the Earth. It’s simple, except for those who thinks that the carbon dioxide is a primary source of heat, comparable to the Sun, that an astronomical unit is 203 meters, that the second law of thermodynamics is imaginary, that don’t know how to eliminate units from a formula, etc. 😀
how stellar physicists can get their chemical compositions from absorption lines if Nassif’s theology is correct.
It’s not a theology, but science; and it is not <bNasif's but astrophysical knowledge that you can find in any book on astrophysics.
As I had told you some posts above, “ignorance is the worst enemy of AGWers”.
how the solar wind going at 400kps makes the GCRs going in the other direction move at less than 400kps.
Again, you ignore quantum mechanics and don’t know a cent about EMPR. Your question is well explained in my article so… READ IT! 😀
But all he can manage is “he doesn’t know!!!!”.
That’s a lie. The problem is that you don’t even know how to make a scientific question. You start your questions with “whys”, and even a high school student knows that the questions begining with “whys” are not scientifically correct.
Read my articles and my posts in this same thread and in my articles. Every one of your ridiculous questions is well explained there. I have shown here and in my articles my formulas and discussed them thoroughly. You don’t see them because you are an illiterate on science.
It’s a waste of time a dialogue with someone like you, who doesn’t know a bit of science.
“Total emissivity is crucial for calculating the load of energy emitted by any thermodynamic system”
So why haven’t you shown this calculation?
“The amount of energy that the carbon dioxide has an insignificant effect on the temperature of the Earth.”
This is incorrect. 1.4W/m2 is not insignificant.
“It is not a primary source of heat”
Never said it was, but doesn’t have to be primary to be significant.
“because heat is a process function, not a state function.”
Nope, heat is energy. Not a process function.
“Have you seen the CO2 burning?”
Every time I turn the gas fire on.
“but astrophysical knowledge that you can find in any book on astrophysics.”
What? *I* know how you can get compositions of stellar atmospheres. But to do so requires that Beers Law doesn’t apply to atmospheres that have a temperature gradient.
Yet your ECO2 pdf tries to apply Beers Law to an atmosphere that has a temperature gradient.
Therefore, if you know astrophysics, you know that your application there of Beers Law is incorrect. So why are you defending it?
“Again, you ignore quantum mechanics and don’t know a cent about EMPR.”
Neither quantum mechanics not EMPR answer the question “how does the solar wind going at 400kps make the GCRs going in the other direction move at less than 400kps.” Of course, feel free to show this here if you can.
But you can’t so you won’t.
“That’s a lie.”
No, it’s the truth. In this message alone, you’ve accused me of not knowing stuff when it’s clear you don’t, you haven’t answered any question, even when you’ve put words up (e.g. “quantum mechanics!!!”.
“Read my articles and my posts in this same thread and in my articles”
I have done. They are hilariously wrong.
“Every one of your ridiculous questions is well explained there.”
No, they are not. And you’re not explaining them here either. Because you cannot explain them.
“You don’t see them because you are an illiterate on science.”
No, I’m quite able to see science and the bastardisation you consider science and tell the difference between them.
When are you going to answer the questions with answers, rather than responses?
Still waiting for all those answers.
He replies, but, although all answers are replies, not all replies are answers.
Nassif, stop trying to sound scienty with techno-babble like “state function”, “photon stream”, “quantum mechanics” or “EMPR”. ESPECIALLY when they don’t say what you assert them to mean.
You don’t even know what a state or a process is in physics.
Heat IS a state. Heat transfer is a process.
Mind you, when Nassif yibbers on about “quantum mechanics and EMPR explain!” I can’t help but imagine Magnus Pike waving his hands about.
Magnus Pike would not have made the mistake of bluffing about what the answer is, mind.
Maybe Nassif will answer this.
You assert in your ECO2 pdf that the radiation intercepted by the earth from the sun is
GPL=QSUN/4*pi*POR^2
Yes?
And from that you get TSI of 1359.02 W/m^2
Yes?
Agree so far?
Nope… You’re wrong. Here the PDF on ECO2. Tell me, where that formula is?
Click to access ECO2.pdf
You’re confused, Mark…
Is that your only disagreement?
So you then have 51% of this being absorbed by the ground.
This takes it to 693.1W/m2
Correct?
Nope, again… Your confusion gets deeper and deeper each time you write. For more info about the amount of energy absorbed by the surface, go to:
http://biocab.org/Annual_Energy_Budget.html
Read, Mark, read… Heh! 🙂
Nope, your paper there is ridiculous and unweildy.
What is YOUR answer. Put it here. Come on. What is YOUR figure for the total radiation from the sun on the earth?
This is called *science*.
181.64 Watts?
Is that your figure for how much solar radiation gets to the earth and warms it up?
Hey, Mark!!! If carbon dioxide burns every time you turn on your stove, why you don’t use carbon dioxide as fuel for cooking instead CH4 or C2H6, or C3H8? Hah! 😀
What does getting energy out of CO2 have to to with burning and CO2?
CO2 is the result of combustion.
😀
Yes, you ARE a funny little man.
So you don’t understand combustion.
You think the only source of heat is burning.
You don’t recognise your own equations.
Yes, a VERY funny little man.
:-O
So already Nassif has a failure.
He stated that GPL=QSUN/4piPOR^2 was all you needed.
Yet that calculation ends up with ~1400 Watts/m2.
But somehow that isn’t the number he uses.
Something missing already.
Where did it come from, Nassif?
Mark says…
181.64 Watts?
Is that your figure for how much solar radiation gets to the earth and warms it up?
Oh! No! It’s not my figure, but the figure given by correct calculations through the proportions taken from the book Ecology by Odum.
Do you know how much temperature 181.64 W of power produce on the Earth’s surface?
I invite you to make the calculation using the following formula:
dT = P/m * Cp
Introduce the magnitudes for soil and/or oceans.
So what is your figure, then?
dT = P/m * Cp
Did you mean
dT = P/(m*Cp)?
Because that’s a VERY different equation YOU gave…
Please, if this is so, try the same calculations with CO2’s figures of P, m and Cp.
@Mark…
So already Nassif has a failure.
He stated that GPL=QSUN/4piPOR^2 was all you needed.
Yet that calculation ends up with ~1400 Watts/m2.
But somehow that isn’t the number he uses.
Something missing already.
Where did it come from, Nassif?
Hah! Again confused, Mark… or perhaps you cannot read?
1402 W/m^2 is the energy received by the most external layer of the Earth. You know where it is? 😀
1364.5 W/m^2 is the average of solar radiation accepted by solar physicists.
One is the bulk, another is the average. You know, the Earth is not always at the same distance from the Sun.
For you know it, we measure the amount of solar energy received on the surface with thermo-photometers. 😀
Yes, but neither of them are 181.64.
So where did that come from?
“One is the bulk,”
None of them are the bulk.
“another is the average”
Well, one is the average.
Still neither is the bulk.
“Do you know how much temperature 181.64 W of power produce on the Earth’s surface?”
Yes.
238K.
Mark says…
“Do you know how much temperature 181.64 W of power produce on the Earth’s surface?”
Yes.
238K.
I give you a chance of reconsidering your cipher. From your standpoint, 238 K is a negative temperature (-35.15 °C), caused by a positive power.
Nope, it’s a positive temperature. 238.
Note the lack of negative at the front, the lack of which by normal mathematical procedures indicates it is a positive number.
Mark… I give you a last chance, but I now will give you three clues:
1. Tbb = 255 K
2. Tstd = 290 K
3. dT is for change of temperature.
Reconsider your cipher. It is a negative change, Ok?
238K is a positive temperature.
Here’s a pointer:
http://en.wikipedia.org/wiki/Kelvin
Kelvin is the unit of temperature.
238 Kelvin is positive.
That is the temperature you get from giving something 181.64 watts per square meter of surface area and wait for it to come to thermal equilibrium.
There’s no need to give me a last chance. The truth is this:
181.64W/m2 => 238K.
And why have you changed again?
before:
“238 K is a negative temperature (-35.15 °C),”
Now you’re talking
“Tbb = 255K Tstd = 290K”
What do these have to do with -35.15C?
Changing your story again?
I’m not changing anything. I’m giving three clues for you reconsider your wrong deduction. You’re saying that 181.64 W causes a decrease of temperature:
Tmark – Tstd = -52 K, which means that, according to your nonsensical deduction, the Earth, instead warming by the energy absorbed, is cooling by 52 K each second.
Tmark – Tbb = -17 K, which means that, according with Mark’s nonsensical deduction, the Earth, instead of warming by the energy absorbed, is cooling by 17 K each second.
Deduce by yourself. Yours is a nonsensical figure.
I forgot to explain the other side of your nonsensical deduction:
T in Celsius = 238 K – 273 K = -35.15 °C
See your silliness and scientific illiteracy? The cipher I gave of -35.15 °C is the conversion from Kelvin to Celsius.
Yes, so the temperature you get from 181.64W/m2 is colder than the freezing point of water (the zero point of the Celsius scale). It’s ~20F colder than the freezing point of Brine. Or about 190C warmer than the frezing point of Nitrogen.
So?
It’s colder than the freezing point of water at the poles.
Where’s the problem?
“Tmark – Tstd = -52 K”
Yes, Tmark is 52 kelvin colder than Tstd.
“the Earth, instead warming by the energy absorbed, is cooling by 52 K each second.”
No, it just means that Tmark is colder than Tstd.
Like my kitchen is 175 degrees colder than my oven when I’m cooking turkey.
“Tmark – Tbb = -17 K”
Yes, Tmark is colder than Tbb by 17 degrees.
“the Earth, instead of warming by the energy absorbed, is cooling by 17 K each second.”
No, it just means it’s colder than Tbb.
That would be “Tmark is colder than Tbb” at the end.
Correction:
T in Celsius = 238 K – 273.15 K = -35.15 °C
Sorry, but you’re only looking for failures when all my calculations are correct and verified by real university scientists, not by blogger trolls.
That calculation is correct. So?
181.64W/m2 becomes a black body radiation temperature of 238K.
Which is positive.
It’s YOUR number.
Tnn = 238K.
Again, the change of temperature is negative. Ok? Hahaha! 😀
No, 238K is positive.
Did you fail maths that hard???
So, now we have the earth according to Nassif gains 181.64W/m2 from the sun.
This is a temperature of 238K, which is, as I stated earlier (much earlier) is far too cold for the actual earth whose average temperature is 288K.
The difference is made up from
a) Nassif is using the numbers incorrectly
Which is what I said earlier
b) The Greenhouse Effect which contributes to the heating by retaining and trapping heat, causing an imbalance in the fluxes at the top of the atmosphere.
Mark says:
No, 238K is positive.
Did you fail maths that hard???
A positive number, Mark; but a negative change of temperature, which is not the same. It is not even the Tbb, so your calculation of a simple three rule thumb is wrong.
This shows how easy you’ve demonstrated by yourself that you don’t know how to obtaind dT or deltaT.
Don’t hide your maths and tell us how did you deduced that 181.64 W causes a change of temperature of 238 K. 😀
For making the things easier to you, here the formula again:
dT = Q/(m*Cp)
Go ahead… Heh! 🙂
Why would I use the wrong equation?
Wrong equation!!! Wow!!! Tell Wilson he has to change that formula from his book on Elementary Physics because the formula is wrong. Hahaha! 😀
“Don’t hide your maths and tell us how did you deduced that 181.64 W causes a change of temperature of 238 K.”
Here:
P=sigmaT^4
Rearranging for T:
T=(P/sigma)^(1/4)
Where
P=181.64W/m2
sigma=5.67×10^-8 W/m^2K^4/
Now, don’t be coy, show your workings.
Well, while you’re trying to work out why your maths is wrong, Nassif, maybe you can clear up your other equation.
dT=P/m * Cp
Correction 1:
I take it you mean
dT=P/(m*Cp)
Where
dT = change in temperature (units: Kelvin)
P = Total Power (units: Joules)
m = Mass (units: Kilogrammes)
Cp = Specific Heat Capacity (units: Joules/Kilogramme/Kelvin)
Units therefore cancel out.
So what m do you use?
Hahaha!!! You don’t know what m to use? Bad thing for you! Ask Tamino for this magnitude… Hah! 😀
No, if you can’t do the maths, then what use were you?
Or don’t you know what m to use?
@Mark…
So, now we have the earth according to Nassif gains 181.64W/m2 from the sun.
This is a temperature of 238K, which is, as I stated earlier (much earlier) is far too cold for the actual earth whose average temperature is 288K.
The difference is made up from
a) Nassif is using the numbers incorrectly
Which is what I said earlier
b) The Greenhouse Effect which contributes to the heating by retaining and trapping heat, causing an imbalance in the fluxes at the top of the atmosphere.
Now you have gotten the compromise of explaining this series of lies about the numbers in my article. Go straightly in your answers and don’t evade.
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
2. What’s the algorithm you applied for obtaining a change of temperature of 238 K from 181.64 W.
3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc.
4. How is it that you conclude that the greenhouse effect is given by the carbon dioxide, i.e. tell us the thermal properties of the carbon dioxide.
If you evade one single of these simple questions, you would be admitting that you don’t know about physics, as you have demonstrated through this thread saying that the astronomical unit is 203 meters, that the massive charged particles travel at c, that the units cannot be eliminated from an algorithm, that 238 K is a positive change of temperature when the Tstd is 290 K, that the “formula” you used for obtaining those 238 K is a cross-multiplication, etc., etc.
You have been evading to answer my straight questions, so you are obliged now to answer these simple questions. If you evade to answer one single of these questions making another question to me, it would be quite evident that you know nothing of physics.
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
Yup, that’s what you said.
Therefore the earth’s temperature from that becomes 238K.
This is your number, which is wrong.
“3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc”
This one:
dT=P/m * Cp
It’s completely wrong.
And where you go through all that rigamarole calculating the solar constant then throw it away for this 181.64W which comes out of nowhere.
“as you have demonstrated through this thread saying that the astronomical unit is 203 meters,”
Your lies keep following you like the smell of a dead hyena.
Where did I say that?
“that 238 K is a positive change of temperature when the Tstd is 290 K,”
Where did I say that?
“that the massive charged particles travel at c, ”
Where did I say that?
“that the units cannot be eliminated from an algorithm”
Well, you can’t. This is why
F=ma
means that Force has units, because m has units and they are different units from the units of a.
It’s called “Dimensional Analysis” and is a basic resource for scientists. That you don’t know what it means speaks volumes.
“You have been evading to answer my straight questions,”
Ah, projecton.
You’ve responded to, for one example among many, to the query “what value of m did you use” with “Ha! You don’t know? Ask Tamino!”.
This is not answering the question.
Still waiting after scores of requests, Nassif’s calculations.
Pity he seems to only have other people’s workings.
Plagiarism is a naughty thing.
If you don’t base your science in the work of other scientists based on experimentation and observation of nature, that is, in others’ theories, then you’re a creator of fantasies, like AGW.
You don’t go writing other people’s work and call it your own.
That’s plagiarism.
You’re quick to pounce on non-answering messages, Nassif.
Very slow on any information, though.
Do you have something to hide?
Nassif: “Do you know how much temperature 181.64 W of power produce on the Earth’s surface?”
Me: “Yes.
238K.”
But still nothing from Nassif about whether HE knows how much temperature 181.64W of power produce on the earth surface.
It’s been several postings from him since then, not one of which gives his answer.
Don’t YOU know how much temperature it produce?
You continue evading my questions.
Your formula is incomplete.
dT = P/(m*Cp) is the appropriate formula for calculating the change of temperature caused by a given power.
Don’t continue evading my questions and answer them straightly:
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
2. What’s the algorithm you applied for obtaining a change of temperature of 238 K from 181.64 W.
3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc.
4. How is it that you conclude that the greenhouse effect is given by the carbon dioxide, i.e. tell us the thermal properties of the carbon dioxide.
Point
You fail to answer.
What value for m do you use?
What number do YOU get for 181.64W/m2.
Or don’t you know the answer?
My questions, please?
“i.e. tell us the thermal properties of the carbon dioxide.”
It’s a triatomic molecule that absorbs heavily in the Infra Red band.
No your questions don’t please. They’re idiotic and incomplete.
My questions. If you can’t answer them then you’ve nothing to say on the temperature of the earth.
What’s the absorptiviy of the carbon dioxide, its emissivity, its Cp, its Cv and its mass fraction at its current concentration in the atmosphere?
BTW, I always give the credit to the people who have worked on the same thing that I’m working. Haven’t you seen the references in my articles?
I have never said that the formulas are my formulas or that such or that investigation is mine. So your accusation on plagiarism is only an ad hominem attack, as it is usual among you, AGWers when your arguments are revealed as pseudoscience.
Answer my questions:
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
2. What’s the algorithm you applied for obtaining a change of temperature of 238 K from 181.64 W.
3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc.
4. How is it that you conclude that the greenhouse effect is given by the carbon dioxide, i.e. tell us the thermal properties of the carbon dioxide.
Awww. Still don’t know the answer?
Poor little mite.
Go on, then ask Tamino what values you got.
Awww. Still don’t know the answer?
Poor little mite.
And to hide your shame you had to ask another dozen!
Nassif, you don’t know what value to use for m, do you.
You don’t know what value you get for dT nor do you know what it means.
Neither do you know Stefan-Boltzmann law.
I think we’re up to 8:
8) Stephan Boltzmann law.
Your list if inabilities is getting longer.
I’ve not failed to answer your questions, Nassif.
Nassif: “Do you know how much temperature 181.64 W of power produce on the Earth’s surface?”
Me: “Yes.
238K.”
Nassif: “i.e. tell us the thermal properties of the carbon dioxide.”
Me: “It’s a triatomic molecule that absorbs heavily in the Infra Red band.”
Nassif: “Don’t hide your maths and tell us how did you deduced that 181.64 W causes a change of temperature of 238 K. ”
That was answered too.
But asking those same questions back to you gets evasion, crybaby antics and more questions.
No answers though.
Maybe you have none.
Answer my questions, please? I know perfectly what value to use for m in every ocassion, so don’t evade my questions.
So what value of m did you use in each occasion?
Or don’t you know, but you’re just bashful?
Nassif can’t answer the questions!
Nassif can’t answer the questions!
“Don’t hide your maths and tell us how did you deduced that 181.64 W causes a change of temperature of NOT 238 K. ”
So, summing up, Nassif says: “Still waiting for your results using the formulas I provided. If you have lost them, here they are again:
GPL = QSUN / 4π (POR)^2
EMPR = U / c”
But then when this is done, ignores it and states that GPL is 181.64W. And never even tries with EMPR.
Seems like even when all you need are the formulas he provides, they aren’t the ones you need to use…
Even Nassif doesn’t think he applies those equations correctly! Why then are you asking me how the are wrong, Nassif?
“Don’t hide your maths and tell us how did you deduced that 181.64 W causes a change of temperature of 238 K.”
Here:
P=sigmaT^4
Rearranging for T:
T=(P/sigma)^(1/4)
Where
P=181.64W/m2
sigma=5.67×10^-8 W/m^2K^4/
Now, don’t be coy, show your workings.
++++
reposted because Nassif has a blind spot when it comes to truth…
As you continue evading my questions, I’ll show in public that you know nothing of physics. Your formula is wrong because it is incomplete and wrong:
You wrote:
T = P / sigma
T = (181 W/m^2 / 5.6697 x 10^-8 W/m^2 K)^1/4
However, power is not W/m^2, but W, alone. So in your formula, you cannot eliminate m^2 because the real introduction of the magnitudes, if your Yahoo’s formula were correct which is not, must be:
T = (181 W / 5.6697 x 10^-8 W/m^2 K)^1/4, and the result would be in m^2 K.
For a complete reference about Power, read:
http://en.wikipedia.org/wiki/Power_(physics), where it says:
“The dimension of power is energy divided by time. The SI unit of power is the watt (W), which is equal to one joule per second.”
The complete formula that you tried to use is as follows, which is the formula I would have applied if I were looking for the absolute temperature, but I am looking for change of temperature:
P = a * A * (sigma) * (T)^4
Now make your calculations.
Answer my questions, please? Point.
P=181.64 W/m2
sigma is 5.67×10^8 W/m2/K^4
P/sigma units cancel out for W, m and leave only Kelvin to the fourth power.
When you take the fourth root, that gives you kelvin.
Which is the unit of temperature.
Epic failure.
As to your equation, that dT is the rate of change of temperature because P is rate of change of energy, not energy.
Oh dear, not only can’t you cancel out units in other people’s equations, you can’t manage it on the ones you yourself use!!!
OMG!!!
Because, Nassif, P is 181.64 Watts per square meter.
The sun shines on each meter under the sun. Not just one of them.
As you continue evading my questions, I’ll show in public that you know nothing of physics. Your formula is wrong because it is incomplete and wrong:
You wrote:
T = P / sigma
T = (181 W/m^2 / 5.6697 x 10^-8 W/m^2 K)^1/4
However, power is not W/m^2, but W, alone. So in your formula, you cannot eliminate m^2 because the real introduction of the magnitudes, if your Yahoo’s formula were correct which is not, must be:
T = (181 W / 5.6697 x 10^-8 W/m^2 K)^1/4, and the result would be in m^2 K.
For a complete reference about Power, read:
http://en.wikipedia.org/wiki/Power_(physics), where it says:
“The dimension of power is energy divided by time. The SI unit of power is the watt (W), which is equal to one joule per second.”
The complete formula that you tried to use is as follows, which is the formula I would have applied if I were looking for the absolute temperature, but I am looking for change of temperature:
P = a * A * (sigma) * (T)^4
Now make your calculations.
Answer my questions, please? Point.
And you’re wrong even in the wrong bit:
“and the result would be in m^2 K.”
No, your equation which YOU got wrong wouldn’t even do that. The result would be K/m^0.5.
Even maths you fail hard.
Just in case you didn’t know, Nassif, this document may help:
http://biocab.org/Annual_Energy_Budget.html
Within it says:
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
Watts per square meter.
Maybe you ought to read some of that stuff on biocab… 8)
Point, Game, Set and Match.
And now, add another question to the previous questions:
Why did you take 181 W/m^2 like power and introduced you into your Yahoo’s formula if the magnitude is for flow of energy and not for power?
Twisting the science, Mark?
Answer my questions.
Oh, look no answers from you again, Nassif.
You don’t know what values you used for m in any cases and don’t know what temperature you get from 181.64W/m2!
Neither do you know why you got the previous post wrong and proclaim P as watts rather than watts per square meter!
You can’t answer, can you.
You can’t say what value to use for m.
You can’t say what temperature YOU get for 181.64W/m2, nor can you say how you get it.
It would be easy to prove me wrong on these three things.
“As you continue evading my questions, I’ll show in public that you know nothing of physics. Your formula is wrong because it is incomplete and wrong:”
It’s got to be hard on you, Nassif, when you start out so strongly and then instead of showing my formula is incomplete and wrong instead you show yourself to be wrong.
Man, that’s gotta hurt.
@Mark
Just in case you didn’t know, Nassif, this document may help:
http://biocab.org/Annual_Energy_Budget.html
Within it says:
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
Watts per square meter.
Maybe you ought to read some of that stuff on biocab…
And that is what I said in one of my previous posts:
Nasif Nahle on July 15, 2010 at 6:45 pm | Reply
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
And I am correct. The load of energy absorbed by the surface is 181.64 W/m^2.
Now, concluding this useless discussion, let’s see the extreme errors made by Mark which demonstrates he never has touched a book of physics:
1. He took an astronomical unit = 203 meters, when an AU is ~150 million kilometers.
2. He said the protons travel at c and was saying that I was wrong.
3. He don’t know how to eliminate units from the formulas, as it was shown in his post:
Mark
Here: “ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]]”
That makes the result have units.
The result have units? 🙂
4. He don’t know a formula for obtaining the change of temperature, and he told the formula I provided was unreal as he tried to invalidate my question #3:
“3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc”
This one:
dT=P/m * Cp
It’s completely wrong.
5. He ignores that EMRP is the pressure exerted by the electromagnetic radiation, which was discovered theoretically by Maxwell and corroborated experimentally by Lebedev, and Nichols and Hull:
http://www.phy.hr/~dpaar/fizicari/xmaxwell.html
http://www.britannica.com/EBchecked/topic/334217/Pyotr-Nikolayevich-Lebedev
http://prola.aps.org/abstract/PRI/v13/i5/p307
6. He says the formula GPL = QSUN / 4π (POR)^2 was invented by me, when it was taken from the book Astrophysics by Maoz, pp. 36-47.
7. Mark doesn’t know that W/m^2 is a unit for flux of energy, not for power, and failed when eliminating units from the formula T = (P/sigma)^1/4 because of his confusion between power and flux of energy.
8. Mark didn’t answer a sole question from all the questions I did.
Thus, it’s quite evident what the purpose of that “Mark” was whith this discussion, i.e. hide the decline… oops! sorry, denigrate the real science with his scientific illiteracy.
So, ciao! 😀
My comment is awaiting moderation? Hahaha!
Maybe because you still aren’t saying what temperature YOU get from 181.64W/m2.
@Mark
Just in case you didn’t know, Nassif, this document may help:
http://biocab.org/Annual_Energy_Budget.html
Within it says:
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
Watts per square meter.
Maybe you ought to read some of that stuff on biocab…
And that is what I said in one of my previous posts:
Nasif Nahle on July 15, 2010 at 6:45 pm | Reply
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
And I am correct. The load of energy absorbed by the surface is 181.64 W/m^2.
Now, concluding this useless discussion, let’s see the extreme errors made by Mark which demonstrates he never has touched a book of physics:
1. He took an astronomical unit = 203 meters, when an AU is ~150 million kilometers.
2. He said the protons travel at c and was saying that I was wrong.
3. He don’t know how to eliminate units from the formulas, as it was shown in his post:
Mark
Here: “ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]]”
That makes the result have units.
The result have units?
4. He don’t know a formula for obtaining the change of temperature, and he told the formula I provided was unreal as he tried to invalidate my question #3:
“3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc”
This one:
dT=P/m * Cp
It’s completely wrong.
5. He ignores that EMRP is the pressure exerted by the electromagnetic radiation, which was discovered theoretically by Maxwell and corroborated experimentally by Lebedev, and Nichols and Hull:
http://www.phy.hr/~dpaar/fizicari/xmaxwell.html
http://www.britannica.com/EBchecked/topic/334217/Pyotr-Nikolayevich-Lebedev
http://prola.aps.org/abstract/PRI/v13/i5/p307
6. He says the formula GPL = QSUN / 4π (POR)^2 was invented by me, when it was taken from the book Astrophysics by Maoz, pp. 36-47.
7. Mark doesn’t know that W/m^2 is a unit for flux of energy, not for power, and failed when eliminating units from the formula T = (P/sigma)^1/4 because of his confusion between power and flux of energy.
8. Mark didn’t answer a sole question from all the questions I did.
Thus, it’s quite evident what the purpose of that “Mark” was whith this discussion, i.e. hide the decline… oops! sorry, denigrate the real science with his scientific illiteracy.
So, ciao!
@Mark
Just in case you didn’t know, Nassif, this document may help:
http://biocab.org/Annual_Energy_Budget.html
Within it says:
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
Watts per square meter.
Maybe you ought to read some of that stuff on biocab…
And that is what I said in one of my previous posts:
Nasif Nahle on July 15, 2010 at 6:45 pm | Reply
1. How is it that you assure I said that the Earth temperature depends of 181.64 W, when I said that it is the energy absorbed by the surface, as it is clearly stated in my article:
http://biocab.org/Annual_Energy_Budget.html
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
And it is stated by Peixoto and Oort in their book “Physics of Climate”, by Odum in his book “Ecology”, and by many other authors.
And I am correct. The load of energy absorbed by the surface is 181.64 W/m^2.
Now, concluding this useless discussion, let’s see the extreme errors made by Mark which demonstrates he never has touched a book of physics:
1. He took an astronomical unit = 203 meters, when an AU is ~150 million kilometers.
Don’t know what value to use for m?
Go on, tell us what value for m you use under every occasion.
And then show us what temperature you get from 181.64W/m2 and how you get it.
If you can’t answer, that’s proof you don’t know the answer.
And quit with the lies
“Nasif Nahle July 13, 2010 at 9:19 pm
Heh… Well, I don’t like your physics; you know, your assertion that an AU = 100 km and other “physics” from you.”
And now “He took an astronomical unit = 203”
You’re busy lying and accusing to avoid telling anyone what value you got.
2. He said the protons travel at c and was saying that I was wrong.
3. He don’t know how to eliminate units from the formulas, as it was shown in his post:
Mark
Here: “ECO2 = 1- [(1.45-1 * 1-1.0001 bar / (1.45 + 0.23) 1 + 1.0001 bar)) * e [-1.47 (Log10 (0.005134 bar cm /0.034 bar cm))2]]”
That makes the result have units.
The result have units?
4. He don’t know a formula for obtaining the change of temperature, and he told the formula I provided was unreal as he tried to invalidate my question #3:
“3. What’s, specifically the incorrect way I used the magnitudes and algorithms taken from books and articles on heat transfer, astrophysics, etc”
This one:
dT=P/m * Cp
It’s completely wrong.
5. He ignores that EMRP is the pressure exerted by the electromagnetic radiation, which was discovered theoretically by Maxwell and corroborated experimentally by Lebedev, and Nichols and Hull:
http://www.phy.hr/~dpaar/fizicari/xmaxwell.html
http://www.britannica.com/EBchecked/topic/334217/Pyotr-Nikolayevich-Lebedev
http://prola.aps.org/abstract/PRI/v13/i5/p307
“”dT=P/m * Cp
It’s completely wrong.”
5. He ignores that EMRP is the pressure exerted by the electromagnetic radiation,”
1) You’ve said 181.64W/m2 is the value and I should use that equation above to calculate the temperature of the earth from it.
Yet you can’t do it.
2) That formula doesn’t come from EMRP and so whether it’s a correct formula doesn’t matter, it isn’t used here.
3) Those links don’t explain why you use it to get 181.64W/m2 or why it would apply in this case
So what do YOU get?
6. He says the formula GPL = QSUN / 4π (POR)^2 was invented by me, when it was taken from the book Astrophysics by Maoz, pp. 36-47.
7. Mark doesn’t know that W/m^2 is a unit for flux of energy, not for power, and failed when eliminating units from the formula T = (P/sigma)^1/4 because of his confusion between power and flux of energy.
8. Mark didn’t answer a sole question from all the questions I did.
Thus, it’s quite evident what the purpose of that “Mark” was whith this discussion, i.e. hide the decline… oops! sorry, denigrate the real science with his scientific illiteracy.
So, ciao!
ciao? This means you don’t know what value of m you use in your equation
dT=P/m*Cp
So that means you didn’t get a dT.
So that means you didn’t get a temperature from that equation for the earth.
So all your wailing and crying about how the IPCC is wrong and how I’m wrong is just because you don’t like the answers, not because you don’t have better ones.
Poor little baby.
You know it would be easy to prove me wrong:
tell us your answer for the temperature from the earth and how you got it.
As to your idiotic attempt to call “wrong”, an energy flux is Power and that is what you get from YOUR “paper” and I quote:
“181.64 W/m^2 are absorbed by the surface of Earth (Land and Oceans).”
So I’m using YOUR figure to work with YOUR formula and YOU haven’t said how YOU did it.
@Mark…
You are applying that formula in a wrong way. Again, a few lessons on physics:
Units for Power (P) = W
Units for flux of energy = W/m^2
You wrote the formula:
equation
dT=P/m*Cp
So that means you didn’t get a dT.
Thus, you must introduce the value of power, which you say it is 181.64 W/m^2; however, it is not power, but flux of energy. 😀
If you introduce a value for power, then the units would be:
T = [W/(W/m^2 K^4)]^0.25, and your result would be K/m^2.
Understood???
The proper units are W/m^2, so your Yahoo formula is incorrect.
The correct formula is T = (Φq/sigma)^0.25
You didn’t read the correct source, biocab.org
On the other hand, I would like you take a look to the energy budget by Trenberth and Kevin at:
Click to access BAMSmarTrenberth.pdf
Now tell me… What is the thermal flux reported by Trenberth and Kevin as the energy absorbed by the surface? hahahahaha!!!
They say the flux of energy absorbed by the surface is 161 W/m^2; therefore, following your criteria and your Yahoo formula, the temperature of the Earth’s surface would be:
T = [161 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 230.84 K 😀
Aren’t Trenberth and Kevin your priests? Hahaha! 😀
So, summing up, Nassif, you don’t know why you get 181.64W/m2. You don’t know how you get a temperature from that and you don’t know how to apply formulae.
Yelling screaming and crying about how bad done by you are doesn’t counter these facts.
Answering how you get 181.64W/m2 and how you get a temperature of the earth from that would at least START to do it, but you KNOW you’re using the wrong formulae and avoiding showing it. Lies cannot stand scrutiny, so you avoid it.
Oh, no! It’s just that you don’t know physics and I have demonstrated it through this thread. 😀
Take a look again to my article and read the diagram where I report the ISR on the surface:
Oooh! You didn’t read it… Well is usual in illiterate people, like you.
Taken from the diagram, almost at the end of the article here:
http://biocab.org/Annual_Energy_Budget.html
13/06/07: ISI (Incident Solar Irradiance) = 469.69 W/m^2, taken with a thermo-radiometer.
Now apply your Yahoo formula, but introduce the correct magnitude, which is not P, as you said, but flux of energy or thermal flux. 😀
Ooh! Then Nasif is correct and Mark is wrong. Simple.
Oh, you still don’t know what m you used with that equation (it isn’t in that link).
Here’s what you said:
“I invite you to make the calculation using the following formula:
dT = P/m * Cp
Introduce the magnitudes for soil and/or oceans.”
So what m and P did you use for the soil and/or oceans?
You didn’t do it there.
You haven’t done it here.
And you squirm to avoid doing so.
Hmm. Yet a third number.
Where did the 181.64W go?
Nassif rushes past, yelling and hoping nobody is listening to him getting all wrong all over again.
“Take a look again to my article and read the diagram where I report the ISR on the surface:”
you don’t calculate the temperature, you’re reporting it.
You stated that you calculate the earths temperature, but you don’t show how you calculate it.
Never have on this site either.
Because you can’t.
“13/06/07: ISI (Incident Solar Irradiance) = 469.69 W/m^2, taken with a thermo-radiometer.”
And that thermo-radiometer doesn’t know the difference between sunlight energy and greenhouse gas energy. Therefore it’s unsurprising that when you plug that equation into SB’s Law you get the right temperature of the earth.
However, this includes the effect of greenhouse gasses.
All you’ve done is proven that you have to have greenhouse gasses to get the earth temperature that you can read on a thermometer.
“The correct formula is T = (Φq/sigma)^0.25”
So what values did you use?
What result do you get?
It’s easy to say “you’ve got it wrong” then put up meaningless figures from the extended ASCII set and say “you should use that”.
So what values did or would you use?
“They say the flux of energy absorbed by the surface is 161 W/m^2; therefore, following your criteria and your Yahoo formula, the temperature of the Earth’s surface would be:
T = [161 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 230.84 K ”
And YOU Said that it should be 181.64W.
Plug those in and you get:
T = [18.641 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 230.84 K ”
237.91K
HA!
This is using YOUR number, not picking another random figure from yet another source. Don’t you have any work of your own?
8)
“They say the flux of energy absorbed by the surface is 161 W/m^2; therefore, following your criteria and your Yahoo formula, the temperature of the Earth’s surface would be:
T = [161 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 230.84 K ”
And YOU Said that it should be 181.64W.
Plug those in and you get:
T = [18.641 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 237.91 K
HA!
This is using YOUR number, not picking another random figure from yet another source. Don’t you have any work of your own?
8)
@Mark…
“They say the flux of energy absorbed by the surface is 161 W/m^2; therefore, following your criteria and your Yahoo formula, the temperature of the Earth’s surface would be:
T = [161 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 230.84 K ”
And YOU Said that it should be 181.64W.
Plug those in and you get:
T = [18.641 (W/m^2)/5.6697 x 10^-8 (W/m^2) K^4]^0.25 = 237.91 K</
HA!
This is using YOUR number, not picking another random figure from yet another source. Don’t you have any work of your own?
And I sustain it. All my methodology on how to obtain those magnitudes is explained in my article:
http://biocab.org/Annual