In Part One we took a look at what data was available for “back radiation”, better known as Downward Longwave Radiation, or DLR.
The fact that the data is expensive to obtain doesn’t mean that there is any doubt that downward longwave radiation exists and is significant. It’s no more in question than the salinity of the ocean.
There appear to be three difficulties in many people’s understanding of DLR:
- It doesn’t exist
- It’s not caused by the inappropriately-named “greenhouse” gases
- It can’t have any effect on the temperature of the earth’s surface
There appear to be many tens of variants of arguments around these three categories and it’s impossible to cover them all.
What’s better is try and explain why each category of argument is in error.
Part One covered the fact that DLR exists and is significant. What we will look at in this article is what causes it. Remember that we can measure this DLR at night, and the definition of DLR is that it is radiation > 4μm.
99% of solar radiation is <4μm – see The Sun and Max Planck Agree. Solar and longwave radiation are of a similar magnitude (at the top of atmosphere) therefore when we measure radiation with a wavelength > 4μm we know that it is radiated from the surface or from the atmosphere.
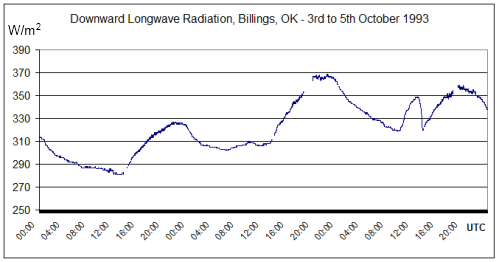
Notice that the night-time radiation (midnight local time = 6am UTC) is not a lot lower than the peak daytime radiation. The atmosphere cools down slower than the surface of the land (but faster than the ocean).
This by itself should demonstrate that what we are measuring is from the atmosphere, not solar radiation – otherwise the night-time radiation would drop to zero.
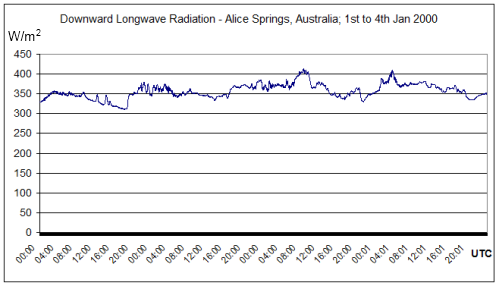
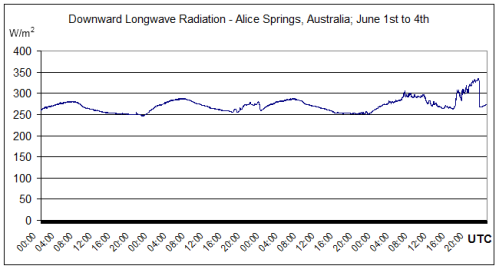
More DLR measurements from Alice Springs, Australia. Latitude: -23.798000, Longitude: 133.888000. BSRN station no. 1; Surface type: grass; Topography type: flat, rural.
Summer measurements over 4 days:
Winter measurements over 4 days:
This radiation is not solar and can only be radiation emitted from the atmosphere.
Properties of Gases – Absorption and Emission
As we can see from the various measurements in Part One, and the measurements here, the amount of radiation from the atmosphere is substantial – generally in the order of 300W/m2 both night and day. What causes it?
If measurements of longwave radiation at the surface are hard to come by, spectral measurements are even more sparse, again due to the expense of a piece of equipment like an FT-IT (Fourier Transform Infrared Spectroscope).
You can see some more background about absorption and emission in CO2 – An Insignificant Trace Gas? – Part Two.
A quick summary of some basics here – each gas in the atmosphere has properties of absorption and emission of electromagnetic radiation – and each gas is different. These are properties which have been thoroughly studied in the lab, and in the atmosphere. When a photon interacts with a gas molecule it will be absorbed only if the amount of energy in the photon is a specific amount – the right quantum of energy to change the state of that molecule – to make it vibrate or rotate, or a combination of these.
The amount of energy in a photon is dependent on its wavelength.
This post won’t be about quantum mechanics so we’ll leave the explanation of why all this absorption happens in such different ways for N2 vs water vapor (for example) and concentrate on a few simple measurements.
The only other important point to make is that if a gas can absorb at that wavelength, it can also emit at that wavelength – and conversely if a gas can’t absorb at a particular wavelength, it can’t emit at that wavelength.
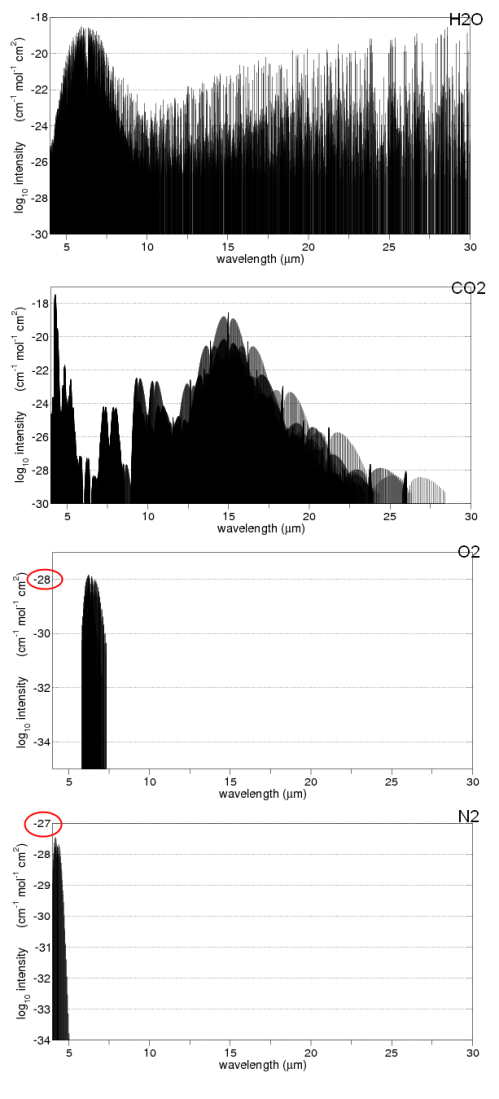
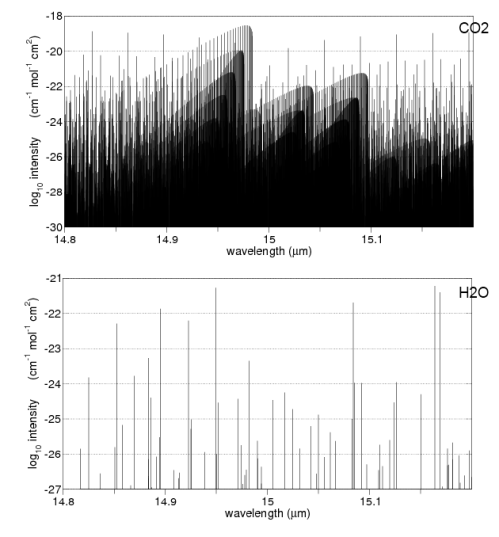
Here are some absorption properties of different gases in the atmosphere:
And for those not used to this kind of graph, the vertical axis is on a logarithmic scale. This means that each horizontal line is a factor of 10.
So if we take the example of oxygen (O2) at 6-7μm the absorption is a factor of 1,000,000,000 times (1 billion times) lower than water vapor at those wavelengths.
Water vapor – as you can see above – absorbs across a very wide range of wavelengths. But if we take a look at CO2 and water vapor in a small region centered around 15μm we can see how different the absorption is:
We know the absorption properties of each gas at each wavelength and therefore we also know the emission properties of each gas at each wavelength.
So when we measure the spectrum of a radiating body we can calculate the energy in each part of the spectrum and calculate how much energy is coming from each gas. There is nothing at all controversial in this – not in physics anyway.
Measured Spectra of Downward Longwave Radiation
Now we know how to assess the energy radiated from each gas we just need some spectral plots of DLR.
Remember in Part One I commented about one of the papers:
Their paper isn’t about establishing whether or not atmospheric radiation exists. No one in the field doubts it, any more than anyone doubts the existence of ocean salinity. This paper is about establishing a better model for calculating DLR – as expensive instruments are not going to cover the globe any time soon.
If we want to know the total DLR and spectral DLR at every point over the globe there is no practical alternative to using models. So what these papers are almost always about is a model to calculate total DLR – or the spectrum of DLR – based on the atmospheric properties at the time. The calculated values are compared with the measurements to find out how good the models are – and that is the substance of most of the papers.
By the way, when we talk about models – this isn’t “predicting the future climate in the next decade using a GCM” model, this is simply doing a calculation – albeit a very computationally expensive calculation – from measured parameters to calculate other related parameters that are more difficult to measure. The same way someone might calculate the amount of stress in a bridge during summer and winter from a computer model. Well, I digress..
What DLR spectral measurements do we have? All from papers assessing models vs measurements..
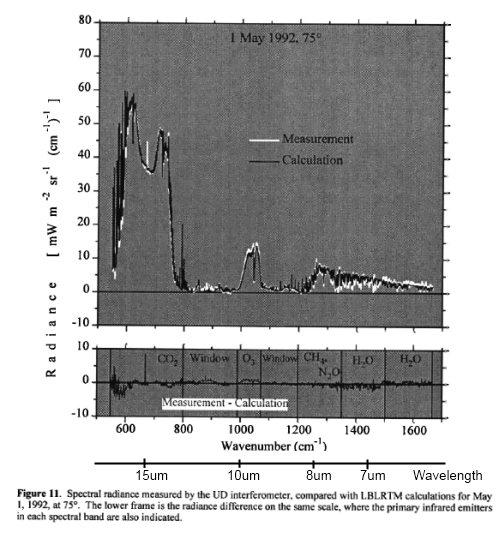
One place that researchers have tested models is Antarctica. This is because by finding the driest place on earth, it eliminates the difficulties involved in the absorption spectrum of water vapor and the problems of knowing exactly how much water vapor is in the atmosphere at the time the spectral measurements were taken. This helps test the models = solving the radiative transfer equations. In this first example, from Walden (1998), we can see that the measurements and calculations are very close:
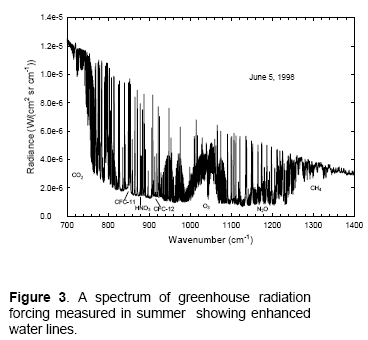
Note that in this field we usually see plots against wavenumber in cm-1 rather than a plot against wavelength in μm. I’ve added wavelength to each plot to make it easier to read.
I’ll comment on the units at the end, because unit conversion is very dull – however, some commenters on this blog have been confused by how to convert radiance (W/m2.sr.cm-1) into flux (W/m2). For now, note that the total DLR value measured at the time the spectrum was taken was 76 W/m2.
We can see that the source of this DLR was CO2, ozone, methane, water vapor and nitrous oxide. Oxygen and nitrogen emit radiation a billion times lower intensity at their peak.
The proportion of DLR from CO2 is much higher than we would see in the tropics, simply because of the lack of water vapor in Antarctica.
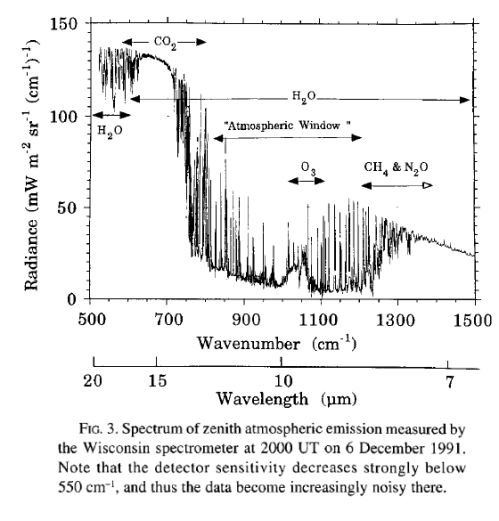
Here is a spectrum measured in Wisconsin from Ellingson & Wiscombe (1996):
We see a similar signal to Antarctica with a higher water vapor signal. Notice, as just one point of interest, that the CO2 value is of a higher magnitude than in Antarctica – this is because the atmospheric temperature is higher in Wisconsin than in Antarctica. This paper didn’t record the total flux.
From Evans & Puckrin (2006) in Canada:
By now, a familiar spectrum, note the units are different.
And a comparison with summer with more water vapor.
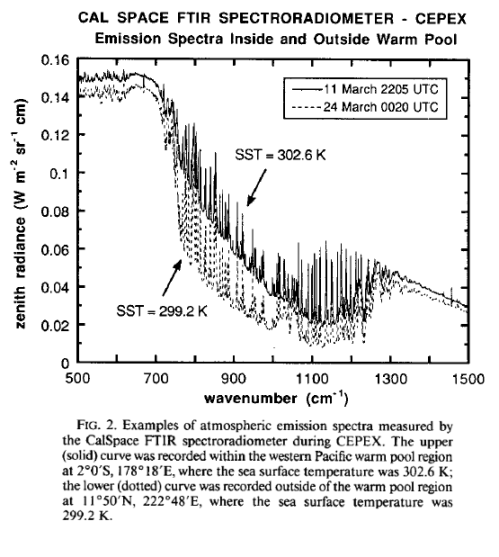
From Lubin et al (1995) – radiation spectrum from the Pacific:
Alternative Theories
Some alternative theories have been proposed from outside of the science community:
- DLR is “reflected surface radiation” by the atmosphere via Rayleigh scattering
- DLR is just poor measurement technology catching the upward surface radiation
A very quick summary on the two “ideas” above.
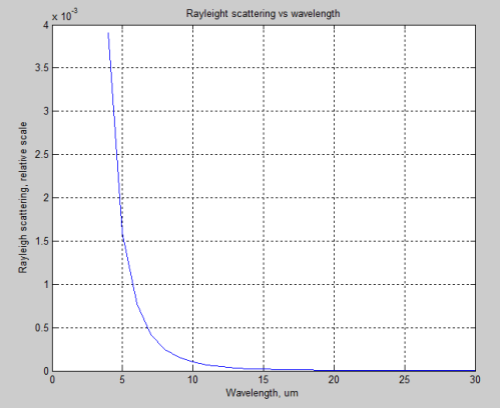
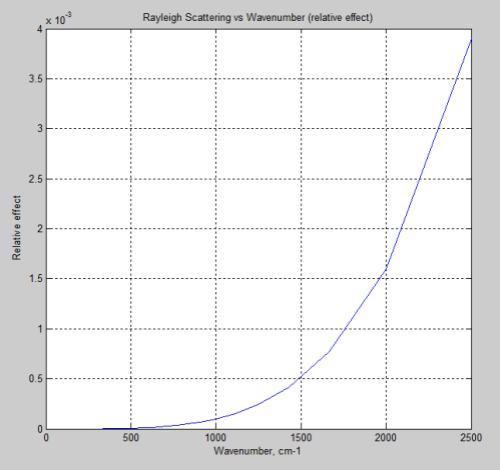
Rayleigh scattering is proportional to λ-4, where λ is the wavelength. That’s not easy to visualize – but in any case Rayleigh scattering is not significant for longwave radiation. However, to give some perspective, here are the relative effects of Rayleigh scattering vs wavelength:
So if this mechanism was causing DLR we would measure a much higher value for lower wavelengths (higher wavenumbers). Just for easy comparison with the FTIR measurements above, the above graph is converted to wavenumber to orientate it in the same direction:
Compare that with the measured spectra above.
What about upward surface radiation being captured without the measurement people realizing (measurement error)?
If that was the case the measured spectrum would follow the Planck function quite closely, e.g.:
(Once again you need to mentally reverse the horizontal axis to have the same orientation as the FTIR measurements).
As we have seen, the spectra of DLR show the absorption/emission spectra of water vapor, CO2, CH4, O3 and NO2. They don’t match Rayleigh scattering and they don’t match surface emission.
Conclusion
The inescapable conclusion is that DLR is from the atmosphere. And for anyone with a passing acquaintance with radiation theory, this is to be expected.
If the atmosphere did not radiate at the spectral lines of water vapor, CO2, CH4 and O3 then radiation theory would need to be drastically revised. The amount of radiation depends on the temperature of the atmosphere as well as the concentration of radiative gases, so if the radiation was zero – a whole new theory would be needed.
Why does the atmosphere radiate? Because it is heated up via convection from the surface, solar radiation and surface radiation. The atmosphere radiates according to its temperature, in accordance with Planck’s law and at wavelengths where gas molecules are able to radiate.
There isn’t any serious theory that the atmosphere doesn’t emit radiation. If the atmosphere is above absolute zero and contains gases that can absorb and emit longwave radiation (like water vapor and CO2) then it must radiate.
And although the proof is easy to see, no doubt there will be many “alternative” explanations proposed..
Update – Part Three now published
Darwinian Selection – “Back Radiation”
References
Measurements of the downward longwave radiation spectrum over the Antarctic plateau and comparisons with a line-by-line radiative transfer model for clear skies, Walden et al, Journal of Geophysical Research (1998)
The spectral radiance experiment (SPECTRE): Project Description and Sample Results, Ellingson & Wiscombe, Bulletin of the AMU (1996)
Measurements of the radiative surface forcing of climate, Evans & Puckrin, 18th Conference on Climate Variability and Change, (2006)
Spectral Longwave Emission in the Tropics, Lubin et al, Journal of Climate (2005)


Another consequence of “backradiation doesn’t exist” is that to be consistent, the earth would be unable to radiate during the day: the Sun is hotter than he Earth, therefore if the air can’t radiate because it’s colder than the earth, the earth can’t radiate at daytime because it’s colder than the sun.
And at night, when temperature inversion takes place (the surface is often cooler than the atmosphere) – the atmosphere starts radiating towards the earth, and the earth’s radiation switches off.
It’s called the “radiative switcheroo” and sadly the climate science community are trapped in their own paradigm and refuse to accept the measurement support and technical backing for this obvious radiative switcheroo.
Look out for the new Gerlich and Tscheuschner paper on this subject..
“So if this mechanism was causing DLR we would measure a much higher value for lower wavelengths (higher wavenumbers). ”
Is this sentence correct? It’s from between the 2 Rayleigh graphs. Because it looks like that is exactly what those 2 graphs show.
Bill Stoltzfus
One graph is the inverse of the other (the first is against wavelength, the second against wavenumber = 10,000/wavelength). The answer is not halfway between. Compare the 2nd graph with the FTIR plots.
In any case, Rayleigh scattering for longwave is negligible but if it was significant you would see 15um (667cm-1) radiation at 5% of 7um (1400cm-1) radiation. (7^4/15^4 = 0.047)
Instead you see 15um radiation much higher than 7um radiation.
OK, thanks–my bad. I was thinking that the “measure a much higher number for lower wavelengths” was referring to the Rayleigh graphs instead of the FTIR graphs.
What happens if “the atmosphere is above absolute zero and” does not “contain gases that can absorb and emit longwave radiation”? Presuming that under those circumstances the atmosphere radiates differently, what becomes othe surface’s temperature?
The atmosphere would find a closest body it can share energy without radiative heat transfer and adobt it’s temperature according to it. Here, it would most probably be the surface and it would exchange heat with it through conduction. And the surface would be at whatever temperature it has to be to maintain radiative balance with the sular flux (a lot colder than we have at the moment).
Forgot to select the ‘notify’ option
I originally started to develope this issue when I read some posting purporting to prove the Stefan-Boltzmann law “wrong” based on lunar temperatures. You might find this link, regarding Newton’s law of cooling, of interest.
http://www.ugrad.math.ubc.ca/coursedoc/math100/notes/diffeqs/cool.html
The law gives this equation:
T(t) = Ta + (T0 -Ta)*1/(e^kt)
Where T(t) gives Temperature, T, as a function of time, t,
Ta is ambient background temperature, and T0 is the starting temperature of the body warming up or cooling off.
My prior post regarding the conservation of heat in the atmosphere was to verify that it is reasonable to assume a constant long wave
flux from the atmosphere over the course of a day. I don’t know how much “average” surface temperature changes over the course of a 24 hour day.
I checked my own locality for last night, and got a high-low difference of about 20 C. I assume the difference is a lot less near an ocean, and most of the world is ocean, so I’m assuming the average diurnal flux over the whole earth is more like 12C.
For my wattage numbers, I’m using Trenbeth’s numbers from Figure 1.1 here:
Click to access 9780521871075_excerpt.pdf
I read that CO2 is thoroughly mixed in the atmosphere, and I immediately jumped to the conclusion that the atmospheric wattage
flux was evenly mixed- I quickly realized my stupid mistake when I saw those long wave figures on your post.
A second point, although the air gains or loses heat on the order of 1% per day, clouds make up about 1/6 of the total greenhouse
effect, and cloud weather can fluctuate rapidly, resulting in changes in of plus or minus 50 watts or so over short intervals, giving us weather rather than climate.
Although there are large fluxes due to earth’s transport of heat from warm to cool regions,making “weather”, for an “average” value, my figures
work okay.
Using Trenbeth’s figures, earth’s surface gets 168 watts from the sun, and 324 from the atmosphere. Of course that isn’t distributed evenly.
During the “daytime” we get 2*168 = 336 watts from the sun, and 324 from the atmosphere (remember my prior post showing the slow change in atmosphere flux.
During the “nighttime” we get 0 watts from the sun and 324 from the atmosphere.
Another adjustment: We lose 102 watts in latent heat, 24 to conduction and 78 to convection- This doesn’t go towards sensibly heating the
earth , so I’m not using it in the Newton Equation. I’ll assume all the latent heat is lost during the daytime, rather than half at day, half at night.
That leaves 336 watts from the sun, 324 from the atmosphere -204 latent heat during the day, for an average flux of 456 watts, and
324 watts-0 latent heat from the atmosphere at night.
Converting those wattage fluxes to temperature, given that for a blackbody,
1000 K gives of a wattage flux of 56,790
and given that temperature is proportional to the fourth root of the wattage flux, we get a
“daytime average” ambient temperature of
(456/56,790)^0.25*1000K =299.35K = Ta for the daytime, and
(324/56,790)^0.25*1000K =274.83K = Ta for the nighttime.
The median of 299.35 and 274.83 is 287.09.
T(t) = Ta + (T0 -Ta)*1/(e^kt)
Let’s start with a 12 hour day and 12 hour night, and a temperature of 293.09 at nightfall.
Let t be in units of daytime or nighttime. Then 1 nighttime is the full 12 hours of darkness, 1/12
unit is 1 hour of darkness, etc.
Then T(t) = 274.83 + (293.09-274.83)*1/e^kt
Let’s assume, for purposes of this example, that k=1.07053 Check the article on newton cooling and you’ll also see how
to derive the k experimentally from 1 hour of cooling, assuming you have a local climate and not local weather.
Then
T(t) = 274.83 + (293.09-274.83)* 1/e^1.07053t At nightfall, when t= 0, you get
T(0) = 274.83 + (293.09-274.83)*1/1 = 293.09
T(1) = 274.83 + (18.26)*1/e^1.07053 = 274.03 +(18.26/2.91693) = 281.09
Halfway through the night, at midnight, assuming climate and not that cloud changing weather, you’ll get
T(1/2) = 274.83 + (18.26)/e^(1/2*1.0753) = 274.83 + 10.67 = 285.5
Since we started at 293.09, the first half the night cooled 7.59 degrees, 63.25% of the total 12 degree cooling for the night.
You’ll get similar figures for the daytime based on the above model, remembering to plug in daytime figures.
Of course the sun isn’t equally high above the horizon all day, a better result might be obtained by
plugging in averages for 10 degree angles, etc.
Thank you scienceofdoom for a very nice post here, your Part Two.
“What happens if “the atmosphere is above absolute zero and” does not “contain gases that can absorb and emit longwave radiation”?”
Then it comes down to the outliers. If 8 molecules with 1/8th the necessary energy hit, then you’ll get emission.
And so on…
I realized that I forgot to add the boring units conversion – because it was so boring. If anyone thinks that the first graph can’t convert into something of the order of 70-80 W/m^2 in total I will be happy to explain.
Yes, I would like to understand that radiance unit. Thanks.
SOD: By units conversion, are you referring to the process of converting W/m2.sr.cm-1 into W/m2? Removing the dependence on sr-1 probably is boring, but it could be useful to understand how it works. Removing the dependence on wavenumber, however, presumably requires calculating the area under the radiance vs. wavenumber curve. There could be a little more excitement here, given that: integration needs to be done over about 3000 cm-1, the instrument detector needs to respond accurately when the energy per photon varies by more than a factor of ten and can only resolve to 1 cm-1 (in Lubin et al), while line-by-line radiative transfer models calculate emission at a resolution of 0.001 cm-1 (in Walden et al). When one considers the spectrum for CO2 shown above between 14.8 um (676 cm-1) and 15.1 um (662 cm-1), there would be 14 points representing observed data and about 14,000 points describing all of those lines. Is 14,000 points really enough? How does 0.001 cm-1 compare with the width at half-height for typical emissions lines at 200-300 degK and 10-1000 mb?
Just for the sake of being a bit mean, I think the concept of back radiation, and espescially measuring it in absolute values, is confusing and somewhat misleading. It seems to imply that the atmosphere is a heat source for the surface, which isn’t necessarily false, but leads to the confusion regarding how heat can flow from a cold body to a warm body (as the surface is warmer than the atmosphere) and all the other weird stuff that seems to pop up now and then.
In other words, the reason for all the confusion regarding it’s existance, is very much down to the fact that it is a rather stupid way to look at what’s going on. From what I’ve understood the amount of back radiation is very much dependant on the temperature of a short distance of gas above the earth plus the reflected radiation (the reflected part actually makes sense to me for some reason). As the atmosphere is supposed to be quite opaque on the absorbtion wavelength already, I don’t see how, for example, increasing the amount of CO2 in the atmosphere would change back radiation that much provided we don’t change the surface temperature.
It would be a lot prettier (in my opinion) to show it as a relationship between emitted radiation by the surface vs the measured atmospheric radiation on ground level or in other words, the value would be shown as a fraction rather than in W/m2.
In the context of radiative processes that affect atmospheric temperatures forget about the Rayleigh scattering. While Rayleigh scattering accounts for the sky being blue and the setting (or rising) sun being red, it has very little effect on the Infra-Red radiation.
In optical fibre, Rayleigh scattering is the main source of attenuation. Typical attenuation at 1.5 microns is ~0.2 dB/km. This means that it takes 15 km of glass (fused silica) to scatter 50% of the light.
By the time one gets to 15 microns where the Earth is radiating strongly, the Raleigh scattering is 10,000 times less than at 1.5 microns. Around 15 microns, Rayleigh scattering is tiny and absorption by atmospheric gases is dominant. I think that is what you have been telling us when talking about an “insignificant trace gas”.
Just one more point. Unlike absorption that changes the wavelength of incident energy, Rayleigh scattering merely redirects the photons without changing their energy.
“It seems to imply that the atmosphere is a heat source for the surface, which isn’t necessarily false, but leads to the confusion regarding how heat can flow from a cold body to a warm body”
It’s only confusing if you’re ignoring that it’s NET flow, *not* absolute flow.
P=signa(t1-t2)^4
is EXACTLY THE SAME as
P=P1-P2
where
P1=sigmaT1^4
P2=sigmaT2^4
Thereby illustrating that there is a flow exactly as equated for a single hot body, but moving in two different directions.
If T1=T2, then the flows balance and no NET flow happens.
If T1>T2 then the NET flow is from T1 to T2, but each is merely radiating what they do irrespective of each others presence.
If T1<T2 then the NET flow is the other way. Still both radiating what they do irrespective of each others presence.
This is the ONLY way you can prove the second law with photon emissions because photons don't interact with each other. One photon cannot stop another from progressing on its journey.
Where's the confusion? It's manufactured to spread FUD.
Regardless of whether the confusion is manufactured or not, I believe it is quite clear it exists (as far as I understand this is the reason behind this article). I’m just not that fond of this particular angle of looking at atmospheric processes (I call everything I don’t like stupid, because it makes me feel smarter).
PS. It’s not really nice to only quote half of a sentence.
“Regardless of whether the confusion is manufactured or not”
It does rather have a great effect.
If the confusion arises naturally, it can be countered and fixed. Just like if your sheep keep dying because there’s a toxic weed in that paddy, you can fix the problem and keep your sheep.
If the confusion arises through actual malice or deed, then it cannot be countered, just as if your sheep are being poisoned, you can’t stop your sheep dying by moving them elsewhere or clearing out the meadow.
“I’m just not that fond of this particular angle of looking at atmospheric processes”
Why don’t you like it?
Photons don’t bump into each other, so the existence or otherwise of another photon going the other way doesn’t cause any back pressure to stop the cooler body radiating.
There’s no gradient to climb for a photon unlike an electrical potential, so there’s nothing to prevent a photon moving where it likes.
Therefore the cooler body radiates whether there is another body nearby.
The second law says nothing about energy being banned from moving from cold to hot, just that the overall effect will be distinctly one way.
But any one photon moving will still move, irrespective of the second law, because thermodynamics have nothing to say about the microscopic world, just the macro one.
PS why is it not nice to quote half a sentence?
If that quotation takes out the context by leaving it, then there is no harm and crying foul is merely petulance.
But to give the context of the return, the part of the sentence quotes was enough to start people off, especially since the rest of the quote was in the direct parent of the post.
I think the hot/cold issue is dead and buried; the colder body will radiate to the warmer [which I believe G&T did not contradict] but the atmosphere of the Earth is not an independent body generating its own heat; it is dependent on the surface [and to a lessor extent, insolation] for its heat; in this circumstance the cooler body [the atmosphere] cannot heat the warmer body [the surface] to a temperature greater than what the warm body was before it heated the cool body; this is the 2nd law, however, the Earth is not a closed system with insolation continuously occuring. So, the relevance of backradiation is that it is in addition to insolation at the surface so that the surface will heat to a level which would otherwise be contradicted by the 2nd law. A number of issues:
1 http://4.bp.blogspot.com/_nOY5jaKJXHM/TDDizFtBw0I/AAAAAAAABMI/Hl_EW6F_-og/s1600/divine.gif
2 For backradiation to heat requires a lag or delay in the upward radiation [Su in Miskolczi parlance] leaving the TOA; we know this occurs because of the Greenhouse temperature of 33C; the issue is how much extra lag is caused by ACO2 so that 33C is increased. Has there been any measure of this lag? TOA OLR is subject to the Lindzen Choi dispute but has backradiation increased over the AGW period?
3 Any increase in backradiation’s contribution to warming would still be subject to the defect of GMST; that is (A + B)^4 > A^4 + B^4 which shows that backradiation, like all Stefan-Boltzman effects, is subject to regionalised variation which defeats any averaging that AGW relies on as a metric.
“in this circumstance the cooler body [the atmosphere] cannot heat the warmer body [the surface] to a temperature greater than what the warm body was before it heated the cool body;”
If you lag your hot water tank the tank WILL get hotter if you have the same power input.
Talk to your plumber or electrician, he’ll tell you.
“2 For backradiation to heat requires a lag or delay in the upward radiation”
No it doesn’t. All it requires is that hot things radiate.
Which CO2 and other greenhouse gasses to in IR.
“like all Stefan-Boltzman effects, is subject to regionalised variation which defeats any averaging that AGW relies on as a metric.”
What? What do you think statistics is all about? There’s a variation in the heights of human beings. Regional ones too. But we still have the ICAO standard man (or woman) with an average height.
IQs also vary but the average is set to 100.
Energy use? Same thing: regional and time variations but we still have an average.
The problem isn’t that it can’t be done, it’s that you can’t do it.
“I think the hot/cold issue is dead and buried; the colder body will radiate to the warmer [which I believe G&T did not contradict]”
Well, you’ll have to tell G&T because they specifically say it’s impossible.
I do find it confusing that there are so many different measurement systems. Can you provide an article or links on how to convert between all of the different systems?
G&T said this in their reply to Halpern et al’s comment:
a) We never claimed — allegedly with reference to Clausius — that a colder body
does not send radiation to a warmer one. Rather, we cite a paper, in which
Clausius treats the radiative exchange.19,20 The correct question is, whether
the colder body that radiates less intensively than the warmer body warms up
the warmer one. The answer is: It does not.
I also think you have missed the point about (A + B)^4 > A^4 + B^4 and how any correlation between GMST and the Earth’s energy balance is negated by it.
“a) We never claimed — allegedly with reference to Clausius — that a colder body”
They did try and prove that thermal energy cannot go from the lower temperature object to the higher one.
“The correct question is, whether the colder body that radiates less intensively than the warmer body warms up the warmer one.”
Then what does that energy do? Hide???
No, it warms the other body just like any other radiation would.
“I also think you have missed the point about…”
No, I noticed it. It’s complete hogwash.
Here:
http://www.engineersedge.com/heat_transfer/black_body_radiation.htm
From engineers who don’t have a pony in the climate sciences.
“hogwash”;
Yes, Hogwash.
Where does that have (T1-T2)^4?
Answer: it doesn’t.
Therefore, though in a trivial sense, (A + B)^4 > A^4 + B^4 is true
a) it doesn’t apply here
b) it still doesn’t mean you can’t have an average
Yes, you can still have an average, it just won’t tell you anything meaningful about the Earth’s energy balance which backradiation is supposedly affecting.
And I note that you haven’t been able to show your link given cast any veracity on your statement about (A+B)^4, either.
Could you not find it?
After all, it could be there and I missed it.
Or were you making stuff up?
Yes you will have something meaningful about the earth’s energy balance.
Because it’s not (T1 + T2) ^ 4.
From the link:
“There’s nothing surprising about this – average a series of numbers and raising the average to the 4th power will almost always give a different answer to first calculating the 4th power for each of a series of numbers and averaging the results.”
SoD then says this:
“The earth by contrast, with less extreme temperatures has this result –
the “average” temperature = 15°C, and converting that to the “average” radiation = 390 W/m2
calculated the correct and painful way, the individually calculated values of radiation from each and every surface temperature around the globe every few hours over a year.. then averaged = 396 W/m2”
And concludes: “The right way to calculate a planet’s average radiation is to calculate it for each and every location and average the results. The wrong way is to calculate the average temperature and then convert that to a radiation. In the case of the earth’s surface, it’s not such a noticeable problem”
I tend to disagree that “its not such a noticeable problem”; Lubos explains here:
http://motls.blogspot.com/2008/05/average-temperature-vs-average.html
And Pielke has an interesting paper on the issue:
Click to access r-321.pdf
The issue is a crucial one which is why our host has a specific thread on it, other than the link I gave, which I’m sure you can find.
But this is not the earth and is not the regional variation you’re talking about and is not in any way giving a non-average temperature.
Sorry, still 100% failure.
Oh, and it also has nothing to do with back radiation.
A fail bonus. cohen.
” 1. By virtue of the second law of Thermodynamics, heat cannot be transferred from a colder to a warmer body, and
2. Since solar energy is the basic source of all energy on Earth, if we do not change the amount of solar energy absorbed, we cannot change the effective radiating temperature of the Earth.
Both of the above statements are certainly true, but as we will show, the so-called “greenhouse theory” does not violate either of these two statements.”
And though you can’t just power up the addition to get the addition of the powers
a) a fractional difference small enough is 4x the difference when run to the fourth power
b) you can still sum the energy and then put the sum to the fourth root and you get a temperature that, if the world were radiating at were a constant and even temperature, would be radiating the same energy.
The latter is the progenitor of the Teff (effective blackbody temperature which is what you get from a photometer reading of temperatures, whereas an optical pyrometer gives you the Wein displacement law Teff, the temperature at which the peak radiation is the same).
At the beginning of this post, SOD listed three “difficulties” about DLR that I personally don’t find difficult. (DLR clearly exists, is emitted by GHGs, and – like all radiation – must warm the earth.) I’d like to suggest two additional difficulties that appear to be far more relevant:
1) Does the simple equation W = oT^4 have anything to do with how DLR is really calculated? If not, why do we see diagrams with a “layer” of atmosphere emitting oT^4, or eoT^4 or (1/2)*eoT^4?
2) Can current GCM’s predict DLR with enough accuracy make useful predictions about GHG-mediated GW? Depending on the situation, errors of a few W/m^2 could be critical when the radiative forcing from 2X CO2 is only 3.7 W/m^2.
Referring to data from several papers, SOD says: “If we want to know the total DLR and spectral DLR at every point over the globe there is no practical alternative to using models.” Are these models really a useful alternative? In most of these papers, the atmosphere is first probed by a radiosonde to determine the exact profile of temperature and humidity vs. altitude producing DLR, an advantage AOGCM’s don’t have. The sky is not cloudy, an advantage AOGCM’s don’t have. One paper comes from the Antarctic, where problem with humidity are minimal. Below are the abstracts from these paper describing how well DLR is calculated EVEN WITH THESE ADVANTAGES:
Lubin et al (1995, couldn’t find in 2005): Longwave emission by the tropical western Pacific atmosphere has been measured at the ocean surface by a Fourier Transform Infrared (FTIR) spectroradiometer deployed aboard the research vessel John Vickers as part of the Central Equatorial Pacific Experiment. The instrument operated throughout a Pacific Ocean crossing, beginning on 7 March 1993 in Honiara. Solomon Islands, and ending on 29 March 1993 in Los Angeles, and recorded longwave emission spectra under atmospheres associated with sea surface temperatures ranging from 291.0 to 302.8 K. Precipitable water vapor abundances ranged from 1.9 to 5.5 column centimeters. Measured emission spectra (downwelling zenith radiance) covered the middle infrared (5–20, μm) with one inverse centimeter spectral resolution. FTIR measurements made under an entirely clear field of view are compared with spectra generated by LOWTRAN 7 and MODTRAN 2, as well as downwelling flux calculated by the NCAR Community Climate Model (CCM-2) radiation code, using radiosonde profiles as input data for these calculations.
In the spectral interval 800–1000 cm−1, these comparisons show a discrepancy between FTIR data and MODTRAN 2 having an overall variability of 6–7 mW m−2 sr−1 cm and a concave shape that may be related to the representation of water vapor continuum emission in MODTRAN 2. Another discrepancy appears in the spectral interval 1200–1300 cm−1, where MODTRAN 2 appears to overestimate zenith radiance by 5 mW m−2 sr−1 cm. These discrepancies appear consistently; however, they become only slightly larger at the highest water vapor abundances. Because these radiance discrepancies correspond to broadband (500–2000 cm−1) flux uncertainties of around 3 W m−2, there appear to be no serious inadequacies with the performance of MODTRAN 2 or LOWTRAN 7 at high atmospheric temperatures and water vapor abundances. On average, CCM-2 flux calculations agree to within 1 W m−2 with downwelling flux estimates from the FTIR data over all sea surface temperatures, although this result has a scatter Of ±12 W m−2 at high sea surface temperatures.
Robert G. Ellingson et al (1996): The fundamental climatic role of radiative processes has spurred the development of increasingly sophisticated models of radiative transfer in the earth-atmosphere system. Since the basic physics of radiative transfer is rather well known, this was thought to be an exercise in refinement. Therefore, it came as a great surprise when large differences (30–70 W/m^2) were found among longwave infrared fluxes predicted by over 30 radiation models for identical atmospheres during the intercomparison of radiation codes used in climate models (ICRCCM) exercise in the mid-1980s. No amount of further calculation could explain these and other intermodel differences; thus, it became clear that what was needed was a set of accurate atmospheric spectral radiation data measured simultaneously with the important radiative properties of the atmosphere like temperature and humidity.
To obtain this dataset, the ICRCCM participants charged the authors to develop an experimental field program. So, the authors developed a program concept for the Spectral Radiance Experiment (SPECTRE), organized a team of scientists with expertise in atmospheric field spectroscopy, remote sensing, and radiative transfer, and secured funding from the Department of Energy and the National Aeronautics and Space Administration. The goal of SPECTRE was to establish a reference standard against which to compare models and also to drastically reduce the uncertainties in humidity, aerosol, etc., which radiation modelers had invoked in the past to excuse disagreements with observations. To avoid the high cost and sampling problems associated with aircraft, SPECTRE was designed to be a surface-based program.
The field portion of SPECTRE took place 13 November to 7 December 199 1, in Coffeyville, Kansas, in conjunction with the FRE Cirrus II field program, and most of the data have been calibrated to a usable form and will soon appear on a CD-ROM. This paper provides an overview of the data obtained; it also outlines the plans to use this data to further advance the ICRCCM goal of testing the verisimilitude of radiation parameterizations used in climate models.
Von P. Walden et al (1998): A 1-year field program was conducted at South Pole Station in 1992 to measure the downward infrared radiance spectrum at a resolution of 1 cm−1 over the spectral range 550–1667 cm−1. The atmosphere over the Antarctic Plateau is the coldest and driest on Earth, where in winter, surface temperatures average about −60°C, the total column water vapor is as low as 300 μm of precipitable water, and the clear-sky downward longwave flux is usually less than 80 W m−2. Three clear-sky test cases are selected, one each for summer, winter, and spring, for which high-quality radiance data are available as well as ancillary data to construct model atmospheres from radiosondes, ozonesondes, and other measurements. The model atmospheres are used in conjunction with the line-by-line radiative transfer model (LBLRTM) to compare model calculations with the spectral radiance measurements. The high-resolution calculations of LBLRTM (≈0.001 cm−1) are matched to the lower-resolution measurements (1 cm−1) by adjusting their spectral resolution and by applying a correction for the finite field of view of the interferometer. In summer the uncertainties in temperature and water vapor profiles dominate the radiance error in the LBLRTM calculations. In winter the uncertainty in viewing zenith angle becomes important as well as the choice of atmospheric levels in the strong near-surface temperature inversion. The spectral radiance calculated for each of the three test cases generally agrees with that measured, to within twice the total estimated radiance error, thus validating LBLRTM to this level of accuracy for Antarctic conditions. However, the discrepancy exceeds twice the estimated error in the gaps between spectral lines in the region 1250–1500 cm−1, where emission is dominated by the foreign-broadened water vapor continuum.
The fourth paper (Evans) is a poster which contains the following data: “Table 3b shows the measured downward surface radiation forcing for three summer cases. The H2O flux has increased [compared with winter] from about 100 W/m2 to 200 W/m2. CO2 is reduced from 33 W/m2 to 11 W/m2.” SOD shows us that DLR may not change much from hour to hour at some sites, but doesn’t show us how much it various from season to season, or from clear to cloudy
For Alexandre and probably others:
Re: explaining how to work out the total flux in W/m^2 from a graph of radiance in W/m2.sr.cm-1.
When I started thinking about this I realized that there was a complication that I’m not sure how to resolve.
However, in another post when one of the these graphs was shown, a couple of commenters became quite entranced with the idea that the amount of DLR was in the order of a few 10s of mW/m^2. So I hope it’s clear at the end of the explanation that the spectral measurements shown do convert into a much higher flux value.
I’ll explain in what might be too basic a way for many – because some people have never seen numerical integration before.
First, note the important point that the x axis is in units of “Wavenumber in cm^-1”.
We could also write cm^-1 as 1/cm – because 1/x = x^-1 (this is just a very standard algebra convention).
Let’s use a simpler example to explain the first step.
Suppose you had a graph from some measurements of your walking speed in miles/hour and you want to calculate how far you had travelled in total:
Notice that you have miles/hour on the vertical and hours on the horizontal.
In the first hour the distance you travelled was between 2.5 and 2.7 miles. You can see this just by looking at the graph.
If you wanted to work out the total distance you could simple look at the graph and get the approximate value of distance for each hour then sum each distance.
Numerical integration or the area under the curve involves this same process, either with some graph paper and a ruler, or using a simple program (e.g. excel) to sum all of the values.
Here is one segment highlighted:
For this first half hour we can see that the distance travelled = average speed x time = (approximately) 2.6 miles/hour * 0.5 hours = 1.3 miles.
The same approach can be used with the more difficult radiance graph by using the area under the curve.
Instead of doing a tedious job with lots of little sections measured out we will just look at the rough values.
Between 600-800 cm^-1 the value on the y-axis is about 45 mW/(m^2.sr.cm^-1).
So this part of the spectrum has a value of 45 mW/(m^2.sr.cm^-1) x 200 cm^-1 = 9000 mW/(m^2.sr) = 9 W(m^2.sr)
We are simply doing a very very rough numerical integration – the area under the curve. We could do it more precisely if we wanted to take some time..
If you add up the other major parts of the measured spectrum in the same way, you can see around 12 x 60 = 720 mW/(m^2.sr) in the ozone part of the band (at around wavenumber 1000cm^-1) and 4 x 300 = 1200 mW/(m^2.sr) over to the right from 1300 to 1600 cm^-1.
If we add these up we get a total of 9 + 0.7 + 1.2 = 11 W/(m^2.sr).
Second, before we look at the part with the complication, we note that this is not the complete spectrum. Measuring spectral intensity accurately across very wide frequency ranges is very challenging, which is why the measurements are between 550-1650 cm^-1 (6-18um). There will be significant radiance above 18um (mostly from water vapor). In the case of this measurement sample we can’t see how large that is.
Third, what is the sr in W/(m^2.sr)? And how to we convert to W/m^2?
W/(m^2.sr) is Watts per m^2 per steradian. Steradian is a solid angle and there are 4π steradians in a sphere.
To convert to a total flux we have to integrate over all solid angles. If you consider a small surface area radiating isotropically (equally in all directions):
– then although there are 2π steradians in a hemisphere, when integrating up the radiation as if it came from a planar surface you only get π steradians. (For reasons that can be explained at some later stage, but it’s not exciting or particularly important).
This is the part where I am now questioning whether in fact it’s possible to convert with confidence to W/m^2 given that only a small beam angle has been measured. Step forward someone with some outdoor measurement experience.
Perhaps the most that can be known without a direct flux measurement is that the conversion from W/(m^2.sr) to W/m^2 is approximately done by multiplying the W/(m^2.sr) value by π (3.14).
In the case of the above spectral measurement, we have a direct comparison of 78W/m^2 independently measured.
And hopefully it is clearer why the values on the vertical axis are so small – we have to “integrate” this value over all wavenumbers (calculate the area under the curve) to convert to W/(m^2.sr).
Frank:
No
Because lots of simple models that illuminate the problem can be built with this equation.
What you see depends on what you look at. Here’s part of a standard derivation from Vardavas and Taylor (2007):
Or you can check out Climate Modeling through Radiative-Convective Models, Ramanathan and Coakley (1978).
Thanks. Now I can begin to see how radiative forcing is calculated from the change in upwelling and downwelling radiation as GHGs change. A closer look at these terms may tell me how emission varies with T and GHG concentration.
Frank:
The width of each spectral line is a function of temperature and pressure, and as pressure varies by a factor of 5 through the troposphere this is important.
For a layer of the atmosphere where pressure and temperature don’t vary (homogeneous) the emission from a GHG will be a linear function of concentration and dependent on T^4. But calculating the actual value yourself isn’t easy because you have to consider each spectral line.
I haven’t really used Modtran, but it is supposed to be a good solution. It uses a band model rather than each spectral line, but that’s fine for reasonably accurate solutions.
Well, I looked at your classification and realised my convective coupling argument (sort of) fell under number 3: “It can’t have any effect on the temperature of the earth’s surface”.
I look forward to part 3, where I assume this will be answered?
Or will it perhaps come under “and it’s impossible to cover them all”?
[…] Part Two we looked at several measured spectra of DLR which clearly demonstrated that this radiation is […]
[…] As you can see, the emission of radiation measured at the earth’s surface corresponds to the missing sections at the top of the atmosphere. See The Amazing Case of “Back-Radiation” and The Amazing Case of “Back Radiation” – Part Two. […]
[…] the downward radiation from the atmosphere – The Amazing Case of “Back-Radiation”, Part Two, […]
[…] 2010 by scienceofdoom In the The Amazing Case of “Back-Radiation” series, which included Part Two and Part Three, someone commented that it would have been good to see more than a few days of DLR […]
I an confused. Most of part 2 explained how the back (down) IR radiation is produced by molecular vibration and rotation relaxation of excited internal energy levels, which occurs at very specific wavelengths and because of a number of reasons — collisions and quantum statistics with Boltzmann distributions and Einstein coefficients e.g. but not because of temperature, and, as you say, virtually only with GHGases. Then in the conclusion you seem to switch hats and say, “…atmosphere radiates according to its temperature, in accordance with Planck’s law…” Planck-type radiation is not molecular relaxation radiation though you seem to imply that it is (??). Which is it?
Sorry I’m late — was just referred to your site; and I hope this wasn’t already covered — I only scanned the comments.
Rod B:
There is only one type of radiation – the emission of photons due to the changing energy states of molecules. The photon energy matches the energy change of the molecule.
Planck’s law, strictly speaking, gives you the blackbody radiance per unit frequency (or wavelength), per unit solid angle, per unit area. It’s the formula for working it out.
For a non-blackbody, Planck’s law is modified by the emissivity of the body. Emissivity is a material dependent property which varies with wavelength (and for non-diffuse surfaces also varies with direction).
For radiatively-active gases the intensity of the radiance at the lines where these gases emit follows the Planck function. And where these lines don’t emit the radiance is zero.
For example, if we view the sun’s spectrum from space:
– we see the “Planck curve” of 5780K.
Thanks for the help, but I must demur. Planck-type radiation is a function only of temperature, and predominately caused by temperature, mostly through collisions that cause charges (electrons, or atomic polarization or charge clouds mostly) to accelerate. It is a broadband radiation. Molecular vibration and rotation relaxation is only partly — and indirectly at that — related to temperature through Boltzmann distribution, and is decidedly (very) narrow band, and is predominately a result of molecular transfer of energy from collisions.
Are you implying that CO2 relaxation at 667 cm^-1 say is really blackbody (greybody) radiation with an emissivity of 0.0 over the entire EM spectrum except an emissivity of 1.0 at 667 +/- maybe 0.1 cm^-1? When that molecule relaxes and emits a photon of 1.3×10^-20joules, what would be its equivalent black/greybody temperature, as determined by the black body spectrum and peak intensity?
I don’t have answers to all of this, but something does not add up.
Perhaps I have a terminology problem that you can put me straight on.
In any case, there is no “switching of hats”, the absorption and emission of radiation by the atmosphere is exactly as originally described – by vibrational and rotational excitation and relaxation of gases.
It does turn out that when we have a radiatively-active gas emitting in a band – like CO2 (see spectrum in the article) – that the emission curve in that band looks like the Planck curve for the temperature of the gas where it is primarily emitting from.
What we call this emission is less important than the mechanisms behind this absorption and emission.
Thanks, again. I think it could be semantics. But, I also think that what it is called is important as it implies the wrong mechanism and is misleading. There is a fair amount of controversy over this subject. Saying ‘the CO2 emission curve looks like the Planck curve for the temperature of the gas where it is primarily emitting from’ is like saying a bicycle looks like a 747. There is an element of truth there (and admittedly, I think some of the math does apply to both) but it is far from scientifically accurate and not very instructive.
You say ‘the absorption and emission of CO2 radiation is exactly as originally described – by vibrational and rotational excitation and relaxation of gases.’ [I’m substituting “CO2” for “atmosphere” here] But earlier you said, “…CO2 radiates according to its temperature, in accordance with Planck’s law…” Those two mechanisms are NOT the same. The intensity of radiation from Planck’s law is a direct function of the temperature of the substance and varies smoothly as a function of the wavelength over a wide spectral band. Whether or not CO2 radiates at all from vibration relaxation is somewhat affected by the temperature, but the intensity of the radiation, within tight margins, is precisely the same, whatever the temperature. It radiates in a spectral band so narrow that it can be considered a line in comparison with wideband Planck. Lastly the physical causes or mechanisms are different for these two types of radiation.
I think it important (assuming I am correct) to clearly distinguish between the two — though many do not. This thread is trying to answer questions or skepticism about back radiation. Describing GHG radiation wrongly, either back or forward, detracts significantly from the credibility of the answer, IMO.
Rod B:
Heavyweights like Richard M. Goody “Atmospheric Radiation: Theoretical Basis”, 2nd ed (1989) equate the monochromatic “source function” (emission) with the Planck function (at that wavelength) for non-scattering atmospheres.
However, I’m all for getting details right, so will investigate further.
“…so will investigate further…”
Waiting.
Thanks. Much of the same mathematics (physical formulas) applies to both types of radiation. The basic Planck formula does not (at least very accurately), but Beers, Kirchoff, and others are directly applicable to both. I surmise that over time they have, in our mind, kinda naturally but inaccurately morphed into the same physical mechanism.
[…] Part One looked at the network of stations that measured DLR and some of the measurements, Part Two reviewed the spectra of this radiation, and Part Three asked whether this radiation changed the […]
While waiting, am wondering…
How does an atmosphere at about 300K, which is 99%
non-radiative and the other 1% partially radiative,
manage to output DLR at 300 W/sq m
?
Well I can aswer my own question.
The total quantity of the radiative matter
is completely irrelevant once a certain minimum
is attained. That minimum is the amount
– spread out on the appropriate surface-
which can absorb 300 W/sq m incident
normally on the surface. And that minimum
can be calculated, and it is much less
than the 1% of the atmosphere mentioned.
Additional radiative matter will merely
increase the emission and absorption
fluxes within the material.
But, then again…; no!
300 K is far too low for this balance to hold.
And, of course, this whole line of reasoning
ASSUMES that when some CO2 (for example),
50 meters above the ground, is at a certain temperature
and is absorbing a photon of ground radiation in a limited
window, we may say this is equivalent IN ALL WAYS to
imagining the CO2 as a black-body absorbing in “a
Planckian way” at the same temperature, just
ignoring most of the spectrum.
Which is what you were going to investigate.
And that brings us back to,
…waiting…
I think this is a very good site, the most informative and balanced I have seen on this very polarised subject.
However, I have the same problem as Rod B, and it is simply this. I believe that ALL objects above absolute zero emit electro-magnetic radiation. The spectrum of frequencies that they emit accords with Plank’s Law. Accordingly, this must apply to all gases in the atmosphere, including Oxygen and Nitrogen. If they have a temperature above absolute zero they must radiate. Is this not true?
In the case of CO2, this gas also absorbs and emits radiation at very specific wavelengths around 15 micron. When the CO2 ‘captures’ a photon it changes energy state for a short time and then re-emits the photon on reverting back to its ‘ground’ state. But surely this is a different mechanism to ‘normal’ temperature-linked blackbody radiation?. The re-emission of the photon at 15 micron by the CO2 molecule is not temperature dependent, it will always be emitted at about 15 microns, and at no other wavelength. The time that CO2 holds onto the captured photon is short (less than a microsecond?) and so once it is captured the CO2 must re-emit it fast, irrespective of its temperature. Monitoring radiation at 15 micron uniquely does not provide an indication of the temperature of the source?
Also, I don’t think that the reason all objects emit electro-magnetic radiation is due to them capturing photons, changing energy states and re-emitting the photon. I think this a very special mechanism similar to that which gives rise to atomic absorption and emission line spectra. I believe that the general Plank type emissions are due to the movement of atoms and molecules, the velocity of which is dependent on their temperature.
So I am confused. Why are N2 and O2 not considered to emit radiation? Is it because their emissivities are so small? If they are above absolute zero the molecules move; molecules contain electrically charged particles; moving charged particles generate electro-magnetic radiation. Is this not right?
Mike,
I’ve had similar questions. Here’s one thing I learned that helped a lot. When a molecule absorbs a photon, the relaxation rate is very fast as you’ve noted. What surprised me though is that the collision rate with other molecules is many times faster. So it’s more likely to give up that increased energy to other molecules through kinetic collisions rather than through re-emission of the same energy photon. I’ve seen this described in a number of places, and makes a lot of things fall into place.
A few other thoughts, not sure how correct they are, but in general shouldn’t be too far off and you might find them relevant to some of your thoughts expressed above:
Moving charged particles will generate EM fields, which isn’t the same thing as EM radiation. EM radiation (photons) are emitted due to quantum changes in electronic, vibrational, and rotational energy states. Blackbody radiation is mostly due to the vibrational and rotational changes. Molecules that absorb and emit a lot have many possible states and therefore many possible changes. O2 and N2 don’t have as many possible (I think because of their symmetry and lack of dipole moment). There are many other things at play, including probabilities of photon capture vs reflection and transmission, etc.
There’s a lot to learn and SOD’s site is great. Just start at the beginning, keep reading, and you’ll find lots of answers. The more I read, the more I find that agrees with my university studies and fills in a lot of gaps that have developed in my memory over time.
Hello Mike B (and others), I have been working on the problems you are positing and have found it is the detectors that are putting us wrong – completely wrong. O2 and N2 do have a absorption emission bands (but only one each) at 2338 and 1556 cm-1 respectively, these are predicted by Schrodinger’s QM equation and only observed by Raman (laser) spectroscopy. All early work on radiation is based on thermo-electrics – including Planks work and John Tyndall’s experiment. The so called GHGs are really only the thermo-electric gases: they generate electricity via the thermopile (and the like) and the Seebeck effect. N2 and O2 do radiate – and just as you say – they my otherwise they contradict QM and thermodynamics – it is just that they do not generate with those said detecters
. I am still writing my work, but have started with this. https://www.youtube.com/watch?v=T0IHKKkOwdU&t=4s and https://www.academia.edu/12043014/Reinterpreting_and_Augmenting_John_Tyndall_s_1859_Greenhouse_Gas_Experiment_with_Thermoelectric_Theory_and_Raman_Spectroscopy
Emissivity, in ‘light’ of thermoelectrics will go.I posit is is just a correction factor between the detector and the substance with respect to thermoelectrics.
Mike B:
The graph under the subheading Properties of Gases – Absorption and Emission is from measurement.
I don’t see any experimental claims from you. The HITRAN database (the source of the graph) represents the work of decades of spectroscopic professionals in many countries – from measurements.
It shows that O2 and N2 do absorb – and therefore emit – but in the longwave band their absorption characteristics are around a billion times less than water vapor, CO2 etc.
This is all measurement based. Your comments appear to be belief based.
You ask “ Why are N2 and O2 not considered to emit radiation?” – the answer is because we measure it.
I don’t know whether it is worth writing a long explanation here because this thread probably has very few visitors.
I see a few other recent unanswered questions above, but not really questions, belief in “conceptual” problems over measurements.
Is it worth an article explaining this? I’m not sure. You seem to have belief trumping experiment – that’s how your comment comes over.
Do you understand that the graph is measurement?
Do you think the measurements are all wrong? And if so do you have a basis for this?
Do you have a specific question you would like me to address in a new article that has some kind of basis in theory or experiment – or at least that hordes of other people also subscribe to?
Science of Doom,
Thank you for you prompt reply. Unfortunately you seem attribute motives or beliefs to me which I really don’t have.
I am a physicist, now retired; climate science is not my field but I have taken up an interest in it recently and am seeking enlightenment. I asked questions because I hoped that you would be able help since, as I said, yours seems to be the most informative and detailed site that I have found. I was not trying to suggest an alternative view of my own, just asking for clarification of the one you put forward. I’m sorry this has been misunderstood. I’m sorry if the questions appeared to be assertions but they represent real difficulties that I have.
I do realise that the graphs are from measurement ( and therefore precious) and do not dispute them in any way. I certainly do not have any experimental claims of my own.However, I do know (or think I know) that ALL objects above absolute zero emit radiation ( is this not accepted? ) and that is why I expect all gases in the atmosphere to do this. And I really am confused as to why emission of a photon at 15 micron from CO2 could be temperature dependent. Understand, I am not saying you are wrong – you obviously know more about this subject than me – but I was hoping for some sort of help to understand why.
Mike B
Mike B:
My apologies.
Lots of people show up making claims with no support. After a while it all blurs and I forget everyone is an individual.
Let me think about your questions and see what I can do to explain.
..and whether a new article is better than a few points down here..
Mike B:
A photon of frequency v has energy, E = hv, where h = Planck’s constant.
Quantum mechanics shows that a photon of energy E can only be absorbed if the molecule absorbing can move from one state to another, with the difference in energy between these states = E.
Each of these matches the energy differences between one vibrational / rotational state and another (frequently a combination of both vibrational and rotational states).
It’s quite involved (!) but diatomic molecules like N2 and O2 don’t have the rotational or vibrational states of molecules like water vapor, CO2, O3, CH4 and NO2.
This is why O2 and N2 are mostly transparent to atmospheric radiation, whereas water vapor and CO2 (and other molecules) are strong absorbers.
As Jimwit comments, the collision time is very much less than the “inherent re-emission time”. In the lower atmosphere, collisions take place on average less than a nanosecond apart and these collisions “thermalize” the energy. This means that the extra energy taken on from photon absorption is more likely to be converted to kinetic energy = temperature, which will be shared among locally-based molecules in the atmosphere.
Molecules that are strong absorbers at a given frequency (wavelength) are also strong emitters. This is for similar reasons that explain absorption. Statistical thermodynamics explains the re-emission proportions.
Think of Planck’s law as the theoretical maximum for a body of molecules. The actual emission will be less and will be determined by the temperature and the emissivity at each wavelength.
If this sounds confusing.. it is. This isn’t a simple subject and conceptual models in the end are only models trying to help us “see” what really happens at molecular levels.
We can measure absorption and emission vs wavelength for each gas.
If it is hard to understand, so be it. We can confirm it by quantum mechanics. More importantly, we can confirm it all by measurement.
I don’t think that the point I was making has been fully understood, perhaps because I didn’t make it too well. Allow me one more try.
All objects emit radiation depending on their temperature. The characteristics of this type of radiation are that the power of this radiation is defined by Stephan’s Law, the peak wavelength is defined by Wien’s law and the spectral distribution is given by Plank’s Law. Let’s call this type of radiation ‘Plank’ radiation. All objects emit it and, because it is temperature related, this enables us to determine the temperature of distant stars by studying the spectrum of their emitted radiation (there is an example of a Plank function spectrum in the article above). Note that Plank radiation is continuous over the whole spectrum – approaching infinity asymptotically
Now, what happens in the case of CO2 absorption of long wave infrared? This is a different mechanism. Here the CO2 molecule must first absorb a photon of radiation from somewhere else before emitting. It absorbs exclusively those photons corresponding to a wavelength of around 15 micron. It selectively absorbs those photons because they have precisely the right amount of energy to raise the CO2 molecule from one internal energy state to another (Jimwit, this is where the rotational and vibrational energy comes in – not in Plank radiation). The CO2 molecule can be thought of as being ‘tuned’ to accept this wavelength whilst ignoring others. The absorption of this photon does not depend on the temperature of the CO2 molecule, just on its absorption cross-section. When the photon is absorbed the molecule is said to be ‘excited’. The excited state is unstable and the molecule almost instantaneously reverts to its original state by giving up a photon of exactly the same energy. This is not Plank radiation; it does not have any characteristics of Plank radiation; it is not temperature dependent; it is a distinctly different mechanism. When the CO2 molecule reverts to its ground state the direction of the re-emitted photon is spherically random, meaning that some will be directed back to the earth’s surface and thus represent an extra heating flux which wouldn’t occur without the presence of CO2. This was my first understanding of the greenhouse effect. In fact, the measurements of downward radiation shown in the article seem consistent with this being due to CO2 (because most of it is in the CO2 band)
However, as Jimwit points out, before the CO2 can release the captured photon it is more likely to collide with another gas molecule. If it does this the energy becomes ‘thermalised’. The gas molecule it collides with gains velocity and the CO2 can no longer emit a photon (its energy has been dissipated). Some sources say that the atmosphere is thus warmed because of the atmospheric CO2 but, if the other gases don’t emit radiation there isn’t going to be any ‘back’ radiation from this process.
Because CO2 absorption and emission is not Plank radiation, the amount of radiation that the CO2 emits depends only on the rate that it absorbs photons from some other source, not it’s own temperature.
So my problem was ‘How is it possible to infer a temperature in the upper atmosphere from the intensity of this radiation’? [Some other sources also suggest that this is done].
I could answer my own question but I was really hoping for an independent corroboration.
Anyway, here is my tentative answer from what I can put together. Some sources (a WattsUpWithThat article) say that the ‘thermalistion’ process is actually a two-way process. The ‘excited’ CO2 molecule can pass it’s energy on to other atmospheric gases but it can also become ‘excited’ by colliding with other molecules in the atmosphere. This may fit in with some comments which say that CO2 has a warming effect at low altitude but helps to cool the atmosphere at high altitude. If this is the case, it is then possible that the rate of CO2 emission is dependent on the temperature of the upper atmosphere.
Is this what happens? – or is everyone lost?
Mike B:
I think you are confused.
There is only one kind of radiation.
Planck’s law defines the theoretical maximum spectral intensity at each wavelength. The actual intensity depends on the ability of that body to emit – this is called its emissivity which is a wavelength dependent material property.
A blackbody has an emissivity, ε = 1.
In practice no material has ε = 1.
For example, the ocean has ε=0.96 (for longwave).
Here is an extract from Fundamentals of Heat and Mass Transfer, Incropera & DeWitt (2007):
Liquids and solids tend to have continuously varying emissivities (but not equal to 1).
Gases do not.
“For example, the ocean has ε=0.96 (for longwave).”
That’s probably for shortwave. Longwave is 0.98-0.99, right?
This is for longwave.
The reflectivity for shortwave is about 10%, which means the absorptivity = 0.9. Of course, even though also equals the emissivity, the ocean would need to be around 5800K for this to be a useful parameter for emission of thermal radiation.
Mike B:
No, this is not true.
1. If the CO2 molecule absorbed absolutely nothing it will still emit.
A body of CO2 molecules will emit radiation at specific wavelengths because energy transitions take place between different rotational and vibrational states.
When a molecule moves from a higher energy state to a lower energy state it emits a photon of energy, E = E2 – E1 = hv, where E2 and E1 are the energy states, h = Planck’s constant and v = frequency.
This is Planck radiation just as much as the ocean emitting radiation.
It does not need to absorb a photon of this energy to emit a photon of this energy.
As an aside, obviously, if the body of molecules continues to emit radiation without absorbing any energy from elsewhere it will cool down.
2. “It absorbs exclusively those photons corresponding to a wavelength of around 15 micron.” – no, CO2 absorbs in many bands, including around 4um. And the 15um band stretches from 12-19μm.
[…] […]
[…] […]
[…] will have those characteristic CO2, O3 and water vapor peaks that were shown in DLR spectra in Part Two. [QUOTE] That he did not even bother to do a spectral analysis, which could have singled out his […]
Not only not single out they missed ~20Wm-2 atmospheric absorption. Do over!
To disperse fuzzy thinking (mine and others’), I need to have all the important assumptions in the open, with some info on which are safe ones. My questions are probably in the “everyone knows” category unavailable to the amateur.
A quick scan indicates the flux and radiance data in question comes in sets which are far from raw, the production of which is clearly down to a fine art, with no technical detail of measurement (that I can find).
SoD above shows that something I’ll loosely call the sky radiates generally downwards. The spectra show that this is far from blackbody (BB). SoD also warns that real (non-BB) things may deviate in spectrum, direction, or both. NASA’s AIRS satellite experiment handles this by transverse scans of a narrow beam (to 49° off nadir) and reporting all spectra, leaving the “averaging” for others. Frank above, in otherwise detailed accounts of surface measurements, doesn’t supply this info.
My guess is that there are two basic types of sensor: Narrow-beam, and hemispherical. Unless the former is scanned, it must be fixed (vertically?) and its limited response assumed representative of the whole sky. The latter reverses this, assuming the aggregate over the 2pi steradians applies to the zenith. I see mention of the pyrgeometer for whole-sky flux measurement. In practice, I wonder if this type is optically limited to just short of the horizon (edges tending to be difficult), with a correction factor for this applied.
Somewhere, somewhen, someone has shown that
a) Hemispherical sensors are linear down to the horizon
b) My ‘sky’ is isotropic at all wavelengths and all angles (and times).
Can anyone report (or point to) these?
Interestingly, JPL’s Ask_AIRS tells me early tests showed no spectral variation with scan angle for the view from above. Does the same rule apply to that from below?
I’ll explain my reasons for asking later.
Pyrgeometers do not have hemispherical detectors. They have a hemispherical dome transparent in the thermal IR (~4-50 μm) covering a flat plate with high absorptivity in the thermal IR. The amount of radiation from the sky seen by a flat plate parallel to the ground is a function of cosine(θ) where θ is the angle measured from the zenith. That means radiation from the horizon contributes nothing and radiation from just above the horizon contributes very little.
For measuring incoming solar radiation there are pyrheliometers and pyranometers. A pyranometer is similar to a pyrgeometer in that it has a flat plate detector meant to be oriented parallel to the ground and a dome cover. A pyranometer thus measures both diffuse and direct solar radiation. A pyrheliometer has a narrow angle of acceptance and is mounted on a tracker to keep it pointed directly at the sun so it measures only direct solar radiation.
Rip,
“Does the same rule apply to that from below?
I’ll explain my reasons for asking later.”
There are local emissivity changes documented which have created issues mainly at the poles. Not really sure why. The south pole flux readings seem to be showing some magnetic interference. With temperatures that low, and extreme inversions, up to about 40 C, that’s a huge inversion, it is hard to tell what is going on.
There were some oddities I noticed in the tropopause with deep convection cloud tops. Those were in temperature ranges of -90C which showed the Atmospheric window spectrum. Lots of stuff seems to be going on between -50 and -100C.
U of W Milwaukee is doing a lot of work on the local emissivity variance which could have a number of causes.
Ta DeWitt Payne & Capt. Dallas
It appears then that the pyrgeometer is designed on the assumption that LWR is isotropic, and reads true only for such. The response at an angle to the zenith varies as sinX.cosX, which is maximum at 45° (not the zenith). Consequently…
I was expecting a group of “everyone knows…” responses exposing my ignorance. The lack of such encourages me to share a line of thought (bear with me, it has to be built):
Imagine we have wideband eyes. Blackbody(BB) radiation becomes visible, and greenhouse absorption bands become characteristic colours.
Through an ideal atmospheric window, the Earth’s surface should appear essentially flat; brightness will vary with local emissivity and insolation, but not with viewing angle (I’m temporarily neglecting clouds). The Sun appears as a flat disc rather than a sphere for two reasons: near-perfect BB isotropy, and a sharp increase in density and opacity with depth through the photosphere. Were this not so, we would see deeper and so brighter in the centre of the image; this isn’t observed (at least by naked eye).
In one of the greenhouse colours, the Earth’s surface (or the sky from below) will be invisible. If opacity here also rises sharply, the effective depth (or rather altitude) of the ‘fog’ will vary little with angle, and the image down (and up) also be close to a featureless disc.
But between these extremes (at the edges of the “window”) we would see a thin ‘fog’. Downward, the surface would be visible, but not at large viewing angles. Towards the horizon, we would ‘see’ to progressively higher altitudes, and so lower temperature and brightness – “limb darkening”. As typical lapse rate is around (vertical) 150m/K, this should readily be detectable by modern instruments. Conversely, from below the 2.7K CMB should be visible overhead, and limb brightening observed.
Apparently, systematic variation with angle is not observed, leaving us with three alternatives:
> Those assembling the vast banks of climate data have been careless (most unlikely);
> I’ve missed something (likely, but I don’t see it);
> SoD (with other climate modellers) has missed something (?).
I need help, in the form of hard facts, preferably from direct observation.
I operated a weather station for years and the intensity of radiations at night is close zero. I suggest that you check your sources. I tried to check your sources but they are unavailable.
If the intensity of radiation at night is about equal to that during the day, then why there is so much difference in land temperature between night and day?
Nabil,
You need to provide some details.
Location, equipment used for measurement, specification, frequency response, calibration certificates, who else verified this amazing result.
Perhaps your pyrgeometer was broken, or not turned on.
Seeing as well-calibrated pyrgeometers in numerous locations around the world measure the values of DLR every few minutes, and these measurements also match the integration of the spectral results measured by well-calibrated FT-IRs you will start a revolution in atmospheric physics if you can reproduce your results.
I think you are referring to the atmospheric radiation, not the total radiation. The sun makes a considerable difference. That’s why daytime is much warmer.
This paper is deceptive. Look at this statement:
“Water vapor – as you can see above – absorbs across a very wide range of wavelengths. But if we take a look at CO2 and water vapor in a small region centered around 15μm we can see how different the absorption is:”
and then they show us 15 mikes, so we think CO2 is a stronger absorber/radiator.
Why do they cherry pick 15, the center of a CO2 band? Why don’t they show us 7 mikes, the center of an H2O band and CO2 window.
Why do they always lie to us?
Your claim that this is deceptive appears to have no merit. Did you not notice the absorption curves from less than 5 to 30 μm for water vapor, CO2, O2 and N2? I don’t see any cherry picking or lying there. CO2 makes a significant contribution to downward emission at 15 μm. It doesn’t at 7 μm. So what? The emission from water vapor is still there and I don’t see anyone here claiming that water vapor isn’t a significant greenhouse gas.
Not to mention that the vast majority of the emission energy from the atmosphere comes from wavelengths longer than 7 μm. The MODTRAN plots, for example, only go to 1500 cm-1 or 6.68μm.
Morgan,
If you want to stay around and learn something about climate science, maybe start with Water Vapor vs CO2 as a “Greenhouse” Gas – which gives a lot of examples from climate science books and climate science papers where water vapor is acknowledged to be the strongest greenhouse gas. It isn’t in dispute.
It is so well known and acknowledged that (in real climate science) much of the time no one even bothers to mention it.
Then take a look through the whole series Visualizing Atmospheric Radiation where you can get to understand the respective roles of CO2 and water vapor in changing terrestrial radiation as it travels through the atmosphere.
And before posting your next edifying comment, please check out the Etiquette.
I have been working on the problem of radiation and have found it is the detectors that are putting us wrong – completely wrong. O2 and N2 do have a absorption emission bands (but only one each) at 2338 and 1556 cm-1 respectively, these are predicted by Schrodinger’s QM equation and only observed by Raman (laser) spectroscopy. All early work on radiation is based on thermo-electrics – including Planks work and John Tyndall’s experiment. The so called GHGs are really only the thermo-electric gases: they generate electricity via the thermopile (and the like) and the Seebeck effect. N2 and O2 do radiate, they must otherwise they would contradict QM and thermodynamics; it is just that they do not generate with those said detecters
I am still writing my work, but have started with this. https://www.youtube.com/watch?v=T0IHKKkOwdU&t=4s and https://www.academia.edu/12043014/Reinterpreting_and_Augmenting_John_Tyndall_s_1859_Greenhouse_Gas_Experiment_with_Thermoelectric_Theory_and_Raman_Spectroscopy
Emissivity, in ‘light’ of thermoelectrics will go.I posit is is just a correction factor between the detector and the substance with respect to thermoelectrics.
*sigh*
See the post titled Etiquette
The field of infra-red spectrometry is considered basic science. Your rantings are not. Raman spectrometers, by the way, use the same type of detectors as absorption and emission spectrophotometers. Photons are photons whether scattered inelastically (Raman) or emitted.
I don`t really know the relevance of this, but perhaps Blair is making storm in a glass of water.
“In remote sensing applications, such as the applications of differential optical absorption spectroscopy (DOAS), atmospheric scattering processes need to be considered since they can modify the observed spectra. Inelastic scattering of photons by N2 and O2 molecules can be observed as additional intensity, effectively leading to filling-in of both, solar Fraunhofer lines and absorption bands of atmospheric constituents. The main contribution is due to rotational Raman scattering, which can lead to changes in observed optical densities of absorption lines up to several percent. Measured optical densities are typically corrected for this effect (also known as Ring Effect). In contrast to that Vibrational Raman scattering of N2 and O2 was often thought to be negligible, but also contributes to this effect. We present calculations of Vibrational Raman cross-sections for O2 and N2 for the application in passive DOAS measurements”
On the impact of Vibrational Raman Scattering of N2/O2 on MAX-DOAS Measurements of atmospheric trace gases, 2015.
Lampel, Johannes; Zielcke, Johannes; Frieß, Udo; Platt, Ulrich; Wagner, Thomas
Clearly stated: “Measured optical densities are typically corrected for this effect (also known as Ring Effect)”
nobodysknowlegde,
Blair’s comment is almost entirely gobbledegook. O2 and N2 do have vibrational bands, but they are not absorption bands since they do not absorb IR. Sunlight is scattered by molecules, that accounts for nearly 30% of the reflection of light by the planet. Short wavelengths are scattered much more strongly than longer ones (the sky is blue). The scattering is mostly elastic, with no change in the energy of either the photon or the molecule. A small fraction is inelastic (Raman scattering), with energy exchanged between the molecule and the photon; the change in energy of the photon can be either positive or negative and is usually small and the change in energy of the molecule can be in either the rotational or vibrational state and does not require IR absorption to occur. There are few thing for which Raman scattering in the atmosphere actually matters.
Thank you for the explanation Mike M. So the scattering of LW radiation by O2 and N2 should be a part of the backradiation by a kind of reflection from the atmosphere. Perhaps so small part that it doesn`t matter. Although, nice to know.
nobodysknowledge wrote “So the scattering of LW radiation by O2 and N2 should be a part of the backradiation by a kind of reflection from the atmosphere. Perhaps so small part that it doesn`t matter. Although, nice to know.”
Yes. And definitely too small to matter. At 0.475 micron (blue light) about 20% of the incoming solar is scattered. Molecular scattering varies as the inverse cube of wavelength. So at 15 micron, it would be a factor of 30,000 weaker; that would be 0.0006%. Total scattering would be quite a bit larger since scattering by small particles is not as wavelength dependent. But I am pretty sure it is still tiny.
Mike M.,
On a clear day with the sun close to directly overhead, ~85% of radiation striking the ground is direct and 15% is diffuse, scattered by molecules and particles. I haven’t been able to find any numbers on how much is molecular and how much is particulate. Diffuse radiation can be as little as ~7% or as high as 40% of the total insolation when the sun is close to the horizon.
Here’s the spectrum of clear blue sky (I hope):https://en.wikipedia.org/wiki/Diffuse_sky_radiation#/media/File:Spectrum_of_blue_sky.svg
I wonder if atmospheric warming leads to more scattering. It would be intuitively more water vapor, reaching a bit higher, and becoming a bit colder. And ice crystals and small water droplets are scattering more and absorbing less than water vapor, and give stronger albedo. This could be a case of an iris mechanism.
Blair: A photon of a particular wavelength doesn’t “know” anything about the molecule that emitted it. When it arrives at a detector, it doesn’t know whether it came from a CO2, an H2O or an O2; nor what the “temperature of the emitting molecule” was. (Technically, temperature is the mean kinetic energy of a group of colliding molecules, which not a property of a single emitting molecule.) Therefore, when a photon of a particular wavelength is absorbed (or scattered) by a detector, the signal produced is independent of the nature of the photon’s source, including its temperature. All detectors (including photomultiplier tubes, photosensitive semiconductors, thermopiles, etc.) have a continuous response to changes in wavelength. Therefore, our technology detects ALL photons important to radiative heat transfer in our climate. Furthermore, we can also calibrate one type of detector against another. No photons are “lost”, “missing”, or “undetectable”.
Visible and infrared electromagnetic radiation interacts with the electrical dipole moment of molecules, which is negligible for symmetrical molecules like N2 and O2. Visible and infrared absorption and emission from these molecules isn’t “missing”, it simply is very WEAK. However, when a symmetrical molecule is colliding with another molecule, it can transiently have a small dipole moment. This (and similar phenomena) produce the weak lines of O2 and N2. To detect these lines directly, we either need an absurdly long path length or we need to study them at high pressure (which changes their absorption lines). Atmospheric scientists know about these weak absorptions, but usually don’t discuss them in the context of climate. Despite the abundance of N2 and O2, their effects are negligible compared with H2O, CO2 and CH4.
Normally, a molecule changes its vibrational, rotational and electronic state by absorbing or emitting a photon with EXACTLY the energy difference between two states. Raman spectroscopy uses a different phenomena – scattering – to detect different energy states in molecules that have weak dipole moments. (The sky appear blue because blue visible light is scattered more than other colors. Nothing in the sky itself emits blue light we see. That light came from the sun and was scattered towards our eye.) As Mike M describes, when visible photons are SCATTERED by gases, a small fraction of the scattering can be “inelastic” – meaning that a small fraction of the scattered photons have a different wavelength after scattering than before. This difference in energy has gone into changing the vibrational and/or rotational state of the molecule that inelastically scattered the photon. Only about 1 in 10,000,000 scattered photons is scattered inelastically, but we have powerful lasers, optics and detectors that can observe a few inelastically-scattered photons. Detecting absorption of 1 out of 1,000 photons (99.9% vs 100% transmission) is challenging. So Raman spectroscopy allows us to learn absorption lines far too weak to modify heat flux by thermal infrared in the atmosphere.
I am in need of measured spectra of downward long wave radiation. I have an ongoing discussion with several of my friend that content that the GHG effect is non-existent or at most inconsequential. They say that there is no evidence that CO2 is a factor in downward long wave radiation. The say that there are no measurements of a CO2 effect. Indeed, finding the actual finger print of CO2 is hard to come by. I have talked with the NOAA people about the SURFRAD program and they say that they only measure total downward radiation. Similarly, the CERES people tell me that the outgoing measurements of energy by their satellites measures only the total energy leaving the Earth. To me, this leaves a big hole in the GHG effect theory.
Your posting of “The Amazing case of back radiation” has one claimed to be “Measured Spectra of Downward Longwave Radiation”.
This section has several spectra measurement.
Your posting CO2 An Insignificant Trace Gas? Part 1 has four sited to actual measured spectra in Figure 6.3, Figure 2.9, Measured and theoretical spectra (from Goody and Yung) and, “Spectra of Zenith Atmospheric Emissions (Wisconsin, Ellington and Wiscombe).
At one time when reading your excellent postings, thought I remembered a response to incoming comments, you were going to or had provided access to many measured spectra of downward long wave radiation. I failed to find that in my re-reading. Perhaps my diligence was not as good as it should have been.
So, could you supply me with links to the measured spectra. I am somewhat surprised the data seems to be about 20 or more years old. Why are SURFRAD and CERES not making the measurements. I know the cost of the equipment is very high. But in SURFRAD’s case, it would not need to do it at all of the stations.
cbdakota,
Do your friends believe the actual measurements of longwave flux measured at the surface? If so, where is the downward longwave flux coming from?
If you look at Part One of this series you can see that we have large numbers of measurements of longwave flux.
These measurements match the calculations. How are the calculations done? By using the Planck law of emission (which depends on temperature) modified by the emissivity of the atmosphere at each wavelength. The emissivity at each wavelength is calculated from the absorption lines of each gas and the amount of each gas.
Why aren’t there large numbers of spectral measurements at the surface published in papers and produced daily by some climate body? The people who did the measurements (for example those shown in this article) are doing them to verify some specific details, and getting FTIR measurements is expensive. No one is any doubt that the spectrum matches the theory. (When I say “no one”, I mean no one who understands radiative physics and has any knowledge of the absorption properties of CO2, water vapor and methane).
Did you notice that there is a large peak at 15μm in each spectra shown? Where do your friends think it is coming from?
What do your friends believe is the correct formula for the surface radiation as a function of wavelength?
Usually people who doubt the existence of atmospheric CO2 emission received at the surface don’t have a clue about the radiative transfer equation, well known for at least 65 years. See Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. I’ve yet to have someone explain what is wrong with these equations and there’s a reason why. The “skeptics” don’t have a clue how to derive the equation of radiative transfer and have probably never even seen it.
Perhaps your friends “think” the equation is spot on but believe that the last few decades of papers in Journal of Quantitative Spectroscopy and Radiative Transfer are all bogus? Just in case, here is a link to the papers behind the HITRAN database.