A lot of people have asked about this. I haven’t been so interested in the subject, but because I came across it in a paper I thought I would post it.
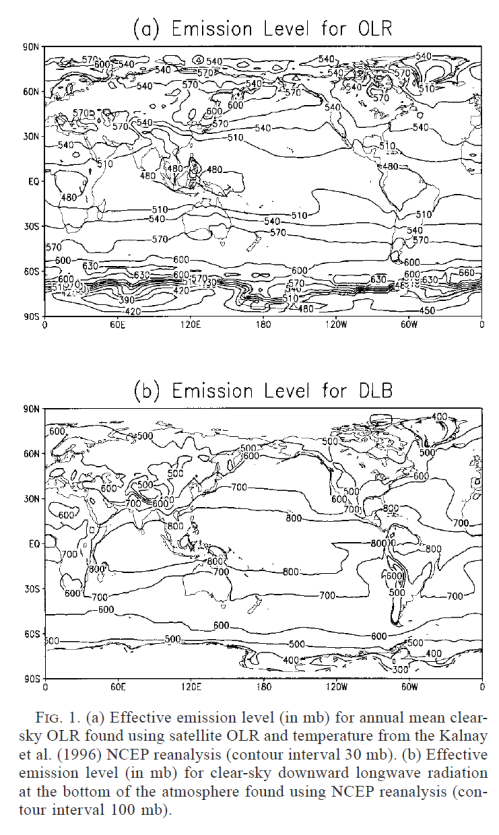
What is the effective height of outgoing longwave radiation? I.e., the radiation from the climate system that leaves the planet.
What is the effective height of downward longwave radiation as measured at the surface?
By effective height we mean that there isn’t just one level that radiation comes from, so it is the average height.
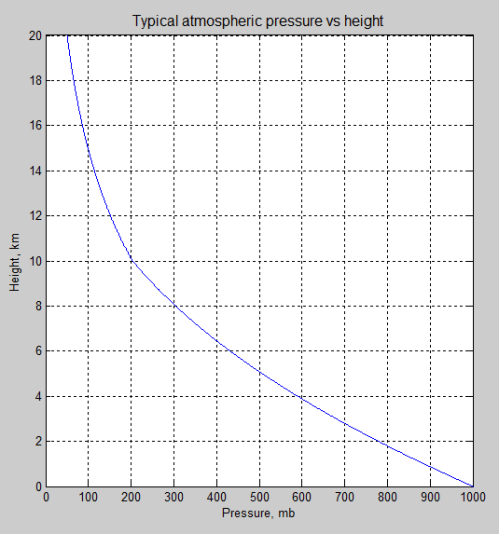
For reference here is a typical pressure vs height comparison (this one is calculated, using the standard hydrostatic equations and ideal gas laws):
So in the tropics the typical emission height of DLR we receive at the surface (called DLB in the paper) is just under 2km and in the mid-latitudes and poles it is around 5km.
Likewise for the OLR, the typical height is around 5km in low latitudes and 4km near the poles.
How is this calculated?
Here the effective emission level is defined as the level at which the climatological annual mean tropospheric temperature is equal to the emission temperature: (OLR/σ)1/4, where σ is the Stefan–Boltzmann constant.
The effective emission level for the downward longwave radiation at the ground is analogously defined as the level at which the climatological annual mean tropospheric temperature is equal to (DLB/σ)1/4 , where DLB is the clear-sky downward longwave radiation at the bottom.
Reference
Tropospheric Water Vapor and Climate Sensitivity, by Schneider, Kirtman & Lindzen, Journal of the Atmospheric Sciences, 1999


Mmmm … well, my copy of Geiger’s “The Climate Near The Ground” begs to disagree. It says that 72% of the DLR at the surface comes from the lowest 87 metres of atmosphere. Another 6.4% comes from the next 89 metres, 4% from the 93 metres above that, 3.7% from the next 99 metres, 2.3% from the next 102 metres, and 1.2% from the next 105 metres.
This means that some 90% of the DLR is coming from the first (lowest) 578 metres of atmosphere …
Don’t know why your figure should be so different from Geiger’s, but the Geiger text cites actual measurements rather than e.g. NCAR reanalyses …
w.
Is Geiger necessarily inconsistent with that definition of effective height? If my reading is correct, the definition of effective height remains agnostic about where the radiation in fact originates from; it just says, Let’s come up with a temperature that corresponds to the radiation intensity and then find the altitude where that temperature prevails. Of course, the atmosphere is sparser as a radiator than a black body, so one should not be surprised that the radiation intensity is as of a black body farther away than the (somewhat transparent) atmosphere.
Since you have characteristically shown insight with which I am blessed only in my fantasies, I’m sure I’m missing something, but I’d be obliged to find out what it is.
You can actually get rough estimate of the DLR height from Kiehl and Trenberth’s figures. With Tg=ground temp=287K,
Te=emission temp
396 W/m2 up = σTg^4
333 W/m2 down = εσTe^4 ε=emissivity of air
Te/Tg=(333/396/ε)^.25=0.9576/ε^.25
If ε=1, Tg-Te would be about 12K, which at a lapse rate of 6K/km is about 2 km. But of course ε is less than 1 because of AW etc.
In fact, a reasonable way of allowing for it would be to deduct K&T’s 40 W/m2 AW flux;
then Te-Tg comes down to 4.75K, and the height to about 800m.
But that’s averaged over all skies, clear and cloudy. Clear would be higher.
I think SoD’s figure of 5km mid-lat is high. 700mbar is about 3km. Remember over land that mb converts to height asl; you have to deduct altitude.
I think the atmospheric window is the key to Willis’ paradox. Yes, 72% of radiation received came from <87m etc. But a chunk of the spectrum is black – the AW, in clear sky about 1/4. This is 0% of radiation received, but it’s big in determining the reduction of DLR relative to air temp. And it’s from that reduction that you calculate the effective height.
On further thought, I think I should retract that AW adjustment that used the reduced 356 W/m2 and led to a 800m height. It’s inappropriate gray-body thinking.
Willis Eschenbach
I’ve had a look at the online portion of that book before and it looks very good.
What page is that from? (maybe I can read it online..) And do they explain their methodology?
The Lindzen paper is really about water vapor in the atmosphere, this calculation isn’t a central feature of the paper. Perhaps they are wrong. Perhaps there are different definitions of this parameter.
On the NCAR reanalyses – a real measurement would always be better than a reanalysis, but I’m guessing some “interpolation” is necessary to calculate (annual average) temperature at each height at each location around the globe..
Rereading the methodology of the Schneider/Lindzen paper I’m not so happy about the “meaning” of their result.
I need to think about it some more – hopefully some additional data – like the approach from Geiger – can provide some enlightenment.
It appears that Schneider et al assumed a sky emissivity of 1.0. BZZT. That resulted in emissivity temperatures that were too cold and pressure altitudes that were too high.
Does this mean you are preparing to finally post your analysis of Miskolczi’s Theory?
David44:
No, it means I am reading lots of papers on water vapor for Part Two of Clouds and Water Vapor
Still, good preparation for having a go at Miskloczi.
The altitude numbers, which derive from the temperature numbers, which in turn derive from OLR and DLR numbers, present a puzzle. They reflect what the K&T energy budget shows, DLR>OLR at the surface and TOA, respectively. But, given (a) the nature of radiation which progresses equally in all directions and implies that at source DLR=OLR, and (b) atmospheric attenuation, which varies directly with density and distance, lower for OLR than for DLR (if these originate around mid-troposphere), then OLR at TOA should exceed DLR at the surface. The puzzle is resolved when DLR is expressed in net terms as negative 26 Wm-2, being the heat transported from the surface to the atmosphere by radiation as implied in K&T. Assuming emissivities equal to unity (where has justification for this ubiquitous assumption in climate science been demonstrated?), the effective temperature of DLR is seen to be about 5K cooler than the surface, putting the effective altitude at less than a kilometre and in accord with Geiger. Presumably, atmospheric attenuation of OLR originating from this low altitude could plausibly reduce OLR flux from about 360 Wm-2 at source to 195 Wm-2 at TOA?
The simplified surface energy budget would read 168 Wm-2 in from the sun balanced by 102 of non-radiative transport to the atmosphere, 26 radiative transport to the atmosphere and 40 Wm-2 radiative transport to space. The atmosphere balance would read: 67 Wm-2 in from the sun and 128 from the surface offset by 195 Wm-2 radiated to space. Gone would be the controversial back-radiation and attendant “problem” with thermodynamic laws, we wouldn’t have to weary our brains with all those thought experiments and we’d all be friends again!
Fig 11-1 from Geiger seems to confirm Aa=Ed, the paradigm of Miskolczi;
http://books.google.com.au/books?id=KaJHBv9FbYIC&printsec=frontcover&dq=Geiger%E2%80%99s+%E2%80%9CThe+Climate+Near+The+Ground%E2%80%9D&source=bl&ots=2vWksoLUjX&sig=uzVQx1QlpuuIgcLfqjFI7x7-Eas&hl=en&ei=t_1oTJy5B5DCcYLg3awP&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBQQ6AEwAA#v=onepage&q=Geiger%E2%80%99s%20%E2%80%9CThe%20Climate%20Near%20The%20Ground%E2%80%9D&f=false
[sorry about the long url]
The diagram and accompanying Tables show the lapse rate of temp from the surface to what appears to be 51 metres; averaged over the 24 hours at different seasons there appears to be an equivalence but I haven’t done an exact calculation.
In addition, while I initially thought Geiger’s findings about the relatively low height of the bulk of backradiation was a contradiction to CO2 being evenly mixed and a possible confirmation of CO2 saturation, it would be merely consistent with S-B’s law because the lower CO2 backradiation is at higher temperature than the backradiation from higher up.
Roy Spencer discusses some “backyard experiments” capable of detecting DLR at:
http://www.drroyspencer.com/2010/08/help-back-radiation-has-invaded-my-backyard/#comments
scienceofdoom
That’s on page 21 of my version of Geiger (sixth edition). Inter alia it says:
followed by the numbers that I gave. They go on to say:
The citation is given as “Czepa, O., and Reuter, H., Uber den betrag der effektiven Ausstrahlung in Bodennahe bei klarem Himmel, Arch. f. Met. (B) 2, 250-2589, 1950.” Which doesn’t help me one bit, but might help someone.
Geiger is a resource well worth buying …
Willis,
I think the confusion results from whether you look at the brightness temperature of the integrated DLR spectrum or the brightness temperature of the most intense parts of the spectrum. The brightness temperature of the most intense part of the DLR spectrum for the US standard atmosphere is close to 288 K, the same as the surface temperature. There’s a big hole, however, from 800 to 1200 cm-1 that has a brightness temperature below 220 K. The low intensity in that region means it doesn’t contribute much to the total, but it does reduce the integrated brightness temperature a lot. If you then convert to a blackbody spectrum that would emit the same integrated flux, the effective pressure becomes much higher.
If we look at the MODTRAN calculated spectrum for the 1976 U.S. standard atmosphere for standard conditions at 0 km looking up we see 258.673 W/m2 flux from 100-1500 cm-1. For a blackbody emitter, adding in the tails from 5-100 and 1500-3000 cm-1, you get a brightness temperature of 265.1 K, which corresponds to a pressure of about 660 mbar or an altitude of ~3.5 km. For the Tropical Atmosphere, the effective pressure level is about 800 mbar or a little over 2 km. So saying that 90% of the DLR comes from below 600 m does not contradict the Schneider, et.al. graph.
The effective pressure becomes lower and the effective altitude becomes higher.
I found this page by luck.
I’ve been playing around with my new IR thermometer, measuring DLR.
But I’ve been reading at least 41.5C colder (min over range of -40C) than the surface on a clear 1.5C day. That has to be pretty high up, and it’s way more than 5K. But at that temp most of the water vapor has been removed from the atm.
I’ve also noticed a lot of max over range of 320C both nearer the Sun (expected), but also on the other side of the sky, where in between it reads min scale of -40. I’m presuming it’s detecting a reflection of Solar IR, maybe off the 4u Co2 absorption band.
I’m curious on your thoughts?
MiCro,
The acceptance cone of an IR thermometer is fairly large. Are you sure you’re not including part of the surface? Clouds are effectively black bodies and will emit at the temperature of the altitude of the base of the cloud. Molecular scattering of IR is normally negligible and I think IR thermometers don’t see wavelengths as short as 4 μm. You can use a handheld IR thermometer to measure vertical column water vapor.
No, I’m sure, I’ve done it 3-4 different times on clear days, and a few times with partly cloudy skies. While taking measurements, I’ve scanned the sky in various directions, and have pretty low horizons in all directions. I can tell when I’m pointing at a cloud, or missing it, and I’ve scanned various objects on the surface to get a feel for what and how it reads.
But being winter time, I’ve not had any warm days to really play with and get an actual measurement (something other than min scale).
Thanks for the link, it’s printing now.
I’m planning on following up with Ryobi, to see what info I can get on the thermometer as well.
Furthermore, unlike Doors made up of fiber glass or the tinted glass
that blurs the vision. That being accomplished, it is recommended that you consult your nearest double glazing company.
Make sure a record is kept of where the resume
and cover letter is sent, and of varying sizes at that – such as a home office.