Without a firm grasp on the basics it can be hard to choose between a good and bad explanation.
In The Hoover Incident I explained what would happen if the atmosphere didn’t absorb or emit radiation – i.e., if the radiatively active gases were “hoovered up”. Have a read of that post for a full explanation, but the essence of it is that with no atmospheric absorption or radiation the surface would be radiating around 390 W/m² into space while receiving only 240 W/m² from the sun. Therefore, the earth would cool down until it was only radiating 240 W/m² (it’s slightly more complicated) – leading to a surface temperature around -18°C (255K).
One of the statements I made was:
And no matter what happens to convection, lapse rates, and rainfall this cooling will continue. That’s because these aspects of the climate only distribute the heat.
Nothing can stop the radiation loss from the surface because the atmosphere is no longer absorbing radiation. They might enhance or reduce the cooling by changing the surface temperature in some way – because radiation emitted by the surface is a function of temperature (proportional to T4). But while energy out > energy in, the climate system would be cooling.
Recently, one commenter said in response to this (but in another article):
Convection etc distributes the heat in ways that affect radiative heat transport from the surface. While the intensity of radiation is a function of temperature, radiative heat transport is a function of a temperature difference. No heat may be exchanged between regions with the same temperature.
In an isothermal atmosphere there would be no temperature difference between it and the surface and therefore no heat loss from the surface. The accumulation of heat in a radiatively-constrained atmosphere by non-radiative means of heat transport from the surface would produce an isothermal atmosphere. Then, energy out = 0 and < energy in and the climate system would be heating.
The comment is confused, so I thought it was worth explaining in some detail.
Radiation and Temperature
Here is the starting point for the Hoover Incident: 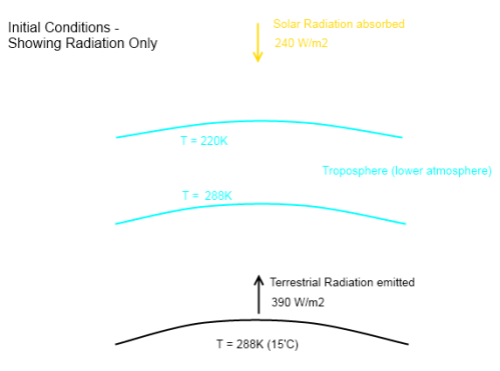
This isn’t showing any heat transfer by conduction or convection, to keep the diagram simple.
The blue area – the troposphere, or lower atmosphere – is shown with a gap between it and the earth’s surface. This is just to make heat transfer values clearer – there isn’t really a gap. Notice that no radiation is emitted by the atmosphere (because this is a thought experiment where radiatively-active gases have been “hoovered” up).
Note as well that we are looking at averages in this diagram. The solar radiation absorbed in any one places is very rarely 240 W/m² – at night it is zero, and at midday in the tropics it is closer to 1000 W/m². If you want to understand why the average value of solar radiation absorbed is 240 W/m² take a look at Earth’s Energy Budget – Part One.
Rather than thinking of this as the average, if it helps, simply think of this as the heat transfer for one location where these are the actual values.
The equation for the emission of thermal radiation by the earth’s surface is only dependent on its temperature and emissivity. The equation is the well-known Stefan-Boltzmann law:
j = εσT4
where ε=emissivity, σ=5.67×10-8, T is temperature in K and j is energy per second per unit area (W/m²)
Emissivity is a value between 0 and 1, where 1 is a “blackbody” or perfect radiator. The surface of the earth has an emissivity very close to 1. See The Dull Case of Emissivity and Average Temperatures.
Now regardless of any heat transfer by conduction or convection with the atmosphere, the surface of the earth will continue to radiate in accordance with that equation. With an emissivity of 1, a surface of 15°C (288K) radiates 390 W/m².
Emission of thermal radiation is independent of any other heat transfer mechanisms and only depends on the temperature of the body and its emissivity.
Now the earth also absorbs solar energy by radiation. So for our initial conditions, the net heat transfer by radiation,
Hrad = 240 – 390 W/m² = -150 W/m² (i.e., a cooling of 150 W/m²)
The only heat transfer mechanism in a vacuum is radiation and therefore heat can only be transferred into and out of the total climate system by radiation. In our thought experiment the atmosphere is unable to absorb or emit radiation.
Therefore the solar energy absorbed at the surface minus the energy radiated from the surface of the earth gives the net heat transfer for the entire climate system.
Radiation, Sensible and Latent Heat
Now with the particular example above let’s add heat transfer between the surface and the atmosphere by conduction and convection. This is often termed sensible heat. Gases have a very low thermal conductivity, so most heat will be transferred by convection (bulk movement of air). This will also include latent heat, which is the heat used in evaporation of water from the surface of the earth.
There is no simple formula for convection because it depends on many factors including the speed of the air movement. The formula for latent heat removal is also complex. So to get started we will use the average value derived by Kiehl and Trenberth in their well-known 1997 paper. Note that their calculation of latent heat was derived from the amount of rainfall (what comes down, must have been evaporated up in the first place).
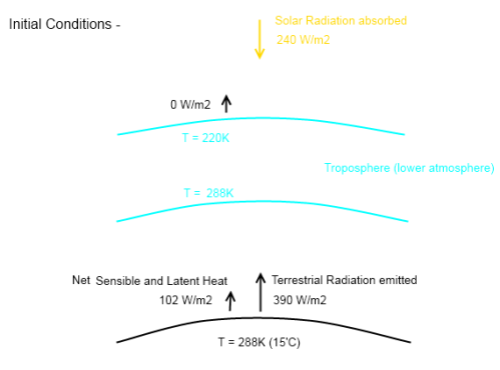
Here is the updated diagram, still showing the initial conditions, just after the Hoover Incident has taken place:
Note that the conduction and convection from the atmosphere into space = 0 W/m².
And with conduction and convection it is conventional to show the net flow of heat – which is why there is no arrow with heat from the atmosphere to the surface. (With radiation, because heat is exchanged across distances it is more usual to show radiation emitted from each body).
What happens now?
To calculate dynamic processes is more difficult, especially if we wanted to do it for all points on the earth.
What everyone should be able to see is that the surface of the earth is losing heat.
If we use the value from K&T for sensible and latent heat removal, we can see that net heat transfer from the surface of the earth at time = 0 is now 252 W/m². That is, a cooling of 252 W/m².
Let’s consider the atmosphere. It is gaining heat from the surface of the earth, and not radiating it into space (or back to the surface), because in this post-Hoover world we have an atmosphere with no ability to emit radiation.
Therefore, within a relatively short space of time, the heat transfer (averaged around the globe) between the surface of the earth and the atmosphere will drop to almost zero. If the atmosphere heats up and the earth’s surface cools down – the result has to be that this heat transfer reduces.
But whatever happens to the temperature difference and heat transfer between the atmosphere and the earth’s surface – the radiation from the earth’s surface into space will still follow the Stefan-Boltzmann law and be proportional to T4. The only way this can change is if fundamental physics turns out to be wrong..
Dynamic Situation
How fast will the earth’s surface cool down?
This is a more challenging question. It involves calculating the heat flow out from the rocks, soil, sand, vegetation and most importantly, from the oceans. For each of these materials we would need to know the thermal diffusivity, which is the ratio of the thermal conductivity (how well heat travels through a material) to the heat capacity (how much heat is stored in a material per K of temperature change). As the earth’s surface cools down the rate of heat loss from radiation will reduce. This is because, using our earlier equation with the term for radiation stated explicitly:
Hrad = 240 – εσT4 W/m² ( = solar radiation absorbed – radiation emitted from the surface)
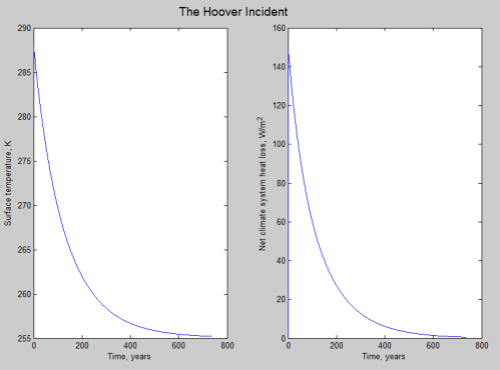
That is, the solar radiation absorbed stays constant while the radiation emitted reduces as the temperature decreases. It’s not so easy to visualize if you haven’t seen this kind of function before. Here is a very simple model of how the temperature (and net radiation) might change with time:
Click for a larger view
This graph is calculated by assuming that the climate system’s heat is stored in an ocean 4km deep and a very high thermal conductivity of water (that is, the heat can flow from the depths of the ocean to the surface with almost no resistance).
A more complete treatment takes account of the thermal conductivity of water. This value varies greatly depending on whether the water is still or well-mixed.
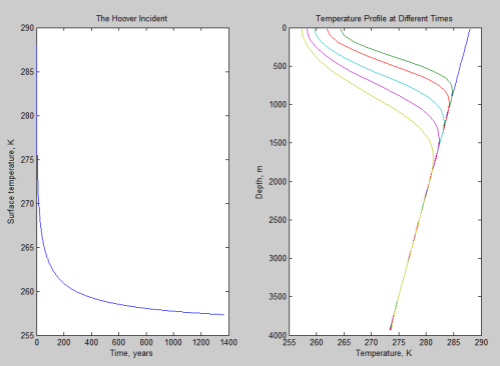
Below, the graph on the left shows the surface temperature against time. The graph on the right is more interesting and shows the temperature profile against depth of ocean for a few different times:
Click for a larger view
In this right hand graph the lower curves are later times. The initial temperature profile against depth is a straight line from 288K at the surface to 273K at 4000m – this is my assumption, my initial conditions.
What you can see from this graph is that the surface is much better at radiating heat away than the ocean is at conducting heat from its depths to the surface. That’s why the temperature stays higher for longer lower down in the ocean.
In this more thorough treatment the surface cools more quickly initially but will take much longer to reach the equilibrium of 255K.
And of course, alert readers will have noticed that it all changes when the surface freezes as the heat conductivity through ice will be different, and the albedo of the earth will change..
In fact, the problem can be made more and more complex, but that doesn’t change the essential elements.
Conclusion
Heat transfer by radiation is conceptually simple.
A surface emits radiation with a well-known formula which depends on temperature of that surface (and its emissivity).
The net heat transfer by radiation depends on how much radiation is incident on that surface from other bodies – whether near or far – and what proportion is absorbed.
In the case of a planet with an atmosphere – if the atmosphere cannot absorb or emit radiation then the equilibrium condition for that climate system will be where the radiation emitted by the planetary surface equals the radiation absorbed by the planetary surface.


SoD, thanks for the post.
A very minor note: the text switches from one graph to the next just below the “Hoover Incident” graph, without expliciting which one it’s about.
Perhaps it would make it clearer if you added something like “ Below, the graph on the left shows the surface temperature against time(…)”
Thanks, updated the article.
Convective heat loss to the atmosphere from the surface would shut down very rapidly because there would be a temperature inversion would develop near the surface. The situation is more complex if you include the daily cycle, but the huge loss at night cannot be completely overcome during the day.
At the new steady state, there will still be convective heat loss from the surface near the equator (and convective heat gain near the poles) because there will still be atmospheric circulation driven by the pressure gradient difference caused by the surface temperature difference between the equator and the poles. That horizontal circulation will cause turbulent vertical mixing that should drive the lapse rate towards the adiabatic rate. There would be the usual temperature inversion near the surface during each polar winter when the sun is below the horizon.
Well SoD, the non radiative atmosphere would still contain the same gases except that they don’t radiate in the IR.
The atmosphere would not be able to lose any heat except by returning it to the surface at night.
Convection and evaporation and condensation all still functioning as with Ocean internal energy storage.
Radiation reflection would still function.
Overall I would expect it to be much warmer during the day and a bit colder during the night.
The atmosphere would still have considerable insulating properties.
The exact balance is hard to nail down.
But that’s not unusual since no climate model, that I have heard of, can cope with convection and phase change in water but some still chance their arm at climate predictions.
I don’t think some comments I added about this post elsewhere are quite right, so we’ll see how I go this time…
I’m still trying to put my thoughts in to words, but basically, I think this scenario is not entirely correct. You’ve suggested that post “hoover” incident the temperature would fall to that of the incoming radiation. Let’s assume that the Trenberth energy budget is reasonably accurate (I’m not convinced, but it’s a good starting point) and go from there:
The situation you’re describing is that the atmosphere cannot interact with longwave radiation, at which point you’re suggesting that the original ~240 W/m^2 is absorbed by the system and that ~396 W/m^2 from the surface reaches space. How have you accounted for the following:
1) Cloud changes? (They appear to influence albedo, outgoing radiation, and back-radiation, it’s only apparent that albedo is unchanged in your scenario. Are clouds able to respond to outgoing radiation post “hoover” incident?)
2) The net increase in to the atmosphere? (This is tricky as the energy budget doesn’t clearly illustrate the amount due to the atmosphere as opposed to that due to clouds. If clouds post “hoover” incident can’t respond to longwave radiation then there should be a net reduction of 176 W/m^2 leaving the atmosphere.)
3) What effect does 2) have on the 97 W/m^2 due to sensible heat in to the atmosphere? (If the atmosphere sees a net increase in energy then it should become warmer causing a net reduction in energy transferred to it via conduction/convection, but not necessarily due to evaporation/latent heat, I’m not sure.)
As I tried to illustrate elsewhere, and what I believe is a mistake I tried to illustrate in the Arthur Smith paper here:
I think there’s confusion between energy budget at TOA vs planet surface and what’s valid when playing with various scenarios.
The temperature profile of the troposphere would similar to the present adiabatic rate.(-9.8K/km)
This is predicted by the Kinetic Theory of Gases in a Gravitational Field.
This in itself would give rise to the next heat transport effect, convection, because of Gravity and Buoyancy.
Since the Earth surface and the Atmosphere cool down at night the pattern will repeat on a daily cycle.
As well as the Heat capacity of the Oceans, you should also allow for the Heat capacity of the Earths land content as your example of the lunar item showed.
Further the Earths geothermal activity will have to feature.
Not quite. In a realistic model of anything at moderate temperatures on Earth (ie nearly everything) you have to use the alternate form of Stefan Boltzmann that contains (T1**4 – Te**4), where Te is the local environmental temperature – which is of course affected hugely by convection. The convection therefore affects the radiation output. That was what your commentator meant in his first paragraph!
So by using that correct form of S-B:
“The net heat transfer by radiation on a body depends on how much radiation is incident on that surface from other bodies” AND the heat flux from convection.
And “A surface emits radiation with a well-known formula which depends on temperature of that surface (and its emissivity)” AND the surrounding fluid temperature.
Bryan:
“Insulating properties“?
Can you explain what you think the atmosphere would change in the emission of thermal radiation from the surface of the planet?
I think that the surface starts off, post-Hoover, by radiating around 390W/m^2.
And I think that means the outgoing longwave radiation from the top of atmosphere = 390W/m^2.
What do you think?
JamesG:
I’m fascinated by this “alternative form“.
I suspect that you have seen an equation in a particular application and believe (incorrectly) that this is something fundamental.
There is only one form of the Stefan Boltzmann equation which you find in thermodynamics and physics textbooks.
This one form is derived by integrating the Planck function across all wavelengths and through all solid angles.
In the particular example of a surface radiating through a radiatively-active gas you will find that the surface still radiates:
j = εσT^4
And the gas radiates back:
ja = εa.σ.Ta^4 (εa = emissivity of the gas, Ta = temperature of the gas)
Therefore, in that particular example the heat exchange is close to the equation you wrote.
Now, in the case when the gas cannot absorb or emit thermal radiation how do you think that equation changes?
Have another think.
If the gas cannot radiate and is transparent to the radiation from the surface, by what mechanism does your equation hold true?
kamilian:
I didn’t spell it out, but the atmosphere not being able to absorb or emit radiation includes shortwave. Therefore, instead of 170W/m^2 absorbed by the surface and 70W/m^2 by the atmosphere (in our current climate), all 240W/m^2 of solar radiation is absorbed by the surface.
1) Cloud changes? (They appear to influence albedo, outgoing radiation, and back-radiation, it’s only apparent that albedo is unchanged in your scenario. Are clouds able to respond to outgoing radiation post “hoover” incident?)
Clouds will still reflect radiation. In the original Hoover Incident I did note that there would be changes to the albedo from clouds changes and increased ice sheets.
Of course no one can be sure what will happen to clouds. But we can be certain that as the climate cools there will be more ice – and therefore a higher surface albedo (less solar energy absorbed).
For the other comments you made I think you haven’t grasped the essence of the problem – the point of the post.
If the atmosphere cannot emit or absorb radiation then its ability to modify the temperature of the planet’s surface is very limited.
If it temporarily “sucks more heat out” (via convection/conduction) then the surface of the earth will be a little cooler and radiate a little slower.
If it temporarily “returns more heat” (via convection/conduction) then the surface of the earth will be a little warmer and radiate a little faster.
But the atmosphere cannot stop the surface radiating according to the Stefan-Boltzmann law. And the atmosphere cannot radiate any heat into space itself.
Sod, the issue is the validity of the starting assumption of the thought experiment, that the predominant component of air cannot emit electromagnetic radiation in the IR range of wavelengths because it cannot absorb them. It sits uncomfortably with basic thermodynamics. Is the thermodynamic axiom, that all matter at a temperature above absolute zero loses heat through electromagnetic radiation, qualified by the proviso that the matter must also absorb EMR? I have not seen it so expressed. If the assumption is invalid then JamesG’s story, with which you appear to agree, comes into play.
Does a frozen world, s you have concluded from the thought experiment, necessarily follow from the starting assumption? Heat stored in the atmosphere during the day resulting from importing sensible heat from the surface would be lost only slowly by conduction at night. The quantity of stored heat would grow, albeit at a decaying rate as the surface temperature fell as a result of radiation directly to space. An isothermal atmosphere would be the logical result of a warming atmosphere and a cooling surface. At this stage the surface would be gaining by conduction from the atmosphere and by absorption of solar radiation what it would be losing by radiation to space. I don’t think we know what the equilibrium temperature would be, other than between 255K and 288K.
Before I take leave for a couple of weeks, could I suggest a revisit to the emissivity issue. K&T show that most of the radiation to space originates from atmosphere. The emissivity of air, therefore, largely determines the temperature of the climate system. The following paper provides a formula which gives values of 0.76 and 0.44 at the surface and tropopause, respectively. A surface temperature of 288K and OLR of 240 Wm-2 at TOA (that is, no atural greenhouse effect) are not obviously incompatible if these emissivities are true.
http://www.ce.utexas.edu/prof/hodges/site2006/…/thermodynamics.pdf
John Millett:
It doesn’t sit uncomfortably with basic thermodynamics. It is basic thermodynamics.
Kirchhoff’s law says that emissivity equals absorptivity (for a body in thermodynamic equilibrium).
If you heat a gas like nitrogen what kind of emission do you think you measure?
If a gas absorbs radiation at 6.27um it will emit radiation at 6.27um.
If a gas can’t absorb radiation at 6.27um it can’t emit radiation at 6.27um.
(These measured properties are explained by quantum mechanics).
Without an understanding of these basic principles any story can sound believable.
Sod:
“Kirchoff’s law says that emissivity equals absorptivity (for a body in thermodynamic equilibrium).”
Wikipedia on Kirchoff’s Law:
“Average and overall absorptivity and emissivity data are often given for materials with values which differ from each other. For example, white paint is quoted as having an absorptivity of 0.16, while having and emissivity of 0.93. [2]. This is because the absorptivity is averaged with weighting for the solar spectrum, while the emissivity is weighted for the emission of the paint itself at normal ambient temperatures. The white paint will serve as a very good insulator against solar radiation, because it is very reflective of the solar radiation, and although it therefore emits poorly in the solar band, its temperature will be around room temperature, and it will emit whatever radiation it has absorbed in the infrared, where its emission coefficient is high”.
Sod:
“If a gas absorbs radiation at 6.27um it will emit radiation at 6.27um.”
K&T:
The atmosphere absorbs solar radiation and emits IR
Am I entitled to take from all this that in general emission and absorption are separate phenomena and that Kirchoff’s law deals with the special case of local thermal equilibrium, which doesn’t apply within the climate system (though the system itself is in long-term equilibrium with the solar flux)?
No, it’s simpler than that. In fact, thermodynamic equilibrium, local or not, is a red herring here. Emissivity and absorptivity are simply properties of materials, as the stated number indicates. And Kirchhoff’s law says they are equal.
But they are frequency dependent. That’s what that Wiki extract is saying. White paint has a reasonably uniform (low) absorptivity in the visible range – that’s why it looks white. They say 0.16 – that’s an average figure across the solar frequencies. But when the paint emits, it does so at the much lower thermal IR range. And there the emissivity (and absorptivity) is much higher.
The frequency dependence is more significant for gases, where absorption and emission is strongly banded with specific peak frequencies.
SoD says
“Insulating properties“?
….”Can you explain what you think the atmosphere would change in the emission of thermal radiation from the surface of the planet?”…..
The atmosphere would not be able to lose any heat except by returning it to the surface at night.
This in itself changes the thermal emission of surface.
Your non radiating atmosphere would have yet another effect.
Because during the day it would be much hotter this would lead to significantly more evaporation.
Hence more cloud, more rain.
Particularly at night as the atmosphere cools.
One raindrop contains 2×10 to the power of 22 molecules.
So with rain and clouds radiation will again occur.
However you might like to exclude liquid water as an emitter.
If you do you will have to revise your surface emission figure as water covers 70% of planet surface.
I’m not quite following why you think it would be hotter during the day. If we remove the radiative insulation properties (or back radiation if you like) of the atmosphere the surface will be able to lose more heat through radiation (talking about net balance for radiation here). Sure the atmosphere can only lose heat to the surface, but it can also only gain heat from the surface – that is the effect of heating can only be temporary. Any excess heat given to the surface by the atmosphere would be quickly radiated away.
SoD says
…”If a gas absorbs radiation at 6.27um it will emit radiation at 6.27um.”……
This needs to be qualified as it is not true in all cases.
For instance in the radiating atmosphere CO2 can absorb radiation of 4.3um and 15um.
Most agree that this radiation is the thermalised into intermolecular KE.
This KE is then shared out by collision with mainly N2 and O2 molecules.
However to get this KE back for emission is very difficult at atmospheric temperatures of say 260K
Using Maxwell Boltzmann statistics
The fraction of co2 molecules who have attained the above average KE to enable them to emit a 15um photon.
Would be 4 emissions per hundred absorptions.
The value for the 4um photon emission probability is 5 per million absorptions.
Bryan
Of course, the ability to emit depends on the temperature – the equation that shows this relationship is the Planck function.
So if a gas molecule can absorb at 0.5um for example, then it would need to be hot enough to emit radiation at 0.5um.
So being specific, the absorptivity of a body is also equal to the emissivity of a body at any given wavelength (and direction, in the case of non-diffuse surfaces).
SoD says
…..”Of course, the ability to emit depends on the temperature – the equation that shows this relationship is the Planck function”…..
Yes I agree and further I suppose that with sudden thermalisation of 4.3um and 15um we would no longer have thermal equilibrium hence the Kirchhoff condition is no longer satisfied .
Mait
………”I’m not quite following why you think it would be hotter during the day. “……..
I think the example of the Moon(with no atmosphere) at about the same distance from the Sun as Earth gives good support to the idea that the Earth would be hotter during daytime.
I think Earth is spinning fast enough and the atmosphere would still be able to move enough heat away from the surface to prevent moonlike daytime temperatures or even hotter than with our current atmosphere.
Mait
Have a look at the actual lunar temperature profile.
Click to access Greenhouse_Effect_on_the_Moon.pdf
See how fast the temperature rises.
Look up some geostationary satellite data to find out what operating surface temperature problems they experience
On the non radiative Earth atmosphere you would get almost 50% more radiation than at present during daylight.
This radiation would have a spectrum centred around 5800K.
The atmosphere would as you say remove heat from the surface during the day but since it cannot lose heat it would also return heat to the surface by night by conduction (if surface temperature dropped below atmospheric)
I see in this example that, at equilibrium, the top 750M or so of the ocean would be frozen. Surface temperatures are -15C or so. So, the Albedo will rise to over 0.5.
Now surface temperatures are even lower another -25C or so.
What is the lapse rate in this atmosphere? What is the atmospheric temperature at 50 metres for example.
There’s a whole thread on lunar surface temperature (Lunar Madness and Physics Basics). The main point is that the lunar surface is hotter during the day and colder during the night because the heat capacity of the lunar surface is much lower than the heat capacity of the Earth’s surface. The slower rotation rate also plays a part. Since the Earth would still have an atmosphere with significant heat capacity and a 24 hour rotation rate, the day/night surface temperature range for an Earth-like planet with a transparent atmosphere would still be much less than for the Moon.
Bryan,
Exactly. That’s why the hypothetical Earth’s surface would not get as warm during the day or as cold during the night as the lunar surface with no atmosphere. Heat capacity is much like capacitance in a series RC circuit. A large capacitor means that the voltage at the junction between the resistor and capacitor varies much less than the signal applied to the resistor. The maximum is not as high and the minimum is not as low. There’s also a phase shift causing the peak voltage across the capacitor to occur later than the peak of the applied signal if the frequency of the applied signal is much greater than the inverse of the RC time constant. The lunar surface has a low heat capacity and the frequency of the radiation is low so there is almost no phase shift. At the Earth’s surface, however, the maximum daily temperature occurs several hours after local noon.
DeWitt Payne
“Heat capacity is much like capacitance in a series RC circuit. ”
Good analogy
Another one would be heating a concrete block with a blowlamp.
The immediate surface would have a large temperature change but deeper down hardly any change at all.
I do not think that the hypothetical Earth’s surface would go just as high as the Lunar surface just that the daytime average would be higher than the present radiative value.
Further the night time value would be somewhat lower.
In your analogy the capacitor would be slightly smaller and the supply voltage somewhat larger.
In my opinion there isnt enough information to be any more definite than that.
Bryan,
The earth, atmosphere included, exists in what is effectively a vacuum. The only way to transfer energy through a vacuum is through radiation. Iff you take the atmosphere out of the radiative transfer process, you’ve only got the surface left. Night and day, the surface will always radiate. With no radiative interference of the atmosphere, the mean surface temp is going to be governed by how much energy is absorbed. Yes, there will be buffering by the atmosphere, and yes, the surface temps will have higher variance between night and day. As an example, consider the temperature swings between night and day in a desert versus in a humid region. However, none of that means that the mean temperature does not lower to that predicted by Stefan-Boltzmann. It has to, or basic thermodynamics is wrong, as has been stated before.
Otherwise,
You might get some interesting effects with clouds, increased surface ice, and the convective currents between night and day might be intensified, but I think all those complexities are beyond the scope of this thought experiment.
I don’t think the temperature is going to be the simple mean of (day mean + night mean)/2. This is because of the 4th power in the equation for energy lost. Even proportional to temperature, more is going to be lost from a part of the body that is, say 10 K, hotter than the mean of the body than will be lost from a 10 K cooler part of a body. I suspect this is merely stating the obvious for a lot of readers here, but I thought it should be said for those for whom it is not obvious.
I think John Millet, in his original comment, simply overlooked that even if convection and conduction between the surface and the atmosphere become negligible, the surface will still radiate. Of course, I may have not understood what he meant to say.
There is an _if_ in my mind that I’ve not found a simple answer to. I haven’t found a reference that explains in not too complex terms how much energy can be absorbed by, say N2 and O2, through collisions, and then emitted at some frenqency(ies) outside the earth’s LW band. Judging from the spectral emission of the earth, I believe the answer is ‘not much’ or ‘none’, but I’m wondering if I can get confirmation of that.
Chris G
“However, none of that means that the mean temperature does not lower to that predicted by Stefan-Boltzmann. It has to, or basic thermodynamics is wrong, as has been stated before.”
There is considerable disagreement as to what the average Earth surface temperature is or even whether it has a strictly defined meaning.
There is no unanimity on the emissivity of the Earth surface.
Hence the calculations of the well know radiation budget produced by K&T are not in the area of undisputed fact.
I would agree with your other point on lack of information on……
….how much energy can be absorbed by, say N2 and O2, through collisions, and then emitted ……
There have been two recent articles in WUWT and the AIR VENT by Tom Vonk and Jeff ID on this topic.
The views ran the full spectrum of possibilities but failed to reach a consensus.
I was impressed by the level of information shown by some of the posters, I found myself mostly in agreement with poster Merrick.
Their comments however addressed only partial aspects of the topic.
It never reached the clarity and depth of the discussion in SoDs excellent recent thread
…”Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion”…..
Perhaps SoD might be persuaded to host a discussion on this topic
Bryan:
I can agree with your first point as I’ve often made it (irrelevant though it is to your conclusion).
Your second point is only true in that a number of people including yourself debate it.
Within the frame of physics, there is zero debate about the subject of the emissivity of the earth’s surface because we can measure it and it is a reproducible parameter. Like every material, emissivity is a function of wavelength.
Measuring the emissivity of different types of earth surface is a tedious but predictable venture. It just requires spectroscopy expertise, equipment and time.
Being pedantic we could say that there is some small area of uncertainty, as there is in just about every measurable parameter – for example, the solar “constant”. We don’t know whether this is exactly 1367 W/m^2 because of instrument uncertainty.
Finally, your conclusion “Hence the calculations of the well known radiation budget produced by K&T are not in the area of undisputed fact.” is wrong because:
1. We do know the emissivity of all the earth’s surface types.
2. The fact that average temperature cannot necessarily be defined is irrelevant. We can still calculate average energy – just total it up from all around the world (because we know temperature and emissivity) and divide by the surface area.
Therefore, we can calculate average emission of thermal radiation.
Once again I can agree that you dispute it.
And I write this comment for others.
Myself, Sylas and probably others have explained these points to you many times, here and on another blog.
And I write this comment for others.
From Wikipedia
..”The average emissivity of the earth is readily estimated from available data. The emissivities of terrestrial surfaces are all in the range of 0.96 to 0.99[5][6] (except for some small desert areas which may be as low as 0.7). Clouds, however, which cover about half of the earth’s surface, have an average emissivity of about 0.5[7]”…….
Now what value is used for instance in K&T diagram of 390W/m2 for Earth Surface – It is exactly 1.00
In the Latest K&T update this has now been increased to 396W/m2 giving a value for e>1.
Sceptics will keep a close eye on any tendency to “round up” be it emissivity or temperature.
By systematically “rounding up” a “problem” can be created out of nothing.
Bryan, did you really get a physics degree? Send it back.
Sylas has explained this to you. I have explained this to you, but I believe you just don’t understand simple maths.
For others..
The K&T (1997) 390W/m^2 was calculated from the Stefan-Boltzmann equation for radiation from an average of 15’C or 288K. This is the arithmetic mean of surface temperatures around the globe, on an annual basis.
j = εσT^4 = 1 x 5.67×10^-8 x 288^4 = 390 W/m^2
But this is not the correct way to do it.
Why?
Because the average temperature to the power of 4 is not equal to all the individual temperatures to the power of 4 then averaged.
This is outlined for, example, in the section How to Average in Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored.
The correct approach is to take the temperature at all points around the globe, calculate the emission of thermal radiation for each of these temperatures, and then, take the average.
And when we do that we find that instead of 390 W/m^2 we get 396 W/m^2. (The updated K&T paper has an explanation of the uncertainties depending on slightly different approaches).
Which is why, as you pointed out without understanding why, average temperature is a slightly useless concept.
But it doesn’t mean that emissivity is greater than 1 in Kiehl and Trenberth’s calculation. Or that Kiehl and Trenberth don’t understand what they are doing.
For anyone else having trouble understanding this point, take a look at the reference for an example.
And for a simple example, suppose I have two equal areas, one of temperature 200K and one of temperature 376K. The average is 288K. Which would radiate at 390 W/m^2 – if the actual temperature was 288K.
And yet one surface is radiating, j = 5.67×10-8 x 200^4 = 91 W/m^2
While the other is radiating, j = 5.67×10-8 x 376^4 = 1133 W/m^2
What is the average radiation from these two areas?
Average radiation = (91 + 1133)/2 = 612 W/m^2. (Not 390 W/m^2)
This new value of average radiation is the correct one to use.
Well, I have no problem with people saying they don’t understand simple maths. But don’t claim insight into physics if you lack this ability..
SoD
So K&T used the rounded up value of 1 for their earlier calculation.
I noticed you skirted neatly around the value that K&T used for emissivity in their calculations for the value in their updated calculation.
What value did they use?
Was it once again the unrealistically high physically maximum possible value of 1?
I don’t see how the surface emissivity is particularly important in the context of K&T diagram (there are no temperature values on the diagram I think?). Using a lower emissivity value would only result in a higher corresponding surface temperature as far as I can tell. It would most probably result in higher sensitivity to the changes in the concentration of gases that absorb longwave radiation.
Mait
If a lower more realistic value of emissivity was used then the surface radiation calculated value would be less.
I said calculated because that what these values are.
If K&T did experiments rather than calculations they would not have to”revise” the value.
An experimental value is final and can only be discarded if there is operator or instrument error.
Bryan
You can call “dealing with the main point Bryan keeps trying to make through a lack of very basic understanding” – skirting around other issues if you like.
It’s one issue at a time with your “ideas”, I’m afraid.
And really, I only comment so that others can learn.
scienceofdoom
Perhaps your right and I’m in need of a refresher course to get up to speed with modern “climate science”
1. In my Physics degree we missed out on the module on “rounding up”.
2. Our laboratory supervisor was a bit of a reactionary. He insisted that if you give a result to three significant figures such as 396W/m2 then all the data used to calculate the result must have the same level of accuracy(3 significant figures) or better.
3. In the old days we did experiments which could possibly give surprising results.
Far better to use the modern technique of a computer program which never disappoints.
You mention Sylas as an authority in the area of Physics.
However Sylas was part of the Halpern Gang of Six who shot themselves in the foot with their attack on Gerhard Gerlich and Ralf d. Tscheuschner.
When asked by G&T to point to the part in the G&T paper to support their main critisism of the paper namely that G&T said that the atmosphere did not radiate the Halpern et al group were stumped.
So you think I don’t know any Physics and that’s also your opinion on Gerhard Gerlich and Ralf d. Tscheuschner.
Do you think that you might possibly be wrong?
Brian,
(I suspect this is a dead subject, but anyway…)
It looks to me that you are missing the point that the later K&T contains 396 where the prior has 390 is not a result of rounding up, but a result of fixing a problem in the math used on the prior paper.
It is nice that they fixed it, but it’s not a huge problem any more than there is a huge difference between 390 and 396.
Chris G
In both calculations K&T assumed the Earth is a perfect black body emitter(e=1)
Even Wikipedia do not go as far as that:
Emissivity is…..
0.96 to 0.99[5][6] (except for some small desert areas which may be as low as 0.7). Clouds, however, which cover about half of the earth’s surface, have an average emissivity of about 0.5[7]“…….
Now you might think that K&T did a rough and ready calculation and just picked the nearest whole number.
However they give the surface radiation as 396W/m2 that is to three figures of accuracy.
Now I suspect that in every well run university physics department the students are told that if they give a result to three significant then all data used to calculate that result should be accurate to three figures or better.
What conclusion can we come to?
K&T don’t know any better and just muddle along?
Or is it a deliberate exaggeration so as to inflate figures to make the so called “Greenhouse effect” appear to have some reality!
FWIW, I found a couple of references that I believe help me with my question at August 24, 2010 at 10:52 pm, that I thought I would share.
http://adsabs.harvard.edu/full/1904ApJ….19..105N
Click to access v230307.pdf
I need to work on this a bit more, but what I am gathering is that there is a lot of energy exchanged through collisions, and that the presence of a molecule capable of emitting at a lower energy state than the others in the mix tends to dampen the emission of molecules that only emit at higher energy states. If so, then even if the other gases have absorption/emission bands at a state higher than the IR, they won’t be stimulated to emit there very much, if at all.
Brian, I wasn’t trying to make a point; I was merely saying I’d like to understand it better.
I have a short note at The Air Vent that might help with your question.
In short, radiation depends on the number of molecules in the excited state. At local thermal equilibrium, the number of molecules in the excited state is an inverse exponential function of the energy of the state and an exponential function of the temperature, i.e. the Boltzmann distribution. Higher energy states have low populations and as a result don’t emit much compared to lower energy states at low temperatures. That means that at 300 K, emission of CO2 is almost entirely from the 15 micrometer band.
Another way of looking at it is the Planck equation. Emission at any given wavelength is the emissivity at that wavelength times the Planck equation at that wavelength.
http://en.wikipedia.org/wiki/Planck%27s_law
A high energy line may have high emissivity, but if the value of the Planck function for the temperature of interest is very low, there will be little emission.
Thank You! That fills in the gaps nicely.
It also allows me to correctly counter an argument I’ve come across occasionally to the effect that excited CO2 molecules rise to a higher altitude and emit from there, thereby lowering the GHE to some negligible level. I’ve long thought that the typical excited molecule really wouldn’t have time to travel very far before emitting, certainly not from some place near the ground to the tropopause. It looks like the hazard function for decay would make that possible only for an extremely small proportion of molecules.
Chris G,
You’re welcome.
[…] 12, 2010 by scienceofdoom This post “follows” on from Heat Transfer Basics and Non-Radiative Atmospheres and Do Trenberth and Kiehl understand the First Law of Thermodynamics? and many other posts that […]
“That is, the solar radiation absorbed stays constant while the radiation emitted reduces as the temperature decreases.”
If temperature decrease the absorption increase. This is an article about heat transfer, and you forget to include heat transfer?
The solar constant acts as a radiating body at ~395 Kelvin. Heat transfers according to difference in temperature to the surface.
“And of course, alert readers will have noticed that it all changes when the surface freezes as the heat conductivity through ice will be different, and the albedo of the earth will change..”
Yes, when the surface gets cold a lot more heat is transferred from the solar constant and other warm locations in the surroundings. With 51% IR in solar radiation the ice and snow is like a blackbody spreading her legs.
Lasse,
Please provide your formula for absorption of solar radiation.
You are just making up random assertions. Please provide a formula. And a reference or a textbook.
I’ll give you a clue. The solar radiation is still solar radiation, with a peak around 0.5μm, and a total flux of around 1360 W/m2.
What has the % of an arbitrary construct known as IR got to do with anything. Provide a formula.
In fact, the reflectivity of snow and ice at solar wavelengths is quite high. That is the snow and ice reflects 30-80% of solar radiation. On the other hand in the longwave radiation range it acts almost as a blackbody.
1360W-390W/4=242.5W=effective temperature
The heat transferred to the surface is what it takes to heat the atmosphere at the same instant. It´s logical that the atmosphere cools the surface and heat is transferred in the same rate it emits.
“I’ll give you a clue. The solar radiation is still solar radiation, with a peak around 0.5μm, and a total flux of around 1360 W/m2”
Always the bad tone with you people.
I´ll give you a clue. The emitted energy depends on temperature only. Is the atmosphere with it´s increasing amount of dry ice a part of the surface internal state?
“In fact, the reflectivity of snow and ice at solar wavelengths is quite high. That is the snow and ice reflects 30-80% of solar radiation. On the other hand in the longwave radiation range it acts almost as a blackbody.”
Wake up, we are talking temperature, not spectral composition. It is only your eyes that makes a difference in visual and infrared radiation. Do you think your eyes has anything to do with the relationship of emission and temperature?
Do you accept the fact that a place with snow, ice and the necessary cold temperatures is a place that receives heat from all locations of higher temperatures in the surroundings?
Lasse,
Textbook and formula please.
Check the Etiquette:
..Basic Science is Accepted – This blog accepts the standard field of physics as proven. Arguments which depend on overturning standard physics, e.g. disproving quantum mechanics, are not interesting until such time as a significant part of the physics world has accepted that there is some merit to them.
The moderator reserves the right to just capriciously delete comments which use as their premise that standard textbook physics is plain wrong..
If you wanted to ask I could have given you the textbook equation but you have arrived with huge confidence that you understand textbook heat transfer.
Ok, so provide the formula.
[That doesn’t mean – randomly put numbers on a page. It means cite a formula under any relevant conditions and note what each element of the formula represents.
It also doesn’t mean – 5 paragraphs of words.]
Stefan-Boltzmann law with inverse square law.
You need more?
“The moderator reserves the right to just capriciously delete comments which use as their premise that standard textbook physics is plain wrong.”
I expect this to happen. Someone is wrong and my posts will be deleted.
SOD:
“..Basic Science is Accepted – This blog accepts the standard field of physics as proven. Arguments which depend on overturning standard physics, e.g. disproving quantum mechanics, are not interesting until such time as a significant part of the physics world has accepted that there is some merit to them.”
I understand that you don´t want discussions about QM being wrong. But why do you use quantum physics to explain bulk properties like temperature? Since when do we count photons to calculate heat transfer?
And why do you base your argument on contradicting the whole theory of emission, temperature and heat if you care so much about arguments being accepted physics?