Following discussions about absorption of radiation I thought some examples might help illustrate one simple, but often misunderstood, aspect of the subject.
Many people believe that radiation from a colder atmosphere cannot be absorbed by a warmer surface. Usually they are at a loss to explain exactly why – for good reason.
However, some have the vague idea that radiation from a colder atmosphere has different wavelengths compared with radiation from a warmer atmosphere. And, therefore, that’s probably it. End of story. Unfortunately for people with this idea, it’s not actually solved the problem at all..
The specific question I posed to one commenter some time ago was very specific:
If 10μm photons from a 10°C atmosphere are 80% absorbed by a 0°C surface, what is the ratio of 10μm photons from a -10°C atmosphere absorbed by that same surface?
It was eventually conceded that there would be no difference – 10μm photons from a -10°C will also be 80% absorbed. This material property of a surface is called absorptivity and is the proportion of radiation absorbed vs reflected at each wavelength.
Basic physics tells us that the energy of a 10μm photon is always that same, no matter what temperature source it has come from – see note 1.
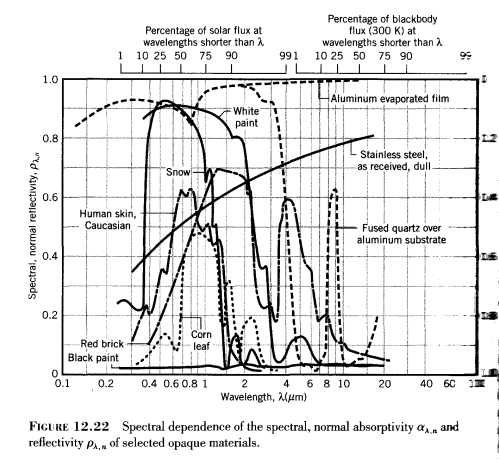
Here’s an example of the reflectivity/absorptivity of many different materials just for interest:
Clearly materials have very different abilities to absorb /reflect different wavelength photons. Is this the explanation?
No.
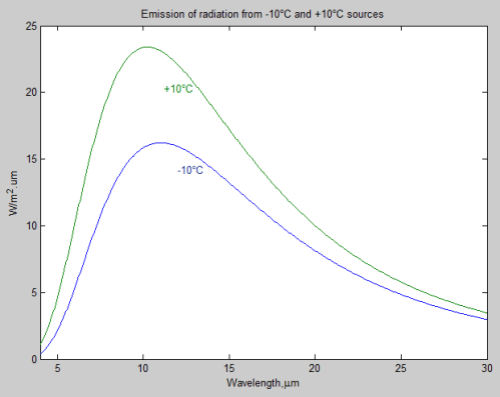
The important point to understand is that even though radiation emitted from different temperature sources have different peak wavelengths, there is a large spread of wavelengths:
The peak wavelength of +10°C radiation is 10.2μm, while that of the -10°C radiation is 11.0μm – but, as you can see, both sources emit photons over a very similar range of wavelengths.
Scenarios
Let’s now take a look at the proportion of radiation absorbed from both of these sources.
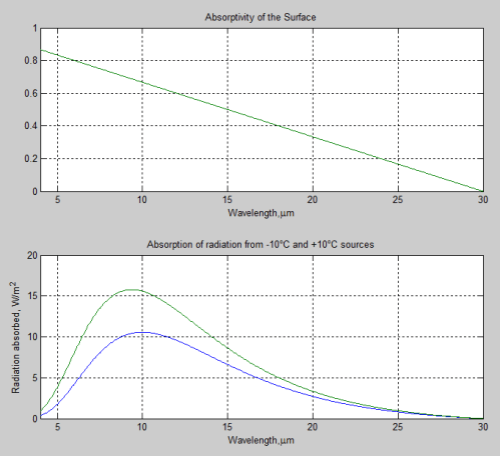
First, with the case where the surface absorptivity is higher at shorter wavelengths – this should favor absorbing more energy from a hotter source and less from a colder source:
The top graph shows the absorptivity as a function of wavelength, and the bottom graph shows the consequent absorption of energy for the two cases.
Because absorptivity is higher at shorter wavelengths, there is a slight bias towards absorbing energy from the hotter +10°C source – but the effect is almost unnoticeable.
The actual numbers:
- 43% of the -10°C radiation is absorbed
- 46% of the +10°C radiation is absorbed
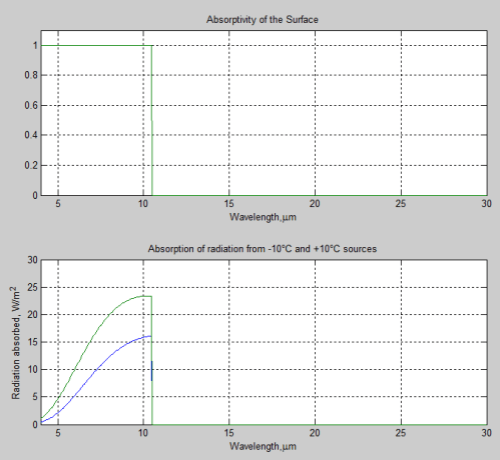
So let’s try something more ‘brutal’, with all of the energy from wavelengths shorter than 10.5μm absorbed and none from wavelengths longer than 10.5um absorbed (all reflected).
As you can see, the proportion absorbed of the energy from the hotter source vs colder source appears very similar. It is simply a result of the fact that +10°C and -10°C radiation have almost identical proportions of energy between any given wavelengths – the main difference is that radiation from +10°C has a higher total energy.
The actual numbers:
- 22% of the -10°C is absorbed
- 27% of the +10°C is absorbed
So – as is very obvious to most people already – there is no possible surface which can absorb a significant proportion of 10°C radiation and yet reflect all of the -10°C radiation.
And If There Was Such a Surface
Suppose that we could somehow construct a surface which absorbed a significant proportion of radiation from a +10°C source, and yet reflect almost all radiation from a -10°C source.
Well, that would just create a new problem. Because now, when our surface heats up to 11°C the radiation from the 10°C source would still be absorbed. And yet, the radiation is now from a colder source than the surface. Red alert for all the people who say this can’t happen.
Conclusion
The claim that radiation from a colder source is not absorbed by a warmer surface has no physical basis. People who claim it don’t understand one or all of these facts of basic physics:
a) Radiation incident on a surface has to be absorbed, reflected or transmitted through the surface. This last (transmitted) is not possible with a surface like the earth (it is relevant for something like a thin piece of glass or a body of gas), therefore radiation is either absorbed or reflected.
b) The material property of a surface which determines the proportion of radiation absorbed or reflected is called the absorptivity, and it is a function of wavelength of the incident photons. (See note 2)
c) The energy of any given photon is only dependent on its wavelength, not on the temperature of the source that emitted it.
d) Radiation emitted by the atmosphere has a spectrum of wavelengths and the difference between a -10°C emitter and a +10°C emitter (for example) is not very significant (total energy varies significantly, but not the proportion of energy between any two wavelengths). See note 3.
The only way that radiation from a colder source could not be absorbed by a warmer surface is for one of these basic principles to be wrong.
These have all been established for at least 100 years. But no one has really checked them out that thoroughly. Remember, it’s highly unlikely that you have just misunderstood the Second Law of Thermodynamics.
See also: The Real Second Law of Thermodynamics
Intelligent Materials and the Imaginary Second Law of Thermodynamics
The First Law of Thermodynamics Meets the Imaginary Second Law
The Amazing Case of “Back Radiation” – Part Three
and Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics
Note 1 – Already explained in a little more detail in The Amazing Case of “Back Radiation” – Part Three – the energy of a photon is only dependent on the wavelength of that photon:
Energy = hc/λ
where h = Planck’s constant = 6.6×10-34 J.s, c = the speed of light = 3×108 m/s and λ = wavelength.
Note 2 – Absorptivity/reflectivity is also a function of the direction of the incident radiation with some surfaces.
Note 3 – For those fascinated by actual numbers – the energy from a blackbody source at -10°C = 272 W/m² compared with that from a +10°C source = 364 W/m² – the colder source providing only 75% of the total energy of the warmer source. But take a look at the proportion of total energy in various wavelength ranges:
- Between 8-10 μm 10.7% (-10°C) 12.2% (10°C)
- Between 10-12 μm 11.9% (-10°C) 12.7% (10°C)
- Between 12-14 μm 11.2% (-10°C) 12.4% (10°C)
- Between 14-16 μm 9.8% (-10°C) 9.5% (10°C)


SoD
You still seem to be missing the point.
If the source temperatures are fairly close the difference though real might be hard to discern.
So lets pick two sources that are quite different.
One BB source produces 200J/s landing on a surface per second with total absorption.
The specrtrum is centred around 2um
The first source is then removed and replaced by the second BB source producing 200J/s but centred around 50UM and is totally absorbed.
If you are correct then the two sources will produce identical effects every second.
I think the 200J of 2um centred radiation will have far more capacity to do WORK than the 200J of 50um centred radiation
Bryan:
Quite amazing.
You are the one claiming that a -10’C atmosphere (peak wavelength at 11.0um) cannot be absorbed by a 0’C surface, while a +10’C atmosphere (peak wavelength at 10.2um) will be absorbed by a 0’C surface.
Or you did..
Do you believe this or not?
If you believe it then this is precisely the example we should discuss, not a completely different one that avoids you having to face up to the contradiction in your ideas.
If you don’t believe it then wonderful. Let the angels sing. We can all celebrate in our own way. Because this would mean that radiation from a colder atmosphere is absorbed by a warmer surface.
So please, once again, for the cameras – if radiation from a +10’C atmosphere is mostly absorbed by a 0’C surface, is radiation from a -10’C atmosphere mostly absorbed by a 0’C surface?
Following the discussion in the previous thread, I’ve expanded my commented on entropy budgetting in a post here. It illustrates this issue of countervailing fluxes, some of which may show entropy reduction, but always combined with a counterflux making a nett entropy increase.
Nick (and Sod), my question relates to necessary and sufficient conditions to be met if a process is to be shown to be in accordance with thermodynamic laws. Showing that a process in which heat flows from cold to hot may exist in a sytem in which entropy increases satisfies a necessary condition. But is that a sufficient demonstration? What about the specific heat-flow statement arising from the general entropic statement of the 2nd law – heat may not spontaneously flow from cold to hot?
In your graphic, Nick, (in which shell temperature and emissivity are related) emissivity is assumed at 100%. Realistically reducing emissivity raises temperature bringing shell temperature closer to ground temperature. For example, an emissivity of 0.6 implies a shell temperature of 275K. This in turn reduces entropy gain in the ground-shell exchange; but it will always be a gain provided the shell is colder than the surface.
This is not the case under the not uncommon condition of temperature inversion on still cold nights (night-time is when the process of heat flowing from cold to hot is most at issue). Then we would expect to have the surface gaining entropy by absorption of radiation from the warmer air aloft. Instead, dew forms, suggesting the surface has lost entropy and that the exchange reduces entropy, violating the 2nd law. The air’s lower emissivity resolves the anomaly- while the air above may be warmer than the surface its power output is less.
Another consequence of lower air emissivity would be a smaller difference than the 50% between the up and down surface-shell energy flows in Nick’s diagram. The 16% difference in K&T’s global mean energy budget implies air emissivity considerably less than the 100% ubiquitously assumed in these discussions.
John,
“heat may not spontaneously flow from cold to hot?”
That’s equivalent to saying that entropy must not decrease. If heat Q flows from temp T1 to higher temp T2, the entropy change is Q*(1/T2-1/T1) $lt; 0 – and vice versa.
“Realistically reducing emissivity raises temperature”
Probably not – Kirchhoff’s Law comes in here. Reduced emissivity means higher temperature needed to emit same heat flux, but also lower absorptivity, so there’s less heat to emit.
Temperature inversion – I think the causality goes the other way. Almost always the surface emits more IR than it receives – overall this is balanced by sunlight, but at night, that is absent. So the ground must then cool, even if the clear air above is warmer. The warm air doesn’t help with the considerable loss through the atmospheric window. If the air is still, the nett IR loss is not compensated by turbulent transport, so the ground gets cold – hence the dew. This is all first law. I don’t think the dew is related to entropy.
Emissivity 100%? I simplified to have an atmospheric window, where the emissivity is 0, and the rest, where it is 1. That is approximate.
Sod
My powers of explanation and your power of comprehension appear to be mismatched.
…….”So please, once again, for the cameras – if radiation from a +10′C atmosphere is mostly absorbed by a 0′C surface, is radiation from a -10′C atmosphere mostly absorbed by a 0′C surface?”…..
My difficulty in accepting full absorption of atmospheric radiation in contrast to you is that you believe the Earth is a perfect black body.
Its not the main point here however and too move on lets say that both radiations are equally absorbed.
My main point which you seem inclined to sidestep is that 200J of radiation from a lower temperature is not exactly thermodynamically equivalent to 200J from a higher temperature.
To make matters crystal clear please, once again, for the cameras
One BB source produces 200J/s landing on a surface per second with total absorption.
The spectrum is centred around 2um
The first source is then removed and replaced by the second BB source producing 200J/s but centred around 50um and is totally absorbed.
If you are correct then the two sources will produce identical effects every second.
I think the 200J of 2um centred radiation will have far more capacity to do WORK than the 200J of 50um centred radiation.
What do you think?
SoD– once again, a clear and helpful explanation, followed by obscure distractions (roughly-“oh yeah? well, look over there!”) from Bryan. I get the impression that Bryan is now aware that his position on back-radiation was just wrong, and wants to change the subject rather than admit his error. Perhaps it’s time to turn to another issue. But I’ll have a go just to try to explain, for others’ more than Bryan’s benefit, why Bryan’s remarks here continue to miss the point and get the physics wrong.
Bryan: “My difficulty in accepting full absorption of atmospheric radiation in contrast to you is that you believe the Earth is a perfect black body.”
SoD has not said or implied or assumed this– Bryan, you owe us a quote if you want to defend this one!
Bryan: “I think the 200J of 2um centred radiation will have far more capacity to do WORK than the 200J of 50um centred radiation.”
This is both a distraction and a misunderstanding. ‘Work done’ is not a way to express the effect on a surface when it absorbs energy. In terms of energy and implications for heat gain, 200J is 200J–a surface that absorbs 200J of radiation gains 200J of energy, translating into the same temperature increase regardless of the frequency of the energy involved. Doing work is a very different matter (work measured as force x distance, and when a quantity of energy flows through a heat engine, the maximum work done depends on the temperature drop between source and sink, not just the amount of energy). But again, work is not the topic here: we’re just talking about the heat energy that winds up in the surface due to back radiation.
[This response has been posted at the earlier thread and is posted also here, since the earlier post seems to ‘fade out’ and since it bears relevance also to the discussion in this post/JanS]
In the post https://scienceofdoom.com/2010/09/27/the-real-second-law-of-thermodynamics/ , ScienceOfDoom aims at proving evidence for that the CO2 greenhouse effect is scientifically sound, that is, that the colder atmosphere will heat the (on average) warmer surface of the earth via so-called back-radiation from greenhouse gases. He initially sets the scene via the following statement:
“Let’s avoid a semantic argument about the correct or incorrect use of the word ‘heat’. … I claim that energy from the atmosphere is absorbed by the surface”.
The problem with this statement is that the difference between good science and bad science hides in the details. It is therefore of utmost importance to clearly define what ‘heat’ is and what it is not. ‘Heat’ is energy, but energy is not necessarily ‘heat’.
‘Heat’ is in thermodynamics defined as: “Thermal energy in transit”. Or, alternatively [http://en.wikipedia.org/wiki/Heat]: “The energy transferred from a high-temperature object to a lower-temperature object is called heat”. It is thus clear that ‘heat’ only refers to the net energy that is actually transferred from a warmer body to a cooler one. This is a consequence of the second law of thermodynamics, stating that the entropy of the system cannot reduce. It may either remain stationary (no change), in case of an equilibrium situation (e.g. no heat transfer between bodies of equal temperature), or increase for spontaneous ‘reactions’ (e.g. heat flows from hot to cold). The mysterious entropy concept is defined as follows [http://en.wikipedia.org/wiki/Entropy]: “The entropy change, δS, of a system at temperature T, absorbing an infinitesimal amount of heat, δq, in a reversible way, is given by δS=δq/T”. Please note here the use of the word ‘heat’ (and not ‘energy’).
SoD uses double accounting to reach his goal and treats ‘heat’ and ‘energy’ as if they were synonymous entities. This must be categorised as bad (and thus untrustworthy) science. It is, however, clear that all objects do emit thermal radiation energy (blackbody radiation). But this does not mean that this energy always is absorbed by (transferred to) other bodies that are exposed to this radiation (see also my comment: https://scienceofdoom.com/2010/09/12/heat-transfer-basics-part-zero/#comment-6546). Only a body that is cooler than the radiating body can absorb part of the incoming radiation energy (in relation to the temperature difference between the objects and to their geometry, etc.). This part of the radiated energy is thus actually transferred and is then called ‘heat’. Non-absorbed radiation energy is directly re-emitted and will not influence the temperature of the irradiated body.
A proper entropy calculation, using the true heat transfer in the equation above, will therefore show that the cooler atmosphere cannot heat the warmer surface of the earth. Such a hypothetical heat transfer would correspond to negative entropy and is thus forbidden by the laws of thermodynamics. This means that the CO2 greenhouse effect cannot exist.
Those of the readers who want to better understand atmospheric physics are recommended to visit Professor Claes Johnson’s blog, for example starting at: http://claesjohnson.blogspot.com/2010/09/lapse-rate-vs-radiative-forcing.html
You are arguing semantics, heat is the net flow of energy between systems, Its the product of the gross energy from the warmer body, minus the gross energy transfer from the cooler body… thus if you increase the temperature of the cooler body, You will decrease the net flow of energy from the warmer body, resulting in a higher equilibrium temperature.
Its basically the same as conduction, at most the warmer body can only transfer half the differential in a given moment, because equilibrium will be reached, and it will require a differential to allow a net flow of energy. (assuming equal thermal capacities o course)
JanS
“It is thus clear that ‘heat’ only refers to the net energy that is actually transferred from a hotter body to a colder one.”
Not so. The quote on which JanS bases this claim says only that the kind of energy that is transferred from a hotter to a colder body (via conduction, convection or radiation) is heat energy, not that all heat energy must be transferred. (After all, if only net transferred thermal energy counted as heat, that would make the amount of ‘heat’ in a system that was always in thermal equilibrium at temperature T zero, while a perfectly similar system that had begun out of equilibrium but has now reached equilibrium would have ‘heat’ equal to the amount transferred during the transition, making ‘heat’ as JanS understands it a very silly concept indeed.)
As for the absurd claim that a body checks (how?) the temperature of a radiation source before absorbing (or rejecting) the individual photons striking the surface (which wear no labels as to their temperature of origin), well, that’s just false, as SoD has been at great pains to explain.
And things only go downhill from there, with JanS concluding that the atmosphere cannot ‘heat’ the surface. But the contribution of the atmosphere to the temperature of the surface does change as greenhouse gases increase. When the atmosphere changes in a way that reduces the rate at which heat radiated to the top of the atmosphere (where radiation into space occurs– the only way heat energy is removed from the earth) and solar radiation received by the surface continues at the same rate, the new equilibrium temperature of the surface is higher. So the change in the atmosphere has caused an increase in the surface temperature, i.e. it has heated the surface. Because the net heat lost to the atmosphere has diminished, the surface gets warmer. We can describe this as a result of diminished cooling of the surface by the atmosphere, rather than warming of the surface by the atmosphere. But that just is the greenhouse effect: the diminished cooling makes the surface warmer than it was– that is, the climate has changed.
This whole heat business is just semantics… Technically in thermodynamics, heat is the net flow of energy between systems… so by definition it can be only one way, that is its definition… o course in everyday English, we refer to the thermal state of a system as heat.
JanS:
Which one of the 4 points a) to d) in the conclusion is wrong?
scienceofdoom
Point c) is wrong.
AFAIK — Peak wavelength = 0.000293 m/Temperature (in Kelvin).
This might help to explain why high temperatures are associated with shorter wavelengths.
Hope this helps.
Live well and prosper.
JanS:
I responded to your claims about “a proper entropy” calculation in second law article. I look forward to seeing your calculation over there.
However, it is worth examining your claim about what happens with the missing energy from the colder body that “reaches” the hotter body.
You might be surprised to find that you are one of the few to actually come up with a real answer.
Well, it’s easy to demonstrate that it’s not true, but at least you didn’t just “clam up”..
There are (at least) three problems with your claim.
First of all, you need a whole new theory for emission of thermal radiation.
As demonstrated in The Amazing Case of “Back Radiation” – Part Three, the EBEX 2000 experiment directly contradicts your claims.
If your claim was true then the measurements of upward surface radiation would be the emission due to the surface temperature, εσT^4 PLUS the reflected/re-emitted radiation of around 300W/m^2.
However, this re-emitted energy isn’t measured – instead we measure exactly the radiation we would expect from a surface with that temperature.
So you need a new theory. One that is not in any textbook.
Secondly, you have to find an as yet unknown mechanism whereby photons of one wavelength can be distinguished by a surface. Current theory is that surfaces have an absorptivity which is wavelength and direction dependent.
I said “as yet unknown” – of course, the Illuminati may have the secrets to be revealed at the appointed time.
But it’s not yet hit a single textbook. They all show the traditional view.
Thirdly, the first law of thermodynamics might well be a casualty due to your claims.
It is pretty easy to demonstrate that the earth’s surface receives a global annual average of around 170 W/m^2 from the hotter sun. That’s it really for energy from hotter sources.
And yet the earth radiates out a global annual average of around 396 W/m^2. Let’s make a few allowances for all kinds of measurement issues and exactly the effect of the emissivity of the deserts and a few other places with low emissivity – but it’s impossible to come up with a value anything close to 170W/m^2. Especially as the oceans have an emissivity of 0.99 and cover 70% of the globe.
All three are major problems with your theory that need addressing.
Mike: No, c) is perfectly correct. A photon has the energy associated with its frequency by Planck’s equation, e=h\nu, not a different energy (or any other property) depending on the temperature of its source. The blackbody curve expresses the statistical distribution of the number of photons (times their individual energy) emitted as temperature radiation (a good experimental version is cavity radiation) by a body at a certain temperature. There is no difference between the individual photons emitted by warmer and colder sources.
Mike Flynn:
You have grabbed Wien’s displacement law which yes, tells you the wavelength at which the energy is a maximum. But not the energy of a photon which is emitted from that source.
If you look at the graphs of +10’C and -10’C radiation in the article you can see the wavelength of peak energy and they correspond to Wien’s law.
What is the energy of a photon of 10um?
=1.99×10^-20 J = hc/λ
Doesn’t matter whether it was emitted from a -50’C or a 500’C source.
Sod: ” …..therefore radiation is either absorbed or reflected”.
That could usefully be elaborated to “absorbed and retained/thermalised, absorbed and re-emitted or reflected”
The latter two processes, while physically different, have the same heat effect on the subject surface, nil, and the 2nd law isn’t an issue. It becomes an issue only in the case of absorption and thermalisation. This requires electrons to transit from lower to higher energy levels in the atom, the opposite of the transition required for the spontaneous process of a warmer body losing heat to its cooler surroundings. Is this the mechanism by which GHGs warm the surface in a relative, not an absolute, sense (relative to the nil-GHG condition)? If this is the general case, then, even at equilibrium, transitions nevertheless continue unabated, nullifying each other, whereas wouldn’t electronic stability be the natural state?
“If heat Q flows from temp T1 to higher temp T2, the entropy change is Q*(1/T2-1/T1) $lt; 0 – and vice versa”.
Admirable parsimony, Nick! The longer version: Taking “$lt;” to mean “less than” and “vice versa” to mean that the entropy change at the other end of the exchange is greater than zero (by a lesser amount); then, the premised process results in an overall loss of entropy for the system which violates the 2nd law of thermodynamics (and contradicts Sod’s demonstration). Have I interpreted your answer to my query correctly?
Sod’s entropy arithmetic always starts with loss from the warmer body. Unsurprisingly the arithmetic demonstrates an increase in entropy because that’s what heat flow from hot to cold does. No other result is possible. Conversely, no result other than a prohibited reduction in entropy is possible when the arithmetic starts with loss from the cooler body. Isn’t this a sufficient demonstration of the Clausius corollary of the entropic 2nd law – that heat may not flow from cold to hot?
“Kirchhoff’s Law comes in here. Reduced emissivity means higher temperature needed to emit same heat flux, but also lower absorptivity, so there’s less heat to emit”.
Kirchoff’s Law and the existence of the atmospheric window mandate atmospheric emissivity less than 100% and a higher effective radiating temperature.
“This is all first law. I don’t think the dew is related to entropy”.
The first and second laws are related, the former dealing with states of nature, the latter with change from one state to another – in this case from a dewless state to a dewy one. The dew forms because the ground loses heat (and entropy) by radiation to its surroundings. However, since the surroundings are warmer than the surface under inversion conditions, this process is impossible by the entropy law. Under this law, assuming 100% emissivity of the surroundings, heat would flow from the surroundings to the surface, precluding dew formation. A lower emissivity, by reducing the heat flux from the surroundings below that from the surface, allows the dew to form, consistent with the entropy law.
John,
I’m not sure what SoD demo you mean, but no – the proposition that entropy cannot in total decline is equivalent (arithmetically) to the proposition that heat cannot nett flow from hotter to cooler. The confusion comes from trying to apply this proposition to parts of the process.
The entropy view may be clearer. You can’t destroy entropy, but you can move it. One region loses, another gains. There’s a local loss of entropy, but it bobs up somewhere else.
The Earth’s entropy budget illustrates this. A lot of entropy is created on the Earth, but it doesn’t build up. It’s exported to space, and a big contributor is the greenhouse effect, which ensures that the primary emission of IR happens at cold high altitude.
You’re missiong the point on Kirchhoff’s law. if trhe emissivity of high GHG is lowered, then so is its absorptivity. It receives and emits less heat. More heat goes through the AW, which is wider.
I don’t agree with your distinction between 1LoT and 2LoT. They both deal with states and changes of state. 1LoT quantifies energy, 2LoT quantifies “free energy” – the ability of the energy to be converted to other states (“do work”).
Nick,
Oops! I see that I tripped up – the test of compliance with 2LoT of a heat exchange between two bodies at different temperatures doesn’t depend on the starting point for the arithmetic. This mistake had confused me.
But I’m still troubled by the idea that the test can’t be applied to parts of the process. The Clausius corollary of 2Lot is straightforward – heat may not flow spontaneously from a cold region to a warmer one. It isn’t qualified with “unless accompanied by a larger flow in the opposite direction”.
Moreover, it implies that in the climate system, say, 1LoT need be seen to apply only at top of atmosphere and not separately at the surface or the atmospheric shell.
On Kirchoff: If I understand Sod correctly, absorptivity and emissivity are properties of the subject material and are wavelength dependent. According to K&T’s energy budget, in the SW, the atmosphere’s properties are reflectivity, 0.23; absorptivity, 0.2; and transmissivity, 0.57. In the IR, transmissivity is 0.1 and, if reflectivity is the same as in SW, absorptivity is 0.67. Adding GHGs reduces transmissivity and increases absorptivity (and emissivity, following Kirchoff). Higher emissivity increases the flux to space. Thus, adding GHGs has opposing effects: it reduces the quantity of the minor heat loss to space from the surface through the AW; and it increases the efficiency of the major heat loss to space from the atmosphere. Its overall effect is ambiguous.
I guess our different takes on 1&2LoT can live in harmony.
John: I’m puzzled by your talk of the arithmetic ‘beginning’ with flows from warmer to colder or from colder to warmer. It’s only the entire process that’s got to fit within the constraints of thermodynamics! What bit of the maths we being with makes no difference, so long as the whole calculation takes everything relevant into account.
For example, we can start calculations re. the earth-moon system by calculating the earth’s gravitational action on the moon or vice-versa, but the complete picture has to include both. Of course when the mass of one object in a two-body system is thousands of times larger than the other’s, an approximation can neglect the influence of the smaller object and get Kepler’s laws for an orbiting planet. But SoD’s figures on radiation emitted by the various sources in the case of the atmosphere and the surface show that we can’t neglect the downward radiation from the atmosphere if we want to get the right results for average surface temperature.
As for the 1st and 2nd laws, any complete picture of an exchange of energy in a system has to reflect the first law. And your closing remarks about emissivity and absorptivity don’t justify skepticism about the ‘greenhouse effect’ at all: this is where the treatment of atmospheric layers (see earlier posts) and in particular the increase in altitude at which emission to space occurs has to come in: your ‘opposing effects’ need to be integrated into a real calculation, not just tossed on the table as an objection to accounts of the ‘greenhouse effect’ that actually do the maths. It turns out, when you do the maths, that the overall effect is not ambiguous.
Bryson,
You’re right on your first point, as I acknowledged above.
I’m a bit puzzled by “we can’t neglect the downward radiation from the atmosphere if we want to get the right results for average surface temperature”. Neglecting downward radiation wouldn’t change the result: entropy would still increase. Neglecting upward radiation on the other hand would give the wrong result – reduced entropy. That’s the basis of my doubt that Sod’s demonstrations, though necessary, are not sufficient to prove heat flowing from cold to warm is in accord with the 2nd law. The question is: if heat flows spontaneously from cold to hot why do we need refrigerators and air conditioners?
Over on another post Bryan suggested that the reason I was writing new articles was to try and avoid answering his excellent question over here.
How I love irony! It’s a beautiful thing. I hope that other readers can learn to love irony in the same way.
Well, on October 2, 2010 at 7:17 am I had asked Bryan some specific questions:
And also:
Simple questions I think.
Bryan’s “answer” was:
First point – not true and not claimed and not part of the argument. What, more red herrings?
Second point – oh, wait up. Pull back the cameras.
Bryan has apparently stated that the atmospheric radiation – from the colder atmosphere – is absorbed by the warmer earth.
Bryan has conceded the point. This is wonderful. I like a drink or three, and I will drink to this.
Bryan, did you really mean that? – The colder atmospheric radiation is absorbed by the warmer earth’s surface?
Note to self – will continue to press Bryan to confirm this point, but for now have to answer a later question from Bryan:
You are wrong.
200J is 200J.
The reason that higher temperature sources (e.g. one centered on 2um vs 50um) do more work is because they radiate more thermal energy.
So if you took two bodies in close proximity with your scenario:
– the one radiating and centered on 2um would have a temperature of 1449K (body 1)
– the other centered on 50um would have a temperature of 58K (body 2)
Body 1 would radiate ε1 x 249,950 W/m^2 while Body 2 would radiate ε2 x 0.64 W/m^2. (Where ε1, ε2 is emissivity of each body, a value between 0 – 1).
We can all agree that the transfer of heat would be from Body 1 to Body 2.
This is why a high temperature source transfers energy to a low temperature source.
But 200J is 200J. Your confusion on the subject is amazing.
scienceofdoom
“But 200J is 200J. Your confusion on the subject is amazing.”
No, I’m afraid to say that you are the one who is completely confused.
However I’m glad that you answered the question .
Now, proof that you are the confused one, read and learn.
Lets say that the surface both radiations impinged on was at 100K
“the one radiating and centered on 2um would have a temperature of 1449K ”
The efficiency of a Carnot Engine operating between these temperatures would be 1-Tcold/Thot
=1-100/1449 =0.93
In other words the 200J from the higher temperature can be converted into other forms of energy with an efficiency of 93%
Now if you like you can try to calculate the efficiency of transferring 200J/s from -58K to 100K
“the other centered on 50um would have a temperature of 58K (body 2)”
I think you can see you are now in la la land.
Efficiency=1- T(100k)/T(58K)
Where does work come into the picture? What we’re talking about is equilibrium temperatures. The efficiency of a Carnot engine is utterly irrelevant to the discussion.
DeWitt Payne
This side issue developed when SoD gave his opinion that 200J/s of radiation centred around 2um was thermodynamically equivalent to 200J/s centred around 50um.
The post above gave an answer that the higher temperature gave radiation of a very high quality that could be readily transferred into other energy types with >90% efficiency in the conditions specified.
On the other hand the radiation characteristic of the lower temperature was of such low quality that no work could be obtained even though the magnitude available was still 200J/s.
You as a chemist should realise the effects that are available to the short wave radiation that are just not possible with radiation of a longer wavelength irrespective of its magnetude.
In terms of heat content, 200 joules is 200 joules. If you add 200 joules to 1 kg of water, the temperature goes up 200/4187 = 0.048 K. That’s the rules. Now the mechanics of heat transfer means that if that a kilogram of water at 300 K is surrounded by a black body at 100 K, there will be a net transfer of energy from the water to the black body and the water will cool, but the water will cool less rapidly than if the walls of the black body were at 10 K. And it wouldn’t cool at all if the walls were at 300 K. But in no case are we talking about doing work. No work is done at all. If you’re trying to convert light into electricity with a PV cell or you’re a plant trying to do photosynthesis, then the photon wavelength is critical, but not when you’re moving heat around.
[…] see Absorption of Radiation from Different Temperature Sources – clearing up a few misconceptions on this […]
Absorption of radiation emitted by air is slowing down the cooling of the surface. This effect can be deduced from the diagram untitled “Emission of radiation from – 10°C and +10°C sources” above. Without the atmosphere the situation would resemble that on the Moon. The surface would lose energy directly to the outer space at the rate corresponding to the area below the green curve in the diagram. With the atmosphere present, the surface gains indeed energy corresponding to the area below the blue curve but it still loses energy below the green one. The net loss corresponds to the area between the green and blue curves. The cooling of the surface is therefore slowed down but it still takes place. There is nothing wrong with the second law of thermodynamics.