When I wrote Do Trenberth and Kiehl understand the First Law of Thermodynamics? I imagined that (almost) no one would have a problem with the model created. Instead, I thought perhaps some might question its relevance to climate.
It was a deliberate choice to use conduction to demonstrate the point – the reason is that radiation is less familiar to most people, while conduction is more straightforward and easier to understand.
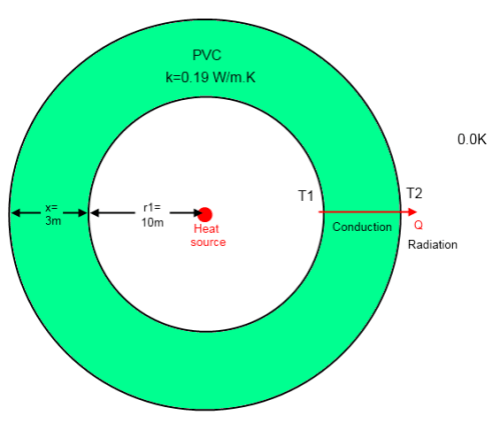
Here is the model from that article – a heat source in a hollow PVC sphere, located in the depths of space:
Many people have experienced a lagged hot water pipe. The more lagging (insulation), the higher the temperature rises. It seems straightforward.
However, the conceptual barrier that some people have is so large that anything – literally – will be put forward to make the model fit their conceptual idea. In case the case of one blog, claiming that energy can be destroyed in an effort to get the “right” result. A delicious irony that the first law of thermodynamics is cast aside to protect.. the first law of thermodynamics.
The reason this PVC sphere model appears so wrong to many people is for similar reasons that the famous Kiehl & Trenberth diagram seems wrong – the radiation “internally” (earth surface) is higher than the external radiation to space. (Note that the radiation values in the K&T diagram can be measured).
Explaining How the Result is Calculated
..in simple terms.
Solving the maths for the model above is straightforward (refer to the first article for the actual maths). Here is the solution in simple terms:
For the steady state condition the energy radiated from the outer surface must equal the energy source in the center (30,000 W). Otherwise the system will keep accumulating energy.
Given the surface area and the stated emissivity the outer surface temperature (T2) must be 133K (to radiate 30,000 W).
The only way that heat can be transferred from the inner surface to the outer surface is through conduction. This means 30,000 W is conducted through the PVC.
Given the (low) thermal conductivity of PVC and the dimensions, the temperature difference must be 290K, making T1 = 423K.
If the temperature differential is any lower then less than 30,000W will be conducted through the wall. And if that was the case then heat would be accumulated at the inner surface – increasing its temperature until eventually 30,000W did flow through.
Conversely, if the temperature was higher than 423K then more than 30,000W would be conducted through the sphere. This would start to reduce the temperature until only 30,000W was conducted.
Simple really. However, when the result doesn’t seem right, people begin their mental gyrations to get the “right” result.
This article is not written to convince people who have their minds made up. It’s written to help those who are asking the legitimate question:
Haven’t you just created energy? And can’t I use that to run a small power station?
Good question.
This article is not about proving what has already been demonstrated, it’s about helping with mental models.
The equations of heat transfer have already been clearly explained in Part One. So far, the arguments against that have been put forward consist of:
- the argument from incredulity
- 3m of PVC can transmit radiation straight through (no it can’t)
- energy disappears under the right circumstances (that was just the first of many flaws in that person’s argument..)
Of course, if someone comes up with yet another alternative calculation of the heat transfer I will be happy to look at it.
In the meantime, let’s create a mental model..
The Power Station
A few people have jubilantly claimed that the model I created, if correct, can run a power station of 1.8 MW, from a source of only 30,000 W.
That’s what it might seem like on the surface. But strangely, the model results were derived by conserving energy. That is, no energy was created or destroyed..
In the steady state condition:
- 30,000 W is produced from the internal source
- 30,000 W is conducted through the PVC “wall”
- 30,000 W is radiated from the outer surface
Energy is not being created or destroyed. Where is the energy accumulation in this model? Where is the usable energy being stockpiled?
- If you want to understand the subject, this point is the one to focus on and think about
- If you don’t want to understand the subject say “he’s created 1.8 MW of energy from 30,000W – ridiculous”, and move on (it sounds good)
The inner surface of the sphere has an area of 1,257 m² (4πr²). Consider one square meter of internal surface, we’ll call it “A” – these kind of models always have catchy names for different components of the model.
- Each second, A receives 23.9 W/m² from the internal heat source (30,000W / 1,257 m²).
- Each second, A conducts 23.9 W/m² through the wall.
- Each second, A absorbs 1,452 W/m² radiated from the rest of the inner wall.
- Each second, A re-radiates 1,452 W/m².
This is another way of saying that no energy is being created or destroyed. Where is the energy to run this power station?
All that happens if we start drawing power out of this system is the temperature internally reduces very quickly.
How Does the Sphere Heat Up?
In my efforts to understand the conceptual problems people have, I believe that this might help. I can’t be certain – this article is about mental models.
Let’s picture the scene when the PVC sphere is “started up”.
Outside it is 0K. Inside it is 0K. Chilly. Very chilly.
Now the 30,000 W heat source is fired up. 30,000 J every second gets radiated out from this source. Every second, 80% of this 30,000 J gets absorbed by the inner surface (with 20% reflected).
At this stage almost no energy is conducted through the PVC sphere. It can’t – because the temperature differential is not nearly high enough. Conduction requires a heat differential. So instead, the energy goes into heating up the inner surface of the sphere.
As the inner surface heats up it begins to conduct heat through to the outer surface – but most of the energy still goes into heating the inner surface.
A necessary consequence of the inner surface being heated up is that it radiates. All of this radiation is absorbed by the rest of the inner surface AND THEN re-radiated. Energy is not being created. This energy can’t be “tapped off” to do anything useful.
A small supply of energy is simply being “bounced around” (not really “bounced” but it might be a useful way to think about it)
This energy is simply the energy that has been accumulated by the inner surface during the initial heating process. It keeps being accumulated until finally the temperature is high enough to conduct the full 30,000 W through to the outer surface.
Now we have reached equilibrium! On our journey to equilibrium, while the inner surface was heating up, it accumulated heat, and this accumulated heat is now radiated, absorbed, re-radiated, absorbed…
You can connect it to a power station and very quickly you will draw down this accumulation of energy. The maximum you can draw out long term will be 30,000 W.
Conclusion
This article is all about mental models – explaining why the actual results for this model don’t violate the First Law of Thermodynamics. The results were calculated from the very simple and standard heat transfer equations.
Analysis of this model, with the results that I have presented (in part one), demonstrates that energy is conserved.
At first glance it might not seem like it to many people – because the inner surface radiation is so high. But the energy is just re-radiated from the energy absorbed. It’s like a small stockpile of energy that is being “bounced around” from wall to wall.
There is only one (legitimate) way to solve the heat transfer equations for this model. Other approaches invent /destroy physics in an attempt to get a low enough value for the radiation emitted from the inner wall.


Teaching thermodynamics is tough, ask any high school or freshman physics teacher.
Willis Eschenbach has taken on the task using similar models several times with similar results. The first was in a comment at ClimateAudit …
… and later as a post at Watts Up With That.
“I’m sorry but I thought the article was tremendous nonsense … If there are physicists watching this weblog then I’m sure they’ll fill you in on exactly why your “steel greenhouse” won’t work … It’s wrong from first principles.”
SoD, I do wish you the best of luck with this. As Speed noted, I tried this with my thought experiment The Steel Greenhouse.
Man, that was fun. I got enough foolishness about thermodynamics thrown at me to last a week of Thursdays.
But don’t let me discourage you, there is obviously still much more educational work to be done on the subject.
I will point out in passing that a “single shell” planetary greenhouse system is not adequate to model the earth, as it does not give enough energy to allow for the known losses in the climate system.
All the best,
w.
Congratulations on yet another patient, clear explanation of the principles and how to go about applying them to a simple illustration. Transmitting this kind of understanding generally goes pretty well in the classroom, where clarity and simple calculations are actually persuasive. Sadly, when the class is full of people who are there to challenge anything you say because they simply don’t like where it leads and have been warned in advance not to accept anything they don’t like (as in a lecture on evolution presented to creationists), it’s a harder row to hoe… But hardscrabble farming may still be the only way to persuade some to take a more serious approach to the issues at hand and find either a defensible form of skepticism, or perhaps even enlightenment.
“a defensible form of skepticism, or perhaps even enlightenment.”
😉 What does enlightenment entail exactly? I think pragmatic reasoning, over emotional reasoning should be the goal, which to my mind comes from conceptual understanding.( even math can be little more than a chant, if you dont know the “why”) And where ever that may lead, will still probably depend a bit on what part of an issue someone focus’s on.
In the comment thread for Willis’ steel greenhouse article at WUWT, one commenter did change his mind and admitted that he had been wrong and Willis was correct. One.
I think a layman’s understanding of this concept is that 30,000 W is the addition of energy to the system per second, which equals 23.9 W/m² reaching the inner surface of your sphere. And 1,452 W/m² radiating back from the inner surface is a peak achieved due to the accumulation of energy inside the system over some time. At this peak the inner surface temperature reaches 423K (at every point on the smaller inner surface), at which stage the system is then able to radiate (lose) a total of 30,000 W from the outside surface at 133K (at every point on the larger outer surface) given the conductivity, thickness and diameter of PVC you used. The system is then said to be in equilibrium – a non-changing state – and no further energy accumulation occurs inside.
So energy isn’t being created; it’s just being accumulated for a time until equilibrium is reached. The system can only generate power equal to the energy being continuously input plus the energy previously accumulated until drained, therefore there’s no power station utility. But things do get much hotter inside the system than might be expected given the relatively small energy source (I see the GHG relevance here). Perhaps such a system could be called a thermal reservoir.
Is this simplified understanding correct?
This thought experiment is just a Bomb Calorimeter we used to use in highschool to get the energy content of food. Soon as the water around the container stopped rising we were at equilibrium and could calcuate the caloric content of the food (chocolate was a favorite to test with).
Hockeyschtick seems to have withdrawn their objection:
“The post originally here entitled Why ‘Science of Doom’ doesn’t understand the 1st Law of Thermodynamics unfortunately contained an error in the analysis and is therefore withdrawn. I apologize to ‘Science of Doom’ for the mischaracterization and the error.”
Instead they have moved on to :
“However, the Science of Doom ‘thought experiment’ does not prove anything relevant to the Kiehl/Trenberth (K/T) Earth energy budget or the earth/atmosphere system as claimed since etc etc”
I repeat my comment I made in Interesting Refutation of Some Basics.
Congratulations to MS on The Hockey Schtick for rewriting their article. It takes great strength of character to do something like this.
My earlier ironic statements about the relevance of this model is something to discuss on a much later day.
Today is a beautiful day.
Just a thought – should we assume the temperature of “empty space” is 0K? I understood the Cosmic Background Radiation effectively made the temperature out there a balmy 2.725K. Not much, I grant, but shouldn’t it be incorporated in theoretical calculations involving radiation to space?
BTW, I thought your detailed explanation above to be a model of clarity, and obeys the First Law of Satisfaction.
Sod:
Thank you for dealing with issues left hanging in your previous article on the subject – the system’s pre-equilibrium retention of 1.8MJ of externally supplied energy. (Supplied at 30,000W the system took about a minute to warm up).
You say:
“Now we have reached equilibrium! On our journey to equilibrium, while the inner surface was heating up, it accumulated heat, and this accumulated heat is now radiated, absorbed, re-radiated, absorbed”.
Wouldn’t it be better to characterise the retained energy as filling the cavity with an electromagnetic field, or a photon gas, in thermal equilibrium with the inner surface? There being no temperature potential between the surface and the gas would obviate the need for the somewhat inelegant model: Radiation, absorption, re-radiation, re-absorption…….ad infinitum….between every infinitesimal bit of surface and every other bit of surface.
MostlyHarmless:
In one sense you are correct (in fact, totally correct that the background temperature is 2.7K). We could also add the dependence of the material properties of PVC (heat conductivity, emissivity) on temperature.
But there is a value in keeping thought experiments as simple as possible because there are less distractions from additional terms.
Find the simplest way to demonstrate a point..
SoundOff:
Your understanding seems correct.
Willis Eschenbach:
I like your steel greenhouse explanation.
Of course many people don’t understand the basics and so they wrote entertaining comments to that effect.
Many more silent readers do want to understand the subject. This is the value.
SoD, thanks for the vote of confidence in my Steel Greenhouse. Someone commented above that only one person changed their mind as a result of my article.
However, I am not pushing to change the minds of the committed. I am interested in providing food for thought for the uncommitted. I write first for the lurkers, and only secondarily for those who will reply to my work.
So keep up the good fight, and don’t be discouraged if only a few people show up to say “hey, I was wrong”. For everyone who posts there are ten lurkers out there who are reading, not to debate, but to further their understanding. Yours is a premier site for that purpose.
w.
SoD:
Does this example work variables reversed? Not to be flippant, but a serious question. In your article Radiation Basics and the Imaginary Second Law of Thermodynamics you challenged me to prove you wrong formulaically. I could not..In fact my longhand calculations supported your supposition. Specifically, within a vacuum two warm bodies will increase one another’s temperatures, without thermal run away, simply due to proximity. My better grasp of this concept is no doubt a result of your challenge …and DeWitt’s reply post. Thanks. Nevertheless, I still plant my flag in the skeptic camp.
Back to my questions, does this example work with variables reversed? That is, if the goal is to maintain cold temperature while outside conditions are hot, will the conclusion be as satisfying. Let me propose a less impracticable, more deductible hypothetical.
The Twin Freezer Paradox:
Two identical freezer, one empty, the second containing 50 one litter bottles of water. Freezer two’s bottles are arranged such that none are touching one another. Both freezers are set to 255K. The room surrounding our twins, is a static 288K. After achieving set temperature, the power in cut for both.
Which freezer reaches surrounding temperature first?
My intuition and experience tells me freezer one will win the race to 288k…yet freezer two a has 50 litters of frozen water and thus more energy. Since freezer two has more LWR reflecting back does that not mean more energy absorption i.e. higher temperature. Will freezer two heat up faster?
The thermal capacity of the freezer with the frozen water will be much greater than an empty freezer… it will take a LOT more energy for it to warm to the ambient temperature , and thus will take longer.
“it will take a LOT more energy for it to warm to the ambient temperature , and thus will take longer.”
I agree…but does not the greater radiated long wave from the water increase the internal energy of number 2 thus increases the temperature of 2 faster….yes?
🙂 No, because with one you will have the air in the freezer radiating the same as two, they are the same temperature, But with one, it will move to equilibrium a lot faster, just because it would require a lot less energy, than with two, the air has greater surface area(gases are still semi transparent to IR, water is opaque, it only receives and emits at the surfaces of the bottles, the dimensions of the bottles would effect the rate, but water still has four times the thermal capacity of air) . The differential in T is the same, the thermal capacities are not.
The radiation from the water, will decrease the rate at which the air can move energy into the water, the closer in T they are, the slower the exchange. The larger the differential the faster the exchange.
By gases are semi transparent to IR, i was specifically meaning air! W
What you are overlooking with your experiment, is that radiation is a product o T, not E, although the water contains more energy than the empty freezer, it has the same entropy, but a much larger capacity to absorb energy, than the empty freezer.
Science of Doom,
I believe the correct units for the energy flux per second should J/m².
But other than that, great site – keep up the good work – even though I may disagree on occasion (but not in this case).
J. Lanier:
Freezer 1 (F1) does reach the race to 288K, as Mike Ewing has already explained (November 15, 2010 at 5:54 am).
Radiation is function of surface temperature, not energy.
All that happens due to the proximity of the F1 and F2 is that F1’s temperature increases slower and F2’s temperature faster than would happen if they were in their own individual “rooms”.
The amount of radiation shared is based on emissivity/absorptivity AND “view factor”.
I will see if I can create some graphs to help visualize the problem.
Concerning the two freezer problem. Is the heat capacity particularly important in the context of the question? If we assumed the heat transfer with the outside would be only through radiation and the freezers would be filled with gas which is transparent to IR (in the sense that it doesn’t absorb/emit at the temperature which it is at), then I’d guess freezer two would reach target temperature faster due it being a better absorber than freezer one (in fact – freezer one’s temperature wouldn’t raise at all if our model gas doesn’t emit any radiation).
To put the question in a bit different wording – if considering only radiative heat transfer – wouldn’t the speed of reaching environment temperature depend on the balance between emissivities of the gas and liquid and the heat capacities.
Hi SoD,
Many thanks for your continued efforts to keep us on the straight and narrow with regard to basic principles of physics.
It is nearly 50 years since I was taught these concepts at school and I am having to pull things out from some very cobwebbed corners of my memory. I must have been very lucky to be exposed to Prévost´s theory of exchanges, the experimental work of Dulong and Petit involving rates of cooling of bodies within evacuated copper spheres and the recognition by Stefan that the rate was proportional to the difference of the fourth powers of the temperature of the shell and the cooling body. This all makes it much easier for me to follow your basic arguments
There are a copuple of points that are puzzling me and I wonder if you would care to comment. The first is that you seem to have involved the emissivity of the PVC when calculating the internal radiation and I am trying to square this up with what I thought was the peculiar property of a cavity that the internal radiation was only dependent on the wall temperature.
The second point is the idea that there is some stored energy inside the sphere. Starting from cold I can quite see that equilibrium will take some time to achieve but my guess is that the only place that energy is stored is in the thermal capacity of the PVC. I cannot convince myself that there is any energy stored in the internal vacuum despite the photons buzzing around.
If this sounds confused it is because I am!
Isn’t the entropy of freezer two much lower than freezer one and that explains why freezer 1 wins the race?
Hmmm thinking thinking…. the level of chaos in both freezers is equal at equal temperatures. But f2 simply requires greater movements of energy to effect a change…
If the water was lower entropy at 255k, than air at 255k… entropy would increase from its higher concentration(air) to the water… it would mean the water should warm more than the air? Entropy is the level of chaos, and T would be what determines this, not energy capacity.
I could be wrong, but thats how i understand it.
S.o.D. says:
Note that the radiation values in the K&T diagram can be measured
If so, why did Minnett calculate the sea surface emission of longwave radiation using the Stefan-Boltzmann equation instead of measuring it directly like the rest of the quantities in his empirical experiment on sea surface ‘skin’ temperatures?
http://www.realclimate.org/index.php/archives/2006/09/why-greenhouse-gases-heat-the-ocean/
Can you point me to empirical measurements of the longwave emission from the sea surface and desciptions of the hardware used to take them?
Thanks
S.o.D has post-edited my contribution to remove the bolding of his use of the word measured as seen on his original post, and my bolding of the word measurement in order to reduce the impact of the point I’m making.
Tut tut S.o.D. Messing around with what people wrote to change meaning and emphasis is very sharp practice.
tallbloke
As you can see in The Amazing Case of “Back Radiation” – Part One and Part Three the measurements of upward and downward longwave radiation at the surface are few and far between due to the expense of the instruments and the setup required.
However, sufficient measurements have been done to be confident that the Stefan-Boltzmann equation is correct and so if the SST is known accurately the emission of radiation is also known accurately.
I’d like a go at this, please don’t reply with complicated maths..
I’m sticking with ‘classic’ 2nd Law, heat always flows spontaneously from hotter to colder, it does not go the other way.
My whole body is the heat source. It’s freezing outside, my oil supply has run out, I live in a stone house, I go to bed to try and sleep. My bed has a thick duvet on it, I add a couple of blankets and put on pyjamas, and pulling the covers around my body into a cocoon am feeling quite warm around my torso, and my hands are warm, but I cannot get to sleep, I’m still shivering sporadically.
Although I do not feel it ‘internally’, my perception of the temperature of my feet is that they’re not that cold, they don’t feel warm either and I wonder why they’re not getting as toasty warm as my hands. I check, my feet are blocks of ice, figuratively speaking, what I was feeling was no feeling, I try to warm them on my calves with no discernible benefit. I realise I’m actually in mild hypothermia and decide I need to do something about it. I get up, put on thick socks, put on more layers of clothing around my torso, and a hat. (The reason my feet are so cold is because my body is extracting heat from my extremities to keep my vital functions alive, to keeping the torso warm.) I begin to warm up as I wait for my body’s torso temperature to reach my feet. When it does, or comes close enough to feel comfortable again, I know that I have put enough insulation around me to block the flow of heat from my body to the cold room, sufficiently thickly to delay the previous higher rate of heat loss to feel comfortable again. The inside of the duvet next to me feels warm, it does not feel warm on the outside, nor do the two blankets on it, they feel cold.
That’s all that is happening, the insulation around me has built up sufficiently to delay my heat loss ‘proportionally?’, for the energy I’m generating internally to now return to warming me up and to continue warming as my body has decided it is now safe for my heart to send warm blood to my feet again. Comfy, if a tad restricted, I fall asleep.
I think that is what is happening in the sphere. There’s no energy flow from my clothes or duvet to me, I am still heating them up, energy is still flowing from hot to cold.
Somehow, the heat source has turned the inner space around it in the sphere into a thermal blanket, insulating it.
It becomes hotter than it began just the same as if I had put on more blankets and clothes on than I actually needed to the point that it raised my body’s normal working temperature. Exactly as being in a hot tropical atmosphere does until one adjusts to living in it.
Whatever that ‘proportion’ is, the thermal blanket the heat source has created around itself in the sphere is probably relative to the amount of space in which this is taking place. Pressure?
Howzat?
Myrrh
Without using maths your take on the situation is spot on.
Some will try to convince you that the radiation from the cloths next to your skin will INCREASE your temperature.
The only reason that the inner clothes feel warm is that you as the prime source heated them.
The clothes now become a secondary source as far as radiation is concerned.
However a source cannot raise the temperature of an object higher than its own temperature.
So next a little bit of maths
Prime source your body skin temperature say 36C will raise the temperature of your inner clothes to say 34C.
The back radiative element from your clothes must influence the temperature of your body < 34C.
So we see that the radiative element of heat transfer obeys the second law.
All elements of heat transfer insulate your body as your sound common sense has made explicit.
Bryan/Myrrh
Skin temp 36, inside blanket surface 34 – a temperature potential; and heat will flow spontaneously from the body to the surrounding air. Myrrh will continue to feel cold and be unable to sleep until temperature equilibrium is reached in the system comprising his body, surrounding air and inner surface of the blanket. At equilibrium, metabolism converts chemical energy to heat at the same rate that the outer surface of the blanket loses heat by convection to the surrounding air. The equilibrium temperature will be a function of the metabolic rate and the depth and conductivity of the blanket. There being no vacuum, there is no need to invoke radiative heat transfer either forward or backward.
Thanks, I’m still sticking with heat flow from hot to cold, so I thought that an example because as you say the blanket is losing heat to cold outside as I’m producing to warm the inside. I don’t understand why vacuum and radiant heat should be any different. Just because the PVC is further away from the heat source doesn’t make it any different in principle.
The space around the heat source in the sphere is in like relation as my body next to the blanket. If my body was space the heat my metabolism was generating would get to the blanket quicker, that’s the only difference I can see. If the PVC blanket is such a bad conductor of heat it will delay the escape of heat into space as would piling more clothes and blankets around my body. I would start getting too hot before the blankets were anywhere near the temperature I was genenerating. What is being described here as ‘back-radiation’ to explain it isn’t necessary, the PVC is simply blocking heat flow which is still flowing from hotter to colder.
My room hasn’t got any warmer in my example, just as the depths of space aren’t affected by what’s going on at the inner surface of the PVC. The inner surface is building up enough temperature to delay the loss of heat from the source while at the same time that heat is being conducted out into space.
It seems to me that this Law simply describes what is happening, if there were exceptions, that this didn’t apply to radiated heat, I am astonished that it hasn’t ever been mentioned directly as an exception in all the years before AGW.
As it stands the Law can appear counter-intuitive, an example I read recently was picking up a snowball. We think in terms of the cold snowball cooling our hand, but it’s the heat flowing from our hand that’s making the hand go cold, the snowball is melting.
Thinking some more about this ‘back-radiating’, how can a colder body even if warm radiate heat out to an even warmer body when it is actually still in the process of being warmed by that warmer body? (because heat always flows from hotter to colder)
I’ve just taken a brisk walk on a warm day and so feeling lots of internal heat plus my body temperature a little up, I walk into a room with a fire blazing and stand in front of it. The fire is radiating a huge amount of heat in my direction, is any radiation from me really going to the fire? Isn’t any heat from my hot body actually overwhelmed by the greater heat coming from the fire to me?
Hi Myrrh,
It’s true that heat flows from hot to cold. In other words, there must always be a net exchange of heat from the warmer object to the cooler object.
You ask how can a colder body radiate heat to a warmer body when it is being warmed by a warmer body? You can also ask the opposite question; if we know that warm bodies must radiate heat, then what physical phenominon prevents that heat from reaching a warmer body?
In any case, I think that I understand what you are asking. You are saying, the cool object is warmed by the warm object, and therefore is cooling the warm object, so how can it also be warming the warm object.
The answer is that the cooler object is not warming the warm object, but in some circumstances it may be slowing the cooling of the warmer object (by reducing the net amount of radiation that is leaving the warm object). In some circumstances the cooler object will accelerate the cooling of the warmer object (like if I hold a block of ice against my chest). But if I am in outer space and a block of ice is a foot away from me, it is actually a source of heat, because even though a net amount of heat is going from me to the block of ice, I would be losing a larger amount of heat into empty space if the block of ice wasn’t there.
Mike has the nub of it in his 2nd paragraph. All I can do is say the same thing in different words.
Look at it this way. America has a balance of trade deficit with China. America buys more stuff from China than China buys from America.
That doesn’t mean there is no flow of money from China to America, just that the flow of money from China to America is smaller than the flow the other way. The NET flow is from America to China.
The 2nd law doesn’t say (except in convenient shorthand) that “heat flows from a hotter to a colder body”, and it definitely doesn’t say that “heat ONLY flows from a hotter body to a colder body”. If we state it precisely rather than in approximate shorthand, it says that “The entropy of an isolated macroscopic system never decreases”. Translating that into heat flows, a precise statement of the same law would be “In a macroscopic system there can be no NET heat flow from a colder body to a hotter body”.
[In technical terms, Entropy is a state function – it does not depend on the processes by which a state is reached. Therefore it imposes no restriction on heat flows, only on net changes which result.]
You see the distinction? Heat can flow both ways, and in the systems we are discussing it does, but the flow from hotter to colder will be greater than the flow the other way. (The term flow may also be misleading here if you are used to thinking in terms of fluids.)
Thermodynamics is often counterintuitive, which is why shorthand forms of the various laws are often stated. But over-reliance on the shorthand forms can lead to wrong conclusions.
S.o.D. says:
measurements of upward and downward longwave radiation at the surface are few and far between due to the expense of the instruments and the setup required.
However, sufficient measurements have been done to be confident that the Stefan-Boltzmann equation is correct and so if the SST is known accurately the emission of radiation is also known accurately.
Please don’t think I’m trying to be disuptive here, as my comment on your previous thread makes clear, I have no problem with the basic theoretical physics. What I’m trying to establish is the applicability of the basic physics to Keihl and Trenberth’s radiation budget diagram.
I’m sure the Stefan-Boltzmann equation is correct, but I’m not so sure about it’s applicability to the question of the amount of upward LW radiation from the ocean, the biological matter covering it’s surface, and the absorption in the moist air between it and the measuring device.
So please could you point me to some, or even just one measurement of the upward longwave radiation from the ocean surface and a description of the hardware used to perform the measurement.
Thanks.
[…] a new post over at Science of Doom entitled Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three the Creation of Energy… S.o.D posits a simple model and offers it as some kind of vindiction of the Keihl Trenberth […]
Jorge asked some good questions:
You are thinking of the cavity with the tiny hole that produces the closest thing to “blackbody radiation”.
The radiation emitted is blackbody radiation even though the surface inside the cavity wall is not a perfect emitter. This is because the radiation that finally escapes has all been emitted, not reflected.
However, this is the specific property of an isothermal cavity with a tiny hole when the exiting radiation is measured.
For radiation from the inner surface of the sphere we need to use the standard equations for emission of radiation.
This is correct, the energy is stored in the PVC. Take a look at Do Trenberth and Kiehl understand the First Law of Thermodynamics? – Part Two – you will see the heating effect through the sphere.
Thank you for your explanations.
It was indeed the cavity with a hole that I was thinking of. I am still not quite sure of the mechanism for black body radiation appearing out of the hole but that is probably a diversion from this topic.
I was impressed with the ease with which you produced the energy time graphs. Do you have some package for this or did you solve the heat flow equations from scratch? I remember seeing a book full of graphs back in the sixties showing the evolution of temperature versus time/distance for a wide range of geometries and forcings.
I have had a rethink about whether there is any energy stored in the photon cloud within the sphere and I now believe there is some. I can´t do the sums but it seems likely that it will be tiny at the temperatures in your example. There certainly does seem to be a concept of energy density in a radiation field and it is measured in Joules per cubic meter. If it is easy to compute the total energy stored within the whole volume it would be interesting to see how it compares to the amount in the PVC.
Again this is wandering away from the basic back radiation and its effects that bothers many of your commenters so it is no big deal.
Here is the energy radiated from the outer surface, vs time:
Energy stored is the difference between energy in (30,000 x time in seconds) AND the “area under the curve” in the graph (energy out).
Energy stored goes into increasing the temperature of the PVC sphere.
Notice that in the early days the energy radiated from the outer surface is almost nothing. Later the energy radiated rapidly increases towards 30,000 W. This happens because the inner surface temperature increases and so heat is conducted through the sphere.
Here is the energy stored in the sphere, which goes into increased temperature:
Note that compared with the 30,000 J per second, this value is quite high.
This is because the PVC sphere is heated by the internal source for a long time before it reaches steady state. The continual increase in temperature as a result is what eventually drives the heat out.
tallbloke:
When you write on your own blog about my recent article: “I think this is something of a trojan horse”.
It indicates that your questions are not ones to spend too much time on.
I try and discuss a subject with people who have questions, or with people have a theory that they want to put forward – because they believe in it or because they want it to be tested.
For people who clearly have a particular theory but won’t articulate it for whatever reason, I’m much less interested.
S.o.D says:
“sufficient measurements have been done to be confident that the Stefan-Boltzmann equation is correct and so if the SST is known accurately the emission of radiation is also known accurately.”
But NASA says:
Click to access 19990100634_1999169386.pdf
“Recent measurements of spectral reflectances of surface
materials have clearly demonstrated that surface emissivities
deviate considerably from unity, both spectrally and
integrated over the broadband. Thus, assuming that a surface
radiates like a blackbody can lead to potentially significant
errors in surface temperature retrievals in longwave surface
energy budgets and in climate studies. ”
On the face of it, your claim that an accurate figure for LW emission can be determined from the Stefan-Boltzmann black body equation and the surface temperature is falsified.
S.o.D says:
For people who clearly have a particular theory but won’t articulate it for whatever reason, I’m much less interested.
I stated my question/theory way back on my blog when you first entered the fray there. It is that the surface of the ocean doesn’t emit longwave radiation in accordance with the Stefan-Boltzmann blackbody equation.
And it appears NASA agrees with me.
Is this relevant?
http://www.agu.org/pubs/crossref/2010/2009JD012758.shtml
My next step would be to do citation back-and-forth trace to find other relevant materials, but a bit bust ATM.
(New to this blog. Some great stuff here SOD.)
You can see test data for Minnett’s instrument in Figure 10 of Minnett, J. Atmos. Oceanic Technol., 18, 994–1013 (2001) http://journals.ametsoc.org/doi/full/10.1175/1520-0426(2001)018%3C0994%3ATMAERI%3E2.0.CO%3B2
It looks like the IR emissivity of water (presumably in the lab) is very near 1.0 for a useful range of temperatures and wavelengths. In the real ocean (with a skin temperature difference arising from evaporative and radiative cooling, wind, waves), there is generally good agreement (<1 degC) between surface temperature calculated from IR (which assumes that the lab measured emissivity is correct) and the bulk temperature when the ocean temperature changed by 20 degC. (Figure 12)
I suspect that NASA is referring to materials other than water that have IR emissivity <1. We can measure sea surface, but not land, temperature from space because the emissivity of land surfaces varies, but water does not.
Your link states that:
“The M-AERI is a robust, accurate, self-calibrating, seagoing Fourier-transform interferometric infrared spectroradiometer that is deployed on marine platforms to measure the emission spectra from the sea surface and marine atmosphere. ”
And Minnett states:
“the emission from the sea surface was calculated from the Stefan-Boltzmann equation using the skin temperature measurements of the M-AERI.”
“I suspect that NASA is referring to materials other than water that have IR emissivity <1."
You need to suspect anything, just read the paper at the link I provided.
Thank you Bryan!
Is it something like ‘pressure’ which is creating this insulation in the sphere?
I have also been trying to work out what made the first plate hotter in the Spencer example if you know that one. Insulation came to mind there, but I couldn’t understand why the first plate had reached an equilibrium before it then got hotter after the second plate heated up or why the second plate didn’t get as hot as the first. But now I see, I think, that the first plate is doing what a human body is doing trying to conserve its heat and stop from freezing which it does by making the barrier to loss thicker. The second plate is acting like the PVC, creating a barrier to heat loss, and so the original heat source can continue to get hotter, by making the space less cold? Like putting on a small electric fire in the room will make the space less cold and so heat from the body doesn’t get extracted as quickly?
Myrrh:
I remain unconvinced by the Spencer thought experiment. Let T1, T2 and T3 be the equilibrium temperatures of the one plate on its own, of that plate in the 2-plate situation and of the second plate, respectively. Let the plates have identical areas, A. In both the single and the 2-plate cases the product of the radiative flux and the area must equal the input power, which is the same for both cases. Therefore:
AT1^4 = A(T2^4 + T3^4)
1 = (T2/T1)^4 + (T3/T1)^4
Since (T3/T1) > 0, (T2/T1) <1 and T2 < T1
That is, the equilibrium temperature of the first plate is lowered by the presence of the second one, the opposite of Spencer's claim.
SoD, Mike Ewing:
“What you are overlooking with your experiment, is that radiation is a product o T, not E, although the water contains more energy than the empty freezer, it has the same entropy, but a much larger capacity to absorb energy, than the empty freezer.”
“The radiation from the water, will decrease the rate at which the air can move energy into the water, the closer in T they are, the slower the exchange.”
Some radiated LW in f2 is lost to the surrounding room…but most is reflected. That portion reflected must go somewhere…won’t the bottles absorb that energy? Won’t that increase the bottles temperature? In fact, will not the middle most bottles, those with limited view factor to freezer walls, receive large amount of LW from neighboring bottles causing them the heat up faster then those on the periphery? Stated otherwise, the cold bottles increase one another’s energy and thus temperature simply due to proximity….yes?
the cold bottles increase one another’s energy and thus temperature simply due to proximity….yes?
No, because they would only be absorbing what they are radiating, it wouldn’t change their T, entropy does not decrease. This is not introducing energy into the system, its simply chaos in motion.
For a change in T, more energy must be introduced into the system, in your freezer experiment, it would over time move from the higher chaotic concentration(warmer room) through the walls, doors, and seals of the freezer into the freezer, and the rate that it is able to move through these(which is a question of the exact material properties/ and condition o seals, T inside freezer etc), is going to set the rate at which each freezer warms, but the simple fact that water requires larger amounts of energy, to effect a change in temperature.
The back radiation, in your examples effect, is going to be to effect the rate at which energy can be exchanged from the freezer walls to the interior of the freezer, that is all. It cannot create more energy, it can effect the rate of movement of energy, however.
By stacking the bottles tightly together, you could further slow the rate it warms, because the bottle surfaces in contact would only be swapping energy(through radiation) back and forth, but not increasing or decreasing the energy content of the touching faces(which is what is also happening internally in a solid when it is at a constant T, the exchanges balance). This would also limit surface area for conductive energy exchange, from the warmer air as it warms, and decrease the surface area to mass ratio available to absorb higher energy LW from the walls/air in the freezer.
Obviously, this is something we are all familiar with… it takes longer for a big chunk o ice to melt, than the same volume broken into many small chunks o ice.
Mike Ewing:
“No, because they would only be absorbing what they are radiating, it wouldn’t change their T, entropy does not decrease. ”
“Absorbing what they are radiating” is exactly what happens in SoD Radiation Basics and the Imaginary Second Law of Thermodynamics post…yet then both bodies increase temperature due to proximity. Surely this radiation does not care about it’s origin or whether it falls on a warmer or colder body. If the LW does not escape and is not absorbed by bottles, where does this radiation go?
tallbloke,
Did you actually read your linked source or just the abstract? In the 8-14 micrometer window, the emissivity of water is about 0.98. How is that not emitting LW radiation in accordance with the S-B equation? Assuming that water emits as a black body causes only a 2% error. That’s good enough for the purposes of SoD’s example but not when you’re trying to close the global energy budget. What the NASA paper is about is improving the accuracy of surface temperature measurements and LW energy budgets. The big errors, and most of them are not big, are not due to the ocean but to features on land with barren and open shrub land needing the largest correction.
Hi DeWitt,
yes, I read the paper, including table 4 which shows that the emissivity of clear lab tested water is assigned to the entire oceans of the Earth. I also looked at the graph for water which shows more than a 2% difference from unity beyond 11um. And I also read the section on the variation of emissivity of soils with changing moisture content, up to 20% below unity. Keihl and Trenberth is out of the window, along with Minnett. They migh undrstand the first law of thermodynamics well enough, but they duffed up their emissivity calcs.
The issue I raised with S.o.D is not so much that we can’t improve on the error, it’s that he was intimating that we should accept K&T because the radiation could be measured. It is not measured, it is modeled using approximations.
I don’t have a problem with that, as long as the facts are explicit. And the reason for that is it’s clear that factors which can cause substantial variation in emissivity over a long timescale such as soil moisture have possibly made as much difference to the LW budget as the rise in co2 has, which raises another issue where attribution and sensitivity calculations are concerned.
If we are going to do proper climate science, we need to start with an honest assessment of uncertainty.
In the careful paper below the claimed climate predictive effects are discussed as well as the errors of observation arising in each case.
In nearly all cases the errors are bigger than the claimed effect making any conclusion vacuous.
On the meaning of feedback parameter, transient climate response, and the greenhouse effect: Basic considerations and the discussion of uncertainties
Authors: Gerhard Kramm, Ralph Dlugihttp://arxiv.org/abs/1002.0883
Problem with link above
Try this link
Cite as: arXiv:1002.0883v1 [physics.ao-ph]
Jorge:
You are correct that there is some energy in the radiation field. I haven’t done the sums either.
I use Matlab, which I got hold of recently. But I wrote the equations “from scratch”. They are very simple – see Part One.
Because of spherical symmetry values of conducted and radiated heat can only vary with radius (and time). Matlab is a great package, lots of features and takes time to learn- but very easy to do complex calculations and churn out graphs.
Matlab would be nice, but $2,000 for the basic program is a little too rich for my blood.
[…] Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three – The Creation of E… […]
[…] Update: Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three – The Creation of E… […]
Does energy have mass? If I feel heat as a wave isn’t that mass? Is this then, my example fire above, what is ‘overwhelming’ any heat I may be generating if I’m standing in front of a blazing fire?
J. Lanier.
“yet then both bodies increase temperature due to proximity. Surely this radiation does not care about it’s origin or whether it falls on a warmer or colder body. If the LW does not escape and is not absorbed by bottles, where does this radiation go?”
Ok, 1st up in SoD’s example with two bodies radiation causing them to warm more, its because its slowing the rate that energy leaves the bodies, whilst there is a separate energy input into the warmer body…. the back radiation is actually causing them to cool more slowly… and because the energy input is constant, they warm. If you stuck your freezers in a vacuum, this would be relevant, but in your example, it is not. The background T to the systems is not 2.7K. If your water bodies were in a vacuum, or the ambient T was lower around the bottles proximity to each other would decrease the rate they lost energy also…
When something radiates, it is moving energy from the body, it is not creating it. So in an isothermal situation, it is simply shuffling energy between molecules. Every time it emits it looses x amount of energy, every time it absorbs, it gains x amount of energy, and by definition in an isothermal situation, these energy exchanges will balance.
If the boundary conditions to your system(freezer) are greater T wise than in it, you will never have more energy leave than arrives… without turning it on, and physically applying work to remove energy.
So for more energy to be leaving the freezers than arriving would require the room where they are situated to be colder than inside the freezers, then if the radiation escapes, it will cause the freezers to cool more.
Mike Ewing:
“the ambient T was lower around the bottles proximity to each other would decrease the rate they lost energy also… ”
Are you saying if the temperature in the freezer is lower the bottles will heat up faster thus f2 warms faster than f1?
“If you stuck your freezers in a vacuum, this would be relevant, but in your example, it is not.”
So proximity warming (slow the cooling) of radiant bodies can only can only spontaneously occur within a vacuum.?
“Are you saying if the temperature in the freezer is lower the bottles will heat up faster thus f2 warms faster than f1?”
No, they would heat up slower than in your example, they would have looses rather than just gains. But their radiation would offset loses, rather than just shuffle energy. So they would effect the rate they cool, how quickly they warm is dependent on energy input. But the water bottles require a LOT more energy to effect a change.
” So proximity warming (slow the cooling) of radiant bodies can only can only spontaneously occur within a vacuum.?”
No also, the back radiation will offset radiative loses if there are loses, if the ambient air T was lower around the bottles for example. if the ambient T is higher, it will offset energy gains(T1^4-T2^4). The vacuum is to isolate radiation from conduction, so there can be no argument as to how the energy moves in SoD’s examples.
I said
“if the ambient T is higher, it will offset energy gains”
This is dependant on view factor, really not enough info, but if you pack the bottles together, they will increase the time it takes to warm, and increase the time it takes to cool also, just because it is limiting surface area to mass/view factor.
I realize you have cancelled my posts…
So you can keep your blog, enjoying to make a censorship of posts that are critical of your opinions…
That’s IPCC system, ridicolous, what are you thinking to do?
Do you really believe your censorship can stop scientific truth?
Keep on with your junk-science…good luck.
Bye, Engineer.
Note for other readers, no posts from Engineer deleted, nothing from this person in the spam queue. Quite a few still on display for those interested in searching for amazing insights.
tallbloke,
I certainly won’t dispute that point, although the mechanism may not be a change in emissivity. If the emissivity goes down, so does the absorptivity, so things may still balance. Nor will Roger Pielke, Sr. His position is that CO2 is only one of several first order climate forcings (main conclusions). Land use/land cover may not be as important globally as CO2, but it definitely has a local effect and in the end, everything is local.
Science of Doom,
Great post.
The only detail that doesn’t seem right to me is that the dimensions of the PVC seems to have no effect on the ‘effective’ conductivity. Is this right? I would think that the actual conductivity would be slightly higher than what it would be for a slab of PVC.
Mike Ewing:
“The vacuum is to isolate radiation from conduction, so there can be no argument as to how the energy moves in SoD’s examples.”
I’m quite aware of the rational behind isolating the hypothetical examples to a vacuum. My original question was “Does this example work variables reversed?” Said otherwise will cold bodies in the absences of a vacuum retard or accelerated their own warming, simply due to proximity This was my thinly veiled attempt to be cleaver, to have SoD argue against atmospheric forcing. And to some degree you have…you thoroughly explained why these bodies retard their own warming….I agree. Herein lies the problem. Proximity warming, save atmospheric forcing, does not exist outside vacuum…as such untestable. If I’m mistaken please elaborate.
Say that a person is totally immersed in an ice bath.
Now take a body sized bag of water at 70F and let the person hug the bag while immersed in the ice bath. Obviously the warm water bag (though lower temperature than the person) will be warm relative to the ice bath.
That same 70F bag of water would be relatively cool if instead we immerse a person in 120F water.
So the 70F bag slows the cooling of the person when in the ice bath and it slows the warming of the person when in 120F bath. Where’s the contradiction here? Is it a contradiction or paradox that the 70F bag doesn’t always have a warming effect?
Mike Blackadder:
I understand your point …yet your example misses the point of my challenge. I’m not questioning relative temperature do to proximity, but rather radiant warming, or lack thereof, due to proximity. Atmospheric forcing (LWR) is a phenomenon which exists alone…outside the bounds of a vacuum. Are there other example of similar processes absent a vacuum?
J Lanier,
It may be that I misunderstand your point. I don’t see why proximity warming (whether or not it is radiant) only exists in a vacuum.
Mike Blackadder:
The proximity warming, to which I’m referring, a colder body’s radiated energy warms, or slows the cooling, of a warmer body thereby increasing the warmer body’s temperature. See SoD post Radiation Basics and the Imaginary Second Law of Thermodynamics. My point, this process can only take place within a vacuum…accept that is for atmospheric forcing. Because it is this hypothesis is untestable and has no applicable equivalent, we are left to arguing data records and the significance to the hypothesis. Unlike most science which develops theories based upon observation, non-vacuous proximity warming is a theory in search of observations…evidence.
There are more variables than what you are allowing for, say you are outside, in winter, its -30C, the sun is rising, there is an exposed rock that has absorbed some of the sunlight, and its T is -15C, you would warm faster if you took shelter in front of the rock, warming yourself in the sun, than what you would in the open.
Or you’re walking home from the pub one night, a frost has formed on the ground, you can feel the cold seeping through your bones, then you go over to the tar seal, and notice it hasnt frozen yet, its colder than you, but you can feel the difference.
But as in all things, its relative.
SOD,
There’s a point about this model and also Willis Eschenbach’s Steel Greenhouse that confuses me.
Let’s say that you have a Steel Greenhouse like Willis proposes, but that the radius of the earth is very small relative to the radius of the Steel greenhouse.
Lets say that the earth and the shell are both blackbodies and that the Earth’s temperature is such that it radiates 235 W/m2 and the Steel Greenhouse is at a lower temperature and so it radiates 200 W/m2 (ie. we are not necessarily in thermal equilibrium yet).
If the greenhouse radius is ~ 4 times larger than the Earth’s radius then is there not approximatly 16 times the wattage radiated towards the Earth than what is radiated away (simply due to the larger surface area of the greenhouse)?
Doesn’t this suggest that the shell which is at a lower temperature is actually increasing the temperature of the planet and therefore is contrary to the 2nd law? What am I missing here?
Mike: When the shell is close to the earth’s surface, essentially all of the radiation emitted inward by the shell gets absorbed by the earth’s surface. When the shell is very far away, some of the radiation emitted by the shell misses the earth and lands on another part of the shell warming it rather than the earth.
Frank,
Thanks for your reply.
This makes sense. The inner surface is emitting radiation isotropically. It isn’t as though radiation is being focused to the middle of the sphere.
tallblokeNovember 16, 2010 at 6:33 pm:
If we are going to be honest evaluators of climate science we should do our homework.
If we can’t do our homework we should at least be honest about that.
Why don’t you do some research and summarize the work of the last few decades on measurements of ocean emissivity?
I look forward to reading about it on your blog. Or you can post your results here.
STill unable to engage with uncertainty S.o.D.?
I’m not surprised.
But thanks for encouraging me to do more homework around the issues of radiative interfaces. Hopefully I can encourage you to do some homework around engineering concepts describing heat engines and the large scale thermodynamics that will help you understand the bigger picture, beyond the narrow focus of radiative physics.
tallbloke:
Instead of you making empty claims, I’m asking you to do some work.
I’m asking you to prove your case – that climate science hasn’t bothered to check the emissivity of the ocean.
I’m sure your literature review will be revealing.
My ‘claims’ about uncertainty are of a more general nature than ocean emissivity, which in any case are proven by links already provided here. I suggest you read Judith Curry’s testimony to congress made yesterday to assist you. http://judithcurry.com/2010/11/17/uncertainty-gets-a-seat-at-the-big-table-part-iv/
Reply to Tallbloke (11/17 8:48): I read your reference and agree with DeWitt. I didn’t find anything there that invalidated the K-T diagram or Minnett. In Figure 9, the largest corrections they found were 6 W/m2 and the global average is less than 3 W/m2, so the corrections are about 0.5% of the upward long wavelength flux from the ground. If you want to use emissivity to subtract 2 W/m2 from K-T’s value for upward long wavelength flux and add it to convection, fine. As for Minnett, their instrument is calibrated vs water temperature under conditions where the bulk water temperature and skin temperature are the same. So they should have an accurate measure of the difference between the skin layer and bulk water in the open ocean. But one doesn’t need Minnett to know that the skin layer must usually be cooler than the surface – the losses to evaporation and net long wavelength radiation are too big to be compensated for by the small fraction of shortwave radiation that gets absorbed by the skin layer.
Click to access 50010017.pdf
The sea surface emissivity in the infrared region is determined on the basis of data
analyses. Net radiation, surface irradiance and other oceanographical and meteorological
variables are measured throughout most of the year at the oceanographical
observatory tower in Tanabe Bay, Japan. We have found that 0.984 ±
0.004 is a reliable emissivity value from the night time data. Surface emission
radiates not from the subsurface water but from the sea surface. The thermal skin
layer on the sea surface, however, is disturbed and disappears under high wind
speed over 5 m/s through the analyses of the radiation observation using the
emissivity value of 0.984. Under low wind speed, the sea surface can be cooler or
warmer than the subsurface due to overlying thermal conditions, and the skin
layer can be neutral as the transient process between them. By using an emissivity
value of 0.984, the temperature difference between the sea surface temperature
and the temperature determined from surface irradiance that has been reported
in the satellite data analyses is found to be reduced by half.
I put it to you that over most of the globe most of the time, here are low winds over the oceans, wich will substantially reduce any differential between skin temperature and immediate subsurface temperature. Minnett seems to think conduction is the primary process for transfer of heat near the surface of the ocean. S.o.D and I are in agreement that this is not the case. Where we differ is that he thinks this means lots of energy from DLR is going to get mixed down into the ocean, whereas I think the buoyancy of the water near the surface means the heat flux is in general going upwards and being lost from the ocean with the latent heat of evaporation.
Perhaps in stepping back and thinking about the ocean-atmosphere as a coupled system, it might be clearer that the various physical processes are going to work together to maximise heat loss from the ocean, since the Earths climate is a heat engine, moving heat from the equatorial regions where most heat enters the system, to the poles where it can most easily lose energy back to space. Somewhere in the mid latitudes, the atmsphere takes over from the ocean as the major heat transporter, so it’s pretty clear that there will be auto-regulation of the process in the shifting north and south of the latitudinal band where the switchover occurs.
It would be informative to calculate jut how far that latitudinal band would have to move to equilibriate for the change in co2 level and it’s forcing, assuming the drop in mid troposphere humidity since 1948 hasn’t offset it anyway.
Apologies for the typos – ancient keyboard.
…there are low winds over the oceans, which will substantially reduce any differential…
Frank said:
“If you want to use emissivity to subtract 2 W/m2 from K-T’s value for upward long wavelength flux and add it to convection, fine.”
I’ll put up a post on free path lengths and we can discuss it there.
Tallbloke: Whatever the mechanism of heat transfer, we know that seasonal warming due to increased insolation penetrates down about 100 m over several months. For example, see Figure 6.7 of http://oceanworld.tamu.edu/resources/ocng_textbook/chapter06/chapter06_04.htm If your speculations are consistent with this observation, there is hope.
If you watch a video of the annual cycle of the arctic ice cap, you may gain a greater appreciation for how important the Gulf Stream is to Arctic temperature, particularly north of Scandanavia. (This experience isn’t offered as proof that the major mechanism of heat transport into the Arctic can’t be the atmosphere. Proof requires real data.)
Frank I try not to speculate.
http://eesc.columbia.edu/courses/ees/climate/lectures/o_atm.html
“While the ocean gains heat in low latitudes and losses heat in high latitudes, the largest heat loss is drawn from the warm Gulf Stream waters off the east coast of the US during the winter, when cold dry continental air spreads over the ocean. An equivalent pattern is found near Japan, where the Kuroshio Current is influenced by the winter winds off Asia. It is in these regions that the atmosphere takes over as the major meridional heat transfer agent.”
So we’re both right, and I should have said ‘high mid latitudes’ rather than just ‘mid latitudes’.
Mike Blackadder:
Conductivity is a material property. The maths for different geometries is different, but the conductivity doesn’t change.
If you take a look at the maths section in Part One:
So you see that the results are a little different for the sphere compared with the slab.
Okay, so you did take into account the geometry. Thanks for the clarification.
Mike Blackadder:
I think it is the geometry.
In Willis’ model the radius of the steel shell is almost the same as the earth.
In your model the radius of the shell is 4x the radius of the earth.
This means the energy incident on the inner surface of the shell is 1/16 of the energy radiated from the surface of the earth. Which changes the equations accordingly.
Does this answer the question?
Mike Ewing:
“Or you’re walking home from the pub one night, a frost has formed on the ground, you can feel the cold seeping through your bones, then you go over to the tar seal, and notice it hasnt frozen yet, its colder than you, but you can feel the difference.”
Lets continue your story..suppose you were to stroll over a bridge, lean over the railing and peer down to the yet frozen river. Surely a large mass of water radiating great quantities LW towards your face will scorch you eyebrows. Does the greater energy radiating from the tar seal or the river increase your skin temperature above 37C. Of course not. However, colder lower energy CO2 apparently raises Earths energy and thus temperature 33 C. So I ask again, does there exist another non-vacuous example of this phenomenon?
Energy content, does not equal radiative power, temperature does, i thought i said that already 😉
With the greenhouse effect, it works because the atmosphere is transparent to shortwave, but not longwave. The only way it has to leave the atmosphere is through radiation.(or alternatively energy would just build up until the gases reached escape velocity) So from what we have discussed, we have determined, that energy flow is limited by the T differential(not just radiativly either, also through conduction and convection)
The ole, heat cant flow from a colder source to a hotter… and by extension, the closer in T a object is with its neighbor, the less net energy can be exchanged(this is what we have been discussing)
So to transport the energy up, through the atmosphere to an altitude where it can escape to space requires a T gradient, and its the density of the greenhouse gases at a given altitude that set this(CO2 is one GHG) So the higher up you go, the less molecules per given area there are, the further radiation can travel, til you reach an altitude where on average it escapes.
Energy flow, is all around you. All you have to do is be observant, a cold wind, will cool you more than a hot wind…even if they are both below your body T. The difference with a planet, is that it does not moderate what it absorbs and emmits to maintain a certain temperature as our bodies do. If you restrict the rate energy leaves, but not the rate it enters the system, it will accumulate. But Temperature is a negative feedback on its own, so it will always work back towards balance.
Mike Ewing:
“Energy content, does not equal radiative power, temperature does”
So on average, what is the temperature of the radiating atmosphere?
tallbloke on November 18, 2010 at 3:17 pm:
If you want to be taken seriously you need to provide specific claims and research rather than throw doubt at something, then when pressed “move on”.
You raised the question about measurements of the emission of radiation from the ocean here on November 16, 2010 at 8:30 am (and on your blog):
I commented:
Then you cite a paper:
The Stefan-Boltzmann equation is:
j = εσT^4
If ε=1 this is a blackbody. If ε<1 this is not a blackbody and yet the Stefan-Boltzmann equation is still true.
So if the emissivity, ε, of the ocean is known then the results for the emission of thermal radiation from the ocean are known (from SST measurements).
You then cite a paper which states that lots of areas of the earth don't emit like a blackbody and say "therefore, your claim is falsified”
I haven’t said that the ocean emits like a blackbody, although in fact it is very close. I have said the ocean emits in accordance with the Stefan-Boltzmann equation.
You haven’t falsified anything. You are just demonstrating that you are quick to jump to conclusions.
Back to my earlier point – you have thrown doubt at the values of ocean radiation. You imply that no one has measured these values.
Shoddy work by climate science once again?
Or zero research by the “skeptic”?
I look forward to an honest assessment by you on this topic.
S.o.D says:
Back to my earlier point – you have thrown doubt at the values of ocean radiation. You imply that no one has measured these values.
Plenty of radiation readings have been taken near the sea surface. What interests me, looking at the hardware design, the methodology and the interpretation, is what is really going on at the sea-air interface, and what it is that the hardware is actually measuring. And what affects energy transfer between an ocean which stores solar energy on seasonal, multidecadal and millenial timescales in stratified layers, and an atmosphere which loses a lot of its energy to space overnight.
I’m interested in those questions rather than your misrepresentations and post editing of what I write.
tallbloke:
“Misinterpretations and post-editing” ?
You stated that you had falsified my claim. Pretty simple. Is this true or not?
It’s not, but rather than acknowledge your own error, why not instead claim bad intentions on my part?
And just state a different question that you are interested in and point out that no one has answered this one. And that’s what you wanted to know all along.
You can never be wrong this way. And anyone who tries to address any claims is “misrepresenting you”.
science of doom,
“I think it is the geometry.
In Willis’ model the radius of the steel shell is almost the same as the earth.
In your model the radius of the shell is 4x the radius of the earth.
This means the energy incident on the inner surface of the shell is 1/16 of the energy radiated from the surface of the earth. Which changes the equations accordingly.
Does this answer the question?”
Agreed. The part that I’m uncertain about is how much heat emitted from the shell will actually reach the planet.
It doesn’t seem possible that all the heat transmitted from the inside of the shell will be incident on the surface of the planet, otherwise you could set up a scenario where a lower temperature shell will transfer a ‘net’ amount of heat to a higher temperature planet (simply due to the much larger surface area it is emitting from). This would obviously be a violation of 2nd law (effectively perpetual motion of the 2nd kind).
Mike Blackadder
The amount that reaches the surface of the earth is the flux from the surface of the shell times the surface of the earth. The surface of the earth sees a sky at constant temperature. The problem can be solved analytically, I think, but it can also be solved numerically. Suppose we have a shell initially at 0 K with an area 16 times the area of the earth. We’ll postulate the sky beyond the shell is at 0 K. The earth has an internal power source that produces sufficient power that 235 W/m2 is radiated. The sphere then sees 235/16 or 14.6875 W/m2. Half of that will be radiated outward and half inward. Now the earth sees 235 W/m2 from the inside and 7.34375 W/m2 from the sky. The temperature goes up enough that 242.34375 radiates from the surface and the shell sees 15.146 W/m2. Keep that up and after 4 iterations things have converged at the 0.0001 W/m2 level. The surface temperature of the earth has increased from 253.7296 K to 255.7515 K and the shell temperature is 107.5303 K. Note that I don’t care anything about what the shell radiates internally that isn’t absorbed by the earth. That radiation will be exactly matched by radiation from the opposite part of the shell.
That makes sense. The larger the outer shell, the smaller the proportion of a 180degree view from a given point on it is taken up by the earth, and the greater the proportion taken up by the outer shell .
And a 180 degree view from anywhere on a surface (assuming its a perfect sphere is going to see the shell)
Thats what you’re saying isnt it?
End o the day, the reality it is more like an onion, than a single shell o course. But the same principle would apply.
Mike Blackadder:
Drawing not to scale, see text.
The equations are quite simple, assuming that the “ring” is totally transparent to solar radiation and totally opaque to terrestrial radiation. And assuming that the surface of the earth is all at the same temperature.
At the surface of the earth, the total incident radiation is S + A. Therefore the earth surface must radiate:
E = S+A [1]
to balance the incoming energy.
The “ring” receives incident radiation, E (and nothing of S).
The ring radiates 2A, where A is the radiation from each surface.
E = 2A [2]
Therefore, A = E/2 [3]
[3]->[1] E = S + E/2
Therefore E – E/2 = S
Therefore E/2 = S
E = 2S
These equations are true if the radius of the ring is nearly equal to the radius of the earth.
As the radius increases, all of the earth’s radiation is still incident on the “ring”. But some of the “ring’s” radiation is now incident on itself, with the balance on the earth’s surface.
This is called “view factor”. The proportion of the radiation from the “ring” incident on the earth’s surface = Ae/Ar, where Ae = surface area of the earth, and Ar = surface area of the “ring”.
Now aside from that, if we want to work out the temperature of the ring, we have to know the radius.
From the Stefan-Boltzmann equation, A = εσT^4.pi.r^2
As the radius of the ring increases the radiation is “shared out” over a larger area, reducing the ring’s temperature.
[Note, I see DeWitt Payne has also answered this while I have been writing]
Does this solve the problem or is it still unclear?
Thanks very much for your explanations (Frank, Dewitt Payne and scienceofdoom).
It all makes sense now.
I was previously trying to work out the proportion of the shell’s radiation that would be incident on the earth by an approach similar to what Mike Ewing described above.
The Ae/Ar ‘view-factor’ definitely simplifies that calculation.
The proportion of shell radiation incident on the earth is exactly equal to the proportional intensity of the earth radiation once it reaches the shell. This makes sense. If for example the Earth and the shell were the same temperature and therefore emitting the same radiation intensity, then there must be no net transfer of radiation between them.
And here are the graphs of temperature and radiation:
The solution to the equations above is achieved by defining:
energy in = energy out
-at the surface and at the ring.
For the purposes of this illustration, the solar radiation absorbed by the surface is the same value as occurs in the current earth. And the ring and earth are treated as a blackbody.
There are still a couple of questions I would like to ask. To be clear, I have no problem with the calculation of the outer surface temperature of the sphere at equilibrium and no problem with the temperature difference to the inner surface.
The first question is to confirm that the emissivity of the inner surface plays no part in these equilibrium calculations and that it played no part in the calculation of the dynamic energy/time graphs.
If this is true my next question is about what would happen if we applied a magic coating to the inside surface of the PVC that reduced its emissivity. Suppose, for example, we change the value from the original 0.8 down to 0.008. Will this change the mysterious internal radiation from 1452 W/sq m to 14.52 W/sq m.
Going further, it would seem we could make the internal radiation arbitarily small by using the magic coating to reduce the emissivity even more. I imagine, in the best case, we could get a zero value and have no internal radiation at all. The problem then arises that I can´t see how the inner surface is ever going to absorb the required 23.9 W/sq m needed to reach equilibrium.
My guess is that this is simply a maths paradox that cannot happen in the real world because the required zero emissivity never occurs.
If I understand your example correctly it appears that the internal radiation is simply an interesting curiosity that has no practical importance. In particular, it has nothing to do with determining the temperatures of the inner and outer surfaces of the sphere. All the important internal consequences have been hidden from view by choosing to use a point source.
Jorge,
The emissivity of the outer surface is very important for determining the temperature. Since the emitted power must be constant at steady state, the temperature of the outer surface will be inversely proportional to the fourth root of its emissivity. That will raise the temperature of the inner surface because the temperature difference to transmit the power through the PVC is still the same. Of course as the temperature goes up the PVC will first melt and then break down.
As long as the interior surface isn’t a perfect reflector and the emissivity of the outer surface is constant, there is no effect on the temperature of the interior surface from changing the emissivity of the interior surface. I’m assuming you mean that the decrease in emissivity is accomplished by increasing reflectivity while transmissivity remains equal to zero. If you look at the interior surface of the sphere, you will still see not only the emitted radiation but also the reflected radiation. So for SoD’s case where the emission is 1452, emission plus reflection is 1452/0.8 = 1815 W/m2.
If you keep the emissivity of the outer surface constant and lower the emissivity of the inner surface to 0.008, emission will be 14.52 W, but the total of emitted and reflected will be 14.52/0.008 = 1815 W/m2, exactly the same as for 0.8. If the emissivity of the PVC was equal to 1, the exterior temperature would be 125 K, the interior would then be 415 and the emission from the interior surface would be 1692 W/m2. Assuming the source has a finite area, its temperature must go up as the reflectivity of the PVC exterior goes up.
DeWitt Payne,
That was a very helpful response. I was already confident that the external temperature was purely a function of the external emissivity, the outer radius and the power to be radiated. Similarly, the temperature difference across the PVC depends on the two radii, the thermal conductivity and the power to be transmitted.
I think you have confirmed that the emission from the internal surface is not very interesting in the case of an closed cavity as it has no effect on the inner or outer temperatures of the sphere.
What I found most valuable was the number 1815 W/m2 that you calculated. This is clearly the radiation to be expected from a black body (emissivity =1) at the temperature of the inside surface. It is now obvious to me why it would be blackbody radiation that would emerge from a small hole in a cavity, dependent only on the internal surface temperature.
My education continues!
Jorge,
On further reflection, (pun intended), the situation is more complicated. If the walls are partly reflective, the blackbody temperature observed through a small hole would be higher than the wall temperature. This is because the energy from the source isn’t all absorbed on the first encounter with the wall. It will all be absorbed eventually, but the extra photons bouncing around increase the apparent flux. That means the total photon flux for an emissivity of 0.8 would look like a blackbody at 424.728 K instead of 423 K with a flux of 1845 W/m2 instead of 1815 W/m2. Things really get ugly at a reflectivity of 0.992. The effective blackbody temperature is 539.4 K with a flux of 4799 W/m2.
This is only true for an internal heat source with heat leaking through the walls. If there is no internal heat source and the walls are maintained at constant temperature, the observed blackbody temperature will be very close to the wall temperature regardless of the emissivity. At low emissivity, though, the observing hole has to be very, very small.
The discussion is interesting.
What I find interesting about many of these discussions, here and on other sites, is that many people are under the impression that a large body only emits in some sort of uniform radial manor with photons only moving away from the object in some orderly fashion and as they move further away the distance between them increases.
They seem to dump those ray tracing diagrams they did at school and focus on those animations of radar (which in any case is a manipulated and managed source of electromagnetic radiation), with radial lines emanating from the transmitter.
They seem to forget the random nature in which emission occurs and that it is only at a distance at a particular point that the photons are travelling towards you.
If there were some sort of uniform emission (like in a radar animation), then we wouldn’t see the ‘perimeter’ of a sphere, no matter where you stood, you would only see the central part.
The fact that the perimeter of the sphere emits in all directions, means we see it as a sphere with crisp outlines and not as a fuzzy blob.
I remember on another blog, with similar discussions to the ones here, someone made claims about point sources and radiating emissions. It is easy to get confused by idealised scenarios, forgetting what is actually happening.
I guess I should point out that I meant a sphere that was a source of emission and not just reflecting electromagnetic radiation (light). Although the principle of why we can see the perimeter and not just a fuzzy central section is the same.
Photons aren’t are particularly good way to look at light anyways (it’s not like they are real or anything), but I wouldn’t call emission random for practical purposes (in large scales it’s pretty constant and small scale isn’t particularly important as photons are really cheap and you can get a lot of them for very little).
“Photons aren’t are particularly good way to look at light anyways (it’s not like they are real or anything)”
Not sure it is worth responding to a statement like that.
One could say that about anything if we start philosophising about life, so it doesn’t make a lot of sense.
The point I made badly (and might do the same again!?) is that I have come across people that don’t understand the nature of emissions, even on a large scale. Emissions from any single point on a spheres surface radiate outwards in a hemisphere shape with the centre at the point of origin of the emission. When you extrapolate this to the whole sphere and traced all the paths to an eye, you would see why the eye (sensor) picks out the image of the emitting sphere.
I disagree about your opinion on particles. The days of separating what happens at the small scale from what happens at the large scale are probably over and have been for quite some time for many.
Although for many engineers and scientists it makes sense to not worry to much about the small scale.
DeWitt Payne,
I had wondered about the effect of not absorbing all the source energy on its first encounter with the inner suface but could not get my head round the implication. It is now much clearer.
In some ways I quite like this model that SoD has devised because it shows that it is the radiation from the outer parts of the atmosphere that has to be balanced by being at the right temperature. The temperature drop across the shell mimics the lapse rate which fixes the temperature of the earth. I am less sure about whether it sheds much light on the question of back radiation.
Of course, a gas shell is much more complicated than a PVC shell, not least, because of the dependence on wavelength when calculating where photons are generated and where they finish up.
Warmcast,
Most of the numbers on radiant power are for power integrated over a full hemisphere (π steradians) and the direction is just the perpendicular to the observing plane. A pyrgeometer, for example, is a small thin flat plate with a coating that has high absorptivity in the thermal IR. It is covered by a dome that transmits radiation with wavelengths from 5 to 50 micrometers, so it sees the whole sky when mounted with the plate parallel to the surface. The temperature of the plate is then proportional to the thermal radiation it absorb and is reported as W/m2. The AERI spectrophotometer has of field of view of 1.3 degrees straight up. So the output would be W/m2/steradian.
[…] While writing a new article – What’s the Palaver? – Kiehl and Trenberth 1997 – I thought that I should separately explain a few things which related to the earlier article: Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three. […]
[…] See also Do Trenberth and Kiehl understand the First Law of Thermodynamics? Part Three – The Creation of E… […]
[…] errori incredibili (e che peraltro l ’autore dell’articolo si guarda bene dal correggere!) apparsi tempo fa in un articolo sul sito “scienceofdoom”, blog molto amato dai paladini delle teorie dell’AGW, e considerato […]
I just finally unsubscribed from the pointless exchange with Joules . I assume you’ve got the calculations correct . You’ve just got two functions to consider , Fourier for conduction , and Stefan-Boltzmann&Kirchhoff for radiation from the surface .
But I continue to fail to see the relevance of a ball with a heat source at its core unless you are considering geothermal heating which I understand to be orders of magnitude less than that from the sun .
The model of interest is an externally radiantly heated colored ball surrounded by a thin colored transparent layer .
The next complication to address is that transparent layer being fluid , indeed compressible , and the much greater complexity convection introduces .
Still , there is only about 10c increase over a gray ball to be explained .
Bob Armstrong:
I’ve explained it to you before many times. If you can’t understand it, so be it. Good luck in your endeavors.
[…] Do Trenberth and Kiehl understand the First Law of Thermodynamics? & Part Two & Part Three – The Creation of Energy? […]
It is conservation of energy not power. You do not seem to understand the basics!
Alan. Technically, you are correct. So what does CoE say and not say about power and power fluxes?
In this example, an internal 30,000 W power source is specified and the system is in a steady-state (the temperature isn’t changing anywhere), so 30,000 W must leave the surface. In one second, that is 30,000 J delivered by the power source and 30,000 J leaving the system. If these quantities weren’t equal, then CoE demands that the difference become “internal energy” or higher temperature – an option inconsistent with a steady-state. Over a year, that would be 0.946 TJ of energy from the power source and 0.946 TJ leaving the system. Have we learned anything new by discussing CoE rather than conservation of power?