I write this article as a placeholder to send people to – and as a request for information.
On another blog, there was a confused article posted about the earth’s energy balance. Within the article was this statement:
Earth is a grey body, because it has volume, a black body does not have volume, simply that is the end of “the controversy”.
As I said in my comment to the article:
I have seen similar inaccurate comments before but can’t fathom where they came from.
A followup comment to mine reinforced the point that I just don’t understand:
- what many people believe about blackbodies, or
- what many people believe conventional climate science believes about blackbodies (and why it’s supposed to be wrong)
So this is a request for clarification of “the problem”
I will post examples of changing temperature for a blackbody and a non-blackbody. But because of my lack of understanding of “the problem” I have no idea if these examples will highlight particular areas of disagreement, or are completely accepted by all.
Just before the examples:
My understanding, gained from dull textbooks on the subject of heat transfer and atmospheric physics:
The difference between a “grey body” and a “black body” is this:
1. A blackbody has an emissivity of 1. So energy radiated in W/m², E = εσT^4, where ε=1.
2. A non-blackbody has an emissivity >0 and <1. So energy radiated in W/m², E = εσT^4, where ε<1.
No other physical properties are related to this parameter called emissivity, or to the difference between “blackbodies” and “non-blackbodies“.
Unrelated parameters:
- Mass
- Specific heat capacity
- Color
- Thermal conductivity
- Viscosity
- Density
I could go on, but I’m sure the point is made.
So, onto the two examples.
Example 1 – A Blackbody
Let’s consider a body of mass, m = 1kg with specific heat capacity, cp = 1000 J/kg.K.
Therefore, heat capacity, C = 1000 J/K.
Surface area, A = 2 m².
Emissivity, ε = 1 (a blackbody).
Temperature (at time, t=0) = 300K
Background temperature = 0K (lost in the vastness of space, see note 1)
No external energy is supplied after time, t=0. The body is suddenly placed in the vastness of space. What happens to temperature over time?
The body radiates:
E = AεσT4 [1] Note, really we should write E(t) and T(t) to show that E and T are functions of time
Change in temperature with time:
dT/dt = E/C [2]
Here is the change in temperature with time:
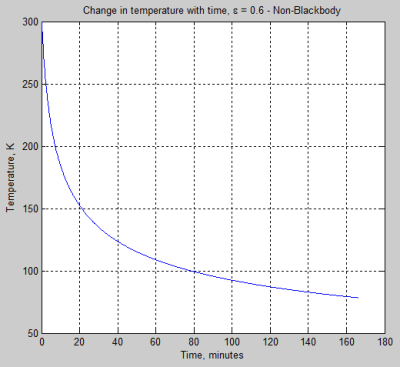
Example 2 – A non-blackbody
Exactly the same as Example 1 – but ε = 0.6 (not a blackbody).
Here is a non-blackbody result:
You can see the form of the result is similar but the temperature drops more slowly – because it is emitting radiation more slowly.
Conclusion
The equations are the same for both examples. The other physical parameters are the same for both. The results are similar. There is nothing startlingly different about a solution with a blackbody and a body with an emissivity less than 1.
Well, that’s my take on it.
Blackbodies appear to be believed to have characteristics unknown in textbooks. I hope some people can explain their “issue” with blackbodies. Or what “the problem” really is.
Notes
Note 1: Yes, the background temperature of space is 2.7K, but using 0K just makes the maths easier for people to follow.



Excellent.
This is off-topic but I don’t know where else to post it.
I’ve just drafted a simple, short (8-pp double spaced), piece on the West Antarctic Ice Sheet (WAIS). If anyone is interested in reading it critically, he or she can contact me off-list at huntjanin@aol.com.
Best,
Hunt Janin
Vught, Netherlands
Emissivity/absorptivity is not completely independent. If the emissivity is less than one, then transmissivity and/or reflectivity must be greater than zero as the three properties must sum to exactly 1. There’s also the problem of direction or angle of incidence which we’re all ignoring.
Speaking as a non-physicist, I would say that Mr. Payne’s comment seems inarguable to me.
I would also like to add that to me it seems self-evident that the emissivity of a non-blackbody is also dependent on the spatial distribution of heat within that body at the start of the experiment, and also on any spatial variation, within the body, of emissivity, transmissivity, and reflectivity.
To Scienceofdoom: take a non-blackbody that is unhomogenous in all of these factors (doesn’t have to be something as large or complicated as Earth) and if you can manage to control for all these factors to a close-enough degree to enable some realistic real-word comparisons, you will have come a long way in convincing me of your position about back-radiation.
I am presently an agnostic on this disagreement. Until yesterday, I had never questioned the orthodoxy regarding back-radiation. Now I am reading some of the debate that has been raging on tAV and Frank Davis and by drroyspencer.com and by Claes Johnson, and I am vacillating. I don’t have the math to try to solve this question myself, but I am irresistibly drawn anyway to try to imagine solutions for it. Several times I have changed my mind about who’s right, but now I must say I just don’t know. I don’t know enough to know. I continue to follow all of this with great interest. As I have relatively little effort invested thus far, it is not personal for me. I feel like I could be perfectly comfortable living in either of the universes that are being described by these two sides — and I am convinced that in both of them, the AGW hypotheses lose big time!
RTF
You may be interested in this quick analysis I did on how randomness affects variations when applied to temperature profiles:
I’m in the process of moving my blog from BlogSpot to here, much better.
Richard T. Fowler:
DeWitt Payne is correct of course. For completeness, I should have included the relationship between emissivity, absorptivity, transmissivity and reflectivity.
And I am sure there are a few less obvious parameters which are related to the emissivity. For example, many metals have a low emissivity and high thermal conductivity. Perhaps there is a relationship there.
But the curious comments and ideas about blackbodies are not about these. These are well-known and basic physics. (I already agree with them myself as you will find in other posts).
No, many people have other ideas that I haven’t been able to get to the bottom of. Like the comment shown in the article and the comment linked.
The questions that you have about backradiation seems to have no relationship to the subject of blackbodies. A nice example in fact.
You can measure backradiation – very easily. See The Amazing Case of “Back Radiation” -Part One.
You don’t need maths to solve it. If you take Claes Johnson, for example, he has a paper full of maths about some fundamental physics and then switches to climate science and claims that back radiation doesn’t exist.
Point a pyrgeometer at the sky and you can prove it does. No maths needed.
I appreciate your comments.
I have to say that the fact that there exists an instrument which can measure certain energy at a certain quantity at Earth’s surface does not convince me, because there has to be sound theory to explain the measurements. As I said, I am not a physicist and lack the mathematical skill to fully assess such theory. Thus, I am forced to sit back and watch as others who are better prepared than I try to “duke it out”.
It seems to me that the question of proving back radiation is a question that has to involve the study and estimation of heat flow. The reason I say this is because if heat flows from one place to another within a body, then that will affect where, in what quantity, in what direction, and at what wavelength it is radiated.
Bear in mind that your argument at some of the threads that I have seen on this subject has been focused on blackbody radiation. The earth is not a blackbody, and neither are Earth’s atmospheric particles. Perhaps this is the source of the disconnect you are seeking to understand.
Thanks again for your comments; I am now going to read the link you just gave me.
RTF
Well perhaps. I have explained blackbody radiation and also in many places I have explained practical radiation.
But why the idea that a blackbody has no mass?
And if the arguments are about the exact emissivity, why do we not see articles which say – “this approximation is not accurate enough because if we use emissivity = 0.96 instead of emissivity =1 we get a change in radiation at location X of so many W/m^2” ??
Instead I see many articles and comments “against blackbodies”.
By people who don’t seem to understand what “blackbodies” are, or the difference between “blackbodies” and “greybodies”.
If you take a look at Emissivity of the Ocean you can see the actual emissivity and you can see the difference in upward surface radiation if e=1 vs e=0.98 is used.
I expect that many people imagine that blackbody approximations are used in climate models when they aren’t.
In any case, I am seeking to establish what people believe about “blackbodies” and why they appear to be associated with “AGW” in some curious fashion rather than associated with “radiation”.
“But why the idea that a blackbody has no mass?”
I can only speak for myself. This will probably sound facetious, but it’s the only thing that comes to mind. If something doesn’t exist, then I do not see how it CAN have mass.
“This blackbody does not exist, but its mass does”? That strikes me as being nonsense.
If I told you that *I* don’t exist, but I nevertheless have a nonzero mass which you can estimate, would you find that believable?
Unless you’re talking about some kind of imaginary nonexistent “mass”, in quotes. And if so, I fail to see what value there is in doing calculations with it. Because again, it doesn’t exist in the real world. Let’s go with a model of something that we agree *can* exist.
—
“And if the arguments are about the exact emissivity, why do we not see articles which say – “this approximation is not accurate enough because if we use emissivity = 0.96 instead of emissivity =1 we get a change in radiation at location X of so many W/m^2” ??”
I imagine it’s because they don’t want to go on the record with their own math, fearing being caught in a mistake, so they’re hoping to get someone else to do it for them.
—
“I expect that many people imagine that blackbody approximations are used in climate models when they aren’t.”
Question: Do climate models assume the existence of back-radiation? And does the proof of back-radiation rely on blackbody approximations? If so, then blackbody approximations *are* used in climate models.
—
“In any case, I am seeking to establish what people believe about “blackbodies” and why they appear to be associated with “AGW” in some curious fashion rather than associated with “radiation”.”
See my answer to your last question.
RTF
You are correct. Every instrument needs a theory to explain how it works. They involves sensing something and converting it to a reading. These include thermistors, radios, flow meters, mass spectrometers, ultrasonic level sensors…
What we are talking about is not a special instrument for measuring backradiation, but an instrument for measuring radiation.
Measurements of radiation done with instruments:
– lower tropospheric temperatures (e.g. UAH figures)
– SST (sea surface temperature) measurement
– solar radiation measurement out in space and at the ground
Interestingly, some people do dispute that a pyrgeometer can measure back radiation.
But I don’t see the same groundswell movement for disputing the UAH temperature measurements, SST measurements, solar radiation.
Perhaps these are all fictional. We have one instrument that everyone believes in – the eye. (Everyone except a few philosophers). It is a very narrow band device, only covering a few hundred nanometers in wavelength.
Everything else for measuring radiation relies on a theory.
I think it’s unproductive for you to spend time arguing that the pyrgeometer must be accurately measuring radiation. The real question that interests me (since I know nothing about pyrgeometers and have no good reason to doubt them) is this: assuming they are accurate, how much of what they measure is attributable to terrestrial radiation, and how much to solar which has passed through the atmosphere?
“Everything else for measuring radiation relies on a theory.”
EVERYTHING relies in part on a theory. What I think is causing the controversy that I have discussed is that there is simultaneously the claim that backradiation cannot reasonably be doubted, combined with a relative paucity of rigorous theoretical exposition on the blogs. Not saying people should have to go to town with the calculus. But there is talking at cross-purposes. The issues that I find important — heat flow, the modeling of blackbodies which don’t exist, and assumptions made about the passage of solar energy through the atmosphere — are not being discussed very much, and not in a sufficiently serious way, to enable me to draw strong conclusions one way or the other about back-radiation.
RTF
RTF
Richard T. Fowler:
Well that’s a very easy one to answer. Check out The Sun and Max Planck Agree – Part Two.
Richard T. Fowler:
Climate models assume the existence of:
-solar radiation
-backradiation
-terrestrial radiation
-absorption and emission of radiation by atmospheric gases
-convection
These are all very believable phenomena. Because they are all measurable and all have excellent theory to support them.
Back radiation does not rely on blackbody approximations. See Theory and Experiment – Atmospheric Radiation for examples of how measurement and theory match up.
Each gas emits and absorbs in very narrow lines. These are used in climate models, or in their place, approximations called “band models” which reduce the huge complexity of the 100,000 lines in the database to something more computationally manageable.
There are many approximations in all areas of physics and engineering.
For example:
– the “ideal gas laws” – but no gas is quite ideal. However, the theory is successfully used because many gases in the atmosphere are close approximations.
– incompressible fluids – no fluid is quite incompressible
If you take a look at any engineering textbook, any physics textbook you find statements like:
“As such and such a parameter is much larger than this other parameter, this equation reduces to a simpler one where we can neglect these terms..”
And this is the staple of real world engineering. Neglecting terms in equations, making approximations, “assuming” some idealisation.
And the test is simply, does it work? Does it match the measurements? Under what circumstances are these assumptions reasonable? What level of accuracy do we need out of this particular model? And so on.
All textbooks which cover radiation start with blackbody radiation. Yet no surface is actually a blackbody. Surely the textbooks should all be thrown out?
Except, first, the blackbody is the measure of a perfect emitter that all others are compared with so a blackbody is a very necessary concept to understand. Second, many emitters are very close. The ocean for example is very close to a blackbody. If you assume the ocean is a blackbody for some purposes the error will be less than 1%. The model is not falsified by assuming a blackbody, unless you need better than 1%. In which case it is falsified.
See Theory and Experiment – Atmospheric Radiation to find how close the measured results come to theory.
Scienceofdoom: “The model is not falsified by assuming a blackbody, unless you need better than 1%. In which case it is falsified.”
You don’t know what you need unless you model a non-blackbody. Therefore, you don’t know whether the blackbody model is falsified unless and until you model a reasonably complex non-blackbody.
By reasonably complex is meant, “sufficient for the deductive purpose that a reasonable person would consider sufficient.”
So the standard is one of reasonability. It is not an objective standard. It is a subjective one. Whether the standard chosen is sufficient to solve a particular problem will not necessarily be known initially, or even after the entire problem is worked through. One could work through it, everything could “tie out” as it’s said in accounting, engineering solutions could be designed, built, tested and used, and later on, all the theory could come spectactularly undone. The reason this can happen is because, as said above, the standard of sufficiency in one’s models is not objective, but completely subjective. Sorry, but that’s science. That’s what science is, and that’s the way it *has* to be.
Most scientists I have been familiar with are tragically ignorant of the fact that they live within the type of reality that I have described here. It doesn’t necessarily make them a bad scientist, because there are many different roles to fill within science, and not all of those roles require awareness of the tentative nature of one’s views.
It sounds to me like you are one who seeks to understand something which you don’t yet understand. If you really, really, want to do so — and you have to WANT it, it’s not enough to just seek, since merely seeking you will NOT find — you must first admit that you MAY not already know everything that must be known in order to definitively answer the question at hand. If you would do this, progress toward further understanding is possible. If instead you would resist this requirement, zero progress is possible, and none will happen. In that case, you may continue at the level you are at. I assure you that no reasonable human being will lose sleep over your lack of progress.
RTF
Here are some extracts from Heat Transfer, by Gregory & Sanford, Cambridge University Press (2009).
I hope they help to dispell a little of the confusion that surrounds “blackbodies”.
Four separate extracts from the “Radiation” chapter:
Science of Doom,
It is just about creating doubt where none exists. Of course the Earth is a greybody, but as you show the principles are the same (Just more complex in application).
Oh I see, so the purpose of those who raise doubts is not to find truth, because even these people have no doubt?
If your comment were directed at a professional scientist, it would constitute an accusation of academic fraud.
I can only suppose that you feel confident in slinging such mud because those who express doubt are generally not entitled to a paid, professional position. In other words, they are an easy target.
So, if I’m wrong that you’re charging fraud, let’s have you name one or more names regarding who is ‘just creating doubt where none exists’. Shouldn’t be a problem if I’m wrong. And if I’m right about your charge but you won’t name a name to go with it, perhaps the charge is inappropriate in this forum and should be retracted?
Speaking for myself, I have doubt, and I have tried to express the nature and quantity of that doubt to the best of my ability, subject to the fact that I don’t want to overwhelm the page with disagreeable material, especially given that it could turn out to be wrong anyway.
After I have done this, you have posted a comment suggesting that my comments are “just about creating doubt where none exists.” I take great offense at your apparent meaning.
Regarding your comment about greybodies, as I understand it, Earth is not a greybody, because a greybody, like a blackbody, does not exist. Is it not true that the reason these two types of bodies cannot exist is precisely because the principles governing their behavior are not identical to those which govern the behavior of real objects?
RTF
Tony O’Brien:
Please check out the Etiquette – we aim to discuss science rather than motivations that might or might not be true.
If someone presents a totally flawed understanding of a subject I would rather assume they just don’t understand the subject than that they aim to confuse.
And the aim is to keep this blog on the science. Other blogs are better places for discussing motivations.
SoD,
I had a look at the article where the comment about volume and black bodies originated. From the context it is clear that the ideas about black and grey bodies are not the conventional definitions where they only vary in their emissivity.
My interpretation of the comment is that the only interesting feature of a (solid) black body is the surface whereas this particular version of a grey body is about the heat flows in the volume beneath the surface as well. It is really the lunar surface temperature variation debate in disguise.
In part, I think some of this kind of confusion comes about because of the huge simplifications that are made when trying to make models of particular aspects of the physics. It certainly is the case that the simplest radiation model treats the earth surface as isothermal and pays little attention to the heat capacity or conductivity below the surface. This is similar to the way that complicated heat flows from convection are removed and replaced by a simple lapse rate to derive the temperatures needed for the TOA radiation calculations.
The idea of trying to find the relationship between a few variables while treating every other factor as fixed is one of the oldest in the physics toolbox and has been very productive. The problem come when everybody knows that these other factors are not really constant at all. It takes quite a mental effort to keep the simplified model apart from the reality. In some cases the disconnect can be so profound that a layman can easily come to believe that the simple model is quite useless.
From what I have read it seems that experts have no problem with the temporal/spatial averaging over the earth that yields single values for the relevant temperatures needed by the simple radiation model. Many laymen look at the variations in temperature with time and place and then wonder whether the averages have any meaning.
I think that the development of the GCMs was partly motivated to remove some of the averaging and replace it with dynamic calculations all over the system. This is hard to do and has its own problems.
Anyway, my understanding of the original comment is that the author has rather mixed up the steady state simple model which only requires the black body surface emissivity/temperature with the dynamic effects that involve heat flows that are influenced by heat capacities and thermal conductivities.
It would be interesting to see what happens to the surface temperature if your model also included thermal resistance as well as a heat capacity. My guess is that the surface temperature would fall rapidly at the start as the whole heat capacity would not be available to replenish the surface loss by radiation in the short term.
Jorge:
Your proposal seems quite unlikely to me. Conductivity goes both ways: the surface will cool faster, but it will also heat up faster as it absorbs radiation, if conduction into the ground is slow. Since both convection at the surface and radiation into the atmosphere from the surface are driven by the surface temperature, the same equilibrium surface temp should result. The only effect I’d expect is that changes in temperature will take place more quickly if conduction is low: the surface would warm faster in the day and cool faster in the night.
Bryson Brown,
Oh dear! My reference was to the curves that SoD showed for his model of how a hot sphere with heat capacity would cool when placed in outer space. This is not cyclical and no new energy is supplied.
This is rather like your night example where I agree that a low conductivity would make the surface cool more rapidly. I also agree that a low conductivity would make the sphere surface warm up more quickly if SoD were to introduce a source of radiant energy at some point.
I think we are in violent agreement about this!
The equilibrium temperature question is a bit more subtle as there is no equilibrium temperature with a cyclic energy forcing unless the heat capacity is vey high and the conductivity is high compared to the forcing frequency. The temperature is also going to cycle up and down and will have an average temperature. I am not sure that this average will be the same if changes in conductivity or heat capacity lead to larger or smaller swings. This is mainly due to the non-linearity introduced by the T^4 variation of the emission.
Jorge:
This is covered in Lunar Madness and Physics Basics.
You can see that the “average temperature” is dependent on the heat capacity. But the average radiation stays the same.
So now we are talking about a model that allows for heat flow, and the average temperature drops. Now if the radiation is the same, is it safe for me to assume that the average wavelength also drops? Sorry if I’m wrong; remember I’m not a physicist.
Thanks.
RTF
Three rather pedantic points.
First, Eli would reserve the term greybody for systems that had uniform (with frequency) but not unit emissivity.
Second, remember that the model for blackbody radiation is a closed volume, in a uniform heat bath that has a small hole in it through which the blackbody radiation emerges (or acts to absorb light from the outside entering through the hole). In that sense, transmission is not a property of a blackbody.
Third, surface emission/absorption is well modeled by the Planck formula with, perhaps, a frequency dependent emissivity, but it is not necessarily simple. For example, skin depth (generally a few wavelengths of the light) plays a determining role in the observed “temperature” at which the surface is emitting. A neat example of this is that the blackbody temperature of the moon, as measured from the earth, is different if you use IR or millimeter wave emission because the former senses the surface temperature, and the latter, the average temperature a few mm down.
Richard T. Fowler:
The point is that average temperature is a problematic concept.
Two scenarios – both surfaces receive the same total radiation and emit the same total radiation but one has similar temperatures across its area and the other has widely varying temperatures across its area.
The two average temperatures will be different even though the two surfaces emit the same total radiation.
It’s easy to demonstrate, as in the link provided and the example below.
Peak wavelength (the wavelength of peak radiation) = 2898 / T.
So when we average the peak wavelength there will also be a non-linear dependence.
The answer might be obvious to people who do complex maths in their head but I needed to punch a few numbers into a calculator.
Here is an example: 3 areas of equal area.
Scenario 1: all at the same temperature of 15’C (288K) – therefore the average radiation from the surface = 390.1 W/m^2
Average temperature = 15.0’C
Scenario 2: T1 = -15’C (258K), T2 = 15’C (288K), T3 = ?
what is T3 to have the average radiation = 390.1 W/m^2?
T3 = 37.8’C (310.8K)
Average temperature = 12.6’C
Scenario 1: Average peak wavelength = 10.1um
Scenario 2: Average peak wavelength = 10.2um
(Note for the detail orientated people – I used 0’C = 273K rather than 273.15K for reasons of laziness).
So the average peak wavelength has increased as the average temperature drops but the total radiation stays the same.
If you define “average wavelength” differently the answer might be different, I can’t be sure. Average of the wavelength of peak radiation is what I used to do this calculation.
And in the example I used “blackbody” radiation to do my calculations.
Clearly the answer is invalidated.
If we used a body with a real-world wavelength-varying emissivity we would probably find the same result. The answer is left as an exercise for the interested student.
This is all very interesting to me, and I thank you greatly for the time you spent on this.
I will be referring back to your blog regularly for further enlightenment.
RTF
Historically, one looked at the peak wavelength, which was related to the temperature of the body by the Wien displacement law
lambda (peak) = b/T where b is 2.90 ×10−3 m·K
So if T falls, wavelength lambda (peak) increases. It gets more complicated for non isothermal, non uniform bodies, but is tractable.
To add another somewhat pedantic point: that formulation of Wien’s displacement law only applies if the spectral power distribution is measured in wavelength space (W/m2/unit wavelength). If one is measuring spectral power density of a black body in frequency space then the peak frequency is proportional to temperature (~2*T for frequency in cm-1 and T in Kelvin). The peak frequency of the spectral power density converted to wavelength will not be the same as the peak wavelength of the spectral power distribution.
SOD: The comment you cite at the beginning of this article (“Earth is a grey body, because it has volume, a black body does not have volume, simply that is the end of “the controversy”) illustrates some of the confusion that arises from misleading terminology combined with slab models of the atmosphere. Your anonymous author understands that blackbody radiation arises from an ideal surface. He knows that the atmosphere doesn’t behave like a blackbody and is often termed a “grey body”, something he appears to sensibly believe has volume in addition to surface area and perhaps an emissivity <1. Unfortunately (as also noted by Eli), we also use the term "grey atmosphere" in other contexts – such as to refer to model atmosphere with an absorbance that is constant with wavelength – which you discussed in your post "Vanishing Nets" (https://scienceofdoom.com/2010/08/08/vanishing-nets/). Interestingly, there is no emissivity term in that post, just an unspecified absorption coefficient that is multiplied times the Planck function, B(T). The relationship between emissivity (a dimensionless quantity) and this absorption coefficient (a quantity with dimensions) is unclear to me. From my (mostly self-taught) perspective, the concept of blackbody radiation from a "slab atmosphere" (modified by an emissivity term) and atmospheric radiation (as described by the Schwartzschild equation) don't really fit together very well.
Climate science might be clearer if it restricted the use of the terms blackbody radiation and emissivity to radiation originating from a solid or liquid surface and never used the term to describe to radiation leaving the surface of a volume of gas. After all, one can't say anything sensible about the radiation leaving a volume of gas until one defines the number and type of GHGs in that volume. How does one map the concept of emissivity (a number between zero and one) onto the concept of GHGs (which can take on any value from zero to infinity)?
By calculating absorptivity at any given wavelength and then integrating over the spectral range.. Absorptivity is also bounded between zero and 1. By Kirckhoff’s Law, absorptivity must equal emissivity when local thermal equilibrium applies. The HITRAN database contains the information about the spectral lines to allow calculation of absorptivity for any temperature, pressure and mixing ratio of a given ghg. The atmospheric profiles of temperature, total pressure and partial pressure of atmospheric components with altitude can be measured or estimated. Emission is then product of the emissivity at a given wavelength and the Planck function for that wavelength and the local temperature integrated over the spectral range.
That should be Kirchhoff, not Kirckhoff.
Dewitt: If I understand correctly, the HITRAN database is a tool for integrating the Schwartzschild equation along a path, for example from the surface of the earth to space. In contrast, blackbody (e=1) and graybody (e<1) radiation tell us how much radiation is emitted by a surface. In both cases, we can consider the simpler problem of emission at a single wavelength, while recognizing that the complete solution is obtained by integrating over all wavelengths. I'm complaining about the problems that develop when the equations for black/graybody radiation are applied to the surface of a slab of atmosphere.
A slab model of the atmosphere says that emission from the surface of the slab depends on emissivity and temperature. However, the Schwartzschild equation makes different predictions about emission:
dI = -Ikrdz + B(T)krdz
where r is the density of GHG and k is the absorption/emission coefficient at a given wavelength. If the density of GHGs in a slab of atmosphere (at a given temperature) increases by 10X, the emission term grows by 10X. If increased by 1,000,000X (producing an atmosphere about like Venus), the emission term will increase by 1,000,000X. When such dramatic changes in GHG content are made, the photons emitted from the surface of a slab of atmosphere will be coming from different depths (and many may be absorbed before they get to the surface). But slab models don't have the flexibility to handle changes in GHGs with an emissivity term – especially when we think of that term as being a constant, as it is for solid and liquid surfaces. Schemes proposing that we can calculate the flux from a slab of the earth's atmosphere using W = eoT^4 (and without integrating along a path, as HITRAN presumably does) seem grossly unrealistic and are the source of some of the confusion SOD presented in the post.
In summary, slab models are simply a trick that allow alarmists focus attention on the absorption term of Schwartzschild's Equation while pretending that emission is fixed by temperature and emissivity (W = eoT^4). In these models, increased GHGs warm by absorption, but do not increase radiative cooling. Perhaps SOD will someday do a post on "Are Slab Models of the Atmosphere an Alarmist Trick?" (Or perhaps his less scrupulous competitors will.)
If a slab of atmosphere is thick enough, then the problem simplifies to blackbody radiation, as shown below. However, optical density of the earth's atmosphere varies greatly with wavelength, so the following mathematics doesn't apply to our atmosphere. If radiation passes far enough through a homogeneous atmosphere, eventually an equilibrium will be reached where emission along the path is exactly balanced by absorption:
dI/dz = -Ikr +B(T)kr = 0
I = B(T) except when k or r = 0
In the limiting case of an optically thick slab of atmosphere, emission will be blackbody, B(T), at absorbing wavelengths. At non-absorbing wavelengths, emission will be due to whatever radiation is coming from behind the slab (the surface of a planet or empty space, both of which emit blackbody radiation at different temperatures than the atmosphere). As the optical thickness decreases, more and more of the emission will originate from behind the slab. In NO case, is radiation a simple fraction (e) of what would be expected from oT^4 – it's always a mixture of radiation from behind diminished by absorption and supplemented by emission.
Frank,
I think the differential form of the Schwarzchild equation is causing confusion. A more appropriate form is:
I = [I0(exp(-κρz))]Tabsorption + {B[1 – exp(-κρ’z)]}Temission
What’s important is the value of exp(-κρz) for absorption and (1-exp(-κρz)) for emission. As the value of κρz, the optical depth τ, increases, the fraction transmitted approaches 0 and emission approaches {B}Temission. Increasing ρ by 1E06 does not increase emission by the same factor unless the value of κρz was vanishingly small to start with.
Let’s see if I got the Greek letters right.
Frank,
You might also want to check out Barret Bellamy’s page on the Schwarzchild equation:
http://www.barrettbellamyclimate.com/page45.htm
He goes into a lot more detail.
Frank,
I just tried a little experiment with MODTRAN. Looking up from the surface, I calculated atmospheric emission at different surface temperature offsets (-5 to +5 C) changing nothing else (1976 US standard atmosphere, clear sky). The intensity was a lousy fit to the S-B equation whether one allowed the emissivity or the exponent to vary. The key is that Teff ( I = σTeff^4) for the atmosphere turns out to be proportional to Tsurf, but the slope isn’t one. The OLS fit has a slope of 0.7395 with an R^2 = 1.
Single slab, gray atmospheres are crude toy models. They’re useful for demonstrating principles, but can’t be considered quantitative.
Dewitt: Thanks for your reply. You are, of course, completely correct in saying that I should have cited the integrated form of the Schwartzschild eqn to describe emission from a slab of atmosphere. Mentioning a 1,000,000X increase in GHG while considering the differential form of the equation is pretty misleading (a problem I partially acknowledged). However, your integrated emission term has a factor of 1-e^(-x). This term increases fairly linearly with x between 0 and 1. My analysis remains correct when x (optical thickness?) is <1.
I did a little more looking into slab models, such as the one at Barret Bellamy’s page and models in Taylor's Elementary Climate Physics. In both cases, they quietly mention an "optically thick" slab of atmosphere. This puts them in the region where the 1-e^(-x) term is 1 and doesn't vary with x. Unfortunately, neither appears to mention that the Earth's atmosphere is not optically thick at many wavelengths. (I remember reading once that the average was 0.7, which may be related to the value you derived above from MODTRAN.)
You said above that: "Single slab, gray atmospheres are crude toy models. They’re useful for demonstrating principles, but can’t be considered quantitative." The principle these models often demonstrate is that emission doesn't depend on GHG mixing ratio. Is this a principle climate scientists should be spreading without a full explanation of its limitations, especially with regard to the earth?
In the past, this problem was particularly acute when I tried to "picture" radiative forcing at the tropopause. This altitude is above roughly 80% of the atmosphere and essentially all of the water vapor, so the atmosphere is optically thin at most infrared wavelengths. If one imagines an optically thick slab atmosphere at this key altitude, one gets the completely misleading idea that emission (ie radiative cooling) doesn't increase as GHGs increase.
I’ll take a stab at the original question.
One can imagine a grad student teaching undergrads an introduction to Planck, Stefan-Boltzmann, and black bodies. In a real world scenario, as a body lost energy through radiation, its temperature would cool. This would lead to too much complication to explain to a student new to the subject; the energy emitted would have to be calculated over the range of temperatures as the body cooled and the surface temperature would also be dependent on the conductive properties of the body. So, for the sake of getting the primary lesson across, the grad student describes the black body as a hollow shell with no volume and a constant temperature. This creates two disjoints between the model and a real world body: a real body is does not emit uniformly under a Planck curve, and a real body of course has volume and internal conduction. In the world of thousands of undergrad students, some will get confused as to the important difference, regarding the absorptivity/emissivity, and the inconsequential one regarding the instruction for the purpose of getting the answer on the test to treat the black body as a hollow shell with constant temperature.
The alternative to the hollow shell is a superconducting solid with infinite heat capacity. Or you put a source of energy at a constant rate inside the shell.
True, of course. The math to describe the radiative output of the different objects, and, if you could take measurements of such hypothetical objects, they would be identical and you could not distinguish between them. I thought of the other types, but decided that it was more likely that new students would be instructed to consider only the surface and the temperature as the only factors that mattered.