In the ensuing discussion on Does Back Radiation “Heat” the Ocean? – Part Four, the subject of the cool skin of the ocean surface came up a number of times.
It’s not a simple subject, but it’s an interesting one so I’m going to plough on with it anyway.
Introduction
The ocean surface is typically something like 0.1°C – 0.6°C cooler than the temperature just below the surface. And this “skin”, or ultra-thin region, is less than a 1mm thick.
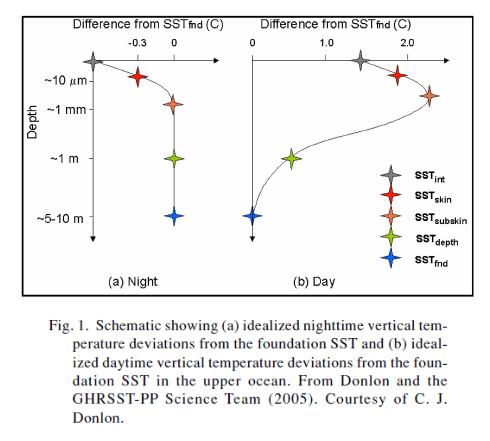
Here’s a diagram I posted in the comments of Does Back Radiation “Heat” the Ocean? – Part Three:
Figure 1
There is a lot of interest in this subject because of the question: “When we say ‘sea surface temperature’ what do we actually mean?“.
As many climate scientists note in their papers, the relevant sea surface temperature for heat transfer between ocean and atmosphere is the very surface, the skin temperature.
In figure 1 you can see that during the day the temperature increases up to the surface and then, in the skin layer, reduces again. Note that the vertical axis is a logarithmic scale.
Then at night the temperature below the skin layer is mostly all at the same temperature (isothermal). This is because the surface cools rapidly at night, and therefore becomes cooler than the water below, so sinks. This diurnal mixing can also be seen in some graphs I posted in the comments of Does Back Radiation “Heat” the Ocean? – Part Four.
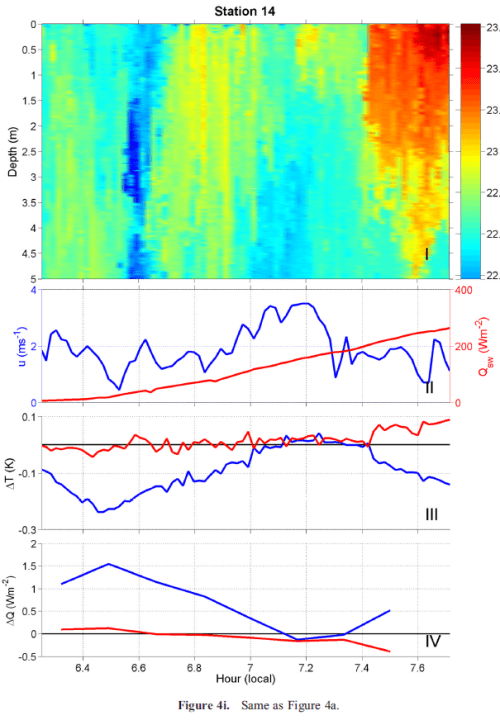
Before we look at the causes, here are a series of detailed measurements from Near-surface ocean temperature by Ward (2006):
Figure 2
Note: The red text and arrow is mine, to draw attention to the lower skin temperature. The measurements on the right were taken just before midday “local solar time”. I.e., just before the sun was highest in the sky.
And in the measurements below I’ve made it a bit easier to pick out the skin temperature difference with blue text “Skin temp“. The blue value in each graph is what is identified as ΔTc in the schematic above. The time is shown as local solar time. 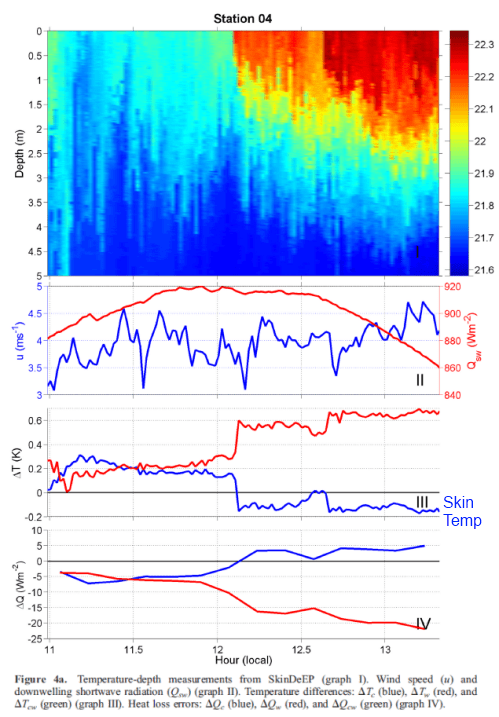
Figure 3
Figure 4
Figure 6
Figure 7
The measurements of the skin surface temperature were made by MAERI, a passive infrared radiometric interferometer. The accuracy of the derived SSTs from M-AERI is better than 0.05 K.
Below the skin, the high-resolution temperature measurements were measured by SkinDeEP, an autonomous vertical profiler. This includes the “sub-skin” measurement, from which the sea surface temperature was subtracted to calculate ΔTc (see figure 1).
The Theory
The existence of the temperature gradient is explained by the way heat is transferred: within the bulk waters, heat transfer occurs due to turbulence, but as the surface is approached, viscous forces dominate and molecular processes prevail. Because heat transfer by molecular conduction is less efficient than by turbulence, a strong temperature gradient is established across the boundary layer.
Ward & Minnett (2001)
Away from the interface the temperature gradient is quickly destroyed by turbulent mixing. Thus the cool-skin temperature change is confined to a region of thickness, which is referred to as the molecular sublayer.
Fairall et al (1996)
What do they mean?
Here’s an insight into what happens at fluid boundaries from an online textbook (thanks to Dan Hughes for letting me know about it) – this textbook is freely available online:
Figure 8
The idea behind turbulent mixing in fluids is that larger eddies “spawn” smaller eddies, which in turn spawn yet smaller eddies until you are up against an interface for that fluid (or until energy is dissipated by other effects).
In the atmosphere, for example, large scale turbulence moves energy across many 100’s of kilometers. A few tens of meters above the ground you might measure eddies of a few hundreds of meters in size, and in the last meter above the ground, eddies might be measured in cms or meters, if they exist at all. And by the time we measure the fluid flow 1mm from the ground there is almost no turbulence.
For some basic background over related terms, check out Heat Transfer Basics – Convection – Part One, with some examples of fluid flowing over flat plates, boundary layers, laminar flow and turbulent flow.
Therefore, very close to a boundary the turbulent effects effectively disappear, and heat transfer is carried out via conduction. Generally conduction is less effective than turbulence movement of fluids at heat transfer.
A Note on Very Basic Theory
The less effectively heat can move through a body, the higher the temperature differential needed to “drive” that heat through.
This is described by the equation for conductive heat transfer, which in (relatively) plain English says:
The heat flow in W/m² is proportional to the temperature difference across the body and the “conductivity” of the body, and is inversely proportional to the distance across the body
Now during the day a significant amount of heat moves up through the ocean to the surface. This is the solar radiation absorbed below the surface. Near the surface where turbulent mixing reduces in effectiveness we should expect to see a larger temperature gradient.
Taking the example of 1m down, if for some reason heat was not able to move effectively from 1m to the surface, then the absorbed solar radiation would keep heating the 1m depth and its temperature would keep rising. Eventually this temperature gradient would cause greater heat flow.
An example of a flawed model where heat was not able to move effectively was given in Does Back-Radiation “Heat” the Ocean? – Part Two:
Note how the 1m & 3m depth keep increasing in temperature. See that article for more explanation.
The Skin Layer in Detail
If the temperature increases closer to the surface, why does it “change direction” in the last millimeter?
In brief, the temperature generally rises in the last few meters as you get closer to the surface because hotter fluids rise. They rise because they are less dense.
So why doesn’t that continue to the very last micron?
The surface is where (almost) all of absorbed ocean energy is transferred to the atmosphere.
- Radiation from the surface takes place from the top few microns.
- Latent heat – evaporation of water into water vapor – is taken from the very top layer of the ocean.
- Sensible heat is moved by conduction from the very surface into the atmosphere
And in general the ocean is moving heat into the atmosphere, rather than the reverse. The atmosphere is usually a few degrees cooler than the ocean surface.
Because turbulent motion is reduced the closer we get to the boundary with the atmosphere, this means that conduction is needed to transfer heat. This needs a temperature differential.
I could write it another way – because “needing a temperature differential” isn’t the same as “getting a temperature differential”.
If the heat flow up from below cannot get through to the surface, the energy will keep “piling up” and, therefore, keep increasing the temperature. Eventually the temperature will be high enough to “drive the heat” out to the surface.
The Simple 1-d Model
We saw a simple 1-d model in Does Back Radiation “Heat” the Ocean? – Part Four.
Just for the purposes of checking the theory relating to skin layers here is what I did to improve on it:
1. Increased the granularity of the model – with depths for each layer of: 100μm, 300μm, 1mm, 5mm, 20mm, 50mm, 200mm, 1m, 10m, 100m (note values are the lower edge of each layer).
2. Reduced the “turbulent conductivity” values as the surface was reached – instead of one “turbulent conductivity” value (used when the layer below was warmer than the layer above), these values were reduced closer to the surface, e.g. for the 100μm layer, kt=10; for the 300μm layer, kt=10; for the 1mm layer, kt=100; for the 5mm layer, kt=1000; for the 20mm layer, kt=100,000. Then the rest were 200,000 = 2×105 – the standard value used in the earlier models.
3. Reduced the time step to 5ms. This is necessary to make the model work and of course does reduce the length of run significantly.
The results for a 30 day run showed the beginnings of a cooler skin. And the starting temperatures for the top layer down to the 20mm layer were the same. The values of kt were not “tuned” to make the model work, I just threw some values in to see what happened.
As a side note for those following the discussion from Part Four, the ocean temperature also increased for DLR increases with these changes.
Now I can run it for longer but the real issue is that the model is not anywhere near complex enough.
Further Reading on Complexity
There are some papers for people who want to follow this subject further. This is not a “literature review”, just some papers I found on the journey. The subject is not simple.
Free
Saunders, Peter M. (1967), The Temperature at the Ocean-Air Interface, J. Atmos. Sci.
Tu and Tsuang (2005), Cool-skin simulation by a one-column ocean model, Geophys. Res. Letters
Paywall
McAlister, E. D., and W. McLeish (1969), Heat Transfer in the Top Millimeter of the Ocean, J. Geophys. Res.
Fairall et al, reference below
GA Wick, WJ Emery, LH Kantha & P Schlussel (1996), The behavior of the bulk-skin sea surface temperature difference under varying wind speed and heat flux, Journal of Physical Oceanography
Hartmut Grassl, (1976), The dependence of the measured cool skin of the ocean on wind stress and total heat flux, Boundary Layer Meteorology
Conclusion
The temperature profile of the top mm of the ocean is a challenging subject. Tu & Tsuang say:
Generally speaking, the structure of the viscous layer is known to be related to the molecular viscosity, surface winds, and air-sea flux exchanges. Both Saunders’ formulation [Saunders, 1967; Grassl, 1976; Fairall et al.,1996] and the renewal theory [Liu et al., 1979; Wick et al.,1996; Castro et al., 2003; Horrocks et al., 2003] have been developed and applied to study the cool-skin effect.
But the exact factors and processes determining the structure is still not well known.
However, despite the complexity, an understanding of the basics helps to give some insight into why the temperature profile is like it is.
I welcome commenters who can make the subject easier to understand. And also commenters who can explain the more complex elements of this subject.
References
A Heat Transfer Textbook, by Prof Lienhard & Prof Lienhard, Phlogiston Press, 3rd edition (2008)
Cool-skin and warm-layer effects on sea surface temperature, Fairall, Bradley, Godfrey, Wick, Edson & Young, Journal of Geophysical Research (1996)
Near-surface ocean temperature, Ward, Journal of Geophysical Research (2006)
An Autonomous Profiler for Near Surface Temperature Measurements, Ward & Minnett, Accepted for the Proceedings Gas Transfer at Water Surfaces 4th International Symposium (2000)








This is off-subject but I don’t know where else to post it.
I’m writing an introductory survey on sea level rise and need to begin it (for the general reader) with a brief and simple chapter on global warming.
Being a mere generalist, I also need to be very sure that I have my scientific facts right. The chapter mentioned above runs to 17 pp. double spaced.
If anyone might be interested in reading it critically and telling me if it contains any errors, please contact me off-list at huntjanin@aol.com.
Many thanks.
Best,
Hunt Janin
Hi ScienceOfDoom,
About this short paragraph:
And in general the ocean is moving heat into the atmosphere, rather than the reverse. The atmosphere is usually a few degrees cooler than the ocean surface.
I assume the temperature difference between ocean and the air right above it is also important, and I get the feeling it got overlooked in this discussion.
If the air right above the ocean gets warmer doesn’t it affect the heat transfer through the interface?
SoD,
These two articles are very interesting and certainly show how hard it is to go from toy models to the real thing when trying to work out the energy balances in the various layers.
I understand what you are trying to do with the finer resolution and the variations on the thermal resistances that you are using to simulate convection.
The code is quite difficult for me to follow and so I hope you don´t mind a few questions. I am not sure of the actual physical interpretation of how you have handled the various ocean layers. Clearly in a lumped model there can only be one temperature, one, possibly variable, thermal resistance and one thermal capacity per layer.
It is my impression that you have actually calculated the temperatures at the middle of the layer and that is where all the thermal capacity resides. The thermal resistance between layers is defined to be the sum of the two resistances divided by two. In effect, each layer is split into two thermal resistances with the thermal capacity attached to the mid point and the layer temperature is calculated at this junction.
Am I correct to assume that any solar heating appropriate to the layer is also fed into this same junction?
This “T” model sometimes encounters some slight problems with the first and last sections. It is not clear to me from the code how the fixed temperature infinite heat sink is joined to the deepest layer but it seems it must be separated from the mid point by the lower half of the thermal resistance of that final layer. Is this right?
At the top layer it seems there is the choice to include the top half of the thermal resistance and feed the DLR into the resistance or to throw away this half of the resistance and feed directly to the junction of the thermal capacity and the lower part of the layer resistance. The same thing applies to the connection of the thermal resistance that is simulating the air/water convection. Could you tell me which of these two options you have simulated?
By retaining this top half of the thermal resistance one would have access to the actual surface temperature which would be more correct for calculating the upward surface radiation. Clearly, if the layer is thin enough it may not make much difference but it seems that this half layer is likely to have quite a high resistance as it is almost certainly pure conduction.
I must say I am still rather surprised by the result that you obtained in the previous article. I am not surprised that DLR could cause the deeper layers to warm but the fact that the temperature profile was virtually identical to penetrating solar was most unexpected.
Anyway, I very much appreciate your approach of using simple models to illustrate the pure physics that most people can accept. I value them for what they are while retaining the right to dispute their relevance to reality!
I find the cold skin argument so obvious that I must be missing something.
A school type experiment would ask you to put a finger into some alcohol and then hold it in the air.
You would feel the finger much colder than usual because of the evaporating alcohol.
The energy to cause the evaporation comes from your finger.
Your finger surface temperature will drop.
Likewise on the Ocean surface.
The surface water molecules will have a range of velocities.
Some will have a high enough velocity to pull away from the attractive bonding forces of neighbouring molecules in the liquid state and so escape.
This energy is now stored in the gaseous phase molecules as potential energy.
The remaining liquid surface will now have lost some average kinetic energy and this is shown by a drop in surface temperature.
Back radiation can only heat the ocean if the air temperature is warmer than the surface skin temperature (back radiation will contribute to the downward energy flux in all cases, but heat transfer, which is the net energy flow, always goes from hot to cold). The air can be warmer than the sea surface in some cases due to a combination of evaporation and radiation from the sea surface through the optical window direct to space on a clear night, removing energy faster than the air could add energy by conduction, or if winds bring in hotter air than the surface film from a different location. Otherwise the air will be cooler.
The reason the air and water are warmer than they would be with no greenhouse gases (and thus have increased radiation both directions) is that the lapse rate combined with the high altitude of outgoing radiation to space gives a higher near surface temperature than otherwise. The back radiation is a consequence of, not cause of, warmer conditions.
Readers interested in nitty-gritty details about what’s happening at / on the compliant interface between the atmosphere and the ocean might try this Google Scholar search for papers by Sanjoy Banerjee.
I recall that Sanjoy’s original investigations into this subject, way back in the late 1960s, were related to gas absorption into liquids; CO2 absorption into the Oceans, for an example.
Over the decades, Banerjee and colleagues have developed a fundamental understanding of the details of the phenomena and processes that occur at these compliant interfaces and captured the essence of these in relatively simple expressions that have very wide ranges of applicability.
Here is a simple school level explanation of why the surface layer in an evaporating liquid is cooler.
Why do you need to make a simple thing complicated?
http://www.school-for-champions.com/science/evaporation.htm
Bryan,
We know why it’s cooler. The difficulty is in the details, like calculating a temperature profile that matches the measured profile and how it varies during the day.
In the ocean the surface layer is cooler because it loses heat by evaporation, radiation upward and conduction to the air. Radiation is the biggest item. It gains some from downwelling IR, but that’s not enough for balance. The rest must be transported from below, which necessitates a temperature gradient.
Yes, this is how I would describe it too.
Bryan and others: Many commenters seem to be confusing a simple change in an energy flux with an automatic change in temperature.
a) Evaporation causes a loss of energy, but cooling can’t be assumed until you’ve analyzed all of the energy fluxes. At night, convection brings as much energy to the surface of the ocean as needed to prevent an unstable temperature gradient from forming, so evaporation doesn’t cool the skin layer of the ocean (without cooling the bulk).
b) AGG- or cloud-enhanced DLR will increase the amount of energy flowing into the skin layer of the ocean. If this extra energy slows convection or conduction into the skin layer, the extra energy may not increase the temperature appreciably.
c) When one uses a forced-air dryer after washing your hands in a restroom, the energy from the warm air tends to prevent your hands from cooling.
Confusing really reigns when we skip temperature change. Extra energy from DLR can’t increase radiation or evaporation until temperature has risen. If increased energy flux doesn’t cause the temperature to rise, emission and evaporation won’t increase.
Actually, I find the thinness of the ocean warm layer about as scary a condition as anything. A bit of mixing, we’re in an ice age and it will be a long time before today’s temps are recovered. Nothing in AGW worries me like an ice age.
SoD : Shouldn’t you have a 10um layer that is the radiating layer? Why stop at 100um? What is your reasoning for that?
The thinner the layer the smaller the heat capacity – so the larger the temperature swings over a given time.
As the layer goes thinner the model therefore needs to have shorter time steps.
The model here is run in 5ms time steps.
If I move to 10μm thick layer I need 0.5ms time steps and so 10 times as long computationally for the same “real world time”.
“If I move to 10μm thick layer I need 0.5ms time steps and so 10 times as long computationally for the same “real world time”.”
I guess thats the price you pay for making the model accurate then…it makes you realise just how coarse the GCMs must be!
The top 10um behaves differently to the next 90um so I dont see how you can avoid it and hope to keep the model accurate in its representation.
Its good to see you’re beginning to see the cool skin in your model though!
SOD: I’m a little confused about how to think about or calculate conduction over relatively short vertical distances at the top of the ocean. I’d like to know how long it takes energy from SWR deposited 1 mm below the surface (subskin) or 5 cm below (the RC experiment) to reach the skin layer by conduction. The size of the temperature gradient driving conduction (about 1 degC for the subskin to skin; 0.2 degC for 5 cm to skin) is clearly an important factor. I’m not sure whether the “answer” to such problems can be expressed as a time for energy transfer or an initial rate or a maximum flux that can be driven by the gradient over a given distance. It seems that the upward flux needed to bring the energy deposited by the SWR needs to be something on the order of 100 W/m^2. This energy is deposited over several meters, so the net upward flux is only 100 W/m^2 very near the surface. Much of this energy may move most of the vertical distance by convection rather than conduction, although conduction presumably becomes practical when the remaining distance is short enough. For example, the night profile changes at a depth of 1 mm. Could this be where conduction is capable of taking over from convection? (I’m sorry my question is so vague.)
SoD,
This is a very good series of articles. Just a couple of quibbles:
1. The viscous sublayer applies to a wall boundary, where there is a no-slip condition. It is a shear region. The ocean surface is different.
2. “In brief, the temperature generally rises in the last few meters as you get closer to the surface because hotter fluids rise. They rise because they are less dense.”
I don’t think that is the reason here. Mainly it’s that the upper levels are absorbing more sunlight. That’s why the peak isn’t there at night.
Yes Nick you are right. The ocean surface is a free surface thus the absence of turbulence at the ocean surface is due to a totally different mechanism to the absence of turbulence in the viscous sublayer of a turbulent boundary layer.
A free surface blocks vertical movement (that traverses the surface) and has zero flux with horizontal movement (parallel to the surface). The combination of these two conditions attenuates the turbulence. This process can’t create the streaky structures that are formed in wall turbulence.
The bottom line is that neither a laminar nor a turbulent boundary layer can exist next to a free surface.
The problem can be considered as a conduction problem next to the free surface exactly because there is no boundary layer.
For the record:
Where walls are involved, the heat transfer in a laminar flow is not the same as heat transfer in a solid.
The temperature profile in a laminar flow is given by
T+ = Pr y+
where T+ = T/T* and y+=u* y/ nu
As the Reynolds number increases u* (the friction velocity) increases. Thus the temperature increases and the heat transfer changes with the local velocity.
Incropera gives the Nusselt number for a laminar boundary layer
Nu = 0.332 Rex^1/2 Pr^1/3
The heat transfer depends on the Reynolds number. The heat transfer of a laminar boundary layer should not be considered as if it was a solid.
Thermal fluctuations are disturbed as they pass through a turbulent flow. Correlations developed for turbulent boundary layers are designed to take into account these perturbations.
An externally generated thermal fluctuation will be significantly distorted as it passes through a turbulent boundary layer. However the same thermal fluctuation will pass through a laminar boundary layer much more easily.
But the ocean surface is a free surface and there isn’t a boundary layer so these aspects become somewhat irrelevant. I leave them in here because there are relevant to plenty of other parts of the ocean/atmosphere system.
“Mainly it’s that the upper levels are absorbing more sunlight. That’s why the peak isn’t there at night.”
Isn’t it likely to be both convection AND distribution of energy from the DSR? Or are you suggesting DSR energy distribution effects >> convection?
Frank,
The problem is that the thermal resistance and the thermal capacity are distributed. I am talking here of a liquid or solid where conduction is the only mechanism for heat transfer. The proper way to do the sums uses diffusion equations. The easy way is to use lumped constants but you really need to string many section in series to simulate the behaviour over any given distance.
The simplest possible approach for a given layer is to take the thermal capacity of the layer and the thermal resistance of the layer. If you multiply them together (using the right units) you should finish up with a simple time constant in seconds. This would show how the temperature would rise at one end of the layer if a step change was made to the temperature at the other end. This does assume that no heat is being lost from the far end.
If you model the same distance but use multiple lumped sections the behaviour changes and the response is more like a delay line. In effect, for a period of time, the far end will not show any increase at all. It then starts to increase fairly slowly, increases in rate and finally slowly reaches the equilibrium temperature. In the case where no heat is being lost from the far end the equilibrium will be the same as the temperature at the driving end.
This is not quite the same as the situation where the driver is a constant supply of heat energy rather than a step temperature change. Using a single lump the output temperature is a simple ramp but with multiple lumps there is a delay before any thing happens. Eventually the ramp shows up at the far end but with a delay.
This is all complicated to visualize but one can get an idea of the time for a layer to respond by taking the product of resistance and capacity for the layer.
There is a nearly perfect mapping of the various heat flow equations with those of electrical current flows. This makes it very tempting to use an electronic simulator like SPICE to do all the calculations. It is over twenty years since I used such a program and it would be hard to get my remaining grey cells to cope with relearning.
Jorge: In Part 4, SOD tells us:
Heat flux between layers (e.g. H54 in the schematic) is calculated using the temperature values for the previous time step for the two adjacent layers then using the conducted heat formula: q” = k.(T5-T4)/d54, where k= conductivity, and d54 = distance between center of each layer 5 to the center of layer 4. For still water, k = 0.6 W/m.K – a very low value as water is a poor conductor of heat … a value for stirred water that I found in a textbook: kt = 2 x 105 W/m.K. What
Can enough energy get from the subskin layer (1 mm below) to the skin layer by conduction or is some faster process required? How about from 5 cm below? I’m still not sure what to do (or if I have asked the right questions). In the long run, the entire SWR absorbed beneath the skin layer needs to get to the skin layer. That’s a global average of 160 W/m^2 minus about 20% absorbed by the skin layer.
Sod : “Because turbulent motion is reduced the closer we get to the boundary with the atmosphere, this means that conduction is needed to transfer heat. This needs a temperature differential”
However from the paper quoted, “Cool-skin simulation by a one-column ocean model – Chia-Ying Tu and Ben-Jei Tsuang”, diffusion is stated as being the “only” mechanism.
“Molecular transport is the only mechanism for the vertical diffusion of heat and momentum in the cool skin and viscous layer”
So perhaps you ought to be using values for heat transfer from diffusion rather than (or as well as) for conduction in the appropriate layers?
This kinda makes it even more important to get its relative sizes of your modelled layers right if they’re all behaving differently 😉
Nick Stokes:
Thanks, you are correct.
I think I have become too entranced by how heat moves from the solar-irradiated layers below up to the surface.
Even though it is moving up continually (during the day), the solar radiation vs depth is the reason for the temperature profile. You are correct again.
“Even though it is moving up continually (during the day), the solar radiation vs depth is the reason for the temperature profile. You are correct again.”
Do you have a reference for this? My understanding was that water was largely transparent to the visible spectrum and that most absorbtion happened due to impurities in the water.
I’m sure I read that somewhere…but am willing to be re-educated!
Damned paywalls 😦
TimTheToolMan:
Check out Does Back Radiation “Heat” the Ocean? – Part One where you can see the absorption profile of water.
It’s true that impurities increase the absorption – but pure water absorbs very well.
“Check out Does Back Radiation “Heat” the Ocean? – Part One where you can see the absorption profile of water.”
It does match very closely doesn’t it. So closely I’ve answered my own question that DSR absorbtion effects really are >> convection in terms of how the temperature profile appears anyway!
TimTheToolMan on January 20, 2011 at 2:42 am:
Heat “diffusion” = “conduction”.
From A Heat Transfer Textbook by the Prof’s Lienhard:
And check out pages 18-19 and around that area in the textbook.
“Heat “diffusion” = “conduction”.”
Calling it conduction and having the same properties as conduction are probably not the same thing.
Alexandre:
Yes it does.
But it also affects the radiative transfer – which is equal to the net radiation between atmosphere and surface.
And the evaporation is also important – which is linked to the specific humidity, temperature and wind speed.
Thanks.
Jorge on January 18, 2011 at 1:24 pm:
With many good questions about the model (from the last article).
Correct.
The temperature is in the middle of the layer:
But strictly speaking the conductivity assigned is the “average” or effective conductivity between each layer. I didn’t assign a value for each layer than calculate the effective thermal resistance.
This is because in Part Four the same value was used throughout. And in this article the values were somewhat arbitrary to see what happened with conductivity values that tended to very low values as the boundary was reached.
Yes. The lowest level uses the somewhat arbitrary distance of “the width of the lowest layer”. In the case of Part Four (v3.5 of the code) it was 70m (100m-30m).
I don’t quite understand this question.
The heat into the top layer follows the normal equations, as shown in the notebook above. The heat out is by convection and radiation. The thermal resistance/conductivity of this layer is not used for the DLR, solar heating, convection and radiation out.
TimTheToolMan:
They are the same thing. From Incropera &DeWitt (2007)
The simplified version of this, i.e. the 1d version of this, is the equation I use in Does Back Radiation “Heat” the Ocean? – Part Four:
q” = k . ΔT/Δx
Take a look at the Lienhard textbook and the section on conduction.
As background, there are three forms of heat transfer:
-conduction
-convection – bulk movement of fluids
-radiation
Plus the “fourth in the trilogy” – phase change, e.g. latent heat – which actually moves by convection.
“They are the same thing. From Incropera &DeWitt (2007)”
Is that referring to a liquid?
Nevermind, I haven’t been able to find any references that suggest that a liquid’s molecule’s ability to move (eg brownian motion) makes any difference to its ability to “conduct/diffuse”
A result I’m surprised at actually.
TTTM and SOD: In a liquid, where the surfaces of molecules are in contact with each other, it seems likely that energy transfer/diffusion by collision is likely to occur much faster than repeated exchanges (by diffusion) of a hotter molecule for a neighboring colder molecule. Furthermore, if diffusion of “hotter” molecules to a new locations were possible, that would appear to create a situation where local temperature equilibrium doesn’t apply.
Since the equations describing diffusion of molecules and diffusion of heat appear to be similar, can the coefficients of these two processes be directly compared?
Frank,
Indeed they can be compared. The ratio of diffusivity of momentum (viscosity) to diffusivity of heat is the Prandtl Number – v important in fluid mechanics. And the ratio of viscosity to mass diffusion is the Schmidt Number. So the ratio of these dimensionless numbers, characteristic of a fluid, is what you want.
SoD,
Thanks for the clarifications.
The normal equation clearly takes account of the lower half of the thermal resistance of the top layer when calculating the heat flow from T2 to T1. I understand that this is not specifically calculated but appears simply by using the distance between the middle of the layers.
It seems clear that any thermal resistance from the middle of the top layer to the “surface” has been ignored and effectively T1 is the “surface”.
Strictly speaking, this has halved the temperature gradient needed to pass the solar energy up through the layer.
This sort of thing is a problem for any lumped model and the only solution is to use more “lumps” for the layer. Of course, one then has to use smaller time steps and the computational burden quickly gets out of hand.
Anyway, keep up the good work.
Ward and Minnett(2001)
This is not really correct. As I indicated above The turbulence dissipates because the surface is a free surface and not because viscous forces dominate.
Frank,
I think that the low levels of conductivity may not be quite as troublesome as you imagine. Look at the conductivity figure of 0.6 W/K.m This says that a 1º temperature difference will cause o.6W/m2 to flow through a 1m thick layer that has an area of 1m2. If we do it the other way round we find that it needs a temperature difference of 1.67º to pass 1W/m2 through a 1m thick layer.
Clearly we would need 267º to pass 160W/m2 which is ridiculous but if the layer is only 1mm thick the temp difference comes down to 0.267º which is not implausible. With a thickness of 5mm we drop 1.33º which seems a bit high.
I realise that this 160W/m2 is an average over a day so this is not a totally realistic way to do the sums but it looks as though it does not need a huge temperature drop to drive the absorbed solar heat through the last few mm below the skin.
It does seem certain that the much lower effective thermal resistance of convection is needed to get the solar energy from the rather deeper parts where some was absorbed.
Jorge: I didn’t have any preconceptions about the implications of the low intrinsic conductivity of water, I was hoping to establish the limitations set by the low conductivity of water. Following your sample calculation, 600 W/m2 of thermal energy to flow through 1 mm of calm water with a temperature gradient of 1 degK. 600 W/m2 is more than we need for all but the most extreme situations situations on earth: a) Full solar in space is 1365 W/m2. b) Global average solar is 160 W/m2 at the surface. c) Globally, the difference between upward and downward long wavelength radiation is about 60 W/m2. If we have a temperature gradient of 0.1-1.0 degK, energy fluxes of this magnitude can travel the last millimeter to the skin layer of the ocean by conduction alone (and escape to the atmosphere). Distances which are more than an order of magnitude longer than 10 mm presumably require convection or some other type of physical mixing.
Looking at SOD’s temperature profiles with depth at the top of this post shows temperature gradients consistent with conductive heat transport in the top 1 mm of the ocean. We could call this the “conductive domain”, but the extent of such a domain depends on assumptions about the temperature gradient and the energy flux. From Part 1, about 20% of sunlight is absorbed in the “conductive domain” and needs no added mechanism to reach the skin layer. About 50% of sunlight is absorbed below 1 m. The vast majority of this energy needs to reach the surface by a different mechanism.
SoD,
This goes beyond the scope of the surface layer, and speaks experientially to the macro temperature profile specifically in the northern Gulf of Mexico but ends with several questions. This area has a fairly characteristic bottom profile of gently sloping white sand bottom to a depth of 20 meters 3 miles offshore, 35 meters 15 miles offshore, and continuing (more or less smoothly) to the continental shelf.
In the summer months through fall, there is a distinctively warmer layer in the top 3 to 5 meters that can be as warm as 88f to 90F (I have always attributed this to solar heating and wave mixing). This top layer can be so much warmer than the deeper water that it often makes me a bit nauseous as I come to the surface after a deep dive. Summer temperature of the large middle layer generally settles into the 76F to 82F range. There is always a thermocline cold layer near the bottom which can be as cold as 68F to 72F, but can vary quite widely in depth and temperature from year to year.
In the winter it is not unusual to experience as many as 3 thermoclines in 20 meters of water with surface temperatures starting in the mid to low 60’s (F).
During the transitional seasons one can often find no distinctive surface layer in the top 3 to 5 meters.
I’d conclude with just a few observations about some of the comments on the topic. Inverted layers where warmer water is trapped below colder water are sometimes encountered. These layers have (in my experience) been most distinctively bounded, and can create an optical boundary as well. I have literally bobbed up and down through the layer at mask level and observed the (quite visible) boundary extending into the distance. It’s a mind-blowing thing to see!
These general consistencies point out again that water layers of differing temperature really do not mix easily and tend to stay distinct.
I wonder if there are any studies on the heat transfer across thermocline layers? Is there something that causes higher resistance to heat flow across those distinctive boundaries? In a normal delta T calculation you would expect the heat transfer to be quite high, but I wonder…
Well I was sure I’d read that it was impurities that were the reason for the absorbtion and not the water itself.
SoD wrote : “Check out Does Back Radiation “Heat” the Ocean? – Part One where you can see the absorption profile of water.
It’s true that impurities increase the absorption – but pure water absorbs very well.”
So from a reference from one of your references revealed the following
http://oceanworld.tamu.edu/resources/ocng_textbook/chapter06/chapter06_10.htm
“The clearest ocean water is called Type I waters by Jerlov (Figure 6.18). The water is so clear that 10% of the light transmitted below the sea surface reaches a depth of 90m.”
So it seems to me that “k” in Beer-Lambert’s law you quoted earlier…
I = I0.exp(-kd)
…varies very much with the properties of the water rather than the water itself.
So the upshot is I’m still not fundamentally clear on the point regarding water’s ability to absorb DSR.
k for water varies a lot with wavelength. There’s a reason that underwater photographers use flash lamps.
http://en.wikipedia.org/wiki/Underwater_photography
That 10% that penetrates to 90 m is all blue.
“That 10% that penetrates to 90 m is all blue.”
Of that I’ve no doubt, but I cant see why the rest of the wavelengths shouldn’t be distributed in a relative fashion to the 90m. And thats quite a different result from essentially all of it being absorbed in the first 5-10m or so.
…and as far as I can see depends on the clarity of the water and isn’t a property of the absorbtion of the molecule H2O.
Having done a bit more research and having thought on it… the only thing I can come up with is that the “light” is actually UV and extreme UV and for whatever reason the atmosphere was letting a lot through on the day it was measured so that it could account for 10% of the total SI.
It still doesn’t feel right, though.
It can’t be all UV. Otherwise you couldn’t see at 90 m, which you can if the water is clear enough.
“It can’t be all UV. Otherwise you couldn’t see at 90 m, which you can if the water is clear enough.”
OK, well if thats the case then unless there is yet another factor at work here, the temperature profile offered by SoD (with the relative depth given of about 2m for about 90% absorbtion) must primarily be due to impurities.
And so that means that daily ocean heating is influenced to a large extent by ocean water clarity. Its not inconceivable that long term heating would be effected as well.
Thats not a result you see quoted much.
90% in 2 m does seem a little too quick. But water clarity isn’t going to affect the total absorption, it just affects the depth profile. The heat will still have to get back to the surface. The other thing to consider is that the 10% transmitted to 90 m probably only refers to the visible part of the spectrum. All the IR is going to be absorbed very close to the surface. So in terms of total power, it’s probably less than 5% transmitted to 90 m.
If anything, turbid water will absorb less energy because it reflects more than clear water.
DeWitt write : “90% in 2 m does seem a little too quick.”
Yes, its actually more like 20m which is still well short of the 90m it can get to.
“But water clarity isn’t going to affect the total absorption, it just affects the depth profile.”
Yes, but its heat moving to the depths that is the only way to “keep it in the ocean”. If its not in the depths, then necessarily the SST must increase and I didn’t think there was an actual trend observed for that…
“So in terms of total power, it’s probably less than 5% transmitted to 90 m.”
Could be. The website quoted 10% for “light”. If you add UV then its more. Take off IR and its less…but either way, that much energy at that depth is significant.
“If anything, turbid water will absorb less energy because it reflects more than clear water.”
There are SO many complicating factors aren’t there!
According to the model outlined by “science of doom”, the upper layer of the surface is free of convection. Heat is transported though this layer by conduction, exclusively. Since the thermal conductivity of water is relatively low, this throttles the escape of heat from the ocean to the air and thus out from the Earth system into space.
If so, then we must see that we do not to contaminate this thin layer by chemicals or in some other way so that the temperature gradient is eradicated. This will allow the mixing process to reach surface and disturb the temperature balance of the oceans.
I am mentioning this in connection to the comment given by Jeff Id on January 19, 2011 at 2:09 am.
In http://en.wikipedia.org/wiki/Sea_surface_temperature, the diagrams of Sea Surface Temperature name the major channels for the heat flow from the surface to the air at the daytime and nighttime.
At the daytime the major losses seems to be related to evaporation emission while at the nighttime the radiation emission is predominant.
This would indicate that if we prevent (intentionally or unintentionally) the evaporation emission during the daytime, the “greenhouse” effect for the ocean will be established. Such an “ocean greenhouse effect” would warm the oceans much more effectively than the increase of the back radiation.
And what about algae covering the see surface (and below)?
Chlorophyll is known to absorb radiation within the band from far violet to blue-green with the absorption peak at about 0.48 um (the absorption coefficient above 80% at the peak value) and the next band covering the yellow – red region with the peak at 0.68 um (the absorption coefficient above 50%). Photons from the green – yelow region are reflected. Similarly, Carotenoids are absorbing photons from the far violet to green with the absorption coefficient of about 60%, see, for example, http://www.physics.umd.edu/grt/taj/104a/104anotessupps.html
Thus, a considerable part of the visible radiation is either absorbed or reflected, the interaction of vegetation with the photons from the visible region making the surface of the lands cooler and greener. Algae, in turn, prevent the heating of water as long as algae are not decomposed. If algae are consumed by the other organisms, the solar energy, stored in algae, is transferred to these organisms.
Any kind of human activity diminishing the vegetation areas and organic life at lands and oceans has a very large impact on the temperature state of the Earth and is working against the mankind itself. It is this that should be called AGW.
I don’t know if anyone is still reading this thread, but if so I have a question.
I recently performed some comparisons that show a close correlation between increasing sea surface temperatures and increasing solar irradiance during the 20th century, which leads me to suspect that solar heating may have caused the increase in SST. Is this physically plausible?
The problem is the magnitude of the increase in solar radiation. It just isn’t large enough to explain the size of the temperature increase. Correlation is not causation. My guess would be that sea surface temperature correlates to global population as well.
The problem here is that we really don’t know how large the 20th-century increase in total solar irradiance was. Estimates range from 0.2 w/sq m (Svalgaard) to 5.2 w/sq m (Beer), with others (e.g. Solanki, Lean, Hoyt, Wang, Krivova) falling anywhere between 0.7 and 4.1 w/sq m. The 0.2 w/sq m estimate adopted by the IPCC is at the absolute bottom of the range.
And then there’s the possibility that changes in TSI generate large positive feedbacks from the related changes in cosmic ray flux. I don’t think anyone has conclusively proved that they do, but no one seems to have proved that they don’t either.
So let me restate my question in a more specific form. Let’s assume that the increase in TSI between 1900 and 1950 (which is when most of the 20th- century increase occurred) WAS in fact large enough to have warmed the upper layers of the ocean. Now we have to explain why the SST record shows about twice as much warming as the surface air temperature record over this period. It seems that we can explain this only if solar heat accumulates at the sea surface and doesn’t get released to the atmosphere or transferred to greater depth. Is this physically plausible?
The problem is that the oceans are not static. You have to figure in circulation, about which, we only know the basics. Warm water flows to the poles, cools, descends and upwells at lower latitudes. The upwelling rates vary with time and location. It’s more or less constant or the thermocline between the deep ocean and the upper layer would be moving up or down. But that’s only more or less. The AMO, for example, looks like it has an oscillation with a period of about 65 years and appears to be correlated to global average temperature.
In the Pacific, you have ENSO and the PDO. Maybe they’re driven by solar cycles, but I doubt it.
In fact, it’s possible to explain ~80% of the variation of global temperature from 1880-2010 using a combination of an exponential function and a sine wave (R=0.93). The best fit sine wave has a period of 67.7 +/- 7.2 years.
Nick, TTTM: The Prandtl number for water is 7. A modest search on the web didn’t produce a Schmidt number for water, but did produce a statement saying that it was 0.1 for most liquids. Looking at the denominators of these dimensionless ratios, the thermal diffusion rate or thermal diffusivity for water is 1.4*10^-7 m/s2. The molecular diffusion rate or mass diffusivity for many small molecules in water are about 1*10^-9 m/s2. So thermal/kinetic energy is diffuses (through collisions) about 100 times faster than the molecules that possess the kinetic energy.
en.wikipedia.org/wiki/Thermal_diffusivity
http://enggyd.blogspot.com/2009/09/diffusivity-and-mass-transfer.html
Roger on January 24, 2011 at 3:28 pm:
on January 24, 2011 at 6:07 pm:
It is, of course, physically plausible that an increase in solar irradiance would cause an increase in SST.
In fact, all other things being equal, an increase in solar irradiance must lead to an increase in SST.
The important question is: how much increase have we seen? And as you correctly point out in your 2nd statement, we don’t really know the values prior to 1978 when satellites began measuring it.
So that makes your 1st statement confusing.
Yes, I guess these two statements were confusing. Sorry.
The point I should have made is that although the solar reconstructions have quite different amplitudes, they all show the same rapid increase between 1900 and 1950 after normalization. So the correlation between TSI and SST persists regardless of the estimated amplitude of the TSI increase.
Which leads to another question. How large an increase in radiative forcing do we need to generate a 1C increase in SST? (Averaging the reconstructions gives an increase in TSI of about 2.0 w/sq m between 1900 and 1950, for what it’s worth.)
Is that TSI at the top of the atmosphere as in 1360 W/m2 or averaged over the area of the planet at 340 W/m2? If it’s 2 in 1360 then the surface forcing would be 2*0.7/4 or 0.35 W/m2, which isn’t much. You’d have to invoke some sort of currently unknown mechanism that makes the system to have higher sensitivity to solar forcing to get 1 C warming from solar alone.
Dewitt:
That’s 2 w/sq m TOA. As you say, 0.35 w/sq m at the surface probably wouldn’t cause a 1C rise in SST (how much would it cause, incidentally?) so I guess I’m going to have to fall back on feedbacks.
The first order effect from Stefan-Boltzmann, and ignoring any change in convective transfer, depends on the surface temperature. If I pick 15C or 288.15 K then adding 0.35 W/m2 that has to be radiated away increases the surface temperature to 288.21 for a change of 0.06 degrees. For the US 1976 standard atmosphere clear sky in MODTRAN, to get an increase of ~0.35 W/m2 at the TOA, the surface temperature has to go up by 0.1 K. In other words, not very much.
I’ve just noticed this thread and am pleased to see it because it addresses the heart of the issue as to whether extra DLR can heat the ocean bulk.
Lets look at that chart again:
https://scienceofdoom.files.wordpress.com/2010/12/ocean-temp-profiles-2-kawai-wada-2007.png?w=490&h=441
To reduce the upward energy flow from the bulk ocean it is not enough to change the temperature of the ocean skin at 10 microns deep. Additionally one has to change the temperature of that 1mm deep subskin.
The depth and intensity of that subskin is a direct indication of the upward energy flow from the ocean bulk below it.
If one only warms the skin (the top 10 microns) without altering the gradient below 10 microns then the upward energy flux is not being affected.
In that diagram that top layer 1mm deep and 0.3C cooler than the ocean bulk remains day and night with no apparent change.
If the change from day to night does not affect it then how can a little more DLR change it ?
The implication is that the subskin temperature is a permanent fixed feature which is not affected by anything that goes on above 10 microns in depth.
Whatever happens in that 10 micron deep layer does not transmit downward.
The reason must be that whatever warming occurs in that 10 micron layer is negated by an increased upward energy flux to the air above from increased upward convection, evaporation, radiation and conduction.
Thanks, you are correct.
Regarding Nick Stokes’ suggestion : “2. “In brief, the temperature generally rises in the last few meters as you get closer to the surface because hotter fluids rise. They rise because they are less dense.”
I don’t think that is the reason here. Mainly it’s that the upper levels are absorbing more sunlight. That’s why the peak isn’t there at night. ”
And SoD’s agreement “I think I have become too entranced by how heat moves from the solar-irradiated layers below up to the surface.
Even though it is moving up continually (during the day), the solar radiation vs depth is the reason for the temperature profile. You are correct again.”
After having carefully considered this, I’m going to disagree with Nick’s suggestion because according to the Wiki diagram (which I’ve seen replicated in a few places) the vast majority of the warm waters are concentrated within the first couple of meters
That isn’t the temperature profile of absorbtion in the ocean. We’ve seen examples where the absorption goes much much deeper than that. And on top of that, convection MUST bring the warmer waters to the surface for radiation.
So whilst I will agree that a portion of the “hook profile” will be due to direct absorption, the majority of it wont be.
As far as the night time observation goes, this is simply due to the fact there is no additional warmth being input into the ocean at depth and convection will quite quickly concentrate it at the top for radiation away.
This would be relatively easy to verify and my prediction would be that once DSR decreases/stops, radiation will continue until such time as the hook disappears and it gets to the night time profile.
This would mean that in the Minnett experiment, the absolute SST would drop but the relative temperatures between the SST and the 5cm depth may well increase for a time because the amount radiated by the ocean must decrease (due to the increased DLR making up the difference) and so convection will tend to increase the 5cm warmth.
If Peter Minnett was to publish his data then we could see what actually happened…at the moment all we have is the reported difference in SST and 5cm depth with no appreciation of absolute temperatures and how they varied.
I should also mention how I know this to be true… over the last few days I spent considerable time fishing and you can clearly see the bottom when the depth (according to the sonar) is 4-5m. Thats a 10m round trip for the light in the visible spectrum without it being absorbed.
TTTM,
About half the energy of solar radiation at the surface (49%) is in the near IR, 780-2500nm. Near IR is strongly absorbed by water. Pretty much all of it will be absorbed in the first meter with most of that happening in the first few cm. Even the red end of the visible spectrum goes away pretty fast. Drop something bright red on the bottom the next time you go fishing and see if it still looks the same. Water isn’t colorless. Over a sufficiently long path, it’s blue.
On rechecking figure 1. above, peak absorption of near IR occurs at about 1 mm.
Yes, but this is the bit that doesn’t penetrate the ocean and as you say, doesn’t contribute to the hook shape at all.
So for Nick to be correct almost all of the non-IR must be absorbed in the next meter or two and thats just not what happens.
Further to that, I have a pool and when its nice and clean, its crystal clear to the bottom. Thats about 1.7m (for a 3.4m return journey) and my scoop is red.
I know for a fact that when I’m scooping stuff off the bottom at the deep end, then scoop is still red.
Absorption is exponential with path length so 3.4 m will absorb a lot less than 10 m. Even so, if you had a something at the surface to compare, you should see a small difference in the color intensity. It will still be red, but not as bright. It will also depend on the exact shade as the absorption is changing a lot with wavelength at the red end of the visible spectrum.
The IR absorption properties of water lead to exactly the observed daytime temperature profile. Peak absorption at 1 mm depth means peak temperature is seen there as well. The temperature then decreases as you move up or down because there’s less heat in and heat will be diffusing out to the lower temperatures of the surface and the bulk.
Where are you getting your 49% for IR and near IR figures from?
At any rate a portion of that 49% is absorbed in the first 10um not the first 1mm
FWIW, look at this Solar Radiation Spectrum by energy graph
Where it appears that about 1/3 of the IR+nearIR energy is absorbed in the first 10um. Thats going to leave 2/3 of the remainder for absorption in that first few meters. (but I’d still like to check against your source)
So that breakdown means…
approximately 17% is absorbed in the first 10um
approximately 33% is potentially absorbed in the “hook region”
approximately 50% is absorbed lower down
Therefore about 60% of the “hook profile” must come from convection because the remaining energy makes its way back out of the ocean from deeper.
It’s gone suddenly quiet so I’ll ask a simple question.
Why is the temperature gradient from the very surface to 1mm deep (where the subskin joins the ocean bulk) identical both by day and by night despite the huge change in energy input from above ?
All that changes between day and night is the gradient below 1mm which is clearly solely a result of changed solar shortwave input.
Neither variations in solar input nor in DLR from above 1mm deep appears to make a scrap of difference to the gradient from 1mm depth to the top.
Sure it changes the absolute temperature but not the gradient.
Yet it is the gradient that matters for the background flux from ocean bulk to the subskin and not the absolute temperature.
So, on the basis of that diagram, changes in energy input from solar or DLR make not a scrap of difference to the gradient from 1mm upwards and therefore cannot be affecting the energy content of the bulk ocean at all.
Slight correction, I said this:
“So, on the basis of that diagram, changes in energy input from solar or DLR make not a scrap of difference to the gradient from 1mm upwards and therefore cannot be affecting the energy content of the bulk ocean at all.”
should read:
therefore cannot be affecting the background energy flux from the bulk ocean at all,
Having made that point it becomes necessary to deal with the matter of cloudiness and it’s effects because the passing over of a cloud with the consequence of a warmed ocean skin layer is put forward (by Realclimate amongst others) as a ‘confirmation’ of the effect of DLR on the skin layer because clouds transmit more DLR downward just as GHGs do.
I think that the two types of phenomena are quite different. When a cloud passes over it reduces both upward radiation (by bouncing it back down) and evaporation (humidity increases due to suppressed convection) and so has an effect on the skin layer by reducing upward energy loss. That will reduce the gradient from 1mm deep upwards both by day and by night and will slow down energy loss from the bulk ocean.
When DLR from a clear sky (either at night or by day) is present it does not significantly decrease upward radiation in the way that a cloud does and it increases evaporation by adding energy to the interacting layer (the top 10 microns) and then allowing maximum convection rather than suppressing it in the way that a cloud does.
So DLR will NOT slow down energy loss from the bulk ocean in the way that a cloud does.
Unless someone can falsify the above it would seem that the comparison between passing cloud cover and DLR changes is utterly misconceived.
Moreover, cloud cover will reflect incident visible & UV upwards, preventing it from reaching the ocean. This cooling effect is by measurement enormously more important to ocean temperature (skin or otherwise) than any IR effect.
We learn from NOAA, for example, that the current La Niña differs from earlier ones in that the strengthened tradewinds have not cleared the cloudiness of the central tropical Pacific — thus slowing the La Niña recharge process and producing what will probably prove to be a multiyear La Niña atmospheric cooling.
Thus evidence as well as theory supports SW’s conclusion that incident IR (solar, greenhouse, whatever) cannot be affecting the bulk ocean temperature.
=====
As an aside, I note that SoD in the earliest posts on this topic emphasized turbulent mixing as the way the IR-absorbing micron surface skin transmitted its heat downwards. We now learn in this post that the whole mm-thick top layer does not participate in turbulent mixing but remains more or less fixed. OK, full speed astern, maties!
Another point about tropical clouds — since the tropics are the major source of heat for the climate system — is that a typical day there sees a relatively clear dawn, with clouds gradually accumulating during the day and precipitation in the afternoon, with the clouds gradually dissipating around dusk. Thus the night sky is frequently clear, allowing any outgoing radiation from the tropical ocean a more or less free ticket to outer space.
The daylight clouds, precipitation, and clear night are all obviously negative feedbacks to any SST increase, in addition to evaporation.
Hi SoD
thanks for the illuminating series. I have a question related to what Stephen is talking about. In Ward (2006), at what depth is the subskin temp measured?
SOD
DSR and DLR are of the same order of magnitude at the oceans surface.
Fig. 1 (Donlon 2005) above shows the sun warmed top 5 to 10 metres cooling and sinking etc. at night to produce zero gradient with cooler skin.
There is no noticeable night time DLR signal in the night time gradient as would be expected given DLR’s continued existance at night and it’s, according to your model in part 4, effect on ocean bulk temperature being as strong and as quick as DSR’s.
I’ve no doubt missed something, but would be interested in how you reconsile Fig. 1 above with your model results in part 4.
Craig Goodrich on February 7, 2011 at 12:21 pm:
By the way, for reasons only known to WordPress the spam filter ate all 4 of your comments – which is why they didn’t appear until now.
In fact, the main mechanism for mixing is the diurnal cooling. The water cools and sinks. You can see the measurements here:
The point about turbulent mixing is not that the top layer stays “fixed” but that turbulence becomes less effective as you move closer to a boundary. The actual fluid mechanics is very complex. But this is to do with turbulent motions of the ocean being transferred to the surface.
It doesn’t stop cold water sinking.
Bob Irvine:
The solar heat penetrates a few meters into the ocean. This causes the temperature gradient. The temperature established during the mid-afternoon is determined by how effectively heat can move back to the surface.
The DLR only penetrates the first few microns so you won’t expect to see any temperature gradient below those few microns.
Does this answer your question?
Stu N
Sorry, I have only just noticed your question.
I had a quick reread of the paper and didn’t find a clear answer. It seems the profiler is measuring a value at “the surface” and the unit has a resolution of about 3mm. It’s clear from everyone else’s work that you can’t actually measure the skin temperature with this kind of device – because of the tiny skin thickness – so the actual “subskin” temperature measured is an average of the top 3mm.
SoD
The IPCC are now saying that 90% of the energy trapped by AGHGs is warming the bulk ocean. This is an attempt to explain (along with aerosols) atmospheric warming being lower than expected and predicted.
Question 1-Does this imply that 300w/m2 (340 x 90% = aprox 300) of DLR is being deposited in the top 10 microns of the ocean then transported to the bulk ocean rather than be radiated or evaporated to the atmosphere or space?
This is a bit hard for me to swallow but I would be interested in your thoughts.
Q 2- In an ideal situation (ie no wind, no clouds, and 24 hours of strong sunlight, no night etc) would the daytime gradient in fig. 1 above be a permanent feature or would it disappear slowly as the system approached equilibrium?
Time is temperature. The theory goes that changes in GHGs hold energy in the system for LONGER before it is released thus warming the system. If it can be shown that a change in DSR puts more energy into the bulk ocean than a similar change in DLR then this implys that DLR is returned more quickly to space and therefore the earth’s heat content sensitivity would be less for DLR than DSR.
DLR sensitivity at the moment is being calculated using DSR data. Annan 2006 (ice ages, volcanic etc.).
The Tangaroa data in light winds indicates that a 100w/m2 increase in DLR under cloud increased the temp. 0.2C. Some of this may be due to decreased evaporation under the cloud.
For arguements sake lets say an increase in DLR of 100w/m2 caused a 0.1C change in ocean temp.
Chelle et al, http://www.ssmi.com/papers/tmi/diurnal_signals_in_satellite_sst_measurements.pdf
(you’ll have to copy/paste to google) show a 120w/m2 change in solar insolation in light winds causes a 1.0C to 2.0C change in upper ocean temperature, a factor of 10 or more higher than Tangaroa.
Q3- Does the difference between Tangaroa and Chelle et al imply that a change in DLR does not heat the ocean as much as a similar change in DSR and, therefore, the earth’s heat content sensitivity is considerably less for DLR than DSR?
Thanks again for taking the time to answer my questions. It’s difficult for an amateur like myself to get this type of opinion.
http://www.remss.com/papers/tmi/diurnal_signals_in_satellite_sst_measurements.pdf
The cool skin of water can be sensed radiometrically in great detail using an infrared interferometer such as M-AERI. This was done in 20 years ago and is detailed in “Sounding the skin of the ocean”, Journal of Atmospheric and Oceanic Technology, Vol. 12, # 6, pp 1313-1328 Dec., 1995 with F. Bretherton, H. L. Huang and W. L. Smith, U Wisconsin
I’m sorry to see much research time has been spent speculating on what is inside this difficult-to-observe region whereas a refined means of observing it is ignored. The interferometric technique results in some 300+ measurements within 0.01 cm.
Walt McKeown
Walt,
The caption for the measurements says:
So I’m not clear what your point is.
I noticed that the distribution of absorption of solar SW with depths is discussed in this thread. I checked the distribution based on the solar spectrum at surface (ASTM G173-3, Direct+circumsolar) and absorption of UV, visible, and IR in pure water as function of wavelength. The results are as follows.
The following values tell the share of absorption in a top layer of several thicknesses from 1µm to 1km for sun at zenith.
Layer absorption
1µm 0.14%
10µm 0.57%
100µm 2.8%
1mm 10.2%
1cm 21.4%
0.1m 37.6%
1m 58.1%
10m 77.0%
100m 93.6%
1km 99.97%
For thermal IR spectrum of 15C corresponding ratios are
1µm 16.6%
10µm 74.9%
100µm 99.8%
1mm 100.00%
The net emission of thermal IR is roughly one third of global average of absorbed solar SW and the maximal solar radiation is around seven times the global average. Thus the layer in radiative equilibrium may be less than 1 mm thick with clear sun at zenith, and a couple of cm, if calculated from the global averages.
Hi,
I should have been clearer in my comment. The paper I mentioned showed how to look inside the top mm of the cool skin and determine the temperature
gradient inside that tiny moving zone. That allows a simple
calculation of heat flux.
Later papers connected the measurement and gradient with gas flux.
Thanks for the feedback.
Walt McKeown
[…] a very high level of consistency over the last 15 years, the authors report. AIRS data reflects skin temperature at the surface of the ocean, land, and snow/ice covered regions. Surface-based data are a blend of two-meter surface air data […]