In Atmospheric Circulation – Part One we saw how the pressure “slopes down” from the tropics to the poles creating S→N winds in the northern hemisphere.
In The Coriolis Effect and Geostrophic Motion we saw that on a rotating planet winds get deflected off to the side (from the point of view of someone on the rotating planet). This means that winds flowing from the tropics to the north pole will get deflected “to the right”.
Taylor Columns
Strange things happen to fluids in rotating frames. To illustrate let’s take a look at Taylor columns.
Figure 1
The static image is quite beautiful, but the video illustrates it better. Compare the video of the non-rotating tank with the rotating tank.
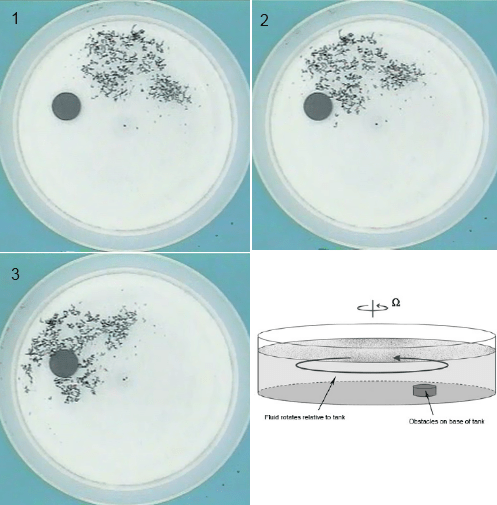
Now to stretch the mind we have a rotating tank with an obstacle on the base – in this case a hockey puck. The height of the puck is small compared with the depth of the fluid. The fluid flow has come into equilibrium with the tank rotation.
We slow down the rotation slightly. We sprinkle paper dots on the surface of the water. Amazingly the dots show that the surface of the fluid is acting as if the puck extended right up to the surface – the flow moves around the obstacle at the base (of course) and the flow moves “around” the obstacle at the surface. Even though the obstacle doesn’t exist at the surface!
Take a look at the video, but here are a few snapshots:
Figure 2
This occurs when:
- the flow is slow and steady
- friction is negligible
- there is no temperature gradient (barotropic)
Under the first two conditions the flow is geostrophic which was covered with examples in The Coriolis Effect and Geostrophic Motion.
And under the final condition, with no temperature gradient the density is uniform (only a function of pressure).
“Thermal Wind”
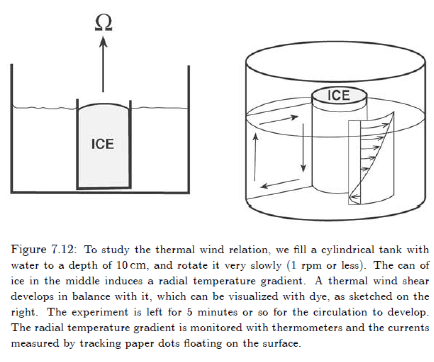
Now let’s look at an experiment with a “cold pole” and “warm tropics”:
Figure 3
The result:
Figure 4
Even better – take a look at the video.
This experiment shows that once there is a N-S temperature gradient the E-W winds increase with altitude.
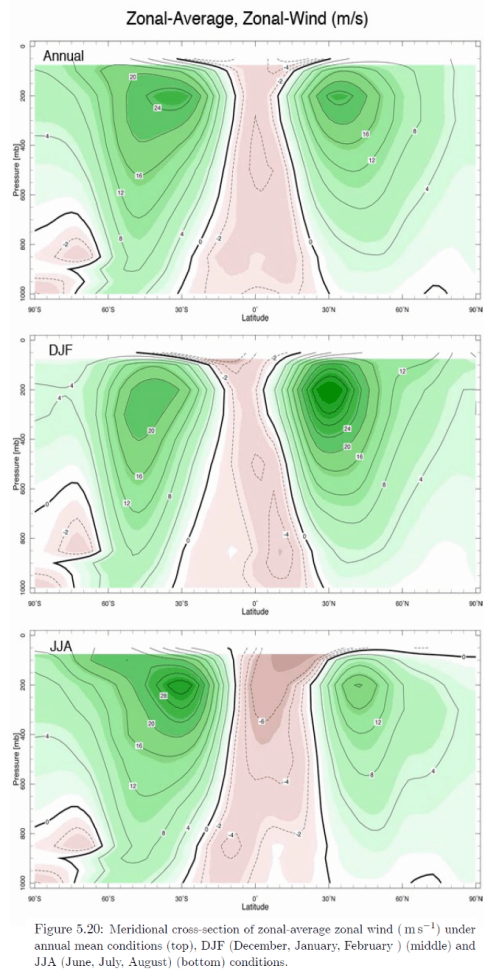
Which is kind of what we find in the real atmosphere:
Figure 5
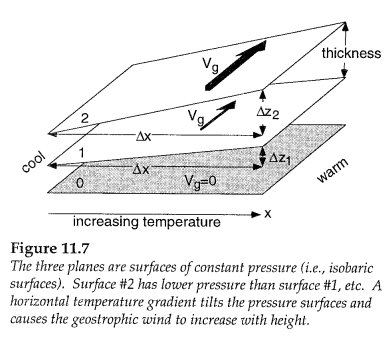
Why does this happen? I found it hard to understand conceptually for a while, but it’s actually really simple:
Figure 6
So the ever increasing pressure gradient with height (due to the temperature gradient) induces a stronger geostrophic wind with height.
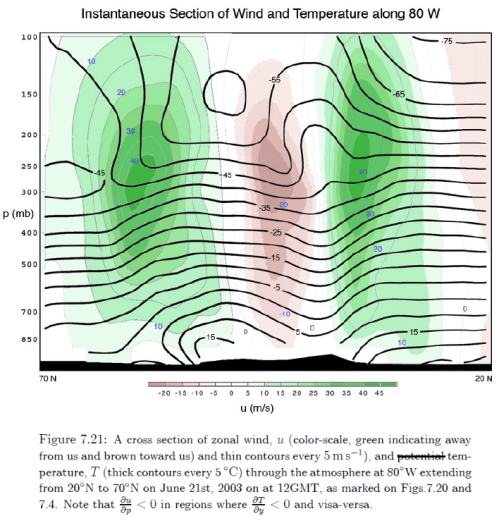
Here is an instantaneous measurement of E-W winds, along with temperature in a N-S section:
Figure 8
The measurement demonstrates that the change in E-W wind vs height depends on the variation in N-S temperature.
The equation for this effect for the E-W winds can be written a few different ways, here is the easiest to understand:
∂u/∂z = (αg/f) . ∂T/∂y
where ∂u/∂z = change in E-W wind with height, α = thermal coefficient of expansion of air, g = acceleration due to gravity, f = coriolis parameter at that latitude, T = temperature, y = N-S direction
It can also be written in vector calculus notation:
∂u/∂z = (αg/f)z x ∇T
where u = wind velocity (u, v, w), z = unit vector in vertical
In the next article we will look at why the maximum effect in the average, the jet stream, occurs in the subtropics rather than at the poles.
References
Meteorology for Scientists and Engineers, Ronald Stull, 2nd edition – Free (partial) resource
Atmosphere, Ocean and Climate Dynamics – An Introductory Text, Marshall & Plumb, Academic Press (2008)




[…] « Temperature Profile in the Atmosphere – The Lapse Rate Atmospheric Circulation – Part Two – Thermal Wind […]
SoD,
The caption of your Figure 8 (Figure 7.21 of Marshall and Plumb) refers erroneously to potential temperature while the values and thick contours present actual temperatures rather than potential temperatures. That’s not your error but may be confusing. You can find the same image with the correct caption as a Powerpoint file from the publishers web page:
http://www.elsevierdirect.com/v2/companion.jsp?ISBN=9780125586917
Check the ppt of Chapter 07.
(Similarly I think that the missing molar mass in the formula of your previous post may be confusing although it’s not essential for understanding your points. As the equation stands the units don’t match. Thus anyone trying to reproduce the formula may have unnecessary difficulties.)
Pekka,
Well spotted. I updated the graphic for figure 8.
On the missing molar mass, I have now clarified the equation in a comment.
R = gas constant for dry air; and is in units of J kg-1K-1
SoD,
I think that some further arguments could be added to explain your formulas. Now you don’t really present any justification for them. You tell the background but skip over the final essential step. Going through the full derivation is perhaps too much but the following basic idea behind the formulas can be given:
A possible situation and the one actually observed is that rather stable geostrophic winds persist. To have such a wind something must balance the force created by the pressure gradient of your Figure 6. The only horizontal “force” available is the Coriolis force. Your formulas represent the requirement that the “pressure force” and the Coriolis force are equal in size and have opposite directions.
Pekka,
Good idea.
Refer to The Coriolis Effect and Geostrophic Motion for the geostrophic wind equations:
ug = – 1/fρ . ∂p/∂y ….[4a]
vg = 1/fρ . ∂p/∂x ….[4b]
where ug = W-E wind speed, vg = N-S wind speed
These equations are derived from:
So from the equations we see that the E-W wind is proportional to the change in N-S pressure, and the N-S wind is proportional to the E-W change in pressure.
It is more convenient to consider the height of a pressure surface rather than the pressure at a given height.
Using the hydrostatic balance equation it’s easy to show that:
(∂p/∂x)z = gρ (∂z/∂x)p ….[5a]
(∂p/∂y)z = gρ (∂z/∂y)p ….[5b]
where (∂p/∂x)z is the change in pressure (at constant height) in the x direction and (∂z/∂x)p is the change in the height of a pressure surface (geopotential height) in the x direction
So combining 4 & 5 we get:
ug = –g/f . ∂z/∂y ….[6a]
vg = g/f . ∂z/∂x ….[6b]
This version of the equation doesn’t include density, ρ, and given that density varies in a compressible fluid like air this is a very helpful version of the equation. It is one reason why pressure is often preferred over height as the vertical coordinate.
And back to the thermal wind equation – if we differentiate equation 4 with respect to height we get the equation shown in the article although the derivation takes a little time to write out.
SoD.
Here you have a great resource on this topic.
http://kiwi.atmos.colostate.edu/group/dave/at605.html
[…] 2012/08/25: TSoD: Atmospheric Circulation — Part Two — Thermal Wind […]
Jon
Thanks for that – it looks like the sort of thing I have been looking for. The following sentence however is a good reminder of how much things have been changing.
“The Arctic ocean is ice-covered all year, while the North Atlantic and the Southern Oceans experience seasonal melting.”
That was then, this is now.
SoD,
This is very impressive work , my friend.
[…] Comments « Atmospheric Circulation – Part Two – Thermal Wind […]