In Planck, Stefan-Boltzmann, Kirchhoff and LTE one of our commenters asked a question about emissivity. The first part of that article is worth reading as a primer in the basics for this article. I don’t want to repeat all the basics, except to say that if a body is a “black body” it emits radiation according to a simple formula. This is the maximum that any body can emit. In practice, a body will emit less.
The ratio between actual and the black body is the emissivity. It has a value between 0 and 1.
The question that this article tries to help readers understand is the origin and use of the emissivity term in the Stefan-Boltzmann equation:
E = ε’σT4
where E = total flux, ε’ = “effective emissivity” (a value between 0 and 1), σ is a constant and T = temperature in Kelvin (i.e., absolute temperature).
The term ε’ in the Stefan-Boltzmann equation is not really a constant. But it is often treated as a constant in articles that related to climate. Is this valid? Not valid? Why is it not a constant?
There is a constant material property called emissivity, but it is a function of wavelength. For example, if we found that the emissivity of a body at 10.15 μm was 0.55 then this would be the same regardless of whether the body was in Antarctica (around 233K = -40ºC), the tropics (around 303K = 30ºC) or at the temperature of the sun’s surface (5800K). How do we know this? From experimental work over more than a century.
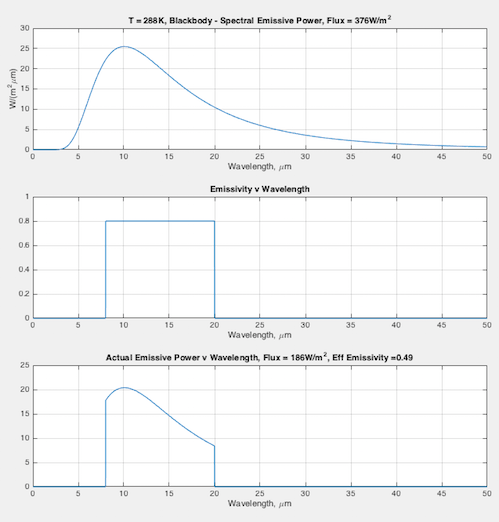
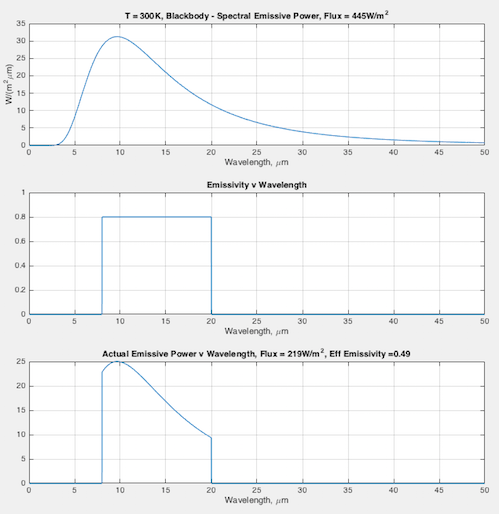
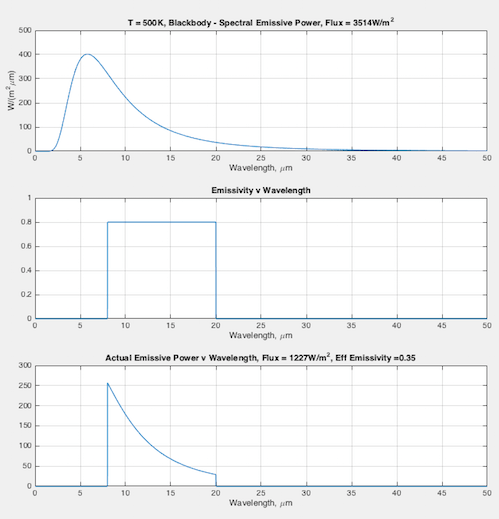
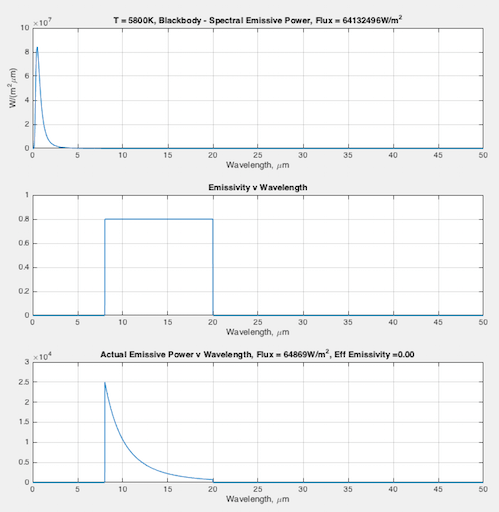
Hopefully some graphs will illuminate the difference between emissivity the material property (that doesn’t change), and the “effective emissivity” (that does change) we find in the Stefan-Boltzmann equation. In each graph you can see:
- (top) the blackbody curve
- (middle) the emissivity of this fictional material as a function of wavelength
- (bottom) the actual emitted radiation due to the emissivity – and a calculation of the “effective emissivity”.
The calculation of “effective emissivity” = total actual emitted radiation / total blackbody emitted radiation (note 1).
At 288K – effective emissivity = 0.49:
At 300K – effective emissivity = 0.49:
At 400K – effective emissivity = 0.44:
At 500K – effective emissivity = 0.35:
At 5800K, that is solar surface temperature — effective emissivity = 0.00 (note the scale on the bottom graph is completely different from the scale of the top graph):
Hopefully this helps people trying to understand what emissivity really relates to in the Stefan Boltzmann equation. It is not a constant except in rare cases. But you can see that treating it as a constant over a range of temperatures is a reasonable approximation (depending on the accuracy you want), but change the temperature “too much” and your “effective emissivity” can change massively.
As always with approximations and useful formulas, you need to understand the basis behind them to know when you can and can’t use them.
Any questions, just ask in the comments.
Note 1 – The flux was calculated for the wavelength range of 0.01 μm to 50μm. If you use the Stefan Boltzmann equation for 288K you will get E = 5.67×10-8 x 2884 = 390 W/m2. The reason my graph has 376 W/m2 is because I don’t include the wavelength range from 50 to infinity. It doesn’t change the practical results you see.



“emissivity … is a function of wavelength.”
That’s why the generalization of the computation with produces the ubiquitous 255K meme in the box on http://cosy.com/Science/RadiativeBalanceGraphSummary.html is a function of dot products of the relevant spectra .
At what temperature radiant emittance of some grey body with reduced absorption coefficient equal to 0.5 is 500 Wt/m2?
Sorrento: Since your question includes both emission and absorption, I presume that Kirchhoff’s Law lies at the heart of your question:
emissivity = absorptivity (or absorptance)
Unfortunately the terminology of radiation is an absolute disaster. Absorptivity, emissivity, transmittance, reflectance, absorptance and exitance are DIMENSIONLESS RATIOS. Sometimes emittance is included in this group, but it apparently has been replaced by exitance to avoid confusion. Absorption, transmission, reflection, emission, and sometime emittance are NON-DIMENSIONLESS quantities sometimes measured in W/m2 or W/sr/m2. When these terms contain the word “spectral”, it refers to power/area per unit wavelength or per unit frequency and only becomes power after integrating over a range of wavelengths or frequencies.
For the emission part of your problem, emissivity (e) is given by:
e = I(lambda)/B(lambda,T) for a single wavelength
e = I/o*T^4 integrating over all wavelengths
where I is the intensity of radiation emitted at all wavelengths and B(lambda,T) is Planck’s function and o is the Stefan-Boltzmann constant.
For the absorption part of your problem, absorptivity I/I_0, where I is the absorbed power and I_0 is the incident power. Absorbance, or formerly optical density, (A or tau, a quantity which differs from absorptance/absorptivity) is given by:
A = ln(I/I_0) except in chemistry where A = log10(I/I_0)
An absorption coefficient is the FRACTION of incident light absorbed per unit distance that radiation travels through a material. Therefore it has units of reciprocal distance (m^-1). An attenuation (or extinction) coefficient is the analogous term when both absorption and scattering occur. An absorption coefficient is the product (n*o) of an absorption cross-section (o, area/molecule) per molecule and the density of absorbing molecules (n, molecules/volume). According to Beer’s Law for homogeneous materials:
A = n*o*s
where n is the density of absorbing molecules, o is the absorption coefficient and s is the length of the path through the absorber. (To confuse matters, chemists use the term “molar extinction coefficient” to refer to the absorption cross-section when the density of the absorber in given in molarity.)
Unfortunately, you haven’t provided enough information (density, path length) to calculate anything about an absorption coefficient. If you meant that the absorptivity of a material were 0.5, I think you now have enough information to answer your question.
SOD: Thanks for the post. It is an beautiful explanation – of one facet of the complex phenomena associated with emissivity/absorptivity. (These two phenomena are tightly linked.)
For the atmosphere, the 15 um CO2 band is located at the peak BB emission for 200 K and perhaps 25% below the peak for 300 K at 10 um.
According to MODTRAN (looking up from 0 km), the emissivity of a US standard atmosphere with 400 ppm of CO2 and no other GHGs is 85 W/m2 / 390 W/m2 = 22%. If I offset the temperature by -33 K (to 255 K), 50/240 = 21%. For 220K, 25.5/133 = 17%. You’ve illustrated this phenomena perfectly.
Note: Modtran uses a fixed lapse rate anchored to a surface temperature (with offset) for 10 km of troposphere and leaves stratospheric temperature without any offset. Any offset disappears between 10 and 11 km. So your examples are simpler and cleaner.
Now for the fun: What happens if I reduce or increase the CO2 concentration (with no temperature offset)? Increase from 1 to 2 ppm: +4.5 W/m2. 2 to 4 ppm: +5.4 W/m2. 20 to 10 ppm: +6.0 W/m2. 100 to 200 ppm: +6.4 W/m2. 1000 to 2000 ppm: +6.72 W/m2. 0.1 to 0.2 ppm: +1.7 W/m2.
Unlike most solids and liquids, emissivity isn’t a property of CO2 itself; it’s a property of the amount of CO2. The relationship appears to be roughly log-linear down to a few ppm. So emissivity for CO2 is a function of both temperature and concentration.
What happens when we put all GHGs in the atmosphere at their normal concentrations? Emissivity in the downward direction is 333 W/m2 / 390 W/m2 (288 K) = 85%. Emissivity in the upward direction is 240 W/m2 / 390 W/m2 = 61%???. About 40 W/m2 of the photons escaping upwards come for the surface, not the atmosphere, so one could argue that the upward emissivity of the atmosphere is closer to 50%. Normal materials usually don’t have emissivities that are different in each direction.
If the downward emissivity of the atmosphere is 85%, does that mean that the upward absorptivity of surface emission by the atmosphere of surface emission is also 85%? The correct answer here is 90% or higher, which is quite reasonable, given that DLR is emitted from a little above the surface where it is cooler than 288 K.
If one carefully accounts for absorptivity, emissivity and transmissivity, everything should work out correctly with absorptivity = emissivity. However, in the case of different upward and downward emissivity from the atmosphere, Grant Petty calculates emissivity using the Schwarzschild eqn.
Frank,
Global annual averages are useful but can obscure more than they reveal.
Downward longwave radiation of 333 W/m2 implies an “effective emissivity” of about 85%. In broad brush this number is probably overwhelmed by the higher humidity tropics. You get a lower number for high latitudes and the arctic.
Downward longwave radiation is nice and simple because it is only sourced from the atmosphere. There is no (significant) longwave radiation from space.
If the atmosphere was only 500m thick then the upward longwave radiation from the atmosphere would be about the same. And the total upward longwave radiation would be greater than 333 W/m2 because some surface radiation would be transmitted through the atmosphere. The total upward radiation would be around 390 W/m2 (a little lower, but not much).
Why is the upward radiation at top of atmosphere a lot lower than 390? Because of all the reasons explained in various series including Visualizing Atmospheric Radiation.
Nick suggests (see later comment) some more explanation and I might draw up some more graphs, without going back into the content of the whole series already linked.
“Downward longwave radiation of 333 W/m2 implies an “effective emissivity” of about 85%.”
But this is a typical gas problem. You can’t deduce any sensible emissivity from 333 W/m2 because you can’t say what the temperature is. It is worse with the frequency dependence. Some frequencies have come from a long way up, while some, eg peak CO₂, from very close.
A paradox is that a thick enough atmosphere with multiple GHGs has emissivity 1 (as an apparent surface), despite the strongly banded spectrum of the gas. You can see this easier by thinking about absorptivity. If it’s think enough everything gets absorbed. There is no reflection or anything else that can happen to the incident radiation.
SoD,
Thanks for a good discussion of emissivity of surfaces. I think it would be a good idea if you wrote something about how to understand emissivity of gases. The flux emitted is no longer proportional to a surface area, but to a volume, and as Frank says, depends on gas concentration in that volume. And in that volume there is also absorption. You have described emissivity as a fraction of what a perfect emitter (BB) would put out, but for a gas the idea of a perfect emitter is less clear.
Nick,
I think the best way to understand it in an atmosphere is as a “layer” – emitting up and down. Of course a volume emits in all directions, but the atmosphere is like a thin piece of paper with the area of a desk, so the “sideways” doesn’t affect the result.
And then emissivity simply depends on the number of molecules, in a non-linear way (1-exp(-n)).
Maybe I will draw some more graphs.
As far as including emission and absorption, I’ll just point people back to the whole series Visualizing Atmospheric Radiation.
Nick wrote: “You have described emissivity as a fraction of what a perfect emitter (BB) would put out, but for a gas the idea of a perfect emitter is less clear.”
Planck’s Law tells us what a perfect emitter would put out, but the derivation starts with an assumption that absorption and emission have reached equilibrium in the medium. As soon as you consider semi-transparent media, this assumption is invalid. (The assumption is still valid if emissivity is produced at a surface.) Can we really apply the S-B eqn. to situations where its derivation is invalid? Having a flexible fudge factor – emissivity – seems to work, but allowing it to be both an intensive property at surfaces and and an extensive property of semi-transparent media is kludgy nomenclature.
The only place that the S-B eqn really causes trouble is the difference between upward and downward emissivity in the atmosphere. Here Grant Petty (p211) still uses the terms emissivity and absorptivity, but he calculates them by integrating the Schwarzschild eqn. IMO, we should admit that Planck’s and S-B don’t apply to semi-transparent materials and say that the Schwarzschild eqn must be used with them.
If Einstein coefficients had been discovered earlier, we might consider Planck and S-B to merely be corollaries of a more fundamental equation – the Schwarzschild eqn. It describes the interaction between radiation and matter without assuming that radiation is in equilibrium with the medium (as Planck assumed). LTE is required so that a Boltzmann distribution of states can be assumed. The Planck function B(lambda,T) and a single cross-section for absorption and emission arise In the process of deriving the Schwarzschild eqn from Einstein coefficients. However, that derivation is complex and generally ignored. Planck and S-B dominate our view of how radiation is emitted by matter and Beer’s Law dominates our view of how radiation is absorbed by matter. The Schwarzschild eqn – which encompasses both processes – isn’t usually even mentioned by name; the synonym “radiative transfer calculation” is used instead.
Best of all, there is no need for emissivity when calculating radiation transfer thorough semi-transparent media using the Schwarzschild eqn.
Since no one seems to agree with this perspective, I’m probably exaggerating the difficulties of using emissivity properly.
SOD: In the idealized Figures in this post, the emitter has no emissivity below 8 um or above 20 um. What phenomena produce changes in emissivity?
1) In some cases, the emitter doesn’t have any QM-allowed transitions outside of a particular region. For example, carbon monoxide has only a single mode of vibration. In that case, we are talking about a material that is partially TRANSPARENT at wavelengths relevant to radiative cooling. In the case of CO (5 um), the atmosphere is a little too cold emit much energy through its allowed vibrational transitions. So are the stretching bands of CO2 (2.5 and 4 um), which is why we usually discuss only the 15 um bending of CO2.
2) In other cases, the emitter may have QM-allowed transitions and a structure that doesn’t permit all radiation to escape through its SURFACE. I assume this is the case with conductive metals like copper and aluminum, which have emissivity around 10%. A thin layer of oxide on the surface of these metals, however, raises their emissivity to around 90%. A thin layer of low emissivity material (fluorinated tin oxide) is deposited on the surface of glass to make low emissivity windows. Mike M. mentioned that silicon (a poor conductor) is transparent to longer wavelengths of IR, so some metals may have low emissivity because they are semi-transparent. However, low-E glass wouldn’t work if the coating on the surface had low emissivity because of transparency.
So – unless I am badly confused (please let me know if I am) – we have at least two mechanisms that produce low emissivity: semi-transparency and reflection/scattering of radiation at the surface of a non-transparent material. It is easy to see why absorptivity must equal emissivity when low emissivity is produced at a surface. For semi-transparency, we need to remember transmissivity when thinking about absorptivity = emissivity.
The surface scattering mechanism makes emissivity a property that is independent of quantity or thickness. The semi-transparency mechanism produces emissivity that varies with the amount of emitter – as I demonstrated for CO2 in the atmosphere.
If most readers are like me, they don’t immediately associate low emissivity with transparency – especially when using the S-B eqn: W = eoT^4. The average emissivity of the Earth’s surface is 97%, but not because 3% of thermal infrared is passing through the Earth (partial transparency). The same is true for a few inches of concrete (e = 0.91). On the other hand, the downward emissivity of the atmosphere (including cloudy areas) is 85-90% is due to semi-transparency in the “atmospheric window wavelengths”. If clouds didn’t interfere with semi-transparency in more than half of the sky, the downward emissivity of the atmosphere would be closer to 70% (according to MODTRAN for a US Standard atmosphere).
This post does a great job of explaining why emissivity can change with significant changes in temperature. It still leaves many booby traps for those who crudely apply the S-B eqn to the atmosphere.
Frank,
Emissivity calculated from total emitted flux and a particular temperature using the S-B equation only has some physical meaning if you know that the emissivity is nearly constant over the wavelength range of interest, as when doing optical pryometry for temperatures greater than about 1000K. An optical pyrometer is also the official interpolation instrument for measuring temperatures above the freezing point of gold, 1337.33K. Otherwise, it’s just a number.
It’s a completely different number if you use the temperature of the atmosphere at 5km, which is the average effective height of emission or assume that the emissivity is one and calculate the effective temperature. Effective temperature may or may not have physical meaning. In the real world, emissivity is always a function of wavelength and for solids or liquids, a function of viewing angle. The same goes for absorptivity and transmissivity.
Saying that the Earth has an emissivity viewed from space of ~0.6 using the S-B equation and the surface temperature of the Earth is a pointless exercise. The same goes for downward radiation from the atmosphere. It wasn’t all emitted from the same altitude and temperature.
DeWitt wrote: “Saying that the Earth has an emissivity viewed from space of ~0.6 using the S-B equation and the surface temperature of the Earth is a pointless exercise.”
I pointed out the difference in directional emissivity/absorptivity of the Earth to illustrate the absurdity of applying the S-B equation in some situations. The question I am trying to get agreement about is: What situations give absurd answers and why? When is the S-B eqn suspect or invalid?
1) Like the Earth and Venus, objects without a homogeneous temperature MAY be suspect. Ocean temperature varies with depth, but the surface has a well-defined emissivity in the thermal infrared, because essentially all of the outgoing photons are emitted and incoming photons are absorbed in the top 1 mm, where the temperature is locally homogeneous. So we need temperature homogeneity within a few tau (optical depth) of the emitting surface. The corona of the sun is much hotter than the 5700 K “surface”, but there is negligible optical density in the corona. The temperature of our thermosphere don’t have any impact on TOA OLR for the same reason.
Interestingly, Wikipedia discusses emissivity in terms of “reduced emission”, but the author(s) of the article about the S-B eqn approach the problem from a different direction. “A body that does not absorb all incident radiation (sometimes known as a grey body) emits less total energy than a black body and is characterized by an emissivity less than 1”. I’d add: “… and equal to its absorptivity (assuming LTE)”. So here a GRAY BODY is defined by its ABSORPTIVITY, which is [mostly] independent of temperature. Emissivity isn’t a fudge factor we can select to correct for temperature inhomogeneity or some other weaknesses of a model. (:))
Those who attempt to treat the atmosphere as a black box with an arbitrary temperature and emissivity run into problems with this definition. The absorptivity of their black box must be the same from the top or bottom. So they aren’t allowed to postulate different emissivities from the top and bottom. (They need to break the atmosphere up into a vertical stack of black boxes thin enough that emissivity is the same in both directions.)
2) Objects that are semi-transparent appear to be OK if they have a homogeneous temperature and W = eoT^4 is applied over a modest range of temperature (less than 2X in degK).
3) The S-B eqn is invalid if it disagrees with the Schwarzschild eqn. The latter properly accounts for the rate of emission and absorption of photons; the former is derived assuming an equilibrium that may not exist. (Grant Petty uses the Schwarzschild eqn when discussing the emissivity and absorptivity of the Earth’s atmosphere.)
Frank,
I think you’ve answered your own question. The key word for emissivity less than one is gray. If the emission spectrum has more or less the same shape as a blackbody but is lower everywhere by very close to the same proportion, then the S-B equation is useful.
The emission spectrum of the Earth’s atmosphere is not even close to gray. Nor is the example given by SoD in this post.
However, the S-B equation can be used to determine total radiative flux even if the flux spectrum isn’t gray. That’s how a pyrgeometer works. It works because the detector has constant emissivity so the effective temperature of the source has physical meaning even though the spectrum isn’t gray. The pyrgeometer measures the effective temperature, but the data out is W/m².
To put it another way: Radiative imbalance is expressed in W/m², not temperature.
But that doesn’t make any difference.
“Prevost also showed that the emission from a body is logically determined solely by its own internal state. The causal effect of thermodynamic absorption on thermodynamic (spontaneous) emission is not direct, but is only indirect as it affects the internal state of the body.
The radiative imbalance is described as a small reduction in emitted intensity, and that is a reduction in temperature. A thing that doesn’t fit with the theory of thermal radiation is that a lowered temperature in the atmosphere cause rising temperature in the surface. I haven’t found that described anywhere else than in the greenhouse theory. An imbalance can happen, but if a rising temperature is involved, the imbalance always originates in the rising temperature body. Temperature never rise as a result of decreasing temperature. Where in the laws of thermal radiation do you find support for that claim? If you give a reference, make sure it is not from a description of the greenhouse effect, everything in the greenhouse effect should be found in ordinary physics.
Another thing, and as you see in the citation above it is general for all bodies:
It says that the emission from a body depends on it’s internal state only. So when you say that the surface temperature rise from a radative imbalance that comes from a decrease in temperature of the atmosphere, how do you mean? The atmosphere is not the surface internal state, or even part of it. A very specific property of the atmosphere is that it is located outside of the heated body.
There is no way to join the radiative imbalance with a rising temperture in the surface, because the emitted intensity of the surface is depending on it’s own temperature only. If you think that the earth is not in equillibrium and that would make it possible, that would not be true either. If earth was in a steady state it would be even harder to argue for the radiative imbalance.
The emission is not dependent on absorption either, absorption is also dependent on temperature, it is clearly shown. But absorption and emission is related to each other through the internal temperature, which determines them both.
Another problem with the radiative imbalance is that increased absorption shown as decreased emission is equal to rising temperature. Absorption is dependent on temperature, and it is shown in heat transfer.
Two bodies of different temperatures emitting intensity according to the fourth power of their respective temperature, shows the absorbed amount in the cooler body from T1-T2, where T2 is the cooler body. Absorption increase when temperature decrease in T2.
When you claim that the troposphere heats up from increased absorption, not from increased emission, you point to the negative radiative imbalance. Indeed, if there is a real imbalance, you are observing increased absorption.
But increased absorption, for whatever reason, is not connected to increasing temperature. It is connected to decreasing temperature, because increased absorption is increased heat transfer from a hotter body.
The laws of thermal radiation clearly say that the observed emitted radiative imbalance, if real, is the result of decreasing temperature. Which is logic if it is caused by increased amounts of dry ice molecules in the atmosphere. Because the energy in the system is finite and already present. If you increase the amount of heat absorbing molecules and the energy is limited and constant, the energy is divided over more molecules.Less energy per molecule is equal to lower temperature, which fits with the rising co2 and the radiative imbalance.
When investigating temperature we must keep to the laws of absorption and emission, which is clearly proven many times to be true. Emitted intensity and absorbed heat are each dependent on temperature only, and related through temperature.
Wavelengths or frequency does not have to be involved, even though the emitted spectrum from the atmosphere confirms the temperature effect of co2 lowering it by showing that it has the emitted intensity of dry ice.
Emission depends on temperature only and absorption depends on temperature only. The theory says it holds for all bodies. All the talk of spectrum is interesting stuff, but it is about other aspects of radiation, like peak intensity and wavelengths. Temperature is independent of that, temperature is oddly enough independent of everything. Everything is dependent on temperature. That is the remarkable discovery made by stefan and boltzmann. That emitted intensity is dependent on the internal state that is equal to the fourth power of temperature.
If temperature is rising it is not dependent on absorption and emission. I know it is a bit unintuitive at first, but that is how it works. Wavelengths is not important because all radiation is thermal. IR or visual is a property of our eyes, not a property of radiation. All radiation in the universe is emitted at an intensity dependent on its internal state only. The tropospheres emitted intensity is dependent on the tropospheres internal state, that according to you show cooling. The surface emitted intensity, that you say is rising, is dependent on the surface internal state only. The solar constant can be considered to be the sun extended to our location, and it is dependant on the suns internal state only.
If the surface has a rising intensity, the laws of thermal radiation that is independent of wavelengths and everything else than the internal state, tells us that an exactly equal amount of heat will be transferred from the solar constant to the surface. The problem is that rising surface intensity and decreasing troposphere intensity also means more transfer to the troposphere. Transfer of heat is energy that is not observed, only calculated. It is added on top of the emitted intensity because it is transferred and depends on the cold bodys internal state, not the hot body.
I don’t understand why you don’t use the laws for temperature instead of wavelengths and other stuff in the greenhouse temperature. As you can see yourself you write things here that violate the relationship between thermal radiation and temperature. The greenhouse theory says that decreasing intensity in the atmosphere causes the internal state of the surface to change. But the laws of thermal radiation says everything depends on the internal state. The atmosphere is not part of the surface internal state, is it?
Does the laws of radiation not apply for earth? It doesn’t matter if the earth is a blackbody or not. The laws of thermal radiated intensity applies to all bodies, black or any shade of gray. The stuff you put into it is about wavelengths of peak intensity and molecular interactions shown as a spectrum. Emissivity concerns individual objects inside the thermal bath present at the surface and in the atmosphere. If you want to know the amount absorbed energy of co2, you look at the spectrum and find that it emits as dry ice, ~130W/m^2. The amount transferred to co2 in the atmosphere then is 260W/m^2 of the emission from the surface. The amount absorbed by co2 is 260W/m^2. 400ppm co2 in 10 km atmosphere, emitting 130W over the whole spectrum overlapping other molecules which also have those internal populated states at that intensity, but it absorbs all of it over a couple of wavelengths. The surface also has those internal states populated, and it is here the term “no heat transfer between equal temperatures” come into play. There is no measurable change or transfer between bodies that have the same energy states populated internally. This is seen in radiative heat transfer that calculate the amount in transfer and the amount absorbed according to the colder bodys internal state. Some call it “net” transfer, but that makes no difference. The net heat transfer from a hot to a cold body includes all energy related to the internal states of both bodies. If there is energy that is not included in “net transfer”, the “net transfer” calculation itself is proof that the excluded energy is not heat and can only be the shared internal energy levels. Which is up to the intensity of co2 or dry ice.
Lasse Kongo: “The radiative imbalance is described as a small reduction in emitted intensity, and that is a reduction in temperature. A thing that doesn’t fit with the theory of thermal radiation is that a lowered temperature in the atmosphere cause rising temperature in the surface. I haven’t found that described anywhere else than in the greenhouse theory. An imbalance can happen, but if a rising temperature is involved, the imbalance always originates in the rising temperature body.”
There is much confusion involved, so I have to ask if it originates in me.
I would think that if an imbalance happens, it would always involve a relationship between two ore more bodies, and originate from these relations. And if there is a rising temperature in the surface It is not from any warming atmosphere, but among plenty other mechanisms from less LW radiation from the surface. And where does the idea of lowered temperature in the atmosphere come from? The temperature near surface seems to be increasing. But the latitudes where LW radiation to space is emitted from is dependent on spectrum. Some latitudes are warmer and some are colder. It will be change in lapse rate that matters. So I have not really understood why cooling of stratosphere should matter when it comes to global warming.
As the LWR emitted from stratosphere to space is very low compared to radiation from lower altitudes.
I think there is related confusing issue here. Usually it is o.k. to assume that thermal flux incident on the earth will be absorbed, even if the emissivity is less than one. But not always, apparently. In Feldmanm et. al. PNAS, no. 46, pp.16297 – 16302 he finds that sometimes reflected thermal IR flux will make it out to TOA but only in a few arid regions. In most places, it is absorbed by water vapor. Of course,and fortunately, sunlight has no problem leaving once reflected, but under most circumstances thermal IR can’t escape.
It’s surprising to find on scienceofdoom.com a resource so precious
about equations.
We will note your page as a benchmark for Basics – Emissivity and the
Stefan Boltzmann Equation .
We also invite you to link and other web resources for equations like http://equation-solver.org/ or https://en.wikipedia.org/wiki/Equation.
Thank you ang good luck!
Lasse Kongo: Many people treat the planet as a graybody with a temperature of 288 K and emissivity of 0.61. This post discusses some aspects of the issue. How reliable is this model? You have raise numerous other issues. Consider picking one, reading about it at scienceofdoom and asking focused questions below the appropriate post – assuming your issue hasn’t already been thoroughly discussed. To get started
The boundary between the Earth and space is the top of the atmosphere or TOA. Heat can only CROSS this boundary by radiation. There is negligible overlap between the spectrum of incoming solar radiation (SWR) and outgoing thermal infrared (LWR). That allows GHG’s to slow down the rate at which LWR escapes to space without interfering with incoming SWR (to a first approximation). The resulting radiative imbalance means that the temperature somewhere below the TOA must rise – until incoming and outgoing radiation are in balance. You can explore some aspects of this process at:
http://climatemodels.uchicago.edu/modtran/
If the Earth behaved like a simple gray- or blackbody, we could easily convert radiation (W/m2) into temperature using the Stefan-Boltzmann equation. The Earth doesn’t behave like a simple gray- or blackbody. How fast, how much and where temperature must rise are complicated questions that depend upon heat transfer by WITHIN our climate system (the atmosphere, the surface and the ocean). Below the TOA, heat transfer includes radiation, convection of simple and latent heat (evaporation and condensation) and conduction very near the surface. These are complicated processes that control how much LWR crosses the TOA.
I am very hesitant to the concept of slowing down heat or radiation using air. Slowing down how much? If we are talking about radiation it moves at lightspeed, no matter how many absorptions on the way up it would not make much difference. I often hear this argument, but I interpret it as another way of saying that it takes a longer way.
“The boundary between the Earth and space is the top of the atmosphere or TOA. Heat can only CROSS this boundary by radiation.”
Of course, but isn’t TOA the tropopause in this case?
” There is negligible overlap between the spectrum of incoming solar radiation (SWR) and outgoing thermal infrared (LWR).”
All radiation is thermal as the emitted intensity from any radiating body is dependent on temperature only. The wavelenght is mainly a relation to the human eye as it consist of mostly the visual part with a bit of IR and UV. It is called infra-Red and ultra-Violet, so these words are clearly related to our vision as well. I don’t think it is useful to use our eyes relation to sunlight and use that as a property of sunlight that affects how it interacts with matter in the whole system.
You can assume I am familiar with the properties of radiation, I will ask if I don’t understand something. So you don’t have to explain the simple things, like overlap in the spectrum. When the subject discussed is temperature, wavelength is not useful. Wavelength is a property of high intensity radiation, and emitted intensity from a radiating body is dependent on temperature only. Wavelength is a property relative to intensity, and therefore it is an effect of temperature.
“That allows GHG’s to slow down the rate at which LWR escapes to space without interfering with incoming SWR (to a first approximation).”
You can also assume I know the greenhouse effect and the claimed mechanisms and properties of GHG’s.
That said, a radiating body does not rise in temperature as a result of how fast or how much radiation that escapes from a cold gas surrounding it. A radiating body emits an intensity dependent on it’s internal state only. That is one of the fundamental discoveries of blackbody radiation. Temperature as a measure of the internal state, and it was found that absorption and emission is dependent on temperature alone. Emission doesn’t depend on absorption, it is related through temperature/the internal state on which they both depend, and that acually makes a differnce in how you approach the problem.
“The resulting radiative imbalance means that the temperature somewhere below the TOA must rise – until incoming and outgoing radiation are in balance.”
Radiative imbalance is not something I have seen in the theory of thermal radiation/blackbody radiation. I don’t think it useful since it simply is a reduced emission and I also doubt very much that it is really possible to measure such a difference. And when we include a term like albedo, which is hard to find an exact description of and it is said to vary by an unknown amount. I haven’t even been able to get an answer to what is included exactly and in what proportions. When it is said to reduce the insolation with 30% and then it is claimed an “imbalance” of single Watts, I don’t think it’s acceptable physics.
In reality the imbalance is much larger when we don’t take away albedo. Albedo is not part of the original theory of thermal radiation, correct me if I’m wrong, but I think it came from astronomy. Anyway, emissivity was used for the relationship between emission and internal state. I don’t think we should use anything else if we are trying to understand temperature on earth, it confuses the strong relationship of emission and temperature that is independent of everything else. We should keep loyal to proven theories that have been tried through well over a hundred years, and assume that they are correct. An imbalance in the emitting bodys surroundings is not possible to include as a cause of the internal state. The theory is very clear about that;
The emission of a body is dependent on the internal state only. The same goes for absorption.
A radiative imbalance in the atmosphere is not part of the internal state of the emitting body.
The temperature “must” not do anything because of something else, everything else is what it is because it is dependent on temperature.
“If the Earth behaved like a simple gray- or blackbody, we could easily convert radiation (W/m2) into temperature using the Stefan-Boltzmann equation.”
In what part of the theory of thermal radiation do you find support for explaining a radiating body by disconnecting the emitted intensity from temperature? If you make a claim about radiation and temperature, and there is a theory that has been confirmed in many many experiments to be true over a century, and is until this very moment regarded as one of the greatest discoveries in physics, you better have a calculation including that teory and numbers that clearly show how and why we should ignore a proven law.
“The Earth doesn’t behave like a simple gray- or blackbody.”
First of all, if you read what Preost stated, you can see it says only “body”. A bit further down on the wikipedia article about blackbody radiation you can read a clarification that it really applies to -any- body. This is my point. Temperature and the emitted intensity dependence on it, IS the whole theory. The other included terms like wavelength, grey or black, displacement of the emission curve etc. are aspects within that relationship. They are facets on the diamond, but they all obey that relationship. If you say that emission in a investigated situation not is dependent on temperature, our response to that, and your own, should be that you have miscalculated, not to ignore a law that has been standing through most part of the evolution of modern physics.
It is not the way laws are treated in physics, a failed attempt to calculate and understand the system investigated according to the theory of the observed phenomenon, is not a base for saying that the law doesn’t apply.
“How fast, how much and where temperature must rise are complicated questions that depend upon heat transfer by WITHIN our climate system (the atmosphere, the surface and the ocean). Below the TOA, heat transfer includes radiation, convection of simple and latent heat (evaporation and condensation) and conduction very near the surface. These are complicated processes that control how much LWR crosses the TOA.”
The theory is not questioned. I think it can be considered to be the strongest consensus there is in all science of all kinds. Why do you think that you can say that the temperature “must” do anything?
It is very clearly written, and it consists of so few parts that if you just read every word in that one sentence you know how to apply it.
The emission depends on temperature only. Which part of it and why do you say is wrong. A statement about that must be connected to evidence disproving that very mechanism, and as far as I see it, there is only one mechanism in there.
From that law of thermal emission from any body of any kind, we can safely assume that a claim where the emission from a (somewhat) hot surface depends on the decreased emission of a cold gas surrounding it, can be said to be untrue. You can’t violate a law of physics because of an imbalance when you have taken away 30% using an unclear term which parts and internal relations and causes is to some extent unknown.
I think this law have been overlooked. And it has not been explained clearly enough, or people haven’t paid attention to the words. It is the entire theory, that radiation depends on temperature, not the other way around. And the other terms are jabout the characteristics of the emission in higher resolution. Heat transfer is the only theory that should be used for temperature and the relation between emitting bodys. It will fit the temperature profile of earth, we can rely on that. It has been standing for a long time.
There is a couple of places in my last post where the word “short” is missing next to “wavelenght”. Sorry.
“short wavelength is mainly a relation to the human eye”
“Short wavelength is a property of high intensity radiation”
Hope that helps if anyone had problems understanding the writing.
LK “From that law of thermal emission from any body of any kind, we can safely assume that a claim where the emission from a (somewhat) hot surface depends on the decreased emission of a cold gas surrounding it, can be said to be untrue.” Are you claiming that the temperature of a surrounding gas doesn`t matter? So your warm food is cooling at the same rate in a refrigerator and in a warm room.
” Are you claiming that the temperature of a surrounding gas doesn`t matter? So your warm food is cooling at the same rate in a refrigerator and in a warm room.”
I don’t think I made that claim. The temperature of the surrounding gas matters for the emission of the gas. The emission of the surface depends on its internal state. That is what the theory say.
It is a bit misleading to say that it is cooling. The food emits depending on its temperature. Whatever assumption you make, it has to fit that law.
Lasse and Nobody: The fundamental “law of thermal emission” uses Einstein’s A21 and B21 for spontaneous and stimulated emission of photons (and a B12 coefficient for absorption). Planck’s Law and the derived S-B equation were derived for systems where radiation has come into equilibrium with the radiation that surrounds it. Technically, they don’t apply to semi-transparent objects like the atmosphere, because the radiation isn’t absorbed and emitted at weakly absorbed wavelengths often enough to create equilibrium. Emissivity less than 1 allows us to adjust the S-B equation so that it agrees with observations.
The S-B is used to calculate emission of radiation from the surface of the planet. The Schwarzschild eqn tells us how that radiation is CHANGED by passing an incremental distance through the atmosphere (or other materials). When thermal emission is negligible, the Schwarzschild eqn simplifies to Beer’s Law for absorption. For long distances traveled through a material (equilibrium), it simplifies to Planck’s Law. The Schwarzschild equation is derived from Einstein coefficients assuming LTE and those coefficients turn into absorption cross-sections.
“Lasse and Nobody: The fundamental “law of thermal emission” uses Einstein’s A21 and B21 for spontaneous and stimulated emission of photons (and a B12 coefficient for absorption).”
I think it would have been hard for Prevost and all the other scientists studying blackbody radiation before Einstein had produced any of his theories, to have used anything in those theories to draw their conclusion. Einstein used thermodynamics in general as his base for developing his theory. E=mc^2 for example, although Einstein defined it differently, is a version of sb*T^4, where energy and the state of matter have a defined relationship in both.
” Technically, they don’t apply to semi-transparent objects like the atmosphere, because the radiation isn’t absorbed and emitted at weakly absorbed wavelengths often enough to create equilibrium.”
Technically they do. Non-equilibrium is not helping the greenhouse theory, it makes it worse. That a transparent atmosphere emits and absorbs poorly in relation to solids means that it is colder and emits less heat, or energy overall. Non-equilibrium doesnt make heat go backwards and disconnects temperature from emitted intensity. If you still claim they do, your have to attach a reference from the theory of thermal radiation, where changes happen that makes the relationship invalid.
“Emissivity less than 1 allows us to adjust the S-B equation so that it agrees with observations”
How does that work? Emissivity does not allow such processes where temperature is disconnected from emission. Emissitivity says that emission and absorption is a fraction of the radiation around the body. It is very clearly explained that if absorption is 0.7 for example, emission is equal.
But it is not said anywhere that emission and absorption is independent on temperature, or that a troposphere that is at an average 255 Kelvin can emit over 300W/m^2. Even if it did, try putting in the surface emitted intensity with that 300W/m^2 in the radiant heat transfer equation, and you will see that the surface still doesnt change it’s emitted intensity.
“The S-B is used to calculate emission of radiation from the surface of the planet. The Schwarzschild eqn tells us how that radiation is CHANGED by passing an incremental distance through the atmosphere (or other materials).”
You mean that it is used for that in the greenhouse theory? Because it wasn’t created for that reason.
Do you mean that you can show with the Schwarzchild equation that the law of thermal radiation doesn’t hold in some situations? That would be a remarkable discovery.
How the radiation is changed happens within the fact proven in many experiments over and over again, that the emission is dependent on temperature alone.
“When thermal emission is negligible, the Schwarzschild eqn simplifies to Beer’s Law for absorption.”
First, when thermal emission is negligible, the temperature is low. Second, Beer’s law does not show how emission is independent on temperature. It has no function where the emitters internal state is dependent on the absorbing body or molecule.
The emitted intensity is dependent on temperature alone. It has never been questioned or proven wrong. Circumstances sometimes make it less distinct and the term emissivity is used for those situations.
Are you saying that the law of thermal radiation where the emission and absorption is not dependent on the internal state?
Lasso: The first step in the derivation of Planck’s Law is to assume radiation in equilibrium with “quantized oscillators”. Technically, you should not use it or the SB eqn where equilibrium does exist – in the atmosphere. Planck ignores the fact that real molecules absorb and emit different wavelengths very differently. Einstein coefficients encompass these aspects of the behavior of molecules that are ignored by Planck. Einstein coefficients become the absorption cross-section and B(lambda,T) terms found in the Schwarzschild eqn, making it “moe fundamental” than Planck and SB. Planck and Beer’s Law can be derived from Schwarzschild.
“There is much confusion involved, so I have to ask if it originates in me.
I would think that if an imbalance happens, it would always involve a relationship between two ore more bodies, and originate from these relations.”
You don’t think it starts in one end, in one of the bodies?
It is pretty clear that it is the decrease in the troposphere emission that is the initial cause of temperature rising in the greenhouse theory. I’m just asking for a reference in the theory of thermal radiation that it is an accepted mechanism. All the information I have seen in the physics of radiation says the opposite.
A dropping temperature never cause temperature to rise.
“And if there is a rising temperature in the surface It is not from any warming atmosphere, but among plenty other mechanisms from less LW radiation from the surface.”
That is a contradiction to the whole theory of thermal radiation. You are saying that the emission from the body is inverse to the internal state.
“And where does the idea of lowered temperature in the atmosphere come from? The temperature near surface seems to be increasing”
That is the theory of thermal radiation:The emission is dependent on the internal state only.
You claim that reduced emission from the atmosphere, the “radiation imbalance”, is not dependent on the internal state. Am I wrong?
. “But the latitudes where LW radiation to space is emitted from is dependent on spectrum.”
No, the spectrum is something we humans produce to have as reference to the physics. It is not cause of anything about temperature or radiation.
Latitude? Not altitude?
What characteristics of emitted radiation have is dependent on temperature.The more intense emission, the shorter the wavelength. Absorption and emission spectrums show the relationship between the absorbing and emitting molecules and present radiation.
Anyway, the spectrum is dependent on emission, not the other way around.
Some latitudes are warmer and some are colder.
“It will be change in lapse rate that matters. So I have not really understood why cooling of stratosphere should matter when it comes to global warming.”
Lapse rate is dependent on temperature. The stratosphere is dependent on temperature. Global warming is caused by the sun with a fixed amount of thermal radiation, without the sun it would be cold. If the surface heats up, less heat is transferred from the solar constant. If the atmosphere would be heating up, less transfer of heat from the surface. As long as the atmosphere is colder there is no transfer of heat to the surface.
Lasse Kongo:
How do you understand the cooling of deserts with your theory?
“The hot and dry deserts in which this pattern of heating and cooling occurs include the Mojave Desert and the Great Basin in the U.S. and the Sonoran and Chihuahuan Deserts in Mexico. The seasons are generally warm throughout the year but get a lot hotter during the summer. Because of the lack of humidity in the area, the ground receives more than twice the radiation heat from the sun during the day and loses twice as much heat during the night in comparison to more humid environments. Hot and dry deserts have a mean annual temperature of 20 to 25 degrees Celsius, and the extreme temperatures can range from 43 to 49.5 degrees Celsius during the day and minus 18 degrees Celsius at night.”
How can lack of humidity influence cooling with your theory?
Nobody:
“How do you understand the cooling of deserts with your theory?”
The lack of cooling and the lack of humidity is very obvious in the daytime in a desert, If there would have been more water present, both vapor and liquid, it would have taken much more energy to reach those temperatures. Just look at tropical areas, they receive about the same amount of radiation from the sun, but all the water with its high heat capacity absorbs heat and evaporate when the energy exceeds the strength of the bindings in the liquid, carrying energy away internally in mass. When reaching a temperature low enough it emits the same amount that was used to change phase into the excited state of a vapor. Think about it, heat is absorbed and carried away by molecules from the surface, where the heat is released again the vapor form clouds, blocking energy at the same time as it releases excess energy from the surface, condensing when the excess is released and cooling the surface even more as it rains. Eventually the sun is let through to heat up the cooled surface again. This is very obvious in the rainforests around the equator where the cycle happens on a daily basis.
Watervapor doesn´t heat the surface, but it reduce the rate of transfer to higher altitude. Reduced transfer is not heating, temperature doesn´t rise in a solid because it transfers less heat to a cool gas. All the way up until the air and the surface has the same temperature there is cooling of the surface to the gas, and at the same temperature the transfer is nonexistant.
Heat transfer is energy that is accounted for on top of the energy that is emitted from a surface. When the sun doesn´t shine, there is no energy to transfer and the surface emits only what the internal state allows.
The air cools rapidly with heat transfer increasing without solar heating replenishing.
If we take the solar constant of 1361W/m^2 and calculate the rate of transfer to the surface emitting 390W/m^2, we get a rate of transfer to the surface of 970W/m^2. That is transferred to the whole surface in average, and the surface transfer that energy towards a surrounding sphere, 970W/4=242W, which is equal to observed mean emitted intensity of the atmosphere, or what is called effective temperature. It works with the surface emission and using mean atmosphere temperature to get the tropopause temperature.
Where the surface is irradiated by the sun, it transfers lots of energy to the air on top of what it emits itself. That is why the temperature drops fast at night in the desert.
Can you think of any other situation where cold water or cold air makes a solid rise in temperature? If not, why would it have the reverse function in the atmosphere? It makes no sense.
Lasse Kongo: “Watervapor doesn´t heat the surface, but it reduce the rate of transfer to higher altitude. Reduced transfer is not heating, temperature doesn´t rise in a solid because it transfers less heat to a cool gas.”
Perhaps we can agree on this. And this is my understanding. In principle short wave radiation from the sun does the heating, and long wave radiation does the cooling. The only heating by LWR is what comes from the sun and is absorbed in the atmosphere and surface. This is a very small part, and has no influence on overall temperature. What matters is how fast this cooling is done, and the transfer depends on water vapor, CO2 and some other gases.
Frank March 18, 2017 at 7:23 pm
“Lasso: The first step in the derivation of Planck’s Law is to assume radiation in equilibrium with “quantized oscillators”. Technically, you should not use it or the SB eqn where equilibrium does exist – in the atmosphere.”
Well, the s-b equation is what the greenhouse theory uses for the atmosphere, so I don´t see the problem. This is what wikipedia says about planck´s law and the power radiated by a blackbody:
“This formula mathematically follows from calculation of spectral distribution of energy in quantized electromagnetic field which is in complete thermal equilibrium with the radiating object.”
Where did you read that it shouldn´t be used?
The s-b equation works very well for equilibrium, what makes you say that it doesn’t? The relationship between temperature and emission of a body in equilibrium is what the s-b equation was used for when it was presented:
From the sb-wikipedia article
“The Stefan–Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan–Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time is directly proportional to the fourth power of the black body’s thermodynamic temperature T”
Black bodies in theory is considered to be in equilibrium.
In the pyrgeometer that greenhouse theorists point at for (false) evidence of DLR heating the surface, the s-b equation is used without emissivity from what i can see. If the technology you use for proof of the theory uses it for measuring atmospheric radiation, then why do you claim it shouldn´t be used?
“Planck ignores the fact that real molecules absorb and emit different wavelengths very differently.”
Planck developed the theory of blackbody radiation further, explaining the distribution of energy over wavelengths. The blackbody is the perfect absorber and emitter, molecules absorb and emit very different indeed. They are much, much worse at both absorbing and emitting being limited to only use parts of the spectrum, where co2 is limited to only a couple of wavelengths.
This means that they don´t absorb as much as a solid and they don´t emit as much as a solid. That makes them even more irrelevant for raising temperature in the solid surface. On the contrary, they are perfect coolers of solids, especially the ones that absorb lots of infrared, like water vapor and co2. That is why they use for example argon and xenon as insulating gases. There is a report on the internet somewhere which comes from a windowmaker that tried co2 as insulator in a windowcasette. It transported massive amounts of heat from the hot side to the cold side, it was the worst gas possible to use for insulation. Not very surprising, considering co2 is practically dry ice.
“the absorption cross-section and B(lambda,T) terms found in the Schwarzschild eqn, making it “moe fundamental” than Planck and SB. Planck and Beer’s Law can be derived from Schwarzschild.”
You are not very clear about what you are saying. The relationship between temperature and emission is as clear as it can be. Emission depends on temperature alone. No exceptions are mentioned anywhere but in the greenhouse theory.
Do you mean that the Schwarzild equation is evidence of that in the greenhouse theory thermal radiation can violate the relationship between emission and the internal state? Does it give proof of the emission of a body being dependent on the state of its exterior?
The emission of a body is not even dependent on absorption, they are related through temperature, but each on their own they depend on temperature alone. Which is clearly illustrated by a body heating up, absorbing much more than emitting, like how co2:s fingerprint is seen in the emission from the atmosphere. Absorbing radiation from the higher temperature below shown as the curve around its wavelengths, but emits at an intensity of a body with temperature ~220K.
nobodysknowledge
“Perhaps we can agree on this. And this is my understanding. In principle short wave radiation from the sun does the heating, and long wave radiation does the cooling. The only heating by LWR is what comes from the sun and is absorbed in the atmosphere and surface. This is a very small part, and has no influence on overall temperature.”
That depends on what you call LWR. Is it IR? Because IR is ~51% of solar radiation. Personally, I think there is quite a lot of atmospheric heating from solar heating, the processes of absorption and diffusion of sunlight is not very clear. With water vapor absorbing large amounts in IR around 1 micrometer and also absorb over almost the whole spectrum, it is not hard to imagine that absorption of high intensity radiation and transformation through kinetic energy transfer, which can be re-emitted from molecules of lower temperature at longer wavelengths.
“What matters is how fast this cooling is done, and the transfer depends on water vapor, CO2 and some other gases.”
But the thing is, the surface internal state doesn´t change much from the cooling by co2 and watervapor. We have to keep in mind that there is a glowing mass just beneath the crust, and that is what balances heat from the sun. At the surface only a small amount of 90 mW/m^2 is said to be the addition from internal heat generation to the emitted intensity. That means that we are observing a surface in almost perfect equillibrium between the sun and the equally hot core and the other internal layers. The cooling of the surface is very small compared to the large amounts of energy in balance between the two glowing bodies of the sun and below the crust. The transfer of heat through the system is tiny compared to what the system contains. That is the reason for the importance of the theory of thermal radiation and its single base that is the totally independent relationship between emission and its dependence on the internal state.
When considering the temperatures of the internal state of earth, it is not hard to see that the relationship to emission and absorption can not be influenced by the tiny, tiny amounts that is included in the atmosphere. We are standing on a very, very thin crust that looks like a “star egg”, with a raging internal heat inside the shell. And the heat source is even hotter and larger, although far away. The temperatures on the surface are farts in comparison, and cooling is a process involving several thousand degrees in the internal mass that cools to a vacuum at 3 Kelvin.
The cooling we experience on the surface is a separate layer of icecold gas that is the product of the surface being heated by two glowing bodies, exciting matter into a low density state of the atmosphere. It is carried by the radiated heat. It is caused by temperature, not a cause of temperature.
They recently did an experiment with particles levitating between two surfaces with a similar temperature difference as the surface of earth and vacuum of space. It seems like the flow of energy between large differences in temperature can cause some interesting things to happen, like lift molecules and even particles against gravity.
The last paragraph is just speculation of my mind around the observed facts in an experiment, where I think the experiment might be a clue to why we have the gaslayer around earth. The main point to always include in the problem of earth surface temperature is that only the internal state of earth is cause of emission and absorption. Cooling or not, the atmosphere is an exact description of something that is not part of the internal state, and it is irrelevant for the emitted heat from the surface.
Considering heat transfer and the fact that it has to be the right theory to use for temperature, because that is what it does, there are some interesting consequences to be considered knowing what causes the rate of transfer to have a certain size. The largest transfer rates inside the system have to be from the equator towards the poles. There has to be enormous amounts being in constant transfer to both poles at all times. The gulf stream is one sign of that. When such large flows are present and the ice caps are still there, half a Watt of radiative imbalance would hardly make any difference even if it was the true cause. The rate of transfer from the internal heat is also very large to the poles for the same reason, half a Watt between a star and a glowing ball of iron and stone is such a strange theory of warming of the surface.
I´m actually starting to wonder if it is a planned deception of humanity because it is a detailed contradiction of physics in all details and in the main argument. I can´t say I think it is a conspiracy for real. But how can people like the anonymous man behind this blog, have read so much of the litterature and using physics as an argument, still miss the foundation of the whole theory of temperature and emission. The probability to miss that fact is smaller than the probability of a conspiracy. And why being anonymous? Or is he?
Lasse,
Longwave radiation is, by convention, radiation greater than 4μm wavelength and shortwave radiation is, by convention, radiation less than 4μm wavelength.
“Longwave radiation is, by convention, radiation greater than 4μm wavelength and shortwave radiation is, by convention, radiation less than 4μm wavelength.”
Some people think everything above the visual range is LW, that´s why I asked. How much solar heating there is from LW is totally irrelevant. If the sun heats something it gets hot no matter if it´s LW or SW
Lasse,
You’ve written some very long comments that I haven’t studied. I’ve scanned them and it looks like you don’t understand some important basics.
Let’s start with a question.
Do you think this diagram (and the text within) is correct?
Likewise I supply a number of heat transfer textbooks in support of heat transfer basics in: Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics. Please have a read and comment.
Hello mr. SOD
“You’ve written some very long comments that I haven’t studied. I’ve scanned them and it looks like you don’t understand some important basics.
Let’s start with a question.
Do you think this diagram (and the text within) is correct?”
Nothing wrong with the diagram, no. There is an unnecessary arrow there, pointing from the vacuum to the body. Why?
What do you mean that this diagram shows?
Lasse,
If you read the text it tells you what that other arrow is – the net.
I wanted to check that you understood that radiation from a cold surface was absorbed by a hot surface.
Many previous discussions with people who believe that radiation from a hot surface is absorbed by a cold surface, but the same people believe that radiation from a cold surface is not absorbed by the hot surface.
Let’s check – do you agree that radiation from a cold surface is absorbed by a hot surface?
“scienceofdoom
Lasse,
If you read the text it tells you what that other arrow is – the net.
I wanted to check that you understood that radiation from a cold surface was absorbed by a hot surface.
Many previous discussions with people who believe that radiation from a hot surface is absorbed by a cold surface, but the same people believe that radiation from a cold surface is not absorbed by the hot surface.
Let’s check – do you agree that radiation from a cold surface is absorbed by a hot surface?”
I don´t have to agree to that, because it doesn´t matter. The energy included in “net” is the only energy that is heat. If there is energy that is not included in “net”, it is not involved in rising temperature. If you say it is, give a reference to the physics of thermal radiation from a NON-greenhouse textbook. This invisible unmeasurable ghost-energy, acting like a religious entity, only exist in the greenhousetheory.
Your previous discussions are full of your statements about how the temperature of the earth surface violates the theory of thermal radiation when you claim that the temperature, the internal state, is dependent on the external cold atmosphere. The theory says clearly: the temperature is dependent on the internal state only. No exceptions are given. The greenhouse is the only one.
Lasse,
This is from a heat transfer textbook, “Fundamentals of Heat and Mass Transfer, 6th edition”, Incropera and DeWitt (2007) – an undergraduate textbook that an engineering student or physics student will use. Likewise the 6 textbooks that I provided in the other link.
As noted in the Etiquette, we accept textbook physics as a given. If you want to say it is all wrong, good for you, but find another blog.
Many people arrive full of confidence, with no idea what is taught in textbooks. Many people leave still full of confidence, still with no idea what is taught in textbooks.
“Many people arrive full of confidence, with no idea what is taught in textbooks. Many people leave still full of confidence, still with no idea what is taught in textbooks”
Where is your textbook explaining how and why the greenhouse effect is an exception from the fact that all bodies emit depending on temperature only. Where do you find support for the claim that earth works in the opposite way, that the surface emission depends on the external state in the atmosphere.
Lasse,
In a few short days you have written about 30 comments on about 10 different articles, each with almost the same content. In the meantime you aren’t able to understand what a textbook is, or an equation.
Contrary to your expectations, none of your insightful comments will be deleted. They will all be retained to demonstrate your clarity of thought for future readers.
Any now you can join the select group of people, the pantheon of greats, who have been banned from further comment, for inability to engage with the concept of physics – specifically:
– to write an equation to explain your idea without ambiguity
– to engage with the ideas in physics textbooks that have been presented to you
Well, just to be clear to new readers, inability to write an equation or have clarity in a physics concept is not a barrier to comment. It is only a barrier if you claim great insights and write non-stop comments with zero appreciation that perhaps your understanding of physics or heat transfer might be flawed.
I could have written the equations for Lasse, but Lasse didn’t want them. Self-confidence in physics without any understanding of physics is an entertaining idea that will be certainly be appreciated in other blogs.
[…] The last post from Lasse was deleted from the discussion under this article https://scienceofdoom.com/2017/02/01/basics-emissivity-and-the-stefan-boltzmann-equation. […]
Writing about Schwarzschild’s eqn forced me to reconsider emissivity. Planck demonstrated that radiation in equilibrium (absorption = emission) with quantized oscillators (obeying a Boltzmann distribution) would obey Planck’s Law. Soon after, quantum mechanics came along to reveal that simple molecules have quantized vibrational, rotational and electronic states and that absorption and emission of photons are fundamentally controlled by Einstein coefficients which control line intensity (but not line width). The SE equation can be derived from Einstein coefficients assuming LTE.
Nevertheless, Planck’s Law is wrong: Emission at a single wavelength or across all wavelengths is usually less than predicted. Sometimes this happens for trivial reasons: 1) Absorption and emission don’t reach equilibrium before radiation leaves an object such as an optically thin layer of atmosphere (too few GHGs, some wavelengths absorb weakly if at all). 2) We have created a variety of devices (lasers, LED and fluorescent light) where a Boltzmann distribution, LTE, and even thermodynamically-defined temperature don’t exist. But this doesn’t explain why most dense materials, take water for example, don’t have unit emissivity.
I believe I first heard the suggestion from DeWitt that emissivity less than unity is caused by internal radiation being internally reflected or scattered at the surface. This attractive hypothesis provides an explanation for why emissivity equals absorptivity, but I haven’t located any references. SOD has an article on the emissivity of the ocean that says emissivity has an angular dependence, exactly what one might expect for a surface phenomena. However, many metals have thermal emissivities less than 0.1. Could that much reduction be due to internal reflection or scattering?
Looking for references, I finally did a search for “Rational for Kirchhoff’s Law absorptivity and emissivity” (rather than emissivity alone) and found that some solid state physicists and other materials scientists are actively pursuing these questions even today. And it suddenly dawned on me that metals, crystalline materials and other solids may not behave like quantized oscillators. That description may be reasonable for molecules with covalent bonds, but not solids with complicated phenomena such as phonons, conduction etc. The propagation of thermal infrared inside a solid is “conductivity”. The most disturbing reference I encountered is given below. (This may be a conference proceeding and not peer reviewed.)
“The Theory of Heat Radiation” Revisited: A Commentary on the Validity of Kirchhoff’s Law of Thermal Emission and Max Planck’s Claim of Universality
Pierre-Marie Robitaille and Stephen J. Crothers. http://www.rxiv.org/pdf/1502.0007v1.pdf
Affirming Kirchhoff’s Law of thermal emission, Max Planck conferred upon his own equation and its constants, h and k, universal significance. All arbitrary cavities were said to behave as blackbodies. They were thought to contain black, or normal radiation, which depended only upon temperature and frequency of observation, irrespective of the nature of the cavity walls. Today, laboratory blackbodies are specialized, heated devices whose interior walls are lined with highly absorptive surfaces, such as graphite, soot, or other sophisticated materials. Such evidence repeatedly calls into question Kirchhoff’s Law, as nothing in the laboratory is independent of the nature of the walls. By focusing on Max Planck’s classic text, “The Theory of Heat Radiation’, it can be demonstrated that the German physicist was unable to properly justify Kirchhoff’s Law. At every turn, he was confronted with the fact that materials possess frequency dependent reflectivity and absorptivity, but he often chose to sidestep these realities. He used polarized light to derive Kirchhoff’s Law, when it is well known that blackbody radiation is never polar- ized. Through the use of an element, dσ, at the bounding surface between two media, he reached the untenable position that arbitrary materials have the same reflective prop- erties. His Eq. 40 (ρ = ρ′ ), constituted a dismissal of experimental reality. It is evident that if one neglects reflection, then all cavities must be black. Unable to ensure that perfectly reflecting cavities can be filled with black radiation, Planck inserted a minute carbon particle, which he qualified as a “catalyst”. In fact, it was acting as a perfect absorber, fully able to provide, on its own, the radiation sought. In 1858, Balfour Stew- art had outlined that the proper treatment of cavity radiation must include reflection. Yet, Max Planck did not cite the Scottish scientist. He also did not correctly address real materials, especially metals, from which reflectors would be constructed. These shortcomings led to universality, an incorrect conclusion. Arbitrary cavities do not con- tain black radiation. Kirchhoff’s formulation is invalid. As a direct consequence, the constants h and k do not have fundamental meaning and along with “Planck length”, “Planck time”, “Planck mass”, and “Planck temperature”, lose the privileged position they once held in physics.
Fortunately for climate science, GHG’s are simple molecules with covalent bonds and no surface to reflect or scatter radiation or produce emissivity less than unity.
Hi ?
Nice post.
What is the effective emissivity of earth according to you ?
Rasmus,
Emissivity is a material property that is wavelength dependent. So you need to rephrase the question.
Besides defining exactly what you mean by “effective emissivity”, you also have to state where the measurement is to be taken.
Anyone here knows the average surface emissivity of the earth please? It said the ocean is about 0.98, but the aluminnum is 0.2 if my memory is right. How come water behave more close to a blackbody while a metal is far from unit?
When a photon interacts with a solid or liquid, it can only be absorbed, reflected or transmitted, so a + r + t = 1. The Second Law requires that emissivity equals absorptivity at any given wavelength. Metals are highly reflective, so that doesn’t leave much room for absorption/emission. Ice can be highly reflective, snow somewhat less. There is also reflection from clouds. For incoming solar radiation, about 30% is reflected by the surface and clouds.
I am reading here for one purpose: to learn. I have absolutely no stubborn bias or position about people and greenhouse gases contributing to global warming beyond that I believe both are true without personally studying all the arguments. I am 100% objective when looking at scientific and logical arguments to the degree I understand them. I know this because lately I’ve been reading discussions like here above and I have never judged a person’s arguments based on their position on the issues. So not only do I think I’m being honest about this, I know I am – I can see it unequivocally in my reactions. I am looking to understand as much as I can about radiative heat transfer (and not global warming) and I haven’t found satisfactory consistent explanations for several issues. But I find myself reading about the global warming debate because its “the place” where the “physics” are. Fascinating indeed, but it still isn’t what’s occupying my mind. I find the posts made by Lasse Kongo to be the most valuable yet in providing coherent explanations for physical “laws”. I didn’t see any meaningful arguments to address his understandable and highly applicable assertions. No follow through whatsoever. Just a claim that he didn’t illustrate with (unnecessary) calculus. Why not? He was decried as a nuisance and banished. Maybe there’s more I haven’t found yet – but based on what’s above, Lasse Kongo is the only one that has my trust.
I don’t know about Lasse Kongo specifically, but people come and go. Pekka Pirila, for example, died in 2015. Very few people have been banned, and those that were definitely deserved it.
As far as understanding atmospheric radiative transfer, I still recommend Grant Petty’s A First Course in Atmospheric Radiation. For a textbook it’s not expensive. You can buy it direct from the publisher at the same price I paid for it several years ago, $36.
https://sundogpublishingstore.myshopify.com/products/a-first-course-in-atmospheric-radiation-g-w-petty
Thank you DeWitt – the book looks to be right up my alley.
I have a few questions. Above you wrote, “The Second Law requires that emissivity equals absorptivity at any given wavelength.” This is an example of a “law” that seems misused to me. If the rest of the law is “at thermal equilibrium” then why even state it without its full definition since it seems to be violated profusely as thermal equilibrium is almost nonexistent in life. Even more, a black object wouldn’t look black if it was near simultaneously emitting the same wavelengths that it absorbed.
How do we see cold objects – by reflected light else they are invisible because we do not absorb radiation from colder things? I don’t think so. Why aren’t these processes explained better?
Where are the explanations for what happens to “rejected” radiated thermal energy?
Can a body/material/surface sense its radiative surroundings in any way and then alter its own radiative emission as a reaction (for example, to radiate more heat)? Can radiation be interactive in any way?
Lasse Kongo’s assertion that emission, absorption, and intensity depend on the internal state of a material only – with internal temperature being the only meaningful relevant factor in most discussions makes too much sense to me to have him summarily dismissed with no argument as to why that isn’t true.
I’m thankful when people provide explanations in English instead of calculus. The calculus is for a select few and it is almost worthless without explanations for reality that do not need to be stated in terms of calculus. It is ok to state what we don’t know. Pretending doesn’t cut it. Our human condition does not allow us to understand but a fraction of “reality” so in significant ways we are arrogant about the limits of our abilities. That said, I expect us to fill in the seemingly large gaps in our understanding of radiation.
Kirchhoff’s law of radiation applies at Local Thermal Equilibrium. In a gas, that means that energy transfer between molecules is dominated by collision (99.99+%), not radiation and the molecules have a Boltzmann energy distribution. Most of the atmosphere (everywhere below about 60km altitude) can be considered to be at LTE. If emissivity doesn’t equal absorptivity, then an object could have a temperature greater or less than ambient with no heat flow. You can’t define temperature under those conditions.
A black body emits radiation according to its temperature, not the spectrum of radiation being absorbed/reflected. If we’re talking about a real object, then emissivity/absorptivity, reflectivity and transmissivity depend on a lot more than temperature. The atoms in a solid can all be considered to be at local thermal equilibrium even if the the solid body is not in equilibrium with its surroundings. A true black body would indeed be hard to see, but no such thing exists in the real world, with the possible exception of a black hole and even black holes emit Hawking radiation. Some radiation will always be reflected from a real object, allowing it to be seen.
Gary,
It makes too much sense to you? But you haven’t learnt any physics so any blah blah blah can sound very convincing.
There’s an equation, found in physics textbooks. I’ll describe it in words.
Absorption of radiation is a proportion of the incident radiation. The proportion is called the absorptivity. It’s a number between 0 and 1. The absorptivity does not depend on the internal temperature of the body. It depends on the material property of the body, which is wavelength (and with surfaces, directionally) dependent.
I’ll leave it you to work it out from intuition if this sounds correct or not.
Intuition is way more reliable than physics textbooks.
Just to finish the story in case you’re still reading.. emission is dependent on the body’s temperature and the emissivity, a wavelength dependent value just like absorptivity.
The body’s emissivity equals its absorptivity at the same wavelength and direction.
Absorptivity is different from absorption. Emissivity is different from emission. Emission does not equal absorption unless a body is in a steady state with no convection or conduction to transfer heat.
No doubt you can decide based on intuition whether these explanations are correct.
Gary: I’ll try a novel explanation for Kirckhoff’s Law, which says that the absorptivity and emissivity of a material must be equal at every wavelength. First, we think of absorptivity and emissivity as properties of a material, but I’m going to argue that they are properties of the INTERFACE between two materials, usually a solid and air (or a solid and vacuum).
Let’s make the two materials liquids that don’t mix, say water and gasoline at the same temperature. Gasoline is a mixture, so let’s replace gasoline with a single pure liquid component of gasoline, octane, Both water and octane emit thermal infrared radiation, aka photons, and let’s consider those of a particular wavelength, say 10 um. The intensity of emission obeys Planck’s Law for this wavelength. When the photons emitted by the water reach the interface with octane, most pass through into the octane, but some are reflected (or scattered) by the interface between the two liquids. So, let’s draw three arrows: one from the water to the interface, one continuing through/from the interface into the octane, and a third arrow from the interface back towards the water. Let’s say 80% of the photons go through the interface (where than can be absorbed by the octane, making octane’s absorptivity 0.8.
If partial reflection and partial transmission sounds weird, think about the partial reflection from glass you see when it is darker outside than inside. Or think of the reflection of mountains seen in the surface of a lake even when you can see rocks at the bottom of the lake in very shallow water.
Now let’s consider the thermal infrared photons emitted by the octane towards the water. Again we will have three arrows, but we will call the arrow leaving the interface the emission from the octane and the fraction of photons passing through the interface the emissivity of octane. If the emissivity of octane is not equal to the absorptivity of octane, then one liquid will start warming and the other cooling due to the unequal radiation/heat flow between them. And this will violate the Second Law of Thermodynamics.
So, I’ve postulated that both liquids emit like blackbodies and that the phenomena of absorptivity and emissivity arise at the interface. (Some people may object to what I’ve done, so I want to make it clear.) Planck derived his law for radiation in black cavities where absorption and emission have come into equilibrium (given the local temperature, which influences emission).
Now let’s replace the octane with air, and we are talking about the absorptivity and emissivity of water being equal. Then let’s freeze the water into ice and we are talking about the absorptivity and emissivity of ice being equal. Finally let’s replace the ice with a non-transparent aluminum block. In this situation, I have a mental block trying to picture thermal infrared photons traveling through the aluminum and passing through or being scattered back into the aluminum at the interface. Despite this difficulty, I’m sure emissivity arises at the interface because the emissivity of many metals depends on how polished and oxide-free their surface is.
[I’m replying to DeWitt’s last post above as the reply option is missing on my iPad]
DeWitt wrote “… If emissivity doesn’t equal absorptivity, then an object could have a temperature greater or less than ambient with no heat flow.”
The problem I have is that the wavelength/frequency of the absorption and emission is stated to be one and the same by the law. Therefore, a black object should appear close enough to that of a white object, or at least not black.
Regarding that we see colder objects by their reflected light. Cannot a colder object emit visible light (as opposed to only reflecting it)? If so, why is it not possible to see that light, or is it? The way you responded leaves me to assume that only warmer objects can omit light visible to the observer.
[I apologize that I have been ridiculously busy and I haven’t even read Frank’s reply yet – although I will as I truly appreciate it!]
I’m starting to think you’re hopeless. The only question is whether you’re being obstinate on purpose.
Kirchhoff’s Law does not require that an object emits thermal radiation at all wavelengths. Nor does it mean that it must emit radiation at all wavelengths it receives from an external source. That is determined by the reflectivity at those wavelengths. The spectral density of emitted thermal radiation is determined by Planck’s Law. An object at 300K does not emit EM radiation at visible wavelengths. It does not mean that you cannot visually distinguish between a white and a black object.
Great – We now firmly believe the other is completely hopeless. I am good at reading and understanding plain English and I have no background in physics. I am better at computer science. In computer science, things can be explained that actually mean what one says, in actual English. I was not being obstinate but rather completely sincere and serious. I understand all the terms, just not the contortions of how it all is supposed to work together despite a hundred different definitions and interpretations. I was hoping to learn something that hadn’t yet been coming out in the words. I seriously have to question the integrity of many, in particular one who can’t recognize sincerity and who can’t relate to an intelligent person with a different background.
Gary wrote: “Cannot a colder object emit visible light (as opposed to only reflecting it)? If so, why is it not possible to see that light, or is it? The way you responded leaves me to assume that only warmer objects can omit light visible to the observer.”
For any object (or more accurately any molecule) to emit radiation, it must be in an excited vibrational, rotational or electronic state. Everyone knows that absorption of a photon creates an excited state, but few realize that excited states are usually “relaxed” by molecular collisions many orders of magnitude faster than an excited state can “re-emit” a photon. This is often called “thermalization” of the absorbed photon, since the photon’s energy becomes kinetic energy of molecular motion in the case of gas and liquid absorbers. (Any time you hear someone mention “re-emission” of an absorbed photon in connection with climate science, you are probably dealing with an unreliable source.)
In climate science, essentially all of the photons that are emitted come from molecules that have been excited by molecular collisions: “Thermal infrared” (or long wavelength radiation, LWR) is emitted by molecules in our climate system between 190 and 310 K. You need much more energetic collisions to reach excited states that can emit visible light light. Visible, near infrared, and near UV light (short wavelength radiation, SWR) is emitted by the surface of the sun at about 5700 K (and by tungsten filaments in incandescent light bulbs at about 2000 K). Otherwise, most visible light you see has been reflected or scattered into your eye. We have invented a few technologies that allow us to excite molecules with electricity rather than heat: LED and fluorescent lights, lasers, and microwave ovens. The phenomena occurring in these devices are not relevant to climate science, but can be sources of confusion. In climate science, photons less than 4 um are SWR emitted by the sun; and if longer, LWR emitted by our climate system.
When molecules are excited by molecular collisions, this produces a Boltzmann distribution of energy among excited state. The probability of a molecule being in an excited state decreases exponentially with -E/kT, where E is the energy of the excited state (and the photon it might emit) and T is temperature. Assuming a Boltzmann distribution of energy among excited states, Planck calculated the spectrum of radiation that would exist at any given temperature IF absorption and emission were in equilibrium and radiation was quantized (consisted of particles called photons). This is called blackbody radiation. Stefan-Boltzmann added up (or integrated) the power emitted by “blackbodies” over all wavelengths and found that it was proportional to T^4 (=oT^4, where o is a constant). However, most objects emit somewhat less, eoT^4, where e is emissivity – and is 1 for blackbodies. Kirckhoff’s Law says that the fraction of radiation that fails to escape through the surface of a “graybody” (1-e) is exactly the fraction of radiation of the same wavelength “fails” to enter a graybody (1-a) – that is reflected or scattered rather than absorbed.
Unfortunately, the simple gas molecules in our atmosphere have negligible ability to absorb and emit photons at many thermal infrared wavelengths: N2 O2, and Ar have negligible emission and absorption at all wavelengths important in our climate system; while “GHGs” like CO2, H2O and CH4 emit and absorb at only some wavelengths. These gases don’t emit like a blackbody (following Planck’s law) for this reason. The surface of the earth emits almost like a blackbody (average e = 0.98?). Therefore. when seen from space, the spectrum of radiation emitted by our planet does not follow Planck’s Law. Nevertheless, many people say our planet emits like a graybody at 288 K with an “effective emissivity” of 0.615. Given the wide range of temperature in our climate system (190-310 K) and the absence of an equilibrium between absorption and emission (the assumption behind Planck’s Law), this crude graybody approximation is useful, but can be misleading in many details.
The lack of equilibrium between absorption and emission at many wavelengths and altitudes in our climate system means that radiation in our atmosphere must be studied using another equation, the little-known Schwarzschild’s equation. When someone says they are doing “radiation transfer calculations”, they are usually using some variant of Schwarzschild’s equation to predict the absorption and emission (and sometimes scattering) of radiation as it travels through our atmosphere. This involves the kind of math you aren’t interested in reading. Unfortunately, the greenhouse effect and the radiative forcing from rising GHGs in our atmosphere are calculated and explained using radiative transfer calculations. There are some decent “handwaving” explanations that allow you to “understand” these concepts, their lack of rigor provides skeptics many opportunities to create doubt about these explanations. For example, for far too long, I KNEW that twice as many CO2 molecules in our atmosphere would absorb AND emit twice as many photons, so I was positive 2XCO2 couldn’t “trap” more heat in our atmosphere. 2XCO2 will reduce the rate at which heat escapes our planet (if nothing else changes) and that reduction is calculated by radiative transfer calculations. These calculations have been validated by experiments in our atmosphere.
Climate scientists have tried to portray the effects of rising CO2 to the public as a simple trapping of heat or an increase in radiation emitted downward by CO2. This has created opportunities for confusion that skeptics have exploited. More technical explanations also have weaknesses. When you get down to the level of radiation transfer calculations – which have been validated by experiments in our atmosphere – you are dealing with the fundamentals of how radiation interacts with GHGs. Most skeptics won’t go there, and their remaining arguments are easily rejected. However, radiation is the simplest part of the problem, After that, you are dealing with climate models and there is plenty of room for skepticism about models.
Frank, I greatly appreciate this explanation which I just read. Your earlier one I only read the first few sentences because I can’t afford to spend any time on this for a few more days. But eventually I will and I won’t be nice to the explanations given by physics related professionals in general regarding the radiative transfer of energy. However, I do not mean you and again I sincerely appreciate your comments and I am 100% sincere in mine and I am not trying to annoy anybody. I only want to understand a few things at the current time and climate science and greenhouses gasses have not been on that short list. (I leave it open now to perhaps try to follow that debate someday in the future because I have found my introduction compelling.) Like most people, I skip through the math because I am not going to need it for any work. I will accept the proofs of others to the extent their colleagues accept it. I am good at a lot of math even though I am more careful than fast. The math classes I took were applicable to computer science and business although I did take two calculus classes and got two A’s and then promptly forgot every bit of it because I never needed it and I was slow at it even though I could follow it. Much of the other math that I got educated on became invaluable and I did not forget.
I have not commented on physics, radiation, or climate science prior to this in any other forum or venue of any kind anywhere. These are my first and only comments to this date. I have no axe to grind other than what I see is the lack of coherence in English explanations. I don’t have any block in trying to understand something necessarily complicated, or even a block over something simple (things which I am unfortunately capable of). My problem isn’t one of those so the advise to read books is misplaced.
Gary wrote: “I won’t be nice to the explanations given by physics related professionals in general regarding the radiative transfer of energy.”
The rules of this blog limit discussions to the accepted laws of physics (but not “the consensus on climate science). If you aren’t interested in what physics tells us about radiation and other important phenomena in our climate system, then you are in the wrong place.
However, I do remember being frustrated and intemperate when I first arrived here and found a community of people who were more knowledgable than I, some of whom were exceptionally generous in helping (especially DeWitt and our host). Beginning a reply with “thanks for the reply” and “what I don’t understand” followed by quoting the key passage can be conducive to learning why we differ, but aren’t very useful for pointing out the idiocy of others.
What I meant by “I won’t be nice” is not going to be personal attacks – not in the least. My frustration with the commonly available accessible information on radiative transfer of energy and thermal radiation – well actually not since thermal radiation is a term people use to mean different things 🙂
I really am overwhelmed by a number of things so I have to wait and pick this up later. Thanks Frank!
Gary,
1. There have been large numbers of visitors to this blog who, with no knowledge of physics, or even with some knowledge of physics, no knowledge of radiative physics. Many often claiming “this is what climate science says” when it obviously isn’t. No references. No textbooks. And of course massive confidence.
That makes it difficult when commenter #1185 shows up. You can probably appreciate this.
2. It’s hard to solve someone’s intuition problem. They say what they think. The person who understands the subject tries to understand their conceptual issue, explains some points.. but it often doesn’t help.
Me for example, I never got z-transforms. I kind of did. But not really. I always had this conceptual block and no one could find the mechanism to solve that. Luckily I never needed them. Likewise I never really grasped electromagnetism during my degree, but I passed my exams. I did need electromagnetism in my first job and had to start from scratch and re-educate myself. Then it all became clear because I had actual problems to solve. But I would never have grasped the key points without a textbook and equations.
There’s only so much that people can write to explain the stuff to someone who hasn’t read a textbook and has still decided that random commenter #1467 made perfect sense. Even when anyone who knows textbook physics can see plain as day that random commenter #1467 was a nutter with zero knowledge of the field.
I started the blog mainly because I thought science was important and lots of people wanted to get some answers about climate science. But, there’s only so much myself and a few fabulous commenters can do. We can’t solve your lack of insights into the physics of radiative transfer. I only understood it myself by reading lots of textbooks.
Has this paradox been covered?
Anthropocentric Climate Science does not follow S-B?
S-B suggests that for a given temp, there is a given emissivity for a Gas?
Contradicting this, Anthropocentric Climate Science suggests that our atmosphere, at the same temp, emits different amounts of IR.
It makes this inference when it claims more IR is “down-welled” when there is more CO2 in the atmosphere, while remaining at the same temp.
That’s fine, more CO2 might change the emissivity.
But if it does, then a consequence of this has to be that the atmosphere cools?
The energy put back into the earth must come from somewhere, and it comes from the atmosphere.
And this apparent ‘cooling’ is exactly what this NASA diagram shows.
Prior to CO2 being added to the atmosphere, one would imagine that the system was in balance, and the energy leaving the atmosphere was the same as that entering it.
So, prior to CO2, one presumes
340.40 W/m2 in
340.40 W/m2 out
This is not stated in the diagram, but can we assume this is the case?
But check the figures in the diagram, and we have
340.40 W/m2 in
339.80 W/m2 out
So presumably, less radiation at Top of Atmosphere (TOA) means it has cooled?
Peter,
It doesn’t mean the atmosphere has cooled. The local temperature in the troposphere decreases with altitude. Increasing the absorbance of the atmosphere means the altitude of effective emission increases. It’s colder at higher altitude, at least until you get to the stratosphere. But most of the emission to space originates in the troposphere.
This is well known. If you haven’t come across it, you haven’t looked very hard.
Note that the emission from the atmosphere to the surface originates quite close to the surface where the atmosphere is warmer. Hence the atmosphere radiates more energy to the surface than it radiates to space.
Peter: You mentioned several different topics. This will address the last part of your remarks covering the net inward imbalance of radiation before CO2 began rising and 0.6 W/m2 today. The link for your Figure presumably is
The energy fluxes shown in this Figure are not measured values; the Figure is compilation of the best estimates from a variety of information, and there is significant uncertainty in many of these values. There is an uncertainty of several (5?) W/m2 in the absolute magnitude of the radiative fluxes measured from space, but changes of a fraction of a W/m2 are believed to be reliable. We don’t have enough instruments measuring SWR arriving at the surface to have a reliable global value for this flux and AOGCMs disagree by more than 10 W/m2. We have a pretty good idea of the flux of latent heat from measurements of global precipitation, but convection/thermals can’t be easily measured. We do know sensible heat is “co-convected” with latent heat/water vapor and some estimates of this ratio have been made. The flux of sensible heat is usually selected to make sure the other fluxes add up properly.
This brings us to the current imbalance of 0.6 W/m2, which is actually the most accurately determined quantity on this figure. (The most up-to-date value is 0.7 W/m2.) The heat capacity of the ocean is enormous compared with the atmosphere or the land (where heat can only move by conduction). For that reason, more than 90% of the energy delivered by the radiative imbalance ends up in the ocean Seasonal changes in radiation warm and cool the ocean down to an average of about 50 m, but heat from the radiative imbalance from rising CO2 has been carried much deeper by convection in the ocean. We know this because we have tracked the co-convection of man-made CFCs and 14C (from atmospheric tests of atomic weapons). Climate scientists have also been trying to measure the tiny increase in temperature of the deeper ocean for a half century. For more than the last decade, the flux of heat into the ocean has been tracked by a network of 4000 Argo floats that measure the temperature from the surface down to 2000 m. From that measured rise in ocean temperature, we know that 0.6 (0.7) W/m2 of heat has penetrated the surface of the ocean over this period and therefore must also represent the radiative imbalance at the TOA. This “imbalance” is the most accurately measured quantity on this Figure. (It may also include some minor adjustments for the melting of ice caps and sea ice and perhaps other phenomena.)
This accumulation of heat in the ocean may be our best observational evidence that rising GHGs are slowing down the rate at which heat escapes to space and causing “global warming”. It doesn’t tell us how much of that warming is localized within a few meters of the surface over land – where we most care about the temperature. Actually, we were sure rising GHGs would slow radiative cooling to space and create a radiative imbalance at the TOA from laboratory measurements on GHGs and radiative transfer calculations – IF nothing else changed. Now we are accurately measuring the consequences of that imbalance. Note that the calculated radiative forcing from rising GHGs has reached more than 3 W/m2 with rising aerosols cancelling some of this forcing; leaving a highly uncertain net anthropogenic forcing of a little more than 2 W/m2. So our warmer climate system (which is a little less than 1 degC warmer at the surface) has responded by sending a little more than 1.4 W/m2 more net radiation to space and taking up 0.6 W/m2 in the ocean. This is roughly consistent with a climate sensitivity of 2 degC/doubling.
Since the Earth was coming out of the Little Ice Age when the Industrial Revolution began and since it takes about a millennium for the ocean to overturn, we believe that a small radiative imbalance (0.15-0.20 W/m2) existed when GHGs began rising. Sea level was also already rising from thermal expansion.
Peter: In the stratosphere, local temperature is controlled by absorption of UV by O2 and O3 and emission and absorption of LWR by GHGs. Since there is little water vapor in the stratosphere, CO2 is the main GHG. Increasing CO2 should be causing the stratosphere to cool and it is cooling. However, some of that cooling is also being caused by destruction of ozone by CFCs.
In the troposphere, temperature is controlled mostly by convection, not by radiation. When air rises, it expands under lower pressure, and cools, If a risen parcel of air is now colder and denser that the air that now surrounds it, that parcel sinks back down. However, if temperature is falling rapidly with altitude (a high “lapse rate”), the air surrounding a risen parcel will be warmer and less dense, and that parcel will keep rising. If moisture condenses and releases some heat, the parcel can keep rising where the lapse rate is lower. Consequently, ON THE AVERAGE in most of the troposphere, temperature drops about 6.5 degC/km. Therefore, if a local parcel of air contained more CO2, radiatively cooled more effectively, and produced a steeper lapse rate, that would simply encourage more warmer air to rise from below to restore the 6.5 degK/km.
Basically our atmosphere is too opaque to thermal infrared to let all of the SWR deposited on the surface escape to space as fast as it arrives. It we could turn off convection, surface temperature would rise to something like 345 degK before incoming and outgoing radiation equalized. However, that would produce too high a lapse rate in the atmosphere, making it unstable to “buoyancy-driven” convection. When convection was “turned back on”, convection would speed up until surface temperature temperature and lapse rate returned to normal.
Frank (aka Franktoo)
Peter,
The physics of the atmospheres “in climate science” is the same as textbook physics on radiation – emission of radiation from a body of gas is isotropic, i.e., the same in all directions.
The emission of radiation is determined by the emission lines of each gas, the concentration of each gas, and the temperature of the gas.
If you take a “layer of the atmosphere” close to the surface it emits the same radiation up and down. Xup and Xdown.
If you take a “layer of the atmosphere” higher up in the atmosphere it also emits the same radiation up and down. Let’s call this Yup and Ydown.
Because the temperature of the atmosphere is lower the higher up you go, Yup is less than Xup. Ydown is less than Xdown.
Also, while CO2 is a well-mixed “greenhouse” gas, water vapor concentration is highly dependent on temperature. Water vapor concentration reduces by something like a factor of 1000 as you go from the surface in the tropics to the top of the troposphere in the tropics.
Therefore, the emission of radiation from a layer high up in the atmosphere is “lower” – compared with near the surface – than you would expect from temperature alone.
Hopefully this makes sense.
I recommend you read through the series Visualizing Atmospheric Radiation.
Yes thank you.
I read your emissivity piece yesterday, it was mostly nice and clear, more pieces falling into place for me.
If additional CO2 can change the emissivity of the gray body atmosphere that can explain the two different levels of IR output for the same temp, although for a perfect S-B BB this would not be true.
On the issue with energy flux in a closed system (if that makes sense) –
Has the upper atmosphere cooled?
Standing back and looking big-picture, if one bit of a closed system warms, another must cool?
The NASA diagram which shows the effect of CO2 has net energy leaving the earth as 339.8 W/m2. Using S-B this implies a lower temp for the upper atmosphere than before?
The fact that IR leaving the atmosphere is lower has to be interpolated.
If we assume that prior to CO2 upsetting things, the system would have been in balance, 340.4 W/m2 insolation, 340.4 W/m2 radiated (or reflected) out.
I thought the NASA pictogram of the Earth Energy Budget was suggesting a cooler upper Troposphere since it shows REDUCED radiation at TOA to counterbalance the increased radiation at ground level, ergo TOA is cooler using S-B.
I have discussed this with the guys at the NASA climate change website.
They point to stratospheric cooling as the counterpoint to terrestrial warming.
I think I would interesting to see some ‘flux’ or ‘energy v temp’ calculations between the upper stratosphere and troposphere if both the earth and troposphere are shown as warming while the stratosphere cools.
If the Earth itself warms as the part of he CC mechanism (reasonable enough?), that implies that the Troposphere receives net reduced energy input from ground-level upwelling, which would tend to cool anything above it, ?
.
My thinking may or may not be entirely clear, but that seems to be one of the refreshing things about your site, thankyou, is actually working through ideas like this.
Peter: Emissivity is a very tricky concept to apply to gases, and confused me for a very long time. The S-B equation for black bodies comes from integrating Planck’s Law over all wavelengths. Planck’s Law was derived assuming that temperature-dependent emission and temperature-independent absorption are in equilibrium. This assumption don’t apply to all altitudes and wavelengths in the atmosphere. There is effectively no absorption and emission at wavelengths in the “atmospheric window” (8-13 um), for example. On the other hand, 90% of the photons most effectively absorbed by CO2 have been absorbed within one meter of travel near the surface – and have been replaced by and equal number of newly emitted photons An equilibrium between absorption and emission exists at this wavelength and location. In this case, we say that absorption is “saturated” and the radiation has the intensity predicted for a blackbody by Planck’s Law. However, if you go high enough in the atmosphere, the density of all GHGs becomes low enough that absorption and emission are no longer in equilibrium at the local temperature, and that temperature varies dramatically with altitude. It turns out that radiative forcing arises mostly at weakly absorbed wavelengths where photons can travel far enough vertically between emission and absorption that the temperature is significantly different. This is why upward flux of thermal infrared drops from 390 W/m2 near the surface to 240 W/m2 at the TOA and why DLR increases from 0 at the TOA to 333 W/m2 at the surface.
The other complicating factor is that emission depends on the number of emitting molecules, but emissivity is usually considered to be a property that is independent of quantity. However, you will find climate scientists referring to “optically thick” layers of atmosphere with an emissivity of 1 and “optically thin” layers of atmosphere whose “emissivity” varies with the amount of GHGs they contains. Furthermore, the emissivity of many metals varies with the roughness of their surface and the presence of an oxide coating. Kirckhoff’s Law says emissivity equals absorptivity, so both phenomena arise from surfaces. Gases don’t have a surface.
Many prefer to ignore these problems and think in terms of a blackbody MODEL for our climate system with a temperature of 255 degK, or a gray body MODEL for our climate system with a temperature of 288 degK and an EFFECTIVE emissivity of 0.615. In the latter MODEL, you can think of rising GHGs as lowering the effective emissivity of our climate system. Such models can be extremely useful in some cases, and they can mislead you in other cases. If the power emitted by our planet is given by W = eoT^4 and we want to know how this emission varies with temperature, we can differentiate to get: dW/dT = 4eoT^3 + oT^4*(de/dT). The first term is called Planck Feedback and is 3.3 W/m2/K at 288K. The second term is not zero because the effective emissivity of our climate system falls with rising temperature. For example. absolute humidity rises with temperature and increasing vapor vapor slows radiative cooling to space, just like CO2. Emissivity also changes, because the lapse rate is reduced by higher humidity. If the height of cloud tops also changes, that effects the emissivity of clouds.
Thankyou Frank.
Can I repeat my understanding of your idea?
More CO2 in the atmosphere increases the effective emission height of the CO2?
Due to the lapse rate this height is colder.
By SB a colder body emits less radiation.
So more heat is trapped in the atmosphere?
This seems odd.
The CO2 gas is still at the same temperature as before, if not warmer?
Kirchoff law applies?
Or not?
Is there a physical mechanism you can point me to that explains this effect ?
You comment was very helpful thank you, but got me pondering the lapse rate. I have some more thoughts on that but first wanted to try and make sense of the idea of the “effective emission height” , which in truth is not clear to me.
Thankyou !
Peter, you cite Frank on the greenhouse effect: “More CO2 in the atmosphere increases the effective emission height of the CO2?
Due to the lapse rate this height is colder.
By SB a colder body emits less radiation.
So more heat is trapped in the atmosphere?”
This comes from the physics of gas radiation. The iconic theory of earth as a greenhouse. But both measurement and models say that there is no IR heat trapping. All new models say the opposite. It is Short Wave Radiation that is warming the earth, by trapping heat into oceans. More CO2 gives less IR radiation out at Top Of Atmosphere. So there is something to counteract the greenhouse effect.
There are many thermostatic mechanisms in the atmosphere, mainly driven by water vapor and clouds. It seems that a warmer surface drives more heat to space. The classical greenhouse theory had a deficient understanding of convection, and how latent heat is lifted higher, among other things. This gives a lot of uncertainty to an understanding of global warming.
Sorry. What I should say is that more CO2 drives more longwave heat out at TOA
nobodysknowledge
This goes into the “so confused and wrong I don’t even know where to start” category.
Maybe as a shorthand we can use the “not even wrong” category?
Frank, thankyou for your comments, I only realised they were there once I posted my new reply.
I think one of the issues with the climate is the massive complexity, one can get overwhelmed with detail.
But the fundamental processed being posited are not complex, taken one by one, and that is the role for thought-experiments and simple mathematical models?
If the earth warms, fair enough as a concept, won’t another part of the atmosphere cool?
One of the confusions with climate is the ‘Goldilocks Temp’ idea of the earth reaching an equilibrium temp. There is no increased insolation to increase the overall heat in the system. Or at least, that is what CC modelling assumes. NASA say this. And in fact NASA readings show slightly reduced insolation over the past 10 years.
Of course the sun is the ultimate source of heat (if we exclude Geo), but in a system which is in balance, 340.4 w/m2 in v 340.4 w/m2 out, if one bit heats, another bit must cool ?
Peter,
I was going to make one more effort to point out your fundamental conceptual error, but I’ve decided that you are completely hopeless and the effort is pointless. Bye.
Peter,
“If the earth warms, fair enough as a concept, won’t another part of the atmosphere cool?”
If you put a lid on a saucepan that’s got heat applied.. if the water in the saucepan warms up won’t some part of the kitchen (or some part of the saucepan) cool down?
(No)
Fine to use analogical reasoning, but the analogy of the saucepan is very loose and not a good match to what is going on I think?
No one has turned any gas up?
That is the physics conundrum.
In fact the analogy is one of the typical things that is confusing at climate change, because there is simply no increase in insolation, is there? So, physically, there must be another mechanism?
In fact, the gas has been turned down a little, insolation has reduced over the past 10 – 20 years according to NASA if you check?
So, that was one of the things that never really made sense to me.
I know this is utterly counter-intuitive, but stay with it a minute !
This is to do with overall reduced IR emissivity of the atmosphere.
A better analogy, I think, is a one-way thermal blanket. It lets sunlight straight through, but slows down IR leaving.
After a long time the system has reached a ‘Goldilocks’ temperature where incoming radiation = outgoing radiation. It has reached equilibrium?
The picture I gave myself was being in a nice toasty room with a cheery log fire (ie the sun). You have this special blanket on. You are magical and don’t need to breathe and there is no air in the room, so just your body, the fire, and the blanket.
It’s a thermal blanket with a tog rating of 10 which is transparent to UV light one way – ie incoming rays from the log fire because it is white hot, and opaque to IR light the other way.
So, just like the earth, the first thing that happens, is your skin warms, which then warms the air (the blanket) which then warms up and eventually reaches an equilibrium point where incoming heat from the fire/sun = outgoing heat from the blanket/air.
What happens when you flick a switch and increase the tog rating of the blanket? (Ie, put more CO2 in the air).
Doesn’t IR leaving your body’s surface slow down through the blanket?
It takes longer for the IR to go from bottom of blanket to top of blanket?
The mean free path of the IR has increased?
So sure, the bottom of the blanket warms. But the top of blanket is getting less IR, so what happens? It used to emit energy at 340.4w/m2, it was in equilibrium. But the NASA diagram shows the TOA is now emitting less, 339.8 W/m2. Boltzmann says the TOA is cooler?
Until the TOA gets back up to temp, and starts re-emitting at 340.4 W/m2 then the system will be back in equilibrium.
But in the meantime, while the system rebalances , the earths surface heats, and the TOA cools.
The extra CO2 will create a different heat gradient between the earth’s surface and the TOA. And while that is happening, temporarily, the TOA cools a bit, as the earth’s surface is stealing more heat from the atmosphere.
No one needs to turn the gas up.
My pic may well not be the whole pic, and it might not even be right (I’ll have to take a close look at what others are saying), but it IS a different heating mechanism, based on the emissivity of the TOA. Reduced Atmospheric IR emissivity due to increased COs, produces a heating effect?
And this is one thing NASA pointed me to when I asked them.
The TOA is cooling, whatever the reasons given….
https://skepticalscience.com/Stratospheric_Cooling.html
https://www.realclimate.org/index.php/archives/2006/11/the-sky-is-falling/
And this an indication NASA gave me –
Stratospheric Cooling.
The mechanism is not the convoluted one described in this piece, it is more like the very simple one of the lid on boiling water and the cooled air-space above the lid.
Less energy is being transmitted upward.
This results in hotter water below, and a cooler upper atmosphere, until things re-equalize?
Stratospheric cooling can be a corollary of global warming, as an interim stage prediction?
Totally counter-intuitive, but it makes sense if you explain climate change by a re-distribution of energy/temp due to changes in atmospheric emissivity.
The pan lid has changed the emissivity of the pan of water ?
https://skepticalscience.com/Stratospheric_Cooling.html
Frank, thankyou for your reply.
Very informative and intelligent.
Ok, I’m saying, going by SB and LWR flux measured leaving the TOA, the upper atmosphere, or (even the whole atmosphere if I want to be really contentious!) cools?
This seems mad and a sort of Climate Warming denialism.
But longer-term, this turns out to be a mechanism which can SUPPORT the idea of overall climate change ?
So although, (clickbait), it seems to be saying climate change is negative, the atmosphere is getting cooler, really it isn’t when taken as a whole, it is more a local effect at TOA balanced by a warming effect lower down? Which is kindof exactly what you are saying happens. Energy is trapped for longer lower down, in the sea, and land and so on, which might temporarily reducing outgoing flux at TOA, but warming the lower atmosphere, sea, land, ice etc? There is an internal flux shift, or energy shift.
Longer term I agree this is a mechanism for a warming climate, but as an intermediary stage, perhaps allow the TOA to cool a bit? As the measurements are actually suggesting?
You write ……
“The law of conservation of energy DEMANDS, that if our climate system gains more energy from SWR than it loses as LWR, then it must warm up.”
I agree, but one of the weird points here is clearly, that you are suggesting that the LWR at the TOA has gone down? That is the paradox we started with. So it would be fair to assume the TOA is a bit cooler if we use SB?
The thing is, doesn’t this actually make a lot of sense?
And, actually, due to mixing from convection, winds, weather, Coriolis etc, and timescale (past 150 years) the actual, measurable effect is probably minimal, it still suggests a mechanism by which outgoing flux is reduced at TOA, allowing more LWR energy to be trapped for longer in the lower atmosphere? So, both you and I are correct.
Overall, long-term, there is more energy in the atmosphere, and it warms.
But as an intermediary stage, there is less LWR flux leaving the TOA, so that part cools a bit.
And actually, NASA are measuring lower temps in the Stratosphere, for which various mechanisms have been proposed. But that info fits quite neatly with this mechanistic idea?
And look at your final phrases –
“More heat immediately starts radiating to space as our climate system begins to warm.”
This is just not born out by the experiments, is it? There is no increase in LWR from TOA
The LWR at TOA is lower than it was before, and in fact the LWR leaving the atmosphere will never be above the incoming energy flux so long as there are factors in the atmosphere which delay the egress of the LWR? What will happen as the atmosphere warms is that the outgoing LWR will slowly increase then reach equilibrium with the incoming flux. And at that point, the climate will stop warming.
Ok,Ok, given a perfect model, granted.
To be honest, this is only an idea I have come across after studying the NASA diagram, but seems to fit to me SB does suggest a lower TOA temp, if exiting LWR flux is reduced, doesn’t it?. Prior to this, claiming a sort of ‘raising temp out of nothing’ really did not fit at all well with me, which is why I was keen to really understand and think through the physics and the mechanisms.
Anyway, my pennyworth for the pot.
Peter: To keep things organized, I am replying to your statements and questions on the narrow topic of stratospheric cooling in a separate comment at the bottom of this thread.
Peter asks: If the earth warms, fair enough as a concept, won’t another part of the atmosphere cool?
No! If ONE PART of the earth warms, ANOTHER PART usually cools. When cold Arctic air penetrated all the way to Texas and caused problems this February, it was almost certainly warmer than normal somewhere in the Arctic. The Arctic air that moved south across the US was replaced by air from somewhere else, and air moving into the Arctic is usually warmer than the air that is normally there. However, THIS PHENOMENA IS WEATHER AND HAS NOTHING TO DO WITH THE SUBJECT OF THIS WEBSITE – “global warming” or “anthropogenic climate change” allegedly caused by rising GHG’s. El Nino, which involves a change in upwelling of cold water off of Peru that lasts for many months, involves vastly more energy, and effects the whole planet – is also WEATHER and has little to do with AGW. As DeWitt noted, we can’t have an intelligent conversation when YOU confuse weather with AGW.
I like to call everything below the TOA our “climate system” – the entire atmosphere, the ocean and a few meters depth of land. AGW OR ANTHROPOGENIC CLIMATE CHANGE IS ABOUT HOW MUCH ENERGY ENTERS AND LEAVES OUR CLIMATE SYSTEM. Our climate system is isolated from below by kilometers of solid crust that totally insulates us from the enormous heat that lies below. (Only about 0.1 W/m2 escapes from below, less than 0.1% of the energy coming in from the sun, so you can forget about geothermal.) Therefore, to understand AGW, we only need to concern ourselves with radiation crossing the TOA in either direction. So let’s restrict our discussion to that until you understand it. So we are going to simplify that complex figure showing the Earth’s energy balance to just three fluxes: a) LWR exiting the TOA. b) SWR absorbed by our climate system. c) SWR reflected by our climate system. While internal energy fluxes modify how we experience climate change where we live – the tiny sliver of the climate system within a few meters of land surfaces – it is a waste of time trying to deal with those complicated internal processes without FIRST understanding what is happening at the TOA. Our climate system (except for the deep ocean) is efficiently mixed by winds, waves and currents. To a first approximation, any GLOBAL WARMING will be somewhat evenly spread around our climate system (except the deep ocean) by the same processes that already control the distribution of heat we already receive.
Fortunately, quantum mechanics. laboratory experiments with GHGs and experiments in the atmosphere itself tell us what we need know about how radiation interacts with the atmosphere and is emitted and absorbed by the surface. Schwarzschild’s equation for radiation transfer (usually referred to as “radiation transfer calculations”) tells us how radiation is modified by absorption and emission on its path from the surface to the TOA. These calculations tell us that rising GHGs slow down the rate at which LWR crosses the TOA and escapes to space – assuming nothing else changes. This reduction is about 3.6 W/m2 for a hypothetical instantaneous doubling of CO2.* Unfortunately, Schwarzschild’s equation is a differential equation which must be solved by numerical integration using data for the composition and temperature of dozens of layers of atmosphere and thousands of absorption lines and wavelengths. Instead of a simple formula like eoT^4 (which creates an impression we understand the physics), all radiation transfer calculations provides is the numerical output from a computer program that automates calculations – like the one at this website.
http://climatemodels.uchicago.edu/modtran/
Radiative transfer calculations show that rising GHGs slow down the rate at which LWR leaves our climate system, but they have no effect on how fast SWR crosses the TOA and enters our climate system. Some SWR is absorbed in the atmosphere and some at the surface, but any changes in where SWR is absorbed are irrelevant to how much energy our climate system contains.
The law of conservation of energy DEMANDS, that if our climate system gains more energy from SWR than it loses as LWR, then it must warm up. The difference becomes “internal energy”, ie higher temperature. This doesn’t tell us how much it will warm, how fast it will warm, where inside the climate system it will warm, or whether that warming will be detectable against the background of other internally or externally driven fluctuation in our climate.
You can – if you wish – imagine a gray body model for our climate system with a surface temperature of 288 K and an effective emissivity of 0.615. However, you must recognize that the effective emissivity of our climate system in this model is not a constant – it depends on the amount of GHGs in the atmosphere. We know from radiative transfer calculations that a doubling of CO2 reduces the emission of LWR from our climate system by about 3.6 W/m2 (1.5% of 240 W/m2). So emissivity will decline to about 0.60 in your gray body model when CO2 doubles. After it warms, there likely will be more water vapor in the atmosphere and that will reduce emissivity further. We can use Modtran to calculate that the increased humidity in the atmosphere after a 1 degC warming will reduce radiative cooling to space by about 1.3 W/m2 if relative humidity rather than absolute humidity remains constant. The reduction in radiative cooling to space caused by rising humidity is comparable to the reduction caused by rising GHGs. If you insist on using gray body models, you will reach the wrong conclusion if you assume emissivity is a constant.
* As soon as I wrote that rising GHGs slow down radiative cooling to space, you probably immediately thought that the same process causes the part of the atmosphere that absorbed more radiation must have warmed and then radiated away more heat. First, the atmosphere has some heat capacity, so its temperature can’t change instantly. The temperature in the atmosphere is controlled by both radiation and convection, so less heat will be convected upward from the surface as the atmosphere warms. And the atmosphere is radiating heat back to the surface of the land and ocean. The ocean, even the upper ocean that warms and cools with the seasons, has vastly more heat capacity than the atmosphere, so most of the “formerly outgoing” radiation the atmosphere absorbs is likely to end up in the ocean in the long run. Weather forecasting models and AOGCMs attempt to simulate these processes, but fluid flow is inherently unpredictable. I’m trying to get you to set aside all of these very complicated INTERNAL energy fluxes and focus on the big picture at the TOA. All I can say for sure is that the heat that GHGs prevent from escaping to space will end up warming our “climate system”, probably somewhat evenly. How much warming it takes to restore a balance between incoming and outgoing radiation at the TOA is the big unknown of climate science? These are problems worth considering, once you fully recognize that there will be warming.
Finally, a 3.5 W/m2 imbalance at the TOA is a enormous amount of energy – or more accurately power. If all of the power from a 3.5 W/m2 imbalance ended up evenly distributed in the top 50 m of the ocean, that part of the ocean would warm at a rate of 0.7 degC/year! Fortunately, it is taking nearly a century to double the amount of CO2 in the atmosphere. All of that heat does not stay in the top 50 m of the ocean. More heat immediately starts radiating to space as our climate system begins to warm.
I re-read your saucepan and surely, Yes, of course, the space directly above the saucepan which was being heated by escaping steam cools?
I mis-read it first time, you are not adding more heat, but you are taking heat away from the atmosphere directly above the saucepan by putting a lid on?
That contained heat needs to heat the saucepan lid up to 100% before the atmosphere above the saucepan will get anywhere near the temp it was before? In the meantime, the atmosphere above the sauce pan, that is no longer receiving heat directly from the water, will dissipate it’s latent heat to equalize with the air around it ?
Dear nobodysknowledge, thank you.
The theory that increased CO2 raises the effective emission height (EEH) of CO2 is crucial part of the ‘greenhouse effect’ theory.
To be honest, I don’t understand it.
I was hoping someone else might be able to describe this mechanism, or at least point me to a website, because I can’t find one that gives details of this mechanism. Even this excellent SoD website explains EEH as an SB identity (x=y), but does not discuss why or how this height changes by adding more CO2.
If anything, I think MORE CO2 hints at MORE shortwave IR leaving the atmosphere if anything, as you suggest?
I’d be very pleased if it is possible to have this explained?
The EEH can be thought of as the altitude where the absorption in layer of atmosphere is equal to 50% of the emitted radiation. Below that altitude the absorption increases until greater than 99% of emitted radiation is absorbed by the layer above it. Absorption decreases with altitude because pressure, and hence the number of molecules per cubic meter, decreases with altitude. Increasing CO2 partial pressure increases the number of CO2 molecules per cubic meter so the EEH increases.
I’m pretty sure that this is discussed somewhere here, but I can’t remember where. It’s definitely discussed in Grant Petty’s A First Course in Atmospheric Radiation, which isn’t very expensive when bought directly from the publisher and should be in the library of anyone who is seriously interested in understanding the physical underpinnings of greenhouse theory.
Thanks DeWitt that was pretty clear and makes sense.
I see two things – my thoughts on the lapse rate.
1. There is MORE CO2. So MORE OLR?
You yourself point out CO2 is a partial gas in the atmospheric mix, so we cannot analogize it’s effects to BB . I see CO2 as at atmospheric coolant.
2. Gravity as a ‘Greenhouse’ effect .
Via pressure + the lapse rate.
Gravity stores energy in the Potential Energy (PE) of molecules at TOA.
This expresses itself as atmospheric pressure.
The lapse rate is created and driven by the radiative bias at TOA.
Molecular radiation is isotropic, but at TOA there is no inbound radiation so molecules cool and this sets up the temp gradient back to earth.
Any increase in temp from anywhere can physically expand the atmosphere, and this is what happens in the tropics.
There are actually 3 lapse rates.
1. Bottom to TOA.
2. Equator to poles.
3. Day to night.
Earths temp swings are damped down or mediated via the storage of potential energy in the molecules at TOA. This gravity driven pressure and temp combination absorbs and buffers temperature fluctuation. Eg zenith solar power input at the equator could easily raise temps to 100C, but this is buffered by hot molecules rising and storing PE at TOA.
Via all the thermodynamic energy transfer mechanisms this energy is ultimately radiated to space via the ‘greenhouse gasses’ which are effectively atmospheruc coolants.
The reduction in SB radiation as a result of increasing height and falling temp could be seen as the storage in PE of the higher molecules?
So as far as any ‘warming’ caused by the suppression of the escape of energy via the CO2 route (if true, and it could be ..), that would be stored as usual in the upper atmosphere as PE until the atmosphere re-equilibrises and radiates the IR to space via another route, if CO2 is blocked?
DeWitt
Another issue I see with your description of the EEH is that it is predicated on there being a finite amount of radiation upwelling from the Earth’s surface, then shared by the IR-active gas. Radiation is simply a symptom of a hot gas. More gas means more radiation.
I think the overall role of ‘greenhouse’ gases in the atmosphere is to enable radiation into space to occur, thereby COOLING our atmosphere.
Energy is stored by gravity in the Potential Energy (PE) of molecules at TOA.
If there was no radiation hapening at TOA, these TOA molecules would eventually reach escape velocity and boil off. We need CO2 and water vapour to release the heat pressure to space to retain our atmosphere. Radiative cooling to outer space means TOA reduces in height? Phew.
A doubling of CO2 within the atmosphere means, pretty much, a doubling of the amount of radiative events (or logarithmic, whatever – IR activity increases)
Your description of the EEH and ‘greenhouse’ effect is as if the atmosphere is trying to transport a given number of IR ‘cars’ from Earth to TOA, and this transport route is being ‘blocked’.
If anything, hasn’t a second transport highway been built? More CO2 means a wider highway?
I would expect to see an INCREASE in IR within the CO2 active range at both TOA and Earth. The difference is the IR radiation at TOA will be lost to outer space. The Earth side will simply be recycled thermodynamically. This is how the Lapse Rate is created.
A hot gas internally generates its own IR.
More CO2 means MORE IR, not less.
There is no finite amount of IR packages to be delivered ?
Now I remember why I stopped replying to you. As SoD says above, you’re ‘understanding’ is so messed up that it’s not even wrong as Pauli once said about a theory that couldn’t be falsified. You should forget almost everything you think you know and start over again. It probably won’t help, though.
Bye again.
More CO2 means more IR
If you double the concentration of a trace gas like CO2 within the earth’s atmosphere, you effectively double it’s partial pressure.
Twice the molecules = twice the pressure.
This is Dalton’s law.
If you double it’s partial pressure, you increase it’s emissivity, and emittancy, the total IR output.
The CO2 gas becomes a bit less of a grey body, a bit more of a black-body, emitting more IR
Here is some data.
Please see the table.
The figures are originally from Hottel
http://www.biocab.org/Emissivity_CO2.html
This is an excellent analysis of the change in EEH, and fiendishly complex from Clive Best. I’m happy to change my mind if someone explains things.
I must say I am bewildered by his conclusions, I don’t mean I disagree, just that I am bewildered, and don’t know what to think.
I think Clive is saying this shows increased CO2 means increased Stratospheric Cooling, which NASA tells me is happening.
Quite how Statospheric Cooling leads to Tropospheric heating I don’t understand … ?
Is Clive even suggesting increased CO2 means more radiation, hend Stratospheric Cooling here?
By the way, for anyone interested my comment about the partial pressure doubling increasing IR is CORRECT, I believe.
What I had not factored in was the Lapse rate, or change of temp with height, which is an incredibly subtle climate effect, which I now appreciate.
Consider a ball of CO2 gas
A denser CO2 partial gas makes the gas slightly more opaque.
A bit less of a grey body, a bit more of a black body.
This raises the effective emission radius from the ball of gas.
Add more CO2 to the ball, and it becomes a bit more solid.
If the whole ball was at the same temp, the overall heat output would INCREASE.
But the ball of gas is actually within in a lapse rate.
And the ONLY radiation we are interested in is the upward component, the final direction IR is lost to the atmosphere.
And I can see now, this IS affected by height due to the lapse rate.
But what is also true is that overall emissivity increases as per the Hottel table I posed earlier, and I think Clive missed this. I will tell him and see if he thinks fit to publish.
Ok, here is the whole summary that turns climate science on it’s head for anyone interested.
I think Dalton’s Law turn the Greenhouse Gas effect on it’s head?
I think Carbon Dioxide is an atmospheric COOLANT.
The general view of climate scientists is that more CO2 WARMS the atmosphere because radiation is ‘blocked’.
And this effect happens.
I agree.
But Dalton also suggest more CO2 leads to MORE IR active molecules and more radiative events AS WELL as being blocked?
More CO2 will lead to more IR radiation leaving the atmosphere simply by dint of there being more molecules, and more radiative events, so COOLING the atmosphere?
And this is what AGW thinkers miss. (AGW = Anthropocentric Global Warming).
I think doubling CO2 in the atmosphere pretty much doubles Global COOLING from CO2?
I think AGW thinkers miss this because –
1. They are focussed on EEH, which is complicated yet true.
2. There is an immense momentum behind the AGW idea.
The AGW ‘CAUSE’ – EEH
The key mechanism Anthropocentric Global Warming (AGW) thinkers describe is to use is something called EEH, Effective Emission Height.
In a nutshell, EEH defines the Global Warming concept.
And this is real.
And true.
I can explain it pretty well.
It works exactly as AGW proponents say it does.
As you go higher in the atmosphere temperature decreases.
Think going up mountains – cooler with snow on top, the higher you go, the cooler it is.
Cooler things emit less radiance.
Think a one bar, not a two bar electric fire? It is cooler.
Here is a much, much more complicated explanation – (http://clivebest.com/blog/?p=4597).
There is also a complicated bit to do with the effective density of a ‘grey body’ sphere, which Clive’s link (above) illustrates, but that’s a bit too complicated to include here, but I think I can describe it simply enough if anyone wants to ask.
EEH works as an idea, and it would REDUCE IR emissions from CO2 leaving the atmosphere, IF a fixed amount of radiation was flowing through the atmosphere. So, does radiation ‘flow’ through the atmosphere is a big question?
So I agree with EEH principles, in general.
CO2 in our atmosphere going from 300ppm to 600ppm will increase the EEH.
Higher means colder.
SB (Stefan Bolzman) calculations rules tell us that colder things emit less heat.
So the EEH idea is a valid one.
A cooler fire means less radiative heat.
But there are 3 mistakes in AGW thinking-
1. Trying to explain heat transfer using radiation flow.
(It is convection that transports most heat, not radiation.)
2. Thinking of radiation as a fixed quantity of energy being transported.
Wrong.
Thermodynamic radiation aspects are much more complicated than this.
3. Not realising the implications of CO2 being a trace gas.
As CO2 molecules increase, there are more IR events.
More CO2 means MORE IR radiation.
Radiative heat is caused by the temperature, but also the QUANTITY of gas.
Double the gas, and pretty much, you double the radiative output.
This is true because CO2 is a trace gas in our atmosphere.
This is also, pretty much, what Dalton’s Law suggests.
Dalton’s law says that double the molecules of CO2 will double it’s partial pressure (https://en.wikipedia.org/wiki/Dalton%27s_law).
And you will see from the empirically measured tables below that a higher partial pressure means MORE radiation.
Outgoing radiation is utterly independent of how much incoming radiation there is.
Stop it.
Stop thinking about radiative flow.
It is wrong !
This is one of the key problems with the idea of radiative AGW.
The heat flow is convection.
On earth we call this ‘weather’.
The outgoing radiation from the atmosphere is utterly independent of the amount of incoming IR that is “upwelled”.
Radiation from a gas is described by the SB (Stephan-Boltzman) rules.
It is dependent on
the temperature of the gas and
the quantity (or ’emissivity’) – my main point today.
It is NOT related to the amount of radiation it receives or is “upwelled”
That is a really tricky one to take in, but believe me, true ( I think ).
Increasing CO2 in the atmosphere has two effects.
These are both to do with what physicists might describe as a ‘grey’ body becoming a bit more ‘black’.
The gas becomes a bit more opaque, and bit denser, a bit more solid.
It’s effective surface gets a bit more solid or ‘higher’.
And this gives two opposing effects :
1 And increase in EEH, which lowers outgoing IR a bit, the IR fire cools
2. An increase in IR from an increased amount of CO2. The IR fire gets bigger.
So the IR fire cools a little, but gets a lot bigger.
And the key to understand key heat transport within the atmosphere is not radiation, it is convection at the equator, where the sun is hottest. This is what Joseph Postma of climatesophistry.com is very good on.
Let go of the idea of heat being ‘blocked’.
Rising air transports massive amounts of energy from the bottom to top of atmosphere where it is stored as potential energy in packets of air (which have weight).
Claes Johnson is good on this.
This creates atmospheric pressure, and is slowly released. Think tropical thunder storms.
Think cold ice caps.
Pure radiation doesn’t create thunder storms.
Sun + convection do though.
Convection is what transports heat from Earth to Top of Atmosphere (TOA).
The met office even has a name for this – CAPE.
CAPE = Convective Available Potential Energy.
https://en.wikipedia.org/wiki/Convective_available_potential_energy
It would be good to quantify this by the way.
Thinking in terms of radiation transporting heat and being ‘blocked’ does not well describe how our atmosphere works, but is the idea that AGW is based on.
Convection is the main heat-transport mechanism.
CO2, believe it or not, is only really a coolant, cooling hotter layers by emitting radiation to lower layers, and cooling outer layers into space.
Here is a table which describes, and pretty much proves (I think) the effect I am on about. Please argue back scientifically, but spare me, don’t rant ?
Ok, rant if you want, I might not reply.
Increasing partial pressure increases radiative output.
More CO2 means More IR will leave our atmosphere.
These figures were calculated about 60 years ago by a man called Hottel.
http://www.biocab.org/Emissivity_CO2.html
I’m happy to be enlightened if wrong if someone has a better set of explanations, but I don’t think I am !
The climate is massively complex.
But more CO2 in our atmosphere means MORE IR being irradiated to space, not less.
We are getting colder?
NASA is currently measuring the Stratosphere cooling, which is what Clive Best calculates above. Clive also seems to think that IR leaves the atmosphere from the Stratosphere.
NASA doesn’t agree with my overall view by the way !
The fact that you link to biocab.org is sufficient reason to justify continuing to ignore you. NN is one of the few people that are banned from posting here. I’m beginning to wonder if you might be a sock puppet of his.
Peter: I see so many mistakes. It takes a long time to correct each address. I’ll try to tackle a few:
You said: “And the key to understand key heat transport within the atmosphere is not radiation, it is convection at the equator, where the sun is hottest. This is what Joseph Postma of climatesophistry.com is very good on.” When I first came to this blog, I was constantly frustrated and all-too-often intemperate about excessive attention being paid to radiation and lack of attention being paid to convection. After a long time, my “world-view” expanded to include two critical points:
1) The heat from the 240 W/m2 of SWR that crosses the TOA can only escape back across the TOA as radiation. Radiation transfer calculations (using the Schwarzschild equation) show that rising GHGs reduce the rate of radiative cooling to space. These calculations have been shown accurately predict what we observe in our atmosphere. Radiation is more fundamental than convection because radiation is the only means by which heat escapes our planet.
2) I used to wonder why convection of heat from the surface to the upper troposphere wouldn’t speed up in response to rising GHGs and limit or negate or perhaps even over-compensate for expected warming. Once in the upper troposphere and above most GHG molecules, that heat can escape more easily to space. In the tropics, the Hadley circulation sweeps heat (and especially latent heat from evaporation) towards the equator. That air rises in the Intertropical Convergence Zone (ITCZ) and the heat it carries is released in the upper tropical troposphere. That air radiately cools as it moves poleward, and it eventually becomes dense enough to sink back to the surface in the sub-tropics. (If you aren’t familiar with the Hadley circulation, see Wikipedia). To some extent, summer and tropical thunderstorms are “miniature local-scale versions” of the Hadley circulation. Willis Eschenbach has postulated that afternoon thunderstorms in the tropics function as a thermostat that regulate how warm the surface can get. Postma may do the same
I repeatedly asked why the Hadley cycle wouldn’t speed up in response to the warming produced by rising GHGs and “air-condition” the surface by moving more heat to the upper troposphere, where it can escape to space.
I didn’t understand is that the THE RATE-LIMITING STEP removing heat from the surface is LWR crossing the TOA. Yes, the Hadley circulation hypothetically could speed up and move more heat to the upper troposphere and make the surface cooler. However, that would reduce the lapse-rate between the surface and the upper troposphere and thereby DECREASE THE RATE OF CONVECTION. The Hadley circulation is a SELF-REGULATING SYSTEM. When the upper atmosphere has gotten too cold from radiating heat to space, the lapse rate become unstable and convection speeds up. And when too much heat has been convected to the upper atmosphere, any parcels of air that attempt to rise will expand, cool – but still be colder and denser than the air they have risen into. In that case, such parcels of air fail to continue rising and sink back to the surface. I like the phrase “buoyancy-driven convection”.
In other words, convection isn’t driven by excess heat at the surface; it is driven by the upper troposphere being cold enough so that warm air from the surface can rise into the upper troposphere, expand and cool under lower pressure – and still be warmer and less dense than the surrounding air. When rising air produces clouds, the heat of condensation partially compensated for the cooling caused by expansion. The rate at which the upper troposphere radiates heat to space controls the rate at which heat can be convected upward from the surface. Convection simply maintains an average lapse rate (a “moist adiabatic lapse rate) equal to the lapse rate where the atmosphere is marginally unstable towards buoyancy-driven convection – about 6.5 degK/km as it turns out.
A more sophisticated analysis actually shows that the Hadley circulation will SLOW as the planet warm, not speed up. And the upper troposphere theoretically will warm about twice as fast as the surface, because rising absolute humidity makes the atmosphere more unstable to convection. (Lapse rate feedback.) However, these factors modestly MODIFY the warming that is caused by the most fundament driver of climate change: Rising GHGs that reduce the rate of radiative cooling to space. That is why this blog and many others correctly pay far more attention to radiation and radiative forcing than they do to convection.
As for Willis Eschenbach and his acolytes, they are correct that afternoon tropical thunderstorms limit daytime warming on tropical islands, where Willis used to live. However, the tropical ocean that surrounds tropical islands – and which covers vastly more of the tropics than islands – actually warms less than 1 degC from daytime sunlight. That usually isn’t enough to drive convective thunderstorm in the afternoon. In fact, most of the rain that falls over tropical oceans falls at night, not in the afternoon when solar-driven convection might be expected to be greatest. Willis’s thermostat hypothesis only applies part of the time to a small fraction of the tropics. Our experience with thunderstorms on hot summer or tropical days fools us into thinking that convection is driven only by surface warming. Convection is mostly limited by the rate at which heat can escape the upper troposphere by radiative cooling to space.
Peter,
Imagine critiquing the equations for motion of the planets around the sun.. using your method of random word salad.. Well, I can imagine it.
Instead, please confirm for me these two question in this article –
Two Basic Foundations
And then we can progress.
Thankyou for engaging all.
In a nutshell, I’m wrong !
I was a bit over-excited wasn’t I.
I think the reason I’m wrong is actually really obvious that I missed what might be called the ‘optical density’ of the atmosphere due to it’s height.
No IR is directly transmitted through the atmosphere, unlike UV going the other way.
Earth’s atmosphere is opaque to IR with an emissivity of 1 if that is correct?
All the IR is abosorbed within a few metres.
If the atmosphere had been a thin layer with a real emissivity of 0.1, I would have been more on the money with this idea.
Increasing density does increase the number of molecules in a cross section, and therefore emissions from that thin layer.
But actually the atmosphere is 10k thick, so all the little layers in ascending height need adding and the atmosphere becomes completely opaque.
Interestingly for me, this seems one way to clarifywhat turns a ‘Grey Body’ atmosphere turn into a virtual ‘Black Body’, the notional level at which all radiation is absorbed.
Great rational website SoD, will check the links.
Thanks Frank a lot to chew over there.
DeWitt, you were the first person who made clear to me what the key element of Greenhouse Mechanics was, the EEH, thanks.
Check about the 9th picture down if interested, the idea of an atmosphere with a single molecule in. More molecules means more interrupted line of sight?
It is a small but useful pic in this respect:
https://scottishsceptic.uk/greenhouse-effect/
Peter: The atmosphere is completely opaque to thermal IR at some wavelengths, partially opaque at others, and nearly transparent at others. I suggest that you spend a hour at the Modtran website and learn how emission and absorption produce and modify the radiation traveling in our atmosphere. I suggest you start by “looking up” from the surface (0 km) at the radiation traveling down towards the surface, emitted by the US Standard Atmosphere. (The default setting is to look down from 70 km (the TOA), but when you look down you see a combination of emission from the surface and from GHGs in the atmosphere. When you look up, you are only seeing emission from the atmosphere.
Notice that emission from the atmosphere is near zero between about 800 and 1200 cm-1 (except for two weak peak’s just above 1000 cm-1 from ozone.) This is called the atmospheric window, and none of the GHGs emit OR ABSORB significantly at these wavelengths. Both absorption and emission are controlled by the same parameter, the absorption cross-section.
Then set the concentrations of all GHGs but one to zero and observe what wavelengths come from which GHGs. You might start with just CO2. In fact, start with 1 ppm CO2, and keep doubling until you get to 512 ppm. Notice that the intensity of radiation from CO2 never rises much above 0.4 W/m2/cm-1, but the peak gets broader. Why?
Planck’s Law was derived by postulating radiation where absorption was in equilibrium with emission. The website has superimposed the emission curves expected for a blackbody – absorption in equilibrium with emission – emission spectrum of radiation arriving at the surface. 0.4 W/m2/cm-1 is the emission expected near 666 cm-1 for a blackbody at 288 K. Now change the settings so that you have 10 ppm CO2 and are looking up from 3 km, where it is about 20 K colder. (Note the temperature vs altitude plot on the far right). Now the maximum emission from CO2 is just above 0.3 W/m2/cm-1, the intensity expected for a blackbody about 265 K. At wavelengths where the intensity of DLR from just CO2 is independent of concentration, but dependent and altitude/temperature, absorption and emission are in equilibrium at the Local temperature. When intensity varies with the amount of a GHG, then some of the DLR photons are arriving from higher in the atmosphere.
When you fully understand the emission that reaches the surface and how it is modified and sometimes reaches equilibrium (blackbody intensity) by absorption, then you might be able to understand the spectrum of OLR crossing the TOA to space = “looking down from 70 km”. However, at the wavelengths of the “atmospheric window” (where there is no DLR), you are also seeing emission from the surface. Again, it makes sense to consider the two most important GHGs (CO2 and water vapor) in isolation. And to vary the altitude from which you “look down” to see where photons are being emitted from. And to vary their concentrations to see what altitudes and wavelengths have absorption and emission in equilibrium with the LOCAL temperature.
As you have noted, doubling CO2 doubles the number of photons emitted and cuts the average distance they travel APPROXIMATELY in half, so doubling CO2 has only a minor effect on OLR crossing the TOA – a 3.3 W/m2 reduction in 298.5 W/m2 reaching space through a clear sky in the US Standard Atmosphere. (The more familiar figure of 240 W/m2 takes into account clouds and averaging over the entire planet.)
You and others like to talk about the “emissivity of the atmosphere”. At some wavelengths and altitudes, absorption and emission are in equilibrium, radiation has “blackbody intensity” and emissivity is 1.00. At other wavelengths and altitudes, the radiation we see depends of the concentration of GHGs and/or how far radiation has traveled from where it was emitted. In this case, “emissivity” doesn’t have its usual meaning. (Normally we think of emissivity a constant that is independent of the amount of a substance.) For this reason, I try to avoid discussing the “emissivity” of the atmosphere; it causes confusion. It is acceptable to talk about a “gray-body” MODEL for our planet with a temperature of 288 K and an emissivity of 0.615. However, this is just a crude model for our atmosphere: Its temperature ranges from 190 to 310 degK. None of the gases in the atmosphere has an emissivity of 0.615, and the “emissivity” of the planet in this MODEL will decrease as GHGs rise.
Seashell,
Thanks for stopping by, but we stick to science here. Many other blogs are suited to politics. Good luck.
Thanks Frank, I think I need to go back to school and read all the points you guys are pointing to don’t I?
Your description was great. The idea of emissivity as 1 is kindof useful conceptually, but an approximation isn’t it?
By the way, I think you have changed my mind. There IS a greehouse effect! I get the mechanism now. By you explaining things clearly, and you actually were the first one to mention the EEH which is the key thing.
In my mind the EEH is a crucial mechanism, and not many people understand it, this is the first place it has become clear, thanks
It’s going to take a while to review and absorb it all.
It also makes sense why we need computer models to model all of this, it really is massively complicated.
I keep trying to poke holes, it just doesn’t *feel* right, but actually the science works doesn’t it?
For scientific disambiguation I meant “emissivity” of 1 for CO2 when limited to the IR wavelengths that CO2 is active in, not the whole spectrum.
An interesting analogy (I thought!) that occurred to me was this is very similar to what happens when regular clouds go across the sun?
We can actually feel the clouds blocking sunlight on our skin, we feel less hot. We no longer see the sun. The clouds have blocked both the visible light and the UV hitting our skin?
In the same way, considering the CO2 spectrum IR, there is a massive great cloud of CO2 molecules around the earth, and the upwelling CO2-window IR is all blocked/absorbed/reflected whatever pretty quickly?
And to be honest this discussion has clarified the power of that ‘blocking’ action for me thanks.
Thoughts on whether there is an energetic interaction between the various layers of Earth’s atmosphere, and how this might affect climate modelling ? –
What is the actual effective height of the ‘Top of Atmosphere (TOA)’ where IR from CO2 escapes to space?
Top of Troposphere?
Top of Stratosphere?
Top of Other-sphere?
There is a tradition of taking the TOA where IR escapes to outer space at the Top of Troposphere. This is a useful simplification, but is it also misleading?
Is there a higher layer than the Troposphere that could be more accurately considered the layer at which CO2 actually radiates IR into outer space, rather than just into the next highest layer within the atmosphere?
Would it be helpful to stratify the “Energy Budget” of the various layers of the earth’s atmosphere for more accurate climate modelling?
For example the Stratosphere –
Doesn’t the Stratosphere ‘Downwell’ IR to the Troposphere in the CO2 IR active window?
Does this down-welling IR need factoring into a Stratosphere – Troposphere IR-CO2 energetic feedback loop to work a more accurate rate of Tropospheric cooling?
Heat is only lost to outer space from the outermost CO2-IR-active layer isn’t it? (Exosphere?)
If heat is a measure of energy within a layer of the atmosphere, isn’t this consideration relevant?
Is there an analysis of such layers of Atmospheric layer ‘energy budgets’ modelled elsewhere ?
The Stratosphere is cooling for at least two reasons –
1. Less upwelling IR from CO2 in the Troposphere
2. More IR being irradiated outward to space due to EEH (Elevated Emission Height) effects within the Stratosphere itself, caused by an increased density of CO2 within the Stratosphere. The Stratosphere get’s warmer as it gets higher.
So more IR is irradiated ‘to space’ by a higher EEH, therefore cooling the Stratosphere?
As a result, doesn’t this mean the Stratosphere will feed back less energy to the Troposphere?
There are two mechanisms involved
1. A cooling Stratosphere emits less IR, both upward and downward.
2 Also, an ‘REH’ effect (Reduced Emission Height) within the Stratosphere at the bottom of the Stratosphere?
Because the CO2 in the Stratosphere has increased in density, just as in the Troposphere, this lowers the height at which it back-wells or downwells IR back to the Troposphere. But conversely to the Troposphere, lower in the Stratosphere means cooler, so this means less IR back to the Troposphere?
Won’t the decrease in downwelling IR from a cooling Stratosphere affect the overall energy budget within the Troposphere?
The following site has some very interesting observations.
The Troposphere seems to be expanding (and heating?), while the Stratosphere seems to be cooling and shrinking.
Might not any reduction in CO2-IR feedback energy from the Stratosphere to the Troposphere be a longer-term mitigation of less CO2-IR energy escaping the Troposphere due to an increase in the EEH of CO2 active molecules within the Troposphere?
https://www.theweathernetwork.com/ca/news/article/stratosphere-shrinking-due-to-greenhouse-gases-carbon-dioxide-emissions
Re IR dynamics between Troposphere and Stratosphere.
I think the previous comment (analysis of Heat/Energy/Flux at the Troposphere/Stratosphere boundary) may be valid because it uses a more detailed study of the energetic dynamics of the two most important interfaces in the Troposphere? As far as I can seen UV is NOT a part of the energetic flux at these boundaries.
Viz –
1. between the Earth’s Surface (ES) and the Troposphere (T)
2. between the Troposphere (T) and Stratosphere (S) (ok, with the Tropopause in between, but for this case ignored because Isothermal)
Of course the UV heating happens as a precursor to heat exchange between these boundaries. But as far as the dynamic energetic flux across the boundaries it can be ignored? Heat exchanges at these boundaries have much more to do with IR + evaporation and forced cooling.
It is taken as given in a steady-state (!) system each boundary will tend towards an equilibrium of energetic flux (entropy), if they go out of equilibrium some event/forcing will tend to happen to make them go back in balance.
And of course the forcing change we are interested in is the change in CO2 levels.
At the earth’s surface the exchanged are mediated by
Up flowing Energy from ES (IR + evaporation + others) = Down flowing energy from T (mostly IR)
And at the top of Troposphere the mechanisms are
Up flowing Energy from T (mostly IR) = Down flowing Energy from S (mostly IR)
Previous modelling that I have seen, such as the Earth Energy Budget tries to equate incidental UV from the sun that reaches the earth surface at 340Wm2 with the outgoing loss of IR at TOA to space. Is this detailed enough to create accurate climate change models?
I think equating incoming solar UV with outgoing IR is not detailed enough to describe all the processes going across the boundaries? The fundamental principle is correct of course, incoming UV must equal outgoing radiation from the earth as a whole, but the intermediary energetic transfer processes are more complex ?
I might be missing something very obvious of course, and happy to have that pointed out. But see no harm in asking questions, even if it goes to prove my point is wrong ?
The main point of all this, is the question, doesn’t reduced down-welling IR from a cooling Stratosphere tend to mediate against Tropospheric heating from reduced upwelling IR from the top of Troposphere?
It strikes me that the climate/weather effects might be very complicated indeed? Or even just minor? But very difficult to predict – which is why we need accurate computer modelling !
And quite where this leaves the overall energetic balance between incoming Solar Radiation and outgoing Terrestrial Radiation seems much less clear ….. except for the fact it must tend to balance .. !
Re upwelling OLR and Downwelling or (DLR) within the atmospheric column.
This 2013 paper examines OLR and DLR at 5 atmospheric levels.
It seems to use the top of Stratspohere as the TOA?
It concludes that the overall effect on OLR leaving Earth at TOA from increased CO2 is neutral, but that flux is redistributed due to temperature variations within the atmospheric column
(ie a varied, mixed bag of effects)
https://journals.ametsoc.org/view/journals/clim/26/5/jcli-d-12-00438.1.xml?tab_body=fulltext-display