Posted in Basic Science on November 17, 2011| 18 Comments »
We all would like this machine that creates time.
In the context of Science of Doom all my time has been diverted into work-related activities and I’m not sure when this will ease up.
Unless someone hands me this machine, and for a price well below market worth, I am not sure when my next post will take place.
I have lots of ideas, but like to do research and gain understanding before writing articles.
Normal service will eventually be resumed.
Posted in Atmospheric Physics, Basic Science on September 2, 2011| 184 Comments »
In a discussion a little while ago on What’s the Palaver? – Kiehl and Trenberth 1997, one of our commenters asked about the surface forcing and how it could possibly lead to anything like the IPCC-projected temperature change for doubling of CO2.
Following a request for clarification, he added:
..We first look at the RHS. We believe that the atmosphere will also increase in temperature by roughly the same amount, so there will be no change in the conductive term. The increase in the Radiative term is roughly 5.5W/m².
The increase in the evaporative term is much more difficult, but is believed to be in the range 2-7%/DegC. So the increase in the evaporative term is 1.5 to 5.5W/m², for a total change on the RHS of 7 to 11 W/m².
Since balance is an assumption, the LHS changed by the same amount. The surface sensitivity is therefore 0.095 to 0.15 DegC/W/m².
Note that this is the sensitivity to changes in Surface Forcing, whatever the source. It is NOT the response to Radiative Forcing – there is no response of the surface to Radiative Forcing, it can only respond to Sunlight and Back-Radiation.
[See the whole comment and exchange for the complete picture].
These are good questions and no doubt many people have similar ones. The definition of radiative forcing (see CO2 – An Insignificant Trace Gas? Part Seven – The Boring Numbers) is at the tropopause, which is the top of the troposphere (around 12km above the surface).
Why is it at the tropopause and not at the surface? The great Ramanathan explains (in his 1998 review paper):
..Manabe & Wetherald’s [1967] paper, which convincingly demonstrated that the CO2-induced surface warming is not solely determined by the energy balance at the surface but by the energy balance of the coupled surface-troposphere-stratosphere system.
The underlying concept of the Manabe-Wetherald model is that the surface and the troposphere are so strongly coupled by convective heat and moisture transport that the relevant forcing governing surface warming is the net radiative perturbation at the tropopause, simply known as radiative forcing.
In essence, the reason we consider the value at the tropopause is that it is the best value to tell us what will happen at the surface. It is now an idea established for over 40 years, although for some it might sound bizarre. So we will try and make sense of it here.
Here is a schematic originating in Ramanathan’s 1981 paper, but extracted here from his 1998 review paper:
From Ramanathan (1998)
Figure 1
The first thing to pay attention to is the right hand side – 1. CO2 direct surface heating – which is shown as 1.2 W/m².
The surface forcing from a doubling of CO2 is around 1 W/m² compared with around 4 W/m² at the tropopause. The surface forcing is a lot less than at the top of atmosphere!
Before too much joy sets in, let’s consider what these concepts represent. They are essentially idealized quantities, derived from considering the instantaneous change in concentrations of CO2.
As CO2 shows a steady increase year on year, the idea of doubling overnight is clearly not in accord with reality. However, it is a useful comparison point and helps to get many ideas straight. If instead we said, “CO2 increasing by 1% per year”, we would need to define a time period for this 1% annual increase, plus how long after the end before a new balance was restored. It wouldn’t make solving the problem any easier – and it would make the results harder to understand – by contrast GCM’s do consider a steadily rising CO2 level according to whatever scenario they are considering.
So, with the idea of an instantaneous doubling, if the surface increase in radiative forcing is less than the tropopause increase in radiative forcing, this must mean that the balance of energy is absorbed within the atmosphere. And also, we have to consider what happens as a result of the surface energy imbalance.
The numbers I use here are Ramanathan’s numbers from his 1981 paper. Later, and more accurate, numbers have been calculated but don’t affect the main points of this analysis. The reason for reviewing his analysis is because some (but not all) of the inherent responses of the climate system are explicitly calculated – making it easier to understand than the output of GCM.
The immediate result of this doubling of CO2 is a reduced emission of radiation (OLR = outgoing longwave radiation) from the climate system into space. See the Atmospheric Radiation and the “Greenhouse” Effect series for detailed explanations of why.
At the tropopause the OLR reduces by 3.1 W/m², and downward emission from the stratosphere into the troposphere increases by 1.2 W/m².
This results in a net forcing at the tropopause of 4.3 W/m². Most of the radiation from the atmosphere to the surface (as a result of more CO2) is absorbed by water vapor. So at the surface the DLR (downward long radiation) increases by only 1.2 W/m² – this is the (immediate) surface forcing. Here is a simple graphical explanation of why the OLR decreases and the DLR increases:
Figure 2 – Click for a larger image
The stratosphere cools and reaches a new radiative equilibrium. This reduces the downward emission from the stratosphere by a small amount. The new value of radiative forcing at the tropopause = 4.2 W/m².
The surface-troposphere warms until a new equilibrium is reached – the radiative forcing at the tropopause has returned to zero.
So let’s now consider the surface. Take a look at Figure 1 again. The values/ranges we will consider are calculated by a model. This doesn’t mean they are correct. It means that applying well-understood processes in a simplistic way gives us a “first order” result. The reason for assessing this kind of approach is because our mental models are usually less accurate than a calculated result which draws on well-understood physics.
As Ramanathan says in his 1998 paper:
As a caveat, the system we considered up to this point to elucidate the principles of warming is a highly simplified linear system. Its use is primarily educational and cannot be used to predict actual changes.
Process 1 is as already described – the surface forcing increases by just over 1 W/m². But the balance of 3 W/m² goes into heating the troposphere.
Process 2 – The warming of the troposphere results in increases downward radiation to the surface (because the hotter the body, the higher the radiation emitted). The calculated value is an additional 2.3 W/m², so the surface imbalance is now 3.5 W/m² and the surface temperature must increase in response. Upwards surface radiation and/or sensible and latent heat will increase to balance.
Process 3 – The surface emission of radiation increases at around 5.5 W/m² for every 1°C of surface temperature increase. But this is almost balanced by increased downward radiation from the atmosphere (“back radiation”). The net effect is only about 10% of the change in upward radiation. So latent heat and sensible heat increase to restore the energy balance, but this also heats the troposphere.
Process 4 – The tropospheric humidity increases. This increases the emissivity of the atmosphere near the surface, which increases the back radiation.
So essentially some cycles are reinforcing each other (=positive feedback). The question is about the value of the new equilibrium point.
From Ramanathan (1981)
Figure 3
In Ramanathan’s 1981 paper he gives some basic calculations before turning to GCM results. The basic calculations are quite interesting because one of the purposes of the paper was to explain why some model results of the day produced very small equilibrium temperature changes.
Sadly for some readers, a little maths is necessary to reproduce the result. It is simple maths because it is based on simple concepts – as already presented. As much as possible I follow the equation numbers and notations from Ramanathan’s 1981 paper.
Energy balance at an “average” surface:
Upward flux = Downward flux
→ LH + SH + F↑ = F↓ + S + ΔR ….[2]
where LH = latent heat, SH = sensible heat, F↑ = surface emitted upward radiation, F↓ = surface downward radiation from the atmosphere, S = solar radiation absorbed, ΔR = instantaneous change in energy absorbed at the surface due to an increase in CO2
And see note 1. We have simple formulas for the left hand side.
F↑ = σT4….[3a]
Latent heat and sensible heat flux have “bulk aerodynamic formulas” (note 2):
LH = ρLCDV (q*M – qS) ….[3b]
SH = ρcpCDV (TM – TS) ….[3c]
Where ρ = density of air = 1.3 kg/m, L = latent heat of water vapor = 2.5 x 106, CD = empirically determined coefficient ≈ 1.3 x10-3, V = average wind speed at some reference height above the surface ≈ 5 m/s, q*M = specific humidity at saturation at the surface temperature of the ocean, qS = specific humidity at the reference height, TM = temperature of the ocean at the surface, TS = temperature of the air at the reference height (typically 10m).
To give an idea of typical values, for every 1°C difference between the surface and the air at the reference height, SH = 8.5 W/m²K, and with a relative humidity of 80% at the reference height (and 100% at the ocean surface), LH = 55 W/m²K.
Now we consider changes.
TM‘ is the change in the surface temperature of the ocean as the result of the increased CO2, and similar notation for other changes in values. Missing out a few steps that you can read in the paper:
TM‘ = ΔR(0) + ΔF↓(2) + ΔF↓(3) ….[13]
[ ∂LH/∂TM + ∂SH/∂TM + 4σTM³] + [ ∂LH/∂TS + ∂SH/∂TS ].TS‘/TM‘
This probably seems a little daunting to a lot of readers.. so let’s explain it:
And the smaller the total under the line, the higher the increase in temperature. And there are two competing terms:
As an interesting comparison, Ramanathan reviewed the methods and results of Newell & Dopplick (1979) who found a changed surface temperature, Tm’ = 0.04 °C as a result of CO2 doubling. Effectively, very little change in surface temperature as a result of doubling of CO2.
Ramanathan states that the calculations of Newell & Dopplick had ignored the red terms and the green terms. Ignoring the red terms means that the heating of the atmosphere is ignored. Ignoring the green terms means that the effect of the ocean surface heating is inflated – if the ocean surface heats and the atmosphere just above somehow stayed the same then the heat transferred would be higher than if the atmospheric temperature also increased as a result. (Because heat transfer depends on temperature difference).
I expect that many people doing their own estimates will be working from similar assumptions.
Here is a graphic from Andrews et al (2009), reference and free link below, which shows the simplified idea:
From Andrews et al (2009)
Figure 4
The paper itself is well worth reading and perhaps will be the subject of another article at a later date.
I haven’t demonstrated that the surface will warm by 3°C for a doubling of CO2. But I hope I have demonstrated the complexity of the processes involved and why a simplistic calculation of how the surface responds immediately to the surface forcing is not the complete answer. It is nowhere near the complete answer.
The surface temperature change as a result of doubling of CO2 is, of course, a massively important question to answer. GCM’s are necessarily involved despite their limitations.
Re-iterating what Ramanathan said in his 1998 paper in case anyone thinks I am making a case for a 3°C surface temperature increase:
As a caveat, the system we considered up to this point to elucidate the principles of warming is a highly simplified linear system. Its use is primarily educational and cannot be used to predict actual changes.
Trace Gas Greenhouse Effect and Global Warming, V. Ramanathan, Ambio (1998)
The role of ocean-atmosphere interactions in the CO2 climate problem, V Ramanathan, Journal of Atmospheric Sciences (1981)
Thermal equilibrium of the atmosphere with a given distribution of atmospheric humidity, Manabe & Wetherald, Journal of Atmospheric Sciences (1967)
A Surface Energy Perspective on Climate Change, Andrews, Forster & Gregory, Journal of Climate (2009)
Note 1: The equation ignores the transfer of heat into the ocean depths
Note 2: The “bulk aerodynamic formulas” – as they have become known – are more usable versions of the fundamental equations of heat and water vapor flux. Upward sensible heat flux, SH = ρcp<wT>, where w = vertical velocity, T = temperature, so <wT> is the time average of the product of vertical velocity and temperature. However, turbulent motions are so rapid, changing on such short time intervals that measurement of these values is usually impossible (or requires intensive measurement with specialist equipment in one location). We can write,
w = <w> + w’, where <w> = mean vertical velocity and w’ = deviation of vertical velocity from the mean, likewise T = <T> + T’.
So:
<wT> = <w><T> + <w’ T’> or, Total = Mean + Eddy
Near the surface the mean vertical motion is very small compared with the turbulent vertical velocity and so the turbulent component, <w’ T’>, dominates. Therefore,
SH = cp ρ <w’ T’>
LH = L ρ <w’ T’>
where cp = specific heat capacity of air, ρ = density of air, L = latent heat of water vapor
By various thermodynamic arguments, and especially by lots of empirical measurements, an estimate of heat transfer can be made via the bulk aerodynamic formulas shown above, which use the average horizontal wind speed at the surface in conjunction with the coefficients of heat transfer, which are related to the friction term for the wind at the ocean surface.
Note 3: The calculation of each of the partial derivative terms is not shown in the paper, these are my calculations. I believe that ∂LH/∂TS = 0, most of the time – this is because if the atmosphere at the reference height is not saturated then an increase in the atmospheric temperature, TS, does not change the moisture flux, and therefore, does not change the latent heat. I might be wrong about this, and clearly some of the time this assumption I have made is not valid.
Posted in Atmospheric Physics, Basic Science on June 12, 2011| 418 Comments »
During a discussion following one of the six articles on Ferenc Miskolczi someone pointed to an article in E&E (Energy & Environment). I took a look and had a few questions.
The article is question is The Thermodynamic Relationship Between Surface Temperature And Water Vapor Concentration In The Troposphere, by William C. Gilbert from 2010. I’ll call this WG2010. I encourage everyone to read the whole paper for themselves.
Actually this E&E edition is a potential collector’s item because they announce it as: Special Issue – Paradigms in Climate Research.
The author comments in the abstract:
The key to the physics discussed in this paper is the understanding of the relationship between water vapor condensation and the resulting PV work energy distribution under the influence of a gravitational field.
Which sort of implies that no one studying atmospheric physics has considered the influence of gravitational fields, or at least the author has something new to offer which hasn’t previously been understood.
Note that I have added a WG prefix to the equation numbers from the paper, for ease of referencing:
First let’s start with the basic process equation for the first law of thermodynamics
(Note that all units of measure for energy in this discussion assume intensive properties, i.e., per unit mass):dU = dQ – PdV ….[WG1]
where dU is the change in total internal energy of the system, dQ is the change in thermal energy of the system and PdV is work done to or by the system on the surroundings.
This is (almost) fine. The author later mixes up Q and U. dQ is the heat added to the system. dU is change in internal energy which includes the thermal energy.
But equation (1) applies to a system that is not influenced by external fields. Since the atmosphere is under the influence of a gravitational field the first law equation must be modified to account for the potential energy portion of internal energy that is due to position:
dU = dQ + gdz – PdV ….[WG2]
where g is the acceleration of gravity (9.8 m/s²) and z is the mass particle vertical elevation relative to the earth’s surface.
[Emphasis added. Also I changed “h” into “z” in the quotes from the paper to make the equations easier to follow later].
This equation is incorrect, which will be demonstrated later.
The thermal energy component of the system (dQ) can be broken down into two distinct parts: 1) the molecular thermal energy due to its kinetic/rotational/ vibrational internal energies (CvdT) and 2) the intermolecular thermal energy resulting from the phase change (condensation/evaporation) of water vapor (Ldq). Thus the first law can be rewritten as:
dU = CvdT + Ldq + gdz – PdV ….[WG3]
where Cv is the specific heat capacity at constant volume, L is the latent heat of condensation/evaporation of water (2257 J/g) and q is the mass of water vapor available to undergo the phase change.
Ouch. dQ is heat added to the system, and it is dU which is the internal energy which should be broken down into changes in thermal energy (temperature) and changes in latent heat. This is demonstrated later.
Later, the author states:
This ratio of thermal energy released versus PV work energy created is the crux of the physics behind the troposphere humidity trend profile versus surface temperature. But what is it that controls this energy ratio? It turns out that the same factor that controls the pressure profile in the troposphere also controls the tropospheric temperature profile and the PV/thermal energy ratio profile. That factor is gravity. If you take equation (3) and modify it to remove the latent heat term, and assume for an adiabatic, ideal gas system CpT = CvT + PV, you can easily derive what is known in the various meteorological texts as the “dry adiabatic lapse rate”:
dT/dz = –g/Cp = 9.8 K/km ….[WG5]
[Emphasis added]
Unfortunately, with his starting equations you can’t derive this result.
What I am talking about?
Most textbooks on atmospheric physics include some derivation of the lapse rate. We consider a parcel of air of one mole. (Some terms are defined slightly differently to WG2010 – note 1).
There are 5 basic equations:
The hydrostatic equilibrium equation:
dp/dz = -ρg ….[1]
where p = pressure, z = height, ρ = density and g = acceleration due to gravity (=9.8 m/s²)
The ideal gas law:
pV = RT ….[2]
where V = volume, R = the gas constant, T = temperature in K, and this form of the equation is for 1 mole of gas
The equation for density:
ρ = M/V ….[3]
where M = mass of one mole
The First Law of Thermodynamics:
dU = dQ + dW ….[4]
where dU = change in internal energy, dQ = heat added to the system, dW = work added to the system
..rewritten for dry atmospheres as:
dQ = CvdT + pdV ….[4a]
where Cv = heat capacity at constant volume (for one mole), dV = change in volume
And the (less well-known) equation which links heat capacity at constant volume with heat capacity at constant pressure (derived from statistical thermodynamics and experimentally verifiable):
Cp = Cv + R ….[5]
where Cp = heat capacity (for one mole) at constant pressure
With an adiabatic process no heat is transferred between the parcel and its surroundings. This is a reasonable assumption with typical atmospheric movements. As a result, we set dQ = 0 in equation 4 & 4a.
Using these 5 equations we can solve to find the dry adiabatic lapse rate (DALR):
dT/dz = -g/cp ….[6]
where dT/dz = the change in temperature with height (the lapse rate), g = acceleration due to gravity, and cp = specific heat capacity (per unit mass) at constant pressure
dT/dz ≈ -9.8 K/km
Knowing that many readers are not comfortable with maths I show the derivation in The Maths Section at the end.
And also for those not so familiar with maths & calculus, the “d” in front of a term means “change in”. So, for example, “dT/dz” reads as: “the change in temperature as z changes”.
There are two basic problems with his fundamental equations:
A sign error might seem unimportant but given the claims later in the paper (with no explanation of how these claims were calculated) it is quite possible that the wrong equation was used to make these calculations.
These problems will now be explained.
Because William Gilbert mixes up internal energy and heat added, the result is a sign error. Consult a standard thermodynamics textbook and the first law of thermodynamics will be represented something like this:
dU = dQ + dW
Which in words means:
The change in internal energy equals the heat added plus the work done on the system.
And if we talk about dW as the work done by the system then the sign in front of dW will change. So, if we rewrite the above equation:
dU = dQ – pdV
By the time we get to [WG3] we have two problems.
Here is [WG3] for reference:
dU = CvdT + Ldq + gdz – PdV ….[WG3]
The first problem is that for adiabatic process, no heat is added to (or removed from) the system. So dQ = 0. The author says dU = 0 and makes dQ = change in internal energy (=CvdT + Ldq).
Here is the demonstration of the problem using his equation..
If we have no phase change then Ldq = 0. The gdz term is a mistake – for later consideration – but if we consider an example with no change in height in the atmosphere, we would have (using his equation):
CvdT – PdV = 0 ….[WG3a]
So if the parcel of air expands, doing work on its environment, what happens to temperature?
dV is positive because the volume is increasing. So to keep the equation valid, dT must be positive, which means the temperature must increase.
This means that as the parcel of air does work on its environment, using up energy, its temperature increases – adding energy. A violation of the first law of thermodynamics.
Hopefully, everyone can see that this is not correct. But it is the consequence of the incorrectly stated equation. In any case, I will use both the flawed and the fixed version to demonstrate the second problem.
This problem won’t appear so obvious, which is probably why William Gilbert makes the mistake himself.
In the list of 5 equations, I wrote:
dQ = CvdT + pdV ….[4a]
This is for dry atmospheres, to keep it simple (no Ldq term for water vapor condensing). If you check the Maths Section at the end, you can see that using [4a] we get the result that everyone agrees with for the lapse rate.
I didn’t write:
dQ = CvdT + Mgdz + pdV ….[should this instead be 4a?]
[Note that my equations consider 1 mole of the atmosphere rather than 1 kg which is why “M” appears in front of the gdz term].
So how come I ignored the effect of gravity in the atmosphere yet got the correct answer? Perhaps the derivation is wrong?
The effect of gravity already shows itself via the increase in pressure as we get closer to the surface of the earth.
Atmospheric physics has not been ignoring the effect of gravity and making elementary mistakes. Now for the proof.
If you consult the Maths Section, near the end we have reached the following equation and not yet inserted the equation for the first law of thermodynamics:
pdV – Mgdz = (Cp-Cv)dT ….[10]
Using [10] and “my version” of the first law I successfully derive dT/dz = -g/cp (the right result). Now we will try using William Gilbert’s equation [WG3], with Ldq = 0, to derive the dry adiabatic lapse rate.
0 = CvdT + gdz – PdV ….[WG3b]
and rewriting for one mole instead of 1 kg (and using my terms, see note 1):
pdV = CvdT + Mgdz ….[WG3c]
Inserting WG3c into [10]:
CvdT + Mgdz – Mgdz = (Cp-Cv)dT ….[11]
which becomes:
Cv = (Cp-Cv) ↠ Cp = Cv/2 ….[11a]
A New Paradigm indeed!
Now let’s fix up the sign error in WG3 and see what result we get:
0 = CvdT + gdz + PdV ….[WG3d]
and again rewriting for one mole instead of 1 kg (and again using my terms, see note 1):
pdV = -CvdT – Mgdz ….[WG3e]
Inserting WG3e into [10]:
-CvdT – Mgdz – Mgdz = (Cp-Cv)dT ….[12]
which becomes:
-CvdT – 2Mgdz = CpdT – CvdT ….[12a]
and canceling the -CvdT term from each side:
-2Mgdz = CpdT ….[12b]
So:
dT/dz = -2Mg/Cp, and because specific heat capacity, cp = Cp/M
dT/dz = -2g/cp ….[12c]
The result of “correctly including gravity” is that the dry adiabatic lapse rate ≈ -19.6 K/km.
Note the factor of 2. This is because we are now including gravity twice. The pressure in the atmosphere reduces as we go up – this is because of gravity. When a parcel of air expands due to its change in height, it does work on its surroundings and therefore reduces in temperature – adiabatic expansion. Gravity is already taken into account with the hydrostatic equation.
The author says:
As we shall see, PV work energy is very important to the understanding of this thermodynamic behavior of the atmosphere, and the thermodynamic role of water vapor condensation plays an important part in this overall energy balance. But this is unfortunately often overlooked or ignored in the more recent climate science literature. The atmosphere is a very dynamic system and cannot be adequately analyzed using static, steady state mental models that primarily focus only on thermal energy.
Emphasis added. This is an unproven assertion because it comes with no references.
In the next stage of the “physics” section, the author doesn’t bother with any equations, making it difficult to understand exactly what he is claiming.
Keeping this gravitational steady state equilibrium in mind, let’s look again at what happens when latent heat is released (condensation) during air parcel ascension.
Latent heat release immediately increases the parcel temperature. But that also results in rapid PV expansion which then results in a drop in parcel temperature. Buoyancy results and the parcel ascends and is driven by the descending pressure profile created by gravity.
The rate of ascension, and the parcel temperature, is a function of the quantity of latent heat released and the PV work needed to overcome the gravitational field to reach a dynamic equilibrium. The more latent heat that is released, the more rapid the expansion / ascension. And the more rapid the ascension, the more rapid is the adiabatic cooling of the parcel. Thus the PV/thermal energy ratio should be a function of the amount of latent heat available for phase conversion at any given altitude. The corresponding physics shows the system will try to force the convecting parcel to approach the dry adiabatic or “gravitational” lapse rate as internal latent heat is released.
For the water vapor remaining uncondensed in the parcel, saturation and subsequent condensation will occur at a more rapid rate if more latent heat is released. In fact if the cooling rate is sufficiently large, super saturation can occur, which can then cause very sudden condensation in greater quantity. Thus the thermal/PV energy ratio is critical in determining the rate of condensation occurring. The higher this ratio, the more complete is the condensation in the parcel, and the lower the specific humidity will be at higher elevations.
I tried (unsuccessfully) to write down some equations to reflect the above paragraphs. The correct approach for the author would be:
One point I think the author is claiming is that the speed of ascent is a critical factor. Yet the equation for the moist adiabatic lapse rate doesn’t allow for a function of time in the equation.
The (standard) equation has the form (note 2):
dT/dz = g/cp {[1+Lq*/RT]/[1+βLq*/cp]} ….[13]
where q* is the saturation specific humidity and is a function of p & T (i.e. not a constant), and β = 0.067/°C. (See, for example: Atmosphere, Ocean & Climate Dynamics by Marshall & Plumb, 2008)
And this means that if the ascent is – for example – twice as fast, the amount of water vapor condensed at any given height will still be the same. It will happen in half the time, but why will this change any of the thermodynamics of the process?
It might, but it’s not clearly stated, so who can determine the “new physics”?
I can see that something else is claimed to do with the ratio CvdT /pV but I don’t know what it is, or what is behind the claim.
Writing the equations down is important so that other people can evaluate the claim.
And the final “result” of the hand waving is what appears to be the crux of the paper – more humidity at the surface will cause so much “faster” condensation of the moisture that the parcel of air will be drier higher up in the atmosphere. (Where “faster” could mean dT/dt, or could mean dT/dz).
Assuming I understood the claim of the paper correctly it has not been proven from any theoretical considerations. (And I’m not sure I have understood the claim correctly).
The heading is actually “Empirical Observations to Verify the Physics”. A more accurate title is “Empirical Observations”.
The author provides 3 radiosonde profiles from Miami. Here is one example:
From Gilbert (2010)
Figure 1 – “Thermal adiabat” in the legend = “moist adiabat”
With reference to the 3 profiles, a higher surface humidity apparently leads to complete condensation at a lower altitude.
This is, of course, interesting. This would mean a higher humidity at the surface leads to a drier upper troposphere.
But it’s just 3 profiles. From one location on two different days. Does this prove something or should a few more profiles be used?
A few statements that need backing up:
The lower troposphere lapse rate decreases (slower rate of cooling) with increasing system surface humidity levels, as expected. But the differences in lapse rate are far less than expected based on the relative release of latent heat occurring in the three systems.
What equation determines “than expected”? What result was calculated vs measured? What implications result?
The amount of PV work that occurs during ascension increases markedly as the system surface humidity levels increase, especially at lower altitudes..
How was this calculated? What specifically is the claim? The equation 4a, under adiabatic conditions, with the additional of latent heat reads like this:
CvdT + Ldq + pdV = 0 ….[4a]
Was this equation solved from measured variables of pressure, temperature & specific humidity?
Latent heat release is effectively complete at 7.5 km for the highest surface humidity system (20.06 g/kg) but continues up to 11 km for the lower surface humidity systems (18.17 and 17.07 g/kg). The higher humidity system has seen complete condensation at a lower altitude, and a significantly higher temperature (−17 ºC) than the lower humidity systems (∼ −40 ºC) despite the much greater quantity of latent heat released.
How was this determined?
If it’s true, perhaps the highest humidity surface condition ascended into a colder air front and therefore lost all its water vapor due to the lower temperature?
Why is this (obvious) possibility not commented on or examined??
The radiosonde profiles in the paper are not necessarily following one “parcel” of air.
Consider a parcel of air near saturation at the surface. It rises, cools and soon reaches saturation. So condensation takes place, the release of latent heat causes the air to be more buoyant and so it keeps rising. As it rises water vapor is continually condensing and the air (of this parcel) will be at 100% relative humidity.
Yet relative humidity doesn’t increase with height, it reduces:
From Marshall & Plumb (2008)
Figure 2
Standard textbook stuff on typical temperature profiles vs dry and moist adiabatic profiles:
From Marshall & Plumb (2008)
Figure 3
And explaining why the atmosphere under convection doesn’t always follow a moist adiabat:
From Marshall & Plumb (2008)
Figure 4
The atmosphere has descending dry air as well as rising moist air. Mixing of air takes place, which is why relative humidity reduces with height.
The “theory section” of the paper is not a theory section. It has a few equations which are incorrect, followed by some hand-waving arguments that might be interesting if they were turned into equations that could be examined.
It is elementary to prove the errors in the few equations stated in the paper. If we use the author’s equations we derive a final result which contradicts known fundamental thermodynamics.
The empirical results consist of 3 radiosonde profiles with many claims that can’t be tested because the method by which these claims were calculated is not explained.
If it turned out that – all other conditions remaining the same – higher specific humidity at the surface translated into a drier upper troposphere, this would be really interesting stuff.
But 3 radiosonde profiles in support of this claim is not sufficient evidence.
There are a few ways to get to the final result – this is just one approach. Refer to the original 5 equations under the heading: The Equations for the Lapse Rate.
From [2], pV = RT, differentiate both sides with respect to T:
↠ d(pV)/dT = d(RT)/dT
The left hand side can be expanded as: V.dp/dT + p.dV/dT, and the right hand side = R (as dT/dT=1).
↠ Vdp + pdV = RdT ….[7]
Insert [5], Cp = Cv + R, into [7]:
Vdp + pdV = (Cp-Cv)dT ….[8]
From [1] & [3]:
Vdp = -Mgdz ….[9]
Insert [9] into [8]:
pdV – Mgdz = (Cp-Cv)dT ….[10]
From 4a, under adiabatic conditions, dQ = 0, so CvdT + pdV = 0, and substituting into [10]”
-CvdT – Mgdz = CpdT – CvdT
and adding CvdT to both sides:
-Mgdz = CpdT, or dT/dz = -Mg/Cp ….[11]
and specific heat capacity, cp = Cp/M, so:
dT/dz = g /cp ….[11a]
The correct result, stated as equation [6] earlier.
Note 1: Definitions in equations. WG2010 has:
Note 2: The moist adiabatic lapse rate is calculated using the same approach but with an extra term, Ldq, in equation 4a, which accounts for the latent heat released as water vapor condenses.
Posted in Basic Science, Climate History on June 5, 2011| 56 Comments »
In Part One we saw:
But we only touched on the satellite data (shown in Trenberth, Fasullo & Smith in comparison to some reanalysis projects).
Wentz & Schabel (2000) reviewed water vapor, sea surface temperature and air temperature from various satellites. On water vapor they said:
..whereas the W [water vapor] data set is a relatively new product beginning in 1987 with the launch of the special sensor microwave imager (SSM/I), a multichannel microwave radiometer. Since 1987 four more SSM/I’s have been launched, providing an uninterrupted 12-year time series. Imaging radiometers before SSM/I were poorly calibrated, and as a result early water-vapour studies (7) were unable to address climate variability on interannual and decadal timescales.
The advantage of SSMI is that it measures the 22 GHz water vapor line. Unlike measurements in the IR around 6.7 μm (for example the HIRS instrument) which require some knowledge of temperature, the 22 GHz measurement is a direct reflection of water vapor concentration. The disadvantage of SSMI is that it only works over the ocean because of the low ocean emissivity (but variable land emissivity). And SSMI does not provide any vertical resolution of water vapor concentration, only the “total precipitable water vapor” (TPW) also known as “column integrated water vapor” (IWV).
The algorithm, verification and error analysis for the SSMI can be seen in Wentz’s 1997 JGR paper: A well-calibrated ocean algorithm for special sensor microwave / imager.
Here is Wentz & Schabel’s graph of IWV over time (shown as W in their figure):
From Wentz & Schabel (2000)
Figure 1 – Region captions added to each graph
They calculate, for the short period in question (1988-1998):
Soden et al (2005) take the dataset a little further and compare it to model results:
From Soden et al (2005)
Figure 2
They note the global trend of 1.4 ± 0.78 %/decade.
As their paper is more about upper tropospheric water vapor they also evaluate the change in channel 12 of the HIRS instrument (High Resolution Infrared Radiometer Sounder):
The radiance channel centered at 6.7 μm (channel 12) is sensitive to water vapor integrated over a broad layer of the upper troposphere (200 to 500 hPa) and has been widely used for studies of upper tropospheric water vapor. Because clouds strongly attenuate the infrared radiation, we restrict our analysis to clear-sky radiances in which the upwelling radiation in channel 12 is not affected by clouds.
The change in radiance from channel 12 is approximately zero over the time period, which for technical reasons (see note 1) corresponds to roughly constant relative humidity in that region over the period from the early 1980’s to 2004. You can read the technical explanation in their paper, but as we are focusing on total water vapor (IWV) we will leave a discussion over UTWV for another day.
Durre et al (2009) updated radiosonde trends in their 2009 paper. There is a lengthy extract from the paper in note 2 (end of article) to give insight into why radiosonde data cannot just be taken “as is”, and why a method has to be followed to identify and remove stations with documented or undocumented instrument changes.
Importantly they note, as with Ross & Elliott 2001:
..Even though the stations were located in many parts of the globe, only a handful of those that qualified for the computation of trends were located in the Southern Hemisphere. Consequently, the trend analysis itself was restricted to the Northern Hemisphere as in that of RE01..
Here are their time-based trends:
From Durre et al (2009)
Figure 3
And a map of trends:
From Durre et al (2009)
Figure 4
Note the sparse coverage of the oceans and also the land regions in Africa and Asia, except China.
And their table of results:
From Durre et al (2009)
Figure 5
A very interesting note on the effect of their removal of stations based on detection of instrument changes and other inhomogeneities:
Compared to trends based on unadjusted PW data (not shown), the trends in Table 2 are somewhat more positive. For the Northern Hemisphere as a whole, the unadjusted trend is 0.22 mm/decade, or 0.23 mm/decade less than the adjusted trend.
This tendency for the adjustments to yield larger increases in PW is consistent with the notion that improvements in humidity measurements and observing practices over time have introduced an artificial drying into the radiosonde record (e.g., RE01).
Brown et al (2007) evaluated data from the Topex Microwave Radiometer (TMR). This is included on the Topex/Poseiden oceanography satellite and is dedicated to measuring the integrated water vapor content of the atmosphere. TMR is nadir pointing and measures the radiometric brightness temperature at 18, 21 and 37 GHz. As with SSMI, it only provides data over the ocean.
For the period of operation of the satellite (1992 – 2005) they found the trend of 0.90 ± 0.06 mm/decade:
From Brown et al (2007)
Figure 6 – Click for a slightly larger view
And a map view:
From Brown et al (2007)
Figure 7
Paltridge, Arking & Pook (2009) – P09 – take a look at the NCEP/NCAR reanalysis project from 1973 – 2007. They chose 1973 as the start date for the reasons explained in Part One – Elliott & Gaffen have shown that pre-1973 data has too many problems. They focus on humidity data below 500mbar as the measurement of humidity at higher altitudes and lower temperatures are more prone to radiosonde problems.
The NCEP/NCAR data shows positive trends below 850 mbar (=hPa) in all regions, negative trends above 850 mbar in the tropics and midlatitudes, and negative trends above 600 mbar in the northern midlatitudes.
Here are the water vapor trends vs height (pressure) for both relative humidity and specific humidity:
From Paltridge et al (2009)
Figure 8
And here is the map of trends:
from Paltridge et al (2009)
Figure 9
They comment on the “boundary layer” vs “free troposphere” issue.. In brief the boundary layer is that “well-mixed layer” close to the surface where the friction from the ground slows down the atmospheric winds and results in more turbulence and therefore a well-mixed layer of atmosphere. This is typically around 300m to 1000m high (there is no sharp “cut off”). At the ocean surface the atmosphere tends to be saturated (if the air is still) and so higher temperatures lead to higher specific humidities. (See Clouds and Water Vapor – Part Two if this is a new idea). Therefore, the boundary layer is uncontroversially expected to increase its water vapor content with temperature increases. It is the “free troposphere” or atmosphere above the boundary layer where the debate lies.
They comment:
It is of course possible that the observed humidity trends from the NCEP data are simply the result of problems with the instrumentation and operation of the global radiosonde network from which the data are derived.
The potential for such problems needs to be examined in detail in an effort rather similar to the effort now devoted to abstracting real surface temperature trends from the face-value data from individual stations of the international meteorological networks.
In the meantime, it is important that the trends of water vapor shown by the NCEP data for the middle and upper troposphere should not be “written off” simply on the basis that they are not supported by climate models—or indeed on the basis that they are not supported by the few relevant satellite measurements.
There are still many problems associated with satellite retrieval of the humidity information pertaining to a particular level of the atmosphere— particularly in the upper troposphere. Basically, this is because an individual radiometric measurement is a complicated function not only of temperature and humidity (and perhaps of cloud cover because “cloud clearing” algorithms are not perfect), but is also a function of the vertical distribution of those variables over considerable depths of atmosphere. It is difficult to assign a trend in such measurements to an individual cause.
Since balloon data is the only alternative source of information on the past behavior of the middle and upper tropospheric humidity and since that behavior is the dominant control on water vapor feedback, it is important that as much information as possible be retrieved from within the “noise” of the potential errors.
So what has P09 added to the sum of knowledge? We can already see the NCEP/NCAR trends in Trends and variability in column-integrated atmospheric water vapor by Trenberth et al from 2005.
Did the authors just want to take the reanalysis out of the garage, drive it around the block a few times and park it out front where everyone can see it?
No, of course not!
– I hear all the NCEP/NCAR believers say.
One of our commenters asked me to comment on Paltridge’s reply to Dessler (which was a response to Paltridge..), and linked to another blog article. It seems like even the author of that blog article is confused about NCEP/NCAR. This reanalysis project (as explained in Part One), is a model output not a radiosonde dataset:
Humidity is in category B – ‘although there are observational data that directly affect the value of the variable, the model also has a very strong influence on the value ‘
And for those people who have a read of Kalnay’s 1996 paper describing the project they will see that with the huge amount of data going into the model, the data wasn’t quality checked by human inspection on the way in. Various quality control algorithms attempt to (automatically) remove “bad data”.
This is why we have reviewed Ross & Elliott (2001) and Durre et al (2009). These papers review the actual radiosonde data and find increasing trends in IWV. They also describe in a lot of detail what kind of process they had to go through to produce a decent dataset. The authors of both papers also both explained that they could only produce a meaningful trend for the northern hemisphere. There is not enough quality data for the southern hemisphere to even attempt to produce a trend.
And Durre et al note that when they use the complete dataset the trend is half that calculated with problematic data removed.
This is the essence of the problem with Paltridge et al (2009)
Why is Ross & Elliot (2001) not reviewed and compared? If Ross & Elliott found that Southern Hemisphere trends could not be calculated because of the sparsity of quality radiosonde data, why doesn’t P09 comment on that? Perhaps Ross & Elliott are wrong. But no comment from P09. (Durre et al find the same problem with SH data, and probably too late for P09 but not too late for the 2010 comments the authors have been making).
In The Mass of the Atmosphere: A Constraint on Global Analyses, Trenberth & Smith pointed out clear problems with NCEP/NCAR vs ERA-40. Perhaps Trenberth and Smith are wrong. Or perhaps there is another way to understand these results. But no comment on this from P09.
P09 comment on the issues with satellite humidity retrieval for different layers of the atmosphere but no comment on the results from the microwave SSMI which has a totally different algorithm to retrieve IWV. And it is important to understand that they haven’t actually demonstrated a problem with satellite measurements. Let’s review their comment:
In the meantime, it is important that the trends of water vapor shown by the NCEP data for the middle and upper troposphere should not be “written off” simply on the basis that they are not supported by climate models—or indeed on the basis that they are not supported by the few relevant satellite measurements.
The reader of the paper wouldn’t know that Trenberth & Smith have demonstrated an actual reason for preferring ERA-40 (if any reanalysis is to be used).
The reader of the paper might understand “a few relevant satellite measurements” as meaning there wasn’t much data from satellites. If you review figure 4 you can see that the quality radiosonde data is essentially mid-latitude northern hemisphere land. Satellites – that is, multiple satellites with different instruments at different frequencies – have covered the oceans much much more comprehensively than radiosondes. Are the satellites all wrong?
The reader of the paper would think that the dataset has been apparently ditched because it doesn’t fit climate models.
This is probably the view of Paltridge, Arking & Pook. But they haven’t demonstrated it. They have just implied it.
Dessler & Davis responded to P09. They plot some graphs from 1979 to present. The reason for plotting graphs from 1979 is because this is when the satellite data was introduced. And all of the reanalysis projects, except NCEP/NCAR incorporated satellite humidity data. (NCEP/NCAR does incorporate satellite data for some other fields).
Basically when data from a new source is introduced, even if it is more accurate, it can introduce spurious trends and even in opposite direction to the real trends. This was explained in Part One under the heading Comparing Reanalysis of Humidity. So trend analysis usually takes place over periods of consistent data sources.
This figure contrasts short term relationships between temperature and humidity with long term relationships:
From Dessler & Davis (2010)
Figure 10
If the blog I referenced earlier is anything to go by, the primary reason for producing this figure has been missed. And as that blog article seemed to not comprehend that NCEP/NCAR is a reanalysis (= model output) it’s not so surprising.
Dessler & Davis said:
There is poorer agreement among the reanalyses, particularly compared to the excellent agreement for short‐term fluctuations. This makes sense: handling data inhomogeneities will introduce long‐term trends in the data but have less effect on short‐term trends. This is why long term trends from reanalyses tend to be looked at with suspicion [e.g., Paltridge et al., 2009; Thorne and Vose, 2010; Bengtsson et al., 2004].
[Emphasis added]
They are talking about artifacts of the model (NCEP/NCAR). In the short term the relationship between humidity and temperature agree quite well among the different reanalyses. But in the longer term NCEP/NCAR doesn’t – demonstrating that it is likely introducing biases.
The alternative, as Dessler & Davis explain, is that there is somehow an explanation for a long term negative feedback (temperature and water vapor) with a short term positive feedback.
If you look around the blog world, or at say, Professor Lindzen you don’t find this. You find arguments about why short term feedback is negative. Not an argument that short term is positive and yet long term is negative.
I agree that many people say: “I don’t know, it’s complicated, perhaps there is a long term negative feedback..” and I respect that point of view.
But in the blog article pointed to me by our commenter in Part One, the author said:
JGR let some decidedly unscientific things slip into that Dessler paper. One of the reasons provided is nothing more than a form of argument from ignorance: “there’s no theory that explains why the short term might be different to the long term”.
Why would any serious scientist admit that they don’t have the creativity or knowledge to come up with some reasons, and worse, why would they think we’d find that ignorance convincing?
..It’s not that difficult to think of reasons why it’s possible that humidity might rise in the short run, but then circulation patterns or other slower compensatory effects shift and the long run pattern is different. Indeed they didn’t even have to look further than the Paltridge paper they were supposedly trying to rebut (see Garth’s writing below). In any case, even if someone couldn’t think of a mechanism in a complex unknown system like our climate, that’s not “a reason” worth mentioning in a scientific paper.
The point that seems to have been missed is this is not a reason to ditch the primary dataset but instead a reason why NCEP/NCAR is probably flawed compared with all the other reanalyses. And compared with the primary dataset. And compared with multiple satellite datasets.
This is the issue with reanalyses. They introduce spurious biases. Bengsston explained how (specifically for ERA-40). Trenberth & Smith have already demonstrated it for NCEP/NCAR. And now Dessler & Davis have simply pointed out another reason for taking that point of view.
The blog writer thinks that Dessler is trying to ditch the primary dataset because of an argument from ignorance. I can understand the confusion.
It is still confusion.
One last point to add is that Dessler & Davis also added the very latest in satellite water vapor data – the AIRS instrument from 2003. AIRS is a big step forward in satellite measurement of water vapor, a subject for another day.
AIRS also shows the same trends as the other reanalyses and different from NCEP/NCAR.
Before reaching the conclusion I want to throw a scenario out there. It is imaginary.
Suppose that there were two sources of data for temperature over the surface of the earth – temperature stations and satellite. Suppose the temperature stations were located mainly in mid-latitude northern hemisphere locations. Suppose that there were lots of problems with temperature stations – instrument changes & environmental changes close to the temperature stations (we will call these environmental changes “UHI”).
Suppose the people who had done the most work analyzing the datasets and trying to weed out the real temperature changes from the spurious ones had demonstrated that the temperature had decreased over northern hemisphere mid-latitudes. And that they had claimed that quality southern hemisphere data was too “thin on the ground” to really draw any conclusions from.
Suppose that satellite data from multiple instruments, each using different technology, had also demonstrated that temperatures were decreasing over the oceans.
Suppose that someone fed the data from the (mostly NH) land-based temperature stations – without any human intervention on the UHI and instrument changes – into a computer model.
And suppose this computer model said that temperatures were increasing.
Imagine it, for a minute. I think we can picture the response.
And yet, this is a similar situation that we are confronted with on integrated water vapor (IWV). I have tried to think of a reason why so many people would be huge fans of this particular model output. I did think of one, but had to reject it immediately as being ridiculous.
I hope someone can explain why NCEP/NCAR deserves the fan club it has currently built up.
Radiosonde datasets, despite their problems, have been analyzed. The researchers have found positive water vapor trends for the northern hemisphere with these datasets. As far as I know, no one has used radiosonde datasets to find the opposite.
Radiosonde datasets provide excellent coverage for mid-latitude northern hemisphere land, and, with a few exceptions, poor coverage elsewhere.
Satellites, using IR and microwave, demonstrate increasing water vapor over the oceans for the shorter time periods in which they have been operating.
Reanalysis projects have taken in various data sources and, using models, have produced output values for IWV (total water vapor) with mixed results.
Reanalysis projects all have the benefit of convenience, but none are perfect. The dry mass of the atmosphere, which should be constant within noise errors unless a new theory comes along, demonstrates that NCEP/NCAR is worse than ERA-40.
ERA-40 demonstrates increasing IWV. NCEP/NCAP demonstrates negative IWV.
Some people have taken NCEP/NCAR for a drive around the block and parked it in front of their house and many people have wandered down the street to admire it. But it’s not the data. It’s a model.
Perhaps Paltridge, Arking or Pook can explain why NCEP/NCAR is a quality dataset. Unfortunately, their paper doesn’t demonstrate it.
It seems that some people are really happy if one model output or one dataset or one paper says something different from what 5 or 10 or 100 others are saying. If that makes you, the reader, happy, then at least the world has less deaths from stress.
In any field of science there are outliers.
The question on this blog at least, is what can be proven, what can be demonstrated and what evidence lies behind any given claim. From this blog’s perspective, the fact that outliers exist isn’t really very interesting. It is only interesting to find out if in fact they have merit.
In the world of historical climate datasets nothing is perfect. It seems pretty clear that integrated water vapor has been increasing over the last 20-30 years. But without satellites, even though we have a long history of radiosonde data, we have quite a limited dataset geographically.
If we can only use radiosonde data perhaps we can just say that water vapor has been increasing over northern hemisphere mid-latitude land for nearly 40 years. If we can use satellite as well, perhaps we can say that water vapor has been increasing everywhere for over 20 years.
If we can use the output from reanalysis models and do a lucky dip perhaps we can get a different answer.
And if someone comes along, analyzes the real data and provides a new perspective then we can all have another review.
On the Utility of Radiosonde Humidity Archives for Climate Studies, Elliot & Gaffen, Bulletin of the American Meteorological Society (1991)
Relationships between Tropospheric Water Vapor and Surface Temperature as Observed by Radiosondes, Gaffen, Elliott & Robock, Geophysical Research Letters(1992)
Column Water Vapor Content in Clear and Cloudy Skies, Gaffen & Elliott, Journal of Climate (1993)
On Detecting Long Term Changes in Atmospheric Moisture, Elliot, Climate Change (1995)
Tropospheric Water Vapor Climatology and Trends over North America, 1973-1993, Ross & Elliot, Journal of Climate (1996)
An assessment of satellite and radiosonde climatologies of upper-tropospheric water vapor, Soden & Lanzante, Journal of Climate (1996)
The NCEP/NCAR 40-year Reanalysis Project, Kalnay et al, Bulletin of the American Meteorological Society (1996)
Precise climate monitoring using complementary satellite data sets, Wentz & Schabel, Nature (2000)
Radiosonde-Based Northern Hemisphere Tropospheric Water Vapor Trends, Ross & Elliott, Journal of Climate (2001)
An analysis of satellite, radiosonde, and lidar observations of upper tropospheric water vapor from the Atmospheric Radiation Measurement Program, Soden et al, Journal of Geophysical Research (2005)
The Radiative Signature of Upper Tropospheric Moistening, Soden et al, Science (2005)
The Mass of the Atmosphere: A Constraint on Global Analyses, Trenberth & Smith, Journal of Climate (2005)
Trends and variability in column-integrated atmospheric water vapor, Trenberth et al, Climate Dynamics (2005)
Can climate trends be calculated from reanalysis data? Bengtsson et al, Journal of Geophysical Research (2005)
Ocean Water Vapor and Cloud Burden Trends Derived from the Topex Microwave Radiometer, Brown et al, Geoscience and Remote Sensing Symposium, 2007. IGARSS 2007. IEEE International (2007)
Radiosonde-based trends in precipitable water over the Northern Hemisphere: An update, Durre et al, Journal of Geophysical Research (2009)
Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data, Paltridge et al, Theoretical Applied Climatology (2009)
Trends in tropospheric humidity from reanalysis systems, Dessler & Davis, Journal of Geophysical Research (2010)
Note 1: The radiance measurement in this channel is a result of both the temperature of the atmosphere and the amount of water vapor. If temperature increases radiance increases. If water vapor increases it attenuates the radiance. See the slightly more detailed explanation in their paper.
Note 2: Here is a lengthy extract from Durre et al (2009), partly because it’s not available for free, and especially to give an idea of the issues arising from trying to extract long term climatology from radiosonde data and, therefore, careful approach that needs to be taken.
Emphasis added in each case:
From the IGRA+RE01 data, stations were chosen on the basis of two sets of requirements: (1) criteria that qualified them for use in the homogenization process and (2) temporal completeness requirements for the trend analysis.
In order to be a candidate for homogenization, a 0000 UTC or 1200 UTC time series needed to both contain at least two monthly means in each of the 12 calendar months during 1973–2006 and have at least five qualifying neighbors (see section 2.2). Once adjusted, each time series was tested against temporal completeness requirements analogous to those used by RE01; it was considered sufficiently complete for the calculation of a trend if it contained no more than 60 missing months, and no data gap was longer than 36 consecutive months.
Approximately 700 stations were processed through the pairwise homogenization algorithm (hereinafter abbreviated as PHA) at each of the nominal observation times. Even though the stations were located in many parts of the globe, only a handful of those that qualified for the computation of trends were located in the Southern Hemisphere.
Consequently, the trend analysis itself was restricted to the Northern Hemisphere as in that of RE01. The 305 Northern Hemisphere stations for 0000 UTC and 280 for 1200 UTC that fulfilled the completeness requirements covered mostly North America, Greenland, Europe, Russia, China, and Japan.
Compared to RE01, the number of stations for which trends were computed increased by more than 100, and coverage was enhanced over Greenland, Japan, and parts of interior Asia. The larger number of qualifying
stations was the result of our ability to include stations that were sufficiently complete but contained significant inhomogeneities that required adjustment.Considering that information on these types of changes tends to be incomplete for the historical record, the successful adjustment for inhomogeneities requires an objective technique that not only uses any available metadata, but also identifies undocumented change points [Gaffen et al., 2000; Durre et al., 2005]. The PHA of MW09 has these capabilities and thus was used here. Although originally developed for homogenizing time series of monthly mean surface temperature, this neighbor-based procedure was designed such that it can be applied to other variables, recognizing that its effectiveness depends on the relative magnitudes of change points compared to the spatial and temporal variability of the variable.
As can be seen from Table 1, change points were identified in 56% of the 0000 UTC and 52% of the 1200 UTC records, for a total of 509 change points in 317 time series.
Of these, 42% occurred around the time of a known metadata event, while the remaining 58% were considered to be ‘‘undocumented’’ relative to the IGRA station history information. On the basis of the visual inspection, it appears that the PHA has a 96% success rate at detecting obvious discontinuities. The algorithm can be effective even when a particular step change is present at the target and a number of its neighbors simultaneously.
In Japan, for instance, a significant drop in PW associated with a change between Meisei radiosondes around 1981 (Figure 1, top) was detected in 16 out of 17 cases, thanks to the inclusion of stations from adjacent tries in the pairwise comparisons Furthermore, when an adjustment is made around the time of a documented change in radiosonde type, its sign tends to agree with that expected from the known biases of the relevant instruments. For example, the decrease in PW at Yap in 1995 (Figure 1, middle) is consistent with the artificial drying expected from the change from a VIZ B to a Vaisala RS80–56 radiosonde that is known to have occurred at this location and time [Elliott et al., 2002; Wang and Zhang, 2008].
Posted in Basic Science, Climate History on June 2, 2011| 32 Comments »
Water vapor trends is a big subject and so this article is not a comprehensive review – there are a few hundred papers on this subject. However, as most people outside of climate scientists have exposure to blogs where only a few papers have been highlighted, perhaps it will help to provide some additional perspective.
Think of it as an article that opens up some aspects of the subject.
And I recommend reading a few of the papers in the References section below. Most are linked to a free copy of the paper.
Mostly what we will look at in this article is “total precipitable water vapor” (TPW) also known as “column integrated water vapor (IWV)”.
What is this exactly? If we took a 1 m² area at the surface of the earth and then condensed the water vapor all the way up through the atmosphere, what height would it fill in a 1 m² tub?
The average depth (in this tub) from all around the world would be about 2.5 cm. Near the equator the amount would be 5cm and near the poles it would be 0.5 cm.
Averaged globally, about half of this is between sea level and 850 mbar (around 1.5 km above sea level), and only about 5% is above 500 mbar (around 5-6 km above sea level).
How do we find IVW (integrated water vapor)?
Frequent radiosonde launches were started after the Second World War – prior to that knowledge of water vapor profiles through the atmosphere is very limited.
Satellite studies of water vapor did not start until the late 1970’s.
Unfortunately for climate studies, radiosondes were designed for weather forecasting and so long term trends were not a factor in the overall system design.
Radiosondes were mostly launched over land and are predominantly from the northern hemisphere.
Given that water vapor response to climate is believed to be mostly from the ocean (the source of water vapor), not having significant measurements over the ocean until satellites in the late 1970’s is a major problem.
There is one more answer that could be added to the above list:
As most people might suspect from the name, a reanalysis isn’t a data source. We will take a look at them a little later.
Pros and Cons in brief:
Radiosonde Pluses:
Radiosonde Minuses:
Satellite Pluses:
Satellite Minuses:
Three names that come up a lot in papers on radiosonde measurements are Gaffen, Elliott and Ross. Usually pairing up they have provided a some excellent work on radiosonde data and on measurement issues with radiosondes.
From Radiosonde-based Northern Hemisphere Tropospheric Water Vapor Trends, Ross & Elliott (2001):
All the above trend studies considered the homogeneity of the time series in the selection of stations and the choice of data period. Homogeneity of a record can be affected by changes in instrumentation or observing practice. For example, since relative humidity typically decreases with height through the atmosphere, a fast responding humidity sensor would report a lower relative humidity than one with a greater lag in response.
Thus, the change to faster-response humidity sensors at many stations over the last 20 years could produce an apparent, though artificial, drying over time..
Then they have a section discussing various data homogeneity issues, which includes this graphic showing the challenge of identifying instrument changes which affect measurements:
From Ross & Elliott (2001)
Figure 1
They comment:
These examples show that the combination of historical and statistical information can identify some known instrument changes. However, we caution that the separation of artificial (e.g., instrument changes) and natural variability is inevitably somewhat subjective. For instance, the same instrument change at one station may not show as large an effect at another location or time of day..
Furthermore, the ability of the statistical method to detect abrupt changes depends on the variability of the record, so that the same effect of an instrument change could be obscured in a very noisy record. In this case, the same change detected at one station may not be detected at another station containing more variability.
Here are their results from 1973-1995 in geographical form. Triangles are positive trends, circles are negative trends. You also get to see the distribution of radiosondes, as each marker indicates one station:
Figure 2
And their summary of time-based trends for each region:
Figure 3
In their summary they make some interesting comments:
We found that a global estimate could not be made because reliable records from the Southern Hemisphere were too sparse; thus we confined our analysis to the Northern Hemisphere. Even there, the analysis was limited by continual changes in instrumentation, albeit improvements, so we were left with relatively few records of total precipitable water over the era of radiosonde observations that were usable.
Emphasis added.
Well, I recommend that readers take the time to read the whole paper for themselves to understand the quality of work that has been done – and learn more about the issues with the available data.
In their 1991 paper, Elliot and Gaffen showed that pre-1973 radiosonde measurements came with much more problems than post-1973.
From Elliott & Gaffen (1991)
Figure 4 – Click for larger view
Note that the above is just for the US radiosonde network.
Our findings suggest caution is appropriate when using the humidity archives or interpreting existing water vapor climatologies so that changes in climate not be confounded by non-climate changes.
And one extract to give a flavor of the whole paper:
The introduction of the new hygristor in 1980 necessitated a new algorithm.. However, the new algorithm also eliminated the possibility of reports of humidities greater than 100% but ensured that humidities of 100% cannot be reported in cold temperatures. The overall effect of these changes is difficult to ascertain. The new algorithm should have led to higher reported humidities compared to the older algorithm, but the elimination of reports of very high values at cold temperatures would act in the opposite sense.
And a nice example of another change in radiosonde measurement and reporting practice. The change below is just an artifact of low humidity values being reported after a certain date:
From Elliott & Gaffen (1991)
Figure 5
As the worst cases came before 1973, most researchers subsequently reporting on water vapor trends have tended to stick to post-1973 (or report on that separately and add caveats to pre-1973 trends).
But it is important to understand that issues with radiosonde measurements are not confined to pre-1973.
Here are a few more comments, this time from Elliott in his 1995 paper:
Most (but not all) of these changes represent improvements in sensors or other practices and so are to be welcomed. Nevertheless they make it difficult to separate climate changes from changes in the measurement programs..
Since then, there have been several generations of sensors and now sensors have much faster response times. Whatever the improvements for weather forecasting, they do leave the climatologist with problems. Because relative humidity generally decreases with height slower sensors would indicate a higher humidity at a given height than today’s versions (Elliott et al., 1994).
This effect would be particularly noticeable at low temperatures where the differences in lag are greatest. A study by Soden and Lanzante (submitted) finds a moist bias in upper troposphere radiosondes using slower responding humidity sensors relative to more rapid sensors, which supports this conjecture. Such improvements would lead the unwary to conclude that some part of the atmosphere had dried over the years.
And Gaffen, Elliott & Robock (1992) reported that in analyzing data from 50 stations from 1973-1990 they found instrument changes that created “inhomogeneities in the records of about half the stations”
Different countries tend to use different radiosondes, have different algorithms and have different reporting practices in place.
The following comparison is of upper tropospheric water vapor. As an aside this has a focus because water vapor in the upper atmosphere disproportionately affects top of atmosphere radiation – and therefore the radiation balance of the climate.
From Soden & Lanzante (1996), the data below, of the difference between satellite and radiosonde measurements, identifies a significant problem:
Soden & Lanzante (1996)
Figure 6
Since the same satellite is used in the comparison at all radiosonde locations, the satellite measurements serve as a fixed but not absolute reference. Thus we can infer that radiosonde values over the former Soviet Union tend to be systematically moister than the satellite measurements, that are in turn systematically moister than radiosonde values over western Europe.
However, it is not obvious from these data which of the three sets of measurements is correct in an absolute sense. That is, all three measurements could be in error with respect to the actual atmosphere..
..However, such a satellite [calibration] error would introduce a systematic bias at all locations and would not be regionally dependent like the bias shown in fig. 3 [=figure 6].
They go on to identify the radiosonde sensor used in different locations as the likely culprit. Yet, as various scientists comment in their papers, countries take on a new radiosonde in piecemeal form, sometimes having a “competitive supply” situation where 70% is from one vendor and 30% from another vendor. Other times radiosonde sensors are changed across a region over a period of a few years. Inter-comparisons are done, but inadequately.
Soden and Lanzante also comment on spatial coverage:
Over data-sparse regions such as the tropics, the limited spatial coverage can introduce systematic errors of 10-20% in terms of the relative humidity. This problem is particularly severe in the eastern tropical Pacific, which is largely void of any radiosonde stations yet is especially critical for monitoring interannual variability (e.g. ENSO).
Before we move onto reanalyses, a summing up on radiosondes from the cautious William P. Elliot (1995):
Thus there is some observational evidence for increases in moisture content in the troposphere and perhaps in the stratosphere over the last 2 decades. Because of limitations of the data sources and the relatively short record length, further observations and careful treatment of existing data will be needed to confirm a global increase.
Weather forecasting and climate modelling is a form of finite element analysis (and see Wikipedia). Essentially in FEA, some kind of grid is created – like this one for a pump impellor:
Stress analysis in an impeller
Figure 7
– and the relevant equations can be solved for each boundary or each element. It’s a numerical solution to a problem that can’t be solved analytically.
Weather forecasting and climate are as tough as they come. Anyway, the atmosphere is divided up into a grid and in each grid we need a value for temperature, pressure, humidity and many other variables.
To calculate what the weather will be like over the next week a value needs to be placed into each and every grid. And just one value. If there is no value in the grid the program can’t run and there’s nowhere to put two values.
By this massive over-simplification, hopefully you will be able to appreciate what a reanalysis does. If no data is available, it has to be created. That’s not so terrible, so long as you realize it:
Figure 8
This is a simple example where the values represent temperatures in °C as we go up through the atmosphere. The first problem is that there is a missing value. It’s not so difficult to see that some formula can be created which will give a realistic value for this missing value. Perhaps the average of all the values surrounding it? Perhaps a similar calculation which includes values further away, but with less weighting.
With some more meteorological knowledge we might develop a more sophisticated algorithm based on the expected physics.
The second problem is that we have an anomaly. Clearly the -50°C is not correct. So there needs to be an algorithm which “fixes” it. Exactly what fix to use presents the problem.
If data becomes sparser then the problems get starker. How do we fill in and correct these values?
Figure 9
It’s not at all impossible. It is done with a model. Perhaps we know surface temperature and the typical temperature profile (“lapse rate”) through the atmosphere. So the model fills in the blanks with “typical climatology” or “basic physics”.
But it is invented data. Not real data.
Even real data is subject to being changed by the model..
There are a number of reanalysis projects. One is the NCEP/NCAR project (NCEP = National Centers for Environmental Prediction, NCAR = National Center for Atmospheric Research).
Kalnay (1996) explains:
The basic idea of the reanalysis project is to use a frozen state-of-the-art analysis/forecast system and perform data assimilation using past data, from 1957 to the present (reanalysis).
The NCEP/NCAR 40-year reanalysis project should be a research quality dataset suitable for many uses, including weather and short-term climate research.
An important consideration is explained:
An important question that has repeatedly arisen is how to handle the inevitable changes in the observing system, especially the availability of new satellite data, which will undoubtedly have an impact on the perceived climate of the reanalysis. Basically the choices are a) to select a subset of the observations that remains stable throughout the 40-year period of the reanalysis, or b) to use all the available data at a given time.
Choice a) would lead to an reanalysis with the most stable climate, and choice b) to an analysis that is as accurate as possible throughout the 40 years. With the guidance of the advisory panel, we have chosen b), that is, to make use of the most data available at any given time.
What are the categories of output data?
Humidity is in category B.
Interested people can read Kalnay’s paper. Reanalysis products are very handy and widely used. Those with experience usually know what they are playing around with. Newcomers need to pay attention to the warning labels.
Bengtsson et al (2004) reviewed another reanalysis project, ERA-40. They provide a good example of how incorrect trends can be introduced (especially the 2nd paragraph):
A bias changing in time can thus introduce a fictitious trend without being eliminated by the data assimilation system. A fictitious trend can be generated by the introduction of new types of observations such as from satellites and by instrumental and processing changes in general. Fictitious trends could also result from increases in observational coverage since this will affect systematic model errors.
Assume, for example, that the assimilating model has a cold bias in the upper troposphere which is a common error in many general circulation models (GCM). As the number of observations increases the weight of the model in the analysis is reduced and the bias will correspondingly become smaller. This will then result in an artificial warming trend.
Bengtsson and his colleagues analyze tropospheric temperature, IWV and kinetic energy.
ERA-40 does have a positive trend in water vapor, something we will return to. The trend from ERA-40 for 1958-2001 is +0.41 mm/decade, and for 1979-2001 = +0.36 mm/decade. They note that NCEP/NCAR has a negative trend of -0.24 mm/decade from 1958-2001 and -0.06mm/decade for 1979-2001, but it isn’t a focus of their study.
They do an analysis which excludes satellite data and find a lower (but still positive) trend for IWV. They also question the magnitudes of tropospheric temperature trends and kinetic energy on similar grounds.
The point is essentially that the new data has created a bias in the reanalysis.
Their conclusion, following various caveats about the scale of the study so far:
Returning finally to the question in the title of this study an affirmative answer cannot be given, as the indications are that in its present form the ERA40 analyses are not suitable for long-term climate trend calculations.
However, it is believed that there are ways forward as indicated in this study which in the longer term are likely to be successful. The study also stresses the difficulties in detecting long term trends in the atmosphere and major efforts along the lines indicated here are urgently needed.
So, onto Trends and variability in column-integrated atmospheric water vapor by Trenberth, Fasullo & Smith (2005). This paper is well worth reading in full.
For years before 1996, the Ross and Elliott radiosonde dataset is used for validation of European Centre for Medium-range Weather Forecasts (ECMWF) reanalyses ERA-40. Only the special sensor microwave imager (SSM/I) dataset from remote sensing systems (RSS) has credible means, variability and trends for the oceans, but it is available only for the post-1988 period.
Major problems are found in the means, variability and trends from 1988 to 2001 for both reanalyses from National Centers for Environmental Prediction (NCEP) and the ERA-40 reanalysis over the oceans, and for the NASA water vapor project (NVAP) dataset more generally. NCEP and ERA-40 values are reasonable over land where constrained by radiosondes.
Accordingly, users of these data should take great care in accepting results as real.
Here’s a comparison of Ross & Elliott (2001) [already shown above] with ERA-40:
From Trenberth et al (2005)
Figure 10 – Click for a larger image
Then they consider 1988-2001, the reason being that 1988 was when the SSMI (special sensor microwave imager) data over the oceans became available (more on the satellite data later).
From Trenberth et al (2005)
Figure 11
At this point we can see that ERA-40 agrees quite well with SSMI (over the oceans, the only place where SSMI operates), but NCEP/NCAR and another reanalysis product, NVAR, produce flat trends.
Now we will take a look at a very interesting paper: The Mass of the Atmosphere: A Constraint on Global Analyses, Trenberth & Smith (2005). Most readers will probably not be aware of this comparison and so it is of “extra” interest.
The total mass of the atmosphere is in fact a fundamental quantity for all atmospheric sciences. It varies in time because of changing constituents, the most notable of which is water vapor. The total mass is directly related to surface pressure while water vapor mixing ratio is measured independently.
Accordingly, there are two sources of information on the mean annual cycle of the total mass and the associated water vapor mass. One is from measurements of surface pressure over the globe; the other is from the measurements of water vapor in the atmosphere.
The main idea is that other atmospheric mass changes have a “noise level” effect on total mass, whereas water vapor has a significant effect. As measurement of surface pressure is a fundamental meteorological value, measured around the world continuously (or, at least, continually), we can calculate the total mass of the atmosphere with high accuracy. We can also – from measurements of IWV – calculate the total mass of water vapor “independently”.
Subtracting water vapor mass from total atmospheric measured mass should give us a constant – the “dry atmospheric pressure”. That’s the idea. So if we use the surface pressure and the water vapor values from various reanalysis products we might find out some interesting bits of data..
from Trenberth & Smith (2005)
Figure 12
In the top graph we see the annual cycle clearly revealed. The bottom graph is the one that should be constant for each reanalysis. This has water vapor mass removed via the values of water vapor in that reanalysis.
Pre-1973 values show up as being erratic in both NCEP and ERA-40. NCEP values show much more variability post-1979, but neither is perfect.
The focus of the paper is the mass of the atmosphere, but is still recommended reading.
Here is the geographical distribution of IWV and the differences between ERA-40 and other datasets (note that only the first graphic is trends, the following graphics are of differences between datasets):
Trenberth et al (2005)
Figure 13 – Click for a larger image
The authors comment:
The NCEP trends are more negative than others in most places, although the patterns appear related. Closer examination reveals that the main discrepancies are over the oceans. There is quite good agreement between ERA-40 and NCEP over most land areas except Africa, i.e. in areas where values are controlled by radiosondes.
There’s a lot more in the data analysis in the paper. Here are the trends from 1988 – 2001 from the various sources including ERA-40 and SSMI:
From Trenberth et al (2005)
Figure 14 – Click for a larger view
As this article is already pretty long, it will be continued in Part Two, which will include Paltridge et al (2009), Dessler & Davis (2010) and some satellite measurements and papers.
Update – Part Two is published
On the Utility of Radiosonde Humidity Archives for Climate Studies, Elliot & Gaffen, Bulletin of the American Meteorological Society (1991)
Relationships between Tropospheric Water Vapor and Surface Temperature as Observed by Radiosondes, Gaffen, Elliott & Robock, Geophysical Research Letters (1992)
Column Water Vapor Content in Clear and Cloudy Skies, Gaffen & Elliott, Journal of Climate (1993)
On Detecting Long Term Changes in Atmospheric Moisture, Elliot, Climate Change (1995)
Tropospheric Water Vapor Climatology and Trends over North America, 1973-1993, Ross & Elliot, Journal of Climate (1996)
An assessment of satellite and radiosonde climatologies of upper-tropospheric water vapor, Soden & Lanzante, Journal of Climate (1996)
The NCEP/NCAR 40-year Reanalysis Project, Kalnay et al, Bulletin of the American Meteorological Society (1996)
Radiosonde-Based Northern Hemisphere Tropospheric Water Vapor Trends, Ross & Elliott, Journal of Climate (2001)
An analysis of satellite, radiosonde, and lidar observations of upper tropospheric water vapor from the Atmospheric Radiation Measurement Program, Soden et al, Journal of Geophysical Research (2005)
The Radiative Signature of Upper Tropospheric Moistening, Soden et al, Science (2005)
The Mass of the Atmosphere: A Constraint on Global Analyses, Trenberth & Smith, Journal of Climate (2005)
Trends and variability in column-integrated atmospheric water vapor, Trenberth et al, Climate Dynamics (2005)
Can climate trends be calculated from reanalysis data? Bengtsson et al, Journal of Geophysical Research (2005)
Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data, Paltridge et al, Theoretical Applied Climatology (2009)
Trends in tropospheric humidity from reanalysis systems, Dessler & Davis, Journal of Geophysical Research (2010)
Posted in Basic Science, Debunking Flawed "Science" on May 15, 2011| 38 Comments »
In previous articles in this series we looked at a number of issues first in Miskolczi’s 2010 paper and then in the 2007 paper.
The author himself has shown up and commented on some of these points, although not all, and sadly decided that we are not too bright and a little bit too critical and better pastures await him elsewhere.
Encouraged by one of our commenters I pressed on into the paper: Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Quarterly Journal of the Hungarian Meteorological Service (2007), and now everything is a lot clearer.
The 2007 paper by Ferenc Miskolczi is a soufflé of confusion piled on confusion. Sorry to be blunt. If I was writing a paper I would say “..some clarity is needed in important sections..” but many readers unfamiliar with the actual meaning of this phrase might think that some clarity was needed in important sections rather than the real truth that the paper is a shambles.
I’ll refer to this paper as M2007. And to the equations in M2007 with an M prefix – so, for example, equation 15 will be [M15].
Some background is needed so first we need to take a look at something called The Semi-Gray Model. Regular readers will find a lot of this to be familiar ground, but it is necessary as there are always many new readers.
I’ll introduce this by quoting from an excellent paper referenced by M2007. This is a 1995 paper by Weaver and the great Ramanathan (free link in References):
Simple models of complex systems have great heuristic value, in that their results illustrate fundamental principles without being obscured by details. In particular, there exists a long history of simple climate models. Of these, radiative and radiative-convective equilibrium models have received great attention..
One of the simplest radiative equilibrium models involves the assumption of a so-called grey atmosphere, where the absorption coefficient is assumed to be independent of wavelength. This was first discussed by Schwarzschild [1906] in the context of stellar interiors. The grey gas model was adapted to studies of the Earth by assuming the atmosphere to be transparent to solar radiation and grey for thermal radiation. We will refer to this latter class as semigrey models.
And in the abstract they say:
Radiative equilibrium solutions are the starting point in our attempt to understand how the atmospheric composition governs the surface and atmospheric temperatures, and the greenhouse effect. The Schwarzschild analytical grey gas model (SGM) was the workhorse of such attempts. However, the solution suffered from serious deficiencies when applied to Earth’s atmosphere and were abandoned about 3 decades ago in favor of more sophisticated computer models..
[Emphasis added]
And they go on to present a slightly improved SGM as a useful illustrative tool.
Some clarity on a bit of terminology for new readers – a blackbody is a perfect emitter and absorber of radiation. In practice there are no blackbodies but some bodies come very close. A blackbody has an emissivity = 1 and absorptivity = 1.
In our atmosphere, the gases which absorb and emit significant radiation have very wavelength dependent properties, e.g.:
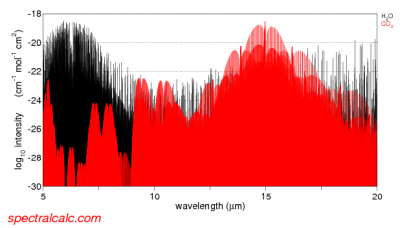
From spectralcalc.com
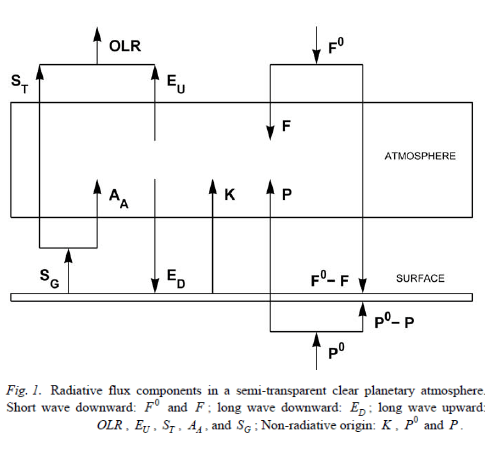
Figure 1
So the emissivity and absorptivity vary hugely from one wavelength to the next (note 1). However, as an educational tool, we can calculate the results for a grey atmosphere – this means that the emissivity is assumed to be constant across all wavelengths.
The term semi-grey means that the atmosphere is considered transparent for shortwave = solar wavelengths (<4 μm) and constant but not zero for longwave = terrestrial wavelengths (>4 μm).
This model is very simple – and is not used to really calculate anything of significance for our climate. See Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations for the real equations.
We assume that the atmosphere is in radiative equilibrium – that is, convection does not exist and so only radiation moves heat around.
Here is a graphic showing the main elements of the model:
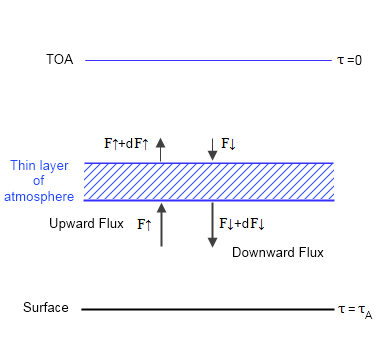
Figure 2
Once each layer in the atmosphere is in equilibrium, there is no heating or cooling – this is the definition of equilibrium. This means energy into the layer = energy out of the layer. So we can use simple calculus to write some equations of radiative transfer.
We define the TOA (top of atmosphere) to be where optical thickness, τ=0, and it increases through the atmosphere to reach a maximum of τ=τA at the surface. This is conventional.
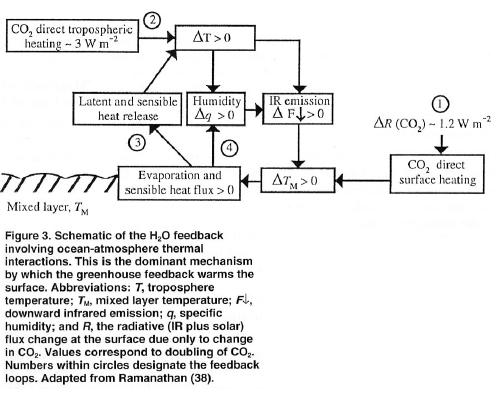
We also know two boundary conditions, because at TOA (top of atmosphere) the downward longwave flux, F↓(τ=0) = 0 and the upwards longwave flux, F↑(τ=0) = F0, where F0 = absorbed solar radiation ≈ 240 W/m². This is because energy leaving the planet must be balanced by energy being absorbed by the planet from the sun.
We also have to consider the fact that energy is not just going directly up and down but is going up and down at every angle. We can deal with this via the dffusivity approximation which sums up the contributions from every angle and tells us that if we use τ*= τ . 5/3 (where τ is defined in the vertical direction) we get the complete contribution from all of the different directions. (Note 2). For those following M2007 I have used τ* to be his τ with a ˜ on top, and τ to be his τ with a ¯ on top.
With these conditions we can get a solution for the SGM (see derivation in the comments):
B(τ) = F0/2π . (τ+1) [1] cf eqn [M15]
where B is the spectrally integrated Planck function, and remember F0 is a constant.
And also:
F↑(τ) = F0/2 . (τ+2) [2]
F↓(τ) = F0/2 . τ [3]
A quick graphic might explain this a little more (with an arbitrary total optical thickness, τA* = 3):
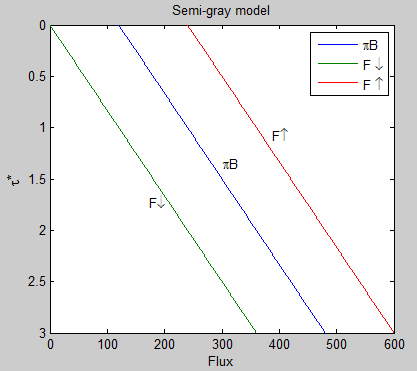
Figure 3
Notice that the upward longwave flux at TOA is 240 W/m² – this balances the absorbed solar radiation. And the downward longwave flux at TOA is zero, because there is no atmosphere above from which to radiate. This graph also demonstrates that the difference between F↑ and F↓ is a constant as we move through the atmosphere, meaning that the heating rate is zero. The increase in downward flux, F↓, is matched by the decrease in upward flux, F↑.
It’s a very simple model.
By contrast, here are the heating/cooling rates from a comprehensive (= “standard”) radiative-convective model, plotted against height instead of optical thickness.
Heating from solar radiation, because the atmosphere is not completely transparent to solar radiation:
From Grant Petty (2006)
Figure 4
Cooling rates due to various “greenhouse” gases:
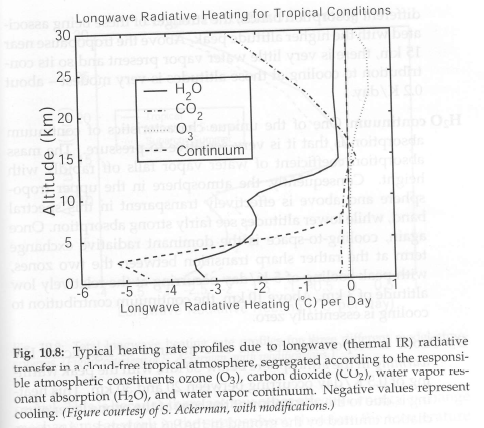
From Petty (2006)
Figure 5
And the heating and cooling rates won’t match up because convection moves heat from the surface up into the atmosphere.
Note that if we plotted the heating rate vs altitude for the SGM it would be a vertical line on 0.0°C/day.
Let’s take a look at the atmospheric temperature profile implied by the semi-grey model:
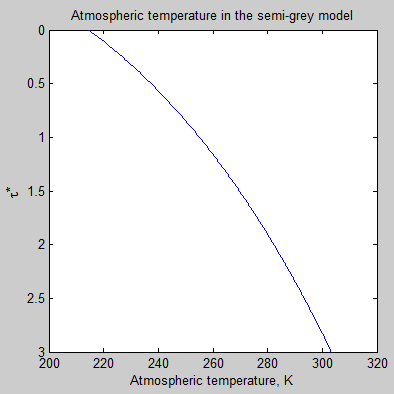
Figure 6
Now a lot of readers are probably wondering what the τ really means, or more specifically, what the graph looks like as a function of height in the atmosphere. In this model it very much depends on the concentration of the absorbing gas and its absorption coefficient. Remember it is a fictitious (or “idealized”) atmosphere. But if we assume that the gas is well-mixed (like CO2 for example, but totally unlike water vapor), and the fact that pressure increases with depth then we can produce a graph vs height:
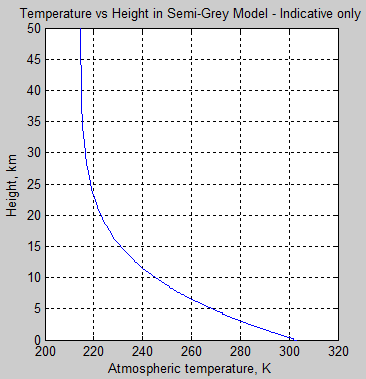
Figure 7
Important note – the values chosen here are not intended to represent our climate system.
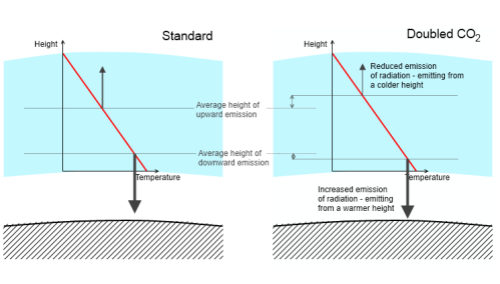
Figure 6 & 7, along with figure 3, are just to help readers “see” what a semi-grey model looks like. If we increase the total optical depth of the atmosphere the atmospheric temperature at the surface increases.
Note as well that once the temperature reduction vs height is too large a value, the atmosphere will become unstable to convection. E.g. for a typical adiabatic lapse rate of 6.5 K/km, if the radiative equilibrium implies a lapse rate > 6.5 K/km then convection will move heat to reduce the lapse rate.
Some comments from M2007:
p 11:
Note, that in obtaining B0 , the fact of the semi-infinite integration domain over the optical depth in the formal solution is widely used. For finite or optically thin atmosphere Eq. (15) is not valid. In other words, this equation does not contain the necessary boundary condition parameters for the finite atmosphere problem.
The B0 he is referring to is the constant in [M15]. This constant is H/2π – where H = F0 (absorbed solar radiation) in my earlier notation. This constant B0 later takes on magical properties.
p 12:
Eq. (15) assumes that at the lower boundary the total flux optical depth is infinite. Therefore, in cases, where a significant amount of surface transmitted radiative flux is present in the OLR , Eqs. (16) and (17) are inherently incorrect. In stellar atmospheres, where, within a relatively short distance from the surface of a star the optical depth grows tremendously, this could be a reasonable assumption, and Eq. (15) has great practical value in astrophysical applications. The semi-infinite solution is useful, because there is no need to specify any explicit lower boundary temperature or radiative flux parameter (Eddington, 1916).
[Emphasis added]
The equations can easily be derived without any requirement for the total optical depth being infinite. There is no semi-infinite assumption in the derivation. Whether or not some early derivations included it, I cannot say. But you can find the SGM derivation in many introductions to atmospheric physics and no assumption of infinite optical thickness exists.
When considering the clear-sky greenhouse effect in the Earth’s atmosphere or in optically thin planetary atmospheres, Eq. (16) is physically meaningless, since we know that the OLR is dependent on the surface temperature, which conflicts with the semi-infinite assumption that τA =∞..
..There were several attempts to resolve the above deficiencies by developing simple semi-empirical spectral models, see for example Weaver and Ramanathan (1995), but the fundamental theoretical problem was never resolved..
This is the reason why scientists have problems with a mysterious surface temperature discontinuity and unphysical solutions, as in Lorenz and McKay (2003). To accommodate the finite flux optical depth of the atmosphere and the existence of the transmitted radiative flux from the surface, the proper equations must be derived.
The deficiencies noted include the result in the semi-gray model of a surface air temperature less than the ground temperature. If you read Weaver and Ramanathan (1995) you can see that this isn’t an attempt to solve some “fundamental problem“, but simply an attempt to make a simple model slightly more useful without getting too complex.
The mysterious surface temperature discontinuity exists because the model is not “full bottle”. The model does not include any convection. This discontinuity is not a mystery and is not crying out for a solution. The solution exists. It is called the radiative-convective model and has been around for over 40 years.
Miskolczi makes some further comments on this, which I encourage people to read in the actual paper.
We now move into Appendix B to develop the equations further. The results from the appendix are the equations M20 and M21 on page 14.
The highlighted equation is the general solution to the Schwzarschild equation. It is developed in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations – the equation reproduced here from that article with explanation:
Iλ(0) = Iλ(τm)e-τm + ∫ Bλ(T)e-τ dτ
The intensity at the top of atmosphere equals..
The surface radiation attenuated by the transmittance of the atmosphere, plus..
The sum of all the contributions of atmospheric radiation – each contribution attenuated by the transmittance from that location to the top of atmosphere
For those wanting to understand the maths a little bit, the 3/2 factor that appears everywhere in Miskolczi’s equation B1 is the diffusivity approximation already mentioned (and see note 2) where we need to sum the radiances over all directions to get flux.
Now this equation is the complete equation of radiative transfer. If we combine it with a simple convective model it is very effective at calculating the flux and spectral intensity through the atmosphere – see Theory and Experiment – Atmospheric Radiation.
So equation B1 in M2007 cannot be solved analytically. This means we have to solve it numerically. This is “simple” in concept but computationally expensive because in the HITRAN database there are 2.7 million individual absorption lines, each one with a different absorption coefficient and a different line width.
However, it can be solved and that is what everyone does. Once you have the database of absorption coefficients and the temperature profile of the atmosphere you can calculate the solution. And band models exist to speed up the process.
And now the rabbit..
The author now takes the equation for the “source function” (B) from the simple model and inserts it into the “complete” solution.
The “source function” in the complete solution can already be calculated – that’s the whole point of the equation B1. But now instead, the source function from the simple model is inserted in its place. This equation assumes that the atmosphere has no convection, has no variation in emissivity with wavelength, has no solar absorption in the atmosphere, and where the heating rate at each level in the atmosphere = zero.
The origin of equation B3 is the equation you see above it:
B(τ) = 3H(τ)/4π + B0 [M13]
Actually, if you check equation M13 on p.11 it is:
B(τ) = 3H.τ/4π + B0 [M13]
This appears to be one of the sources of confusion for Miskolczi, for later comment.
Equation M13 is derived for zero heating rates throughout the atmosphere, and therefore constant H. With this simple assumption – and only for this simple assumption – the equation M13 is a valid solution to “the source function”, ie the atmospheric temperature and radiance.
If you have the complete solution you get one result. If you have the simple model you get a different result. If you take the result from one and stick it in the other how can you expect to get an accurate outcome?
If you want to see how various atmospheric factors are affected by changing τ, then just change τ in the general equation and see what happens. You have to do this via numerical analysis but it can easily be done..
As we continue on working through the appendix, B6 has a sign error in the 2nd term on the right hand side, which is fixed by B7.
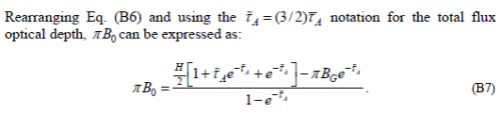
This B0 is the constant in the semi-gray solution. The constant appears because we had a differential equation that we integrated. And the value of the constant was obtained via the boundary condition: upward flux from the climate system must balance solar radiation.
So we know what B0 is.. and we know it is a constant..
Yet now the author differentiates the constant with respect to τ. If you differentiate a constant it is always zero. Yet the explanation is something that sounds like it might be thermodynamics, but isn’t:
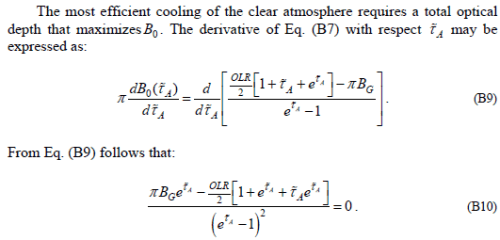
If someone wants to explain what thermodynamic principle create the first statement – I would be delighted. Without any explanation it is a jumble of words that doesn’t represent any thermodynamic principle.
Anyway B0 is a constant and is equal to approximately 240 W/m². Therefore, if we differentiate it, yes the value dB0/dτ=0.
Unfortunately, the result in B10 is wrong.
If we differentiate a variable we can’t assume it is a constant. The variable in question is BG. This is the “source function” for the ground, which gives us the radiance and surface temperature. Clearly the surface temperature is a function of many factors especially including optical thickness. Of course, if somewhere else we have proven that BG is a constant then dBG/dτ=0.
It has to be proven.
[And thanks to DeWitt Payne for originally highlighting this issue with BG, as well as explaining my calculus mistakes in an email].
A quick digression on basic calculus for the many readers who don’t like maths – just so you can see what I am getting at.. (you are the ones who should read it)
We will consider just the last term in equation [B9]. This term = BG/(eτ-1). I have dropped the π from the term to make it simpler to read what is happening.
Generally, if you differentiate two terms multiplied together, this is what happens:
d(fg)/dx = g.df/dx + f.dg/dx [4]
This assumes that f and g are both functions of x. If, for example, f is not a function of x, then df/dx=0 (this just means that f does not change as x changes). And so the result reduces to d(fg)/dx = f.dg/dx.
So, using [4] :
d/dτ [BG/(eτ-1)] = [1/(eτ-1)] . dBG/dτ + BG . d [1/(eτ-1)]/dτ [5]
We can look up:
d [1/(eτ-1)]/dτ = -eτ/(eτ-1)² [6]
So substituting [6] into [5], last term in [B9]:
= [1/(eτ-1)] . dBG/dτ – eτ.BG /(eτ-1)² [7]
You can see the 2nd half of this expression as the first term in [B10], multiplied by π of course.
But the term for how the surface radiance changes with optical thickness of the atmosphere has vanished.
end of digression
So the equation should read:
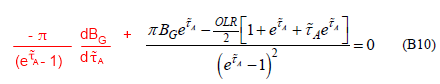
Where the red text is my correction (see eqn 7 in the digression).
Perhaps the idea is that if we assume that surface temperature doesn’t change with optical thickness then we can prove that surface temperature doesn’t change with optical thickness.
This (flawed) equation is now used to prove B11:
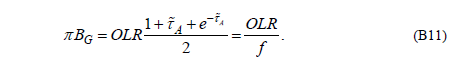
Well, we can see that B11 isn’t true. In fact, even apart from the missing term in B10, the equation has been derived by combining two equations which were derived under different conditions.
As we head back into the body of the paper from the appendix, equations B7 and B8 are rewritten as equations [M20] and [M21].
Miskolczi adds:
We could not find any references to the above equations in the meteorological literature or in basic astrophysical monographs, however, the importance of this equation is obvious and its application in modeling the greenhouse effect in planetary atmospheres may have far reaching consequences.
Readers who have made it this far might realize why he is the first with this derivation.
Continuing on, more statements are made which reveal some of the author’s confusion with one part of his derivation. The SGM model is derived by integrating a simple differential equation, which produces a constant. The boundary conditions tell us the constant.
Equation [M13] is written:
B(τ) = 3H/4π + B0 [M13]
Then [M14] is written:
H(τ) = π (I+ – I-) [M14]
So now H is a function of optical depth in the atmosphere?
In [M15]:
B(τ*) = H (1 + τ*)/2π [M15]
Refer to my equation 1 and you will see they are the same. The only way this equation can be derived is with H as a constant, because the atmosphere is in radiative equilibrium. If H isn’t constant you have a different equation – M13 and 15 are no longer valid.
..The fact that the new B0 (skin temperature) changes with the surface temperature and total optical depth, can seriously alter the convective flux estimates of previous radiative-convective model computations. Mathematical details on obtaining equations 20 and 21 are summarized in appendix B.
Miskolczi has confused himself (and his readers).
There is an equation of radiative transfer and it is equation B1 in the appendix of M2007. This equation is successfully used to calculate flux and spectral intensity in the atmosphere.
There is a very simple equation of radiative transfer which is used to illustrate the subject at a basic level and it is called the semi-grey model (or the Schwarzschild grey model). With the last few decades of ever increasing computing power the simple models have less and less practical use, although they still have educational value.
Miskolczi has inserted the simple result into the general model, which means, at best, it can only be applied to a “grey” atmosphere in radiative equilibrium, and at worst he has just created an equation soufflé.
The constant in the simple model has become a variable. Without any proof, or re-derivation of the simple model.
One of the important variables in the simple model has become a constant and therefore vanished from an equation where it should still reside.
Many flawed thermodynamic concepts are presented in the paper, some of which we have already seen in earlier articles.
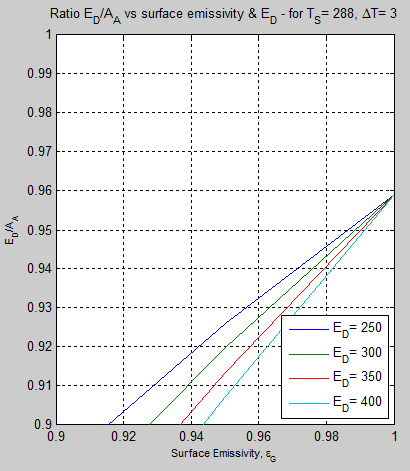
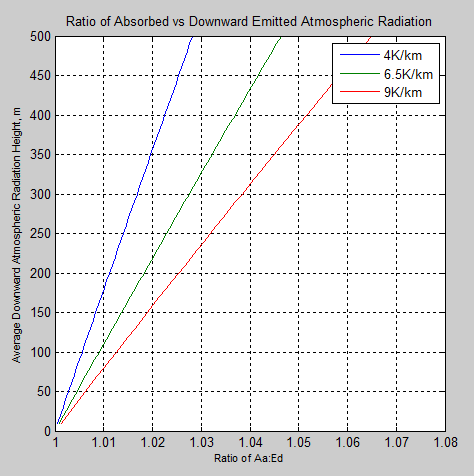
M2007 tells us that Ed=Aa due to Kirchhoff’s law. (See Part Two). His 2010 paper revised this claim as to due to Prevost.. However, the author himself recently stated:
I think I was the first who showed the Aa~=Ed relationship with reasonable quantitative accuracy.
And doesn’t understand why I think it is important to differentiate between fundamental thermodynamic identities and approximate experimental results in the theory section of a paper. “My experiments back up my experiments..”
M2007 introduces equation [M7] with:
In Eq. (6) SU − (F0 + P0 ) and ED − EU represent two flux terms of equal magnitude, propagating into opposite directions, while using the same F0 and P0 as energy sources. The first term heats the atmosphere and the second term maintains the surface energy balance. The principle of conservation of energy dictates that:
SU − (F0) + ED − EU = F0 = OLR
Note the pseudo-thermodynamic explanation. The author himself recently said:
Eq. 7 simply states, that the sum of the Su-OLR and Ed-Eu terms – in ideal greenhause case – must be equal to Fo. I assume that the complex dynamics of the system may support this assumption, and will explain the Su=3OLR/2 (global average) observed relationship.
[Emphasis added]
And later entertainingly commented:
You are right, I should have told that, and in my new article I shall pay more attantion to the full explanations. However, some scientists figured it out without any problem.
Party people who got the joke right off the bat..
M07 also introduces the idea that kinetic energy can be equated with the flux from the atmosphere to space. See Part Three. Introductory books on statistical thermodynamics tell us that flux is proportional to the 4th power of temperature, while kinetic energy is linearly proportional to temperature. We have no comment from the author on this basic contradiction.
This pattern indicates an obvious problem.
In summary – this paper does not contain a theory. Just because someone writes lots of equations down in attempt to back up some experimental work, it is not theory.
If the author has some experimental work and no theory, that is what he should present – look what I have found, I have a few ideas but can someone help develop a theory to explain these results.
Obviously the author believes he does have a theory. But it’s just equation soufflé.
Other Articles in the Series:
The Mystery of Tau – Miskolczi – introduction to some of the issues around the calculation of optical thickness of the atmosphere, by Miskolczi, from his 2010 paper in E&E
Part Two – Kirchhoff – why Kirchhoff’s law is wrongly invoked, as the author himself later acknowledged, from his 2007 paper
Part Three – Kinetic Energy – why kinetic energy cannot be equated with flux (radiation in W/m²), and how equation 7 is invented out of thin air (with interesting author comment)
Part Four – a minor digression into another error that seems to have crept into the Aa=Ed relationship
Part Six – Minor GHG’s – a less important aspect, but demonstrating the change in optical thickness due to the neglected gases N2O, CH4, CFC11 and CFC12.
Further reading:
New Theory Proves AGW Wrong! – a guide to the steady stream of new “disproofs” of the “greenhouse” effect or of AGW. And why you can usually only be a fan of – at most – one of these theories.
Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Miskolczi, Quarterly Journal of the Hungarian Meteorological Service (2007)
Deductions from a simple climate model: factors governing surface temperature and atmospheric thermal structure, Weaver & Ramanathan, JGR (1995)
Note 1 – emissivity = absorptivity for the same wavelength or range of wavelengths
Note 2 – this diffusivity approximation is explained further in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. In M2007 he uses a different factor, τ* = τ . 3/2 – this differences are not large but they exist. The problems in M2007 are so great that finding the changes that result from using different values of τ* is not really interesting.
Posted in Basic Science, Commentary on May 1, 2011| 293 Comments »
In Part Two we looked at the claimed relationship ED=AA in Miskolczi’s 2007 paper.
I showed that they could not be exactly equal. Ferenc Miskolczi himself has just joined the discussion and confirmed:
I think I was the first who showed the AA≈ED relationship with reasonable quantitative accuracy.
That is, there is not a theoretical basis for equating AA=ED as an identity.
There is a world of difference between demonstrating a thermodynamic identity and an approximate experimental relationship. In the latter situation, it is customary to make some assessment of how close the values are and the determining factors in the relationship.
But in reviewing the 2007 paper again I noticed something very interesting:
From Miskolczi (2007)
Figure 1
Now the point I made in Part Two was that AA ≠ ED because the atmosphere is a little bit cooler than the surface – at the average height of emission of the atmosphere. So we would expect ED to be a a little less than AA.
Please review the full explanation in Part Two to understand this point.
Now take a look at the graph above. The straight line drawn on is the relationship ED=AA.
The black circles are for an assumption that the surface emissivity, εG = 1. (This is reasonably close to the actual emissivity of the surface, which varies with surface type. The oceans, for example, have an emissivity around 0.96).
In these calculated results you can see that Downwards Emittance, ED is a little less than AA. In fact, it looks to be about 5% less on average. (And note that is ED = Absorbed Downwards Emittance)
Of course in practice, εG < 1. What happens then?
Well, in the graph above, with εG = 0.96 the points appear to lie very close to the line of ED=AA.
I think there is a calculation error in Miskolczi’s paper – and if this is true it is quite fundamental. Let me explain..
Here is the graphic for explaining Miskolczi’s terms:
From Miskolczi (2007)
Figure 2
When the surface is a blackbody (εG =1), SU = SG – that is, the upwards radiation from the surface = the emitted radiation from the ground.
The terms and equations in his 2007 are derived with reference to the surface emitting as a blackbody.
When εG < 1, some care is needed in rewriting the equations. It looks like this care has not been taken and the open circles in his Fig 2 (my figure 1) closely matching the ED=AA line are an artifact of incorrectly rewriting the equations when εG < 1.
That’s how it looks anyway.
Here is my graphic for the terms needed for this problem:
Figure 3
As much as possible I have reused Miskolczi’s terms. Because the surface is not a blackbody, the downward radiation emitted by the atmosphere is not completely absorbed. So I created the term EDA for the emission of radiation by the atmosphere. Then some of this, Er, is reflected and added to SG to create the total upward surface radiation, SU.
Note as well that the relationship emissivity = absorptivity is only true for the same wavelengths. See note 4 in Part Two.
Now for some necessary maths – it is very simple. All we are doing is balancing energy to calculate the two terms we need. (Updated note – some of the equations are approximations – the real equation for emission of radiation is a complex term needing all of the data, code and a powerful computer – but the approximate result should indicate that there is an issue in the paper that needs addressing – see comment).
And the objective is to get a formula for the ratio ED/AA – if ED=AA, this ratio = 1. And remember that in Figure 1, the relationship ED/AA=1 is shown as the straight line.
First, instead of having the term for atmospheric temperature, let’s replace it with:
TA = TS – ΔT [1]
where ΔT represents the idea of a small change in temperature.
Second, the emitted atmospheric downward radiation comes from the Stefan-Boltzmann law:
EDA = εAσ(TS – ΔT)4 [2]
Third, downward atmospheric radiation absorbed by the surface:
ED = εGEDA [3]
Fourth, the upward surface radiation is the emitted radiation plus the reflected atmospheric radiation. Emitted radiation is from the Stefan-Boltzmann law:
SU = εGσTS4 + (1-εG) EDA [4]
Fifth, the absorbed surface radiation is the upward surface radiation multiplied by the absorptivity of the atmosphere (= emissivity at similar temperatures):
AA = εASU [5]
So if we put [2] -> [3], we get:
ED = εGεAσ(TS – ΔT)4 [6]
And if we put [4] -> [5], we get:
AA = εGεAσTS4 + EDεA(1-εG)/εG [7]
We are almost there. Remember that we wanted to find the ratio ED/AA. Unfortunately, the AA term includes ED and we can’t eliminate it (unless I missed something).
So let’s create the ratio and see what happens. This is equation 6 divided by equation 7 and we can eliminate εA that appears in each term:
ED/AA = [ εGσ(TS – ΔT)4 ] / [ εGσTS4 + ED(1-εG)/εG ] [8]
And just to make it possibly a little clearer, we will divide top and bottom by εG and color code each part:
ED/AA = [ σ(TS – ΔT)4 ] / [ σTS4 + ED(1-εG)/εG2 ] [8a]
And so the ratio = blackbody radiation at the atmospheric temperature divided by
( blackbody surface radiation plus a factor of downward atmospheric radiation that increases as εG reduces )
We didn’t make a blackbody assumption, it is just that most of the emissivity terms canceled out.
Take a look at the green term – if εG = 1 this term is zero (1-1=0) and the equation simplifies down to:
ED/AA = (TS – ΔT)4 / TS4
Which is very simple. If ΔT = 0 then ED/AA = 1.
Let’s plot ED vs AA for a few different values of ΔT and for TS = 288K:
Figure 4
Compare this with figure 1 (Miskolczi’s fig 2).
Note: I could have just cited the ratios of ED/AA, which – in this graph – are constant for each value of ΔT.
And we can easily see that as ΔT →0, ED/AA →1. This is “obvious” from the maths for people more comfortable with equations.
That’s the simplest stuff out of the way. Now we want to see what happens when εG < 1. This is the interesting part, and when you see the graph, please note that the axes are not the same as figure 4. In figure 4, the graph is of ED vs AA, but now we will plot the ratio of ED/AA as other factors change.
Take a look back at equation 8a. To calculate the ratio we need a value of Ed, which we don’t have. So I use some typical values from Miskolczi – and it’s clear that the value of Ed chosen doesn’t affect the conclusion.
Figure 5
You can see that when εG = 1 the ratio is almost at 0.99. This is the slope of the top line (ΔT=1) in figure 4.
But as surface emissivity reduces, ED/AA reduces
This is clear from equation 8a – as εG reduces below 1, the second term in the denominator of equation 8a increases from zero. As this increases, the ratio must reduce.
In Miskolczi’s graph, as εG changed from 1.0 → 0.96 the calculated ratio increased. I believe this is impossible.
Here is another version with a different value of ΔT:
Figure 6
Perhaps I made a mistake in the maths. It’s pretty simple – and out there in the open, so surely someone can quickly spot the mistake.
Of course I wouldn’t have published the article if I thought it had a mistake..
On conceptual grounds we can see that as the emissivity of the surface reduces, it absorbs less energy from the atmosphere and reflects more radiation back to the atmosphere.
This must reduce the value of ED and increase the value of AA. This reduces the ratio ED/AA.
In Miskolczi’s 2007 paper he shows that as emissivity is reduced from a blackbody to a more realistic value for the surface, the ratio goes in the other direction.
If my equations are correct then the equations of energy balance (for his paper) cannot have been correctly written for the case εG <1.
This one should be simple to clear up.
Update May 31st – Ken Gregory, a Miskolczi supporter appears to agree – and calculates ED/AA=0.94 for a real world surface emissivity.
Other articles in the series
The Mystery of Tau – Miskolczi – introduction to some of the issues around the calculation of optical thickness of the atmosphere, by Miskolczi, from his 2010 paper in E&E
Part Two – Kirchhoff – why Kirchhoff’s law is wrongly invoked, as the author himself later acknowledged, from his 2007 paper
Part Three – Kinetic Energy – why kinetic energy cannot be equated with flux (radiation in W/m²), and how equation 7 is invented out of thin air (with interesting author comment)
Part Five – Equation Soufflé – explaining why the “theory” in the 2007 paper is a complete dog’s breakfast
Part Six – Minor GHG’s – a less important aspect, but demonstrating the change in optical thickness due to the neglected gases N2O, CH4, CFC11 and CFC12.
Posted in Basic Science, Commentary, Debunking Flawed "Science" on April 26, 2011| 123 Comments »
In Part One we looked at the calculation of total atmospheric optical thickness.
In Part Two we looked at the claim that the surface and atmosphere exchanged exactly equal amounts of energy by radiation. A thermodynamics revolution if it is true, as the atmosphere is slightly colder than the surface. This claim is not necessary to calculate optical thickness but is a foundation for Miskolczi’s theory about why optical thickness should be constant.
In this article we will look at another part of Miskolczi’s foundational theory from his 2007 paper, Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Quarterly Journal of the Hungarian Meteorological Service.
For reference of the terms he uses, the diagram from the 2007 paper:
From Miskolczi (2007)
Figure 1
On pages 6-7, we find this claim:
Regarding the origin, EU is more closely related to the total internal kinetic energy of the atmosphere, which – according to the virial theorem – in hydrostatic equilibrium balances the total gravitational potential energy. To identify EU as the total internal kinetic energy of the atmosphere, the EU = SU / 2 equation must hold.
Many people have puzzled over the introduction of the virial theorem (note 1), which relates total kinetic energy of the atmosphere to total potential energy of the atmosphere. Generally, there is a relationship between potential energy and kinetic energy of an atmosphere so I don’t propose to question it, we will accept it as a given.
By the way, on the diagram SU = SG, i.e. SU = upwards radiation from the surface. And EU = upwards radiation from the atmosphere (cooling to space).
Kinetic Energy of a Gas
For people who don’t like seeing equations, skip to the statement in bold at the end of this section.
Here is the equation of an ideal gas:
pV = nkT (also written as pV = NRT) [1]
where p = pressure, V = volume, n = number of molecules, k = 1.38 x 10-23 J/K = Boltzmann’s constant, T = temperature in K
This equation was worked out via experimental results a long time ago. Our atmosphere is a very close approximation to an ideal gas.
If we now take a thought experiment of some molecules “bouncing around” inside a container we can derive an equation for the pressure on a wall in terms of the velocities of the molecules:
pV = Nm<vx²> [2]
where m = mass of a molecule, <vx²> = average of vx², where vx = velocity in the x direction
Combining [1] and [2] we get:
kT = m<vx²>, or
m<vx²>/2 = kT/2 [3]
The same considerations apply to the y and z direction, so
m<v²>/2 = 3KT/2 [4]
This equation tells us the temperature of a gas is equal to the average kinetic energy of molecules in that gas divided by a constant.
For beginners, the kinetic energy of a body is given by mv²/2 = mass x velocity squared divided by two.
So temperature of a gas is a direct measure of the kinetic energy.
The Kinetic Error
So where on earth does this identity come from?
..To identify EU as the total internal kinetic energy of the atmosphere..
EU is the upwards radiation from the atmosphere to space.
To calculate this value, you need to solve the radiative transfer equations, shown in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. These equations have no “analytic” solution but are readily solvable using numerical methods.
However, there is no doubt at all about this:
EU ≠ 3kTA/2 [5]
where TA = temperature of the atmosphere
that is, EU ≠ kinetic energy of the atmosphere
As an example of the form we might expect, if we had a very opaque atmosphere (in longwave), then EU = σTA4 (the Stefan-Boltzmann equation for thermal radiation). As the emissivity of the atmosphere reduces then the equation won’t stay exactly proportional to the 4th power of temperature. But it can never be linearly proportional to temperature.
Many people have puzzled over the equations in Miskolczi’s 2007 paper.
On p6:
The direct consequences of the Kirchhoff law are the next two equations:
EU = F + K + P (M5)
SU − (F0 + P0 ) = ED − EU (M6)
Note that I have added a prefix to the equation numbers to identify they as Miskolczi’s. As previously commented, the P term (geothermal energy) is so small that it is not worth including. We will set it to zero and eliminate it, to make it a little easier to see the problems. Anyone wondering if this can be done – just set F’ = F0 + P0 and replace F0 with F’ in the following equations.
So:
EU = F + K (M5a)
SU − F0 = ED − EU (M6a)
Please review figure 1 for explanation of the terms.
If we accept the premise that AA = ED then these equations are correct (the premise is not correct, as shown in Part Two).
M5a is simple to see. Taking the incorrect premise that surface radiation absorbed in the atmosphere is completely re-emitted to the surface: therefore, the upward radiation from the atmosphere, EU must be supplied by the only other terms shown in the diagram – convective energy plus solar radiation absorbed by the atmosphere.
What about equation M6a? Physically, what is the downward energy emitted by the atmosphere minus the upward energy emitted by the atmosphere? What is the surface upward radiation minus the total solar radiation?
Well, doesn’t matter if we can’t figure out what these terms might mean. Instead we will just do some maths, using the fact that the surface energy must balance and the atmospheric energy must balance.
First let’s write down the atmospheric energy balance:
AA + K + F = EU + ED [10] – I’m jumping the numbering to my equation 10 to avoid referencing confusion
This just says that Surface radiation absorbed in the atmosphere + convection from the surface to the atmosphere + absorbed solar radiation in the atmosphere = energy radiated by the atmosphere from the top and bottom.
Given the (incorrect) premise that AA = ED, we can rewrite equation 10:
K + F = EU [10a]
We can see that this matches M5a, which is correct, as already stated.
So first, let’s write down the surface energy balance:
F0 – F + ED = SU + K [11]
This just says that Solar radiation absorbed at the surface + downward atmospheric radiation = surface upward radiation + convection from the surface to the atmosphere.
Please review Figure 1 to confirm this equation.
Now let’s rewrite equation 11:
SU – F0 = ED – F – K [11a]
and inserting eq 10a, we get:
SU – F0 = ED -EU [11b]
Which agrees with M6a.
And as an aside only for people who have spent too long staring at these equations – re-arrange the terms in 11b:
Su – Ed = F0 – Eu; The left side is surface radiation – absorbed surface radiation in the atmosphere (accepting the flawed premise) = transmitted radiation. The right side is total absorbed solar radiation – upward emitted atmospheric radiation. As solar radiation is balanced by OLR, the right side is OLR – upward emitted atmospheric radiation = transmitted radiation.
Now, let’s see the mystery step :
In Eq. (6) SU − (F0 + P0 ) and ED − EU represent two flux terms of equal magnitude, propagating into opposite directions, while using the same F0 and P0 as energy sources. The first term heats the atmosphere and the second term maintains the surface energy balance. The principle of conservation of energy dictates that:
SU − (F0) + ED − EU = F0 = OLR (M7)
This equation M7 makes no sense. Note that again I have removed the tiny P0 term.
Let’s take [11b], already demonstrated (by accepting the premise) and add (ED -EU) to both sides:
SU – F0 + (ED – EU) = ED – EU+ (ED -EU) = 2(ED -EU) [12]
So now the left side of eq 12 matches the left side of M7.
The M7 equation can only be correct if the right side of eq 12 matches the right side of M7:
2(ED -EU) = F0 [13] – to be confirmed or denied
In concept, this claim is that downward radiation from the atmosphere minus upward radiation from the atmosphere = half the total planetary absorbed solar radiation.
I can’t see where this has been demonstrated.
It is not apparent from energy balance considerations – we wrote down those two equations in [10] and [11].
We can say that energy into the climate system = energy out, therefore:
F0 = OLR = EU + ST [14] (atmospheric upward radiation plus transmitted radiation through the atmosphere)
Which doesn’t move us any closer to the demonstration we are looking for.
Perhaps someone from the large fan club can prove equation 7. So many people have embraced Miskolczi’s conclusion that there must be a lot of people who understand this step.
I’m confused about equation 7 of Miskolczi.
Running with the odds, I expect that no one will be able to prove it and instead I will be encouraged to take it on faith. However, I’m prepared to accept that someone might be able to prove that it is true (with the caveat about accepting the premise already discussed).
The more important point is equating the kinetic energy of the atmosphere with the upward atmospheric radiation.
It’s a revolutionary claim.
But as it comes with no evidence or derivation and would overturn lots of thermodynamics the obvious conclusion is that it is not true.
To demonstrate it is true takes more than a claim. Currently, it just looks like confusion on the part of the author.
Perhaps the author should write a whole paper devoted to explaining how the upwards atmospheric flux can be equated with the kinetic energy – along with dealing with the inevitable consequences for current thermodynamics.
Update 31st May: The author confirmed in the ensuing discussion that equation 7 was not developed from theoretical considerations.
Other Articles in the Series:
The Mystery of Tau – Miskolczi – introduction to some of the issues around the calculation of optical thickness of the atmosphere, by Miskolczi, from his 2010 paper in E&E
Part Two – Kirchhoff – why Kirchhoff’s law is wrongly invoked, as the author himself later acknowledged, from his 2007 paper
Part Four – a minor digression into another error that seems to have crept into the Aa=Ed relationship
Part Five – Equation Soufflé – explaining why the “theory” in the 2007 paper is a complete dog’s breakfast
Part Six – Minor GHG’s – a less important aspect, but demonstrating the change in optical thickness due to the neglected gases N2O, CH4, CFC11 and CFC12.
Further Reading:
New Theory Proves AGW Wrong! – a guide to the steady stream of new “disproofs” of the “greenhouse” effect or of AGW. And why you can usually only be a fan of – at most – one of these theories.
Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Miskolczi, Quarterly Journal of the Hungarian Meteorological Service (2007)
Note 1 – A good paper on the virial theorem is on arXiv: The Virial Theorem and Planetary Atmospheres, Victor Toth (2010)
Posted in Basic Science, Commentary, Debunking Flawed "Science" on April 25, 2011| 87 Comments »
In Part One we looked at the usefulness of “tau” = optical thickness of the atmosphere.
Miskolczi has done a calculation (under cloudless skies) of the total optical thickness of the atmosphere. The reason he is apparently the first to have done this in a paper is explained in Part One.
The 2010 paper referenced the 2007 paper, Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Quarterly Journal of the Hungarian Meteorological Service.
The 2010 paper suggested an elementary flaw, but referenced the 2007 paper. The 2007 paper backed up the approach with the same apparently flawed claim.
The flaw that I will explain doesn’t affect the calculation of optical thickness, τ. But it does appear to affect the theoretical basis for why optical thickness should be a constant.
First, the graphic explaining the terms is here:
From Miskolczi (2007)
Figure 1
The 2010 paper said:
One of the first and most interesting discoveries was the relationship between the absorbed surface radiation and the downward atmospheric emittance. According to Ref. 4, for each radiosonde ascent the
ED = AA = SU – ST = SU(1− exp(−τA)) = SU(1− TA ) = SU.A (5)
relationships are closely satisfied. The concept of radiative exchange was the discovery of Prevost [17]. It will be convenient here to define the term radiative exchange equilibrium between two specified regions of space (or bodies) as meaning that for the two regions (or bodies) A and B, the rate of flow of radiation emitted by A and absorbed by B is equal to the rate of flow the other way, regardless of other forms of transport that may be occurring.
Ref. 4 is the 2007 paper, which said:
According to the Kirchhoff law, two systems in thermal equilibrium exchange energy by absorption and emission in equal amounts, therefore, the thermal energy of either system can not be changed. In case the atmosphere is in thermal equilibrium with the surface, we may write that..
What is “thermal equilibrium“?
It is when two bodies are in a closed system and have reached equilibrium. This means they are at the same temperature and no radiation can enter or leave the system. In this condition, energy emitted from body A and absorbed by body B = energy emitted from body B and absorbed by body A.
Kirchhoff showed this radiative exchange must be equal under the restrictive condition of thermal equilibrium. And he didn’t show it for any other condition. (Note 2).
However, the earth’s surface and the atmosphere are not in thermal equilibrium. And, therefore, energy exchanged between the surface and the atmosphere via radiation is not proven to be equal.
Dr. Roy Spencer has a good explanation of the fallacy and the real situation on his blog. One alleged Miskolczi supporter took him to task for misinterpreting something – here:
With respect, Dr Spencer, it is not reasonable, indeed it verges on the mischievous, to write an allegation that Miskolczi means that radiative exchange is independent of temperature. Miskolczi means no such thing. To make such an allegation is to ignore the fact that Miskolczi uses the proper laws of physics in his calculations. Of course radiative exchange depends on temperature, and of course Miskolczi is fully aware of that.
and here:
..Planck uses the term for a system in thermodynamic equilibrium, and the present system is far from thermodynamic equilibrium, but the definition of the term still carries over..
I couldn’t tell whether the claimed “misinterpretation” by Spencer was of the real law or the Miskolczi interpretation. And this article will demonstrate that the proper laws of physics have been ignored.
And I have no idea whether the Miskolczi supporter represented the real Miskolczi. However, a person of the same name is noted by Miskolczi for his valuable comments in producing the 2010 paper.
Generally when people claim to overturn decades of research in a field you expect them to take a bit of time to explain why everyone else got it wrong, but apparently Dr. Spencer was deliberately misinterpreting something.. and that “something” is very clear only to Miskolczi supporters.
After all, the premise in the referenced 2007 paper was:
According to the Kirchhoff law, two systems in thermal equilibrium exchange energy by absorption and emission in equal amounts, therefore, the thermal energy of either system can not be changed. In case the atmosphere is in thermal equilibrium with the surface, we may write that..
Emphasis added.
So if the atmosphere is not in thermal equilibrium with the surface, we can’t write the above statement.
And as a result the whole paper falls down. Perhaps there are other gems which stand independently of this flaw and I look forward to a future paper from the author when he explains some new insights which don’t rely on thermodynamic equilibrium being applied to a world without thermodynamic equilibrium.
If you put two bodies, A & B, at two different temperatures, TA and TB, into a closed system then over time they will reach the same temperature.
Let’s suppose that TA > TB. Therefore, A will radiate more energy towards B than the reverse. These bodies will reach equilibrium when TA = TB (note 1).
At this time, and not before, we can say that ” ..two systems in thermal equilibrium exchange energy by absorption and emission in equal amounts”. (Note 2).
Obviously, before equilibrium is reached more energy is flowing from A to B than the reverse.
Let’s consider a case like the sun and the earth. The earth absorbs around 240 W/m² from the sun. The sun absorbs a lot less from the earth.
Let’s just say it is a lot less than 1 W/m². Someone with a calculator and a few minutes spare can do the sums and write the result in the comments.
No one (including of course the author of the paper) would suggest that the sun and earth exchange equal amounts of radiation.
However, they are in the condition of “radiative exchange”.
The earth’s surface and the bottom of the atmosphere are at similar temperatures. Why is this?
It is temperature difference that drives heat flow. The larger the temperature difference the greater the heat flow (all other things remaining equal). So any closed system tends towards thermal equilibrium. If the earth and the atmosphere were left in a closed system, eventually both would be at the same temperature.
However, in the real world where the climate system is open to radiation, the sun is the source of energy that prevents thermal equilibrium being reached.
The bottom millimeter of the atmosphere will usually be at the same temperature as the earth’s surface directly below. If the bottom millimeter is stationary then it will be warmed by conduction until it reaches almost the surface temperature. But 10 meters up the temperature will probably reduce just a little. At 1 km above the surface the temperature will be between 4 K and 10 K cooler than the surface.
Note: Turbulent heat exchange near the surface is very complex. This doesn’t mean that there is confusion about the average temperature profile vs height through the atmosphere. On average, temperature reduces with height in a reasonably predictable manner.
According to Miskolczi:
AA = ED [4]
Referring to the diagram, AA is energy absorbed by the atmosphere from the surface, and ED is energy radiated from the atmosphere to the surface.
Why should this equality hold?
The energy from the surface to the atmosphere = AA+ K (note 3), where K is convection.
The energy absorbed in total by the atmosphere = AA + K + F, where F is absorbed solar radiation in the atmosphere.
The energy emitted by the atmosphere = ED + EU , where EU is the energy radiated from the top of the atmosphere.
Therefore, using the First Law of Thermodynamics for the atmosphere:
AA + K + F = ED + EU + energy retained
i.e., energy absorbed = energy lost – energy retained
No other equality relating to the atmospheric fluxes can be deduced from the fundamental laws of thermodynamics.
In general, because the atmosphere and the earth’s surface are very close in temperature, AA will be very close to ED.
It is important to understand that absorptivity for longwave radiation will be equal to emissivity for longwave radiation (see Planck, Stefan-Boltzmann, Kirchhoff and LTE), therefore, if the surface and the atmosphere are at the same temperature then the exchange of radiation will be equal.
Where does the atmosphere radiate from, on average? Well, not from the bottom meter. It depends on the emissivity of the atmosphere. This varies with the amount of water vapor in the atmosphere.
The atmospheric temperature reduces with height- by an average of around 6.5 K/km – and unless the atmospheric radiation was from the bottom few meters, the radiation from the atmosphere to the surface must be lower than the radiation absorbed from the surface by the atmosphere.
If radiation was emitted from an average of 100 m above the surface then the effective temperature of atmospheric radiation would be 0.7 K below the surface temperature. If radiation was emitted from an average of 200 m above the surface then the effective temperature of atmospheric radiation would be 1.3 K below the surface temperature.
For people still thinking about this subject, a simple mathematical proof.
Temperature of the atmosphere, from the average height of emission, Ta
Temperature of the surface, Ts
Emissivity of the atmosphere = εa
Absorptivity of the atmosphere for surface radiation = αa
If Ta is similar to Ts then εa ≈ αa (note 4).
(In the paper, the emissivity (and therefore absorptivity) of the earth’s surface is assumed = 1).
Surface radiation absorbed by the atmosphere, AA = αaσTs4 .
Atmospheric radiation absorbed by the surface, ED = εaσTa4 .
Therefore, unless Ta = Ts, AA ≠ ED .
If Roy Spencer’s experience is anything to go by, I may now be accused of deliberately misunderstanding something.
Well, words can be confused – even though they seem plain enough in the extract shown. But the paper also asserts the mathematical identity:
AA = ED [4]
I have demonstrated that:
AA ≠ ED [4]
I don’t think there is much to be misunderstood.
Two bodies at different temperatures will NOT exchange exactly equal amounts of radiation. It is impossible unless the current laws of thermodynamics are wrong.
As a more technical side note.. because εa ≈ αa and not necessarily an exact equality, it is possible for the proposed equation to be asserted in the following way:
AA = ED if, and only if, the following identity is always true, αa(Ts)σTs4 = εa(Ta)σTa4 .
Therefore:
Ts/Ta = (εa(Ta)/αa(Ts))1/4 [Equation B]
– must always be true for equation 4 of Miskolczi (2007) to be correct. Or must be true over whatever time period and surface area his identity is claimed to be true.
Another quote from the 2007 paper:
The popular explanation of the greenhouse effect as the result of the LW atmospheric absorption of the surface radiation and the surface heating by the atmospheric downward radiation is incorrect, since the involved flux terms (AA and ED) are always equal.
Emphasis added.
Note in Equation B that I have made explicit the dependence of emissivity on the temperature of the atmosphere at that time, and the dependence of absorptivity on the temperature of the surface.
Emissivity vs wavelength is a material property and doesn’t change with temperature. But because the emission wavelengths change with temperature the calculation of εa(Ta) is the measured value of εa at each wavelength weighted by the Planck function at Ta.
It is left as an exercise for the interested student to prove that this identity, Equation B, cannot always be correct.
In Fig. 2 we present large scale simulation results of AA and ED for two measured diverse planetary atmospheric profile sets. Details of the simulation exercise above were reported in Miskolczi and Mlynczak (2004). This figure is a proof that the Kirchhoff law is in effect in real atmospheres. The direct consequences of the Kirchhoff law are the next two equations:
EU = F + K + P (5)
SU − (F0 + P0 ) = ED − EU (6)The physical interpretations of these two equations may fundamentally change the general concept of greenhouse theories.
From Miskolczi (2007)
Figure 2
This is not a proof of Kirchhoff’s law, which is already proven and is not a law that radiative exchanges are equal when temperatures are not equal.
Instead, this is a demonstration that the atmosphere and earth’s surface are very close in temperature.
Here is a simple calculation of the ratio of AA:ED for different downward emitting heights (note 5), and lapse rates (temperature profile of the atmosphere):
Figure 3
Essentially this graph is calculated from the formula in the maths section and a calculation of the atmospheric temperature, Ta, from the height of average downward radiation and the lapse rate.
Reading the claims by the supporters of Miskolczi at Roy Spencer’s blog, you read that:
So the supporters claim.
Read the paper, that’s my recommendation. The 2010 paper references the 2007 paper for equation 4. The 2007 paper says (see larger citation above):
..This figure is a proof that the Kirchhoff law is in effect in real atmospheres..
In fact, this is the important point:
Anyone who didn’t believe that it was a necessary consequence of Kirchhoff would be writing the equations in the maths section above (which come from well-proven radiation theory) and realizing that it is impossible for AA = ED.
And they wouldn’t be claiming that it demonstrated Kirchhoff’s law. (After all, Kirchhoff’s law is well-proven and foundational thermodynamics).
However, it is certain that on average ED < AA but very close to AA.
From time to time, Miskolczi fans have appeared on this blog and written interesting comments. Why the continued fascination with the exact amount of radiation transmitted from the surface through the atmospheric window?
I have no idea whether this point is of interest to anyone else..
One of the comments highlighted the particular claim and intrigued me.
Yes, indeed, that’s right: Simpson discovered the atmospheric window in 1928. It was not till the work of Miskolczi in 2004 and 2007 that it was discovered that practically all the radiative cooling of the land-sea surface is by radiation direct to space.
Apart from the (unintentional?) humor inherent in the Messianic-style claim, the reason why this claim is a foundational point for Miskolczi-ism is now clear to me.
If exactly all of the radiation absorbed by the atmosphere is re-radiated to the surface and absorbed by the surface (AA = ED) then these points follow for certain:
A curiosity only.
Miskolczi claims:
The physical interpretations of these two equations may fundamentally change the general concept of greenhouse theories.
He is being too modest.
If it turns out that AA = ED then it will overturn general radiative theory as well.
Or demonstrate that the atmosphere is much more opaque than has currently been calculated (for all of the downward atmospheric radiation to take place from within a few tens of meters of the surface).
This in turn will require the overturning of some parts of general radiative theory, or at least, a few decades of spectroscopic experiments, which consequently will surely require the overturning of..
How is it possible to claim that AA = ED and not work through the basic consequences (e.g., the equations in the maths section above) to deal with the inevitable questions on thermodynamics basics?
Why claim that it has fundamentally changed the the general concept of the inappropriately-named “greenhouse” theory when it – if true – has overturned generally accepted radiation theory?
Interested observers might wonder about the size of the error bars in Figure 2. (And for newcomers, the values in Figure 2 are not measured values of radiation, they are calculated absorption and emission).
As already suggested, perhaps there are useful gems somewhere in the 40 pages of the 2007 paper, but when someone is so clear about a foundational point for their paper that is so at odds with foundational thermodynamic theory and the author doesn’t think to deal with that.. well, it doesn’t generate hope.
Update 31st May – the author comments in the ensuing discussion that Aa=Ed is an “experimental” conclusion. In Part Four I show that the “approximate equality” must be an error for real (non-black) surfaces, and Ken Gregory, armed with the Miskolczi spreadsheet, later confirms this.
Other Articles in the Series:
The Mystery of Tau – Miskolczi – introduction to some of the issues around the calculation of optical thickness of the atmosphere, by Miskolczi, from his 2010 paper in E&E
Part Three – Kinetic Energy – why kinetic energy cannot be equated with flux (radiation in W/m²), and how equation 7 is invented out of thin air (with interesting author comment)
Part Four – a minor digression into another error that seems to have crept into the Aa=Ed relationship
Part Five – Equation Soufflé – explaining why the “theory” in the 2007 paper is a complete dog’s breakfast
Part Six – Minor GHG’s – a less important aspect, but demonstrating the change in optical thickness due to the neglected gases N2O, CH4, CFC11 and CFC12.
Further Reading:
New Theory Proves AGW Wrong! – a guide to the steady stream of new “disproofs” of the “greenhouse” effect or of AGW. And why you can usually only be a fan of – at most – one of these theories.
Greenhouse Effect in Semi-Transparent Planetary Atmospheres, Miskolczi , Quarterly Journal of the Hungarian Meteorological Service (2007)
The Stable Stationary Value of the Earth’s Global Average Atmospheric Planck-Weighted Greenhouse-Gas Optical Thickness, Miskolczi, Energy & Environment(2010)
The Theory of Heat Radiation, Max Planck, P. Blakiston’s Son & Co (1914) : a translation of Waermestrahlung (1913) by Max Planck.
Note 1 – Of course, in reality equilibrium is never actually reached. As the two temperatures approach each other, the difference in energy exchanged is continually reduced. However, at some point the two temperatures will be indistinguishable. Perhaps when the temperature difference is less than 0.1°C, or when it is less than 0.0000001°C..
Therefore, it is conventional to talk about “reaching equilibrium” and no one in thermodynamics is confused about the reality of the above point.
Note 2 – Max Planck introduces thermodynamic equilibrium:
Note 3 – Geothermal energy is included in the diagram (P0). Given that it is less than 0.1 W/m² – below the noise level of most instruments measuring other fluxes in the climate – there is little point in cluttering up the equations here with this parameter.
Note 4 – Emissivity and absorptivity are wavelength dependent parameters. For example, snow is highly reflective for solar radiation but highly absorbing (and therefore emitting) for terrestrial radiation.
At the same wavelength, emissivity = absorptivity. This is the result of Kirchhoff’s law.
If the temperature of the source radiation for which we need to know the absorptivity is different from the temperature of the emitting body then we cannot assume that emissivity = absorptivity.
However, when the temperature of source body for the radiation being absorbed is within a few Kelvin of the emitting body then to a quite accurate assumption, absorptivity = emissivity.
For example, the radiation from a source of 288K is centered on 10.06 μm, while for 287 K it is centered on 10.10 μm. Around this temperature, the central wavelength decreases by about 0.035 μm for each 1 K change in temperature.
An example of when it is a totally incorrect assumption is for solar radiation absorbed by the earth. The solar radiation is from a source of about 5800 K and centered on 0.5 μm, whereas the terrestrial radiation is from a source of around 288 K and centered on 10 μm. Therefore, to assume that the absorptivity of the earth’s surface for solar radiation is equal to the emissivity of the earth’s surface is a huge mistake.
This would be the same as saying that absorptivity at 0.5 μm = emissivity at 10 μm. And, therefore, totally wrong.
Note 5: What exactly is meant by average emitting height? Emitted radiation varies as the 4th power of temperature and as a function of emissivity, which itself is a very non-linear function of quantity of absorbers. Average emitting height is more of a conceptual approach to illustrate the problem.
 | pjmacha on Extreme Weather #17 – Mo… |
 | E. Schaffer on Clouds & Water Vapor – Par… |
| E. Schaffer on Clouds & Water Vapor – Par… |
 | Rok Adamlje on Clouds and Water Vapor –… |
| Everything You Need… on Sensible Heat, Latent Heat and… | |
 | Philip Schmidt on The “Greenhouse” E… |
| Philip Schmidt on The Real Second Law of Th… |
 | Barton Paul Levenson on Opinions and Perspectives… |
| Your Guide to Gambli… on Natural Variability and Chaos… | |
 | Mane Oliva on The Amazing Case of “Bac… |
 | Tucker C on Heat Transfer Basics – P… |
 | Alll Teens Relate on Stratospheric Cooling |
 | DeWitt Payne on Clouds & Water Vapor – Par… |
| DeWitt Payne on The Imaginary Second Law of… |
 | Ivan on The Imaginary Second Law of… |
The Science of Doom 
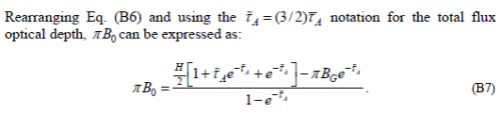
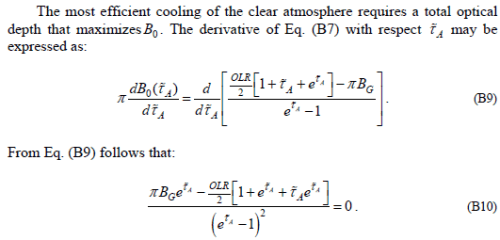
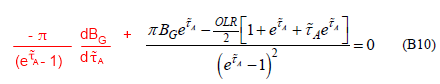
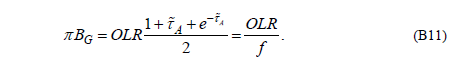
Kramm & Dlugi On Illuminating the Confusion of the Unclear
Posted in Basic Science, Commentary on January 3, 2012| 242 Comments »
Many people are confused about science basics when it comes to the inappropriately-named “greenhouse” effect.
This can be easily demonstrated in many blogs around the internet where commenters, and even blog owners, embrace multiple theories that contradict each other but are somehow against the “greenhouse” effect.
Recently a new paper: Scrutinizing the atmospheric greenhouse effect and its climatic impact by Gerhard Kramm & Ralph Dlugi was published in the journal Natural Science.
Because of their favorable comments about Gerlich & Tscheuschner and the fact that they are sort of against something called the “greenhouse” effect I thought it might be useful for many readers to find out what was actually in the paper and what Kramm & Dlugi actually do believe about the “greenhouse” effect.
Much of the comments on blogs about the “greenhouse” effect are centered around the idea that this effect cannot be true because it would somehow violate the second law of thermodynamics. If there was a scientific idea in Gerlich & Tscheuschner, this was probably the main one. Or at least the most celebrated.
So it might surprise readers who haven’t opened up this paper that the authors are thoroughly 100% with mainstream climate science (and heat transfer basics) on this topic.
It didn’t surprise me because before reading this paper I read another paper by Kramm – A case study on wintertime inversions in Interior Alaska with WRF, Mölders & Kramm, Atmospheric Research (2010).
This 2010 paper is very interesting and evaluates models vs observations of the temperature inversions that take place in polar climates (where the temperature at the ground in wintertime is cooler than the atmosphere above). Nothing revolutionary (as with 99.99% of papers) and so of course the model used includes a radiation scheme from CAM3 (=Community Atmospheric Model) that is well used in standard climate science modeling.
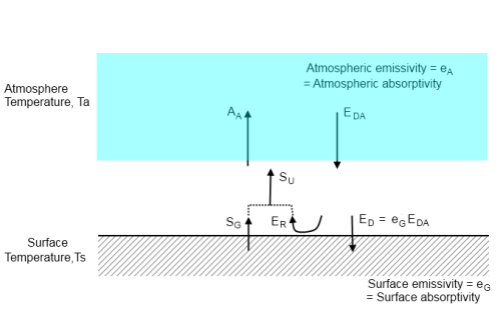
Here is an important equation from Kramm & Dlugi’s recent paper for the energy balance at the earth’s surface.
Lots of blogs “against the greenhouse effect” don’t believe this equation:
Figure 1
The highlighted term is the downward radiation from the atmosphere multiplied by the absorptivity of the earth’s surface (its ability to absorb the radiation). This downward radiation (DLR) has also become known as “back radiation”.
In simple terms, the energy balance of Kramm & Dlugi adds up the absorbed portions of the solar radiation and atmospheric longwave radiation and equates them to the emitted longwave radiation plus the latent and sensible heat.
So the temperature of the surface is determined by solar radiation and “back radiation” and both are treated equally. It is also determined of course by the latent and sensible heat flux. (And see note 1).
As so many people on blogs around the internet believe this idea violates the second law of thermodynamics I thought it would be helpful to these readers to let them know to put Kramm & Dlugi 2011 on their “wrong about the 2nd law” list.
Of course, many people “against the greenhouse thing” also – or alternatively – believe that “back radiation” is negligible. Yet Kramm & Dlugi reproduce the standard diagram from Trenberth, Fasullo & Kiehl (2009) and don’t make any claim about “back radiation” being different in value from this paper.
“Back radiation” is real, measurable and affects the temperature of the surface – clearly Kramm & Dlugi are AGW wolves in sheeps’ clothing!
I look forward to the forthcoming rebuttal by Gerlich & Tscheuschner.
In the followup article, Kramm & Dlugi On Dodging the “Greenhouse” Bullet, I will attempt to point out the actual items of consequence from their paper.
Further reading – Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part One and New Theory Proves AGW Wrong!
Note 1 – The surface energy balance isn’t what ultimately determines the surface temperature. The actual inappropriately-named “greenhouse” effect is determined by:
Read Full Post »