The Science of Doom

In Part Two, we looked at the beginnings of a very simple 1-d model for examining how the atmosphere interacts with radiation from the surface.

Simplification aids understanding so the model has some fictious gases which absorb radiation – pCO2 (pretend CO2) and pH2O (pretend water vapor). We saw that as the concentrations of pCO2 were increased we stopped seeing a change in “top of atmosphere” (TOA) flux.

That is, the “greenhouse” effect became “saturated” as the pCO2 concentration was increased.

Of course, the model was flawed. The model only included absorption of radiation by the atmosphere, with no emission. There are other over-simplifications and progressively we will try and consider them.

Emission

Once the atmosphere can emit as well as absorb radiation the results change.

The model has been updated, and for these results is now at v3.1 (see note 5).

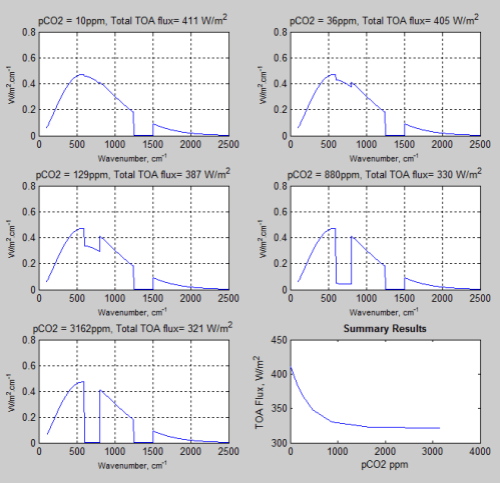
Here is a comparison of “no emission” vs “emission”. In each case 10 runs were carried out of different pCO2 concentrations. Each graph shows:

• TOA spectral results for runs 1, 5 and 10
• Surface spectral downward radiation (DLR or “back radiation) for the last run
• Temperature profile for the last run
• Summary graph of flux vs concentration changes for all 10 runs

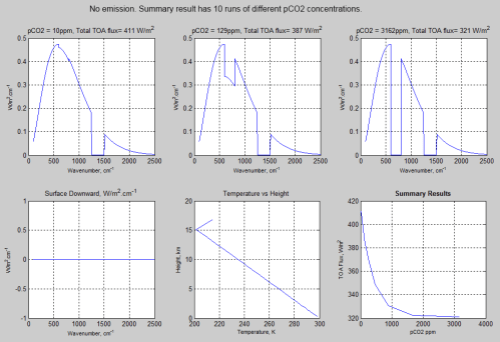
No emission:

Figure 1 – Click for a larger view

Note that the surface downward radiation is zero. This is because the atmosphere doesn’t emit radiation in this model.

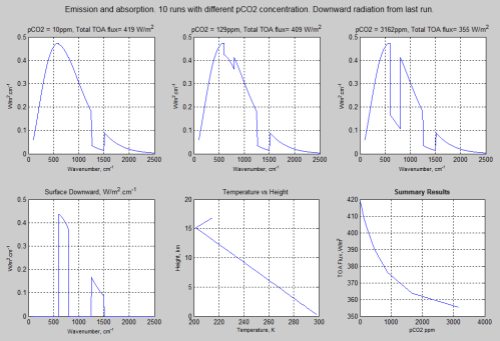
With emission:

Figure 2 – Click for a larger image

If you compare the spectral results you can see that in the “no emission” case the “pretend water vapor” (pH2O) band of wavenumbers 1250-1500 cm^-1 is in “saturation”, whereas in the “emission” case, it isn’t.

This is just the natural result of an atmosphere that re-emits – and of course, gases that absorb at a given wavelength also emit at that same wavelength. (See Planck, Stefan-Boltzmann, Kirchhoff and LTE).

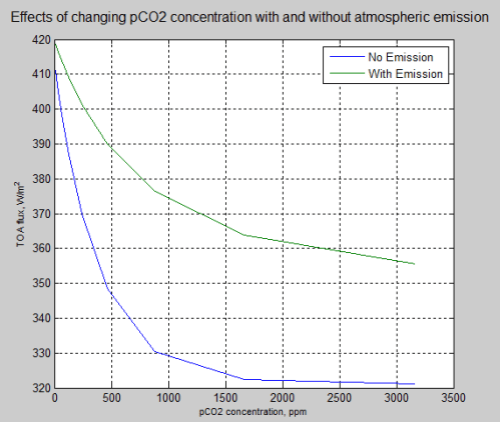
And a comparison of the 10 runs between the two models:

Figure 3

As the concentration of pCO2 increases the TOA flux reduces. Of course, we can see that this effect diminishes with more pCO2.

One interesting idea is to show these results as radiative forcing. (You can find a more formal definition of the term in CO2 – An Insignificant Trace Gas? Part Seven – The Boring Numbers – although here it is not calculated according to the strict definition of allowing stratospheric adjustment)

In essence radiative forcing is the change in TOA flux. When less flux escapes this is considered a positive radiative forcing. The reason is this: less flux radiated from the climate system means that less energy is leaving, which means the climate will heat (all other things being equal).

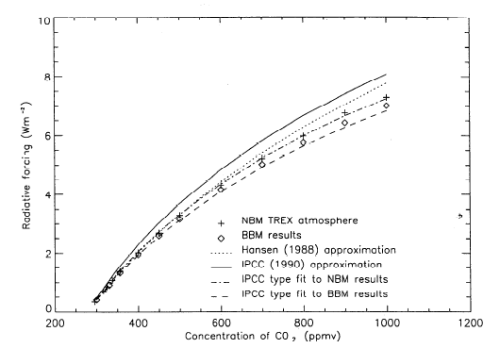
Here is the same graph expressed as radiative forcing:

Figure 4

If you compare it with the IPCC graph in Part Two (or Part Seven of the CO2 series) you will see it has some similarities:

Figure 5

Note that the actual values of radiative forcing in this model are much higher – in part because we are comparing the results of a gas with made up properties and also because we are comparing the effect from ZERO concentration of the gas vs a very high concentration.

However, one point should be clear. Using the very simple Beer-Lambert law of absorption, and the very well-known (but not so simple) Planck law of emission we find that the “radiative forcing” for changing concentrations of one gas doesn’t look like the Beer-Lambert law of absorption..

Real World Complexity

The very simple model here – with emission – will eventually reach “saturation”.

The much more complex real-world “line by line” models eventually reach “saturation” but at much higher concentrations of CO2 than we expect to see in the climate.

This model is still a very simple model designed for education of the basics – and to allow inspection of the code.

The model has no overlaps between absorbing molecules and has no effects from the weaker lines at the edges of a band.

Reducing Emission and “The Greenhouse Effect”

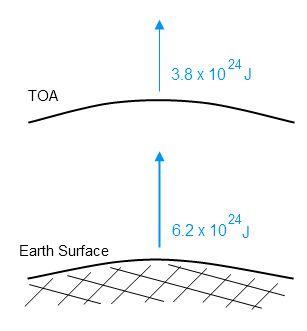
As emission of radiation is reduced due to increases in absorbing gases, with all other things being equal, the planet must warm up. It must warm up until the emission of radiation again balances the absorbed radiation (note 1).

Another way to consider the effect is to think about where the radiation to space comes from in the atmosphere. As the opacity of the atmosphere increases the radiation to space must be from a higher altitude. See also The Earth’s Energy Budget – Part Three.

Higher altitudes are colder and so the radiation to space is a lower value. Less radiation from the climate means the climate warms.

As the climate warms, if the lapse rate (note 3) stays the same, eventually the radiation to space – from this higher altitude – will match the absorbed solar radiation. This is how increases in radiatively active gases (aka “greenhouse” gases) affect the surface temperature (see note 4).

The Model

The equations will be covered more thoroughly in a later article in this series.

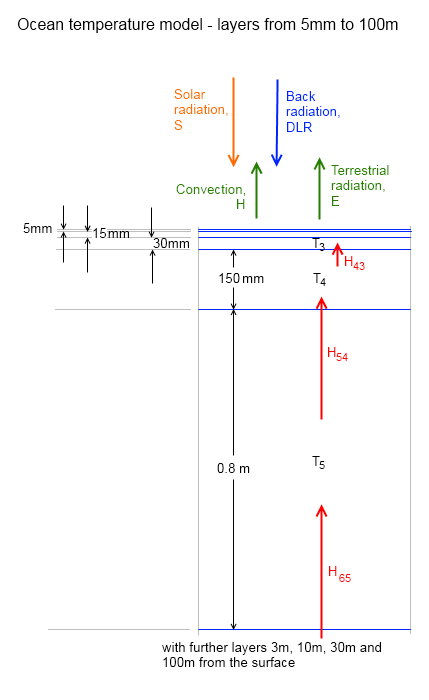
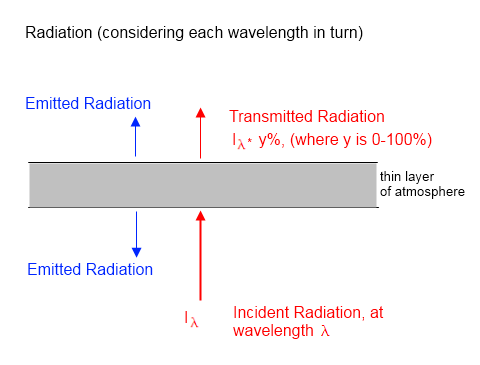
The essence of the model is captured in this diagram for one “layer”:

Figure 6 – One layer from the model

The atmosphere is broken up into a number of layers. In these model runs this was set to 30 layers with a minimum pressure of 10,000 Pa (about 17km). The “boundary condition” for radiation from the surface was Planck law radiation from a surface of 300K (27°C) with an emissivity of 0.98. And the “boundary condition” for radiation from TOA was zero.

This is because we are considering “longwave radiation”. A further complication would be to consider an absorber (like CO2) which absorbs solar radiation, but this has not been done in this model. Absorbers of “shortwave” radiation trap energy in the atmosphere rather than allowing it to be absorbed at the surface. Therefore, they affect the “in planetary balance” but don’t significantly affect the total energy absorbed.

The transmissivity at each wavenumber for each layer was calculated. Absorptivity = 1- transmissivity (note 2).

So for each layer – and each wavenumber interval – the transmitted radiation (incident radiation x transmissivity) was calculated for each wavenumber. This was done separately for up and down radiation. The emitted radiation was calculated by the Planck formula and the emissivity (= absorptivity at that wavenumber).

The net energy absorbed as a result changed the temperature, and the model iterated through many time steps to find the final result.

With the very simple pCO2 and pH2O properties the number of timesteps made almost no difference to the TOA flux. The stratospheric temperature did vary, something for further investigation.

The wavenumber interval, dv = 5cm^-1, was changed to see the results. Very small changes were observed as dv changed from 5cm^-1 to 1cm^-1. This is not surprising as the absorbing properties of these molecules is very simple.

Conclusion

The model is still very simple.

The changes in TOA fluxes are significantly different for the unrealistic “no emission” case vs the “emission” case. This is to be expected.

As concentration of pCO2 increases the TOA flux reduces but by progressively smaller amounts.

When we review the results as “radiative forcing” we find that even with this simple model they resemble the IPCC “logarithmic forcing result”.

There’s more to think about with real-world gases and absorption.

Hopefully this article helps people who are trying to understand the basics a little better.

And surely there must be mistakes in the code. Anyone who sees anything questionable, please comment. You will probably be correct.

People trying to do these calculations in their head, or with a pocket calculator, will be wrong. Unless they are mathematical savants. Playing the odds here.. when someone says (on this subject): “I can see that …” or “It’s clear that..” without a statement of the radiative transfer equations and boundary conditions plus their solutions to the problem – I expect that they haven’t understood the problem. And mathematical savants still need to explain to rest of us how they reached their results.

Other articles:

Part One – a bit of a re-introduction to the subject

Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only

Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.

Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”

Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies

Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking

And Also –

Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.

Notes

Note 1: Simplifications aid understanding. But in the current “climate” where many assume that climate science doesn’t understand complexity it is worth explaining a little further. Words from others neatly describe the subject of “equilibrium”:

The dominant factor determining the surface temperature of a planet is the balance between the net incoming solar radiation and outgoing thermal infra-red radiation.

That is, radiative equilibrium can be assumed for most practical purposes, although strictly speaking it is never achieved, as time-dependent and non-radiative processes are always present..

I.M. Vardavas & Prof. F.W. Taylor, Radiation and Climate, Oxford University Press (2007)

Note 2: Scattering of solar radiation is important, but scattering of longwave (terrestrial radiation) is very small and can be neglected. Therefore, Absorption = 1 – Transmission.

Note 3: Lapse rate is the temperature change with altitude – typically a reduction of 6.5K per km. This is primarily governed by “adiabatic expansion” and is affected by the amount of water vapor in the atmosphere. See Venusian Mysteries and the following articles for more.

Note 4: The explanations here do not include the effects of feedback. Feedback is very important, but separating different effects is important for understanding.

Note 5: The model still has many simplifications. The Matlab code:

RTE v0.3.1

It is easier to read by downloading the word doc. But pasted here below for reference. The two functions called are already documented in Part Two (and have not changed).

Matlab has many great features, but they also mean that some aspects of the code might not be clear. Feel free to ask questions.

I already see that a comment doesn’t match the code. The time step, tstep=3600*3 is 3 hrs not 12 hrs, as the comment says. However, this doesn’t alter the results.

======= v 0.3.1 ================

% RTE = Radiative transfer equations in atmosphere

% Objective – allow progressively more complex applications

% to help people see what happens in practice in the atmosphere

% v0.2 allow iterations of one (or more) parameter to find the TOA flux vs

% changed parameter

% v0.3 add emissivity = absorptivity ; as a function of wavelength. Also

% means that downward and upward radiation must be solved, plus iterations

% to allow temperature to change to find stable solution. Use convective

% adjustment to the lapse rate

% v0.3.1 changes the method of defining the atmosphere layers for radiation

% calculations, to have roughly constant mass for each layer

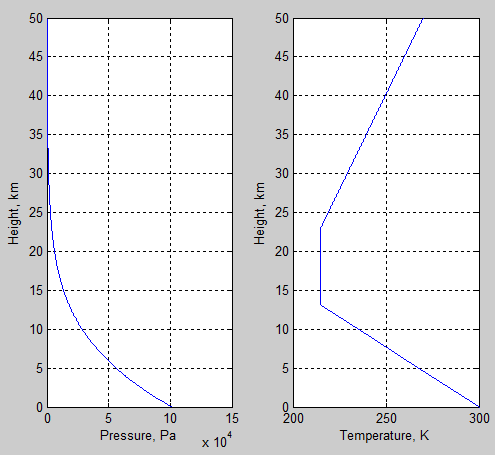
% Define standard atmosphere against height

% zr = height, pr = pressure, Tr = temperature, rhor = density, all in SI units

Ts=300; % define surface temperature

ps=1.013e5; % define surface pressure

% nmv=2.079e25; % nmv x rho = total number of molecules per m^3, not yet

% used

maxzr=50e3; % height of atmosphere

numzr=2001; % number of points used to define real atmosphere

zr=linspace(0,maxzr,numzr); % height vector from sea level to maxzr

[pr Tr rhor ztropo] = define_atmos(zr,Ts,ps); % function to determine (or lookup) p, T & rho

% Consider atmosphere in a coarser resolution than used for calculating

% pressure, temperature etc

% z, p,T,rho; subset of values used for RTE calcs

numz=30; % number of layers to consider

minp=1e4; % top of atmosphere to consider in pressure (Pa)

% want to divide the atmosphere into equal pressure changes

dp=(pr(1)-minp)/(numz); % finds the pressure change for each height change

zi=zeros(1,numz); % zi = lookup vector to “select” heights, pressures etc

for i=1:numz % locate each value

zi(i)=find(pr<=(pr(1)-i*dp), 1); % gets the location in the vector where

% pressure is that value

end

% now create the vectors of coarser resolution atmosphere

z=zr(zi);   % height

p=pr(zi);   % pressure

T=Tr(zi);   % original temperature

rho=rhor(zi);  % density

for i=2:numz

dz(i)=z(i)-z(i-1); % precalculate thickness of each layer

end

% ============ Set various values =========================

lapse=6.5e-3; % environmental lapse rate in K/m ** note potential conflict with temp profile already determined

% currently = max lapse rate for convective adjustment, but not used to

% define initial temperature profile

ems=0.98; % emissivity of surface

cp=1000; % specific heat capacity of atmosphere, J/K.kg

convadj=true; % === SET TO true === for convective adjustment to lapse rate = lapse

emission=true; % ==== SET TO true ==== for the atmosphere to emit radiation

% work in wavenumber, cm^-1

dv=5;

v=100:dv:2500; % wavenumber (=50um – 4um)

numv=length(v);

rads=ems.*planckmv(v,Ts); % surface emissive spectral power vs wavenumber v

% ============== Introducing the molecules ==============================

% need % mixing in the atmosphere vs height, % capture cross section per

% number per frequency, pressure & temperature broadening function

nummol=2; % number of radiatively-active gases

mz=ones(nummol,numz); % initialize mixing ratios of the gases

% specific concentrations

% pH2O = pretend H2O

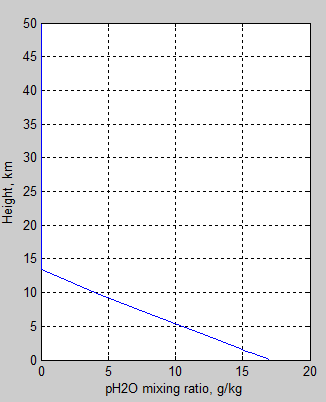
emax=17e-3; % max mixing ratio (surface) of 17g/kg

mz(1,:)=(ztropo-z).*emax./ztropo; % straight line reduction from surface to tropopause

mz(1,(mz(1,:)<0))=5e-6; % replace negative values with 5ppm, ie, for heights above tropopause

% pCO2 = pretend CO2

mz(2,:)=3.6e-4; % 360ppm

% absorption coefficients

k1=0.3; % arbitrary pick – in m2/kg while we use rho

k2=0.3; % likewise

a=zeros(nummol,length(v)); % initialize absorption coefficients

a(1,(v>=1250 & v<=1500))=k1;  % wavelength dependent absorption

a(2,(v>=600 & v<=800))=k2;    % ” ”

% === Scenario loop to change key parameter for which we want to see the effect

%

nres=10; % number of results to calculate

flux=zeros(1,nres); % TOA flux for each change in parameter

par=zeros(1,nres); % parameter we will alter

% this section has to be changed depending on the parameter being changed

% now = CO2 concentration

par=logspace(-5,-2.5,nres); % values vary from 10^-5 (10ppm) to 10^-2.5 (3200ppm)

% par=0.01; % kept for when only one value needed

% ================== Define plots required =======================

% last plot = summary but only if nres>1, ie if more than one scenario

% plot before (or last) = temperature profile, if plottemp=true

% plot before then = surface downward radiation

plottemp=true; % === SET TO true === if plot temperature profile at the end

plotdown=true; % ====SET TO true ==== if downward surface radiation required

if nres==1   % if only one scenario

plotix=1;  % only one scenario graph to plot

nplot=plottemp+plotdown+1;  % number of plots depends on what options chosen

else     % if more than one scenario, user needs to put values below for graphs to plot

plotix=[1 round(nres/2) nres]; % graphs to plot – “user” selectable

nplot=length(plotix)+plottemp+plotdown+1; % plot the “plotix” graphs plus the summary

% plus the temperature profile plus downward radiation, if required

end

% work out the location of subplots

if nplot==1

subr=1;subc=1;  % 1 row, 1 column

elseif nplot==2

subr=1;subc=2;  % 1 row, 2 columns

elseif nplot==3 || nplot==4

subr=2;subc=2;  % 2 rows, 2 columns

elseif nplot==5 || nplot==6

subr=2;subc=3;  % 2 rows, 3 columns

else

subr=3;subc=3; % 3 rows, 3 columns

end

for n=1:nres  % each complete run with a new parameter to try

% — the line below has to change depending on parameter chosen

mz(2,:)=par(n);

% First pre-calculate the transmissivity and absorptivity of each layer

% for each wavenumber. This doesn’t change now that depth of each

% layer, number of each absorber and absorption characteristics are

% fixed.

% n = scenario, i = layer, j = wavenumber, k = absorber

trans=zeros(numz,numv); abso=zeros(numz,numv); % pre-allocate space

for i=2:numz   % each layer

for j=1:numv   % each wavenumber interval

trans=1;  % initialize the amount of transmission within the wavenumber interval

for k=1:nummol  % each absorbing molecule

% for each absorber: exp(-density x mixing ratio x

% absorption coefficient x thickness of layer)

trans=trans*exp(-rho(i)*mz(k,i)*a(k,j)*dz(i)); % calculate transmission, = 1- absorption

end

tran(i,j)=trans;  % transmissivity = 0 – 1

abso(i,j)=(1-trans)*emission;  % absorptivity = emissivity = 1-transmissivity

% if emission=false, absorptivity=emissivity=0

end

end

% === Main loops to calculate TOA spectrum & flux =====

% now (v3) considering emission as well, have to find temperature stability

% first, we cycle around to confirm equilibrium temperature is reached

% second, we work through each layer

% third, through each wavenumber

% fourth, through each absorbing molecule

% currently calculating surface radiation absorption up to TOA AND

% downward radiation from TOA (at TOA = 0)

% has temperature changed loop.. not yet written

% not changing pressure and density with temperature changes – only

% minor variation

tstep=3600*3; % each time step in seconds = 12 hour

for h=1:100  % main iterations to achieve equilibrium

radu=zeros(numz,numv); % initialize upward intensity at each height and wavenumber

radd=zeros(numz,numv); % initialize downward intensity at each height and wavenumber

radu(1,:)=rads;  % upward surface radiation vs wavenumber

radd(end,:)=0;  % downward radiation at TOA vs wavenumber

% units of radu, radd are W/m^2.cm^-1, i.e., flux per wavenumber

% h = timestep, i = layer, j = wavenumber

% Upward (have to do upward, then downward)

Eabs=zeros(numz); % zero the absorbed energy before we start

for i=2:numz   % each layer

for j=1:numv   % each wavenumber interval

% first calculate how much of each monochromatic ray is

% transmitted to the next layer

radu(i,j)=radu(i-1,j)*tran(i,j);

% second, calculate how much is emitted at this wavelength,

% planck function at T(i) x emissivity (=absorptivity)

% this function is spectral emissive power (pi x intensity)

radu(i,j)=radu(i,j)+abso(i,j)*3.7418e-8.*v(j)^3/(exp(v(j)*1.4388/T(i))-1);

% Change in energy = dI(v) * dv (per second)

% accumulate through each wavenumber

Eabs(i)=Eabs(i)+(radu(i,j)-radu(i-1,j))*dv;

end  % each wavenumber interval

end  % each layer

% Downards (have to do upward, then downward)

for i=numz-1:-1:2   % each layer from the top down

for j=1:numv   % each wavenumber interval

% first, calculate how much of each monochromatic ray is

% transmitted to the next layer, note that the TOA value

% is set to zero at the start

radd(i,j)=radd(i+1,j)*tran(i,j);

% second, calculate how much is emitted at this wavelength,

radd(i,j)=radd(i,j)+abso(i,j)*3.7418e-8.*v(j)^3/(exp(v(j)*1.4388/T(i))-1);

% accumulate energy change per second

Eabs(i)=Eabs(i)+(radu(i,j)-radu(i-1,j))*dv;

end  % each wavenumber interval

dT=Eabs(i)*tstep/(cp*rho(i)*dz(i)); % change in temperature = dQ/heat capacity

T(i)=T(i)+dT; % calculate new temperature

% need a step to see how close to an equilibrium we are getting

% not yet implemented

end  % each layer

% now need convective adjustment

if convadj==true  % if convective adjustment chosen..

for i=2:numz  % go through each layer

if (T(i-1)-T(i))/dz(i)>lapse  % too cold, convection will readjust

T(i)=T(i-1)-(dz(i)*lapse); % adjust temperature

end

end

end

end   % iterations to find equilibrium temperature

flux(n)=sum(radu(end,:)*dv);   % calculate the TOA flux

% === Plotting specific results =======

% Decide if and where to plot

ploc=find(plotix==n);  % is this one of the results we want to plot?

if not(isempty(ploc))  % then plot. “Ploc” is the location within all the plots

subplot(subr,subc,ploc),plot(v,radu(end,:))  % plot wavenumber against TOA emissive power

xlabel(‘Wavenumber, cm^-^1′,’FontSize’,8)

ylabel(‘W/m^2.cm^-^1′,’FontSize’,8)

title([‘pCO2 = ‘ num2str(round(par(n)*1e6)) ‘ppm, Total TOA flux= ‘ num2str(round(flux(n))) ‘ W/m^2’])

grid on

end

end   % end of each run with changed parameter to see TOA effect

if plotdown==1  % plot downward surface radiation, if requested

plotloc=nplot-plottemp-(nres>1); % get subplot location

subplot(subr,subc,plotloc),plot(v,radd(2,:))  % plot wavenumber against downward emissive power

title(‘Surface Downward, W/m^2.cm^-^1’)

xlabel(‘Wavenumber, cm^-^1′,’FontSize’,8)

ylabel(‘W/m^2.cm^-^1′,’FontSize’,8)

grid on

end

if plottemp==1  % plot temperature profile vs height, if requested

plotloc=nplot-(nres>1); % get subplot location

subplot(subr,subc,plotloc),plot(T,z/1000)

title(‘Temperature vs Height’)

xlabel(‘Temperature, K’,’FontSize’,8)

ylabel(‘Height, km’,’FontSize’,8)

grid on

end

if nres>1 % produce summary plot – TOA flux vs changed parameter

subplot(subr,subc,nplot),plot(par*1e6,flux)

title(‘Summary Results’,’FontWeight’,’Bold’)

ylabel(‘TOA Flux, W/m^2′,’FontSize’,8)

xlabel(‘pCO2 ppm’,’FontSize’,8) % ==== change label for different scenarios =========

grid on

end

In Part One I said:

In the next part we will consider more advanced aspects of this subject.

However, although that is where we are heading, first I want to look at a very simple model and progressively increase its complexity. It may be illuminating.

The discussions on the Radiative Transfer Equations at the very informative blog of Judith Curry’s were very interesting. Many comments showed an appreciation for the very basics with a misunderstanding of how they fit together, for example:

IPCC declares that infrared absorption is proportional to the logarithm of GHG concentration. It is not. A logarithm might be fit to the actual curve over a small region, but it is not valid for calculations much beyond that region like IPCC’s projections. The physics governing gas absorption is the Beer-Lambert Law, which IPCC never mentions nor uses. The Beer-Lambert Law provides saturation as the gas concentration increases. IPCC’s logarithmic relation never saturates, but quickly gets silly, going out of bounds as it begins its growth to infinity.

There have also been many questions asked at this blog about the various aspects of radiation and atmosphere, so I thought some examples – via a model – might be beneficial.

The Model

The main purpose of this model is to demonstrate the effect of the basic absorption and emission processes on top of atmosphere fluxes. It is not designed to work out what troubles may lie ahead for the climate.

This model is designed to demonstrate some basic ideas about what are known as the radiative transfer equations – how radiation is absorbed and emitted as it travels from the surface to the top of atmosphere (and also from the top of atmosphere to the surface).

I aim to bridge a gap between the “blackbody shell” models and the line-by-line climate models – in a way that people can understand. Ambitious aims.

The advantage of this model should be that we can try different ideas. And the code is available for inspection.

Absorption and Beer-Lambert

The equation of absorption is known as the Beer-Lambert law – you can see more about it in CO2 – An Insignificant Trace Gas? Part Three.

In essence the Beer-Lambert law demonstrates that absorption of radiation of any wavelength is dependent on the amount of the molecule in the path of the radiation & how effective it is at absorbing at that wavelength (note 1):

Figure 1 – Beer-Lambert Law

Simple Model – v0.2 – Saturation

The simple model (v0.2) starts by creating an atmosphere. First of all, atmospheric temperatures, “created”, by definition. Second, using the temperatures plus the hydrostatic equation to calculate the pressure vs height. Third, the density (not shown) is derived.

The surface temperature is 300K.

Figure 2

In this first version of the model (v0.2), we introduce two radiatively-active molecules (=”greenhouse” gases):

• pH2O – pretend H2O
• pCO2 – pretend CO2

They have some vague relationship with the real molecules of similar names, but the model objective is simplicity, so of course, these molecules aren’t as complex as the real-life water vapor and CO2. And their absorption characteristics are in no way intended to be the same as the real molecules.

The mixing ratio of pH2O:

Figure 3 – water vapor mixing ratio

The pCO2 mixing ratio is constant with height, but the ppm value is varied from model run to model run.

So onto our top of atmosphere results. I’ll refer to “top of atmosphere” as TOA from now on. These results are at 20km, a fairly arbitrary choice.

The results are shown against wavenumber, which is more usual in spectroscopy, but less easy to visualize than wavelength. Wavenumber = 10,000/wavelength (when wavelength is in μm and wavenumber is in cm^-1.

• 15 μm = 667 cm^-1
• 10 μm = 1,000 cm^-1
• 4 μm = 2,500 cm^-1

The “notch” that starts to appear around 600-700 cm^-1 is from pCO2 as we increase its concentration. The effect of pH2O is held constant. You can see the effect of pH2O as the “notch” around wavenumbers 1250-1500.

Note that the final graph summarizes the results – TOA Flux vs pCO2 concentration:

Figure 4

What we see is that eventually we reach a point where more pCO2 has no more effect – saturation!

We see that as the concentration keeps on increasing we get a reduction in the TOA flux down to a “saturated” value.

And when we plot the Summary Results we get something that looks very like the Beer-Lambert law of absorption! Nothing like the IPCC result shown in CO2 – An Insignificant Trace Gas? Part Seven – The Boring Numbers:

Figure 5

So, case closed then?

Flaws in the Model

This model is very simplistic. Most importantly, it only includes absorption of radiation and does not include emission.

Simplifications:

• no emission from any layers in the atmosphere
• no dependence of line width on pressure and temperature
• no weaker “wings” of an absorption band
• no overlapping of absorption (absorption by 2 molecules in the same band)

In fact, the model only represents the Beer Lambert law of absorption and therefore is incomplete. If the atmosphere is absorbing energy from radiation, where is this energy going?

The next step is to add emission.

Another important point is that the total number of people involved in creating, testing and checking this model = 1.

Surely there will be mistakes.. I welcome comments from sharp-eyed observers pointing out the mistakes.

Other articles:

Part One – a bit of a re-introduction to the subject

Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.

Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.

Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”

Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies

Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking

And Also –

Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.

Notes

Note 1 – The Beer-Lambert law is written in a number of slightly different forms. The transmission of incident monochromatic radiation is reduced like this:

I(λ) = I₀(λ).exp(-σ(λ)nz)

where I(λ) = transmitted radiation of wavelength λ, I₀(λ) = the incident radiation, σ(λ) = “capture cross section” at wavelength λ, n = number of absorbers per unit volume, z = length of path. And this equation relies on the number of absorbers remaining constant per unit volume. The equation can be written differently to deal with the case when the density of absorbers through the path changes.

Note 2 – If there was no radiatively-active atmosphere, then the top of atmosphere flux would be the same as the surface. With an emissivity of 0.98 and a temperature of 300K, the emission of radiation from the surface = 450 W/m².

It is actually calculated in the program by numerically integrating the spectrum of surface radiation, with a result of 447 W/m² (due to not integrating the waveform with enough precision at high wavelengths/low wavenumbers).

Note 3 – The Matlab program used to create this data:

RTE v0.2

and two functions called from RTE:

define_atmos

planckmv

==== RTE v0.2 =========

% RTE = Radiative transfer equations in atmosphere

% Objective – allow progressively more complex applications

% to help people see what happens in practice in the atmosphere

% v0.2 allow iterations of one (or more) parameter to find the TOA flux vs

% changed parameter

% Define standard atmosphere against height

% zr = height, pr = pressure, Tr = temperature, rhor = density, all in SI units

Ts=300; % define surface temperature

ps=1.013e5; % define surface pressure

nmv=2.079e25; % nmv x rho = total number of molecules per m^3

maxzr=50e3; % height of atmosphere

numzr=1000; % number of points used to define real atmosphere

zr=linspace(0,maxzr,numzr); % height vector from sea level to maxzr

[pr Tr rhor ztropo] = define_atmos(zr,Ts,ps); % function to determine (or lookup) p, T & rho

% Consider atmosphere in a coarser resolution than used for calculation

% z, p,T,rho; subset of values used for RTE calcs

numz=20; % number of layers to consider

maxz=20e3; % height of atmosphere to consider in meters

zi=round(logspace(0.3,log10(numzr),numz)); % zi = lookup vector to “select” heights, pressures etc

% approximately logarithmically as pressure is logarithmic

z=zr(zi);

p=pr(zi);

T=Tr(zi);

rho=rhor(zi);

% various values

lapse=6.5; % environmental lapse rate ** note potential conflict with temp profile already determined

% could be max lapse rate for convective adjustment

ems=0.98; % emissivity of surface

% work in wavenumber, cm^-1

dv=5;

v=100:dv:2500; % wavenumber (=50um – 4um)

numv=length(v);

rads=ems.*planckmv(v,Ts); % surface spectral intensity against frequency v

% ====== Introducing the molecules ============

% need % mixing in the atmosphere vs height, % capture cross section per

% number per frequency, pressure & temperature broadening function

nummol=2; % number of radiatively-active gases

mz=ones(nummol,numz); % initialize mixing ratios of the gases

% specific concentrations

% pH2O = pretend H2O

emax=17e-3; % max mixing ratio (surface) of 17g/kg

mz(1,:)=(ztropo-z).*emax./ztropo; % straight line reduction from surface to tropopause

mz(1,(mz(1,:)<0))=5e-6; % replace negative values with 5ppm, ie, for heights above tropopause

% pCO2 = pretend CO2

mz(2,:)=3.6e-4; % 360ppm

% absorption coefficients

k1=.3; % arbitrary pick – in m2/kg while we use rho

k2=.3; % likewise

a=zeros(nummol,length(v)); % initialize absorption coefficients

a(1,(v>=1250 & v<=1500))=k1;  % wavelength dependent absorption

a(2,(v>=600 & v<=800))=k2;

% === Loop to change key parameter for which we want to see the effect

%

nres=10; % number of results to calculate

flux=zeros(1,nres); % TOA flux for each change in parameter

par=zeros(1,nres); % parameter we will alter

plotix=[1 3 5 8 10]; % graphs to plot

nplot=length(plotix)+1; % plot the “plotix” graphs plus the summary

% work out the location of subplots

if nplot==1

subr=1;subc=1;  % 1 row, 1 column

elseif nplot==2

subr=2;subc=1;  % 2 rows, 1 columns

elseif nplot==3 || nplot==4

subr=2;subc=2;  % 2 rows, 2 columns

elseif nplot==5 || nplot==6

subr=3;subc=2;  % 3 rows, 2 columns

else

subr=3;subc=3; % 3 rows, 3 columns

end

% parameter values to try – this section has to be changed depending on the

% run

% CO2 concentration

par=logspace(-5,-2.5,nres);

for n=1:nres  % each complete run with a new parameter to try

% — this line below has to change depending on parameter chosen

mz(2,:)=par(n);

% === Main loops to calculate TOA spectrum & flux =====

% first we work through each layer

% then through each wavenumber

% currently calculating surface radiation absorption up to TOA

rad=zeros(numz,numv);

rad(1,:)=rads;  % surface radiation vs wavenumber

for i=2:numz   % each layer

for j=1:numv   % each wavenumber interval

abs=1;  % initialize the amount of absorption within the wavenumber interval

for k=1:nummol  % each absorbing molecule

% for each absorber: exp(-density x mixing ratio x

% absorption coefficient x thickness of layer)

abs=abs*exp(-rho(i)*mz(k,i)*a(k,j)*(z(i)-z(i-1))); % calculate absorption

end

rad(i,j)=rad(i-1,j)*abs; %

end

end

flux(n)=sum(rad(end,:)*dv);   % calculate the TOA flux

% decide if and where to plot

ploc=find(plotix==n);  % is this one of the results we want to plot?

if not(isempty(ploc))  % then plot. “Ploc” is the location within all the plots

subplot(subr,subc,ploc),plot(v,rad(end,:))  % plot wavenumber against TOA emissive power

xlabel(‘Wavenumber, cm^-^1′,’FontSize’,8)

ylabel(‘W/m^2.cm^-^1′,’FontSize’,8)

title([‘pCO2 = ‘ num2str(round(par(n)*1e6)) ‘ppm, Total TOA flux= ‘ num2str(round(flux(n))) ‘ W/m^2’])

grid on

end

end

% final plot – TOA flux vs changed parameter

subplot(subr,subc,nplot),plot(par*1e6,flux)

title(‘Summary Results’,’FontWeight’,’Bold’)

ylabel(‘TOA Flux, W/m^2’)

xlabel(‘pCO2 ppm’) % this x label is up for changing

====== end of RTE v0.2  =========

====== define_atmos ============

function [pr Tr rhor ztropo] = define_atmos(zr, Ts, ps)

% Calculate pressure, pr; temperature, Tr; density, rhor; from height, zr;

%  surface temperature, Ts; and surface pressure, ps

% By assuming a standard temperature profile to a fixed tropopause temp

% zr is a linear vector and starts at the surface

pr=zeros(1,length(zr)); % allocate space

Tr=zeros(1,length(zr)); % allocate space

rhor=zeros(1,length(zr)); % allocate space

% first calculate temperature profile

lapset=6.5/1000; % lapse rate in K/m

Ttropo=215; % temperature of tropopause

htropo=10000; % height of tropopause

Tstrato=270; % temperature of stratopause

zstrato=50000; % height of stratopause

ztropo=((Ts-Ttropo)/lapset); % height of bottom of tropopause in m

for i=1:length(zr)

if zr(i)<ztropo

Tr(i)=Ts-(zr(i)*lapset);  %  the troposphere

elseif (zr(i)>=ztropo && zr(i)<=(ztropo+htropo))

Tr(i)=Ttropo; % the tropopause

elseif (zr(i)>(ztropo+htropo) && zr(i)<zstrato)

Tr(i)=Ttropo+(zr(i)-(ztropo+htropo))*(Tstrato-Ttropo)/(zstrato-(ztropo+htropo)); % stratosphere

else

Tr(i)=Tstrato; % haven’t yet defined temperature above stratopause

% but this prevents an error condition

end

end

% pressure, p = ps * exp(-mg/R*integral(1/T)dz) from 0-z

mr=28.57e-3; % molar mass of air

R=8.31; % gas constant

g=9.8; % gravity constant

intzt=0; % sum the integral of dz/T in each iteration

dzr=zr(2)-zr(1); % dzr is linear so delta z is constant

pr(1)=ps; % surface condition

for i=2:length(zr)

intzt=intzt+(dzr/Tr(i));

pr(i)=ps*exp(-mr*g*intzt/R);

end

% density, rhor = mr.p/RT

rhor=mr.*pr./(R.*Tr);

end

======= end of define_atmos  =================

======= planckmv ==================

function ri = planckmv( v,t )

%  planck function for matrix of wavenumber, v (1/cm) and temp, t (K)

%  result in spectral emissive power (pi * intensity)

%  in W/(m^2.cm^-1)

%  from

%  http://pds-atmospheres.nmsu.edu/education_and_outreach/encyclopedia/planck_function.htm

[vv tt]= meshgrid(v,t);

ri =  3.7418e-8.*v.^3./(exp(vv.*1.4388./tt)-1);

end

============ end of planckmv =================