The Science of Doom

Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics

October 7, 2010 by scienceofdoom

Probably many, most or all of my readers wonder why I continue with this theme when it’s so completely obvious..

Well, most people haven’t studied thermodynamics and so an erroneous idea can easily be accepted as true.

All I want to present here is the simple proof that thermodynamics textbooks don’t teach the false ideas circulating the internet about the second law of thermodynamics.

So for those prepared to think and question – it should be reasonably easy, even if discomforting, to realize that an idea they have accepted is just not true. For those committed to their cause, well, even if Clausius were to rise from the dead and explain it..

On another blog someone said:

Provide your reference that he said heat can spontaneously flow from cold to hot. And not from a climate ‘science’ text.

I had cited the diagram from Fundamentals of Heat and Mass Transfer by Incropera and DeWitt (2007). It’s not a climate science book as the title indicates.

However, despite my pressing (you can read the long painful exchange that follows) I didn’t find out what the blog owner actually thought that the writers of this book were saying. Perhaps the blog owner never grasped the key element of the difference between the real law and the imaginary one.

So I should explain again the difference between the real and imaginary second law of thermodynamics once again. I’m relying on the various proponents of the imaginary law because I can’t find it in any textbooks. Feel free to correct me if you understand this law in detail.

The Real Second Law of Thermodynamics

1a. Net heat flows from the hotter to the colder

1b. Entropy of a closed system can never reduce

1c. In a radiative exchange, both hotter and colder bodies emit radiation

1d. In a radiative exchange, the colder body absorbs the energy from the hotter body

1e. In a radiative exchange, the hotter body absorbs the energy from the colder body

1f. This energy from the colder body increases the temperature compared with the case where the energy was not absorbed

1g. Due to the higher energy radiated from a hotter body, the consequence is that net heat flows from the hotter to the colder (see note 1)

The Imaginary Second Law of Thermodynamics

2a. – as 1a

2b. – as 1b

2c. – as 1c

2d. – as 1d

2e. In a radiative exchange, the hotter body does not absorb the energy from the colder body as this would be a violation of the second law of thermodynamics

Hopefully everyone can clearly see the difference between the two “points of view”. Everyone agrees that net heat flows from hotter to colder. There is no dispute about that.

What the Equations Look Like for Both Cases

Now, let’s take a look at the radiative exchange that would take place under the two cases and compare them with a textbook. Even if you find maths a little difficult to follow, the concept will be as simple as “two oranges minus one orange” vs “two oranges” so stay with me..

Here is the example we will consider:

Radiant heat transfer

We will keep it very simple for those not so familiar with maths. In typical examples, we have to consider the view factor – this is a result of geometry – the ratio of energy radiated from body 1 that reaches body 2, and the reverse. In our example, we can ignore that by considering two very long plates close together.

E₁ is the energy radiated from body 1 (per unit area) and we consider the case when all of it reaches body 2, E₂ is the energy radiated from body 2 (per unit area) and we consider that all of it reaches body 1.

We define E_net1 as the change in energy experienced by body 1 (per unit area). And E_net2 as the change in energy experienced by body 2 (per unit area).

Radiation Exchange under The Real Second Law

E₁ = εσT₁⁴; E₂= εσT₂⁴ (Stefan-Boltzmann law)

E_net1 = E₂ – E₁ = εσT₂⁴ – εσT₁⁴

E_net2 = E₁ – E₂ = εσT₁⁴ – εσT₂⁴

Therefore, E_net1 = -E_net2

Under The Imaginary Second Law

E_net1 = – E₁ = -εσT₁⁴

E_net2 = E₁ – E₂ = εσT₁4⁴ – εσT₂⁴

Therefore, E_net1 ≠-E_net2 ; note that ≠ means “not equal to”

This should be uncontroversial. All I have done is written down mathematically what the two sides are saying. If we took into account view factors and areas then the formulae would like slightly more cluttered with terms like A₁F₁₂.

In the case of the real second law, the net energy absorbed by body 2 is the net energy lost by body 1.

In the case of the imaginary second law, there is some energy floating around. No advocates have so far explained what happens to it. Probably it floats off into space where it can eventually be absorbed by a colder body.

Alert readers will be able to see the tiny problem with this scenario..

What the Textbooks Say

First of all, what they don’t say is:

When energy is transferred by radiation from a colder body to a hotter body, it is important to understand that this incident radiation cannot be absorbed – otherwise it would be a clear violation of the second law of thermodynamics

I could leave it there really. Why don’t the books say this?

Engineering Calculations in Radiative Heat Transfer, by Gray and Müller (1974)

Note that if the imaginary second law advocates were correct, then the text would have to restrict the conditions under which equation 2.1 and 2.2 were correct – i.e., that they were only correct for the energy gain for the colder body and NOT correct for the energy loss of the hotter body.

Heat and Mass Transfer, by Eckert and Drake (1959)

Note the highlighted area.

Basic Heat Transfer, M. Necati Özisik (1977)

Note the circled equations – matching the equations for the “real second law” and not matching the equations for the “imaginary second law”. Note the highlighted area.

Heat Transfer, by Max Jakob (1957)

Note the highlighted section, same comment as for the first book.

Principles of Heat Transfer, Kreith (1965)

Note the highlighted sections. The second highlight once again confirms the equation shown at the start, that under “the real second law” conditions, E_net1 = – E_net2. Under the “imaginary second law” conditions this equation doesn’t hold.

Fundamentals of Heat and Mass Transfer, Incropera and DeWitt (2007)

Note the circled section. This is false, according to the advocates of the imaginary second law of thermodynamics.

And the very familiar diagram shown many times before:

From "Fundamentals of Heat and Mass Transfer, 6th edition", Incropera and DeWitt (2007)

Conclusion

There are some obvious explanations:

1. Professors in the field of heat transfer write rubbish that is easily refuted by checking the second law – heat cannot flow from a colder to a hotter body.

2. Climate science advocates have crept into libraries around the world, and undiscovered until now, have doctored all of the heat transfer text books.

3. (My personal favorite) Science of Doom is refuted because these writers all agree that net heat flows from the hotter to the colder.

4. Look, a raven.

Relevant articles – The Real Second Law of Thermodynamics

Notes

Note 1 – Strictly speaking a hotter body might radiate less than a colder body – in the case where the emissivity of the hotter body was much lower than the emissivity of the colder body. But under those conditions, the hotter body would also absorb much less of the irradiation from the colder body (because absorptivity = emissivity). And so net heat flow would still be from the hotter to the colder.

To keep explanations to a minimum in the body of the article in 1e and 1f I also didn’t state that the proportion of energy absorbed by each would depend on the absorptivity of each body.

Posted in Basic Science, Debunking Flawed "Science" | 324 Comments »

Does Back-Radiation “Heat” the Ocean? – Part One

October 6, 2010 by scienceofdoom

In the three part series on DLR (also known as “back radiation”, also known as atmospheric radiation), Part One looked at the network of stations that measured DLR and some of the measurements, Part Two reviewed the spectra of this radiation, and Part Three asked whether this radiation changed the temperature of the surface.

Very recently, on another blog, someone asked whether I thought “back radiation” heated the ocean. I know from a prominent blog that a very popular idea in blog-land is that the atmospheric radiation doesn’t heat the ocean. I have never seen any evidence for the idea. That doesn’t mean there isn’t any..

See note 1 on “heat”.

The Basic Idea

From what I’ve seen people write about this idea, including the link above, the rough argument goes like this:

solar radiation penetrates tens of meters into the ocean
atmospheric radiation – much longer wavelengths – penetrates only 1μm into the ocean

Therefore, solar radiation heats the ocean, but atmospheric radiation only heats the top few molecules. So DLR is unable to transfer any heat into the bulk of the ocean, instead the energy goes into evaporating the top layer into water vapor. This water vapor then goes to make clouds which act as a negative feedback. And so, more back-radiation from more CO2 can only have a cooling effect.

There are a few assumptions in there. Perhaps someone has some evidence of the assumptions, but at least, I can see why it is popular.

Solar Radiation

As regular readers of this blog know, plus anyone else with a passing knowledge of atmospheric physics, solar radiation is centered around a wavelength of 0.5μm. The energy in wavelengths greater than 4μm is less than 1% of the total solar energy and conventionally, we call solar radiation shortwave.

99% of the energy in atmospheric radiation has longer wavelengths than 4μm and along with terrestrial radiation we call this longwave.

Most surfaces, liquids and gases have a strong wavelength dependence for the absorption or reflection of radiation.

Here is the best one I could find for the ocean. It’s from Wikipedia, not necessarily a reliable source, but I checked the graph against a few papers and it matched up. The papers didn’t provide such a nice graph..

Absorption coefficient for the ocean - Wikipedia

Figure 1

Note the logarithmic axes.

The first obvious point is that absorption varies hugely with the wavelength of incident radiation.

I’ll explain a few basics here, but if the maths is confusing, don’t worry, the graphs and explanation will attempt to put it all together. The basic equation of transmission relies on the Beer-Lambert law:

I = I₀.exp(-kd)

where I is the radiation transmitted, I₀ is the incident radiation at that wavelength, d is the depth, and k is the property of the ocean at this wavelength

It’s not easy to visualize if you haven’t seen this kind of equation before. So imagine 100 units of radiation incident at the surface at one wavelength where the absorption coefficient, k = 1:

Figure 2

So at 1m, 37% of the original radiation is transmitted (and therefore 63% is absorbed).

At 2m, 14% of the radiation is transmitted.

At 3m, 5% is transmitted

At 10m, 0.005% is transmitted, so 99.995% has been absorbed.

(Note for the detail-oriented people, I have used the case where k=1/m).

Hopefully, this concept is reasonably easy to grasp. Now let’s look at the results of the whole picture using the absorption coefficient vs wavelength from earlier.

Figure 3

The top graph shows the amount of radiation making it to various depths, vs wavelength. As you can see, the longer (and UV) wavelengths drop off very quickly. Wavelengths around 500nm make it the furthest into the ocean depths.

The bottom graph shows the total energy making it through to each depth. You can see that even at 1mm (10^-3m) around 13% has been absorbed and by 1m more than 50% has been absorbed. By 10m, 80% of solar radiation has been absorbed.

The graph was constructed using an idealized scenario – solar radiation less reflection at the top of atmosphere (average around 30% reflected), no absorption in the atmosphere and the sun directly overhead. The reason for using “no atmospheric absorption” is just to make it possible to construct a simple model, it doesn’t have much effect on any of the main results.

If we considered the sun at say 45° from the zenith, it would make some difference because the sun’s rays would now be coming into the ocean at an angle. So a depth of 1m would correspond to the solar radiation travelling through 1.4m of water (1 / cos(45°)).

For comparison here is more accurate data:

From "Light Absorption in Sea Water", Wozniak (2007)

Figure 4

On the left the “surface” line represents the real solar spectrum at the surface – after absorption of the solar radiation by various trace gases (water vapor, CO2, methane, etc). On the right, the amount of energy measured at various depths in one location. Note the log scale on the vertical axis for the right hand graph. (Note as well that the irradiance in these graphs is in W/m².nm, whereas the calculated graphs earlier are in W/m².μm).

From "Light Absorption in Sea Water", Wozniak (2007)

Figure 5

And two more locations measured. Note that the Black Sea is much more absorbing – solar absorption varies with sediment as well as other ocean properties.

DLR or “Back radiation”

The radiation from the atmosphere doesn’t look too much like a “Planck curve”. Different heights in the atmosphere are responsible for radiating at different wavelengths – dependent on the concentration of water vapor, CO2, methane, and other trace gases.

Here is a typical DLR spectrum (note that the horizontal axis needs to be mentally reversed to match other graphs):

Pacific, Lubin (1995)

Figure 6

You can see more of these in The Amazing Case of Back Radiation – Part Two.

But for interest I took the case of an ideal blackbody at 0°C radiating to the surface and used the absorption coefficients from figure 1 to see how much radiation was transmitted through to different depths:

Figure 7

As you can see, most of the “back radiation” is absorbed in the first 10μm, and 20% is absorbed even in the first 1μm.

I could produce a more accurate calculation by using a spectrum like the Pacific spectrum in fig 6 and running that through the same calculations, but it wouldn’t change the results in any significant way.

So we can see that while around half the solar radiation is absorbed in the first meter and 80% in the first 10 meters, 90% of the DLR is absorbed in the first 10μm.

So now we need to ask what kind of result this implies.

Heating Surfaces and Conduction

When you heat the surface of a body that has a colder bulk temperature (or a colder temperature on the “other side” of the body) then heat flows through the body.

Conduction is driven by temperature differences. Once you establish a temperature difference you inevitably get heat transfer by conduction – for example, see Heat Transfer Basics – Part Zero.

The equation for heat transfer by conduction:

q = kA . ΔT/Δx

where k is the material property called conductivity, ΔT is the temperature difference, Δx is the distance between the two temperatures, and q is the heat transferred.

However, conduction is a very inefficient heat transfer mechanism through still water.

For still water, k ≈ 0.6 W/m.K (the ≈ symbol means “is approximately equal to”).

So, as a rough guide, if you had a temperature difference of 20°C across 50m, you would get heat conduction of 0.24 W/m². And with 20°C across 10m of water, you would only get heat conduction of 1.2 W/m².

However, the ocean surface is also turbulent for a variety of reasons, and in Part Two we will look at how that affects heat transfer via some simulations and a few papers. We will also look at the very important first law of thermodynamics and see what that implies for absorption of back radiation.

Update – Does Back-Radiation “Heat” the Ocean? – Part Two

Reference

Light Absorption in Sea Water, Wozniak & Dera, Atmospheric and Oceanographic Sciences Library (2007)

Notes

Note 1 – To avoid upsetting the purists, when we say “does back-radiation heat the ocean?” what we mean is, “does back-radiation affect the temperature of the ocean?”

Some people get upset if we use the term heat, and object that heat is the net of the two way process of energy exchange. It’s not too important for most of us. I only mention it to make it clear that if the colder atmosphere transfers energy to the ocean then more energy goes in the reverse direction.

It is a dull point.

Posted in Basic Science, Debunking Flawed "Science", Ocean Physics | 45 Comments »

Absorption of Radiation from Different Temperature Sources

October 2, 2010 by scienceofdoom

Following discussions about absorption of radiation I thought some examples might help illustrate one simple, but often misunderstood, aspect of the subject.

Many people believe that radiation from a colder atmosphere cannot be absorbed by a warmer surface. Usually they are at a loss to explain exactly why – for good reason.

However, some have the vague idea that radiation from a colder atmosphere has different wavelengths compared with radiation from a warmer atmosphere. And, therefore, that’s probably it. End of story. Unfortunately for people with this idea, it’s not actually solved the problem at all..

The specific question I posed to one commenter some time ago was very specific:

If 10μm photons from a 10°C atmosphere are 80% absorbed by a 0°C surface, what is the ratio of 10μm photons from a -10°C atmosphere absorbed by that same surface?

It was eventually conceded that there would be no difference – 10μm photons from a -10°C will also be 80% absorbed. This material property of a surface is called absorptivity and is the proportion of radiation absorbed vs reflected at each wavelength.

Basic physics tells us that the energy of a 10μm photon is always that same, no matter what temperature source it has come from – see note 1.

Here’s an example of the reflectivity/absorptivity of many different materials just for interest:

Reflectivity vs wavelength for various surfaces, Incropera (2007)

Reflectivity vs wavelength for various surfaces, Incropera & DeWitt (2007)

Clearly materials have very different abilities to absorb /reflect different wavelength photons. Is this the explanation?

No.

The important point to understand is that even though radiation emitted from different temperature sources have different peak wavelengths, there is a large spread of wavelengths:

The peak wavelength of +10°C radiation is 10.2μm, while that of the -10°C radiation is 11.0μm – but, as you can see, both sources emit photons over a very similar range of wavelengths.

Scenarios

Let’s now take a look at the proportion of radiation absorbed from both of these sources.

First, with the case where the surface absorptivity is higher at shorter wavelengths – this should favor absorbing more energy from a hotter source and less from a colder source:

The top graph shows the absorptivity as a function of wavelength, and the bottom graph shows the consequent absorption of energy for the two cases.

Because absorptivity is higher at shorter wavelengths, there is a slight bias towards absorbing energy from the hotter +10°C source – but the effect is almost unnoticeable.

The actual numbers:

43% of the -10°C radiation is absorbed
46% of the +10°C radiation is absorbed

So let’s try something more ‘brutal’, with all of the energy from wavelengths shorter than 10.5μm absorbed and none from wavelengths longer than 10.5um absorbed (all reflected).

As you can see, the proportion absorbed of the energy from the hotter source vs colder source appears very similar. It is simply a result of the fact that +10°C and -10°C radiation have almost identical proportions of energy between any given wavelengths – the main difference is that radiation from +10°C has a higher total energy.

The actual numbers:

22% of the -10°C is absorbed
27% of the +10°C is absorbed

So – as is very obvious to most people already – there is no possible surface which can absorb a significant proportion of 10°C radiation and yet reflect all of the -10°C radiation.

And If There Was Such a Surface

Suppose that we could somehow construct a surface which absorbed a significant proportion of radiation from a +10°C source, and yet reflect almost all radiation from a -10°C source.

Well, that would just create a new problem. Because now, when our surface heats up to 11°C the radiation from the 10°C source would still be absorbed. And yet, the radiation is now from a colder source than the surface. Red alert for all the people who say this can’t happen.

Conclusion

The claim that radiation from a colder source is not absorbed by a warmer surface has no physical basis. People who claim it don’t understand one or all of these facts of basic physics:

a) Radiation incident on a surface has to be absorbed, reflected or transmitted through the surface. This last (transmitted) is not possible with a surface like the earth (it is relevant for something like a thin piece of glass or a body of gas), therefore radiation is either absorbed or reflected.

b) The material property of a surface which determines the proportion of radiation absorbed or reflected is called the absorptivity, and it is a function of wavelength of the incident photons. (See note 2)

c) The energy of any given photon is only dependent on its wavelength, not on the temperature of the source that emitted it.

d) Radiation emitted by the atmosphere has a spectrum of wavelengths and the difference between a -10°C emitter and a +10°C emitter (for example) is not very significant (total energy varies significantly, but not the proportion of energy between any two wavelengths). See note 3.

The only way that radiation from a colder source could not be absorbed by a warmer surface is for one of these basic principles to be wrong.

These have all been established for at least 100 years. But no one has really checked them out that thoroughly. Remember, it’s highly unlikely that you have just misunderstood the Second Law of Thermodynamics.

Intelligent Materials and the Imaginary Second Law of Thermodynamics

The First Law of Thermodynamics Meets the Imaginary Second Law

The Amazing Case of “Back Radiation” – Part Three

and Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics

Note 1 – Already explained in a little more detail in The Amazing Case of “Back Radiation” – Part Three – the energy of a photon is only dependent on the wavelength of that photon:

Energy = hc/λ

where h = Planck’s constant = 6.6×10^-34 J.s, c = the speed of light = 3×10⁸ m/s and λ = wavelength.

Note 2 – Absorptivity/reflectivity is also a function of the direction of the incident radiation with some surfaces.

Note 3 – For those fascinated by actual numbers – the energy from a blackbody source at -10°C = 272 W/m² compared with that from a +10°C source = 364 W/m² – the colder source providing only 75% of the total energy of the warmer source. But take a look at the proportion of total energy in various wavelength ranges:

Between 8-10 μm 10.7% (-10°C) 12.2% (10°C)
Between 10-12 μm 11.9% (-10°C) 12.7% (10°C)
Between 12-14 μm 11.2% (-10°C) 12.4% (10°C)
Between 14-16 μm 9.8% (-10°C) 9.5% (10°C)

Posted in Basic Science, Debunking Flawed "Science" | 29 Comments »

The Real Second Law of Thermodynamics

September 27, 2010 by scienceofdoom

Many people often claim that the atmosphere cannot “heat” the earth’s surface and therefore the idea of the inappropriately-named “greenhouse” effect is scientifically impossible. The famous Second Law of Thermodynamics is invoked in support.

Let’s avoid a semantic argument about the correct or incorrect use of the word “heat”.

I claim that energy from the atmosphere is absorbed by the surface.

This absorbed energy has no magic properties. If the surface loses 100J of energy by other means and gains 100J of energy from the atmosphere then its temperature will stay constant. If the surface hasn’t lost or gained any energy by any other means, this 100J of energy from the atmosphere will increase the surface temperature.

I also claim that because the atmosphere is on average colder than the surface, more energy is transferred from the surface to the atmosphere compared with the reverse situation.

Let’s consider whether this violates the real second law of thermodynamics..

The Conceptual Problem

In Heat Transfer Basics – Part Zero a slightly off-topic discussion about the “greenhouse” effect began. One of our most valiant defenders of the imaginary second law of thermodynamics said:

An irradiated object can never reach a higher temperature than the source causing the radiation

I have demonstrated previously in The First Law of Thermodynamics Meets the Imaginary Second Law that a colder body can increase the temperature of a hotter body (compared with the scenario when the colder body was not there).

In that example, there was more than one source of energy. So, with this recent exchange in Heat Transfer Basics it dawned on me what the conceptual problem was. So this article is written for the many people who find themselves agreeing with the comment above. As a paraphrased restatement by the same commenter:

If the atmosphere is at -30°C then it can’t have any effect on the surface if the surface is above -30°C

Entropy Basics and The Special Case

Entropy is a difficult subject to understand. Heat and temperature are concepts we can understand quite easily. We all know what temperature is (in a non-precise way) and heat, although a little more abstract, is something most people can relate to.

Entropy appears to be an abstract concept with no real meaning – nothing you can get your hands around.

The second law of thermodynamics says:

Entropy of a “closed system” can never reduce

Before defining entropy, here is an important consequence of this second law:

Increasing entropy means that heat flows spontaneously from hotter to colder bodies and never in reverse

This fits everyone’s common experience.

Ice melts in a glass of water
A hot pan of water on the stove cools down to room temperature when the heat source is removed
Put a hold and cold body together and they tend to come to the same temperature, not move apart in temperature

And all of these are easier to visualize than a mathematical formula.

What is entropy? I will keep the maths to an absolute minimum, but we have to introduce a tiny amount of maths just to define entropy.

For a body absorbing a tiny amount of heat, δQ (note that δ is a symbol which means “tiny change”), the change in entropy, δS, is given by:

δS = δQ / T, where T is absolute temperature (see note 1)

It’s not easy to visualize – but take a look at a simple example. Suppose that a tiny amount of heat, 1000 J, moves from a body at 1000K to a body at 500K:

Example 1

The net change in energy in the system is zero because 1000J leaves the first body and is absorbed by the second body. This is the first law of thermodynamics – energy cannot be created or destroyed.

However, there is a change in entropy.

The change in total entropy of the system = δS₁ + δS₂ = -1 + 2 = 1 J/K.

This strange value called “entropy” has increased.

Notice that if the energy flow of 1000J was from the 500K body to the 1000K body the change in entropy would be -1 J/K. This would be a reduction in entropy – forbidden by the real second law of thermodynamics. This would be a spontaneous flow of heat from the colder body to the hotter body.

Updated note Sep 30th – this example is intended to clarify the absolute basics.

Think of the example above like this – If, for some reason, in a closed system, this was the only movement of energy taking place, we could calculate the entropy change and it has increased.

The example is not meant to be an example of only one half of a radiative energy exchange. Just a very very simply example to show how entropy is calculated. It could be conductive heat transfer through a liquid that is totally opaque to radiation.

The Special Case

The simplest example demonstrating the second law of thermodynamics is with two bodies which are in a closed system.

Let’s say that we have a gas at 273K (Body 1) and a solid (Body 2) surrounded by the gas. The solid starts off much colder.

What is the maximum temperature that can be reached by the solid?

273K

Easy. In fact, depending on the starting temperature of the solid and the respective heat capacities of the gas and solid, the actual temperature that both end up (the same temperature eventually) might be a little lower or a lot lower.

But the temperature reached by the solid can never get to more than 273K. For the solid to get to a temperature higher than 273K the gas would have to cool down below 273K (otherwise energy would have been created). Heat does not spontaneously flow from a colder to a hotter body so this never happens.

This defining example is illuminating but no surprise to anyone.

It is important to note that this special case is not the second law of thermodynamics, it is an example that conforms to the second law of thermodynamics.

The second law of thermodynamics says that the entropy of a system cannot reduce. If we want to find out whether the second law of thermodynamics forbids some situation then we need to calculate the change in entropy – not use “insight” from this super-simple scenario.

So let’s consider some simple examples and see what happens to the entropy.

Simple Examples

What I want to demonstrate is that the standard picture in heat transfer textbooks doesn’t violate the second law of thermodynamics.

What is the standard picture?

From "Fundamentals of Heat and Mass Transfer, 6th edition", Incropera and DeWitt (2007)

This says that two bodies separated in space both emit radiation. And both absorb radiation from the other body (see note 2).

The challenging concept for some is the idea that radiation from the colder body is absorbed by the hotter body.

We start with Example 1 above, but this time we consider an exchange of radiation and see what happens to the entropy of that system.

Example 2

What I have introduced here is thermal radiation from Body 2 incident on Body 1. We will assume all of it is absorbed, and vice-versa.

According to the Stefan-Boltzmann equation, energy radiated is proportional to the 4th power of temperature. Given that Body 2 is half the temperature of Body 1 it will radiate at a factor of 2⁴ = 2 x 2 x 2 x 2 = 16 times less. Therefore, if 1000J from Body 1 reaches Body 2, then 62J (1000/16) will be transmitted in the reverse direction. However, the exact value doesn’t matter for the purposes of this example.

So with our example above, what is the change in entropy?

Body 1 loses energy, which is negative entropy. Body 2 gains energy, which is positive entropy.

δS₁ = -(1000-62)/1000 = -938 / 1000 = -0.94 J/k
δS₂ =(1000-62)/500 = 938 / 500 = 1.88 J/K

Total entropy change = -0.94 + 1.88 = 0.94 J/K.

So even though energy from the colder body has been absorbed by the hotter body, the entropy of the system has increased. This is because more energy has moved in the opposite direction.

There is no violation of the second law of thermodynamics with this example.

Now let’s consider an example with values closer to what we encounter near the earth’s surface:

Example 3

This isn’t intended to be the complete surface – atmosphere system, just values that are more familiar.

Surface: δS₁ = -(390-301)/288 = -89 / 288 = -0.31 J/k
Atmosphere: δS₂ = (390-301)/270 = 89 / 270 = 0.33 J/K

Total entropy change = -0.31 + 0.33 = 0.02 J/K.

So even though the temperatures of the two bodies are much closer together, when they exchange energy, total entropy still increases.

Energy from the colder atmosphere has been absorbed by the hotter surface and yet entropy of the system has still increased.

Now, the example above (example 3) is an exchange of a fixed amount of energy (in Joules, J). Suppose this is the amount of energy per second (Watts, W) or the amount of energy per second per square meter (W/m²).

If the atmosphere keeps absorbing more energy than it is emitting it will heat up. If the earth keeps emitting more energy than it absorbs, it will cool down.

If example 3 was the complete system, then the atmosphere would heat up and the earth would cool down until they were in thermal equilibrium. This doesn’t happen because the sun continually provides energy.

The Complete Climate System

The earth-atmosphere system is very complex. If we analyze a long term average scenario, like that painted by Kiehl and Trenberth there is an immediate problem in calculating the change in entropy:

From Kiehl & Trenberth (1997)

[Note from Sep 28th – This section is wrong, thanks Nick Stokes for highlighting it and so delicately! Preserved in italics for entertainment value only..] If we consider the surface, for example, it absorbs 492 W/m² (δQ = 492 per second per square meter) and it loses 492 W/m² (δQ = -492 per second per square meter).

Net energy change = 0. Net entropy change = 0.

Why isn’t entropy increasing? We haven’t considered the whole system – the sun is generating all the energy to power the climate system. If we do consider the sun, it is emitting a huge amount of energy and, therefore, losing entropy. But the energy generation inside the sun creates more entropy – that is, unless the second law of thermodynamics is flawed.

[Now the rewritten bit]

Previous sections explained that calculations of entropy “removed” (negative entropy) are based on energy emitted divided by the temperature of the source. And calculations of entropy “produced” are based on energy absorbed divided by the temperature of the absorber. In a closed system we can add these up and we find that entropy always increases.

So the calculation in italics above is incorrect. Change in entropy at the surface is not zero.

Change in entropy at the surface is a large negative value, because we have to consider the source temperature of the energy.

So as Nick Stokes points out (in a comment below), we can draw a line around the whole climate system, including the emission of radiation by the sun (see example 4 just below). This calculation produces a large negative entropy, because it isn’t a closed system. This is explained by the fact that the production of solar energy creates an even larger amount of positive entropy.

Example 4

The Classic Energy Exchange by Radiation

I was in the university library recently and opened up a number of heat transfer textbooks. All of them had a similar picture to that from Incropera and DeWitt (above). And not a single one said, This doesn’t happen.

In any case, for someone to claim that an energy exchange violates the second law of thermodynamics they need to show there is a reduction in entropy of a closed system.

But one important point did occur to me when thinking about this subject. Let’s reconsider our commenter’s claim:

An irradiated object can never reach a higher temperature than the source causing the radiation

As I pointed out in the The Special Case section – this is true if this is the only source of energy. Yet the surface of the earth receives energy from both the sun and the atmosphere.

If the colder atmosphere cannot transfer energy to a warmer surface, and the second law of thermodynamics is the reason, the actual event that is forbidden is the emission of radiation by the colder atmosphere. When the colder atmosphere radiates energy it loses entropy.

After all, the entropy loss takes place when the atmosphere has given up its energy. Not when another body has absorbed the energy.

Our commenter has frequently agreed that the colder atmosphere does radiate. But he doesn’t believe that the surface can absorb it. He has never been able to explain what happens to the energy when it “reaches” the surface. Or why the surface doesn’t absorb it. Instead we have followed many enjoyable detours into attempts to undermine any of a number of fundamental physics laws in an attempt to defend “the imaginary second law of thermodynamics”.

Conclusion

Entropy is a conceptually difficult subject, but all of us can see the example in “the special case” and agree that the picture is correct.

However, the atmosphere – surface interaction is more complex than that simple case. The surface of the earth receives energy from the sun and the atmosphere.

As we have seen, in simple examples of radiant heat exchange between two bodies, entropy is still positive even when the hotter body absorbs energy from the colder body. This is because more energy flows from the hotter to the colder than the reverse.

To prove that the second law of thermodynamics has been violated someone needs to demonstrate that a system is reducing entropy. So we would expect to see an entropy calculation.

Turgid undergraduate books about heat transfer in university libraries all write that radiation emitted by a colder body is absorbed by a hotter body.

That is because the first law of thermodynamics is still true – energy cannot be created, destroyed, or magically lost.

Notes

Note 1 – There are more fundamental ways to define entropy, but it won’t help to see this kind of detail. And for the purists, the equation as shown relies on the temperature not changing as a result of the small transfer of energy.

If the temperature did change then the correct formula is to integrate:

ΔS = ∫Cp/T. dT (with the integral from T1 to T2) and the result,

ΔS = Cp log (T2/T1), this is log to the base e.

Note 2 – This assumes there is some “view factor” between the two bodies – that is, some portion of the radiation emitted by one body can “hit” the other. Just pointing out the obvious, just in case..

Posted in Basic Science, Debunking Flawed "Science" | 159 Comments »

Clouds and Water Vapor – Part Three

September 18, 2010 by scienceofdoom

In Part One we had a look at Ramanathan’s work (actually Raval and Ramanathan) attempting to measure the changes in outgoing longwave radiation vs surface temperature.

In Part Two (Part Zero perhaps) we looked at some basics on water vapor as well as some measurements. The subject of the non-linear effects of water vapor was raised.

Part One Responses attempted a fuller answer to various questions and objections about Part One

Water vapor feedback isn’t a simple subject.

First, a little more background.

Effectiveness of Water Vapor at Different Heights

Here are some model results of change in surface temperature for changes in specific humidity at different heights:

From Shine & Sinha (1991)

For newcomers, 200mbar is the top of the troposphere (lower atmosphere), and 1000mbar is the surface.

You can see that for a given increase in the mixing ratio of water vapor the most significant effect comes at the top of the troposphere.

The three temperatures: cool = 277K (4°C); average = 287K (14°C); and warm = 298K (23°C).

Now a similar calculation using changes in relative humidity:

From Shine & Sinha (1991)

The average no continuum shows the effect without the continuum absorption portion of the water vapor absorption. This is the frequency range between 800-1200 cm-1, (wavelength range 12-8μm) – often known as the “atmospheric window”. This portion of the spectral range is important in studies of increasing water vapor, something we will return to in later articles.

Here we can see that in warmer climates the lower troposphere has more effect for changes in relative humidity. And for average and cooler climates, changes in relative humidity are still more important in the lower troposphere, but the upper troposphere does become more significant.

(This paper, by Shine & Sinha, appears to have been inspired by Lindzen’s 1990 paper where he talked about the importance of upper tropospheric water vapor among other subjects).

So clearly the total water vapor in a vertical section through the atmosphere isn’t going to tell us enough (see note 1). We also need to know the vertical distribution of water vapor.

Here is a slightly different perspective from Spencer and Braswell (1997):

Spencer and Braswell (1997)

This paper took a slightly different approach.

Shine & Sinha looked at a 10% change in relative humidity – so for example, from 20% to 22% (20% x 110%)
Spencer & Braswell said, let’s take a 10% change as 20% to 30% (20% + 10%)

This isn’t an argument about how to evaluate the effect of water vapor – just how to illustrate a point. Spencer & Braswell are highlighting the solid line in the right hand graph, and showing Shine & Sinha’s approach as the dashed line.

In the end, both will get the same result if the water vapor changes from 20% to 30% (for example).

Boundary Layers and Deep Convection

Here’s a conceptual schematic from Sun and Lindzen 1993:

The bottom layer is the boundary layer. Over the ocean the source of water vapor in this boundary layer is the ocean itself. Therefore, we would assume that the relative humidity would be high and the specific humidity (the amount of water vapor) would be strongly dependent on temperature (see Part Two).

Higher temperatures drive stronger convection which creates high cloud levels. This is often called “deep convection” in the literature. These convective towers are generally only a small percentage of the surface area. So over most of the tropics, air is subsiding.

Here is a handy visualization from Held & Soden (2000):

Held and Soden (2000)

The concept to be clear about is within the well-mixed boundary layer there is a strong connection between the surface temperature and the water vapor content. But above the boundary layer there is a disconnect. Why?

Because most of the air (by area) is subsiding (see note 2). This air has at one stage been convected high up in the atmosphere, has dried out and now is returning back to the surface.

Subsiding air in some parts of the tropics is extremely dry with a very low relative humidity. Remember the graphs in Part Two – air high up in the atmosphere can only hold 1/1,000th of the water vapor that can be held close to the surface. So air which is saturated when it is at the tropopause is – in relative terms – very dry when it returns to the surface.

Therefore, the theoretical connection between surface temperature and specific humidity becomes a challenging one above the boundary layer.

And the idea that relative humidity is conserved is also challenged.

Relationship between Specific Humidity and Local Temperature

Sun and Oort (1995) analyzed the humidity and temperature in the tropics (30°S to 30°N) at a number of heights over a long time period:

Sun and Oort (1995)

Note that the four graphs represent four different heights (pressures) in the atmosphere. And note as well that the temperatures plotted are the temperatures at that relevant height.

Their approach was to average the complete tropical domain (but not the complete globe) and, therefore, average out the ascending and descending portions of the atmosphere:

Through horizontal averaging, variations of water vapor and temperature that are related to the horizontal transport by the large-scale circulation will be largely removed, and thus the water vapor and temperature relationship obtained is more indicative of the property of moist convection, and is thus more relevant to the issue of water vapor feedback in global warming.

In analyzing the results, they said:

Overall, the variations of specific humidity correlate positively at all levels with the temperature variations at the same level. However, the strength of the correlation between specific humidity variations and the temperature variations at the same level appears to be strongly height dependent.

Sun & Oort (1995)

Early in the paper they explained that pre-1973 values of water vapor were more problematic than post-1973 and therefore much of the analysis would be presented with and without the earlier period. Hence, the two plots in the graph above.

Now they do something even more interesting and plot the results of changes in specific humidity (q) with temperature and compare with the curve for constant relative humidity:

Sun & Oort (1995)

The dashed line to the right is the curve of constant relative humidity. (For those still trying to keep up, if specific humidity was constant, the measured values would be a straight vertical line going through the zero).

The largest changes of water vapor with temperature occur in the boundary layer and the upper troposphere.

They note:

The water vapor in the region right above the tropical convective boundary layer has the weakest dependence on the local temperature.

And also that the results are consistent with the conceptual picture put forward by Sun and Lindzen (1993). Well, it is the same De-Zheng Sun..

Vertical Structure of Water Vapor Variations

How well can we correlate what happens at the surface with what happens in the “free troposphere” (the atmosphere above the boundary layer)?

If we want to understand temperature vertically through the atmosphere it correlates very well with the surface temperature. Probably not a surprise to anyone.

If we want to understand variations of specific humidity in the upper troposphere, we find (Sun & Oort find) that it doesn’t correlate very well with specific humidity in the boundary layer.

Sun & Oort (1995)

Take a look at (b) – this is the correlation of local temperature at any height with the surface temperature below. There is a strong correlation and no surprise.

Then look at (a) – this is the correlation of specific humidity at any height with the surface specific humidity. We can see that the correlation reduces the higher up we go.

This demonstrates that the vertical movement of water vapor is not an easy subject to understand.

Sun and Oort also comment on Raval and Ramanathan (1989), the source of the bulk of Clouds and Water Vapor – Part One:

Raval and Ramanathan (1989) were probably the first to use observational data to determine the nature of water vapor feedback in global warming. They examined the relationship between sea surface temperature and the infrared flux at the top of the atmosphere for clear sky conditions. They derived the relationship from the geographical variations..

However, whether the tropospheric water vapor content at all levels is positively correlated with the sea surface temperature is not clear. More importantly, the air must be subsiding in clear-sky regions. When there is a large-scale subsidence, the influence from the sea is restricted to a shallow boundary layer and the free tropospheric water vapor content and temperature are physically decoupled from the sea surface temperature underneath.

Thus, it may be questionable to attribute the relationships obtained in such a way to the properties of moist convection.

Conclusion

The subject of water vapor feedback is not a simple one.

In their analysis of long-term data, Sun and Oort found that water vapor variations with temperature in the tropical domain did not match constant relative humidity.

They also, like most papers, caution drawing too much from their results. They note problems in radiosonde data, and also that statistical relationships observed from inter-annual variability may not be the same as those due to global warming from increased “greenhouse” gases.

Articles in this Series

Part One – introducing some ideas from Ramanathan from ERBE 1985 – 1989 results

Part One – Responses – answering some questions about Part One

Part Two – some introductory ideas about water vapor including measurements

Part Four – discussion and results of a paper by Dessler et al using the latest AIRS and CERES data to calculate current atmospheric and water vapor feedback vs height and surface temperature

Part Five – Back of the envelope calcs from Pierrehumbert – focusing on a 1995 paper by Pierrehumbert to show some basics about circulation within the tropics and how the drier subsiding regions of the circulation contribute to cooling the tropics

Part Six – Nonlinearity and Dry Atmospheres – demonstrating that different distributions of water vapor yet with the same mean can result in different radiation to space, and how this is important for drier regions like the sub-tropics

Part Seven – Upper Tropospheric Models & Measurement – recent measurements from AIRS showing upper tropospheric water vapor increases with surface temperature

References

How Dry is the Tropical Free Troposphere? Implications for Global Warming Theory,

Spencer & Braswell, Bulletin of the American Meteorological Society (1997)

Humidity-Temperature Relationships in the Tropical Troposphere, Sun & Oort, Journal of Climate (1995)

Distribution of Tropical Tropospheric Water Vapor, Sun & Lindzen, Journal of Atmospheric Sciences (1993)

Sensitivity of the Earth’s Climate to height-dependent changes in the water vapor mixing ratio, Shine & Sinha, Nature (1991)

Some Coolness concerning Global Warming, Lindzen,Bulletin of the American Meteorological Society (1990)

Notes

Note 1 – The total amount of water vapor, TPW ( total precipitable water), is obviously something we want to know, but we don’t have enough information if we don’t know the distribution of this water vapor with height. It’s a shame, because TPW is the easiest value to measure via satellite.

Note 2 – Obviously the total mass of air is conserved. If small areas have rapidly rising air, larger areas will have have slower subsiding air.

Posted in Atmospheric Physics, Climate Models, Feedback | 44 Comments »

On Missing the Point by Chilingar et al (2008)

September 17, 2010 by scienceofdoom

Someone on another blog reminded me about this paper – Cooling of Atmosphere due to CO2 Emission, by Chilingar, Khilyuk and Sorokhtin (2008).

It’s clearly impressed many people, but it’s not a good paper. It’s main strength is misdirection.

Traditional anthropogenic theory of currently observed global warming states that release of carbon dioxide into atmosphere (partially as a result of utilization of fossil fuels) leads to an increase in atmospheric temperature because the molecules of CO2 (and other greenhouse gases) absorb the infrared radiation from the Earth’s surface. This statement is based on the Arrhenius hypothesis, which was never verified (Arrhenius, 1896).

The proponents of this theory take into consideration only one component of heat transfer in atmosphere, i.e., radiation. Yet, in the dense Earth’s troposphere with the pressure pa > 0:2 atm, the heat from the Earth’s surface is mostly transferred by convection (Sorokhtin, 2001a). According to our estimates, convection accounts for 67%, water vapor condensation in troposphere accounts for 25%, and radiation accounts for about 8% of the total heat transfer from the Earth’s surface to troposphere. Thus, convection is the dominant process of heat transfer in troposphere, and all the theories of Earth’s atmospheric heating (or cooling) first of all must consider this process of heat (energy)– mass redistribution in atmosphere..

Emphasis added.

The highlighted statement from the 2nd paragraph is false. Open any atmospheric physics textbook and you will find a treatment of convection.

Here are the first two pages of contents from The Physics of Atmospheres, by John Houghton, 2nd ed, 1986, Cambridge University Press:

Here are the contents from Atmospheres, by Richard Goody (1972), Prentice-Hall Inc:

Here is the first part of the contents from Elementary Climate Physics, by Prof. F.W. Taylor (2005), Oxford University Press:

If readers would like citations and extracts from many papers to demonstrate the point further, just ask.

So the writers of this “paper” conclude:

Thus, convection is the dominant process of heat transfer in troposphere, and all the theories of Earth’s atmospheric heating (or cooling) first of all must consider this process of heat (energy)– mass redistribution in atmosphere

The dominant theories of atmospheric heating and cooling do consider this. If the paper provided some evidence that this is “not considered” we could address the evidence but instead they just go on to claim:

This physical system (multiple cells of air convection) acts in the Earth’s troposphere like a continuous surface cooler. The cooling effect by air convection can surpass considerably the warming effect of radiation.

For the easily impressed this might seem like something noteworthy. And yet this is the staple of every textbook and every paper reviewing the effect of the inappropriately-named “greenhouse” effect.

For example, Lindzen (1990):

It is worth noting that, in the absence of convection, pure greenhouse warming would lead to a globally averaged surface temperature of 72°C given current conditions. Our current average temperature, 15°C, is actually much closer to the blackbody temperature without any greenhouse warming than to the pure greenhouse result. The relative ineffectiveness of the greenhouse effect is due to convection which carries heat past the bulk of the water vapor (which has a scale height of about 2km)..

Or Ramanathan & Coakley (1978):

A comparison of the radiative equilibrium temperatures with the observed temperatures has indicated the extent to which the other atmospheric processes, such as convection, large-scale circulation, and condensation processes, influence the thermal energy balance of the system. In most planetary atmospheres, radiative equilibrium temperatures cannot be sustained in the lower regions of the atmosphere..

Convection aids radiation in transporting energy from the surface of the planet to the atmosphere. The vertical transport of heat by convection tends to minimize the magnitude of dθ/dz..

And so Chilingar et al move to the “greenhouse” effect:

Therefore, the present-day greenhouse effect is approximately equal to +33°C. The term “greenhouse effect” is confusing from the physical point of view and leads the general public astray.

And like G&T, they point out that a greenhouse works differently from the atmosphere without noting that greenhouses are not used by atmospheric physicists to prove the effect of radiatively-active gases in the atmosphere. Instead atmospheric physics uses the fundamental equations (the radiative transfer equations) which determine absorption and emission of radiation by water vapor, CO2, methane, and other trace gases.

Proof of Negative Feedback

Now Chilingar and his colleagues bring out the simple equation balancing the effective radiation temperature of the earth with the solar radiation absorbed. But then they make the curious comment:

The water vapor condensation in troposphere begets clouds, which to a considerable degree determine the reflective properties of the planet, i.e., its albedo A. The latter gives rise to a strong negative feedback between the surface temperature Ts and the temperature of “absolutely black body” Tbb, which is determined by the solar radiation S reaching the Earth’s surface at its distance from the Sun.

Indeed, any increase in surface temperature intensifies the water evaporation and increases the Earth’s cloudiness, which, in turn, increases the Earth’s albedo. As a result, the reflection of solar heat from the clouds into space increases and the heat influx to the Earth’s surface decreases and the average surface temperature decreases to the previous level. Strong negative feedback in any system leads to linear dependence of system’s output on its input.

Why curious?

Because they provide no evidence for the claim of negative feedback. No papers, no equations, no research..

It might be true, but for us skeptics, we like to see evidence.

Anthropogenic Imact on the Earth’s Climate – Tiny

In their piece de resistance they start with:

The adiabatic theory allows one to evaluate quantitatively the influence of anthropogenic emission of carbon dioxide on the Earth’s climate.

And continue:

To evaluate the effect of anthropogenic emission of carbon dioxide on global temperature, one can use the adiabatic model together with the sensitivity analysis (Sorokhtin, 2001; Khilyuk and Chilingar, 2003, 2004). At sea level, if the pressure is measured in atmospheres, then p = 1 atm and

ΔT ≈ T α Δp (12)

If, for example, the concentration of carbon dioxide in the atmosphere increases two times (from 0.035% to 0.07%), which is expected by the year of 2100, then the atmospheric pressure will increase by Δp = 1.48 10^-4 atm (Sorokhtin, 2001). After substitution of T = 288 K, α = 0.1905, and Δp = 1.48 10^-4 atm into Eq. (13), one obtains ΔT = 0.00812 °C..

Thus, the increase in the surface temperature at sea level caused by doubling of the present-day CO2 concentration in the atmosphere will be less than 0.01 °C, which is negligible in comparison with natural temporal fluctuations of global temperature.

From these estimates, one can deduce a very important conclusion that even considerable increase in anthropogenic emission of carbon dioxide does not lead to noticeable temperature increase. Thus, the hypothesis of current global warming as a result of increased emission of carbon dioxide (greenhouse gases) into the atmosphere is not true.

Awesome. Who could argue with that. It is in a peer-reviewed paper and has a lot of equations. Climate scientists, shame on you for neglecting convection. CO2 has almost no effect on the earth’s temperature..

The Conjuring Trick

It’s all very well to produce some equations, but in the interests of accuracy it’s important to produce the correct ones.

The conjuring trick in this paper is discussing the movement of heat from the surface to the troposphere (lower atmosphere) without discussing how the surface AND atmosphere lose heat to space.

Suppose that heat was transferred from the surface to the troposphere 100% by convection.

What would it prove? It would certainly be quite a different climate but there would still be an important question to ask.

One important question for all students of climate science is:

How does the earth’s climate system (surface, troposphere, stratosphere) lose heat to space?

Solar radiation heats the earth. In equilibrium, the earth and the atmosphere radiate the same amount of heat out to space. Imbalances between solar heating and radiative cooling change the amount of heat in the climate system.

Convection (and conduction) cannot move heat into space, only radiation can do this.

Increasing the concentration of “greenhouse” gases like CO2 has an important effect unmentioned by Chilingar and his colleagues. This effect is explained in The Earth’s Energy Budget – Part Three.

The higher the concentration of “greenhouse” gases, the more optically thick the atmosphere, and therefore radiative cooling to space takes place from higher up in the atmosphere.

The higher up you go, the colder it gets. The explanation is somewhat involved, so check out the link and also the series: CO2 – An Insignificant Trace Gas?

The important point is that Chilingar and his colleagues don’t mention this. They don’t prove the fundamental equations wrong. They don’t comment..

Perhaps they don’t understand the subject. Who knows?

Conclusion

The paper demonstrates nothing about the effect of increased CO2 on the earth’s climate.

It doesn’t show a problem in established arguments, like from Manabe and Strickler (1964), Ramanathan and Coakley (1978) or any other paper. The authors of this 2008 paper just imagine the established science away.

Understanding how the earth and atmosphere cool to space via radiation is a critical component in understanding surface temperature changes.

References

Cooling of Atmosphere Due to CO2 Emission, Chilingar et al, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects (2008)

Some Coolness concerning Global Warming, Lindzen, Bulletin of American Meteorological Society (1990)

Climate Modeling through Radiative-Convective Models, Ramanathan and Coakley, Reviews of Geophysics and Space Physics (1978)

Posted in Debunking Flawed "Science" | 12 Comments »

Heat Transfer Basics – Part Zero

September 12, 2010 by scienceofdoom

This post “follows” on from Heat Transfer Basics and Non-Radiative Atmospheres and Do Trenberth and Kiehl understand the First Law of Thermodynamics? and many other posts that cover some basics.

It’s clear from comments on this blog and many other blogs that a lot of people have difficulty understanding simple scenarios because of a lack of understanding of the basics. Many confident (but erroneous) comments state that particular scenarios can never occur because they violate this or that law..

I know from my own experience that until a concept is conceptually grasped, a mathematical treatment is often not really helpful. It might be right, but it doesn’t help..

So this post has a number of examples that paint a picture. It has some maths too.

Enough examples might help some readers unfamiliar with thermodynamic concepts grasp the essence of some heat transfer basics.

Ignore the details if you like and just check the results from each example. Some maths is included to make it possible to check the results and understand the subject a little better.

Conduction

We will use the example of a “planar wall”. What exactly is that?

It’s a wall that extends off to infinity in both directions.

For those thinking this is some kind of climate madness, it’s simply physics basics – draw up a problem with simple boundary conditions and find the answer. If we start with some massively complex problem that approximates the real world then unfortunately there will be no conceptual understanding. And this article is all about conceptual understanding. Start with simple problems and gradually extend to more complex problems.. (The wall can just be a long wall if that makes you happier).

Example One is a wall, made out of PVC, with both sides held at a constant temperature (probably by a fluid at a constant temperature pumped over each side).

Example One – constant temperature conduction

We want to calculate the heat flux (heat flow per unit area) travelling through this wall of PVC.

The basic equation of heat conduction is:

q = kA . ΔT/Δx (see note 1)

where ΔT is the temperature difference, Δx is the thickness of the wall, A is the area, k is the conductivity (the property of the material) and q is the heat flow.

To make things slightly easier we consider heat flux – heat flow per unit area, q”:

q” = k . ΔT/Δx

For PVC, k=0.19W/m.K

And for the case of this wall, T1 = 50°C, T2 = 10°C and therefore ΔT = 40°C

So,

q” = 0.19 x 40 / 2 = 3.8 W/m²

In this example, because the system is holding both surfaces at a constant temperature we have a constant (and continuous) flow of heat between surfaces.

You can see that not much heat is flowing because PVC is a very good insulator.

Example Two – constant temperature conduction, thinner wall

q” = 0.19 x 40 / 0.2 = 38 W/m²

So with the wall 10x thinner, the heat flux is 10 times greater. Hopefully, for most, this is intuitively obvious – put thinner insulation on a hot water pipe and it loses more heat; wear a thinner coat out in the cold and you get colder..

If we changed the PVC for metal then the heat flow would be very much higher, as metal conducts heat very effectively.

Now what’s supplying the heat? The liquid or gas being pumped over the higher temperature surface to keep it at that temperature.

Note that these surfaces will be radiating heat. However, this doesn’t affect the calculation of conducted heat between the two surfaces.

In simple terms, heat flow due to conduction depends on the temperature difference, the material and the dimensions of the body.

Example Three – no temperature differential

Now both sides of the wall are held at the same temperature,

q” = 0.19 x 0 / 2 = 0 W/m²

This is very simple, but obviously confuses some people, including some visitors to this blog. It is temperature difference that drives conduction of heat. If there is no temperature difference, there will be no conduction.

In these three examples we have constrained the temperature on each side to see what happens to heat flow. Now we will change these boundary conditions.

Conduction and Radiation

Example Four – constant heat supply one side, fixed temperature the other

This is example two but with a constant heat supply instead of a constant temperature on one side.

This example is now more complex. The right side of the wall is held at a constant temperature of 10°C, as with the first few examples, but the other surface of the wall now has a constant input of heat and we want to find out the temperature of that surface.

The heat source for the left side is incident radiation. We will assume that the proportion of radiation absorbed (“absorptivity”) is 80% or 0.8. And we will assume that the emissivity of the surface is also 0.8. See note 2.

How do we now calculate the surface temperature T₁?

It’s quite simple in principle. We use the first law of thermodynamics – energy cannot be created or destroyed. And we will calculate the equilibrium condition – which is when steady-state is reached. This means no heat is being retained to increase the temperature.

So all we have to do is balance the heat flow terms at the surface (the left surface). Let’s take it step by step.

Energy absorbed from radiation:

E_in(absorbed) = E_in x 0.8

This is because 80% is absorbed and 20% is reflected, due to the material properties of PVC.

For energy balance, once the surface has reached a steady temperature:

E_in(absorbed) = q” + E_out (see the diagram)

q” is the heat flux through the wall, and E_out is the radiated energy. At this point we are assuming no convection (perhaps there is no atmosphere for example) to keep things simple.

Hopefully this is quite a simple concept – the heat absorbed from radiation is balanced by the heat radiated from the surface plus the heat conducted through the wall.

We can calculate the energy radiated using the well-known Stefan-Boltzmann equation,

E_out = εσT⁴

where ε = emissivity (0.8 in this example), σ is the Stefan-Boltzmann constant (5.67 x 10^-8) and T is absolute temperature in K (add 273 to temperature in °C).

Except we don’t yet know the temperature.. Still, let’s put it all together and see what happens:

E_in(absorbed) = q” + E_out

Now put the numbers in that we know:

500 x 0.8 = 0.19 x ΔT / 0.2 + 0.8 x 5.67×10^-8 x T₁⁴

Now ΔT is the temperature difference between T₁ and T₂. T₂ is held constant at 10°C so ΔT=T₁-10. However, the first term on the right is expressed in °C and the second term in absolute temperature (K). We will express both as absolute temperature, so ΔT = T₁-283.

So now the equation is:

400 = 0.19 x (T₁-283) / 0.2 + 0.8 x 5.67×10^-8 x T₁⁴

The important point to note for those a little bewildered by all the numbers – we have used the first law of thermodynamics, the equation for emission of radiation and the equation for conducted heat and as a result we have an equation with only one unknown – the temperature.

This means we can find the value of T₁ that satisfies this equation. (See note 3 for how it is found).

T₁ = 302.80 K = 29.65°C

And using this value, conducted heat, q” = 18.7 W/m² and radiated heat, E_out = 381.3 W/m².

In this case, there is a lot more heat radiated compared with conducted.

Example Five – as example four with a thinner wall

With a much thinner wall or a much higher conductivity the balance changes.

Changing the thickness of the wall from 0.2m to 2mm, keeping everything else the same and so using exactly the same equations as above, we get:

T₁ = 284.24 K = 11.09°C

Note that this means the temperature differential across the wall has reduced to only (just over) 1°C.

And using this value, conducted heat, q” = 103.6 W/m² and radiated heat, E_out = 297.4 W/m².

Example Six – as example four with increased “colder” temperature

Now with the 0.2m wall (example four) we increase the temperature of the colder side, from 10°C to 25°C.

Using the same maths we find that the temperature, T1, has increased:

T₁ = 305.16K = 32.01°C

An increase of 2.36°C.

Most people are probably asking “why this example? it’s obvious that increasing the temperature of one side will lift the other..”

However, many people believe that a colder atmosphere cannot affect the temperature of a warmer surface. See, for example, The First Law of Thermodynamics Meets the Imaginary Second Law. This reasoning is due to a misunderstanding of the second law of thermodynamics.

However, as conduction is quite familiar and more intuitive I expect that this example will be more easily accepted. And perhaps this last example will help a few people to see that a colder body can affect a warmer body without violating any laws of thermodynamics.

Conclusion

In Do Trenberth and Kiehl understand the First Law of Thermodynamics? I presented a hollow sphere in space with a heat source at its center. Some people were (and still are) convinced that there is something wrong with the results from that example. One person (at least) is convinced that the inner surface must be at the same temperature as the outer surface.

The only correct approach to calculating heat transfer and temperatures is to apply the relevant equations of conduction, convection and radiation to the particular problem in question.

Conduction of heat is proportional to the temperature difference across a material
Radiation of heat is proportional to the 4th power of (absolute) temperature of a surface
The first law of thermodynamics is used to solve these problems: energy in – energy out = energy retained, for any particular part of a system that you analyze

Many people rely on intuition for determining whether a solution is correct. However, intuition is not as reliable as applying the basic equations of heat transfer.

Note that the example in Do Trenberth and Kiehl understand the First Law of Thermodynamics? uses exactly the same equations and approach as the examples here. If these six examples are correct you will have trouble finding the flaw in the hollow sphere example.

Notes

Note 1 – Conventionally the equation of heat conducted has a minus sign because heat travels in the opposite direction to the temperature gradient. And for the purists, the more general equation of conduction is:

q” = -k∇T

where ∇T is the three dimensional version of the “change of T with respect to distance”

Note 2 – Emissivity = Absorptivity at a particular wavelength (and direction for “non-diffuse” surfaces). In the case of a surface receiving radiation and emitting radiation there is no reason why these two values should be the same. This is because the incident radiation will be at one wavelength (or range of wavelengths), but the wavelength of emission depends on the temperature of the surface.

Note 3 – One simple way to find the value that satisfies the equation is to plot the equation for a wide range of temperatures and look up the temperature value where the result is correct. This is what I did here. It is the work of a minute with Matlab.

Update – added Sep 15th

A graph of temperature vs wall thickness for Examples Four & Five (with T2 = 10°C):

Update – Added Sep 15th

3D graph for examples 4 to 6 – of how T1 varies with wall thickness and T2:

Click for a larger image

Update – added Sep 16th

3D graph of how T1 varies with emissivity. First, when absorptivity = emissivity:

Click for a larger image

Now with absorptivity (the proportion of incident radiation absorbed) set at 0.8, while the emissivity varies.

Click for a larger image

Notice that when the absorptivity and emissivity are equal the temperature T1 is pretty much independent of the actual value of emissivity/absorptivity – why is that?

And when emissivity varies while absorptivity is fixed (and therefore absorbed energy is fixed) the temperature T1 is pretty much independent of emissivity for very thin walls – why is that?

Posted in Basic Science | 161 Comments »

Clouds and Water Vapor – Part One – Responses

August 29, 2010 by scienceofdoom

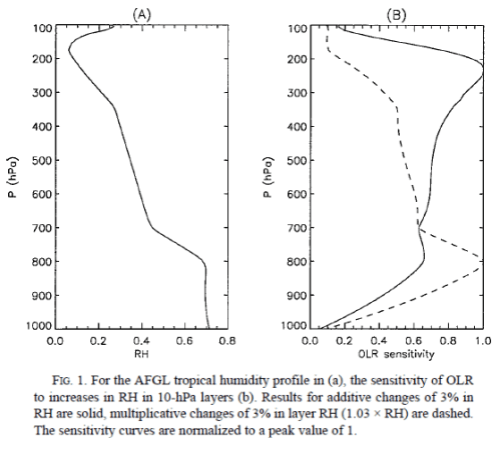
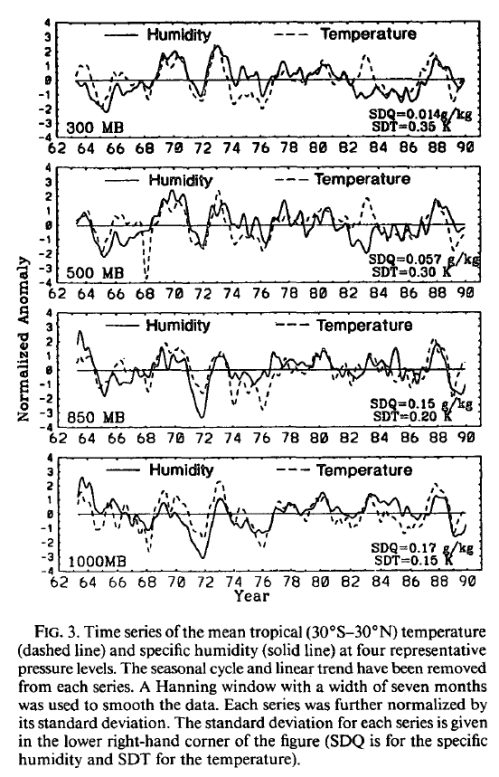
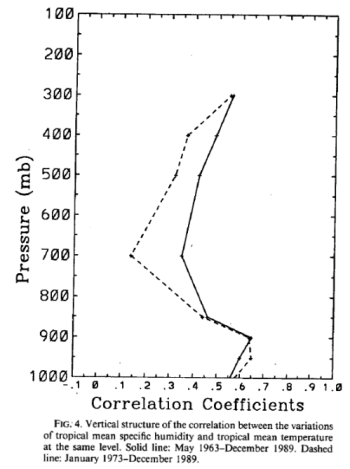
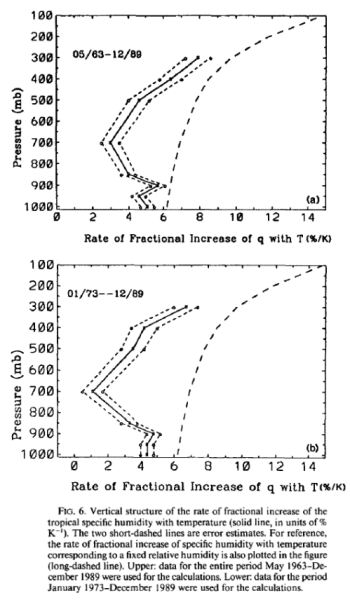
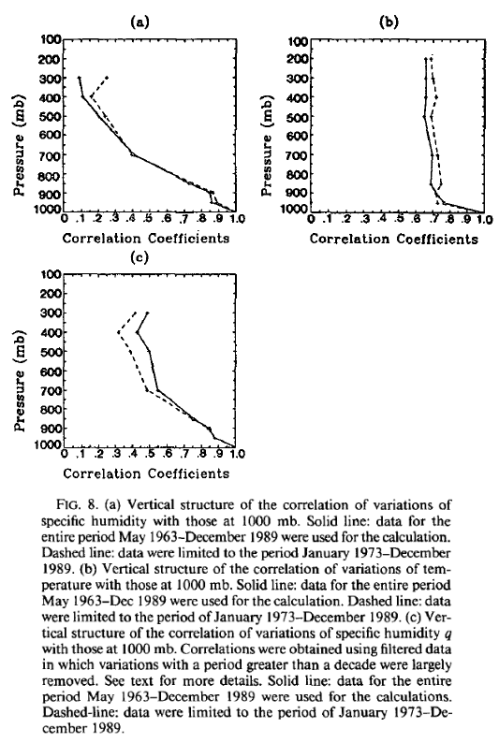
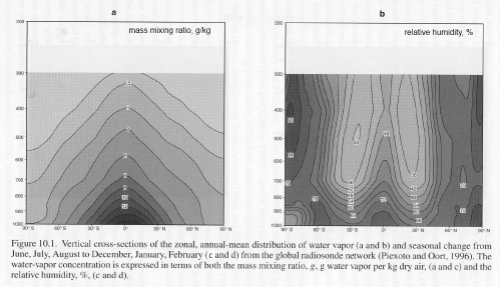
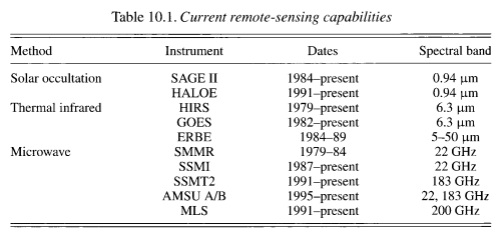
After posting Part Two on water vapor, some people were unhappy that questions from Part One were not addressed.

I have re-read through the many comments and questions and attempt to answer them here. I ignore the questions unrelated to the feedbacks of water vapor and clouds – like the many questions about the moon, answered in Lunar Madness and Physics Basics. I also ignore the personal attacks from a commenter that my article(s) was/were deceptive.

The Definition

The major point from the perspective of a few commenters (including critics of Part Two) was about the radiometric definition of the “greenhouse” effect.

Ramanathan analyzed the following equation:

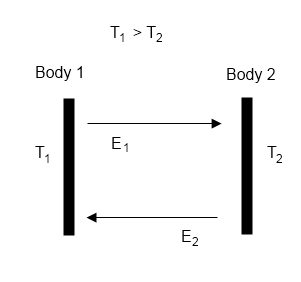
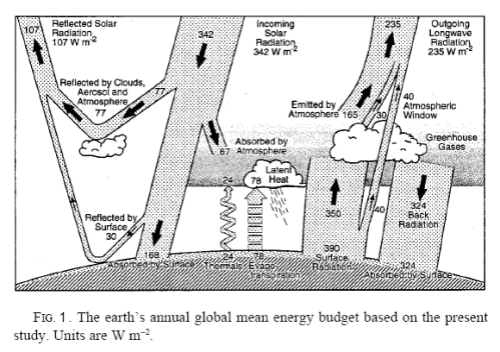
F = σT⁴ – G

where F is outgoing longwave radiation (OLR) at top of atmosphere (TOA), T is surface temperature, and G is the “greenhouse” effect.

For newcomers, F averages around 240 W/m² (and higher in clear sky conditions).

The first term on the right, σT⁴, is the Stefan-Boltzmann equation which calculates radiation from a surface from its temperature, e.g., for a 288K surface (15°C) the surface radiation = 390 W/m².

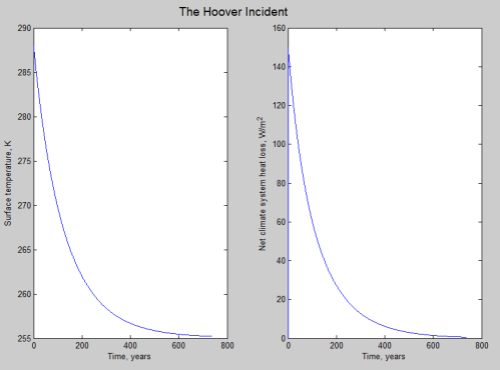
If the atmosphere had no radiative absorbers (no “greenhouse” effect) then F= σT⁴, which means G=0. See The Hoover Incident.

The approach Ramanathan took was to find out the actual climate response over 1988-89 from ERBE scanner data. What happens to the parameters F and G when temperature increases?

Why is it important?

If increasing CO2 warms the planet, will there be positive, negative or no feedback from water vapor? Apparently, Ramanathan thought that analyzing the terms in the equation under changing conditions could shed some light on the subject.

However, the equation itself was brought into question, mainly by Colin Davidson, in a number of comments including:

..In the section “Greenhouse Effect and Water Vapour”, he introduces an equation:

F = σTs^4 – G

I didn’t understand what this equation was trying to say. How are the Surface Radiation and the Outgoing Long Range Radiation linked, noting that there are other fluxes from the Surface into the Atmosphere? And one of these (evaporation) is stronger than the NET Surface radiation, while direct Conduction is also a significant flux?
The sentence “So the radiation from the earth’s surface less the “greenhouse” effect is the amount of radiation that escapes to space.” is not accurate.

Missing from this sentence are the following:
Incoming Solar Radiation Absorbed by the Atmosphere(A);
Evaporated Water from the Surface(E);
Direct Conduction from Surface to Atmosphere(C)
Back-Radiation from Atmosphere to Surface (B)

Writing down the fluxes for the atmosphere as a black box:
F= A+(S-B)+E+C (where S=Stephan-Boltzmann Surface Radiation),
Making G = S-F = B-A-E-C

So G doesn’t appear to me to make much PHYSICAL sense, and is certainly NOT the “Greenhouse Effect”, as the evaporative and conductive species are not greenhouse animals, but B and A certainly belong in the zoo..

And:

..I have shown that both those claims are incorrect. G does not represent the “Greenhouse” effect of an IR active atmosphere, as it contains terms (Evaporation and Conduction) which are plainly IR insensitive, nor does it represent the upward surface flux less the amount of longwave radiation leaving the planet.

What G represents is anyone’s guess, but it is not an easily identifiable physical quantity.

Hence my problem with the equation F=S-G as a starting point for any analysis – it doesn’t seem to represent anything coherent. Why not start with the TOA balance, the Surface balance, or the Atmospheric balance?

I am concerned about this. Is the whole theorem of climate sensitivity based on the incorrect notion that the factor G represents the Greenhouse Effect?

As well as:

In this post I summarise some of my concerns.

1. F= Sunlight – Reflected sunlight. Unless the earth’s short-wave albedo changes, the Outgoing Long-Wave Radiation(F) is constant, whatever the state of the Greenhouse. So dF/dTs does not represent the Greenhouse Effect, but is a representation of the change of surface temperature with cloudiness.

2. F= S(urface Radiation) + G, but G= E(vaporation) +C(onduction) + A(bsorbed Solar Radiation) – B(ack Radiation). Of these terms, only A and B are Greenhouse dependent. C and E are Greenhouse independent. dG/dTs is therefore not a measure of the Greenhouse Effect.

3. It is unclear if the amount of radiation from the surface escaping “through the window” direct to space is constant. If CO2 concentration increases we expect some tightening of the window, but not much. On the other hand any increase in surface temperature will increase the amount of radiation, so the two processes may balance. Kiehl and Trenberth keep this constant at 40W/m^2 despite raising the surface temperature over time by 1DegC, suggesting that it may be close to constant.

Assuming that is so, the fluxes warming the atmosphere from the Surface are constant, the (B)ack radiation increasing by roughly the same as the sum of the increases in Radiation from the Surface(S) and (E)vaporation. Basically when the surface temperature increases, the increase in Evaporation is balanced by a
decrease in Net Surface Radiation Absorbed by the Atmosphere.
As the heat entering the lower atmosphere is unchanged (though the amounts entering at each height will change), the overall Lapse Rate to the tropopause will be unchanged. So the temperature at the Tropopause will always be the Surface Temperature minus a Constant. The sensitivity of the Tropopause temperature is therefore the same as (and driven by) the sensitivity of the Surface temperature to changes in “forcing” (either solar or back-radiation).

This sensitivity is between 0.095 and 0.15 DegC/W/m^2.

And a search in that post will highlight all the other comments.

My attempts at explaining the concept did not appear successful. I don’t think I will have any more success this time, but clearly others think it is important.

I find Colin’s comments confused, but I’ll start with the main point of Ramanathan (paraphrased by me):

What happens if the climate warms from CO2 (or solar or any other cause) – will water vapor in the climate increase, causing a larger “greenhouse” effect?

That’s the question that many people have asked. These people include well-known figures like Richard Lindzen and Roy Spencer, who believe that negative feedbacks dominate.

Scenarios to Demonstrate the Usefulness of the Definition

If the surface temperature in one location goes from 288K (15°C) to 289K (16°C) the surface radiation will increase by 5.4 W/m². (The Stefan-Boltzmann law). How can we determine whether positive or negative feedbacks exist?

Condition 1. Suppose under clear skies when the temperature was 288K we measured OLR = 265 W/m² and when the temperature increased to 289K we measured OLR = 275 W/m². That means OLR has increased by 10 W/m² for a surface radiation increase of 5.4 W/m². Let’s call this condition Good.

Condition 2. Suppose instead that when the temperature increased to 289K we measured OLR = 265W/m². That means OLR has not changed when surface radiation increased by 5.4 W/m². Let’s call this condition Bad.

In condition Good we have negative feedback, where the atmospheric “greenhouse” response to higher temperatures is to reduce its absorption of longwave radiation
In condition Bad we have positive feedback – the situation where more heat has been trapped by the atmosphere – the atmosphere has increased its absorption of longwave radiation

Whether or not more heat also leaves the surface by evaporation or conduction doesn’t really matter for this analysis. It doesn’t tell us what we need to know.

In fact, it’s quite likely that if evaporation increases we might find that positive feedback exists. However, that depends on exactly where the water vapor ends up in the atmosphere (as the absorption of longwave radiation by water vapor is non-linear with height) and how this also changes the lapse rate (as the moist lapse rate is less than the dry lapse rate).

It’s possible that if convective heat fluxes from the surface increase we might find that negative feedback exists – this is because heat moved from the surface to higher levels in the atmosphere increases the ability of the atmosphere to radiate out heat. This is also part of the lapse rate feedback.

But all of these different effects are wrapped up in the ultimate question of how much heat leaves the top of atmosphere as a function of changes in the surface temperature. This is what feedback is about.

So for feedback we really want to know – does the absorptance of the atmosphere increase as surface temperature increases? (see note 3).

That’s as much as I can explain as to why this measure is the useful one for understanding feedback. This is why everyone that deals with the subject reviews the same fundamental equation. This includes those who believe that negative feedbacks dominate.

See Note 2 and Note 3.

Colin Davidson’s points

Colin often makes very sensible statements and points but many of the statements and claims cited earlier suffer from irrelevance, inaccuracy or a lack of any proof.

Missing the point – as I described above – was the main problem. In the interests of completeness we will consider some of his statements.

The third comment cited above indicates one of the main problems with his approach:

..Unless the earth’s short-wave albedo changes, the Outgoing Long-Wave Radiation(F) is constant, whatever the state of the Greenhouse. So dF/dTs does not represent the Greenhouse Effect..

This is not the case. Suppose that absorbed solar radiation is constant. This does not mean that OLR (=”F” in Colin’s description) will be constant. From the First Law of Thermodynamics:

Energy in = Energy out + energy added to the system

In long term equilibrium energy in = energy out. However, we want to know what happens if something disturbs the system. For example, if increased CO2 reduces OLR then heat will be added to the climate system until eventually OLR rises to match the old value – but with a higher temperature in the climate. The same is the case with any other forcing. (See The Earth’s Energy Budget – Part Two).

In fact we expect that for a particular location and time OLR won’t equal solar radiation absorbed. We also have the problem that any “out of equilibrium” signal we might try to measure at TOA is very small, and within the error bars of our measuring equipment.

I didn’t understand what this equation was trying to say. How are the Surface Radiation and the Outgoing Long Range Radiation linked, noting that there are other fluxes from the Surface into the Atmosphere? And one of these (evaporation) is stronger than the NET Surface radiation, while direct Conduction is also a significant flux?

This is a very basic point. The surface radiation and outgoing longwave radiation (OLR) are linked by the equations of atmospheric absorption and emission (see note 4). With no absorption, OLR = surface radiation. The more the concentration of absorbers in the atmosphere the greater the difference between surface radiation and OLR. If we want to find out the feedback effect of water vapor this is exactly the relationship we need to study. Surface radiation and OLR are linked by the very effect we want to study.

A similar problem is suggested in the second comment cited:

..Hence my problem with the equation F=S-G as a starting point for any analysis – it doesn’t seem to represent anything coherent. Why not start with the TOA balance, the Surface balance, or the Atmospheric balance?

How is it possible to extract positive or negative feedback from these?

We expect that at TOA and at the surface the long term global annual average will balance to zero. But we can’t easily measure evaporation or sensible heat. Without carefully placed pyrgeometers we can’t measure DLR (downward longwave radiation) and without pyranometers we can’t measure the incident solar radiation at the surface. In any case even if we had all of these terms it doesn’t help us extract the sign or magnitude of the water vapor feedback.

If we had lots of measurement capability at a particular location it might help us to estimate the evaporation. But then we have the problem of where does this water vapor end up? This is a problem that Richard Lindzen has frequently made – and is also made by Held & Soden in their review article (cited in Part Two). Approaching the problem (from the surface energy balance) without knowing the answer to where water vapor ends up we can’t attempt to calculate the sign of water vapor feedback.

Colin also makes a number of other comments of dubious relevance in the last section of text I extracted.

He states that evaporation and conduction are “greenhouse independent” – but I question this. More “greenhouse” gases mean more surface irradiation from the atmosphere, and therefore more evaporation and conduction (and convection).

The amount of radiation escaping through the so-called “atmospheric window” is not constant (perhaps a subject for a later article). The rest of the statement covers the belief in some kind of simplified atmospheric model where everything is in balance – and therefore a positive feedback is defined out of existence:

Basically when the surface temperature increases, the increase in Evaporation is balanced by a decrease in Net Surface Radiation Absorbed by the Atmosphere.
As the heat entering the lower atmosphere is unchanged (though the amounts entering at each height will change), the overall Lapse Rate to the tropopause will be unchanged. So the temperature at the Tropopause will always be the Surface Temperature minus a Constant. The sensitivity of the Tropopause temperature is therefore the same as (and driven by) the sensitivity of the Surface temperature to changes in “forcing” (either solar or back-radiation).

When surface temperature increases, evaporation is not balanced by a decrease in net surface radiation absorbed by the atmosphere. In fact, when surface temperature increases, surface radiation increases and possible atmospheric absorption of this radiation increases (due to humidity increases from more evaporation). Exactly what change this brings in DLR (atmospheric radiation received by the surface) is a question to be answered. By saying everything is in balance means that the solution about positive feedback is already known. If so, this needs to be demonstrated – not claimed.

The rest of the statement above suffers from the same problem. None of it has been demonstrated. If I understand it at all, it’s kind of a claim of climate equilibrium which therefore “proves” (?) that there isn’t water vapor feedback. However, I don’t really understand what it might demonstrate.

Other Comments Needing Response from the Original Article

From Leonard Weinstein:

Since the issue is not resolved that the temperature in the upper troposphere has increased, and the relative humidity has not stayed nearly constant (it has clearly decreased) over the period of greatest lower troposphere temperature increase, the argument seems less than resolved. The lack of increased water vapor in the stratosphere pushes that point even further.

The argument isn’t resolved by this piece of work. This is one attempt to measure the effect over a period of good quality data.

Finely, the data and analysis of Roy Spencer seems to lead to different conclusions even on the data interpretation. Can you point out his errors and respond to those issues?

Roy Spencer’s analysis doesn’t address this period of measurement. His paper is about the period from 2000-2008.

From NicL:

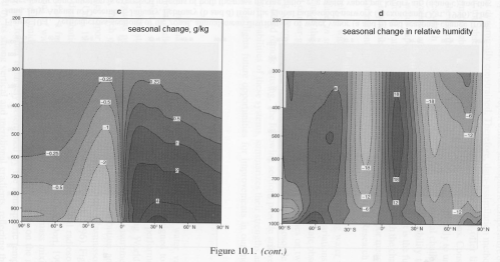
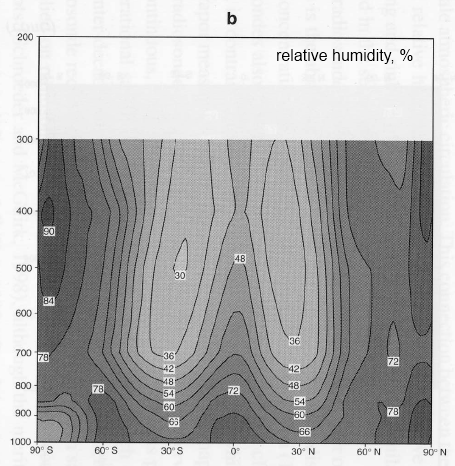
However, I take issue with your statement “It should be clear from these graphics that observed variations in the normalized “greenhouse” effect are largely due to changes in water vapor.” The spatial maps referred to merely indicate a correlation between these two things. It is unscientific to infer causation from correlation. Ramathan himself goes no further than to say the graphics suggest that variations in water vapour rather than lapse rates contribute to regional variations in the greenhouse effect.

It’s unscientific to infer causation from correlation in the absence of a theory that links them together. It’s solidly established that water vapor absorbs longwave radiation from the surface, and it’s solidly established that CO2 and other “greenhouse” gases are well-mixed through the atmosphere, while water vapor is not. Therefore, there is a strong theoretical link.

I think, in common with various other repondants, that changes in lapse rates and in the height of the tropopause are key issues in modelling the greenhouse effect, yet they seem rarely discussed. Ramanathan’s chapter does not really cover them.

What makes you say they are rarely discussed? There are many papers discussing the different processes involved in modeling water vapor feedback. However, Ramanathan’s chapter is primarily about measurements. Of course he refers to the different aspects of feedback in the chapter.

Conclusion

One commenter in part two said:

I want to give him a chance to reflect on whether he wants to defend the Ramanathan analysis in Part 1 or separate himself with dignity, which he can still do..

The primary question seemed to be the approach, and not the results, of Ramanathan.

Ramanathan tested the changes in atmospheric absorptance of longwave radiation with temperature changes. To claim this is inherently wrong is a bold claim and one I can’t understand. Neither can Richard Lindzen or Roy Spencer, at least, not from anything I have read of their work.

There are other possible approaches to Ramanathan’s results. Other researchers may have replicated his work and found different results. Other researchers may have analyzed different periods and found different changes.

There are also theoretical considerations – whether changes in the equilibrium temperature as a result of increased CO2 can be considered as the same conditions under which seasonal changes indicated positive water vapor feedback.

The question for readers to ask is: Did Ramanathan find something important that needs to be considered?

Ramanathan himself said:

However, our results do not necessarily confirm the positive feedback resulting from the fixed relative humidity models for global warming, for the present results are based on annual cycle.

If I someone can point out the theoretical flaw in Ramanathan’s work then I might “separate myself with dignity” otherwise I will be happy to stand by the idea that he has demonstrated something that needs to be considered.

Articles in this Series

Part One – introducing some ideas from Ramanathan from ERBE 1985 – 1989 results

Part Two – some introductory ideas about water vapor including measurements

Part Three – effects of water vapor at different heights (non-linearity issues), problems of the 3d motion of air in the water vapor problem and some calculations over a few decades

Part Four – discussion and results of a paper by Dessler et al using the latest AIRS and CERES data to calculate current atmospheric and water vapor feedback vs height and surface temperature

Part Seven – Upper Tropospheric Models & Measurement – recent measurements from AIRS showing upper tropospheric water vapor increases with surface temperature

Note 1.

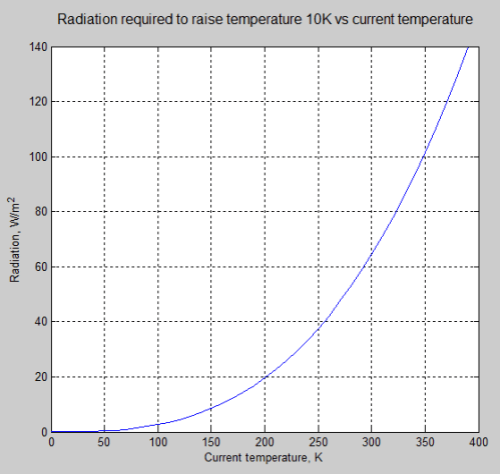
The actual change in emission of radiation for a 1°C rise in temperature depends on the temperature itself, one of the many non-linearities in science. The example in the article was for the specific temperature of 288K, along with the desire to avoid confusing readers with too many caveats.

Here is the graph of radiation change for a 1°C rise vs temperature:

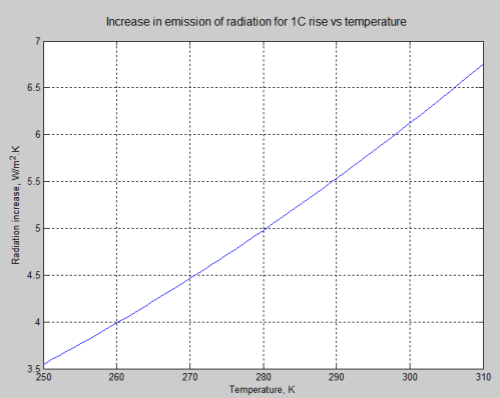
For the mathematicians it is an easy exercise. For non-mathematicians, the change in radiation = 4σT³ W/m².K (obtained by differentiating the Stefan-Boltzmann equation with respect to T).

Note 2.

This article is about a specific point in Ramanathan’s work queried by some of my readers. His explanation of how to determine feedbacks is much more lengthy and includes some important points, especially the demonstration of the relationships in time between the various changes. These are important for the determination of cause and effect. See the original article and especially the online chapter for more a detailed explanation.

Note 3.

The rate of change of surface radiation with temperature, σdT⁴/dT = 4σT³ W/m².K (see note 1) is 5.4W/m² per K at 288K. However, the rate of change of OLR, dF/dT, for the no feedback condition is slightly more challenging to determine and not intuitively obvious.

Ramanathan, based on his earlier work from 1981, determined the “no feedback” condition (i.e., without lapse-rate feedback or water vapor feedback) was dF/dT=3.3 W/m².K. And for positive feedback this parameter, dF/dT would be less than 3.3.

Roy Spencer and William Braswell in their just-published work in JGR, On the diagnosis of radiative feedback in the presence of unknown radiative forcing has exactly the same value as the determination of the no feedback condition.

Note 4.

There are many different formulations of the solutions to the radiative transfer equations. This version is from Ramanathan’s chapter in Frontiers of Climate Modeling:

This is just to demonstrate that there is a strong mathematical link between surface radiation and OLR, and one that is very relevant for determining whether positive or negative feedbacks exist.

Posted in Atmospheric Physics, Feedback | 105 Comments »

Clouds and Water Vapor – Part Two

August 25, 2010 by scienceofdoom

In Part One we covered a lot of ground. In this next part we will take a look at some basics about water vapor.

The response of water vapor to a warmer climate is at the heart of concerns about the effect of increasing the inappropriately-named “greenhouse” gases like CO2 and methane. Water vapor is actually the major “greenhouse” gas in the atmosphere. But unlike CO2, methane and NO2, there’s a huge potential supply of water vapor readily available to move into the atmosphere. And all it takes is a little extra heat to convert more of the oceans and waterways into water vapor.

Of course, it’s not so simple.

Before we dive into the subject, it’s worth touching on the subject of non-linearity – something that doesn’t just apply to the study of water vapor. Some people are readily able to appreciate the problem of non-linearity. For others it’s something quite vague. So before we’ve even started we’ll digress into slightly more familiar territory, just to give a little flavor to non-linearity.

A Digression on Non-Linearity

People who know all about this can just skip to the next section. For most people who haven’t studied a science or maths subject, it’s a natural assumption to assume that the world is quite a linear place. What am I talking about?

Here’s an example, familiar to regular readers of this blog and anyone who has tried to understand the basic concept of the “greenhouse” effect.

If the atmosphere did not absorb or emit radiation the surface of the earth would radiate at an average of around 240 W/m² (see The Hoover Incident, CO2 – An Insignificant Trace Gas? and many other articles on this blog).

This would mean a surface temperature of a chilly 255K (-18°C).

With the “greenhouse” effect of a radiating atmosphere, the surface is around 288K (+15°C) and radiates 390 W/m².

As one commenter put it (paraphrasing to save finding the quote):

Clearly you haven’t done your sums right. If 240 W/m² means a temperature of 255K, then 390 W/m² means a temperature of (390/240)x255 which is way more than the actual temperature of 288K (15°C).

Now that commenter spelt out the maths but many more people don’t even do that and yet feel instinctively that something is wrong when results can’t be simply added up, or fitted on a straight line.

In the case of that approach, the actual temperature – assuming a linear relationship between radiation and temperature – would be 414K or 141°C. That approach is wrong. The world is not linear.

How much radiation does it take to raise the equilibrium surface temperature by 10°C (or 10K)? This assumes a simple energy balance where more radiation received heats up the surface until it radiates out the same amount.

The answer might surprise you. It depends. It depends a lot. Here’s a graph:

So if the surface is at 100K ( -173°C), it takes only 2.6 W/m² to lift the temperature by 10K (10°C).

At 200K (-73°C), it takes 20 W/m²
At 300K (27°C), it takes 65 W/m²
At 400K (127°C), it takes 151 W/m²

The equation that links radiation to temperature is the Stefan-Boltzmann equation, and the relationship is j=εσT⁴,where T is temperature.

If the equation was something like j=kT, then it wouldn’t matter what the current temperature was – the same amount of energy would lift the temperature another 10K. For example, if it took 10 W/m² to lift the temperature from 100K to 110K, then it would take 10W/m² to lift the temperature from 300K to 310K. That would be a linear relationship.

But he world isn’t linear most of the time. Here are some non-linear examples:

radiation from surfaces (and gases) vs temperature
absorption of radiation by gases vs pressure
absorption of radiation by gases vs wavelength
pressure vs height (in the atmosphere)
water vapor concentration in the atmosphere vs temperature
convective heat flow

It’s important to try and unlearn the idea of linearity. Intuition isn’t a good guide for physics. At best you need a calculator or a graph.

Digression over.

Water Vapor Distribution

Let’s take a look at water vapor distribution in the real world (below).

Both graphs below have latitude along the horizontal axis (x-axis) and pressure along the vertical axis (y-axis). Pressure = 1000 (mbar) is sea level, and pressure = 200 is the top of the troposphere (lower atmosphere).

The left side graph is specific humidity, or how much mass of water vapor exists in grams per kg of dry air.

The right side graph is relative humidity, which will be explained. Both are annual averages.

Water Vapor Observations, Soden – “Frontiers of Climate Modeling”, chapter 10

Click for a larger view

As a comparison the two graphs below show the change in specific humidity and relative humidity from June/Jul/August to Dec/Jan/Feb:

Water Vapor Observations, Soden – “Frontiers of Climate Modeling”, chapter 10

Click for a larger view

The most important parameter for water vapor is the maximum amount of water vapor that can exist – the saturation amount. Here is the graph for saturation mixing ratio at sea level:

You can see that at 0°C the maximum mixing ratio of water vapor is 4 g/kg, while at 30°C it is 27 g/kg. Warmer air, as most people know, can carry much more water vapor than colder air.

(Note that strictly speaking air can become supersaturated, with relative humidities above 100%. But in practice it’s a reasonable guide to assume the maximum at 100%).

Here’s the graph for temperatures below zero, for water and for ice – they are quite similar:

Relative humidity is the ratio of actual humidity to the saturation value.

Saturation occurs when air is in equilibrium over a surface of water or ice. So air very close to water is usually close to saturation – unless it has just been blown in from colder temperatures.

The Simplified Journey of a Parcel of Moist Air

Let’s consider a parcel of air just over the surface of a tropical ocean where the sea surface temperature is 25°C. The relative humidity will be near to 100% and specific humidity will be close to 20 g/kg. The heating effect of the ocean causes convection and the parcel of air rises.

As air rises it cools via adiabatic expansion (see the lengthy Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion).

The cooler air can no longer hold so much water and it condenses out into clouds and precipitation. Eventually this parcel of air subsides back to ground. If the maximum height reached on the journey was more than a few km then the mixing ratio of the air will be a small fraction of its original value.

When the subsiding air reaches the ground – much warmer once again due to adiabatic compression – its relative humidity will now be very low – as the holding capacity of this air is once again very high.

Take a look at the graph shown earlier of relative humidity:

Annual averages don’t quite portray the journey of one little parcel of air, but the main features of the graph might make more sense. In a very broad sense air rises in the tropics and descends into the extra-tropics, which is why the air around 30°N and 30°S has a lower relative humidity than the air at the tropics or the higher latitudes.

Why isn’t the air higher up in the tropics at 100% relative humidity?

Because the air is not just made up of air rising, there is faster moving rising air, and a larger area of slowly subsiding air.

Held & Soden in an excellent review article (reference below), said this:

To model the relative humidity distribution and its response to global warming one requires a model of the atmospheric circulation. The complexity of the circulation makes it difficult to provide compelling intuitive arguments for how the relative humidity will change. As discussed below, computer models that attempt to capture some of this complexity predict that the relative humidity distribution is largely insensitive to changes in climate.

(Emphasis added).

The Complexity

The ability of air to hold water vapor is a very non-linear function of temperature. Water vapor itself has very non-linear effects in the radiative balance in the atmosphere depending on its height and concentration. Upper tropospheric water vapor is especially important, despite the low absolute amount of water vapor in this region.

Many many researchers have proposed different models for water vapor distribution and how it will change in a warmer world – we will have a look at some of them in subsequent articles.

Measurement of water vapor distribution has mostly not been accurate enough to paint a full enough picture.

Measurements

There are two ways that water vapor is measured:

radiosonde
satellite

Radiosondes (instruments in weather balloons) provide a twice-daily high resolution vertical profile (resolution of 100m) of temperature, pressure and water vapor. However, in many areas the coverage is low, e.g. over the oceans.

Radiosondes provide the longest unbroken series of data – going back to the 1940’s.

Measurements of humidity from radiosondes are problematic – often over-stating water vapor higher up in the troposphere. Many older sensors were not designed to measure the low levels of water vapor above 500hPa. As countries upgrade their sensors it appears to have introduced a spurious drying trend.

Comparison of measurements of water vapor between adjacent countries using different manufacturers of radiosonde sensors demonstrates that there are many measurement problems.

Here’s a map of radiosonde distribution:

From “Frontiers of Climate Modeling” (2006)

Satellites provide excellent coverage but mostly lack the vertical resolution of water vapor. One method of measurement which gives the best vertical resolution (around 1km) is solar occultation or limb sounding. The satellite views the sun “sideways” through the atmosphere at a water vapor absorption wavelength like 0.94μm, and as the effective height changes the amount of water vapor can be calculated against height.

This method also allows us to measure water vapor in the stratosphere (and in fact it’s best suited for measuring the stratosphere and the highest levels of the troposphere).

Here are the established satellite systems for measuring water vapor:

From “Frontiers of Climate Modelling” (2006)

Here is a water vapor measurement from Sage II:

From “Frontiers in Climate Modeling” (2006)

There are many disadvantages of solar occultation measurement – large geographic footprint of measurement, knowledge of ozone distribution is required and measurements are limited to sunrise and sunset.

The other methods involve looking down through the atmosphere – so they provide better horizontal resolution but worse vertical resolution. Water vapor absorbs and emits thermal radiation at wavelengths through the infrared spectrum. Different wavelengths with stronger or weaker absorption provide different “weighting” to the water vapor vertical distribution.

The new Earth Observing System, EOS, which began in 1999 has many instruments for improved measurement:

Mostly these provide improvements, rather than revolutions, in accuracy and resolution.

Finally, an interesting picture of upper tropospheric relative humidity from Held & Soden (2000):

Upper tropospheric humidity, Held & Soden (2000)

You can see – no surprise – that the relative humidity is highest around the clouds and reduces the further away you move from the clouds.

Conclusion

Understanding water vapor is essential to understanding the climate system and what kind of feedback effect it might have.

However, the subject is not simple, because unlike CO2, water vapor is “heterogeneous” – meaning that its concentration varies across the globe and vertically through the atmosphere. And the response of the climate system to water vapor is non-linear.

Measurements of water vapor are not quite at the level of accuracy and resolution they need to be to confirm any models, but there are many recent advances in measurements.

Articles in this Series

Part One – introducing some ideas from Ramanathan from ERBE 1985 – 1989 results

Part One – Responses – answering some questions about Part One

Part Three – effects of water vapor at different heights (non-linearity issues), problems of the 3d motion of air in the water vapor problem and some calculations over a few decades

Part Four – discussion and results of a paper by Dessler et al using the latest AIRS and CERES data to calculate current atmospheric and water vapor feedback vs height and surface temperature

Part Seven – Upper Tropospheric Models & Measurement – recent measurements from AIRS showing upper tropospheric water vapor increases with surface temperature

References

Frontiers of Climate Modeling, ed. J.T. Kiehl & V. Ramanathan, Cambridge University Press (2006)

Water Vapor Feedback and Global Warming, I.M. Held & B.J. Soden, Annual Review of Energy and the Environment (2000)

Posted in Atmospheric Physics, Feedback | 32 Comments »

Heat Transfer Basics and Non-Radiative Atmospheres

August 22, 2010 by scienceofdoom

Without a firm grasp on the basics it can be hard to choose between a good and bad explanation.

In The Hoover Incident I explained what would happen if the atmosphere didn’t absorb or emit radiation – i.e., if the radiatively active gases were “hoovered up”. Have a read of that post for a full explanation, but the essence of it is that with no atmospheric absorption or radiation the surface would be radiating around 390 W/m² into space while receiving only 240 W/m² from the sun. Therefore, the earth would cool down until it was only radiating 240 W/m² (it’s slightly more complicated) – leading to a surface temperature around -18°C (255K).

One of the statements I made was:

And no matter what happens to convection, lapse rates, and rainfall this cooling will continue. That’s because these aspects of the climate only distribute the heat.

Nothing can stop the radiation loss from the surface because the atmosphere is no longer absorbing radiation. They might enhance or reduce the cooling by changing the surface temperature in some way – because radiation emitted by the surface is a function of temperature (proportional to T⁴). But while energy out > energy in, the climate system would be cooling.

Recently, one commenter said in response to this (but in another article):

Convection etc distributes the heat in ways that affect radiative heat transport from the surface. While the intensity of radiation is a function of temperature, radiative heat transport is a function of a temperature difference. No heat may be exchanged between regions with the same temperature.

In an isothermal atmosphere there would be no temperature difference between it and the surface and therefore no heat loss from the surface. The accumulation of heat in a radiatively-constrained atmosphere by non-radiative means of heat transport from the surface would produce an isothermal atmosphere. Then, energy out = 0 and < energy in and the climate system would be heating.

The comment is confused, so I thought it was worth explaining in some detail.

Radiation and Temperature

Here is the starting point for the Hoover Incident:

This isn’t showing any heat transfer by conduction or convection, to keep the diagram simple.

The blue area – the troposphere, or lower atmosphere – is shown with a gap between it and the earth’s surface. This is just to make heat transfer values clearer – there isn’t really a gap. Notice that no radiation is emitted by the atmosphere (because this is a thought experiment where radiatively-active gases have been “hoovered” up).

Note as well that we are looking at averages in this diagram. The solar radiation absorbed in any one places is very rarely 240 W/m² – at night it is zero, and at midday in the tropics it is closer to 1000 W/m². If you want to understand why the average value of solar radiation absorbed is 240 W/m² take a look at Earth’s Energy Budget – Part One.

Rather than thinking of this as the average, if it helps, simply think of this as the heat transfer for one location where these are the actual values.

The equation for the emission of thermal radiation by the earth’s surface is only dependent on its temperature and emissivity. The equation is the well-known Stefan-Boltzmann law:

j = εσT⁴

where ε=emissivity, σ=5.67×10^-8, T is temperature in K and j is energy per second per unit area (W/m²)

Emissivity is a value between 0 and 1, where 1 is a “blackbody” or perfect radiator. The surface of the earth has an emissivity very close to 1. See The Dull Case of Emissivity and Average Temperatures.

Now regardless of any heat transfer by conduction or convection with the atmosphere, the surface of the earth will continue to radiate in accordance with that equation. With an emissivity of 1, a surface of 15°C (288K) radiates 390 W/m².

Emission of thermal radiation is independent of any other heat transfer mechanisms and only depends on the temperature of the body and its emissivity.

Now the earth also absorbs solar energy by radiation. So for our initial conditions, the net heat transfer by radiation,

H_rad = 240 – 390 W/m² = -150 W/m² (i.e., a cooling of 150 W/m²)

The only heat transfer mechanism in a vacuum is radiation and therefore heat can only be transferred into and out of the total climate system by radiation. In our thought experiment the atmosphere is unable to absorb or emit radiation.

Therefore the solar energy absorbed at the surface minus the energy radiated from the surface of the earth gives the net heat transfer for the entire climate system.

Radiation, Sensible and Latent Heat

Now with the particular example above let’s add heat transfer between the surface and the atmosphere by conduction and convection. This is often termed sensible heat. Gases have a very low thermal conductivity, so most heat will be transferred by convection (bulk movement of air). This will also include latent heat, which is the heat used in evaporation of water from the surface of the earth.

There is no simple formula for convection because it depends on many factors including the speed of the air movement. The formula for latent heat removal is also complex. So to get started we will use the average value derived by Kiehl and Trenberth in their well-known 1997 paper. Note that their calculation of latent heat was derived from the amount of rainfall (what comes down, must have been evaporated up in the first place).

Here is the updated diagram, still showing the initial conditions, just after the Hoover Incident has taken place:

Note that the conduction and convection from the atmosphere into space = 0 W/m².

And with conduction and convection it is conventional to show the net flow of heat – which is why there is no arrow with heat from the atmosphere to the surface. (With radiation, because heat is exchanged across distances it is more usual to show radiation emitted from each body).

What happens now?

To calculate dynamic processes is more difficult, especially if we wanted to do it for all points on the earth.

What everyone should be able to see is that the surface of the earth is losing heat.

If we use the value from K&T for sensible and latent heat removal, we can see that net heat transfer from the surface of the earth at time = 0 is now 252 W/m². That is, a cooling of 252 W/m².

Let’s consider the atmosphere. It is gaining heat from the surface of the earth, and not radiating it into space (or back to the surface), because in this post-Hoover world we have an atmosphere with no ability to emit radiation.

Therefore, within a relatively short space of time, the heat transfer (averaged around the globe) between the surface of the earth and the atmosphere will drop to almost zero. If the atmosphere heats up and the earth’s surface cools down – the result has to be that this heat transfer reduces.

But whatever happens to the temperature difference and heat transfer between the atmosphere and the earth’s surface – the radiation from the earth’s surface into space will still follow the Stefan-Boltzmann law and be proportional to T⁴. The only way this can change is if fundamental physics turns out to be wrong..

Dynamic Situation

How fast will the earth’s surface cool down?

This is a more challenging question. It involves calculating the heat flow out from the rocks, soil, sand, vegetation and most importantly, from the oceans. For each of these materials we would need to know the thermal diffusivity, which is the ratio of the thermal conductivity (how well heat travels through a material) to the heat capacity (how much heat is stored in a material per K of temperature change). As the earth’s surface cools down the rate of heat loss from radiation will reduce. This is because, using our earlier equation with the term for radiation stated explicitly:

H_rad = 240 – εσT⁴ W/m² ( = solar radiation absorbed – radiation emitted from the surface)

That is, the solar radiation absorbed stays constant while the radiation emitted reduces as the temperature decreases. It’s not so easy to visualize if you haven’t seen this kind of function before. Here is a very simple model of how the temperature (and net radiation) might change with time:

Click for a larger view

This graph is calculated by assuming that the climate system’s heat is stored in an ocean 4km deep and a very high thermal conductivity of water (that is, the heat can flow from the depths of the ocean to the surface with almost no resistance).

A more complete treatment takes account of the thermal conductivity of water. This value varies greatly depending on whether the water is still or well-mixed.

Below, the graph on the left shows the surface temperature against time. The graph on the right is more interesting and shows the temperature profile against depth of ocean for a few different times:

Click for a larger view

In this right hand graph the lower curves are later times. The initial temperature profile against depth is a straight line from 288K at the surface to 273K at 4000m – this is my assumption, my initial conditions.

What you can see from this graph is that the surface is much better at radiating heat away than the ocean is at conducting heat from its depths to the surface. That’s why the temperature stays higher for longer lower down in the ocean.

In this more thorough treatment the surface cools more quickly initially but will take much longer to reach the equilibrium of 255K.

And of course, alert readers will have noticed that it all changes when the surface freezes as the heat conductivity through ice will be different, and the albedo of the earth will change..

In fact, the problem can be made more and more complex, but that doesn’t change the essential elements.

Conclusion

Heat transfer by radiation is conceptually simple.

A surface emits radiation with a well-known formula which depends on temperature of that surface (and its emissivity).

The net heat transfer by radiation depends on how much radiation is incident on that surface from other bodies – whether near or far – and what proportion is absorbed.

In the case of a planet with an atmosphere – if the atmosphere cannot absorb or emit radiation then the equilibrium condition for that climate system will be where the radiation emitted by the planetary surface equals the radiation absorbed by the planetary surface.

Posted in Climate Models | 49 Comments »

« Newer Posts - Older Posts »

	. on The Amazing Case of “Bac…
	pjmacha on Extreme Weather #17 – Mo…
	E. Schaffer on Clouds & Water Vapor – Par…
	E. Schaffer on Clouds & Water Vapor – Par…
	Rok Adamlje on Clouds and Water Vapor –…
	Everything You Need… on Sensible Heat, Latent Heat and…
	Philip Schmidt on The “Greenhouse” E…
	Philip Schmidt on The Real Second Law of Th…
	Barton Paul Levenson on Opinions and Perspectives…
	Your Guide to Gambli… on Natural Variability and Chaos…
	Mane Oliva on The Amazing Case of “Bac…
	Tucker C on Heat Transfer Basics – P…
	Alll Teens Relate on Stratospheric Cooling
	DeWitt Payne on Clouds & Water Vapor – Par…
	DeWitt Payne on The Imaginary Second Law of…

Evaluating and Explaining Climate Science

What the Equations Look Like for Both Cases

What the Textbooks Say

Conclusion

The Basic Idea

Solar Radiation

DLR or “Back radiation”

Heating Surfaces and Conduction

Reference

Notes

Scenarios

And If There Was Such a Surface

Conclusion

The Conceptual Problem

Entropy Basics and The Special Case

The Special Case

Simple Examples

The Complete Climate System

The Classic Energy Exchange by Radiation

Conclusion

Other Relevant Articles

Notes

Effectiveness of Water Vapor at Different Heights

Boundary Layers and Deep Convection

Relationship between Specific Humidity and Local Temperature

Vertical Structure of Water Vapor Variations

Conclusion

Articles in this Series

References

Notes

Proof of Negative Feedback

Anthropogenic Imact on the Earth’s Climate – Tiny

The Conjuring Trick

Conclusion

References

Conduction

Example One – constant temperature conduction

Example Two – constant temperature conduction, thinner wall

Example Three – no temperature differential

Conduction and Radiation

Example Four – constant heat supply one side, fixed temperature the other

Example Five – as example four with a thinner wall

Example Six – as example four with increased “colder” temperature

Conclusion

Notes

The Definition

Other Comments Needing Response from the Original Article

Conclusion

Articles in this Series

A Digression on Non-Linearity

Water Vapor Distribution

The Simplified Journey of a Parcel of Moist Air

The Complexity

Measurements

Conclusion

Articles in this Series

References

Radiation and Temperature

Radiation, Sensible and Latent Heat

Dynamic Situation

Conclusion

Pages

Recent Posts

Recent Comments

Categories

Climate Websites

Science of Doom Key Pages

Subscribe by RSS

Subscribe by Email

Archives

Meta