This post covers some foundations which are often misunderstood.
Radiation emitted from a surface (or a gas) can go in all directions and also varies with wavelength, and so we start with a concept called spectral intensity.
This value has units of W/m².sr.μm, which in plainer language means Watts (energy per unit time) per square meter per solid angle per unit of wavelength. (“sr” in the units stands for “steradian“).
Most people are familiar with W/m² – and spectral intensity simply “narrows it down” further to the amount of energy in a direction and in a small bandwidth.
We’ll consider a planar opaque surface emitting radiation, as in the diagram below.
Hemispherical Radiation, Incropera and DeWitt (2007)
The total hemispherical emissive power, E, is the rate at which radiation is emitted per unit area at all possible wavelengths and in all possible directions. E has the more familiar units of W/m².
Most non-metals are “diffuse emitters” which means that the intensity doesn’t vary with the direction.
For a planar diffuse surface – if we integrate the spectral intensity over all directions we find that emissive power per μm is equal to π (pi) times the spectral intensity.
This result relies only on simple geometry, but doesn’t seem very useful until we can find out the value of spectral intensity. For that, we need Max Planck..
Planck
Most people have heard of Max Planck, Nobel prize winner in 1918. He derived the following equation (which looks a little daunting) for the spectral intensity of a blackbody:
where T = absolute temperature (K); λ = wavelength; h = Planck’s constant = 6.626 x 10-34 J.s; k = Boltzmann’s constant = 1.381 x 10-23 J/K; c0 = the speed of light in a vacuum = 2.998 x 108 m/s.
What this means is that radiation emitted is a function only of the temperature of the body and varies with wavelength. For example:
Note the rapid increase in radiation as temperature increases.
What is a blackbody?
A blackbody:
- absorbs all incident radiation, regardless of wavelength and direction
- emits the maximum energy for any wavelength and temperature (i.e., a perfect emitter)
- emits independently of direction
Think of the blackbody as simply “the reference point” with which other emitters/absorbers can be compared.
Stefan-Boltzmann
The Stefan-Boltzmann equation (for total emissive power) is “easily” derived by integrating the Planck equation across all wavelengths and using the geometrical relationship explained at the start (E=πI). The result is quite well known:
E = σT4
where σ=5.67 x 10-8 and T is absolute temperature of the body.
The result above is for a blackbody. The material properties of a given body can be measured to calculate its emissivity, which is a value between 0 and 1, where 1 is a blackbody.
So a real body emits radiation according to the following formula:
E = εσT4
where ε is the emissivity. (See later section on emissivity and note 1).
Note that so long as the Planck equation is true, the Stefan-Boltzmann relationship inevitably follows. It is simply a calculation of the total energy radiated, as implied by the Planck equation.
The Smallprint
The Planck law is true for radiant intensity into a vacuum and for a body in Local Thermodynamic Equilibrium (LTE).
So that means it can never be used in the real world
Or so many people who comment on blogs seem to think. Let’s take a closer look.
The Vacuum
The speed of light in a vacuum, c0 = 2.998 x 108 m/s. This value appears in the Planck equation and so we need to cater for it when the emission of radiation is into air. The speed of light in air, cair = c0/n, where n is the refractive index of air = 1.0008.
Here’s a comparison of the Planck curves at 300K into air and a vacuum:
Not easy to separate. If we expand one part of the graph:
We can see that at the peak intensity the difference is around 0.3%.
The total emissive power into air:
E = n²σT4, where n is the refractive index of air
So the total energy radiated from a blackbody into air = 1.0016 x the total energy into a vacuum.
This is why it’s a perfectly valid assumption not to bother with this adjustment for radiation into air. In glass it’s a different proposition..
Local Thermodynamic Equilibrium
The meaning, and requirement, of LTE (local thermodynamic equilibrium) is often misunderstood.
It does not mean that a body is at the same temperature as its surroundings. Or that a body is all at the same temperature (isothermal).
An explanation which might help illuminate the subject – from Thermal Radiation Heat Transfer, by Siegel & Howell, McGraw Hill (1981):
In a gas, the redistribution of absorbed energy occurs by various types of collisions between the atoms, molecules, electrons and ions that comprise the gas. Under most engineering conditions, this redistribution occurs quite rapidly, and the energy states of the gas will be populated in equilibrium distributions at any given locality. When this is true, the Planck spectral distribution correctly describes the emission from a blackbody..
Another definition, which might help some (and be obscure to others) is from Radiation and Climate, by Vardavas and Taylor, Oxford University Press (2007):
When collisions control the populations of the energy levels in a particular part of an atmosphere we have only local thermodynamic equilibrium, LTE, as the system is open to radiation loss. When collisions become infrequent then there is a decoupling between the radiation field and the thermodynamic state of the atmosphere and emission is determined by the radiation field itself, and we have no local thermodynamic equilibrium.
And an explanation about where LTE does not apply might help illuminate the subject, from Siegel & Howell:
Cases in which the LTE assumption breaks down are occasionally encountered.
Examples are in very rarefied gases, where the rate and/or effectiveness of interparticle collisions in redistributing absorbed radiant energy is low; when rapid transients exist so that the populations of energy states of the particles cannot adjust to new conditions during the transient; where very sharp gradients occur so that local conditions depend on particles that arrive from adjacent localities at widely different conditions and may emit before reaching equilibrium and where extremely large radiative fluxes exists, so that absorption of energy and therefore populations of higher energy states occur so strongly that collisional processes cannot repopulate the lower states to an equilibrium density.
Now these LTE explanations are far removed from most people’s perceptions of what equilibrium means.
LTE is all about, in the vernacular:
Molecules banging into each other a lot so that normal energy states apply
And once this condition is met – which is almost always in the lower atmosphere – the Planck equation holds true. In the upper atmosphere this doesn’t hold true, because the density is so low. A subject for another time..
So much for Planck and Stefan-Boltzmann. But for real world surfaces (and gases) we need to know something about emissivity and absorptivity.
Emissivity, Absorptivity and Kirchhoff
There is an important relationship which is often derived. This relationship, Kirchhoff’s law, is that emissivity is equal to absorptivity, but comes with important provisos.
First, let’s explain what these two terms mean:
- absorptivity is the proportion of incident radiation absorbed, and is a function of wavelength and direction; a blackbody has an absorptivity of 1 across all wavelengths and directions
- emissivity is the proportion of radiation emitted compared with a blackbody, and is also a function of wavelength and direction
The provisos for Kirchhoff’s law are that the emissivity and absorptivity are equal only for a given wavelength and direction. Or in the case of diffuse surfaces, are true for wavelength only.
Now Kirchhoff’s law is easy to prove under very restrictive conditions. These conditions are:
- thermodynamic equilibrium
- isothermal enclosure
That is, the “thought experiment” which demonstrates the truth of Kirchhoff’s law is only true when there is a closed system with a body in equilibrium with its surroundings. Everything is at the same temperature and there is no heat exchanged with the outside world.
That’s quite a restrictive law! After all, it corresponds to no real world problem..
Here is how to think about Kirchhoff’s law.
The simple thought experiment demonstrates completely and absolutely that (under these restrictive conditions) emissivity = absorptivity (at a given wavelength and direction).
However, from experimental evidence we know that emissivity of a body is not affected by the incident radiation, or by any conditions of imbalance that occur between the body and its environment.
From experimental evidence we know that the absorptivity of a body is not affected by the amount of incident radiation, or by any imbalance between the body and its environment.
These results have been confirmed over 150 years.
As Siegel and Howell explain:
Thus the extension of Kirchhoff’s law to non-equilibrium systems is not a result of simple thermodynamic considerations. Rather it results from the physics of materials which allows them in most instances to maintain themselves in LTE and this have their properties not depend on the surrounding radiation field.
The important point is that thermodynamics considerations allow us to see that absorptivity = emissivity (both as a function of wavelength), and experimental considerations allow us to extend the results to non-equilibrium conditions.
This is why Kirchhoff’s law is accepted in thermodynamics.
Operatic Considerations
The hilarious paper by Gerlich and Tscheuschner poured fuel on the confused world of the blogosphere by pointing out just a few pieces of the puzzle (and not the rest) to the uninformed.
They explained some restrictive considerations for Planck’s law, the Stefan-Boltzmann equation, and for Kirchhoff’s law, and implied that as a result – well, who knows? Nothing is true? Not much is true?Nothing can be true? I had another look at the paper today but really can’t disentangle their various claims.
For example, they claim that because the Stefan-Boltzmann equation is the integral of the Planck equation over all wavelengths and directions:
Many pseudo-explanations in the context of global climatology are already falsified by these three fundamental observations of mathematical physics.
Except they don’t explain which ones. So no one can falsify their claim. And also, people without the necessary background who read their paper would easily reach the conclusion that the Stefan-Boltzmann equation had some serious flaws.
All part of their entertaining approach to physics.
I mention their papertainment because many claims in the blog world have probably arisen through uninformed people reading bits of their paper and reproducing them.
Conclusion
The fundamentals of radiation are well-known and backed up by a century and a half of experiments. There is nothing controversial about Planck’s law, Stefan-Boltzmann’s law or Kirchhoff’s law.
Everyone working in the field of atmospheric physics understands the applicability and limits of their use (e.g., the upper atmosphere).
This is not cutting edge stuff, instead it is the staple of every textbook in the field of radiation and radiant heat transfer.
Notes
Note 1 – Because emissivity is a function of wavelength, and because emission of radiation at any given wavelength varies with temperature, average emissivity is only valid for a given temperature.
For example, at 6000K most of the radiation from a blackbody has a wavelength of less than 4μm; while at 200K most of the radiation from a blackbody has a wavelength greater than 4μm.
Clearly the emissivity for 6000K will not be valid for the emissivity of the same material at a temperature of 200K.
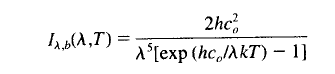
SoD,
A very good explanation.
My vernacular version of LTE is that the process of energy exchange between molecules by collision happens faster than any other process you need to worry about. And it fails when this process slows down (rarefaction).
So for example, emission by GHG’s is not affected by a molecule’s history (prior absorption). At this level energy has no history (or locality).
And as you say, the restrictive conditions that people sometimes want to apply to Kirchhoff’s Law don’t make sense. Emissivity and absorptivity, if they are meaningful, are just numbers (material properties) that belong to objects. You can look them up in books. There’s a dependence on wavelength, but not on the current state of heat fluxes. They are coefficients.
Nike says: “My vernacular version of LTE is that the process of energy exchange between molecules by collision happens faster than any other process you need to worry about.”
To be more specific, what one needs to worry about is whether there has been time for collisions to maintain an equilibrium Boltzmann distribution of energy across a group of molecules when you are considering their interactions with radiation.
SoD quoting G&T
……”Many pseudo-explanations in the context of global climatology are already falsified by these three fundamental observations of mathematical physics.”……
G&T make 2 of the 3 comments here relate to the MISUSE of Stefan-Boltzmann equation rather than as SoD says;
….”reach the conclusion that the Stefan-Boltzmann equation had some serious flaws”…..
…”All part of their entertaining approach to physics”…..
Point 2
The constant in the T^4 Law is not a universal constant but depends strongly on the geometry of the problem.
G&T give a reference for this statement.
So presumably if this is ignored errors will arise.
Point 3
The T^4 Law will not hold if one integrates over a limited spectrum such as found in real world situations.
two curves are shown on a graph one for black body source and one for a filtered 3um to 5um source.
They are clearly different.
The T^4 Law does not hold for the filtered case.
So SoD if these points are as hilarious as you contend they should be easily exposed
Bryan:
They are easily exposed by the fact that everyone in the field of atmospheric physics understands them and no one makes these mistakes. They are claiming that schoolboy errors are made by professionals in the field.
Take Ramanathan and Coakley (1978) for example. Or, for a textbook, Radiation and Atmosphere by Vardavas and Taylor (2007). Or Atmospheric Radiation: Theoretical Basis by Goody and Yung.
Why am I even bothering to answer your ridiculous point. They make unsubstantiated claims and you believe them.
The joke is on you.
And hopefully, now that you’ve read this article you won’t make so many mistakes in your future comments. Here’s hoping.
SoD says of G&T
……..”They are claiming that schoolboy errors are made by professionals in the field.”………
So Michael Mann, Phil Jones and Kevin (wheres the heat) Trenberth don’t make errors!
Now who’s being hilarious!
As with the Second Law, absorptivity, emissivity and Kirchhoff’s Law are concepts developed for large numbers of molecules that may become clearer when analyzed on a molecular level. Unfortunately, my physics is a little rusty, so any corrections of what is below would be appreciated.
When a molecule is interacting with radiation, there are two states we need to consider from a quantum mechanical point of view. State 1: a molecule in an excited (electronically, vibrationally or rotationally) state. State 2: the same molecule in a lower energy state plus a photon whose frequency depends on the energy difference between the two states. The probability (which comes from the amplitude squared) of going from State 2 to State 1 (which gives rise to the bulk property called absorptivity) in a given period of time is the same as going from State 1 to State 2 (which give rise to the bulk property called emissivity). This is why the absorption and emission coefficients in Schwartzschild’s equation are identical. So I’ll suggest that Kirchhoff’s Law may arise from more fundament principles of quantum mechanics. However, there are two complications that must be considered first.
dI = (-kprI)ds + [kprB(T,lamba)]ds
Complication 1: The probability of a molecule being in excited State 1 depends on temperature (and is given by Boltzmann’s distribution another equation derived from the statistical behavior of large numbers of molecules). This means that the emission from large numbers of molecules (the bulk property) depends on temperature while the molecular emissivity does not and must be multiplied by the Boltzmann function in Schwartzschild’s equation.
Complication 2: The probability of a molecule being in State 2 depends on the local “concentration” of photons. This accounts for the factor of I in the term describing absorption in Schwartzschild’s equation.
When you say that Kirchhoff’s Law only applies in situations of thermodynamic equilibrium with an isothermal enclosure, these limitations could be translated to the molecular level: Isothermal is equivalent to saying that B(T,lamba) is the same for all molecules. Enclosure is equivalent to saying that no photons are being lost or gained by the system keeping the “concentration” of photons constant. Under these circumstances, the (kprI)ds and [kprB(T,lamba)]ds terms of the Schwartzschild equation are equal in magnitude.
“Laws” for bulk materials such as Kirchhoff’s or the Second Law can be confusing when one isn’t sure whether the “law” should be applied to a given situation. Then one needs to look at the fundamental physics underlying the behavior of bulk materials. For absorption and emission, that physics can be found in Schwartzschild’s equation – which unfortunately is expressed in differential form and doesn’t convey much information to me in integrated forms. I’ve posted previously on why – looking at physics at a molecular level – it is crazy to apply the Second Law to DLR.
In the above post, I discussed the Schwartzschild eqn and the QM probability that a photon will be emitted or absorbed in a given period of TIME. The Schwartzschild eqn, however, discusses how radiation changes with distance (ds) rather than time (dt). For photons, ds = c*dt and we could have an equation that shows how intensity changes with time rather than distance
Before making this connection, I had previously thought of absorption as something that happens as light “passes through” a substance or bumps into the molecules of a substance while emission was something that happened “to” the molecules of a substance. If photons weren’t required to move at the speed of light, it would be easier to think about the excited state of a molecules converting into and back from to a lower energy state and a photon – making the idea of the “local concentration” of photons more appealing. Indeed scientists have recently found that the speed of light in some media (Bose-Einstein condensates?) can be many orders of magnitude less than the speed of light in air or a vacuum.
“Note the rapid increase in radiation as temperature increases.”
Note also the small amount of radiation for the wavelengths co2 emits at at the temperatures found in Earth’s atmosphere.
Sod, it’s good to revise the basics. Thank you. Two points:
1. You use “total emissive power” and “total energy radiated” interchangeably. But possessing the power to do something is not the same as doing it. Two vehicles, each with the power to accelerate from 0-100 in x secs, will go nowhere when positioned in contact against each other.
Of course, the difference in meaning dissolves in a vacuum in which, facing no resistance, the power to radiate is exercised spontaneously and completely in accordance with Stefan-Boltzmann. But, in a material medium such as the earth’s atmosphere (at the end of the day, what is happening there is what we’re trying to understand) calculating the magnitude of the radiative flux must take the medium’s temperature into account, as required by the entropy law. Thus:
Total emissive power = emissivity*sigma*T^4
Total energy radiated = ditto and ditto*(T^4 – T(m)^4)
If this view is correct, the need for “back-radiation” to satisfy the first law of thermodynamics at the surface disappears and with it the “problem” with the second law.
2. “Note 1 – Because emissivity is a function of wavelength, and because emission of radiation at any given wavelength varies with temperature, average emissivity is only valid for a given temperature”.
And average emissivity of the climate system must decline as emission occurs higher and colder in the atmosphere, making somewhat heroic the assumption that the planet cools as an exclusively theoretical blackbody would, and somewhat questionable the calculated 33 degrees Celsius natural greenhouse effect. Another set of assumed emissivities would reduce the effect to single digits.
John Millett:
You have invented some physics. You are free to think whatever you like, but don’t expect serious response.
Emission of thermal radiation is a function of temperature of the body (and a function of emissivity, a material property) and that’s that.
The status of the outside world has no effect on emission of thermal radiation.
This is the view presented in every thermodynamics textbook, every paper, and is beyond dispute.
John Millett wrote 10/27/10 10:16 am:
“Sod, it’s good to REVISE the basics.” Was this a Freudian slip (or did you really mean “review”)? I’d like to revise what the IPCC says about climate physics, but I appreciate SOD’s review of how the laws of the physics apply to the atmosphere.
“Two vehicles, each with the power to accelerate from 0-100 in x secs, will go nowhere when positioned in contact against each other.” Infrared photons leaving the earth’s surface to do not “push against’ or block infrared photons emitted by the atmosphere. SOD has posted experimental evidence that DLR of the expected intensity and wavelength is striking the earth’s surface at night. Roy Spencer has describe a backyard experiment where you can personally explore how DLR prevents air from cooling at night as much as it would without DLR.
“Total energy radiated = emissivity*sigma*(T^4 – T(m)^4)”
When the surface of the earth is emitting blackbody radiation upwards, it doesn’t “look” at the number and temperature of GHG molecules in the atmosphere above and then decide how much energy to irradiation upward. Nevertheless it is simple to make your statement correct (for blackbodies and reasonably accurate for other situations); all you have to do say:
Upward energy flux = emissivity*sigma*T(g)^4
Downward energy = n*k*emissivity*sigma*T(a)^4
Net upward energy flux = difference between these terms.
T(g) = temperature of the ground
T(a) = temperature of air
n = amount of GHG radiating
k = geometric factor to correct for the fact that GHG’s radiate horizontally as well as vertically.
The emissivities of the ground and GHGs are different.
“If this view is correct, the need for “back-radiation” to satisfy the first law of thermodynamics at the surface disappears and with it the “problem” with the second law.” Experiments tell us that “back-radiation” exists; the first law tells us that this back-radiation must make the surface warmer than it would be otherwise. In the comments to Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics, you seemed to accept the conclusion the 2LoT applied to the net flux, not what individual photons.
Frank:
My reply to Sod tells evidencewhat bothers me.
I take this opportunity to revisit the phenomenon of molecular collisions which arose in another thread. You said, if I understood correctly, that the fact of the distribution of velocities at equilibrium necessitated some collisions transferring energy from slower molecules to faster ones. This was given as corroborating evidence that heat flows from cold to hot. I don’t follow the logic. In the thermodynamic process towards equilibrium, molecular speeds will be faster and slower than at equilibrium. Collisions must close the speed gaps. Collisions that transfer energies from fast to slow would do that but reverse transfers would enlarge the gap, taking the process away from equilibrium.
SOD: Writing John raised some awkward question in my mind. So that “—–ers” aren’t confused by my questions, given the experimental evidence and theory supporting the existence of DLR, I don’t question its existence – just the ability of computer models to calculate DLR accurately enough (<1%, the forcing expected for 2X CO2) to make useful predictions about climate change.
Can you provide an explanation of why interference is not important when upward and downward photons cross in the atmosphere? I know that in a double slit experiment, the total flux of the light striking a surface on the far side of the slits doesn't change, interference simply distributes the photons unevenly (without violating the law of conservation of energy). I wonder if some upward and downward photons meeting in the atmosphere could interfere with each other and go off in different directions. If that happened, an equal number of horizontally moving photons could interfere and gain a vertical component of motion.
Do pulses of light crossing in optical fibers interfere in any way?
Scienceofdoom:
“The status of the outside world has no effect on emission of thermal radiation”.
Yet it is the central effect on heat flow, both magnitude and direction, between matter and its surroundings.
Thermal radiation and heat flow are at least closely related, if not exactly the same, making for an apparent inconsistency in these two views of the status of the outside world in thermodynamic processes.
I understand your claim that there is no inconsistency, the entropy law applying only to the net flux between, say, the planetary surface and the surrounding atmospheric boundary layer. What I don’t understand is the logical end, at the surface at the atomic level, to your claim. That is, the apparent chaos of electrons transitioning both upwards and downwards between energy orbits. I think it was Mait, responding when I raised this issue in another thread on your excellent site, who said this couldn’t happen in individual atoms, but perhaps the transitioning was towards higher energy in some atoms and towards lower in others -absorption and emission, respectively. My question then, and now, is: How do the atoms know whether they are absorbers or emitters?
Frank,
The cross section for photon-photon scattering, which is, I think, the phenomenon you are describing, is infinitesimal for IR photons. Interference doesn’t change the overall energy flux, it changes the spatial distribution of the flux. One still gets the same interference pattern even if the intensity is so low that there is only one photon present in the apparatus at any given time.
Thanks for the useful answer, Dewitt
John Millett: the atomic-level picture goes something like this. I’m going to take a somewhat unusual approach by trying to describe both the surface and the atmosphere at the molecular level.
A molecule at the surface (say, a water molecule in the surface layer) gets hit by another molecule and as a result gets excited to a vibrationally excited state. (Since we’re talking about IR radiation, the quantum states involved are the vibrational states of molecules rather than the electronic states of atoms, but the fundamental principles are the same.) Most of the time it gets rid of that energy by bumping into another molecule, converting that internal energy back into translational motion of the molecules with respect to each other. This is going on all the time. Averaging over time and over large numbers of molecules, at any time a definite fraction of the molecules are in vibrationally excited states when the system as a whole is in thermodynamic equilibrium. That fraction is, of course, given by the Boltzmann distribution and increases with the temperature of the system.
However, there is a small chance that a vibrationally excited molecule will emit an IR photon instead of losing its energy in a collision. This probability also depends on temperature; it is given by a formula called the “Einstein A Coefficient.” (Yes, that’s *the* Einstein.) The time at which any given emission takes place is absolutely random. This is “spontaneous emission”. However, the probability per unit time that a molecule will emit is definite – it depends on the kind of molecule, the temperature, the frequency of the radiation that is emitted (which is determined by the energy level spacing in the molecule) and perhaps some details about the local environment (the “radiative lifetime” of a water molecule in liquid water won’t be exactly the same as that of water vapor), but upon very little else.
Now let’s consider the effect of photons coming into the system from outside. The molecules can absorb these photons, becoming vibrationally excited. Just as with emission, the time of any particular absorption is random, but the probability per unit time that any molecule will absorb the photon is definite. It is proportional to the light intensity (number of photons coming in per unit time.) The proportionality constant is the “Einstein B coefficient.” It also depends on frequency, temperature and molecular properties. Both the A and the B coefficients can be calculated from quantum mechanics (Dirac solved this problem in 1927.) They are the molecular-level analogs of absorptivity and emissivity. Quantum mechanics also shows that A and B are proportional, with a proportionality constant that depends only on frequency (it’s c^2/hnu^3, where c is the speed of light, nu is frequency, and h is Planck’s constant.) In 1917, before quantum mechanics had been invented, Einstein had already shown that if A and B are related in this way, then the spectrum of the emitted radiation is given by Planck’s Law. This same relationship leads directly to Kirchhoff’s Law. Thus all of these laws follow from quantum mechanics (the most quantitatively successful theory in all of physics) and the assumption of thermodynamics equilibrium (which you may notice has been invoked, explicitly or implicitly, as several points in this argument.
(Cognoscenti will have noticed that I have skipped past a third process, stimulated emission, in which a photon arriving at a molecule that is already excited causes it to emit, instead of absorbing that photon. One photon in, two out. That’s what happens in lasers. It’s of no practical importance here since the intensities of the radiation are much too low, although it does need to be included in order to complete Einstein’s argument.)
Notice that the second law of thermodynamics has not appeared anywhere in this argument. That’s because it’s entirely microscopic, whereas thermodynamics is a macroscopic theory. Nevertheless, one can show, via statistical mechanics, that when the relationships described here hold at the microscopic level, then the macroscopic properties will obey the laws of thermodynamics. We don’t need to invoke thermodynamics because we’re guaranteed that anything that we calculate from the microscopic theory will, as long as we do not make a mistake or an inappropriate approximation, obey thermodynamics.
Thus, I view Kirchhoff’s and Boltzmann’s original derivations of Kirchhoff’s law and the Stefan-Boltzmann law, which did invoke the laws of thermodynamics as, in some sense, having been superseded. By requiring that macroscopic properties obey thermodynamics, Kirchhoff and Bunsen derived relationships that any microscopic theory of radiation-matter interactions would have to satisfy. This was of enormous importance for the historical development of the microscopic theory. Nevertheless, we now have a successful microscopic theory the interactions between radiation and matter. As noted above, Dirac wrote down the essentials in 1927.
This is an interesting article and somewhat useful. The problem is that it is so limited in readership. Few people without significant amounts of scientific background can follow it.
I fully agree that the troposphere acts as a blackbody and radiates as such. On a macro scale the individual photons are irrelevant and treating the atmosphere as a normal body is fine. The only real adjustment is that it acts as several bodies as the different GHG’s act on only specific portions of the spectrum.
There is no real question that it is in a LTE until the density drops off above the troposphere/tropopause.
I still struggle with how to explain this to people that have never taken radiative heat transfer or thermodynamics….
I’m guessing I didn’t get the context correctly, but wouldn’t it be really, really dark on the surface all the time, if troposphere acted as a blackbody?
It depends what wave length you are talking about, in the visible spectrum’s(shortwave, red to blue), yes, a black body means a black body, thats why something appears black, it is absorbing all the light, in wave lengths longer than red, it just means a perfect absorber/emitter in the IR spectrums(Infra red, means longer than red, a longer wave length than is visible to our eyes)
I dont know about the audience, I cant argue a singe bit of the math, I do learn an awful lot from your non math explanations, and I greatly appreicate them.
There are a great number of people incapable of understanding the math, but more than capable of grasping the concept.
Every time I visit this site I learn something about the world around me that I can use.
I am suree that I am not alone. Thank you for your time, I will reinvest it in someone else, another colliding electron, togehter we will raise the temperature of human understanding, and awareness.
Robert P: Thank you for this peek into the exotic domain of quantum mechanics. From a position at the beginning of the learning curve I must have missed something: Sod, following Kirchoff, says emissivity = absorptivity, given wavelength; you say Einstein’s coefficients A and B are micro analogs of emissivity/absorption and are proportional, not equal. This looks like a contradiction.
Paraphrasing, spontaneous emission results from a proportion of molecular collisions producing a photon rather than the usual inter-molecular transfer of energy. Is this process universal or limited to collisions involving only radiatively-active molecules such as GHGs? (as Sod argues is the case in the atmosphere, implying that the numerically predominant N2 and O2 molecules, which gain heat from the surface mainly through non-radiative means, must find a non-radiative way to transfer the heat gain to the trace GHGs for ultimate radiation to space – a dynamic seemingly lacking natural parsimony and elegance and contrarily implying a warmer planet in the absence of GHGs).
If the probability of emission is limited to the population of collisions involving GHGs, it would relate in the water surface layer to all collisions but to a much smaller population of collisions in the surrounding air layer. Thus, while “collision density” might be comparable in the water and air layers, emissive “photon density” (coefficient A) would be very much greater in the water than in the air layer. It would likewise be greater than absorptive “photon density” (coefficient B) in the water surface layer, since air layer photon emission constitutes the supply of water layer photon absorption. Within each layer, the energy quanta of emitted and absorbed photons must be equal, being related to the energy level spacing in the molecule and the layer temperature. These will be different in the two layers. Thus absorption in the water surface layer of a photon emitted in the air surface layer would depend on the compatibility between the energy level spacings in the water and air surface molecules.
Question: Is such compatibility certain, positively or negatively, or is there another probability or coefficient in play?
If compatibility is certain, guaranteeing absorption, the asymmetric quantities of emitted and absorbed photons would nevertheless result, unphysically, in a cooling water surface layer even under conditions of thermal equilibrium between the two layers. This would appear to invalidate the premise that only collisions involving GHGs may result in emission. In turn, that would appear to allow all atmospheric molecules to be radiatively-active some of the time, through ubiquitous mutual collisions, and contribute directly to cooling the planet.
Question: Do all atmospheric molecules radiate, substantively, some of the time?
If, on the other hand, the energy quantum of the photon emitted in the air surface layer, consistent with layer temperature and molecular energy level spacing, is inconsistent with the molecular energy level spacing in the water surface layer, presumably it is not absorbed and remains in the photon energy field pervading the atmosphere. This outcome would have implications for the notion of atmospheric back-radiation slowing the cooling rate of the surface, thereby warming the planet.
Question: Are energy quanta universally portable – emitted from any source, absorbed in any sink?
It depends on what you mean by substantively. All atmospheric molecules do radiate and absorb. Oxygen has a magnetic dipole moment so it absorbs and radiates in the microwave and a few other wavelengths. The 60 GHz microwave band for oxygen is used for satellite air temperature measurements. In addition there is collision induced radiation. When two molecules collide, there is a small probability that the electric field will be distorted enough by the collision for a photon to be absorbed or emitted. This results in a continuum rather than line or band spectrum. Peak absorption/emission is at about 100 micrometers. CIA absorption/emission from N2 and O2 can be neglected in the lower atmosphere where water vapor dominates the spectral region. There is a school of thought that the water vapor continuum spectrum is caused by CIA. The same mechanism that produces CIA is also the likely cause of pressure broadening of spectral lines.
That should have been collision induced absorption (CIA).
DeWitt Payne:
Thank you for that. I meant by “substantive”, sufficient to release the heat gained by non-radiative means from the surface. I have great difficulty with the notion that this heat has first to be transferred by non-radiative means to the GHGs for radiation to space. Given that the molecular collisions occur in space, it would be neater for them to induce emission at a rate sufficient to maintain thermal equilibrium without the need for intermediation by GHGs.
[...] equation is called the Stefan-Boltzmann equation. More about it in Planck, Stefan-Boltzmann, Kirchhoff and LTE. It is a well-proven equation with 150 years of evidence behind it – and from all areas of [...]
[...] More about this formula and background on the material properties in Planck, Stefan-Boltzmann, Kirchhoff and LTE. [...]
[...] This is just the natural result of an atmosphere that re-emits – and of course, gases that absorb at a given wavelength also emit at that same wavelength. (See Planck, Stefan-Boltzmann, Kirchhoff and LTE). [...]
[...] lastly, the Stefan-Boltzmann equation, correct and accurate though it is (check out Planck, Stefan-Boltzmann, Kirchhoff and LTE) is not used in the actual equations of radiative transfer in the atmosphere. Nor is any assumption [...]
[...] that absorptivity for longwave radiation will be equal to emissivity for longwave radiation (see Planck, Stefan-Boltzmann, Kirchhoff and LTE), therefore, if the surface and the atmosphere are at the same temperature then the exchange of [...]
[...] The atmosphere also emits radiation, and the emission lines are the same as the absorption lines. More about that in Planck, Stefan-Boltzmann, Kirchhoff and LTE. [...]
[...] is emissivity? It turns out, explained in Planck, Stefan-Boltzmann, Kirchhoff and LTE, that emissivity = absorptivity (for the same [...]