Recap
Part One opened up the topic and introduced the simple “billiard ball” or zero-dimensional analysis of the earth’s climate system. The sun radiates “shortwave” energy which is absorbed in the atmosphere and the earth’s surface. This heats up the earth’s climate system and it radiates out “longwave” energy.
The longwave energy gets significant absorption from water vapor, CO2 and methane (among other less important gases). This absorption heats up the atmosphere which re-radiates long wave energy both up and back down to the earth’s surface.
It is this re-radiation which keeps the earth’s surface at around +15°C instead of -18°C.
Part Two looked at why different gases absorb and radiate different proportions of energy – what the factors are that determine the relative importance of a “greenhouse” gas. Also why some gases like O2 and N2 absorb almost nothing in the longwave spectrum.
The Part Three introduced Radiative Transfer Equations and finished up with a look at what is called the gray model of the atmosphere. The gray model is useful for getting a conceptual understanding of how radiative transfer creates a temperature profile in the atmosphere.
However, part three didn’t finish up with enlightenment on the complete picture of CO2. The post was already long enough.
In this post we will look at “band models” and explain a little about saturation.
Band Models
Many decades ago when physicists had figured out the radiative transfer equations and filled up books with the precise and full derivations there was an obvious problem.
There was clearly no way to provide an analytical solution to how longwave radiation was absorbed and re-emitted through the atmosphere. Why? Because the actual absorption is a very complex and detailed function.
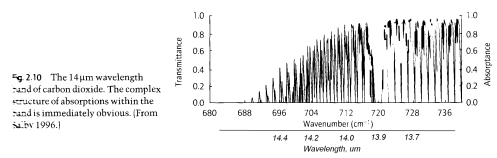
For example, as shown in an earlier post in the series, here is one part of the CO2 absorption spectrum:
The precise structure of the absorption is also affected by pressure broadening as well as a couple of other factors.
So long before powerful computers were available to perform a full 1-d model through the earth’s atmosphere, various scientists started working out “parameterizations” of the bands.
What does this mean? Well, the idea is that instead of actually having to look up the absorption at each 0.01μm of the longwave spectrum, instead you could have an equation which roughly described the effect across one part of the band.
Goody in 1952 and Malkmus in 1967 proposed “narrow band” methods. Subsequently others proposed “wide band” methods. Later researchers analyzed and improved these band paramaterizations.
Without using these parameterizations, even today, with very powerful computers, it is weeks of computational time to calculate the 1-d radiative transfer function for the atmosphere for one profile.
It’s important to note that the parameterizations can be tested and checked. Kiehl and Ramanathan did a big study in 1983 and showed that many of the models were well within 10% error compared with the detailed line by line calculations.
Here is one band model:
Looks ugly doesn’t it? But it makes the calculations a million times easier than the detailed spectral lines all the way from 4μm up to 30μm.
The first term, TΔν, is transmittance – it’s just how much radiation gets through the gas.
If you don’t mind a little maths – otherwise skip to the next section
Let’s explain the equation and what it means for saturation.
First of all what are the variables?
TΔν – is the transmittance in the spectral interval Δν. Transmittance is the fraction of radiation that passes through: 0 – no radiation gets through; 1 – all the radiation gets through.
S, α and δ are all part of the band model: S – average line strength; α – line width; δ – line spacing
u – the absorber amount in the path (this is the important one to keep an eye on)
By the definition of Transmittance,TΔν = e-χ, where χ is optical thickness. It’s the Beer Lambert law that we already saw in part three.
An alternative way of writing this is χ = – log (TΔν) , that is, the optical thickness is the log of the transmittance
Well, even the tricky band model equation can be simplified..
If Su/πα << 1 (this means if the expression on the left side is a lot less than 1 – which happens when there isn’t “very much” of the absorbing gas)
Then the above question can be simplified to:
TΔν = exp (-Su/δ)
This means the optical thickness of the path is directly proportional to the amount of gas, u
So in part three when we looked at the Beer-Lambert law we saw this shape of the curve:
But we couldn’t properly evaluate the expression because the absorption variable was a complex function of wavelength.
What the band model allows us to do is to say that under one condition, the weak condition, the optical thickness is a linear function of absorber amount, and therefore that the amount of radiation getting through the atmosphere – the Transmittance – follows this form: e-χ
And in another condition, if
If Su/πα >> 1 (much greater than 1, which means there is “lots” of the absorbing gas)
Then the band model can be “simplified” to:
TΔν = exp (-(Su)1/2/( δ √(πα)) )
Ok, not too easy to immediately see what is going on? But S, δ and α are constants for a given absorbing gas..
So it is easy to see what is going on:
TΔν is proportional to exp (-u1/2), i.e., proportional to exp (-√u)
Or as optical thickness, χ =- log (TΔν),
Optical thickness, χ is proportional to √u
The optical thickness, in the strong condition, is proportional to the square root of the amount of the absorber.
“Saturation” and how Transmittance and Optical Thickness Depend on the Concentration of CO2
If you skipped the maths above, no one can blame you.
Recapping what we learnt there –
In the weak condition, if we double the concentration of CO2, the optical thickness doubles and in the strong condition if we increase the concentration of CO2 by a factor of 4, the optical thickness doubles
And what were the weak and strong conditions? They were mathematically defined, but keeping it non-technical: weak is “not much” CO2 and strong is “a lot” of CO2.
But we can say that in the case of CO2 (in the 15μm band) through the troposphere (lower part of the atmosphere) it is the strong condition. And so if CO2 doubled, the optical thickness would increase by √2 (=1.4).
Simple? Not exactly simple, but we made progress. Before, we couldn’t get any conceptual understanding of the problem because the absorption spectrum was lots of lines that prevented any analytical formula.
What we have achieved here is that we have used a well-proven band model and come up with two important conditions that allow us to define the technical meaning of saturation – and even better, to see how the increasing concentration of CO2 impacts the absorption side of the radiative transfer equations.
But it’s not over yet for “saturation”, widely misunderstood as it is.. Remember that absorption is just one half of the radiative transfer equations.
Before we finish up, optical thickness isn’t exactly an intuitive or common idea, and neither is e-√χ. So here is a idea of numerically how transmittance changes under the weak and strong conditions as the concentration increases. Remember that transmittance is nice and simple – it is just the proportion of radiation that gets through the absorbing gas.
Suppose our optical thickness, χ = 1.
T = 0.36 =exp(-1)
Under the weak condition, if we double our optical thickness, χ = 2; T = 0.13 =exp(-2)
and double it again, χ = 4; T = 0.017 =exp(-4)
Under the strong condition, double our optical thickness, χ = 2; T = 0.24 =exp(-√2)=exp(-1.41)
and double it again, χ = 4; T = 0.13 =exp(-√4) = exp(-2)
Note: these numbers are not meant to represent any specific real world condition. It just demonstrates the kind of change you get in the amount of radiation being transmitted as the gas concentration increases under the two different conditions. It helps you get an idea of e-χ vs e-√χ. Assuming that a few people would want to know..
Conclusion
To carry out the full 1-d radiative transfer equations vertically through the atmosphere climate scientists usually make use of band models. They aren’t perfect but they have been well tested against the “line by line” (LBL) absorption spectra.
Because they provide a mathematical parameterization they also allow us to see conceptually what happens when the concentration of an important gas like CO2 is increased. We can calculate the transmittance or absorptance that takes place.
It helps us understand “saturation” – which we have done by looking at the “strong” and “weak” conditions for optical thickness.
This term “saturation” is widely misused and conveys the idea that CO2 has done all its work and adding more CO2 doesn’t make any difference. As we will see in a future part of this series, due to the fact that gases that heat up also radiate, adding more CO2 does increase the radiative forcing at the surface – even if CO2 could have no more effect through the lower part of the atmosphere.
Well, that’s to come. What we have looked at here is some more detail of exactly how transmittance and optical thickness increase as CO2 increases.
The next post will look at the 1-dimensional model results..
Update – Part Five now published
Reference
CO2 Radiative Paramaterization Used in Climate Models: Comparison with Narrow Band Models and With Laboratory Data, J.T. Kiehl and V. Ramanathan (1983)





[…] – Part Four is now online Possibly related posts: (automatically generated)Carbon dioxide and its greenhouse […]
Hi Science
Nice post. Are you going to gather all four parts together in one place and top and tail them so it can be read as one article?
Tonyb
Keep posting! Your efforts are greatly appreciated. I’m still “absorbing” it all. Probably some questions to come. . .
I may get bored when we get to part 999 (have you any idea just what you have started here…! ) but for the moment – thanking you for a very coherent and interesting read.
Regarding the figure ‘From “Handbook of Atmospheric Sciences”, Hewitt & Jackson 2003’ shouldn’t absorptance be the inverse of transmittance (assuming no reflection)?
And the prize goes to Lynn E..
Great to see someone actually reads and checks the details!
You are correct. They got their graph wrong.
In some fields, absorbance refers to -log10 (I/I(0)). In other words, the A = 1 means that 10% of the light gets through the sample, A =2 means that 1% of the light gets through the sample, etc. Absorbance therefore is directly proportional to the concentration of absorbing species directly in the path of the light
[…] Three and Four got a little more technical – an unfortunate necessity. Part Three introduced Radiative […]
Eagerly waiting for an update on the discussion on what happens after saturation.
Thanks
Ani:
Can you explain a little more what you are looking for?
[…] up in the atmosphere), or not. Some feedback from water vapor, or not. Different band models (see Part Four). And also different comparison points of CO2 […]
Your excellent posts on atmospheric modelling give rise to a speculative thought.
AFAIK water vapour does not affect the albedo, but droplets of condensed water in suspension (i.e. clouds) certainly must do. I remember reading that cumulus clouds are the next brightest thing to the sun, so they must be very good reflectors.
So it might be possible to set up the model to produce the amount of albedo increase required in order to produce a no warming effect from a doubling of CO2. And then a set of assumptions should get a rough idea of the amount of increased cloud cover that ought to be observable, in this case.
Do you know if anyone has done this kind of investigation?
Tony
I’ve seen that discussion touched on in a few places. It’s a good question, and hopefully something that will get addressed on this blog.
[…] profile through the atmosphere. Solving those equations, as you can see in CO2 – Part Three, Four and Five – requires knowledge of the temperature profile as well as the concentration of the […]
[…] on these equations, see the CO2 – An Insignificant Trace Gas series, especially Part Three, Four and […]
When I came to know this blog this series was already too long for me. Now I see it’s definetly worth the time of reading it. Very instructive. Thanks again for the great work and generosity.
One question: one professor called Modtran a line-by-line model. But it takes only a few seconds to run in its online version. So is it really a band model?
Alexandre:
Thanks for the kind comments.
I believe you are correct. From what appears to be the Modtran website
This means, it is not LBL “line by line”.
scienceofdoom
If we are discussing:
http://geoflop.uchicago.edu/forecast/docs/Projects/modtran.orig.html
Then it is indeed a band model.
Dig into the “saved” data from a run and it lists the bands and a LOT of very insightful, if a little arcane, data.
The bands are on 2/cm wavenumber centres from 100/cm (100 microns) to 1500/cm (6.667 microns).
The saved data is very rich and includes just about everything of interest. Transmittance, absorption, path length radiance, mole densities by height, etc.
Also the ability to view at different heights (both up and down) allows insight into such questions as energy balance by layer.
All in all a very useful bit of kit.
Alex
Miskolczi, slightly simplified to
2 = tau + ( exp ( – tau ) )
gives tau, the optical depth, as
1.58
(the more exact formula will give 1.867)
http://www.friendsofscience.org/assets/documents/The_Saturated_Greenhouse_Effect.htm
He also gives considerable data showing that
this is a correct value and that the climate
is in a homeostatic energy balance which
maintains the 1.867 value, nearly regardless
of the atmospheric CO2 concentration. As a result,
the sensitivity of temperature to a doubling of
CO2 is less the 0.5 deg K/doubling.
oops
change that “1.58” to “1.85”
james kennedy
What does he put forward to show that the atmosphere has a constant optical depth?
radiosonde measurements i believe… i have no idea as to the validity o these claims mind.
This lil slide show was all i could find that documents it mind. Id be interested in your take on it all… i slaved my way through his paper years ago… And came to the definite conclusion it was well above my head.
Have the band models been verified experimentally? In my dreams, someone will shine a giant variable-wavelength infrared laser at a detector in space and obtain an actual spectrum of the infrared absorption of the earth’s actual atmosphere. The laser would need to be able to compete with “earthshine” at infrared wavelengths, totaling about 240 W at all infrared wavelengths.
Such an experiment would demonstrate whether or not these extremely complicated calculations are correct. Since the temperature of the atmosphere and the height of the tropopause vary with latitude, one would like to place the laser in different locations. By looking at different wavelengths, one could determine which components in the atmosphere were or were not behaving as predicted.
Frank … I think much the same thing. It must be a powerful CO2 laser, and it must be shone upwards at night, so that there is almost no earthshine. Then we can parse the data on a satellite and see if the AGW group is right.
Frank:
Well, the calculations of absorption and emission in the atmosphere – the radiative transfer equations – using the “line by line” method have been verified against many experiments (e.g. see CO2 -Part Six – Visualization ).
And the band models have been verified against the “line by line” calculations. For example, in the reference given in the article.
[…] even numbers in the series shouldn’t be ignored either, especially Part Four which explained band models vs line by line (LBL) […]
[…] 1: See CO2 – An Insignificant Trace Gas? Part Four for more explanation of ”band models”. A “model” doesn’t mean […]
Reblogged this on Climate- Science.
Attenuation/absorbtion
Late question regarding gasses absorbtion or attenuation versus length.
I understand the formulas, but as electrical engineer i would like to have it in dB/m or whatever distance unit and referenced to existing levels of concentration.
I believe the dB figure for each component would be proportional to the concentration of that component (more or less).
It will be very dependent of wavelength, but to make it even simpler then state how many dB the power from 290K surface (~400W/m2) would be attenuated .
per meter by the different components in the present atmosphere.
3dB means half the power is lost and 10dB means only a tenth comes out.
I read the posts from time to time and gain new insight and come up with some questions.
Svend: In spectroscopy, optical depth (tau, formerly optical density or optical density units) is a dimensionless measure of absorption that may be analogous to dB:
I/I_0 = e^(-tau) in physics and = 10^(-tau) in chemistry
where I_0 and I are the fluxes of a beam of radiation entering and exiting an absorbing material of thickness s.
tau = n*o*s
(or = the integral of n(s)*o(s)*ds when n or o aren’t constant over a path, which they aren’t in the atmosphere)
where n is the density of absorbing molecules and o is their absorption cross-section at a particular wavelength (absorption coefficient in chemistry). If the material both absorbs and scatters radiation, then we talk about attenuation/extinction and an extinction coefficient.
HOWEVER, all molecules that absorb radiation of a particular wavelength emit radiation at the same wavelength. In the laboratory, we use intense radiation (from a filament at several thousand degK) that allows us to neglect emission of thermal radiation by a sample (and all other surfaces in the laboratory). In the atmosphere, absorption and emission of thermal IR are EQUALLY IMPORTANT. If you think ONLY OF ABSORPTION by the atmosphere in terms of optical depth or dB, you will be GROSSLY MISLED. Thermal radiation traveling downward in our atmosphere gets STRONGER the further it travels!
At the wavelength most strongly absorbed by CO2, 90% of the photons emitted upward by the surface are absorbed within 1 m – and replaced by an equal number of photons emitted by CO2 molecule along that 1 m path. When absorption and emission are in equilibrium, thermal radiation has blackbody intensity. Planck derived his law by assuming radiation in equilibrium with quantized oscillators. For this reason, the intensity of blackbody radiation appears to be independent of the number of molecules emitting and absorbing it. And Planck assumed a Boltzmann distribution of excited states produced by molecular collisions – not excited states produced by absorption of a photon. (Excited states produced by absorption are “relaxed” by collisions much faster than they can “re-emit” a photon.)
HOWEVER, our atmosphere changes temperature, becomes less dense with altitude and doesn’t interact strongly with radiation at some wavelengths. Therefore an equilibrium between absorption and temperature-dependent emission doesn’t always exist, and the atmosphere does not emit like a black-body. The radiation at the wavelengths in the “atmospheric window” have negligible interaction with the atmosphere. Unlike black- or gray-body radiation, radiative fluxes in the atmosphere depend on the density of GHGs present.
Climate scientists sometimes speak of optically-thick layers of atmosphere – which are postulated to emit radiation of blackbody intensity – and optically-thin layers of atmosphere – which emit and absorb in proportion to the density of GHGs they contain. Confusing. In the general case, we use Schwarzschild’s equation for radiative transfer to determine radiative fluxes in the atmosphere using programs such as MODTRAN. (Schwarzschild was an astrophysicist interested in star, so climate scientists rarely use his name.)
dI = emission – absorption
dI = n*o*B(lambda,T)*ds – n*o*I*ds
When absorption and emission cancel along a path, dI is 0 and radiation has blackbody intensity (I = B(lambda,T). For more see,
https://en.wikipedia.org/wiki/Schwarzschild%27s_equation_for_radiative_transfer
“tau = n*o*s
(or = the integral of n(s)*o(s)*ds when n or o aren’t constant over a path, which they aren’t in the atmosphere)
where n is the density of absorbing molecules and o is their absorption cross-section at a particular wavelength ”
My problem is that i dont know the n and o for the different molekules in the atmosphere, and i have even less knowledge of the wavelenghts, so i have hoped you could give som estimates of the attenuation/absorbtion in a given length of air, for a signal with a spectrum like 390K (but of higher power).
I asked because i would like to know if it is possible to measure (at a kitchen table) that the absorbtion could heat the gas more if it had CO2.
I personally doubt it, but would like som facts and fysics to back it up.
I realize the problems with measuring attenuation, like if you measure cable loss with signals very close to the noise limit.
Knowing the attenuation can tell you how much energi is lost in the cable from an external signal..
Kind regards
Svend Ferdinandsen (Danmark)
If you go to the Archer MODTRAN website ( http://climatemodels.uchicago.edu/modtran/ ) you can get all sorts of information on concentration and absorption when you get the raw data output from an atmospheric calculation by clicking on the ‘Show Raw Model Output’ button. Note that some of the units are not what you might be used to seeing, particularly ATM CM/KM. What that means is the height of a column of the pure gas in centimeters at standard temperature and pressure per kilometer of altitude. For example, at the surface, the contribution of nitrogen in the first kilometer would be about 78,084cm, oxygen, 20,947cm and argon, 934cm.
If you scroll down toward the end of the data, you get information on emission and transmittance for 2 cm-1 frequency ranges from 2 to 2200 cm-1 from the point of reference specified in the input, which in the base case is 70km altitude looking down.
Svend: I’ve never personally tried to perform any calculations of tau for CO2. At the kitchen table, your first problem is that glass blocks thermal infrared. A clear polyethylene container might work. If you fill the container with CO2, the strongest bands are certain to be saturated, meaning that there will be just as much absorption as emission and therefore no warming. A GHE exists in our atmosphere only because temperature decreases with altitude. An isothermal atmosphere with GHGs would have no GHE.
When you double the number of CO2 molecules in the atmosphere, you double the number of photons emitted and cut the mean free path between absorption and emission roughly in half. Doubled CO2 results in very large change in emission and absorption of photons that nearly cancel, leaving a 3.5 W/m2 reduction in outward flux at the TOA (radiative forcing).
SOD has two posts on heating rates produced by absorption of thermal IR by the atmosphere:
In spectroscopy, attenuation is a term that refers less than 100% transmission of a beam of radiation due to either absorption or scattering or both. Extinction is a synonym.
Thanks
It explains why attempts to measure the warming has failed.
I wonder why they do not try to estimate the result before they make the experiment.
These 3.5W/m2 for the whole column of air should give some indication of the experiments outcome.
-Svend
Svend,
You can approximate the simple model of the atmosphere as a single layer by comparing glass, which is nearly opaque in the thermal IR to thin polyethylene film ( cling film is now polyethylene ), which is nearly transparent in the thermal IR wavelength range. Both have similar transparency in the solar wavelength range. If you cover the open end of a box that is well insulated on five sides with a layer of polyethylene and cover a similar box with glass and expose both to sunlight, the glass covered box will get a lot warmer. This is similar to the infamous Wood experiment that the noted physicist managed to screw up. The result is that some people, including our host, think that ‘greenhouse’ is an inaccurate designation for the effect of thermal IR absorbing/emitting gases like water vapor and carbon dioxide on the global average surface temperature.
Somewhere on this site are posts by me describing results I obtained with my version of the above apparatus. You can also read about Horace de Saussure and his solar oven. https://en.wikipedia.org/wiki/Horace_B%C3%A9n%C3%A9dict_de_Saussure
Because there is significant circulation inside a box tilted to make the incident solar radiation perpendicular to the bottom of the box, a better experiment would be to put a heating element on the side of the box that is opposite the opening and mount the box with that side up. That should drastically reduce circulation and allow for the accurate measurement of energy input.