General Circulation Models or Global Climate Models – aka GCMs – often have a bad reputation outside of the climate science community. Some of it isn’t deserved. We could say that models are misunderstood.
Before we look at models on the catwalk, let’s just consider a few basics
Introduction
In an earlier series, CO2 – An Insignificant Trace Gas we delved into simpler numerical models. These were 1d models. They were needed to solve the radiative transfer equations through a vertical column in the atmosphere. There was no other way to solve the equations – and that’s the case with most practical engineering and physics problems.
Here’s a model from another world:
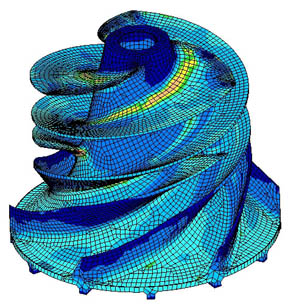
Here’s a visualization of “finite element analysis” of stresses in an impeller. See the “wire frame” look, as if the impeller has been created from lots of tiny pieces?
In this totally different application, the problem of calculating the mechanical stresses in the unit is that the “boundary conditions” – the strange shape – make solving the equations by the usual methods of re-arranging and substitution impossible. Instead what happens is the strange shape is turned into lots of little cubes. Now the equations for the stresses in each little cube are easy to calculate. So you end up with 1000’s of “simultaneous” equations. Each cube is next to another cube and so the stress on each common boundary is the same. The computer program uses some clever maths and lots of iterations to eventually find the solution to the 1000’s of equations that satisfy the “boundary conditions”.
Finite element analysis is used successfully in lots of areas of practical problem solving, many orders simpler of course, than GCMs.
Uses of Models
One use of models is to predict, no project, future climate scenarios. That’s the one that most people are familiar with. And to supply the explanation for recent temperature increases.
But models have more practical uses. They are the only way to provide quantitative analysis of certain situations we want to consider. And they are the only way to test our understanding of the causes of past climate change.
Analysis
On this blog one commenter asked about how much equivalent radiative forcing would be present if all the Arctic sea ice was gone. That is, with no sea ice, there is less reflection of solar radiation. So more absorption of energy – how do we calculate the amount?
You can start with a very basic idea and just look at the total area of Arctic sea ice as a proportion of the globe, and look at the local change in albedo from around 0.5-0.8 down to 0.03-0.09, multiply by the current percentage area in sea ice to find a number in terms of the change in total albedo of the earth. You can turn that into the change in radiation.
But then you think a little bit deeper and want to take into account the fact that solar radiation is at a much lower angle in the Arctic so the first number you got probably overstated the effect. So now, even without any kind of GCM, you can simply use the equation for the reduction in solar insolation due to the effective angle between the sun and the earth:
I = S cos θ – but because this angle, θ, changes with time of day and time of year for any given latitude you have to plug a straightforward equation into a maths program and do a numerical integration. Or write something up in Visual Basic or whatever your programming language of choice is. Even Excel might be able to handle it.
This approach also gives the opportunity to introduce the dependence of the ocean’s albedo on the angle of sunlight (the albedo of ocean with the sun directly overhead is 0.03 and with the sun almost on the horizon is 0.09).
This will give you a better result. But now you start thinking about the fact that the sun’s rays are travelling in a longer path through the atmosphere because of the low angle in the sky.. how to incorporate that? Is it insignificant or highly significant? Perhaps including or not including this effect would change the “radiative forcing” by a factor of two? (I have no idea).
So if you wanted to quantify the positive feedback effect of melting ice your “model” starts requiring a lot more specifics. Atmospheric absorption by O2 and O3 depending on the angle of the sun. And the model should include the spatial profile of O3 in the stratosphere (i.e., is there less at the poles, or more).
It’s only by doing these calculations that the effect of sea ice albedo can be reliably quantified. So your GCM is suddenly very useful – essential in fact.
Without it, you would simply be doing the same calculations very laboriously, slowly and less accurately on pieces of paper. A bit like how an accounts department used to work before modern PCs and spreadsheets. Now one person in finance can do the job of 10 or 20 people from a few decades ago. Without an accountant someone can just change an exchange rate, or an input cost on a well-created spreadsheet and find out the change in cash-flow, P&L and so on. Armies of people would have been needed before to work out the answers.
And of course, the beauty of the GCM is that you can play around with other factors and find out what effect they have. The albedo of the ocean also changes with waves. So you can try some limits between albedo with no waves and all waves and see the change. If it’s significant then you need a parameter that tells you how calm or stormy the ocean is throughout the year. And if you don’t have that data, you have some idea of the “error”.
Everyone wants their own GCM now..
Of course, in that thought experiment about sea ice albedo we haven’t calculated a “final” answer. Other effects will come into play (clouds).. But as you can see with this little example, different phenomena can be progressively investigated and reasonably quantified.
Past Climate
Do we understand the causes of past climate change or not? Do the Milankovitch cycles actually explain the end of the last ice age, or the start of it?
This is another area where models are invaluable. Without a GCM, you are just guessing. Perhaps with a GCM you are guessing as well, but just don’t know it.. A topic for another day.
Common Misconception
The idea floats around that models have “positive feedback” plugged into them. Positive feedback for those few who don’t understand it.. increases in temperature from CO2 will induce more changes (like melting Arctic sea ice) that increase temperature further.
Unless it’s done very secretly, this isn’t the case. The positive feedbacks are the result of the model’s output.
The models have a mixed bag of:
- fundamental equations – like conservation of energy, conservation of momentum
- parameterizations – for equations that are only empirically known, or can’t be easily solved in the “grid” that makes up the 3d “mesh” of the GCM
More on these important points in the next post.
“Necessary but Not Sufficient”
A last comment before we see them on the catwalk – the catwalk “retrospective” – is that models matching the past is a necessary but not sufficient condition for them to match the future. However, it is – or it would be – depending on what we find.. a great starting point.
Models On the Catwalk
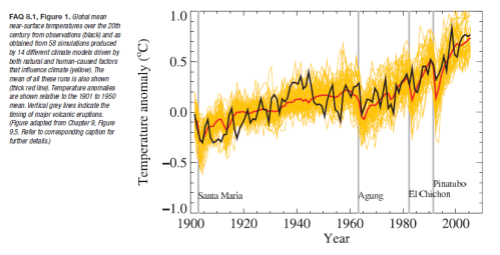
Most people have seen this graph. It comes from the IPCC AR4 (2007).
The IPCC comment:
Models can also simulate many observed aspects of climate change over the instrumental record. One example is that the global temperature trend over the past century (shown in Figure 1) can be modeled with high skill when both human and natural factors that influence climate are included.
In summary, confidence in models comes from their physical basis, and their skill in representing observed climate and past climate changes. Models have proven to be extremely important tools for simulating and understanding climate, and there is considerable confidence that they are able to provide credible quantitative estimates of future climate change, particularly at larger scales. Models continue to have significant limitations, such as in their representation of clouds, which lead to uncertainties in the magnitude and timing, as well as regional details, of predicted climate change. Nevertheless, over several decades of model development, they have consistently provided a robust and unambiguous picture of significant climate warming in response to increasing greenhouse gases.
Now of course, this is a hindcast. Looking backwards. One way to think about a hindcast is that it’s easy to tweak the results to match the past. That’s partly true and, of course, that’s how the model gets improved- until it can match the past.
The other way to think about the hindcast is that it’s a good way to test the model and find out how accurate it is.
The model gets to “past predict” many different scenarios. So if someone could tweak a model so that it accurately ran temperature patterns, rainfall patterns, ocean currents, etc – if it can be tweaked so that everything in the past is accurate – how can that be a bad thing? Also the model “tweaker” can change a parameter but it doesn’t give the flexibility that many would think. Let’s suppose you want to run the model to calculate average temperatures from 1980-1999 (see below) so you put your start conditions into the model, which are values for 1980 for temperature and all other “process variables” and crank up the model.
It’s not like being able to fix up a painting with a spot of paint in the right place – it’s more like tuning an engine and hoping you win the Dhaka rally. After you blew the engine halfway through you get to do a rebuild and guess what to change next. Well, analogies – just illustrations..
Obviously, these results would need to be achieved by equations and parameterizations that matched the real world. If “tweaking” requires non-physical laws then that would create questions. Well, more on this also in later posts.
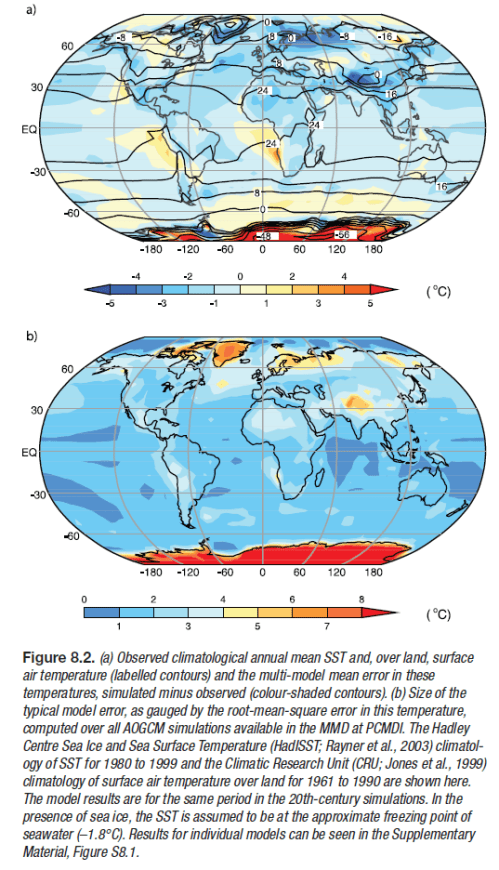
More model shots.. The top graphic is the one of interest. This is actual temperature (average 1980-1999) in contours with the shading denoting the model error (actual minus model values). Light blue and light orange (or is it white?) are good..
The model error is not so bad. Not perfect though. (Note that for some reason, not explained, the land temperature average is over a different time period than sea surface temperatures).
Temperature range:
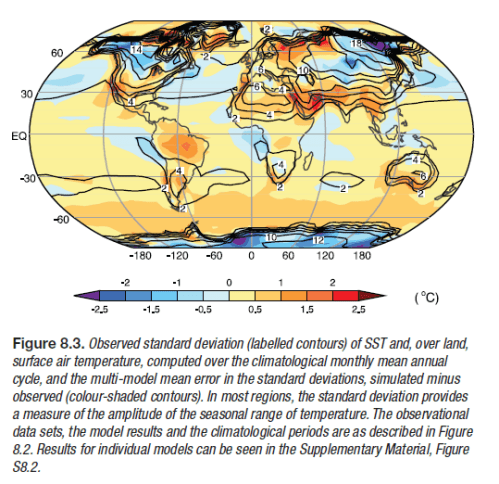
The standard deviation in temperature gives a measure of the range of temperatures experienced. The colors on the globe indicate the difference between the observed and simulated standard deviation of temperatures.
Simplifying, the light blue and light orange areas are where the models are best at working out the monthly temperature range. The darker colors are where the models are worse. Looks pretty good.
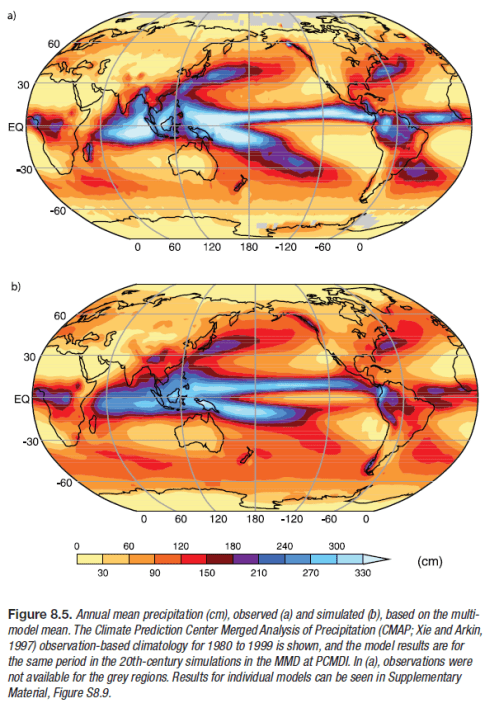
Rainfall:
This one is awesome. Remember that rainfall is calculated by physical processes. Temperature, available water sources, clouds, temperature changes, winds, convection..
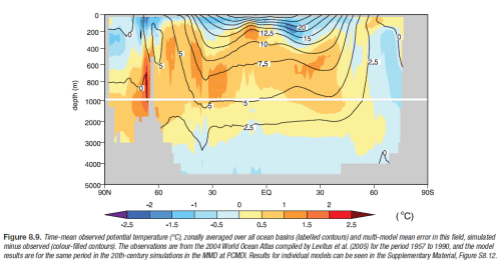
Ocean temperature:
Ocean potential temperature, what’s that? Think of it as the real temperature with unstable up and down movements factored out, or read about potential temperature.. Note that the contours are the measurements (averaged over 34 years) and the shaded colors are the deviations of actual – model. So once again the light blue and light orange are very close to reality, the darker colors are further away from reality.
This one you would expect to be easier to get right than rainfall, but still, looking good.
Conclusion
It’s just the start of the journey into models. There will be more, next we will look at Models Off the Catwalk. So if you have comments it’s perhaps not necessary to write your complete thoughts on past climate, chaos.. Interesting, constructive and thoughtful comments are welcome and encouraged, of course. As are questions.
Hopefully, we can avoid the usual bunfight over whether the last ten years actual match the model’s predictions. Other places are so much better for those “discussions”..
Update – Part Two now published.


Great post, very interesting. Have you read “Storms of My Grandchildren,”? Hansen talks about models a bit there — he seems to feel that models are less than reliable over the long term, and a better bet is to look at periods in history with comparable forcings and look at what the conditions were then. Your thoughts?
And another question that has defeated my Google-fu: Do you know offhand what kind of assumptions the current models make about future changes methane levels?
I would think it would be difficult to estimate, given that we don’t know why methane levels leveled off there for a while, nor why it has resumed its climb over the past three years.
I am wondering what the consequences would be if the current trend of 0.5% growth in methane continues (knowing full well that by even speculating about a trend from three years of growth I risk the wrath of Gaussia, Muse of Statistical Significance. But I do wonder.)
Robert:
I haven’t read the book. You ask the big questions right at the start.. models, reliability, history.. well, we will work through these things I hope.
No idea on methane either, but why not take a look at IPCC AR4 p793 Chapter 10 Climate Projections:
“10.4.3 Simulations of Future Evolution of Methane, Ozone and Oxidants”
I’m sure there will be a good explanation of scenarios and results..
The SRES scenarios assume +6 ppb yr–1. Others assume little to no increase. Estimates of the change in the CH4=ozone forcing range from -0.05 to +0.18 to +0.30 W/m^2 for the MFR, CLE, and A2 scenarios. They don’t give a number for the SRES scenario. Although they talk about the increase under a SRES scenario.
I may be just a tad out of my depth here.
Robert
Hansen tends to be rather selective in choosing the periods to look at, although the basic approach of looking at what has gone before and basing future suppositions on that is a good one.
The major storms over the last two thousand years have been very well documented by Hubert Lamb, the first director of CRU. This shows storms/floods/hurricanes etc literally shaping landscapes and destrying whole villages in the past and there is nothing comparable over the last 100 years or so.
Whilst his book is -as its title infers-confined to a part of the Northern Hemisphere it is a very well documented part
“Historic storms of the North Sea, British Isles and Northwest Europe” by Hubert Lamb ISBN 0-521-61931-9 published by Cambridge University Press.
When you look at history it is very difficult oi be alarmist about todays events!
Science of Doom -just wanted to say how much I enjoy reading your articles and the even handed manner in which things here are conducted.
Tonyb
I know climate scientists, well the IPCC anyway, claim there is no known climate driver that can explain the recent warming other than increased CO2. But what if there is an unknown driver?
They had models for ocean waves for many years indicating that the reported rogue waves by ships crews had to be exaggerations. It wasn’t until the 90s that sattelites confirmed the commonality of rogue ocean waves. They are developing new wave models now based on observations.
An article on that subject can be seen with the below link.
http://www.livescience.com/environment/050503_monster_waves.html
I think there may in fact be an input to the models that forces the positive feedback to appear. This is the assumption of constant relative humidity. In fact, the best data available shows a reduction in relative humidity at the higher altitudes associated with the feedback. The exact trend is complex, and there may have a small positive feedback in the 1990’s, but there appears to be a negative feedback in the 2000 to 2010 time frame (Soloman, et, al.).
Leonard Weinstein
By enormous coincidence I am just finishing an article on Historic CO2 readings which commences with referencing the paper written by you;
‘Limitations on Anthropogenic Global Warming’ carried on The Air Vent
My follow up concentrates primarily on Co2 measurements through History, the people who took them, the circumstances, and the instruments and methods used.
This all appears to indicate Ernst Beck probably has a very good case and levels were similar to today during the 19th Century.
If you have the time to have a quick read through it before release please send me a message by clicking on my name. Thanks
Tonyb
Robert,
The emissions scenario’s are probably one of the places with the greatest amount of disagreement. Scenario A1 predicts 52 Gt/yr CO2 emissions by 2030 and Scenario B2 predicts 37 Gt/yr CO2 by 2030.
Current EIA projections are 40 Gt/yr by 2030.
Methane gets even more complicated.
Ive got a Q… so for the initial input data what is required? Do you need to know the “weather” at all the grids at that time? or will they work of basic atmospheric approximations(averages for grids)? And for the oceans, are they modeled as well? or more just surface conditions?
Leonard Weinstein:
This is a key point. If relative humidity is assumed but not true..
Hopefully we will get into this critical point in due course..
Mike Ewing
Each grid section is pretty big, more than 1′ x 1′ (lat x long). And yes there is a big database of past conditions that is used to find the right average starting value for each grid section for each parameter.
There are lots of different models. The bigger ones are AOGCMs – atmosphere-ocean GCMs. In these the oceans are modeled as well. Usually they can be decoupled if required, so really there are 2 models joined together.
In the next post in this series there will some more about a top model named CCSM3.
Solomon et al is about stratospheric water vapor, not water vapor in the troposphere, which is where (somewhat) constant relative humidity is presumed and backed up by observations (recently via detailed observations at various altitudes in the troposphere using the AIRS sensor on the AQUA satellite, which match model predictions very closely).
Water vapor content in the stratosphere is very low and doesn’t get there through the normal evaporation/convection/mixing process seen in the troposphere. The relative humidity argument for the troposphere isn’t challenged by Solomon.
Solomon’s paper addresses natural variability, not the underlying trend. She doesn’t argue that this contradicts anything important in regard to AGW. Note that if there’s a higher than previously known negative feedback as stratospheric water vapor increases, then when it decreases, the decrease in that negative feedback will also be higher than previously known. Bigger swings around the trend, not a different trend, if I understand correctly.
Also note that Solomon’s paper is just one paper, and like most scientific work that presents novel results, should be taken with a grain of salt until more work is done in the area.
Thanks harrywr2, sometimes I just need to be told when something is above my pay grade!
[…] 23, 2010 by scienceofdoom In Part One, we introduced some climate model basics, including uses of climate models (not all of which are […]
I’ve been reading some of the articles on this site, and I think they are quite good.
I do feel compelled to comment on your characterizations of hind casts. It is of course good and perhaps necessary for a model to work accurately against a known record. But the true test of a model is its ability to continue to work with data that was not available to the modeler. Unfortunately for climate modelers most of the detailed data comes from the relatively short current period.
Continuing to refine models against a very well known data set is interesting, but does little to improve confidence against unknown data sets. (One example of which is the future.)
Having said this the scientific consensus on the gross temperature impact of doubling CO2 has changed very little over the last 30 years, and there is no reason to believe it is incorrect.
For some time it has puzzled me that GCMs do a decent job of hindcasting the 20th century, for example as we just looked at in the IPCC figure, while at the same time they have sensitivities that vary by over a factor of three.
How does that circle get squared?
SOD: In “Common Misconceptions”, you state that “The idea floats around that models have “positive feedback” plugged into them. ” Feedback and climate sensitivity are obviously not parameters that are directly entered into a model. However, I have read (but can’t find my original source) that some skeptics assert that climate sensitivity is an innate property that is built into a model – not a number that calculated from experiments with GCM’s. While attempting to find my earlier source, I ran across a relevant 2005 Nature paper by Stainforth (http://ww.lse.ac.uk/collections/cats/papersPDFs/66_EvaluatingUncertainty_Nature_2005.pdf) where about 1000 versions of the the HADCM3 model were run with different sets of physically relevant parameters. They found “model versions as realistic as other state-of-the-art climate models, but with climate sensitivities ranging from less than 2 K to more than 11 K.” In other words, the climate sensitivity of the HADCM3 model (3.4 degK/2XCO2) turns out to be determined by an arbitrary choice of unconstrained parameters. Since the choice of parameters appears to be arbitrary, there may be some truth to the claim that climate sensitivity is an input into models (via cloud parameterization).
These results shouldn’t be surprising, because the difference between a climate sensitivity of 2 and infinity is a modest change in total feedback – 1.7 vs 3.3 W/m^2/degK if my calcs are correct.
Question: Does this mean that discerning climate scientists believe that climate sensitivities derived from the IPCC’s models are essentially meaningless? If one really believed that high-sensitivity, low-sensitivity and standard versions of HADCM3 really were equally good at representing today’s climate, this would seem to be an appropriate conclusion. (One could choose among these models using past climate, but climate sensitivity has already been limited to 1.5-4.5 using this approach without GCM’s.)
Lindzen claims that most models use too large a value for thermal diffusivity in the oceans. It would be interesting to know if thermal diffusivity is one of the parameters Stainforth et al varied through the full possible range.
Later Stainforth publications suggest that he is focusing on cloud parameters and thermal diffusivity probably hasn’t been varied – if it is an input parameter that is normally modified. Attempts to select the best models from ensembles weren’t particularly successful:
http://www.pnas.org/content/104/30/12259.long
Click to access qump1.pdf
Click to access SandersonBM_KnuttiR_etalii_2008.pdf
Frank:
Hard question to answer. You can see what climate scientists think in papers they write and, for a few, in their textbooks.
From the survey by Dennis Bray and Hans von Storch there is quite a spectrum of opinions.
Well worth a read.
Thank you for the reply. I read the survey – which was interesting, but out-of-date and not directly relevant to my difficult question. If you don’t think it is unreasonable to discount the predictions models make about feedbacks and climate sensitivity because those predictions depend greatly on unconstrained parameters, your might consider revising the section on “Common Misconceptions”.
The follow up papers by Stainforth mentioned above show that all of his versions of HADCM3 are not equally good as reproducing current climate (especially outgoing radiation), but the ensemble doesn’t narrow the range of any parameter based on deteriorating performance.
Question: Has any useful work been done on the reliability of the parameter models use for the rate at which heat penetrates the oceans (thermal diffusivity)? The issue is relevant to: interpreting the changes seen after Mt. Pinatubo, the idea that 0.5 degK of further warming is “in the pipeline” (even if we stabilized GHG levels today), and probably climate sensitivity itself.
[…] For a bit of background generally on models, take a look at the Introduction in Models On – and Off – the Catwalk. […]
Dear SoD
Re your intro to GCM’s, in fact many if not most GCM’s rely on a method that is almost exactly Finite Elements (FE), called Spectral Methods (SM’s). In techno-bable, the primary difference is that FE have local basis functions, while SM’s have global basis functions. The SM’s are used to solve the models “in the plane” (i.e. horizontally)
If the GCM includes a third (upward) dimension, then that is usually managed with Finite Difference (FD).
The reason for splitting the solution into SM/FD format is a little technical, but basically there is a lucky coincidence for GCM’s that allows SM’s to be much more computationally efficient (c.f. doing the whole thing FD, or FE).
BTW, I only saw this page today, and that you had made use of AR4 Fig 8.1 as an illustration of model verification. In fact, as you know by now, I had commented on the “cheating” that is used in exactly that image, previously on another part of your blog.
I can repeat some of those illustrations of the pathologies in those models here (not sure if repetition is desired), or if you like, I have posted a “no volcano cheating” version of IPCC AR4 Fig 8.1 to here (http://www.thebajors.com/climategames.htm) you are welcome to copy it if you wish.
BTW, it is a relatively easy matter to show people, say, the heat equation, to show how the FD version is created, and even how that can be whacked into a spreadsheet (yes, your very own FD PDE solver in a spreadsheet, no coding required).
Cheers
PS. not trying to be picayune, but your statement about the “solutions satisfying the boundary conditions”, should read more like “solutions that satisfy the model equations plus their BC’s and IC’s” The entirety of (P or ODE) models is the PDE’s together with IC’s/BC’s.
[…] In this article we will start to consider what GCMs can do in falsifying these theories. For some basics on GCMs, take a look at Models On – and Off – the Catwalk. […]
Just wanted to point out that even though your impeller finite element analysis is a good example, its not as simple as it looks on the outside, nor are typical calculations very accurate in absolute terms. That’s why destructive testing is still the gold standard and there are still a lot of failures such as the famous side of body join failure for the Boeing 787 in ground testing.
The problem here is that even though the standard models used for structural stress analysis are elliptic and thus are well posed in a mathematical sense, i.e., small changes to the shape and boundary conditions give small changes in the calculated stresses, typical structures have sharp edges, fastener holes, etc. These features give rise to stress singularities. The result is that rigorous error analysis shows that typical finite element calculations are in error by 5% – 20% in the L2 norm. This is proven in the papers of people like Ivo Babuska and Leszek Demkowicz from Univ. of Texas at Austin. Of course the Navier-Stokes equations are not well posed as an initial value problem and are a much harder problem to solve numerically.
Finite element modeling has revolutionized the design of structures, but one needs to be careful to accurately disclose the limitations and often rather large errors in the calculations.
There has recently been some discussion of climate sensituvity. observations and climate models. One of the issues is the temperatures at the surface. What will be the changes in air temperatures over ocean and how do the ocean surface change?. This will have much to say when it comes to changes in wind, evaporation. moisture and surface heat flux.
A paper from 2008 adressed these issues: Muted precipitation increase in global warming simulations: A surface evaporation perspective
Ingo Richter, Shang-Ping Xie
http://onlinelibrary.wiley.com/doi/10.1029/2008JD010561/full
“A 90-year analysis of surface evaporation based on a standard bulk formula reveals that the following atmospheric changes act to slow down the increase in surface evaporation over ice-free oceans: surface relative humidity increases by 1.0%, surface stability, as measured by air-sea temperature difference, increases by 0.2 K, and surface wind speed decreases by 0.02 m/s. As a result of these changes, surface evaporation increases by only 2% per Kelvin of surface warming, rather than the 7%/K rate simulated for atmospheric moisture. The increased surface stability and relative humidity are robust across models. The former is nearly uniform over ice-free oceans while the latter features a subtropical peak on either side of the equator. While relative humidity changes are positive almost everywhere in a thin surface layer, changes aloft show positive trends in the deep tropics and negative ones in the subtropics. The surface-trapped structure suggests the following mechanism: owing to its thermal inertia, the ocean lags behind the atmospheric warming, and this retarding effect causes an increase in surface stability and relative humidity, analogously to advection fog.”
“Under GHG forcing, the simulated SST increases more slowly than surface air temperature, which increases surface stability. This acts to suppress latent heat release from the ocean and appears as a negative term in our decomposition.”
And much more than that. So I think “The future world according to models” can give some food for thoughts
And from the same Ingo Richter: “Global climate models experience great difficulties simulating eastern boundary regions, with one of the most notable shortcomings being warm sea-surface temperature biases that often exceed 5 K. These model biases are due to several reasons. (1) Weaker than observed alongshore winds lead to an underrepresentation of upwelling and alongshore currents and the cooling associated with them. (2) Stratocumulus decks and their effects on shortwave radiation are underpredicted in the models. (3) The offshore transport of cool waters by mesoscale eddies is not adequately represented by global models due to insufficient resolution. (4) The sharp vertical temperature gradient separating the warm upper ocean layer from the deep ocean is too diffuse in the models.”
This shows that scientists who are working with models are better to see their shorcomings.
nobodysknowledge.
If we assume that the land surface is 30% of the surface of the Earth, then the average temperature increase adjusted for area is 0.3 x 0.9 + 0.7 x 0.44 = 0.58. That’s pretty close to 0.55. Again, there is no evidence that the air above the sea surface is warming faster than the sea surface.
Model behavior is not evidence.
Nic Lewis at Climate Audit:
One would logically expect that SST and SAT would be closely linked. IMO, model behavior in the surface boundary layer is suspect.
I had a comment to Nic Lewis at Climate Audit:
“”Nor is there good observational evidence that air over the open ocean warms faster than SST.”
Perhaps niclewic is on thin ice here. I have done some eye-balling on temperatures since 1980, and the difference seems clear. From wood for trees. Ocean surface temperatures increase 0,44 deg C, total global increase 0,55 deg C, land air increase 0,9 deg C, low troposphere (RSS and UAH) 0,45 deg C. I think you would get much of the same impression of the differences with a different timespan.
For me it is important to get this so right as possible, and I think it is wise to let the data speak. When it comes to the estimates of TCR, I think it starts in the wrong end. I would like to know more about natural variations first. And what interest me more is how climate warming sets itself through in the climate system. I would ask you to say something about that before you ask me to believe in the strength of forcings and sensitivity. “
As Frank has said:: “The most fundamental question when it comes to sesitivity is: How can you say something of climate sensitivity without having a good measure of natural variation?”
I clicked on the wrong reply button. See my reply above:
I have reconsidered. I think Nic Lewis had a point.
HadMAT1 (ocean air temperatures) and HadSST (ocean water temperatures) seem to follow each other very close through a timescale from 1870 to 2000.
After a paper from N A Rayner et. al 2003 http://badc.nerc.ac.uk/data/hadisst/HadISST_paper.pdf
nobodysknowledge,
“HadMAT1 (ocean air temperatures) and HadSST (ocean water temperatures) seem to follow each other very close through a timescale from 1870 to 2000.
After a paper from N A Rayner et. al 2003”
Are you referring to Figure 15? Of course they look a lot alike after massive averaging that implicitly assumes that everything is linear. The effect in question is, I think, due to the non-linear T dependence of vapor pressure. So I think that a proper comparison must be point by point.
You quote Lewis as saying ”Nor is there good observational evidence that air over the open ocean warms faster than SST.” Absence of evidence is not evidence of absence. The effect may be just too small to see in noisy data. For lack of evidence to be significant, you must be able to show that the effect should produce an observable effect in data of the available quality.
Mike M.
You are right. I was referring to fig. 15.
Simple calculations concerning surface energy balance conflict with TOA radiative balance when climate sensitivity is high.
TOA balance: If ECS is 3.7 K/doubling and 3.7 K / 3.7 W/m2, then the planet needs to emit or reflect an additional 1 W/m2/K to space as it warms.
Surface balance: On the average, OLR rises 5.5 W/m2/K as it warms. At 277 K (blackbody emission of 333 W/m2), DLR rises 4.8 W/m2/K. Evaporation transfers 80 W/m2 of latent heat. If evaporation rises 7%/K, that would be 5.6 W/m2/K. Total: 6.3 W/m2/K.
Obviously, the surface flux rise can’t be 6.3 W/m2/K if the TOA flux rise is only 1 W/m2/K. AOGCMs with high climate sensitivity must eliminate this difference somehow.
A decrease in SWR reflected by clouds back to space (albedo) could account for some or all of this difference. Currently, about 100 W/m2/K, so the difference could be eliminated by a 5%/K decrease in albedo. That is huge; 6 K of warming would eliminate all clouds. Decreasing reflection of SWR appears unlikely to close the majority of the gap.
Therefore, AOGCMs must reduce the increase in evaporation to half or less of the 7%/K that saturation vapor pressure increases – otherwise their climate sensitivity would be lower. If albedo does not change, 90% of the rise in evaporation must be suppressed. Why do we associate high climate sensitivity with water vapor and cloud feedback when suppression of evaporation is critical?
The rate of evaporation is proportional to wind speed and to “under-saturation” (how much more water vapor can be added to the air without condensation). Reductions in either factor can suppress evaporation.
If relative humidity remains unchanged, under-saturation remains unchanged. If relative humidity over the oceans rises from 80% to 81%, under-saturation decreases by 5%. This is can reduce the increase in evaporation from 7%/K to 2%K, eliminating most of the discrepancy.
Higher relative humidity in the boundary layer over the ocean must(?) be caused by a decrease In mixing between the boundary layer and free atmosphere. What causes this? Won’t a boundary layer with higher relative humidity have more boundary layer clouds at the top, where it is colder. AOGCMs presumably don’t have the resolution to properly model the interface between the boundary layer and free atmosphere. This is fertile ground for skepticism.
Frank,
You wrote: “TOA balance: If ECS is 3.7 K/doubling and 3.7 K / 3.7 W/m2, then the planet needs to emit or reflect an additional 1 W/m2/K to space as it warms.”
At equilibrium, total emitted + reflected is the same as before any change. It must balance what comes in from the sun. Before equilibrium is reached, the total outgoing radiation is reduced.
“Surface balance: …”
I see no reason to believe that you do a meaningful calculation in such a simple manner. The calculation requires considerable justification of both the method and specific numbers.
Mike: I’m looking at climate sensitivity from the perspective of what I understand (mostly self-taught) to be the climate feedback parameter (CFP). When the surface of the Earth warms 1 K, how much more radiation escapes to space. If the answer is 3.7 W/m2, then the CFP is 1 W/m2/K. ECS is the reciprocal of the CFP, or 1 K/(W/m2). MUltiplying by 3.7 W/m2/doubling gives an ECS of 3.7 W/m2/doubling. If CFP is 2 W/m2/K (twice as much heat escapes per K of warming), ECS is 1.8 K/doubling. If CFP is 3.7 W/m2/K, ECS is 1 K/doubling. A blackbody at 255 K has a “CFP” of 3.7 W/m2/K.
Heat can escape to space as OLR or by reflection of SWR. Normally we think a warmer planet radiates more OLR to space, but IIRC the increase in reflected SWR is bigger in many models.
Mike wrote: “I see no reason to believe that you do a meaningful calculation in such a simple manner. The calculation requires considerable justification of both the method and specific numbers.”
I treated the surface (emitting OLR) and the lower atmosphere (emitting DLR) as blackbodies and assumed that the temperature difference between them (lapse rate) didn’t change. A blackbody that emits 333 W/m2 would be 277 K or about 2 km above the surface, a reasonable estimate for the altitude and temperature of the GHGs emitting DLR. Issac Held discusses evaporation and some other aspects of this problem from a different perspective at:
http://www.gfdl.noaa.gov/blog/isaac-held/2014/06/26/47-relative-humidity-over-the-oceans/
I should have mention that observations show precipitation increasing with GMST 7%/K with a 95% ci of about 3.5%/K.
Frank,
“When the surface of the Earth warms 1 K, how much more radiation escapes to space.”
If you keep the lapse rate the same and the concentrations of greenhouse gases the same (so that the emission altitude stays the same), then I think you would increase emission by about 3.3 W/m^2 (although I have seen estimates that would imply as much as 3.7 W/m^2). But then there would be more radiation going out than coming in, causing temperature to fall until the radiative balance was re-established.
If you instantaneously double CO2 (which you can do in a model) so that lapse rate and T have no chance to respond, then the emission would go down by 3.7 W/m^2. That would mean that the radiation going out is less than coming in, causing the system to get warmer, until a new balance is established. The initial radiative imbalance is the radiative forcing and the eventual increase in average surface T is the climate sensitivity.
Mike: Temperature change can be forced or unforced. Warming forced by rising GHGs is too slow for us to be able accurately measure small, slow changes radiative balance at the TOA and the forcing agent causes changes in both temperature and radiative cooling to space (including increased reflection of SWR). Let’s consider temperature change that is “unforced”: A sudden increase or decrease of currents between the deep ocean could easily change surface temperature by several K. (This is basically what happens during El Niño – changing winds reduce upwelling in the eastern Pacific and down welling in the west, but let’s imagine more dramatic change). Now we can ask how radiative cooling to space varies with surface temperature without any complications the climate feedback parameter. As long as we wait a few months (possibly only weeks) all of the fast feedbacks (humidity, lapse rate, clouds, seasonal snow cover) will be amplifying or suppressing radiative cooling to space. We would only be missing changes in surface albedo due to shrinking ice caps. I believe the climate feedback parameter on this time scale is the reciprocal of the effective climate sensitivity rather than the equilibrium, but I find some of this nomenclature confusing.
Now consider the surface and TOA flux change per K of unforced surface warming that I discussed above.
Then consider GHG-mediated warming after a doubling of CO2. Temperature change lags behind forcing, because heat is flowing into the deep ocean, making the situation complicated. When those complications diminished after several centuries, CO2 will have reduced OLR by 3.7 W/m2 and surface warming will have increased radiative cooling to space by 3.7 W/m2. In other word, AGW can be analyzed as an instantaneous forcing compensated by CFP*dT, where dT is warming.
If you don’t use anamalies to remove seasonal changes, GMST warms 3.5 K every summer in the NH, because the heat capacity of the NH is smaller than the SH. If ECS is 3.7 K/doubling and CFP therefore 1 W/m2/K, the increase in radiative cooling to space will be 3.5 W/m2. If ECS is 1 K/doubling and the CFP therefore 3.7 W/m2/K, the increase in radiative cooling to space will be 13 W/m2. These huge difference develop over 6 months (rather than a century) and are replicated ever year. We can easily observe changes in both the LWR and SWR channels from both clear and cloudy skies, and thereby some aspects of feedbacks. Unfortunately, seasonal warming is not an ideal model for global warming. Manabe (2013) PNAS shows that climate models do a lousy job of reproducing seasonal feedback.
Pinatubo’s effect on temperature and radiative cooling has been studied. Lindzen notoriously found negative feedback in the tropics in response to rapid temperature change during El Niño.
Frank,
The temperature profile of the planet can change such that the average temperature goes up or down without changing the total emission to space. Hölder’s Inequality says that the average temperature of a non-isothermal sphere exposed to sunlight on one side will always be less than the average for an isothermal sphere. In the case of a non-rotating sphere, it’s a lot less. According to UAH v. 6.0 data, the recent El Nino raised the global average near surface temperature, tlt, by less than 1K, and this was quite a large one. So it’s not at all clear that at the peak, emission to space increased by ~3 W/m².
Frank,
OK, I think I see what you are doing. I would comment that the warming associated with El Nino is more likely associated with changes in clouds than with heat transfer to/from the ocean (at least if I understand the things that Roy Spencer has written).
“TOA balance: If ECS is 3.7 K/doubling and 3.7 K / 3.7 W/m2, then the planet needs to emit or reflect an additional 1 W/m2/K to space as it warms.”
Implying, perhaps, that clouds are letting in an extra 1W/m^2. Or 2 W/m^2 using an ECS half as large, as implying by observational data.
“Surface balance: On the average, OLR rises 5.5 W/m2/K as it warms. At 277 K (blackbody emission of 333 W/m2), DLR rises 4.8 W/m2/K. Evaporation transfers 80 W/m2 of latent heat. If evaporation rises 7%/K, that would be 5.6 W/m2/K. Total: 6.3 W/m2/K.”
You also have to consider sensible heat flux.
“Obviously, the surface flux rise can’t be 6.3 W/m2/K if the TOA flux rise is only 1 W/m2/K.”
Why not? With AGW, the surface flux increases but the TOA flux is unchanged.
“AOGCMs with high climate sensitivity must eliminate this difference somehow.”
The increased atmospheric water vapor increases vertical heat transfer and reduces lapse rate (the negative “lapse rate feedback”). That would reduce the small contribution from OLR-DLR (smaller T difference) and decrease sensible heat transfer (same reason). It would also increase T at the emission altitude. Not clear that there is a problem.
But if your point is that satellite observations of radiative changes associated with El Nino might provide a helluva natural experiment, then I think that is an good point.
“Manabe (2013) PNAS shows that climate models do a lousy job of reproducing seasonal feedback.”
I did not know that. The IPCC report seems to say almost nothing about seasonal effects. Can you provide a full reference? Is it Tsushima and Manabe, “Assessment of radiative feedback in climate models using satellite observations of annual flux variation”, published in PNAS? That paper did not impress me much, but maybe I need to give it another look.
Frank: wrote: “Manabe (2013) PNAS shows that climate models do a lousy job of reproducing seasonal feedback.”
Mike replied: “I did not know that. The IPCC report seems to say almost nothing about seasonal effects. Can you provide a full reference? Is it Tsushima and Manabe, “Assessment of radiative feedback in climate models using satellite observations of annual flux variation”, published in PNAS? That paper did not impress me much, but maybe I need to give it another look.”
Frank continues: You identified the right paper.
http://www.pnas.org/content/110/19/7568.full
To be honest, the authors concluded: “Here, we show that the gain factors obtained from satellite observations of cloud radiative forcing are effective for identifying systematic biases of the feedback processes that control the sensitivity of simulated climate, providing useful information for validating and improving a climate model.”
When looking at how models differ from observations – and disagree with each other in so many different ways – I characterized their output as a lousy job. I was impressed by this paper for the following reasons:
We need to wait roughly a century to see how a 3 K (1.5-4.5 K) increase in the GMST anomaly changes OLR and reflected SWR using different satellites. This paper shows us the change for five seasonal 3.5 K warmings with two different satellites. Nowhere else can you see changes in temperature and TOA fluxes that are this robust. Look at the tiny error bars!
Seasonal warming has been analyzed before this paper beginning with a paper by Ramanathan discussed here at SOD. This is the first comparison between satellites and AOGCMs. Seasonal warming is not global warming. It is the net result of warming in the NH and cool in the SH. Since the heat capacity of the mixed layer in the SH than the NH (60% vs 80% coverage, deeper mixed layer), seasonal temperature swings are 2X bigger in the NH than the SH. Unfortunately those differences mean global feedbacks could be different from seasonal hemispheric feedbacks. For example, the seasonal change in SWR reflected by clear skies is caused by the relative paucity of seasonal snow cover in the SH. So I don’t think one can estimate ECS for global warming from the data in this paper. However, climate models should be just as capable of properly reproducing seasonal changes in temperature and radiation in response to seasonal changes as they are supposed to be to global changes in temperature anomaly and radiation in response to GHGs.
Whenever anyone says that no one has observed feedbacks, I point out the data in this paper: There is about a 3 W/m2 difference between the dotted lines in Figure 1 for no-feedbacks and for observations. The error bars are a tiny fraction of this difference. Clearly combined water vapor plus lapse rate feedback is positive and about 1 W/m2/K herein. This is the one feedback AOGCMs agree with each other on and with observations. I’m not sure what to think about cloud feedback, except that models clearly disagree with each other. (I find it confusing to think of cloud feedback as the difference in gain between clear and cloud skies rather than just the gain from cloudy skies alone.)
Frank,
You wrote: ” I was impressed by this paper for the following reasons …”.
You must be a lot more patient than I am (not all that hard). I once again gave up on a paper that I found so wretched that I ended up concluding that I could not tell if what they are doing is correct and saw no reason to take it on faith.
Did you understand how there can be a temperature dependence of albedo under clear sky conditions?
Did you understand why the signs of the gain factors from Figures 1 and 2 are the same, even though the signs of the slopes are opposite?
Didn’t SoD deconstruct this method for cloud feedbacks?
I tend to figure that if peer reviewers did not catch major presentation problems, they they are unlikely to have caught major errors and conclude that, in effect, such a paper has not been properly peer reviewed.
Mike: Additional comments:
1) There are many phenomena associated with El Nino. It is my understanding that a slackening in trade winds blowing from east to west slows down upwelling of cold water off of South America and downwelling of warm water in the Pacific Warm Pool. So I look at this as an example of unforced (internal) climate variability associated chaotic variation in heat exchange between the surface and the deeper ocean. This over-simplified picture ignores clouds and probably other important factors, but hopefully still correctly show that warming does not need to be FORCED.
If I understand correctly, sensible heat is conduction of heat 1 cm (1 mm?) between the surface and air that is not adhering to the surface – air that can be mixed by wind and rise by convection. If we assume that the temperature difference across this gap remains constant with surface warming, sensible heat flux will remain constant during warming.
240 W/m2 of post-albedo SWR enters the atmosphere and 168 W/m2 reaches the surface. At steady-state, a total net flux of 168 W/m2 needs to leave the surface through the lowest few meters of the atmosphere and that flux needs to increase to 240 W/m2 by the TOA for a steady state to exist. That increase is the result of a decrease in DLR with altitude. At the surface, latent heat provides the largest flux, but it and most DLR aren’t present at or above the tropopause. The downward flus of energy must equal the upward flux of energy at all altitudes, otherwise a steady state won’t exist and the atmosphere would warm or cool indefinitely.
What happens after the surface has warmed by X degK? Net radiation carries a net increase in radiative flux upward from the surface of 0.7 W/m2/K. If wind and relative humidity remain constant, the upward flux of latent heat will increase by 5.6 W/m2/K. Therefore, if 6.3 W/m2/K (or 6.3*X W/m2) of heat escapes from the surface, while only 1 W/m2/K (1*X W/m2) escapes the TOA if ECS is 3.7 K/doubling, the atmosphere will warm indefinitely and a steady state will not exist. The RATE of increase in flux from the surface per K of surface warming and from the TOA must be equal at all times during warming. A 5.6 W/m2/K decrease in albedo is unlikely given that albedo only reflects 100 W/m2 of SWR back to space right now.
Mike wrote: “But if your point is that satellite observations of radiative changes associated with El Nino might provide a helluva natural experiment, then I think that is an good point.”
The biggest change in GMST is seasonal change (3.5 K) and this produces the biggest change if TOA OLR and reflected SWR. This change develops over 6 months and is easy to measure from space.
The biggest change in GMST ANOMALY is associated with El Nino. That change is less than 1 K in the troposphere and less at the surface. The change also develops over about 6 months. Lindzen and Choi reported negative feedback for the TROPICS associated with El Nino warming of the tropics.
Pinatubo is the other large temperature perturbation that has been observed by ERBE or CERES.
Frank wrote: “sensible heat is conduction of heat 1 cm (1 mm?) between the surface and air that is not adhering to the surface”
Yes, and it is also the transfer at any given height due to convection across that height.
Frank wrote: “If we assume that the temperature difference across this gap remains constant with surface warming, sensible heat flux will remain constant during warming.”
Yes, but then we would not have energy balance. If latent heat transfer goes up by more than the net radiative change, then sensible heat transfer must go down to compensate. Either that or the surface T will have to change to restore the balance. I think the mechanism is that latent heat transfer cools the surface and warms the atmosphere (when it condenses) and therefore reduces the temperature difference. That results in less sensible heat flux.
“Therefore, if … the atmosphere will warm indefinitely and a steady state will not exist.”
I might be missing your point, but I think the end result of that argument is that it is very difficult for changes in ocean-atmosphere heat transfer to produce large surface T changes that last for any length of time. There is just no way to sustain such a large energy transfer. But El Nino produces much less cloudiness in the tropical Pacific, allowing much more sunlight in. I think the tropical Pacific is something like 15% of the Earth’s surface, so that could be significant.
“A 5.6 W/m2/K decrease in albedo is unlikely given that albedo only reflects 100 W/m2 of SWR back to space right now. ”
Yes, that seems rather high. But with an ECS of 1.8 K and a 10% reduction in sensible heat transfer, that gets knocked down to about 2 W/m^2. I do not claim the latter number is the correct one; I only point out that in dealing with small differences in large numbers, slightly different assumptions make a huge difference. Which is the reason for my skepticism about the utility of this type of calculation. It is the sort of thing that probably can only be addressed by a proper model.
“climate models should be just as capable of properly reproducing seasonal changes in temperature and radiation in response to seasonal changes as they are supposed to be to global changes in temperature anomaly and radiation in response to GHGs.”
I agree. That is the sort of thing that the modelers ought to carefully examine as part of model validation. It frustrates me that they don’t seem to do much of that.
Mike: I think we agree that net inward and outward heat flux must be equal at all altitudes at steady state. If we set aside changes in inward SWR flux (albedo) as likely to be small, then the RATE of increase in outward flux per K of surface warming must be the same at all altitudes. I’m focused on the rate of increase at two locations, the interface between the surface and the atmosphere and at the TOA. You are correct in applying this requirement to all altitudes and sensible heat transport is important within the atmosphere, but there is turbulent mixing (entrainment?) between rising and descending air masses. Due to these complications, I prefer to focus on the two interfaces where where heat transport is simplest, the surface/air and TOA.
Sensible heat flux at the surface/air interface is something I understand poorly. The transport of water molecules and “hot” molecules across this interface presumably is controlled by the same physics. Somewhere at this blog I have learned to think of this as conduction driven by a temperature gradient.
High climate sensitivity (3.7 W/m2 gives nice round numbers) implies that the RATE of rise of net upward heat flux at the TOA and the surface must be 1 W/m2/K. And that is grossly incompatible with the rate of evaporation rising with saturated vapor pressure (7%/K). Modest changes in albedo won’t fix this problem.
So there must be “feedbacks” that suppress the “no-feedbacks” increase in evaporation (7%/K). Those feedbacks include a rise in relative humidity, and a decrease in wind speed. A decrease in albedo with warming can reduce the need for such “feedbacks”.
Mike wrote: “That is the sort of thing that the modelers ought to carefully examine as part of model validation. It frustrates me that they don’t seem to do much of that.”
IMO, modelers think their models are better than observations (though I doubt they would say so publicly). This statement isn’t ridiculous. For most of their careers, we didn’t have observations with the accuracy, resolution, or long time baseline to tell us anything that could usefully contradict model output. You can tune your model to match many aspects of climate (such as albedo) perfectly. And you can do experiments with models in a few week that would take decades, even if we had dozens of Earths to with which to experiment. When governments wanted immediate answers, all science had to offer were models. Even if some observations did contradict models, the observations could be wrong. A decade plus pause in warming was just eliminated from some temperature records. Radiosondes and other records were “homogenized”. RSS is inflating its estimate of possible systematic error. An honest skeptic citing contradictory observations always has been standing on quicksand.
Isaac Held had a post on Pinatubo that focused on what models say happened. Notice his reply when commenter Paul_K told him observations contradict his model. The idea that observations contradict a model in a meaningful way may be inconceivable. (Paul_K had a great analysis at the Blackboard showing Pinatubo data is most consistent with low climate sensitivity. Paul knows that that data is incompatible with the high climate sensitivity. However, that data could be inaccurate.)
http://www.gfdl.noaa.gov/blog/isaac-held/2014/08/02/49-volcanoes-and-the-transient-climate-response-part-i/
http://rankexploits.com/musings/2012/pinatubo-climate-sensitivity-and-two-dogs-that-didnt-bark-in-the-night/
Frank,
At the very least you need to run a one dimensional radiative/convective model before you blithely assert how much latent heat transfer will change with increasing temperature. Latent heat transfer can be estimated by global precipitation, so you’re assuming that precipitation will increase by about 6%/K. However, according to the IPCC FAR:
Here’s an article on measure the Earth’s albedo which includes a graph of the albedo anomaly from 3/1/2000 to 12/31/2011.
http://earthobservatory.nasa.gov/IOTD/view.php?id=84499
DeWitt (and Mike): For observational evidence that evaporation/precipitation has been rising at 7%/K or higher, see
Frank J. Wentz, et al. Science 317, 233 (2007);
DOI: 10.1126/science.1140746
http://
images.remss.com/papers/rsspubs/Wentz_Science_2007_more_rain.pdf
Climate models and satellite observations both indicate that the total amount of water in the atmosphere will increase at a rate of 7% per kelvin of surface warming. However, the climate models predict that global precipitation will increase at a much slower rate of 1 to 3% per kelvin. A recent analysis of satellite observations does not support this prediction of a muted response of precipitation to global warming. Rather, the observations suggest that precipitation and total atmospheric water have increased at about the same rate over the past two decades.
Also see http://journals.ametsoc.org/doi/full/10.1175/2007JCLI1714.1
Yu (2006)
Global estimates of oceanic evaporation (Evp) from 1958 to 2005 have been recently developed by the Objectively Analyzed Air–Sea Fluxes (OAFlux) project at the Woods Hole Oceanographic Institution (WHOI). The nearly 50-yr time series shows that the decadal change of the global oceanic evaporation (Evp) is marked by a distinct transition from a downward trend to an upward trend around 1977–78. Since the transition, the global oceanic Evp has been up about 11 cm yr1 (10%), from a low at 103 cm yr1 in 1977 to a peak at 114 cm yr1 in 2003. The increase in Evp was most dramatic during the 1990s. The uncertainty of the estimates is about 2.74 cm yr1. By utilizing the newly developed datasets of Evp and related air–sea variables, the study investigated the cause of the decadal change in oceanic Evp. The decadal differences between the 1990s and the 1970s indicates that the increase of Evp in the 1990s occurred over a global scale and had spatially coherent structures. Larger Evp is most pronounced in two key regions—one is the paths of the global western boundary currents and their extensions, and the other is the tropical Indo-Pacific warm water pools. It is also found that Evp was enlarged primarily during the hemispheric wintertime (defined as the mean of December–February for the northern oceans and June–August for the southern oceans). Despite the dominant upward tendency over the global basins, a slight reduction in Evp appeared in such regions as the subtropical centers of the Evp maxima as well as the eastern equatorial Pacific and Atlantic cold tongues.
This is based on re-analysis data of observational data and theoretical expectations for how wind and humidity influence evaporation. AOGCMs rely on the same principles.
I need to see what the IPCC has said about this evidence concerning precipitation.
Your evidence says albedo didn’t change appreciably during “the pause”. I doubt that we can turn that into a number in terms of W/m2/K that is meaningfully different from 0. The slope is certainly less than a 0.1% decrease in albedo per decade which is 0.1 W/m2/decade. If warming were 0.1 K/decade during the Pause, we are talking about something on the order of 1 W/m2/K. This is in agreement with my opinion that a change in albedo can’t supply the 5 W/m2/K needed IF evaporation rises at the same rate as saturation vapor pressure.
There is nothing unusual in my conclusion; I’m simply presenting it from the a different perspective. Without “feedbacks” that suppress the “no-feedback” increase in evaporation rate, climate sensitivity must be low. In general, the consensus ignores this issue and the projection of a 1% increase in relative humidity over the oceans attract little discussion.
Frank,
AR5, Table 2.9, gives an increase in globally averaged precipitation of about 2 cm (very uncertain) for 1901-2008. So that would be a bit under 2% for a T change of maybe 0.8 K. Consistent with the numbers you quote for the models, but not the WHOI numbers.
You wrote: “Without “feedbacks” that suppress the “no-feedback” increase in evaporation rate, climate sensitivity must be low.”
OK, but without feedbacks, climate sensitivity IS low. So is there any contradiction here?
Frank,
Are you including the increase in DLR from an increase in temperature and humidity? MODTRAN for the tropical atmosphere at constant RH and zero altitude looking up shows 347.912 W/m² for zero temperature offset and 355.448 W/m² for a 1K increase. That’s an increase of 7.536 W/m². OLR at the surface goes from 417.306 to 422.33 or an increase of 5.02. So the surface sees a net increase of 2.5 W/m². And that’s just the water vapor feedback. Doubling CO2 adds another ~1.5 W/m² to the DLR.
That’s a quick and dirty calculation. I really should adjust the CO2 so that the OLR at the tropopause is equal to the value before adding CO2 and raising the surface temperature. That would lower the contribution from CO2 somewhat. A 1K increase requires an increase of 570ppmv CO2 to balance the OLR at the tropopause. Then DLR at the surface is 356.39 W/m² or an increase of 8.478 W/m² and a net of 3.46W/m².
Mike asked: “OK, but without feedbacks, climate sensitivity IS low. So is there any contradiction here?”
I’ve gotten too tricky with my language here. Most/all conventional feedbacks are changes that inhibit outgoing or enhance outgoing radiation. One could also look at lapse rate feedback as a factor that corrects for the fact that a lower lapse rate means the upper atmosphere will warm more than the surface. Therefore “Planck feedback” is calculated assuming that warming is equal at all altitudes.
Suppression of evaporation has nothing to do with transport of heat by radiation. It happens at the interface between the surface and the atmosphere. Do the feedbacks that interfere with OLR also interfere with evaporation?
The physics that controls evaporation are wind speed and undersaturation of the boundary layer. It would be interesting to know if relative humidity in the boundary layer over the oceans increases with SST. If transport out of the boundary layer slows with warming, relative humidity probably rises. To some extent, the need for such transport is greatest where it is warmest, as is the upper limit of convection (the tropopause). Wind speed also depends on the intensity highs and lows, which I also presume are dependent on vertical convection. I’ve seen data that wind speed increases with SST.
So, I think you are correct. The traditional radiative feedbacks that control radiative cooling from the upper troposphere (mostly water vapor) probably also determine if transport out of the boundary layer slows upon warming. In the real world, increasing SSTs are associated with stronger convection, and a higher, drier, colder tropopause. In climate models, GHG-mediated warming in the tropics is associated with less convection, higher humidity in the upper troposphere and a hot spot. I can’t decide which is correct.
OK, so to summarize the pieces scattered over many posts:
Postulate an increase in surface T and ask what happens to energy balance. Try assuming that boundary layer RH and wind speed stay constant (I will call this the “first guess”). Then net evaporation should increase in proportion to vapor pressure; I’m getting 6.4% /K at 288 K. That represents a large increase in net upward latent heat transfer. That must be balanced by other changes. Candidates are: (1) more upward IR out the top of the atmosphere, (2) less net upward sensible heat and IR at the surface, (3) less net evaporation than expected. I think the last is what Frank means by “suppression of evaporation”.
Both (1) and (2) certainly occur; the question is whether together they fully balance the first guess estimate of latent heat flux. Frank argues that they can’t. I am not so sure, especially given the very large water vapor induced change in DLR computed by DeWitt.
Frank wrote: “The physics that controls evaporation are wind speed and undersaturation of the boundary layer. It would be interesting to know if relative humidity in the boundary layer over the oceans increases with SST.”
If memory serves, AR5 states that boundary layer RH has remained pretty much constant as average global temperature has risen. I am pretty sure that is considered a robust result of both measurements and models (unlike free troposphere RH).
Frank wrote: “In the real world, increasing SSTs are associated with stronger convection, and a higher, drier, colder tropopause. In climate models, GHG-mediated warming in the tropics is associated with less convection, higher humidity in the upper troposphere and a hot spot. I can’t decide which is correct.”
It could be that both are correct. You’ve got to be really careful about correlation vs. causation here. The association of high SST with stronger convection etc. does not mean that high SST causes stronger convection. Both are associated with greater solar energy input. But in models, the changes are due to a different cause, so one might get different effects.
Mike and DeWitt: I agree with DeWitt that using MODTRAN would have been better than assuming DLR rises with surface temperature as a blackbody. I certainly agree that water vapor feedback will change DLR and that I didn’t account for it. Increasing WV lowers the effective emission altitude of DLR, thereby increasing DLR.
I don’t agree with DeWitt about doubling CO2. With an ECS of 3.7, a 1K increase in surface temperature would be driven by about 20% of a doubling, 400 ppm to 480 ppm. If ECS is 3.0, 1 K is about 25% of a doubling, or 400 ppm to 500 ppm. I used the latter in calculations below (1.25XCO2). The increase in DLR per degK of surface warming doesn’t change much (0.1-0.2 W/m2) whether warming is driven by rising CO2 or by some other factor (internal or solar, for example).
Above, I calculated that the net increase in radiative cooling from the surface was 0.5 W/m2/K. If I include water vapor feedback in MODTRAN and use the US Standard Atmosphere, the net is -0.1 to 0.1 W/m2/K (with or without clouds or 1.25XCO2). As the surface warms, DLR and OLR increase at nearly the same rate.
As DeWItt noted above, the tropics behave differently. Without clouds, DLR increases 2.6-2.7 W/m2/K faster than OLR and therefore provide about half of the heat needed to increase evaporation at 7%/K. However, as soon as you add clouds, the influence of water vapor feedback diminishes. Both clouds and water vapor compete to lower the effective emission altitude of DLR. I couldn’t figure out what clouds were best to use and ended up with average height stratus/stratocumulus somewhat by chance. If they are representative of tropical clouds, DLR increases only 0.5 W/m2/K faster than OLR and provides only 10% of the heat needed to increase evaporation at 7%K.
If half of tropical skies are cloudy, then maybe 30% of the needed heat comes from increasing DLR. (In the tropics, I probably should use 6%/K.) If half of all skies are tropical, then increasing DLR in the tropics contributes only 15% globally of the heat needed to increase evaporation at 7%/K.
Above, I said that total upward flux increases at 6.3 W/m2/K at the surface and only 1 W/m2/K at the TOA (for ECS = 3.7). These corrections lower 6.3 W/m2/K to about 4.8 W/m2/K. My conclusion STANDS that high climate sensitivity requires dramatic suppression of evaporation below the rate expected from the increase in saturation vapor pressure, but the numbers are different. (I presume the literature I cited convinced you of the need for suppression of evaporation even though you questioned my calculations. And, as always, I appreciate your comments.)
Removing water vapor feedback shows that my blackbody slab at 277 K emitting DLR wasn’t a great model. The real increase in net radiative cooling without water vapor feedback is 1.4-1.8 W/m2/K , not 0.5 W/m2.
Some notes on MODTRAN oddities below.
Assuming Blackbody Slab Emits DLR
T 278 K DLR 338.7 W/m2 T 289 K OLR 395.5 W/m2
T 277 K DLR 333.8 W/m2 T 288 K OLR 390.1 W/m2
Rate: DLR 4.9 W/m2/K OLR 5.4 W/m2/K
Net Rate OLR-DLR: 0.5 W/m2/K
Modtran US Standard atm no clouds
constant absolute humidity (no VW feedback)
T 289.2 K DLR 261.1 W/m2 OLR 365.2 W/m2
T 288.2 K DLR 258.2 W/m2 OLR 360.5 W/m2
Rate: DLR 2.9 W/m2/K OLR 4.7 W/m2/K
Net Rate OLR-DLR: 1.8 W/m2/K
Modtran US Standard atm no clouds
constant relative humidity (with WV feedback)
T 289.2 K DLR 263.0 W/m2 OLR 365.2 W/m2
T 288.2 K DLR 258.2 W/m2 OLR 360.5 W/m2
Rate: DLR 4.8 W/m2/K OLR 4.7 W/m2/K
Net Rate OLR-DLR: 0.1 W/m2/K
Modtran US Standard atm no clouds
1.25XCO2 + constant relative humidity (with WV feedback)
T 289.2 K DLR 264.0 W/m2 OLR 365.2 W/m2
T 288.2 K DLR 259.2 W/m2 OLR 360.5 W/m2
Rate: DLR 4.8 W/m2/K OLR 4.7 W/m2/K
Net Rate OLR-DLR: -0.1 W/m2/K
Modtran US Standard atm stratus/stratocumulus clouds
constant absolute humidity (no VW feedback)
T 289.2 K DLR 263.6 W/m2 OLR 365.2 W/m2
T 288.2 K DLR 358.9 W/m2 OLR 360.5 W/m2
Rate: DLR 4.7 W/m2/K OLR 4.7 W/m2/K
Net Rate OLR-DLR: 0 W/m2/K
Modtran US Standard atm stratus/stratocumulus clouds
constant relative humidity (with WV feedback)
T 289.2 K DLR 263.6 W/m2 OLR 365.2 W/m2
T 288.2 K DLR 258.9 W/m2 OLR 360.5 W/m2
Rate: DLR 4.7 W/m2/K OLR 4.7 W/m2/K
Net Rate OLR-DLR: 0 W/m2/K
Modtran Tropical atm no clouds
constant absolute humidity (no VW feedback)
T 300.7 K DLR 351.4 W/m2 OLR 442.2 W/m2
T 299.7 K DLR 347.9 W/m2 OLR 417.3 W/m2
Rate: DLR 3.5 W/m2/K. OLR 4.9 W/m2/K
Net Rate OLR-DLR: 1.4 W/m2/K
Modtran Tropical atm no clouds
constant relative humidity (with WV feedback)
T 300.7 K DLR 355.4 W/m2 OLR 442.2 W/m2
T 299.7 K DLR 347.9 W/m2 OLR 417.3 W/m2
Rate: DLR 7.5 W/m2/K OLR 4.9 W/m2/K
Net Rate OLR-DLR: -2.6 W/m2/K
Modtran Tropical atm no clouds
1.25XCO2 + constant relative humidity (with WV feedback)
T 300.7 K DLR 356.1 W/m2 OLR 442.2 W/m2
T 299.7 K DLR 348.5 W/m2 OLR 417.3 W/m2
Rate: DLR 7.6 W/m2/K OLR 4.9 W/m2/K
Net Rate OLR-DLR: -2.7 W/m2/K
Modtran Tropical atm stratus/stratocumulus clouds
1.25XCO2 + constant relative humidity (with WV feedback)
T 300.7 K DLR 423.3 W/m2 OLR 442.2 W/m2
T 299.7 K DLR 417.9 W/m2 OLR 417.3 W/m2
Rate: DLR 5.4 W/m2/K OLR 4.9 W/m2/K
Net Rate OLR-DLR: -0.5 W/m2/K
Modern doesn’t believe that the surface emits like a blackbody. OLR looking down from 0.001 and 0.01 km is 361.7 W/m2 at 288.2 K (US Standard). BB is 391.1 W/m2. Emissivity is only 92.5%. Looking down from 0.1 km. OLR rises to 362.4 W/m2 (92.6%) and begins falling above 0.15 km. Emissivity for the tropical sounding is 91%. (The values I cite for OLR above, except my calculations, were from MODTRAN looking down from 0.001 km. Assuming higher emissivity won’t cause an important change)
The lowest clouds – stratus (0.33 km) and nimbostratus (0.16 km) in a US Standard Atmosphere produce more DLR than OLR. For nimbostratus, the difference is 5.6 W/m2 and an emissivity of 95% if the cloud bottoms are 1 degK cooler than the surface.
I really wish MODTRAN had a “global setting” which would account for the fact that X% of the earth is tropical with clear skies, Y% tropical with cumulus clouds, Y’% with tropical stratus clouds, Z% with midlatitude clear skies, etc. These percentages must have been worked out at some point.
Frank,
The actual emissivity used for the surface in MODTRAN is 0.98. The reason it looks like less than that is that MODTRAN only integrates emission from 100-1500 cm-1. The emission from 0-100 and 1500→&inf; (I hope I got the symbols right) cm-1 account for the rest of the missing emission intensity. I’ve got a spreadsheet somewhere with the actual numbers calculated from the Planck equation, but I’m not interested in looking right now.
DeWItt: Thanks. I presume that estimates of both DLR and OLR are low for the same reason and therefore the difference between these two is reasonably accurate.
Frank,
That’s correct. The low and high frequency ends of the spectra are very close to the Planck equation because there’s little structure in the emissivity and are only slightly different with temperature.
Got one of them right, but not the other. 1500→∞
I checked out Mike’s reference to changes in precipitation in AR5. All estimates of the observed increase in global precipitation over the last century or half-century have large errors. Some show precipitation increasing for the century and decreasing for the last half-century.
Section 12.4.1.1 discusses projected changes in precipitation (and temp):
“The processes that govern global precipitation changes are now well understood and have been presented in Section 7.6. They are briefly summarized here and used to interpret the long-term projected changes. The precipitation sensitivity (about 1 to 3% °C–1) is very different from the water vapour sensitivity (~7% °C–1) as the main physical laws that drive these changes also differ. Water vapour increases are primarily a consequence of the Clausius–Clapeyron relationship associated with increasing temperatures in the lower troposphere (where most atmospheric water vapour resides). In contrast, future precipitation changes are primarily the result of changes in the energy balance of the atmosphere and the way that these later interact with circulation, moisture and temperature (Mitchell et al., 1987; Boer, 1993; Vecchi and Soden, 2007; Previdi, 2010; O’Gorman et al., 2012). Indeed, the radiative cooling of the atmosphere is balanced by latent heating (associated with precipitation) and sensible heating. Since AR4, the changes in heat balance and their effects on precipitation have been analyzed in detail for a large variety of forcings, simulations and models (Takahashi, 2009a; Andrews et al., 2010; Bala et al., 2010; Ming et al., 2010; O’Gorman et al., 2012; Bony et al., 2013).
Global precipitation sensitivity estimates from observations are very sensitive to the data and the time period considered. Some observational studies suggest precipitation sensitivity values higher than model estimates (Wentz et al., 2007; Zhang et al., 2007), although more recent studies suggest consistent values (Adler et al., 2008; Li et al., 2011b).
Zhang, X. B., et al., 2007: Detection of human influence on twentieth-century
precipitation trends. Nature, 448, 461–U464.
Wentz, F., L. Ricciardulli, K. Hilburn, and C. Mears, 2007: How much more rain will global warming bring? Science, 317, 233–235.
Li, L., X. Jiang, M. Chahine, E. Olsen, E. Fetzer, L. Chen, and Y. Yung, 2011b: The recycling rate of atmospheric moisture over the past two decades (1988–2009). Environ. Res. Lett., 6, 034018.
Adler, R. F., G. J. Gu, J. J. Wang, G. J. Huffman, S. Curtis, and D. Bolvin, 2008: Relationships between global precipitation and surface temperature on interannual and longer timescales (1979–2006). J. Geophys. Res., 113, D22104.
Section 7.6.3. Radiative Forcing of the Hydrological Cycle
In the absence of a compensating temperature change, an increase in well-mixed GHG concentrations tends to reduce the net radiative cool- ing of the troposphere. This reduces the rainfall rate and the strength of the overturning circulation (Andrews et al., 2009; Bony et al., 2013), such that the increase in global mean precipitation would be 1.5 to 3.5% °C–1 due to temperature alone but is reduced by about 0.5% °C–1 due to the effect of CO2 (Lambert and Webb, 2008). The dynamic effects are similar to those that result from the effect of atmospheric warming on the lapse rate, which also reduces the strength of the atmospheric overturning circulation (e.g., Section 7.6.2), and are robustly evident over a wide range of models and model configurations (Bony et al., 2013; see also Figure 7.20). These circulation changes influence the regional response, and are more pronounced over the ocean, because asymmetries in the land-sea response to changing concentrations of GHGs (Joshi et al., 2008) amplify the maritime and dampen or even reverse the terrestrial signal (Wyant et al., 2012; Bony et al., 2013).
The dependence of the intensity of the hydrological cycle on the tropospheric cooling rate helps to explain why perturbations having the same RF do not produce the same precipitation responses. Apart from the relatively small increase in absorption by atmospheric water vapour, increased solar forcing does not directly affect the net tropospheric cooling rate. As a result the hydrological cycle mostly feels the subsequent warming through its influence on the rate of tropospheric cooling (Takahashi, 2009). This is why modeling studies suggest that solar radiation management (geoengineering) methods that maintain a constant surface temperature will lead to a reduction in globally averaged precipitation as well as different regional distributions of precipitation (Schmidt et al., 2012b; Section 7.7.3).
Above, I showed that high climate sensitivity requires that the rate of evaporation increase with surface temperature much less than saturation vapor pressure (7%/K). If relative humidity also increases at 7%/K, same the same thing about changes in relative humidity and evaporation. The rate (R) at which water is returned from the atmosphere to the earth is simply the precipitation rate (R) divided by the total column water vapor and at steady state P = E (evaporation).
and at steady state P = E (evaporation).
R = P/W = E/W
This is the formula that tell us that the average water molecule remains in the atmosphere for about 9 days. R is a measure of “hydraulic intensity” or the rate at which the atmosphere is being turned over by convection.
If we take the derivative of this formula and do a little algebra, we find:
(dR/dt)/R = (dP/dt)/P – (dW/dt)/W = (dE/dt)/E – (dW/dt)/W
If you integrate over at period of time (or multiply both sides by dt)
dR/R = dP/P – dW/W = dE/E – dW/W
where dR is now deltaR, not an infinitesimal. dR/R, dP/P, dE/E and dW/W are the percentage change in R, P, E, and W.
If relative humidity remains constant, then dW/W is 7%/K. If temperature is rising at a rate of 0.14 K/decade, then dW/W is 1% a decade. If dE/E is much less than dW/W, then the rate at which the atmosphere is being turned over by convection must go down. This slow down is not an incidental side effect of global warming – if is a mathematical requirement for high climate sensitivity. (As noted above, a decrease in albedo can reduce the needed slow down, but probably not eliminate it.)
Therefore, the reliability of climate sensitivity from AOGCMs depends on how well they deal with convection and precipitation and whether these processes -which occur on scales smaller than grid cells – are accurately represented.
Current grid cells are about 100×100 km. If precipitation everywhere within that area is relatively uniform, then the model is capable of reproducing it in detail. That is often true in the mid-latitude in winter, but not summer; and is rarely true in the tropics and where the terrain is uneven (mountains, coasts). If you look at weather radar which shows areas of “rain” (cloud top temperature?), you can see how much convection and precipitation vary across a grid cell.
Frank,
“Therefore, the reliability of climate sensitivity from AOGCMs depends on how well they deal with convection and precipitation and whether these processes -which occur on scales smaller than grid cells – are accurately represented.”
Yes, and in a nutshell why climate models are useless for climate prediction. I thought current grid cells have gotten down to 10 km x 10 km, but I could be wrong. In all likelihood you would need something down to more like 1 cm x 1 cm, and even then it would require the models to be objective and not arbitrarily adjusted or ‘tuned’.
Surely, the hydrological cycle of surface water –> evaporation –> clouds –> precipitation –> surface water is the underlying mechanism or physical process that maintains the energy balance, i.e. a stable global average despite the random dynamic chaos associated with weather. But how does it work and how can we discern it amongst all the short term noise and chaos?
‘Guru’ George White’s work on feedback analysis supports Lindzen’s work on climate sensitivity, and he even derives the same feedback factor of around 0.7C per 3.7 W/m^2 of forcing as Lindzen does.
Regarding Lindzen’s analysis where they get a fairly strong net negative feedback back in the tropics, which is then weakened when ‘shared’ with the whole globe:
This is supported by George White’s analysis of the data above, which is the net radiative cooling effect of clouds is strongest in the tropics and gets progressively weaker as you head out of the tropics toward the poles, and where eventually the net radiative effect of clouds actually becomes warming as you cross the 0C surface temperature threshold (which is roughly where the surface is or is not snow/and or ice covered).
*Note that the inflection point around 0C is where the net effect of increasing/decreasing clouds switches from cooling to warming and warming to cooling. That this inflection point is roughly where the surface reflectivity, due to the presence or not of snow and ice, clearly indicates why the net effect of clouds changes in response to a change in surface reflectivity. Above about 0C, the average net effect of clouds is to cool, i.e. more solar energy is reflected than is delayed beneath the clouds, where as below about 0C, the average net effect of clouds is to warm, i.e. more solar energy is delayed beneath than is reflected away in total (due to the reflectivity of snow and ice being about the same as the clouds.
Water vapor saturation occurs in the tropics, where the combination of cloud caused cooling (from solar reflection) and evaporative caused cooling of the surface is so strong it effectively prevents the surface temperature from ever exceeding about 300K over the oceans, no matter how much atmospheric water there is. Note there is nearly a full 3 cm range where there is virtually no difference in surface temperature, and in fact in both hemispheres, if anything the high point of the range is slightly cooler even than the preceding concentrations below it (i.e. it curls back the other way a bit).
*Note at approximately the same point that the clouds start to increase again (above 0C) in the prior above plot is also where increased water concentration in the above plot no longer results in further rise in temperature. The fundamental physical mechanism(s) behind this is beyond a certain temperature there is so much water being evaporated, removing so much heat from the surface (as the latent heat of evaporation), providing so much ‘fuel’ (i.e. water) for cloud formation, that the combination of cloud caused (from solar reflection) and evaporative caused cooling overwhelms any increase in atmospheric IR opacity from increased water vapor.
While the first plot of surface temperature to cloud amount doesn’t establish causation in either direction, it establishes that above about 0C when there are more clouds on monthly average per grid area, it tends to be cooler, and when there are fewer clouds, it tends to be warmer. This relationship becomes even more pronounced as you get closer and closer to the tropics where eventually water saturation occurs. Where as, below about 0C, when there are more clouds, it tends to be warmer, and when there are fewer clouds it tends to be cooler.
When you consider that the vast majority of energy from the Sun arrives in the area of about 23N to 23S, i.e. the tropics, and the least amount arrives in the area of above 63N and below 63S, i.e. the frigid zone, where much of the surface is snow and/or ice covered, it’s of little consequence that the net effect radiative effect of clouds is to warm in these areas. Moreover, if anything, in a warming world there would be less snow and ice.
This analysis is completely consistent with the validity Lindzen is claiming in extrapolating from the tropics to the poles, and the net feedback of clouds and water vapor operating in the subtropics and further out would only somewhat lessen the strength measured in the tropics.
Trying to model the climate as what is essentially the chaos of weather is useless. This is because climate change is fundamentally a change in the average steady-state surface temperature of the system. The short term behavior and net effect of clouds and water vapor is largely chaotic and unpredictable, where as if you look at the long term averages, a clear pattern of net average behavior emerges. The idea is the plots provide the average net dynamics of clouds and water vapor (albeit separated by hemisphere), and which is what is applicable for how the average dynamics would change in response to climate change.
*For the satellite data plots, each small dot represents a monthly average for one grid area for a 2.5 degree slice of latitude. The green and blue dots are the 25 year averages for each 2.5 degree slice of latitude (1983-2008). From right to left, it goes from the tropics to the poles.
RW wrote: “Surely, the hydrological cycle of surface water –> evaporation –> clouds –> precipitation –> surface water is the underlying mechanism or physical process that maintains the energy balance, i.e. a stable global average despite the random dynamic chaos associated with weather.”
It is always a temptation to believe that surface temperature is controlled by convection. And wrong.
The global energy balance is determined at the TOA, the only place energy can enter and leave our planet. The distribution of heat (provided by net radiation) between the upper and lower atmosphere and the surface is controlled by the lapse rate.
As the earth warms (or cools), it emits more (or less) OLR to space which we can quantify in terms of W/m2 per degK of surface warming or simply W/m2/K. As temperature changes, clouds may reflect more (or less) SWR to space, which can be combined with the change in OLR to produce the climate feedback parameter (also in terms of W/m2/K). The reciprocal of the climate feedback parameter is called the effective climate sensitivity, quantified in terms of K/(W/m2) and usually multiplied by 3.7 W/m2/doubling to give K/doubling. If we work backwards from an ECS of 3.7 W/m2/doubling, we get a climate feedback parameter of 1 W/m2/K. This means that the earth emits or reflects only an addition 1 W/m2 when surface temperature rises – whether due to internal variability, an increase in solar output or rising GHGs. To maintain a stable state, the warming surface of the earth must transfer only 1 W/m2/K more heat to the atmosphere.
If the increase in evaporation/precipitation were proportional to the increase in saturation vapor pressure, about 5.5 W/m2/K more heat would be transferred from the surface to the atmosphere. Unfortunately, evaporation at the surface can’t “push” heat into space. Only radiation transfers heat to space and that rate depends on the temperature and composition of the upper atmosphere. Latent heat can’t become high temperature until air rises and water vapor condenses, and the air won’t rise until the upper atmosphere has radiatively cooled enough to produce an unstable lapse rate and convection.
Evaporation can’t lower climate sensitivity – but the increase in evaporation with warming and ECS are mathematically linked to each other.
Frank,
“It is always a temptation to believe that surface temperature is controlled by convection. And wrong.”
By convection alone — no, of course not. Convection via evaporation is the source of atmospheric water, which is what condenses to form clouds. The underlying mechanism is how this process of cloud formation dynamically modulates incoming solar energy into the system to maintain a steady global average surface energy balance, despite being so chaotic an unpredictable in the short term.
“As temperature changes, clouds may reflect more (or less) SWR to space,”
Yes, because clouds are changing or varying for reasons other than just temperature changes, and different type of clouds have different net radiative effects. This would appear to make the problem ultra complex to understand and solve.
Notice in the plots I referenced above that it only includes the total cloud amounts with no breakdown of the proportions of the types of clouds that make up the total amount? For each grid area monthly average sample (the small orange dots). This is very significant.
Take a look at these gain plots from the same data set:
Do you see how, for the data averaged over 25 years, as the energy from the Sun increases and the surface temperature increases, the total cloud coverage increases, and as energy from the Sun decreases and the surface temperature decreases, the cloud coverage decreases? And as the energy and temperature increases, the gain decreases below its average and vice versa?
In this plot from before:
What is the relationship between surface temperature and cloud amount? The overall pattern is, above about 0C, the more cloud covered surface there is, the cooler it tends to be, and the less cloud covered surface there is, the warmer it tends to be (on monthly average per grid area).
The supports that the underlying mechanism that maintains the energy balance is increasing clouds coverage on the whole causes cooling, i.e. more solar energy is reflected back out into space than is delayed, and decreasing cloud coverage causes cooling, i.e. more solar energy is absorbed than exits to space. These two counter balancing mechanisms dynamically maintain the energy balance of the surface.
Note: the relationship below around 0C, which is also roughly where the surface becomes snow and/or ice covered, is the opposite. That is, the more clouds there are, the warmer it tends to be, and the few clouds there are the cooler it tends to be. This is because the reflectivity of clouds and that of snow and ice are roughly the same, but clouds are substantially better IR absorbers than the clear or cloudless sky is. And if there is no Sun, clouds still warm for the same reason.
The advantage of this approach is the use of long term averages (multiple decades). This is because climate change is fundamentally a change in the average steady-state surface temperature of the system. The short term behavior and net effect of clouds and water vapor is largely chaotic and unpredictable, where as if you look at the long term averages, a clear pattern of net average behavior emerges. The idea is the plots provide the average net dynamics of clouds and water vapor (albeit separated by hemisphere), and which is what is applicable for how the average dynamics would change in response to climate change.
As I said, this analysis of the data I’ve outlined is completely consistent with the results Lindzen is getting looking at tropical data (and then extrapolating to the poles) in his latest 2011 paper with Choi, where they get a fairly strong net negative feedback in the tropics which then becomes weaker when ‘shared’ over the globe.
RW: I’m interested in the relationship between surface temperature and cloud cover, but some of you plots are misleading.
Surface temperature does mostly fall between 220 and 310 K, but I don’t pay much attention to anything below about 270 K. Anything below represents only a small fraction the surface of the earth and an even smaller fraction of the heat flux. The tropics – a little less than half of the surface and probably more than half of the heat flux is that blob around 300 K, where there is no apparent relationship between Ts and cloud cover.
The tropics also complicates the relationship between seasonal changes in albedo and surface temperature. Your figure shows clouds increasing with hemispheric warming, but that doesn’t mean that clouds increase outside the tropics where the warming occurs. The ITCZ moves north and south with the seasons, but those seasonal changes aren’t associated with much warming. And the ITCZ is not symmetrically located with respect to the equator. Nor is land/ocean. I’m interested whether seasonal warming is associated with an increase or decrease in cloud cover and/or albedo. That would suggest whether cloud feedback is positive or negative. However, I do need to see something more sophisticated that considering a whole hemisphere at one time.
Linden showed only that feedback is negative in the tropics during rapid warming and cooling in the tropics associated with major El Nino and La Nina events. An El Nino event is not global warming. Seasonal warming in one hemisphere and cooling in the other is also not global warming. Both are good models for proving that AOGCMs do a poor job of reproducing the feedbacks associated with these phenomena. Neither is a good model for the climate feedback parameter (1/ECS) associated with global warming.
Frank,
“RW: I’m interested in the relationship between surface temperature and cloud cover, but some of you plots are misleading.
Surface temperature does mostly fall between 220 and 310 K, but I don’t pay much attention to anything below about 270 K. Anything below represents only a small fraction the surface of the earth and an even smaller fraction of the heat flux.”
Yes, this is why the net average radiative effect of clouds being to warm below about 273K doesn’t matter much relative to the whole.
The tropics – a little less than half of the surface and probably more than half of the heat flux is that blob around 300 K, where there is no apparent relationship between Ts and cloud cover.”
But there is, and that is as the average cloud cover increases as you get into the tropics note that the surface temperature quickly comes to a hard upper limit of around 300K (and even curls back the other way a little in the northern hemisphere). This is point at which the combination of cloud caused cooling (from solar reflection) and evaporative caused cooling is so strong it prevents the Sun from heating the surface (at least where there is water) beyond about 300K.
“The tropics also complicates the relationship between seasonal changes in albedo and surface temperature. Your figure shows clouds increasing with hemispheric warming, but that doesn’t mean that clouds increase outside the tropics where the warming occurs. The ITCZ moves north and south with the seasons, but those seasonal changes aren’t associated with much warming. And the ITCZ is not symmetrically located with respect to the equator. Nor is land/ocean. I’m interested whether seasonal warming is associated with an increase or decrease in cloud cover and/or albedo. That would suggest whether cloud feedback is positive or negative.”
Here are more regional specific plots from the same data set:
http://www.palisad.com/co2/plots/wbg/plots.html
It’s important to keep in mind that the overwhelming amount of absorbed solar energy entering the system occurs in the tropics. Something like 2/3rds or more I believe. Global warming is essentially a further extension of the tropics towards the poles and a shrinkage of the poles (or the so-called ‘frigid zone’)
“However, I do need to see something more sophisticated that considering a whole hemisphere at one time.”
Why? The data shows there is virtually no net exchange of absorbed solar energy across the equator, and this is fully expected since the 2nd law says energy flows from hot to cold and not the other way around.
“Linden showed only that feedback is negative in the tropics during rapid warming and cooling in the tropics associated with major El Nino and La Nina events. An El Nino event is not global warming.”
Why not? Moreover, why and/how could the feedback mechanisms distinguish one from the other? They respond to the temperature change, independent of the cause.
“Seasonal warming in one hemisphere and cooling in the other is also not global warming.”
No, but it does clearly show that the net feedback acting on the seasonal changes in solar flux is not only negative, but gets stronger and stronger negative the higher the temperature and incident solar energy goes. The sign of the measured feedback is independent of the time rate of response, so it doesn’t matter that the changes never reach equilibrium. Note the gain is 180 degrees out of phase with the incident solar energy, which is the universal signature of the system whose net feedback is negative.
“Both are good models for proving that AOGCMs do a poor job of reproducing the feedbacks associated with these phenomena. Neither is a good model for the climate feedback parameter (1/ECS) associated with global warming.”
It’s important to note that Lindzen doesn’t claim there are not any positive feedbacks acting outside the tropics (clouds or otherwise), only that the feedback measured in the tropics is that which is dominant for the whole. Moreover, when he shares the feedback measured from the tropics with the whole, it is (appropriately) weakened — not strengthened.
You’re making an assertion that specific humidity and precipitation are linearly correlated. I don’t think I’ve seen any evidence that’s true. It could also be true that at constant RH, the precipitation rate doesn’t change or changes at a rate less than the specific humidity. P=E at steady state is a truism. The expected lifetime of a water molecule in the atmosphere, however, is not necessarily a constant.
Frank wrote: “Therefore, the reliability of climate sensitivity from AOGCMs depends on how well they deal with convection and precipitation and whether these processes -which occur on scales smaller than grid cells – are accurately represented.”
Closely related to that are clouds, which the models deal with via unproven parameterizations. They don’t seem to be very good, since comparisons of modeled cloud radiative effects with observations are terrible. So if they can’t model the present, why should we believe their projections of the future? High climate sensitivity (ECS greater than about 2 K) requires positive cloud feedbacks. AR5 says (in section 7.2.5.1) they have “high confidence in a positive feedback contribution from increases in high-cloud altitude”. That seems to be the most certain of the cloud feedbacks. And they say in the same section “observed cloud height trends do not appear sufficiently reliable to test this cloud-height feedback mechanism”. So it seems there is no observational evidence for the various feedbacks.
So far as I can tell, there is no actual scientific evidence in favor of high climate sensitivity. That does not prove that sensitivity is not high, but there is observational evidence for low sensitivity. And there seems to be some weak evidence for Lindzen’s ‘iris effect’, which is a negative cloud feedback not in the models.
Also, thank to Frank for the earlier excerpts on model precipitation.
Bryan:
I looked at the plots regional plots you linked at:
http://www.palisad.com/co2/plots/wbg/plots.html
The key parameters are % cloud cover and reflectivity in the SWR channel and % cloud cover and emissivity/cloud top temperature in LWR channel.
In the NH, there are fewer clouds (“cloud amount”) in the summer – positive feedback (amplification) and less “cloud reflect” which could mean several different things but probably imply positive feedback. “Cloud temp” rises with surface temperature. If cloud tops are higher in the summer, they aren’t high enough to be colder than in winter.
In the SH, the opposite is true: There are more clouds and reflection in the summer – negative feedback. As in the NH, “Cloud temp” rises with surface temperature. If cloud tops are higher in the summer, they aren’t high enough to be colder than in winter.
In the tropics, there are big seasonal changes. More clouds when it is warmer. (negative feedback), but also colder cloud tops when it is warmer (positive feedback).
The IPCC tends to focus on what climate models project for cloud feedback in response to global warming. It is interesting to see if clouds respond in similar way to regional seasonal warming as the IPCCs models predict. The most interesting test would be to see if AOGCMs reproduce these seasonal changes in clouds.
Seasonal warming or ENSO warming aren’t ideal models for global warming. Global warming will be greatest in the Arctic, not the equator. Seasonal warming means one hemisphere is warming will the other is cooling, rather than both warming at one time. If AOGCMs do a good job of predicting regional seasonal changes in cloud cover, height and reflectivity, maybe they can be trusted to represent cloud feedback in global warming.
Frank,
“I looked at the plots regional plots you linked at:
http://www.palisad.com/co2/plots/wbg/plots.html
The key parameters are % cloud cover and reflectivity in the SWR channel and % cloud cover and emissivity/cloud top temperature in LWR channel.
In the NH, there are fewer clouds (“cloud amount”) in the summer – positive feedback (amplification) and less “cloud reflect” which could mean several different things but probably imply positive feedback. “Cloud temp” rises with surface temperature. If cloud tops are higher in the summer, they aren’t high enough to be colder than in winter.
In the SH, the opposite is true: There are more clouds and reflection in the summer – negative feedback. As in the NH, “Cloud temp” rises with surface temperature. If cloud tops are higher in the summer, they aren’t high enough to be colder than in winter.”
Where do you see this? In both hemispheres, there is more cloud coverage in their corresponding summers than in their winters. That is, cloud coverage increases from January to July in the NH and increases from July to January in the SH.
The most important relationship to observe is that in each hemisphere the gain is 180 degrees out of phase with the incident solar flux, and the data shows there is little to no net exchange of absorbed solar energy from one hemisphere to the other. Which means they are mostly responding independently to one another, making them a good (albeit somewhat rough) measure of the net feedback acting on the system as a whole.
Do you know and/or understand that climate sensitivity can be directly expressed as dimensionless gain in W/m^2? The global average or absolute gain is around 1.6, i.e. the surface at around 287K emits 385 W/m^2 in order to offset the incoming post albedo solar flux of around 239 W/m^2 (385/239 = 1.6). The global average gain of about 1.6 is equivalent to the ‘zero feedback’ parameter of about 3.3 W/m^2 at the TOA per 1C of warming, i.e. +1C = +5.3 W/m^2 of surface radiation, and 5.3/1.6 = 3.3. An incremental gain in response to an imposed imbalance less than 1.6 indicates net negative feedback and an incremental gain above 1.6 indicates net positive feedback.
The average gain in the hemispheres is 1.7 and 1.8, which is very close to the global average of around 1.6. In standard control theory and systems analysis, sensitivity to some stimuli is always quantified as a dimensionless gain of output divided by input, but climate science has more or less made up its own rules and metric for quantifying sensitivity to muddy the waters.
There is a lot more detail on a lot of this here, which maybe you have seen (or maybe not). I can’t remember:
http://www.palisad.com/co2/eb/eb.html
No one here seems to be able to understand this kind of analysis at all, which I find bizarre. This is the kind of analysis one would use to reverse engineer and unknown, but measurable system.
Mind you, a sensitivity of 3.3C per 3.7 W/m^2 of forcing (the IPCC’s best estimate) requires a gain of 4.8, i.e. +3.3C = +18 W/m^2 of net surface gain and 18/3.7 = 4.8.
Frank wrote: In the SH, the opposite is true: There are more clouds and reflection in the summer – negative feedback. As in the NH, “Cloud temp” rises with surface temperature. If cloud tops are higher in the summer, they aren’t high enough to be colder than in winter.”
Bryan asked: Where do you see this? In both hemispheres, there is more cloud coverage in their corresponding summers than in their winters. That is, cloud coverage increases from January to July in the NH and increases from July to January in the SH.
Frank replies: See albedo graphs S MID MONTH ALBEDO, “cloud amount” line. Actually it has two maxima and two minima a year, with the lowest in Jun and Jul (winter).
Bryan wrote: “The most important relationship to observe is that in each hemisphere the gain is 180 degrees out of phase with the incident solar flux, and the data shows there is little to no net exchange of absorbed solar energy from one hemisphere to the other. Which means they are mostly responding independently to one another, making them a good (albeit somewhat rough) measure of the net feedback acting on the system as a whole.”
Frank: Without the formula used to calculate gain, I haven’t tried to interpret this curve. (I don’t have experience in signal processing and electronics, so I need to see the equations.) I also don’t see what proves there is little to no transport of energy across the equator, though I suspect little is.
Bryan: Do you know and/or understand that climate sensitivity can be directly expressed as dimensionless gain in W/m^2?
Frank: W/m2 is not a dimensionless ratio. Climate sensitivity doesn’t appear to be a dimensionless ratio either, but can be dimensionless with some caveats. The usual units are K/doubling, but you can divide by 3.7 W/m2/doubling to get K/(W/m2). Heat capacity (J/m3 or J/kg*kg/m3) is the factor that allows one to convert a change in energy (J) into a change in temperature. Watts are J/s, so you need to multiply by time (s). During climate change, the radiative imbalance gradually shrinks over time and eventually approaches zero, so we do the multiplication by integrating/summing W(t)*dt from t=0 to t=equilibrium. (Sorry about the calculus.) To complete the dimensional analysis, we have W/m2 and J/m3 and we need to know the depth (m) of the material being warmed so we can calculate W/m3. For some problems (but not ECS), depth is the depth of the mixed layer near the surface that warms seasonally (within several months), about 50 m.
So, if you specify a:
1) TIME – traditionally long enough to reach equilibrium and reduce the imbalance at the TOA to zero – and
2) DEPTH – with different amounts of warming at different depths we need to do another integration/summation here –
then ECS is dimensionless (:)).
At WUTW, Willis regularly complains that large volcanoes (say a peak forcing near -3.7 W/m2, similar in magnitude but opposite direction compared with 2XCO2) don’t produce 3 K of cooling. Volcanic forcing doesn’t last long enough to reach equilibrium. Watt*time is energy and energy is proportional temperature. Watts alone are proportional to a RATE of temperature change (dT/dt).
Bryan: “No one here seems to be able to understand this kind of analysis at all, which I find bizarre. This is the kind of analysis one would use to reverse engineer and unknown, but measurable system.”
I haven’t read (or retained) much of what George White has written, but it doesn’t make sense to me to underestimate what some commenters at this blog understand. (Nor does it make sense to assume they are motivated by anything besides generous sharing of experience.) Info that passes through you is often distorted.
You sometimes talk about the 1.6:1 dimensionless ratio of surface OLR (390 W/m2) to TOA OLR (240 W/m2). This is a measure of the greenhouse effect. The difference (150 W/m2) is also a measure of the greenhouse effect. AFAIK, there is no advantage to presenting this information in dimensionless terms.
Frank,
Engaging with RW (not Bryan) is a waste of time.
Frank,
I only have time at the moment for a quick reply, but the formula for the gain is just Psurf/Pi, where Psurf is the surface radiated flux density in W/m^2 according to the measured surface temperature (dictated by S-B) and Pi is the post albedo solar input flux density in W/m^2.
A ratio of W/m^2/W/m^2 is of course dimensionless. Climate sensitivity can be directly quantified in this way, whether the net feedback is positive or negative (real or unreal), and has the exact same physical meaning as when sensitivity is quantified in degrees C per W/m^2 of forcing, as climate science does.
It is (or should be) easy to see this. Take for example a sensitivity of 3.3C per 3.7 W/m^2 of forcing (the IPCC’s supported best estimate). If the surface, from a baseline temperature of around 287K, is to increase by 3.3C it will radiate about an additional 18 W/m^2, which corresponds to a dimensionless gain of about 4.8, i.e. 18/3.7 = 4.8. 4.8 is greater than the absolute gain of 1.6 (385/239 = 1.61), indicating net positive feedback (of around 300%). On the other hand, a sensitivity of 0.8C from a forcing of 3.7 W/m^2 corresponds to gain of only about 1.16, i.e. 4.3/3.7 = 1.16, which is less than the absolute gain of 1.6, indicting net negative feedback (of about -30%).
The absolute gain of 1.6 is equivalent to the ‘zero-feedback’ measure at the TOA of 3.3 W/m^2 per 1C of warming, i.e. +1C equals about +5.3 W/m^2 of surface radiation, and 5.3 W/m^2/1.6 = 3.3 W/m^2.
Frank,
“Frank replies: See albedo graphs S MID MONTH ALBEDO, “cloud amount” line. Actually it has two maxima and two minima a year, with the lowest in Jun and Jul (winter).”
I thought you were looking at the full hemispheres. Yes, I see that, but the minimum still occurs at mid winter.
” I also don’t see what proves there is little to no transport of energy across the equator, though I suspect little is.”
The data only shows a small net flux into the southern hemisphere I believe, which is consistent since the SH is slightly cooler on average than the NH. The key word is *net* energy transfer. No doubt there is some energy transfer/movement across the equator due to weather systems at least.
GW also cites (in the paper): “Another indication of the independent hemispheric response is the nearly linear sinusoidal relationship between the output variables, energy flux and surface temperature, and the sinusoidal incident solar energy. This would not be the case if there was a substantial energy flux flowing between hemispheres, where each hemisphere’s response would exhibit some signature of the other and be equal in magnitude.”
Which does seem logical to me. The key point is there are responding mostly independently to one another, making them a good test and/or measure of whether the net feedback acting on the system is positive or negative.
But you must understand what he’s quantifying as gain, and that the gain in the plots is directly measured with no assumption of mechanism whatsoever.
Above all, the gain is just output/input and is just the most basic engineering measure of the response or sensitivity of something to some stimuli. For the climate system, the input is around 239 W/m^2 of post albedo solar power and the output (based on all of the effects, radiant and non-radiant, known and unknown) is around 385 W/m^2 of radiant black body power emitted from the surface, i.e. the absolute gain of the system is around 1.6 (385/239 = 1.61).
If you can’t see and fully understand this, then there is no way you can understand and evaluate his analysis.
“I haven’t read (or retained) much of what George White has written, but it doesn’t make sense to me to underestimate what some commenters at this blog understand. (Nor does it make sense to assume they are motivated by anything besides generous sharing of experience.) Info that passes through you is often distorted.”
The only thing in there I know that overtly conflicts with what commenters here ‘understand’ is GW’s claim that the 3.7 W/m^2 calculated per 2xCO2 is only equal to about half that (1.85 W/m^2) of post albedo solar power entering the system in its *intrinsic* ability to act to ultimately further warm the surface. Or that so-called GHG ‘forcing’ is only equal to about half of the 3.7 W/m^2. We’ve discussed that ad nauseam here and no one understands why or how he’s deducing/calculating that, and/or vehemently disagrees. So be it.
I think you would agree that the notion of the net feedback being negative due to clouds is not an extraordinary claim, as most everyone in the field knows and/or agrees its easily possible (if not probable). In the end, that’s one of the main things he claims his analysis shows.
RW wrote: Above all, the gain is just output/input and is just the most basic engineering measure of the response or sensitivity of something to some stimuli. For the climate system, the input is around 239 W/m^2 of post albedo solar power and the output (based on all of the effects, radiant and non-radiant, known and unknown) is around 385 W/m^2 of radiant black body power emitted from the surface, i.e. the absolute gain of the system is around 1.6 (385/239 = 1.61). If you can’t see and fully understand this, then there is no way you can understand and evaluate his analysis.
Frank replies: A gain is one way of quantifying the greenhouse effect from our current atmosphere. 390-240=150 W/m2 is another. Both of these measures are flawed because the earth would not emit or absorb 240 W/m2 without any GHGs because the planet would be much colder and have a different albedo and humidity. So, none of these numbers tells us how radiative transfer transfer will change when CO2 doubles in the future; radiative transfer calculations such as MODTRAN do. These calculations are based on real physics, not ad hoc extrapolations from ratios or differences
RW wrote: I think you would agree that the notion of the net feedback being negative due to clouds is not an extraordinary claim, as most everyone in the field knows and/or agrees its easily possible (if not probable). In the end, that’s one of the main things he claims his analysis shows.
Frank replies: IMO, anyone who thinks they know that cloud feedback is negative OR positive is probably over-confident. The complications are enormous: changing cloud top altitude/temperature, changing cloud top emissivity and reflectivity, changing regional distribution of clouds, has the upper atmosphere been drying as the planet warmed (Partridge)?, the putative missing hotspot, and – most of all – the limited ability of observations and AOGCMs (with tuned parameters) to shed light on these issues. Thus my interest in seasonal changes in clouds – which can be large and driven by large changes in surface temperature. If AOGCMs can’t properly reproduce cloud feedback associated with large seasonal change in temperature, then there is no reason to trust their ability to handle GHG mediated warming. See link below. Note that AOGCM’s disagree with each other about feedbacks associated with seasonal change; they are internally inconsistent, so most models must be wrong. None is particularly good at reproducing all observed aspects of seasonal changes in clouds. Nevertheless, I can’t convince myself that the data says cloud feedback is negative or positive. As best I can tell, there is little difference between clear and cloudy skies in the LWR channel AND the SWR channel. And the SWR channel from clear skies changes with surface albedo (seasonal snow cover) and the two hemisphere have very different amount of seasonal snow cover.
http://www.pnas.org/content/110/19/7568.long
Frank,
“A gain is one way of quantifying the greenhouse effect from our current atmosphere. 390-240=150 W/m2 is another. Both of these measures are flawed because the earth would not emit or absorb 240 W/m2 without any GHGs because the planet would be much colder and have a different albedo and humidity. So, none of these numbers tells us how radiative transfer transfer will change when CO2 doubles in the future”
Correct, it would not. I never claimed the absolute gain directly tells us or quantifies the sensitivity. I only claimed that whether the incremental gain (in response to some forcing) is greater or less than the absolute gain determines if the net feedback acting on the system is positive or negative.
At least for the separate hemispheric responses, the net feedback acting on the gain is unambiguously net negative, as its directly measured from the data. Now whether than can be extrapolated to global feedback also being negative is really the question. My point is without at least understanding what is being measured and quantified by the gain, you would have no way to understand and assess the analysis.
IMO, anyone who thinks they know that cloud feedback is negative OR positive is probably over-confident.”
With absolute certainty? No, but it follows from basic physical logic that the combined or net feedback of clouds and water vapor is almost certainly negative and not positive. This is because immensely dynamic and chaotic, yet extremely stable systems don’t behave or function that way. All the dynamic chaos converges on a global average temperature that barely moves by more than a few tenths of a degree, which strongly suggests the climate is some form of a control system. Control systems can’t even function or exist unless the net feedback acting on them is negative. There must be some underlying, counter balancing, mechanism amongst the dynamic chaos that maintains such a tight balance. The obvious mechanism is via clouds through their ability to reflect incoming solar energy and precipitate out of the atmosphere the evaporated water from the surface.
A case can be (and is) made that this underlying mechanism can be extrapolated from the separate hemispheric responses — if one knows what to look for. Part of the problem is most people are looking at globally averaged data, where all the dynamics of the system are averaged out and can’t be seen or analyzed. This leads a lot of heuristics and guessing, or just to the proclamation that the system is too complex determine it.
Let me ask, do you understand that those plots are that of the 25 year average responses of the hemispheres? If you plotted each year separately, the results would be a little different from year to year.
All of the hullabaloo about the heat wave in England prompted me to look into the Extreme Weather Chapter of AR6. On page 1550 (end of 11.3.2), it says:
“Annual minimum temperatures on land have increased about three times more than global surface temperature since the 1960s, with particularly strong warming in the Arctic (high confidence).”
Click to access IPCC_AR6_WGI_Chapter11.pdf
I wonder why the candid gentlemen who wrote this report didn’t tell us how much annual maximum temperature on land had increased? And why they chose to express the change in the minimum on land as a multiple of the change of the average GLOBAL temperature?
If I understand correctly, SST are not reported as average of a daily high and a daily low, as 2m surface temperature on land is reported. Looking at Nick Stokes temperature viewer, CRUTEMP5 (land) has warmed 1.41 K between 1960 and 2020, HADSST4(ocean) warmed 0.85 K and HadCRUT5 (global) warmed 1.06 K. That means minimum temperature on land warmed 3.18 K and maximum temperature on land rose only 0.15 K over 60 years, about 5% of the rise in minimum temperature on land.
Double check
70% * 0.85 ocean increase
+15% * (3*1.06) land minimum increase
+15% * 0.15 land maximum increase
= 1.06 K global warming
Then I remembered that BEST looked in the predicted decrease in diurnal range with rising GHGs. They said the rise in Tmax was 0.91 K and Tmin 1.06 K from “1950s to 2000s”, a much more reasonable result – until you remember their diurnal range fell until 1980 and then began rising.
Click to access Results-Paper-Berkeley-Earth.pdf
Any comments?
Frank,
IIRC, the diurnal range of SST is quite small, so max/min is not particularly relevant even if you could have measured it reliably. Traditionally, SST was measured by ships sampling the surface with a canvas bucket and measuring the temperature of the water in the bucket with a mercury thermometer and then recording the date, time and position. Now it’s mostly measured by radiometers in satellites. But there should also be data from the ARGO system and other buoys, fixed or floating free. While you could conceivably put something like an AWS on a buoy at a height of 2 m, you wouldn’t have been able to take daily readings with a traditional max/min liquid in glass thermometer over the ocean. Hence water surface temperature being the number of interest. Or that’s my understanding anyway.