A long and interesting discussion followed Venusian Mysteries. One commenter posed an excellent thought experiment:
Consider Venus with its existing atmosphere, and put a totally opaque enclosure (to incoming Solar radiation) around the entire planet at the average location of present outgoing long wave radiation. Use a surface with the same albedo as present Venus for the enclosure.
What would happen to the planetary surface temperature over a reasonably long time?
For this case, NO Solar incoming radiation reaches the surface. I contend that the surface temperature will be about the same as present.
Now assume the gas temperature and distribution are initially different from present levels, but no gases are condensed other than those that form the present clouds. I contend the temperature will go to about the present distribution and level. The only reason for this not to not match exactly the same as the actual atmosphere would be due to the fact that for the atmosphere, outgoing radiation actually leaves from a finite gas thickness, but the present version is a surface.
With further clarification:
Assume the surface has a black body emissivity for the long wave outgoing radiation. Also assume it is a thin but good conducting material.
And also answered that the opaque enclosure radiates in both directions (both outgoing to space and to the surface of the planet).
The First Simple Model
Here’s a very simple radiative balance below. The “opaque enclosure” is E, and the surface is S. This has one layer of opaque atmosphere,1, to get us started: 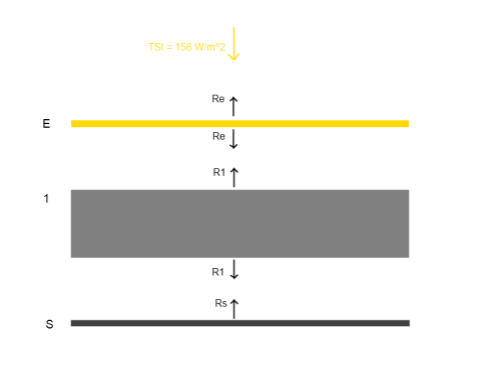
The gaps in the diagram are simply to enable us to see the radiation values from each layer more easily – they don’t represent any kind of physical discontinuity.
I started with a many layer model of the atmosphere – as described a little in Venusian Mysteries.
As a result of the solution to the equations, it made sense to explain a one layer model of the atmosphere first. I started by assuming that the initial conditions were that the enclosure and surface were initially very cold to see what happens.
Because E is a “thin but good conducting layer” we assume that E is “isothermal” – all at the same temperature. And because it is thin we assume that it heats up quickly when irradiated by solar energy – i.e., its heat capacity is low so it doesn’t take long to reach equilibrium.
Because gases have very low conductivity, and because radiation from the inside surface of the “opaque layer” is taking place, we assume that radiation to the surface is “much greater” than conductivity.
In this simple (unrealistic) one layer model, we also assume that the atmosphere is isothermal (all at one temperature). This is just to get us started. We can add a many layer model later, where each layer is isothermal, but each layer is at a different temperature from the ones above and below.
A Little Maths
Reviewing the diagram above, assuming that radiation is the only heat transfer mechanism, and assuming that the solar radiation is equally spread (note 1 at end):
TSI + R1 = 2RE [1]
2R1 = RS + RE [2]
RS = R1 [3]
So:
[3] -> [2] 2RS = RS + RE, or RS = RE [4]
[4], [3] -> [1] TSI + RS = 2RS, or TSI = RS
And so, in equilibrium (after every layer has heated up to steady state):
RS = R1 = RE = TSI
That is, each layer radiates the same as every other, and at the same value as the solar irradiance of 158 W/m2 (absorbed solar radiation).
Which means that the enclosure layer will reach an equilibrium temperature of 229K – and this will also be the equilibrium planetary surface temperature.
If these are the equilibrium temperatures what will drive conduction or convection of heat? Nothing. With the surface, the atmosphere and the “enclosure layer” of our thought experiment, all at the same temperature there will be no convection or conduction.
The Many Layer Model
The example above can be extended to many layers of opaque atmosphere. I checked out a 3-atmospheric layer model and the same results are obtained. (It’s tedious writing down the 5 equations and showing the substitutions to solve, especially as wordpress doesn’t do subscripts easily).
But the more realistic many-layer models solve exactly the same way. So with an outer atmospheric layer absorbing the solar radiation and then heating up and radiating in to the surface (and out to space), we find that the surface is no hotter than the outer atmospheric layer.
Compare this with the many layer model in the original article (under How Can the Surface Get so Hot? An Over-Simplified Climate Model), where, because the surface was heated by solar irradiance, the surface could become much hotter due to “backradiation” from the many layers above.
Then, in that model, as a result of the high surface temperatures, convection was initiated which moderated the high temperatures.
In this model, radiation can’t create those conditions – at least from a cold starting condition.
[Note added, 25th June – This model is aimed at demonstrating that radiative effects through an opaque atmosphere are totally different when the solar radiation is received at the outer layer of the atmosphere compared with at the surface. The “isothermal” model of the atmosphere (=the atmosphere all at the same temperature) is just for the purposes of constructing this radiation model – and as Leonard Weinstein points out, his thought experiment explicitly stated that the atmospheric temperature varies. In a “many layer” model with low conductivity (as found in gases) the radiation model would still be valid, even though the temperature varies from night to day and at different latitudes. Therefore, another mechanism of significant heat transfer is required to get the surface temperature of “thought experiment Venus” (TEV) to the temperature of actual Venus.
So in normal Venus we have a mechanism – radiation – for driving the temperature so high. But in TEV we need another mechanism.]
What about the Real World Effects?
In practice, one half of the atmosphere is heated during the day while the other half cools, and vice-versa for the night. This doesn’t affect conduction which has a tiny effect.
Does this create a stronger heating through to the surface and initiate some convective activities? How about if we started with a hot surface (from volcanic activity), would we reach a different equilibrium effect?
In both of these cases, there is no explanation for why any convective lapse rate would be maintained – unless a high source of internal heat from something like volcanic activity was maintained.
If we started with a hot initial condition (but no ongoing source of heat) instead of a cold initial condition, convection would simply move heat up to the top of the atmosphere until the same steady state condition was reached – where each layer was at the same temperature.
Convection is the bulk movement of heat as gases or liquids carry heat from one location to another. But something needs to drive convection. In the case of the earth’s atmosphere it is the relatively high surface temperature (from radiation) heating gases which expand and so are less dense. Gases that are less dense rise – and so heat is moved more effectively from the surface than can be achieved by radiation.
When heating the atmosphere from the top – with the vacuum of space above – there is no explanation for high temperatures in layers below.
In the case of the real Venus we at least saw what a totally opaque atmosphere could achieve. In the case of this thought experiment we see a totally different result.
Perhaps someone can produce a more comprehensive model which shows how the surface could radiate at 16,000 W/m2 in this thought experiment. I doubt that it can be done.
Note 1: If we assume that the solar radiation is equally spread across all surface elements, we get the result in the 1-layer or many-layer model. Strictly speaking this is not the case – as the solar radiation only heats one side of the planet at any one time, and that somewhat unequally. Is this a good approximation? Yes, if the heat capacity of the atmosphere is sufficiently high.
If the heat capacity is lower we simply get a relatively hotter surface temperature during “the day” and a relatively colder surface temperature during “the night”. No mechanism for Venusian surface temperatures.
Update – New article – Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion


I don’t think you have really engaged Dr Weinstein’s argument. Your atmosphere exhibits no gas properties, nor any response to gravitation. Dr Weinstein is correct insofar as an atmosphere in motion and with gravity does pump heat downwards until the adiabatic lapse rate is reached (in the absence of other fluxes). But a positive lapse rate also induces an upward flux, principally by radiative transfer. These come into some sort of balance, depending on the energy available to keep the atmosphere in motion and driving the heat pump.
There is a significant real world effect, in that parts of the shell will be cooler than others, depending on incident sunlight. This will induce circulation, driven by the heat engine source of flux from warm to cool.
But it will be much less than the current atmosphere on Venus. We know that because the mixing on Venus is currently so great that there is little temperature difference from night to day, or equator to pole. If that continued to be true with the shell, there is no differential to drive a heat engine. So something has to give. The turbulence and mixing will reduce, raising the temperature differential, until there is enough heat engine energy available to sustain the reduced circulation.
This will produce a positive lapse rate, but much less than the current one. The reason is than One big downflux, sunlight, has been blocked, and the other, adiabatic pumping, has much less energy available. Since the up and down fluxes must balance, that means that the lapse rate which determines the upflux, must be greatly reduced too.
SOD,
Nick has it basically correct. The conduction (due to molecular diffusion) and convection will drive the process to regain the lapse rate. The temperature near the planet surface would tend to nearly constant due to the huge thermal mass and high pressure at the surface, but the temperature would develop to be not as constant at different locations from lower to higher latitudes (due to lower input from the Solar angle) at higher altitudes. This difference would eventually drive the high wind velocities found above a few km altitude. The non-uniform barrier temperature and planetary rotation would generate convection, but even just conduction (gas diffusion) would eventually drive the lapse rate, since it is in the end mainly caused by conversion of potential energy to kinetic energy. The low optical transmission makes radiation heat transfer very low and not directly important (its importance is as a cause to raise the altitude where outgoing radiation does become important). For the case of the opaque shell, the radiation to space would be from the shell, and energy to the shell would have been carried up by mainly convection to near the shell, and the last distance by radiation to the shell from the lower density gas. The final temperature distribution and atmospheric wind velocities would likely be some different from an open atmosphere, due to the different location where Solar energy is absorbed (most of the present absorption is likely at the clouds). It is NOT necessary for the Solar energy to actually hit the ground to heat it, although if some does hit the ground, the rate of movement toward equilibrium may be faster, and there would be some difference in convection currents.
Nick,
The eventual average lapse rate would be the same, it is the time scale to reach it that is different. There would be differences in wind currents, as the boundary conditions are different, but the lapse rate in the end comes from g/Cp as long as either conduction (gas diffusion) and delta T driven convection are available, even if their time scale is different.
A major point seems to have been missed here. You do not even need radiation to space from the atmosphere to have a lapse rate. If the Solar radiation went through a totally non-absorbing atmosphere (for all wavelengths), the ground temperature would be developed to be in radiation balance with incoming Solar radiation. The gas above the ground would be heated by contact with the ground and that would produce lift to generate convection. However, as it rose it would cool from rising in the gravity (or from expansion-which in the end is the same thing). this would carry energy up, but due to low latitude to high latitude currents, the energy would then go back down and in the end would result in a lapse rate and warming of higher latitude ground from lower latitude ground.
“You do not even need radiation to space from the atmosphere to have a lapse rate.”
True, but will you get enough heat transfer from low to high latitude to create an adiabatic lapse rate even at the equator. Remember that any meridional movement will be bent by the Coriolis effect creating geostrophic winds at altitude like the jet streams on Earth. That’s going to act as a barrier to heat flow, I think.
Nick,
I think I see where you got a bit off. The ideal lapse rate does not transmit or require a net energy flux. The equilibrium value is a purely a result of g/Cp. Heat transfer from a variety of sources (radiation, conduction, and convection, as well as phase changes) result in non-equilibrium values which effectively change the lapse rate measured, but are not the cause of the ideal lapse rate. Some energy transmission is need to reestablish the level if it is somehow changed, and the level can be distorted if non-equilibrium processes dominate.
Leonard,
I do believe that maintenance of a near ideal lapse rate requires a constant flux of energy. With a temp gradient, there are transfers that must happen. Conduction down the gradient, or more significantly, the quasi-conduction of gas to gas radiative transfer. These are lossy, irreversible, and constantly create entropy. They can only be balanced (to keep a contsant lapse rate) by a forced counter-flux, which the heat pumping of atmospheric processes provides. But that is pumping against a gradient, and requires energy, which comes from the atmosphere. In turn, that energy must be replenished by the various kinds of heat engines that the atmosphere has, where convection takes heat from hot places to cold.
There may be no net flux, but that is because two fluxes balance. And the flux against the temperature gradient requires energy to maintain.
That is why I suggest that both energy and entropy should be tracked through the system. With the shell, there is much less free energy available, and the ability to export entropy to space is inhibited. All this points to much less motion, and a much reduced lapse rate.
I’ve written about this here, and I’m hoping to get another post written there tomorrow.
Bad wording – by “maintenance … requires a constant flux of energy” I mean a constant supply of energy.
Leonard,
“The law that says one surface can’t be heated more than the source does not apply if other sources of energy (potential to kinetic) are available.
That would only be true if the molecule that left the shell surface stuck to the ground. When it rebounds, it carries away just as much energy as it deposited unless the surface is hotter than the surrounding sphere. In that case, it will carry more energy back to the sphere than it deposited. The end result will be the surface and the sphere will have the same temperature, as they must to comply with the Second Law.
A gravitational field is not a source of energy. You can’t obtain free energy by lifting an object to high altitude and dropping it back to the surface. If the motion is one way only as in gravitational collapse, you do convert potential to kinetic energy, but only once.
DeWitt,
The excess amount carried to the ground due to gravity would be lost again on the upward rise back (gravity gives, and gravity takes). The ground would be hotter, but this heat would not be a source of energy to the shell in average equilibrium (however, there probably would be local variation both ways at different locations). Due to energy storage terms (thermal mass of ground and gases) and unbalanced initial conditions there would be net energy fluxes before average equilibrium is established, but that is not what I am talking about.
The 1D system you describe, with molecules gaining KE as they fall, and losing when they rise, sounds conservative. But it isn’t reversible. When a molecule falls, the KE gain relates to 1 degree of freedom (vertical motion). But when it reaches the ground, total KE may be preserved, but will be partitioned among available dof – say 3 for argon. It isn’t all available to send another molecule back to the shell. This is the entropy gain of the process, and energy must be supplied to overcome it.
Nick,
The single molecule falling was just to make the point that energy is gained as you go down the potential well. For a real gas, multiple collisions along the way with other molecules would redistribute the higher thermal energy (equipartition), so the collision with the ground would be more of the same.
DeWitt,
The gas takes energy from collision with the shell. It then adds gravitational potential energy as it goes down and heats the ground. If the ground is less hot than at equilibrium, the gas is slightly cooler at the ground from giving some of its energy to the relatively cooler ground. Now when it goes back up, it is cooler than the Solar heated shell, and again absorbs energy from contact. The net effect is the transport of Solar energy as absorbed from the shell to heat the ground, with a delta T at the ground of the produce of the lapse rate and altitude. When the ground reaches average equilibrium, the gas is not transporting to or taking energy from the shell. All the energy then would be at a static average level, and the shell would be at a temperature so that absorbed Solar energy is all radiated back out. There would be radiation, conduction, and convection actually carrying energy back and forth, but that would be due to regional variation in Solar heating, and internal convection currents and radiation. On the average, the interior would be at a constant energy content.
SOD,
On re-reading you initial text, I noticed you concluded that I meant good conductivity meant isothermal for the entire surface. That was not what I meant. I only meant there was no temperature variation in its thickness, not over its whole area. I specifically stated latitude and rotation caused variation, so I thought that was clear. Using the whole area as isothermal loses the latitude variation and day to night variation needed for significant convection. Even for that case, the diffusion would eventually move toward the correct temperature lapse rate, but diffusion is so slow, that radiation would be strong enough to change the actual value to a smaller level (the radiation does not have the gravity effect, so is different from both conduction and convection).
Leonard Weinstein:
You were clear.
I didn’t do a good job of explaining what that assumption was about or why it was there.
It was simply to create a radiation model which could be easily solved to demonstrate one major contrast between “thought experiment Venus” (TEV) and real Venus.
It actually only needs to be the case for one localized area to solve for that area.
So not well explained and something I might note in the article.
Of course, there will be temperature variations in the atmosphere in TEV, but can they get to anything like the values of Venus? I can’t see a mechanism to drive it.
I will read your other comments some more and think.
Now noted in the article.
scienceofdoom,
I want to add here that the conversion of potential energy is not done directly to surface kinetic energy as I stated. That was a notional representation. The actual gravity enters as a method of causing a pressure variation with altitude and using the adiabatic temperature variation with pressure. They are not quite the same, but have the same source-gravity. Also, since the actual lapse rate is about 7.7 K/km, and theory shows about 9 K/km, then a combination of real gas effects and some radiation conduction is present to cause the difference. All discussions were simplified to point out the features I wanted to emphasize.
Leonard,
I think I see what you’re saying, but you’re still wrong.
First, do you agree that in a perfect vacuum inside the shell that the planet surface and the surface of the shell will be at the same temperature?
At a pressure where the mean free path is on the order of the distance between the shell and the surface, you are very far from LTE and it’s not clear to me that the concept of a lapse rate even applies. Besides, any heat transferred to the surface will be collision at that rate will be immediately radiated away.
Now let’s add a neon atmosphere. Neon has close to the same heat capacity as dry air. For simplicity, make the shell isothermal at 230 K at an altitude of 80 km and make the surface pressure 91 bar. We’ll also ignore any collision induced absorption at the high surface pressure. What’s the surface temperature? Remember if the surface temperature is higher than the shell, you’ll have to have convective heat transfer from the cooler shell to the warmer surface to transport the excess heat that will be radiating from the surface back from the shell since the flux outward from the shell cannot exceed 158 W/m2. Then there’s the problem that vertical convection at the adiabatic lapse rate does not require work, it also doesn’t transfer heat in the absence of a condensable gas. But heat will still diffuse to the shell if there’s a temperature gradient as well as radiate away. You can transfer heat by convection if the lapse rate is less than adiabatic, but you have do do work against the buoyancy force and with an isothermal shell, I see no source for that work.
If the shell isn’t isothermal, then the situation is much more complicated, but the total flux over the entire surface of the planet will still equal the total flux from the surface of the sphell. So the temperature at the equator will be less than the simple radiative model in the absence of an atmosphere and the temperature at the poles will be higher. The average temperature should be slightly less than the average temperature for an isothermal planet. Any work done against a lapse rate less than the adiabatic rate will just make the surface temperature more uniform, not hotter.
Oh for an edit function. That’s …any heat transferred to the surface [by] collision at that rate will be immediately radiated away.
And what would be the effect of say the atmosphere/shell being bombarded/compressed by the solar winds?
Would that have an effect on Venus’s climate? And the energy absorbed by the atmosphere? or would the losses on the leeward side balance?
This Q was just a curiosity, im aware its moving the goal posts as far as the TEV is concerned… Just one o those things thats peculiar about venus, (i suppose mars is in the same boat… but lacks an atmosphere, probably because o it)
But ive never seen mention o the fact that the atmosphere directly interacts with the solar winds in regards to its current climate, Is that because of the basic effect youve described with the shell model? (not effecting lower levels above equilibrium taken in isolation)
Interesting question, but far beyond my job description. Or, I dunno. Considering it’s taken me years to get to where I am on atmospheric and radiative physics (and I still have a long way to go), I’m not motivated to start on an almost completely new project that looks entirely too much like work with little prospect for payback. Not that this rewards anything but my curiosity.
DeWitt,
If the gas in the shell was not a radiation absorber, the average ground temperature would be the same as the planet with no greenhouse gas and no shell, and even the same as for no atmosphere. It would be cool. The radiation to the shell would be absorbed and radiate both ways, so would be the same temperature as the ground. The thin gas near the shell and the dense gas near the ground would be the same average temperature. However, the heat transfer rates at the ground from conduction to the gas and convective currents would be orders of magnitude different. The net result is that the temperature going down from the shell would decrease over a moderately short distance then start increasing back toward the adiabatic lapse rate. If the mass of gas is sufficient to cause the atmosphere to be effectively very tall (as the one on Venus), the lapse rate times altitude gives too large a temperature difference, so condensation and other processes would greatly complicate the actual case.
Please excuse my incompetence, but I’m trying to learn… When it is said that the average energy received by, say, the Earth, is X W/square meter, does it imply that it is the average energy considering the Earth as a flat disk with due correction for the latitude and the relevant atmosphere thickness at that latitude ? If so, where can I find a formula stating this value ?
If this seems preposterous for you specialists, please bear with me… I don’t want to die uneducated !
DeWitt,
First, the shell and surface would be the same temperature if they both had the same emissivity and absorptivity in a vacuum or near vacuum. Second the lack of gas or very long MFP would make the concept of lapse rate meaningless, although the thermal velocity of individual molecules would increase as they fell. The point I was making with the sub discussion is how gravity can make a gas have different thermal velocity as a function of altitude. It was a separate issue from the rest of the discussion. Note this is not a violation of the second law. It is also true the immediate radiation gets rid of the excess heat when the molecule hits the surface, but again the only point I was making is that the molecule would be “hotter” near the ground going down. If you use optically transparent gases, the high radiation heat transfer would dominate any convection, so the lapse rate would be very small or even near zero WITH THE SHELL PRESENT. Note that in the case of an actual atmosphere, there is no absorbing and re-radiating shell, so the radiation would be directly to space, and the lapse rate would be dominated by the convection and diffusion. For that case, you would have a modestly temperature surface, and a cooling atmosphere with increasing elevation. Please note the actual case in question has a nearly optically opaque atmospheric property for long wave radiation, so the actual radiation heat transfer is very small compared to convection, and my argument basically holds for the Venus atmosphere in a shell. I think we are talking across each other on some of the issues.
Wouldn’t we get a rather weird temperature profile with the scenario DeWitt presented, where, when we start from the surface), the temperature would at first raise with altitude and at some point start falling again. The reason for this is that we need to raise the temperature from the shell downwards due to gravity, and at the surface, we lose energy due to radiation, and we again need to cool it down (surface is cooling the atmosphere).
Nick Stokes:
I agree that there will be a small temperature gradient. But there isn’t much to drive it.
When I read your comment I think that I almost agree with it – but it’s all a question of degree which is the reason for writing the post in the first place – to clarify which end of the spectrum we are all at and why.
When you say “But a positive lapse rate also induces an upward flux, principally by radiative transfer.” – what kind of value are we talking about?
We can see that in the absence of convection and conduction that the many layers are in radiative balance, transferring around 160 W/m^2 from each layer.
So to perturb this sufficiently we need to see a value in this kind of order from the motion of the atmosphere and gravity.
Do you think that can happen?
Or was your statement a qualitative kind of statement?
I may have given the impression that the atmosphere would be isothermal – my mistake. But would it be close to isothermal? Yes, I think so.
So it’s all a question of degree:
– Is the atmosphere in TEV isothermal? No
– Is the atmosphere close to isothermal? Yes
– Is the surface temperature closer to 230K or 730K? Much closer to 230K.
And so yes I agree with your conceptual statement. But are you saying that gravity and planetary motion generate enough heat transfer to make “a dent” in 160W/m^2?
SoD,
I’ve just put up a post trying to quantify some of these aspects . The first thing to say is that only a small part of that 160 W/m2 actually reaches the surface – the atmosphere absorbs a lot of SW too. At each level, the upflux which is the sum of IR and convection has to balance the SW downflux at that level.
As to the balance between IR and convection – I don’t know for sure. Leonard thinks there is not much IR transport near the surface – however, there isn’t much flux in total either – because of reduced SW. As the pressure reduces, so does the opacity, giving IR a greater role.
But yes, I think gravity and winds can make a dent in 160 W/m2. Venus emits almost uniformly, night/day, pole/equator. Since insolation varies a lot, that means big horizontal heat fluxes from hot to cold – a substantial fraction of total heat absorbed. It’s true that the temperature difference at emission isn’t so large, but it’s still potentially a big heat engine, which could drive a big heat pump. It could drive a significant fraction of the 160 W/m2 over a big temperature differential.
Whether it actually does depends on whether the actual lapse rate is less than or greater than the adiabat.
Oops, left out the link, which is here.
SOD,
You continue to state that the radiative flux would be close to 160 W/msquare, which would be needed to drop the lapse rate to a small value. However, the mean radiation absorption path is so small on Venus (near the ground), that this radiation flux is much smaller than that due to back radiation nearly balancing forward radiation. Since the actual lapse rate for Venus is about 7.7 instead of 9, I would state that while the radiation flux effect is not insignificant, it is not nearly dominate. Also, if the surface were at a lower temperature, the radiation flux would be even much lower. Gravity causes heating AND cooling (i.e., adiabatic compression of downward moving gas heats the gas, but expansion of upward moving gas cools the gas). At near equilibrium, there is no net flux from convection, only local variation. Away from equilibrium, the net flux does occur to drive the system back toward average equilibrium. The fact of a hot surface does not imply that there needs to be a large energy flux from the surface. It is trapped heat. There will be some net radiation, but it is small.
SOD,
Consider a case for no convection where essentially all of the radiation up is absorbed in 1 m then re emitted up and down. The lapse rate of 7.7 degrees K/km results in the temperature dropping 0.0077 K in 1 m. Assume you are near the surface. Now assume the lower layer is 750 K, then the layer 1 m above (which absorbed the radiation) is 749.9923 K due to the actual lapse rate on Venus. The energy transfer due to radiation would be 0.8 W/msquare for that case. Even if the near total absorption length were 10 m, the radiation energy flux would only be 7.5 W/msquare. You can’t get 160 W/msquare radiation heat transfer for the case of Venus.
Leonard Weinstein:
I know I’m addressing points out of order (and after I started writing this you have made new comments..), but this one intrigued me:
What do you mean by equilibrium value?
I might be reading too much into this, of course..
The equilibrium value of lapse rate is either the actual temperature gradient or – when that becomes sufficiently high, the atmosphere becomes convectively unstable and so it (the equilibrium value) becomes the adiabatic lapse rate.
So if the heat transfer processes in the atmosphere mean that the environmental lapse rate is lower than the adiabatic lapse rate, there will be no convection from this process.
For example (for newcomers), suppose the environmental lapse rate is 1K/km (temperature decreases at 1K/km). The adiabatic lapse rate is around 9K/km which means that if a parcel of air is forced up 1km it will be 9K cooler. This will be 8K cooler than the the actual environment so this air will be more dense and will tend to sink. (Writing this paragraph not for you but for many readers).
So did I just misunderstand you?
If radiation and/or conduction don’t generate a lapse rate of sufficient magnitude then there will be no convection from this process. And the value of g/Cp will just stay as the maximum achievable lapse rate.
Agree? Or Disagree?
cdc
What it really means is that the earth has absorbed a total of Z Watts of solar radiation (incident radiation – reflected radiation). This value is usually averaged globally annually.
And Z / surface area = X W/square meter.
Check out Earth’s Energy Budget – Part One as it might answer some basic questions.
SOD,
I agree. However, my point is that the adiabatic lapse rate came from initial non equilibrium values causing some driver (convection or diffusion) to happen so that eventually the adiabatic level is reached. In reality, it never is exactly balanced, so convection does occurs. However, it can be ON THE AVERAGE balanced, with convection always tending to re balance it locally, and the actual lapse rate will tend toward the adiabatic value. In that case there may be no net heat transfer, just movement from one area to another. That is the case for nonuniform heating of a planet. The radiation from the surface and from the atmosphere do result in an energy flux, which is needed to balance the input energy from the Sun that went into the surface or atmosphere, and since the radiation does not have a gravity effect, can shift the value of the lapse rate depending on its local magnitude relative to the size of the convection.
SOD,
You said several things and my agreement was only on part of it. The point is that something sets up the lapse rate. It is not a given. You have to have at least diffusion or convection to initially establish it. Once it is established, if there were no radiation to space, and no radiation heat transfer it would stay at that level, not go to zero. Putting in radiation, but constraining convection is a false assumption for the case with the shell.
SOD,
3 cm of Venus’s lower atmosphere has as much CO2 as all of the Earth’s atmosphere.
One last model. We know polished Gold has a very low absorption and emission coef. at a large range of wavelengths. Let us assume a thin metal is used for the shell that is a perfect reflector and zero emitter on the side facing down (like an idealized case for gold), but has a exterior paint coat so that it has an albedo like Venus on the outside for Solar wavelengths, and is a near black body at the outgoing temperature. This gives the metal shell an average temperature close to the value for the present upper atmosphere, with latitude and day to night area variation. Actually the shell temperature would be more extreme in that low energy storage would give more extreme cooling, but assume here that the temperature is close to the present average at Venus’s upper atmosphere. Now assume the gas has the density and specific heat close to the present, but is totally optically transparent to all wavelengths present. Now the radiation up from the ground is not absorbed by either the gas or shell. The only method of heating the gas here is collisions with the ground, the shell, and between molecules from convected or conducted flow. I contend that the ground will be just about as hot as Venus (or even slightly hotter due to total lack of radiation heat transfer), and the lapse rate will be close to the ideal g/Cp. Note this is a case for NO greenhouse gas at all, and radiation on the interior has been removed from the problem. If this is valid, the case for Venus’s temperature is basically as I claim.
Can we get some sort of summary as to where we are at in this debate? As I understand Leonard the radiative flux on Venus, given the ~ balance between OLR or 160W/m2 and the same reaching the surface, is consistent with the surface heat and the lapse rate[s], adiabatic and non-adiabatic. Where does that leave the core issue of pressure vs greenhouse causing the exceptional surface and atmospheric temperature profile of Venus?
I have a question on the assumption that Venus’s atmosphere is totally opaque to all Infrared radiation. Do you have links to empirical tests run on CO2 at the high pressure of Venus atmosphere? I could not find any. CO2 at Earth pressure will absrob only about 8% of the total IR spectrum. The bands broaden under pressure but I have not found any information that demonstrates they will go beyond the few resonance frequencies of the Carbon Oxygen bonding.
There are alternate theories on why Venus is so hot beyond CO2 in atmosphere. How much of the IR Spectrum will CO2 absorb at the higher pressure?
Scientists claim the Venus surface is only 500 million years old. Maybe it is a new planet and that explains its thick atmosphere (did not blow off when Sun was born). If so it could still be cooling from a much hotter state and the thick atmopshere is just a good insulator so the heat is only slowly leaving.
The Electric Universe concept is that there are other forms of energy transfer beyond the photon interaction (radiatioin). I know a metal pan can be heated by magnetic energy alone. The theory is the Sun is able to transfer energy to Venus through an electrical coupling mechanism.
Why is it assumed that Venus was Earthlike and had a “runaway Greenhouse”. And why isn’t 92% of the 16,000 watts per meter getting through the CO2 atmosphere and going out into space.
Final thought. Since science should be an empirical system (math is a useful tool but if initial assumptions are wrong, even correct math will still result in an incorrect conclusion), the theory above can best be tested via surface probe that actually measures the downwelling radiation to see if it is indeed 16,000 watts per meter.
Cohenite,
The 160 W/m2 is the amount of average Solar radiation absorbed, probably mostly at the cloud layer. That has to be the amount leaving on average to be in a constant average temperature (i.e., no storage source taking in or removing more than the average levels in and out). The outgoing radiation is mainly at the very high level of the atmosphere, near 80 to 90 km, but some may be coming from the cloud layer, and possibly a small amount may be from the surface. However, there is neither a need or likely hood that 160 W/m2 of Solar energy ever reaches the surface. If any at all reaches the surface, it is very small. The rest of the action is all convection, a small amount of conduction, and a small amount of radiation from the surface, and larger amount at higher altitudes. If you look at my June 23 7:16 model, you can see that there is no need for the greenhouse gas to have a lapse rate. The only net effect of the greenhouse gas is to raise the location of outgoing radiation from the surface to a high altitude, and the lapse rate does the rest.
Norman,
I suspect the Sulfuric acid clouds have a large part in absorbing wave lengths not absorbed by the CO2. I am not expert on the amount of pressure (and temperature?) broadening of CO2, so I do not know its limits. There is a trace of H2O and other gases that also may contribute. My whole point has to do with the fact that the only effect of ANY greenhouse gases on surface temperature is to move the location of outgoing radiation up from the surface to a higher altitude. The gravity and specific heat properties of the gas (any gas) will form a lapse rate =g/Cp in the basic case. Convection from lateral variations in temperature carry energy up and down and drive the value to it’s average level. This value of 7.8 K/km is almost exactly the ideal value for CO2, and the ground temperature based on the known location of the tropopause plus the lapse rate times the altitude of the tropopause (which is thought to be the general location of most of the outgoing radiation) gives the ground temperature. I thought the ideal value for CO2 was 9 for Venus based on Earth ambient temperatures, but I found that the higher temperature of Venus caused Cp to increase, and 7.8 is in fact the value of Cp for CO2 for the actual temperatures encountered.
Norman,
I meant the troposphere temperature plus lapse rate time altitude gives ground temperature.
Norman:
No it’s not. In Venusian Mysteries I said:
Some of this discussion is a conceptual one to demonstrate how an opaque atmosphere does increase surface temperature.
There is some comment about the real situation under the heading “Real Solutions” in Venusian Mysteries.
Leonard,
The net flux at the surface must be equal to the solar flux absorbed at the surface. Anything absorbed by the clouds and the atmosphere before it gets to the surface doesn’t count. K&T97 has for the Earth 235 W/m2 total absorption, but 67 W/m2 of that is absorbed by the atmosphere. The net flux at the surface is then 168 W/m2, 102 by convection and 66 by radiation. According to this ( http://www.lpi.usra.edu/vexag/nov_2007/presentations/crisp.pdf page 4), the solar flux absorbed by the surface of Venus is ~17 W/m2 on a global average so a radiative flux of 0.8 W/m2 would be about 5% of the total. Also, while the atmosphere is opaque at wavelengths greater than 3 micrometers, peak emission at 730 K is at 4 micrometers, so there is still lots of energy in the emission spectrum of the surface where the atmosphere isn’t totally opaque and the net radiative flux from the surface could be greater than 0.8 W/m2.
That would also make peak net solar flux at the surface at the Venusian equator with the sun directly overhead 2636*0.24*0.1 = 63 W/m2, not very much compared to ~1,000 W/m2 for the surface of the Earth on a clear day.
Leonard,
“If you look at my June 23 7:16 model, you can see that there is no need for the greenhouse gas to have a lapse rate.”
Not true. An isothermal atmosphere will not have a greenhouse effect because the top layer of the atmosphere will emit exactly the same flux as the bottom layer.
A perfectly reflective shell in the LW but transparent in the SW and a surface with an emissivity of one would make the surface temperature rise to a level that it would emit sufficient SW to balance incoming radiation. For calculation purpose let’s say the reflectivity is 1 for greater than 3 micrometers and 0 for less than three micrometers. For a flux out through the shell of 158 W/m2, the surface temperature would be 539 K. At a cutoff of 4 micrometers, the surface temperature drops to 454 K. I don’t see how you get an adiabatic lapse rate from those numbers.
DeWitt,
I have said several times that if radiation effects on the system dominated conduction and convection, the lapse rate could be reduced. Making strange radiation pass and cutoff filters can make these occur. These are not representative of any realistic simulation. The shell I postulated was just to assure no Sunlight reached the ground, and showed why there would still be a lapse rate and hot ground. If there were no greenhouse gas and no shell, there would still be a lapse rate, but there would almost certainly be condensation and other changes if the gas were still as dense as on Venus (the lapse rate time altitude exceeds the available temperature range). Other strange shell properties can produce a wide range of results, but they simulate nothing useful.
DeWitt Payne,
I think Weinstein was saying (again, sorry if I’m wrong) that you don’t need greenhouse gases for there to be a lapse rate. In other words, lapse rate would still be there due to gravity (and gases being mostly vacuum with some molecules mixed in), if there were no absorbing gases in the atmosphere.
I don’t quite understand how you would get a isothermal atmosphere even in model conditions, if you don’t eliminate gravity?
Re SOD and Weinstein June 23, 2010 at 12:56 pm
Is there general agreement that the net vertical transfer of energy by radiation in an optically thick atmosphere can be very small?
If s is the mean free vertical path of a photon (which is SQRT(1/3) smaller than the mean free path of a photon), Wu is the net upward flux of energy from a certain altitude, a, Wd is the net downward flux of energy from altitude a+s, Wn is the net flux (halfway between), and L is the environmental lapse rate for this region of the atmosphere (a negative number):
Wu = 0.5*o*T^4
Wd = 0.5*o*(T+L*s))^4
Wd = 0.5*o*T^4 + 2*o*T^3*L*s + smaller terms
Wn = -2*o*T^3*L*s = -2*(2*Wu/T)*L*s
= Wu*(4*(-L)*s/T)
So Wu is reduced by a factor of -4Ls/T by an optically thick atmosphere. This can be a big reduction even if s is relatively long. For example, if s were 1 km near the surface of earth or high in the Venusian atmosphere, Wn would about only about 10% Wu.
A complete analysis would take into account how s varies with wavelength and then integrate over all emitting wavelengths. And s increases inversely with pressure and therefore increases exponentially with altitude. (And needs limitation so that Wn is never greater than Wu, a problem that may arise from neglecting the “smaller terms” of the expansion.)
Frank,
The problem is that we don’t know whether the atmosphere is all that thick at short wavelength. The short wavelength tail of spectrum still has a lot of energy. At 730 K, the flux for wavelengths shorter than 3 micrometers is about 800 W/m2. It doesn’t take much of a drop in emissivity of the atmosphere in that range to get a substantial radiative flux.
Shorter than 2 micrometers, It’s still 86 W/m2.
DeWitt,
My wording was not clear. I mean you do not need to have a greenhouse gas to be the atmospheric gas in order to have a lapse rate. Diffusion and convection will make any initial isothermal condition go to the lapse rate. I have been using a model with the assumption of an optically thick atmosphere for all wavelengths, and went to the extreme of assuming it was so optically thick that all radiation from the ground and incoming from the Sun were near totally absorbed by the ground. I modified the incoming rate of absorption to match Venus. This model is not the exact case for Venus, but looking at the model, you can see that it is not the energy from The Sun directly hitting the ground that makes the ground hot, or that causes the lapse rate. The actual case is more complex, but basically follows the same logic. The ground is hot due to the in/out radiation level being at a high altitude and the lapse rate due to gravity effects does the rest.
DeWitt,
Correction (sloppy words): Were totally absorbed before it reached the ground.
DeWitt,
If the shorter wavelength radiation passes straight through, why can we not see the surface at those wavelengths? I expect the sulfuric acid clouds probably stop those and since they are much cooler than the surface, their emission is at longer wavelengths. The cloud layer is also probably where most of the absorption and reflection takes place. Once the longer wavelength is dominate, the CO2 above the clouds takes a larger roll again, although there probably is some direct long wave to space component.
This is terrific; if I understand things correctly, SoD says a pressure theory will not provide a heat transfer mechanism; Leonard says a greenhouse will explain the height of the emission layer but is not necessary to explain the heat transfer from surface to TOA and therein the surface temperature.
Is that right guys? Where do you stand De Witt? I won’t ask Nick because he will beat me up as usual.
If you put me on one end and Leonard on the other, I think Nick is closer to me than to Leonard. I could be wrong about that. He might not be on the direct line at all.
Cohenite,
You got my idea almost correct. There is no NET heat transfer to or from the ground. There is some net radiation up and some convective transfer of energy up and down, but they average to be matched to keep the average ground temperature constant.
Leonard,
We can’t see the surface of the Earth through clouds either, but it’s not pitch dark on a cloudy day. There’s forward scattering too, which gives diffuse light. The Venera 9 probe took available light black and white pictures of the surface before it failed.
“Venera 9 measured clouds that were 30–40 km thick with bases at 30–35 km altitude. It also measured atmospheric chemicals including hydrochloric acid, hydrofluoric acid, bromine, and iodine. Other measurements included surface pressure of about 90 atmospheres (9 MPa), temperature of 485 °C, and surface light levels comparable to those at Earth mid-latitudes on a cloudy summer day. Venera 9 was the first probe to send back black and white television pictures from the Venusian surface showing shadows, no apparent dust in the air, and a variety of 30 to 40 cm rocks which were not eroded.”
http://en.wikipedia.org/wiki/Venera_9
cohenite,
Except for the very small (if any) direct radiation from the Sun that reaches the ground, that then has to eventually go back to space, there is no other heat transfer ON THE AVERAGE from the ground to space. The temperature gradient present in the lapse rate would only transfer AVERAGE energy by radiation, not conduction or convection. The only heat transfer out is due to the need to match the absorbed Solar radiation in (at a constant average condition), and that input energy is probable almost all or all absorbed in the high cloud layer. There is a heat transfer up, down, and sideways by convection, but it just moves energy around, with an average of zero. The 16,000 W/m2 from the hot ground is balanced ON THE AVERAGE by back radiation of nearly the exact same amount from both short range gas heated by absorption, and by absorption and re emission back down and reflection back by the clouds, so it is actually trapped energy. Think of a blanket holding in heat. The difference is with a blanket on a person, the heat source is the person. A blanket without a heat source is not warm. Shining a heat lamp on the blanket causes a hot air layer to form under the blanket, hotter than the air above. The lapse rate just comes from the effect of gravity on an atmosphere, and is a gas in gravity property.
What I am trying to say is that once the lapse rate is formed, and it always forms from conduction and convection, that as long as the upper atmosphere is maintained at a given temperature, there is NO net heat transfer needed to or from the ground for the ground to be hot.
DeWitt,
The lag between comment and display has us talking a bit past each other. I agree some Sunlight probably reaches the surface after scatter, but is probably very small, and not important. I also agree that clouds and other gases make the problem more complex. However, I am trying to look at an idealized situation to show that the net effect of the greenhouse gases and clouds is only to move the location of the average radiation to space (that was absorbed from Solar radiation) to a high altitude, and that the lapse rate from g/Cp of the average gas (CO2) times the altitude added to the temperature of the effective location of the outgoing radiation gave the ground temperature. The source of the lapse rate is only gravity and the mass and type of gas. It turns out the g/Cp of CO2 at about 750 K down to about 400 K, and using the local gravity, is near 7.8 K/km, which is the actual value of Venus’s lapse rate. The lapse rate actually varies from a temperature dependent Cp, but this doesn’t change the above result much. The variations in local Solar input from different latitudes and planet rotation are the source of convection, which set up the average lapse rate fairly rapidly. Given the above, the extreme concepts of “Runaway greenhouse effect”, or surface heated by internal energy sources are not needed and are likely false. The actual Venus is more complicated, but in the end it is basically the same process that drives its average ground temperature.
DeWitt,
If the Venus atmosphere were perfectly transparent to incoming Sunlight (but the same as present outgoing), it would be the surface that absorbed the average 160 W/m2, and there would be a net heat transfer of 160 W/m2 up. This would be transferred mainly by convection. The net effect might be a tiny fraction of a degree difference in ground temperature, and a microscopic shift in lapse rate due to an average energy convection, but the final ground temperature and lapse rate result would be about the same as the totally opaque shell in the upper atmosphere that I postulated.
DeWitt,
The Earth’s Solar insolation on a cloudy day varies, but a typical value might be 50 W/m2. I know that a light shining through even strongly scattering diffusers may keep some collimation, so a shadow on the surface is not unreasonable. I am not denying Solar energy reaching the ground at that energy level. I am saying it doesn’t matter for the ground temperature where in the atmosphere the energy is absorbed, as long as it is absorbed at the intensity matching the effect of the actual albedo.
DeWitt,
To expand a little on the previous, it doesn’t matter where the energy is absorbed, it does matter where it leaves.
Norman,
Of course the back radiation to the surface has to be near 16,000 W/m2. Otherwise the excess radiation would be a net heat transfer that would have to go into space and would rapidly cool the surface. The Solar input is what it is (160 W/m2), and that is all that goes out of the atmosphere other than the reflected Sunlight. You can’t get extra energy to replace the lost radiation from any other possible source other than a subsurface process, which is surely not present in any significant level.
Leonard Weinstein,
Here is an article that challenges your assumption.
“I have noted that this is in sharp disagreement with with actual findings, and that astronomers have made a habit of doctoring the findings and have actually found themselves in the position of having to explain AWAY 100% of the raw data. All of the probes which carried infra-red flux (upward vs. downward readings) meters to the surface measured a sharp upward ir flux, which is in keeping with Velikovsky’s version, but not that of Sagan. Astronomers have posted oficial position papers (Revercomb/Suomi et. al) explaining the manner in which each and every such probe “failed”, without bothering to try to explain why they should not all be fired for failing to oversee the proper manufacture of so simple an instrument in even one case out of at least four (instruments were not all the same). ”
Quote from article. Link to the full article.
Debate on cause for Venus High Temp.
Norman,
I looked at your suggested article. I want to point out three things:
1) The Solar intensity changes some over periods of decades to centuries, and thermal lag of the huge atmosphere and ground would result in some variation over time from a fully balanced condition. This may be the cause of some of the in vs out unbalance.
2) Accuracy of scientific instruments and exactly where they are used can vary a lot. I am not convinced that much of the difference is not just due to those causes.
3) The ignorance of many if not all scientists on many levels is profound. I do not know if something like what Velikovski thought is true, and I do NOT think the issue is closed. However, The basic greenhouse gas effect combined with gas lapse rate is already sufficient to explain the approximate hot surface temperature. Velikovski is a separate issue.
Norman,
One final point. The upward radiation CAN be larger than the downward radiation at a particular location. It is only on the AVERAGE that they have to balance. During the day or near the equator, I would expect an unbalance up. At the higher latitudes and at night it is probably reversed.
DeWitt,
Please re read my perfect internal reflector case (all wavelengths) and completely optically transparent gas (with matched Cp and density height) case for June 23 at 7:16. This case has no radiation absorption (by definition), and radiation is trapped (up = down) by the assumption of a perfect reflector. This still has conduction, convection, and a lapse rate that would be equal to Venus. Tell me why not if you disagree. If the mirror were removed, but the gas were still transparent and passed all of the radiation, the temperature that would cause the 160 W/m2 out would be the surface, and the atmosphere would be cold, with a temperature at the same initial lapse rate, but higher altitudes would get so cold they would condense, so the problem is more complex. Thus the optically absorbing greenhouse gas is necessary for a hot surface, but only to change the location of outgoing radiation (what I have been saying all along). Cutting the amount of CO2 but retaining total mass and Cp would only cut surface temperature due to lowering the outgoing radiation location.
Nope. If you have a perfect reflector, then it doesn’t matter if the atmosphere is opaque or not. Heat will have to transfer by eddy diffusion, which requires a lapse rate less than adiabatic. That assumes that a perfect reflector can actually have a temperature and transmit heat even by collision, which is not at all clear to me. In the end, photon exchange is necessary for collisions. If the surface cannot emit or absorb photons, how can it exchange energy by collision?
Solar radiation penetrating to the surface is critical and 17 W/m2 globally is enough to maintain a 730 K surface temperature if the resistance to heat flow is high enough.
A perfect reflector (note the reflector is on one side only facing down – think paint on the outside) can have a temperature and transmit heat by collision. Do you think polished gold is not a thermal conductor and heats a gas touching it? It has a reflectivity of up to 98%, and the remaining 2% is not why it can conduct and heat a gas by collision. Photon exchange is not necessary for gas to solid collisions, with heating, it is only necessary for radiation transfer. It is molecular kinetic collisions that transfers the conducted energy.
Leonard,
I’ve changed my mind on at least some of this. A transparent atmosphere will have a lapse rate close to the adiabatic rate. Or a potential temperature gradient close to zero. In most atmospheric soundings above the boundary layer the potential temperature increases with altitude, that is the lapse rate is less than adiabatic, moist or not.
But I’m not budging on a totally opaque atmosphere, though. If there is no penetration by short wave radiation then the potential temperature will have to increase with altitude a lot. That’s the only way that heat can flow down to the surface. That would mean a near isothermal atmosphere or or even an increase of temperature with altitude and a surface temperature lower than the cloud layer.
If 90% of the CO2 were replaced with an inert, transparent gas, then the surface temperature would drop on the order of 100 K, the average temperature of the atmosphere would drop, resulting in a denser atmosphere with a lower cloud layer and a similar lapse rate.
DeWitt,
I do agree the replacing 90% of the CO2 would drop the surface temperature, and I would guess less than 100 K, but you may even be right on that level. This would still leave the ground very hot. However, the reason would not be due to a large drop in lapse rate, but due to lowering the effective location where the outgoing radiation comes from. That lower height would then be where the atmospheric temperature would be pinned to a level to match the in and out levels of radiation. Since ground temperature is that temperature plus lapse rate time altitude that it comes from, the lower height results in the lower ground temperature level. There could be a decrease in convection, so the offset from exact average adiabatic rate could be a bit more, but not by much.
Here is yet another article that challenges the hypothesis that Venus experienced a “runaway greenhouse”.
The Sagan hypothesis is based upon mathematical theory. The counter is based upon empirical measurements.
I still ask, Why does anyone assume Venus and Earth were formed at the same time? Why is it impossible that Venus is a newcomer to the Solar System?
Here is the article with the empirical data challenging the hypothesis that Venus is so hot because of a Greenhouse effect.
Empirical data collected by probes indicating the Upwelling IR does not match the Downwelling IR.
Norman:
It’s quite a confused article. For myself, I’m not particularly interested in the origins of Venus, but when I read the paper it doesn’t have a coherent explanation of the current observations, and it doesn’t appear that the writer really understands the subject.
And as for the “empirical observations” – precedence appears to be given to possibly suspect sources:
Thanks Leonard at 1.57pm; as I understand it the difference between you and De Witt is that you say Venus heats down whereas De Witt reckons Venus must heat from the surface up because a down heating effect would require an isothermal atmosphere or even an inverted temp gradient. Venus’s temp gradient cools with height but the atmosphere is nearly opaque with little sunlight heating the surface although De Witt says about 17W/m2 of the solar flux is absorbed by the surface; I have read elsewhere that 10% of the TOA solar flux of ~ 2600W/m2 actually reaches the surface; that’s about 260W/m2; only about 160W/m2 is leaving the TOA so what is the exact figure of surface flux?
That aside, if De Witt is right about the problems with a down heating effect wouldn’t a sub-surface heating source overcome those problems? Why has that been dismissed apart from Nick’s comment that if the surface is emitting 16000W/m2 that has to be matched by TOA outgoing; that objection has been addressed by Leonard’s argument that immediate to the surface backradiation will match that upward 16000W/m2, plus the little [assuming it is not 260W/m2] solar flux.
Nick Stokes (from June 23, 1:02pm )
I don’t want to assume I’ve understood your point, so tell me if I’ve gone wrong somewhere.
I agree, of course, that the night/day variations – and latitude variations – of solar insolation will have a significant effect in the radiative balance. And therefore, the radiative balance is a function of latitude and time.
So, for example, instead of saying the energy received is an average of 160 W/m^2 we could say that the energy received at equatorial latitudes during the day is closer to 400-600 W/m^2 (peak at 659 W/m^2 for midday), while during the night it is 0.
But if radiation – assuming our mythical totally opaque atmosphere – is balanced from the top of atmosphere to the surface, then unless planetary rotation is adding some surface heat, how can the average surface temperature be anything higher than the average at the top of atmosphere?
(Average can be defined as the radiative average of T^4, or the average of T, let’s leave that aside while we consider the main point).
I’ve described here (third section) the adiabatic heat pump, which is independent of radiation. It takes energy from air to pump heat downwards. Provided the lapse rate is less than the dry adiabat, both rising and falling air pump heat down.
This is partly an answer to your next question to LW. This pump steepens the temp gradient, forcing it towards the adiabat. As it approaches, it has diminishing effect, and at the adiabat, rising and falling gas heat and cool at the same rate as ambient, and convey no heat. With lapse rate above the ambient, signs change. Rising air warms relative to ambient as it rises, and accelerates.
This is a heat engine, and promotes convection. It is the region of convective instability. The energy comes from moving gas from warm to cool. But it then lowers the gradient, bringing the lapse rate back towards the adiabat.
My point about uneven temperature (poles etc) is that if the lapse rate sits below the adiabat, as it often does on Earth, and if winds continue to blow, even though the convective stability is draining energy from them, then you need to find a heat engine to provide the KE. That comes from conditions where there is a big heat flux from warm to cold. Equator-pole circulations are one such KE source.
Leonard Weinstein from June 24, 2010 at 11:06 pm :
and,
June 25, 2010 at 1:57 am:
I still don’t know whether I understand your argument.
From these comments: in the first comment it looks like there is a perceived inevitability about the atmosphere moving to “the lapse rate”?
– This could be 0.001K/km?
– Or do you mean the adiabatic lapse rate?
In the second comment, it looks like there may be initial conditions that happened to move the atmosphere to an adiabatic lapse rate condition – and once there – it is in a new equilibrium..
With a different set of starting conditions, this situation wouldn’t have been reached?
I am still trying to understand the set of conditions that would move the surface to radiating 16,000 W/m^2 (on average).
In the original article I proposed the (over-simplified) radiation conditions that could significantly lift the surface temperature – and in this article I explained the difference (where radiation conditions can at most keep the surface at the temperature of the top of atmosphere).
Can you find a way to quantify your heat transfer mechanisms to show how your concepts could create such a high surface temperature – quantitively?
Leonard,
The scale height of the atmosphere is a function of the harmonic mean temperature (Tm, Caballero uses different notation).
H(z) = RTm/g
See section 2.4 et. seq. in Cabellero’s Phys. Met. lecture notes starting on page 22. ( http://maths.ucd.ie/met/msc/PhysMet/PhysMetLectNotes.pdf ). The surface temperature could be a lot lower and still have a near adiabatic lapse rate. I should actually do the math, but I have to go out of town this weekend and I need to start packing the car now.
SOD,
I mean the adiabatic lapse rate. As an example of how to get a hot surface, assume a cooler initial surface and cooler efficient long wave radiation absorbing gas (but not liquified) and look what happens when the Solar absorption goes to (average) 160 W/m2. The system is initially non equilibrium, with a lower lapse rate. Since the gas and surface are relative colder, they would initially act as energy sinks, so that more energy is absorbed than re-radiated to space at this time. This is a modestly small energy flux, so it would take a long time for the atmosphere and surface to heat up, but they eventually would. The Solar energy absorption could be at the surface, or in the atmosphere, or at the clouds, but it would get distributed by conduction (diffusion of the gas) and mostly by convection from the non-uniform energy at different latitudes and from rotation of the planet. The sink of energy and effect of distribution would drive the atmosphere toward the adiabatic lapse rate. If long wave radiation has a low energy flux back up compared to the convective energy transmission, the lapse rate would tend to the adiabatic level. The effective height from where the radiation went to space would lock the atmospheric temperature level at that height, and the lapse rate and stored energy would be the source of heating the ground.
DeWitt,
This case would only occur if the outgoing radiation were through an optically this atmosphere. I stated that the ground could be cold and the lapse rate would be the same adiabatic lapse rate, except that the upper atmosphere at the high atmospheric mass at Venus would get so cold that condensation would occur and the atmosphere would be different due to phase change. You are not saying anything I did not already say.
SOD,
I did a back of envelope calculation. It would take order of 100 years to go from 250 K for the ground and atmosphere near the ground (and low initial lapse rate) to heat to 750 K from the specific heats, the mass, and assuming the heat only has to penetrate a couple of hundred meters to reach a low value of conduction to greater depth. This assumes most of the 160 W/m2 are absorbed before the radiation to space approaches the input. Obviously this is a crude but reasonable approximation. The sink effect would result in local energy storage, and convection would then drive the lapse rate toward the adiabatic value.
I think DeWitt and possibly others don’t get what I am saying. The adiabatic lapse rate for an atmosphere is where the actual lapse rate will go unless there is phase change. If the atmosphere has small radiative heat flux, the location of outgoing radiation will be near the top of the atmosphere, and the lapse rate will result in a hot surface. If the atmosphere is nearly transparent to outgoing radiation, the ground will be where the radiation balance is, and the ground will be much cooler, but the lapse rate will still be the adiabatic rate, resulting in dropping temperature with altitude. For in between systems (with significant radiation energy flux), the ground will be in between temperature, but not due to lower lapse rate, but due to a lower level where radiation to space occurs. Venus is mainly the case of small radiative flux compared to convection, so the ground is hot. For all cases, the lapse rate is about the same as the adiabatic lapse rate as long as there is no condensation. Earth is somewhat in between, and the drop from adiabatic lapse rate is mainly due to condensation of water vapor.
SOD,
Yes a tendency toward the adiabatic lapse rate is inevitable if convection is at all available, and convection dominated the radiation energy flux. There will always be variation in lapse rate due to lack of perfect equilibrium but the average always tend toward that value for dry gases. Condensation changes the level some, but the idea is the same. Top down or bottom up heating all can do the job, but top down is slower.
Cohenite,
17 W/m2 is probably a reasonable average level for radiation to the ground as DeWhitt stated
(out of 160 W/m2 absorbed totally), and this probably speeds up the convective mixing, but is not critical for the process to work. Down heating does not require an isothermal or reverse gradient atmosphere. It only requires that the local higher altitude temperature is warmer than it would be if it were at average adiabatic conditions. This is excess energy for that elevation and when forced downward by induced convection (generally from currents from lower to higher latitudes and day to night), this relatively over hot gas heats the lower atmosphere from the excess heat energy available after adiabatic compression occurs at the lower elevation.
SOD,
When I described moving from one initial condition to the adiabatic lapse rate, I was trying to point out that for any initial variation from the adiabatic lapse rate, the tendency is always to drive back toward the adiabatic lapse rate. You are never in exact equilibrium due to non uniform heating, so convective currents are formed, and they always tend to try to restore the adiabatic lapse rate. On the average, they appear to get close. My example was to show a logical process to do the job from most or all of the Solar input heating occurring at high altitude, and showing how it eventually still makes the surface hot. The time lag in some replies being posted sometimes results in our talking across each other. In addition, the limited amount of words in a reply, along with my limited wordsmith skills make my replies sometimes come out less clear than I intend.
Leonard,
Where do you see radiation in the equation for the scale height? It’s proportional only to g, R and mean temperature. Does the adiabatic lapse rate calculation change if the atmosphere is opaque or transparent? No. So there is no reason to believe that the relationship between scale height and temperature has anything to do with optical properties either.
DeWitt,
The relation between scale height, temperature, and radiation come from the fact that optical properties change the mean temperature by trapping heat in the ground and atmosphere. That is what the greenhouse effect is. However the trapping is done by moving the location of the outgoing radiation to a higher location in the atmosphere. The lapse rate does not change, the location along it that is heated to a temperature in balance with the Solar radiation is changed by the optical properties. It is only the optical properties in the region controlling the final outgoing radiation that enters in the process, and for Venus, that is the very uppermost part of the thick atmosphere. Since the amount of greenhouse gas in Venus is 230,000 times as much as for Earth, even a fairly large drop in fraction of greenhouse gas (but replacing it with a non-greenhouse gas) would only change the ground temperature a modest amount (by changing the altitude where the outgoing radiation exits). The high temperature on Venus is both due to the high altitude of outgoing radiation, which is due to the very high mass of the atmosphere and presence of a reasonable amount of greenhouse gas. The adiabatic lapse rate is a gradient of temperature. The absolute level depends where along the altitude the absolute temperature is forced to go.
“The high temperature on Venus is both due to the high altitude of outgoing radiation, which is due to the very high mass of the atmosphere and presence of a reasonable amount of greenhouse gas. “
But the altitude of outgoing radiation is not fixed by the mass of the atmosphere alone. It depends on the heat content of the atmosphere below it. The heat content depends on the opacity. The opacity depends on the concentration of CO2. Even at 96% CO2, the Venusian atmosphere isn’t totally opaque to thermal IR. And, as Nick has pointed out, there’s still radiative diffusion, the Rosseland model, for highly opaque atmospheres Replacing CO2 with a transparent gas would reduce the opacity and by doing so, increase the radiative loss rate and lower the surface temperature. A lower surface temperature would mean a lower scale height and a lower emission altitude.
Unfortunately, Spectralcalc won’t do Venus or I’d do something more quantitative.
DeWitt,
I don’t think we are basically disagreeing with each other on most of the points, only picking at the margins. The basic issue is why is the surface of Venus hot as it is. Keep in mind that the altitude of the effective outgoing radiation times the lapse rate plus the temperature of the atmosphere at the altitude of the effective outgoing radiation is the source of the surface temperature reaching its average level. The reason Venus has a very great height atmosphere is due in part to the mass of gas in the atmosphere. There also has to be enough greenhouse gas to block, and therefore trap, most of the direct radiation from the ground. These facts set up the temperature level. Yes there will be some direct radiation out and some direct Solar energy in. That changes the exact numbers, but not the concept. You keep pointing at the increased radiative loss with less CO2. I think that is less clear than you think due to the cloud layer and other gases present. Since the present amount of CO2 is 230,000 times the amount on Earth, and since the drop in partial pressure is not linear with altitude, reducing the partial pressure of CO2 by a factor of 10 would only lower the height to match the partial pressure for outgoing radiation by less than 10 km (out of about 90), so Venus would still be very hot. Reducing it by a factor of 100 would probably reduce the level less than 20 km, with the details confused by the cloud layer. I can’t calculate the accurate numbers, but was pointing out that the quantity of gas is the dominate cause of a hot Venus as long as there was even a modest amount of greenhouse gas able to raise the height of the outgoing radiation to great enough height. The mean path for absorption is not important to a first order as long as it is much smaller than the height of the atmosphere. The unabsorbed wavelengths do not matter unless they lower the effective radiation height significantly, and I don’t think they will with the clouds in the way. Please tell me where you disagree with the above.
DeWitt,
I have several times repeated that if all of the greenhouse gas on Venus were replaced with an optically transparent gas (and no cloud layer or other blocking layer were present), the surface would be relatively cool. You seem to imply I did not state that. I said a reasonable amount of greenhouse gas is necessary for the surface to be hot, as well as the need for a high gas mass. The point I make is that a super excess of the greenhouse gas is not needed, and only adds a small extra temperature.
And we disagree on that point. There is no super excess and no upper limit, other than the surface temperature of the sun, to the effect of adding more CO2, if there is any left on Venus, which seems unlikely. To put it another way, if instead of replacing the CO2 with a transparent gas, you just removed it, the temperature would drop by about the same amount. Lowering the surface pressure would decrease the line broadening near the surface so I would expect the lower pressure example would be slightly cooler, but the difference between the two cases would be small compared to the total temperature reduction from the starting conditions.
DeWitt,
Removing all of the greenhouse gases or replacing all of them by non-greenhouse gases would result in a cool surface. Removing 90% and replacing it with an equivalent amount of non-greenhouse gas would only drop the temperature by less than 100 degrees C out of 750. Do you disagree with that?
DeWitt,
If you retained 96% CO2 but lowered the surface pressure by 90% (which would require 90% less total atmospheric gas), do you not agree that the surface temperature would drop to much nearer to Earth’s temperature?
Thank you SOD, Leonard, dewitt and co for the fascinating thread.
From what ive read i think most people agree that the Venusian “climate” is due to its atmospheres density and composition…. Ok so 10% o the solar radiation is absorbed by the planet, and 10% o that at the surface, with 90% of it absorbed in the UV spectrum by the clouds… so its a mix o the shell and surface absorption o SW. (at least if what is written here resembles reality http://www.esa.int/esaMI/Venus_Express/SEMFPY808BE_0.html )
So i suppose the real Q here is how did it get that way… If at one time it had a similar surface and atmosphere to earth. And it is often presented as a look into our future by people… it was caused by a runaway greenhouse effect, al la Hansen:-)
Ok, so earth is now how venus was once. Now switch off the magnetic field on earth… and what would the solar wind do to our atmosphere? Id imagine it would immediately start stripping the atmosphere on the night side o the planet, disassociate H2O, H would escape atmosphere, only denser gases wouldnt reach escape velocity, the surface would be left unshielded from the sun, and given time, we would have venus two, or mars two… depending on how much C was available on the surface… I personally think this is as realistic a hypothesis as the runaway greenhouse, that fits what is known of Venus…. and Mars… and is the obvious difference between earth and mars and Venus.
I had heard of the solar wind hypothesis a long time before the runaway greenhouse hypothesis. Both stories end the same i suppose, and could be a combination o the two… http://www.esa.int/esaMI/Venus_Express/SEM0G373R8F_0.html
A lil correction o wording for This “with 90% of it absorbed in the UV spectrum by the clouds…” what i meant was 90% is absorbed in the atmosphere, with the majority being at the cloud level in the UV spectrum…
I have been following the two Venus threads for the past week or so and have finally reached the last comment. I didn’t want to post anything until I was sure it hadn’t already been covered. It hasn’t been so here are my thoughts – I hope I’m not too late.
Leonard is absolutely correct in his analysis, but he is having a little bit of a hard time getting others to understand. Let me approach the problem in a slightly different way to see if that will help. I will use the first law of thermodynamics (dU = dQ – dW) for an adiabatic system under the influence of a electromagnetic field (sun) and a gravitational field (Earth/Venus). For an ideal gas in an unconstrained system (constant pressure) the first law can be expressed as:
dU = CpdT or (1)
dU = CvdT – PdV (2)
I this case CvdT = dQ and PdV = W. This relationship is valid in an electromagnetic field. But for the system to be adiabatic , dQ = 0, and this is not possible for a simple gaseous system in an electromagnetic field unless the net energy flux is zero. But this is not the case in a planetary atmosphere heated by the sun. That is where the gravitational field comes in and a term for potential energy must be added to eqn. (2):
dU = CvdT + gdh –PdV (3)
Now dQ = CvdT + gdh. In the case where thermal flux is added to the system, dT is positive, the system will perform work (PdV) on the surroundings via expansion and the parcel density will decrease causing buoyancy and the parcel will rise. CvdT will decrease due to the expansion and gdh will increase due to the vertical displacement. In the presence of a gravitational field the PV work by the system on its surroundings is derived from its internal thermal energy and converted to potential energy. As a result, for a gaseous system in a gravitational field, dQ =0 (adiabatic) and dU = 0. This also true for a cooling parcel except that PV work is done on the parcel and potential energy is converted to thermal energy during subsidence (what goes up must come down). Thus in a gravitational field eqn. (1) becomes:
CpdT + gdh = 0 or
dT/dh = – g/Cp (4)
which is the lapse rate formula you guys have been working with.
The atmospheric temperature at any height is a function of the local pressure, or vertical mass (PV = nRT), and the total energy contained in the parcel via the net electromagnetic flux resulting from solar absorption/surface heating and emission to space. Radiation does not play a role in the atmospheric thermodynamics since each layer is in local thermodynamic equilibrium with its surroundings and there is no net radiation heat transfer between layers or between the surface/atmospheric boundary. This was covered nicely by Leonard and is empirically supported by the work of Miskolzci (especially in his newest paper which is about to be published in E&E).
I tried to cover a lot in a short space so I hope this intelligible and helps explain what Leonard has been pointing out. Latent heat (Ldq) can also be handled in this manner but I will hold off on that for now.
This comment for WilliamCG follows my one below. I think this is a good analysis, but it is all adiabatic. No conductivity is mentioned. Adiabatic is a useful short-term approximation, but cannot hold in the long run. Conductive, and more importantly radiative transfer accumulates. In the presence of a thermal gradient, it causes constant entropy gain, which can only be removed from the system by doing work. Gas motion does this, but loses KE, which has to be replaced.
Many thanks for this informative and polite discussion.
I understand if this post is snipped/ignored for being barely on-topic or just plain ignorant.
Gas giants as large as Jupiter radiate more light than they absorb. I assume that this energy is created via gravity squeezing the molecules together. They repel each other and the resultant heat is emitted as LW, at which point the newly cooled molecules can be heated again by gravity. I may be *totally wrong* on this and instead a constant slow contraction of the planet is the source. Otherwise:
The reason I mention this is that measurements of the Venusian albedo from Earth and early probes sent there reported it as 0.8 bond. But it is instead listed as 0.76. Could the 0.8 figure be correct and the shortfall is made up by Venus’ thick atmosphere producing heat via gravity?
I know Venus is in no way comparable to Jupiter, and those I’ve mentioned this to have accused me of creating a perpetual motion machine. But if Venus could be shown to be a net producer of heat I think that would prove that pressure creates heat in planetary atmospheres.
Thanks again and sorry for the interruption, I really had to get that off my chest.
Pressure is a catalyst for chemical/nuclear reactions. With gas giants it depends on their mass, if they are big enough they can initiate a fusion reaction. End o the day, a star is just a really big gas giant.(i doubt a gas giant would ever have free oxygen available in any quantity before it instantly reacts with hydrogen.. i dont think chemical reactions could have a lasting effect on a gas giant)
Im sure its “possible” that at some stage the pressure on venus set off planet wide combustion of the more volatile elements present, but it will/has in time ended up with an inert atmosphere. And this would be a short term effect in the greater scheme o things.
BCassidy,
Venus gravity and atmosphere are too small for the gravitational contraction to be a significant factor. In addition, the hard surface is not present on the gas giants until almost at the center, but is only 90 km below the effective top of the Venus atmosphere. The difference in albedo may be just measurement error or may be due to the fact that it actually changes slightly (up and down) with time. Earth’s albedo changes day to day and even year to year due to cloud and surface ice variation so that would not be a surprise.
BCassidy,
Please note that no one here is saying that pressure creates heat as a cause of Venus surface temperature. The heat comes from the Sun. The optical absorption (so called greenhouse effect) traps some of this energy and keeps it in the atmosphere and on the ground. The pressure and gravity cause the temperature variation to be generated, resulting in the hot surface and cooler upper atmosphere.
williamcg,
“Radiation does not play a role in the atmospheric thermodynamics since each layer is in local thermodynamic equilibrium with its surroundings and there is no net radiation heat transfer between layers or between the surface/atmospheric boundary.”
If there is no radiation heat transfer and the temperature profile is adiabatic so no heat can be transferred vertically by convection, then how does the solar flux to the surface get transmitted back to space? If there’s a temperature gradient, then there’s radiative flux because the layer above will emit slightly less energy to the level below than the level below emits to the level above.
DeWitt,
There is probably some Solar radiation that reaches the surface and a small amount of thermal radiation that is transmitted up and out. However, these are not the basic mechanism that heats Venus. The radiation can all be absorbed both ways by the clouds and or atmosphere and there would be no basic difference. CONVECTION does the main job of carrying net energy both ways up to the high altitude where radiation can finely go to space (actually there is little net energy carried, and most is carried from lower latitudes to higher latitudes). Any Solar flux to the surface is carried up by wind currents produced by insolation variations. The temperature lapse rate value is adiabatic on the average, but locally can vary up and down due to the non uniform input. It is this LOCAL variation that generates the wind.
The layer above a given layer does transmit a bit less down, and the layer below transmits a bit more up. There is a net heat transfer from the radiation, but with an absorption effective length very small (say <1 m), the lapse rate only gives a temperature difference of <0.008 K, and the flux transferred is less than 1 W/m2. At higher altitudes the absorption length greatly increases, but the gas temperature is lower, so the radiation heat transfer does not increase very rapidly until you are at a very high altitude. The temperature profile shows a deviation from the adiabatic lapse rate at these high altitudes, and this is due to the radiation heat transfer increasing.
DeWitt,
Leonard’s explanation is correct in that the radiation heat transfer between adjacent layers is very small (negligible) since the corresponding ∆T is very small. However there is another aspect of the system that makes that small effect even more insignificant. You have to realize that a dry atmosphere under the influence of a gravitational field will assume the dry adiabatic lapse rate at equilibrium. Convection is not the means of obtaining the adiabatic lapse rate but is instead the mechanism for maintaining the adiabatic lapse rate equilibrium temperature profile. The atmosphere is trying to maintain an isentropic state of constant energy per unit mass. U = CpT + gdh where dU = 0. (The 2003 paper by Hans Jelbring does a good job of laying out the underlying theory and can be found here http://ruby.fgcu.edu/courses/twimberley/EnviroPhilo/FunctionOfMass.pdf)
An ideal atmospheric system under the influence of a gravitational field, isolated from any ingoing or outgoing energy flux, will assume an equilibrium dry adiabatic lapse rate (dT/dh = -g/Cp). The atmosphere will not be isothermal as is commonly believed. Each atmospheric layer will have the same internal energy content with the lower elevations having a higher temperature (CpT) and the higher elevations having a lower temperature but a higher potential energy (gh). But the sum of the two energy components will be equal at every layer. (The value of the constant U is determined by the overall energy content of the atmosphere). As for the very small radiation heat transfer component between layers, the only effect will be to insure the atmospheric is not static. The lower layer will slightly heat the upper layer and that layer will rise and cool and displace the cooler layer above it. The uppermost layer will descend (at some point) and warm. Everything returns to its original state. The reverse happens for the lower layer. It will cool and sink and displace a lower hotter layer which will rise and cool. Heat is not transferred through the atmosphere but the heat transfer will cause mini PV work events to take place causing some mixing action. But the dry adiabatic lapse rate is maintained. Convection maintains the isentropic equilibrium state.
An ideal atmospheric system under the influence of a gravitational field, undergoing a perfectly uniform steady state energy flux (incoming = outgoing), will also exhibit the dry adiabatic lapse rate. If a parcel of atmosphere experiences a gain or loss of internal thermal energy (a deviation from the adiabat), the parcel will expand or compress and trade off thermal/potential energy via ascending or descending due to the ∆P of the parcel and its relation to its surroundings. Convection will maintain the dry adiabatic lapse rate via transferring mass throughout the atmosphere. That is why radiosonde data in a dry desert at midday will show a dry adiabatic lapse rate and a constant potential temperature profile throughout the troposphere.
An isothermal atmosphere is impossible under the influence of a gravitational field since that would require a net increase in parcel energy content (increased potential temperature) with increasing altitude. That is not an achievable equilibrium condition. Of course in the real world nothing in the atmosphere is at equilibrium and will never be so. But it is probably always trying.
Comments would be greatly appreciated in case I have gotten something wrong or I have not explained my logic clearly.
“Leonard’s explanation is correct in that the radiation heat transfer between adjacent layers is very small (negligible) since the corresponding ∆T is very small.”
This is only true in the limit of high opacity. Otherwise much of the radiation comes from further away, and the gas seen at a point is significantly hotter below than above, hence nett flux. That is the point of my calculation here. Even highly opaque gas can transfer significant radiative flux at the high Venus temperatures.
Williamcg,
Thanks for the more rigorous explanation. I think you got it right. I would like to see a response from SOD at this point if possible. By the way, the: http://en.wikipedia.org/wiki/Atmosphere_of_Venus site gives a lot of discussion on Venus, and points out that there is large convection, including 3-D motion, and even extends to the surface, although the speeds are much lower near the ground.
Williamcg,
I just read your reference by Hans Jelbring. I am sorry but he has it wrong. The factor he left out is that the need for the radiation to space requires a gas that does radiate to space in order to pin the balance of in and out energy at the top of the atmosphere. Since the thermal radiation emission line width of the gases at the local temperature only radiate at the black body rate for those line widths, the upper atmosphere can’t remove the energy received by the surface or by the gases or clouds unless those line widths dominate the energy spectrum. The net result for no greenhouse content is that the surface temperature rather than top of the atmosphere temperature is where the input to outgoing radiation balance, and the surface is cool as if the atmosphere were not significant. There is still an adiabatic atmospheric lapse rate, but it drops going up from the surface value rather than rises coming down from the upper atmosphere. If there is sufficient greenhouse gas, the net effect is to move the radiation in/out balance layer up in the atmosphere, thus with the same adiabatic lapse rate, results in a hotter surface. You do need the greenhouse gas, and the issue is where the outgoing radiation effectively is located.
I agree with almost all that, and I like the use of U. The problem is that maintenance of the lapse rate requires work to overcome losses by heat diffusing down the temperature gradient, either by conduction or gas-to-gas radiative transfer. You have alluded to this
“the heat transfer will cause mini PV work events”
The energy to do that work has to come from somewhere.
My contention is that when you have a positive lapse rate, heat transfer by conduction and radiation must occur. The processes are not reversible, and create entropy. For the lapse rate to be maintained, the heat must be pumped back. Gas in motion does this, bringing the gradient back towards the dry adiabat.
But it draws KE from the flow, which must be replaced. So I disagree – without an energy supply, gas under gravity will become isothermal. In motion, with a source of KE, it moves towards the dry adiabat, but can’t reach it, through this mechanism alone. The reason is that the heat pump loses afficiency as the adiabat is approached.
The usual source of energy is a heat engine resulting from the flux of solar energy.
This comment was meant for WilliamCG
Leonard Weinstein:
I do hope to reply in detail within the next few days, and certainly by the weekend. I have half-written several replies in the last few days as the discussion has progressed without the opportunity to complete them.
Unfortunately, “FirstLife” has recently taken over.
Nick Stokes,
You do not get conductive heat transfer up the temperature gradient due to the lapse rate. The lapse rate is in fact the condition of no conduction of heat, since the gravitational potential energy to kinetic energy variation is exactly the cause of the lapse rate. You can get conduction of heat by radiation, but I indicated that if it small enough (as on Venus), that it is not the main mechanism for the action. These are not cases of all or nothing, but a mix with a need for several processes. I do agree that the analysis by Jelbring is not quite valid due to the radiation conduction being left out to set the location of radiation to space, but it does show how the radiation in fact helps drive the mixing that maintains the average lapse rate.
Leonard, I disagree. Fourier’s Law is a Law. If there is a temperature gradient, there will be conduction down it.
The carriage of heat by convection, modified by compression/expansion, is a different process with a distinct mechanism. It can carry an equal and contrary flux, but it cannot prevent conduction, or the similar radiative transfer process.
You can quantify the conduction rate of entropy production per unit volume – it is k(L/T)^2, where k is the conductivity and L the (actual) lapse rate. That entropy has to go somewhere, and, of course, its creation is irreversible.
Nick Stokes,
There would be radiation either from a greenhouse gas to space, or from the surface to space if there is no greenhouse gas in the atmosphere. Without Sunlight, the continual outgoing radiation would make the entire system get colder and colder. Thus you need input energy to have a system that does not go to zero energy. This is why your statement that you need a source of energy is valid, not because it lets the system go isothermal (the isothermal would be absolute zero).
You could have your atmosphere with a shell, uniformly and constantly irradiated. That would create an atmosphere with stable uniform positive temperature and no flux.
Nick,
Conduction in a non convecting gas is actually only diffusion of molecules with more kinetic energy to regions with less kinetic energy. If at the same time there is a loss or gain of velocity from the conversion of gravitational potential energy to kinetic energy the two effects can and will exactly balance out without a supply of replacement energy. This is not the same as conduction in the absence of a gravitational potential well. The molecules do not need continued input of energy to continually trade between the two effects off UNLESS there is radiation loss, which does not use gravitational potential energy to kinetic energy to maintain the lapse rate. The Solar energy input is only needed to replace the radiation energy lost. williamcg showed that, although he looked at the case of no radiation, which is not exactly true, but the logic is the same for small radiation levels.
Leonard,
I think I’m convinced by your argument that gravity does modify molecular conduction, so that at the adiabat, there is no conduction upward, and no need for heat to be pumped downward to balance. So I was wrong about the absoluteness of Fourier’s Law.
However, this doesn’t apply to the other, much greater radiative transfer which acts like enhanced conduction. This is unaffected by gravity and will cause heat to flow along the gradient. I’ve been describing this as Rosselande conduction, but I notice that the formula I’ve been citing is just Eq 1 of Ramanathan and Coakley, so I’ll cite that:
q=(16 F0/3)*a*(L/T)
where q is flux, F0 is BB flux, a is absorption length, L is lapse rate and T is temp. DeWitt says a may be hundreds of metres. Let’s say at the venus surface F0=16,000 W/m2, a=0.1 km, L=7 K.km, T=700K, then
q=85 W/m2, which is actually a lot more than the downward insolation at that point.
Even if a is 10m, the gradient is sufficient to carry almost the entire flux to balance sunlight reaching the surface..
Nick,
As was pointed out by williamcg, the radiation that is absorbed is converted to a small local temperature increase which then caused some buoyancy which mixes the gas to restore the unbalance. The slightly warm layer is also continually radiating upward to the next layer, and the net effect of the radiation flux is to help drive the mixing. Keep in mind that there is latitude and rotational input variation, so it is not a sheet effect, but local regions. In addition, if you look at a picture of Venus, you see structure in the clouds, so albedo varies a lot locally. The only location that actually has a forced average temperature is where the final radiation leaves to space that matches the absorbed incoming temperature. The fact that this is not in a thin sheet but a finite depth make the problem more complicated, but not basically different. The upper surface of the clouds may in fact be the beginning of the main location of outgoing radiation, since it likely blocks all direct radiation from below.
Leonard, I can’t agree with that. There’s no reason why you couldn’t have a steady state radiative flux, which is what the Rosselande (or R&Coakley) model envisages. Air wouldn’t heat and rise; it absorbs and emits at the same rate, but the temperature gradient ensures that the nett result is a flux as if conducted.
In any case, I don’t understand the rise and fall argument as presented. At the adiabat, it wouldn’t convey nett heat at all; it is just an exchange of gas. Below the adiabat it would – that’s my heat pump notion. But that then requires energy.
Nick,
“Leonard, I disagree. Fourier’s Law is a Law. If there is a temperature gradient, there will be conduction down it. “
Are you now adopting my old position which I’ve abandoned? Shouldn’t the correct measure be the potential temperature gradient not the absolute temperature gradient? If the potential temperature gradient is negative then convection will act to increase it. If it’s positive, eddy diffusion will transfer heat from higher to lower altitude.
Leonard and Williamcg,
A gray atmosphere model isn’t really accurate once you get above the surface because it implies redistributing radiative energy across the whole spectrum at each level, but it should be a fairly good approximation at the surface. At 730 K surface temperature the net surface flux to the first 0.5 kilometer is a very strong function of the optical thickness:
optical thickness %transmission net flux
10.0 0.0045% 0.013 W/m2
9.00 0.0123% 0.035
8.00 0.0335% 0.096
7.00 0.0912% 0.260
6.00 0.2479% 0.708
5.00 0.6738% 1.934
1.00 36.788% 168.8
Given that ~5% of the flux at 730K is at wavelengths shorter than 3 microns where even at 91 bar CO2 starts to become transparent, I seriously doubt the optical thickness at the surface is as high as 10. A reduction in optical thickness from 10 to 5 is equivalent to replacing 50% of the atmospheric CO2 with a transparent gas.
If you make the optical thickness infinite, then you force the atmosphere to be isothermal because any reduction of temperature with altitude by convective transfer will create a radiation imbalance, forcing the level with lower temperature to warm and the level with higher temperature to cool.
The above calculations are for a lapse rate of 6.5 K/km. A higher lapse rate would make the rate of increase of net flux with decreasing optical thickness even greater.
DeWitt,
No, it’s been my belief all along that conduction, both molecular and radiative, occur and their flux balanced by convection effects. I’m thinking more about Leonard’s (and, I think, WilliamCG’s) proposition that it is just balancing PE against KE for individual molecules. But there’s no eddy diffusion there, or thoughts of moving parcels of air.
Nick,
Molecular diffusion would do the job. In fact, that is all that causes heat transfer in gases.
Using the HITEMP database for SpectralCalc, the average transmittance for a 0.5 km path at 92 bar and 730 K from 500-5500 cm-1 is 0.091 ( http://i165.photobucket.com/albums/u43/gplracerx/Venusatmosphere05kmthickatsurfaceco.png ). That’s rather a long way from an optical thickness of 10, 2.4 in fact. Using a black body emission curve with an emissivity of 1 and a temperature of 730 K and assuming that transmission at less than 500 cm-1 is zero, the fraction of the surface emission that reaches an altitude of 0.5km is 8.72% or 1,400 W/m2. Obviously, very little of that gets to space. However, for radiative transfer purposes, the Venusian atmosphere cannot be considered opaque at all wavelengths over path lengths less than the whole atmosphere and radiative flux ignored compared to convective flux.
For an atmosphere that transparent, a gray model isn’t appropriate and I can’t calculate a net radiative flux at the surface easily. There will be too much contribution from higher altitudes. If I wanted to spend that much time, I could calculate the radiance and absorptivity at 0.5 km intervals and add it all up, but that seems like a lot of work.
Leonard,
“The lapse rate is in fact the condition of no conduction of heat, since the gravitational potential energy to kinetic energy variation is exactly the cause of the lapse rate”
So you are arguing that the lapse rate g/Cp will occur even if no solar radiation hits the surface. You have persuaded me!
But in the case of real Venus and Earth everyone is already convinced that we do have a lapse rate, and your argument seems also to imply that a large part of the reason for the hot surface is the amount/mass of the atmosphere (and some ghg for starters).
Let’s make a thought experiment on earth:
If we raise the surface about 5 km and keep the atmosphere above 5 km (now 0 km) the same as before. Would that not mean a surface temperature ca 33 C colder, ie -18 C. That temperature is the same as the bare Stefan- Boltzmann calculation
T=(solar constant*(1-albedo)/4/SB)^1/4
would give. In that case the often stated greenhouse effect of 33 C vanish! ??
But I guess that does not say much about the greenhouse effect, only that the often cited 1st approximation with the Stefan-Boltzmann calculation is rubbish?
“Would that not mean a surface temperature ca 33 C colder, ie -18 C. That temperature is the same as the bare Stefan- Boltzmann calculation”
No. It would be colder, but not 33K colder. You’ve removed about half the atmosphere if you take away the lower 5 km. Teff would still be 255 K, but now the radiative altitude would be ~3km above the surface and the surface temperature would be 15-20 K higher than Teff. That’s just a crude estimate, though. It might even be warmer because Teff changes with albedo and there might be fewer clouds resulting in a lower albedo, or colder because there would be more ice. In fact a snowball earth might be likely. But there would still be a greenhouse effect and Tsurf would be higher than Teff.
I decided that I didn’t really need to do more than 5 km and that’s within reach. Unfortunately, Spectralcalc produces a different number of points at different pressure and I’m struggling to get around that. But as a starting point with a blackbody surface at 695K at 5 km and 7 K/km lapse rate, the net radiative flux at 4.5 km is on the order of 19.6 W/m2 upward. Maybe I should just look at the first 0.5 km and use 50 m layers at constant pressure.
DeWitt,
First, there is significant water vapor on Venus (20ppm but at 92 bar), and there is SO2 to add to absorption. There is also a lot of pressure broadening. However, even if the lower atmosphere were more transparent, the haze and cloud layers dominate most of the rest, and they are optically very thick. One question to consider is what is the outgoing spectral distribution. If it is mostly shorter wavelengths consistent with the surface temperature, then the atmosphere should be passing a lot of surface energy out, and the total energy radiated out should exceed the small Solar input. This would cool the surface to a lower temperature. The fact it does not indicates this radiation is not transmitted.
I looked at the pressure and temperature profiles measured for Venus and looked at the relative radiation transmitted layer to layer (for one effective absorption length) relative to the value at the ground, and found that if you assume a gray atmosphere (uniform wavelength absorption), that the length of the equal energy absorption path at 50 km is only 2 X that of the ground, even though the pressure has dropped from 92 bar to 1 bar. The reason is that the relayed absorbed radiation intensity has dropped due to lower local temperatures, and the T^4 driver, which is a much larger effect than the pressure drop. The transmission in the lower atmosphere is not the cause of the outgoing radiation, the transmission in the upper atmosphere is. If you dropped the partial pressure of CO2 by 10 X, the new height to match that partial pressure of CO2 would only drop about 10 km out of 90, and thus only drop the temperature increase by 670 K. If you dropped it by 100X, the drop to match the new pp would be a little below 80 km, so the temperature at the surface would be possibly >605 K. I think the resulting temperatures would be grater than those shown values, due to readjustment of the temperature at the new atmospheric levels from the existing values (it is effective density, not pressure that is important).
DeWitt,
>670 K, not by 670 K.
SpectralCalc fixed the bug that was keeping the blackbody source from working correctly in the gas cell emission calculator. For a path length of 500 m with a lapse rate of 7 K/km, a surface temperature of 730K, average pressure 90.5 bar, gas temperature average 728.25 K and a blackbody source at 726.5 K at 500 m, the net upward flux at the surface is 52.13 W m-2 sr-1. For 100 m with temperatures adjusted, it’s 11.73 W m-2 sr-1. I also calculated for 200, 300 and 400 m, plotted and fitted a linear trend to extrapolate net emission to zero path length. R^2 = 0.9998. The intercept was 1.905 W m-2 sr-1 or 5.98 W m-2. That’s 35% of the estimated average solar radiance reaching the surface of 17 W m-2. That’s very comparable to the 39 % of net surface emission by radiation from the Earth ( 100*66/168).
That may actually be an underestimate because I’m including path lengths that are too short. The blackbody approximation for the top of the cell will result in too high radiance and too low net emission at very small path lengths.
Leonard Weinstein,
“I just read your reference by Hans Jelbring. I am sorry but he has it wrong.”
I think you missed what he was trying to communicate. There was great confusion back in 2003 as to what the GE really was. He was pointing out that it is the lapse rate that determines the atmospheric temperature profile and not GHG radiation. The GE is simply determined by the optical depth of the atmosphere (D) and the lapse rate determined by the gravitational field. His model sets the altitude (D) at which radiation escapes to space as an arbitrary quantity. But the lapse rate is independent of whether or not GHG are part of the atmospheric composition or the total mass of the atmosphere. The reason I cited the paper was for the following points that were being discussed on the thread:
• The atmosphere is trying to reach an equilibrium where there is constant energy per unit mass.
• The dry adiabatic lapse rate will exist in a static atmosphere as well as a uniform dynamic one.
• The solar radiation does not have to reach the surface for the dry adiabatic lapse rate to form.
• The surface temperature can be determined by counting backwards from the atmospheric temperature at a given altitude.
williamcg,
Jelbring is, as Pauli once said, is not even wrong. How is his model anything at all like the real world? How can you even calculate a delta T between the surface and the shell if you don’t know the energy content, which isn’t specified anywhere? But let’s throw some numbers in just to see what happens. Say the surface is at 300 K and the the distance between the shell and the surface is 10 km and the atmosphere is transparent. If the dry adiabatic lapse rate is the only determinant of the shell temperature then it will be at ~200 K. But wait, the surface will be radiating at 459 W/m2, but the shell will be radiating only 91 W/m2. That means that the rate of convective transfer from the shell to the ground must be 368 W/m2. But you can’t transfer energy by convection if the lapse rate is at the adiabatic rate. So the only way this works is if the spacing between the shell and the surface is vanishingly small. But that makes it a trivial case. Seems like a gaping logic hole to me.
4.55 billion years ago, a big ball of gas next to us reached temperatures of 10,000,000K in its core (before nuclear fusion started) despite the fact that incoming radiation was limited to a miniscule amount of star-light and cosmic background radiation.
Atmospheric Physics models based on the greenhouse effect only are obviously incomplete.
williamcg,
I see your point. He is correct, except that the need to show the temperature at a given altitude does require additional information, and that information was just left hanging. That is where the absorbed Solar energy and average location of outgoing radiation comes in.
DeWitt,
The lapse rate is only applicable if the location of the outgoing radiation that matches the absorbed incoming radiation is found between the ground and the upper atmosphere. This sets bounds on possible temperatures, and thus energy flux out. By selecting an arbitrary temperature outside this range, you can force the expected outgoing radiation location to be outside the possible limits and this is not physically possible so is an ill-posed problem. In order to get a real possible answer, first you find the location and level of outgoing energy that matches the absorbed incoming energy, and thus determine the temperature at that level, and then apply the lapse rate below this level to the ground to find the ground temperature. If the atmosphere is transparent to radiation, the ground is where the temperature is determined, and you then apply the decreasing temperature upwards corresponding to the lapse rate. At some point, the temperature reverses due to ionization and dissociation effects, and Solar wind input.
DeWitt,
Did you read my second post located here? https://scienceofdoom.com/2010/06/22/venusian-mysteries-part-two/#comment-3485. Some of the answers to your statements are there, but maybe I didn’t explain things clearly. Jelbring purposefully left his paper qualitative rather than quantitative as he explains at the end of the paper. He was trying to lay out general physics/meteorological principles with respect to atmospheres under the influence of a gravitational field. His primary purpose was to show that the Greenhouse Effect (GE) was independent of atmospheric mass, atmospheric energy content or radiative properties of the atmospheric gases. He did state that if the temperature (not energy content) were known at any given height, then the surface temperature could be calculated by working backwards using the adiabatic lapse rate.
As for your example, you are letting your radiation paradigm get in the way of basic thermodynamics where mass is just as important as energy fluxes. (If your world is only composed of W/m2, your world is two dimensional like Aristotle’s Cave). Let’s take your example and put some mass related numbers to it. The surface is at 300K. Assuming earth atmospheric properties, the energy content at the surface is 300.9 J/g. Assuming a zero net energy flux to and from the atmosphere (this can be either a static or steady state condition but incoming solar = OLR), the energy content at 10 km is also 300.9 J/g. The only difference in the energy content is that at the surface all 300.9 J/g exists as thermal energy (mCpT). But at 10 km, thermal energy content is only 202.9 J/g with 98 J/g existing as potential energy (mgh). That is why the temperature profile follows the dry adiabatic lapse rate. The total energy content on a mass basis (U) is not changing from the surface upwards, only the thermal energy component is changing. And remember that this lapse rate profile will exist in a stable atmosphere (at equilibrium) no matter whether the atmosphere is static (no convection) or steady state (with convection). Convection transfers mass, not heat. This is a common misconception. Heat transfer initiates convection but plays no role in the actual mass movement. The actual mass movement is driven by ∆P not ∆T.
Your radiation energy flux analogy between the surface and 10 km makes no sense. Radiation heat transfer plays no significant role in the troposphere. The various layers are at LTE and are just trading photons with each other. At lower elevations they are just trading more photons with each other than at higher elevations. No net radiative energy flux occurs across the atmosphere (see my post above).
I hope this clears up some of your questions.
“No net radiative energy flux occurs across the atmosphere (see my post above).”
That statement is a demonstrably false assertion even for Jelbring’s shell model. The only way it could be true for the shell model is if both surfaces were perfect reflectors. But IIRC, it was stated that the shell was black, which would imply an emissivity of 1 and a reflectivity of 0.
That the molecules in a thin layer are in LTE says nothing at all about the equilibrium between layers. Radiative emission/absorption doesn’t care about gravity or gravitational potential energy. The Planck equation uses absolute temperature not potential temperature. You cannot simply wave away atmospheric radiative energy transfer by saying it doesn’t exist when it obviously does.
DeWitt,
I think we are talking about different assumptions put in at different times. The discussion has been morphing back and forth, and I am not even sure which point we are in the discussion. If it about my comment at June 23 at 7:16, if the planet surface were an emitter due to its temperature, and the shell a perfect reflector on the side facing the ground, the NET radiation transfer would be zero. The outward facing side could still be a black body radiator. Think a sheet like polished gold (but a perfect reflector) painted black on the outside. All radiation up would be reflected back. The radiation energy would be trapped and uniform in the atmosphere. i.e, no NET radiation flux. The atmosphere would go to the adiabatic lapse rate and be maintained with mainly induced convection and some small amount of diffusion driven by the temperature variation on the outer shell (from latitude variation and rotation) unequally heating the gas just under it. It would be a less energetic mixing than if heated from below, but would still drive the mixing enough to maintain the lapse rate on the average. A perfectly reflecting surface is still fully capable of direct contact heat transfer, which is a molecular collision effect, not radiation effect.
DeWitt,
Think perfect thermos bottle as far as radiation effect.
Leonard,
If the atmosphere has any absorptivity in the thermal IR and there is a positive lapse rate (temperature decreases with altitude) then there will be radiative diffusion (for lack of a better word) from higher to lower absolute temperature. If the lapse rate is less than the adiabatic rate (potential temperature increases with altitude) there will be heat transfer from higher to lower potential temperature. The actual lapse rate will then be less than the adiabatic rate but more than isothermal. That calculation looks to be non-trivial.
Molecular heat transfer by convection or (eddy) diffusion cares about total energy so the rate depends on the potential temperature gradient. Radiative heat transfer could care less about gravity and gravitational potential energy because it depends only on the absolute temperature gradient.
It doesn’t matter whether the shell is perfectly reflective or perfectly absorptive or anything in between as long as the transmissivity is zero. The flux down at the shell surface will be exactly the same.
DeWitt,
“You cannot simply wave away atmospheric radiative energy transfer by saying it doesn’t exist when it obviously does.”
I didn’t say that atmospheric radiative energy transfer doesn’t exist. I said that NET radiative heat transfer is nil across any significant distance through the atmosphere. I also hope you realize that I am only speaking about the gaseous phase of the atmosphere. Solids and liquids such as clouds, water droplets, dust, aerosols, etc. are a different story. As far as equilibrium between the layers, I discussed that in the previous post that I linked to.
“Radiative emission/absorption doesn’t care about gravity or gravitational potential energy.”
It’s not the form of heat transfer that matters. It’s what happens to the system after heat transfer occurs that matters. A parcel of air will act the same whether or not the heat transferred to the system is via conduction, convection, radiation or latent heat. The process of heat transfer doesn’t matter, just the atmospheric behavior that results from the transfer. Thus it’s immaterial whether the heat transfer process cares about gravity or potential energy. But the mass receiving the heat will care very much about those things. Remember the first law: dU = dQ – PdV; which can be expressed as dU = mCvdT + mgdh – PdV for a gaseous atmosphere. There are three terms that constitute the energy of the system; only one of those terms is solely dependent on temperature. The other two are potential energy (which does care about gravity) and work energy (which also cares about gravity). And more importantly, energy can be transformed from one to the other in the system. Any approach to model a thermodynamic system that only considers temperature will almost always be wrong, especially when the system is influenced by two separate fields (electromagnet and gravitational).
“The Planck equation uses absolute temperature not potential temperature.”
Yes it does. But also remember that potential temperature includes the potential energy component which is ignored by the Planck equation. That is why you can’t look at the system from a purely radiative heat flux standpoint.
I agree with Leonard that the discussion has gotten off track.
williamcg,
No the discussion has not gone off track. Re-read the original post. This is exactly the topic of interest, that is, the temperature gradient of an atmosphere inside a closed shell with the shell temperature fixed. Leonard and I agree, I think, that if there is no atmosphere or the atmosphere is perfectly transparent, then the shell temperature and the surface temperature will be the same. The difference between us is about what happens as the atmosphere becomes more opaque in the thermal IR. I may be bending on that a little. If the atmosphere were perfectly opaque at all altitudes, which is impossible in a real atmosphere, then radiative diffusion would vanish and thermal diffusion would force an adiabatic lapse rate. Maybe.
My reading of your position is that even for a perfectly transparent atmosphere, the surface temperature will be higher than the shell temperature with the magnitude determined only by the adiabatic lapse rate and the distance between the shell and the surface. In other words, you ignore radiative transfer completely. That position violates basic physics.
I thought maybe some simple calculations might help make things a bit clearer why we can ignore temperature, heat and radiative properties in some respects of the lapse rate (I’ll probably mess them up though), so here goes.
Let’s take TEV2 as our base and assume that it receives energy in the amount of 160 W/m^2 . Which means the shell would have a blackbody temperature of approx. 230 K (I used spectralcalc, but it comes from the j=sigma*T^4). Now we’ll assume our atmosphere consists of single atom gas with a molecular mass of 40 g/mol (which gives a particle mass of mp=M/N=6,64*10^-26 kg).
For a single atom gas, we should be able to find the average kinetic energy of a paricle, from this formula Ek=3/2*k*T. Where k is the Boltzmann constant (k=1,38*10^-23 J/K). From here we can find the average Ek of our gas paricle:
Ek=3/2*k*T=4,76*10^-21 J
As Ek = 1/2*m*v^2 we get the speed of the paricle by average:
v=(2*Ek/m)^½=(2*4,76*10^-21/6,64 * 10^-26)^½= 379 m/s
Now as it is really high up in the sky (let’s say 10 km) it will have a long way to fall down to earth and the gravitational acceleration is 8,9 m/s^2, we can find the speed of the particle on ground by
vg=(2as+v^2)^½=(2*8,9*10^5+379^2)^½=566,94 m/s
Now going back to kinetic energy:
Ek2=1/2*m*v^2=1,07*10^-20
And to Temperature:
T2=2*Ek2/(3*k)= 2*1,07*10^-20/(3*1,38*10^-23)= 515,45 K
The same calculation can ofcourse be made in more direct ways, but I distanced it from Temperature and heat as much as possible on purpose.
I also assumed that the paricles would be freefalling through the atmosphere, wich is ofcourse directly not true (they will collide with other particles almost immediately). However as gases are mostly empty (the electomagnetic potential to counteract gravity is rather small) and Sir Isaac was hit in the head with large fruit, went quite insane, and forbid stuff to lose momentum when colliding with other stuff, this calculation should hold true, despite individual particles really not falling that much (the momentum is still carried on).
Leonard,
I have more than a sneaking suspicion that any molecular collision with a perfect reflector will always be elastic. In the end, all energy transfer, at normal thermal energies anyway, is by photon exchange and the exchange with a perfect reflector must by definition always balance. Most gas collisions, for example, are elastic.
Leonard Weinstein:
Can you clarify some points? As the discussion has moved to and fro with different models in view it’s likely that specific comments lined up with something different from the original assumptions of TEV (thought-experiment Venus, aka the article).
On June 23, 2010 at 7:16 pm you said:
Later, at June 29, 2010 at 1:19 am you said:
Now probably the 2nd statement was not TEV. And the first one was TEV modified by the change of an optically transparent atmosphere.
This optically transparent atmosphere is most interesting – considering that you believe the surface will be similar to real Venus.
SOD,
You left out the critical part out of my statement for June 23 at 7:16. A shell is placed at the average altitude where present outgoing radiation goes to space. The shell is assumed to be a perfect reflector down. This trapped the radiation like in a thermos bottle. The shell temperature was set by the external balance of Solar input and outgoing radiation (the outside of the shell was defined as an absorbing and radiating body with the same temperature distribution as Venus upper atmosphere at that altitude). Inside the shell, the gas hitting the surface was assumed to be in thermal equilibrium after collision. There may be an issue of whether a perfect mirror has the thermal conduction to a gas in contact like real materials, but near perfect mirrors do, so I assume this still holds. Given that any planet surface radiation is now exactly balanced by back radiation from the reflection, there is no net radiation heat loss from the planet surface (just like there would be no net heat loss from a thermos bottle due to radiation). Since the gas was assumed to be totally non absorbing of radiation, the presence of a large amount of radiation has no interaction with the gas. Radiation is now out of the picture. The only thing that sets the resulting gas temperature is gas interaction by collision with the outer shell, which was defined as having a temperature distribution like the upper atmosphere of Venus. Now the adiabatic lapse rate will form on the average, and be maintained on the average by diffusion and convection of the gas. This lapse rate times the altitude plus the shell temperature gives the hot surface temperature.
The second statement I made to DeWitt on June 29 at 1:19 wasmeant to refer to the case with NO outside shell and an optically transparent atmosphere (direct radiation to space). I later realized that I may not have made the distinction clear which model I was referring to, and that is why I made the statement about “different assumptions put in at different times. The discussion has been morphing back and forth, and I am not even sure which point we are in the discussion”.
SOD,
If you read the June 29 1:19 statement to DeWitt, please note “(and no cloud layer OR OTHER BLOCKING layer were present)”. I think this is actually clear which case I was referring to for that statement.
This string has gotten so long and discussion gone back and forth on different variations of assumptions that it is getting difficult to keep everything straight. This is made even more confusing by answers coming at greatly different times.
SOD,
Please note that the optically transparent atmosphere and mirror shell almost exactly match what a near perfect optically absorbing atmosphere and no shell will do if the altitude where absorbed Solar input and radiation out is the same as the shell height, and the absorbed Solar energy matched the actual level into Venus. There would be radiation heat transfer, but it would be very very small, since back radiation would be almost exactly the same as radiation up until the upper atmosphere is reached. Again the upper atmosphere energy balance would set a reference temperature, and the adiabatic lapse rate set a temperature increase to the surface.
I have difficulty visualizing the effect of large-scale atmospheric movements creating the massive difference in temperature between a 730K surface and a 230K TOA.
Trouble visualizing could be my problem.
But most of the arguments in favor of this have been qualitative, not equations which can be solved. I realize large scale convection is not an easy mathematical problem to solve.
I’m not sure I can get my arms around this problem to distill down the different ideas presented, especially as I realize that the “problem” in understanding may be mine, not others..
With that proviso, some comments here and in following comments – please pull me up if these are misrepresentations of your ideas.
Nick Stokes June 25, 2010 at 1:20 pm explains how rising and falling gases will follow the adiabatic lapse rate.
At other times, maybe explained that not enough work will be present in TEV (thought-experiment Venus) to do this.
Leonard Weinstein has explained at June 23, 2010 at 12:56 pm that in an opaque atmosphere:
And yes this is correct for a 1m layer. Now let’s consider a 10km layer. The radiation into the layer from below is from a 730K surface, or about 16,000 W/m^2.
The radiation from the top of the layer (653K) out is 10,300 W/m^2. Therefore we still need a substantial source of energy to maintain this.
In real Venus we have it in a radiative mechanism of an atmosphere transparent (almost) to solar radiation and opaque to longwave (note this is idealized). In TEV, we don’t have a radiative mechanism.
What I have trouble visualizing is how large scale movements of the atmosphere can create this exact same effect.
Others do not?
SoD,
I think in this quote, Leonard was doing the same calc that I was using the Ramanathan Eq 1 (and getting similar results). It’s for nett radiative flux in the presence of a temp gradient. The 1m layer is related to the absorption length.
I draw a different conclusion. Near the surface, the nett flux is small – 10 W/m2 or less. It balances the amount of insolation that reaches the surface. At much higher levels where the flux is 160 W/m2, the opacity is much less. Against this, so is the temperature. But still, it seems to me that the role of IR flux (gas-to-gas) is important. It’s nett, so it isn’t the 16,000 W/m2.
Here’s what I take from the discussion so far:
1. I now agree with LW and WCG that the adiabat can be seen as a uniform U requirement, and in the absence of GHG the adiabat can be maintained without work.
2. However, with GHG there is a substantial down-gradient IR flux. If that balances insolation, fine. But with the TEV (insolation blocked), there is a problem.
3. Forced convection can in principle pump heat down, countering the IR flux. However, the energy required is on the scale of the original insolation, and it’s hard to see where it could come from.
4. With low opacity, as DeWitt has said, IR exchange would force a near temp balance between shell and surface. And if no shell, then the surface would be kept Eartyh-like by heat loss to space. In either case a cool surface.
Leonard Weinstein
I’m really not trying to put words in your mouth. It’s the 4th time of reading through the comments and wanting to be sure I understand what people are really trying to say.
Let me just ask instead.
If we had all of the solar radiation received close to the top of atmosphere (like TEV), and then an optically transparent atmosphere below to the surface, you believe the surface would be the same temperature (or hotter) as real Venus?
SOD,
Also please note the statement leading to the present discussions (a shell that is a optical absorber and radiator on both sides) was used with an optically absorbing atmosphere assumed. The only purpose for this shell was to show that transmission of Solar energy to the surface of Venus was not needed for the hot surface to result. This became confused with other issues. If some sunlight hits the surface, the convection would be more energetic, but convection still occurs when heating from the top. A lot of the following discussion by me was an effort to show where the temperature gradient causing the eventual hot surface came from. williamcg did a good job of formalizing the mechanism I was verbally trying to explain.
SOD,
I just got your 11:40 question after I made the other statements. We are talking some past each other. In response to your last question, this is the difficult one. Radiation from the planet surface would be in balance with the shell, and the shell has to radiate to space what it gets from the Sun. It appears the surface would be cool (the shell temperature). However, the adiabatic lapse rate still tends to form. A cool surface would tend to cool the air above it by conduction, thermal diffusion, and convection (not radiation), and the cool layer would be lie close to the ground and act like an insulating layer. The net result would be a reduced lapse rate at higher altitudes, going to a negative effective lapse rate above the surface to eventually match the ground temperature to the shell temperature. Please note this is the most unrealistic case possible. The realistic ones are for the gas to be optically absorbing for this shell case, or a shell mirror for an optically transparent gas.
Leonard,
This last transparent gas with shell case is interesting. As I understand, you say that the adiabat is the zero-flux gradient, and isothermal would imply a conductive downward flux, which would indeed tend to move the slope to adiabat. However, that flux is very small. If the surface warms to above shell temperature, then there is an IR flux (nett) back. So I think the answer is a very small positive lapse rate, which would imply a small conductive flux down, and a balancing IR flux up.
Nick,
The gas would tend to act like you say except for the fact that colder gas is more dense, and thus would tend to make a relatively stable layer close to the surface. Thermal diffusion (conductivity) is a very slow process compared to convection, so this layer would tend to act like an insulator, and thus more likely allow the steeper lapse rate above the near wall layer than the uniform convective case. I would guess that the cold layer would be only a few km thick at most, and possibly less. The gravity effect is small in a few km, so it would not take much heat transfer to to support this. Please note the reason the air above Earth and Venus atmospheres are not mixing much above where the lapse rate reverses is due to the stable effect of that reverse gradient.
Nick and SOD,
I ran a case of using Argon to replace CO2 as an optically transparent atmosphere. If the lapse rate heated the atmosphere to 750 K and the shell was 200 K, the surface would be just a small amount above 200 K, but the gas would still heat going down from the shell to near 750 K. Assume the gas cooled near the ground by purely thermal conduction in a cold and stable ground layer. If the gas cooled from 750 K to 250 K in just the last 500 m, the conductivity of Argon would result in only about 0.016 W/m2 thermal conduction. The excess radiation (of 0.016 W/m2) needed from the ground to the shell to maintain that cold ground would then be taken from the shell by downward conduction from the shell, and so the energy would circulate in that way. There would still be large scale convection above the ground layer to maintain the lapse rate in changing latitude and rotation positions.
Nick and SOD,
Please note that a ground layer even only 5 m thick with a temperature drop of 500 K in that short distance still would only conduct 1.6 W/m2! This relatively very cold layer would have a density increase of a factor of about 3 in that short distance so would be very stable.
Leonard,
It may be only 1.6 W/m2, but where does the heat come from, and how? That’s the reason I don’t think you can have kinks in the profile – there’s no heat source in the Ar.
Nick,
The reversed lapse rate due to conducting the energy out of the gas next to the wall results in local conduction and convection for the gas ABOVE that reversed layer being slightly out of balance for the adiabatic lapse rate. This slight unbalance in the presence of the increasing convection occurring at higher levels tends to restore the adiabatic lapse rate. In the end the energy come from the upper shell being slightly out of equilibrium with the gas directly under it, and thus transfer the small amount of average energy needed, which large scale convection moves the energy around. It is a small amount of energy, so it does not take much to supply it. Thus only the gas diffusion caused conduction is enough to supply the trace of energy to the wall, and the wall radiates this to the upper shell, and the shell conducts it to the gas. The result is a small deviation from the adiabatic lapse rate until very near the ground.
Nick,
Based on the total atmosphere thickness, it would show the temperature profile as being about the same as a hot surface with a radiation absorbing gas. Near the ground, the kink would probably not be sharp, but rounded over a modest height 10’s to 1000’s of m thick, with details depending on wind patterns. The entire assumptions for this case are strange and non obvious.
Thanks DeWitt for clarifying that the discussion was still centered around the shell (TEV) model. All of my comments were based on an open atmosphere with no shell. Sorry for any confusion I may have created. Also I have limited time to read this thread and my posts are not as timely as I would like. You guys move fast.
I am also not sure which shell model is being discussed at any one time. There seem to have been many versions. I will try to go back and review some previous posts to get back up to speed. It would help if the model being discussed at any one time would be clearly stated. But based on what I think is the model, Leonard’s recent posts seem to make a lot of sense.
Nick, your comment about where the energy is coming from deserves some attention. I will come back later with some comments. But for now remember what I pointed out in a previous post: at 10 km approximately 33% of the total internal energy is potential energy.
We need some definitions. [updated in a later comment]
TEV1 is thought experiment Venus – as originally described.
– solar radiation is completely absorbed in a thin layer near the top of atmosphere (at the altitude where radiation to space from Venus currently takes place)
– this thin layer radiates as a blackbody
TEV2 is a modified concept (also proposed by Leonard Weinstein).
– solar radiation is completely absorbed in a thin layer near the top of atmosphere (at the altitude where radiation to space from Venus currently takes place)
– this thin layer cannot radiate to the atmosphere below or absorb radiation from the atmosphere below, but exchanges heat via conduction
TEV3 is as TEV2 except:
– the atmosphere is IR transparent
Leonard Weinstein, have these captured your concepts at different times correctly?
Do we need any more?
SOD,
Thanks for the definitions. That will save me some time from searching back posts. I have two questions.
1. Leonard made the statement a few posts ago: “The shell temperature was set by the external balance of Solar input and outgoing radiation (the outside of the shell was defined as an absorbing and radiating body with the same temperature distribution as Venus upper atmosphere at that altitude)”. Does this mean that the model has a day side and night side and the solar insolation decreases with higher latitude?
2. Shouldn’t there be a default case where there is no shell. We could call that TEV0.
SOD,
TEV1 is a black body shell for all radiation except for the constraint that Solar radiation absorbed is the same as actual at Venus (albedo value, day/night and latitude variation included). The gas underneath is the same as actual Venus. This is intended to do only one thing different than actual Venus: It assures no Sunlight reaches deeper than the shell. In fact it would change the convection pattern a lot, but I don’t think that is a significant factor in final temperature results.
TEV2 is correct except it would be conduction and convection, with convection dominating in the gas away from surfaces. It also would match the day/night and latitude levels on the shell, and radiate out the same amount as input (at shifted wavelength).
TEV3 is correct.
The basic discussion comes from the question: how does the surface of Venus get to the high temperature it has. Several of the introduced models were input to respond to specific issues. For example TEV1 was used to show that radiation did not have to reach the planet surface to drive convection or the final high surface temperature. TEV2 was in response to the issue of maintaining lapse rate for an opaque gas until almost to the shell location, which is an extreme ideal case for radiation blockage, but probably realistic if clouds and haze are included. The surface would be hot in that case. TEV3 showed that the lapse rate would be maintained for a hot gas to near the surface even if the surface could cool off by radiating to the shell.
williamcg,
The case for no shell would have 2 versions:
TEV0 is the ideal case with no shell and an assumed atmosphere that is very opaque to long wave radiation (close to actual Venus, but not exactly due to some transmission at low altitudes, but also thick clouds up higher). Solar input absorbed and radiation output are assumed to match actual Venus level with distribution.
TEV00 is a case with no shell and is assumed to be transparent to all radiation
I contend that TEV0 is effectively equal to TEV1
I contend that for TEV00, the planet surface temperature will be close to the value of the shell of TEV1 (relatively cool) except for surface storage of heat smoothing and wind redistribution of energy over the surface. However the atmosphere would still have the same average lapse rate with dropping temperature with altitude until the level of temperature dropped so low that condensation occurred. Then the problem becomes more complicated.
In all cases, I assumed the temperature variations did the same as if uniformly average values occurred. That is I assumed non-linear effects were not introduced by day to night and latitude variations. This is not exactly true and also the assumptions of none or all optical transmission is not exactly true. These were simplified models to show the points I tried to make.
Updated definitions. Including the additions suggested.
TEV00 is Venus with an atmosphere transparent to all radiation – i.e., no absorption of radiation at any wavelength within the atmosphere
TEV0 is closest to real Venus, with an atmosphere highly opaque to Venusian “longwave” radiation (i.e., a more idealized atmosphere). And see note at end.
TEV1 is thought experiment Venus – as originally described in this article.
– albedo is the same as real Venus
– solar radiation not reflected is completely absorbed in a thin layer near the top of atmosphere (at the altitude where radiation to space from Venus currently takes place)
– this thin layer radiates as a blackbody
TEV2 is a modified concept (also proposed by Leonard Weinstein).
– solar radiation is completely absorbed in a thin layer near the top of atmosphere (at the altitude where radiation to space from Venus currently takes place)
– this thin layer cannot radiate to the atmosphere below or absorb radiation from the atmosphere below, but exchanges heat via conduction (perfect conduction across the boundary layer)
TEV3 is as TEV2 except:
– the atmosphere is transparent to Venusian radiation
Note: in this last point “Venusian radiation” is like the longwave (terrestrial) / shortwave (solar) distinction on earth. There is a very small overlap on earth, and a slightly higher overlap on real Venus. But saying “transparent to IR” might cause confusion for others because half of solar radiation is IR.
SOD,
Don’t forget Leonard’s important assumption:
“Solar radiation absorbed is the same as actual at Venus (albedo value, day/night and latitude variation included)”.
I assume this holds for all shell constructs. This is important when considering mass transfer behavior.
Leonard Weinstein:
I kept TEV2 as earlier described for now. This is because I picture this layer of gas with its unique properties as not able to mix with the rest of the Venusian atmosphere.
Given the various properties of the atmosphere this seems to be the case.
Therefore heat would be transferred by conduction across the boundary layer, and then by convection away from this surface.
It might be a minor difference of no impact but important to be precise.
However, it can be up for discussion, after all they are your models!
Leonard Weinstein:
In TEV2, if the planet was not rotating what do you believe about the final surface temperatures?
There is a way of heating your house cheaply with a thermal pump. Pipes buried in your garden full of refrigerant absorb heat, and pumps (located outside) compress it (increasing the temperature) into radiators in your house. As the refrigerant cycles, the pressure is released, the fluid cools below the ambient outside temperature, and returns to the start of the cycle outside in the garden again. The inside of the house can achieve a temperature above ambient, with no internal heat sources, and far more efficiently than with a simple conventional heater.
If you take a long tank of fluid, and heat the top surface of the tank at one end, and cool the top of the tank at the other, how will the fluid inside flow? Will it not flow along the top of the tank from warm to cold, descend to the bottom of the tank (getting compressed), and then flow along the bottom from cold to warm? Is this not a way for heat to descend vertically, even though there is no internal heat source? If horizontal flows are fast enough to be turbulent, would that not also lead to vertical flow, even without convection?
(I realise that all this has already been alluded to, but it wasn’t clear to me the first time.)
What drives the winds on Venus, if the atmosphere and surface are horizontally nearly isothermal? Does the fact that the heat flux is not uniform make a difference? Is it not the sun and outer space that act as hot and cold heat reservoirs?
The greenhouse effect on Earth is reported to make a 33 C difference in temperature. Why, then, is the top of the troposphere nearly 70 C colder than the surface? What keeps it so cold? If you look at the top half of the troposphere rather than the bottom half, what is the mechanism by which this temperature difference is maintained now? Back radiation, perhaps?
scienceofdoom,
Venus rotates very slowly as is. I think if there were no rotation the latitude and day/night shell temperature variation would drive large convection winds and result in nearly the same result as present. The main difference is that the shell would get very cold in some areas from radiation out, so conduction heating from the gas below, carried by the convection currents, would be the only source of heat in those areas.
SOD,
I think you are considering the shell in TEV2 as a thin gas shell. In that case you are correct. I was thinking of it as a thin metal shell, so no convection in the shell. I was referring to the heat transfer in the gas as you moved away from the shell when I said convection.
Nullius in Verba,
It is in fact the differences of temperature at different locations on Venus that drive the winds. The winds are efficient enough to transfer heat, so that the temperature differences are maintained fairly small but not isothermal at the surface. The variation in the higher atmosphere is larger than the surface, and wind velocities larger there.
It is the adiabatic lapse rate (modified somewhat on Earth by water vapor phase change) that causes the upper atmosphere to be a lot colder than the surface.
I meant to leave this as a comment rather than a reply actually (SoD maybe you can delete the previously added one). Sorry about the spam:
I thought maybe some simple calculations might help make things a bit clearer why we can ignore temperature, heat and radiative properties in some respects of the lapse rate (I’ll probably mess them up though), so here goes.
Let’s take TEV2 as our base and assume that it receives energy in the amount of 160 W/m^2 . Which means the shell would have a blackbody temperature of approx. 230 K (I used spectralcalc, but it comes from the j=sigma*T^4). Now we’ll assume our atmosphere consists of single atom gas with a molecular mass of 40 g/mol (which gives a particle mass of mp=M/N=6,64*10^-26 kg).
For a single atom gas, we should be able to find the average kinetic energy of a paricle, from this formula Ek=3/2*k*T. Where k is the Boltzmann constant (k=1,38*10^-23 J/K). From here we can find the average Ek of our gas paricle:
Ek=3/2*k*T=4,76*10^-21 J
As Ek = 1/2*m*v^2 we get the speed of the paricle by average:
v=(2*Ek/m)^½=(2*4,76*10^-21/6,64 * 10^-26)^½= 379 m/s
Now as it is really high up in the sky (let’s say 10 km) it will have a long way to fall down to earth and the gravitational acceleration is 8,9 m/s^2, we can find the speed of the particle on ground by
vg=(2as+v^2)^½=(2*8,9*10^5+379^2)^½=566,94 m/s
Now going back to kinetic energy:
Ek2=1/2*m*v^2=1,07*10^-20
And to Temperature:
T2=2*Ek2/(3*k)= 2*1,07*10^-20/(3*1,38*10^-23)= 515,45 K
The same calculation can ofcourse be made in more direct ways, but I distanced it from Temperature and heat as much as possible on purpose.
I also assumed that the paricles would be freefalling through the atmosphere, wich is ofcourse directly not true (they will collide with other particles almost immediately). However as gases are mostly empty (the electomagnetic potential to counteract gravity is rather small) and Sir Isaac was hit in the head with large fruit, went quite insane, and forbid stuff to lose momentum when colliding with other stuff, this calculation should hold true, despite individual particles really not falling that much (the momentum is still carried on).
Mait,
Your approach seems very valid on first glance. My recollection of kinetics is a little rusty but the equations seem correct. (One correction, the acceleration of gravity is 9.8 m/s^2 rather than 8.9 if I remember correctly. This would bring the surface temperature up to 567.57K if I did the calculation correctly). This confirms some earlier statements that the gravitational effect accounts for the bulk of the temperature differential from the surface to the TOA.
I have often resorted to looking at the system from a molecular standpoint when I get tangled up in the classical thermodynamic approach. This is especially true when working with a gravitational field which is sometimes cumbersome with classic thermodynamics. The molecular approach is also handy when trying to emphasize that the final state of a system does not depend on what processes (e.g., heat transfer mechanism) were performed for the system to reach that thermodynamic state. Kinetic energy is kinetic energy.
I do have a question for the quantum mechanics experts in the group. This reflects kinetic energy only. What are the relative energy levels for rotational and vibrational energies versus kinetic energy within a molecule? Would taking these parameters into account widen the altitude temperature differential even more, or are these parameters independent of kinetic energy?
Yes, the molecular viewpoint (kinetic gas theory) is a more fundamental viewpoint than what you call the classical thermodynamic approach.
Isn’t this where the misunderstandings lie? Kinetic gas theory gives us the lapse rate although a bit slower, no large scale convection (air parcel) is necessary.
Williamcg,
I think the 8.9 is Venus. 9.8 is Earth. The vibrational mode would not apply to a single molecule gas.
williamcg,
I meant a single atom molecule gas.
Mait and willialcg,
Mait used a starting height of only 10 km. Obviously starting much higher gives a lot more potential to kinetic conversion. Distributing this over the 3 spatial modes by multiple collisions (rotation is not needed for a symmetrical atom) cuts the velocity gain in any one direction, and gives the final g/Cp result.
Leonard,
Thanks, you are correct about the acceleration. Sometimes I forget which planet I’m on let alone whether there is an outer shell or not.
The kinetic energy calculation works for atoms or molecules. Since most atmospheric gases are diatomic or triatomic molecules I was wondering how these other energy states vary (or not) with kinetic energy. I have not read anything on that.
Leonard and Mait,
Come to think of it, the constant “3/2” in the equation Ek=3/2*k*T may change depending on whether it is an atom or diatomic or triatomic molecule. I know it does for heat capacity calculations. Anyone know?
williamcg,
Well, according to my textbook on kinetic gas theory:
3/2kT is only translational energy wich applies at very low temperatures ca 20K.
5/2kT is also with rotational energy which apply at normal temperatures and,
7/2kT is with vibrational energy too, which apply at very high temperatures ca 4000 K
Jonas,
The rotational and vibrational will not apply for the atomic rather than molecular gas, so 3/2kT is valid at all temperatures under consideration.
Thanks Jonas,
I assume this means that Mait’s analysis is correct even for diatomic molecules since 3/2kT applies only to translational energy (which we have been calling kinetic energy).
Your statement “Kinetic gas theory gives us the lapse rate although a bit slower, no large scale convection (air parcel) is necessary” is important. This supports the contention that the lapse rate does not require convection for it to form. The lapse rate is the equilibrium or stable state even for a static system. This proves an isothermal atmosphere is not in the cards.
williamcg,
The need for the convection is to restore the lapse rate when it has been distorted by local energy input (or by a given initial condition which does not have the lapse rate). For example, ground or gas absorption of radiation, or conduction of heat from a locally hot spot on the ground to the gas above (or below) forces the production of the convection current, which tends to re balance the local g/Cp value. If you initially had an isothermal system it would be an initially unbalanced system, and diffusion and convection will re balance it toward the lapse rate. The case of the cold planet surface where the lapse rate would give a high temperature as you go down toward the surface (case TEV3) is a special case where local gas conduction to the cold surface (cooled by radiation of the extra energy up to a cold shell) results in a thin cold layer under the hot gas near the surface, but the lapse rate analysis is still valid (it is just overwhelmed very close to the wall).
Leonard,
Thanks, you are putting some meat on the statement I made back in an earlier post:
“Convection is not the means of obtaining the adiabatic lapse rate but is instead the mechanism for maintaining the adiabatic lapse rate equilibrium temperature profile. The atmosphere is trying to maintain an isentropic state of constant energy per unit mass. U = CpT + gdh where dU = 0.”
Your examples are good. I haven’t totally completed the TEV3 case in my mind yet but your analysis seems similar to what I had been thinking.
williamcg,
You wording (and SOD’s) is much better and more to the point than mine. I know what I mean, but do not always say it as compactly or clear as I would like. Thanks for helping convey the message.
Leonard,
Thank you. But I find your writing very good also. It was your posts that convinced me to participate in this thread.
I don’t believe that TE1-TE3 have a surface temperature anything like real Venus.
That doesn’t mean I’m right.
But I see a gas heated from the top with a certain amount of forced convection from heating variations and rotation. Gases heated from the top don’t usually generate hotter temperatures below.
I can’t solve the equations in my head and probably no one else can.
I’m considering TEV3 because it is simplest. I’m considering an initial Venusian surface temperature of 300K. We have to start with something (I do anyway).
And I’m interested in seeing if we can establish any temperature profiles before we start spinning the planet.
Where the sun is directly overhead, the absorbed solar radiation = 632 W/m^2, at 60′ zenith = 316 W/m^2 and at 90′ zenith = 0 W/m^2.
Net radiation from the Venusian surface is zero. Radiation is totally reflected from the inside of the “shell” and no absorption takes place in the atmosphere. Therefore it all arrives back at the surface. So the surface temperature is only affected by conduction and convection, likewise with the atmosphere.
Rt1 is the radiated energy from the “shell” and Ct1 is the conducted energy across the boundary layer to the atmosphere. Likewise for 2 and 3.
Reaching a steady state:
Rt1 + Ct1 = 632
Rt2 + Ct2 = 316
Rt3 + Ct3 = 0
And Tt1 (not marked on the graphic) but the temperature of this part of the “shell”:
σ.T1^4 + Ct1 = 632
T1 = ((632 – Ct1)/σ)^1/4
To calculate Ct1 we need to know the temperature of the gas and its conductivity and then we will have a pair of equations to solve.
We can assume that the atmospheric temperature at t (time)=0 is 300K and isothermal – to see what happens and how it changes. With perfect conduction through to the shell and a low specific heat capacity of the shell, the shell will also start at 300K.
Therefore, Rt1 = 459 W/m^2 at the start. It can only radiate out of its upper surface.
Any problems with this so far?
And maybe I will shortly realize I have to buy Matlab..
SOD,
TEV3 (or TE3) is not claimed to have a high surface temperature, but the atmosphere will tend toward the actual high level until near the surface, where it cools back to a low level. I think it would be more instructive to examine one case at a time to minimize confusion, even if there is some commonality in TEV1 (TE1), TEV2 (TE2), and TEV3 (TE3). I also do not see in your comment the latitude and night/day shell variation. These are there with or without planet rotation. I have not yet had time to carefully go over your last analysis, so I will hold comments a while.
SOD,
What I meant was that the gas cooling and heating of the shell changes the local temperature from balance with the Sun. The net effect is that the average outgoing radiation will balance incoming Solar radiation, but local values will not in general balance. This results in heat input from the shell to the gas in the high Solar intensity areas, and heat input from the gas to the shell in the low or no Solar intensity areas.
SOD,
Please excuse my misstatements. You are considering the gas to shell effect. The signs may vary (conduction in as well as out of the shell), and your symbols were not clear to me at first. I await where you go from here. Keep in mind that even though it is very slow compared to convection, that diffusion (resulting in conduction heat transfer in a gas) always occurs, and by itself would establish a lapse rate unless heat fluxes from convection locally overwhelm it.
SOD,
Stop the press. I just went over the previous discussions and realized some confusion (by me). TEV3 is the reflective shell, so the ground will be hot. The other case, discussed July 3 at 11:40 was a black body shell in facing the ground, with a transparent atmosphere. That is the cool ground but hot atmosphere to near the ground case. If you want, we can call this case TEV4, or just leave it out.
SOD,
A simplified solution to your model would be that the convective and conduction effects would tend to make the atmosphere temperature approach constant average value at all locations under the shell (the key term is approach, as a difference is required to drive convection). This average value case would give a shell temperature based on 632/4 or 158 W/m2 (plan area over surface area). The average temperature of the shell would approach 229 K. Now convection and diffusion (gas conduction) going to lower levels in the atmosphere would heat up due to the altitude potential energy to thermal kinetic energy, and carry the increasing temperature all the way to the surface. Initially the radiation out (and shell temperature) would be lower than the final level due to the need for excess energy to overcome the heat storage needed to heat the lower gas and the ground. After this unbalance goes on long enough, the average radiation out would balance the input. The system would never be in full balance locally, but the out of balance would be the driver to tend to restore and maintain the lapse rate.
SOD,
Here are some calculations:
Cp of CO2 at 300 K is about 0.8 J/g/degree K
Density at 0.1 bar (.001 Venus surface pressure) is 190 g/m3
Using a delta T of 1 K and a velocity of 10 m/sec (very mild)
Transport 1,520 W/m2 stream tube cross section.
This means that even a very modest convection current can carry many time the level of radiation out energy, and it would be easy to move the energy from one place on the shell to another and from the shell to the atmosphere and down. Also keep in mind that the time scale of transmitting the energy down can be much longer than across the underside of the shell (i.e, the vertical convection and diffusion only need to eventually carry the energy down, but the lateral movement under the shell needs to be larger, due to continuing Solar input).
SOD,
Thanks for putting together this scenario. It should help to focus the discussion.
First I need to question one of your initial conditions. I have no problem with the shell fluxes or the 300K starting point for the surface temperature. But your assumption of an isothermal atmosphere does not reflect reality. Recent posts have shown beyond a doubt (at least to me) that the natural equilibrium state for the atmosphere is a negative lapse rate with increasing altitude. This has been demonstrated from both a classical thermodynamics standpoint as well as by kinetic gas theory. This will result in a much larger rate of conductive heat transfer (Ct) from the shell to the atmosphere than your assumption.
With that said, I will try to lay out a step by step overview of the basic thermodynamics/physics processes that I envision taking take place beginning with the initial conditions (including an initial lapse rate). There are a number of less significant nuances that can be important but I will try to avoid them for now so as to simplify the model construct. I will number these steps so it will be easier to refer back to a particular assumption in later discussions (hopefully).
1. The shell and the underlying atmospheric layer will have a decreasing temperature profile as you move from the equator to the poles.
2. This decreasing temperature gradient in the upper atmosphere will result in a decreasing pressure gradient along the shell path (PV = nRT).
3. This decreasing ∆P will result in mass transfer of the upper atmosphere from the equator towards the poles. (Remember that ∆P is the driving force for mass transfer just as ∆T is the driving force for heat transfer).
4. At some point this moving mass of warmer air will overpower the cooler air parcels and force them downwards (visualize the Hadley Cell structure at the Earth’s equator). While this is primarily a ∆P driven event, the fact that the cooler air parcels are denser they will tend to sink relative to the warmer air parcels.
5. As the cooler air parcels are forced downwards they undergo compression from the increasing air mass above them and warm.
6. The descending air parcels will warm at the adiabatic lapse rate, g/Cp.
7. Assuming that the parcels had received positive conductive heat transfer from the shell, they will be warmer at the surface than was the initial state surface air parcels.
8. Positive heat transfer will occur from the surface air parcel to the surface, warming the surface.
9. Since the shell is a reflector, the surface radiation transfer between the surface and the shell is zero. The surface will remain warmer.
10. The warmer air parcels at the surface will be forced towards the equator by the convective downward stream of air parcels from the shell (same as the Hadley Cells).
11. Since these equator driven parcels are working against a pressure gradient (the equator is at a higher pressure than the higher latitudes) more compression and warming will occur further heating the surface. (The initial condition of a constant surface temperature independent of latitude presents a problem with reality here, but let’s ignores that for now).
12. As the parcel warms it becomes buoyant relative to the cooler parcels above and the parcel will start to rise.
13. Convection of the parcel will continue upwards to the shell due to the decreasing pressure gradient from the surface to the shell. (The pressure gradient is what causes the lapse rate temperature gradient).
14. The arriving air parcels at the shell will be warmer than the original air parcels and the conductive heat transfer from the shell will be reduced.
15. This convective cycle will continue until the upper air parcels are at the same temperature as the shell. At this point conductive heat transfer ceases between the shell and the upper atmosphere.
16. Incoming solar radiation flux = OLR.
17. The surface temperature is warmer than the shell by a factor of g/Cp*h degrees K, where h is the shell height.
This is basically identical to the case with no shell but an opaque atmosphere. In both cases the surface temperature is elevated due to the OLR originating at a higher, cooler location. The higher surface temperature is due to the variable ∆P and multi-stage compression generated as a result of the gravitational field.
I may have missed some things here and I am looking forward to comments.
williamcg
It’s not reality.
To attempt to solve some equations I need a starting point at t=0. This is the simplest starting condition I can think of.
Suppose this starting condition demonstrates that TEV3 cannot get to the conditions you describe (I have no idea yet, I can’t do it in my head). This would be an interesting result and would argue against the inevitability of a final hot surface on TEV3. It wouldn’t prove it because the right combination of initial conditions might lead to another result.
All hypothetical at this stage since the answers are not yet known, but this is the reason for simple t=0 boundary conditions.
SOD,
I don’t remember if the initial conditions (other than the surface temperature) you are using are those based on Venus or not. If they are just pick the temperature for the effective emission height for Venus and use that as the upper atmosphere temperature. That would give you a starting point to see if the surface temperature will increase. But I’m not sure what you are trying to calculate. If the final steady state condition will mean that incoming solar radiation = OLR, then since OLR is originating by definition at the shell, you know the final T based on the incoming solar. Ct will also be zero at steady state. From that T you can calculate the surface temperature from the lapse rate. There is no radiation heat transfer from the surface to the shell if the shell is a reflector.
I hope I am understanding your question and the model correctly.
williamcg,
The item 15 is not valid. The balanced final state would still have the uprising gas cooler than the shell when it reaches that height, and always continue to take in energy from the shell at that location to drive the circulation current. The net effect is to cool the shell at the equator, heat the shell poleward, and drive some continuing circulation at near steady state conditions. Depending on the efficiency of the circulation current, the shell temperature could vary a lot from just the local radiation balance value, and circulation speeds also vary a lot. On Venus, winds in excess of 100 m/sec are driven by this type of process at higher altitudes, but are a lot slower near the surface due to much higher densities.
Leonard,
Thanks for the input. Good observation but I think I disagree. But it’s making me think. For there to be a final balanced state (assuming you could ever get a balanced state in the real world), incoming solar IR must equal OLR. If Ct were not zero (on average) then OLR would be less than incoming IR and the system would not be balanced.
Under balanced conditions there would still be convection circulation from the equator to the poles due to the horizontal ∆P and ∆T between lower and higher latitudes in the upper atmosphere. And because the ∆P and ∆T are greatest at the higher altitudes, the wind speeds would be highest there. This is the opposite for an earthlike planet where the primary heat source is the surface. There the greatest horizontal ∆P and ∆T are at the surface and the differences diminish with altitude (ignoring the effect of friction directly at the surface and the jet streams which are primarily a result of planet rotation – but I’m not sure about that last statement). The temperature and pressure gradients, caused by the solar energy variation along with the constant gravitational force, are what drives the circulation (it is not a perpetual motion machine).
Great topic. I have written this and my previous responses to SOD rather quickly and I may still be missing something important. I am not completely sure about the wind thing (shell vs. surface as the heat source) but I’m sure there’s a meteorologist around here somewhere that can correct me if I screwed that up.
williamcg,
The final state has the average outgoing radiation energy equal to the average incoming Solar. The low latitudes get more than average Solar, and higher latitudes get lower than average. The upwelling current is near the average due to excess heating at low latitudes followed by excess cooling before it goes downward near the high latitude. It has to be at near the average upper atmosphere temperature when it goes down. The net effect is to cool the over-hot shell some near the equator, and heat the over cool shell near the poles, but be near the average temperature after circulation. Thus it is always cooler than the shell coming up, and the Solar energy drives the circulation. After steady state is reached, there is no net energy transfer down, only circulation (I am ignoring viscous dissipation here). If dissipation is included, temperatures will adjust slightly to re balance the net.
williamcg,
Rereading your last post, I am not even sure we are disagreeing on the net process. However, that statement is not made by your previous statement 15, which states the the upwelling stream temperature matches the wall (i.e., no heat input there to the stream). This would lead to heat transfer from the gas to the shell at the high latitudes, resulting in the whole system cooling down, and excess radiation out from high latitudes driving the excess cooling.
williamcg:
Leonard Weinstein contends that the surface temperature will be similar to real Venus with a hypothetical Venus-like planet with TEV3 conditions.
I believe that the surface temperature will not be anything like the real Venus.
And so this surface temperature is what I am trying to calculate.
So really the only prescribed conditions are those identified in the TEV3 description – and definitely not the planetary surface temperature, or current atmospheric movements.
I was planning to start with effects of conduction, and see if that leads to any convection, then start spinning the planet and see what happens as a result.
Possibly some insights might be gained. Possibly I might feel like the guy rowing out into the North Sea with a spare afternoon, a few steel pipes and the aim of building an off-shore oil rig..
SOD,
The hotter shell region causes a pressure rise if the gas is initially cooler than the shell. The colder shell region at higher latitudes or night side causes a pressure drop. A weak flow current starts. The movement increases the heat transfer rate and thus increases pressure change levels. At some point the large physical scales cause instabilities to form and eddy motion greatly increases the heat transfer into the gas by eddy mixing rather than molecular diffusion. I have already shown how large an energy flux can be carried by a very modest flow. Large temperature differences and higher velocities can easily carry enough of the excess heat from low latitude wall locations to high latitude ones, and the colder flow at the higher latitudes will eventually go down toward the surface (due to being higher density) and establish a circulation. You can input different initial conditions, but the details of the problem are very complex. A walk through the likely process with order of magnitude values showing there is enough energy to drive the process, and the fact that the adiabatic lapse rate is the eventual level an atmosphere has to go toward makes the rest seem reasonable.
However, I want to point out that if the flow over the shell does not do what I said, the cooled gas temperatures next to the cold shell at high latitudes will still result in a downward current in exactly the same way as gas over a hot ground will rise. This dropping flow would start some circulation, and this dropping flow will adiabatically heat as it goes to to lower altitudes. However even if there were no circulation, molecular diffusion would eventually form the lapse rate (although this would be a very slow process). That is, the average result of a hot ground is inevitable independent of process, although the local ground temperature variation can be somewhat different depending on which process dominated.
To be honest I’m slightly confused why we’ve made it more complicated by making it round and non isothermal. Wouldn’t it make more sense to start with an isothermal shell (let’s say it’s rotating really fast around a few axes)? The redistribution can only make a quantitative difference, but the general direction (hotter than/colder than) shouldn’t change.
The conductive properties shouldn’t really be that important either, as they can mainly only change the time at which an equilibrium is achieved, and we should have quite a lot of that time thing.
Actually I’m not even quite sure we wouldn’t reach a higher surface temperature really, really fast as we are still talking about air falling out of the sky and it would take about 11 minutes for it to fall from the sky to the surface on Venus (t=(s/2a)^½). But I must admit this feels quite crazy even for me – not just quite sure where I’ve got lost.
A small addendum: The lapse rate would be established very quickly (it would get very cold close to the shell), but as our energy content is lower than the equilibrium, it would take time for the system to heat up.
Mait
I just need a starting point that’s easy. If only I had a pliable GCM with a nice user interface..
Instead it’s a case of visualizing the problem, adding equations, doing simulations to check it makes sense – adding more equations, doing more simulations..
The problem is simulating convective flow which is the nub of the problem anyway..
Mait,
I think you are looking at a free falling gas, but that is not the present model we are looking at. The present model being discussed is TEV3, which is a dense gas model, with a perfect reflector lower shell surface and a non optically absorbing gas. The gas would eventually go all the way down, but very much slower than a free fall (by convection and diffusion), and would eventually establish the lapse rate and hot surface.
The shell would have to turn really fast to approach isothermal if you wish to examine that version, but rapid rotation itself makes other things happen. We could impose an isothermal condition by assuming a surrounding uniform heat source rather than the Sun, and this is a possible model, although the uniform heating would eliminate the lateral currents and slow things down considerably, but diffusion and naturally organized local convection would eventually get the same end temperatures.
Mait,
That free falling gas molecule discussion was a separate discussion just trying to point out how gravitational potential energy converts to higher kinetic energy (temperature) as the molecule goes from higher to lower.
SOD,
I want to be sure we are on the same page. We are presently looking at TEV3. If the atmosphere were optically transparent and there was no shell at all, the ground would be cold, but that is case TEV00. I just wanted to make sure you do not think that I am claiming ALL possible cases lead to a hot surface.
I’m clear.
SoD is of course right, and Leonard Weinstein is completely wrong in the discussion here. Sorry Nick, but you’re wrong too, though headed in the right direction regarding conduction vs. adiabatic convection – and we’ve had this discussion before.
Understanding this requires no calculations, but rather an understanding of basic thermodynamic principles.
First, the real Venus (or Earth) is not an ‘isolated’ system to which simple equilibrium and near-equilibrium thermodynamics applies. The primary reason for this is the steady-state influx of low-entropy sunlight reaching the surface. That energy source means the planet has access to energy for all sorts of lower-temperature processes from convection to the water cycle to biology (in Earth’s case).
But Weinstein’s absorbing shell completely cuts off that low-entropy energy source from the planetary surface. The entire planet underneath the shell is essentially isolated from the rest of the universe. It is a system enclosed in a constant (or slightly varying)- temperature box, with no access to the rest of the universe.
And that means standard equilibrium thermodynamics directly applies to this hypothetical planet. In particular, it will tend towards a constant, uniform, temperature, as does every such isolated system. The variations in temperature across the enclosing “box” may induce some slight variations in temperature below, but there will be some important conditions on those variations.
In particular, heat can only flow from warmer to colder regions. That means that any region of the planet inside the box that is hotter than any portion of the box surface will not receive any input energy from the box; it will lose energy until its temperature is lower than the box maximum, at least.
The maximum temperature of the enclosing box becomes the absolute limit on temperatures inside the box. Convection induced by temperature differences cannot cause any temperature to be higher than that.
Arthur,
I would suggest you go back and read the past posts over the last few days. You could start here: https://scienceofdoom.com/2010/06/22/venusian-mysteries-part-two/#comment-3472. You obviously do not understand the atmospheric thermodynamics when a gravitational field is involved. Just about everything you said is incorrect and the correct answers are in the past posts. A lot of thought and subsequent coherent discussion has taken place by several people during that time. Read and then come back and we can talk. If by chance you have read it, then be specific about why you think the thermodynamics we have discussed is incorrect and give us the version that explains your points. Generalities won’t cut it.
Arthur,
Please show me even one place where I am wrong. Keep in mind that several models were discussed one time or another, and the present one being examined is called TEV3 (see SOD’s description). The atmosphere is in contact with the outside universe through the absorption of sunlight and thermal conduction between the barrier and the atmosphere. In fact, all real planetary atmospheres are in contact with the outside universe essentially the same way, with the added possibility of some sunlight reaching deeper in the atmosphere. The input and absorbed solar energy balances ON THE AVERAGE the outgoing longer wave radiation (local values can and will be unbalanced) once the system reaches equilibrium. The special properties of the TEV3 case are the assumption of optical transparency of the atmosphere, the blocking of sunlight from passing through the outer surface, the assumption of a perfect reflecting of radiation by the lower surface of the barrier, and allowing thermal conduction from the barrier to the atmosphere.
TEV1-3 all have all incoming sunlight absorbed by the thin enclosing layer, as far as I can see discussed here, so the same very general thermodynamic considerations apply.
And please, gravity does not trump thermodynamics! A gravitational field is like any other potential energy field, and standard thermodynamics has no trouble dealing with it.
The fundamental problem with Weinstein’s arguments is exactly what SoD identified in the article: convection requires low-entropy energy, because it dissipates energy to heat through the friction of moving air masses and through mixing of air masses of different temperatures. Where is that low-entropy energy coming from? It has to come from a point of higher temperature than the temperature of the air masses involved. But you have cut off all access to the low-entropy energy from the sun by introducing an absorbing shell. Thus there is nothing to drive convection. It really doesn’t need further discussion of imaginary gradients of various sorts.
Leonard,
The free falling part wasn’t actually a condition, but more like a statement (that particles in a gas are essentially always freefalling in a gas). Gases ought to be quite empty things, meaning the actual electromagnetic interactions are relatively small (it becomes increasingly relevant with higher densities). In an optically transparent atmosphere, we can only have atmosphere as high as the surface can ‘bounce’ the gas particles. Doubling the mass of gas in such an environment would have little effect on lapse rate (g/Cp essentially says the same thing).
I still don’t see why we need conduction or convection in this environment to establish a lapse rate.
PS. I don’t quite agree with Arthur on that standard thermodyamics has no trouble handling gravityl. From my observations it usually gets quite confused about it. But I never liked the thermodynamics part of Physics that much (1st law is stolen and the 2nd one isn’t even a law) so I might be a bit biased about this.
Let’s consider a completely different system, just to have a thoughtful analogy of Leonard Weinstein’s assertions here.
Oxygen is a paramagnetic gas; that means it has lower potential energy in a higher magnetic field. So a magnetic field gradient can act on a container of oxygen pretty much the way a gravitational field acts on a planet’s atmosphere. Suppose the high field is on the right side of the container, and the low field on the left. The same hydrostatic balance issues come into play so you get a density gradient from lower density on the left to higher on the right. Suppose the left side is held at a constant temperature (similar to Weinstein’s shell) and the right side is insulated so there’s no heat flux through it (similar to the planetary surface, with the exception of the small geothermal flux we’ve been ignoring).
Standard thermodynamics tells you that, whatever the initial state of this container of oxygen, it will move towards a constant temperature at the temperature of that left-hand side. Yes, right-moving molecules gain kinetic energy due to the potential energy gradient, and left-moving molecules lose kinetic energy – but that is balanced by the fact that there are more molecules on the right than on the left. The density gradient results in hotter, faster equilibrated molecules having a net left-ward flow. Net energy flow is zero. Even cranking up the magnetic field gradient to neutron-star levels will not alter that constant-temperature equilibrium state. There is no way for this container to maintain a much hotter right side than left side; the two sides will always tend to the same temperature.
Similarly there is no way for Weinstein’s hypothetical Venus to maintain a surface temperature any higher than the temperature of the shell.
Arthur,
I don’t quite understand how can having more molecules balances out kinetic energy gain. Could you elaborate on this?
Mait,
The effect of increasing the mass of the atmosphere is not to increase the lapse rate (=g/Cp), but to increase the height of the atmosphere. The lapse rate times the altitude gives the total temperature increase. The discussions were based on a hypothetical atmosphere mass comparable to Venus, and assumes a high altitude to the edge.
Arthur,
I don’t know where you get your statements from, but either you do not understand atmospheric physics or you are deliberately trying to confuse the issue. The energy is obtained from the sun heated shell heating the gas at the lower latitudes and day side. Once enough energy is obtained to result in equilibrium, the gained energy in by conduction is matched by the energy lost at the higher latitudes and night side along the shell. The differential heating drives the convection currents. The falling gas at the lower temperature parts of the shell (which is made higher density from the cooling and falls down exactly analogous to a hot gas rising) is adiabatically compressed and heats up by trading gravitational potential energy for kinetic energy (higher temperature). This is done at constant total energy, so no laws of thermodynamics are violated.
Arthur,
Here is a simple thought experiment. Assume you are on Venus and you build a room 1 km on a side but 100 km tall. Assume the wall is a perfect thermos bottle with no heat storage capacity (like a mass-less perfect insulator). Assume the room is initially empty. Now slowly admit from the top a gas that is optically transparent and similar mass to CO2 (Argon is close). Assume the gas is initially 300 K. Fill the room until the included mass is similar to that of the atmosphere of Venus in a same sized room. What do you think the pressure and temperature distribution down the room will be after any currents die out? Consider what will happen over a long additional time if no gas currents remain, and no energy goes in or out.
Leonard, responding to your “simple thought experiment” – Since you are adding the gas at the top, each molecule gets 100 km*g*m potential energy above what it would get being added at the bottom. Since most of the gas will end up near the bottom (exponential density and pressure dependence) the added energy on average per molecule will be quite substantial – by my rough calculation for Ar it would be add the equivalent of about 500 K worth of energy per molecule.
Nevertheless, under these conditions of no energy in or out, the final temperature in the “room” will be uniform from top to bottom, say around 750 K. In fact, optical transparency will have no effect, nor will the total included mass – you’ll get the same temperature whether you put in 1%, or 100% or 100 times Venus’ atmospheric density.
Do you expect something different?
Arthur,
It was interesting to see more molecules go one way than the other without changing the mass balance. You got that one wrong also.
Mait,
You need conduction or convection to initially establish the lapse rate in the fact that the gas has to come from somewhere (released gas from volcano activity?) and the gas establishes an initial atmosphere. After that, the conduction and convection are self generated restoring actions if heat in or out perturbs the gas. If there is no radiation out and no heat transfer, you don’t need conduction or convection to maintain the lapse rate.
Leonard, you seem to be misinterpreting my earlier comment; Mait also questioned it, so a little more detail.
Let’s stick with my oxygen container analog – I hope you agree it’s the same issue as with the gravitational field problem. I’ll get to what the fundamental problem is with any non-isothermal end-point in a moment.
What I said was “right-moving molecules gain kinetic energy due to the potential energy gradient, and left-moving molecules lose kinetic energy – but that is balanced by the fact that there are more molecules on the right than on the left. The density gradient results in hotter, faster equilibrated molecules having a net left-ward flow.”
This is assuming a steady-state situation where temperatures and densities have adjusted to their final conditions, which I assert are a uniform temperature and a density gradient increasing from left to right, according to the change in potential. (Explicitly if molecular potential varies as -ax where x is the left-right dimension, then density has to vary as exp(ax/kT) from basic statistical mechanics).
Now one argument that this cannot be a constant temperature situation has been expressed above in the gravitational case, that molecules will gain kinetic energy as they move to the right. This is true, but it is only half of the kinetic-energy flow question. The other half is that there are more molecules to the right. Imagine a vertical boundary somewhere in the container. Right-going molecules through the boundary have their distribution of kinetic energies shifted up by the potential; left-going molecules have their distribution of kinetic energies shifted down. But there are *more* molecules coming from the right, heading left. Because the rate at which they go through the boundary depends on their speed (kinetic energy), under these conditions both the net kinetic energy flow and the net molecule flow are zero. It’s a surprisingly subtle calculation, but if you do it you’ll see the constant-temperature condition is the only way this can happen.
But suppose I’m wrong, suppose there was a mechanism for the right side of the container to heat up under these conditions. We could then relax the insulation on the right side just a bit and pull out some of that high-temperature energy and do some work with it, then re-inject that energy at low temperatures on the left side.
That means the oxygen container in a magnetic field gradient would be a perpetual motion machine!
That’s what the second law of thermodynamics prevents. It’s not sufficient to satisfy the first law; you must always satisfy the second as well.
Arthur,
“But there are *more* molecules coming from the right, heading left.”
I fail to see how that can be the case in a steady-state.
“That means the oxygen container in a magnetic field gradient would be a perpetual motion machine!”
No it doesn’t! The work you get from the heat engine is lost to the system, so you will end up cooling the gas.
Jonas – all the extracted energy could be returned to the left-hand-side constant-temperature heat bath and there would be no loss of energy from the system. But you would have extracted work. That’s the condition for any perpetual motion machine.
Any equilibrium system that maintains a temperature gradient (like my example, and as Leonard claims for a hypothetical planetary atmosphere) would similarly be a perpetual motion machine. That’s why thermodynamic equilibrium always requires a single uniform temperature.
Two bodies in thermal equilibrium have the same temperature – this is often referred to as the zeroth law of thermodynamics – Google it for plenty of references.
Arthur,
You seem to have gotten all tangled up in your attempt to handle the thermodynamics. Let me help. I will only deal with your second post. First you seem to have become infatuated with “low entropy energy”. Why I don’t know. But I think it’s based on a misapplication of the second law that seems prevalent in most of Climate Science. I will discuss that in a second.
First you need to understand that all of the atmospheric models being discussed on this thread are isentropic. To refresh your memory, that means that there is no increase or decrease of entropy in any of these systems. And contrary to your statement that “convection requires low entropy energy”, convection is considered a reversible adiabatic process and is by definition isentropic. I’m not sure where you picked up that little gem but it is false.
As to your infatuation with “low entropy energy”, my guess is that you got it from the Climate Scientists who say that the atmosphere is a producer of entropy since the entropy of solar energy entering the atmospheric system is much less than the entropy of the OLR that is leaving the system. That is because they have no clue that the gravitational field must be included in the thermodynamics – but they almost never do. The atmospheric system (as an ideal model – not in the real world) is in fact isentropic. The entropy of the incoming and outgoing energies is exactly the same. How can that be?
The definition of entropy is dS = dQ/T. Since the temperature at the surface is much higher than the temperature at the effective emission height, then this fallacy must be true, they say. But their mistake is in the definition of dQ. As I pointed out in a previous post, which I don’t think you read, in an electromagnetic field:
dU = dQ – dW. This can be rewritten as
dU = CvdT – PdV for an ideal gas.
But if you add a gravitational field the first law now becomes:
dU = CvdT + gdh – PdV where now
dQ = CvdT + gdh
Thus if you use this definition of dQ you will see that there is neither “low entropy energy” nor “high entropy energy”. The atmosphere as a total ideal system does not produce entropy. Potential energy is basically “stored heat” and must be considered in the thermodynamics.
Sorry for the hint of sarcasm above, but your condescending statements “SoD is of course right, and Leonard Weinstein is completely wrong…” and “It really doesn’t need further discussion of imaginary gradients of various sorts” really ticked me off. Learn some basic thermodynamics and then come back. As for your oxygen/magnetic field soliloquy – it is nonsensical.
Responding to williamcg…
You honestly believe that moving masses of air within the atmosphere involves no viscosity or friction or redistribution of that energy? Each parcel of air just smoothly goes up and down, never exchanging molecules with any other parcel of air? Really?
Yes, “adiabatic” means no change in entropy – that’s because “adiabatic” is an *approximation*. Specifically, under the adiabatic approximation there is no exchange of heat with surrounding systems – dQ = 0. In reality, it is impossible to satisfy the adiabatic approximation. You get closer to adiabatic by moving your air parcels around quickly, so they have less time to exchange heat with their surroundings. But you will *never* have perfect adiabatic motion, it’s an idealization.
And as soon as you lose adiabaticity, you start increasing entropy, because what happens is you have heat flow from hotter to colder air parcels – dQ/T_cold – dQ/T_hot. The energy spreads itself out – that’s an essential characteristic of the laws of thermodynamics; energy wants to spread out as much as possible among all the degrees of freedom available. That leads to uniform temperatures at equilibrium, for a system otherwise isolated from the rest of the universe.
As to my “infatuation with low-entropy energy”, I have found that to be a high-information-density expression for what in technical terms is known as “free energy”, or “exergy” – or what I have called “useful energy”. Low-entropy energy or “free energy” is the only way to drive mechanical systems such as atmospheric convection that would otherwise wind down and cease any macroscopic motion due to viscous and friction forces.
williamcg:
The models I was envisaging have normal thermodynamic processes like the real atmosphere. We placed some constraints on the system (like different radiative schemes) but this wasn’t one of them.
I agree with Arthur Smith that convection is not considered a reversible adiabatic process.
The idealization of an adiabatic process helps to define the dry, and moist, lapse rates. But that doesn’t mean that parcels of air move up and down in the real atmosphere without ever exchanging energy with other parcels of air.
I’m still keen to do simulations on TEV3, impossible dream though that probably is.
For Arthur Smith – I am wondering whether there is a source of energy in addition to the “shell” conducting heat into the atmosphere. This is the rotation of the planet potentially driving some compression of gases.
If there was no additional energy source then I agree that the max average temperature has to be the average “shell” temperature.
And maybe even with this rotating work source maybe the above is the case. There is no certainty to the fact that gases will “plummet” 90km to the surface. And even if they did they can’t do it without exchanging some heat on the way down, ie it can’t be a reversible process.
I can’t figure it all out from just thinking, which is why I thought a model might help.
Rotation is just like a gravitational field (it modifies the vector g slightly with an axial component) once you switch to a rotating frame of reference. In particular, there’s no way to extract low-entropy energy from the rotation itself.
Interaction of the rotation with outside bodies (tides from the Moon and Sun) can result in energy exchange. But the tidal energy flow for Earth is very low – around the same scale as geothermal. And for Venus it’s far less, with no moon and much slower rotation.
Arthur and SOD,
What I and williamcg have been trying to say is that the ideal lapse rate is an adiabatic and isentropic concept. However, in the real world there are always processes that push the levels from balance. These include input variations due to latitude and rotation, internal processes (radiation, volcanos) varying albedo, etc. Those all still end out giving the average input solar radiation equals average output radiation, but sets up convection currents which tend to re balance the local offsets. The re balance is never perfect, so there is local entropy increase. However, that is not due to the ideal lapse rate but due to the currents in the non uniform real world. Please don’t confuse the two. The continual solar input and radiation out drive the process.
Arthur,
Your response to my room to space question is wrong. The gas at the bottom will be hot and dense, and the gas at the top will be 300 K and low density. Please tell me how the gas at the top gets any hotter once currents are gone and equilibrium reached.
SOD,
Please also respond to my room to space (keep in mind the lid is also like the walls, so no radiation out the top) problem and tell me if you agree with Arthur or me. This seems to be the basis of Arthur not understanding the issue. This room model is basically the same as the end point of TEV3, so if we can’t get agreement on the room model, and if you agree with him we have a basic problem.
Leonard, I was going to show you this in some detail, but I think a simple answer is best for now – you ask “Please tell me how the gas at the top gets any hotter once currents are gone and equilibrium reached.” – the answer is simply that the gas at the top, whether or not there are currents, mixes with the gas lower down simply through the direct motion of gas molecules. The Maxwell-Boltzmann distribution describes the distribution of vertical velocities of gas molecules, and some of them from lower down will head up. This exchange is sufficient to thermalize the whole system to a single temperature, with or without any radiative exchange.
Arthur,
You still miss the entire point of gravitational potential energy. As a molecule moves up, it cools by giving up some kinetic energy for the gained potential energy. Alternately, you could say it went from a higher pressure to a lower pressure, and the adiabatic expansion (which means no heat transfer case) lowered its temperature to exactly match the gas at the higher location. If you look at individual molecules, the mean free path is so small that many collisions occur for a small net movement. This redistributes the vertical velocity loss over all directions ans results in a very small temperature change in a small distance. However, this goes on and the cumulative effect is as stated. Maxwell-Boltzmann gives a velocity distribution in a local small region. It says nothing pro or con about conversion of gravitational potential energy to kinetic energy conversions.
Leonard – no, I do not misunderstand at all. The acceleration effect you describe is *exactly* what I was trying to explain with my “oxygen container” example, which obviously did not communicate clearly enough. So let’s talk about your “room” instead.
Single molecule behavior is somewhat different from that of a clump of gas (which does behave as you describe, cooling as it rises) because of what I mentioned earlier: there is a *distribution* of molecule velocities, coupled with density varying with height.
If you put in a hypothetical plane partition across your “room” at any given height, the number of molecules crossing that partition in a given time interval is weighted by the vertical component of their velocity.
To understand this: let n(vz) be the number of molecules in a local region of the gas with vertical velocity component vz. Let’s say the region in question is just below the plane, so that molecules with positive vz will cross the plane. In a given amount of time t, a molecule moving at vz goes a vertical distance vz * t. That means that, in time t, the number of molecules crossing the plane with velocity vz is given by n(vz) * vz * t.
That is, all plane-crossings are weighted more heavily to higher kinetic energies, due to this velocity effect.
Since there are *more* molecules below the plane than above the plane, this velocity effect implies a net flux of kinetic energy from below to above.
However, the gravitational acceleration effect acts in the opposite direction, seeming to produce a net flux of kinetic energy downwards. When the temperatures on both sides of the plane are equal, the net flux of kinetic energy goes to zero, and things reach equilibrium, just as they should.
Arthur and SOD,
There are reversible flows that are isentropic. However, in the real world, if turbulence forms, or the dissipation is non reversible, this dissipation is not isentropic. However the issue of isentropic or not is not even the issue of this basic discussion. All that is required to continue to maintain an average near adiabatic condition in the presence of dissipation is a continual input of forcing (solar energy coming in with a distribution of input and radiation leaving with a slightly different distribution). If there were no input or output, and the enclosed atmosphere currents all died out, and the temperature at the top of the atmosphere were selected to be 300 K, the surface temperature would be very hot (depending on g/Cp times altitude). There would be the same condition as the room sub problem.
Leonard – the problem is in all your hypothetical planets here you are thermalizing that input solar energy. What is required to “continue to maintain [anything] in the presence of dissipation” is indeed a continual input of something – that something is what I’ve referred to as low-entropy energy, “exergy”, “free energy”, whatever you choose to call it.
By thermalizing the input solar energy at 300 K, or whatever that top level is, you have removed all the free energy available at 300 K. It is now thermal equilibrium energy, “waste heat”, which can do no work, unless put in contact with a heat bath at *lower* temperature. In particular, it cannot force any “atmospheric currents” that build up or sustain any higher temperature below it.
Suppose we started with one of these hypothetical planets having a 750 K surface temperature and 300 K shell of this sort. As long as the vertical temperature gradient is below the adiabatic lapse rate, the convective instability that drives large-scale atmospheric motion will be suppressed. But simple conductive (and radiative) exchange of energy will still be in effect, and the heat on the bottom will continue to cool off through exchange with the top of the atmosphere over time. The only question is how fast the process will be.
Arthur,
First, I defined how solar input and shell radiation output result in non uniform shell temperatures and output radiation at different latitudes and night/day locations. These differences are what drives the convection currents.
If you consider an example with a totally isolated and uniform system and allow some radiation heat transfer (i.e., an absorbing but not totally opaque gas) you will have a very low lapse rate depending on the relative magnitudes of the radiation and thermal diffusion heat fluxes. However, this is not the model (or the actual planet) we were discussing.
The tall room example was for a non-absorbing ideal gas, so radiation heat transfer TO THE GAS is zero even though the photons are flying around. Thus even diffusion (also called conduction) heat transfer would maintain the adiabatic lapse rate. All the examples we are discussing are defined by SOD and all would do just as I have stated. If you wish to discuss a different model, define it and I will agree or disagree depending on the details, but don’t argue a different model and say that is why my model is wrong.
Artur,
Reading back, I saw you claim adiabatic means isentropic. This is wrong. Adiabatic means no heat transfer. You can have an adiabatic process that is not isentropic. A convecting flow up or down in an atmosphere will result in cooling or heating the gas with no heat transfer due to trading kinetic energy for potential energy (it is generally shown as cooling or heating by expanding or compressing with change in altitude, but gravity is the root cause).
Arthur,
Reading back I just noticed that you think temperature is function of density or pressure of the gas. In fact it is only a function of average kinetic energy per molecule. You can relate temperature to pressure and density, but that is not the same, since both terms have to be considered. Compressing a gas does work on it, so you have to be careful of the process leading to changes in pressure or density.
Stating what “I think” seems rather odd when you give no citation of me saying anything of the sort; as far as I understand what you are saying here, I agree with it completely (other than your claim on what “I think” about it).
williamcg,
Smooth slow convection is often approximated as being isentropic to make solution of problems easier. However, it is a low level non isentropic source, so Arthur is correct on that but I also agree that it is for practical purposes it is effectively near isentropic. The only effect of being non isentropic is the need to supply a source to continue driving the convection to re balance the local offsets from non uniform heating.
williamcg,
I know you stated that the IDEAL situation was isentropic, and Arthur emphasized the REAL WORLD had some non isentropic character. You were both right based on what you were referring to. The result was a side issue of no real value. Please don’t get caught up in this issue.
Leonard,
Sorry to be so late getting back to you concerning our discussion on Step 15. I have been very busy and I took my available time yesterday to respond to Arthur. I understand your viewpoint and have no problem with it. I think we agree on the basics and this doesn’t invalidate any of the overall system assumptions with respect to its behavior. As I said when I outlined the model process flow:
“There are a number of less significant nuances that can be important but I will try to avoid them for now so as to simplify the model construct.”
I think this falls into the “nuance” category.
Arthur,
“You honestly believe that moving masses of air within the atmosphere involves no viscosity or friction or redistribution of that energy? Each parcel of air just smoothly goes up and down, never exchanging molecules with any other parcel of air? Really?”
SOD,
“The idealization of an adiabatic process helps to define the dry, and moist, lapse rates. But that doesn’t mean that parcels of air move up and down in the real atmosphere without ever exchanging energy with other parcels of air.”
In case you missed it, I have these two statements in the post you are referring to: “The atmospheric system (as an ideal model – not in the real world) is in fact isentropic.” and “The atmosphere as a total ideal system does not produce entropy”. We are talking about a model that is fairly well defined. Don’t go changing the subject. Stick with the model thermodynamics.
I am sure both of you are very familiar with the literature that unequivocally states that the earth’s atmosphere very closely follows adiabatic behavior. I also have experience dealing with radiosonde data and I have been amazed at how closely the real world follows the theoretical thermodynamics in this respect. Let’s don’t get off on a tangent. It’s not constructive.
Arthur,
“all the extracted energy could be returned to the left-hand-side”
You can google “carnot heat engine” and find that the heat energy taken from the hot side of your container will be more than what you can return to the container. The difference is the extracted work. (Unless you have some other source of low-entropy energy)
The gas container will therefore loose energy, and your counterexample is invalid.
And where does the extracted work go? Eventually it gets used up, turned into friction, dissipated as its own waste heat. Which, if you’re worried about cooling in the gas container, can be returned to the gas via the left-hand side. The same goes with a Carnot engine – the idea of the heat engine is that it goes through a *cycle*, where things return once again to their starting point. In this case similarly everything about the gas container at the end is identical to that at the start. But work has been extracted – and can continue to be, without end… if Leonard here is right that a temperature differential of this “lapse rate” sort is forced by such a potential energy gradient.
“turned into friction, dissipated as its own waste heat…
can be returned to the gas via the left-hand side”
You can’t just return dissipated heat into the container. That’s pure fantasy.
Arthur,
Re. your magnetic gas example: First, the magnetic force directly produces a pressure, not density difference. If the temperature also increased, density could either be larger or smaller (rho=p/RT) depending on which term dominated. If the temperature ended out the same, the density would have to be higher where the pressure was higher. However, as molecules diffused across the sides, the net mass transfer HAS to be zero after steady state was reached. Thus equal numbers of molecules go each way. However the molecules gain kinetic energy one way and lose kinetic energy the other. Thus the temperature has to be different. For realistic magnetic field strengths and sized box, the pressure and temperature difference would be very small, but still real.
Keep in mind the Venus lapse rate is only about 7.8 K /km or 0.0078 K/m. These are small effects that only matter due to the very large scale of the problem.
Yes, net mass transfer HAS to be zero at steady state.
So does net kinetic energy transfer.
My point (perhaps expressed poorly earlier) is that balancing the kinetic energy transfer effect from left to right is a velocity*density-weighted kinetic energy transfer effect from right to left. This is because higher velocity molecules move faster, and so the higher-kinetic-energy molecules are more heavily weighted. Since there are more of them on the right than on the left, that leads to a right-to-left K.E. flux. Which balances the left-to-right K.E. flux caused by the potential, at equilibrium.
But the balance is *only* there if temperature is uniform.
I am nor sure what you are trying to point out here. At equilibrium all net transfers are zero. Nevertheless, one side will be hotter than the other and one side will have a higher pressure. The magnetic gradient causes it just as gravity on a planet causes pressure to drop with altitude and temperature to also drop with altitude. You can’t separate the thermodynamics of the gas from the effect of the magnetic compression. Both are part of the full problem.
A question to Arthur:
What would happen with our atmosphere in TEV3, if we started with an isothermal 300 K (surface, shell, atmosphere) with the shell at 100 km, and then suddenly increased the height of the shell to, let’s say, 1 astronomical unit?
Mait,
I need to jump in here. The height of an atmosphere is not well defined, but there are some practical guides. One is to reach a selected fraction of ground pressure (say 0.0001 times or some other selected value). Another is to select the effective location where outgoing radiation to space matches incoming that is absorbed. For Venus, a reasonable locations is about 80 km (near the top of the clouds). The atmospheric temperature there is about 200 K. For the present examples, we instead selected 100 km and a temperature there of 300 K. This would give a higher temperature than Venus, but was just used as examples. We assumed similar mass of gas as Venus as this would give a tall atmosphere. Now givena gas like Argon at 300 K, an approximate thermal velocity would be 1000 ft/sec. This means that the gas could not rise very high before gravity pulled it back. In fact it could only rise about 30 km more. The Maxwell-Boltzmann distribution has variation, but not enough to make molecules go much higher. If you raised the heated mirror shell above where any gas could climb, it would not heat the gas at all, so the problem would be the same as a given initial condition going to final condition based on the available system energy.
Leonard,
I know that, but I was trying to find out Arthur’s thought process, as raising the shell height to heights where atmosphere makes no sense, seems to create some serious problems for the isothermal theory.
Mait – so if I understand, the very distant shell is still at 300 K, and atmosphere and surface are as well, and there’s no introduction of any other factors? Then nothing would change, all would remain at 300 K. What is it you’re thinking would be different?
So we would have 100 km of gas at 300 K and then suddenly nothing?
Mait – well, I’m assuming Earth (or Venus)-type gravity for which after 100 km the density (yes, and pressure) of the air is around a millionth or less of that at the surface. Integrating out to infinity of the continued exponential decline in gas density would add only another part per million of gas molecules, at most.
So, yes, there would be a very slight effect on the order of 1 part in 1 million. But there are other effects at that sort of low level too to worry about (part of the thermal velocity distribution being over planetary escape velocity, for instance) and I don’t think any of us are trying to be that precise here.
So yes, the 100 km of gas at 300 K would imperceptibly expand outward (which would result in slight cooling until/unless thermal exchange with the shell could resume) but it would make only about 1 part per million difference.
Arthur,
A simple point: What happens if a single molecule with random thermal velocity the same as a 300 K gas molecule moved from the top of the room (empty otherwise) to the bottom. It undergoes specular elastic collisions with the wall to keep it within the room. I contend it will end out with a kinetic energy at the bottom as if it heated several hundred degrees (=g/Cp X altitude + 300). Now assume its reflected upward from the bottom and goes back up to the top. I contend it will again be cool with kinetic energy like 300 K. What gravity gives, gravity takes back. This is exactly what will happen to the gas in the room as I stated.
Ah, but a single molecule is actually a quite different case from local thermodynamic equilibrium. In particular, since it’s going faster in the lower portion of the “room”, it spends less time there, and therefore the effective density of molecules in this single-molecule case is *lower* at the bottom of the room, and *higher* at the top. You get into weird stuff like this in the upper reaches of our atmosphere, but at that point temperature itself is not well-defined.
Arthur,
If you look at the motion of one or two or a bunch of molecules at a long enough time their statistical distribution of positions and velocities is the same. The average number of location events at the bottom is much larger, and the average velocities at the bottom is larger. The collisions with the walls should be diffuse rather than specular for best results, but if the walls are not exactly 90 degrees but even off by atomic dimensions, the statistics of the process will approach random in long enough time. The top will be 300 K and bottom will be (g/Cp times height + 3000 K.
Leonard, repsonding to your “motion of one or two or a bunch of molecules at a long enough time their statistical distribution of positions and velocities is the same”
If the molecules are not colliding, i.e. they have a mean free path greater than the 100 km size of the “room”, then that is one case – “equilibrium” and temperature are simply not well defined, certainly there is no local equilibrium without inter-molecular interaction. You can perhaps talk about the “temperature” of the entire room as a whole, but there’s no meaning to the temperature of the “top” or the “bottom”, because there’s no population of molecules that inhabits such a region for any period of time and equilibrates together to allow for temperature to be measured.
If they have a shorter mean free path between collisions, then you do start to get local equilibrium – and that’s the “two and more” molecule case we were talking about below.
I have no idea what you mean by “number of location events at the bottom is much larger” – how can that be, if non-colliding molecules are zooming through the bottom of the “room” at breakneck speed before returning to their leisurely stroll around the top? If you’re referring to the equilibration process that accompanies many collisions, I agree, and that’s quite a different situation from the single-molecule example.
Arthur,
I don’t mean to be rude but you do not understand atmospheric physics.
I have to conclude that Arthur is what is called a troll. He knows just enough to make semi-reasonable statements but is mainly interested in confusing and disrupting the discussion. If this is not true I am sorry, but the level of his responses are out of logical bounds. He appears to be trying to jerk us around. Please do not reply to him unless he make a logically supportable statement.
Um, really Leonard?
How are my “level of response [] out of logical bounds”?
If you can’t answer why, for instance, kinetic energy flow should be zero in equilibrium, then I think you have a pretty serious problem with your understanding of this problem…
You have asked questions about my statements, and I have responded to clarify them, in a fashion that I believe gives logical support. If you want further references or mathematical proofs I can give you that too. What particularly do you actually have a question about right now, that I’ve said, that you find not “logically supportable”?
I put this down before but the posts are out of order in some cases due to answers after new entries.
I am nor sure what you are trying to point out here. At equilibrium all net transfers are zero. Nevertheless, one side will be hotter than the other and one side will have a higher pressure. The magnetic gradient causes it just as gravity on a planet causes pressure to drop with altitude and temperature to also drop with altitude. You can’t separate the thermodynamics of the gas from the effect of the magnetic compression. Both are part of the full problem.
You assert that “all net transfers are zero”, but you don’t seem to have done the calculation to verify it. Take a look at writing down the equations to make net kinetic energy transfer balance to zero, as well as net mass transfer.
Here’s another thought experiment for you all – how about Leonard’s “room” with 2 molecules, instead of just 1. They start out both in the 1-molecule state mentioned in the original suggestion, bouncing up and down, but at some point they collide. Assuming there are no internal degrees of freedom to worry about, the collision results in some vertical kinetic energy being lost from one and given to the other. If this happens in the lower part of the “room” and the vertical energy loss is great enough, this molecule would no longer have enough energy to even reach the top of the “room”; it will have a maximum height before turning around and returning. Now you’re starting to build up the density in the lower half, and reduce the density in the upper half.
So we have one slow molecule confined to the lower half, one fast molecule that bounces back and forth. Net molecular flow averaged over time is zero, and net kinetic energy flow over time is zero (put the plane high enough, and the fast molecule goes through going down, then comes back a little while later with the same energy – net zero).
Now add some more molecules. The energy available will gradually spread among them all, but there will be a distribution, so that some are fast enough to go all the way to the top, some only part way, and some are stuck near the bottom. Once you’ve reached equilibrium, the same principle applies: zero net mass flow, zero net kinetic energy flow. And the distribution of energies is such that, with all those slow molecules at the bottom, the temperature at the bottom is actually just the same as the temperature of that one fast molecule that can still make it to the top.
Make sense?
Arthur,
It just goes on. If the molecules have a head on elastic collision, the momentum is conserved. They bounce off each other and just exchange directions and velocity. It is the same as if they passed through each other. Nothing changed. If the collision is offset, they change vectors. It is true with just two that temporarily one or both can lose the ability to now go very high, but at a later time they will collide again, eventually they regain the ability to go high. Add more molecules, and the average density will be higher at lower elevations, but in all cases any molecule can develop the ability to go to the top after enough collisions. However, at the higher levels the average velocities will be lower and at the lower level, they will be higher. The larger the number of molecules, the more smoothly the density distribution will be and the more collisions a molecule will have before going up or down, which more smoothly distributes the velocity variation with height. There would be zero net mass flow and zero net energy flow at long enough times, but individual molecules would always move up and down, and always trade kinetic energy for potential energy as they move up.
I have to ask you, where do YOU think the lapse rate comes from?
Leonard, you ask “where do YOU think the lapse rate comes from?”
The lapse rate in a planetary troposphere is *caused* by having a planetary surface hotter than the air above it (in Earth and Venus’ case, by greenhouse and cloud effects and for Earth differential night/day insolation).
The lapse rate is *limited* due to the convective instability that arises when vertical temperature gradients are too negative. If convection is able to carry away a sufficient fraction of the necessary energy flow from surface to mid-atmosphere, then it will bring down the lapse rate to around or below that instability limit – the “adiabatic lapse rate” in the case of a dry atmosphere. Where you have latent heat from phase changes (as with water on Earth) convection can couple with latent heat transport to bring the lapse rate down further (to the “moist” rate).
If an atmosphere was for some reason highly viscous (or even solid!) then convective heat flow would be limited and you could get a larger lapse rate than the convective instability limit suggests.
But more often you see lower ones – often much lower. Temperature inversions happen when the surface is colder than the air above it, so the temperature gradient becomes positive (to a moderate height) rather than negative. The air becomes stratified in that case, suppressing convection. In a planet with a weak greenhouse effect and little day/night temperature variation the temperature gradient may never reach the instability limit so convection wouldn’t come into play there either.
It’s worth reading Ramanathan and Coakley (Rev. Geophys. Vol. 16, p. 465, 1978) which presents the standard 1-dimensional “radiative-convective” model – equations (1) and (2) cover the origin of any dT/dz temperature gradient in radiative equilibrium, and then in following equations how to handle the convective instability that results. That, in essence, is “where [..] the lapse rate comes from”.
On the 2- or few-molecule example – I certainly agree that “any molecule can develop the ability to go to the top after enough collisions”. But why do you believe “at the higher levels the average velocities will be lower and at the lower level, they will be higher.”? Whichever molecules are slower at a given point are necessarily confined to the lower half, say, so that you will have a lot of slow molecules in the lower half, and only the faster ones able to go to the upper half (where they will be slowed down by the potential energy increase).
Yes, individual molecules would “always trade kinetic energy for potential energy as they move up” – that’s given from the potential energy field we start with. And similarly, they would gain kinetic energy as they move down. That means that, if nothing else was going on, whenever a pair of molecules crosses a given plane, one going up and the other going down, you have zero net mass transfer, but you have a net increase in kinetic energy in the lower half and a decrease in the upper half. That is real nonzero kinetic energy flow.
Where does that kinetic energy flow end? How do you balance it?
Leonard, evidently you disagree with the Zeroth law of thermodynamics for a system in a gravitational field (or a magnetic field gradient).
But thermodynamics is applied to systems in potential energy fields of all sorts all the time. Anybody familiar with the topic should understand for example the partition function of statistical mechanics, and in particular that the probability distribution of any microstate is proportional to exp(-energy/kT) in equilibrium, which describes the distribution of occupation of different states by individual molecules. In a gravitational field that equilibrium distribution encompasses both the Maxwell-Boltzmann distribution and the hydrostatic effect:
Total energy of a molecule of mass m is
E = gmz + 1/2 m v^2
so probability of any given position z and velocity v is proportional to exp(- (gmz + 1/2 m v^2)/kT)
For any value of height z, the velocity distribution is the
same. As it must be, given that temperature in equilibrium is the same everywhere (zeroth law).
Leonard and All,
I have just now finished reading the posts subsequent to my last post this morning. I agree with you that further discussions with Arthur are a waste of time. Good progress was being made in laying out the physics of the various scenarios until his misdirection or total misunderstanding (I don’t know which) of the thermodynamics sidetracked everything.
I would like to briefly point out some of his misstatements so everyone can get back on track and put his remarks where they belong – in the garbage can.
• “The Maxwell-Boltzmann distribution describes the distribution of vertical velocities of gas molecules, and some of them from lower down will head up. This exchange is sufficient to thermalize the whole system to a single temperature, with or without any radiative exchange.”
And
“Maxwell-Boltzmann gives a velocity distribution in a local small region. It says nothing pro or con about conversion of gravitational potential energy to kinetic energy conversions.”
The Maxwell-Boltzmann distribution is but a special case of the Boltzmann distribution. The Boltzmann distribution is much broader and more general. The Maxwell- Boltzmann distribution only deals with kinetic energy where E = 1/2mv2. But the Boltzmann distribution can also be used in a gravitational field where both kinetic and potential energies can be considered and E = ½mv2 + mgh. And guess what the temperature does as elevation is increased using this Boltzmann distribution? You guessed it!
• “The energy spreads itself out – that’s an essential characteristic of the laws of thermodynamics; energy wants to spread out as much as possible among all the degrees of freedom available. That leads to uniform temperatures at equilibrium, for a system otherwise isolated from the rest of the universe.”
But if you look at the first law equation for a gaseous atmosphere under the influence of a gravitational field you get:
dU = CpdT + gdh
If you require that the atmospheric temperature be isothermal throughout, then the internal energy of the system will increase with elevation. In fact at 10 km the internal energy per unit mass will be 133% greater than at the surface. An isothermal atmosphere doesn’t “spread out” the energy very effectively. OOPs, another Arthur theory bites the dust.
• “Low-entropy energy or “free energy” is the only way to drive mechanical systems such as atmospheric convection that would otherwise wind down and cease any macroscopic motion due to viscous and friction forces.”
As far as I can tell, “low entropy energy” is a term invented by environmentalists and is used in sustainability arguments. (One site where I found the term is named “dieoff.com). It is also sometimes used to define what I call “energy density”. But it is not a classical thermodynamic term as far as I can tell.
But “free energy” is a very useful term and simply defines the amount of energy “free” to do work. So Arthur is close here. The equation for Helmholtz free energy is:
∆A = ∆U – T∆S
Since T∆S = ∆Q, ∆A is simply the internal energy able to perform ∆W. But it has nothing to do with “low” or “high” entropy only the change in entropy relative to the change in total energy and whether or not a process is “spontaneous”.
• “Leonard, you ask “where do YOU think the lapse rate comes from?”
“The lapse rate in a planetary troposphere is *caused* by having a planetary surface hotter than the air above it (in Earth and Venus’ case, by greenhouse and cloud effects and for Earth differential night/day insolation).”
What? It is caused by EVERYTHING!
• “And please, gravity does not trump thermodynamics! A gravitational field is like any other potential energy field, and standard thermodynamics has no trouble dealing with it.”
Based on the above statements of his, he never got to that part during that school thing. He sure has trouble dealing with it!
I’m done!
Umm, williamcg?
Point 1: “And guess what the temperature does as elevation is increased using this Boltzmann distribution?”
That’s a good question. Boltzmann distribution applies in equilibrium, to a system *at constant uniform temperature*!!!
Point 2: “internal energy [per unit mass] of the system will increase with elevation”
I agree with this. Internal energy of any given molecule also increases with its velocity. By “spreading out” I didn’t mean that energy is distributed exactly equally among all molecules in the gas. Rather it is distributed using, as you conveniently bring up, the Boltzmann distribution. That’s why there are exponentially fewer molecules at those greater heights (with higher internal energy per unit mass).
Point 3: If you have a given quantity of total internal energy U in a system, how do you get the greatest quantity of free energy at a given temperature? The more general form of what you write is:
A = U – T S
Since entropy S is always greater than zero, as is temperature, the way to maximize A is for S to be zero. The lower S is, the more free energy you have. That’s what “low-entropy energy” means when I talk about it. I won’t commit to anything about what anyone else says about it.
In particular, driving any process (such as convection) requires nonzero A. Thermalization – production of waste heat – means going to thermodynamic equilibrium, i.e. maximizing entropy, bringing A to zero (assuming zero points of A and U have been appropriately defined). The only way to drive anything more with that given quantity of internal energy, once you’ve hit entropy level S = U/T, is to find a lower-temperature heat bath (T2 < T), which allows you to regain a bit of free energy and do a bit more work.
Point 4: "It is caused by EVERYTHING!" – no, only those things that can drive a temperature difference between surface and mid-atmosphere. Which I specifically listed.
Point 5: ? I don't think you had any specific objection here?
Arthur,
First look at an atmosphere like Earths except with ZERO RADIATION ABSORPTION (no greenhouse gas or clouds). The Solar energy heats the ground and the the ground radiates to space. Where is the lapse rate going to come from? According to your concept, the conduction and then convection from the ground will heat the atmosphere at the ground level and eventually transfer energy to the highest level and make the atmosphere approach isothermal (except for latitude and night/day variations). In fact, this would have the same lapse rate as present except for the water vapor condensation effect (=g/Cp).
On the kinetic energy thing, gravity gives and gravity takes. At any given height the AVERAGE kinetic energy going down is exactly the AVERAGE going up as that is a location of a fixed potential energy. The only difference is direction. The kinetic energy flux is zero and the mass flux is zero at a plane. This is true for all planes. I can elaborate, but the statistics of concentration (greater at lower levels) can be calculated (as one of several approaches) by examination of what happens statistically above and below a given plane.
I suggest you do the calculations on kinetic energy and mass flow and see. I’ve done it and I know that it only works at constant temperature.
As to an atmosphere with “ZERO RADIATION ABSORPTION (no greenhouse gas or clouds)” – that also means the atmosphere has zero radiation emission. So how would the upper atmosphere cool down?
You are indeed correct that such an atmosphere would “approach isothermal (except for latitude and night/day variations).”
But it’s another hypothetical planet so it will evidently be hard to prove which of us is right on this. I suggest you try the kinetic energy flow calculation first.
Arthur, this is my final reply to you. The greenhouse gas on Earth is quoted as only causing about 33 deg K increase for the actual temperature on the ground, compared to the case with no greenhouse gas. The Maxwell equation including gravity gives the solution to the lapse rate (the kinetic energy of the gas near the ground decreases at it rises due to increased potential energy).
What does 33 K warming of the surface (which is partially reduced by convection and latent heat flows – without those it would be more than 33 K) have to do with the surface-mid-atmosphere temperature difference?
What you are talking about as a “cause” is not a cause, it is a *limit* caused by convective instability. Read Ramanathan and Coakley.
williamcg,
Sorry we are getting posted past each other. You have got it right. I personally think Arthur may be trying to be correct, and has some reasonable background, but is just out of his depth here. It is either that or the troll thing.
Arthur,
Sorry, that is Boltzmann distribution, not Maxwell equation.
Wow, a lot of “final reply” statements… If you really will not answer further too bad, I’m certainly willing to engage, though we don’t seem to be making much progress. But the one question I’d like you to answer clearly is:
* on what calculations or other grounds do you base your disagreement with the zeroth law of thermodynamics?
Arthur,
Coming back to the high shell thingy, so I understand that in your opinion an optically transparent atmosphere would evaporate? As we will always have particles on the top of the atmosphere with relatively high kinetic energy, which means it’s pretty much only a matter of time before they reach escape velocity (or more precisely end up high enough for their velocity to be escape velocity for that altitude).
Doesn’t the zeroth law state that if T(A)= T(C) and T(B)=T(C) then T(A)=T(B)?
If so, then how is this relevant at the moment (what are A, B and C), and who and where has disagreed with it?
I’m still way way behind everyone else and only write this comment because I don’t want people to think that I have lost interest.
Because of the pace of the conversation and “FirstLife” disruptions I had skated over some of the curious comments. But now I have stepped back and am considering williamcg’s comment from June 30, 2010 at 1:52 am
Sometimes people’s comments make you question what you think and this is the case here. Once I have got my thoughts straight I will post accordingly. I just can’t promise to be as quick as everyone else..
And on a personal note, I very much appreciate the discussion that has taken place so far.
When I wrote this article (about “thought experiment Venus” aka TEV1) I felt that I had a good grasp of the essential points.
The fact that I’m now reading some thermodynamics textbooks and papers means that I’m not so certain.
Perhaps I am right, perhaps I am wrong, but the opportunity to have ideas – and understanding – tested like this is refreshing.
Williamcg:
Now I have had the opportunity to read the Hans Jelbring article referred to earlier – http://www.tech-know.eu/NISubmission/pdf/Politics_and_the_Greenhouse_Effect.pdf
Are you the part author in the 2nd part of the paper: “Atmospheric Temperature Distribution in a Gravitational Field“?
This statement in the paper is quite confused:
The reason it is a confused statement is this same equation, derived with a different approach, is in every atmospheric physics (climate science) text book that I have read.
So the claim appears to be that this is ignored. But it’s not. If you like I can list half a dozen text books, maybe a dozen, and you will find this formula is always there.
Or that it “refutes the radiation heat transfer model..” – but it’s not the case.
The lapse rate is an integral part of the solution to the temperature profile of the atmosphere. If there was no convection (or a higher lapse rate) the greenhouse effect would be stronger.
So the implication is that the simple formula is ignored – QED climate science is flawed and the inappropriately-named “greenhouse” effect is wrong.
In another post I will try and compare your approach to finding the adiabatic lapse rate with the standard solutions.
Seeing as all the atmospheric text books come up with the same answer as you, it’s not that you’ve found some fatal flaw in this approach.
However, it will be interesting to compare the derivations.
SOD,
Would you please respond to the model of a room I posted earlier “Here is a simple thought experiment. Assume you are on Venus and you build a room 1 km on a side but 100 km tall. Assume the wall (including ends) is a perfect thermos bottle with no heat storage capacity (like a mass-less perfect insulator). Assume the room is initially empty. Now slowly admit from the top a gas that is optically transparent and similar mass to CO2 (Argon is close). Assume the gas is initially 300 K. Fill the room until the included mass is similar to that of the atmosphere of Venus in a same sized room. What do you think the pressure and temperature distribution down the room will be after any currents die out? Consider what will happen over a long additional time if no gas currents remain, and no energy goes in or out.” While I don’t necessarily agree that most or even many people may believe “It is remarkable that this very simple derivation [dT/dh = -g/Cp] is totally ignored in the field of Climate Science simply because it refutes the radiation heat transfer model as the dominant cause of the GE.”, Nevertheless Arthur does not understand it’s consequence. Others seemed to also have problems with the basic issue. For example DeWitt initially resisted that it was total energy rather than kinetic energy that was preserved with altitude. He later accepted it. Nick first agreed now seems confused. The result is that there does seem to be an issue with that concept.
When reviewing some basic derivations I found something interesting in a book I hadn’t read before – The Physics of Atmospheres by John Houghton, 1986.
After deriving the adiabatic lapse rate (like every other atmospheric physics text book), he brings up the subject of Sandstrom’s Theorem, something I hadn’t seen before, but seems at least interesting and very relevant to this discussion.
The idea is around a body receiving energy at the top rather than the bottom..
There is a great lecture about Sandstrom’s theory at –
Click to access 03Sandstr.pdf
Of course there is a significant difference between the oceans and the atmosphere but many of the discussion points seem relevent to the TEV discussions.
And a related paper “Vertical Mixing, Energy and the General Circulation of the Oceans” by Carl Wunsch and Raffaele Ferrari – Annual Review of Fluid Mechanics (2004)
Click to access wunsch_ferrari04.pdf
Wiki article on Sandstrom at
http://en.wikipedia.org/wiki/Johan_Sandstrom
williamcg:
I’m intruiged by this statement from July 4, 2010 at 11:45 pm
Which is similar to July 1, 2010 at 2:30 am:
I don’t want to put words in your mouth, so can you explain your perspective on this – once the atmosphere starts thinning out, around the tropopause, the atmosphere does become isothermal, then tends towards a positive temperature gradient due to the ozone effect in the stratosphere.
From your comments above, this appears to be something that can’t happen, but I might well have misunderstood what you are explaining..
Conventional atmospheric physics explains the troposphere as being dominated by convection – because this is more effective at redistributing energy than radiation – while the stratosphere becomes isothermal because radiation (in the more rarefied atmosphere) is much more effective at moving heat than convection.
SOD,
By the way, the basic mistake in the Hans Jelbring article you mentioned above was that he neglected to include the fact that the change in effective altitude of the outgoing radiation was what the added greenhouse gases affected. However claims that the lapse rate is changed are often made by pro AGW supporters, so I see where he is coming from. The lapse rate is not changed (with certain special conditions it can, but that is not the basic issue here), but the location of a particular temperature was. I agree that greenhouse gases affect the surface temperature. However the amount of effect, especially wrt feedback is the big issue with me. In the case of Venus, the issue seems to be entirely different than for Earth for many in the pro AGW camp, and the issue brought up by williamcg and Jelbring do seem to apply for what is claimed for Venus (claims of tipping point and runaway greenhouse).
SOD,
The tropopause and heating above a certain altitude would exist even for no optically absorbing gas at normal sunlight wavelengths. It has nothing to due with the fact that outgoing radiation is free to leave. The solar wind and strong space radiation interact with the outer atmosphere and dissociate and ionize some atoms and molecules. These become very hot. Heat transfer by diffusion downward would cause a temperature reversal even in this case. The presence of Oxygen adds Ozone which absorbs UV and heats, and this changes the magnitude and altitude of the reversal, but the point is that a reversal can and will always happen. The presence of aerosols also enters this problem as they absorb sunlight. The physics of these issues does not change the basic nature of normal atmospheric lapse rate and effect of greenhouse gases.
Leonard Weinstein:
Great question. I will, once I’m sure I’ve got the answer right.
Leonard Weinstein from July 8, 2010 at 12:43 pm:
I’m just trying to make sure I understand williamcg’s statement:
It is the “impossibility because of the gravitational field” that I am struggling with.
Well, it seems like the explanation is part of the different approach to calculating the adiabatic lapse rate.
Perhaps something of importance to pick away at.
SOD,
I have to comment on your claim that “– while the stratosphere becomes isothermal because radiation (in the more rarefied atmosphere) is much more effective at moving heat than convection.” If there were no greenhouse gas on Earth, are you saying that the atmosphere would be isothermal? Look at my room example. You do seem to be saying that lapse rate is not -g/Cp.
Leonard Weinstein:
If there were no greenhouse gas on Earth everything would be different.
My comment is about the point where radiation becomes more effective than convection at moving heat.
Perhaps it is not the right terminology but we could think of a radiative “lapse rate” – as the atmosphere becomes optically thinner heat transfer takes place more effectively via radiation than convection.
The convective lapse rate is “the constant” – for want of a better expression. Lower in the troposphere convection takes over because radiation moves heat quite ineffectively between different heights. As the atmosphere thins out, radiation becomes more effective.
That’s why the temperature profiles don’t follow the adiabatic lapse rate above a certain height. Without ozone, the tropopause and up into the stratosphere would be isothermal.
SOD,
The point williancg has repeated is that TOTAL energy is conserved, and this has a kinetic energy and potential energy component. You can look directly at that total energy conversion physics, or indirectly by looking how the gas in gravity changes density with altitude, and using the density change to derive the adiabatic lapse rate. Both are based on the same physics, and should give the same answer. It is not a different concept, just looking at basic cause in different ways. The lapse rate is due to the fact that going to higher altitude corresponds to converting kinetic energy to potential energy and thus the gas is lower temperature. This happens always unless local events (e.g., selective layers of radiation absorption) modify the result. The lapse rate and absolute temperature levels are totally different things. Fixing the temperature at a particular level (ground or at some altitude) does not change the lapse rate.
SOD,
Without ozone and if there were no space or energetic solar radiation interacting with the gas, the gas would NOT be isothermal, it would continue the adiabatic lapse rate until the gas condensed. The gravity and kinetic energy trade off with altitude continues until gas cannot go any higher due to gravity (a finite gas kinetic velocity below escape velocity limits maximum altitude just as for larger objects). Again, look at an Earth without a greenhouse gas. Do you think the atmosphere would be isothermal?
SOD,
There seems to be some confusion in terms. There is no convective lapse rate. The convection is a restoring mechanism when the lapse rate varies from ideal (due to non uniform ground heating, and day/night variation) the lapse rate is the condition that naturally occurs in the absence of local unbalanced forcing. Calling a term convective lapse rate seems to imply that the convection generated the lapse rate, not the basic physics. Likewise, the location where radiation goes to space is where the incoming and outgoing radiation balance, and thus determines a specific temperature. Now the lapse rate both up and down are applied to this specific temperature at a specific level to find the ground and higher altitude temperatures. The fact that the radiation to space leaves over a range of altitudes makes the problem more complicated, but does not change the basic concept.
Mait – on “an optically transparent atmosphere would evaporate?” – it is true that *every* atmosphere will eventually evaporate if you give it long enough time. But it’s a small, slow effect (at least for molecules heavier than hydrogen on a planet with Earth-like gravity and temperatures). Ignoring that small effect, and the small effect of a tiny fraction of the atmosphere existing beyond 100 km (on Earth, 100 km is considered the start of “outer space”, and those who reach that altitude were, at least until recently, considered astronauts) there’s at most only a tiny difference between having the enclosing shell at 100 km or at 1 AU or higher. What do you see as the difference? What were you expecting from the example you presented?
And on the zeroth law – what it means is that in a system in equilibrium you can always measure a consistent single temperature. Let your system – Leonard’s 100 km room – be component ‘A’, in equilibrium. Let ‘B’ be a thermometer at the surface. Let ‘C’ be a thermometer at 100 km. The zeroth law then says, if all three are in equilibrium, then the temperature measured by ‘B’ has to be the same as the temperature measured by ‘C’. It’s a very basic principle.
Leonard, I really would like to hear why you think you have some violation of this basic thermodynamic law under a gravitational field.
You also still haven’t answered the issue of net kinetic energy flow. Here’s another approach that may illuminate where you’re going wrong, and why this is an issue.
When you talk about the acceleration that individual molecules feel under gravity you are taking account of the gravitational force. This is indeed true – molecules falling accelerate, molecules rising decelerate, due to gravity.
But if gravity were the only force involved, there would be nothing to prevent the entire air column from completely collapsing to the bottom – in fact, there would be no bottom, molecules would continue accelerating downwards forever (until the gravitational field changes at least).
What you are neglecting in this argument is the other force that allows this to be an equilibrium situation – the force associated with the collision of molecules with the surface, at the bottom of your “room”. This is a force pushing the molecules back up. It only acts at the instant they collide, but it is enough to reverse their momenta. On a macroscopic scale, that force is communicated upwards via the pressure field; that pressure field counters the acceleration from gravity. It needs to be properly accounted for, just as the downward acceleration needs to be properly accounted for. And when you do, you find that the equilibrium state with no net kinetic energy flow or net mass flow requires a constant temperature.
I would expect the kinetic energy of gas particles(and hence Temperature), to be zero on “top” of the atmosphere. If it were not, they would just keep flying on and the atmosphere would evaporate (rather quickly I would say). I don’t quite understand how you think it wouldn’t to be honest.
Arthur,
You honestly seem to be discussing your issues, so I will continue the communication. The molecular collisions cause what is called a pressure which is enough to prevent collapse of all of the gas, nevertheless the pressure at any height is the weight of all the gas above it. As a group of molecules moves up, they move to a lower pressure, and adiabatic expansion results in the lower temperature. This is actually a different way of looking at the effect of gravity on temperature, but is the same cause. There is no pressure FIELD only molecular collisions.
*IF THEY MOVE UP ADIABATICALLY* then adiabatic expansion results in a lower temperature. Adiabatic motion is motion fast enough that there is no heat exchange with the surroundings. In the real world, there is always some heat exchange. When you move slowly enough – reversibly – the expansion process becomes isothermal, not adiabatic.
Arthur,
I am sorry but you are either without understanding on this topic or deliberately trying to confuse the issue. Any more such statements out of ignorance and I won’t waste time on you. That is a shame because others seem to be enjoying the discussion.
SOD,
I think I need to elaborate on the temperature reversal issue in the upper atmosphere. This effect is not due to anything related to the basic lapse rate physics at all. It does affect the actual temperature profile due to being a forcing factor. This is caused by a set of imposed conditions that do not exist at lower elevations. If an atmosphere did not have oxygen so that ozone could not form, and if there were no aerosols, a reversal and rising temperature would still form at some altitude, although it would be at higher level. This new source of heating is not part of the lapse rate issue, but is a separate condition that eventually counteracts the lapse rate effect. The tropopause is generally near the location of the main source of outgoing radiation, but does not have to be so. If there were no green house gases or clouds at all, there would still be a tropopause.
Arthur Smith
…”.that pressure field counters the acceleration from gravity. It needs to be properly accounted for”……
Surely in this example the pressure is a secondary effect not a causal effect.
The vector sum of number of particles and their momentum crossing the defined area will give a change in momentum per unit time, hence force, hence pressure.
This is a result of gravity acting on particles who have acquired initial internal energy from the surface and subsequently exchanged between them by collision.
I don’t think a pressure field is a useful concept here.
Bryan, if there is a net force, you do not have equilibrium. What provides the counter-force to gravity, to balance things when you reach steady unchanging macroscopic conditions?
SOD,
I left out that not only would there be a tropopause, but heating to higher temperatures beyond it. It never would go to a isothermal condition as you went out.
Here are a few interesting numbers for thought. On the Earth, near the equator, the energy absorbed by the Earth and it’s atmosphere during daylight is about 1.5E7 J/m2. This is about the amount that leaves at night (some is carried to higher latitudes by wind). The mass of a m2 atmosphere all the way to space is about 1E4 kg/m2. With a Cp of about 0.4 cal/g/K, this means the air will heat and cool about 1 K day to night if all processes were uniform. Venus has nearly 100 times the atmosphere mass and actually less absorbed energy. Thus on Venus even with a day over 100 times as long, the atmosphere will heat and cool only about 1 K from day to night if energy is distributed. The latitude variation and most of the day/night variation is actually mostly smoothed out by induced winds. I think you can safely use average numbers to model the approximate temperature distribution, and the only purpose of the need for wind is to distribute the energy.
I don’t know about the rest of you viewers, but I have changed my view and understanding on some items over this discussion. I still think my overall positions are basically correct, but some of the details I had claimed would change if I restated them. I think this kind of discussion is very useful, and want to thank SOD for his patience and thoughtful replies. Those who also made some changes in position show flexibility. Those who do not are either right or stubborn. Either way I hope we can continue until a reasonable consensus is reached from discussing opposite views rather than just from one side saying that this is the way it is and you are criminal if you disagree.
Leonard, you still have not responded on my main question… let me repeat:
* on what calculations or other grounds do you base your disagreement with the zeroth law of thermodynamics?
Arthur,
Where did I ever disagree with the zeroth law of thermodynamics. If you reply that conduction up a gravity well does not prevent the temperature from becoming a constant, you clearly still do not get it.
? I believe we’ve been talking about, with your “room” example, or my “oxygen container” example, the approach to thermodynamic equilibrium. You seem to feel that even under equilibrium there will still be a temperature gradient, temperatures will not be uniform. But that clearly violates the zeroth law.
SOD,
“And on a personal note, I very much appreciate the discussion that has taken place so far……Perhaps I am right, perhaps I am wrong, but the opportunity to have ideas – and understanding – tested like this is refreshing.”
Glad to hear that. That’s exactly how I feel. I generally don’t participate in public science blogs but this one felt good so I jumped in. The participants are knowledgeable and are willing to discuss all sides in an objective manner. It’s rare these days. I have a hard time objectively analyzing my ideas when I am only talking to myself. Funny, but I find I am not a great critic of my own opinions. That’s why a quality blog like this is very useful. I actually find out when I’m wrong and I always learn something new to generate more ideas. I have enjoyed this Venus thread of yours. I think a lot of progress in understanding has been made. Keep up the good work.
“Are you the part author in the 2nd part of the paper: “Atmospheric Temperature Distribution in a Gravitational Field“?”
Yes, that’s me. I would have used my full name for this blog but I was already registered on Word Press as “Williamcg” so I just stayed with it. The first thing to remember about that paper was that it was not meant as a scientific paper, but as a political one. Hans Jelbring wrote it as a private policy letter in April 2009 to a select number of members of the Swedish Parliament just prior to one of their hearings on Climate Change. I am a member of a private blog called “Climate Skeptics” and Hans was a member (as are a lot of well known serious scientists of the skeptical persuasion – I am lucky to be there). I had posted a version of this simplified derivation of the lapse rate formula and he asked me if I would write something up to include in his letter. He felt it was simple enough that it may be understood by the not so scientific minded parliamentarians. I don’t know if they understood it. I’m not sure how it became public.
You quote me as saying:
“It is remarkable that this very simple derivation [dT/dh = -g/CpT] is totally ignored in the field of Climate Science simply because it refutes the radiation heat transfer model as the dominant cause of the GE.”
And you said:
“This statement in the paper is quite confused: The reason it is a confused statement is this same equation, derived with a different approach, is in every atmospheric physics (climate science) text book that I have read.”
I did not say that this equation was not known; I said that this equation was “ignored”. But I also said in an earlier section:
“I became interested in Climate Science some four years ago because it seemed to be a perfect fit with my Chemical Engineering background (large, complex, multivariant
systems involving significant heat and mass transfer processes) and I thought I may be
able to contribute something. I was immediately amazed at the paltry level of scientific
competence that I found, especially in the basic areas of heat and mass transfer. Even the
relatively simple analysis of atmospheric temperature distributions were misunderstood
completely.”
So I’m not quite sure if it is just ignored or the general educational level of “Climate Scientists” in basic meteorology is abysmal. Based on the recent discussions with Arthur on this blog, I am still not sure which one it is. I know his background and he is considered to be knowledgeable in thermodynamics by his peers.
As for the classical textbook derivation of the lapse rate that you mention, it is quite cumbersome. They start out with the first law, and then insert the derivative of the ideal gas law. They then insert the hydrostatic equation (which only applies to constant temperature gaseous systems) and then fiddle around to get dT/dh = – g/Cp. My derivation uses only the first law and takes two steps. That’s why Jelbring wanted to use it. I am not saying that I was the first to use this derivation; I just haven’t seen it elsewhere. It is just too damn simple not to have been thought of before.
PS: How do you get things like bold, italics, indentation, etc., to work on this blog. It doesn’t take it when I post. Am I missing something basic?
On the admin note “PS: How do you get things like bold, italics, indentation, etc., to work on this blog. It doesn’t take it when I post. Am I missing something basic?”
Now let’s see if that worked.
William, if you have talked about this already I apologize, but I don’t see it in any of your previous comments that I’ve reviewed again just now. You also seem to disagree with the zeroth law of thermo (under a gravitational field) – but you’ve expressed your reasoning that this is true under the conditions that processes are adiabatic (dQ = 0).
Why do you believe atmospheric processes are adiabatic?
In particular, dQ can be non-zero without any total entropy increase (reversibly) if the heat exchange happens between two bodies at the same temperature. One body (gaining heat) increases in entropy, but the other body (losing heat) reduces entropy by the same amount, so no net change. That’s the isothermal case.
Arthur,
I have to comment on your comment. No one said all atmospheric processes were adiabatic. There are always variations in temperature at a constant altitude (due to different latitudes, night and day, and different local albedo) that result in heat transfer, so the mixing processes are not adiabatic. What was said was that a gas increasing in elevation undergoes an adiabatic cooling exactly to the tune of the adiabatic lapse rate. I also said that real heat transfer is what drives the formation of wind and circulation, and these currents are a negative feedback that tend to restore the adiabatic lapse rate. On the average, the net process is the same as an adiabatic process would be if there were no thermal unbalances, and the resulting average lapse rate is the adiabatic lapse rate.
William’s analysis relies on the claim that dQ = 0. If it is not always forced to be zero, then his claim on dT/dh is wrong.
SOD,
Thanks for the reference to Sandstom’s Theorem. I was unaware of it. I will read it as soon as I can. This thread is moving very fast and I’m having trouble keeping up. I better read it quickly.
As to your question regarding the isothermal to positive lapse rate above the tropopause, I think Leonard covered it pretty well. There are two reasons. First, the exothermic reaction of UV, oxygen and Ozone dominate the thermodynamics up there. The exothermic reaction is strongest at the higher elevations where the UV first enters the system and tails off as it approaches the tropopause. Second, the atmosphere seems to have a minimum density at which the lapse rate thermodynamics dominate. This occurs at about 0.1 atmospheres if my memory serves me correctly. That’s why Mars has no appreciable thermodynamic lapse rate but all the other planets with significant atmospheric densities do. They all have a tropopause at about 0.1 atm., if I remember correctly.
Arthur Smith
..”Bryan, if there is a net force, you do not have equilibrium. “..
If the temperature drops as the altitude increases I would not expect to have equilibrium.
Bryan,
Why do you state “If the temperature drops as the altitude increases I would not expect to have equilibrium”? If you followed the discussion you would realize that if the temperature drop rate with increasing altitude followed the lapse rate, that is the ideal equilibrium value. You can be out of equilibrium if force, but that introduces a negative feedback going back toward the lapse rate. Think a ball in a cup that is pushed up the wall a distance and released.
Bryan,
Equilibrium does not mean no molecular motion, only that it is macroscopically in average balance.
Leonard Weinstein
The temperature drop is determined by gravity.
The lapse rate follows the temperature drop it doesn’t determine it.
The lapse rate I am referring to is the Environmental lapse rate – which refers to the actual change of temperature with altitude for a stationary dry atmosphere (i.e. the temperature gradient)
The equilibrium I was referring to was the thermodynamic equilibrium.
On reflection I think Arthur was referring to hydrostatic equilibrium.
I’m not sure how useful a concept this is for a gas.
I think I will observe only for the moment so as not to muddy the waters.
Bryan – the conditions Leonard has set up essentially isolate the atmosphere of the planet from the rest of the universe. Such a system should always tend towards thermodynamic equilibrium – which includes hydrostatic equilibrium as a consequence.
And, which includes uniform constant temperature as a consequence as well (zeroth law).
Bryan,
Please stay in. On our difference, I think it is only usage of words, and limited room for details that causes disagreement.
Arthur,
When you say “the conditions Leonard has set up essentially isolate the atmosphere of the planet from the rest of the universe” this is true for the room problem but not the others. Is this the case you are referring to? If it is, how do you not understand E=1/2 mv2+mgh as causing a temperature gradient in the tall enclosed room. It is E, not T that becomes constant in the zeroth law for the case of gravity.
You say “E … becomes constant” – since your “E” is the internal energy of a single molecule, that means all the molecules would run around with exactly the same velocity (at a given height).
But that is not what happens. There is a distribution of velocities, and so a distribution of energies at a given height. And the same distribution also gives you a distribution of heights. Molecules collide and exchange energy with one another, and the statistical properties force a particular distribution – the Boltzmann distribution we’ve discussed before here.
Arthur,
Yes a distribution, with the gravity term included.
Arthur,
The E refers to the macroscopic average. When you talk about a velocity distribution you can still define a single gas temperature, even though individual molecules vary. Pressure and temperature only have meaning with group statistics relative to a reference frame.
Arthur,
A simple question to you. What do you think the pressure distribution in the isolated tall room would be?
Leonard – you say “The E refers to the macroscopic average”. I assume you mean an intensive quantity such as total internal energy per unit mass, or something of that sort?
But what is your basis for the claim that this quantity is locally constant throughout a system in equilibrium? I’ve never heard such a claim elsewhere in my study of the subject.
Whereas constant temperature of a system in equilibrium is very definitely the standard result (zeroth law).
The pressure distribution in the “room” would of course match the density distribution (since I assert temperature is constant, and we’re talking about ideal gases) – decreasing exponentially with height from bottom to top.
Let me have another attempt to reframe the basics of the statistical mechanics of this problem. A system in thermodynamic equilibrium at a single temperature T should follow the canonical (or Gibbs) ensemble where individual molecules occupy states of molecular energy E with probability
p(E) = c . exp(-E/kT)
for some constant c (the Boltzmann distribution).
My “oxygen container” example was explicitly in this condition, with a constant-temperature left-hand-side in thermal contact, fixing the temperature.
Leonard’s “room” example is very slightly different because it specified total energy of the system, not providing a bounding temperature bath – but the probability distribution at equilibrium is very similar in the end; we can discuss the minor differences later if necessary.
Now, what does the Boltzmann distribution imply? Higher energy molecular states are exponentially less likely. It doesn’t matter whether that higher energy is kinetic or potential. For free molecules with no potential field, the Boltzmann distribution reduces to the Maxwell-Boltzmann distribution of probability exp(-1/2mv^2/kT). So higher velocities are exponentially less likely according to the ratio of their kinetic energy to the temperature.
If you add a gravitational field, the Boltzmann distribution still applies: probability of height z and velocity v is then proportional to exp(-mgz/kT – 1/2 mv^2/kT) which is the product:
p = c exp(-mgz/kT) . exp(-1/2mv^2/kT)
That is, molecules are exponentially less likely to be higher up, according to the ratio of that gravitational potential energy to temperature. But whatever the height ‘z’, the distribution of velocities v at that height is the same. Which it has to be, since the temperature is constant.
Arthur,
You are making a circular argument. In the end you say the temperature is constant because the temperature is constant. And yes I mean the total energy per unit mass. A simple way to see the flaw of your argument is to look at a single molecule going straight up and having a reasonably long path before collision. It’s velocity wrt the walls is DECREASING as it goes up (kinetic energy lost to gravitational potential energy). In other words, it’s contribution to the temperature is dropping as it goes up. Coming down is just the opposite. I don’t see how you can misread that.
Arthur,
There will be a Boltzmann distribution at the higher level, it’s mean will have been shifted down.
Leonard, I don’t think you’ve done the actual calculation needed to prove your assertion. The full analysis is a bit complicated, but here’s an outline that gives the general idea:
Consider molecules (density n0) at height z0 with temperature T0, so the M-B distribution of velocities goes as exp(-1/2mv^2/kT0). This is our starting distribution.
Now suppose we look at all the molecules from this distribution that head up a distance dz. If their initial z-ward velocity was vz, their new z-ward velocity is sqrt(vz^2 – 2 g dz) (because their K.E. has been reduced by m g dz).
In particular, any molecules with vz sqrt(2 g dz); probability n0 exp(- 1/2 m vz^2/k T0), new vz’ = sqrt(vz^2 – 2 g dz)
and a removed distribution from this layer of:
vz 0; probability = n0 exp(-1/2 m (vz’^2 + 2 g dz)/k T0)
which = n0 exp(-m g dz/k T0) * exp(-1/2 m vz’^2/kT0)
I.e. the two distributions are identical *only* if:
n1 = n0 exp(-m g dz/k T0)
and T1 = T0.
Sorry, that was garbled by html – fixed version of the last half as best as I recall:
In particular, any molecules with vz < sqrt(2 g dz) would not reach the new level.
Similarly, there is a distribution of molecules leaving the new level at height z1 = z0 + dz; set the density to n1 and temperature to T1, then all molecules with negative vertical velocity component vz < 0 would leave in a downward direction.
In equilibrium the incoming number and kinetic energy distributions should match (though vertical velocities are reversed).
So the distribution of molecules entering the new level is defined by:
vz > sqrt(2 g dz); probability n0 exp(- 1/2 m vz^2/k T0), new vz’ = sqrt(vz^2 – 2 g dz)
and the removed distribution from this layer is:
vz < 0; probability n1 exp(-1/2 m vz^2/k T1)
Changing variables from vz to the new velocity vz’ in the first distribution gives us:
probability = n0 exp(-1/2 m (vz’^2 + 2 g dz)/k T0)
which = n0 exp(-m g dz/k T0) * exp(-1/2 m vz’^2/kT0)
I.e. the two distributions are identical *only* if:
n1 = n0 exp(-m g dz/k T0)
and T1 = T0.
Arthur,
If you have a web site put the entire analysis in it and give the web address for that writeup on this blog. I think that you forgot that different levels contribute to a given level both up and down (but there is not enough in the analysis to be clear to me). You cannot just look at two adjacent heights. The incoming numbers and average kinetic energy at a single level have to match, but a range of different levels above and below are needed.
Well, you’re the one making the assertions that counter the zeroth law of thermodynamics, I think you ought to run the numbers yourself, no?
All,
Just remember that Arthur is the hit man they brought in to try and rebuke the G&T “Falsification…” paper. (He wasn’t very successful and now there are two papers out there rebuking Arthur’s rebuke). There was a very organized intelligent discussion going on in this thread until Arthur successfully created misdirection and introduced dead end theories and misleading logical fallacies.
I will admit he’s pretty good at it though.
Remember that Venus is the Mount Sinai in Hanson’s religious epic of AGW. These people take their religion very seriously.
“they brought in”? Who would this “they” be? And why would they need me?
But since you seem to admire G&T, tell me how you can believe Leonard’s claims that “TEV1-3” could result in transfer of heat from the cool shell to the hot interior when one of their main arguments is how the greenhouse effect is impossible because it would violate the second law restriction on transferring heat from cooler to warmer bodies?
In the case of the greenhouse effect, of course, that sort of transfer does *not* occur. But your argument on dT/dh above and Leonard’s discussion of TEV1-3 require it.
williamcg:
In this blog we try and stay with the science and the arguments, not attempt to attack people for what we believe they haven’t done or have done elsewhere.
Please check out the Etiquette and for the spirit of the blog, About this blog
It’s easy to claim that someone is creating misdirection.
What’s important is to demonstrate it.
A good demonstration will make it clear to other readers.
From a moderation point of view I rarely have to resort to deleting comments which derail a discussion by continual repetition without taking up points made by others.
But I will delete future comments from anyone which stray into personal attacks.
SOD,
It was a compliment.
Arthur,
from the first law of thermodynamics
dQ = dU + deltaW = n · cv dT + P dV = 0
where cv is given in units of erg/K/mole and n is the number of moles. The derivative of the ideal gas law, P · V = n R T, is
V dP + P dV = n R dT
equating P dV and noting that R = cp – cv yields
dQ = n cv dT – V dP + n (cp-cv) dT
dQ = n cp dT – V dP = 0 for adiabatic
Cp = cp/ and rho = n · /V so that
dT/dP = V/(n · cp) = 1 /(Cp · rho)
From hydrostatic equilibrium and the gas law we can convert from pressure to height coordinates:
dP = – g rho dz
dT/dz|a = -g/Cp
Gammaa ident -dT/dz|a = g/Cp
Leonard – once again your argument requires dQ = 0. But this is not valid, as I’ve been explaining – it requires all processes in the atmosphere to be adiabatic. They are not.
Leonard, note that in a comment above you stated:
SOD,
I read one comment on a blog at Real Climate (yes I read on all sides of issues) that bragged how several people that supported them were attempting to confuse the blogs of skeptics with well placed misdirection. This may put the comment of williamcg in perspective. This type of activity makes it more difficult to keep the discussion on track. The problem with ignoring such people is that then they can say those that disagree with them are not able to respond. In the case of Arthur, I eagerly await his response to my June 10, 2:26 comment.
Leonard – nobody is “placing me” or coordinating what I do or doing anything of the sort. I’ve followed SoD a little and commented on previous posts several times in the past, complimented several of the presentations, pointed out a few weaknesses. I find your insinuation appalling, but indicative of the conspiracy mindset that seems prevalent among those who call themselves “skeptics”.
If your *July* 10, 2:26 comment was intended to be a response to my question on the zeroth law, I’m sorry, but a handful of equations that depend on adiabaticity are not a response. The zeroth law is a very fundamental part of thermodynamics – it gets to the heart of what “temperature” and “equilibrium” mean in the first place. It’s the sort of thing that should be conveyed clearly in a first course in the subject, but sadly many seem to have missed something there.
In any case, I already added 2 reply comments to your comment, so I’m not sure what you’re “eagerly awaiting”!
“Several people” – do you have their names? People who have a different point of view have it for a reason. Rarely because they are paid up members of an evil empire, so I just ask that on this blog we take the charitable approach and assume that people come with genuine motives.
Ask yourself this – are you more likely to convince someone of something by first attacking their character and their motives or by assuming the best and discussing their arguments?
Are you more likely to convince bystanders by attacking the character of others? Or not?
SOD,
I have never initiated a personal attach on a person. However, I have responded when I was attacked. It is possible that I misjudged what was said as an attack, and if so I am sorry. You are reasonable and polite, but that is not what I have observed on many of the pro AGW blog sites. I think many of the skeptics have developed a negative response as reaction to continual negative words used against them. There are exceptions, but this is clearly true of any sizable group. I have always tried to convince by logic not by attacking. I do not plan to continue responding to Arthur, because he is going round and round on what I think is a basic error. I truly am convinced he knows better and is jerking the discussion around.
Arthur,
The analysis we are talking about here is for the the room problem. This is a closed system that has come to steady state. The definition of adiabatic is no heat transfer in the gas. If there were heat transfer to make the gas isothermal, at the end the steady state gas would again be adiabatic, so that assumption of not being adiabatic is an invalid statement. We are talking about the actual room of gas end point where all currents have died out.
The other statement is for the planet with external heating variation from the sun heated shell with latitude and day/night variation. In that case the currents and heat transfer are part of a negative feedback to try to restore the adiabatic condition. They don’t cause it to be adiabatic, they try to counter externally imposed forces that try to unbalance it, and succeed very well in most cases.
I know going over several models and discussions is a source of confusion, but I think that was clear. If the room problem is correct, and a reasonable argument can show how the case with a shell over the atmosphere can induce self balancing atmospheric currents, than I think my arguments can be supported.
Leonard – your equations were not explained with adequate text, but they describe a *process* that involves a change in temperature, volume, height, and pressure (all the items with ‘d’s). That is not a description of the state of an entire system, for which none of those things would be changing. It is a description of *part* of the system.
While your “room” is completely isolated from the rest of the universe so dQ would be zero, so would dV, dp, dT, and dz, because the volume, pressure (distribution), temperature (distribution or single-value) and height are not changing for the room as a whole, in equilibrium.
So your equations must refer to a subsystem. But that subsystem can, and under most circumstances will, exchange heat with other subsystems within the “room”.
What sort of part could you be describing? Though you did not explain this, let’s assume the equations you use are appropriate for a parcel of gas within the system that changes its altitude. Your equations do require ‘dn = 0’ (i.e. no change in number of molecules in the subsystem) so that identification seems warranted.
So dp is the change in pressure of this parcel of gas, dV is the change in volume, dT is the change in its temperature, and dz the change in its height.
If the parcel of gas rises quickly enough that it does not exchange very much heat with its surroundings (i.e. no radiative exchange, no molecules crossing between parcel and surroundings) then the adiabatic assumption dQ = 0 is close to correct.
But if that parcel rises more slowly, that gives more time for conductive exchange with surroundings. dQ becomes larger, and dT becomes smaller (less negative). As the rate of rise slows, it becomes more isothermal, less adiabatic.
Now you specified that we were interested in the limiting case where all currents had stopped. That means the limit where all motion of such parcels ceases. That is, precisely, the isothermal limit.
Arthur,
My responses were made before yours were shown. There is a lag in the system, I guess due to SOD checking the responses for improper statements, so we sometimes talk past each other. However, I have refuted your response. The final room gas will be adiabatic in the steady state, so the analysis holds.
Arthur,
The definition of an adiabatic system is an enclosed system with no heat transfer through the boundary of the system. Once you have a trapped quantity of gas, it does not even matter if local currents and heat transfer is occurring, the system as a whole is adiabatic by definition. For the room, after a fixed amount of gas was introduced from the top at a gas temperature of 300 K (given initial condition). The room was sealed and allowed to come to a steady state equilibrium. The lack of heat transfer in the final state, independent of whether the temperature is constant or a fixed gradient (remember we are talking about all heat transfer and gas bulk motion dying out) would result in all subsets of gas being at adiabatic conditions by definition, as well as the room as a whole. There is no way to avoid the definition of adiabatic conditions here. I showed that if adiabatic conditions existed, there would be a temperature gradient. Therefore isothermal is not possible for this case.
williamcg
You are welcome (and so is everyone else) to discuss the paper of Gerlich and Tscheuschner in the article – On the Miseducation of the Uninformed by Gerlich and Tscheuschner (2009).
We won’t discuss their paper on this thread, but I would welcome your comments on the article over there.
Arthur,
Your slow rising parcel of gas is a perfect example of why you do not seem to understand (or are trying to distract) on the problem. The rising parcel will expand (you admit to pressure dropping with height), and cool without heat transfer other than that from the excess imposed at the initial location. This mixing actually acts to smooth out the unbalance caused by the excess and restores the adiabatic lapse rate. By the way, where do you get the excess from? Once all currents die out what is left is an adiabatic gas with pressure and temperature gradients as stated. If it were isothermal, it would also be adiabatic, and that leads to a non isothermal condition. Can’t do that!
Leonard, the forces in this system are gravity and pressure. If a parcel of gas rises it does so due to a pressure difference that exceeds the gravitational pull on the parcel. The rate at which it rises depends on the magnitude of that excess. As the system reaches equilibrium, pressure differences away from hydrostatic equilibrium will gradually vanish, and motion becomes slower and slower.
How do you enforce a “without heat transfer” condition on a parcel of gas that is just a portion of a much larger system? You can’t – heat will move around, at least through the motion of individual molecules. And that means the motion will not be adiabatic. But it will, in the limit of slow motion, be isothermal.
williamcg,
I am afraid I do not agree with all of the G&T analysis.
Arthur,
The zeroth law of thermo is NOT a law. It is a fact that follows from other laws under certain conditions. The cases we have been discussing are not within those conditions. I am afraid that the first law of thermodynamics combined with the fact that there is no more heat transfer at the end point trumps the zeroth law.
Leonard, I linked to the wikipedia definition of “zeroth law” which mentions only the conditions of thermodynamic equilibrium. Please cite a source for your “certain conditions” claim.
The first law certainly does *NOT* trump the zeroth law – for a given quantity of energy in a system, temperature can be uniform or nonuniform. The equilibrium state is the one where temperature is uniform.
SOD and Leonard,
I did not say that I agreed with the G&T paper. I just pointed out that Arthur was heavily involved in trying to rebuke it. But his rebuke was also very shaky and is being challenged. I personally find the G&T paper unintelligible in places and not to the level of a “Falsification”. I also disagree with certain statements and I don’t think the paper completely backs up some of its conclusions. But the paper did cause quite a stir in the AGW camp that seems to continue to this day. But that’s another thread – and I probably would not participate in it.
Leonard Weinstein:
An interim comment just so you don’t think I have lost interest in your questions and comments.
I think that I now understand your point of view a lot better and I think that the non-radiatively absorbing atmosphere is very different from the radiatively absorbing atmosphere.
So if we think about my comments about an isothermal condition (like the tropopause on earth) it is a very different situation from TEV3. (And in the discussion following I wasn’t sure what scenario was under consideration, mainly my fault I think).
Your excellent question about the room 100 km high has got me thinking.
The question of radiation is important. But you specified optically transparent like TEV3 and I’m starting to think that in this case you have a point.
However, Arthur’s comments are also intriguing, possibly correct, even though you seem to think no one could possibly entertain this viewpoint.
Like I said, an interim comment that I haven’t lost interest in this thread – far from it.
SOD,
I know that having several models and issues has confused the discussion. Keep in mind that the zeroth law of thermodynamics (which is not a separate law but a result derived from the actual laws of thermodynamics) says: If two thermodynamic systems are each in thermal equilibrium with a third, then they are in thermal equilibrium with each other. This is NOT the same as saying they are the same temperature. Also keep in mind that if a gas was isothermal and steady state with no heat transfer through walls, it is by definition adiabatic. If it is adiabatic, my analysis holds.
I don’t like to make disparaging remarks to Arthur, and he may simply misunderstand the facts, but when he came into the discussion with the remark that I was wrong on everything he pushed my button. His lack of being able to see the facts of my arguments seemed in conflict with his obvious abilities, so it appeared he was deliberately trying to distort the discussion. It now appears the facts are not as clear to others as I thought, but the latest analysis should satisfy that particular sub discussion.
SOD,
A little added discussion. On the zeroth law, the temperature at the boundary of contact foe two regions of gas had to be the same for no heat transfer. Think of two finite regions of gas at different altitudes. The temperature varies with height due to the lapse rate. However, the top of the lower region is a particular temperature. Also the top of the lower region is the same temperature as the bottom of the upper region. Now the two regions touch at the boundary of matched temperature. There is no heat transfer. This satisfies the zeroth law and is an adiabatic gas with a lapse rate.
Leonard, local temperature continuity is not sufficient to satisfy the zeroth law. I explained earlier, but I will explain again, since perhaps you missed what I wrote earlier.
Let A = the “room” we have been talking about. Let B = a thermometer at z = 0. Let C = a thermometer at z = 100 km. Any sort of thermometer will do – in particular it need not have any dependence on gravitation. If A is in equilibrium with B that means the thermometer B is reading a certain temperature that represents the temperature of A at z = 0. If A is in equilibrium with C, then thermometer C is reading a certain temperature representing the temperature of A at z = 100 km.
What the zeroth law says is that, if A is in equilibrium with B and A is in equilibrium with C, then B is also in equilibrium with C. In particular, the temperature measured by B must be the same as the temperature measured by C.
What you propose to be the case for your “room” is a clear violation of the zeroth law.
Also please note there is no such thing as “an adiabatic gas”, nor any such thing as an adiabatic system as a whole. A boundary can be adiabatic if it allows no heat through, but that does not prevent heat from being exchanged between different subsystems inside the boundary. What is generally meant by adiabatic is a *process* during which certain properties of a system or subsystem are changing. Wikipedia has an adequate definition of such processes, of course they are as we have discussed, requiring dQ = 0.
But there is no reason for dQ to be zero for slowly moving parcels of gas within such a system as we’ve been discussing. If heat moves in to such a parcel, it’s moving out of another parcel – but that’s the same issue as we have if the volume of the parcel is increasing, then some other volume must be decreasing; if the height is increasing, then some other parcel must be coming in to replace it at the original height.
Any process of motion of a subsystem of this “room” will involve exchanges of heat, volume, location with other subsystems, even though the system as a whole does not allow in any heat, does not change volume, and does not move. Only when all macroscopic motion has ceased (at equilibrium) do all such changes end. There is no particular restriction on heat imposed from the boundary. The gas is certainly not forced to only undergo adiabatic processes.
Since G&T have been mentioned out of context readers might like to know that they have produced a new paper on this very topic.
Adiabatic as well as Isothermal atmospheres are included.
Venus is explicitly discussed.
Click to access 1003.1508v2.pdf
Let’s talk about a completely different system to gain a little perspective on what statistical mechanics and thermodynamics give us, in particular this “zeroth law” issue.
Spins in magnetic fields are a very typical system for statistical mechanical discussion – the Ising model and variants, for example, to describe ferromagnetism. Even simpler would be a collection of non-interacting spins in an external field B. The energy of such a spin in the “up” state (parallel to B) would be something like mu . B, while the energy in the “down” state would be the opposite negative value, -mu . B.
Now each of these spins is attached to a particle of some sort that has other modes of motion (kinetic or vibrational energy, at least) so a temperature could be ascribed just looking at that energy-of-motion side of things without considering the magnetic field.
If Leonard’s argument about the gravitational field was right, that the higher-potential-energy particles have a lower temperature than the lower-potential-energy particles, then the same thing should hold in this system: the spin-up particles have a high potential energy, while the spin-down particles have a low potential energy. So by Leonard’s argument, the temperature of the “spin-up” particles should be lower than that of the “spin-down” particles.
In reality, in equilibrium both “spin-up” and “spin-down” have to be the same temperature. If you couple a thermometer just to the “spin-down” particles, and another just to the “spin-up” particles, then they have to read the same temperature, by the zeroth law.
The same Boltzmann distribution we’ve been talking about in the gravitational case applies perfectly here: in equilibrium the number density of the spin-up particles is reduced relative to spin-down particles by a factor exp(-2 mu B/kT) since the energy difference between the two states is 2 mu B.
But Leonard would argue that when a particle undergoes a process of flipping from spin-up to spin-down, it gains that 2 mu B energy. Therefore its “temperature”, as measured by its energy of motion, should have increased.
Instantaneously, it is true that the spin flip must dissipate its energy somehow, and for uncoupled spins it has to do it through the energy of motion. But that energy won’t stay confined to a single particle – the spin-flip process is not “adiabatic” – the heat spreads out and the particle returns quickly to an energy-of-motion level determined by the local temperature. And eventually the reverse process happens, enough energy gathers on a single particle to flip it the other way.
All of these processes and probabilities happen in equilibrium according that Boltzmann distribution, so the exponentially lower number density in the “up” state is maintained at about that level. All happening through random processes *at a single temperature*.
And the same is true in the gravitational field case we’ve been discussing.
SOD,
I do confess to loose use of the term adiabatic gas. The enclosed system is an adiabatic system would be the correct terminology. This is a system with no resulting heat transfer through the boundary, and can refer to the system as a whole or sub sections of the entire volume of gas under consideration. Once a gas has come to equilibrium, and is not conducting energy from one part to another, it will be thermodynamically an adiabatic system at all macroscopic scales. If it were isothermal and all currents died out, and there were no heating through any portion of the gas (macroscopic average, not individual molecular motion), the analysis will result in dQ=0. This was all that was needed in addition to the first law of thermodynamics to show the process is adiabatic and in the presence of gravity there is a lapse rate. If the result showed that isothermal was not possible in the presence of gravity that does not violate what has been called the zeroth law. Keep in mind that normal fluid problems are generally so small that the gravity effect is neglected. This is not true with atmospheric scales.
Leonard, SOD,
I agree with Leonard’s discussion of adiabatic systems. In a static atmospheric system under the influence of a gravitational field the system much approach a condition of constant energy per unit mass. U = CpT + gh since there is no PV work occurring (first law). In this state Q = CpT + gh as well. There is a term in classic meteorology called potential temperature which I’m sure is familiar to both of you. That is loosely defined as the temperature that a parcel of air at any elevation would exhibit if it were moved to h = 0. In other words it is an expression that consists of both CvT and gh and converts the gh potential energy term into equivalent thermal energy. A profile of potential temperature from the surface to the troposphere in this atmosphere would show a constant potential temperature profile throughout. And dQ = 0 from the surface to the tropopause. This satisfies the 0th law. This also explains why the atmosphere is isentropic.
This is also true for an atmosphere in dynamic steady state. Look at any radiosonde reading from an atmosphere in a dry, stable condition and you will see a constant potential temperature profile from the surface to the tropopause.
Of course this equilibrium condition requires an adiabatic lapse rate dT/dh = -g/Cp. An isothermal atmosphere would require that U increase with elevation. This is an unstable state and would violate the 0th law. (But it may produce something like “low entropy” if you have an active imagination).
Potential temperature is used by Ramanathan and Coakley (standard work on 1-dimensional radiative-convective climate models that’s been discussed here before). But note that it is not “loosely defined” as:
but precisely defined as:
Note the word you left out of your definition: adiabatically. This is precisely what we’ve been discussing.
Yes, when atmospheric motions are fast, they tend to be close to adiabatic, and the adiabatic lapse rate prevails, the gradient in potential temperature is brought close to zero. However, when motions slow down, there is no such constraint; the lapse rate can be arbitrarily larger than that.
The most important feature of the adiabatic lapse rate is that it represents *the onset of instability*. If the lapse rate is more negative, so the gradient of potential temperature is negative, that situation is unstable to the onset of free convection. If the convecting atmosphere can carry away heat fast enough, it will return the situation quickly to the adiabatic lapse rate. Because the convective motion is quite fast, adiabaticity is a good approximation.
But when things slow down, which they do at night, near the tropopause and throughout the stratosphere, under some cloud conditions, sometimes near the poles in winter months, etc. the environmental lapse rate can be more positive than the adiabatic one – sometimes we even see temperature inversions.
If your arguments were as solid as you claim, the adiabatic lapse rate would hold always and everywhere throughout the atmosphere. But it does not.
Leonard, William, do *either* of you have a reference to any standard work in thermodynamics or statistical mechanics that supports your claims that:
* the system [must] approach a condition of constant energy per unit mass
(this is no constraint I have ever heard of in any source on the subject)
* a system in equilibrium can contain subsystems with different temperatures
(violation of the zeroth law)
* any coherent definition of what “thermodynamically an adiabatic system at all macroscopic scales.” could possibly mean?
(the only sense I can make of this would be a system with identically zero heat conductivity, no ability to convect, no radiative absorption, no latent heat, i.e. no way to convey energy around at all – but I don’t think an ideal gas-type system such as we have been discussing could ever meet those conditions).
I’ve referenced my discussion to very basic definitions of the zeroth law, and the definition of adiabatic vs diabatic processes, and these contradict the things you all are saying. You’ve provided no reference at all, other than a paper cowritten by William himself (and Bryan’s reference to one by G&T)! I think it’s about time you came up with some piece of standard accepted textbook science to support what you’re saying…
Arthur,
My last comments to you. The concept of fast or slow used in the definition of adiabatic process are only invoked due to the possibility of heat transfer of moved parcels of gas that move into regions where their temperature at that pressure and height is different from their surrounding. If the heat transfer is not going to occur, fast is not either meaningful or needed. Adiabatic processes are only processes with no heat transfer through boundaries. Defining 1000 mbar for anything is only invoked because that is Earth’s ground level ideal pressure. It has nothing to do with anything else. The zeroth law never refers to constant temperature, it refers to situations where no heat will flow through connecting boundaries. all of the derivations shown and definitions are straight from textbooks.
Leonard – heat moves from hot to cold regions. Do you deny that? The only way to prevent it is for the heat transfer coefficient in Newton’s law of cooling to be zero. Do you have proof that the heat transfer coefficient in the atmosphere, or your “room”, has to be zero for every subsystem? If not, then if there are *any* temperature differences between subsystems, heat transfer will occur. You cannot prevent it by just asserting it.
Yes, 1000 mbar is z=0; that was not the issue I raised with William, it was his noticeable omission of the word “adiabatic” from his definition of potential temperature.
Most importantly, the zeroth law does indeed refer to constant temperature. I cited wikipedia before, but here’s a quote from a textbook I have just next to me on my shelf – and I have a few more if this doesn’t satisfy you:
From “Thermal Physics”, P. C. Riedi, 2nd Edition (Oxford Science, 1988). Chapter 2, section 2.1: “Zeroth law and scale of temperature”:
Thermal equilibrium implies a single temperature; the zeroth law is all about defining what temperature is and allowing it to be compared.
And one more item – Leonard, you claim that “all of the derivations shown and definitions are straight from textbooks.” But what about these specific that you have stated, and *not* derived, which I have not found in any textbook:
* the system [must] approach a condition of constant energy per unit mass
(this is no constraint I have ever heard of in any source on the subject)
* a system in equilibrium can contain subsystems with different temperatures
(violation of the zeroth law)
?
Ok, can’t resist, here’s another from the shelf next to where I’m sitting, “Statistical Physics”, 3rd Edition Part 1, Landau and Lifshiftz (Vol. 5) (Pergamon Press, 1980) – Chapter II, “Thermodynamics Quantities”, Section 9 – “Temperature”. They take a different tack, defining temperature in terms of entropy and proving constancy of temperature in equilibrium from the second law and the understanding that entropy is a maximum in the equilibrium state:
Note in particular the temperature so defined, for an equilibrium system, must be “constant throughout the system”. As I’ve been trying to explain here…
It’s starting to make sense to me now. That’s the benefit of people with opposite points of view stating and restating them.
That doesn’t mean I can convince anyone of anything, but at least I have convinced myself, rightly or wrongly, that I understand the subject better than before. Some think that their point of view should be blindingly obvious to the other party..
In the narrow case of no radiative transfer of energy and of a 1m^2 area, 1km high “room” of gas – what is the picture?
Firstly, if we take a gas at temperature Th at 1km high, and “drop” the gas into this 1km room, the average temperature, T, will go up in accordance with the conversion of potential energy to kinetic energy. So T > Th.
This is the same as dropping a cannon ball from a great height – its potential energy is converted into kinetic energy, or height is converted into speed. But the exact calculation of T depends on a number of factors, including the amount of gas.
(For example, with a very small amount it will end up almost on the surface and therefore almost the entire 1km of potential energy will be converted to potential – contrast that with a much larger amount where the 1km height “fills up”.)
Secondly, the adiabatic movement of “a parcel” of gas involves no change in heat content and therefore a change in temperature if a gas is moved up (or down) in height.
This second point is related to the first point and an equation for temperature change with height, dT/dz, is usually derived via the ideal gas laws (PV = NkT or PV = nRT) and the hydrostatic balance equation of dp = -gρdz.
The value is for adiabatic expansion – which, for stalwart beginners making it this far, adiabatic expansion is a change in conditions with no heat absorbed or lost from this “parcel of air”. A slower change in conditions might be an isothermal change where there is no temperature change, but instead a change in heat content.
Thirdly, what value (or parameter) balances, in equilibrium, in this 1km high column?
This point is perhaps one of the dividing points in the debate so far.
Every standard thermodynamics textbook says that, in equilibrium, temperature will equalize. There is no requirement for “potential energy” either gravitational potential or chemical potential to equalize.
Heat is the property that spontaneously flows from higher potential (hotter) to lower potential (colder).
-This is where I am up to. The concept of potential energy converting to kinetic energy is good and true. But once the gas has settled into equilibrium, temperature will equalize throughout the gas (not kinetic plus potential energy). This seems to be the interpretation of any standard work on thermodynamics. Heat – measured by temperature – flows from the higher potential to the lower potential. Work doesn’t flow. And internal energy is irrelevant unless it can be made to do work.
This isn’t the end of the story if “potential energy” can be made to do work..
More later.
SoD – you say:
but this is surely wrong – a gas by definition “fills” its container, no matter what the quantity of gas involved. You just get a lower pressure with less gas, and higher pressure with more. Under gravity more are forced towards the bottom, but you still get the same distribution of molecules with height (is there some reason you’re using 1 km rather than Leonard’s much more dramatic “100 km”?)
On “potential energy converting to kinetic energy” – what I’ve been saying all along in various different attempts to communicate with Leonard is that he’s not taking into account the pressure of the underlying gas. That’s a real force, just as gravity is. Gravity pulls the gas molecules down; the pressure of the molecules below (exhibited as collisions more from below than above) push the gas molecules back up again. Under hydrostatic equilibrium that’s all balanced – any gain in vertical velocity and thus kinetic energy from falling molecules under gravity is offset by a loss in vertical velocity from those collisions, and things balance. Otherwise you would have a net flow of energy in equilibrium, unbalanced forces – which can’t happen. But that’s a complex process and it’s much easier to understand simply from the zeroth law consideration that temperature has to be fixed, which is what I’ve been trying to get through lately. But all those different arguments are consistent – equilibrium means balance and constant temperature.
SoD
….”Heat – measured by temperature – flows from the higher potential to the lower potential. Work doesn’t flow. And internal energy is irrelevant unless it can be made to do work.”…..
The internal energy of the molecule is the sum of its KE and PE.
The Temperature is directly proportional to the KE.
Heat travels from high T to lower T, but by which method?
(a) Conductive diffusion, say several centimetres per second.
(b )Convection, arising from buoyancy, more like metres per second.
There is no way of stopping convection in gases if there is a temperature difference.
So convection is the main method of heat transfer.
This implies that the atmosphere is best described as being adiabatic.
Arthur,
You truly seem sincere, so I will reply. This is especially needed since SOD is not yet convinced of my claims. Look at your reference:”The argument may be made more concrete by considering two containers of gas of equal mass and volume which are completely isolated from external influences (Fig 2.2).”
The flaw with your argument comes from the part that says “are completely isolated from external influences”. GRAVITY IS AN EXTERNAL INFLUENCE! That example is not for the case of gravity as an effect.
Keep in mind that the concept of heat transfer in a gas comes from nothing but the movement of molecules. If a group of molecules go upward they loses some kinetic energy (converted to potential energy), therefore cool. If you do the statistics correctly, you get the lapse rate for a process that is in equilibrium. The point that the temperature being different from the lapse rate destabilizes the atmosphere and causes currents is exactly the source of negative feedback effect I stated. In the absence of net heat transfer or induced wind, the temperature profile will be at the adiabatic lapse rate unless some other effect modifies it. The restoring efforts may not totally succeed, as is the case with phase change of water vapor, and a modified (wet) lapse rate can be forced.
Oh come on. That was just an illustrative example anyway on how to define temperature. Perhaps you didn’t notice that it explicitly referenced the isotherm as defining mutual equilibrium – constant temperature.
But in fact your suggestion (2:22 pm comment) to raise one box in this context illustrates exactly how you have things wrong. Notice that it’s not raising the box that actually changes the state, but that you have to “make the container larger”. And since the container is adiabatic, of course the expansion process you are forcing on it is adiabatic, and you get cooling. Your citations (3:14- 3:15 comments) similarly rely on things being adiabatic. I don’t dispute that you’ve got the adiabatic formulas correct – the problem is that you’re using them inappropriately.
Consider the “raised box” (1) and the “nonraised box” (2). The function f(P, V) is still just as valid – the macroscopic parameters pressure (P) and volume (V) completely define the internal state of these containers, height has nothing to do with it. Since you have increased V1 and lowered P1 in an adiabatic fashion, f(P1, V1) has been reduced. So f(P1, V1) is now not equal to f(P2, V2).
That means the “raised box” (1) and the “nonraised box” (2) are no longer in equilibrium. If they are thermally connected, they will exchange energy and come to a new mutual equilibrium at an intermediate temperature – if V1 and V2 are constrained then P1 and P2 will adjust so the isotherms match again.
And that is precisely what happens in a real gas subject to any potential field – in equilibrium the states of subsystems along the potential lie on the isotherm – they are at the same temperature. The adiabatic formulas are simply inappropriate to the thermal equilibrium case.
Arthur, look at the balloon enclosures example. I am not enlarging the enclosure when it is raised. When you raise it, the pressure is lower, so it will expand itself to match the surrounding pressure. There is nothing I am doing to cause the expansion except move the enclosure up. In order to again bring it back in contact with the lower enclosure, YOU HAVE TO LOWER IT BACK DOWN, WHICH RE COMPRESSES IT AND BRINGS IT BACK TO THE SAME TEMPERATURE. Now you connect the enclosures and nothing happens. Re separate and enclose and repeat. The point is that you can’t bring the two enclosures together when they are at separate altitudes.
Leonard, this is where you are absolutely wrong in a fundamental way:
“bring the enclosures together” requires only the exchange of heat between them. This could be done by any of hundreds of mechanisms that *do not involve* bringing them to the same altitude again. For instance you could move an object with some moderate heat capacity back and forth between them, allowing them to exchange energy through that third body. If they were in equilibrium, there would be no heat flow. But under the conditions you have given, heat will flow because they are out of equilibrium.
But more importantly, in the real atmosphere we have some of those same conditions – molecules are continually moving around, heat really does flow from hotter to colder areas. It flows slower when you are below the adiabatic lapse rate and the convective instability is suppressed, but it still certainly flows whenever temperature differ.
Bryan,
You are right that convection is generally by far the largest source of atmospheric heat transfer. However, it would not even matter if the conductive diffusion was the only source of heat transfer in a quiescent atmosphere, the atmosphere would still be adiabatic. The main effect of the convective heat transfer is more rapid negative feedback restoring forced offset.
SOD,
The thermodynamic texts you refer to are discussing gases “completely isolated from external influences”. However, gravity is an external influence! Those examples are not for the case of gravity as an influence. Please refer to a (meteorology?) text that includes gravity effects.
If the molecules go to the bottom they heat up. You admitted that. If they diffuse back up, they cool off for exactly the same reason.
For Arthur’s example of two boxes brought in contact and matching temperature, if you then raise one box, and at the same time you make the container larger by the correct amount (remember the pressure and density are lower at higher elevations), the gas inside will cool, with no heat transfer through the wall. If you re lower it and reduce the container size the correct amount, the gas will heat. This is one way of observing what the gravity effect does to the column of gas.
SOD and Arthur,
Here are a couple of sources on the web. The NASA one is the one I used above. The only change I would make is that the CP of CO2 increase to slightly larger than 1 at the temperatures near the surface of Venus, and thus g/Cp goes to about 7.8. The second reference uses the concept of a parcel of gas in section 2.5 as in an enclosure like a balloon, but with no heat or mass transfer through the wall. As this parcel is raised to different heights the balloon expands and temperature drops. This can be raised very slowly or not, it does not matter. This volume can be used as a sensor to examine the resulting temperature and pressure at different heights. If the parcel is in exact balance with the surrounding in temperature and pressure at any initial location, it will be in exact balance with the surrounding at all heights if the surroundings are quiescent.
Sorry, forgot to put the sources in.
http://atmos.nmsu.edu/education_and_outreach/encyclopedia/adiabatic_lapse_rate.htm (this is from NASA)
http://books.google.com/books?id=GokPgjyMz1QC&pg=PA40&lpg=PA40&dq=adiabatic+lapse+rate+derivation&source=bl&ots=jqUVwMt6MU&sig=xMjZI6jxnW_YXs6OoadXHPvd8C8&hl=en&ei=1tg5TIOFLsWblgeI2MzSBw&sa=X&oi=book_result&ct=result&resnum=5&ved=0CCIQ6AEwBDgK#v=onepage&q=adiabatic%20lapse%20rate%20derivation&f=false (look at all of chapter 2)
Leonard, nobody disputes that you have the adiabatic formulas right. Please find a source for your claims that:
* the system [must] approach a condition of constant energy per unit mass
(this is no constraint I have ever heard of in any source on the subject)
* a system in equilibrium can contain subsystems with different temperatures
(violation of the zeroth law)
or retract them.
SOD,
Please go over what I have included up to here and tell me if you are yet convinced for the room analysis (by the way it is 100 km, not 1 km). I have more discussion I think would help if you think it would be necessary.
Arthur,
Assume for the moment that a column of gas is tall enough to have a significant pressure difference top to bottom. Also for now assume for now that the temperature followed the value calculated by the adiabatic lapse rate. The top is T1, half way down it is T2, and at the bottom it is T3, where T1<T2<T3. Now cut the container in half, but assume the cut is a perfect seal like the rest of the container (which is assumed to be like a perfect mirror, is non conducting, and has zero thermal capacity). The two halves are brought upright to a slab of conducting material being maintained at exactly T2. The slab is first brought to the bottom of the top half of the tube, and then the bottom barrier is removed from the tube so that the gas is in direct contact with the slab. There will be no heat transfer, since that location was defined as having T2, the same as the slab. The same action is done to the top of the lower tube, and again no heat transfer occurs. Now the top and bottom are rejoined and opened to each other. Again, no heat transfer occurs.
Hay, I just satisfied the Zeroth law of Thermodynamics under my assumptions. I did not violate it. That alone does not prove that my assumption of a temperature gradient is valid, but it shows that the assumption DID SATISFY THE ZEROTH LAW, and thus is not excluded. The rest is history.
You just satisfied the condition of mutual equilibrium by carefully restricting the condition to only joining components that were already at the same temperature. But the zeroth law applies if you took that conducting slab and attached it to the top of the first container, not just the bottom. And it applies if you took that conducting slab and attached it to the bottom of the second, not just the top. And under those conditions, if you had a temperature gradient within your containers, there would indeed by heat transfer; the containers and slab are *not* in mutual thermal equilibrium.
Leonard, you seem to be very careful to construct artificial examples (like parcels of gas contained in adiabatic balloons) that satisfy your conception of what the constraints are. But the real atmosphere is simply not composed of a collection of separate parcels of gas in adiabatic balloons. Try addressing reality, instead of imaginarily constrained versions of it!
Arthur,
I am very curious what you attribute the cause of actual measured lapse rates of Earth (exactly within in the range of wet adiabatic lapse rate), and Venus (exactly within the range of lapse rate when variation of Cp with temperature is included). The greenhouse gas and or clouds do affect the absolute level of the ground temperatures (as I have stated), but where do you think the gradients are coming from. According to you, these should be close to constant temperature (i.e., lapse rate close to zero), or they violate the zeroth law.
As I’ve said before, a temperature gradient needs an energy flux to drive it – the ultimate source for Venus, Earth, and any other planet is solar flux absorbed by the surface. The heat then flows from the hot surface through successively cooler layers of the atmosphere until it can escape into space. So that is *not* a thermodynamic equilibrium situation, it is explicitly a situation with heat flowing through it.
But your “room” does not have heat flowing through, and your TEV1-3 do not have a heat flux from the surface, because incoming solar radiation never reaches the surface. Very different conditions.
No reason why I started writing 1km instead of 100km, except not enough sleep.
For Arthur Smith:
My writing about the gas density in the latter part of my first point was unclear and incorrect – although not the main point.
You are right in your comments.
However, if the total mass changes, the total pressure changes. This made me think the final result of temperature change would be different for different quantities of gas. If I think in pressure terms this seems right. If I think in potential energy terms this seems wrong.
Well, not my main point – and either I will get around to figuring out the right way to think about it, or more likely, someone else will point it out..
For Leonard Weinstein from July 11, 2010 at 2:22 pm:
One text I have been looking at is The Physics of Atmospheres by John Houghton (1986). He comments on available potential energy:
– and he goes on to talk about Lorenz from 1955 and available potential energy.
Possibly nothing anyone would disagree with in this?
But this way of thinking about potential energy seems to be the crux of the matter.
Perhaps I can introduce a slightly modified thought experiment in our (restored 100km) tall room. Suppose that somehow all of the gas had become isothermal (for newcomers, the same temperature).
What happens next?
I’m certain that nothing happens next. It stays the same temperature.
What drives adiabatic convection? Nothing.
If a small parcel of gas is somehow disturbed and moves up a distance dz, its temperature drops by dT (where dT=dz x lapse rate for this gas).
So it becomes more dense and sinks back to its original position.
Perhaps you are in agreement? I thought I should ask.
Remember the ideal gas law is pV = nRT – there’s an important ‘n’ factor there. Keep all else the same (V and T) and raising ‘n’ increases ‘p’. That’s all that’s at issue as you add gas molecules – no effect on T.
Is the significance of this discussion whether pressure/gravity can contribute to an atmospheric temperature profile [and create a lapse rate] or whether such profile is entirely to do with the radiative properties of ghgs; that is the greenhouse effect causes the temp profile and pressure/gravity contributes nothing. Arthur’s position seems to be best summed up at July12, 12.57am, where he maintains isothermality via Zeroth’s Law and states this:
” Gravity pulls the gas molecules down; the pressure of the molecules below (exhibited as collisions more from below than above) push the gas molecules back up again. Under hydrostatic equilibrium that’s all balanced – any gain in vertical velocity and thus kinetic energy from falling molecules under gravity is offset by a loss in vertical velocity from those collisions, and things balance. ”
Leonard, if I understand him correctly says that Zeroth’s law is to do with a thermo equilibrium [or heat content] whereby a temp gradient will exist but where potential and kinetic energy at different heights will mean an equilibrium at each height despite different temps.
I’m not sure but has Arthur ignored, in equating gas pressure and gravity that the density of gas with altitude must be a factor of gravity; doesn’t that make his argument circular? And what about Casimir, or doesn’t that work between gas molecules?
Does anyone have any idea how much of the gravitational potential is counteracted by the “size” of the gas particles (electromagnetic field). From what I’ve understood gases are mostly empty, but at least at some point, while density increases it should become quite relevant.
Hi Mait – size is relevant to the “mean free path” between collisions, which relates to how dense the gas is at the point where it transitions from the poorly-thermodynamically-defined “single molecule” sort of states to the collective statistically described state of normal “macroscopic” physics. A typical way of defining molecular size is the “cross-section” b, the area that one molecule presents to other moving molecules.
As one molecule moves a distance ‘l’, it essentially carves out a volume l * b. The probability of collision (at low densities) is then the product of the density rho of other molecules with this volume:
collision prob = rho * l * b
The “mean free path” of a molecule is the approximate distance the average molecule goes before colliding with another, which is then given roughly by l ~ 1/(rho * b)
So the smaller the effective “size” of the molecules for a given molecule density, the farther each one travels before colliding. This is definitely a relevant number for accurate estimates of gas properties…
Earlier –
July 8, 2010 at 12:06 pm – I mentioned a lecture on Sandstrom’s Theorem at –
Click to access 03Sandstr.pdf
It’s worth pulling a few points out of the lecture here for interest:
(Annotation added in blue)
The writer goes on to explain that the whole story is a little more complex but I think the explanation, especially with reference to the well-known Carnot cycle and to the experiments – is relevant to this discussion.
The effects of stratification would allow the warmer upper layer and colder lower layer to be in a quasi-stable condition. Also, a ball on the top of a hill can also be quasi-stable if no disturbing influence ever occurred. That still does not make the result stable. One can chill pure water slowly with no vibration and reach a liquid well below 0 degrees K, but that does not mean the laws of thermodynamics are wrong. Those are cases where local limited conditions can exist to reverse the naturally stable situation. For the case of stratification, keep in mind that the temperature gradient from the adiabatic lapse rate for Venus would only be 7.8 degrees K per km. If the initial conditions were imposed with a MUCH larger reverse gradient such as done by Sandstrom, the problem is totally dominated by this imposed gradient, and no natural method of getting close to the lapse rate can occur as long as it is imposed. I have said that if forcing is large enough, you can get any behavior you desire. I suspect Sandstrom had a forcing (heating from the top) that resulted in a strong quasi-stable situation. If he removed the heating and cooling and waited long enough for diffusion to adjust the temperature, it would have reverted. Since his study was small scale, the gravity efffect is so small this would take a very long time, and would not be observed in a lab. I will continue on this in a while, I have an appointment.
SOD,
The stratification that occurs in a room of normal dimensions can be driven to form and be maintained by heating from the top, or can occur if sufficient local heating from the side or below to locally cause the heated air to raise the top with a plume that displaces the air already there. The concept of the buoyancy of locally significantly hotter air is well understood. However, it has nothing to do with the natural adiabatic lapse rate. The heating rates for these types of situations are so large compared to natural adiabatic gradients in the short distance available that they totally dominate the situation. For example, in a room 3 m tall on Earth, the adiabatic lapse rate would only tend to cause a top to bottom temperature variation of <0.03K. Any IMPOSED temperature gradient much larger that that would not be able to be overcome as long as the large inverse gradient is maintained. However, if the source of heating were to stop, the room were then perfectly insulated, and the wall heat capacity were zero, then even molecular diffusion (thermal conduction) would eventually drive the room air to near constant temperature. The thermal conductivity of gases without convection is a slow process, but eventually gets there. The thermal conduction would then continue after the state of near constant temperature was reached until the adiabatic lapse rate were reached. The process is described next.
The process would involve molecules that have an upward component of velocity losing some velocity (to the gravitational potential energy) as they go up. Now the mean free path is sufficiently small that they do not go very far before having numerous collisions with surrounding molecules AT THE SLIGHTLY HIGHER ELEVATION. Since these molecules that went up now have a lower net velocity (e.g., lower temperature) than the constant temperature case, the net effect is that when they interact with the surrounding molecules they slightly lower their average velocities somewhat and effectively cool the air above their initial position. Those that go downward gain kinetic energy (temperature) and through collisions transmit that to the surrounding lower gas molecules. The net effect is to cool the gas above a given level and heat the gas below. This is true through the entire volume. This effect eventually forces the container of air to reach the adiabatic lapse rare, WHICH IS THE CONDITION OF EQUILIBRIUM.
Leonard, you are so close here to getting things right. You have it exactly right up to the point where you say
But you are proposing thermal conduction *causing* a temperature gradient. The formula for thermal conduction is:
Q = k . A . dT/dx
(A = area of the region conducted through, k = thermal conductivity of the material, dT/dx = temperature gradient through the material, Q = heat flux).
That is, when dT/dx = 0, Q = 0. Thermal conductivity simply cannot drive anything under constant-temperature conditions.
Arthur,
First realize that the heat transfer in a gas is by either convection or diffusion of molecules (ignoring radiation for now). the molecules have to move a significant distance relative to their size in order to collide with other molecules to transfer kinetic energy. If the fact of movement also caused them to change temperature by time they had the collision, that relationship is misleading. That formula assumes the molecules temperature is the same at the beginning and end of their path. If we define a temperature of a molecule as a function of the absolute magnitude of it’s velocity wrt the room, the magnitude drops for upward moving molecules and increases for downward moving before any collisions. This means that the appropriate temperatures to use for no net heat transfer would be a cooler upper region and warmer lower region by exactly the adiabatic lapse rate. It seems this effect is not obvious, but it is a fact.
Leonard, there’s no such thing as “molecule temperature”; temperature has no meaning for individual particles, it is defined in the aggregate – *after lots of collisions* – and that aggregate determines a distribution of molecular energies in a given energy landscape. It really doesn’t matter what that energy landscape looks like in phase space, the Boltzmann distribution applies. But you can’t go around talking about what the temperature would be in the absence of collisions, it’s meaningless.
You still haven’t done the calculation, have you? I gave a rough outline above, you indicated how to improve it. Go ahead and give it a try! Mait’s discussion of molecular size and mean free path might help.
The problem is that your “fact” is “not obvious” because it is not a fact.
SOD,
If a room or experimental enclosure is heated from the top at one side of the enclosure, and cooled AT THE TOP at the other side of the enclosure, you would get a mixing current formed. It might mot be large enough to avoid some average stratification, but would not be the static no flow case seen by Sandstrom. His work in no way is equivalent to the cases we have been discussing.
I also want to point out that in the 100 km tall room problem on Venus that we were discussing, there was no natural way for the isothermal condition to initially form. The falling gas would be hot near the bottom, and cooler near the top at all stages. However, I showed how even if you imposed the constant temperature condition as an initial condition, it would still go to adiabatic lapse rate.
SOD,
If the assumption is made that the gas became constant temperature and if that condition resulted in no more heat transfer, then dQ=0 is valid. However, if you again read my July10 post at 2:26, you see that the first law of thermodynamics and the assumption of dQ=0 is exactly what is required for the adiabatic lapse rate. It then follows that the constant temperature case CANNOT be dQ=0, and so the conduction will go on until the adiabatic profile forms.
I have skimmed the comments since I last posted. The equilibrium condition seems to be the point of contention. Let me approach the problem from a different perspective. I will look at the Helmholtz free energy for an answer:
dA = dU – TdS
As I have shown previously for a gaseous system under the influence of a gravitational field: dU = CpdT + gdh, therefore:
dA = CpdT + gdh –TdS
The free energy is basically the energy available or “free” to do work. For a system that is spontaneous, dA 0, then work must be done to the system for the process to proceed.
Let’s look at the constant temperature system proposed by Arthur and SOD. In that case dU (CpdT + gdh) increases with altitude. That means that dA > 0 and the system could not be isothermal unless work is done on the system to achieve the increased internal energy at the higher altitudes. It is neither spontaneous nor at equilibrium.
But take the system that demonstrates an adiabatic lapse rate, dT/dh = -g/Cp. In this system dU = 0 as the altitude increases. TdS (dQ) also equals zero since it is adiabatic. Thus dA =0. The system has minimum free energy and is at equilibrium. And the process used to get it to equilibrium is spontaneous.
Thus the adiabatic lapse rate is the equilibrium state. The isothermal atmosphere is not at equilibrium and is also impossible to achieve unless an outside system provides work.
If this is not enough to put the question to bed, let me provide references to two peer reviewed papers:
Click to access GG.pdf
where it states;
And:
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6X42-46BXYN4-CM&_user=10&_coverDate=02%2F28%2F1965&_rdoc=1&_fmt=high&_orig=search&_sort=d&_docanchor=&view=c&_searchStrId=1397988562&_rerunOrigin=google&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=bdae61671a05723bb712f6b0ef32db49
where it states;
Can we move on to some of the other proposed models now?
What you mean by your differentials is not clear – ‘dU’ etc. should be applied to a single system. So what is it you are talking about when you refer to the change in ‘dU’ with altitude? What for that matter is ‘dh’ if we’re in equilibrium and nothing’s moving? Your argument on the thermodynamic differentials is incoherent.
To make it coherent we need to be talking about a subsystem of the atmosphere – a “parcel of gas”. And we return to the issue of whether its rise through the atmosphere would be adiabatic or not. And again, adiabatic is a fine approximation if it moves quickly enough that there is little molecular (or radiative) exchange with surrounding parcels. It is *not* such a good approximation if motion is slower.
Let’s take the isothermal case. dT = 0 then. Suppose we have a slowly rising parcel of gas, which means it has increasing internal energy, dU = gdh is positive. But for no change in free energy (which there shouldn’t be at equilibrium), dA can still be zero as long as TdS is also positive, and equal to gdh.
That means the entropy of the gas parcel must increase as it rises. But its density and pressure also decrease (and volume increases) so that’s not unexpected: dilution increases entropy generally.
Now TdS positive means there has to be some heat influx to our parcel. So it’s not adiabatic. Again, that’s consistent with all the discussion here so far. No work is done, there’s no change in free energy, but heat is moving around between any parcels of gas that happen, through some some sort of small cycle, to displace one another.
On your two references – I don’t suppose you noticed they contradict one another? Just because something appears in a peer reviewed journal doesn’t make it right, but the second one looks considerably more plausible than the first – it happens to be discussing a very small gravitational red-shift effect (from general relativity), and ends up noting that what this really means is the definition of temperature is slightly adjusted in G.R. But it has nothing to do with adiabatic lapse rates…
Perhaps you can come up with a clear textbook-level source that justifies your and Leonard’s continued claims that:
* the system [must] approach a condition of constant energy per unit mass
* a system in equilibrium can contain subsystems with different temperatures
Your two referenced articles would perhaps satisfy the second – if they agreed with one another and were supported by any subsequent review. Otherwise you’re violating very basic fundamental laws on very flimsy grounds.
For some reason the following paragraph came out garbled when I sent it. I had some symbols in there and I think that screwed things up. Here it is without symbols.
“The free energy is basically the energy available or “free” to do work. For a system that is spontaneous, dA is less 0. For a system at equilibrium dA = 0. If dA is greater than 0, then work must be done to the system for the process to proceed.”
Arthur,
You make the point that if a parcel moves up it has to move fast to be adiabatic. This is for a parcel that was assumed to be at thermal balance before it moved. This is not so, BY DEFINITION, if the gas has an adiabatic lapse rate, thus the heat transfer is zero. The question then may be made, what then made the parcel move. Well, you are the one that supposed that the parcel was slowly rising. What did you think made it move? Also your objections to the common differential conventions are puzzling. You seem to be trying to make a point here but I am not seeing it.
Arthur,
A lot of words you have. But unfortunately they have little meaning. dA = 0. The system is at “equilibrium”. But you have dS as a positive entity. Where did you learn that?
Enough already!
At equilibrium certainly there would be no changes, so all the ‘d’s would be zero. You’re the one who introduced the differential notation and tried to argue something from it, not me. If you’re trying to argue something about the equilibrium state using dU, dA, dh etc. terms that are identically zero, you’re making less sense than I thought you were, when I assumed the question was concerning a near-equilibrium parcel in (slow) motion.
So, Leonard and William, I repeat my question: does pressure from the atmospheric gas mass/gravity contribute to the temp profile of that atmospheric gas mass [and surface]; or is it as good old Arthur claims, via Zeroth, not the case and only radiative/greenhouse processes can achieve that?
Arthur,
I read the text books and definitions also. I know the point keeps being made in them and by you that an unconfined parcel of gas moving to another location where conditions may be different enough to cause heat transfer to occur is only considered to be an adiabatic process if it happens so fast that diffusion and heat transfer at the edges of the parcel can’t have time to happen. This comes from the definition of adiabatic, that is, without heat transfer at the boundary. This is totally irrelevant if the parcel is in thermal and pressure balance at one location and moves slow enough to be in an effectively quiescent gas that has an adiabatic lapse rate. PLEASE NOTE, UNCONFINED PARCELS OF GAS SLOWLY MOVING AROUND IN A GAS WITH AN ADIABATIC LAPSE RATE ARE FREE FROM HEAT TRANSFER. It also is an adiabatic parcel if it is confined by a hypothetical adiabatic barrier (but one free to expand or contract to match the surrounding), even if the gas it moves into is not at adiabatic lapse rate conditions. This has been made clear several times. It is also clear that if an adiabatically shielded parcel rises in a gas that was constant temperature, and then the shield dropped, the gas would cool the surrounding, driving it toward the adiabatic lapse rate. Those approximations were only needed to show that the quiescent and equilibrium state is the one with the adiabatic lapse rate. This has been the whole point of the last many entries.
It is also true that outside forcing (over hot ground, selective radiation absorption, hot wind) can perturb the lapse rate from the adiabatic level. When the effective lapse rate is too large, the gas is strongly self correcting toward the adiabatic lapse rate by buoyancy forces. If the lapse rate is too small, the correcting forces may or may not be able to correct it (for this case, winds from other locations and diffusion try to restore the adiabatic lapse rate, but can be more easily be overcome by forcing). However, in the case of real atmospheres, there are correcting forces tending to drive the lapse rate close to the adiabatic lapse rate almost all of the time. Keep in mind that the restoring forces are negative feedback from the unbalanced adiabatic lapse rate.
The point of the recent discussion was to determine the vertical temperature distribution in the 100 km room with no forcing after conditions became quiescent. Has anyone changed their mind at this point?
Cohenite,
I guess you’ve been away for awhile. I don’t blame you. The answer is “yes” to the first part of your question. Radiation heat transfer plays no significant role in the low to middle troposphere temperature profile. The optical depth is such that LTE exists at all layers with respect to radiative heat transfer. This was discussed in detail somewhere back in earlier posts. I can find it if you want. This is also supported by the empirical radioaonde data presented in Miskolzci’s latest paper in E&E.
Cohenite,
When you say pressure causing the temperature, that is misleading for the stated model. The model of the enclosed room (the present line of discussion) only specifies that you have to have enough gas to reach the entire room height with some reasonable pressure remaining by the top. This WILL lead to a very high ground pressure due to the great height, but the exact pressure is not critical if the conditions are met otherwise. If that condition is satisfied, it is the height of the location where the gas was put in, and known temperature at that height that determined the temperature at the bottom. The absolute pressure at a specified height can be different as long as the stated conditions are met and the temperature is the same. For the enclosed room example, it is the adiabatic lapse rate (-g/Cp) time height plus input temperature at the top that is the total reason for the very hot lower level and relatively cool upper level. That room did not have a greenhouse gas at all, so the high temperature is shown to not be caused by the greenhouse gas FOR THAT SPECIAL CASE.
For real atmospheres, it is the effective height where outgoing radiation is leaving from that sets a local temperature at that height. That means you do need either an atmosphere with enough greenhouse gas or a thick cloud layer to move the outgoing radiation to a large altitude to get the high heating. However, again it is not the greenhouse gas that heats the ground, it’s only function is to move the radiation to space location upward from the ground to a high altitude. Now the lapse rate going down (generally close to the adiabatic lapse rate) determines the ground temperature. The top of the atmosphere is higher if there is more gas in it, and that leads to higher ground pressure. That is why higher pressure is related to higher temperature. Venus has a pressure 91 times that of Earth, and the effective top of the atmosphere where outgoing radiation occurs is about 6 times as high as Earths.
The room problem had a slightly differently defined set of boundary conditions than a planet, so is an idealized model to show certain behavior.
Thanks Leonard; I posted below before I read your reply.
Just to nitpick a bit, I don’t think it’s entirely correct to say that high pressure is caused by height. The pressure at every level should actually be a function of mass above it (mass and height are quite directly . Likewise, I think it would be more correct to say that high ground temperature is a result of the great mass of the atmosphere (you need more energy, to ‘bounce’ the atmosphere to a height where it can get rid of it’s energy as it’s ‘heavier’).
I’m a bit wary of the -g/Cp as well to be honest, as it assumes that the gas particles. It might be that the effect of them not being that is negligable, but I’m not entirely convinced of it yet.
Thanks William; and credit to you and Leonard for your perserverence. I’m familiar with the new Miskolczi paper but being a layman without the technical background of you guys I tend to forget these damned technical points as soon as I’ve spent a day or 2 understanding them!
This is a crucial point and an aspect of this debate, like many others, where I felt intuitively that something was amiss when the issue of ‘pressure’ contribution to atmospheric warmth was dismissed.
The point for me, and this may be OT, but does any pressure component of atmospheric temp contribute to the ‘greenhouse’ 33C which Arthur concluded in his paper;
http://arxiv.org/abs/0802.4324
And while I don’t want to get into the whole G&T, Smith Kramm and Halpern gerfuffle the thing which interests me is the validity or not, of the GMST, or a global average temp, to reflect global TOA energy balances; with that in mind would it matter if Leonard’s room became a circle rather than a square or oblong?
Cohenite,
Hey, don’t put down us laymen. The laymen are the only ones who seem to possess any scientific common sense in this Climate Science thing. I think it was Lindzen who said that most of the people in Climate Science were dropouts from the traditional or applied sciences; and the river of government grant money only made things worse.
It’s been awhile since I read Arthur’s paper so I don’t feel I could comment on it without going back and reading it again. I last read it when it first came out and got a lot of publicity. I read a rather long blog that was discussing it (I think it was Jennifer Marohasey’s old blog and I think you were a frequent contributor there – I never participated though). My impression is that Arthur’s paper was mostly convenient rather than correct science, much like his comments here.
I think the global energy balance diagrams can be of some help but the existing ones are critically flawed since they primarily deal with radiation heat transfer and push the important energy flows of convection and latent energy into the background. Nowhere do you see any indication of PV work, potential energy or even mass.
I will let Leonard comment on his room analogy. I lost track of the discussion when Arthur got involved and it became somewhat convoluted. I thought Leonard had some very good observations, however.
Sorry I’m not much help.
William, on the layman scale I think I am below you and Leonard. Dealing with Arthur is always informative; for instance his linked article is to work done by one of the Verlinde brothers; if gravity is ‘nothing’ more than quintissential entropy with a black hole being pure entropy then light speed is the highest form of order [assuming there is no FLS which would seem to be contradicted by superposition]: how to marry that to Leonard’s room? Arthur says this at July 12, 3.04pm:
“Remember the ideal gas law is pV = nRT – there’s an important ‘n’ factor there. Keep all else the same (V and T) and raising ‘n’ increases ‘p’. That’s all that’s at issue as you add gas molecules – no effect on T.”
But that’s not true; if you are adding more gas molecules you are adding more entropy/gravity. Arthur also said this at July 12, 12.57am:
” Gravity pulls the gas molecules down; the pressure of the molecules below (exhibited as collisions more from below than above) push the gas molecules back up again. Under hydrostatic equilibrium that’s all balanced – any gain in vertical velocity and thus kinetic energy from falling molecules under gravity is offset by a loss in vertical velocity from those collisions, and things balance. ”
This assumes an equality between the upward collisional force, which is anti-entropic, and the downward gravitational force which is entropic. But this is not true; gravity is quicker/stronger than light [ie a blackhole] so it must be that gravity will be stronger and there will be no balance. This would explain LTE layering and the temp profile; the equilibriums between different layers is a product of the entropy/non-entropy mix which is in inverse relationship with temp; ie higher entropy/lower temp; at every level there is not an energy equilibrium but an equilibrium ratio between entropy and non-entropy relative to that height. This is a vertical equilibrium
Zeroth’s law would apply to areas of equal entropy or gas volume. All things being equal that would be a horizontal equilibrium.
William, I found your comment on LTE and Miskolczi at June 30, 1.52am; you say this:
“The atmospheric temperature at any height is a function of the local pressure, or vertical mass (PV = nRT), and the total energy contained in the parcel via the net electromagnetic flux resulting from solar absorption/surface heating and emission to space. Radiation does not play a role in the atmospheric thermodynamics since each layer is in local thermodynamic equilibrium with its surroundings and there is no net radiation heat transfer between layers or between the surface/atmospheric boundary. This was covered nicely by Leonard and is empirically supported by the work of Miskolzci (especially in his newest paper which is about to be published in E&E).”
That would mean, therefore, that all backradiation is coming from the immediate air layer to the surface?
Cohenite,
Yes. And that would also be true for any atmospheric layer that you observe. There is a slight differential in temperature involved, but that would only cause what I called “mini PV work events” in a later post. Radiation heat transfer has no major impact on the atmospheric thermodynamic profiles. Convection (PV work and mass transfer) and latent heat release are the primary drivers.
Arthur,
WRT your comment on molecular temperature, I know what defines the temperature. However, all molecules have a single velocity vector at a single time. That will generally have a side component and either an up or down component. If it has an upward component, going up reduces that component over the time of travel, due to gravity, without changing the side component, until a collision occurs. This reduces the total velocity wrt the frame of the room for the travel time. This single vector wrt the room was DEFINED BY ME FOR THE DISCUSSION as representing the molecules temperature. This is a valid representation, since the average of all molecules velocity wrt the room frame of reference would show this temperature drop before collision, and you can show the effect on a molecule by molecule basis. Going down adds to the vector length before collision thus heats.
Leonard, you have repeated this argument about the single molecule many times, but I repeat again that it is wrong. It can be seen as wrong for many reasons:
* it necessarily results in a flux of energy from colder (higher) to hotter (lower) regions, violating the second law
* it implies an equilibrium state with a temperature gradient, violating the zeroth law
* it implies zero net heat flow under a temperature gradient, requiring some explanation for why heat transfer coefficients must become zero
* literally taken it leads to a net unbalanced force on the molecules that brings them ever downwards. That cannot be there in equilibrium.
* Where does the balancing reverse force come from? The pressure gradient, due to greater rates of collisions with the denser regions below, and ultimately the hard floor of the surface/container. You have essentially neglected this factor and its impact on velocity distributions in all your discussion so far.
* The Boltzmann distribution is enough to ensure that any given molecule is unlikely to be in a high potential energy region – potential and kinetic energies are simply summed in the gravitational case, and separable. So the distribution of kinetic energies at any given height, under the standard Boltzmann distribution, is always the same. But the likelihood of being at high altitude is exponentially diminished – matching the pressure gradient required for hydrostatic equilibrium.
* The variation in density, as with the variation in pressure, is again something you neglect, and from that perspective also balances the potential variation.
If you really believe your “single molecule” argument is strong, do a formal calculation of what it implies for the distribution of molecular velocities and density under the equilibrium constraint, and see what it implies for the temperature gradient. The evidence against your point of view is pretty overwhelming.
Arthur,
I love your statement “Just because something appears in a peer reviewed journal doesn’t make it right”. I think I have been making that argument for a long time now.
Since we’re discussing speculative papers – recent work suggests that gravity is actually a consequence of the laws of thermodynamics (that thermodynamics is more fundamental):
Discussing Verlinde’s work would probably be a lot more fruitful than this endless runaround of claims that adiabatic behavior under gravity somehow transcends basic thermodynamic understanding.
This is almost entirely offtopic, but I’ve never quite understood why people think thermodynamics is fundamental. From what I’ve understood it’s just physics with some statistical mathematics mixed in. Or in other words, it’s a result of laws in other fields and hence not that fundamental, but rather a derivate field. Either way, the origins of the gravity field are not particularly relevant to the discussion at hand, as we can probably agree that it’s still there.
Thermodynamics introduced entropy to the world; the 20th century saw the rise of “information”, which turned out to have a very deep relation to entropy. Entropy’s increase is intimately related to the “arrow of time” – essentially all other physical laws are time invariant. The second law’s constraints seem to lie at the heart of every physical process, for some reason. Understanding why is the question – there’s no theory that justifies it (other than Verlinde’s which is a little sketchy just yet) but most experienced physicists would be far less surprised by a violation of the laws of quantum mechanics or general relativity than by a violation of the second law.
Arthur,
I can’t understand how you miss the point that each molecule is a height above the floor and thus has potential energy as well as the velocity which gives the temperature. As it goes lower, it gains kinetic energy, but gives up an equal amount of potential energy. There is no flux of energy down, only a conversion. That conversion is symmetrical, so it reverses going up. The full statistical analysis is very long and difficult, and I might be up to it, but it would be a major effort. If you are confident you are right, why don’t you do the full analysis, with suitable references. That would be a good argument from you. No outline, the full thing.
By the way, the balancing force is the combined increasing pressure, density, and temperature at lower elevations.
williamcg from July 13, 2010 at 1:08 am:
I’d like to pick up this point in another post, or later in this discussion. That’s partly because there is already a lot to think about already and partly because the atmosphere under discussion here (at least for much of this discussion) was defined as optically transparent (TEV3).
For now, I’ll just note my disagreement with it – as with any slowly changing process the change can always be defined as “small” in one “layer”. The same goes for pressure changing vertically through the atmosphere and yet at 50km the pressure is 1/1000th the value at the surface.
Leonard Weinstein from July 12, 2010 at 3:01 pm:
I’m glad we’ve all worked hard to try and understand how other points of view are formed.
This explanation seems like the key piece of the puzzle in my understanding of your point of view.
And without this understanding any kind of simulation or solution wouldn’t have addressed the critical elements.
I’d like to have a think about how to explain where I believe it is flawed.
For Leonard Weinstein following July 13, 2010 at 10:47 am:
First of all, the standard description of the adiabatic lapse rate in atmospheric physics uses the concept of a “parcel of air”.
This parcel is heated (by the ground for example) and expands, it therefore rises due to buoyancy forces (it is lighter than the surrounding air).
Because no heat is exchanged between the parcel of air and the surrounding air the process is adiabatic (by definition). Therefore the temperature drops according to the lapse rate formula.
Now everyone in the discussion seems ok with this.
(Another mechanism would be “forced convection” where air was forced up and cooled down, for example, via wind pushing air up over a hill or mountain).
There are two important points here:
1. There has to be a “forcing mechanism” for convection
2. The standard discussion is not about a molecule but about a much larger collection of molecules called a “parcel of air”
I have my main question on point 2, but of course I would be interested in your opinion on point 1.
On point 1 – Convection.
This is one of the three mechanisms of heat transfer (along with conduction and radiation) – but it is really mass transfer.
The heat is transferred with the material when the material (gas or liquid) actually moves. There needs to be a “driving force” for moving the mass, it doesn’t happen spontaneously.
Or to put it another way, if it does happen “spontaneously” this needs a very complete explanation.
Heat transfer from hotter to colder happens spontaneously. Mass transfer needs the right circumstances and as a general rule does not move “spontaneously”.
On point 2 – The “parcel of air”.
If we consider the parcel of air formulation, does your earlier explanation hold up?
That’s not to say a molecule can’t be considered on its own, but let’s first consider a parcel of air.
If a parcel of air heats up, expands and rises – then its temperature will decrease. (Alternatively, a parcel of air could be forced vertically up by wind and the shape of the ground). Because this has happened adiabatically, by definition it hasn’t exchanged any heat with the surrounding air.
Therefore, if it is now cooler than the surrounding air it will sink.
I don’t believe we can now say – “it starts exchanging heat with its surroundings and therefore it will stay here”. It didn’t exchange heat fast enough before, when it was rising adiabatically, so now it will fall before it has time to reach an equilibrium via conduction.
This is the standard approach to solving the problem of the atmospheric temperature profile – convection takes place only under certain conditions.
For example, if the lapse rate was 8K/km and the temperature in the atmosphere decreased by 1K/km then convection wouldn’t take place. If the lapse rate was 5K/km and the temperature in the atmosphere decreased by 10K/km then convection would take place.
This is the standard explanation in atmospheric physics. Convection needs a mechanism to drive it and this mechanism is forced convection, or buoyancy.
(I’ll take a look at the “molecule approach” later)
scienceofdoom
….”This is the standard explanation in atmospheric physics. Convection needs a mechanism to drive it and this mechanism is forced convection”……
We often focus on the rising parcel of air.
Same with an air bubble rising through water.
However it might be better to think of gravity pulling the water down.
Likewise gravity pulling the a colder parcel of air down.
SOD,
If there are any imposed currents due to forcing boundary conditions, or as a residue from initial conditions, the parcels (real parcels with no fake adiabatic enclosure) will move, including some up and down motion. If the temperature distribution of the atmosphere system is not close to the adiabatic case, these parcels can carry local excesses or deficiencies of temperature relative to their new local surrounding. If the motion is slow, the heat transfer will occur along the path of motion. If it is fast enough it will mainly occur at the final location. In all cases, the direction of heat transfer is toward adjusting the surroundings toward adiabatic conditions. If the forcing continues and is strong enough, the system can remain in a non-adiabatic condition. However if all forcing stops and the atmosphere system were adiabatically enclosed, the currents would eventually die out, and the system would asymptote to an adiabatic lapse rate. This is the condition that occurs when small random perturbations of parcels would not result in any heat transfer. The parcel temperatures would always be at the correct local temperature at different heights due to the adiabatic expansion or contraction that occurred as the parcels moved.
Alternately, if the temperature was constant at different elevations, as parcels moved up or down, the parcels would be at different temperature from the surrounding, and transfer heat. The transfer would be in the direction of adjusting the atmosphere toward the adiabatic lapse rate.
Thus the stable and quiescent atmosphere has an adiabatic lapse rate. The case of a lapse rate lower than the adiabatic one is a case where lateral variation has to generate the correcting currents in a real atmosphere. If there were no lateral generated currents for this case, the only remaining corrective driver is diffusion. This is a slow process and it would not take much outside forcing to continually dominate the temperature profile. However this condition is generally not dominate in real atmospheres, and would not naturally occur in the room problem as stated.
Ah, you’re talking about the effect of the moving parcel of air on the *surroundings*. However, the effect of the surroundings on the moving parcel of air is the opposite – to adjust the parcel *away* from the adiabatic conditions (toward whatever the local temperature is). If the surroundings are slightly cooled, the parcel is more significantly heated (assuming the parcel is small relative to surroundings). The effect on the parcel is large, the effect on surroundings small.
Moreover, a moving parcel isn’t just moving into a vacuum – it has to be part of a cycle of other moving parcels that removes air from where our parcel is going and restores air back to where our moving parcel originated from. Each of those parcels will similarly exchange heat with their surroundings – essentially opposite to the heat exchange of “our” parcel. So the net effect of all that motion is the heating or cooling of the moving parcels, with essentially no effect on surroundings, particularly if the motion is relatively slow.
SOD,
The analogy using enclosed parcels with a adiabatic wall was to use the parcels as sensors to show where they would be in equilibrium at any height. This use was to avoid the fast/slow issue. It was also used to discuss the zeroth law issue with Arthur. The fact is, the presence of actual heat transfer is needed to show that a constant temperature profile is not a stable one. This is essentially a small perturbation type of analogy. The only totally stable state under the unforced condition is the adiabatic system.
SOD,
I think the point that we disagree on has to do with the statistical result of diffusion of individual molecules as compared to the macroscopic motion of “parcels” of gas. They give the same result! The only difference is that eddy motion is generally much faster than diffusion. This means that being in a quiescent atmosphere with a reduced lapse rate will tend toward the same result as a gently stirred atmosphere.
This is probably a very much a chicken-egg problem, but I think it would be better (or just another way) to say that convection is driven by differeneces in pressure, rather than temperature. In order for the parcel of air to rise, the difference in pressure (pressure increases if you heat the gas) has to be bigger than the force imposed by gravity.
Arthur Smith,
“Leonard, you have repeated this argument about the single molecule many times, but I repeat again that it is wrong. It can be seen as wrong for many reasons:
* it necessarily results in a flux of energy from colder (higher) to hotter (lower) regions, violating the second law
* it implies an equilibrium state with a temperature gradient, violating the zeroth law
That’s what I used to think. Things are actually much more complicated. See for example Priestly and Swinback, Vertical transport of heat by turbulence in the atmosphere, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences © 1947 The Royal Society.
Abstract here: http://www.jstor.org/pss/97858
“A necessary consequence of the classical theory of the turbulent transfer of heat in the atmosphere is that the flux of heat is in the direction from high to low potential temperature, and this normally involves the flux being from low to high actual temperature. On examination this is shown to be consistent with the second law of thermodynamics.” [my emphasis]
and
“It is shown that a component of heat flux, here called ‘convective turbulence’, must result from the buoyancy forces. This is always directed upwards and is thus opposed to the general downward transfer of mechanical turbulence.”
Thank you De Witt, that’s what I was trying to say here:
July 13, 2010 at 5:56 am
Well, the real-world atmosphere that Priestly and Swinback are presumably talking about is quite different from the equilibrium state Leonard is arguing for. The real atmosphere is in steady state with the flow of incoming solar energy driving everything (and the large-scale flow of heat is definitely from the surface up, not top down). But I haven’t read the paper – the abstract doesn’t tell us how they resolve the second law issue or exactly how they define it. Perhaps you can explain if you’ve read it.
I want to summarize my thoughts at this point.
The tall room problem was a very limited special case. It was intended to show how the very high temperature at the ground could result even without a greenhouse gas. The room problem supplied the modest value of the temperature at the top of the room by putting the gas in at that location. The great height required a large quantity of gas to fill the room and still retain a reasonable pressure at the top, but the exact pressure at the top was not critical. The adiabatic lapse rate formed due to gravity acting on the gas. The temperature at the bottom would be very high.
The room model does not mean greenhouse gases and/or clouds are not needed for Venus. Forcing the temperature to have a specific value near the top of the very tall atmosphere is still required to allow the lapse rate to result in the high ground temperature. The only issue there is how high an altitude this specific temperature level forms, and it will be very high for even a modest fraction of greenhouse gas and/or clouds if the atmosphere is very high like that of Venus.
I think one thing SOD and Arthur gets hung up on is what would happen if a lower lapse rate than the adiabatic one, or even a constant temperature profile ever formed from some forcing. It is stable from macroscopic buoyant self-correction (but not diffusion), and unless lateral forcing stirs it up, it would not drive toward an adiabatic lapse rate at a significant speed. Under these conditions and using the assumption from Arthur’s definition of the zeroth law, he assumes the conduction would drive the temperature toward a uniform constant value. This thought is wrong due to the misunderstanding of the concept of potential temperature. However, there are almost always some strong currents in real atmospheres even if heating and cooling both occur at the top of the atmosphere due to latitude insolation variation and day/night variation. As long as induced currents mix the atmosphere, it is not even necessary for sunlight to reach the ground. The wind speed on Venus varies from 2 to 3 m/s near the ground (which is strong convection at the high pressures there) to over 100 m/s at some locations in the atmosphere, and ground absorption of sunlight is probably not a dominant factor in this. This circulation restores the temperature lapse rate to near the adiabatic value. Note that I said restores, not forms.
Arthur,
The gas that was introduced into the top of the tall room was introduce at 300 degree K. If the gas filled the room with a reasonable pressure at the top (say 0.1 bar), what uniform temperature do you claim the entire room temperature would go to after a long time to settle out?
I believe I already answered this – about 750 K. And that result is independent of the pressure at the top, as long as that pressure was high enough that statistical properties like temperature are meaningful, and not so high that you’re inducing phase changes in the bottom portion.
“Potential” temperature has meaning only under adiabatic conditions (rapidly moving currents), and those conditions require some sort of driving energy flux (low-entropy energy, free energy, whatever you want to call it) such as that from the sun. On Venus, about 2% of incoming sunlight does make it to the surface, and that’s sufficient to drive the upward convective flux and induce the adiabatic lapse rate. Cut that 2% completely to zero and you’d have an isotherm up to wherever the solar absorption was occuring.
Arthur,
For the room problem, I did not say the gas had to be introduced rapidly. As a very small amount is introduced, the gas fills the room and the mfp gets smaller and smaller very quickly. The gas can be oozed in so that quickly is not a factor. This violates your comment on the need for quickly to be needed for adiabatic. Next as the mfp gets smaller (very early in introduction of the gas), the continual introduction of gas goes in at the top and stays near the top until it is slowly pushed down by new gas coming in on top of that. This continues until all gas is inside. Note the room was an adiabatic system to the gas inside, i.e., had no heat transfer through the wall. There was no energy added to the gas through the wall after it entered the room. We thus put a gas with internal energy corresponding to a temperature of 300 K, and did not heat it from the outside. We also did things slow as we choose. Where is the added heat coming from? According to your clear definitions, the temperature should be 300 K. In fact it varies from 300 K at the top to (300+100*g/Cp) at the bottom. The added temperature does come from the gravitational potential energy, but if the gas is introduced slowly enough, your concept would not allow this to happen.
Leonard, the gas won’t “stay near the top”. Every molecule of gas added will very quickly end up near the bottom (and then only rarely make it back up to the top again). Gas density and pressure increase exponentially from top to bottom, with most of the gas near the bottom. That doesn’t depend on total gas mass; any new added gas will spread out similarly.
The reason the final temperature has to be much higher than 300 K is because you’re forcing the average internal energy per molecule to be very high – that determines the sum of all internal energies (total energy). Then apply the Boltzmann distribution to find the temperature under constraints of number of molecules and that total energy value, and you get a high temperature.
But consider your “room” example with the gas introduced at the bottom at 300 K instead of the top. Again that determines the total internal energy, distributed among the molecules in the room according to the Boltzmann distribution; since a small number head high up the gravitational potential, the resulting temperature level will be slightly less than 300 K. Same analysis gives you a consistent result. But by your adiabatic (constant internal energy per molecule) argument, none of the molecules could possibly reach the top of the room, because their temperature would be negative! That’s clearly unphysical.
Leonard Weinstein:
Taking the macro view rather than the molecular view, with convection via pressure difference (Mait rightly suggests this as the best description of what forces convection), I think it will be very easy to show that a parcel of air rising up loses heat via adiabatic expansion and falls back down long before any significant conduction of heat took place. (Assuming an environmental lapse rate smaller than the adiabatic lapse rate, of course).
A 10m diameter sphere of warmer air rising up 1km where the environmental temperature decreases by 1K through this distance. And an adiabatic lapse rate of 9K/km (doesn’t much matter).
Choose some typical rates of movement and see what happens..
Perhaps I will have a chance to explore this in a few days time.
Anything wrong with this experiment?
By the way, if you are correct that any atmosphere tends to move towards the adiabatic lapse rate regardless of the source of heating or the temperature profile established at the start (t=0) then you will have redefined atmospheric physics.
Every text book has convection establishing the temperature profile if – and only if – the environmental lapse rate without convection is larger than the adiabatic lapse rate.
That doesn’t mean you are wrong. But if you are right then some professors of physics will be a little embarrassed..
Arthur,
I pointed out that no heating of the ground at Venus is needed if lateral currents are introduced that are sufficient to avoid local low lapse rates. These currents can and will be introduced by variation in the location of heating AND COOLING from the top. That doesn’t mean there is no heating at the surface, only that it is not necessary. Also forced mixing is only needed if the lapse rate is smaller than adiabatic, but there is not any normal mechanism that tends to cause this at quiescent conditions (a cold ground can cause this, but is not there if we have reached quiescent conditions, so is a transient condition).
SOD,
First you have to define the parcel of air. Is is without boundary, in a balloon, or a fixed volume? I think you mean the first. In that case, what was the cause of the upward motion, was it warmer than the local air or was it pushed from some other source? I assume you mean it was warmer. If this is so and the lapse rate was the adiabatic lapse rate, then even with no heat transfer, the parcel will cool as it rises, but so will the surrounding be cooler. In fact, the parcel will always be warmer than the local level as it rises (and expands) until heat transfer with the surrounding heats the region it is going through, and this spreads to reestablish the adiabatic condition. If the lapse rate were less than adiabatic, it would be limited in how high it would rise, but there would be some heat transfer until it reached a slightly higher level and matched surrounding temperature. Nothing I have said violates the text books. They look at a single temperature profile with out lateral variation, and that is not what I discussed for planets. The case of the room can be considered a single profile, but there is no mechanism to form any but an adiabatic profile as the gas fills the room. If a constant temperature profile was introduced by forcing, and if macroscopic forces (convection) are the only ones allowed, any lapse rate can exist less than the adiabatic lapse rate and be stable. Diffusion is a very slow process, and can’t overcome even tiny forcing. This is why it is neglected for these analysis. However, we were talking about a hypothetical case of ultimate profile without mixing, whatever the initial condition was, and even diffusion will eventually form the adiabatic condition for that case.
SOD,
I want to make another point on your example. Assume an initial constant temperature average profile, but allow small local parcels to have small temperature variations. A parcel that is warm wrt the surrounding will rise and and it rises transfer some heat from the edges. However we can neglect that effect for now. As the parcel rises, it expands to maintain the pressure. It also adiabatically cools. It will rise to the height where buoyancy forces go to zero (matched temperature to surrounding). It may slightly overshoot and then settle back to that new height, that is not important. The displacement up of a parcel has to displace down an equal amount of atmosphere (but spread out). The downward displaced atmosphere heats by adiabatic compression, but since it is spread out will actually just result in some net heat transfer downward. The cold parcels will cause heat transfer downward. If cold and hot parcels match (no net excess of energy), since both directions result in a gradient being established moving toward adiabatic conditions, the parcel version is actually a more efficient version of how the lapse rate drives toward adiabatic.
Arthur,
You admit that all lapse rates equal to or less than the adiabatic lapse rate are stable wrt buoyancy. The only issue is the effect of diffusion (the source of heat transfer in gases). Now assume that a tall quiescent room is forced to initially have the adiabatic lapse rate. Now look at a plane location at any given height. By definition, the temperature of the bottom surface of the upper volume is exactly the same as the upper surface of the lower volume. In addition, the kinetic energy of the average molecule going through the plane exactly matches in both directions, and the numbers exactly match (or there would be mass transfer). As the molecules go up they lose KE. As the molecules go down they gain KE both before the next collision. The gain and loss makes them (on the average) exactly match the average KE of surrounding molecules at the new average height exactly as a finite parcel that was in equal temperature wrt the surrounding and that is displaced up in an adiabatic gas would do. This clearly means there is no heat transfer for the adiabatic profile. Any other profile will have heat transfer driving it toward the adiabatic profile unless outside forcing overwhelms it.
Don’t know if it’s going to bring you all down, but Nassif has the solution for Venus’ temperature over on the Lunar thread.
Nasif doesn’t have a solution to anything. As I pointed out in that thread, he has problems doing simple algebra correctly. Further repetition of the many reasons why he is wrong appears to be pointless.
Aye, he doesn’t even know how he does it himself. Yet doesn’t know he doesn’t know.
Which is some sort of minor miracle of self delusion (remember, just because it’s not nice, doesn’t mean it’s not a miracle. If you’re killed by a 1-in-a million freak asteroid hit, it’s STILL a miracle!).
Arthur Smith,
The Priestly & Swinback paper doesn’t go into any detail about the second law. It’s available for free until 7/30/2010 for anyone that’s interested.
http://rspa.royalsocietypublishing.org/content/189/1019/543.full.pdf+html?sid=c535c03b-3cca-4e90-96b9-1bd74a84c499
What’s conserved by the First Law in the free atmosphere is CpT + gz. When the lapse rate is less than the adiabatic rate, entropy increases with altitude. This is expressed in meteorology using potential temperature defined as s = Cp*ln(theta) where s is the specific entropy, Cp is the constant pressure heat capacity and theta is the potential temperature. Theta(z) = T(z) + gamma*z, where gamma is the adiabatic lapse rate. If theta increases with altitude, then heat may flow from higher potential temperature to lower potential temperature without decreasing total entropy, so the Second Law is not violated.
As for the zeroth law, a one dimensional atmosphere with a vertical temperature profile equal to the adiabatic lapse rate is in thermal equilibrium.
And yet the zeroth law states that the temperature at the bottom and at the top must be the same.
DeWitt – thanks, that paper was quite interesting. However, it’s not saying what you seemed to imply it’s saying. It’s actually all about distinguishing between two types of “turbulent diffusion”, first the “classical” case of “eddy diffusion” or “mechanical turbulence”, where a parcel of air at the ambient temperature is somehow pushed up (or down) a bit, and does basically what Leonard’s been talking about here, move temperatures toward the adiabatic lapse rate. But second, they add in something else, “convective diffusion” which has an added “buoyancy term”, where a parcel of air that for some reason is a little warmer than the ambient region spontaneously rises.
That is, the “classical”, “mechanical” term, which has that odd property of moving heat from colder to hotter temperatures, has to be driven by something else, it cannot arise spontaneously. As they discuss in explaining why it’s not a second-law violation (section 3):
But if it was not part of such a larger process of transfer of heat from hot to cold regions, it *would* violate thermodynamics…
True. But it’s a heat pump. You can transfer a lot of heat up and down with a relatively small amount of work generated by moving heat horizontally from hot to cold.
Thank you DeWitt. I don’t seem to be able to convince Arthur and SOD with my arguments. I don’t know what I left out that is any better than what you just posted.
Leonard, maybe the problem is that you’re talking past. Correcting a mistake that exists only in your formulations, not SOD’s.
DeWitt’s explanation is already known in meteorlogical circles as “CAPE”.
Convectively Available Potential Energy.
And these lead to thunderstorms that end up with a lapse rate that is below the moist adiabat.
Your other problems may be in your abuse of adiabat.
There are two:
Moist adiabat
Dry adiabat
An adiabat between the moist and dry adiabat is CONDITIONALLY STABLE. And the moist adiabat is still stable, even though it’s lapse rate less than the dry adiabat. Just conditionally so (based on moisture content).
So when DeWitt says:
“When the lapse rate is less than the adiabatic rate, entropy increases with altitude.”
This is only definitely true if the lapse rate is less than the MOIST adiabatic lapse rate.
Failing to explain precisely what is meant (especially when you start going on about heat capacity which MAJORLY changes when moisture is added/taken away or reaches saturation) makes an argument so poorly made as to be “not even wrong”.
And in any case, an atmosphere with a temperature gradient can NEVER be said to be in thermal equilibrium. That meaning is far too vague.
If it’s thermal equilibrium as in “no movement of heat” it’s obviously wrong. There has to be. If you mean that temperatures at any level will be, generally, stable, then that’s accurate (in bulk: local heating HAS to have an effect, as must orography and other sub-global effects). That is *an* equilibrium, but not thermal.
It IS a stable atmosphere.
But if heat is moving, you can’t call it thermal equilibrium unless you mean stable, or LTE equilibrium, which is somewhat tautological.
Mark,
I think you have missed much of the discussion above. We are mainly talking about a model with gas in a tall room with a dry gas. Moist adiabatic does not enter this problem. We know about moist adiabatic effects. Also the stable condition is wrt buoyancy conditions which is a macroscopic stability and has to be overcome to go to an adiabatic lapse rate. However, without an external forcing, diffusion effects would eventually form the final temperature profile, which would be the adiabatic lapse rate profile. Heat transfer in a gas in gravity is not the same as with no gravity. Why do you think we have lapse rates at all? The no heat transfer condition is exactly the corresponding adiabatic lapse rate, not the constant temperature case. Arthur and SOD disagree with this and DeWitt and williamcg agree with me. The other comments about actual planet atmospheres were side comments referring back to previous discussion.
The lapse rate does require that you have enough energy coming in to the system to maintain it.
And that means energy is transferring up the slope.
Which means there is a temperature gradient, it’s real, and energy slides along it.
Which is, as far as I can see it, what Arthur and SoD is saying.
Cheers.
Arthur,
Let me try one more time. Have an atmosphere with an adiabatic lapse rate that is stable over reasonable time frame (thermal conduction without convection is a very slow process with very small gradients, and the lapse rate is <0.01 K/m). Now look at a parcel of the atmosphere that displaces upward with a very small drift rate. As it rises, it expands and cools at EXACTLY the lapse rate. Thus it is NEVER exchanging heat with the surrounding, i.e., no heat transfer. The movement up requires an equal amount of atmosphere to be moved down (conserving mass). As the gas is moved down, it compresses and EXACTLY maintains the same temperature as its surrounding. Thus no heat transfer. This can be done so slow that kinetic energy of the movement is not a factor. If the gas was constant temperature, the movement results in heat transfer. Thus the only stable profile is the adiabatic lapse rate. It is true that if the lapse rate is lower than adiabatic, or even a uniform temperature, that the profile is a stable condition wrt buoyancy conditions, which is a macroscopic stability and has to be overcome to go to an adiabatic lapse rate. However, without an external forcing, diffusion effects would eventually reform the final temperature profile, which would be the adiabatic lapse rate profile.
The zeroth law of thermodynamic is a generalization about the thermal equilibrium among bodies, or thermodynamic systems, in contact, and for most systems this means no temperature difference. However you keep leaving out IN CONTACT, which is not the same as everywhere. The only thermal equilibrium for an atmosphere such as the one in the room is the adiabatic one. I clearly showed how this is so and do not understand how you do not get it.
Leonard, what is the temperature profile in your 100 km-high room if the gas is added at 300 K at the bottom? What if it’s added at 100 K at the bottom? 10 K (assuming it’s helium and so hasn’t solidified)? Pressure can be as high as you like.
You are quite misunderstanding the zeroth law. Thermometers need have no dependence on gravity, so a thermometer at 100 km and one at 0 km can themselves be brought into thermal equilibrium with one another, and then moved without any change in their equilibrium state. If one is in equilibrium with your “room” while the other is not (i.e. different temperatures top and bottom), then your room is not in equilibrium. End of story. Temperature is not gravity-dependent.
Arthur,
If you introduced the gas at a low temperature at the bottom, the dry adiabatic lapse rate would still try to establish. However, once the temperature fell low enough as the altitude increased, even helium would turn to a liquid and start to fall as drops, but these would re evaporate as they fell. I think the term for rain that does this is virga. This would change the temperature profile a lot. The maximum height possible as a function of pressure would depend on the change in profile, and it is possible that adding more and more gas, that eventually the pressure can go all the way to the top, but that case would have a very small temperature gradient due to the “wet” laps rate effect due to phase change, which is not what we were looking at. The lower the initial temperature, the lower the altitude would be that condensation would occur. The bottom temperature would be the introduced temperature (300 K or 100 K or 10 K).
You keep talking about a thermometer. It is not the thermometer that is gravity dependent, but the exchange of potential energy for kinetic energy of the gas. You really need to study the definition of equilibrium, as the adiabatic lapse rate for the dry gas is the only state of equilibrium. Consider what has to be true for equilibrium-like what does a small perturbation do? I have discussed two types of perturbations, a small hot spot, and a small nudge in position, for both constant temperature, and adiabatic lapse rate, and showed the equilibrium case was adiabatic.
Arthur,
I looked up Helium. It’s Cp is so high that its adiabatic lapse rate is only about 1.6 K/km. This means that 100 km tall would only drop 160 K. If you start at 300 K, it would stay gas to the top with enough pressure put in, and be 140 K there. The 100 K and 10 K cases would do as I described with condensation below the top.
Arthur,
Sticking thermometers at different locations at different heights measures the local temperatures. What the heck does that have to do with the zeroth law. If the thermometer is at a fixed location, and sample volumes of gas from an adiabatic lapse rate are forced up or down to that location, the gas automatically adjusts in pressure and temperature to the same temperature. This is how the gas has to be measured to determine if there would be heat transfer, and the zeroth law refers to conditions that result in no heat transfer between different samples at those locations. The adiabatic lapse rate is the profile with no conduction.
Leonard, I provided two textbook derivations of the “zeroth law” and a wikipedia definition earlier, and yet you still seem not to understand it.
The “zeroth law” states that thermal equilibrium is a transitive property. Two thermometers which are measuring the same temperature are, by the definition of temperature, in thermal equilibrium with each other. So if one of them is in equilibrium with your system, whatever altitude it’s placed at, then the other must be also. The temperature *must* be uniform.
Also, the zeroth law implies that all macroscopic subsystems of a system in thermal equilibrium are in thermal equilibrium with one another; there can be no temperature gradients in thermal equilibrium.
Arthur Smith,
Most thermometers are constant volume devices so the variation in external pressure doesn’t change the indicated temperature. For a kg of gas in the free atmosphere, volume and temperature depend on pressure. So it only makes sense to compare gas temperatures at the same pressure with the pressures being equalized adiabatically. Obviously that means that an atmosphere with an adiabatic lapse rate is indeed in thermal equilibrium even though the absolute temperature decreases with altitude.
I still think you may be correct about a totally opaque atmosphere being isothermal, but I could be wrong about that. The analogy would be the ocean and the concept of potential temperature applies there too. But the Venusian atmosphere isn’t totally opaque to either short or longwave radiation.
The tall narrow room example works both ways. A one dimensional vertical isothermal atmosphere will not eventually develop an adiabatic lapse rate. Turbulent mixing that might transfer heat down the potential temperature gradient would not exist. For turbulence to develop, you need a horizontal temperature and resulting pressure gradient. But horizontal temperature gradients do exist on spherical planets illuminated by plane parallel radiation on one side. So even a transparent planetary atmosphere will exhibit a near adiabatic lapse rate over most of the lower atmosphere.
DeWitt, you’re wrong:
“Most thermometers are constant volume devices ”
The commonest meteorlogical thermometer is the mercury bulb thermometer. The volume HAS to change because otherwise you can’t read temperatures.
Please be a bit more specific. In your case, this statement is not necessary anyway.
Thermometers read temperature BY FIAT. This is why metrology (not meteorology) tells you when you use a mercury thermometer, when you’d use a pyrometer, when you’d use any of the scores of other temperature measurement devices.
The problem with the ocean analogue is the thermohaline layer. Salt exists in the ocean and this helps create a layering which stops convection and the much less effective conduction is needed.
The ONLY way you’re going to be able to answer the opaque atmosphere is to do a full dynamical model of the atmosphere and have a look. Even then you’re going to have to relax “opaque”: it won’t be opaque across all wavelengths.
But the shortcut would be: a completely opaque atmosphere is a black body and is there temperature stratification in such an atmosphere?
Well, in a venus, yes: the sun only shines (on TV), sorry, in daytime.
And you don’t need a horizontal temperature gradient to start turbulence: the gas is entropic.
Think of it this way: the accretion disk of the solar system didn’t need a horizontal temperature gradient.
Such gradients can force turbulence to start, but this only makes the return to stability quicker, it isn’t a requirement. Only time, which is a requirement for the idea of entropy itself, so rather already built-in.
The volume of the liquid in glass device doesn’t change and it’s immune, to a first approximation, to external pressure. Then there are electrical resistance thermometers like thermistors and platinum resistance thermometers, not to mention IR radiance.
A gas thermometer, OTOH, is not a sealed device and is dependent on the reference pressure.
An accretion disk is not one dimensional. Besides, you’re ignoring conservation of angular momentum. If the angular momentum of the system before gravitational collapse were zero, there would be no accretion disk because nothing would ever be in orbit.
“I looked up Helium. It’s Cp is so high that its adiabatic lapse rate is only about 1.6 K/km. This means that 100 km tall would only drop 160 K.”
This will still require enough energy to maintain that lapse rate.
DeWitt,
The tall room case would have a hot bottom and cool top form as the gas was introduced, since the continual introduction of the gas would adiabatically compress the lower portions downward as it was added. Once currents died out, there is no mechanism to cause the gradient to be initially different from this adiabatic lapse rate. If the gas thermal conductivity was a mechanism of reverting to a lower lapse rate, the conduction alone would take thousands of years (do the conduction alone problem). However, I think you agree if the adiabatic lapse rate were the initial condition, that is the equilibrium case, so there would be no heat transfer by conduction. The gray gas case in the room condition also would have the adiabatic lapse rate as I will show later.
Mark,
DeWitt was wrong about the physical thermometers being constant volume, but I think he meant the volume was not dependent on gas pressure. The volume change is a small change due to the coefficient of thermal expansion and is external pressure independent. Also, you stated that you needed some mechanism to maintain the adiabatic lapse rate. Tell me, maintain the lapse rate from what forcing that moves the profile from the adiabatic lapse rate? Enough forcing and you can get any profile, but that is not the equilibrium case we were talking about.
Science of Doom,
We are now going to look at a different model of the same room: 1 km X 1km X 100 km tall. The only significant difference is the gas properties. Again the assumption is no heat transfer at walls (including top and bottom), but the walls and top are perfect mirrors. The difference is that we now make the gas an arbitrary path length absorbing gas for any or all of the wavelengths. Also assume the floor acts like a black body at the gas temperature at the bottom, but has no heat storage capacity. Some wavelengths can be selected to pass through the entire gas if desired, and some absorbed and re radiated in any selected effective length. Again start by filling the room from the top with a gas initially at 300 K and fill until the density is close to that of Venus’s atmosphere. The system is now closed and allowed to come to equilibrium. What is the pressure and temperature distribution?
As a starting point let us assume the pressure and temperature are the values for an adiabatic system. The pressure increases going down and the temperature increases going down by the adiabatic lapse rate, which adds to the temperature at the top to get the temperature at the bottom. If that assumption is wrong, the system will adjust to a new balance, so that is as reasonable a place to start as any.
The very hot floor will radiate upward a huge amount (T floor= g/Cp X 100 km + 300). Note that Cp may vary some with temperature, but assume it does not for simplicity here. Some of that radiation passes unimpeded to the top (if desired), reflects back down, and as was shown previously, does not affect the temperature profile at all if it is not absorbed. Other parts of the radiation upward are absorbed by some selected distance above the floor, and re radiated in all directions including upward. The re radiated energy upward slightly exceeds the re radiated energy downward at this point in the analysis, so that there is a net energy transfer up. This can be as large as desired by selecting the absorption length! Now continue all the way to the top. There is a net radiation energy flux to the top wall. However, that wall reflects all of that energy back downward. You can think of it as a back radiation matching the forward radiation for that top layer. The layer that matched upward and back radiation levels exactly (thus did not change temperature) now passes down the reflected energy as if it came from the next lower absorbing layer directly to the upper wall and was directly reflected back to that layer. That is the next absorbing layer down also will have a matching back radiation to upward radiation, and will not change temperature due to the radiation. This continues all the way to the floor. That is, the reflection makes all layers have back radiation exactly matching forward radiation, and thus there is no radiation net heat transfer. The temperature is exactly that of the adiabatic lapse rate for this approximation with one possible exception. This simplified analysis did not allow for the wavelength shift of the radiation due to temperature change in the gas as the radiation passed up, and its bias on absorption length. Thus the result may not be an exact solution for real gases, and this might distort the temperature profile some, but there would still be a large lower wall heating and cool upper level. If the gas were a perfect gray gas (wavelength independent), the result would be exactly the same as an adiabatic lapse rate.
SOD,
Please retract that last entry of mine, I have rethought it am am not so sure for that case.
My post on the absorbing gas was wrong. The absorbing gas in the room would move toward constant temperature, since even a small radiation energy flux would be large compared to the tiny thermal conduction trying to restore the adiabatic lapse rate, and would transfer heat to the upper level. However both energy fluxes are small for a highly absorbing gas (back radiation almost equals upward radiation), so a modest amount of forced convection could restore the adiabatic lapse rate. This is what would and does happen in the planetary atmosphere cases, but would not happen in the room.
“Also, you stated that you needed some mechanism to maintain the adiabatic lapse rate. Tell me, maintain the lapse rate from what forcing that moves the profile from the adiabatic lapse rate? Enough forcing and you can get any profile, but that is not the equilibrium case we were talking about.”
Not entirely sure because I think you misspelled a few words.
And your retraction may make this redundant.
Yes, you need something to maintain the lapse rate, else it will cool down.
“Moves the adiabatic lapse rate” which way?
Shallower and more stable: energy loss from the system.
Steeper and less stable: extra energy into the system.
Enough forcing is impossible for several profiles. E.g. :
Inverted through column requires trans-infinite energy to maintain. Or (as you get with lasers) a barrier.
Leonard,
Your mechanism of introduction is designed to produce an initial temperature gradient. Suppose we place a superconducting rod with lots of surface area reaching from top to bottom in the room. That will equalize the absolute temperature at all altitudes. Now remove the rod. Will a vertical temperature gradient form? I don’t think so. It takes work to move heat down a potential temperature gradient when the lapse rate is less than adiabatic because buoyancy is working against you. There is no temperature difference to produce that work.
Mark,
It would cool down in real world systems from radiation from the higher temperature. However, I defined the room as not having any radiation effect (all mirror perfect insulating walls, and totally radiation non absorbing gas). For that case I am correct. The point was to show it was possible to get an adiabatic lapse rate at equilibrium.
DeWitt,
If you forced the uniform temperature as an initial condition, the only restoring mechanism available would be thermal conduction (diffusion). I estimated that it would take thousands of years to do this in the tall room due to the very low conductivity of the gas and the small gradient difference between the constant temperature and adiabatic lapse rate profiles (<0.01 K per m over 100 km), so this is only an issue for an idealized case.The temperature difference that is the equilibrium value (adiabatic lapse rate) comes from the asymmetry of gravitational effects on diffusion up vs down. In the real world this does not matter since any forcing at all would dominate it. However the inverse problem is the issue here. If the initial profile were the adiabatic lapse rate, would the conductivity tend to drive the temperature toward a constant temperature profile as Arthur (and SOD?) seem to think. That is where we disagree.
Mark,
I think your confusion comes from my talking about an optically absorbing gas at a recent post. This is not the condition that we were debating, but a new entry following the previous. I then retracted the later post. Look at my problem definition from much earlier. I know the back and forth with different subjects gets confusing, but that is the way this discussion has gone, and you have to follow the string to keep up. It is additionally confusing due to the delay for posting some inputs, although that seems to have speed up lately. Also please tell me which words I misspelled. I try to catch most, but may miss some.
SOD,
I am curious how you agree that the assumption of dQ=0 which allows the derivation of the adiabatic lapse rate equation can result in T=constant on a profile. Even Arthur agrees the derivation is correct with the assumption of dQ=0, but then invokes a zeroth law that says adiabatic is not dQ=0. This is a logical contradiction I truly fail to see.
A definition from the web is: adiabatic equilibrium—A vertical distribution of temperature and pressure in an atmosphere in hydrostatic equilibrium such that an air parcel displaced adiabatically will continue to possess the same temperature and pressure as its surroundings, so that no restoring force acts on a parcel displaced vertically.
A layer in adiabatic equilibrium has uniform equivalent potential temperature.
” am curious how you agree that the assumption of dQ=0 which allows the derivation of the adiabatic lapse rate equation can result in T=constant on a profile.”
Because dQ is with respect to a constant height. Adiabatic means no work done on the surroundings. If you moved it up, then work could be done, but that is no longer its surroundings, therefore adiabatic assumptions are not in force.
A lapse rate requires you compare dT with dH, differing heights.
Adiabatic equilibrium != thermal equilibrium. Adiabatic equilibrium requires a steady vertical heat flux. Thermal equilibrium has all fluxes zero.
According to this AMS glossary, there’s an important condition you left out of the definition:
Mark,
Where on Earth did you get the assumption that dQ=0 was defined only at constant altitude. See:
http://atmos.nmsu.edu/education_and_outreach/encyclopedia/adiabatic_lapse_rate.htm (this is from NASA)
Guys,
I am sure I am right for the special case I stated, and you are sure you are right. We may not resolve it any further. If you want we can continue the present discussion, but I don’t see either side changing. However, I ran a calculation on how long it would take to go from either an adiabatic lapse rate to a constant temperature or a constant temperature to adiabatic lapse rate if only thermal conduction through an Argon atmosphere were the means to do the conversion. For the 100 km tall room, and assuming moderate pressures (say 100 bar at the bottom), it would take 10’s of MILLIONS of years either way. Since I think you would all agree the method of filling the room from the top would almost certainly form an initial lapse rate close to adiabatic, this is how it would stay for a very long time even if the tendency were to try to go uniform. This implies that the discussion is not even relevant in all real atmospheres. Convection for Argon, and a combination of convection and radiation for CO2 and cloud conditions will totally drive the processes.
I think you all agree that the actual lapse rate for Earth and Venus is close to the corresponding wet or dry adiabatic lapse rate. I think we can go on from here and agree that it does not matter who is right on the room problem, but that for real cases, if the gradient is close to the adiabatic lapse rate it would not take much energy to maintain that. If it were significantly lower, and there were not enough restoring convection, it would stay lower for practical time scales.
Real planets stick around longer than 10 million years.
But the real problem involves radiative heat transfers, which will equilibrate a system much more quickly than diffusive conductivity.
Arthur,
I don’t disagree, but that was not the issue. Also over 10 million years, I am sure other processes, including convection would make the conduction moot. I think there are still three main issues.
1) Can heating and cooling just from the top of an atmosphere generate enough circulation to maintain near adiabatic lapse rate?
2) Is the fact that the outgoing radiation is at a very high altitude, combined with the lapse rate sufficient to heat the ground of Venus, or is something more needed (such as some radiation to the ground)?
3) Can a reduction of a large factor (90% drop for example) of greenhouse gasses on Venus (but still maintaining clouds and the total pressures) still keep MOST of the high temperature on the surface of Venus?
My answer to all three is yes.
I pretty much figured that, leonard, when it was all “no heat in or out and mirrored top/bottom”.
At that point, you might as well say “made of unobtanium in gas form”…
DeWitt and Leonard,
I like the problem with the superconducting rods. But we must stop thinking primarily about temperature and forgetting about total internal energy (CpT + dz). With the rods in place, the total internal energy (potential temperature) will increase with altitude. When the rods are removed, the adiabatic lapse rate will form almost immediately and return to equilibrium demonstrated by a uniform internal energy/potential energy profile. (I can demonstrate this with the Helmholtz free energy calculation if you would like. I tried to do that earlier, but I don’t think I did a good enough job of explaining it).
With the rods in place, the increased temperature due to the increased pressure at lower altitudes is offset by the dQ transfer from the parcel to the rods. Thus both the temperature and pressure are lower than they would be without this heat transfer through the rods and back to the upper altitudes (dQ offsets the gravitational dW). When the rods are removed, dQ = 0, and both the pressure and temperature of the lower parcels increase immediately. The system returns to a constant potential temperature profile (adiabatic lapse rate) immediately. Diffusion will play no role.
I am assuming the room is completely adiabatic (no gain or loss of heat to/from the outside). I know the room conditions have changed a few times in the discussion so I hope I am dealing with the correct room conditions. Let me know if I have this wrong.
William – why would there be any dW, or dQ, in equilibrium? What are your d’s referring to? Pressure and temperature increasing “immediately” is physically impossible – it requires large-scale motion of mass and energy “immediately”, but there should be no such motion at all in the constant-temperature equilibrium system.
DeWitt and Leonard,
I need to make a correction to my last post. Since the pressure at the lower levels is determined by the quantity of mass above it, the volume will decrease rather than the pressure when the rods are in place. Thus you would end up with a higher mass density at the bottom and a lower density at the top than without the rods.
williamcg,
I think we can come up with different special condition that do strange things. Solutions may be complex enough to be an effort to verify, and add nothing at this point. I think your basic position on the room problem and mine are the same and DeWitt probably agrees that the adiabatic condition is the stable one. Arthur and SOD seem to think constant temperature is correct as basically the stable end point. It doesn’t matter in the practical world, so we should move on, since we seem to be at an impasse, and there are other issues.
Leonard,
What other issues?
williamcg,
I agree the issue of the correct thermodynamics regarding the lapse rate is one important issue needed to have a chance to fully understand of all the details about planetary atmospheres. However, we have said about what is reasonably possible to say in the limited time and format here to show the basic equations and definitions, and described the physical processes involved, and still appear to be at an impasse. I am not happy about this, but I am not smart enough to coach the facts any better, so encourage moving on where those issues are not show stoppers. I think there are still at least three main issues we need to discuss.
1) Can heating and cooling just from the top of an atmosphere generate enough circulation to maintain near adiabatic lapse rate?
2) Is the fact that the outgoing radiation is at a very high altitude, combined with the lapse rate, sufficient to heat the ground of Venus, or is something more needed (such as some radiation to the ground, or volcanoes)?
3) Can a reduction by a large amount (90% drop for example) of greenhouse gases on Venus, while still maintaining clouds and the total pressures, keep MOST of the high temperature on the surface of Venus?
My answer to all three is yes.
Mark,
The discussion was to make a particular point. Conduction is real and often significant. The fact that for the special cases of the quoted problem it does result in a prohibitively long time constant does not make the fundamental point less important. The reason I suggested going on was that we seemed to be at an impasse and it did not seem useful to spend more time, not that the issue is not relevant. The boundary conditions and choice of gas and method of filling the room are all quite reasonable inputs for a model. We still have not agreed on a very important basic issue, and thus this is an unfinished issue for the participants.
williamcg,
The reason I introduced the tall room model was to show that greenhouse gases are not necessary to heat the ground. Their contribution was to move the lapse rate to a high altitude. The model as described would clearly initially attain that lapse rate and temperature and maintain it for a very long time whether or not the conduction later tended toward constant temperature or not. I am sure it would continue to retain the adiabatic lapse rate for all time scales, and some others are not. However, the required forces to retain the adiabatic lapse rate either way are so small it does not matter in most practical situations. This is a fundamental issue, and if you can be more persuasive go for it.
Leonard, on your 3 questions:
1) Can heating and cooling just from the top of an atmosphere generate enough circulation to maintain near adiabatic lapse rate?
Not near-adiabatic, but some temperature gradients will surely be present even if all heating and cooling is higher up, if that heating leaves a non-uniform pattern of higher-up temperatures. But the maximum temperature below will be at most the maximum temperature “higher up”, it cannot be higher (simple second-law consequence).
2) Is the fact that the outgoing radiation is at a very high altitude, combined with the lapse rate sufficient to heat the ground of Venus, or is something more needed (such as some radiation to the ground)?
The lapse rate does not heat the ground! The lapse rate represents cooling of the ground through the various heat transfer processes that take heat from hotter to colder places. It is absolutely necessary that the ground receive direct heat input from somewhere – either the sun or some substantial planetary interior source – if the ground is at a higher temperature than the atmosphere.
3) Can a reduction of a large factor (90% drop for example) of greenhouse gasses on Venus (but still maintaining clouds and the total pressures) still keep MOST of the high temperature on the surface of Venus?
Yes, I do agree on this – because GHG effects are much less than linear in GHG concentration. Venus CO2 concentrations are several hundred thousand times Earth’s, but its total greenhouse effect is only about 8 times as large. So going from 300,000 times Earth to 30,000 times Earth might be expected to drop Venus’ greenhouse effect by 10-20%, which I agree doesn’t put a large dent in the high surface temperature.
But I myself would like to better understand what in the combination of atmospheric pressure/temperature and GHG concentration determines tropopause height and the rough point in the atmosphere where radiation escapes to space. What would be the impact of reducing Venus’ atmospheric pressure by a factor of 10, along with GHG concentrations? That reduces pressure broadening in the upper atmosphere, for instance, so effective radiating altitude should drop. But how much? Would it be another 10-20% effect, or more significant?
Leonard,
“3) Can a reduction of a large factor (90% drop for example) of greenhouse gasses on Venus (but still maintaining clouds and the total pressures) still keep MOST of the high temperature on the surface of Venus?”
Isn’t it more interesting to rephrase that to:
3a) Can a reduction to earthlike concentrations of greenhouse gasses on Venus (but still maintaining clouds and the total pressures) still keep MOST of the high temperature on the surface of Venus?
or
3b) Would carving off say 50 km of the earth surface and replace it with more atmosphere in a continuous way (keeping the present atmosphere with present temp and pressure) and keeping albedo etc, result in a considerable higher surface temperatures according to the lapse rate formula?
Arthur,
“But I myself would like to better understand what in the combination of atmospheric pressure/temperature and GHG concentration determines tropopause height and the rough point in the atmosphere where radiation escapes to space”
Would you agree that my example 3b would keep the level of LW escape (that was my intention) and just add 50 km of lapse rate below the present atmosphere?
It would have a minor impact on the level of LW escape since some LW leaves from the surface now – so the average escape altitude would drop slightly (but not 50 km!) Assuming the lower 50 km had the same GHG composition as the upper 50 km, radiative absorption would be very strong (due to pressure broadening), so as long as some SW solar input was reaching the surface, yes you’d definitely get close to 50 km of lapse rate added on to surface temperatures.
On the other hand if the lower 50 km was completely radiatively transparent (no additional GHG’s), you would have a radiative short-circuit from surface to the present atmosphere, and surface temperatures couldn’t get higher than about the standard sqrt(2) times the radiating temperature that you get from single-radiative-layer considerations.
I.e. with 50 km of additional GHG’s you’d get something like 600 K for Earth’s surface temperature, while with 50 km of IR transparent gas it would be limited to about 360 K.
Arthur,
As a start, let us go back to the room model. Do you agree that as the atmosphere is vented in and fills the room (from the top), the temperature would form at close to the adiabatic lapse rate WITH A HOT BOTTOM? Do you also agree the conduction away from that level would be very slow, so that very little energy is needed to maintain the adiabatic lapse rate? Keep in mind the assumptions on optical transparent and no losses to the outside for that model. Once you respond to this we can go on.
Jonas B1,
If the total atmosphere is thinner or thicker, and the location of outgoing radiation scales with that thickness, the lapse rate takes the temperature to different levels, since the delta T is lapse rate times height. The location of the outgoing height doing the radiating to space is the critical issue for real greenhouse gases and clouds.
Yes, that would be roughly the situation in the “room” example at first, but of course it’s pretty artificial – it’s effectively like saying what the temperature of a box of lead would be after dropping it from the edge of space. Of course it’s going to be hot at the bottom, and that’s going to stir considerable vertical mixing which is the condition for the adiabatic lapse rate.
But what happens after that? Suppose you have a small column within the room that stays slightly unstable (like a “thermal” in a desert area) – that buoyancy instability is convecting heat from the bottom to the top. That cools the bottom and heats the top. As long as you have spontaneous natural convection of that sort going on, you don’t have to wait for molecular diffusion to bring things closer in temperature. So I’m not sure how close to the “adiabatic” it would actually be after a while – convection is pretty complicated and chaotic and the approximation of a single smooth temperature gradient is surely not what such a real system would exhibit.
Arthur,
If the temperature is initially at the adiabatic lapse rate, there is NO buoyancy instability. Under these conditions, when a convective current (from the initial flow not having become quiescent yet) moves gas upward in a gravitational field. IT COOLS ADIABATICALLY, which means it would do nothing. There is NO convective heating upwards. The only mechanism for heating upwards is radiation, and we kept that out of this problem. That was exactly why I chose those conditions to show how there is no mechanism to move the heat from the lower level gas up. Even if diffusive conduction was capable (which I disagree) it is so weak and slow a process as to not be a factor.
Jonas B1,
Yes to your 3 a), but I am not sure how much of the wavelength range is not absorbed by the CO2, so other trace gases and the high clouds are part of the details. A highly absorbing gray gas assumption would clearly be a yes.
3 b) is complicated by the fact that only about 10% of the Earth surface temperature is due to greenhouse gases and clouds trapping energy. A much thicker atmosphere would increase the temperature, but the final effective location of the outgoing radiation is much more complicated if the outgoing radiation comes from the entire volume of the atmosphere and includes the surface. In addition, the higher temperature would increase the absolute water vapor content, so the wet lapse rate with an increasing fraction of water vapor also complicates the issue. The issue on Venus is much easier to consider due to the nearly fully blocking cloud layer and extremely high greenhouse concentration.
Arthur,
Please read this:
adiabatic equilibrium—A vertical distribution of temperature and pressure in an atmosphere in hydrostatic equilibrium such that an air parcel displaced adiabatically will continue to possess the same temperature and pressure as its surroundings, so that no restoring force acts on a parcel displaced vertically.
A layer in adiabatic equilibrium has uniform equivalent potential temperature.
Displaced adiabatically means you did not heat or cool it to make it move, and the imposed kinetic energy of motion is not large enough to dissipate into a measurable temperature.
SOD,
Are you still interested in this string. I do not want to just go back and forth with just Arthur. He has some stimulating arguments, but not enough to make this as interesting as it could be. It might even be better to start a separate string with a fresh starting point to avoid scanning long distances to see what was said and responded.
Definitely interested. A fresh start might be a good idea, I’m still trying to figure out whether I’m right or wrong before that though..
SOD,
I don’t know about you and others, but I found this type of discussion very stimulating and useful. I have slightly modified some of the ideas I had going in, and hope others have also, as points are discussed. In some cases, I suspect we will reach impasses where agreement is not reached. In many other cases, I think we can converge on a reasonable and hopefully correct agreement. These results can make clear the differences as well as agreements, and allow each of us to see why differences occur, and see if we can find evidence to overcome it. This is how science should be conducted. Taking positions behind walls and being negative to the opposite views is certainly not a good approach.
Arthur,
Solar heating of the top of the atmosphere of Venus inputs in energy and sets the temperature at that elevation. If an adiabatic lapse rate is established for whatever reason, the convection currents that carry atmosphere downward will be adiabatically compressed and heated (gravity to kinetic energy exactly as the room problem) and carried to the surface where the gas would heat the ground. After the ground was INITIALLY heated, no more heat would be needed except that lost to radiation and conduction upward. We agree conduction is totally unimportant at this scale, so radiation is the only thing the downward convecting currents need to overcome to maintain the hot lower level.
If the radiation mean path were 1 m, the delta T between radiation layers would be 0.078 K (the lapse rate per m). The forward radiation would be about 16,000 W/m2, and the back radiation about 15,993 W/m2. The radiation heat transfer would be about 7 W/m2.
If a 1 m2 convecting current this size near the ground) were carrying only 1 K excess temperature (at each height, due to adiabatic compression on the way down) from solar heating at the top of the atmosphere, and was moving downward at 1 m/sec, when it reached the ground level, it would be transporting 1.7E6 W of excess energy. I think this is more than enough to make radiation unimportant.
The question naturally arises how the convection currents occur, since the lapse rate is stable to upward buoyancy. The answer is DOWNWARD BUOYANCY from the top of the atmosphere at the higher latitudes and night side inducing currents.
Leonard,
The problem is that you don’t get vertical velocities of 1 m/s in the Earth’s atmosphere over large areas. For the much higher density Venusian atmosphere, the velocity near the surface would be much, much lower. Horizontal velocity at the surface is only ~2 m/s when the wind is blowing. The other problem is transferring heat to the surface from the atmosphere. Even if the atmosphere were transporting that much heat, you would need an enormous temperature gradient at the surface to transport even 7 W/m2. Average sensible heat transport upward for the Earth is 24 W/m2, but the Earth gets ten times more solar flux at the surface than Venus.
Vertical velocity in the Earth’s atmosphere is measured in fractions of a Pascal/sec at 500 hPa. 1 Pa/sec at 500 hPa for tropical atmosphere is 0.12 m/s. See this figure for the Earth:
According to the data from SpectralCalc using the HITEMP database for CO2 and H2O, the mean transmittance for the Venusian atmosphere (92 bar, 0.96 VMR CO2 and 0.00003 VMR H2O) for a 1 m path from 500-5500 cm-1 is 0.51. So the back radiation from the first meter is only going to be about 8092 W/m2, not 15,993 W/m2. It’s 11,511 W/m2 for 10 m, 14,748 W/m2 for 100 m and 16,006 W/m2 at 1 km and 16,102 at 10 km and beyond. So even for a path length of 1 km, the radiation deficit is still nearly 100 W/m2, not 7 W/m2 at 1 m. SO2 isn’t in the HITEMP database and it would make a contribution, but it wouldn’t change things by an order of magnitude. I’ve also used constant temperature for each path length, which is an error in the opposite direction. The atmosphere of Venus is nowhere near as opaque in the IR as you think.
The discussion of diffusion has brought back memories from college and graduate school studies in electrochemistry. In general, diffusion control can only be maintained on small scales for short times in the presence of a gravitational field. For larger scales, convection will always develop and at somewhat larger scales, that convection will always be turbulent. It takes a great deal of care to maintain laminar flow. For a 100 km tall column to be diffusion controlled only, the horizontal dimensions would have to be very small, cm or possibly smaller. 1 km would definitely be too large.
OTOH, the equilibrium lapse rate would be less than the adiabatic rate because eddy diffusion would work in both directions, as pointed out by Priestly and Swinback.
Leonard,
I think you’re doing the calculation incorrectly anyway. If the mean free path is 1 m, doesn’t that mean that I/Io = 1/e for a 1 m path? You have effectively 100 % % of the back radiation coming from the first 1 m. That would imply a mean free path less than 0.1 m, possibly much less.
“If the mean free path is 1 m, doesn’t that mean that I/Io = 1/e for a 1 m path? ”
Yes, it does.
However…
In illustrative cases (such as Optical Depth, used widely in stellar astrophyics: http://en.wikipedia.org/wiki/Optical_depth) and as the definition of the radiative surface of other atmospheres (e.g. Earth’s).
I.e. the effective radiating temperature of the Sun at any wavelength is given by the temperature at the depth in the atmosphere where the atmosphere is at 1optical depth.
At strongly absorbing frequencies (e.g Ha wavelengths), this happens earlier going down the atmosphere and so the effective temperature at Ha wavelengths is lower.
And, according to S-B law, the radiating energy which depends on the temperature to the fourth power is much lower.
Same thing with the earth’s atmosphere.
The use of 1 optical depth is because of the natural logarithms.
The chance that a photon will be absorbed at or before 0.5 optical depths before getting out is 1/e^0.5, a larger fraction, but there are fewer of them. At or before 2 optical depths, 1/e^2 which though smaller is a greater number. Weighted average mean is 1 optical depth.
So Leonard is right to use “1 optical depth” as the averaged effect of absorption and if his layers are set there (appropriately), then he’s basically following what G N Plass did in 1956.
Where his examples get hairy is that the optical depth changes with frequency…
I may not have explained that too well.
Oopsie.
The EMISSION from an atom in the first half an optical depth has a 1/e^0.5 chance of getting out to freedom. But that contains a smaller volume.
And so on…
I haven’t had any time this week so I have some catching up to do on this post, making sure I understand the comments that have been written and reading some of the references that were given.
DeWitt,
The choice of 1 m/s was just notional. Even at 10 cm/sec, the energy flux at ground level for a 1 K difference is 174,000 W/m2. This exceeds all of the radiation up even if there were no absorption. Also there is no reason the delta T should be limited to 1 K. 10 K is not an unreasonable variation. Also, the wind velocity is as much as 100 m/sec at higher altitudes, with vertical velocities sometimes a large fraction of that. However, the point I was trying to make is that convection is likely very dominate in energy transfer in Venus’ (and Earth’s) atmospheres. The actual lapse rate on Venus is almost exactly that of the dry adiabatic lapse rate when the correct value of Cp for CO2 is used at the actual temperatures, so the offset is small.
DeWitt,
Eddy diffusion (or eddy convection) in the room problem would be adiabatic due to the pressure gradient (except at the very start when the room was starting to fill with gas). No significant net heat transfer would occur, and the lapse rate would be the adiabatic value once large currents died down.
Leonard Weinstein:
I agree wholeheartedly. Perhaps you would be interested in us creating a post outlining our different points of view. That is when I have worked out what my point of view is..
I was thinking that I could write one part explaining my view, then you could add the second part and explain your point of view and what was wrong with mine – then readers could have a useful summary without having to go through 500+ comments. What do you think?
I’m thinking that my point of view is quite close to Arthur Smith’s – but if it turns out differently then Arthur would also be welcome to write a section.
SOD,
Sounds good. I would be glad to give it a try.
Leonard,
High altitude is not the surface. The jet streams in the Earth’s upper atmosphere are also pretty fast. According to Wikipedia, a wind speed of 398 kph has been measured, although it’s usually closer to 100 kph. You also can’t come within many orders of magnitude of transferring 176,000 W/m2 if the temperature difference is only 1 K. You can’t arbitrarily change the surface temperature either because it’s fixed by radiative equilibrium so it must be as warm or warmer than the gas above it. A difference of 1 K would be 90 W/m2 less emission. Which also means that heat must flow from the surface up, not the other way around.
I finally got around to doing the radiative flux calculations. I sliced the atmosphere into 10 m layers for the first 1 km and assumed a blackbody source at 722.2 K at 1 km and a surface temperature of 730 K (7.8 K/km). I used the transmittance at the surface because SpectralCalc has a nasty habit of changing the number of data points when you change the pressure. The net radiative flux upward from the surface is ~5.8 W/m2. If the value of 17 W/m2 for short wavelength solar surface irradiance is correct, then radiation accounts for ~34% of the net flux upward, leaving the rest to convection.
Note that this flux cannot be transferred to the surface by conduction. That can only happen if the surface is cooler than the atmosphere above it. If that happens then the surface has to also gain heat by radiation. Since it isn’t losing heat by radiation or convection, it must warm until it radiates as much as it receives. But then it will be as warm as the gas above it and it can’t gain energy by convection. But then what happens to the solar flux? It may be small, but it’s there.
So we’re back to the greenhouse effect again with incident solar radiation determining the surface temperature.
A side note: I did the calculations in Excel. WinXP Pro (32 bit) and Office XP couldn’t deal with the very large amount of data (the dreaded insufficient resources error). Win7 (32 bit) and Excel 2003 could. I was pleasantly surprised. I may repeat the calculation with a VMR for CO2 of 0.096 instead of 0.96. I suspect I’ll have to use a thicker slice if I do that.
“Note that this flux cannot be transferred to the surface by conduction. That can only happen if the surface is cooler than the atmosphere above it.”
No *net* flux..
🙂
Oh, I would suggest too that you get R for windows.
http://www.r-project.org/
Used a lot in Universities and in science based businesses (cheaper than Mathematica, even without the cost of license compliance!)
I have it. Two problems. I’m not a very good programmer and 32 bit R has fairly severe memory limitations too.
DeWitt,
You keep forgetting adiabatic compression. If the gas is warmer than the local value at any height (say 310 K where the surrounding was 300 K at a large altitude), and the convection currents brought it down to the surface, it would still be 10 K hotter than the surface. This would heat the surface. As long as convection can carry as large a heat flux down that can match the radiation losses, the hot ground can be maintained without solar radiation reaching the ground. If the current were a pressure driven pattern making a large enough current size the edge losses by heat transfer on the way down would be small enough so that most of the excess temperature would be retained all the way down.
If it’s 10 K hotter than the surface, where’s your adiabatic lapse rate? The surface temperature of Venus is very nearly constant. The diurnal temperature range is effectively zero. Unless the surface heat capacity is very high, which seems unlikely, then the atmospheric temperature profile near the surface can’t change much either. A change in surface temperature of 0.01 K changes the radiant flux by nearly 1 W/m2.
The surface of Venus can’t be cooler than the atmosphere above it. That would be a a temperature inversion and that only happens if the surface can radiate some energy directly to space. That can’t happen on Venus.
Suppose the surface were cooler than the atmosphere resulting in a net transfer of 50 W/m2 of sensible heat from the atmosphere to the surface. If that were the case, then the surface must also see a net transfer of radiant energy from the atmosphere to the surface because the atmosphere is warmer than the surface. The surface can’t radiate that 50 W/m2 away and stay cooler than the atmosphere above it. You can’t have any sensible heat transfer to the surface on average. The transfer must be in the other direction because there is incoming solar radiant energy that has to be dealt with.
DeWitt,
When you are at 750 K, 740 K is considered near the same temperature. When they say the surface temperature is near constant, they mean it does not vary a lot. I don’t know the actual numbers I am just trying to point out the fact that convection can carry a lot of energy, and could easily replace energy on the ground lost with the modestly small radiation losses. Also, there is surely some solar energy reaching the ground, but again the point I was trying to make was that it is NOT necessary for solar energy to reach the ground for it to be hot (adiabatic compression of convected atmosphere does that). That is just another source of energy that participates in making convection and radiation to keep near the adiabatic lapse rate. I was not intending to show exact numbers. It is likely that with no solar energy reaching the ground, the ground would be a few degrees cooler, but not much.
As to your sensible heat transfer, the adiabatic lapse rate heats the GAS not the ground. If we assumed there were no solar heating of the ground, it is possible for the ground to be heated to a small amount cooler than the gas directly above, even at equilibrium, so that there could be some heat transfer. The distance over which that inversion might occur may be very small (cm) and the temperature difference a tiny fraction of a degree. The black body radiation out would not all be absorbed by the CO2, and that amount of penetrating radiation could carry out the small amount of heating. However, with some absorbed solar heating occurring, the inversion would not be necessary once the ground reached close to the local level value of the adiabatic lapse rate or a small amount higher, so the adiabatic compression may just keep the atmosphere lapse rate steady and not transfer heat to the ground. It all depends on the level of solar radiation to the ground. The point is that solar heating of the ground is not necessary for the hot ground, it works either way.
DeWitt,
You also mentioned conduction. The conduction is too small to be a player except very close to the ground. However, again it is not the temperature gradient that determines heat transfer, but the potential temperature gradient. Since the adiabatic lapse rate is so small (0.008 K/m), the difference between the two definitions is not significant for realistic cases of importance. However, over large distances, it is the factor that makes the high ground temperature what it is.
Sensible heat transfer between the atmosphere and the surface can only happen by conduction through a boundary layer. What convection does is to keep that boundary layer thin so the temperature gradient can be large. But it’s still conduction.
DeWitt,
I thought that is what I said (“except very close to the ground”), but your version is clearer.
Leonard,
I don’t know why this has eluded me for so long. I knew that forcing from CO2 was higher in the tropics than the Arctic because the atmosphere in the tropics is thicker, but somehow the obvious connection didn’t occur to me until now.
Obviously, the thickness of the Venusian atmosphere is very important, dominant in fact. I haven’t run the numbers yet, but I suspect that when I reduce the CO2 VMR from 0.96 to 0.48, the forcing at the surface will only be a couple of W/m2 and the resulting temperature change will be fairly small. If you added sufficient nitrogen to the Earth’s atmosphere to double the mass and changed nothing else, the surface temperature forcing would be very large because the altitude for emission to space would nearly double. It would almost certainly be large enough to cause a thermal runaway. I suspect that the range of the mass of the atmosphere required to keep water liquid at the surface of the Earth is, in fact, quite small. SETI is looking more and more like a waste of time and money.
DeWitt,
Any possibility of a very large thermal runaway for Earth (hundreds of degrees) would have to be caused by a runaway water vapor condition. The higher the temperature becomes from the combination of a taller atmosphere (due to hypothetical higher mass) with a reasonable amount of greenhouse gas, the higher the water vapor partial pressure will be, and the higher the fraction of total pressure it will be. Since the oceans have such a large available source to evaporate, to add to the atmospheric mass in a feedback mode, this could lead to runaway until the oceans fully evaporated, producing a huge atmosphere. I don’t think just doubling the present total mass would even come close to that critical point, because the present greenhouse gas only adds about 33 K compared to an atmosphere with no greenhouse gas (according to accepted levels), and doubling the mass would increase the altitude much much less than double. At some point though, with enough mass added, it could possibly reach the runaway condition. However, for Earth, that is not a realistic fact with the atmosphere mass we presently have. Even if the amount of greenhouse gas increased 10 times or more while maintaining the approximate present total mass of the atmosphere, the only effect on ground temperature would be due to a small increase in effective increase in altitude of outgoing radiation. This slight increase in altitude combined with the adiabatic (wet or dry) lapse rate, would only slightly raise the temperature a few degrees K, which is not near a large runaway.
There is a relatively small shift up in temperature possible related to decreasing the albedo of the Earth by melting most of the polar sea ice. This not as big a shift as the above version, and I would not call it a runaway, but a state shift, and would only correspond to a few degrees K (that condition existed several time in geological time scales). However, the present increase in Antarctic sea ice has almost exactly matched loss in Arctic sea ice, so this is not a present factor.
You are a pessimist De Witt; what about Europa?
I have a feeling that an equlibrium state of our model atmosphere is at neither thermal nor ‘convective’ equilibrium. Or to put it in another way, it is at dynamic equilibrium. The reason for this comes from the following assumptions (for an atmosphere with defined mass):
* In order to be convectively stable (no mass transfer), the pressure profile must be set by the gravity field. Or to put it in another way, if we look at a certain level in the atmosphere, the pressure under it has to equal the ‘weight’ of the gas above it. Otherwise pressure vs gravity is not equal and we would have movement of mass either up or down depending on which is higher – gas pressure below or weight above.
* If we consider that in an atmosphere, pressure is determined by large part by the mass of air above it (weight again), we will also have a certain density profile that would be needed to achieve this pressure profile (otherwise the change in mass above wouldn’t change the way we need it to in order to achieve the pressure gradient).
* As we have defined two of the three variables in the ideal gas law, pressure and density(density is considere to be n/V*R at the moment) the third one, temperature, ought to be a function of those two. While it is possible (I haven’t done any calculations) that it would give us a constant temperature, I believe it to be somewhat unlikely.
An important thing to note here is that if we remove all methods of heat transfer besides convection we can have an equlibrium state which is not isothermal. There is no violation with the zeroth law because top of the atmosphere and bottom of the atmosphere are thermally isolated. In order for the zeroth law to make any sense there has to be heat transfer and as we’ve shown that convection doesn’t happen any more, there is no heat transfer.
Now to more realistic situation where there is heat transfer.
If my guess is correct and the corresponding temperature profile is not constant we would get a situation where all static solutions would be unstable, as long as there is any amount of heat transfer. The reason for this lies in the ideal gas law and second law of thermodynamics. Ideal gas law says that we can’t change the temperature without messing up density and pressure, which means that any change in temperature will cause convection and the second law says that the temperature will change (Heat *will* move from hotter to colder areas). So we have the situation where neither is happy with any given solution and hence the stable one is determined by the balance between the speed of convection and the speed of thermal heat transfer.
So my understanding of the situation at the moment is that we have two extremum states between where the actual temperature profile lies. The first state is convectively stable state (no convection) which is achieved if thermal conductivity is zero, and the second state is isothermal, which requires thermal conductivity to be infinity (which is ofcourse impossible as well as things can’t really move faster than the light, at least in this context).
I must admit something seems terribly wrong with this line of logic at the moment, so I would very much appreciate where I’ve gotten lost.
Mait,
The pressure is the weight of the gas above a given location. However the temperature profile and density can vary over a wide range. If the lapse rate is larger than the adiabatic lapse rate, buoyancy forces make the gas unstable and cause currents trying to lower it. If it is at or below the adiabatic lapse rate, the atmosphere would be stable wrt buoyancy, but likely would still have convection currents from lateral temperature variations (latitude and night/day differences). The density would vary with both temperature and pressure, so a range of values is possible. The net effect of realistic forcing causing convection tends to drive many actual atmospheres toward the adiabatic lapse rate, and that is what Earth and Venus have to at least near the tropopause. Mars has such a low density atmosphere that convective forces do not reach the adiabatic lapse rate, so it’s lapse rate is lower.
How can density vary over a wide range if the change of mass with height determines the pressure profile. As soon as we change the density in this situation, we change the mass distribution and hence the pressure profile – which means we have an unstable system.
I’m actually guessing the downward pressure is actually dependent on temperature as well to some extent which would change the conditions considerably. I just haven’t seen any equations or something of the sort to explain how temperature might play a role in this.
Mait,
If the quantity of gas in the atmosphere stayed the same, the pressure at the ground would be exactly the same. If the temperature profile changed, rho=P/RT shows that increasing the temperature while holding pressure constant changes the density. Since the mass is the same and the temperature is different, the density is different, but the only way that can happen with constant total mass is to make the height of the atmosphere different by the exact amount to preserve the total mass. The net effect is to change to pressure profile so that except for the ground level, the pressure would be different at different altitudes. Thus your statement that pressure at a given altitude does depend on temperature is correct except at the ground level. The equations are very straight forward. Wikipedia or other sources can give you as much detail as you need.
Mait,
The temperature profile would be the adiabatic one if there were no forcing large enough to prevent it. However if forcing such as radiation was large enough, the temperature profile could be any thing between the adiabatic lapse rate and near constant temperature. The density has both a pressure and temperature term in the equation rho=P/RT. There is a unique pressure profile for each temperature profile, and the effect of gravity would be the same for all profiles, i.e., the pressure at a given height is due to the weight of the gas on top of it. A unique solution for both pressure and density comes from any assumed or measured temperature profile, but these vary from each other if the temperature profile varies. There is no instability, only different solutions.
You are right ofcourse that we can have different sets of parameters (otherwise there would only be one possible temperature for the atmosphere I think). I think I got a bit lost with the gas pressure in a gravity field. I’m guessing the upward pressure of a gas in a gravity field is dependent on temperature (previously assumed to be equal in all directions).
However I still disagree with the direction you’ve chosen. Convection is driven by changes in pressure not temperature, hence it would be more correct to state that pressure levels need to meet certain criteria which are set by the gravity field. Density and temperature can be derived from this profile.
This still doesn’t change the final conclusion that much, which is that a realistic atmosphere can never actually be at either thermal nor ‘convective’ equilibrium and that the lapse rate is going to between the lapse rate set by the necessary pressure profile (I’m guessing that to be the adiabatic lapse rate) and isothermal. The exact point at which it settles depends on thermal conductivity and the speed at which convection can take place (pressure balance can be restored).
Mait,
The average lapse rate for Earth’s troposphere is almost exactly the appropriate wet adiabatic lapse rate except for a few special exceptions (such as near the poles). The lapse rate for Venus’s troposphere is very near exactly the dry adiabatic lapse rate when the correct value of Cp is used. There is no significant in between for these cases. Other planets have to be considered on their separate conditions, but we were talking about Earth and Venus.
Gravity does not determine the pressure distribution separately from the temperature profile. The temperature profile plus gravity plus total mass of atmosphere determine the pressure distribution. The temperature profile is determined by the balance of forcing compared to feedback restoring forces for an adiabatic lapse rate.
The basic restoring forcing is a weak pressure field caused by temperature differences. If enough solar insolation hits and is absorbed by the ground, local excessive lapse rates may occur and buoyancy effects would also cause mixing. Radiation from the ground (and different layers of gas) are the main forcing that tends to decrease the lapse rate, but does not succeed in overcoming the restoring forcing on Earth or Venus. Most of the restoring forcing is caused by mixing due to lateral insolation and upper atmosphere heating difference, which cause the atmosphere to expand or contract enough to cause convection currents (wind and turbulent mixing). The driving pressure differences to create wind and turbulent mixing are generally very small, so it does not take much to force these currents, which mix the atmosphere enough to keep it near the adiabatic lapse rate.
I don’t think you quite understood what I was trying to say. Basically, I said that if something pushes you up harder than other stuff is pulling you down, you will go up and vice versa. As pressure and gravity are the only forces I can come up with that we have to consider in our environment at this point, they have to play nicely together in order for stuff not to go up or down.
Mait,
I more than got it.
Why is it cooler on a hot day under an umbrella? After you figure that one out, why is it even cooler under a light colored umbrella?
Eli,
What kind of question is that supposed to be? What point are you trying to make? By the way, if is a hot day and the sky is solid clouds, the umbrella has little effect. Temperature is a result of forcing and response. The forcing would be convected air temperature and input solar flux (if it is sunny) without the umbrella. If an umbrella is used you are blocking one of the forcings. So what? What does a light color for the umbrella have to do with anything?
Eli,
The light umbrella vs dark is just different absorption of sunlight and re radiation due to umbrella absorption and possibly emission coefficients. So what?
Leonard Weinstein:
I’ve had the chance to catch up, and to read the paper that DeWitt Payne provided (by Priestley and Swinbank) and to think a little more.
It’s probably worth the two of us writing up what we think – and why – so that 500+ responses don’t need to be studied for someone to work out what we think and why.
Before we do that I’ll just run an idea past you based on one thing you’ve said most recently (which crystallizes the concept) and note what I think you think and what I think in response.
This is because I keep wondering if I’ve missed the point you are making.
From July 15, 2010 at 5:27 pm
dQ=0 – or no exchange of heat in a rising parcel of air – is relevant when a parcel of air rises. (I’ll deal with just rising – expanding – cooling to keep it simpler).
What I think you think – there is always some movement of air and this creates the condition of an adiabatic expansion & cooling. This allows an exchange of heat and so the atmosphere is always pushed back to the adiabatic equilibrium.
What I think – under the circumstances when the actual temperature profile (environmental lapse rate) is less steep than the adiabatic lapse rate there won’t be any movement by “natural convection”. So air that is moved, let’s say just by pressure gradients will simply sink back to its original position long before conduction equalizes any temperature between the air forced to rise and its surroundings.
And therefore convection is a process which can move heat upwards, but not downwards. So if the ground, or lower atmosphere, is hot enough for whatever reason – convection will move heat up.
If the ground, or lower atmosphere, is not hot enough – convection won’t operate. Random movements of air, and pressure differentials, will only push air into positions where it will sink (or rise for the opposite case) back to its original position with little or no exchange of heat (because conduction operates so slowly).
So, in summary, I agree 100% that air that is moved by convection will change its temperature adiabatically – and we all agree – but I believe that convection won’t actually re-distribute any heat if the environmental temperature profile is less steep than the adiabatic lapse rate.
I think we are probably still in the same disagreement as when we started?
Did I summarize your point correctly? (Even if not fully)
If you are still interested I’d be happy to try and jointly write an article explaining our points of view – email me at scienceofdoom [at] gmail.com so we can work out the mechanics. I’m happy to write the first side and let you write your section subsequently before we publish it.
Revised slightly:
What I think you think – there is always some movement of air and this creates the condition of an adiabatic expansion & cooling. This allows a subsequent exchange of heat with the surrounding atmosphere and so the atmosphere is always pushed back to the adiabatic equilibrium.
SoD
SoD
Let me hark back to the arguments I made near the start of this thread, because I think they are relevant. Yes, sub-adiabat air is stable to convection. What that means is that up-down motions extract kinetic energy. This energy goes into pumping heat. The pumping is downward, whether the air itself is moving up or down.
Despite the stability, air is always moving up or down – turbulent eddies. So heat is being pumped, and it’s a question of where the energy comes from. The answer is from other heat transfers, which have a heat engine effect,
The downward heat pumping is actually set out in the first sentence of the abstract of that P&S paper. With lapse rate below the adiabat, potential temp rises as you go up. So turbulent motions force heat down.
SOD,
Why do you think convection driven by buoyancy is critical? Do you believe there is no mixing from convection driven by any other source? The lateral and circulating winds caused by uneven temperatures at different latitudes and by day/night variation cause mixing and heat transfer that tend to restore the adiabatic lapse rate. If there were no winds or turbulence the lower lapse rates could form and be stable, but that is not what happens. The convection can be formed without solar energy directly reaching the ground by reverse buoyancy. i.e., by cooling at the upper edge of the atmosphere causing a downward flow of atmosphere which then forms a circulation pattern that reaches the ground and an up draft that rises to the regions of higher warming at the edge of the atmosphere. However, there probably is some solar energy reaching the ground, and even though this was not needed for the mixing to occur, it enhances it. The question of whether it was needed to come close to the adiabatic lapse rate depends on the details, but there clearly is a path to the convection without it. If there is adequate down flow, the adiabatic compression heats the dropping gas to the very high temperature, and this can maintain the hot ground as I have described several times.
Thank heavens you’re here Nick; eli is picking on me; he asked me this umbrella question over at Jo Nova’s. I’m having enough trouble following the discussion without having to interpret it through some esoteric analogy or application of what ever processes you guys think apply.
I did do some research on umbrellas but gave up when I discovered that there were umbrellas made out of human skin; do you think that’s what eli meant? Put in a good word for me.
Alas Coho, I looked into that thread, but it’s too complicated for me, tho I don’t think M of B is a member of the H of L.
But this is a good one.
Yes he’s a Lord without a house; perhaps we can put him in Leonard’s tall room; failing that one of eli’s umbrellas may stop him ascending adiabatically.
Nick Stokes:
I should have made it clearer that I was talking about a clearer description of the process which allowed us to see more clearly the difference between Leonard Weinstein and myself. This was the comment from July 12, 2010 at 3:01 pm.
This may be a reason why this thread and it’s parent were created:
http://wah-realitycheck.blogspot.com/2008/09/khilyuk-and-chilingar.html
The idea that the lapse rate is causing warming is a repeated scientific paper published in the less reputable journals every now and then.
Mark,
I think your comment on “less reputable journals” is a very bad choice of words. However, you clearly don’t get it. The warming is caused by the SUN! the lapse rate is a result of adiabatic compression of the atmosphere as we go lower. The greenhouse gas or clouds set the altitude of balance of outgoing and incoming energy, and thus the temperature at that altitude. The lapse rate results in the hot ground under those circumstances, but it is a mode of heat trapping, not heat generation.
Mark,
You really need to look at the room model we discussed in great detail to understand how a cool gas gets hot just by changing altitude, and makes the ground hot.
Leonard Weinstein:
In your comment from July 15, 2010 at 5:27 pm you suggested that there is a tendency to create a convective lapse rate once any instability appears (what I think you think). You described it in some detail and I might have misunderstood the context, or – like me many times in this discussion – you might have made a point that you don’t now feel is really the essence of your case.
If I have got your comment wrong or out of context, let me know. I have been relying on that comment to give me insight into “what I think you think”.
Onto what I think – “Do you believe there is no mixing from convection driven by any other source?” – of course not. I have already said this. But what happens after a pressure differential drives convection depends on the environmental lapse rate vs adiabatic lapse rate.
Perhaps you mean something different by mixing?
SOD,
I think you at least partially misunderstand what I am saying. I am saying that the equilibrium temperature profile in an atmosphere is the adiabatic lapse rate. I also later concluded that this made no difference, except at the ground, for molecular conduction since that is so slow a process for real forcing. Any forcing that tends to lower the lapse rate from the natural level of the adiabatic lapse rate, such as radiation up, has to be balanced by convective mixing that carries energy from the location in the atmosphere, where energy balance forces a specific temperature to occur, downward to balance the radiation going upward, or the result will be lower than the adiabatic lapse rate. The net for balancing is zero average energy transfer (up =down), and near balance back to the adiabatic lapse rate. It is not an instability but a forcing from radiation that caused the offset. I specifically agreed with “But what happens after a pressure differential drives convection depends on the environmental lapse rate vs adiabatic lapse rate”. If the forced convection is too weak, there will be a lapse rate lower than adiabatic, but Earth and Venus are both very close to their appropriate adiabatic lapse rates, so the convection is adequate.
SOD,
The first law of thermodynamics, plus the assumption of dQ=0 results in the derivation of the adiabatic lapse rate ( http://pds-atmospheres.nmsu.edu/education_and_outreach/encyclopedia/adiabatic_lapse_rate.htm ). Thus then misusing the zeroth law to say that dQ=0 forces a constant temperature is wrong. The zeroth law says that if you measure the temperature at two locations, and the locations were put into contact there would be no heat transfer. This is how a thermometer is shown to represent temperature. However, this has nothing to do with the fact that the adiabatic lapse rate is in fact the condition of no heat transfer in the absence of forcing. The equations of thermal conductivity that include delta T MUST also include the effect of gravity to be applicable for the present case. This means use the “potential temperature”, not measured temperature at a one location.
“I think your comment on “less reputable journals” is a very bad choice of words. ”
Got any substantiation of that assertion? Didn’t see any. But they aren’t a reputable journal for Climate Science and they’ve managed to throw up a couple of real big blunders. Fred Singer is on the editorial staff… ’nuff said.
“However, you clearly don’t get it.”
Here we have projection, I reckon.
“The warming is caused by the SUN!”
BINGO!
“the lapse rate is a result of adiabatic compression of the atmosphere as we go lower.”
But (and this is why that paper is so very wrong) that has nothing to do with the temperature at the surface.
However (and this is where YOU clearly don’t get it), the reason why this adiabatic lapse is given such tremendous visibility is because a peoplewhodontagreewithus-ist [moderator’s note – check the etiquette otherwise whole comments may start being deleted] can go “and therefore the pressure causes the temperature at the surface of the earth. ERGO, AGW is false! Hallelujah!”.
“The first law of thermodynamics, plus the assumption of dQ=0 results in the derivation of the adiabatic lapse rate”
More correctly, the hydrostatic equilibrium (see Rabbett: http://rabett.blogspot.com/2008/08/life-is-too-short-to-occupy-oneself_21.html ).
Mark,
OK
SOD,
Let me make it clear. I do not believe that a lapse rate less than adiabatic lapse rate causes mixing to spontaneously occur. That is not what I ever said. I always said that any processes that cause mixing tend to drive unbalance from the adiabatic lapse rate back toward the adiabatic lapse rate, and that these forced mixings are caused on planets by latitude and day/night input energy variations.
SOD,
I think I need to make a point here. You seem to think convection down can’t transfer heat nearly as well as convection up caused by buoyancy since molecular conduction is so slow. That is not how the atmospheric heat transfer works. Convection along with turbulent mixing brings the different temperatures close enough for molecular conduction to do quite well. If the ground is hotter than the lapse rate, and radiation up occurred, the ground would have to cool, since nothing is able to heat it to replace the loss. The ground has to be at or below the lapse rate to be maintained. There is no mechanism other than radiation to make it cooler than the ground level of the lapse rate. If the lapse rate is very close to the adiabatic lapse rate, that shows that downward convection and heating match radiation loss.
“Convection along with turbulent mixing brings the different temperatures close enough for molecular conduction to do quite well.”
Citation Needed.
Mark,
The scale, density, and speed of atmospheric convective flows produces turbulent mixing (very high Reynolds numbers for the shear and BL flows and stream tubes. Turbulent mixing results in molecular conduction to do quite well in local heat transfer. Any book on fluid mechanics will get you there.
It does get you to turbulent mixing.
What it DOESN’T get you to is how this allows molecular conduction to do quite well.
Taylor-Aris Theory. Here’s the paper by GI Taylor on shear-enhanced diffusion and the relation to turbulence.
The point is that the kinetic theory of temperature requires that the exhibition of temperature is by average velocity.
However, in a gravitational field, anything moving up will lose kinetic energy to potential energy.
Therefore any gas molecules going up will lose “temperature”.
But don’t forget the pressure, which acts as a force to counter gravity – the net effect of collisions on individual molecules is to produce net upward acceleration countering gravity. So the net effect, if the gas is not moving as a whole, should be zero, no net gain or loss of “temperature” in vertical motion of individual molecules (including both gravity and collisions).
“But don’t forget the pressure, which acts as a force to counter gravity”
The pressure is DUE to gravity.
The weight of all those other molecules higher up.
Arthur,
Collisions cause pressure and collisions prevent gravity from collapsing the gas. However, that in no way describes the temperature profile. Saying the gas is not moving as a whole implies constant temperature is invalid. If you consider molecules or small gas packets, the only condition that is unconditionally stable when there is no significant forcing is the adiabatic lapse rate.
Mark – actually, pressure is equal to “the weight of all those other molecules higher up” only under conditions of hydrostatic equilibrium. The actual cause of the upward pressure force that counters gravity is ultimately the floor of the container, the surface normal force. Which individual molecules experience when hitting the floor and bouncing back. That gets propagated upward through the gas as the forces associated with pressure – inter-molecular collisions. The pressure differential (in hydrostatic equilibrium) balances the gravitational potential so the net force experienced by the average molecule is zero – there should be no additional heat flux associated with the gravitational force once you’ve reached hydrostatic equilibrium, whatever the temperature profile is.
The point there being that pressure is not relevant to the kinetic theory of temperature. Molecules only see collisions with neighbours with different kinetic energies.
Temperature, pressure are macro level shortcuts.
Mark and Arthur,
Pressure is only a result of the average kinetic energy of each molecule times the density of molecules at a location. Gravity does not directly enter in pressure except through its forcing to determine the density for a given total mass and temperature profile. Molecules collide with other surrounding molecules whatever their kinetic energy as long as their paths meet. Definitions can be taken different ways but I would say that pressure does not counter gravity but is a consequence of gravity, total mass of gas, and temperature profile. You can say this means pressure counters gravity, and I would not disagree except it implies to me a different cause and effect sequence.
Arthur, you keep insisting the net result of gravity is not to affect the temperature profile, so that constant temperature is the natural result. It is true that any lapse rate between adiabatic and constant temperature results in a stable profile from buoyancy effects if there is no other forcing, but that is not the same as saying the constant temperature is the natural profile. In fact if you had a highly thermally conductive gas, the temperature profile would always move toward the lapse rate. Any forced mixing, and the actual lapse rate goes toward the adiabatic lapse rate anyway. Don’t you wonder why it doesn’t go toward the constant temperature?
“Pressure is only a result of the average kinetic energy of each molecule times the density of molecules at a location.”
WRONG!
Pressure is the result of all the other molecules hitting each other and bouncing off any walls.
Using the law of large numbers (avogadro’s number is REALLY big!) and statistical techniques (which talk of emergent trends and expectations), you can infer several laws that can use the pressure as defined by that.
But, just like the image of your retina is not “the result of the light being focussed on your retina”, pressure is NOT what you say there.
If one wall was taken away, that surface would be a free surface and molecules would leave the box forthwith.
They would be slowed down in that exodus by collisions with any gasses outside that box, however, and they would also be replaced by ones that they passed on the way out, where they were trying to get in (not “trying” in an anthropomorphic sense).
Therefore you get pressure equalising and diffusion.
But the molecules are all just happily jumping around, ignorant of these things called “pressure” and “density”.
Leonard, try this:
Take all the molecules of temperature T. They are all going the same speed, the speed appropriate with thermodynamic laws:
1/2 mv^2 = kT
Then put a potential field there so that any molecule at one wall is in a higher potential field than the molecules at the opposing wall.
mgh + 1/2mv^2 = constant throughout.
(so you can see that without the potential field, all would have the same velocity).
When you add this potential field, the gas at one end is going to go slower.
Solve this and find the velocity average as you go from one end of the box to the other.
Now convert that velocity back to temperature by the same method:
1/2 mv^2 = kT
What do you get?
Mark,
A gas in a container causes a pressure on the walls. However, the pressure in the middle of an atmosphere has no walls. Are you saying the gas in the middle of the atmosphere has no pressure? Look I don’t want to argue basic fluid mechanics (that is my field of expertise). You don’t have it correct.
On the imposed potential field thing, if your box (with no forcing) was tall enough and you waited long enough, the molecular velocity (thus measured temperature) would adjust by diffusion if necessary (very slow) or by convective mixing if available (much faster), and go to the adiabatic lapse rate. If you then removed the potential field, the conduction and convection would go toward the constant temperature (and it would take some time to do so). So what?
“Arthur,
Collisions cause pressure and collisions prevent gravity from collapsing the gas.
Correct.
“However, that in no way describes the temperature profile. ”
Wrong.
“The actual cause of the upward pressure force that counters gravity is ultimately the floor of the container, the surface normal force”
I know what you *mean* to say, but you’re not saying it.
Gas clouds (and gas giants, and stars) have a pressure in space.
Despite having no floor.
The pressure is due to the weight of all those other particles above.
The ones coming down will gain energy and when they bounce off another molecule down there, they’ll hit it harder.
Because it’s gained potential energy on the trip.
Ones going up will hit another molecule up there more gently because it’ll slow down in climbing that potential, losing kinetic energy on the trip.
Pressure (defined in the kinetic theory as “how hard a molecule hits you”) at the upper side of a defined layer is less than the pressure at the lower side.
No need for a surface.
Just a potential energy field that changes with linear distance along a defined local axis.
And in bulk, because “pressure” is based on a continuous distribution model of a gas, this is realised with giving the pressure at any point the weight of the molecules above it.
Both views give the same answer.
And they have to.
In one, it’s individual molecules barreling past each other and whacking into obstructions. Here it’s potential energy gained (mg x dh + 1/2 mv^2, solve for dp, momentum which is proportional to pressure)
In the other, it’s a stratiform infinitesimally thin layer that doesn’t pass through another but abuts it firmly, in which case, (rho x g x a x dh integrated because each layer is incompressible becomes MgT (thickness T) ).
Well, self-gravitating systems are a bit different – yes, there’s no floor, but the gravitational potential goes to zero gradient at the center (no g force) since there’s no mass inside to pull, and in a sense there’s a “floor” of r = 0 (molecules don’t “hit” it in the sense of any physical change in momentum, but in terms of radius r from the center of mass, they do “bounce” in a similar way).
Anyway, your statement implying that “pressure at any point [must equal] the weight of the molecules above it” applies only to a non-moving system, with forces balanced. The actual value of the pressure is determined by *local* temperature and density, and does not necessarily equal that “above”. Density is a consequence of the confinement (walls, floor, or self-gravitation).
For a system not quite in dynamical equilibrium, temperature and density, and therefore pressure, can fluctuate, which is why we’ve been talking about parcels of gas moving around – the 2 forces making things move are gravity and gradients in pressure. Once things settle down, those forces balance, but the pressure is determined by gravity only in that equilibrium state.
Well short version Arthur is “wrong”.
Your problem is that you’re saying “this is THE ONE RIGHT WAY to consider it”.
But pressure, temperature and all that stuff done in thermodynamics are all shortcuts. The molecules don’t know what pressure they are under.
What you say is right. Where you’re wrong is saying that it is the One True Way to consider it.
THAT is wrong.
Leonard:
“A gas in a container causes a pressure on the walls.”
Yes.
“However, the pressure in the middle of an atmosphere has no walls. ”
Yes.
“Are you saying the gas in the middle of the atmosphere has no pressure?”
No.
“You don’t have it correct.”
Yes I do. At least DK isn’t in effect.
“On the imposed potential field thing, if your box (with no forcing) was tall enough”
NO NEED to have it “tall enough”. No need to have height at all. E.g. charge up two opposite walls and use ions rather than neutral gasses.
“and you waited long enough, the molecular velocity (thus measured temperature) would adjust by diffusion”
Nope, you wouldn’t have to wait long enough.
It would change at the speed of light.
” if necessary (very slow) or by convective mixing if available (much faster),”
No need. It’s not that the temperature is moving around, it’s that what WAS temperature is now partly expressed in terms of potential energy.
Why do you think that diatomic molecules use 5/2RT when monatomic ones use 3/2? Why triatomic molecules have 7/2?
“If you then removed the potential field, the conduction and convection would go toward the constant temperature (and it would take some time to do so).”
No it wouldn’t: it would be as instant as special relativity allows.
“So what?”
You have it wrong. If that’s the case, then you may not see the what.
I thought I posted it here, but anyway.
With the gedanken experiment above, when you come to putting a potential energy field in, make the potential field balance out to zero, else you’ve removed energy from the system. That will affect the system since bulk matter has to move.
Mark,
I was talking about gravity.
So?
A gravitational potential energy field is always negative, therefore adding one in subtracts energy from the system.
However, this is not the only way to get a potential energy field.
Go on, try the thought experiment.
Here’s a hint: you get an adiabatic lapse rate.
This despite the fact that the gas started up at the same temperature and NO energy had to move away from where it was in the molecules.
The bare fact is that your assertion is wrong. It is not that thermal energy has to drop down from higher to lower levels but that by the mere fact of being HIGHER UP in a potential field, the gas exhibits lower temperature.
Hell, there’s no need to set that scheme up.
Consider:
Average molecule at temeprature T at height h. Velocity is what?
Lets say it moves upward, doesn’t hit anything else on the way, so no way for this to be called conduction.
This average molecule is now at height h + dh. Velocity is what?
Temperature T + dT from MB-equation is what?
You will find that it’s colder.
An adiabatic lapse.
After all
a) it’s higher
b) it hasn’t surrendered any energy to the rest of the gas molecules
dQ=0.
N’est pas?
And nothing had to be transferred around (as long as all other molecules it finds have the same mass).
Just did a rough calculation and I get an N2 atmosphere with a lapse rate of 13C per km.
Our atmosphere isn’t just N2, but I can’t find any authoritative source on whether that’s expected to be over or under.
Gut feeling is that an N2 atnosphere would have a higher lapse rate because there are triatomic (and bigger) molecules, and they’d hide energy in vibrational states at the same height.
I wouldn’t have thought THAT much higher, though.
Mark,
If you read my earlier comments, you will find that you have made some of the same points I did. I pointed out the adiabatic lapse rate is the condition of no heat transfer with molecular motion or parcel of gas motion, and was thus the equilibrium state. It is a constant temperature profile in the same gravity as the adiabatic case that requires an energy transfer during molecular motion, and thus constant temperature is not the equilibrium state. Turning potential fields on and off is different, but that is not the cases we have been arguing this site.
The definition of the pressure of an ideal gas is P=rhoRT. While formally pressure is defined as a force per unit area, and a real wall is needed to have the force acting on it, direct measurement of rho and T also give the value as defined, and that is why I use it that way.
Mark,
I think the basis of our different comments is related to what problem we are considering. The one Arthur and I have been arguing is what happens to a gas in a gravity field that had a constant temperature profile IMPOSED on it as an initial condition, and no other forcing are imposed. Note that gravity stays the same. I contend mass and energy migration will convert it to an adiabatic lapse rate temperature profile, since any molecular or convection mixing (and at least molecular mixing has to occur) will transfer energy until the no heat transfer condition of the adiabatic lapse rate occurs. If molecular motion is the only source of mixing, this would be a very slow process, but it is the direction it would go.
You are saying the adiabatic condition is the one that would form initially. That is exactly what I have said all along.
Aye, that’s a major difference.
It comes from both of you are considering the ONLY way to consider an atmosphere is to use the MACROSCOPIC shortcuts of pressure, density, temperature, etc.
But temperature in a gas doesn’t exist: it’s merely the AVERAGE velocity of a gas in a whole pile of other gasses.
And averages only exist in a mathematical sense, they have no intrinsic absolute existence (you’ll never see someone with the average number of legs, for example).
The other way you can consider it is the kinetic theory.
The problem I’ve have with both of you is that you don’t seem to be able to realise that they produce THE SAME RESULTS.
It’s just that proving changes with the kinetic theory is quite a bit harder than using the shortcuts like pressure and entropy.
That’s why they were invented, for crying out loud!
So walls, floor, temperature, pressure and all those nice shortcuts DO NOT EXIST to the molecule that is actually doing all the existential stuff of “being a gas molecule”.
A molecule at the 500mb height may never see the ground in the lifetime of the earth. How can its existence affect the molecule?
And working on that allows you to see how a lapse rate is merely the realisation of potential energy as a store of particle energy, just exactly the same as rovibrational states “hide” thermal energy and cause the reduction of temperature seen at the same molecular energy.
And the lovely thing about it is that BOTH METHODS OF MODELLING produce the same result.
It’s very similar to the particle/wave duality. Depending on what you want to explain, you use one model (photoelectric effect == photon, heat capacity == molecule), or the other (double slit == wave, convection and heat transport == continuous fluid). And ignoring one when it is appropriate is how you can get your knickers in a twist in working out reality from the model.
It’s one of the reasons why I like physics so much.
Mark – “rovibrational states “hide” thermal energy and cause the reduction of temperature seen at the same molecular energy.” – what? “rovibrational states” increase heat capacity per molecule, but calling that a “reduction of temperature” is rather odd.
Your error is the same as Leonard and William have been making all along – there is no law of “constant internal energy per molecule” that applies to thermodynamic systems like this. The law that describes the allocation of energy in equilibrium is the zeroth law: uniform temperature. And the Boltzmann distribution describes the translation of that from macroscopic energies and temperatures and so forth into individual molecular energies, which fully accounts for external potentials, whatever their nature.
The pressure/density variation required for hydrostatic balance takes care of the external field – there is no additional requirement on temperature (which in thermal equilibrium must be constant). Which I’ve been trying to explain one way or another all along here, apparently not getting through at all…
A monatomic gas has 3 states to store energy.
x velocity
y velocity
z velocity
All are independent.
Heat capacity =3/2R
A diatomic gas has five states:
x, y, z velocities as before
Compression along the axis
spinning and over end
(spinning along the long axis doesn’t change things so doesn’t store any energy)
Heat capacity = 5/2R
Triatomic molecules, 7 . Heat capacity 7/2 R
http://en.wikipedia.org/wiki/Heat_capacity#The_simple_case_of_the_monatomic_gas
So energy will be removed from a gas that climbs a potential energy well in the same way as it makes a CO2 molecule go “whangwhangwhang” or an N2 one go “Boingoingoing”.
EXACTLY THE SAME.
“but calling that a “reduction of temperature” is rather odd.”
Only because we can’t manipulate potential energy fields. So we generally have gases “on earth”, in a negative potential energy field and we can’t put it in and take it out.
Rather like when someone started using “temperature is a negative feedback”. It was rather odd because temperature is usually the RESULT of calculation, not a feedback response.
Same here.
If the energy is hidden into a newly created PE field, it will reduce the temperature the same as if it managed to elongate into a rod like a diatomic molecule.
If that were possible for a monatomic to do en mass, what would happen to the temperature if you changed NOTHING ELSE?
Cp would increase, but internal energy wouldn’t.
So they’d repartition the energy in the new degree of freedom.
So temperature would drop.
Why do you think the atmosphere would be in thermal equilibrium?
Mark,
I generally use kinetic theory explanations when I can. The problem is that most other people are not comfortable with that approach, so I often have to use the continuum representations. I am fully aware of the averages and discrete nature of the actual physics, so don’t assume because I use continuum terms that I don’t get it. By the way, I have a physic background as well as engineering, and I think having both is very helpful. For the present issue, I have (on several posts) described the heat conduction as diffusion of molecules, and pointed out the asymmetry of motion to try to get the details across, but the others don’t seem to get anything out of that approach. Meanwhile saying such things as temperature doesn’t exist is foolish. It is defined as a macroscopic average and we all know there are individual molecules and a velocity distribution. I am fully aware of the dual nature of the molecular and continuum representations.
“so don’t assume because I use continuum terms that I don’t get it.”
No, I assume quite rightly that when you say that the continuum terms are the ONLY right way to describe things that you don’t get the discrete version.
BOTH are right.
When you say that it is only due to (insert continuum measure like pressure or temperature here), then this indicates that you don’t understand the discrete model.
Like here:
“I have (on several posts) described the heat conduction as diffusion of molecules”
Heat conduction doesn’t REQUIRE the diffusion of molecules. Else you wouldn’t be able to get conduction in solids.
Heat conduction is the transmission of kinetic energy in the constituents by collision. In a gas, this generally ALSO means a rearrangement of the positions of the molecules but this is merely because a molecule can pass some other members before hitting another and transferring its energy.
You may understand the discrete model, but your fluid mechanics background means you don’t really know it well enough.
Leonard Weinstein:
Thanks for taking the time to help me understand your approach. I’m definitely further along although I don’t think I am quite there yet.
One question from July 19, 2010 at 2:32 pm:
And I have a change from the earlier thought experiment with the gas in a 100km tall room. Now we make the gas radiatively active – so like the Venusian atmosphere of mostly CO2.
I’ve confused myself as we have journeyed through these 500 comments but I’m clearer (perceive myself to be clearer..) on this point now. What do you think happens once the atmosphere is optically thin?
Does the environmental lapse rate match the adiabatic lapse rate – or become lower?
SOD,
In the enclosed room case, if the gas was radiatively active, and there were no mechanism for forced mixing, the environmental lapse rate would tend toward near zero gradient. The only balance would be from thermal conduction down and radiation up. Since thermal conduction (gas diffusion) is so slow to transport heat, any modest radiation would totally dominate. This would be true even for a very small amount of radiation heat transfer. However, it is also true that if it were not at all radiatively active it would go to the adiabatic lapse rate and stay there. For the enclosed room with radiation, the temperature would be MUCH hotter than the 300 K due to the gravitational potential energy of the lower gas being converted to kinetic energy.
I want to point out that this was only so for the room model, due to the assumption of no convective mixing. In the actual case of Venus, this mixing is sufficient to strongly overcome the modest radiation, and the environmental lapse rate ends out at close to the adiabatic lapse rate, with a hot ground.
Leonard,
Can you refer me back to a posting that outlines the parameters that describe the enclosed room case? My last involvement was with the shell models and I’m not sure what the boundary parameters of the enclosed room are.
Thanks for the help.
williamcg,
The enclosed problem was first defined July 7 at 12:13 am
I would still say that the lapse rate would be still be quite far from the room being isothermal for any realistic gas. Heat would have to be transfered instantly all over the room for it to be perfectly isothermal. The reason for this is that from my understanding there is still only one stable pressure profile for a given gravity field, mass and energy content (I forgot the last one before) if there are no other forms of heat transfer. This means that there is always forcing towards the mentioned profile if there is some sort of heat transfer because we can’t really change the temperature without changing pressure as well and the temperature will change because of the heat transfer. So we have the zeroth law that is forcing the system into isothermal and laws of sir Isaac that are forcing it into a certain pressure profile (which would give us the adiabatic lapse rate for temperature I’m guessing). The end result, or equilibrium if you will, depends on the strength of this forcings.
From what I’ve understood you actually agree with most of this at least to some extent. We seem to be disagreeing on the speed of which the adiabatic lapse rate would be achieved. My guess would be that it happens fairly quickly as pressure differences move mass pretty fast (at least compared to conduction in a gas). What would happen if you took 100 m at an arbitrary height in your room, and magically radiated all of it’s energy away so it would go to 0 K (essentially causing a vacuum).
Disclaimer: Please do regard this as a question rather than something else, as I don’t really know what I’m talking about. It just seems to add up this way for me at the moment.
Mait,
The enclosed room problem and all real planetary atmospheres would initially tend to go toward an adiabatic lapse rate from the start unless otherwise prevented. Forcing such as imposed initial or boundary conditions can result in other variations of lapse rate if they are strong enough. However, for Earth and Venus, the forcing which tended to move the lapse rate away from the adiabatic lapse rate, which comes from radiation absorption and emission from the ground and gas, is compensated for by a restoring forcing powered by the lateral and day/night variation in solar energy input and in some cases by buoyancy induced convection from solar heating of the ground. In all cases, the compensation is dominated by convection, since large scale conduction is too slow. The convection is pressure driven by the differential heating as previously described, and can come from the top or bottom. The compensation is easily able to overcome the small radiation forcing, so the adiabatic lapse rate is maintained.
SOD,
I think one basic problem I am having, is convincing you that the heating of the ground of Venus comes from the fact that a cool gas at a high altitude will become a hot gas on the ground. No energy is added, only gravitational potential energy is converted to kinetic energy. If you re-read the July 16, 12:07 pm comment and responses, this may help. Please note some times are out of order, so look around for that time. Another time following is 2:03 pm. Even Arthur agrees with this basic issue, so I don’t understand why he and you still have a problem with my explanations.
I emphatically do not agree that “the heating of the ground of Venus comes from the fact that a cool gas at a high altitude will become a hot gas on the ground”.
I do agree that if you drop a bucket of “cool gas” from a high altitude and let it hit the ground it certainly does become a “hot gas”. But that has nothing to do with Venus.
Arthur,
If you read what I said rather than what you misinterpreted from what I said, you would not make such comments. I specifically said a cool gas at high altitude becomes a hot gas at ground level (from adiabatic compression, caused in the end by gravity). You agreed with that. It is the obvious logical follow up- that this is the source of heating of the ground and lower atmosphere of Venus you seem to have a problem with.
Venus’ atmosphere does not originate at high altitude; your starting conditions are artificial and have nothing to do with the real planet.
Moreover, such an explanation would only suffice to warm the surface for a brief period – as long as it had *any* mechanism for cooling off, it would do so, and there would be no way to re-boost the atmosphere to 100 km.
The only way to get the molecules up that in the first place is to provide them with free energy such as that coming directly from the sun to Venus’ surface. Absent that, the whole question is hypothetical.
From what I’ve understood what Arthur is saying (a bit dumbed down by me and sorry if I got it wrong), is that while the momentum of the gas particle “falling” down increases due to gravity, it shares it with more and more particles, and the average momentum/kinetic energy stays the same. For example if we start off with a particle with a momentum of 7 and let it fall so much that it increases to 14, and let it bounce with two other particles, they will each get half, and the average momentum (or temperature), remains 7.
How would you “drop” gas through Venus’ atmosphere anyway? And isn’t the point there that if you DID, you’d be adding energy to the system (so really rather unsurprising that heat content goes up).
Also, “cold” is a relative concept.
If you dropped gas that was “cold” compared to the atmosphere at that height, it would still be colder when it got to the bottom, yes?
Mark,
A relatively cool (i.e., at temperatures found in the upper atmosphere) gas (i.e., cooler that the average for that altitude due to lower solar insolation from being at higher latitudes or being at night) will have negative buoyancy wrt the overall atmosphere below it, and will form a dropping current that will compress and heat as it drops. However, if the lapse rate is essentially at the adiabatic lapse rate, the relatively cool current will remain SLIGHTLY cooler than the surrounding gas even though it is heating as it drops. It would go all the way to the ground, and establish a circulating atmospheric flow like the Hadley cells. In fact that is exactly what it does. The amount cooler may only be a few degrees, or even less, but adiabatic compression heats the gas to a much hotter level than it had in the upper atmosphere.
Your nitpicking words is not useful here. I don’t want to have to include a dictionary definition of every obvious word used in the context of this discussion. No one is “adding energy to the system” as the gas falls, the potential energy is being converted to kinetic energy as the gas falls, and converting back as it rises back up (there is no net global down flow or all the gas would end on the ground). Use of cool or hot is obviously in reference to high in the atmosphere of Venus, and hot is near the surface. The fact of being “colder” only biases the final temperature a few degrees or less out of several hundred, so does not change the basic result.
“The amount cooler may only be a few degrees, or even less, but adiabatic compression heats the gas to a much hotter level than it had in the upper atmosphere.”
Fail to see how this heats Venus, mind.
I guess the problem is nobody knows where you’re going.
Try getting there first.
Leonard, specifically this:
“the heating of the ground of Venus comes from the fact that a cool gas at a high altitude will become a hot gas on the ground”
Is wrong because if you dropped a colder gas into Venus, Venus would actually get colder.
And, specifically, how does the 400C overheating on Venus get explained by this?
The lapse rate is defined by the composition of the atmosphere and gravity in that gas.
T(h) = T(0) + Ah
So A is defined by gravity (given the same atmosphere).
But the temperature of Venus’ surface is T(0) and that is not defined by that method.
That is defined by (essentially) the sun shining on the planet.
This doesn’t change with the gravity.
Mark,
Most of the input sunlight is reflected from the cloud layer in the upper atmosphere of Venus. Most of the remaining amount is absorbed, mostly at the cloud level, and heats the region where it is absorbed. The clouds pass, at most, a very small amount of sunlight to the surface. The warmed regions in the upper atmosphere that absorbed the sunlight slightly expand. The regions that get less sunlight, such as at higher latitudes and night side get less and the atmosphere there is somewhat less expanded (you can say it contracts compared to the average). The difference produces convective flows that circulate all the way to the ground. If a gas has a temperature of 200 K at an altitude of 70 km, and the adiabatic lapse rate is 7.8 K/km, the ground layer of atmosphere that convected down will heat to 746 K due to adiabatic compression. If this is higher than the ground temperature, the gas will heat the ground. If it is lower, it will cool the ground. After a reasonable while, the ground will go to the average value of the lower level of the atmosphere and no more heat transfer will be needed unless other forcing is present. Two other possible forcings can and do occur. One is the small amount of direct solar heating. That adds extra energy to the ground. The other is differential radiation, i.e., the blackbody radiation up from the hot ground minus the back radiation from the hot absorbing and re radiating greenhouse gas. This removes extra energy from the ground. All three forcings occur, but the convection is the largest. It would heat the ground to nearly the same final temperature without the sunlight reaching the ground. The greenhouse gas is necessary to cut the radiation heat transport to a low enough level to allow the convection to dominate, and it does. It would even at a much lower greenhouse gas level, but at some point the radiation could dominate, and this would lower the lapse rate below the adiabatic lapse rate. Once the atmosphere and ground system are brought to a constant average final level, All of the absorbed solar energy has to eventually radiate back out to space to maintain the average energy of the system. The absorbing greenhouse gas and clouds eventually pass all of the energy (that was also used to create the convection flows) back to space from a high altitude. If there were no clouds, the radiation out effective altitude would have probably have been somewhat lower than it is, and the clouds may actually be the main location for the actual case. Either way, the effective height where the outgoing radiation leaves from is where the atmospheric temperature is forced to have a specific absolute level. If it did not have the correct effective temperature, the level of outgoing radiation would not match incoming, and the system would not be balanced. In the end it is the sun that heats the planet, and uneven heating that make the circulation. However, since the temperature is forced to a particular value at a large altitude, there is a lot of gravitational potential energy available to make the gas temperature rise as it falls (resulting in adiabatic compression), and the high gas temperature heats the lower atmosphere and ground. As long as the restoring mixing from the convection can dominate the direct solar and radiation and absorbing forcing, the atmosphere will remain close to an adiabatic lapse rate, and it does.
“Most of the input sunlight is reflected from the cloud layer in the upper atmosphere of Venus.”
How much? Energy wise. The Russian lander produced pictures whose lighting level was similar to that of a cloudy midday on earth.
The difference between cloudy and clear on earth is merely 30W.
“The clouds pass, at most, a very small amount of sunlight to the surface. ”
I doubt, but if you have calculations and physics and evidence to back that up, have at it, hoss.
TL;DR but skimmed the rest. Doesn’t seem to be any sort of explanation about how T(0) is determined by the gas pressure at all.
I stand by my earlier statement and cannot see where or how you have given reason to doubt it.
SOD and Arthur,
Look at the enclosed web site, and these specific comments taken from it.
Some comments from: https://courseware.e-education.psu.edu/simsphere/workbook/ch05.html
* “if we return to the classic conduction laws and our discussion of resistances, we note that heat should be conducted down a temperature gradient. Since we are talking about sensible heat, the appropriate gradient for the conduction of sensible heat is not the temperature but the potential temperature. The potential temperature is simply a temperature normalized for adiabatic compression or expansion”
* “When the environmental lapse rate is exactly dry adiabatic, there is zero variation of potential temperature with height and we say that the atmosphere is in neutral equilibrium. Under these conditions, a parcel of air forced upwards (downwards) will stay where it is once moved, and not tend to sink or rise after released because it will have cooled (warmed) at exactly the same rate as the environment”.
Leonard Weinstein:
There’s nothing that I disagree with in the link. Or anything that was new to me either.
Combined with your recent clarifications (e.g. July 19, 2010 at 1:21 pm and especially July 20, 2010 at 10:34 pm), this has me wondering if our different views are substantial or more about interpretations of how events in specific situations might unfold.
Like this comment from you, which, in an earlier form prompted this article:
Which I’m inclined to doubt – but this is more about how much energy there is to drive this process – perhaps a bit like the Johan Sandstrom debate which has continued for 80+ years – rather than about adiabatic temperature changes.
I don’t want to do a “Church of England” where we all pretend we agree even though we don’t but I am starting to wonder if there is actually a difference of understanding of basic mechanisms or instead a difference of understanding of how processes unfold in more complex environments (i.e., which mechanism dominates).
SOD, I think (at least in Arthur and my case) that we disagree with Leonard’s assertion that the surface temperature on Venus is due to pressure and the adiabatic heating from it.
Maybe if Leonard could more clearly show where this is proven and stands up to scrutiny in a peer reviewed journal (this is, after all, an extraordinary claim) and since this is very old science where pressure/temperature and the gas law all are ancient science, this effect, if it were relevant, would have been discovered a long time ago.
But I’ve never heard of it, except in some peoplewhodontagreewithus-ist blogs “proving” the IPCC is all wrong and it’s a big scam.[moderator’s note, please check the Etiquette]
Hardly reputable sources.
Mind you, both Arthur and myself could be wrong in our reading and Leonard DOESN’T mean what I said at the beginning. In which case clarification is needed.
Mark,
The albedo of Venus is about 0.75. That means 75% of sunlight is reflected. Of the remaining, 25%, I think that only about 10 to 20 W/m2 reach the ground near the equator at mid day (someone please correct this if I am wrong). If that is correct, the average would be about 1/4 of that due to latitude variation and night. In fact, the ground does not absorb all of this but reflects a portion.Thus the average solar heating of the ground is probably less than 5 W/m2. On Earth, a clear sky passes 980 W/m2. A cloudy day can vary a lot but a reasonable typical level might be about 100 W/m2. Thus the energy reaching the surface of Venus is not near zero, but is small compared to Earth. DeWitt has made some calculations showing the net radiation flux from the ground (out minus back radiation)is about 7 to 17 W/m2 (check me on that DeWitt). These are both small levels of energy compared to the Earth (Earth surface radiation directly to space is about 80 W/m2). Since the surface of Venus has 92 times the pressure as Earth, and has a large wind speed in the higher atmosphere due to latitude and night/day variation. Even at the surface, the wind speed is 2 to 3 m/s, and due to the high density, can pick up and carry dust and light objects. Convection, driven by differences of energy input at different latitudes and day to night, is far the dominate cause of heat transfer.
Leonard, the albedo of Earth is 0.7, which means 30% gets reflected.
Our earth’s surface temperature is still based on the power required at TOA to balance what comes in.
“I think that only about 10 to 20 W/m2 reach the ground near the equator at mid day”
And 10 to 20 watts won’t be able to get out because it’s really quite dense (the clouds keep in 75% of that!)
So what happens is that the surface gets hotter and hotter. The volume the gas occupies gets bigger and the top of the atmosphere gets higher.
That reduces the TOA temperature and the amount of energy leaving.
And so the venusian surface gets hotter.
And hotter.
Until it is radiating ~15,000 Watts per square meter into the lower atmosphere.
The lapse rate means that at the TOA, that tremendous store of energy in the atmosphere leaks out at about the same rate as energy is coming in.
The temperature at the surface rises until the TOA is hot enough to reradiate the energy that the surface receives.
I still don’t see where T(0) is being defined by the pressure of the planet’s atmosphere, I’m afraid.
Mark,
The albedo of Earth is 0.3 which means that out of about 1400 W/m2 at Earth’s location, 980 W/m2 reaches the ground and atmosphere and is absorbed. On Venus, any absorbed radiation from Sunlight and any outgoing radiation that penetrated far enough so that back radiation cause a net energy flux do need to be balance out to not have them cause the high temperature. They are factors. However, the convective transport throughout the atmosphere is very large, and almost surely the dominant mode of heat transfer. All the convection has to do is maintain the adiabatic lapse rate, which it does, to completely cause the hot ground.
OK, got it the wrong way around on albedo.
Peak surface radiation is 672W, mind, not 980 (four times the average).
“On Venus, any absorbed radiation from Sunlight and any outgoing radiation that penetrated far enough so that back radiation cause a net energy flux do need to be balance out to not have them cause the high temperature.”
I’m afraid I don’t understand what you’re saying here. Maybe because I’m trying to find out how this relates to the thesis that T(0) is set by the pressure.
“However, the convective transport throughout the atmosphere is very large”
Yes, but they’ve got to get 1500W out. And, as you’ve already pointed out, they’re already being loaded with sunlight coming in, so they have to deal with internal backradiation too.
“All the convection has to do is maintain the adiabatic lapse rate, which it does”
Convection, conduction and radiation, you mean.
“to completely cause the hot ground.”
Convection can’t heat the ground.
What causes the hot ground is the need to release 1500W/m2 from the grounds baking heat.
Convection isn’t bigger, because the atmosphere is heated internally by the sunlight being absorbed and it has to go much higher to get to a height it can radiate to space.
Worse, there’s no phase change water vapour (in comparison to the transport energies involved in the CO2 atmosphere) to help dump energy out at higher altitudes.
The only contribution convection can make to the surface temperature is to be too weak to remove energy from the ground and get it to radiative TOA.
You still haven’t shown your position, except to restate it again.
SOD,
I thought you were convinced that conduction heat transfer was zero only if the temperature lapse rate was zero rather than the adiabatic lapse rate. I don’t know your present position on that but the July 2, 6:54 pm comment should answer that in favor of the adiabatic lapse rate.
I also thought you were not convinced (and still are not) that the modest temperature high altitude gas could heat the ground when it transferred energy to lower levels by mixing and convection down, and the adiabatic compression converted gravitational potential energy to higher temperature. Thus, the issue of whether direct sunlight is needed vs purely induced circulation due to variation in upper atmosphere heating to create enough mixing to maintain the adiabatic lapse rate is the main issue here. If you can maintain the adiabatic lapse rate, that plus the fixed level of temperature at the higher altitude where outgoing radiation matches absorbed sunlight levels clearly indicates that the atmosphere temperature near the ground would be the source of the high surface temperature. I think we both agree some circulation would occur without heating the ground with sunlight, and the issue is how much. I tried to show that the amount of energy in a modest delta T fairly low speed convection is easily much larger than the small direct Solar heating and radiation out levels, so easily could dominate those processes. That does not show that is in fact what happens, so a model with computation would be helpful.
I think we also still disagree on the amount of greenhouse gas needed to cause the high temperature. My contention is that as long as the radiation transfer level is not too large for convective heat transfer to dominate, it is the height of the atmosphere where the outgoing radiation balance occurs that determines the ground temperature, and going to any super level of radiation absorption does not increase the temperature, as long as the outgoing height is near the same.
SOD,
The known surface flow rates on Venus are about 2 m/s. If turbulent mixing eddy motion has just 5% of that level (10 cm/sec vertical mixing speeds), and knowing the adiabatic lapse rate is 0.0078 K/m, then the vertical energy flux available from this very low level of convection is 52 W/m2 (based on Cp and density). This is significantly larger than the solar heating of the surface, or the radiation flux out of the surface. At higher altitudes, the wind speed quickly picks up, and would increase the mixing energy flux available far more. This order of magnitude analysis shows that the source of even a modest surface wind speed can dominate the ground radiation loss and solar heating effects. The only remaining issue is the capability of upper atmosphere generated circulation to cause the modest ground currents.
We know from measured values that the lower troposphere lapse rate is the adiabatic lapse rate (for the correct Cp at the local temperature) within measurement accuracy, so the question arises – what is the source of the large winds on Venus. I like DeWitts analysis that since the higher latitudes and night side get less heating in the atmosphere, the height of the atmosphere is slightly lower to the same pressure, and the atmosphere flows by pressure from the higher elevation to the lower. This river of atmosphere flow is the main source that induces the entire atmospheric circulation pattern. There has to be a return flow below this and induces circulation all the way to the ground.
The Johan Sandstrom debate is about a fixed upper wall condition and is limited to the basic resistance to free circulation in a problem driven purely by buoyancy effects. It is not relevant to the present issues.
Mark,
I don’t have a clue what you are trying to say. What 1500 W has to be removed? Where are you getting a peak surface solar radiation of 672 W/m2? From the sites I looked at the peak surface sunlight corresponds to about 5,000 lux or possibly a bit more. This is 1/20 the Earth max., and so corresponds to 49 W/m2. Only part of this is absorbed due to albedo of surface. I assume an albedo of about 0.5 (may be a bit more or less). Thus a maximum of about 25 W/m2 is absorbed, and the average over the globe is 1/4 that (planer to surface areas), so the surface average is 6 W/m2. It could be a bit more but not much. Also you still obviously don’t understand the effect of adiabatic compression and sensible heat.
“I don’t have a clue what you are trying to say. What 1500 W has to be removed? ”
The 15000 (sorry, dropped a 0, but that’s nothing, right?) watts is what the ground heats up to and emits.
Imagine instead of an atmosphere, you lagged Venus. 99% lagged. Deep space (3K). 200W goes in for each square meter.
The body will heat up because for every 200W going into venus, only 2W comes out.
Until venus warms enough to emit 20,000W per square meter. Then 200W is going out for every 200W going in.
The lagging maintains a temperature drop appropriate with its conductivity and thickness.
Just like the atmosphere maintains a temperature drop appropriate with the lapse rate.
Pressure doesn’t come into it for an atmosphere.
A source gives the incident solar energy absorbed by Venus at 132_+13 W/m2 and that radiated as 153_ + 13 W/m2; that absorption amount is a bit different from the 160W/m2 that I think Nick Stokes came up with at the beginning of this thread; however, if Leonard is right about the amount reaching the surface of 6W/m2 then with ~153W/m2 leaving the heat imbalance on Venus is not +ve but -ve; how would that reflect on either the pressure or greenhouse argument?
“if Leonard is right about the amount reaching the surface of 6W/m2 then with ~153W/m2 leaving the heat imbalance on Venus is not +ve but -ve”
I’m afraid that the 153 only appears in your post, cohenite.
However, I would suggest that you are ignoring the temperature of the atmosphere. It’s also pretty close to 450C and radiating like a good ‘un.
Here’s one model that may help illuminate:
The thicker the atmosphere is optically, the closer to the ground the radiation the ground sees is coming from.
And, since the lower down in the atmosphere you are, the closer you are to the temperature of the surface, the thicker the atmosphere, the less the temperature difference and the lower the net flux into the atmosphere will be.
“I’m afraid that the 153 only appears in your post, cohenite.”
Click to access fvenuspaper.pdf
I just play ’em as I see ’em.
Cohenite,
One problem with the theory of formation of Venus from an impact with Jupiter just 6,000 years ago is straight orbital dynamics. You don’t just go into an orbit, there has to be conservation of momentum and energy, which would prevent such an event. The planets formed when there was enough gas, dust, and many small planetestimals in an accretion disk around the early solar system, and accretion and multiple collisions, along with viscous drag from the gas formed planets and nearly circularized their orbits. It is likely that major collisions between early protoplanets affected the result (a collision of a large body with early Earth is thought to be the way our moon formed), and Venus may have collided with Jupiter, but it would have been over 4 billion years ago, while other material was present to convert the orbit. If that is so, the surface would not have a great subsurface heat source.
You don’t need a subsurface heat source to explain the high temperature of the surface of Venus. It follows from the very thick atmosphere caused by the high mass of the atmosphere and presence of some greenhouse gases and high clouds. That is enough to fully explain the temperature.
Cohenite and Mark,
The amount of energy leaving Venus (not including reflected energy) has to match the amount absorbed (assuming the average temperature is not changing). However, little or even none has to be leaving the ground. All of the absorption and radiation can be in the clouds and atmosphere. There is actually a small amount of energy that reaches the ground and is absorbed, and as Mark points out some net radiation from the ground goes out (with only a small difference in the forward radiation and back radiation). The net outgoing radiation level does not have to exactly match the absorbed solar energy, since convective heating from the hot lower atmosphere could also supply the energy to replace the energy from radiation from the ground. It is not clear what the exact balance is between convection, radiation in and radiation out at the ground, and it does not matter a lot for the process to be able to keep the ground hot. The absorbed heat in the atmosphere is not uniform at different locations (day/night and different latitudes), and this creates winds that mix the atmosphere and maintain the adiabatic lapse rate. Combining that along with the high effective altitude where the outgoing radiation leaves from is all that is needed for the temperature on Venus to be explained.
“The amount of energy leaving Venus (not including reflected energy) has to match the amount absorbed (assuming the average temperature is not changing).”
Indeed.
At the top of the atmosphere.
What happens underneath is nothing to do with that. After the first absorption, the original photon emitted by the sun no longer exists.
“However, little or even none has to be leaving the ground.”
If there was none leaving the ground, then either
1) the ground is at 0K or
2) the atmosphere is hotter than the ground, or
3) the atmosphere is warming
“The net outgoing radiation level does not have to exactly match the absorbed solar energy,”
No, indeed not, as in the case of the (still collapsing) Jupiter Gas Giant.
Venus is, however, rocky.
“since convective heating from the hot lower atmosphere could also supply the energy to replace the energy from radiation from the ground.”
Convection cannot create heat.
“Combining that along with the high effective altitude where the outgoing radiation leaves from is all that is needed for the temperature on Venus to be explained.”
Well, you don’t even need to know all that. Ignore the convection and mixing winds and so on and you’ve already explained the temperature on the surface of Venus by balancing the radiation at TOA with incoming absorbed radiation and calculating what atmosphere would generate that TOA radiative temperature with Venuses atmosphere.
““I’m afraid that the 153 only appears in your post, cohenite.”
…link to pdf…
I just play ‘em as I see ‘em.”
Hmmm. Accuracy:
cohenite: “if Leonard is right about the amount reaching the surface of 6W/m2 then with ~153W/m2 leaving the heat imbalance on Venus is not +ve but -ve”
It wasn’t played to be seen.
Citations next time.
williamcg a long way back on July 8, 2010 at 8:56 pm:
Atmospheres by Richard M. Goody and James C.G. Walker, Prentice-Hall 1972 has this approach to deriving the lapse rate on p142.
Thanks SOD,
I will try to find it. Do you have a link?
It’s a book.
SOD,
I know that. Some books have links. I was hoping this one did.
Ok, sorry. No, no idea if there is a link, I have the physical book.
SOD,
No problem. I appreciate the reference.
Mark from July 22, 2010 at 8:12 am:
I disagree with it as well.
However, as we disentangle our disagreements, it’s important to understand what points we have issues with.
If it’s about basic physics processes then it should be easier to resolve it.
If it’s about a thought experiment Venus, or the real Venus, it might be more difficult.
I think one problem Leonard (and many armchair commentators) has is that they aren’t considering the consequence of their model.
What *would* happen if pressure could create temperature merely by existence?
You’d have energy from nowhere:
Energy=Force x distance
Pressure = Force (no distance moved)
If pressure can create temperatures beyond the mere expression of potential energy (required to make Venus surface 450C), we already know
Temperature = Energy.
Therefore, despite no work done, Pressure can create energy.
Such an effect would make the Steam Engine *really* efficient!
I’m fairly certain we are talking about how energy is distributed inside a system, not how much of it there is. We can have all the energy in a very small area of “space” without conflicting with any of the energy conservation laws. We are looking a very specific part of the observed body (where gaseos system is switched to a solid/liquid one) and we are interested in what the temperature will be in that particular area. Furthermore from my understanding, Leonard didn’t say that the high temperature was caused by the pressure, but rather the “height” of the atmosphere.
I’m not an armchair commentator Mark; I’m on the edge of my seat. If a greenhouse determines temperature above the temperature caused by incipient radiation [255K on Earth] then the ghgs in themselves should be the cause of that temperature in proportion to their atmospheric concentration. Mars and Venus have similar atmospheric concentrations of CO2 but Venus’s surface temperature is much higher than it would be without its atmosphere; Mars is about the same; the mass of Mar’s atmosphere is much less than Earth’s and Earth’s is much less than Venus’s but the total mass of CO2 on Mars is much greater than the total atmospheric mass of CO2 on Earth [ > 100 times]; the mass of other gases on Venus is much greater than the mass of the other atmospheric gases on Mars even though the ratio is ~ =. Obviously, in the first instance, the key is mass not the relative proportion of CO2; if air pressure is the force exerted by the weight of a column of air above a particular location; and mass is the amount of matter that a body contains then the larger the mass of the atmosphere then the more pressure will occur; it is that pressure which is consistent with temperature on Earth, Venus and Mars not any other property, mix or proportion of the atmosphere. To say that pressure does not contribute to the temperature is to ignore the contribution that mass makes to the atmospheric and surface temperatures on all 3 planets.
cohenite:
Not really. The equations are complex and not linear.
If you are looking for differences between Mars and Earth you also have to take account of the width of the absorption lines with pressure (the Martian pressure is less than 1% of the Earth’s pressure).
You have to include the water vapor with CO2 on earth.
You have to solve the RTE (radiative transfer equations).
If it was just a linear problem then we could all do it in our heads. Books that explain the subject in detail have over 100 pages on this subject. Some of it is derivation of formulae of course, but it’s not one line.
“then the ghgs in themselves should be the cause of that temperature in proportion to their atmospheric concentration.”
Why?
The cause of toxicity in your body is not equally meted out to the various elements that have toxic results on human physiology based solely on their relative concentrations.
And I thought it was all “cow farts are FAR more dangerous than my SUV!!!” …
Mark,
The source of the energy is the SUN. The solar energy that is absorbed heats the atmosphere. That portion of the atmosphere that is at very high altitudes has a combination of kinetic energy and potential energy from it’s height. When that portion of the atmosphere is convected and mixed down to lower elevation, it total available energy is expressed as a higher temperature. The high density feature was important as being needed to make the atmosphere thicker. Some greenhouse gas was necessary to prevent the surface radiation heat transfer from carrying away surface heat too rapidly to be replaced by convective heating by the atmosphere (solar heating is in there but a small factor and not necessary for the process to work). What you keep saying shows you have no clue on the issue. SOD’s main disagreement is based (I think) on the issue of whether the solar flux to the ground is a main driver or not, and if it is critical to the process.
“The source of the energy is the SUN. ”
Gosh darn it, don’t blind me like that!
“When that portion of the atmosphere is convected and mixed down to lower elevation, it total available energy is expressed as a higher temperature.”
Only, as you said before, if it has positive potential temperature, else it will either stay at height or cool the atmosphere it is falling through.
Since it’s been to TOA and been able to dump its energy out of the system as per spec, this parcel of air is going to have a negative potential temperature.
If it had a positive one, it would have to be pushed down somehow.
“SOD’s main disagreement is based (I think) on the issue of whether the solar flux to the ground is a main driver or not, and if it is critical to the process.”
Disagreement with your position? Yes. As to whether the solar flux is a main driver, no. I don’t think there’s a lot of uncertainty there: it is. Is it critical to the process? Yup.
Except for gas giants, especially ones like Jupiter who produce from collapse more energy (from their continuing collapse) than they get from the sun (IIRC).
Even then, the lapse rate would still be produced by gravity and the intercept would be set by the TOA balance requirements.
“Why?’; ask Jimmy Hansen, I’m not advocating it, I was playing devil’s advocate with the contrary evidence; and I wish people would not revert to CO2 is a poison analogy; if CO2 is a poison then temperature isn’t the symptom as cointegration analysis has shown.
““Why?’; ask Jimmy Hansen, I’m not advocating it, I was playing devil’s advocate ”
Then, playing devil’s advocate here, why bother answering rhetorical questions like that?
Until you can come up with actual questions, you’re assigned to the NWOR bin.
Leonard Weinstein:
I’ve read all your comments and I still think that on the basic elements except perhaps conduction, we are in agreement. (Haven’t focused on conduction because it is so small in comparison with radiation and convection).
We don’t agree on the results of warming an atmosphere from the top, but I don’t think that is about the absolute basic principles but on the application.
Although I still think that the Johan Sandstrom theory is relevant..
I’ve learnt a lot from having to think about this so much. Whether I really understand it now is open to question.
I still think it will be a worthwhile exercise for us to do an article where we both summarize our points of view.
I would like to invite Arthur Smith to write a section as well, not to do a 2 vs 1 but because I think he may explain some aspects better than me and because, why not?
On the other hand – writing something is time consuming – and you may feel that summarizing this is not a good use of your time – as interested parties can simply read the exchange.
I would totally understand that as well. In any case, I have appreciated the opportunity to learn.
SOD,
I would be glad to write a section as you describe. I am not sure of the best format. It seems there are a small number of issues we disagree on, and many we agree on. The ones we disagree on are in some cases probably not even important to the final real world results of Earth and Venus (such as the conduction problem tending to adiabatic or constant temperature), even though they are important to the room problem and total understanding of what is going on. I think you even agree that the issue of sunlight reaching the ground may not be clear cut (although you do take a particular position on it), but may depend on the exact details of relative magnitudes. I think the Johan Sandstrom theory is relevant when buoyancy forces are very dominant to a setup, and overwhelm any much smaller adiabatic lapse rate effects, but it is not useful to draw conclusions on planetary lapse rate physics.
At any rate, please tell me the format you would prefer, and I will do the best I can. I think sections by DeWitt and williamcg might also be useful, but I leave that to you.
SOD,
I also feel I have learned more from the exchange, and greatly appreciate your courtesy. I wish more of the sites of proponents of AGW being a problem were as open minded and reasonable as yours has been. There is a site at: http://ourchangingclimate.wordpress.com/2010/07/21/the-risk-of-postponing-corrective-action/#comment-6882 by Bart Verhaggen that I have been responding on. There is a person at Bart’s site that uses sod as a name. Is that you or someone else? I would appreciate if you go to that site and see how I am treated.
It’s not me on that site. If I comment anywhere it is as ScienceofDoom.
I am glad it was not you as that person was not as nice as you.
SOD – I’d like to know exactly what the question is we’re writing about, but yes, I’d be happy to write something. I assume you have my email if I don’t happen to catch the request further here? Thanks
Leonard; sod and dhogaza are seasoned warriors for the cause and have no connection to this sedate and informative site. Great job incidentally; for me, along with saturation, average global temperature, climate sensitivity and backradiation, the issue of pressure is the other big aspect of AGW.
cohenite,
I don’t understand the point of “seasoned warriors for the cause”. I thought the issue was to sort out and find the most reliable facts and understanding about a possible problem of AGW. I am not fighting a religious war, I am a scientist. I would gladly join in supporting pushing for action if a reasonable case could be made of a danger, but none has to my opinion and to the opinion of numerous good scientists, so the problem as I see it is that all scientists will lose prestige in the public eyes when the temperature fails to continue climbing. This will be a classic case of yelling about the wolf coming when it did not, so that when a real problem comes up. it will be ignored.
Obviously there is a possibility of dangerous warming. There is also a possibility of dangerous cooling (which I actually think is the bigger danger). There is also possibilities of an asteroid strike, of super volcanoes, etc. We have to do our best to put all of these in perspective and hopefully make at least preliminary plans how to respond if we get better information, but jumping from one fad terror to another with poor understanding is not a good approach.
SOD,
I assume the articles would be on Venus, as including Earth, Mars, and other planets confuses the points I was trying to make, since each has different ranges of conditions.
Leonard,
I am loking forward to the new thread you are working on. You have done an outstanding job so far. Feel free to use anything I have written on this thread if you think it will help (cited or uncited, it’s up to you). Let me know if I can help in any other way.
Leonard Weinstein:
Yes on Venus – but really about the mechanisms under discussion – as much of our discussion has really been about a mythical Venus – TEV3 and then the very tall gas room.
[…] Venus (Venusian Mysteries), Leonard Weinstein suggested a thought experiment that prompted a 2nd article of mine. Unfortunately, it really failed to address his […]