I didn’t think that a Part Two would be needed after the initial installment – The Sun and Max Planck Agree
Anyway, I always appreciate commenters explaining why the article hasn’t done its job, and so following various comments, hopefully, this article can address the deficiencies of the first.
I recommend reading the First Article before diving into this one. The main thrust of the article was to explain that solar radiation and terrestrial radiation have quite different “signatures”, or properties, which enable us to easily tell them apart.
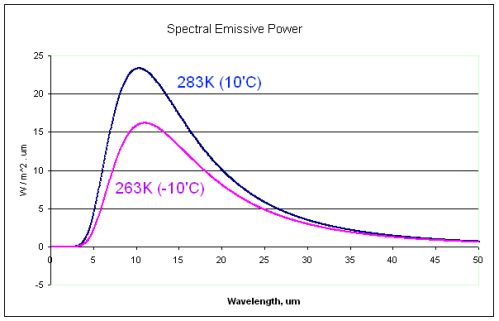
For reader unfamiliar with how radiation varies with wavelength, here are two “blackbody” curves:
What you can notice is that the curve for 10°C radiation is – at all wavelengths – greater than the curve at -10°C radiation. The peak radiation for both of these curves occurs around 10μm. This is Wien’s law where the peak occurs at:
λpeak = 2898/T
where λpeak is the wavelength of peak radiation. So for 283K (10°C) the peak wavelength = 10.6μm. But radiation – as you can see – occurs at all wavelengths.
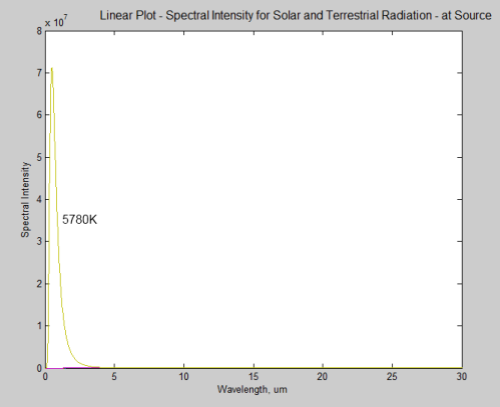
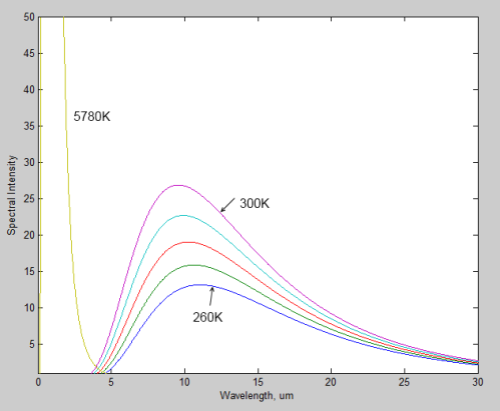
The total radiation from a body varies in proportion to T4, and here is the comparison of solar (at 5780K) and terrestrial radiation (at 260-300K):
Where is the terrestrial radiation? It can’t be seen on a linear plot, it is so small.
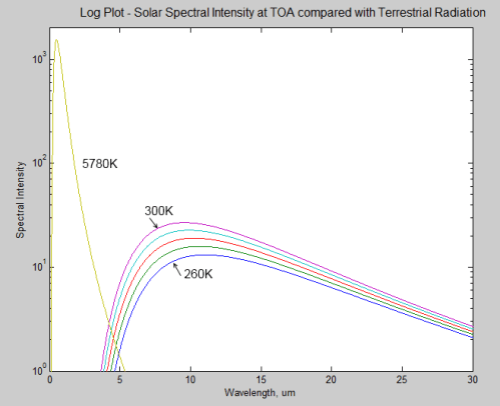
Let’s see it on a log plot:
For those not used to seeing log plots, check out the left hand side axis – the peak of the 300K radiation is around 1000x lower than the solar radiation at that wavelength (each major division corresponds to a factor of 10). And the spectral intensity of the higher temperature radiation exceeds the value of the lower temperature radiation at every wavelength.
This is the radiation measurement you would get from a spaceship parked just off the surface of the sun (for the solar radiation at 5780K) and just off the earth (for the terrestrial radiation of 260 – 300K).
The earth is some distance away from the sun and so the radiation at the top of the earth’s atmosphere will be reduced quite a lot.
If we consider the radiation from the sun expressed as per m2 then the solar radiation incident on the earth’s atmosphere will be reduced by a factor of (rsun / distancesun-earth)2 – this is known as the inverse square law – and there is a nice explanation at Wikipedia.
The amount the solar radiation is reduced for top of atmosphere = (696×106/150×109)2 = 1 / 2152 = 1 / 46,225.
(If we calculated it the other way, we would work out the total solar radiation from the whole surface area and conclude that this value must be divided by 2×109).
So if we look at the incident solar radiation at top of atmosphere (TOA) compared with terrestrial radiation:
We can see that the cross-over is quite small.
And this is not the whole story. Some solar radiation is reflected from the earth (on average around 30%). And depending on the angle of the sun from the zenith, the amount of solar radiation per m2 will be reduced accordingly.
So the above graph is the best case.
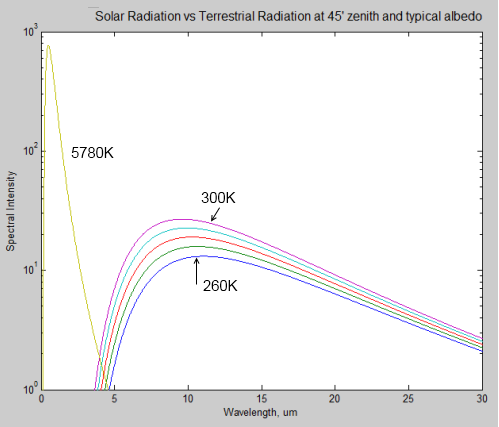
If we take the average of 30% of solar reflected, and at an angle from the zenith of 45°, we will have these curves:
You can see the crossover is very low.
Just for completeness, here it is on a linear plot, with the crossover section clear:
Hopefully, it’s clear, hopefully, there is no possibility of confusion – solar radiation can be easily distinguished from terrestrial radiation within the earth’s climate system.
If we measure radiation > 4μm we can conclude it is terrestrial and if we measure radiation < 4μm we can conclude it is solar.
Of course, at night, it is even clearer.



I think this is a powerful argument, but I prefer another one. Perhaps you can explain it in detail in part III 😉
The one I prefer has to do with the source term in the radiative transfer equation and the directionality of both kinds of radiation. I know it is complex to explain that in a blog, but may be you find a way. That’s the reason you are a blogger and I am not 😉
Regards
“And the spectral intensity of the higher temperature radiation exceeds the value of the lower temperature radiation at every wavelength.”
Quite so. And your log plot at source shows this. But subsequent charts are at odds with the statement. The reason is that, in translating the sun’s radiation at source to TOA, the inverse square law requires a reduction of the spectral intensity across the full spectrum, not a truncation of the spectrum which these charts show.
[…] – followup article – The Sun and Max Planck Agree – Part Two Possibly related posts: (automatically generated)The Imaginary Second Law of ThermodynamicsCO2 – […]
John Millett:
In Part One, you said:
And I explained. And this post expands on that at length.
In this post you said:
What exactly is your point?
Do you see that taking the Planck curve at 5780 and dividing by 46,000 will move it below the terrestrial curves at longwave? Or not?
I can do curves out to 1000um if it would make you happy but you will see that the 5780K solar curve is way below the terrestrial curve at every wavelength.
The correct maths is to take the spectral intensity at each wavelength and divide by 215^2.
Do you think this is wrong? Would you like to explain the correct maths?
“The correct maths is to take the spectral intensity at each wavelength and divide by 215^2.”
This is where the problem lies.
That there is a problem can be deduced in two ways. First, begin with your chart showing curves for temperatures of 273K and 263K, the former enveloping the latter. Add another, say 300K; it would envelop the other two. Add one for 394K, the effective radiating temperature of the solar flux at TOA, and it would envelop all three. It wouldn’t drop below the others at long wavelengths. Its spectrum wouldn’t be truncated.
Second, K&T’s global energy budget shows the atmosphere absorbing a quarter of incoming solar radiation. Since the atmosphere is transparent to short wave radiation it must be absorbing long wave.
Perhaps the solution to the problem is to reduce the sun’s maximum spectral intensity at source by 46,225 to obtain its intensity at TOA, viz, about 1370 Wm-2. Derive the effective radiating temperature for that flux, viz, 394K. Then derive the blackbody curve for that temperature?
Here’s the curves out to 500um, solar radiation divided by 215^2 directly overhead with no reflection, compared with 260-300K curves:
Informative, isn’t it?
And here’s the same one on a log plot, out to 500um:
As you can see the vertical axis has been extended down to miniscule levels of radiation.
For those who don’t mind some truncating to see the important points of a graph, here it is to only 50um, with grid lines overlaid:
At 50um the terrestrial radiation is over 18,000x greater than the solar radiation at TOA (when the sun is overhead and there is no solar radiation reflected).
At 10um the terrestrial radiation is only around 400x greater than the solar radiation (same conditions).
At 15um the terrestrial radiation is around 2,000x greater than the solar radiation (same conditions) – important for analyzing the possible source of 15um radiation.
Note that with a typical albedo of 30% and with the sun not directly overhead the solar radiation would be multiplied by a factor of 0.7 x cos θ (where θ is the angle from zenith). Not that it matters too much.
John Millett:
On my comment:
“The correct maths is to take the spectral intensity at each wavelength and divide by 215^2.”
Said:
There’s no problem there at all, this is actually correct and very very basic.
You appear so confident explaining where “the problem” lies and yet here you asking “perhaps?”
If you take the radiating temperature for a body of 394K you get a body that radiates with a peak wavelength of 2898/394 = 7.3um. (See Wien’s law in the article)
And yet the solar spectrum when measured at TOA by satellite has a peak wavelength around 0.5um – the peak wavelength for a body of 5780K.
This is a simple subject. Radiation gets attenuated according to the inverse square law. You can see a nice representation of it on the wikipedia article I linked earlier.
If you don’t understand the subject that’s fine – but in that case it’s better to ask questions than make pronouncements.
If you have a coherent theory please explain it.
If you don’t then maybe you might want to entertain the possibility that the article is correct.
Sod, you ignored the other parts of the post. They need your attention.
John, what’s the power output from the sun, in toto.
How big a shell has that energy passed out to by the time it gets to earth?
Divide one by the other.
That is the peak flux when the sun is at zenith at TOA. Divide that by 4 to get the same area spread over the entire earth globe. Call that A.
Now, for the BB radiation of ~5700K, what proportion of the energy is longer wavelength than 4um? Lets call this B (will be 4um wavelengths. Let’s call that C.
Now, we have here 324W/m^2 from backradiation from a body (the air) at about 280K. It’s already at the earth’s surface, so no change there.
Calculate the proportion of 280K radiation below 4um. Call that Y (will be less than 1).
Multuply X by Y. Call it Z.
Compare C with Z.
Which is biggest?
By what proportion?
Even if you multiply C by 4 to find the peak, how well do they compare? If you do that, please remember, no sunlight at night, and very little far north or south, or in the mornings and evenings.
Oops. missed out “Multiply A by B”. Let’s call that C.
John Millett from July 28, 2010 at 11:24 am:
Why don’t you explain exactly what you think has been ignored.
And does that mean you have understood and accepted my comments of July 27, 2010 at 2:01 am?
I can see that my perceived inconsistency between your article and K&T’s energy budget was unfounded. Terrestrial radiation occurs in the far infra-red and solar in the near infra-red, the cross-over is minimal and the atmosphere absorbs both.
I am still perplexed by your charts 3 and 4. Do the labels to the curves say “this is the planck curve for a body of temperature T”? If so, the charts show the label “5780K” for solar radiation both at source and at TOA. This doesn’t sound right for TOA. Nor does it look right for the effective radiating temperature of the solar flux at TOA, 394K, which one would expect to look like chart 1. The question in my mind is: what blackbody temperature would be consistent with the solar curve in chart 4?
The Earth emission spectrum is theoritically supposed to follow the 255K line (give or take the reflected short-wave solar radiation).
It looks to me though that the spectra where long-wave absorbing molecules operate emit at as low as 200K and, in the atmospheric windows, the thermal emission operates at as high 298K.
So, we just have a weighted average emission of 255K (which varies from 200K to 296K at different wave-lengths depending on the amount of absorptions). Less energy gets out in the CO2 and H20 spectra, more energy gets out in the windows.
Obviously, “some molecules” are emitting in the windows. Maybe the majority of these would be solid or liquid surface molecules but how many of the high-energy 296K emissions would come from atmospheric molecules. Are any of these high energy emissions coming from atmospheric molecules excited to these higher-energy levels following collisions with CO2 and H20 molecules (or even surface molecules).
“The Earth emission spectrum is theoritically supposed to follow the 255K line (give or take the reflected short-wave solar radiation).”
Why is it supposed to do that? It’s supposed to follow the 290K line. And it does.
That graph you posted a link to shows the temperature of the surface that is radiating out to space averaged over the entire globe.
“Obviously, “some molecules” are emitting in the windows.”
Lots of them, actually. Practically all of them. The ground, is most of them (which is why it’s 295K radiative power). The number from a higher level would be radiating at a colder temperature (adiabatic lapse) and therefore would reduce the temperature at that frequency nearer the 200K line.
And at the 15um range, it’s only the very top of the atmosphere that’s radiating, and that’s ~90C colder.
Bill Illis:
Not quite.
From the top of the atmosphere the earth actually and theoretically emits 239W/m^2. This equates to an “effective blackbody radiating temperature” of 255K. It’s more like a shorthand way of relating radiation to temperature.
If you take a look at The Earth’s Energy Budget – Part Three you will see a more detailed discussion, including this graphic:
The picture shows shortwave radiation (or in other words absorbed radiation). Aren’t we talking about emitted radiation at the moment (which would be longwave).
I said “give or take the reflected short-wave radiation” because the Earth can be photographed in visible light and therefore emits/reflects visible short-wave as well as emits in infrared.
Interesting Earth pic in infrared.
http://bobqat.com/Essays/disteyes/ir-2.html
My main point in bringing this up is that some seem to believe Nitrogen and Oxygen play no role at all in the radiation transfer of thermal infrared from Earth.
But they are warmed to an average of 288K at the surface and therefore emit blackbody radiation just like all molecules do. If they emit in the atmospheric windows, the infrared emissions mostly escape to space. If they emit in the CO2 absorption/emission spectrum, the photons are likely to be absorbed again by CO2/H20.
How do the Nitrogen and Oxygen atmospheric molecules increase to 288K (or 296K in warm latitudes). Through collision with other atmospheric (including CO2) and surface molecules.
So what we have are particular spectrum of CO2 where photons are less likely to get out. The surface and atmosphere warms but the surface and non-GHG atmosphere molecules are still radiating yesterday’s solar heat to space, mostly through the atmospheric windows and less so through spectra where absorption is likely from GHGs.
This is a significantly different perspective than the greenhouse theory is usually described as.
CO2 absorbs at 15 um – hits a N2 molecule and average 0.0000000015 seconds later (shorter than the average emission timeline of CO2 which is 0.000005 seconds) – which makes the N2 warmer and the N2 molecule emits a photon over an emission spectrum of 296K, and a large proportion of those photons are in the atmospheric window and escape to space.
Less photons are emitted at 15 um (only 220K worth of) but more are emitted in the windows (296K) and the equilibrium 255K is still maintained. Increase CO2 and reduce the amount of photons escaping through the 15 um spectrum and the surface and the atmosphere will warm until the equilibrium can be reached again. But this is only requires an increase of 0.6C or 0.7C in surface and atmospheric temperatures per doubling of CO2 to allow the 255K to be maintained.
“But they are warmed to an average of 288K at the surface and therefore emit blackbody radiation just like all molecules do. ”
Bill, they are a reservoir of energy that can refill the IR bands exhausted by emitting CO2/H2O/… molecules.
“If they emit in the atmospheric windows, the infrared emissions mostly escape to space.”
They don’t: those windows exist because, except in rare cases, the molecules in the atmosphere do not interact with those photons.
The matrix structure of solids allows resonance to act on wavelengths of the order of their size and less (harmonics), therefore the solids can radiate much more readily, since they don’t have to wait for another collision to fill the resevoir before radiating.
” If they emit in the CO2 absorption/emission spectrum, the photons are likely to be absorbed again by CO2/H20.”
Correct. And this will continue until somewhere around 1 optical depth into the atmosphere where the photon has a good chance of never hitting another absorber again.
FREEDOM!
“CO2 absorbs at 15 um – hits a N2 molecule and average 0.0000000015 seconds later (shorter than the average emission timeline of CO2 which is 0.000005 seconds) – which makes the N2 warmer”
Absolutely right.
” and the N2 molecule emits a photon over an emission spectrum of 296K,”
Absolutely wrong.
N2 will likely hit another CO2 molecule without an excited 15um state, losing that energy in an inelastic collision and exciting the CO2 molecule. Or maybe the ground. What goes around, comes around…
The 296K radiation is coming from the earth surface. Not (in any measurable sense on the scale of that graph) from the atmosphere.
Bill Illis:
Take a look at The Amazing Case of Back Radiation – Part Two. This might help.
But in any case, gas molecules don’t emit “blackbody radiation”. And some gas molecules emit 1-100 billion times more radiation than others.
It all depends on the molecule. N2 and O2 are very low emitters and absorbers of 4-50um radiation, and are so far below water vapor, CO2, CH4, NO2 that they can be safely ignored in all of the calculations.
The reason why the radiation on top of the atmosphere has lower temperature radiation on absorbtion lines is that all the higher temperature radiation closer to the surface is absorbed by the higher layers of the atmosphere. Actually, if you increased the amount of absorbing gases, the radiating temperature on the absorbtion lines would fall because the radiation we can measure on top of the atmosphere, would originate from higher layers of the atmosphere, which are colder. And the higher temperature radiation in the window should be mostly from the surface. The ability of the atmosphere to radiate in the atmospheric window wavelengths is negligable (hence the window part).
[…] By the time the solar radiation has reached the earth it has reduced in intensity by a factor of around 46,000 (see the Inverse Square Law or The Sun and Max Planck Agree – Part Two): […]
[…] The most challenging part is that energy flowing in – shortwave radiation from the sun – passes through these “greenhouse” gases like they don’t exist (although strictly speaking there is a small effect from CO2 in absorption of solar radiation). That’s because solar radiation is almost all in the 0.1-4μm band (see The Sun and Max Planck Agree – Part Two). […]
[…] For more on this, see The Sun and Max Planck Agree – Part Two. […]
[…] To see how we can differentiate the solar and terrestrial radiation, take a look at The Sun and Max Planck Agree – Part Two. […]
[…] The solar radiation has been normalized to the value at the earth’s surface (because it’s a long way from the sun to the earth – check out The Sun and Max Planck Agree – Part Two): […]
[…] I have the same argument about this one graph from Goody & Yung’s textbook. You can see my equivalent graph in 4th & 5th figures of The Sun and Max Planck Agree – Part Two. […]
[…] 99% of solar radiation is shortwave, while 99% of all terrestrial radiation is longwave. This makes it easy to separate the two. See The Sun and Max Planck Agree – Part Two. […]
[…] system is “shortwave radiation”, which by convention means radiation below 4 μm. See The Sun and Max Planck Agree – Part Two for […]
As CO2 absorbs most strongly in three bands of ~2.7, 4.3 and 15 micrometres it is definitely going to absorb far more energy from the incoming solar radiation than it is from the feeble radiation emitted by the Earth’s surface.
The Earth’s radiation will not impact the 2.7 and 4.3 bands – effectively zero absorption – whilst they will absorb significant amounts from the solar insolation as it is significantly more powerful.
You show a scale factor of 10 to the minus 6 in your posts.
All the literature I can find states ~50% of the solar radiation is infrared.
The 2.7 band coincides with a calculated temperature of ~1073 K and the 4.3 band coincides with a calculated temperature of ~673 K whilst the 15 band coincides with a temperature of ~193 K.
Why would absorbing radiation with a peak generated by 193 K have more thermal effect than radiation with peaks of 1073 and 673 K ?
It doesn’t make sense.
The solar radiation is heating CO2 on the way in far more than the feeble outgoing radiation ever could.
Rosco,
You seem to forget that the Sun is far away.
The Sun emits about 2 billion times more than the Earth surface, but the distance of the Earth from the Sun is large and the amount of solar radiation that hits the Earth is less than the radiation from the Earth surface. The emission from the Earth to the space must be nearly equal to the amount of solar radiation absorbed by by the Earth. Part of the solar radiation is reflected, and the radiation from the Earth to space is less than the emission from the surface. For this reason the radiation from the Earth surface can be larger.
Only 1.5% of the energy of solar radiation is at wavelengths of more than 2.3 µm. Therefore the absorption of the 2.7 µm band has only a small effect. Changes in that absorption from added CO2 are really minimal.
At 4 µm the solar radiation is much weaker in the atmosphere than the radiation from the atmosphere itself or from the Earth surface.
Rosco,
I don’t think you understood the article at all.
The solar radiation absorbed by the earth is approximately equal to the terrestrial radiation emitted by the climate system. How can this possibly be when sun is so much hotter? It’s some kind of mystery..
Then let’s pick one point, the 15um band..
Under the text “If we take the average of 30% of solar reflected, and at an angle from the zenith of 45°, we will have these curves:”
– we have a graph which shows that the terrestrial radiation at 15 μm is much higher than solar radiation. I’m travelling and don’t have a computer to hand but it’s at least 100x greater.
If you can find a way to get solar radiation at 15um greater than terrestrial radiation at 15um on or around the earth’s climate system you will have either disproved Planck’s law or the inverse square law.
So I’m not sure what your point was except to demonstrate that you haven’t read the article and didn’t try to follow the basic maths.
Roscoe: Perhaps it will help to distinguish between visible (0.4-0.7 um), solar infrared (0.7-4.0 um), and thermal infrared (4.0-100 um). Visible and solar infrared combined are called SWR (short-wavelength radiation). You are correct when you say that solar infrared comprises about 50% of the downward SWR flux. Thermal infrared, the wavelengths emitted by the earth and atmosphere, are called LWR (long-wavelength radiation).
CO2’s 15 um band absorbs where LWR is near its maximum and doesn’t absorb SWR at all. CO2’s 2.7 um band absorbs where SWR is ONLY about 1% of its peak intensity in the visible and it doesn’t absorb LWR. CO2’s 4.3 um band absorbs little SWR and LWR. For the earth to maintain a constant temperature, “post-albedo” incoming SWR (after reflection by clouds) must be equal to outgoing LWR. So CO2 has a bigger effect on outgoing LWR than incoming SWR.
When you associate 15 um radiation and 193 degK, you are using Wien’s displacement law, which tells you the relationship between a blackbody’s temperature and the wavelength of peak emission. Unfortunately, Wien’s displacement law causes much confusion, because a blackbody also emits more power at EVERY WAVELENGTH as its temperature rises. (Check the plots above and elsewhere.) So CO2 emits far more power at 15 um when its temperature is 300 degC than when it is 193 degC. To a first approximation: 1) Absorption of radiation is independent of the absorber’s temperature. 2) Total emission increases with the 4th power of temperature, the Stefan-Boltzman Law. Technically, the S-B law applies to only blackbodies; gases are more complicated. 3) Don’t use Wien’s law for anything (except the emission maximum.)
You can see a clearer picture with the log of wavelength on the x-axis at the link below (the last graph in the post). Note the vertical axis has been “normalized” so that the areas underneath are equal.
Frank,
The common wavelength distribution is also drawn to have equal areas underneath to represent equal power. Distortion of the areas is thus not the misleading factor in having the 15 µm peak significantly off the maximum. The misleading factor is in not noticing that the absorption peaks get broader with increasing wavelength. The widths of the peaks are less dependent on the wavenumber (inverse of wavelength) when considered as function of wavenumber. For that reason the spectrum vs. wavenumber gives a more correct view of the importance of absorption of various absorption peaks than the spectrum vs. wavelength. The CO2 absorption peak of 667 1/cm (15 µm) is close to the maximum of the wavenumber spectrum of the Earth surface.
The power of emission at a fixed wavelength grows exponentially (with decreasing 1/T) at low temperatures, when the wavelength is a small fraction of that at the maximum point of the energy spectrum for the temperature. Far on the other side the power grows linearly with temperature. Thus the power grows always over the whole temperature range and for all wavelengths, but the faster growth at shorter wavelengths leads to Wien’s displacement law and also to the Stefan-Boltzmann’s law of fourth power that’s between the linear and exponential behaviors in speed of growth.