In the model simulations up until now the pCO2 band has been a constant – a fixed absorption band between the wavenumbers 600-800 cm-1. In this article we will see what happens when the band shape changes, but the “area under the curve” stays the same.
If you are new to the series, take a look at Part Two (and probably a good idea to take a look the subsequent parts to see how the model and the results develop). pH2O and pCO2 are not the real molecules, but have a passing resemblance to them. This allowing us to see changes in top of atmosphere (TOA) flux and DLR (back radiation) as they take on different characteristics, and as the concentration of pCO2 is changed.
In Part Four we saw the effects of the pH2O band overlapping the pCO2 band. The models results in this article keep the same concept, but have widened the pH2O absorption slightly (extended to a lower wavenumber = higher wavelength).
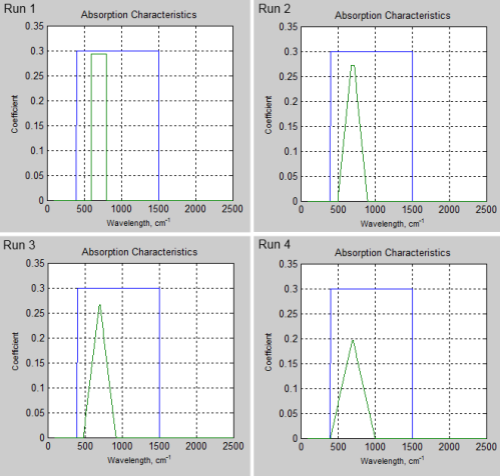
The absorption characteristics for the four model runs:
Figure 1 – Blue is pH2O absorption, Green is pCO2 absorption
What happens is that the total band absorptance (the area under the curve) is the same for each run. The pCO2 absorption profile in Run 1 is the same as in all the previous articles in the series. Then in subsequent runs the edges of the band are widened, the “top” is made thinner, and the peak value is adjusted to keep the “total band absorptance” the same.
The code in the notes is specifically for Run 4. The code has to slightly change for each run, as I am changing the shape of the band in each run.
Each model run simulates 20 different pCO2 concentrations. The TOA spectrum for a few results is shown, along with temperature profile, absorption characteristics and the summary of TOA flux vs pCO2 concentration.
The stratospheric temperature is fixed at 215K – to understand why I’ve chosen to fix it, see the discussion in Part Five.
Run 1:
Figure 2 – Click on the image for a larger view
Run 2:
Figure 3 – Click on the image for a larger view
Run 3:
Figure 4 – Click on the image for a larger view
Run 4:
Figure 5 – Click on the image for a larger view
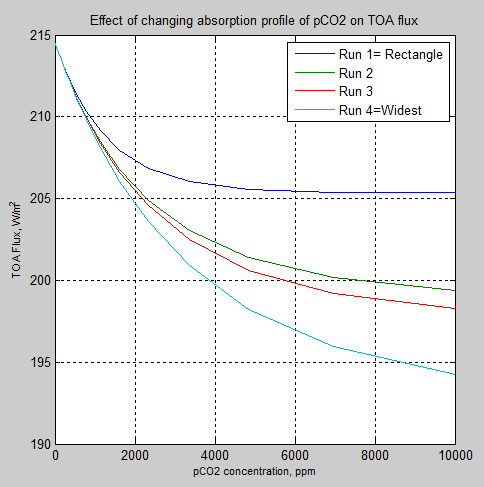
Now let’s compare the summary results from each of the four models:
Figure 6 – Changes in TOA flux
And also a reminder that as the TOA flux reduces, the radiative forcing increases – because a reduction in TOA flux means less energy radiated from the planet, and therefore (all other things being equal) a heating effect.
So if we plot the results as radiative forcing instead:
Figure 7 – Radiative Forcing
Effect of Band Shape
The reason for adding this complexity to the model is because real CO2 has an absorption band which is not “rectangular”. The band has a peak absorption around 667 cm-1 (15 μm) which then falls off on either side.
In the results up until now we have seen that different effects contribute to the eventual “saturation” of increasing pCO2 . The particular conditions determine where that saturation takes place.
What these results show is that with a “rectangular” absorption profile the “saturation” takes place much sooner than with a wider band.
Perhaps that is not very surprising to many people.
If it is surprising, then for a conceptual model think about a very strong, very narrow band reaching saturation quite quickly. Whereas if you spread the same absorption over a wider band then each wavelength/wavenumber can contribute more as each wavelength takes longer to reach saturation.
I find it hard to write a good conceptual explanation. Perhaps better to suggest that readers who find the results surprising to reread Part Two to Part Five and review the results from each of the models.
Logarithmic Slopes
I also played around with a logarithmic fall-off instead of a straight line slope. The results were very similar but not identical. I applied the same normalization to the area under the curve as in the previous models.
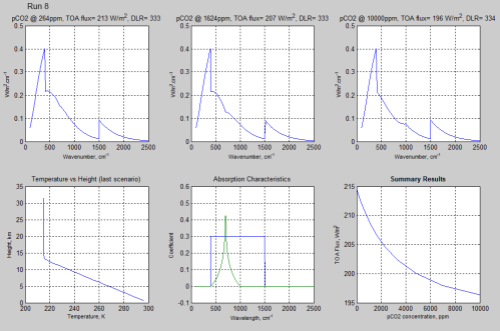
For example, Run 8, which is similar to Run 4 (similar in that the wavenumbers for the zero points and the “flat top” are identical):
Figure 8 – Click on the image for a larger view
The value of TOA flux at the highest pCO2 concentration of Run 8 was 196.3 W/m², compared with 194.3 W/m² in Run 4.
As less absorption has been “moved out” to the “wings” of the band we would expect that the logarithmic slopes have slightly less effect than the straight line slopes.
Reducing pH2O Effectiveness
I also tried halving the absorption characteristics of pH2O to see the effect. Runs 1-4 were repeated as Runs 9-12 with the only change being the halving of the absorption coefficient of pH2O:
Figure 9
Of course, the total TOA flux is higher in all cases – as pH2O’s effectiveness has been reduced. If you compare the results with Figure 6 you see that curves are quite similar.
Conclusion
Most of the ideas that people have about “saturation” of CO2 are based on a very limited appreciation of how radiative transfer takes place.
The fact that CO2 has very strong absorption in the central part of its band has led to a false conclusion that, therefore, more CO2 can have no further effect.
As we have seen in Part Three, just considering the basic fact of emission totally changes that perspective.
Then we see the effects of emitting from different heights in the atmosphere, and how changing temperature profiles (Part Four) affects that emission.
Another area of confusion is with the idea that because water vapor has absorption across the CO2 band and because water vapor has a much higher concentration than CO2 in the lower troposphere, therefore there is nothing more for CO2 to affect. We saw in Part Four that even making the absorption coefficient of pH2O the same as pCO2 – so that the DLR (back radiation) results were swamped from pH2O – even then the TOA flux was considerably affected by increasing concentrations of pCO2. And in the real world, the real water vapor molecule has considerably less absorption than CO2 around the 15 μm / 667 cm-1 band.
Finally we have seen how a band with a different shape causes quite different results – having a “spreading band” more like the real-world molecules also increases the effect of pCO2 at higher concentrations (less “saturation”).
Well, these are all “model results”
Which means they are the solution to some mathematical equations. If the equations are wrong, then the model is wrong (and if the model writer and his huge team made a mistake in implementation, this model is also wrong).
Yet most of the criticism of “the standard results” in the literature (and as reported by the IPCC) only shows that the critics don’t even know what the equations are.
The usual “explanations” of why the standard results are wrong fall into two categories:
- The writers don’t state and solve the radiative transfer equations (see Part Six), but solve something else entirely. They don’t critique the standard equations, a necessary step to demonstrate the standard theory wrong. Going out on a limb, I would say that they don’t know what the standard theory is.
- The writers create poetic words with no equations, or happily state one particular fact or figure as a breathless QED. For example, the relative concentration of water vapor vs CO2, the fact that 95% of surface radiation is absorbed within y meters by CO2 at wavelength x.
I hope that most people who have read this series have :
- a better understanding of how radiative transfer works
- a vague idea at least of what equations we would expect to see in a successful “critique”
- an appreciation of how complex the real world is and why a 2 minute calculator result is unlikely to provide insight
There may be more to come from this model. I would like to be able to include some real data on CO2 and play around with it. That might be too much work. You never know until you start.
And of course, requests and suggestions of model results you would like to see are welcome, even if no guarantees are made that the requests will be fulfilled.
Other articles:
Part One – a bit of a re-introduction to the subject.
Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only.
Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.
Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.
Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”
Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies
Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking
Part Eight – interesting actual absorption values of CO2 in the atmosphere from Grant Petty’s book
Part Nine – calculations of CO2 transmittance vs wavelength in the atmosphere using the 300,000 absorption lines from the HITRAN database
Part Ten – spectral measurements of radiation from the surface looking up, and from 20km up looking down, in a variety of locations, along with explanations of the characteristics
Part Eleven – Heating Rates – the heating and cooling effect of different “greenhouse” gases at different heights in the atmosphere
Part Twelve – The Curve of Growth – how absorptance increases as path length (or mass of molecules in the path) increases, and how much effect is from the “far wings” of the individual CO2 lines compared with the weaker CO2 lines
And Also –
Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.
Notes
Note 1: Sharp-eyed observers will eventually point out that I didn’t make use of the diffusivity approximation from Part Six in my model.
Note 2: The Matlab code, v0.5.0
The code is easiest seen by downloading the word doc, but here it is for reference:
======= v0.5.0 ======================
% RTE = Radiative transfer equations in atmosphere
% Objective – allow progressively more complex applications
% to help people see what happens in practice in the atmosphere
% v0.2 allow iterations of one (or more) parameter to find the TOA flux vs
% changed parameter
% v0.3 add emissivity = absorptivity ; as a function of wavelength. Also
% means that downward and upward radiation must be solved, plus iterations
% to allow temperature to change to find stable solution. Use convective
% adjustment to the lapse rate
% v0.3.1 changes the method of defining the atmosphere layers for radiation
% calculations, to have roughly constant mass for each layer
% v0.3.2 tries changing lapse rates and tropopause heights
% v0.3.3 revises element boundaries as various problems found in testing of
% v0.3.2
% v0.4.0 – introducing overlap of absorption bands
% v0.4.1 – warmer stratosphere to show “saturation” of simple bands
% v0.5.0 – introducing some band “shapes” – instead of just “rectangular”
% absorption bands. pH2O band widened to a min of 400cm^-1
clear % empty all the variables, so previous runs can have no effect
disp(‘ ‘);
disp([‘—- New Run —- ‘ datestr(now) ‘ —-‘]);
disp(‘ ‘);
% SI units used unless otherwise stated
% ============= Define standard atmosphere against height ================
% first a “high resolution” atmosphere
% zr = height, pr = pressure, Tr = temperature, rhor = density
Ts=300; % define surface temperature
ps=1.013e5; % define surface pressure
Ttropo=215; % define tropopause temperature
% nmv=2.079e25; % nmv x rho = total number of molecules per m^3, not yet
% used
maxzr=50e3; % height of atmosphere
numzr=5001; % number of points used to define real atmosphere
zr=linspace(0,maxzr,numzr); % height vector from sea level to maxzr
[pr Tr rhor ztropo] = define_atmos_0_3(zr,Ts,ps,Ttropo); % function to determine (or lookup) p, T & rho
% Create “coarser resolution” atmosphere – this reduces computation
% requirements for absorption & emission of radiation
% z, p,Tinit,rho; subset of values used for RTE calcs
numz=30; % number of boundaries to consider (number of layers = numz-1)
minp=1e3; % top of atmosphere to consider in pressure (Pa)
% want to divide the atmosphere into approximately equal pressure changes
dp=(pr(1)-minp)/(numz); % finds the pressure change for each height change
zi=zeros(1,numz); % zi = lookup vector to “select” heights, pressures etc
for i=1:numz % locate each value
zi(i)=find(pr<=(pr(1)-i*dp), 1); % gets the location in the vector where
% pressure is that value
end
% now create the vectors of coarser resolution atmosphere
% z(1) = surface; z(numz) = TOA
% T, p, rho all need to be in the midpoint between the boundaries
% T(1) is the temperature between z(1) and z(2), etc.
z=zr(zi); % height
pb=pr(zi); % pressure at boundaries
Tb=Tr(zi); % starting temperature at boundaries
rhob=rhor(zi); % density at boundaries
% now calculate density, pressure and temperature within each layer
for i=1:numz-1
dz(i)=z(i+1)-z(i); % precalculate thickness of each layer
Tinit(i)=(Tb(i+1)+Tb(i))/2; % temperature in midpoint of boundary
p(i)=(pb(i+1)+pb(i))/2; % pressure in midpoint of boundary
rho(i)=(rhob(i+1)+rhob(i))/2; % density in midpoint of boundary
end
% ============ Set various values =========================
lapse=6.5e-3; % environmental lapse rate in K/m ** note potential conflict with temp profile already determined
% currently = max lapse rate for convective adjustment, but not used to
% define initial temperature profile
ems=0.98; % emissivity of surface
cp=1000; % specific heat capacity of atmosphere, J/K.kg
convadj=true; % === SET TO true === for convective adjustment to lapse rate = lapse
isothermal_strato=true; % ======= SET to true === for fixed and isothermal stratospheric temperature
emission=true; % ==== SET TO true ==== for the atmosphere to emit radiation
tstep=3600*12; % fixed timestep of 1hr
nt=100; % number of timesteps
% work in wavenumber, cm^-1
dv=5;
v=100:dv:2500; % wavenumber (=50um – 4um)
numv=length(v);
rads=ems.*planckmv(v,Ts); % surface emissive spectral power vs wavenumber, v
disp([‘Tstep= ‘ num2str(tstep/3600) ‘ hrs , No of steps= ‘ num2str(nt) ‘, numz= ‘ …
num2str(numz) ‘, minp= ‘ num2str(minp) ‘ Pa, Lapse= ‘ num2str(lapse*1e3) ‘ K/km’]);
% ============== Introducing the molecules ==============================
% need % mixing in the atmosphere vs height, % capture cross section per
% number per frequency, pressure & temperature broadening function
nummol=2; % number of radiatively-active gases
mz=ones(nummol,numz-1); % initialize mixing ratios of the gases
% specific concentrations
% pH2O = pretend H2O
emax=17e-3; % max mixing ratio (surface) of 17g/kg
mz(1,:)=(ztropo-z(1:numz-1)).*emax./ztropo; % straight line reduction from surface to tropopause
mz(1,(mz(1,:)<0))=5e-6; % replace negative values with 5ppm, ie, for heights above tropopause
% pCO2 = pretend CO2
% mz(2,:)=3162e-6; % a fixed mixing ratio for pCO2
% absorption coefficients
k1=0.3; % arbitrary pick – in m2/kg while we use rho
k2=0.3; % likewise
a=zeros(nummol,length(v)); % initialize absorption coefficients
a(1,(v>=400 & v<=1500))=k1; % wavelength dependent absorption
% define some parameters for the pCO2 band to make it easier to adjust
% and then “normalize” this to the original total band absorptance =
% integral(k.dv) which was 0.3 x 200cm-1 = 60
% note that v1-4 need to be multiples of dv
kint=60; % original total
v2=695;v3=705; % peak “flat top” of band
v1=400;v4=1000; % edges where band absorption coefficient falls to zero
% now optical thickness will fall off as a straight line, later we can try
% transmittance = exp(-tau) falling off as a straight line
% find the location within vector v of these points
vi1=find(v>=v1,1);vi2=find(v>=v2,1);vi3=find(v>=v3,1);vi4=find(v>=v4,1);
a(2,(v>=v2 & v<=v3))=k2; % flat top of band
for i=vi1:vi2 % rising edge of band
a(2,i)=(v(i)-v1)/(v2-v1)*k2;
end
for i=vi3:vi4 % falling edge of band
a(2,i)=(v4-v(i))/(v4-v3)*k2;
end
knint=sum(a(2,:))*dv; % this adjusts the whole band absorption to make the
% integral the same as the original
a(2,:)=a(2,:)*kint/knint;
disp([‘v1-4= ‘ num2str(v1) ‘, ‘ num2str(v2) ‘, ‘ num2str(v3) ‘, ‘ num2str(v4) ‘, total abs for pCO2 = ‘ num2str(sum(a(2,:))*dv)]);
% plot(v,a) % to show absorption characteristics if required
% return % if want to early for review of absorption plot
% ========== Scenario loop to change key parameter =======================
% for which we want to see the effect
%
nres=20; % number of results to calculate ******
flux=zeros(1,nres); % TOA flux for each change in parameter
fluxd=zeros(1,nres); % DLR for each change in parameter, not really used yet
par=zeros(1,nres); % parameter we will alter
% this section has to be changed depending on the parameter being changed
% now = pCO2 conc.
par=logspace(-5,-2,nres); % values vary from 10^-5 (10ppm) to 10^-2.5 (3200ppm)
% par=1; % kept for when only one value needed
% ================== Define plots required =======================
% last plot = summary but only if nres>1, ie if more than one scenario
% plot before (or last) = temperature profile, if plottemp=true
% plot before then = surface downward radiation
plottemp=true; % === SET TO true === if plot temperature profile at the end
plotdown=false; % ====SET TO true ==== if downward surface radiation required
plotabs=true; % SET TO true ======= if absorption characteristics required
if nres==1 % if only one scenario
plotix=1; % only one scenario graph to plot
nplot=plottemp+plotdown+plotabs+1; % number of plots depends on what options chosen
else % if more than one scenario, user needs to put values below for graphs to plot
plotix=[round(nres/2) round(nres*3/4) nres]; % graphs to plot – “user” selectable
% plotix=[]; % don’t want to plot any scenarios
nplot=length(plotix)+plottemp+plotdown+plotabs+1; % plot the “plotix” graphs plus the summary
% plus the temperature profile plus downward radiation, if required
end
% work out the location of subplots
if nplot==1
subr=1;subc=1; % 1 row, 1 column
elseif nplot==2
subr=1;subc=2; % 1 row, 2 columns
elseif nplot==3 || nplot==4
subr=2;subc=2; % 2 rows, 2 columns
elseif nplot==5 || nplot==6
subr=2;subc=3; % 2 rows, 3 columns
else
subr=3;subc=3; % 3 rows, 3 columns
end
for n=1:nres % each complete run with a new parameter to try
% — the line below has to change depending on parameter chosen
% to find what the stability problem is we need to store all of the
% values of T, to check the maths when it goes unstable
mz(2,:)=par(n); % this is for CO2 changes
% lapse=par(n); % this is for lapse rate changes each run
disp([‘Run = ‘ num2str(n)]);
T=zeros(nt,numz-1); % define array to store T for each level and time step
T(1,:)=Tinit; % load temperature profile for start of scenario
% remove??? T(:,1)=repmat(Ts,nt,1); % set surface temperature as constant for each time step
% First pre-calculate the transmissivity and absorptivity of each layer
% for each wavenumber. This doesn’t change now that depth of each
% layer, number of each absorber and absorption characteristics are
% fixed.
% n = scenario, i = layer, j = wavenumber, k = absorber
trans=zeros(numz-1,numv); abso=zeros(numz-1,numv); % pre-allocate space
for i=1:numz-1 % each layer
for j=1:numv % each wavenumber interval
trans=1; % initialize the amount of transmission within the wavenumber interval
for k=1:nummol % each absorbing molecule
% for each absorber: exp(-density x mixing ratio x
% absorption coefficient x thickness of layer)
trans=trans*exp(-rho(i)*mz(k,i)*a(k,j)*dz(i)); % calculate transmission, = 1- absorption
end
tran(i,j)=trans; % transmissivity = 0 – 1
abso(i,j)=(1-trans)*emission; % absorptivity = emissivity = 1-transmissivity
% if emission=false, absorptivity=emissivity=0
end
end
% === Main loops to calculate TOA spectrum & flux =====
% now (v3) considering emission as well, have to find temperature stability
% first, we cycle around to confirm equilibrium temperature is reached
% second, we work through each layer
% third, through each wavenumber
% fourth, through each absorbing molecule
% currently calculating surface radiation absorption up to TOA AND
% downward radiation from TOA (at TOA = 0)
for h=2:nt % main iterations to achieve equilibrium
radu=zeros(numz,numv); % initialize upward intensity at each boundary and wavenumber
radd=zeros(numz,numv); % initialize downward intensity at each boundary and wavenumber
radu(1,:)=rads; % upward surface radiation vs wavenumber
radd(end,:)=zeros(1,numv); % downward radiation at TOA vs wavenumber
% units of radu, radd are W/m^2.cm^-1, i.e., flux per wavenumber
% h = timestep, i = layer, j = wavenumber
% Upward (have to do upward, then downward)
Eabs=zeros(numz-1); % zero the absorbed energy before we start
for i=1:numz-1 % each layer
for j=1:numv % each wavenumber interval
% first calculate how much of each monochromatic ray is
% transmitted to the next layer
radu(i+1,j)=radu(i,j)*tran(i,j);
% second, add emission at this wavelength:
% planck function at T(i) x emissivity (=absorptivity)
% this function is spectral emissive power (pi x intensity)
radu(i+1,j)=radu(i+1,j)+abso(i,j)*3.7418e-8.*v(j)^3/(exp(v(j)*1.4388/T(h-1,i))-1);
% Change in energy = dI(v) * dv (per second)
% accumulate through each wavenumber
% if the upwards radiation entering the layer is more than
% the upwards radiation leaving the layer, then a heating
Eabs(i)=Eabs(i)+(radu(i,j)-radu(i+1,j))*dv;
end % each wavenumber interval
end % each layer
% Downwards (have to do upward, then downward)
for i=numz-1:-1:1 % each layer from the top down
for j=1:numv % each wavenumber interval
% first, calculate how much of each monochromatic ray is
% transmitted to the next layer, note that the TOA value
% is set to zero at the start
radd(i,j)=radd(i+1,j)*tran(i,j); % attentuation..
% second, calculate how much is emitted at this wavelength,
radd(i,j)=radd(i,j)+abso(i,j)*3.7418e-8.*v(j)^3/(exp(v(j)*1.4388/T(h-1,i))-1); % addition..
% accumulate energy change per second
Eabs(i)=Eabs(i)+(radd(i+1,j)-radd(i,j))*dv;
end % each wavenumber interval
dT=Eabs(i)*tstep/(cp*rho(i)*dz(i)); % change in temperature = dQ/heat capacity
if isothermal_strato && z(i)>=ztropo % if we want to keep stratosphere at fixed temperature
T(h,i)=T(h-1,i);
else
T(h,i)=T(h-1,i)+dT; % calculate new temperature
if T(h,i)>500 % Finite Element analysis problem
disp([‘Terminated at n= ‘ num2str(n) ‘, h= ‘ num2str(h) ‘, z(i)= ‘ num2str(z(i)) ‘, i = ‘ num2str(i)]);
disp([‘time = ‘ num2str(h*tstep/3600) ‘ hrs; = ‘ num2str(h*tstep/3600/24) ‘ days’]);
disp(datestr(now));
return
end
end
% need a step to see how close to an equilibrium we are getting
% not yet implemented
end % each layer
% now need convective adjustment
if convadj==true % if convective adjustment chosen..
for i=2:numz-1 % go through each layer
if (T(h,i-1)-T(h,i))/dz(i)>lapse % too cold, convection will readjust
T(h,i)=T(h,i-1)-(dz(i)*lapse); % adjust temperature
end
end
end
end % iterations to find equilibrium temperature
flux(n)=sum(radu(end,:))*dv; % calculate the TOA flux
fluxd(n)=sum(radd(1,:))*dv; % calculate the DLR total
% === Plotting specific results =======
% Decide if and where to plot
ploc=find(plotix==n); % is this one of the results we want to plot?
if not(isempty(ploc)) % then plot. “Ploc” is the location within all the plots
subplot(subr,subc,ploc),plot(v,radu(end,:)) % plot wavenumber against TOA emissive power
xlabel(‘Wavenumber, cm^-^1′,’FontSize’,8)
ylabel(‘W/m^2.cm^-^1′,’FontSize’,8)
title([‘pCO2 @ ‘ num2str(round(par(n)*1e6)) ‘ppm, TOA flux= ‘ num2str(round(flux(n)))…
‘ W/m^2, DLR= ‘ num2str(round(fluxd(n)))])
% —
%subplot(subr,subc,ploc),plot(T(end,:),z(2:numz)/1000)
%title([‘Lapse Rate ‘ num2str(par(n)*1000) ‘ K/km, Total TOA flux= ‘ num2str(round(flux(n))) ‘ W/m^2’])
%xlabel(‘Temperature, K’,’FontSize’,8)
%ylabel(‘Height, km’,’FontSize’,8)
grid on
end
end % end of each run with changed parameter to see TOA effect
if plotdown==true % plot downward surface radiation, if requested
plotloc=nplot-plottemp-plotabs-(nres>1); % get subplot location
subplot(subr,subc,plotloc),plot(v,radd(2,:)) % plot wavenumber against downward emissive power
title([‘Surface Downward, W/m^2.cm^-^1, Total DLR flux= ‘ num2str(round(fluxd(n))) ‘ W/m^2’])
xlabel(‘Wavenumber, cm^-^1′,’FontSize’,8)
ylabel(‘W/m^2.cm^-^1′,’FontSize’,8)
grid on
end
if plottemp==true % plot temperature profile vs height, if requested
plotloc=nplot-plotabs-(nres>1); % get subplot location
subplot(subr,subc,plotloc),plot(T(end,:),z(2:numz)/1000)
title(‘Temperature vs Height (last scenario)’)
xlabel(‘Temperature, K’,’FontSize’,8)
ylabel(‘Height, km’,’FontSize’,8)
grid on
end
if plotabs==true % plot show absorption characteristics if required
plotloc=nplot-(nres>1); % get subplot location
subplot(subr,subc,plotloc),plot(v,a) %
title(‘Absorption Characteristics’)
xlabel(‘Wavelength, cm^-^1′,’FontSize’,8)
ylabel(‘Coefficient’,’FontSize’,8)
grid on
end
if nres>1 % produce summary plot – TOA flux vs changed parameter
subplot(subr,subc,nplot),plot(par*1e6,flux)
title(‘Summary Results’,’FontWeight’,’Bold’)
ylabel(‘TOA Flux, W/m^2′,’FontSize’,8)
xlabel(‘pCO2 concentration, ppm’,’FontSize’,8) % ==== change label for different scenarios =========
grid on
end
disp([‘—- Complete End —- ‘ datestr(now) ‘ —-‘]);








ScienceOfDoom – thanks for doing these posts! Even for those of us very familiar with the equations and with some physical intuition on how it all works, your specific simple models are quite instructive.
Have you thought about writing some of this up as a more formal review paper? At least to post on arXiv.org, and maybe there are some journals that would appreciate it (I’m thinking something along the lines of RP’s recent Physics Today article for instance).
Perhaps one paper for American Journal of Physics, oriented to teachers? Thanks for writing your posts,
An exponential decay of the line wings is effectively equivalent to a Doppler broadened line. You only see that at low pressures corresponding to high altitudes. A Lorentz profile has much broader wings. I suppose you will get to that in a post later in the series.
In fact, it might be useful to describe why lines have a finite width at all. Perhaps that’s in an earlier post I missed.
I definitely plan to cover that subject, whether I can usefully cover it in the model is what I’m wondering. Well, I will see how I go.
“nmv=2.079e25; % nmv x rho = total number of molecules per m^3, not yet
% used”
Avogadro’s number = 6.022141 × 10^23
One mole equals 22.4 liters.
6.022141×10^23
mol−1
1 l = .001 m^3
1000/22.4= 44.6428 mol/m^3
44.6428 * 6.0221415e23 = 2.68845e25 molecules per m^3
Why the difference? Curious.
If you look at the MODTRAN text report, the concentrations are in atmosphere centimeters/kilometer (effectively mass*path length standardized to 1 atmosphere partial pressure and a path length of 1 cm) not molecules/m3. For example, oxygen at the surface is 1.9E4 atm cm/km. That means that if all the oxygen molecules in a kilometer vertical path starting at the surface were put in a container with wall perpendicular to the surface at 1 atm pressure, the container would have a height of 19,000 cm or 19% by volume. Mass path is a more convenient number because all you have to do is multiply it by the absorption coefficient (with the correct units) and you get optical depth.
That’s also the concept that he who shall not be named failed to grasp.
Hello SOD
RE: J. Kauffman’s IR Spectrum of Philadelphia Summer Air.
He used a Perkin-Elmer Spectrum 1000 FT-IR operating in absorbance mode and 7 cm gas cell with new KBr windows.
The cell was first filled argon and the automatic baseline program was run to give a baseline”flat” to within +/- 0.002 absorbance unit.
Outside was drawn into the cell by aspiration and the spectrum was the recorded. The date was June 28, 1999. The concentration of CO2 at this date was ca 368 ppmv for dry air.
The area under the peaks was determined with a planimeter. Water vapor was 92% of the peak area and carbon dioxide was 8%
The earth’s thermal IR emision peaks at ca 500 wave numbers and there is little thermal IR emission above 1,000 wave numbers.
The absorbance of the CO2 peak at ca 670 wave numbers is about 0.025. A cell 7 meters (23 feet) in lenght filled with this air would absorb greater than 99 % of the thermal IR at 670 wave numbers. At lower temperature (e.g.. 15 deg C) and humidity the CO2 peak would have a slightly greater absorbance.
Note that the CO2 peak is a very sharp spike.
Unfortunately this short paper in J. Chem. Ed. is behind a pay wall. I used my son’s account at SFU to obtain the article thru the university’s server.
Harold Pierce Jr:
And what do you conclude from this paper?
(And can you cite it – title, date, journal).
Harold Pierce Jr.,
Eyeballing the spectra calculated at SpectralCalc, that looks about right. If anything, it’s too high for CO2. But then the experiment was carried out in a city. It’s likely that the surface concentration of CO2 was a lot higher than 368 ppmv. At 368 ppmv CO2, the minimum transmittance at 667 cm-1 for a 7 cm cell is about 0.75. Calculating the water vapor spectrum requires knowing the relative humidity and temperature. Is that data in the paper?
Scanning the spectrum from the paper and uploading the image should fall under fair use. What was the range covered by the spectrum?
Btw, the path length of the atmosphere as a column at 1 atmosphere is about 8E8 cm. While the mixing ratio of water vapor is higher at the surface, it falls off rapidly with altitude, CO2 mixing ratio doesn’t.
I can make it even worse looking. Taking the mid-latitude summer atmospheric profile and calculating radiance observed at the surface at 375ppmv CO2 by MODTRAN gives 310.42 W/m2 for clear sky conditions. Setting CO2 to zero gives 297.39 W/m2. So CO2 only contributes 4.2 % of the total IR radiation seen by the surface. Less than that if you include the radiance from 0-100 cm-1 and above 1500 cm-1.
I’ll echo SoD here: What do you conclude from that?
And before you answer, read Part Four and Part Five.
Helllo SOD!
Here is the reference:
“Water in the Atmosphere”
Joel M. Kauffman
Department of Chemistry and Biochemistry
University of the Sciences in Philadelphia
Philadelphia, PA 19104
Journal of Chemical Education, 2004, B81(8), p 1229-30
Publication Date: August 1, 2004
SOD asks, “And what do you conclude from this paper?”
I conclude that CO2 contributes little to the so-called greenhouse effect and that you are wasting a lot of time and effort on a non-problem.
Harold: I’ll try to explain where Kauffman has gone wrong with his IR analysis. (Some of the rest of the paper is similarly flawed.) Perhaps then you will understand why DeWitt said: “Kauffman’s paper is embarrassingly bad. Passing out copies isn’t going to do your reputation any good. Worse, it makes the rest of us who don’t buy into catastrophic global warming look bad too.”
Absorbance coefficients for more than 2.5 million lines for atmospheric components can be found in the HITRAN database, but this information is not very accessible to non-specialists. So Professor Kauffman did something all good science teachers encourage their students to do – he performed a simple experiment. Unfortunately he made a few mistakes and compounded them by publishing in journals unprepared to properly review his work. (According to their website, JSE publishes “original research on consciousness, quantum and biophysics, unexplained aerial phenomena, alternative medicine, new energy, sociology, psychology, and much more”. This ain’t JACS.) Citing Masterton& Hurley (a first-year general chemistry textbook), Kauffman says that the earth’s thermal emission lies between 3 and 30 um (3,333 and 333 cm-1). As you can see from plots of blackbody radiation, a more sensible range is 125 to 2000 cm-1 (98% of energy) or 300 to 1300 cm-1 (80% of energy) The %s are from Wikipedia for 288 degK . So the standard IR spectrum (4000 cm-1 to about 400 cm-1) is only marginally useful: there is negligible energy flux via the stretching bands >2000 cm-1, the H2O bands around 1500 cm-1 are in a region where energy flux is low, and data for <400 cm-1 is missing. The strongest energy flux is through the CO2 band around 670 cm-1 and the partially cut off water bands at 400-600 cm-1.
Kauffman used a 7 cm path length. If pressure were constant with altitude, the atmosphere would be about 100,000 times thicker (8 km). A species that has an absorbance of 0.001 for a given wavelength in Kauffman's spectrum is lost in the baseline noise, but would have an absorbance of 100 (and permit a transmittance of only 10^-100!) passing through the earth's atmosphere. So Kauffman's spectrum misses many relevant bands (including bands from minor isotopes like C-13 and a huge families of transitions involving changing rotational energy levels superimposed on the vibrational excitation). This explains why the emission spectra you see from climate scientists have a massive CO2 band from about 600-800 cm-1, while Kauffman shows a sharp spike in the same region. (And why scientists in the publication mentioned by DeWitt below are working with a path length of 116 meters while amateurs like Kauffman are using 7 cm.)
Finally, the energy balance of the earth is determined by both absorption and emission (using a single coefficient), but the fraction of radiation absorbed depends on the intensity of the incoming radiation while the amount of radiation emitted depends on temperature (via Planck's function). Absorption is only half the story.
What answer would Kauffman have obtained if he could have done the "right" experiment? 9% or 9-26% of the greenhouse effect can be attributed to CO2. See: http://www.realclimate.org/index.php/archives/2005/04/water-vapour-feedback-or-forcing/
There is plenty of room for responsible disagreement with the IPCC's consensus without Kauffman's flawed work.
Harold Pierce Jr:
Thank you for the reference.
Did you read Part Four and Five?
The change in TOA flux from CO2 is the value you should be interested in.
Yes However, I am organic chemist and this atuff is really tough and a struggle for me.
Repost reply to DP First attempt didn’t show up
Hello DeWitt Payne
You can find the spectrum at:
Click to access climate-change-re-examined.pdf
The temperature, rel humidity and air pressure were 28 deg C 76% and 750 torr, resp. The spectrum was recorded from 4000 to 400 wave numbers. KBr has a cut off at ca 400 wavenumbers. There are addditional water vapor absorptions below 400 wave numbers.
You should read his paper “Climate Change Reeamined.” In particular check out Table 1. Note the UHI effect.
BTW Kauffman is an orgainic chemist and earned his PhD at MIT in 1963. At that time, MIT had one of the best organic chemisty section on the planet and it still does. I earned by BSc (Hon) at U of Ill-UC in 1967 which was about tied with MIT in the top ten chem dept rankings. Harvard was always first in those days. Lured by the poker tables in Gardena, I then went to UC Irvine and got a PhD in 1973 where I specialized in organic chemistry.
How much CO2 was in the cell? Good question. Probably depends on the time of day the air was taken and the direction of the wind. If the sample taken early in the moning, the sea breeze might contain extra CO2 from the chemical plants and refineries in New Jersey and from big ships in the Delaware river.
Harold Pierce Jr:
Ok. It’s not an easy subject. But neither is organic chemistry.
What happens at the surface is just a consequence of what happened earlier at the top of atmosphere.
Analogy warning. Analogies prove nothing. I know. I offer it only as a conceptual guide.
Let’s say you are feeding a particular catalyst down a tube into some kind of container where a reaction is taking place.
The reaction is the thing you are really interested in – it’s where the action is.
But the actual cause that changes the reaction is how much of the catalyst you feed down the tube.
So if you want to know why the temperature and rates of your mixture are what they are, it’s all about the amount of catalyst at the surface right now.
But to know what temperature and reaction rates you will get, you therefore need to know what controls the influx of the catalyst.
Analogy over warning.
Perhaps that might be a useful analogy, perhaps not.
In lining up analogy with real world I point out that the “influx of catalyst” is actually being related via analogy to the “amount of energy leaving the planet via TOA”.
To explain the actual surface temperature at any given place on any given day you need to know (among other facts) the value of downward flux (back radiation).
But to explain how the atmosphere got to the temperature that caused it to radiate so high you need to know what has happened to the TOA flux over the last few years/decades.
If less energy leaves the planet than is absorbed by the planet, the planet heats.
So to work out how the TOA flux will change you need to know (among other factors) what effect increases in CO2 will have on the reduction in TOA flux.
Many people have repeatedly calculated this to be around 3.7W/m2 pre-feedback for a doubling of CO2.
I don’t know what the models show for immediate changes in back radiation as a result of doubling CO2. It might be zero. But that isn’t the important factor.
scienceofdoom.
I really don’t know where you are comming from here SOD. Your workshop seems to be based on altitudes above the tropopause, but you imply near surface! Just what ‘do’ you imply? 🙂
Your analogy doesn’t make sense.
Best regards, Ray Dart.
“Ray Dart”! OOPS! My ‘handle’ should be ‘suricat’.
A ‘first post’ isn’t always easy.
Best regards, Ray Dart.
I don’t know, but maybe this will help bridge a gap in understanding, if it still exists.
The article cited by Harold appears to be more directed at calling for an update to textbooks to more accurately reflect the state of the science. It’s possible that is a pretext to say that there are pervasive omissions within the science, but I’m not able to make a judgment on that. At face value, it merely argues that water vapor is not discussed as much as it should be in textbooks, which is not the same as an argument that it is ignored or omitted in the research taking place.
I’m not an expert, but it would appear that anyone who knows much about radiative physics understands that water vapor and clouds are indeed significant factors. Here is a post from RealClimate that might bridge the gap between where Harold is, and the more technical nature of ScienceOfDoom’s posts.
Salient points of the RealClimate post are:
a) Yes, we are aware that H20 and CO2 have overlap in their absorption spectra. We are also aware that H20 absorbs more than CO2 in the lower atmosphere.
b) You can establish maxima and minima values for attribution of how much each gas contributes. An estimate for the real value has to be between those two.
c) The amount of water vapor in the air is more of a feedback than a forcing.
You could argue against the use of models to make this point, but you’d have to demonstrate that there is something wrong with our understanding of how humidity relates to temperature and the absorbtivity of the gases in question, the rules for which are incorporated into the models.
http://www.realclimate.org/index.php/archives/2005/04/water-vapour-feedback-or-forcing/
Relating to what is taught in classrooms compared to what is known by researchers, it is also generally understood that one of the reasons that CO2 is not saturated has a lot to do with the expansion of the wings around the 15 micron peak. As far as what is covered in science courses, for example, David Archer covers this in his course designed for non-science majors; so, I have to believe that it is well covered in the courses designed for science majors.
http://geoflop.uchicago.edu/forecast/docs/lectures.html
I’ll see if I can wrap up my understanding in a nutshell, and I wouldn’t mind if someone corrects it.
In my mind, CO2 is not saturated on two accounts:
a) At increasing concentrations, the amount absorbed at the wavelengths to either side of the 15 micron peak increases. A picture of CO2’s absorptivity can be found here.
http://webbook.nist.gov/cgi/cbook.cgi?ID=C124389&Units=SI&Type=IR-SPEC&Index=1#IR-SPEC
b) When you increase the amount of any GHG, you raise the altitude of mean emission. Stated another way, when you increase the amount of a GHG, you raise the altitude at which a photon has a certain chance of escaping to space. The environmental lapse rate is not constant, but it has a mean which will not be changed significantly by the changes we are talking about. When you raise the mean emission altitude, you raise the altitude of the lowest temperature within the atmosphere. From there, you can follow the mean environmental lapse rate down to a higher temperature at the surface.
Final side note: What we are really talking about with climate change is an increase in energy content within the biosphere; an increase in temperature is just one of many ways that increase can manifest itself.
Harold Pierce Jr.,
Here are two observed IR atmospheric emission spectra taken simultaneously at the surface looking up and at 20 km looking down.
Note the large dip in emission in CO2 band in the 20 km looking down spectrum. That’s what causes the greenhouse effect. That deficit in emission has to be made up by higher emission at other frequencies. That can only happen if the surface is warmer than it would be if there were no dip in the emission.
Here’s a description of an FT-IR spectrometer used to measure atmospheric emission in the IR.
http://www.arm.gov/instruments/aeri
Kauffman does have a valid point that water vapor should be included in the discussion of atmospheric emission, but, as I think I showed in the MODTRAN results, it is fully understood by those actually working in the field.
Thanks, DeWitt Payne, for the diagrams in
The experimental results in “(a) 20 km looking down” for the upward radiation might be explained by the Schwarzschild equation.
The diagram labeled “(b) Surface looking up” shows on the other hand an interesting drop of radiation down to the level 160K. This would indicate that the radiative active molecules “sack” the energy from the air by converting the kinetic energy of molecules into the radiative one? This would be the cooling effect which Frank has mentioned in one of his comments, if I am correct. Is there any other interpretation of this drop?
The drop in emission in the upward looking spectrum is because there isn’t much emission in that region. That’s the 800-1200 cm-1 ‘window’.
http://amsglossary.allenpress.com/glossary/search?id=atmospheric-window1
The low apparent temperature is because the emissivity in that region is much less than 1.
In other words, air is a ”gray body”, at least in this region. I had the similar thought.
A very light gray, almost transparent.
“The low apparent temperature is because the emissivity in that region is much less than 1.”
Disagree. What the up looking instrument sees in the atmospheric window is radiation at 160K in the lower stratosphere. This is what upward looking instruments always see in the window. Surface photons are running away from the instrument.
The above are both up looking, one at Barrow and the other in the tropical Pacific. Notice the similarity and difference between Barrow and Kauffman’s “somewhere on the arctic ice”.
The above digitized spectra are qualitatively useful and show nothing out of line in Kauffman’s spectrum. It even compares well with a modern instrument from 5 km in the Andes.
What is interesting and difficult to explain is the dip to lower temperature/radiance in the saturated CO2 bands at Barrow.
gymnosperm,
Are you disagreeing that the total column absorptivity/emisivity in the window is less than one? If so, you’re wrong. At 900 cm-1, for example, the transmittance to space from the surface for the Tropical Atmosphere is 0.51. You’re seeing emission from the entire column, not a specific altitude.
The dip in the CO2 band at Barrow is easy to explain. There’s a temperature inversion during the winter. The atmosphere near the surface is colder than the atmosphere above it.
It is interesting comparing the spectrum in the Kaufmann article to the upward and downward spectra linked by DeWitt. If you read the caption, DeWitt’s comes from a polar region (little water vapor) while Kauffman’s comes from a part of the planet which is somewhat “more representative” of the atmosphere the average photon is passing through. (The 28 degK temperature is higher than average, but the average photon comes from warmer regions.) The Kauffman spectrum has the units, range and orientation normally used by organic chemists with the higher energy stretching vibrations on the left and the bending vibrations on the right. The other spectrum has energy increasing from left to right (the opposite direction) and has none of the vibrational lines because they are relatively unpopulated by blackbody radiation at 300 degK. The Kauffman spectrum is an absorption spectrum (probably with the chemist’s definition of absorbance (base 10 rather than base e). Full scale probably represents 10% of the light being absorbed by the air in the cell. A standard path length is 1 cm, but these instruments also hold 10 cm path length cells. The “looking upward” spectrum linked by DeWitt is an emission spectrum with unknown path length, but (if I remember DeWitt correctly), there would be 19? km (10? km) of atmosphere overhead if it were all present at 1 atmosphere. So the difference in path length could be up to 100,000-fold longer, but the light leaving an optically thick region of atmosphere emit a maximum of oT^4. If the maximum absorptivity of CO2 is about 2.5% in Kauffman’s spectrum, so is the emissivity. So it only takes a path length about 100 times longer (10 m) before emission begins to saturate at the blackbody limit. With roughly 1000 times more atmosphere overhead, even absorptions 1000 times weaker than the center of the CO2 band will be near the blackbody limit. So the thin spike due to CO2 at about 700 cm-1 in the Kauffman spectrum is a 100 cm-1 wide band radiating at an effective temperature of about 267 degK (about right for air near the surface of a polar ice sheet in the summer)
The mass path of the atmosphere looking upward is ~8 km at 1 atmosphere. But as you say, for top of the band you don’t need anywhere near that distance. A cold summer day looks about right. If it were winter, there would probably be a temperature inversion with the CO2 band having a higher temperature than the surface. The CO2 band looking down would be colder too.
So what was the absorbance at the CO2 peak in the Kauffman spectrum?
The spectrum was on p 735 of http://suesam.files.wordpress.com/2008/01/climate-change-re-examined.pdf I found the original citation for the spectrum at http://gamma.physchem.kth.se/~3b1740/greenhouse/H2O_FEL_LAEROBOK.PDF
The peak CO2 absorbance at 700 cm-1 was approximately 0.025 for a 7 cm path length. For a chemist, this probably implies a transmittance of 10^-0.025 (rather than e^-0.025) or 95%. So if absorptivity over a 7 cm path is about 5%. If I did the math correctly, absorbance (base 10) is 1 (90% absorptivity/emissivity) for a 2.8 m path or 2 (99% absorptivity/emissivity) for about 5 m. At the very center of this narrow spike, equilibrium between emission and absorption is developed in a very short distance.
That spectrum makes no sense. For that spectral range, water vapor absorption should be much higher relative to CO2. Maybe it’s a function of the resolution of the spectrometer. I’d need to subscribe to SpectralCalc to generate lower resolution spectra. Most of the spectral range isn’t significant for thermal IR either, so the relative areas don’t mean much. In fact, most of the CO2 area is from the 4 μm lines which are significant for absorption of incoming solar radiation but insignificant for the outgoing IR.
For a 7 cm cell at a CO2 mixing ratio of 0.00038 and a temperature of 28 C, SpectralCalc gives a transmittance minimum of 0.76, which would be an absorbance of 0.12. But that’s at maximum resolution and is limited at that temperature and pressure by the line width.
My guess would be that he didn’t allow the cell to properly equilibrate with the air and the water vapor was adsorbed by the oxide layer on the aluminum cell wall. 76% relative humidity at 28C corresponds to a water vapor mixing ratio of 0.0285. In a 7 cm cell, the transmittance minimum at 420 cm-1 is ~0.3 for an absorbance of about 0.5, not 0.05.
Frank,
I signed up for a month on SpectralCalc. I can’t reproduce Kauffman’s spectrum. It doesn’t look like the resolution is constant over the spectral range when you compare the 4 μm (2350 cm-1) CO2 line to the 15 μm (667 cm-1) line. Also the relative sizes of the central peak and the rotational branches of the 15 μm (667 cm-1) look wrong. There’s probably been some baseline drift too. Then there’s the nonlinear x axis. That spectrum looks to be qualitative only. I can see the water and CO2 spectral features, but it isn’t quantitative quality. But then, one usually doesn’t try to do quantitative analysis by IR.
Kauffman is using the type of spectrophotometer used by “every” organic chemist who wants to record the IR absorption spectrum of a newly prepared molecule. 4000-400 cm-1 covers all of the common stretching and most of the bend vibrations in organic molecules. It’s normally used for taking spectra of “thin films” of undiluted organic liquids, finely powdered organic solids suspended in an inert matrix (KBr) or solutions of organics solids dissolved in CHCl3 or CCl4 (with the solvent’s spectrum subtracted). Kauffman’s instrument using Fourier transform, so I’m not sure how accurately it can reproduce the shapes of very sharp peaks of gases.
For me, these absorption spectra with short path length look much more familiar than the observations climate science takes of the “real world” where the intensity is often zero or blackbody. Since SOD has done an excellent job of impressing on me that absorptivity = emissivity for gases (as well as solid and liquids), I immediately asked what this absorption spectrum implied about emission. Of course, all one can see is the narrow peak associated the strongest CO2 band, there are lots of others lost in the baseline. A spectrum for a path length of about 1 m would be more instructive.
Finally, chemists often define one absorbance unit as 10% transmittance, not 1/e transmittance.
Frank,
Here are a couple of calculated spectra at different resolutions for 301 K, 76% RH and 380 ppm CO2:
2 cm-1
1 cm-1

I still don’t have the x-axis quite right, but it looks like 2 cm-1 is close to the right resolution. There are obvious problems, though. The absorbance for CO2 is off by at least a factor of two, Then there’s the big hump at ~3300 cm-1. I’m guessing that’s liquid water. If the humidity outside at 28 C was 76%, and then he brought the sample back to the lab which was 5 C colder, some water condensed on the windows, among other places, reducing the amount of water vapor relative to CO2 and adding the hump.
DeWitt: Are you in danger of saying the results of an experiment “can’t be right” because the results doesn’t agree with theory – ie the absorption coefficients and peak width algorithms in SpectraCalc? Reality doesn’t come out of a computer – even though climate scientists sometimes act like it does. Personally, I’d really like to see the best experimental spectra and the calculated spectra used by climate models for a variety of situations. I certainly don’t think that Professor Kauffman’s spectrum comes close to representing the best available experimental spectra. The local concentration of CO2 near the surface of the earth varies substantially, so there is no reason to assume that Kauffman’s cell actually contained 380 ppm CO2. (I used his spectrum to make “order of magnitude” estimates about how how long a path length is needed to reach equilibrium between absorption and emission and therefore have an emissivity near 1.)
I found the calculated spectral lines in Pierrehumbert’s article in Physics Today interesting. ( Figure 2 of http://climateclash.com/2011/01/15/g6-infrared-radiation-and-planetary-temperature/ ) The lines are narrower than 1 cm-1 and vary 100-fold between peak and valley. It makes me wonder how accurately we integrate the absorption under each peak when calculating radiative forcing. (Perhaps SOD will do a post on how well experimental lines agree with theoretical ones or someone will provide a reference.)
Frank,
For IR spectroscopy, one can argue that an experiment that doesn’t agree with calculated data isn’t ‘right’, especially when it looks like it was not performed very carefully. It’s that well understood.
The problem here is that I don’t have all the information I really need. I don’t know the apodization function used in inverting the interferogram in that particular spectrometer. Which means I don’t know the instrument resolution. SpectralCalc calculates the actual line widths from the pressure and temperature and they are indeed much less than 1 cm-1. However the spectrum would look a lot different if the resolution of the instrument was as good as or better than the line width. Because the central CO2 line at 667 cm-1 is so narrow, the peak height is strongly dependent on the instrument resolution. That’s much less true for the band at 2400 cm-1
The presence of the hump at ~3300 cm-1 argues very strongly for the presence of liquid water on the cell windows and the low ratio of the absorbance of the water vapor lines to the CO2 lines is additional evidence that condensation has occurred in the cell. The CO2 concentration is almost certainly higher than 380 ppmv. That’s what I was trying to estimate. But I can’t because the measurement was not carried out at the same temperature as the sampling conditions and I don’t know that temperature either.
Sloppy, very sloppy.
ATTN: DeWitt
The PE Spectrum 1000 FT-IR has a resolution of 1 wave number. The spectral range is 4,000 to 450 wave numbers.
You don’t know the lab temperature so you must assume it was 28 deg C as stated. The hump between 4000 to 3000 wave numbers is due to hydrogen bonding between water molecules. This can occur in the gas phase at high humidity.
Some IR spectrometers has a feature that allows it to be constantly purged with dry purified air to elimate problems due to water vapor, CO2 and any other IR absorbing gases.
ATTN: Frank
In general Al hardware used in spectroscopy is anodized and is black. It is possible that he first drew air thru the cell and recorded the spectrum. He then did this until the spectrum remained constant. It would be rookie mistake not to do this. And he is no rookie. Often these minor details are not mentioned in the experimental procedures.
Your calculations re absorption of IR by CO2 are correct. The center peak has an absorbance of 0.025 for a 7 cm path lenght. For an absorbance of 2 (i.e., 99% of incidence light absorbed) then path of the cell would be: pl = 7 cm x 2/0.025 = 280 cm.
The small peaks on either side of the main peak have an absorbance of ca 0.01 Thus for a cell with a path length of 1,400 cm, 99% of the incident IR would be asborbed.
At the pressure and temperature the spectrum was recorded, the excited CO2 molecules would undergo collisional de-activation so rapidly that they would never have a chance re-radiate (i.e., flouresce) the absorbed IR. That is to say, the N2 and O2 molecules would take away (i.e., thermalize) the absorbed IR energy of the “hot” CO2 molecules and consequently warm up slightly. A lot more energy would taken away from the water molecules.
The claim by the climate scientists that CO2 causes “global warming” is absolute nonsense, and this spectrum of “real air” proves that they just flat out wrong.
BTW Are you a chemist? You are quite knowledgeable of what we organic chemists routinely do.
BTW How did you find the J. Chem. Ed paper? I am old guy and don’t much about using the net to find stuff. I usually go the library at SFU.
The big climate Kauna Kevin T is coming to SFU in Burnaby BC in a few weeks to give a seminar on the role of oceans on climate change. I’m going to be there and be passing out free copies of JK’s paper and of John-Daly’s plot of the annual mean temperatures from the weather station at Furnace Creek in Death Valley.
While the instrument is capable of 1 cm-1 resolution, the spectrum looks like the actual resolution was much less. If it were 1 cm-1, there should have been a lot more structure in the CO2 band at 2400 cm-1. That band, btw, plays no significant role in greenhouse warming. Including it in the spectrum demonstrates Kauffman’s lack of understanding of the actual mechanism.
It does no such thing. The very same program that calculates the forcing for doubling CO2 calculates a spectrum that is in qualitative agreement with Kauffman’s spectrum. It can also calculate atmospheric emission spectra that are in quantitative agreement with measured spectra. But since that fact doesn’t agree with your prejudices, you ignore it.
Hydrogen bonding like that only happens in the liquid phase. If it wasn’t temperature induced condensation it was due to absorption of water by the hygroscopic cell windows.
Kauffman’s paper is embarrassingly bad. Passing out copies isn’t going to do your reputation any good. Worse, it makes the rest of us who don’t buy into catastrophic global warming look bad too.
Harold: I found the J Chem Ed paper by finding the paper’s title at the journal website and then pasting it into Google Scholar. Google Scholar will direct you to all copies of the paper Google has found and highlight those not behind a paywall.
If you are going to a talk by KT on the ocean and climate change, you might want to take along Douglass’s latest paper. Now that we have a network of sensors properly designed to track heat flux into the ocean, the results (unchallenged so far?) are surprising. http://www.pas.rochester.edu/~douglass/papers/KD_InPress_final.pdf
(For me, Kauffman’s “kitchen sink” paper contains too much dubious material to be taken seriously. You may want to look at it more critically.)
Arrrgh!!!! In the above calculation, 280 cm should be 580 cm!
I need donut and more coffee!!!
You’re ignoring the drift in the baseline. The absorbance of the P and R branches of the 667 cm-1 line is a lot less than 0.01. At 1 cm-1 spectrometer resolution and a 1400 cm cell, the transmittance is about 0.5, not 0.01.
Here’s the transmittance spectrum of liquid water:
http://webbook.nist.gov/cgi/cbook.cgi?Spec=C7732185&Index=1&Type=IR&Large=on
Frank,
There’s no danger. I’m saying it flat out. The HITRAN 2008 database used by SpectalCalc is first of all a compilation of measured parameters, not theory. Are you saying that the Beer-Lambert and whoever Law only works sometimes? That’s most of the theory behind line-by-line spectral calculations. Second, if someone claimed to have determined that g is 4.9 m/s2, I would say he muffed the experiment. There is no way that I know of for the the absorbances of CO2 at 667 cm-1 and 2350 cm-1 in Kauffman’s spectrum to both be correct. The ratio is off by at least a factor of two. There was something, or multiple somethings, wrong with the experiment.
Not that the experiment actually proves what he and Harold Pierce, Jr. claim it does even if the spectrum had been correct.
P.S.
If you want to get into that sort of thing, there’s always Beck’s compendium of surface CO2 analyses that purport to show high variability of atmospheric CO2. I’ll say that those measurements have little relation to the average CO2 concentration in the whole atmosphere too. Experimental data can be seriously flawed by systematic error. See Cold Fusion for another example.
Dewitt: Isn’t more than a simple absorption coefficient involved in this situation? Aren’t a number of “assumptions” made when calculating and observing the peak shape of any absorption or emission line, assumptions which can reduce or increase the maximum of the peak? “Assumptions” isn’t quite the right word – accepted theories that describe how QM uncertainty, temperature and pressure change the shape of a peak. How well does this combination of theories generate peak shapes that agree with experiment? Do the same factors control peak shapes for all lines? (Probably.) At some pressures, we aren’t necessarily observing signals from purely monomeric species – which I gather is the case for water vapor in the earth’s atmosphere. (Then we have the issue of whether a particular instrument has the ability to properly resolve narrow peaks.) Someday, I’d like to see comparison between theory and observation. Unfortunately, some of the experimental verification might be quite old and not readily accessible. When I’ve managed to educate myself on this subject (references would be appreciated), I may agree with your assessment that Kauffman’s spectrum is like an experiment determining that g is 4.9 m/s2.
Kauffman (and our discussion?) may also be confusing global and local concentration of CO2. If my memory is correct, local levels of CO2 near the ground vary with photosynthesis (daylight), respiration (especially soil bacteria), mixing by the wind, and anthropogenic use of fossil fuel. I remember reading that a plant in a sealed jar will reduce CO2 to about 100 ppm and then close its stomata to reduce water loss. At Mauna Loa, CO2 data is collected only at night when downdrafts over the cooler land deliver “virgin” air which hasn’t been recently modified by life processes (or volcanic emissions). The experimental data showing CO2 levels >400 ppm before 1950 cited in Kauffman’s paper may very well be accurate for local, but not global, CO2.
Water vapor continuum absorption, which is probably due to water dimer (that’s controversial, though) is most important at longer wavelengths (l< 400 cm-1). It’s considered by most to be Collisional Induced Absorption (CIA) which involves three bodies, two molecules and a photon. That’s usually calculated using an empirical equation, the CKD model, and is a function of the partial pressure of water vapor squared. It’s not included in Spectralcalc for gas cell transmittance spectra, or at least I don’t think it is. CIA also exists for nitrogen and oxygen, but is only important for limb paths through the atmosphere at high altitudes where the humidity is very low.
Here’s a paper investigating water vapor continuum absorption. Note that they use the HITRAN 2004 database to calculate and remove the rotational/vibrational water vapor lines:
http://www.nist.gov/customcf/get_pdf.cfm?pub_id=841141
Note the path length for figure 6., 116 m.
The line shape parameters are also determined experimentally. The HITRAN database is the result of decades of measurements that started with the Air Force wanting to be able to hit targets with IR viewing missiles and be able to image ground targets from space through all sorts of weather.
Clough, the C in CKD, was also one of the originators of line-by-line radiative transfer programs.
DeWitt: Thanks for the reference. I noticed the subtraction of peaks using Hitran to leave behind the continuum, but I would be better served by far more basic comparisons between observed and calculated.
Frank,
This didn’t do it for you?
Remember when you’re calculating a forcing, it’s a difference between spectra and most systematic errors in the calculation will cancel.
You could also try starting here:
http://rtweb.aer.com/
Then there’s Clough’s articles on LBL models like:
http://www.agu.org/journals/ABS/1992/92JD01419.shtml
I really don’t understand your problem with calculating spectra. It’s not rocket science and it can be done with high precision. The big uncertainty in atmospheric radiative transfer is the atmospheric profiles, not the molecular spectral parameters.
The FORTRAN code for LBLRTM is free. You do need a FORTRAN compiler to run it in Windows.
http://rtweb.aer.com/lblrtm_frame.html
Here’s a tech note from Perkin-Elmer on how water vapor and CO2 lines can be removed from measured spectra in non-purged instruments by using calculated spectra.
Click to access tch_avcftir.pdf
It seems to work just fine.
ATTN: DeWitt
DEWitt says:
Kauffman’s paper is embarrassingly bad. Passing out copies isn’t going to do your reputation any good. Worse, it makes the rest of us who don’t buy into catastrophic global warming look bad too.
J. Chem. Ed. is _ a peer-reviewed journal_.
A measured spectrum always trumps any theoretical calculation. The measured spectrum is what it is.
As I mentiond, “Kauffman is no rookie.”
“Kauffman’s paper is embarrassingly bad.”
What qualifies you to make that claim? Unless you have at least B.Sc. in chemistry or physic (aka hard science) and have much practical experience in spectroscopy, hush your mouth.
I reviewed this paper and find the experimental procedures OK.
I have been recording and analyzing NMR, mass, IR and UV-Vis spectra for about 40 years and I do know what I’m talking about.
“Passing out copies isn’t going to do your reputation any good. ”
When you start paying hefty carbon taxes on fossil fuels as shown below for BC, you won’t give a damn about your reputation.
BC carbon taxes on fossil fuel based $20 per tonne of CO2 equivalent as of July 1 ,2010:
Gasoline 4.45 ¢/litre
Diesel 5.11 ¢/litre
Jet Fuel 5.22 ¢/litre
Propane 3.08 ¢/litre
Natural Gas 3.80 ¢/cubic metre
Coal, high heat value 41.54 $/tonne
Coal, low heat value 35.54 $/tonne
The actual tax on nat gas is $0.9932 per gigajoule which costs $4.976 per gigajoule. On July 1, 2012 the carbon taxes will increase by 50%. I will then pay a tax of $1.50 on a gigajoule of nat gas which I use for space and water heating.
This is outrageous! I’m being heavily taxed to take a shower, to wash clothes and dishes, and to heat my house. Fortunately, Metro Vancouver has a mild climate. There are no free passes on these taxes for those who live in the cold regions of the province. Indeed, there are no free passes at all on carbon taxes.
For the last billing period for nat gas usage, I paid a carbon tax of $13.31. Do you have how much yummy fruits and veggies I can buy for that amount of tax? LOTS! These guys are taking food out my and my son’s mouths!
When you get wacked upside the head with carbon taxes, your view of “climate science” will change PDQ!
ATTN: DeWitt
Fast Forward to July 1, 2012 in BC. The above $13.31 carbon tax will zoom to $19.96.
At the local Safeway, frozen Delissio Deluxe Pizzas (907 g) go on sale for $4.99. I can buy 4 pizzas with that amount of tax.
Now do you understand why I just gotta gun down The Big Kauna Kevin?
Gobal warming and climate change fun and games are over!!!
ATTN: Frank
The Mauna Loa CO2 data is valid only PURIFIED BONE-DRY AIR and bears no relationship to the MASS of CO2 in real air at any site.
GCM usually use the conc of CO2 in ppmv and are thus fatally flawed.
If a volume of air contains clouds, you have no way of knowing the MASS of CO2 in the gas phase. A slight change in pressure or temperaure wiil affect the amount of CO2 as well as water vapor added to or removed from the gas phase.
Howard Pierce, Jr
My patience has a limit that you have now exceeded by a wide margin.
*plonk*
I thought you would get the idea of where the logaritm factor comes in when I saw your diagrams 2 and 3, showing traiangluar peaks.
I originally was introduced to the concept of an n layer
atmosphere in “realclimate”, but they subsequently deleted the post. Here is an equivalent link.
Click to access bookchap7.pdf
or
Click to access chap2.pdf
in general, with n opaque atmospheric layers,
the surface will have a flux of n + 1 and a temperature of
(n+1)^0.25 times that of a 0 atmosphere surface.
Another way of writing this factor of n+ 1 is
1/(1/n) at the surface, and I’ll explain where I got this if anybody cares.
With that triangular figure, the AVERAGE atmospheric
height is
1/( integral of 1(/n+1) from 0 to n.
That gives you 1/ 1/ln N, which would be the effective height of an absorbing atmosphere with a min of 0 and a peak of n.
I am rather new here. Let me start with thanking for a very informative website. In the second part of these post about atmospheric radiation and greenhouse effect SienceofDoom say:
“Each layer in the atmosphere absorbs radiation from below (and above). The gases that absorb the energy share this energy via collisions with other gases (thermalization), so that all of the different gases are at the same temperature.”
These posts are about radiation of course, but it seems to be the only explanation of how the atmosphere gets warmer. The thermalization, the collisions beetween the CO2 and N/O-molecules are a sort of conduction in the air, but are all other kinds of conduction irrelevant? Is conduction from the ground completly left out of account? (I can’t find it in the “budgets”.) Is it a general conseption that there is no considerable warming from the ground to the atmosphere via conduction?
Trond A:
Conductivity is negligible in the atmosphere – gases are poor conductors of heat.
Air has a conductivity of approx, k=0.02 W/m.K
Take an example of the temperature difference across 1 km of air = 6.5K.
The heat flow from conductivity, q = kA . ΔT/Δx
We want to know W/m2, so
q” = k . ΔT/Δx
so q” = 0.02*6.5/1000 = 0.13 mW/m2
Convection, the transfer of heat via the bulk movement of fluids, on the other hand is very important. And the radiative transfer calculations have to include it, as you can see, for example, in Part Four.
Probably too late, but rehabilitating Frank’s comment from February 25, 2011 at 7:28 pm out of the spam queue:
Check out the original comment.
Sciencofdoom, thanks for the answer, but still, it does not answer my question which maybe was not clear enogh. The question is about a combination of conduction and convection. Let’s imagine a tropical desert where the temerature can reach 45C. The sun is warming the ground which both radiates energy and transfers energy by collisions with molecules in the air (I guess).
The molecules near the ground will get energy by conduction form this very hot ground. I guess they will rise by convection and leave the place for cooler air above. It does not have to happen very fast. One meter rise per hour for example would be sufficient to do the job. This would transfer a lot of energy to the N/O molecules, an energy that they would not loose very fast because of bad counduction (as you pointed out) through the air. It is hard to imagine that all those molecules (a bulk) which are responsible for what we call the “temperature” get all their energy from collisions with the CO2 molecules available. Then one CO2 molcule will have to do the job for about 2500 N/O molecules. Wouldn’t the the amount of collisions between N/O molecules and the ground be much larger than between CO2 molecules and N/O molecules in, let’s say, a cube of 1m3 “on the ground”, the very place we localize the temperature?
When it comes to total energy in/out it’s of course totally dependent of radiation, but what happens in between is not very well explained from my point of view. And it is this “in between” which is resposible for the experienced temperatures and gives rise for the debate of warming.
Trond A:
In my original response, of February 27, 2011 at 9:03 pm, I said:
It seems you are asking me why I have ignored convection in my response?
Please confirm.
SienceofDoom said: “It seems you are asking me why I have ignored convection in my response?”
No i don’t do that. It’s about the energy transfer from the ground to the air. My question is, if it is considered that all (most of) the energy transfer form the ground to the atmosphere is via radiation from the ground to greenhouse gases like CO2 and then via collisions with N/O molecules, OR, if there also can be a considerably transfer from the ground to the air, by conduction from gound to air to be precise. The convection will follow of course. The situation with the tropical desert could be a good example to shed some light on the problem so to speak. Why does it get so hot, is it all about grenhouse gases, or does the more than 99% of the air get it’s energy, it’s temperature directly from the ground via conduction?
The reason for my question is of course that i can’t find anything about it in these posts about atmospheric radiation (which is understandable in a way). But they are all about warming, and it seems to be an understanding that all the warming of the air (not the surface) comes from the greenhouse effect(?). (Or at least the last 33 degrees.)
If there were no greenhouse gases in the atmosphere, (speaking hypothetically), would the ground (supposed to be 33 deegres colder) still heat the air and what would be the temperature of the air at the surface?
These are simple underlying questions that I would like to understand better, and I think it is important even seen in the light of radiation.
With kind regards and thanks for a website with lot of interesting posts to read!
Trond A:
For background, have a read of The Hoover Incident.
And yes, if the surface was colder the ground would still heat the air at the surface.
The reason is that – in the case of an atmosphere with no “greenhouse” gases – the surface would be warmed by the sun and then would transfer heat from the surface to the air by conduction and convection.
To understand why the surface is so hot (all around the world, not just the deserts) we need to consider the energy fluxes at the surface.
In essence radiation from the sun heats the surface and the downward atmospheric radiation reduces the cooling from the surface (this has a huge effect). But convection acts to cool the surface. It is a more effective mover of heat from the surface to higher up in the atmosphere.
If there was no convection the surface would be hotter.