In the last article we looked at some results from Grant Petty.
In essence they demonstrate the huge variation in the transmittance of CO2 through the atmosphere with the wavelength of radiation.
I decided it might be interesting to try and reproduce these results using the HITRAN database. This allows a closer examination of which mechanisms cause which results.
Line Shapes and Pressure Broadening
The energy in a photon is given by a very simple equation:
E = hν
where h = Planck’s constant = 6.63 x 10-34 J.s, and ν = frequency (ν=c/λ where c=speed of light and λ = wavelength)
So, for example, a 15μm photon has an energy of 1.3 x 10-20 J.
A photon can be absorbed by a molecule if the energy of the photon matches the exact energy required to change the state of that molecule.
Now, if a photon was only absorbed at one exact wavelength then atmospheric radiation would be irrelevant.
An easy concept for people who have done a lot of maths or physics, but not so obvious to many others.
Let’s take a different example. If you start your car up and accelerate steadily up to 60 miles per hour over 1 minute, how long do you spend at the speed of 34.5698895549034592345123 miles per hour? Not much. And the more precise I make this speed, the less time you will have spent at it.
If we consider how much energy is transferred in terrestrial radiation from the surface at 14.995698895549034592345123 μm, the answer is “not much”. The same goes for any other vanishingly small interval of wavelengths.
So if each absorption line was exactly one wavelength then the amount of energy absorbed by a finite number of lines would be zero.
However, each absorption line has a finite width. Part of this is due to the uncertainty principle described by quantum mechanics – the small time a higher energy state is occupied produces an uncertainty in the energy of that state.
This is called natural broadening and is a very small effect.
The easiest broadening mechanism to understand is Doppler broadening. Molecules in the atmosphere are zipping around in all directions at speeds of around 500 m/s. Compared with the speed of light this is small, but the difference in the relative speed between a photon and a molecule is slightly changed, leading to a change in the absorption frequency (see note 1 for more details). This is “relatively easy” to understand from first principles and the mathematical treatment is straightforward.
The dominant line broadening mechanism in the lower atmosphere is pressure, or collisional, broadening. This is more challenging from a theoretical point of view but is certainly a measurable value.
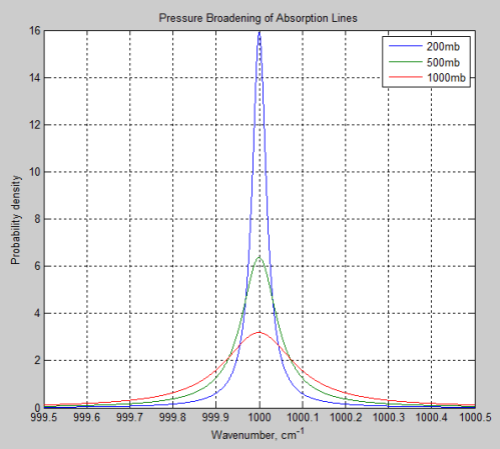
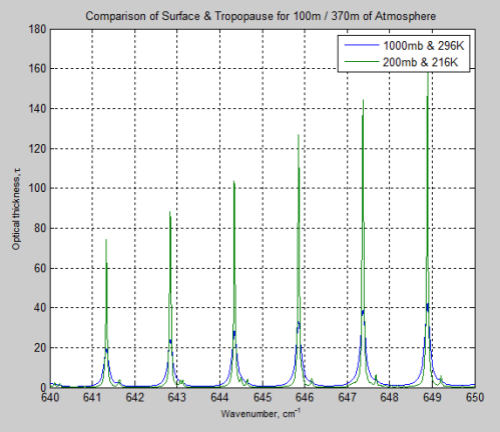
The main effect of pressure broadening is to “spread out” the absorption line. Here is a typical example, where 1000mb is at the earth’s surface, and 200mb is at the “tropopause”, or top of the lower atmosphere:
Figure 1
So the absorption at the center of the line is reduced, while more absorption takes place out to the sides.
The parameter which describes how much broadening has taken place is called the half-width – and is the width of the line when the value has dropped to half the peak value.
Typical values of pressure broadening half width are 0.01 – 0.1 cm-1 at 296 K and pressure of 1000 mb (surface atmospheric pressure).
The function which approximates this effect is the Lorentz line shape:
f(ν-ν0) = αL/π((ν-ν0)²+αL²) [1]
where ν0 is the frequency of the absorption, ν = frequency and αL = half-width at half of the maximum
And the half-width at any given temperature and pressure is given by this formula:
αL = α0(p/p0).(T0/T)γ [2]
where α0 = lab measured half-width at pressure p0 and temperature T0, and γ is also a lab measured parameter, typically around 0.5 – 0.7.
That’s a lot to take in if you haven’t seen it before. Take a look back at Figure 1 – this is what these formulas describe.
The atmospheric pressure where pressure broadening is comparable to Doppler broadening is about 10 mbar. This is around 30km above the surface, so in the troposphere Doppler broadening is unimportant.
In a later article we might explore the experimental results vs theoretical results of pressure broadening in more detail. Or at least, how much inaccuracies might affect radiative transfer calculations.
HITRAN database
You can read more about the HITRAN database here. The most recent update of the database is described in The HITRAN 2008 molecular spectroscopic database, by L.S. Rothman et al, and the earlier 2004 update: The HITRAN 2004 molecular spectroscopic database, by L.S. Rothman et al.
This database is the result of a huge amount of work by thousands of researchers over a few decades. If you look at the references in the 2008 paper you find almost 400 papers.
In the previous articles in this series I created two fictitious molecules, pCO2 and pH20, and solved the radiative transfer equations for a variety of conditions for these two molecules through the atmosphere.
The aim of this simplification was illumination.
Given that the HITRAN database contains over 300,000 absorption lines for CO2 (and 2.7M lines in total), I thought that replicating some standard results (e.g. see Part Eight) might be a little too much of a challenge. However, the hardest part was actually reading the database, which is in text form – and the problems were just due to my novice status with MATLAB.
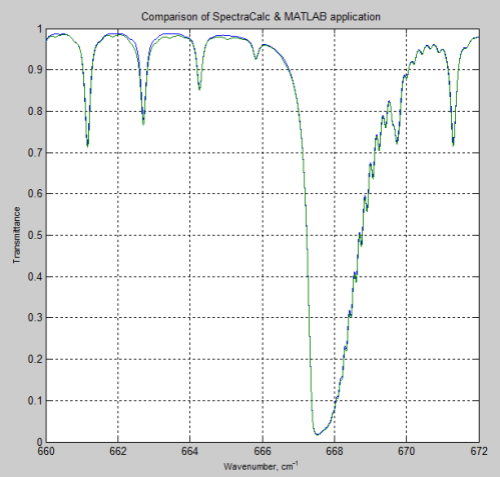
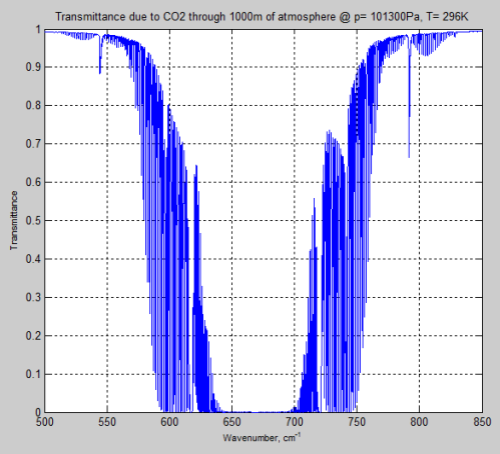
DeWitt Payne kindly offered me some results he obtained from SpectralCalc (via subscription). These were from 660-672 cm-1 through a 1 meter path at standard temperature and pressure, and CO2 concentrations of 380 ppm.
Here is the comparison with my MATLAB program:
Figure 2
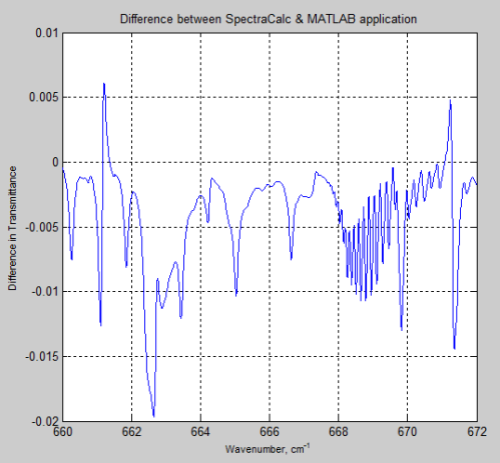
And here is the difference between the two results (the SpectralCalc results minus the MATLAB results):
Figure 3
The MATLAB program, for the results above, only considered the main isotopologue of CO2, which accounts for over 98% of the concentration of CO2 in the atmosphere. However, including the absorption lines for all isotopologues had almost no effect and the small differences remain.
As the differences are small, it seems worth showing some initial results from the program.
Results
First, let’s see the effect of “pressure broadening”.
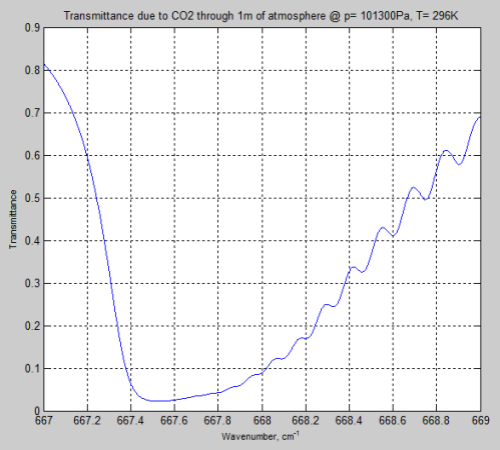
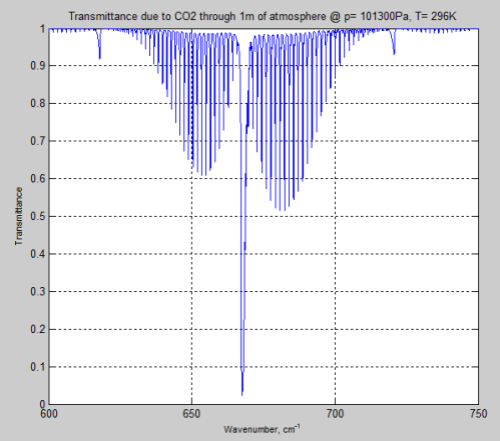
Here is the result through 1m of atmosphere at the earth’s surface, around the peak absorption wavenumber of CO2:
Figure 4
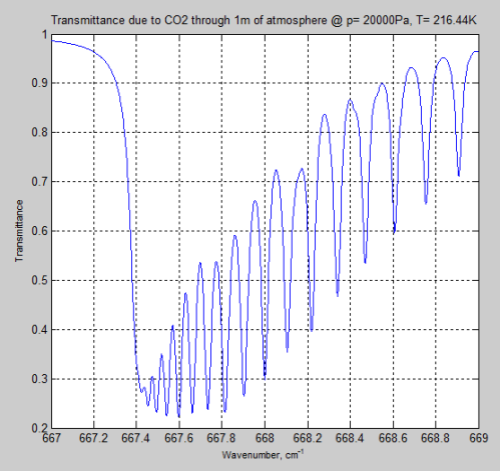
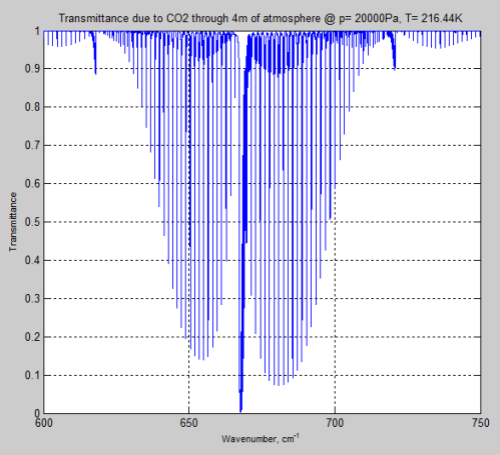
And the result for the same 1m of atmosphere at the tropopause (top of the troposphere) at 200mbar (typically around 12km):
Figure 5
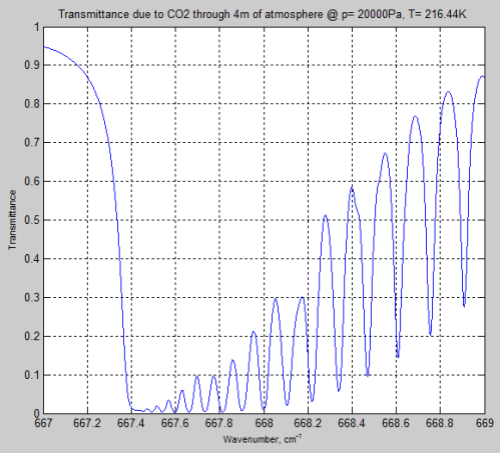
Now at 200 mbar there is less atmosphere so the comparison isn’t truly a fair one. Increasing the path length to get the same number of CO2 molecules we get this result:
Figure 6
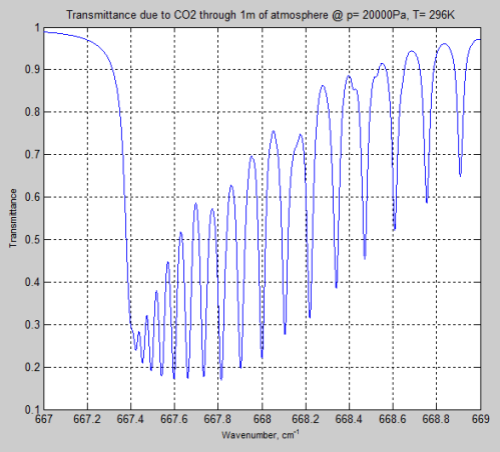
Both pressure and temperature have changed so it’s worth seeing the result if we apply the surface temperature to the Figure 5 results:
Figure 7
We can see from the result (and it’s also clear from the equations earlier) that the parameter having the most effect is the pressure – which changes by a factor of 5. The temperature reduction from 296K to 216K has a much smaller impact.
However, the difference between Figure 4 and Figure 6 is very significant – individual lines are “smeared out” at the earth’s surface, but distinct lines higher up in the atmosphere.
Let’s take a look at a wider range of wavenumbers / wavelengths.
From 600 – 750 cm-1 (13.3 – 16.7 μm) at the surface through 1 meter of atmosphere:
Figure 8
And the same amount of CO2 at the tropopause:
Figure 9
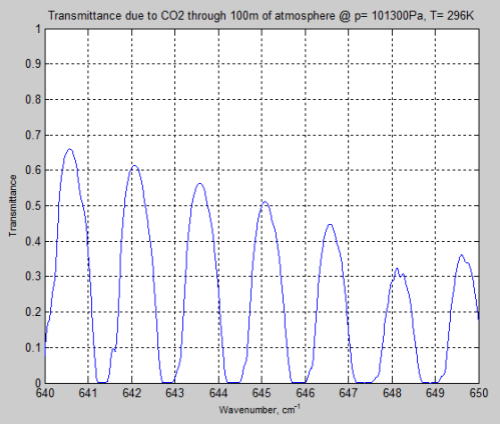
Let’s look at a longer path of 100m through the atmosphere and “zero in” on one part of the bandwidth, 640-650 cm-1:
Figure 10
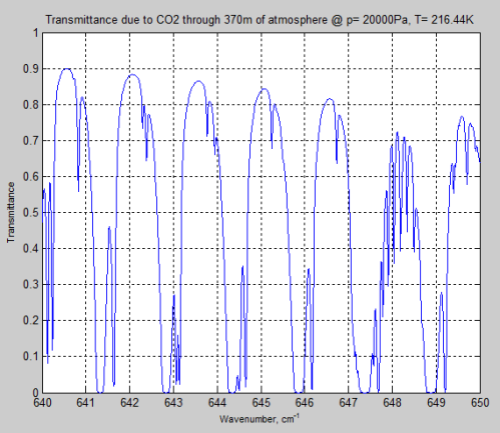
And let’s compare it with the tropopause, again through a longer path, to keep the CO2 quantity the same:
Figure 11
Just for interest I compared the optical thickness of the surface and tropopause for these wavenumbers on the same graph. Optical thickness increases as transmittance decreases. Check out the heading Optical Thickness & Transmittance in Part Six if this isn’t clear.
Figure 12
We can see that the peaks of absorption are indeed lower but the widths of the absorption lines are wider (for the surface results).
Saturation Revisited
As I commented in Part Eight, many people have heard about the high absorption of CO2 at 15 μm and have not understood the huge variation in absorption across the wide bandwidth of CO2. (Also there is the most important subject of re-emission).
Here is the result of the simple “slab” model, which calculates the transmittance through 1km of atmosphere (a slab model means that the pressure and temperature are constant through the “slab” – a very simple model):
Figure 13
As you can see, around 570 – 600 cm-1 (16.7 – 17.5 μm) and 730 – 770 cm-1 (13.0 – 13.7 μm) the transmittance through the atmosphere is nowhere near “saturated”.
If 1 km of atmosphere has a transmittance of 0.7 (i.e., 70% of radiation is transmitted) at some wavelengths then clearly more CO2 will reduce this transmittance.
The Matlab Code
The results were all created using my code: HITRAN_0_2. However, each run has slightly different parameters, which are adjusted by changing the code rather than anything more elegant. See Note 2 for the code.
The code at this stage has provision for different layers of different temperatures, pressures, and densities – but at this stage the code doesn’t use it – just one “slab”.
The core part of the code is very simple:
- Take each absorption line in turn and use its measured line strength, half width, and other parameters
- For the pressure and temperature, calculate the half width for those conditions (equation 2)
- Now for each line, take each wavenumber in turn (defined via a start, stop and interval) and apply the formula in equation 1 to calculate the optical thickness
- Add the optical thickness at this wavenumber to the optical thickness already calculated for this wavenumber
The code could be more “speed efficient” – by only calculating equation 1 close to the absorption line. I started out simpler to see what happened and it went so fast that I didn’t improve it.
Multiple Atmospheric Layers
As the pressure and temperature change with height through the atmosphere the single slab model is limited in value.
So I extended the model to multiple layers – v0.3 (see Note 2).
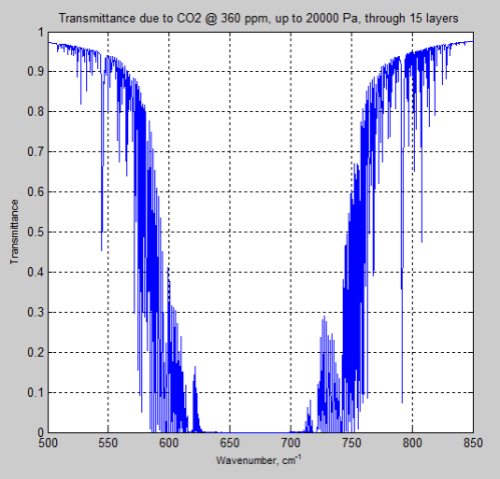
Here is the result of transmittance up to 200mb (20,000 Pa) from CO2 at 360 ppm with a 15 layer model:
Figure 14
And, of course, the question many people have – what is the difference between the atmosphere at 280 ppm and 560 ppm – or a doubling of CO2 from pre-industrial levels:
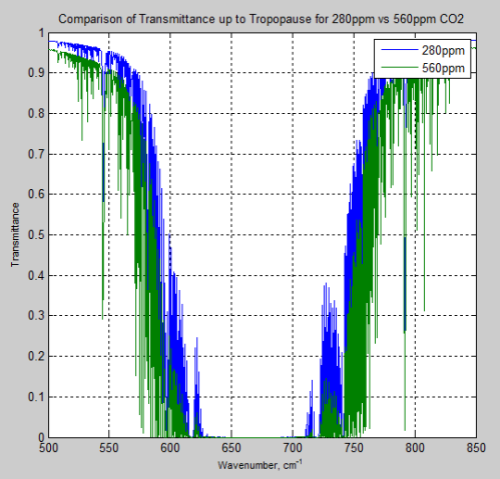
Figure 15
And the difference between the two, the “delta”:
Figure 16
Remember – or note, if this is new – the atmosphere absorbs and also re-emits. The question of radiative forcing cannot be answered by only considering transmittance.
However, these graphs of the change should at least indicate to people that the issue of the very high optical thickness = very low transmittance at 667 cm-1 = 15 μm is not the complete story, even only considering transmittance.
Limitations
The model has the limitation at the moment that it doesn’t take into account Doppler broadening. If we extend the model up into the stratosphere Doppler broadening starts to become important. I might get around to including this by introducing the Voigt function which combines pressure broadening and Doppler broadening.
There is also the possibility that my model has a mistake. However, I have compared it to the results from SpectralCalc and it is very close, and to results published in Grant Petty’s book, which look the same.
Other articles:
Part One – a bit of a re-introduction to the subject.
Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only.
Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.
Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.
Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”
Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies
Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking
Part Eight – interesting actual absorption values of CO2 in the atmosphere from Grant Petty’s book
Part Nine – calculations of CO2 transmittance vs wavelength in the atmosphere using the 300,000 absorption lines from the HITRAN database
Part Ten – spectral measurements of radiation from the surface looking up, and from 20km up looking down, in a variety of locations, along with explanations of the characteristics
Part Eleven – Heating Rates – the heating and cooling effect of different “greenhouse” gases at different heights in the atmosphere
Part Twelve – The Curve of Growth – how absorptance increases as path length (or mass of molecules in the path) increases, and how much effect is from the “far wings” of the individual CO2 lines compared with the weaker CO2 lines
And Also –
Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.
References
The HITRAN 2008 molecular spectroscopic database, by L.S. Rothman et al, Journal of Quantitative Spectroscopy & Radiative Transfer (2009)
Notes
Note 1 – The energy absorbed from a photon, E = hv, where h = Planck’s constant, and ν= frequency. The energy of the photon has to match precisely the energy required for the change in state of the molecule.
However, due to the motion of atmospheric molecules, the actual frequency, ν’ = ν(1-ν/c), where c = speed of light, ν = frequency measured by a stationary observer.
In essence, there is now a very small (but measurable) range in frequencies (with respect to a “stationary” planet) that can be absorbed to give the precise energy level required for a transition of this molecule – and so the faster the molecules are moving, the more the absorption line “spreads out”.
Molecular speeds are given by the Maxwell-Boltzmann distribution.
Note 2 –
And the code for v0.2 reproduced here for convenience:
====== HITRAN v0.2 ===================
function [vmin vmax dv cco2 T p d vt tau ] = HITRAN_0_2()
% Absorption through atmosphere of defined temperature & pressure
% uses the HITRANS database
%
% v0.1 – Basic calculations to get out of the starting blocks
% v0.2 – Tidy up and allow a “slab” to be at any pressure and temperature
% with line width determined by the pressure & temperature
clear
disp([‘—- New Run —- ‘ datestr(now) ‘ —-‘]);
disp(‘ ‘);
% =========== Basic definitions =====================
p0=1.013e5; % std pressure for the HITRANS database in Pa
T0=296; % std temperature for HITRANS database in K
cco2=360e-6; % concentration of CO2
Na=6.02e23; % Avogradro’s number
mair=29e-3; % molar mass of air
% now define the fractional abundance of each isotopologue of CO2
isoprop=[0.98420 0.01106 0.0039471 0.000734 0.00004434 0.00000825 0.0000039573 0.00000147];
ignoreiso=false; % allows easy switching between main isotopologue only or all of them
% =========== Define wavenumber ranges ==============
vmin=640; % min wavenumber to consider (overall)
vmax=650; % max wavenumber to consider (overall)
dv=0.001; % resolution of wavenumber
% because absorption lines below the lower boundary (and above the upper
% boundary) can still affect the wavenumbers under consideration we need to
% extend the boundaries of which absorption lines to consider
rvmin=0.98; % ratio below lower boundary to consider
rvmax=1.02; % ratio above upper boundary to consider
%vt=vmin:dv:vmax; % vt = wavenumbers we will calculate optical depth for
vt=linspace(vmin,vmax,1063);
vtmax=length(vt);
tau=zeros(1,vtmax); % set optical depth to zero as a starting point
% =========== Read in CO2 data and select vmin-vmax data ========
% selected paramaters for complete HITRAN CO2 database already stored in file: co2.mat
load(‘co2’);
if ignoreiso==true
% select only main isotopologue between the wavenumber boundaries
iv=find(iso==1 & v>vmin*rvmin & v<vmax*rvmax); % select upper and lower bounds
else
% select all isotopologues and between the wavenumber boundaries
iv=find(v>vmin*rvmin & v<vmax*rvmax); % select upper and lower bounds
end
% select subset of CO2 spectral data for evaluate
iso=iso(iv); v=v(iv); S=S(iv); gama=gama(iv); nair=nair(iv);
ivmax=length(v);
% ============= Define standard atmosphere against height ================
% reuse code from rte_0_5_0 to define std atmosphere and number of levels
% SI units used unless otherwise stated
% first a “high resolution” atmosphere
% zr = height, pr = pressure, Tr = temperature, rhor = density
Ts=296; % define surface temperature at same value as HITRAN measurements
ps=1.013e5; % define surface pressure
Ttropo=215; % define tropopause temperature
% nmv=2.079e25; % nmv x rho = total number of molecules per m^3, not yet
% used
maxzr=50e3; % height of atmosphere
numzr=5001; % number of points used to define real atmosphere
zr=linspace(0,maxzr,numzr); % height vector from sea level to maxzr
[pr Tr rhor ztropo] = define_atmos_0_3(zr,Ts,ps,Ttropo); % function to determine (or lookup) p, T & rho
% Create “coarser resolution” atmosphere – this reduces computation
% requirements for absorption & emission of radiation
% z, p,Tinit,rho; subset of values used for RTE calcs
numz=10; % number of boundaries to consider (number of layers = numz-1)
minp=2e4; % top of atmosphere to consider in pressure (Pa)
% want to divide the atmosphere into approximately equal pressure changes
dp=(pr(1)-minp)/(numz); % finds the pressure change for each height change
zi=zeros(1,numz); % zi = lookup vector to “select” heights, pressures etc
for i=1:numz % locate each value
zi(i)=find(pr<=(pr(1)-i*dp), 1); % gets the location in the vector where
% pressure is that value
end
% now create the vectors of coarser resolution atmosphere
% z(1) = surface; z(numz) = TOA
% T, p, rho all need to be in the midpoint between the boundaries
% T(1) is the temperature between z(1) and z(2), etc.
z=zr(zi); % height
pb=pr(zi); % pressure at boundaries
Tb=Tr(zi); % starting temperature at boundaries
rhob=rhor(zi); % density at boundaries
% now calculate density, pressure and temperature within each layer
for i=1:numz-1
dz(i)=z(i+1)-z(i); % precalculate thickness of each layer
Tinit(i)=(Tb(i+1)+Tb(i))/2; % temperature in midpoint of boundary
p(i)=(pb(i+1)+pb(i))/2; % pressure in midpoint of boundary
rho(i)=(rhob(i+1)+rhob(i))/2; % density in midpoint of boundary
end
% ===============
% but in the first version we ignore this and just calculate at std temp
% and pressure (later iterate through each layer, i
% work in cm for volumes and distances (absorption coefficients are in cm)
p=p0;
rhop=rhor(find(pr<=p,1)); % lookup density at pressure = p
T=Tr(find(pr<=p,1)); % lookup temperature at pressure = p
na=(Na*rhop/mair)/1e6; % number of air molecules per cm^3
Nco2=na*cco2; % number of CO2 molecules per cm^3
d=100*100; % path length in cm *** just a starting point
% ======== Iterate through each absorption line ======
% for one slab of depth, d
for j=1:ivmax % each absorption line
% v(j)=line center, S(j)=line strength, gama(j)=half width
% first do a code inefficient method – calculate the profile for each
% across the entire wavenumber range
if ignoreiso==true % if we only want to consider the main isotopologue
prop=Nco2;
else
prop=isoprop(iso(j))*Nco2;
end
ga=gama(j).*(p/p0).*(T0/T).^nair(j);
% ======== Iterate through each wavenumber ====
for k=1:vtmax % each wavenumber
% vt(k) is the wavenumber under consideration
dtau=prop*d*S(j)*ga/pi/((vt(k)-v(j))^2+ga^2);
tau(k)=tau(k)+dtau;
end
end
plot(vt,exp(-tau))
title([‘Transmittance due to CO2 through ‘ num2str(round(d/100))…
‘m of atmosphere @ p= ‘ num2str(p) ‘Pa, T= ‘ num2str(T) ‘K’])
ylabel(‘Transmittance’,’FontSize’, 8)
xlabel(‘Wavenumber, cm^-^1′,’FontSize’, 8)
grid on
disp([‘Range = ‘ num2str(vmin) ‘ – ‘ num2str(vmax) ‘ cm^-1, dv = ‘ num2str(dv) ‘, lines = ‘ num2str(ivmax)]);
disp([‘Number of CO2 molecules per cm^3 = ‘ num2str(Nco2) ‘, path length = ‘ num2str(d/100) ‘ m’]);
disp([‘p= ‘ num2str(p) ‘ Pa, T= ‘ num2str(T) ‘ K’]);
disp([‘—- Complete End —- ‘ datestr(now) ‘ —-‘]);
======== end of HITRAN v0.2 =====================
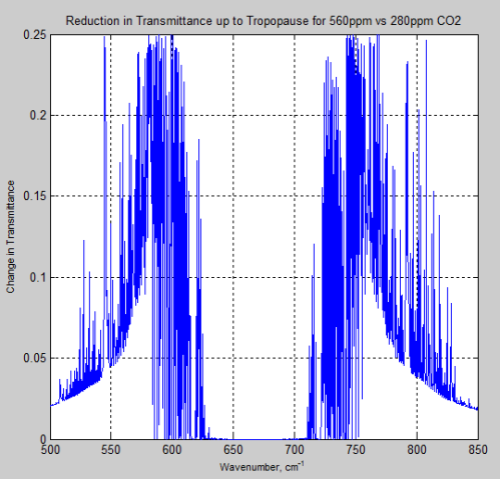


If I take the derivative of the “change in transmittance upon doubling CO2” with respect to the initial CO2 amount and set that derivative to zero, the maximum change in transmittance occurs at wavelengths where the initial transmittance is 0.5 and drops to 0.25 upon doubling. The maximum change in transmittance is 0.25. This agrees reasonably with your graph of the change in transmittance.
T1 = exp(-nos)
T2 = exp(-2nos)
o is absorption cross-section, s = path length, n is number of CO2 (constant over path), T1 and T2 are transmittance before and after doubling.
T1-T2 = exp(-nos) – exp(-2nos)
d(T1-T2)/dn = -os*exp(-nos) + 2os*exp(-2nos)
At max: 2os*exp(-2nos) = os*exp(-nos)
2*exp(-nos) = 1
exp(-nos) = 1/2 = T1
If we go a little further, we can calculate how the change in transmittance upon doubling varies with the initial transmittance.
T1-T2 = exp(-nos) * [1 – exp(-nos)]
T1 * (1 – T1)
If T1 is 0.2 or 0.8, T1-T2 = 0.16
If T1 is 0.1 or 0.9, T1-T2 = 0.09
sod,
Very nice addition to the web. Could you put up (or link to) your CO2.mat file?
Chris Colose:
Thanks.
I just had a quick check and as a MATLAB file it is not useful in a text reader.
I will turn it into a comma delimited file and post up. (Might take a little time, watch this space).
I’m curious what happens when you integrate the area under the change in transmittance curve and average. Or better, multiply the change in transmittance by the Planck function for a 288 degC earth before integrating and calculate the change in power absorbed. As you noted, this isn’t radiative forcing until we include the additional radiation emitted by 2X CO2. I’d like to understand both components (increased absorption and emission) of radiative forcing, not just the net change.
Estimated Absorption Change: If 40-100 W/m2 (10-25%) of the 390 W/m2 emitted by a 288 degK earth is emitted through the 500-850 cm-1 channel and if the average change in transmittance upon doubling CO2 is 5-10% (estimated from your figure), then the power absorbed is 2-4 to 5-10 W/m2.
Estimated Emission Change: CO2 radiates strongly through only about 40% of the 500-850 cm-1 channel. The emission temperature for photons that actually escape the earth is probably around 220 degK, or 75% of the surface. This factor gets raised to the fourth power by S-B and becomes about 30%. So CO2 is emitting roughly about 12% as much as the surface of the earth in this channel. IF twice as many emitters actually emitted twice as much radiation, emission would increase by 5 to 12 W/m2 – more power than absorbed. Of course, twice as many emitters don’t succeed in doubling the upward flux because some of the additional flux is absorbed by the added CO2.
Neither of these estimates is “kosher”. Saying emission doubles as the number of CO2 emitters doubles, implies optically thin. Emission at 220 degK comes from blackbody radiation, implying optically thick. CO2 absorbs photons emitted by the atmosphere as well as by the surface, so only part of the absorption is considered. Perhaps all attempts to develop an intuitive, semi-quantitative understanding are doomed.
Frank:
No. I think it is possible – as well as very desirable. This is why I started doing these models, and also deriving the transmittance from the HITRAN database.
I will post up some more analysis in the comments.
The configuration I ran this time was:
– 15 levels from the surface up to 200 mbar (around 12 km)
– wavenumber resolution of 0.01 cm-1
– 280 ppm then 560 ppm
– wavenumber range of 500-850 cm-1
The average transmittance for 280ppm = 0.498
The average transmittance for 560ppm = 0.437
(Output files of transmittance to follow)
I thought it might be useful to show an expanded view (horizontal axis) so click on each of these for a larger view:
Zooming in to one part:

And zooming again:

Here is the Transmittance Output File.
It is a comma delimited file – ONLY NAMED as .doc because WordPress doesn’t upload .txt files.
It is of the form – wavenumber, transmittance at 280ppm, transmittance at 560ppm.
Chris Colose:
Here is the CO2 extract created from HITRAN 2008.
It is ONLY NAMED as .doc because WordPress doesn’t upload .txt files.
It is a comma separated file of the form:
– isotopologue (sequential numbering, see p 148 of the journal article on HITRAN 2004)
– v, wavenumber in cm-1 of the line center
– S, line strength in cm-1/(molecule.cm-2)
– γair, air-broadened half width at 296K and surface pressure
– nair, temperature-dependence exponent for γair
And see p 143 of the journal article on HITRAN 2004 for the complete description of all available parameters.
And if anyone produces anything from the data, please cite the HITRAN 2008 article.
By the way, if anyone wants an easy way to view a large file like this I recommend Notepad++ (free) and very fast.
Frank:
As a simplistic approach, with a surface temperature of 288K, the energy radiated from the earth’s surface between 500-850 cm-1 is around 140 W/m2.
With a transmittance of 0.498 vs 0.437:
ΔEout = 8.5 Wm2.
If we took a range of temperatures seen on the earth’s surface and area weighted them there would likely be a small change in this value.
On the one hand an upwards shift in the number due to the 4th power dependence on temperature.
On the other hand a downward shift due to the reduced proportion of radiation in that bandwidth (as temperature increases, radiation shifts to shorter wavelengths, higher wavenumbers)
The reason that radiative forcing is only 3.7 W/m2 for CO2 doubling is because the transmitted surface radiation is only part of the jigsaw puzzle.
SOD: Thanks for the calculations. With your numbers, the channel from 500-850 cm-1 should emit about 17 W/m2 (1% of 140 W/m2). To a first approximation, IF doubling CO2 doubled the emission near the top of the atmosphere, the increase in emission from 2X CO2 would be twice the power absorbed by the 2X CO2. I still haven’t come up a second approximation that gets closer to the correct answer.
Does the model you have put together allow you to look at the emission from any one layer of the atmosphere – for example, an altitude you think is some representative of the tropopause? Can you double CO2 and ask how much upward emission changes? At wavelengths where the slab is optically thick, doubling should have no effect on emission. At wavelengths that are transparent to CO2, there will be no emission before or after doubling. So doubling CO2 will cause the greatest increase in emission from the wavelengths that are between these extremes. (This is analogous to what happens with absorption.)
The energy required to excite an electron for it shifts from a lower quantum microstate to the next higher quantum microstate is 5.4468 x 10^-19 J. Ref. 5
5. Castellan, Gilbert W. Physical Chemistry-3rd Edition. Addison-Wesley-Longman Publishing Company, Inc. 1998.
http://jennifermarohasy.com/blog/2011/03/recycling-of-heat-in-the-atmosphere-is-impossible/#more-7668
I found the above energy statement at the link provided. If true then it take multiple IR CO2 photons to get to that energy level and given the collison rate most would never get there.
mkelly:
The article is a study in confusion.
A huge body of experimental work shows that photons of many different wavelengths are absorbed by CO2.
This is what is reported in journals like Journal of Quantitative Spectroscopy & Radiative Transfer.
CO2 is measured as having over 300,000 absorption lines. Let’s take an example. One of these lines is at 663.99 cm-1. This is a wavelength of 15.06 μm.
The energy in a photon of 15.06 μm= 1.33 x10-20 J.
This means CO2 absorbs a photon with an energy of 1.33 x10-20 J as this energy moves the molecule to a new rotational state.
That’s just one of thousands in this region.
This is all very testable and repeatable spectroscopy.
If you have understood the author of that article correctly (and it just looks like a confused jumble of words to me) then he is saying that the HITRAN database has at least 157,000 mistakes. This is the number of measured absorption lines of CO2 with an energy less than that claimed as the minimum.
These are collectively reported by a large number of different spectroscopy professionals in many different countries over decades.
What you say may possibly be true but you did not address the issue. How much energy does it take to excite an electron from lower to higher state? If true the energy imparted by a photon of 1.33e-20 is not sufficient to cause a jump to higher state if 5.4e-19 is needed.
mkelly: CO2 absorbs IR radiation by going to an excited vibrational state, not an excited electronic state. So the entire argument is founded on a false premise.
Fair enough. What is the amount of energy required to change the vibrational state of CO2?
Robert P.
How does a photon excite CO2 via vibration….impact?
J. Lanier:
A photon can be absorbed if the energy of that photon matches the energy difference between two states of the molecule which absorbs it.
This is a basic element of quantum mechanics – that molecular vibrational and rotational energy states are quantized.
Different molecules have different energy states, for example, O2 and N2 are totally different from CO2, NO2 and CH4.
Energy absorbed can be used in:
– moving an electron to a higher energy state
– increasing the vibrational energy of the molecule
– increasing the rotational energy of the molecule
And if we take a specific example like oxygen in the stratosphere, very high energy photons (low wavelength) break up O2 into O + O.
No, not impact. Was your question “proof by ridicule”?
Everyday experience is not a useful guide for quantum mechanics.
What is a useful guide is 100 years of experimental results and theoretical work.
Describing it in everyday language isn’t always possible, although often attempted to overcome “conceptual barriers”.
SoD;
Being quantized, energy above and below these specific values will have no effect…correct?
When a photon of correct wavelength is absorbed, the target molecule’s valance electron is “stepped” up to the next higher valance level. When returning to it’s unexcited state, a photon of slightly lower energy (longer wavelength), then was originally absorbed, is released …correct?
How does an absorbed photon increase the vibrational energy and/or rotational energy of the molecule? Can any of these quantized energy states occur simultaneously?
J. Lanier:
In most cases a photon being absorbed has no effect on the electron states.
These (excited electronic states) are usually higher energy transitions (=shorter wavelength).
Most of the absorption lines in CO2 are associated with rotational/vibrational energy changes.
You ask “How does an absorbed photon increase the vibrational energy..“. I don’t think it’s an easy question to answer. Like “How does work turn into heat?”
That is a challenging question as well.
Where “challenging” = “answering the question so people say, oh of course, I get it”.
Yet we are talking about atoms, photons and quantum mechanics. How can we “get it”?
“The first law of thermodynamics”, if that helps with an “I see” type of answer.
The point is, it happens.
It’s actually not that complicated, SOD. Molecular vibrations and rotations behave fairly classically (since they involve motions of atomic nuclei, which are thousands of times more massive than electrons), so classical pictures work pretty well (mostly) although of course you need quantum to get the numbers right.
IR radiation is an electromagnetic field that varies in time and space. CO2 is a molecule with an uneven distribution of electric charge: the oxygens are more negative, the carbon more positive. The electric field of the light grabs these partially charged atoms and moves them against each other (“induces a dipole moment”), either by squeezing one CO bond and stretching the other, or by bending the molecule (the latter is the main contributor to the greenhouse effect.) However, the absolute strength of the field is weak compared to the static fields within molecules, so you will only get significant stretching/bending if the frequency of the field is resonant with one of the “natural” frequencies (normal mode frequencies) of the molecule, i.e. the frequencies at which it vibrates when not being forced. In the harmonic approximation, these classical “natural” frequencies are exactly equal to the energy spacing between quantum states, divided by Planck’s constant.
How do you determine the absolute strength of the field? If the CO2 is continuously within this field, why would it ever “recoil” releasing IR radiation..propagating an atmosphere electromagnetic field? That is, this terrestrial emitted field (IR) is relatively constant, so why will a “bent” CO2 molecule return to a non-excited state while within the emf?
Is the electromagnetic field a function of the photon stream, or is yours a pure wave, not particle (photon) argument?
It doesn’t “recoil” (usually) – it transfers its vibrational energy to another molecule (most likely nitrogen or oxygen) which returns it to its ground state. That’s where the “warming” comes from. But, once in a great while, the energy ends up in another CO2 bend, and once in an even greater while, that CO2 emits that energy as radiation instead of handing it off to another molecule. This is spontaneous emission, completely uncorrelated with the original absorption. You can understand spontaneous emission classically as the radiation generated by the oscillating charges in the molecule as it vibrates – the molecule behaves like an antenna. But again you need quantum to get the numbers right.
The equations of radiative transfer, which SOD has expounded so eloquently on this blog, take all of these phenomena into account, but they do so implicitly – the “once in a while” and “once in a great while” are buried in the magnitudes of the absorption and emission coeffcients.
Yes, this picture relies upon a classical wave picture of the radiation. You can translate it all into quantum language, but it becomes much more abstract and harder (or impossible) to visualize.
You can explain rotational transitions the same way. The electric field exerts a torque on a molecule having a dipole moment, and “spins it up.” That’s why water absorbs microwave and IR radiation, while CO2 only absorbs IR: water has a dipole moment that the field can grab and twist, CO2 only develops a dipole moment when it vibrates.
mkelly:
As a very general guide:
Electronic transition: Wavelength less than 1 μm = Wavenumber greater than 10,000 cm-1 = Energy greater than 2 x 10-19 J
Vibrational transition: Wavelength 1 μm – 20 μm = Wavenumber 500 – 10,000 cm-1 = Energy = 1 x 10-20 – 2 x 10-19 J
Rotational transition: Wavelength greater than 20 μm = Wavenumber less than 500 cm-1 = Energy less than 1 x 10-20 J
Usually vibrational changes are accompanied by rotational changes.
DeWitt Payne said (on email – following his sending of the SpectralCalc results for comparison):
This is something I will try and check.
mkelly and J. Lanier,
A condensed introduction to molecular absorption and emission of radiation can be found in Chapter 5, Atmospheric Radiation, in R. Caballero’s Lecture Notes in Physical Meteorology starting at page 96 of the pdf. The pdf is now approaching 30 MB so downloading might take a long time if you don’t have a fast connection.
Click to access PhysMetLectNotes.pdf
Asking someone at a blog to hold your hand through an introduction to quantum mechanics is asking too much. Find a local community college with an adult education program and sign up for a course in Physics.
scienceofdoom,
Here’s the plot of the residual transmittance from subtraction of 12C16O2 from the all major isotopologue transmittance after interpolation so the wavenumbers match. There’s still a little aliasing, if that’s the correct term, but it looks more like a spectrum and particularly it looks a lot like the spectrum of 13C16O2 at the appropriate mixing level which I, unfortunately, didn’t save and my subscription has since expired.
Here’s the same plot with the spectra for 13C16O2, 12C16O18O and 12C16O17O overlaid. It’s pretty ugly, but it’s the best I could do for free. Note that almost all the features are there. The problems are likely due to rounding errors in the wavenumber interpolation. Also, the overlay spectra were calculated using the HITRAN2004 database while the difference spectrum used HITRAN2008. That might explain the difference in location of the minor line at ~667.4 cm-1.
DeWitt:
I’ve been caught up in too much work the last week or so to spend the time on this – but it’s not forgotten. I do want to get to the bottom of the subject.
Take your time.
After I did the above graphs, I realized that I really should have converted to absorbance and then subtracted. I did that and it cleaned up the 13C16O2 peak but made the rounding error problems at the 12C16O2 peak worse.
That’s the 12C16O18O peak. The 13C16O2 main peak isn’t in the 660-672 range. It’s at 648.5 cm-1
A couple of questions and verifications: Although it is heavily weighted in most discussions, isn’t pressure broadening pretty insignificant? Isn’t the “spreading” of the wings almost entirely due to rotational energy levels. A rule of thumb that I’ve picked up is that typical pressure spreading is roughly 0.03 to 0.1 cm^-1 for half-width half max intensity, though it spreads further at lower intensities as indicated in your Figure 1. (I’m not sure I’m using “intensity” the right way here…) So if a center vibration wavenumber is 667 the maximum range of absorption would be 666.9 to 667.1 cm-1, and it’s likely half that. But the differential of rotation levels is about 0.5 cm-1 or so plus there are tens to hundreds of these levels about the center vibration level. I think the graphs shown in the pressure broadening discussion actually show rotation energy lines with pressure broadening having only a small effect connecting the bottoms of the peaks. Am I thinking right here?
If so, isn’t the oft used explanation that ‘saturation is not reached because the absorption capability spreads because of greater collision broadening from additional CO2 molecules’ missing the boat? (I haven’t thought it through but my gut tells me that as CO2 populations increase higher rotation quantum levels probably absorb more — though I have no idea by how much…)
Your explanation of the uncertainty spreading is technically off the mark, IMO. The energy associated with a 20 teraHz signal is the same as a 19.999978569 teraHz signal. The uncertainty depends on the time of excitation. Though your point was well made so I’m just nit-picking here.
I think the description of the HITRAN database is a little more gee-whiz than helpful. The vast majority of the 300-400,000 CO2 lines have insignificant (…well, very small…) effect on overall absorption. Many are at the extremes of the rotation set and most are from different isotopologues of CO2, as is pointed out. I would guess (never actually counted) that two or three of the isotopologues would easily cover 99.9+% of the concentration (though isotopologues do have a noticeable effect on rotation energy levels.)
HITRAN questions: 1) Like the MATLAB uses only one isotopologue, I heard that HITRAN somehow takes the isotopologue distribution into account in its calculations. Do you know if this is right? 2) the exponent γ in the half-width equation: does this vary with isotopologues or other factors? And since it (the precise number) is not physics derived but is an estimated figure based on empirical lab experiments, do the users have an option of varying the exponent or do HITRAN database owners select their best estimate? 3) the a0 of the equation also has an elusive factor — collisional cross-section. This has a significant impact yet varies with many parameters including isotopologue and relative concentration and is also empirically estimated (though physics theory gets pretty far). Same question: does HITRAN preselect this factor and does it vary with concentration, e.g., or can the user vary this factor?
I have a couple of other questions/comments but I think this is mixed-up enough. Plus I haven’t gotten through all of this thread yet, so if I’m old hat, sorry.
Look at it as reduced pressure narrowing rather than broadening. If the lines didn’t narrow a lot as the pressure went down, the stratosphere would be a lot colder.
HITRAN is a database. It doesn’t do calculations. You have to do those yourself, obtain a program that does like LBLRTM or you can subscribe to SpectralCalc
http://www.spectralcalc.com/info/about.php
DeWitt, thanks for the help.
I’m not sure there’s much difference between pressure broadening and low pressure narrowing. The former seems more apt as the normal line is naturally very narrow, enhanced only by minuscule doppler and even more minuscule uncertainty broadening. My point (question) is whether pressure broadening is anywhere near as significant ala concentration and saturation (or not) because of bandwidth increases as it is often stated.
I didn’t ask the other question right. The data base for radiation transfer stuff contains a lot of independent variables that have sometimes considerable ranges that are not determined mathematically but must be assumed. Like the gamma exponent of temperature ratio in the broadening equation which HITRAN said (1998) could be anywhere from 0.49 to 0.78 for CO2. Though I don’t know if their range was an average for all CO2 and might be smaller for individual isotopologues. The average base pressure-broadened half width has a range of a factor of two primarily from the estimate of collision cross sections which also vary some by isotopologue and alot by concentration. There are others. Before calculation runs can be made the selection of these variables must be made. My question is does HITRAN select the precise variables based on their best estimate, or does the user pick the individual variables, or maybe it’s optional; and are the selected variables an overall average or by individual molecular case, or by isotopologue distribution? Or even maybe HITRAN combines it all and simply provides an optical thickness factor?
I may be getting way too deep in the mud for a blog, but if anyone happens to know, top of their head….
Rod B,
The range in gamma is for all lines of all isotopologues. Each line has a unique gamma factor, actually two separate gamma factors, one for self and one for air. If you go to the HITRAN site to the documentation page, there are links to all sorts of papers describing the database.
http://www.cfa.harvard.edu/HITRAN/
Table 3 in the paper describing the 1996 edition shows a very small selection from the database covering 800.451076 to 800.484334 cm-1. Appendix A goes into great detail on definitions and usage of the parameters.
Thanks
DeWitt:
On isotopologues, I have this definition in the program:
isoprop=[0.98420 0.01106 0.0039471 0.000734 0.00004434 0.00000825 0.0000039573 0.00000147]
which means 1st isotopologue is 98.4%, 2nd is 1.11%, 3rd is 0.39% etc.
I’m not sure why I only included the first 8, and if I want to improve speed at some stage I should probably just pick from the top three.
The proportional values come from the “Hitran facts” link on the left pane of http://www.cfa.harvard.edu/hitran/ – and match what you gave in your email.
I will rerun the test for the main isotopologue only, at 380ppm for this one type, making sure the frequencies match your test.
DeWitt:
I extracted the wavenumbers from your file (2a) and fed them in as the source wavenumbers for my program – so there was no chance of a subtle frequency shift.
I had the ppm of CO2 (primary isotopologue) as 380ppm, same as you.
1m path through 296K, 1013mbar.
But there is a difference between our results (and not the same as the earlier comparison):
Click for a larger image
However, it looks like a very slight scaling issue when we plot the difference:
Click for a larger image
I put in the exact pressure (1013.25 instead of 1013, but that wasn’t it.
Perhaps I have slightly the wrong number density of molecules? Or some other rounding issue?
I have:
Number of CO2 molecules per cm^3 = 9281304920693130; because rho = 1.1766 kg/m^3
and Avogadro’s number, Na=6.02×10^23
So, I check the two files and the problem becomes clearer:
At the 537th item in the list, wavenumber = 666.0056 cm^-1, your tau = 0.0422, my tau = 0.0409 – a ratio of 1.0318.
At the 104th item, v = 661.1586, your tau = 0.3446, my tau = 0.3340 – a ratio of 1.0315.
At the 662nd item, v = 667.4049, your tau = 3.0918, my tau = 2.9975 – a ratio of 1.0315.
A constant ratio of optical thickness wherever we are on the graph.
Therefore, I have 3.15% less molecules than SpectralCalc in my working calcs.
Any idea why?
I get 1.193 kg/m3 as the density of dry air at 296 K and 101325 Pa (dry air effective MW 28.97). That’s about half. The only thing I can think of for the other half is that your program is actually calculating for 98.4% of 380 ppm for 12C16O2. I think you’ll find that if you take my file #2 rather than 2a and correct for the density difference, it will be the same as yours.
By the way, I calculate rho (density) from the ideal gas equation. Does SpectralCalc assume 1.2 kg/m^3? Is this the 3%?
You left out argon. Or at least that’s the only way I can get your density for dry air.
SpectralCalc says they always scale the VMR to the isotopologue fraction.
No, I definitely have 380ppm of CO2 main isotopologue – and none of the others.
I had the molar mass of air with a typo in the “define_atmos” routine – 28.47 x 10^-3 kg/mole. It should be 28.97 x 10^-3.
Rerunning, I get the correct density = 1.1925 kg/m^3.
The errors now halve in the comparison.
So it’s clear that we have a scalar error to do with the number of CO2 molecules in the path.
I’m happy with that – the results come up the same as SpectralCalc and if we could stipulate the same number of molecules the results would be identical.
It’s possible that SpectralCalc is making an error. It may be that the VMR actually corresponds to the major isotopologue and then they add the minor ones. I’ll ask. That should mean that my file 2 should agree with your data and 2a will be greater by ~1.5%.
[…] this is because of the reduction in pressure broadening at lower pressures = higher altitudes (see Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Nine). This effect causes the absorptivity of CO2 to reduce at higher altitudes meaning that the […]
[…] a look back at Part Nine. Here is the calculated change in transmittance from the surface to the tropopause for a doubling […]
[…] little while ago I managed to recreate the CO2 transmittance in the atmosphere – as shown in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Nine. This was done using the HITRAN database in a MATLAB model I […]
Sorry, I am still at level zero (like Kung fu panda says). And in what litttle free time I have I think about a semi-grey model. How can I use the data of figure 15 for example to come up with a corresponding ‘grey’ optical depth? Is is simply a matter of averaging the transmittance over the short wave spectrum? (4 mu-m to ~ 30 m-um) or the corresponding value for cm-1?
Andrejs Vanags:
If you took the average of this transmittance over the terrestrial spectrum (4 – 100 μm, or 100 cm-1 – 2500 cm-1) then you would have something useful for the effective transmittance of CO2.
One important point to note is that to get a correct answer you would need to “Planck-weight” the average for a given surface temperature.
This is because the importance of transmittance at 5 μm is much less than the importance of transmittance at 10 μm, because the emission of radiation is much less at 5 μm than 10 μm.
Perhaps I might get around to doing it at some stage.
And the result would not be very sensitive to surface temperature – so if you did it for 288K it would be very close to the answer for 263K.
But if you just average the spectrum from fig 15 over an unweighted 4-100 μm you would get a very different number.
Science of Doom:
I went ahead and got the HITRAN_0_3.m program you posted running, by adding the Ttropo parameter to define_atmos_0_2.m (the one I had) and calling it define_atmos_0_3.m, then I used your hitran_co2_keyparams1.txt file and saved it as Co2.mat, assigning the columns to ‘iso’,’S’,’v’,’gama’, and ‘nair’. It all seemed to work. THANKS!!
Then I had the hardest time trying to create a Bgamma curve using the wavenumber, I figured the wavenumber was 1/wavelength (some people use 2*pi/wavelength) and could not get the integral of the Bgamma curve (spectral radiance) to match sigma*T^4 (stefan Bolztman law). Never got it working using wavenumbers, had to convertt them to wavelengths. After some reading I figured that the Stefan Boltzman energy radiated per surface area goes in all directions from the surface, and the Bgamma curve is only perpendicular to the surface. The integral of the Bgamma curve vs gamma = sigma*T^4 divided by pi.
Ok, after all that I could generate the black body radiation at 296K and integrate it, then run the HITRAN_0_3 program (with the wave number range increased to vmin=1 to vmax=2500 and get the transmittance. Then I multiplied the transmittance to the black body curve, integrated it, and got the ratio of the two integrals and then I call that the effective transmittance, and -ln(that) I call the grey optical thickness. I hope I did not go off the deep end there. The results for CO2 ppm’s of 70,140,280,560,1120 then seem to follow the relation tautotal = 0.0495*(CO2ppm)^0.2618
If the total optical thickness for the atmosphere is about 1.9 then that means that at ~ 280ppm the percent contributed by CO2 is 0.216/1.9 or 12%
1) Could you post, or direct me to where I could get a similar file as the CO2 data, but for H2O?
2) I ran the HITRAN_0_3 at 0 CO2 ppm and got transmittance of 1.0. So it does not appear to include any other species. Is the air (N2 and O2) totally transparent to IR? or do we also need to get similar files for air? Or O2 and N2?
Could you comment on the approach?. And thanks again for making the programs available so we can use them.
I think I figured it out by brute force.
It seems that Spectralcalc will give you the Hitran data at:
http://www.spectralcalc.com/spectral_browser/db_data.php
Select Hitran2008 from the line list.
Select H20 from the species.
Select the range of wave numbers (I used 1 to 2500)
Select datafile format as csv.
then click on ‘Extract data’
then rigth click on ‘View lines’ and save as *.csv
To read it into matlab I had to delete the header information and just keep the first 10 columns (the rest are codes and some have alphanumeric characters)
Then to figure out what columns did SOD use for his values of:
S, gama, iso,nair,v I downloaded the same data for CO2 and plotted all the columns until I matched the SOD variables that he uses in his co2 matlab file for HITRAN_0_3.m:
column 1 is the species code (H20 or CO2, etc)
iso is column 2, the isopotologue code
v is column 3, labeled as frequency
S is column 4, labeled as intensity
gama is column 6, labeled as air_halfwidth
nair is column 9, labeled as t_exponent
the list of isopotologue concentrations is from the document describing the 2004 Hitran edition:
http://www.cfa.harvard.edu/hitran/docs.html
for H2O there are 6 with the following concentrations:
isoprop=[0.997317 0.0199983 0.000372 0.00031069 0.000000623 0.000000116];
I was then able to recreate the CO2 transmittance graphs (using CO2 data) and create similar ones for H2O (using H2O data). Now I am off going to figure out how to define H2O concentrations in the atmosphere, and how to do combined CO2 and H2O runs.
Thanks to all for making this available to me 🙂
Very nice addition to the web. Could you put up (or link to) your define_atmos_0_3.m and define_atmos_0_2.m file? I am in urgent need!
thank you very much.
Van Minh Nham,
The link to define_atmos_0_5.m is given in post
That might satisfy your needs. (The file has the ending .doc, but it’s really a .m file.)
Very nice addition to the web. Could you put up (or link to) your define_atmos_0_3.m and define_atmos_0_2.m file? I am in urgent need!
thank you very much.
Asking questions are actually good thing if you are not
understanding anything entirely, howevger ths paqragraph
presents pleasant understanding even.