In the first two parts we looked at some basic statistical concepts, especially the idea of sampling from a distribution, and investigated how this question is answered: Does this sample come from a population of mean = μ?
If we can answer this abstract-looking question then we can consider questions such as:
- “how likely is it that the average temperature has changed over the last 30 years?”
- “is the temperature in Boston different from the temperature in New York?”
It is important to understand the assumptions under which we are able to put % probabilities on the answers to these kind of questions.
The statistical tests so far described rely upon each event being independent from every other event. Typical examples of independent events in statistics books are:
- the toss of a coin
- the throw of a dice
- the measurement of the height of a resident of Burkina Faso
In each case, the result of one measurement does not affect any other measurement.
If we measure the max and min temperatures in Ithaca, NY today, and then measure it tomorrow, and then the day after, are these independent (unrelated) events?
No.
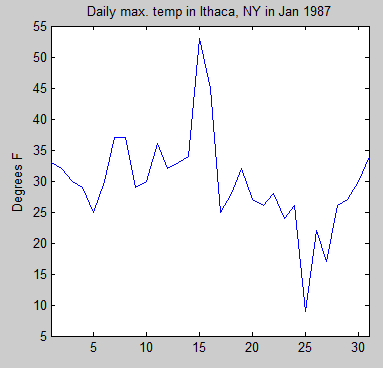
Here is the daily maximum temperature for January 1987 for Ithaca, NY:
Figure 1
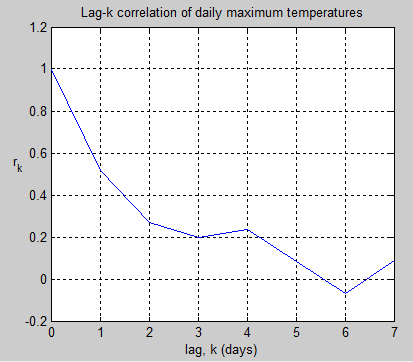
Now we want to investigate how values on one day are correlated with values on another day. So we look at the correlation of the temperature on each day with progressively larger lags in days. The correlation goes by the inspiring and memorable name of the Pearson product-moment correlation coefficient.
This correlation is the value commonly known as “r”.
So for k=0 we are comparing each day with itself, which obviously has a perfect correlation. And for k=1 we are comparing each day with the one afterwards – and finding the (average) correlation. For k=2 we are comparing 2 days afterwards. And so on. Here are the results:
Figure 2
As you can see, the autocorrelation decreases as the number of days increases, which is intuitively obvious. And by the time we get to more than 5 days, the correlation has decreased to zero.
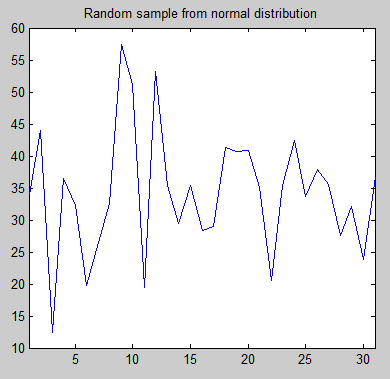
By way of comparison, here is one random (normal) distribution with the same mean and standard deviation as the Ithaca temperature values:
Figure 3
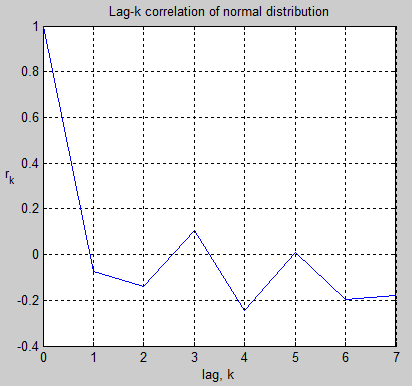
And the autocorrelation values:
Figure 4
As you would expect, the correlation of each value with the next value is around zero. The reason it is not exactly zero is just the randomness associated with only 31 values.
Digression: Time-Series and Frequency Transformations
Many people will be new to the concept of how time-series values convert into frequency plots – the Fourier transform. For those who do understand this subject, skip forward to the next sub-heading..
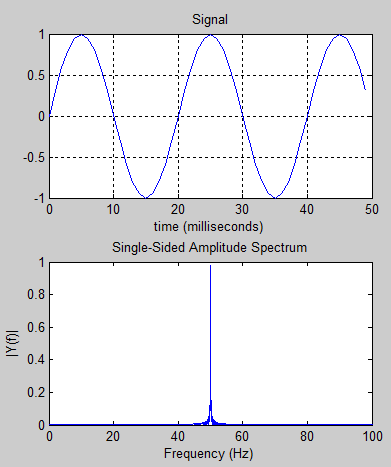
Suppose we have a 50Hz sine wave. If we plot amplitude against time we get the first graph below.
Figure 5
If we want to investigate the frequency components we do a fourier transform and we get the 2nd graph below. That simply tells us the obvious fact that a 50Hz signal is a 50Hz signal. So what is the point of the exercise?
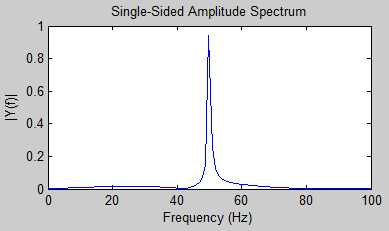
What about if we have the time-based signal shown in the next graph – what can we tell about its real source?
Figure 6
When we see the frequency transform in the 2nd graph we can immediately tell that the signal is made up of two sine waves – one at 50Hz and one at 120Hz – along with some noise. It’s not really possible to deduce that from looking at the time-domain signal (not for ordinary people anyway).
Frequency transforms give us valuable insights into data.
Just as a last point on this digression, in figure 5, why isn’t the frequency plot a perfect line at 50Hz? If the time-domain data went from zero to infinity, the frequency plot would be that perfect line. In figure 5, the time-domain data actually went from zero to 10 seconds (not all of which was plotted).
Here we see the frequency transform for a 50Hz sine wave over just 1 second:
Figure 7
For people new to frequency transforms it probably doesn’t seem clear why this happens but by having a truncated time series we have effectively added other frequency components – from the 1 second envelope surrounding the 50 Hz sine wave. If this last point isn’t clear, don’t worry about it.
Autocorrelation Equations and Frequency
The simplest autocorrelation model is the first-order autoregression, or AR(1) model.
The AR(1) model can be written as:
xt+1 – μ = φ(xt – μ) + εt+1
where xt+1 = the next value in the sequence, xt = the last value in the sequence, μ = the mean, εt+1 = random quantity and φ = auto-regression parameter
In non-technical terms, the next value in the series is made up of a random element plus a dependence on the last value – with the strength of this dependence being the parameter φ.
It appears that there is some confusion about this simple model. Recently, referencing an article via Bishop Hill, Doug Keenan wrote:
To draw that conclusion, the IPCC had to make an assumption about the global temperature series. The assumption that it made is known as the “AR1” assumption (this is from the statistical concept of “first-order autoregression”). The assumption implies, among other things, that only the current value in a time series has a direct effect on the next value. For the global temperature series, it means that this year’s temperature affects next year’s, but temperatures in previous years do not. For example, if the last several years were extremely cold, that on its own would not affect the chance that next year will be colder than average. Hence, the assumption made by the IPCC seems intuitively implausible.
[Update – apologies to Doug Keenan for misunderstanding his point – see his comment below ]
The confusion in the statement above is that mathematically the AR1 model does only rely on the last value to calculate the next value – you can see that in the formula above. But that doesn’t mean that there is no correlation between earlier values in the series. If day 2 has a relationship to day 1, and day 3 has a relationship to day 2, clearly there is a relationship between day 3 and day 1 – just not as strong as the relationship between day 3 and day 2 or between day 2 and day 1.
(And it is easy to demonstrate with a lag-2 correlation of a synthetic AR1 series – the 2-day correlation is not zero).
Well, more for another article when we look at the various autoregression models.
For now we will consider the simplest model, AR1, to learn a few things about time-series data with serial correlation.
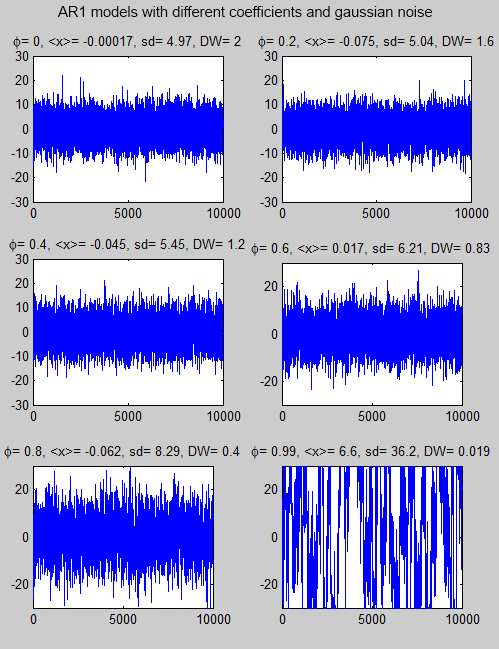
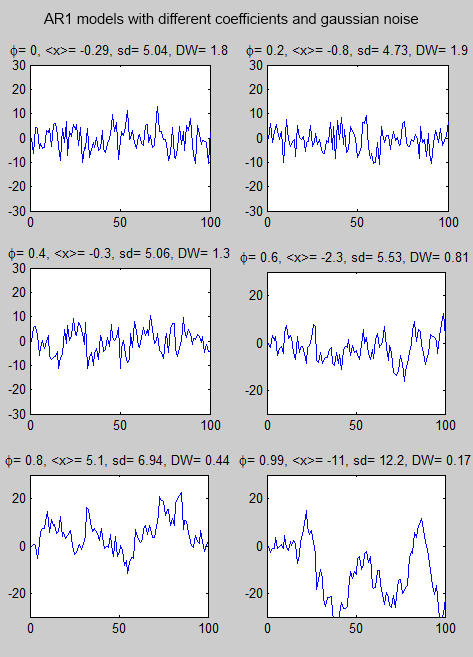
Here are some synthetic time-series with different autoregression parameters (the value φ in the equation) and gaussian (=normal, or the “bell-shaped curve”) noise. The gaussian noise is the same in each series – with a standard deviation=5.
I’ve used long time-series to make the frequency characteristics clearer (later we will see the same models over a shorter time period):
Figure 8
The value <x> is the mean. Note that the standard deviation (sd) of the data gets larger as the autoregressive parameter increases. DW is the Durbin-Watson statistic which we will probably come back to at a later date.
When φ = 0, this is the same as each data value being completely independent of every other data value.
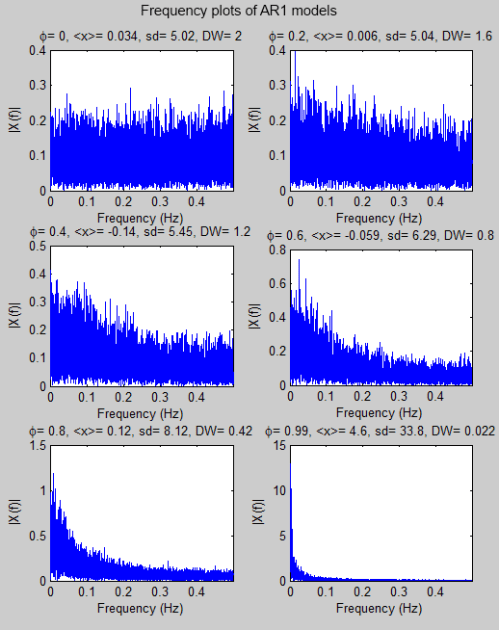
Now the frequency transformation (using a new dataset to save a little programming time on my part):
Figure 9
The first graph in the panel, with φ=0, is known as “white noise“. This means that the energy per unit frequency doesn’t change with frequency. As the autoregressive parameter increases you can see that the energy shifts to lower frequencies. This is known as “red noise“.
Here are the same models over 100 events (instead of 10,000) to make the time-based characteristics easier to see:
Figure 10
As the autoregression parameter increases you can see that the latest value is more likely to be influenced by the previous value.
The equation is also sometimes known as a red noise process because a positive value of the parameter φ averages or smoothes out short-term fluctuations in the serially independent series of innovations, ε, while affecting the slower variations much less strongly. The resulting time series is called red noise by analogy to visible light depleted in the shorter wavelengths, which appears reddish..
It is evident that the most erratic point to point variations in the uncorrelated series have been smoothed out, but the slower random variations are essentially preserved. In the time domain this smoothing is expressed as positive serial correlation. From a frequency perspective, the resulting series is “reddened”.
From Wilks (2011).
There is more to cover on this simple model but the most important point to grasp is that data which is serially correlated has different statistical properties than data which is a series of independent events.
Luckily, we can still use many standard hypothesis tests but we need to make allowance for the increase in the standard deviation of serially correlated data over independent data.
References
Statistical Methods in the Atmospheric Sciences, 3rd edition, Daniel Wilks, Academic Press (2011)



I found this comment useful:
Statistical Considerations in the Evaluation of Climate Experiments with Atmospheric General Circulation Models, Laurmann & Gates, Journal of the Atmospheric Sciences (1977)
The paper covers some statistical theory in serially correlated data, but is unfortunately behind a paywall.
Another interesting paper is Taking Serial Correlation into Account in Tests of the Mean, Zwiers & von Storch, Journal of Climate (1995).
And later, on AR1 models:
A good explanation of why an AR(1) type model is not correctly described by Doug Keegan:
From Wilks (2011).
Correct me if I’m wrong but I read the article and I believe he is saying that the use of AR1 is incorrect because ” For the global temperature series, it means that this year’s temperature affects next year’s, but temperatures in previous years do not. ” I believe he is saying BECAUSE temperature in one year cannot be used to “Predict” the temperature in the next year, the use of AR1 or any form of statistics is incorrect. In other words, statistics my be OK for Math and Graphs but dont use it for temperature or Lottery numbers.
Nice article. Thanks.
Very good series SoD. I will be showing my age with this comment, but I remember attending a seminar by Dr Edward Deming some time ago. As you know, he was a pioneer in statistical quality assurance.
One thing Dr. Deming constantly preached over and over was that even though its important for manufacturing managers to have a working knowledge of statistical quality control, they must also have access to a competent theoretical statistician that will understand when the standard canned statistical tools are not appropriate and can then develop a more proper tool. My sense is that this would be even more true for something as complex as the earth’s climate.
Do you know if climate scientists use theoretical statisticians in their work or at least to review their work prior to publication? or do they typically use canned plug and play tools without a theoretical statistician’s involvement?
Several statisticians have criticized the climate science community (particularly paleoclimatologists) for statistically dubious practices. You could read:
McShane & Wyner (2010) http://www.e-publications.org/ims/submission/index.php/AOAS/user/submissionFile/6695?confirm=63ebfddf
The Wegman Report: http://republicans.energycommerce.house.gov/108/home/07142006_Wegman_Report.pdf
The NRC report on the Hockey Stick: http://books.nap.edu/openbook.php?isbn=0309102251
and lots of one-sided stuff at climateaudit.org
The big problem with climate science often is that the data is very noisy, the time span is limited and experiments can’t be repeated under carefully controlled conditions. Often, the more rigorous the statistical analysis, the greater the uncertainty and the less likely you will produce a high-impact publication. From my cynical perspective, who needs the advice of a professional statistician when Nature, Science and the IPCC are willing publish alarming results without a thorough statistical review and when your colleagues continue to cite your work? However, it is difficult to know whether such cynicism should be applied to a trivial or significant fraction of important climate science publications.
My article states “only the current value in a time series has a DIRECT effect on the next value” [emphasis added]. That statement is correct.
My article also states “For the global temperature series, it means that this year’s temperature affects next year’s, but temperatures in previous years do not”. The point is that once we have knowledge of the present, knowledge of previous years gives no additional information.
My post further states “For example, if the last several years were extremely cold, that ON ITS OWN would not affect the chance that next year will be colder than average” [emphasis added]. Again that is correct, assuming we have knowledge of the present year.
You should read more carefully before criticizing. This is basic stuff.
Douglas J. Keenan:
I apologize if I have misunderstood your statement. I am still not sure I understand your point.
But I will update my article.
You agree – under the assumption of an AR(1) model – that there is a relationship between the previous year’s and next year’s value – even though next year’s value is only mathematically dependent on this year’s value?
scienceofdoom, I’m glad to have this clarified.
Yes, under AR(1), there is a relationship between the previous year’s and next year’s value.
The main point of the paragraph is just to give readers a rough idea of what AR(1) is. Early drafts of the article said only that the IPCC made an assumption called “AR1”, but did not explain what AR1 was; feedback that I got on those drafts indicated that there should be some elaboration.
Once the elaboration was included, I thought some comment was appropriate; so I put in “the assumption made by the IPCC seems intuitively implausible”. This point, though, is tiny for the article.
Still no mention of temperature……Mmmmmm. Maybe in statistics the previous year has a relationship..However, statistics is not evidence. As Douglas has mentioned, ” In other words, the assumption used by the IPCC is simply made by proclamation. Science is supposed to be based on evidence and logic. The failure of the IPCC to present any evidence or logic to support its assumption is a serious violation of basic scientific principles. ” The temperature of one year has no influence on the years after. Just look at BC. Here we have the coldest spring and summer in recorded history. Where is the statistical support for this?
OH yeah, its just weather right?… LOL
Bruce James, Are you just repeating Douglas Keenan’s claim, or are you independently confirming it?
In IPCC AR4 chapter 3, Observations:Surface and Atmospheric Climate Change, p.243 (which is p.9 of the chapter)
I take this to be a statistical argument that the temperature trends have been evaluated for a higher order autoregression than AR(1).
Reviewing Appendix 3.A:
[Emphasis added].
Cohn & Lins is Nature’s style: Naturally trendy (free link) published in Geophysical Research Letters. This paper opens up a wealth of other research on the topic of detecting statistical significance trends under the persistence exhibited by atmospheric values.
Extract:
All very interesting stuff.
But this claim by Douglas Keenan:
“The IPCC chapter, however, does not report doing such checks. In other words, the assumption used by the IPCC is simply made by proclamation. Science is supposed to be based on evidence and logic. The failure of the IPCC to present any evidence or logic to support its assumption is a serious violation of basic scientific principles.” appears flawed. [Update – see comment below.]
The test and the support cited may well be flawed or lead to different conclusions, I have no comment or claim about that. This is a subject I still have much to learn about.
Cohn & Lins is well-worth reading, although of course, has a pre-requisite of some statistical knowledge.
They say:
And in their conclusion:
Something for everyone in this paper.
But I have digressed, we are still getting to understand the questions of statistical significance in the simplest model of serial correlation..
Steve McIntyre has investigated the statistical correctness of the above Table 3.2 of AR4. He is skeptical that the IPCC has properly dealt with long term persistence.
Now I have followed some more of the trail of Doug Keenan’s article – Supplement to “How scientific is climate science?” – I realize he is well ahead of me.
I think his statement that I cited above (“The IPCC chapter, however, does not report doing such checks..“) is, to the reader, misleading. But given his followup work, I don’t want to take issue with him.
In a few years when I understand the subject better I will have more comment.
scienceofdoom
If you are going to claim that the IPCC did a test for AR(1), then specify the test.
The paper of Cohn & Lins is discussed in my article’s supplementary technical details: see the link at the end of the article.
Since the article was published, I have written more about the models treated by C&L: see
http://www.bishop-hill.net/blog/2011/6/6/koutsoyiannis-2011.html
That shows, in particular, that the IPCC’s “physical realism” argument for rejecting the C&L models is invalid.
Douglass,
In your article you state: ‘The paper does not analyze the global temperature series, but previous work of Koutsoyiannis does and shows that the formula fits the series well.’
Do you have a specific citation for this? I’ve seen his analyses of single grid points and the continental USA but not the global mean temperature.
It seems intuitively obvious to me that we can look at the earth’s weather and from second to second the current state is strongly determined by the previous state.
That argument seems to work out to a few days but at about the time we can no longer predict the weather, it completely breaks down.
I believe the IPCC is saying that some aspect of the earth’s climate, namely surface temperature anomoly, can still be determined by previous values despite the fact that we can demonstably no longer predict them.
And not necessarily the same previous values either. Sometimes one needs to look further back to get to suitably lower values and their argument is based on conservation of energy consideration wrapped up in a plausible but unproven mechanism.
What that theory fails to appreciate is that the earth will adjust its atmospheric and oceanic processes to maximum its energy loss and instead predicts increasing and accelerating temperature gradients.
Science of Doom,
I think that particular care may be need to distinquish between two type of confidence.
In the statement:
“Global mean surface temperatures have risen by 0.74°C ± 0.18°C when estimated by a linear trend over the last 100 years (1906–2005). The rate of warming over the last 50 years is almost double that over the last 100 years (0.13°C ± 0.03°C vs. 0.07°C ± 0.02°C per decade).”
Are we asking the question is the trend real or are we asking is the trend significant.
The first requires knowledge about the measurement errors which in this case might require examination of the metadata provided by the provider and other known sources of measuremetn error. This should be reasonably straight forward.
The second would require knowledge of the statistical behaviour of the system. It answers the question, given the trend is real (not a artefact of the measurement procedure) could it be a chance event. One asks how often would this trend occur spontaneously. If we know the correct model for the system we can deduce its statistical properties and attempt to anwser that question. Unfortunately this is not known in this case and hence the choice of model somewhat subjective.
Given the accuracy with which the statement is made I would presume that it is simply answering the question “is the warming real?”. In which case only knowledge relating to measurement errors is required.
That said, the IPCC seemed to have gone a bit further in that they would appear to be answering the question is the trend real after allowing for weather phenomena including El Nino. (Appendix 3.A).
That is getting close to asking the question “is the trend significant” but not quite providing they are only removing phenomena that are short term and of a periodic or quasi-periodic nature. Just as they have removed the season variation by using anomalies in the first place.
Now if that statement is not anwsering the question “is it significant” then a deep knowledge of the model e.g. its long term persistence is not necessary.
I suspect that the statement is only trying to answer the question “is it real”, and the question of significance is dealt with in Chapter 9:
“It is extremely unlikely (<5%) that the global pattern of warming during the past half century can be explained without external forcing, and very unlikely that it is due to known natural external causes alone."
That statement is open to challenge on the basis of the model chosen to derive the system's statistics.
I do fear that you, Douglas J. Keenan, and I, may all be arguing passed each other. I am trying to emphasise the clear distinction in my mind between detection and attribution, the "is it real" and "is it significant" questions, in case this is a source of unnecessary debate.
It is normally the "is it significant" question that gets people excited although there are some that do argue that no detectable warming has occurred.
Alex
Alexander Harvey,
I think you have written a useful and interesting summary.
My only comment in this arena was not to say “it is significant”. My comment was to observe that the IPCC appeared to have stated a reason for applying AR(1) to the temperature series.
If the statement by Douglas Keenan had been “The IPCC have made a vague and unfalsifiable claim which is in any case disputed by the paper they cite in support..” or words to that effect, then I might have left it there until such time (if ever) that I could make a contribution to that debate. In fact, the only reason I went looking was because another commenter repeated the original claim and it made me wonder..
The important point being – I am not saying/claiming that the global average temperature series is an AR(1) series with the results that follow according to the IPCC AR4. And I am not saying/claiming that the global average temperature series is not an AR(1) series..
But I believe you right on the money with the distinction between:
a) is there a trend?
b) is there a statistically significant trend?
And one reason for writing this series is to help those few who know less than me on stats understand what the caveats are behind the idea of “statistically significant”.
Question / thought experiment: you’ve been kidnapped, drugged and locked up for months by a dastardly villain in a state of near-coma. He wakes you up at some point, but is keeping you imprisoned in a cell with a yard. The yard has a little weather station and a record book, and an open roof.
Now: the villain demands that you tell him whether you’re heading towards winter or summer. You’ve been under for so many months, there’s no way of knowing. You can take as long as you like, but of course you’ll still be imprisoned. If you get it right, he’ll free you. However, if you get it wrong, he’ll drug you again – so you want to be as sure as you can that you’re accurate.
Let’s presume you know what latitude you’re at. Say, London, UK. How much data do you need to collect before you’re going to feel safe to declare what season you’re going towards?
Statistically, I’ve got a number of questions about this, as compared to climate trends. The basic similarity: too short a period and any detected trend stands a chance of being randomly wrong. For both, you only need to know the direction of the trend, and make a judgement on what p value to aim for. So, you might decide to wait until you were only risking a 5% chance of being wrong about which season you’re in. Of course, the season example is complicated by the fact that the trend is more pronounced at the Vernal and autumnal equinox: not the same issue for climate trend detection.
Aside from that, how do they differ, how are they the same? We have prior knowledge of course: for seasons, we know there will be a cyclical trend – but that’s not the question being asked by our villainous captor. He just wants you to make a judgement call on the trend. What I take from that is, you actually can’t get any information on physical mechanism from time series trend detection – that’s not what it’s for.
I think it would help me if I understood the issues from this thought experiment point of view. All of the stuff in the comments above about the IPCC just confused matters. ScienceofDoom, this is a really good series to be doing, thanks. Let’s hope you can cut through the confusion and keep shining some clarity on the basics. Thanks, Dan.
Sorry, forgot vital part of thought experiment: no open roof! Locked up in darkened basement, with only weather station temperature data fed through to you. (Otherwise you could just measure sunlight change.)
So you have to judge the season direction by temperature only.
danolner,
Do you have continuous data or just max and min? If it’s continuous, you can probably get an estimate of the length of the day from the temperature/time series in a few days, one if there is no cloud cover. If it’s just max and min, it will take longer, weeks or months.
DeWitt: ah, good point. I think I’d have to say – one temperature sample per day, same time, say midday (no BST!) Or, basically, anything to avoid being able to detect length of day by proxy.
It could be more than a thought experiment. HadCET (Central England) daily temperature data from 1772-present is available at http://www.metoffice.gov.uk/hadobs/hadcet/data/download.html. If you can find a way to make random variable length selections of date sequences you can test what amount of data is required to say something significant with high confidence.
You might have to tighten up on the conditions for detection though. You’re talking about trend detection but at certain times of year absolute temperatures are probably more helpful for determining what season you’re in and therefore where you’re heading. For example you could get 3 months of high temperatures and conclude that you must be heading towards Winter – because you must be at or near the end of Summer – despite there being very little in the way of a trend.
Peharps a further stipulation would be that temperatures will be in anomaly form rather than absolute. In that case I would suggest a minimum 10 weeks of data is needed to make a high confidence declaration but that length of time could be considerably higher for certain start dates.
“It could be more than a thought experiment”. Yeah: at some point I’d like to actually work the example up with real data as a way into learning/teaching how to make a judgement when someone says “no significant climate warming” – as the Daily Mail headline did with Phil Jones. (I do a bit of java/processing based visualisation (example), so I’d like to do it using that, to give an intuitive feel for the problem.)
Still learning about time series stats, though – so this series is very timely. You’re right about time of year too, so yes: either daily difference, or stipulate that you get woken up at or near the vernal or autumn equinox (or whichever point happens to have the closest mean twice-yearly temp, since that might be different.)
The thing I still need to understand: AFAIK, in this thought experiment, you do not need to know anything about the physical processes involved. All you’re doing is looking for a point where, say, there’s only a 5% chance of a detected trend being random. What I’m not clear on: what’s the difference between autocorrelation in systems with underlying boundaries / physical processes, and autocorrelation from say a random walk? Vitally, does it change your ability to use p values to make a statistical significance test?
In the seasons example, is it not possible to simply say, I want to know whether there’s a trend of any sort? Can that not be kept conceptually separate from *whatever* underlying process there is?
p.s. couple of promising related stats links, anyone else got any related material?
MIT opencourseware on time series (econometrics related but some theory)
Duke Uni, forecasting. E.g. good-looking stuff on random walks.
danolner,
In terms of statistical modeling, SoD has only touched on the AR (autoregressive) part of ARIMA models. The I stands for integrated. A value of 1 for I (or an AR coefficient of 1) gives a random walk because the next data point is added to the sum of all previous data points. You can make a case that I cannot be 1 for any real physical process like a temperature time series. MA (moving average) means the next data point is influenced by the average of n previous data points. Then there’s fractional integration models (ARFIMA or FARIMA) where the value of I is not an integer.
Whether a process is stationary is also important. A random walk process is not stationary by definition. Then there’s ergodicity. I’m anticipating a lot of fun with that one, if it ever gets that far.
Danolner,
Your thought experiment and question is very interesting. I had been waiting for an opportunity to ask SoD about a similar thought exercising me.
I have read elsewhere that choosing your starting point (in time) when simulating Earth’s climate can lead to substantially different outcomes. (Something for all people with an opinion on the matter.) With this in mind, I asked myself what tests of a model’s self-consistency can be asked by those who are not actively engaged in climate modelling and don’t have access to either the data or the computing suites?
One (admittedly fanciful, possibly ridiculous) answer that I came up with is this: Taking (arbitrarily) the three dates of, say, 1990, 2000 and 2010, I might run a model from 1990 to 2000, using the measured data for 1990 as the starting point. I would then take the measured data from 2010 and run the simulation backwards in time from 2010 to the year 2000. Aside from the need to write a program that ran in the opposite direction to the normal arrow of time, would the simulation be expected to produce two near identical sets of trends or projected data for the year 2000? If it didn’t, what would that tell us? I’m making the working assumption here that it is theoretically possible to construct such a model based on making incremental changes (of the opposite sign to those that occur during the forward passage of time), and recalculating the properties of the system. (Or maybe I am making some incorrect assumptions about how current simulations are constructed?)
As an example in a rather different context of molecular structure, I am more familiar with the concept of calculating around a complete thermodynamic cycle of the type thus:
A, B, C and D are conformational isomers of the same molecule that reversibly changes it’s structure when heated and cooled. A is the starting point and C is the end ‘product’. (That is they are the two lowest energy structures that are both detectable) B and D are discrete putative intermediates on two different possible pathways to the same product, C.
The reaction pathway A >> B >>C >> B >> A is one possibility, and the pathway A >> D >> C >> D >> A is another possibility. Examining the relative energies of B and D may help to illuminate the mechanism, even if they are too transient to be detected. The hypothetical pathway A >> B >> C >> D >> A, does not occur, but allows for an internal check of the validity of the calculations.
Obviously, by the First Law, whatever the accuracy of calculations regarding the energies of the intermediates, when one arrives back at the starting point, A, then the sum of the thermodynamic changes must be precisely zero (by whatever pathway that actually occurs). If the sum is not zero, then there is an error in the calculations.
One of the reasons for my curiosity similar to Danolner, is the treatment of historical lag time between reconstructed temperatures and CO2 concentrations where the temperature change appears to precede the rise in CO2 concentrations. I have seen some explanations given for this, (and I’m still wrestling with my own thoughts about it). But I have also seen these explanations criticised for failing to adequately address the reverse process, i.e.-what happened when CO2 levels were declining from a maximum. That’s probably too far off-topic for this thread though.
A very enjoyable and educational blog though, SoD. It’s the only one I’ve read so far that is commended by people from both ends of the spectrum.
michael hart,
I’m also a layman, so have that in mind while reading my reply.
AFAIK, wheather projections are highly sensitive to the starting point, or more accurately, to the initial conditions.
Climate projections are usually done with many (100’s) runs, with diferent starting conditions, the climate projection being the average of these runs, like this. They are sensitive to boundary conditions: if you change the terrain, or atmopheric composition, or intensity of the solar irradiance (among others, of course), this average will move.
The statement
“Trends with 5 to 95% confidence intervals and levels of significance (bold: <1%; italic, 1–5%) were estimated by Restricted Maximum Likelihood (REML; see Appendix 3.A), which allows for serial correlation (first order autoregression AR1) in the residuals of the data about the linear trend. The Durbin Watson D-statistic (not shown) for the residuals, after allowing for first-order serial correlation, never indicates significant positive serial correlation."
itself contains an elementary error. The IPCC estimate an autoregressive model, but every undergraduate econometrician knows that the DW statistic is invalid for autoregressive models. Its this level of statistical incompetence that makes people wonder….
nikep:
According to Wikipedia:
Similar in my statistics textbook. And the Matlab function for the Durbin-Watson statistic correctly identifies first order autocorrelation (in my own tests e.g. figure 8 )
Do think the above statement is incorrect, or am I misunderstanding what you are claiming?
The same, I think, Wikipedia article says, quite correctly that
“An important note is that the Durbin–Watson statistic, while displayed by many regression analysis programs, is not relevant in many situations. For instance, if the error distribution is not normal, if there is higher-order autocorrelation, or if the dependent variable is in a lagged form as an independent variable, this is not an appropriate test for autocorrelation.”
It’s the last qualification I was referring to. Because the IPCC tested an AR1 model they were using as dependent variable a lagged form of the dependent variable, hence use of the DW statistic is inappropriate (is in fact biased towards the value 2, indicating no autocorrelation). Pity the IPCC did not read the Wiki entry.
This qualification has been known for a very long time and appears in every econometrics text.
The context of this part of the IPCC report is also of interest. Here is Ross Mckitrick’s take on this – he was involved as an expert reviewer.
“As for the review process, the First Draft of the IPCC report Chapter 3 contained no discussion of the LTP [Long term persistence] topic yet made some strong claims about trend significance based on unpublished
calculations done at the CRU. I was one of the reviewers who requested insertion of some cautionary text dealing with the statistical issue. Chapter 3 was revised by adding the following paragraph on page 3-9 of the Second Order Draft:
Determining the statistical significance of a trend line in geophysical data is difficult, and many oversimplified techniques will tend to overstate the significance. Zheng and Basher (1999), Cohn and Lins (2005) and others have used time series methods to show that failure to properly treat the pervasive forms of long-term persistence and autocorrelation in trend residuals can make erroneous detection of trends a typical outcome in climatic data analysis.
Similar text was also included in the Chapter 3 Appendix, but was supplemented with a disputatious and incorrect claim that persistence models lacked physical realism. I criticized the addition of that gloss, but other than that there were no second round review comments opposing the insertion of the new text. Then, after the close of Expert Review, the above paragraph was deleted and does not appear in the published IPCC Report, yet the disputatious text in the Appendix was retained. There was no legitimate basis for deleting cautionary evidence regarding the significance of warming trends.
The science in question was in good quality peer-reviewed journals, the chapter authors had agreed to its inclusion during the review process and there were no reviewer objections to its inclusion. But, evidently, at some point, one or more of the LA’s decided they did not want to include it anymore, and the IPCC rules do not prevent arbitrary deletion of material even after it has been inserted as a result of the peer review process. Also, the authors proceeded with an
incorrect method of evaluating trend significance, rather than obtaining expert advice.10
10
They used an AR-1 model, then checked the residuals using a Durbin-Watson statistic, despite the fact that the dw statistic is not valid in an autoregressive model. ”
I was referring to the incorrect method of evaluating trend significance. Note that the test was never peer reviewed. I am sure it would have been picked up if it had been included in the draft sent to peer reviewers rather than the final draft.
nikep:
which is the first problem. I am also guessing that ScienceOfDoom believes they are norma and that AR(1) is a reasonable noise model. But climate fluctuations are neither normal, nor described by AR(1).
Wrong guess.
I was kind of hoping you would chime in. 😉
The relevant IPCC pages, in case anyone would like a look.
– Appendix 3a
– 3.2.2.1
nikep,
There are lots of reasons why the DW test may fail, but the data being AR(1) isn’t one of them. The DW test is designed specifically to test for AR(1).
Click to access DWTest.pdf
Obviously if the ε aren’t stationary and normally distributed, the test will fail. Also if the data are AR(2+), MA(1) or I(1) the test is likely to fail.
Carrick,
I don’t think we’re far enough along for that sort of guess. All we’ve been shown so far is that autocorrelation must be considered when testing for trend significance.
De Witt
You have misunderstood what the DW test is a test of. It’s a test of whether there is first order autocorrelation of the RESIDUALS, not the data. And it’s an elementary point that the test does not work properly if the independent variable is a lagged version of the dependent variable, which is what an AR1 temperature process uses. Don’t take my word for it. Look it up in any decent econometrics/statistics book.
Going back to the original question: “how likely is it that the average temperature has changed over the last 30 years?”
I’m missing why we need to get dragged into this “IPCC is naughty” stuff here, maybe someone can explain it to me, perhaps I’m being dumb. But cf. this old Realclimate post: compare the 7,8 and 15 year moving trendlines – all easy enough to knock up from a data series without anything in the way of time series stats sophistication. The point there: you can clearly grasp that a trend only emerges when those trendlines stop changing sign often. 7 and 8: no. 15: getting there.
It’s not mathematically precise, of course, but it illustrates a point – same as I was making above, and same as SoD’s question: if you want to know whether temperature has changed, that requires only finding a trend, and that only requires finding out – as with the realclimate graphical approach – at what sort of period a trendline stabilises, if at all.
Isn’t the rest just finding a more mathematical way of saying the same thing? It’s the same for the seasons example above: there’s absolutely no need for recourse to physical explanations if all you’re after is detecting a trend. No?
Gah: badly formed URL, here’s that realclimate post.
Whether the trends are significant or not depends on the time series sophistication. The ordinary significance tests only work if the errors/residuals are well behaved in well defined ways. Serially correlated errors mess up standard significance tests and the “degrees of freedom adjustment” often applied in climate work is an approximation which only is appropriate for first order autoregression in the errors. For some real sophistication see
Click to access d1771.pdf
nikep,
Comparing global temperature time series analysis with econometrics is somewhat questionable. Econometrics, as near as I can tell, looks for trends first and then tries to explain them. Obviously there are going to be a lot of spurious trends in econometrics. Someone uncharitable might say they’re nearly all spurious because there’s no adequate theory behind most of them.
nikep,
Econometricians have stubbed their toes before by applying econometric statistical tests to climate data. Beenstock and Reingewertz and cointegration comes to mind.
DeWitt,
Whatever you think about econometrics, the fact remains that if you fit an equation with the lagged dependent variable as an explanatory variable the DW test for whether the residuals of the equation will be biased towards recording a value of 2, which in “ordinary” circumstances would indicate no serial correlation of the residuals.
Anyone able to tell me if this is wrong: a simplistic “do trendlines stop changing sign” approach (as in the realclimate article) means it’s entirely possible to answer SoD’s “how likely is it that the average temperature has changed over the last 30 years?” Stats-wise, you just need to assume stationarity to answer that question, don’t you?
That is a *different* question to “how likely is it that any change is significant, given the physical properties of the system?” But the first one is completely straightforward, yes? Can we not conceptually separate the two?
“how likely is it that the average temperature has changed over the last 30 years?” Is a perfectly straightforward question. The temperature is what it is and it’s easy to see whether it’s higher now than it was 30 years ago. All the complications arise when, looking only at the average temperature series itself as evidence, we try and work out whether the rise in observed temperature means that it is following a smooth upward time trend with random movements around trend, whether it is just varying randomly about a fixed value, or whether it is following a stochastic trend (the simplest example of which is the random walk) where the “trend” varies from year to year, or whether it is following a stochastic trend combined with a time trend (e.g. a random walk with drift).
nikep,
Temperature cannot be a random walk. It may be fractionally integrated and show long term persistence, but even that is controversial. A unit root is not physically possible.
You’re saying that if I take a linear trend, add AR(1) noise and do an OLS linear fit the DW test will always show no autocorrelation of the residuals? Somehow I doubt that. I’ll have to crank up R and try it.
No, you misunderstand my point. If your dependent variable is temperature in year t and one of your explanatory variables is temperature in year t-1 ( i.e. your equation suggests that temperature follows an AR1 process)and you test the residuals to see if they are serially correlated using the DW statistic, then the DW test is biased (nb biased, not always produces) towards 2.
You are right that I could/should have included fractional integration.
nikep,
You’re right, I don’t understand your point. I have a hard time understanding why T(t-1) would be used as an explanatory variable for T(t). If one doesn’t just use a linear or other function of time, then it’s usually something related to radiative forcing such as ln(pCO2). I don’t see that the IPCC analysis uses a fit where T(t-1) is an explanatory variable. Clearly one of us is missing something.
When testing for autocorrelation in R, there’s two functions, acf and pacf. acf is just a straight autocorrelogram. pacf tests to see if there is higher order than lag 1 autocorrelation. Something like that is what it looks to me was done in the example from IPCC AR4 quoted above.
DeWitt:
Could you elaborate on why you think a unit root isn’t physically possible?
The sorts of 1/f^nu noise distributions I considered here in a previous thread, all have a variance that increases with the observation time for nu ≥ 1. (I went through the math in a thread on Lucia’s blog.) I would assume any noise distribution with an unbounded variance is unphysical…is this what you were thinking of?
danoiner:
In principle you can do better than this, if you can model the noise (see e.g., Tamino’s and Lucia’s blog posts on using MEI and stratospheric aerosols to reduce the variance in the observed data).
But in general I agree with you… I prefer a period of ≥ 30 years for estimating the temperature trend. (Most of the stuff I do uses 60 year trends, but that isn’t useful if you want to look at just the post-1975 warming.)
The trouble with this is humans care about things that happen on times scales of say 5 years,
One wants a more quantitative approach than “eyeballing curves”. Eyeballing is good because it’s graphical and explanatory to people who don’t have the math background. Personally, I use a Monte Carlo based approach to estimate the effect of the measurement period on the estimate of the trend.
Cart before the horse, or at least apples and oranges; Doug Keenan’s interesting article on Koutsoyiannis quotes this:
“that the temperature from some year a century ago affected the temperature this year—and that is not physically plausible. Koutsoyiannis resolves the problem. The temperature from some year a century ago does not have a significant effect on the temperature this year. Rather, the temperature from the last century has a significant effect on the temperature this century, etc.”
Isn’t it the case that what caused the temperature a century ago may have a significant effect on the current temperature? Unless you can relate to phenomena and causation the correlation between seperated temperatures is meaningless. The process becomes especially difficult when you have long term periodicity, potential resonance, both amplifying and dampening and one offs.
For this reason I’m not sure statistically DeWitt is right in saying temperature does not have unit root; what it does have is a range of values but within that range the walk is random.
Carrick,
My argument on unit roots is more physics based. Basically it’s the tank leaks argument I made at lucia’s during the whole B&R flap. The tank also has a finite size in any real physical system. In either case, a unit root model eventually fails.
If you have a tank with water in it and you randomly remove or add a bucket of water at fixed intervals, the level in the tank is a random walk (unit root). But in a random walk, the level can be arbitrarily far from the starting point as time progresses. The variance increases linearly with time. If the tank has a finite size, it will eventually empty or overflow. The tank emptying is related to the gambler’s ruin problem.
cohenite,
If the range is bounded, it can’t be a random walk. It might look like a random walk for short time intervals though.
DeWitt, here’s another way of looking at it:
Standard deviation versus measurement interval.
At very short time intervals, you are dominated by the noise floor of the measurement system. While there is a range of time intervals over which the standard deviation increases, for long enough a time interval it is bounded.
(This is real world data btw, not a simulation. It is from one of my sensors measuring turbulence in the atmosphere.)
Saying the variance of the measure approaches an asymptote is the same as saying the system is bounded.
This bounded property of the system is not only manifest in the relatively narrow range of temperature over the paleoclimatic history but is also properly discussed in respect of forcing. The IPCC attributes ACO2 as being the forcing agent, F, for this scenario, with water vapor the feedback, f, and temperature, t, the parameter for the change; the interaction of these variables is measured by the state vector, S, which would itself change if F has the effect the IPCC alleges. IPCC represents this dynamic thus:
dS/dt=S/f+F
IPCC assumes that f is +ve so if we intergrate by dividing both sides by fS+F, and multipling both sides by f*dt we get:
(S2+F/f)/(S1+F/f)=exp(f*(t2-t1))
The problem with this is because it predicts that as the final value of t, t2, approaches infinity, the value of S2 becomes infinite. There is no boundary.This is wrong because if there is a climate forcing in operation, at infinite time, the temperature anomaly should approach its finite equilibrium value even if there is positive feedback. This is shown by Venus which is paraded by AGW supporters as being the inevitable result of AGW; but, if there was any greenhouse effect on Venus it has now stopped despite high levels of CO2 and obviously its equilibrium was less than infinity. The correct formula for measuring feedback is done by Spencer and Braswell:
Click to access Spencer-and-Braswell-08.pdf
Their equation 2 is:
Cp*T/*t=-^T+N+f+S
The difference with S&B’s equation is that it introduces a term for the stochastic properties of clouds, N and breaks F into -^T and f; f is ACO2 and -^T is a total feedback term which must be negative so that an infinite equilibrium is impossible.
The point, as I see it, is that temperature is inherently unpredictable, it randomly walks, but is constrained by boundaries which are the product of feedbacks which moderate any trend created by forcings.
cohenite,
The greenhouse effect on Venus hasn’t stopped. Since the atmosphere of Venus is mostly CO2, though, in order to increase the surface temperature, the total mass of the atmosphere would have to increase. Absent a large comet colliding with Venus, this isn’t going to happen. All the carbon in the crust and everything else volatile was cooked out long ago.
Carrick,
I’m more used to instruments where the noise floor is shot noise limited (photon counting in emission spectrometry, e.g.). In that case the standard deviation decreases with increasing sampling time (Poisson statistics) until flicker noise and instrumental drift (~1/f) take over. Sample throughput usually dictates the counting time rather than minimum s.d. Well, sample throughput and other sources of uncertainty like sampling being larger than the measurement uncertainty.
This type of response is typical of systems that have “blue noise” in them (increasing noise with frequency, nu < 0 in my notation).
Newer instrumentation amplifier topologies (like the AD8230) that reduce 1/f noise & drift have promise for significantly lowering your attainable noise floor for measurements of this sort.
De Witt,
Sorry to be absent for a bit. I assume when the IPCC corrects for first order autocorrelation in the residuals, it follows the standard procedure. This involves assuming that the measured residuals from the original specification follow an AR1 process, i.e.
e(t)=be(t-1)+u(t)
where b is the autoregressive parameter which is between 0 and 1. If you then want to test whether you have got rid of all the autoregression you can have a look at the properties of u(t). But you can see at once that if you use the equation above it includes a lagged dependent variable. And if you go back to the original equation and use the equation above to substitute out the e(t), your equation then contains a term in e(t-1) which can be replaced using the lagged version of the original equation so that temperature appears in lagged form in the RHS of the adjusted equation with residual term u(t). So either way, the process of adjusting for an AR1 residual term produces an equation with a lagged dependent variable on the RHS, invalidating the use of the DW statistic.
Incidentally there are other test these days for autocorrelation which test for higher order autocorrelation as well and can be used with lagged depednent variables. See e.g. the Breusch Godfrey test
http://en.wikipedia.org/wiki/Breusch%E2%80%93Godfrey_test
Note also that these days, after much experience of things going wrong out of sample, the first reaction of most econometricians to finding serial correlation in the residuals of their equations is to wonder whether the model is correctly specified. Serial correlation in the residuals implies that there is systematic variation in the dependent variable which is not being accounted for by the explanatory variables.
SOD: You showed above that daily mean temperatures in Ithaca are correlated for about one week. If one calculated weekly mean temperatures, would they be correlated over several weeks? If I remember correctly, the Santer/Douglass controversy about autocorrelation involved monthly mean temperature anomalies that were correlated over several months. Long-term temperature records appear to be based on yearly means. Do they ever show autocorrelation?
A second factor may be the area involved. Warm dry air in Ithaca may blow into Vermont after a few days, but it might not escape from the Northeast US Mean. I think Santer/Douglass covered the whole tropics.
Frank,
I don’t know the answer. Although I have lots of preconceived ideas about how the results will pan out.
I hope to get into that by downloading some data from reanalysis projects and having a play. But need to get the theory sorted out clearly in my head first. I have a few books including Box & Jenkins, Time-series analysis and a number of papers. Lots to study.
I certainly didn’t mean to present the Ithaca temperature results as the gold standard for climate autocorrelation – more as one example that demonstrates there is such a thing as serial correlation of time-series climate data.
SOD: Nothing you said about Ithaca mislead me about the generality of the observations you made about auto-correlation of temperature there. I associated auto-correlation most with the monthly tropical data in the Douglass-Santer controversy. Your first example turns out to be autocorrelation in daily data for one city. Comments in the same post discuss the possibility of long-term persistence (how is this technically different from autocorrelation?) in annual global temperature.
Autocorrelation in temperature series isn’t merely a statistical phenomena; it should reflect of the time scale over which temperature returns towards normal (an attractor?) during its chaotic/forced behavior. For that reason, it’s hard to justify the IPCC’s reporting 20th-century temperature rise as a linear trend without adequate discussion. They could have simply reported the MAGNITUDE of the temperature rise for the last century (1895-1905 mean vs 1995-2005 mean) and half-century. This would probably produce larger uncertainties (the difference in the means of 11 years) than the linear trend extracted from 100 years of (non-linear) data. The only thing linear about temperature rise is associated with the logarithmic increase in forcing with CO2 and exponentially rising CO2. Even the IPCC recognizes that CO2 is only a fraction of the anthropogenic forcing. So why abstract a linear trend?
[…] with the radiative “noise” as an AR(1) process (see Statistics and Climate – Part Three – Autocorrelation), vs the autoregressive parameter φ and vs the number of averaging periods: 1 (no averaging), 7, […]