It is not surprising that the people most confused about basic physics are the ones who can’t write down an equation for their idea.
The same people are the most passionate defenders of their beliefs and I have no doubts about their sincerity.
I’ll meander into what it is I want to explain..
I found an amazing resource recently – iTunes U short for iTunes University. Now I confess that I have been a little confused about angular momentum. I always knew what it was, but in the small discussion that followed The Coriolis Effect and Geostrophic Motion I found myself wondering whether conservation of angular momentum was something independent of, or a consequence of, linear momentum or some aspect of Newton’s laws of motion.
It seemed as if conservation of angular momentum was an orphan of Newton’s three laws of motion. How could that be? Perhaps this conservation is just another expression of these laws in a way that I hadn’t appreciated? (Knowledgeable readers please explain).
Just around this time I found iTunes U and searched for “mechanics” and found the amazing series of lectures from MIT by Prof. Walter Lewin. A series of videos. I recommend them to anyone interested in learning some basics about forces, motion and energy. Lewin has a gift, along with an engaging style. It’s nice to see chalk boards and overhead projectors because they are probably no more in use (? young people please advise).
These lectures are not just for iPhone and iTunes people – here is the weblink.
The gift of teaching science is not in accuracy – that’s a given – the gift is in showing the principle via experiment and matching it with a theoretical derivation, and “why this should be so” and thereby producing a conceptual idea in the student.
I haven’t got to Lecture 20: Angular Momentum yet, I’m at about lecture 11. It’s basic stuff but so easy to forget (yes, quite a lot of it has been forgotten). Especially easy to forget how different principles link together and which principle is used to derive the next principle.
What caught my attention for the purposes of this article was how every principle had an equation.
For example, in deriving the work done on an object, Lewin integrates force over the distance traveled and comes up with the equation for kinetic energy.
While investigating the oscillation of a mass on a spring, the equation for its harmonic motion is derived.
Every principle has an equation that can be written down.
Over the last few days, as at many times over the past two years, people have arrived on this blog to explain how radiation from the atmosphere can’t affect the surface temperature because of blah blah blah. Where blah blah blah sounds like it might be some kind of physics but is never accompanied by an equation.
Here’s the equation I find in textbooks.
Energy absorbed from the atmosphere by the surface, Ea:
Ea = αRL↓ ….[eqn 1]
where α = absorptivity of the surface at these wavelengths, RL↓ = downward radiation from the atmosphere
And this energy absorbed, once absorbed, is indistinguishable from the energy absorbed from the sun. 1 W/m² absorbed from the atmosphere is identical to 1 W/m² absorbed from the sun.
That’s my equation. I have provided six textbooks to explain this idea in a slightly different way in Amazing Things we Find in Textbooks – The Real Second Law of Thermodynamics.
It’s also produced by Kramm & Dlugi, who think the greenhouse effect is some unproven idea:
Now the equation shown is a pretty simple equation. The equation reproduced in the graphic above from Kramm & Dlugi looks a little more daunting but is simply adding up a number of fluxes at the surface.
Here’s what it says:
Solar radiation absorbed + longwave radiation absorbed – thermal radiation emitted – latent heat emitted – sensible heat emitted + geothermal energy supplied = 0
Or another way of thinking about it is energy in = energy out (written as “energy in – energy out = 0“)
Now one thing is not amazing to me – of the tens (hundreds?) of concerned citizens commenting on the many articles on this subject who have tried to point out my “basic mistake” and tell me that the atmosphere can’t blah blah blah, not a single one has produced an equation.
The equation might look something like this:
Ea = f(α,Tatm-Tsur).RL↓ ….[eqn 2]
where Tatm = temperature of the atmosphere, Tsur = temperature of the surface
With the function f being defined like this:
f(α,Tatm-Tsur) = α, when Tatm ≥ Tsur and
f(α,Tatm-Tsur) = 0, when Tatm < Tsur
In English, it says something like energy from the atmosphere absorbed by the surface = 0 when the temperature of the atmosphere is less than the temperature of the surface.
I’m filling in the blanks here. No one has written down such ridiculous unphysical nonsense because it would look like ridiculous unphysical nonsense. Or perhaps I’m being unkind. Another possibility is that no one has written down such ridiculous unphysical nonsense because the proponents have no idea what an equation is, or how one can be constructed.
My Prediction
No one will produce an equation which shows how no atmospheric energy can be absorbed by the surface. Or how atmospheric energy absorbed cannot affect internal energy.
This is because my next questions will be:
- Please supply a textbook or paper with this equation
- Please explain from fundamental physics how this can take place
My Challenge
Here’s my challenge to the many people concerned about the “dangerous nonsense” of the atmospheric radiation affecting surface temperature –
Supply an equation.
If you can’t, it is because you don’t understand the subject.
It won’t stop you talking, but everyone who is wondering and reads this article will be able to join the dots together.
The Usual Caveat
If there were only two bodies – the warmer earth and the colder atmosphere (no sun available) – then of course the earth’s temperature would decrease towards that of the atmosphere and the atmosphere’s temperature would increase towards that of the earth until both were at the same temperature – somewhere between the two starting temperatures.
However, the sun does actually exist and the question is simply whether the presence of the (colder) atmosphere affects the surface temperature compared with if no atmosphere existed. It is The Three Body Problem.
My Second Prediction
The people not supplying the equation, the passionate believers in blah blah blah, will not explain why an equation is not necessary or not available. Instead, continue to blah blah blah.
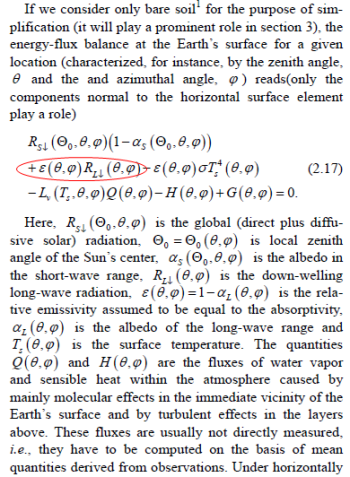


(Knowledgeable readers please explain)
It’s from conservation of linear momentum, which follows from F=ma. Suppose you have a set of particles, m_i, velocity v_i, position relative to arbitrary origin r_i.
Then ang mom M = Σ m_i r_i × v_i
Derivative = Σ m_i r_i × a_i
a = accel, since dr/dt=v and v × v = 0
But Σ m_i r_i × a_i = Σ r_i × F_i = torque (F=ma)
So rate of change of ang mom = torque, and =0 if zero torque.
This works if the particles are stuck together – continuum.
SoD,
Cannot help but admire your dedication here! Unfortunately I believe that you are challenging peoples “core” beliefs (which one could argue is a form of religion) and this is a battle you can never win. i.e. some people are capable of looking at science and data and learning from it and some people are not. An unfortunate consequence of the human make up.
😉 Good luck
I’ll check on this post regularly to see if someone is up to the challenge. Not very promising, but there’s always that dim possibility of it being enlightening for those who persue it.
I’m sorry, but you did ask:
Computational Blackbody Radiation by Claes Johnson
Click to access blackbodyslayer.pdf
First the “Blah! Blah! Blah!”:
“A blackbody acts like a transformer of radiation which absorbs high-frequency
radiation and emits low-frequency radiation. The temperature of the blackbody determines a cut-off frequency for the emission, which increases linearly with the temperature: The warmer the blackbody is, the higher frequencies it can and will emit. Thus only frequencies below cut-off are emitted, while all frequencies are being absorbed.
A blackbody thus can be seen as a system of resonators with different
eigen-frequencies which are excited by incoming radiation and then emit
radiation. An ideal blackbody absorbs all incoming radiation and re-emits
all absorbed radiation below cut-off.
Conservation of energy requires absorbed frequencies above cut-off to be stored in some form, more precisely as heat energy thus increasing the
temperature of the blackbody.
As a transformer of radiation a blackbody thus acts in a very simple
way: it absorbs all radiation, emits absorbed frequencies below cut-off,
and uses absorbed frequencies above cut-off to increase its temperature.
A blackbody thus acts as a semi-conductor transmitting only frequencies
below cut-off, and grinding coherent frequencies above cut-off into heat in
the form of incoherent high-frequency noise.”
As you can see, this is exceptional “Blah!”. I do not think I have seen a more unphysical theory of radiation. However, as per request, it does have equations, commencing on page 174. I know enough to know the “Blah!” is complete nonsense in this case. It follows that the equations, to the extent that they disagree with Planck’s law are empirically refuted. However, while I can see how he has butchered Wein’s Displacement Law, I cannot follow his own equations. Would you care to eviscerate?
The blog policy, to save the patience of the moderator and of most (but not all) readers, includes:
And so this saves me the effort of reading too much “off beat” material. If Claes “no photons” Johnson is successful in his endeavor to persuade the world that photons don’t exist then it will be a fascinating year (whichever year it is) – or decade – for physics. The field of molecular spectroscopy will be scratching their collective heads, no doubt, as will many other fields. Until that time..
Yes, this got torn to shreds at Curry House a few months ago. The problem is that (among other things) it requires a Maxwell Demon with a frequency meter on every piece of matter in the universe.
It is an adaptation of an old and discredited way of dealing with the ultraviolet catastrophe for black body radiation by imposing an artificial cut off.
” Perhaps this conservation is just another expression of these laws in a way that I hadn’t appreciated? ”
Newton’s laws work well : rotationally.
Force is defined as the rate of change of linear momentum.
Torque is defined as the rate of change of angular momentum.
SoD says
“Energy absorbed from the atmosphere by the surface, Ea:
Ea = αRL↓ ….[eqn 1]
where α = absorptivity of the surface at these wavelengths, RL↓ = downward radiation from the atmosphere
And this energy absorbed, once absorbed, is indistinguishable from the energy absorbed from the sun. 1 W/m² absorbed from the atmosphere is identical to 1 W/m² absorbed from the sun.”
The key “once absorbed” is very important for without that qualification its a totally different ball game.
In the past you have denied that radiation has a “quality” as well as a quantity(number of Joules).
This is very easy to prove since as you know the amount absorbed depends strongly on the wavelength.
Think of the various wavelngths of solar radiation and how different absorbing surfaces behave.
Just to comply with your new enthusiasm for equations I’d better stick one in.
The photoelectric effect illustrates the ‘quallity’ difference in radiation.
To free an electron from a photosensitive surface a minimum frequency is required
Work Function = hFo
h = Plancks constant
Fo = minimum frequency required for emission.
If Frequency F > Fo the electrons will be emitted and any excess energy turns into KE of electron
If Frequency F < Fo then there will be no emission despite shining the radiation for eternity and using up endless quantities(Joules) of lower quality radiation.
What’s your equation for atmospheric radiation absorbed by the surface?
If the surface can be irradiated by Sun
Total radiation arriving at surface = Pt = Pd +Pi + Pb
Pd = direct to surface
Pi = indirect to surface
Pb = fraction returned by atmosphere due to absorption from surface
Pa = (what SoD asked for) = (1 – R)Pt
Where R = Reflection co-efficient between atmosphere and surface.
People are so idiots mistaking convection with radiative heat transfer……let the idiots explain how a laser can cool an object …
drtskoul,
As you are new (I hope you are new), this is retrieved from the spam queue, comments that are ranting, essays, off-topic, offensive – all have good chances to be snipped or deleted.
If you have something of interest to say on the subject of back radiation, equations, angular momentum or a question related to this topic, please go ahead.
If your level is the comment above, please choose another blog where your comments will get a wider audience. This is a science blog.
In addition to Nick’s proof (which may be a bit hard to follow without typesetting, anyway he left a term out in his derivative, which was zero but he didn’t justify the step 😉 ), there’s a simple introduction to mechanics here, which includes a proof that angular momentum is conserved when the net torque is zero.
According to a famous theorem proved by Emily Noether (I’m sure I have the spelling of her name wrong), all conservation laws are the result of a symmetry of nature. The conservation of energy results from the fact that the laws of physics are symmetric wrt time. Linear momentum from symmetry wrt translation in space. Angular momentum from symmetry wrt rotations in space.
http://en.wikipedia.org/wiki/Noether's_theorem
[…] Comment […]
Apologies…Just too upset with the imaginary physics some people invoke.
As for angular momentum or any energy conservation, it relates to Newton’s law of inertia and independent degrees of freedom.
Each solid body has six degrees of freedom. A body in vacuum will conserve energy at each DOF. Elsewhere with external forces there’s energy transfer between various DOFs. Linear momentum being more separated from Angular momentum
This post made me sad, because I have such an interest in this subject, and think I “understand” much of the science, but only understand it on the level of “blah, blah, blah.” What I mean is, I understand and agree with the consensus view, which SoD has eloquently explained many times, and which allows for a cooler body to affect the temperature of a warmer body. So I believe in the (inappropriately named) Greenhouse effect, but my level of understanding (which is high for the average population), is still grounded in the world of “blah, blah, blah” even though it’s the GOOD blah blah blah, and not the other.
Which leads me to conclude that if I cannot express myself using the equations described (which pre-supposes that I understand the equations) then I will forever be a second-hand adopter of information. Note in my first paragraph how I said “believe” in these things. Am I forever relegated to “belief” rather than “understanding” if I can only express my views as “blah, blah blah?”
I don’t know if that made sense. What I am trying to say is that my beliefs IN the GhG seem to be no more legitimate than others beliefs AGAINST it, since I am simply accepting an explanation which “makes sense to me” which is exactly what they are doing also, but for which I can provide no mathematical proofs. I believe there’s something about authority bias and the nature of knowledge in here somewhere, but I can’t tease it out at the moment.
Anyways, perhaps another way to illustrate this effect (again, more blah, blah blah) would be to imagine two bodies in space, with no external energy inputs. Set one body at a given temperature (so it has some energy content), and the other nearby body at a somewhat lower temperature. Start the system operating, and observe both objects as their temperatures decrease.
To deny the GhG, one would have to assert that the presence of the nearby cold(er) object would have no impact on the rate of cooling of the warmer object, yes? As they are radiating to each other and to space, the cooler object will certainly not be “warming” the warmer object, but it will be causing it to lose heat less quickly as it radiates some amount of energy back at the warmer object (though less than would be required to warm it), and of course the warmer object would itself be radiating to the cooler object, some of which would be re-radiated back to the warmer object again. Now if you introduce an energy source into this system, one can see how the cooler object can indeed affect the temperature of the warmer object in a system “similar” to the earth’s atmosphere.
Tell me if I’m off base here.
purgatus
There’s nothing wrong with understanding something conceptually. My calculus classes are so far back that my rusty knowledge and limited time prevents me from really following the equations when they exceed two in the same post. So I consider myself to be in the same club as you are.
SoD’d challenge here – if I got the idea right – is just to sort out real “alternative theories” from pompous wording that passes for science to the layman. If the “alternative” has any ture basis, its defender should be able to express it in a mathematical language, following conventional physics.
Bryan’s attempt above suggests it may work…
Alexandre – Don’t get me wrong, I didn’t take it as an attack from SoD. Rather I took it as a challenge. I accept the consensus view of the (inappropriately named) Greenhouse Effect, but I cannot express it mathematically. Until I can understand and express the concepts at that level, I am accepting the explanation, to some extent or another, “on faith.” This gets you in trouble no matter which side of an argument you are on.
I have since my initial comment consoled myself with the knowledge that I could at least express the theory visually, using vectors, etc. I could also build a pretty swell model of it in Stella using a basic systems analysis. My challenge to myself now is to go out and actually do this. To build, from scratch, a (HIGHLY) simplified climate model, to increase my level of understanding. I think this would be an excellent means for me to then integrate the real formulas into my model, and address any shortcomings in my understanding.
I took this as a personal challenge more than anything, and I understood this wasn’t SoD’s main (or even secondary) point. But I’m a student, and I still feel like I should be able to figure it all out, so I guess I will give it a shot.
purgatus
I’m very pleased to read (both) your comments – I find myself in a very similar position. I have a fair amount of conceptual understanding but I would struggle to use equations to communicate that understanding to others. I worry too, that maybe I’m just appealing to an authority that suits my biases?
However, your second comment was an expression of something similar I’ve thought myself – a wandering body in deep space. Internal heat source, external temp a constant 223K. Giving off heat [in my layman’s language] everywhere it goes. Does not reflect other radiation, merely stays at 223K.
An astronaut, cruelly abandoned in deep space has a choice. Rather rapidly cooling to death he can hail the passing body and ask it to park up alongside him, or can hope that his spacesuit will slow his cooling long enough for him to be alive when his ‘friends’ return at some point in the future.
Is he better off with the presence of the body, will it make no difference or will it make things worse? The body will remain at 223K giving out heat in all directions. He, however has a surface temperature of 273K, so the body is a depressing 50K colder than him.
In this situation I’m saying “Oi, you, over here, quick!”. And assume that my life might be saved by the heat emanating from the cooler body. It may indeed only slow my cooling but that also means keeping me warm[er than I would otherwise have been]
Energy really will move from colder to warmer.
Now, if I happened to have some super-combusto-carb food that was just enough to keep me at about 273K, the arrival of the good-natured, colder body might warm me enough for me to reach a survivable temperature allowing me to plan my revenge on my fellow astronauts should they return.
That’s the clearest way I can conceptualise energy moving from colder to hotter. I’d be glad to know if that is an explanation that is meaningful for anybody else..
P.S. Having said that, I’ve now forgotten why the ‘lagging on a hot water pipe’ isn’t an even simpler idea. The lagging doesn’t need to be a heat source, but ‘heats’ the surface of the pipe nonetheless. And is always colder than the pipe.
SOD,
As soon as you mentioned iTunes u I thought you were going to talk about Walter lewin’s lectures. I watched a couple of them yesterday- wonderful stuff.
SOD predicted: “No one will produce an equation which shows how no atmospheric energy can be absorbed by the surface. Or how atmospheric energy absorbed cannot affect internal energy.”
“Atmospheric energy” or DLR that is not reflected is obviously absorbed by the surface. I’ll try to show that absorbed DLR may not increase the internal energy of the surface.
SOD provide an appropriate equation for the internal energy balance of the surface of the earth.
“Solar radiation absorbed + longwave radiation absorbed – thermal radiation emitted – latent heat emitted – sensible heat emitted + geothermal energy supplied = 0”
Let’s convert these words to symbols and explicitly show which ones depend on GHG mixing ratio, the temperature of the surface of the earth (Te) and the temperature of the atmosphere (Ta). I’ll put questions marks by relationships that might need further discussion. The geothermal term is supposed to be negligible, so I’ll omit it.
SWR + DLR(GHG,Ta) = OLR(Te) + LH(Te?,Ta?) + SH(Te?,Ta?) Eqn 1
SWR doesn’t change with GHGs (to a first approximation) and OLR will not change if Te remains constant. This leaves
dDLR =? dLH(Te?,Ta?) + dSH(Te?,Ta?)
IF the change in DLR is compensated by a change in convection, DLR can increase without the surface warming. IF SOD wants to prove that an increase in DLR does warm the surface, he MUST prove that convection can’t fully compensate. Presumably, neither of us can PROVE anything about this subject because the equations of fluid flow with time can’t be solved explicitly.
Even though we can’t solve these equation, there are good reasons to believe that convection can compensate for increased DLR. We know convection occurs where the lapse rate is unstable. Due to weather and diurnal variation in radiation, local lapse rates vary widely. Globally, however, we often assume that the lapse rate is fixed at borderline stability (g/Cp). If the average surface temperature warms 1, 0.1 or even 0.01 degK due to increased DLR, heat will flow upward until surface temperature returns to “normal”. Unlike radiation, we can’t calculate the rate of energy transfer from first principles, but we (K&T diagram for the earth’s energy balance, for example) usually assume convection will get rid of whatever extra energy can’t escape by radiation…
… but only as long as the atmosphere remains at a constant temperature. There is a region of gas high in the troposphere (the critical emission level) whose temperature is controlled by radiative equilibrium. It emits the 238 W/m2 of energy received from the sun minus the 40 W/m2 that escapes directly through the atmospheric “window” to space. Changing CO2 doesn’t change the 238 W/m2 or the 40 W/m2. The temperature at the critical emission level controls surface temperature and lower troposphere temperature via the lapse rate.
DLR reaching the surface – emitted mostly by GHG’s within 1 km of the surface – has nothing to do with the temperature at the critical emission level. Therefore DLR reaching the surface of the earth doesn’t change its temperature/internal energy.
Question 1: What happens to the extra energy reaching the earth’s surface from enhanced DLR? The lower troposphere is cooled by emitting enhanced DLR, so it intercepts enough extra LH and SH flowing upward to restore its temperature and maintain a stable lapse rate. If dramatically more GHGs in only the first 1 km of atmosphere increased DLR from the current by 100 W/m2, convection of LH and SH could also increase by 100 W/m2, leaving the temperature of both unchanged.
Question 2: Does this mean GHGs don’t cause global warming? Of course not. GHGs reduce OLR at and above the critical emission level, causing that level to warm until OLR and SWR are in balance. Read Leonard Weinstein at SOD or Lindzen’s “Taking Greenhouse Warming Seriously”.
SoD,
Can I get some clarification. The equation proves back radiation can warm the surface but doesn’t prove it is the cause of the warming of the past few decades. Is that right?
Frank: “I’ll try to show that – (paraphrase:this special energy can’t have the effect any other energy would have ) – absorbed DLR may not increase the internal energy of the surface.”
Frank, energy is energy. If you are right, the surface must be as hot as it can get regardless of inputs. Riiight. I can’t decide if you are just pulling Sod’s patient leg or what. One thing I can tell you is that your statement made me laugh. But unless there are a lot of leg pullers around, Sod’s careful physics somehow attracts the most unphysical commenters.
Pete Dunkelberg: Energy is energy. I said additional absorbed DLR might not end up warming the surface because all or most of it could be removed from the surface by increased convection. Elsewhere I’ve ridiculed the idea that the surface somehow knows how to absorb photons emitted by warmer sources (the sun) and reflect photons emitted from cooler sources (the atmosphere).
According to 1-D models, increased GHG’s will raise the altitude of the critical emission level (where radiative equilibrium controls the temperature). Surface temperature is controlled by the lapse rate (convection) between the surface and the upper atmosphere. This mechanism can be found in textbooks by respected scientists (Taylor’s “Elementary Climate Physics”, p 113), publications by respected skeptics scientists (Lindzen’s Taking Greenhouse Warming Seriously), and posts by SOD. As best I can tell, this mechanism implies that DLR emitted by increased CO2 and water vapor feedback will not cause surface warming.
www-eaps.mit.edu/faculty/lindzen/230_TakingGr.pdf
Is the surface almost as hot as it can get? It may be in the tropics. The skewed distribution of sea surface temperatures (28-29 degC is most frequent, >31 degC occurs <1% as often) suggests that negative feedback limits tropical SSTs. See Pielke Sr and references to peer-reviewed publications therein:
pielkeclimatesci.wordpress.com/2012/02/14/on-self-regulation-of-the-climate-system-an-excellent-new-analysis-by-willis-eschenbach/
In an unpublished manuscript, VanAndel estimated by two methods that an additional 20 W/m2 of energy is required to raise tropical SST from 30 to 31 degC. That's a local climate sensitivity of about 0.2 degC for 2XCO2.
The validity of CAGW depends whether most of the energy flux from increased DLR (emitted by more CO2 and water vapor feedback) leaves the surface by convection or – after raising surface temperature – leaves as radiation. Since the grid cells used by climate models are far too coarse to properly describe convection, they don't provide a satisfying answer.
When I have gone astray, I appreciate SOD's patient attempts to correct my physics. If you have intelligent criticisms of my comments, skip the insults and explain where you think I've gone wrong.
Frank
The surface forcing is totally different from the TOA forcing – which is also known as “radiative forcing”.
More about this in Radiative Forcing and the Surface Energy Balance.
And interesting that Ramanathan 1981 also computed similar numbers to VanAndel (caveat, this is from memory). The surface forcing is very high compared with the TOA forcing. Important to understand that.
HR
Correct.
To be one step ahead of pedants let’s say the equation proves back radiation can increase the temperature of the surface above what it would be in the absence of said “back radiation”. Which is quite pithy really.
The equation can in no way prove that “back radiation” is the cause of the warming of the past few decades because this would require a massive proof of herculean proportions and not a one line equation which balances surface fluxes.
“IF the change in DLR is compensated by a change in convection, DLR can increase without the surface warming.”
Convection is driven by the temperature difference between the atmosphere and the surface. Since the atmosphere is colder than the surface (see lapse rate) and the absorbed long wave radiation warms the atmosphere, holding the surface temperature constant will decrease convection, not increase it.
Eli wrote: “Since the atmosphere is colder than the surface (see lapse rate) and the absorbed long wave radiation warms the atmosphere, holding the surface temperature constant will decrease convection, not increase it.”
The only sources that provide heat to the lower troposphere are the surface of the earth (via LWR or convection from the surface) and a warming of the upper troposphere (which will shut down convection from the lower troposphere until the lower troposphere has warmed enough to produce an unstable lapse rate). Adding more CO2 to the lower troposphere will not appreciably narrow the atmospheric window, so the lower troposphere will still absorb 390-40 = 350 W/m2 of LWR from the surface – as long as surface temperature remains unchanged. Therefore, the lower atmosphere should be cooled when increased CO2 increases emission of DLR, INCREASING the lapse rate, not decreasing it. The extra energy from enhanced DLR will be absorbed by the surface and returned to the lower troposphere (restoring the lapse rate) by two mechanisms: a) surface warming, which will increase the 390 W/m2 emitted upward LWR, OR b) increased convection. The fundamental physics of the situation doesn’t tell us which pathway will occur.
Frank, your hypothetical moved MORE energy off the surface by convection and held the temperature of the surface constant. Pray tell where that excess energy goes. It goes to heat the lower troposphere, but if you heat the lower troposphere, then it is warmer and convection is lower.
Frank,
If we reach the point where the “greenhouse is wrong” (GIW) coalition say:
1. The equation for surface energy balance includes the term for the absorption of energy from the atmosphere (eqn 1 in the article). The whole energy balance equation is something like Kramm & Dlugi’s equation.
2. 1W/m2 absorbed from the (colder) atmosphere is no different from 1W/m2 absorbed from the (hotter) sun in that both increase the internal energy of the surface (compared with the situation if this energy was not absorbed).
– Then my work on this subject is done.
[Or almost done because still we would want to confirm that the coefficient of absorption was understood and not somehow believed to be zero for radiation from a colder source..]
Because what you are describing is not confusion over very fundamental physics but a question about feedback as a result of a given change in surface energy balance.
A much more complex problem.
[Of course, for reasons already described many times it is really the balance at the top of atmosphere that better defines the “greenhouse” effect, but that is not at all the point of this article or the many that precede it].
SOD: Is your work really done on this subject? Isn’t climate science “a fascinating subject and something really worth trying to understand” or something to defend against “an evil empire of disinformation”.
1) If increased DLR from water vapor (which is mostly found near the surface) causes mostly increased convection (rather than a rise in surface temperature), then water vapor feedback might be negligible, eliminating about 1 degK of climate sensitivity.
2) Today we send about 100 W/m2 from the surface to the lower troposphere by convection. If DLR increased from 333 W/m2 to 356 W/m2 (a 4% increase in total radiation reaching the earth), the result could be a 1% (2.9 degK) increase in surface temperature by purely radiative equilibrium, which we might call a “climate sensitivity” of 8 W/m2/degK. However, if only 2.4 W/m2 of outward heat flux comes from surface warming of 0.29 degK and the rest from increased convection, the “climate sensitivity” goes up to 80 W/m2/degK. Do AOGCMs have the ability to correctly partition increased DLR into increased convection and surface warming? Models presumably get today’s partitioning approximately right: If they sent 23 W/m2 too little energy upward as convection, surface temperature would need to be 2.9 degK higher to radiate away the extra 23 W/m2. With many adjustable parameters, however, models can get some things right by making the “wrong” adjustment.
3) Are intelligent people who clearly understand your points 1 and 2 above (Kramm, G&T, ?) saying that DLR doesn’t warm the surface of the earth for the reasons similar to the ones I suggest (or related reasons that I don’t understand concerning the 2LoT)? I’ve re-read the papers several times and found no clear indication they think convection prevents surface temperature from rising. I hate all of this obscurity about how the 2LoT applies: Sometimes they appear to say that the 2LoT says that net heat can’t be transfered from the cool atmosphere to the warm surface by radiation and, as a result, make the atmosphere cooler and the surface warmer. Cooler than what? Warmer than what? The temperature relationship produced by the lapse rate? Can both end up warmer? In contrast, I think the 2LoT only says:
Entropy change from DLR + Entropy change from SLR >= 0
(-dQae/Ta + dQae/Te) + (-dQea/Te + dQea/Ta) >= 0
Rearranging terms:
(dQea – dQae) * [ (Te-Ta)/Te*Ta ] >= 0
where dQae is heat transfered by DLR and dQea is heat transfered by upward by surface LWR (in infinitessimal form which needs integration). If Te>Ta, the right hand term is positive and the left hand term must also be positive. None of this determines what happens to any temperature at equilibrium. One must total all of the heat fluxes and work done (and integrate over time?) until some sort of steady state is reached
Wasn’t the blackbody radiator dreamed up as a simple case of things too complicated for equations… like atmospheres? Maybe the interesting question is how does an atmosphere differ from a blackbody radiator and how many equations would it take to account for all the differences.
blah blah woof woof
Frank
My work on the subject of educating the blog world on this super-basic fundamental of radiative transfer.
That’s all.
My interest is in trying to really understand climate science. Along the way, I write articles like this. Not my main interest at all. But still worth the effort, especially because the effort is about 1/100th of writing an article about water vapor feedback.
cheers for SOD!
people are always yelling at me that water vapor will save the world… but books tell me that while it influences heat transfer in the atmosphere, it is not a forcing factor because.. because.. it get saturated and then it rains?
do you have a water vapor post up? (I’ll look around but I didn’t see it before)
Start with Clouds and Water Vapor – Part One.
Bryan,
And let’s confirm:
1. R = 1-α , where α = absorptivity at the wavelengths in question (because no energy can be transmitted through the surface – so energy is either reflected or absorbed).
2a. R is a materially dependent property which is a function of wavelength and direction.
2b. Energy reflected = ∫ Pt'(λ).R(λ).dλ
– which says in words that the energy reflected is the integral (summation) of the energy at each wavelength x the reflection coefficient at that wavelength
– and on a slightly technical note this means that Pt = ∫ Pt'(λ).dλ so Pt'(dλ) is in slightly different units – Pt might be in W/m2 while Pt'(λ) is in W/m2.μm.
Please confirm.
SoD says
1. R = 1-α , where α = absorptivity at the wavelengths in question
2a. R is a materially dependent property which is a function of wavelength and direction.
2b. Energy reflected = ∫ Pt’(λ).R(λ).dλ
Yes that looks ok
In a physics textbook it would be more common to see
R = (n1-n2)^2/(n1 + n2)^2
Where n1 = refractive index of material 1
Where n2 = refractive index of material 2
R would vary for each wavelength.
However n1 for a vacuum or gas = 1
Bryan,
So pressing on..
ΔT = ΔQ / C
ΔT = change in temperature of a body, ΔQ = change in energy of a body, C = heat capacity of a body
And to supply an example, if the surface was in equilibrium and solar flux increased so that the surface absorbed an increase of 1 W/m2 for 1 second, then ΔQ = 1 J/m2 and ΔT = 1/C. [Of course the temperature change would result in a change in energy leaving the surface].
And to supply a similar example, if the surface was in equilibrium and atmospheric radiation increased so that the surface absorbed an increase of 1 W/m2 for 1 second, then ΔQ = 1 J/m2 and ΔT = 1/C. [Of course the temperature change would result in a change in energy leaving the surface].
All ok?
On angular momentum..
..what started me off on the track of wondering about angular momentum was the thermal wind equation.
This is an equation derived from the force = mass x acceleration part of the equations of fluid motion. All for a later article.
But the result (based on a warmer equation and colder poles) is high velocity W-E winds somewhere between the subtropics and poles.
Yet conservation of angular momentum also predicts high velocity W-E winds somewhere between the subtropics and poles.
Ok, I’ve oversimplified because it will take some time to explain in an article.
But conceptually how do the two different physics laws lead to the same result. Which one caused it? Did both cause different bits of it independently? Is conservation of angular momentum just a different way of writing Newton’s law of motion?
That’s how I got to wondering about angular momentum anyway.
I will digest the angular momentum explanations from a few readers and comment in due course.
HankHenry,
Perhaps you are thinking of simple teaching models which use blackbody radiation from the atmosphere as the climate 101 lecture for showing how the surface temperature can increase when the atmosphere is transparent to solar radiation (shortwave) yet opaque to terrestrial radiation (longwave). [Note 1]
We can simple write down a value for the emission of radiation from the atmosphere without any assumptions about “blackbodies”:
a) we can measure it
b) we can solve the radiative transfer equations for a given temperature profile and concentration of radiatively-active gases
With a given value of DLR (“back radiation”) the surface energy balance equations are very simple. Some clarity provided here.
Note 1: Strictly speaking this definition is not a “blackbody”. A blackbody has an emissivity of 1 at all wavelengths.
Thanks. I will take some time to read your links.
My curiosity is about how the stirrings of convective (as opposed to radiative) transfer is expressed and calculated. The question I have is whether surface energy balance equations are merely an interesting blackboard exercise or if they produce numbers meaningful to real world considerations. So far, I don’t see how we can say much more than: there is a degree of warming on earth due to the ability of certain gases to absorb and radiate terrestrial radiation. It seems you need laboratory conditions to utilize these equations in a very precise way. How far do you think we can go in saying what the amount of warming is?
HankHenry,
This article was written to assist people in understanding radiative heat transfer 101 (via demonstrating that those “against the greenhouse effect” can’t write down an equation for energy balance that matches what is found in textbooks).
That is all.
A climate model (GCM) has to use the physics of atmospheric and ocean dynamics and heat transfer to attempt to calculate the future climate under various conditions.
Clearly if the fundamental physics is misunderstood the GCM has no chance.
If fundamental physics is understood then the GCM has a chance. So this is what we might call a “necessary but not sufficient condition”. That is, fundamental physics is necessary but by itself does not guarantee the success of the venture.
Surface energy balance not really a condition of an GCM, instead something like:
Solar radiation absorbed + atmospheric radiation absorbed – surface radiation emitted – latent heat flux – sensible heat flux = net energy absorbed = heat capacity x temperature change
where latent and sensible heat are what you are thinking of for the convective transfer of heat.
The question of the parameterization of convective and sensible heat is an important part of the question about GCMs.
At a very basic level the increased energy absorbed by the climate as a result of increased concentration of “greenhouse” gases is a technical but “simple” and accurate exercise.
This basic level does not include the changes to the climate (feedback) that result from this increase in energy absorbed
I think I’m best off carefully reading what you’ve already written. There is a lot for me to take in and digest. I have worked through some video’s produced by Dr David Archer on Stefan-Boltzmann. I consider your stuff as advanced from that.
“Energy absorbed from the atmosphere by the surface, Ea:
Ea = αRL↓ ….[eqn 1]
where α = absorptivity of the surface at these wavelengths, RL↓ = downward radiation from the atmosphere”
Continuing:
RL(down) = (e*S-B)a where S-B is the well-known equation which relates energy density to temperature; “e” is emissivity, a wavelength-dependent, radiating surface property and the subscript “a” denotes atmosphere.
Therefore, Ea = alpha*(e*S-B)a = energy absorbed by the surface (E_in)
Energy emitted by the surface (E_out) = (e*S-B)s
At surface temperature equilibrium, E_in = E_out
That is, alpha*(e*S-B)a – (e*S-B)s = 0
At temperature equilibrium between surface and atmosphere, S-B disappears and the equilibrium equation reduces to:
alpha*ea – es = 0………[eqn 2]
This can be true only when all terms in eqn 2 = 1
That is, when the surface and the atmosphere behave as black-bodies, an unphysical condition.
John Millett,
For the condition of equilibrium between surface and atmosphere –
if the only flux received by the surface is from the atmosphere then the equilibrium condition must be that atmosphere and surface finish at the same temperature.
The extract from Kramm & Dlugi in the article shows the more complete equation. The surface also absorbs radiation from the sun. And it also transfers energy to the atmosphere via latent & sensible heat.
SOD,
Replace “surface” and “atmosphere” with “body” and “surroundings”, respectively, and the argument presented concludes that Prevost’s 1792 theory of exchanges, on which the AGW concept of back-radiation depends, holds only for blackbodies.
John Millett,
Your equations ignored reflection.
For energy balance between two surfaces with non-zero emissivity (non black-bodies) you need to include the reflected radiation from each surface.
So the irradiation at the surface is not equal to εa σ Ta4
[where εa = emissivity of the atmosphere, Ta = temperature of atmosphere]
But instead includes the portion of the surface radiation reflected back from the atmosphere.
So Ein ≠ αs εa σ Ta4
where αs = absorptivity of the surface (previously written just as α)
Noether’s theorem (Wikipedia)
* the invariance of physical systems with respect to spatial translation (in other words, that the laws of physics do not vary with locations in space) gives the law of conservation of linear momentum;
* invariance with respect to rotation gives the law of conservation of angular momentum;
* invariance with respect to time translation gives the well-known law of conservation of energy
Eli wrote:
“Frank, your hypothetical moved MORE energy off the surface by convection and held the temperature of the surface constant. Pray tell where that excess energy goes. It goes to heat the lower troposphere, but if you heat the lower troposphere, then it is warmer and convection is lower.”
If increasing GHG’s in the lower troposphere increase DLR arriving at the surface by 50 W/m2, convection can increase by 50 W/m2. If GHG’s increase DLR by 100 W/m2, convection can increase by 100 W/m2. Etc. (Increasing GHG’s include both anthropogenic GHG’s and water vapor assumed to cause “feedback”.) This scenario would leave the temperature of the surface and lower troposphere and the lapse rate unchanged. Without a solution to the Navier-Stokes equations, no one can say whether this scenario is right or wrong.
Yu (2007) http://journals.ametsoc.org/doi/pdf/10.1175/2007JCLI1714.1 shows that evaporation has increased by 10% between 1977 and 2003, an 8 W/m2 increase in latent heat flux. GISS surface temperature anomaly rose 0.4 degK during the same period, that would amount to a 2.0 W/m2 increase in radiative cooling. If AOGCMs don’t capture some of this increase in evaporation, they will overestimate surface warming.
And convection gets the heat where exactly?? We know how much radiaton comes in (SUN), we know how much radiation goes out (Satelites). And we know the amount that leaves is less than the amount received. So HEATING UP. By the way you cannot get convection unless there is a temperature gradient to set the density difference for flow. So the surface will heat up. What you say makes no sence in a dissipative system.
DrTskoul:
1) Convection gets the heat away from the surface (where it can effect people and the environment). It takes it to the upper atmosphere where GHGs no longer prevent heat from escaping to space. The tropopause is the lowest altitude where GHG are thin enough that all of the SWR not reflected (238 W/m2) can escape upwards by radiation without any assistance from convection.
2) A temperature gradient already exists to produce buoyancy-driven convection. In one-dimensional models, we assume the environmental lapse rate is equal to the adiabatic lapse rate. On the earth itself, we have many convectively unstable regions with no obvious limits on how much heat can pass through them by convection. The Hadley cell gathers excess heat from the entire tropics and pumps it through the convectively unstable ITCZ.
The surface already receives far more heat from SWR than it can get rid of by LWR through the atmosphere. Look at the K&T global energy flows: SWR reaching the surface, 168 W/m2; Net surface radiative cooling by LWR (SLR-DLR); 390-324 = 66 W/m2. Convection 102 W/m2. More heat is already escaping the surface through regions with unstable lapse rates than escaping by net LWR.
From my point of view, a fundamental question is: Why is convection not 16% (16 W/m2) stronger or weaker than it currently is, which would make the surface 4% (3 degC) cooler or warmer than it currently is? Why do with think climate models (with their limited ability to model convection) will get this right as DLR increases in the future?
I don’t understand enough about dissipative systems and non-equilibrium thermodynamics to understand why you think my scheme makes no sense. Any references would be greatly appreciated. Paltridge has formulated a maximum entropy production hypothesis for the earth’s atmosphere:
homepage.mac.com/bradmarston/Papers/Ozawa%20etal%20(2003).pdf
Frank,
Just as a note that’s a useful but very broad brush approximation. Take a look at Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Eleven – Heating Rates:
Radiative cooling to space takes place from near the surface in the slightly appropriately named “atmospheric window”, and from a range of altitudes for other wavelengths.
It doesn’t all take place at the tropopause.
“Energy absorbed from the atmosphere by the surface, Ea:
Ea = αRL↓ ….[eqn 1]
where α = absorptivity of the surface at these wavelengths, RL↓ = downward radiation from the atmosphere”
So your equation concerns the amount energy the surface receives from the atmosphere.
How much energy is received per second per square meter?
And the source of this energy is the atmosphere. And it’s radiation coming from some distance?
It seems that if you had a 100 watt light it matters how far away the light bulb is from a surface which absorbing this light.
With sunlight the difference in amount energy received doesn’t matter much if within say 1 million km range. The reason for this is because sunlight is coming from long distance away. In comparison the sky is a very short distance away. The power of any electromagnetic radiation will be affect by it’s distance. I.e:
“Light and other electromagnetic radiation
The intensity (or illuminance or irradiance) of light or other linear waves radiating from a point source (energy per unit of area perpendicular to the source) is inversely proportional to the square of the distance from the source; so an object (of the same size) twice as far away, receives only one-quarter the energy (in the same time period).”
So if you had one 100 watt light bulbs per square meter, they deliver more energy to the surface if 1 meter above the surface compared to 10 meter above the surface. This also the case if have light bulb every square meter for 1 km square area.
So you are not disputing the equation, but suggesting that the value for DLR is ?
Amazingly we can measure it. Globally annually averaged it is in excess of 300 W/m2.
This is measured with an instrument at the surface pointing up at the sky. So there is no doubt about its value, or that it is significant.
If you want a conceptual way to help you understand why it is significant..
The atmosphere is a very thin layer completely surrounding a very large object. The radius of the earth is 6,400 km and the troposphere is about 12km. Most of the DLR (“back radiation”) is emitted from within the first few km.
And the atmospheric downward radiation has nowhere else to go but reach the surface. If you put a light bulb up 1km in the sky it would be hard to see. Suppose instead you packed the entire sky 1km up with light bulbs. Then the reduction in intensity from one light bulb from the 1km distance would be made up by the fact that light was reaching you from millions of light bulbs.
If these help you conceptually that’s great. If not, remember that the value is measured not invented nor calculated.
SOD wrote:
“Your equations ignored reflection…………….So the irradiation at the surface is not equal to εa σ Ta4”
and later:
“So Ein ≠ αs εa σ Ta4
where αs = absorptivity of the surface (previously written just as α)”
This suggests that the “unequal sign” was a keystroke mistake. If so, I think we have identical expressions for Ein:
Therefore, Ea = alpha*(e*S-B)a = energy absorbed by the surface (E_in)
If there was no mistake, what is the equation for Ein?
Actually I’m not sure what I was writing. The reflected component of surface radiation by the atmosphere will be negligible, the surface radiation will be absorbed or transmitted by the atmosphere.
The surface absorbs the proportion αs and reflects the proportion 1-αs. Nothing is transmitted through the surface.
So it’s clear now (I hope).
CASE 1 – Two concentric plates
If we took a case where there were two opaque concentric spherical plates with no transmitted radiation through the outer plate and emissivity, ε < 1, then the equation of energy balance for the inner plate would include reflection and the equation of energy balance for the outer plate would include reflection from the inner plate.
I haven’t worked out the equations (yet) but I expect there will be a simple approach to solving it and a complex one. The simple one will be equating temperatures and energy in = energy out and the complex one will be an infinite series of reflections (which might have an analytical solution). I vaguely remember seeing this all solved in a textbook some time ago..
CASE 2 – Surface & atmosphere
Now if we take the atmospheric case, the surface is reflecting some atmospheric radiation back, but the atmosphere will either absorb the surface radiation or transmit the surface radiation. This means that energy will be continually lost to space and both will cool down with the atmosphere always staying colder than the surface.
If we wanted a thermal equilibrium between atmosphere and surface we would need to stop energy being lost and the only way to do that would be to have an opaque shield outside the atmosphere reflecting everything back into the climate system. In this case, it reverts back to something like case 1.
SOD,
Let’s go back to my original argument, before consideration of temperature equilibrium between surface and atmosphere:
“Therefore, Ea = alpha*(e*S-B)a = energy absorbed by the surface (E_in)
Energy emitted by the surface (E_out) = (e*S-B)s
At surface temperature equilibrium, E_in = E_out
That is, alpha*(e*S-B)a – (e*S-B)s = 0”
The term (e*S-B)a can be expressed relative to the term (e*S-B)s thus:
alpha*z*(e*S-B)s = (e*S-B)s (z 1, an unphysical condition.
I’ll try again.
Let’s go back to my original argument before consideration of equilibrium between surface and atmosphere:
“Therefore, Ea = alpha*(e*S-B)a = energy absorbed by the surface (E_in)
Energy emitted by the surface (E_out) = (e*S-B)s
At surface temperature equilibrium, E_in = E_out
That is, alpha*(e*S-B)a – (e*S-B)s = 0”
Now, the term (e*S-B)a can be expressed relative to the term (e*S-B)s thus:
alpha*z*(e*S-B)s = (e*S-B)s (z less than 1)
That is, alpha*z = 1
This implies alpha greater than 1, an unphysical condition.
John Millett,
How did you prove surface temperature equilibrium? You just assumed it.
The 1st law of thermodynamics tells you that Ein – Eout = C x ΔT, where C = heat capacity in J/K.
[Assuming no phase change like evaporation]
When the surface absorbs less energy than it loses it cools down.
If you have a condition of constant temperature then Ein = Eout.
And of course you need to consider all of the sources of energy in – so you must include solar radiation, and all the mechanisms of energy out – radiation, convection and conduction.
“So you are not disputing the equation, but suggesting that the value for DLR is ?”
Obviously it’s an equation for DLR. You saying, “Energy absorbed from the atmosphere by the surface will be represented by: Ea. And Ea is the absorbtion of the wavelengths of this energy.
What quantity, what significant, how much?
“Amazingly we can measure it. Globally annually averaged it is in excess of 300 W/m2”
Are you say Ea equals 300 watts absorbed per square meter per second?
That the earth on average gains 300 watts per square meter?
That it accumulates 300 times 3600, times 24, times 365 watts/joules per sq meter per year? Times 10 per decade. Times 100 per century?
And it isn’t affected by day or nite. Or where on planet or what temperature the surface is?
Weird idea.
“This is measured with an instrument at the surface pointing up at the sky. So there is no doubt about its value, or that it is significant.”
Wow, then it must be true then.
“And the atmospheric downward radiation has nowhere else to go but reach the surface. If you put a light bulb up 1km in the sky it would be hard to see. Suppose instead you packed the entire sky 1km up with light bulbs. Then the reduction in intensity from one light bulb from the 1km distance would be made up by the fact that light was reaching you from millions of light bulbs.”
No it wouldn’t. A million 100 watts in one 1 square km and 1 km high would not heat the ground- sorry, guess again. That fact that it would be dimmer, should give you a clue.
gbaikie,
Citing me: “Amazingly we can measure it. Globally annually averaged it is in excess of 300 W/m2″
Said:
Yes.
You don’t understand absolute basics.
Globally annually averaged values aren’t affected by whether it is day or night. That is what “globally annually averaged values” means.
At this point I should probably stop, but perhaps others are equally confused yet less certain in their confusion.
“..Are you say Ea equals 300 watts absorbed per square meter per second? That the earth on average gains 300 watts per square meter?..”
Strictly speaking I am saying that the DLR, RL↓ > 300 W/m2, but α is almost =1.0 so Ea > 300 W/m2.
We measure it, so yes.
If you want to see how it varies with location and time, take a look at The Amazing Case of “Back-Radiation”
For example:
And here is one sample location, Billings, Oklahoma over 14 days:
“..That it accumulates 300 times 3600, times 24, times 365 watts/joules per sq meter per year? Times 10 per decade. Times 100 per century?..”
What do you mean “accumulates”?
The surface absorbs radiation and so the surface emits radiation. Therefore it won’t “accumulate”, but the temperature will be at the point where absorbed energy is approximately equal to emitted energy. (This will be via radiation and convection).
Yes, that is what “measured” means.
The value can also be mathematically calculated from the radiative transfer equations. It matches the measurements, which is why it is proven physics.
When you write in this way you demonstrate that you have a conceptual problem.
Good luck in your journey.
SOD wrote:
“[Or almost done because still we would want to confirm that the coefficient of absorption was understood and not somehow believed to be zero for radiation from a colder source..]”
Well, the coefficient of absorption would be zero except for emission from molecules close to the surface, wouldn’t it, owing to diminishing energy density with distance from source. The sun’s 1 Wm-2 entering at TOA, already diminished by distance from source, strikes the surface at 1 Wm-2. The atmosphere’s 1 Wm-2, generated by CO2 molecules with radii of 10^-10 m (mostly from the upper, dry troposphere?) is diffused into the surrounding electromagnetic field,making no direct contact with the surface.
John Millet,
Coefficient of absorption, called absorptivity = the proportion of radiation absorbed.
The coefficient of absorption is nothing at all to do with the quantity of radiation received.
Let’s say α = 0.9.
If the irradiation at the surface = 0.001 W/m2, ie 1 mW/m2, then absorbed radiation = 0.9 mW/m2.
If the irradiation at the surface = 1 W/m2, then absorbed radiation = 0.9 W/m2.
If the irradiation at the surface = 100 W/m2, then absorbed radiation = 90 W/m2.
John Millett,
Clearly you have some strange idea about radiation. I could try and explain but what’s the point?
The measurements prove your idea wrong. Physics proves your ideas wrong because the calculation (using the radiative transfer equations) of the emission of radiation from the atmosphere that reaches the surface matches the values measured.
How is it that the measuring equipment that measures solar radiation at typical values of 160 W/m2 measures atmospheric radiation at typical values of > 300 W/m2?
But it’s fascinating how many people have so many incompatible ideas about atmospheric radiation.
Here’s a selection:
1. It doesn’t exist.
2. It’s tiny because CO2 has almost no emissivity
3. It gets absorbed into the surrounding something because of the inverse square law
4. It can’t affect the surface temperature because that would violate the second law of thermodynamics
5. “..back-radiation cannot warm the surface to any temperature above the one of its source..”
6. “..DLR can only compensate or back radiate the lower energy waves and not add energy in the higher ranges..”
7. It can’t do anything because of the “quality” of radiation
8. “..It selectively absorbs those photons because they have precisely the right amount of energy to raise the CO2 molecule from one internal energy state to another..”
9. “..It does not get converted to thermal energy and so cannot affect the rate of thermal energy leaving the surface. It is merely immediately radiated out again with the same frequency and intensity, never having been converted to thermal energy..”
I could go on, there are more. And none of the above claims are in textbooks.
Hopefully, some readers find it useful to see the desperately confused and incompatible claims of the no textbook crowd?
Please tell me there’s a point. At least there’s alcohol..
SOD,
How is it strange to think that the intensity of radiation from a molecule in the atmosphere will be subject to the same decay with distance relative to radius as that from the sun?
I agree with your point on absorptivity – poor expression on my part.
Talking of textbooks, in the many you have consulted in preparing your articles, have you happened upon an experimental demonstration of Prevost’s theory of exchanges? French’s “Principles of Modern Physics” (1962), otherwise replete with descriptions of such validation of theory, lacks it in respect of theory of exchanges writing only that: “This asserts that a body emits radiant temperature at all temperatures…………When a body has settled down to a constant temperature, it has not stopped radiating, but receives from its surroundings just as much energy as it emits in given time. In other words the equilibrium is dynamic, not static”
French gives some background. The intuition at the time was that radiation did cease at temperature equilibrium but scientist’s couldn’t understand how bodies ” although entirely separated from each other physically, know when they ought to stop radiating, through an awareness of each other’s temperatures”
But are bodies entirely separated from each other? Aren’t they surrounded by an electromagnetic field, always and everywhere? Such fields, according to French, exhibit properties of energy density, mass, momentum and pressure. Is it not plausible that a body in such a medium would be sensitive to at least one of these properties and would know when to stop radiating?
“You don’t understand absolute basics.
Globally annually averaged values aren’t affected by whether it is day or night. That is what “globally annually averaged values” means.”
It is said that sun gives average of 240 watts per square meter.
And Wiki says:
“Radiation balance
The vast majority of the energy which affects Earth’s weather comes from the Sun. The planet and its atmosphere absorb and reflect some of the energy, while long-wave energy is radiated back into space. The balance between absorbed and radiated energy determines the average temperature.”
http://en.wikipedia.org/wiki/Radiative_forcing
It seems that average of 300 watts per square meter generated by the atmosphere is more than averaged 240 watts per square meter caused by the Sun.
And same wiki article it say CO2 radiative forcing is 1.5 watts per square meter.
““..That it accumulates 300 times 3600, times 24, times 365 watts/joules per sq meter per year? Times 10 per decade. Times 100 per century?..”
What do you mean “accumulates”?”
Warms up.
Absorbs the 300 watts per meter per second. let’s look at melting snow at rate of 300 watts per second- accumulate a watt or joule or as you said:
“And this energy absorbed, once absorbed, is indistinguishable from the energy absorbed from the sun.”
If you have 10 hours of absorbing 300 watts per meter per second that would
be 300 times 3600 times 10- 10.8 million joules. Which is equal in melting ice: 334 kJ/kg.
So at the rate 32 kg ice per square meter for 10 hours- at nite if temperature are at or above freezing. Or about 3 cm thickness of ice or about 1 foot of snow.
Keeping in mind water- or snow and ice absorb at this wavelength very well [doesn’t reflected as it does with sunlight].This would mean if temperature are at or near freezing, one doesn’t need to shovel snow off the driveway in the morning.
Which is odd as I have lived in areas where it has snow at night just above freezing and the snow lasts for days. As example, you could have situation where during afternoon the temperature could around 38 F, and you get wet snow/rain mixed with snow, and as it gets towards night, temperature could lower to 36 F and get snow, also during nite it might lower to 32 F, and if so, wake up to icicles hanging from eaves. And could have clear or partly cloudy skies. If it rains, the snow will disappear quickly- within hours, otherwise if snow is a few inches or more lasts couple days.
gbaikie
You said: “And same wiki article it say CO2 radiative forcing is 1.5 watts per square meter.”
Wherever you read this they were probably talking about the anthropogenic rise of CO2 forcing, like in this link. It’s not a parameter you can compare with total DLR, since they’re two different things.
“It seems that average of 300 watts per square meter generated by the atmosphere is more than averaged 240 watts per square meter caused by the Sun.”
If you really want to understand this apparent “paradox”, take some time to read the article linked here.
Wherever you read this they were probably talking about the anthropogenic rise of CO2 forcing,
http://en.wikipedia.org/wiki/File:Radiative-forcings.svg
from:
http://en.wikipedia.org/wiki/Radiative_forcing
The anthropogenic forcing is also around 1.5 watts, but quite significant error bar of .5 to 2.0 Watts per square meter.
I was going to get around to mentioning the precise of these apparent measurement, also
gbaikie
Please make sure you know what the figures you’re looking at mean. Unless, of course, you’re not interested, which would be a game I’m not interested in.
The greenhouse gas columns you’re looking at are “positive forcing from [anthropogenically] increased greenhouse gases”, as the description explains.
gbaikie
Your wikipedia graph can also be checked directly in its source, the IPCC AR4, with lengthier explanation about its contents:
http://www.ipcc.ch/publications_and_data/ar4/wg1/en/faq-2-1.html
It’s human caused increase. Not total DLR. Neither total CO2-related DLR.
“It’s human caused increase. Not total DLR. Neither total CO2-related DLR.”
Alright.
So 1.5 watts per square meter is from increase from CO2 since 1750.
And we still going for idea that DLR causes more energy to be absorbed by surface than the sun- and to be clear this actually mostly water vapor causing this.
And by water vapor causing this, we aren’t referring to transport energy of water vapor due to evaporation [which is an enormous amount energy, nor talking about droplets of water in clouds, but rather water vapor as a gas and this gas radiating heat.
Is this summary correct?
Or we mixing together everything do water in the sky in as droplets in clouds and the transport of the latent heat of water vapor.
It seems to me as a guess if you pointing instrument at the sky you would not be measuring the energy of latent heat of water gas, nor would pointing the instrument at clouds.
The point I want to focus is the measuring of DLR- it’s accuracy in sense that instrument tells something and the inference that this temperature or watt per square measuring device is having an effect of warming the surface by 300 watts per square meter.
As example, of what mean. One can measure the sunlight. Say at noon, and your instrument could indicate that the solar flux is 1000 watts per square meter. One should NOT therefore conclude that the sun is heating the surface by 1000 watt per meter per second.
Nor would it be correct to say something like- “well, obviously if surface was white it wouldn’t be, but if black then mostly it is absorbing 1000 watts per square meter”.
Rather it would only be true [that the surface absorbing 1000 per square meter] if the surface was black body and it’s temperature was 0 K. Of course it nice if we actually had a blackbody, so such measurement could occur- maybe it could more than 1000 watts per meter. And since there isn’t a blackbody, one would have find something close to a blackbody, and probably something close to 0 K.
But for simpler way it seems my example measuring loss from snow, when at or near freezing, could get you somewhere in the ballpark.
If you agree that idealized perfect black body at 0 K would absorb more energy than the “average” earth surface. Then we have examine how one measuring how much energy the surface is actually absorbing.
I refer you to lecture scienceofdoom gave reference to:
http://ocw.mit.edu/courses/physics/8-01-physics-i-classical-mechanics-fall-1999/video-lectures/
More specifically the second lecture:
http://ocw.mit.edu/courses/physics/8-01-physics-i-classical-mechanics-fall-1999/video-lectures/lecture-1/
And more precisely, where Prof. Walter Lewin says:
“Any measurement you make without any knowledge of the uncertainity is meaningless!”
He repeated it twice, and also mentioned that textbooks tend not talk about it. Then he went on a “proved” why it was important.
I would add, that this is the foundation of science- if you are ignoring it, you are not doing science. And seems with what has been offered regarding these DLR claims have nothing to do with science.
ScienceofDoom,
The thought that back radiation, resulting from the presence of optically absorbing gases in the atmosphere, causes increasing ground temperature, is erroneous. These gases do cause temperature increase at the surface, but not from back radiation (not any more than an insulation layer causes a heat strip to be hotter by back conduction). The result in an atmosphere is more complicated than insulation on a heat strip, but the analogy is similar. The following is a limited analysis, but if you clearly understand it, you should start to better understand what I have been trying to say for a while. To show this, a simplified model atmosphere is examined. Assume we are looking at a process with no feedback or albedo change. Also assume that convective mixing due to buoyancy and wind maintains an adiabatic lapse rate, and that the Cp of the atmosphere is not changed significantly by having more or less of the absorbing gas fraction. For that approximation (and only considering averages), the temperature is highest at the ground, and drops linearly with altitude in most of the lower part of the atmosphere.
Assume the atmosphere absorbs essentially all thermal radiation wavelengths before it radiates to space if the optical thickness is large enough (no transmission window for radiation for simplicity sake), and assume that there is a scale length where essentially full absorption occurs one time. This length increases with increasing altitude (due to dropping pressure) until radiation goes to space. Increasing concentration of the absorbing component of the gas would raise the effective altitude of the outgoing radiation (due to increasing concentration at higher altitudes where the radiation would leave from). The increasing concentration would also shorten each scale length, thus increasing the number of times absorption and radiation occur before the radiation exits.
First consider the concentration of absorbing gas small enough, so that the effective absorption path length is fairly long. As long as solar energy continues to heat the ground, there will be heat energy continually convected upwards from the ground, due to buoyancy and convective mixing, and a net radiation heat transfer up, maintaining the temperature gradient of the adiabatic lapse rate. Estimation of the net radiation transfer near the surface allows the required convective heat transfer to be calculated. An equation is needed here to start to make the critical points needed:
E=5.67E-8(Thot^4-Tcold^4) assuming black body behavior to simplify (1)
An example atmosphere is considered with an adiabatic lapse rate of 6 K per km, a ground temperature with no atmosphere of 270 K, and an initial atmosphere with some absorbing gas resulting in a surface temperature of 280 K (selected numbers are just to show reasonable order of magnitude effects). I assume Tcold for space is 0 K., for simplicity, which is a bit low but not important. The power from surface to space for no atmosphere is thus:
E= 5.67E-8 x (270)^4= 301 W/m2
With the initial atmosphere and with some absorbing gas, the surface was 280 K, so the surface radiation up is:
E=5.67E-8 x (280)^4 = 348.5 W/m2
Only 301 W/m2 goes to space, so this increased surface temperature resulted in an increase of 48.5 W/m2 in surface radiation, and there is also energy convection up, so something happens between the surface and exit location. There is an average effective altitude where the temperature as seen from space is 270 K, and where effective radiation to space matches the solar heated surface input of 301 W/m2. Due to the lapse rate of 6 K per km, this occurs at an effective average altitude: 10/6=1.67 km.
A simple equation is used to represent the surface temperature for concentrations greater than that needed to raise the surface temperature more than the initial 10 K case. This is given as a function of relative partial pressure increase, p2/p1, where p1 was the partial pressure of absorbing gas that resulted in a surface temperature of 280 K. The resulting equation is:
T=280+1.73 ln(p2/p1) (2)
If an increase in the fraction of absorbing gas produces a temperature increase of 1.2 K per doubling (as is claimed for CO2), and 5 doublings occur, then p2/p2=32, and T=286 K. Now outgoing radiation would leave effectively at an altitude: 16/6=2.67 km (same lapse rate). We now look at the comparison of effects for the two concentrations of absorbing gas, the value that increased the surface 10 K, and the value for 16 K.
The partial pressure ratio is the same at all altitudes. Thus the scale length is 32 times shorter for the 32 times concentration case. Determining the scale length is not easy, but for the trend of the result, this is not exactly needed. For the following, I assume the scale length is 1000 m for the 280 K case, and: 1000/32=31.2m for the 5 doublings.
Case 1: The first case has a temperature drop to the first full absorption of 6 K to 274 K. The net radiation up minus down between that layer and ground is:
E=5.67E-8 x [(280)^4 –(274)^4]= (348.5 -319.6)=28.9 W/m2
The value of 28.9 W/m2 is all of the NET radiation heat transfer up, even though there is 348.5 W/m2 surface radiation up from the surface and 319.6 W/m2 back radiation. However, only the NET radiation contributes to heat transfer, and the convective heat transfer is thus: (301-28.9)=272.1 W/m2
Case 2: This case has a temperature drop to first full absorption of: 6/32=0.188 K. The net radiation up minus down for that case is:
E=5.67E-8 x [(286)^4 –(285.812)^4]= (379.36 -378.36)=1 W/m2
The value of 1 W/m2 is all of the NET radiation heat-transfer up, even though the surface radiation up is even larger that the previous case at 379.36 W/m2, and the back radiation is up to 378.36 W/m2. The convective heat transfer is now up to 300 W/m2, or 99.67% of all surface heat-transfer up.
If the absorbing gas concentration increased even more, the radiation heat transfer would tend to ZERO, and all energy would be carried up by convection to an altitude where it radiated to space.
The point is that more absorbing gas does increase the surface temperature by raising the altitude of outgoing radiation, but not by virtue of the increasing back radiation. The radiation heat transfer is of no separate importance beyond the determination of altitude of outgoing radiation. It is a small player in heat conduction at reasonably high concentrations, and actually reduces radiation heat transfer as concentration increases.
Leonard Weinstein,
All I am attempting to achieve here is to demonstrate that the “no greenhouse coalition” have no idea how to write an equation for the absorption of atmospheric radiation by the ground.
I’m sure you don’t want to claim that atmospheric radiation is not absorbed by the surface. Or that the absorption of 1W/m2 of atmospheric radiation does not cause the same change in temperature of the ground as 1W/m2 of solar radiation (all other things being equal).
If this wasn’t the case, the surface would be much cooler. And the first law of thermodynamics would be in trouble (along with all the textbooks on radiative heat transfer).
The relationship between surface temperature, convection, lapse rate and emission of radiation to space from the troposphere is of course the most important determinant of the surface temperature.
That is not what I am trying to explain here.
The reason I keep writing about “back radiation” is the steady stream of textbook-unencumbered people who passionately believe the many (contradictory) fairy stories they have read on the internet.
However, you are welcome to write your explanation of how the atmospheric “greenhouse” functions each time and explain it as if I didn’t agree with you.
As I comment each time – I agree with you. (Caveat – I haven’t read your whole comment this time, but I assume you haven’t changed your mind from all the previous times and have explained it the same way.)
SoD
You said: “So you are not disputing the equation, but suggesting that the value for DLR is ?
Amazingly we can measure it. Globally annually averaged it is in excess of 300 W/m2.
This is measured with an instrument at the surface pointing up at the sky. So there is no doubt about its value, or that it is significant.”
How do the instruments, which measure DLR, work? Specifically, do they not actually compute DLR based on the same formulae used to calculate DLR? And don’t these instruments need be calibrated to account for ambient temperature? That is, in order to “measure” DLR the receiver temperature must be cooled below ambient…must be colder then radiation source, in this case the atmosphere?
L.J. Ryan:
The calculation of DLR is from fundamental physics, which is why the equations of radiative transfer can also reproduce the spectrum of DLR, for example like this where the measurement is from a Fourier transform infrared spectroscope:
You can see the fundamental physics equations derived in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations.
In contrast, the measurement of DLR flux is done using a pyrgeometer which simply relies on net energy absorbed/emitted changing the temperature of a device. The temperature change is measured. Energy emitted is easily calculated from the Stefan-Boltzmann equation. Therefore, energy absorbed can be calculated.
However, it is true that temperature measurement is a very suspect practice and relies on circular reasoning where the whole idea of temperature has to be assumed to measure temperature.
Beware those carrying thermometers!
By the way, if you want to put forward your equation for absorption by the surface of downward radiation from the atmosphere we can move forward.
Armed with this equation we can then evaluate whether there is some way in which pyrgeometer measurements are invalid.
Without an equation it will be impossible to evaluate the impact of any claims you would like to make.
LJ, why not do some research? There’s a whole internet out there.
SoD,
Your equations are no different then mine…I think. However, I question the conclusions drawn from the calculated answers…the conclusion that radiation from the cooler atmosphere will increase the temperature of a warmer surface or object. Case in point, a pyrgeometer. In order to “measure” DLR the receiver temperature must be cooled below ambient…must be colder then radiation source, in this case the atmosphere. Do I have this right?
L.J. Ryan,
No, you don’t.
DSL has already provided a number of links including one to how the pyrgeometer works.
Have you read it? Do you understand it?
Internally the pyrgeometer measures a temperature difference. It can measure a positive difference or a negative difference.
If you have the same equation as me, then what happens when the atmosphere radiates 1 W/m2 more than currently?
Let’s say the surface absorptivity, α = 0.9. This means that the surface now absorbs 0.9 W/m2 more than before.
Where does this energy go?
All thermodynamics textbooks that I have read are quite clear. The absorbed radiation increases the internal energy. This is an inevitable consequence of the first law of thermodynamics. And internal energy is related to temperature via the parameter called heat capacity (as shown in an earlier comment).
So temperature goes up and as a result all kinds of consequences follow. The surface emits more radiation, the convection increases.. at this stage we are not interested in the feedbacks or the ultimate new equilibrium temperature.
Only in what happens to the surface when the incident radiation (irradiation) increases by 1 W/m2 and absorbs 0.9 W/m2.
The result is exactly the same as if some change had resulted in the surface absorbing 0.9 W/m2 more solar radiation.
Exactly the same, even though the first case the absorbed energy is from a colder source and in the second case the absorbed energy is from a hotter source.
If you think differently provide your equations of absorption of energy by the surface, or your equations of temperature change due to changes in energy. With these equations we can do some calculations.
SoD:
You said “No, you don’t.
DSL has already provided a number of links including one to how the pyrgeometer works.
Have you read it? Do you understand it?”
Well…my understanding, according to the primers DSL provided, the receiver temperature is reduced/subsidized. Specifically, from DSl’s link:
“To derive the absolute downward long wave flux, the temperature of the pyrgeometer has to be taken into account. It is measured using a temperature sensor inside the instrument, near the COLD junctions of the thermopile”
Please explain.
As to the radiative transfer equations and text books, in what instances do the equations not hold?
A paper on calibration of pyrgeometers can be found at:
Click to access stoffel_t.pdf
Frank
Right at the bottom of your paper page one an error figure is given.
It appears that two properly calibrated pyrgeometers could be as much as 17W/m2 apart.
This instrument has a long and troubled history.
Bryan,
Only in your mind.
As much as 17 W/m² would imply either two or three sigma. Let’s say conservatively two sigma so sigma would be 8.5 W/m² out of ~400 W/m² or ~2%. That’s amazingly good for an instrument of this sort.
DeWitt Payne says
“As much as 17 W/m² would imply either two or three sigma. Let’s say conservatively two sigma so sigma would be 8.5 W/m² out of ~400 W/m² or ~2%. ”
Call me old fashioned but I prefer to use percentage error.
The way resistors are sold
For 400 with an error of 17W/m2
% error =4.25%
For night time values of around 200W/m2
% error = 8.5%
However I agree with your next comment
“That’s amazingly good for an instrument of this sort.”
Yes for a very crude device its not bad.
Most people don’t know that when used in its normal mode(pointed to the cold sky) there is more radiation leaving the pyrgeometer than entering it.
As a proof of a CO2 greenhouse problem where an effect of the order of 1W/m2 is postulated its completely useless.
Bryan,
Then you don’t understand resistor tolerance either. A tolerance of 1% for a 100&Omega: resistor means that the maximum difference between two resistors could be as much as 2Ω, i.e. 101-99. And that’s probably 99.7% confidence or ±3σ. Which would mean that 95% of all pyrgeometers could be in the range of ±6W/m². And there are lots of pyrgeometers out there making measurements so the error of the mean will be significantly lower than the error of an individual measurement or instrument. Oh, and if we’re looking at anomalies, the absolute accuracy of the instrument mostly cancels out.
Moving the goalposts again are we? You don’t need to close the energy balance to a precision less than 0.1 W/m² to make a convincing argument that the radiative transfer calculations are correct. Which means, all other things being equal, that doubling CO2 must cause some warming of the surface. The calculated spectra and the total flux agree with measurements to within experimental error. You seem to vary wildly between taking the position that downwelling long wavelength radiation doesn’t exist at all, or at least isn’t absorbed, to saying that while DLR may exist, we cannot measure it precisely enough.
DeWitt Payne commenting on Bryan, said:
Bryan has so far confirmed that he accepts the equations that demonstrate the existence of the greenhouse effect.
If there’s one thing that all the “against greenhouse coalition” believes it’s.. that the “greenhouse” effect doesn’t -and can’t – exist.
Actually that’s the only thing.
The rest is pretty much up in the air. And disputed among the coalition.
There are some ways forward for Bryan:
1. The radiation from the atmosphere, DLR = 0.00 W/m2
Notes on 1:
a) saying a measured value of 300 W/m2 is out by 10 W/m2 or even 150 W/m2 still means there is a “greenhouse” effect. The DLR needs to be 0.00.
b) given the acceptance of the equation of absorption of DLR, Bryan has accepted the principle behind the pyrgeometer which measures DLR. Of course, with the pyrgeometer there is always the sticky question of temperature, which is clearly an invented concept by climate science. All of the measurements of temperature actually assume the concept called temperature to begin with, which is obviously a circular argument and needs no further debunking.
2. A formula which demonstrates that no matter how much radiation from the atmosphere increases, temperature of the surface does not increase.
Note on 2: of course we expect the equation to back this up, see my comment to L.J. Ryan offering my assistance.
DeWitt Payne says
“Oh, and if we’re looking at anomalies, the absolute accuracy of the instrument mostly cancels out.”
Sorry for the belated reply but I was on holiday
A 100ohm resistor with a 5% relative error would be expected to be within the range 95 to 105 ohms.
When we combine quantities to find a value we certainly cannot assume as you put it they “mostly cancels out.”
For a simple example to find the specific heat(S) of a substance the following equation was used
S = VIt/MdT
Where V = voltage across heater with 2%re
Where I = current through heater with 1%re
Where t = time heater was on 0.1%re
Where M = mass being heated with 2%re
Where dT = temperature rise 3%re
Total relative error = 8.1%
So if the calculation of measured values was S = 2000 J/kgK
Then we could be confident that the result would be between the region 1838 and 2162
You might think that this is an over pessimistic method of dealing with measurement errors but it can be mathematically justified.
The result assumes there are no other sources of error.
https://ece.uwaterloo.ca/~dwharder/NumericalAnalysis/01Error/Error/
SOD (reply to February 5, 2012 at 12:34 am): I didn’t mean to imply that all of the OLR originates at the tropopause. The outward flux of energy at all altitudes needs to be equal to the energy from SWR absorbed by the surface and the atmosphere below that altitude. Looking at the K&T Energy Flows, 235 W/m2 of SWR is absorbed below the tropopause and 168 W/m2 is absorbed by the surface. For SURFACE balance, the net outward flux of LWR (66 W/m2) plus convection (102 W/m2) must amount to 168 W/m2. For balance higher in the atmosphere (which I assume (without evidence) is the tropopause), 235 W/m2 of outward flux must exist and this must be all radiation, since the lapse rate near the tropopause no longer supports convection. So I meant to say that the tropopause is the lowest altitude where the outward flux is composed all of radiation.
I do have only a vague idea of where most outgoing OLR originates (except for the 40 W/m2 that goes through the window). The wonderful calculations you have shown before show how the outward flux originating at the surface is changed by absorption and emissions as it moves up through the atmosphere. By the time we get to the top of the atmosphere, few of the original photons emitted from the surface are left and I don’t have a good feeling for what has been happening to the photons emitted by the atmosphere. Unlike the surface, which emits at both strongly- and weakly-absorbed wavelengths; the atmosphere emits most strongly at the wavelengths that it absorbs best, and never emits wavelengths it can’t absorb. On the K&T diagram, 40 W/m2 escape directly to space, 26 W/m2 eventually make it to space and the rest returns to the ground to try again. How many cycles of emission and absorption are need to get that measly 26 W/m2 through the atmosphere?
Could you calculate what happens to a photon emitted upward or downward from a CO2 molecule from given altitudes, for example 0.2, 0.5, 1, 3, 6, and 10 km? One way to set up the problem is to imagine a box of air at each of these altitudes that is 1 m2 wide and tall enough to weigh 100 kg, or 1% of the atmosphere above every m2 of surface.
For the box at each altitude, we might calculate:
1) % of photons reaching the surface and W/m2 carried by them.
2) % of photons emitted downward absorbed before reaching the earth, average vertical distance traveled (preferably weighted by energy carried), and W/m2 carried this average distance.
3) % of photons emitted upward but absorbed before reaching space, average vertical distance traveled (preferably weighted by energy carried), and W/m2 transported this average distance.
4) % of photons reaching space and W/m2 carried by them.
5) Height of the box that contains 100 kg.
Sod,
Here is another attempt:
From Newton’s thrid law:
“To every action there is always opposed an equal reaction:” (Google Translation)
The conservation of both linear and angular momentum can be seen as consequences of the term “opposed”.
Opposed can be seen as having two aspects which I will combine in the phrase “collinearly opposed”.
Without the (“co[l]”) the remaining “linearly opposed” is sufficient to conserrve linear momentum. The “co-” part is necessary to conserve angular momentum.
Simply put the “co-” part states that the opposed reaction is in alignment (along the line) of the action. Otherwise the forces could only be in opposed directions.
The “co-” aspect was not left to be deduced from the non “co-” aspect. Newton’s usage of opposed is read to imply both.
Here is a modern rendering courtesy of Wikipedia:
“The mutual forces of action and reaction between two bodies are equal, opposite and collinear.”
The “co-” part establishes that a closed system cannot subject subject itself to a spontaneous net torque. This prevents the need to speculate on whether such a system could convert some other internal energy into a spontaneous rotation or vice versa. Such a rotation would not of itself change the linear momentum thus statisfying its conservation.
Mentions above of Noether are correct but are not additional to Newton’s Laws. The existence of the stated symmetries are inherent to those laws.
Alex
SOD wrote, in answer to Leonard Weinstein:
“The relationship between surface temperature, convection, lapse rate and emission of radiation to space from the troposphere is of course the most important determinant of the surface temperature”
Isn’t it necessary to distinguish between temperature level and variation?Climate system processes determine the variations (diurnal, seasonal and inter-glacial) in surface temperature, not its level (Ts) which reflects the internal energy of the whole planet. The internal energy of the climate system, a fraction of that of the whole, is reflected in its effective radiating temperature (Ta) which, therefore, must be less than Ts. Kramm and Dlugi’s endorsement of G&T’s finding, that the arithmetical excess of Ts over Ta is a “meaningless number” (and says nothing about the greenhouse effect), is warranted.
[…] […]
SOD wrote:
“How did you prove surface temperature equilibrium? You just assumed it”.
I neither assumed temperature equilibrium nor set out to prove it. Rather, I set the condition for equilibrium in the same way you do. The argument, coupled with related comments, is a general one about the limited applicability of the theory of radiative exchange – it applies only to blackbodies and, by definition, doesn’t apply in the climate system.
Experiments in the late 19th century showed that the rate of cooling of a body is a function of the temperatures of both the body and its surroundings. The smaller the temperature difference, the slower the cooling rate. As the body cools (by losing energy), its temperature and, hence, the temperature difference both fall, further slowing the rate of energy loss. Eventually, the rate of energy loss reduces to zero (Eout = 0) and the body is in temperature equilibrium with its surroundings. At temperature equilibrium, Eout = Ein = 0.
That is, the body is neither gaining energy from, nor losing it to, its surroundings, a condition of simultaneous temperature and radiative static equilibria.
If radiation from the cooler atmosphere is to affect the surface temperature by slowing its rate of cooling, it would have to either reduce the surface temperature or increase that of its surroundings, the atmospheric boundary layer. Reducing surface temperature is the opposite of the hypothesised effect and must be rejected. Raising the temperature of the boundary layer, except in the case of temperature inversion, requires energy transport from a cooler region to a warmer one, violating thermodynamic laws. Observations show that in the pre-dawn hours, surface temperature is very nearly stable, that is, Eout = Ein = 0 approx. As argued above that is the condition for simultaneous temperature and radiative static equilibria, the implication of which is that DLR = 0.
How, then, do pyrgeometers measure DLR, proving its existence despite (imagined in SOD’s reference frame) conflict with thermodynamic laws? That is the subject of a separate comment.
John Millett
In response to my statement of February 6, 2012 at 2:45 am:
“How did you prove surface temperature equilibrium? You just assumed it”.
Responded:
Maybe you didn’t realize you assumed temperature equilibrium. And maybe you can’t even read your own words.
Here’s what you wrote:
And if you didn’t mean to write your own words, you did assume these words.
Ein = Eout – is not the first law of thermodynamics, or a result of the first law of thermodynamics.
Ein – Eout = Change in Internal Energy – is a result of the first law of thermodynamics.
You asserted Ein = Eout, which is only true when internal energy is not changing and therefore only true when temperature is constant.
That is why using this flawed hypothesis you managed to “disprove” a basic theory about radiation.
If you can’t grasp these elements, there’s not much point me explaining anything further. Expect me to ignore your subsequent ramblings.
SOD, you’ve really confused me. Consider the following statements, identified by author:
John Millett wrote: At surface temperature equilibrium, E_in = E_out.
SOD wrote: You asserted Ein = Eout, which is only true when internal energy is not changing and therefore only true when temperature is constant.
Recognising that the words “constant” and “equilibrium” are contextually equivalent, our statements mean the same thing, don’t they?
John Millet,
Constant and equilibrium are not identical in meaning. Temperature could be constant in a system far from equilibrium but at steady state. The Earth is never at equilibrium because there is a constant flux of energy in and out. The surface of the Earth is neither at equilibrium nor at steady state even when averaged over a long time.
February 6, 2012 at 6:43 am
L.J. Ryan
A thermocouple nominally has a hot junction and a cold junction. That’s only nominally, though. The “hot” junction can be hotter or colder than the “cold” junction. If the hot junction is hotter than the cold junction then the potential measured is positive, but the potential is negative if the hot junction is colder than the cold junction. A thermopile is a large collection of thermocouples wired in series to increase the voltage sensitivity so small temperature differences can be measured.
In a pyrgeometer or an IR thermometer, the hot junctions of the thermopile are separated from the cold junctions by a thin layer of insulating material with precisely known thermal conductivity. The cold junctions are then placed in thermal contact with a block of material with high heat capacity and high thermal conductivity. The temperature of this block is measured. The hot junctions are covered with, in the case of a pyrgeometer, a silica dome treated to transmit radiation in the ~5-50μm range and reflect radiation < 5μm. The hot junctions are treated to have high emissivity in the 5-50μm wavelength range. If the device is then pointed at the sky, the hot junctions are emitting radiation at less than, the same or more than they are receiving from the sky. If there is a difference in emitted vs absorbed, heat will flow from the sky into the block or from the block into the sky creating a temperature difference across the insulator. Since we know the thermal conductivity of the insulator, the temperature difference converts directly to a negative or positive power difference per unit area. Since we know the temperature of the block and the emissivity of the hot junctions, the total flux from the sky can be calculated by adding the heat flow across the insulator to the heat flow calculated from the SB equation for the temperature of the block.
Hand held IR thermometers work the same way except an IR thermometer has a lens over the detector with a restricted field of view instead of a dome. The temperature of the detector must be known, but it doesn’t have to be colder than the measured temperature. And, strictly speaking, it doesn’t measure temperature, it measures radiative flux that is converted to an effective temperature using the SB equation.
Hand held IR thermometers are not expensive. Buy one that has a lower temperature limit of -60C and you can measure the temperature of the sky (unless it’s a really cold night). I’m currently getting day time readings of -25 to -35 C for a clear sky at the same elevation angle (but not direction) of the sun. The day time vertical effective clear sky temperature measured with a hand held IR thermometer has been shown to correlate well with total column precipitable water vapor ( http://journals.ametsoc.org/doi/pdf/10.1175/2011BAMS3215.1 ). You’ll also find that on an overcast day, the cloud temperature will be very close to the ground temperature.
DeWItt: What is a pyrgeometer “looking at? If I place my detector at the bottom of a long tube, I know what direction the photons are coming from. This works well with visible light because the walls of the tube are too cool to emit many visible photons. At thermal infrared wavelengths, most of photons arriving at the detector may have been emitted from the walls of the tube, unless the tube is cooled with liquid helium.
A pyrgeometer appears to collect all the light from a hemisphere, but it doesn’t seem likely that photons arriving at the detector from shallow angles will be detected as efficiently as photons coming nearly vertically.
GHG molecules emit IR in all directions. When OLR is calculated, we abstract only the component of the flux moving perpendicular to the surface.
How does a purgeometer deal with these issues. Is the angle irrelevant? Do we directly obtain the component of the flux moving perpendicular to the surface or do we process the signal to get the perpendicular component?
Frank,
A pyrgeometer measures the total radiation flux from a hemisphere impinging on a flat surface integrated over all wavelengths. In fact, that’s the number usually quoted for DLR in units of W/m². The direction is simply perpendicular to the plane of the disk. You also see flux in units W/m²/cm-1/sr or W/m²/μm/sr. That’s the number you calculate with the Planck equation. To get the total flux in a hemisphere you integrate over the wavelength range and multiply by π. The factor of two disappears because the area of a hemisphere is twice the area of a disk of the same radius. The W/m² number is also the same as the flux between two parallel planes of infinite extent.
I don’t care about the blah blah blah. These people are just blabbering nonsense. What I find truly amazing and disturbing are those who use a lot of equations and still blabber nonsense. Gerlich and Dr. T come to mind.
My take on the conservation of angular momentum is that it can be derived from Newton’s laws of motion and gravity. But I think the conservation law is more fundamental than the laws of motion. This explains why Newtonian mechanics can be reformulated by Lagrangian mechanics based on the conservation of energy and momentum.
L.J. Ryan from February 6, 2012 at 6:43 am,
The equations are true while the atmosphere is in LTE (local thermodynamic equilibrium).
LTE is all about, in the vernacular:
Molecules banging into each other a lot so that normal energy states apply
It does not mean temperature is not changing, nor that the atmosphere is in thermal equilibrium with the surface (or any other part of the atmosphere).
It means that the speeds of the gas molecules follow the Maxwell-Boltzmann distribution.
And as a result the Planck equation, for emission of thermal radiation, holds true.
More about LTE in Planck, Stefan-Boltzmann, Kirchhoff and LTE.
..And the atmosphere is in LTE below 70km for most molecules in the atmosphere.
Perhaps a bit more formally, that the distribution of population in all modes of motion can be described by the same temperature. Note that this excludes the radiation field. Chemists tend to do that, physicists not so much.
The ease with which nonsense can be translated into equations affords a splendid means of impressing the majority of the population who cannot read equations.
This opens up exciting new careers in demagogy for those who can do both
The ease with which nonsense can be translated to scientific-looking rethoric (=blah blah blah) affords a splendid means of impressing the majority of the population who cannot really grasp the science.
This opens up exciting not-so-new careers in demagogy for those who can do at least the rethoric bit.
Remember, Russel: at least equations can be tested. Anything against that?
DeWitt Payne…..February 6, 2012 at 6:43 am
Thanks very much for your very detailed description of the inner workings of a pyrgeometer….I think I got it.
The hot junction of the thermopile radiates via the lens toward space. Simultaneously, hot junction conducts heat to the cold junction via the thermal conductive insulator. This conduction induces a potential difference, which corresponds to temperature (previously established). This temperature is plugged SB equation to calculate a flux.
The cold junction sinks to the block. This temperature is taken, plugged into SB equation and it’s corresponding flux is calculated
Now, if the pyrgeometer could radiated directly to space, the block temperature will drop (equal to the cold junction)…the conduction, via the thermal conductive insulator, will be from the block side to the hot junction. These two fluxes will be equal and opposite translate to 0 W/m^2 DLR.
If GHG are in the line of sight of pyrgeometer, DLR incident on the lens will offset some of all radiated via lens. Therefore, a positive DLR will be calculated.
Do I have this right?
If I read you correctly, then that’s about right. However, I think you would run into linearity/calibration problems long before the DLR reached zero. For one thing, the dome covering the pyrgeometer sensor or the lens in a hand held IR thermometer has some emissivity. As a result of this, the dome temperature in a pyrgeometer is measured and its emission is included in the calculation of observed DLR. Hand held IR thermometers also have lower temperature reporting limits because of this. The standard lower limit for the inexpensive models is either -20 or -60 C. A pyrgeometer is probably most accurate when there is no flux into or out of the block. This happens most often for a cloud covered sky. The sky can be warmer, i.e. have a higher Teff, than the surface if there’s a temperature inversion. Clear skies, OTOH, usually have a lower Teff than the surface.
DeWitt Payne wrote:
“A pyrgeometer measures the total radiation flux from a hemisphere impinging on a flat surface integrated over all wavelengths. In fact, that’s the number usually quoted for DLR in units of W/m². The direction is simply perpendicular to the plane of the disk. You also see flux in units W/m²/cm-1/sr or W/m²/μm/sr. That’s the number you calculate with the Planck equation. To get the total flux in a hemisphere you integrate over the wavelength range and multiply by π. The factor of two disappears because the area of a hemisphere is twice the area of a disk of the same radius. The W/m² number is also the same as the flux between two parallel planes of infinite extent.”
If I understand correctly, you are saying that a pyrgeometer is recording radiation (integrated over all IR wavlengths) from all directions of the “hemisphere” of atmosphere overhead in units of W/m²/sr and we simply divide by two to get W/m2?
The diffusivity factor used to convert spherical radiation to plane-parallel radiation is therefore a totally different subject and not relevant to this situation. (Reviewing the subject, the diffusivity factor seems to be a correction factor applied to the vertical component of the path length to produce the full path length and appropriate absorption, emission and scattering along that path length.)
Do you believe that any flat sensor is going to have equal sensitivity to radiation coming from both steep and shallow angles? I guess we need to know how the absorptivity of sensor varies with the angle of incidence.
Frank,
You don’t divide by two, you multiply by π to convert, after integrating over all wavelengths, W/m²/sr to W/m²
Frank,
It’s a bit tedious to reproduce the maths (the maths isn’t tricky but all the definitions and integrals are painful to write out), but think of it like this..
If you had a hemispherical surface (half a sphere) radiating out, the hemispherical power would have 2π steradians of solid angle, because all directions have equal power.
Now consider a flat surface radiating out. Directly above you get the “full power” but at almost 90′ (π/2 radians) you get almost no power because of the angle. Here’s a not great graphic from Incropera & DeWitt (2007):
So if you integrated the spectral intensity, I, from a hemispherical surface the total hemispheric emissive power, E, would total up to E = 2πI
But if you do the same from a flat surface, because you are integrating the same relationship with a cosθ in the equation, E = πI
The total emissive power is half what you might expect at first sight from the number of steradians in a hemisphere but this is actually what you measure. The calculation (the integral) just clarifies why the measurement is what it is.
As you correctly comment, the surface needs to be “diffuse” – emissivity/absorptivity not a function of direction.
I’ll let DeWitt comment on the specifics of the pyrgeometer.
On the diffusivity factor..
This is a mathematical approximation which allows us to use the 1D solution to the radiative transfer equations for a hemisphere. So it’s something different.
Integrate the equations over a hemisphere and replace the optical thickness with optical thickness x the diffusivity factor and voila.. all in the radiative transfer equations link.
Dewitt Payne
I thank you for your intervention.
My argument is better presented within a simple model – a body suspended in a vaccuum enclosed by impervious walls. Entropy law says that, irrespective of the body’s initial temperature, the system (walls, body and electromagnetic field) will reach thermal equilibrium at which time the wall and body temperatures are constant and equal. Radiative exchange theory posits accompanying dynamic radiative balance, the body receiving as much energy from the walls as it radiates to them. The theory holds for blackbody walls and bodies, but fails with assignment of different surface emissivities and absorptivities. Introducing the energy field into the analysis allows dynamic radiative exchange between the field and the walls and body, independenty. Why nature would exchange energy in this nil-result way is unclear. The more natural outcome, cessation of radiation at thermal equilibrium, has been attributed to Prevost:
“Pierre Prévost’s theory of heat and radiation exchange, stating that cold is the absence of heat, hot bodies radiate continually and that a lack of radiation indicates equilibrium with surroundings temperature”. (www.omega.math.albany.edu)
The apparent internal contradiction – “hot bodies radiating continually”…..”lack of radiation” disappears when “hot” is taken in the relative sense rather than the absolute – hot relative to surroundings.
Not needed. Problem has been long thought of and that’s why they sell integrating spheres
SoD from February 5, 2012 at 6:45 am
It’s absorbed…and re-radiated. It does not however, increase the surface temperature beyond current brightness. That is, all power is not the same. Before you retort Blah…Blah…Blah, consider the the photoelectric effect. As you are aware,
“The energy of the emitted electrons does not depend on the intensity of the incoming light, but only on the energy or frequency of the individual photons.“
So the frequency of the incident radiation is the pertinent variable, not the magnitude of the flux.
Umm, the photoelectric effect is not relevant. You need a surface in a pretty good vacuum to observe electron emission caused by absorption of radiation. OTOH, you can get thermionic emission of electrons from a heated filament with no absorption of radiation (also in a vacuum). That’s how vacuum tubes work, as opposed to photomultiplier tubes. Thermionic electrons have a continuum energy spectrum unlike photoelectrons.
L.J. Ryan,
So let’s now write down the equation for emission of thermal radiation, Er:
Er = εσT4
At least that’s what we find in textbooks on radiative heat transfer.
But what you are saying is that Er is not a function of T. Or at least changes in absorbed radiation somehow allow Er to change without any temperature change. You are saying that the change in absorbed radiation is just reradiated without any change in surface temperature.
Perhaps you propose:
Er = εσT4 + αΔRL↓
where ΔRL↓ is the change in downward longwave radiation.
Is that what you are proposing?
[moderator’s note – retrieved from the spam queue]
DeWitt Payne Feb 7,
Thank you for your intervention.
Testing the theory of radiative exchange is clearly better attempted with a simpler model than the surface-atmosphere one – a body suspended in a vaccuum within impervious walls. Entropy law says that, irrespective of the initial temperatures of the walls and body, the system (walls, body and electromagnetic field/photon gas) will come to thermal equilibrium. Then, the temperatures of the walls and the body will be equal and constant. Exchange theory posits an accompanying dynamic radiative equilibrium – the body gaining as much energy from the walls as it loses to them. The theory holds for blackbody walls and body. It fails when different emissivities and absortivities are assigned to the radiating surfaces.
Introducing the electromagnetic field into the analysis allows for dynamic radiative equilibrium between the field and the walls and the body, independently – a localised closed-cicuit energy flow. Why nature would trade energy in this nil-result way is not obvious. The more natural outcome, cessation of radiation, has been attributed to Prevost:
“Pierre Prévost’s theory of heat and radiation exchange, stating that cold is the absence of heat, hot bodies radiate continually and that a lack of radiation indicates equilibrium with surroundings temperature”. (www.omega.math.albany.edu)
The apparent internal contradiction – “hot bodies radiate continually” …….”lack of radiation” disappears when “hot” is taken in relative rather than absolute sense – hotter than the surroundings.
DeWitt Payne
What? Do you mean as an assembled panel or the individual cell manufactured?
Regardless, let me amend my statement of February 9, 2012 at 8:16 pm : In a vacuum, the frequency of the incident radiation is the pertinent factor, not the magnitude of the flux.
BTW do agree with my pyrgeometer description of February 8, 2012 at 4:48 pm .
Sod
Before I answer your proposition, let me ask you a question How is that radiation actually confers heat in the surface? Does it not require the excitation of electrons within the surface molecules?
Scienceofdoom,
A good deal of comment relates to “observation” by pyrgeometers of longwave radiation from the sky of around 300 Wm-2 (DLR) providing incontrovertible evidence of atmospheric backradiation and the greenhouse effect. I find the evidence uncompelling for two reasons.
First, the instrument reading is in fact the arithmetical sum of an observed X flux and the computed S-B surface flux. KippZonen, an instrument maker, gives X values (negative) ranging from 5 to 90 Wm-2 for overcast and clear sky conditions, respectively. Stoffel reports pyrgeometer precision of +/- 15 Wm-2 or 30% of X for average sky conditions.
Second, the instrument is programmed to give an X observation consistent with DLR. This can be seen in the linear regression equation used in the calibration process which takes the form:
Wbb = K0 – K1*V – K2*(S-B)r – K3*{(S-B)d – (S-B)r}
where Wbb denotes the blackbody radiation from the calibrating radiating hemisphere;
V denotes the instrument’s thermopile output voltage;
(S-B) denotes the well-known equation relating energy flux and temperature;
the subscripts “r” and “d” denote the instrument’s receiver-detector plate and dome, respectively; and
K0 and Ki (1-3) are, respectively, the constant and coefficients to be derived from the regression.
That is, the sky is modeled in the pyrgeometer as a blackbody surface radiating according to its temperature; and the model output faithfully “observes” that to be the case.
Specifying the regression equation consistent with thermodynamic law, energy flowing in one direction only, from hot to cold, would produce a different set of coefficients in the laboratory calibration and, hence, a different reading in the field.
Nope. Net energy flow in a pyrgeometer is only from hot to cold. A pyrgeometer only measures net energy flow. You can convert the measurement into an effective temperature using the SB equation, but that doesn’t mean that a pyrgeometer requires the atmospheric emission to have a black body spectrum, only that the detector emits and absorbs as something close to a black body with reasonably constant emissivity over the wavelength range of interest. And, of course, it does.
I agree with what you say. I make a different point. If I understand Tom Stoffel correctly (ARM Pyrgeometer Calibration and Field measurements; p24 Appendix. Tom Stoffel December 2005),
calibration involves regressing Wbb against V, (S-B)r, {(S-B)d – (S-B)r} to estimate the coefficients Ki (1-3).
An alternative regression, say, {Wbb – (S-B)r} against V and {(S-B)d – (S-B)r}
would yield coefficients Ji (1-2).
I would expect that two pyrgeometers calibrated with the alternatively specified regression equations would produce different DLR values in the field.
In another thought comparison, what difference in DLR, if any, would you expect from two pyrgeometers, one without the dome, that is, open to the atmosphere?
The dome is critical in two ways. For measuring DLR, it has an interference filter coating that transmits wavelengths from ~3.5-50μm while reflecting shorter wavelength radiation. Without that coating, the device would respond to short wavelength diffuse and direct solar radiation as well as long wavelength atmospheric radiation. Those are important data in their own right and are measured separately. But the most important reason for a dome is to minimize heat transfer by conduction/convection so the instrument isn’t sensitive to wind velocity.
A typical instrument array mounted on a solar tracker can be found here: http://www.eppleylab.com/ (select ‘shading devices’). The instruments are a precision infrared radiometer (pyrgeometer) and a precision spectral pyranometer with shading disks. The shaded pyranometer measures diffuse solar radiation. Direct normal solar radiation is measured with a normal incidence pyrheliometer and an absolute cavity radiometer. For complete measurement of the local radiation budget, you would need another pyranometer and pyrgeometer pointed at the ground to measure reflected solar radiation and upwelling long wavelength radiation.
Your assertion in the absence of actual calculations has no merit. Any difference would have to be small and probably be caused by fewer adjustable parameters in your equation. The calibration equations used provide results that agree with independent measurements using FT-IR spectrophotometers. Both are in agreement with spectra calculated using the radiative transfer equations.
So John Millet, go buy an IR thermometer from your local electronics store.
When you take the IR thermometer out of its box and turn it on and point it at the sky, what is it you think you are measuring?
When you point that IR thermometer at your hand, what do you think it is measuring? Does that temperature correspond to body temperature? Does that temperature change when you point it at someone from a long distance or short distance? As long as the person covers the instrument’s field of view.
Point the thermometer at the ground. What is it measuring?
Point it at the horizon. What is it measuring?
Increase the angle at 10 degree increments until you point straight up. Measure the temperature each time. Do the temperatures you find at increasing heights correspond to the lapse rate?
Take a big sheet of cling film and stretch it over a frame. Measure the temperature of the sky through the film. Is the temperature you get the temperature of the film or the temperature of the sky?
So John, less philophising and more hands on for you.
I would add that after measuring through the cling film, measure through a sheet of glass. And also measure the temperature of something hot through the cling film and through the glass.
SoD
I asked :
“How is that radiation actually confers heat in the surface?”
and
“Does it not require the excitation of electrons within the surface molecules?“
Since you have not replied, I assume you agree with the poignant
context of the questions; In order to confer heat to the surface, radiation must excite the electrons within the surface molecules.
So similar to photoelectric effect, frequency of the incident radiation is the pertinent variable, not the magnitude of the flux. The DLR. as you submitted, has insufficient energy raise surface temperature. Looking specifically at 700 cm^-1 and using the equation Ephoton =hc/l (lambda), the corresponding energy is .086 eV. Now I realize, IR can not excite an electron from ground to n2 state, but the partial increase will have to be greater then the partial increase already realized via solar radiation. That is, if SW radiation translates to 1 eV, a parallel input of .086 eV does not result in 1.086 eV,..parallel inputs differ to the higher potential.
L.J. Ryan,
Poignant. Very nice.
By the way your explanation is not quite correct. In order for a photon to be absorbed the energy of the photon must match the changed energy state of a molecule. This is usually rotation/vibration energy changes.
E=hc/λ is a correct equation. To complete the picture you need to know whether any photons can be absorbed at a given wavelength, λ.
And if any photons can be absorbed, what proportion are absorbed. This is called the absorptivity and is a function of wavelength:
Absorptivity, α(λ)
You incorrectly claim (as far as I can tell what you are claiming from your statement) that the absorptivity of a typical earth’s surface is zero for wavelengths typical of the atmosphere.
You can look up absorptivity in a textbook. It is experimentally measured.
Here is the reflectivity (left vertical axis) of some typical surfaces at a range of wavelengths, and absorptivity = 1- reflectivity:
From Fundamentals of Heat and Mass Transfer, Incropera & DeWitt (2007)
If you were correct then snow, for example, would have a reflectivity of 1.0 for wavelengths around 5-20 μm. But it doesn’t. In fact, snow reflects solar radiation quite well but absorbs most longwave radiation.
Water has a very high absorptivity in longwave as well. Note that emissivity = absorptivity for the same wavelength and direction:
From The Emissivity of the Ocean.
Solids and liquids absorb across a continuum of wavelengths, unlike gases which have sharp absorption lines corresponding to changed rotational/vibrational energy.
I’m going to hazard a guess that you have never looked up absorptivity/reflectivity in a textbook and that these graphs are a surprise to you.
SoD
I’m aware of absorptivity…and reflectivity and emissivity. I am not suggesting the earth’s surface has zero absorptivity. What I am suggesting, absorption of flux does not necessarily translate to a increase in temperature.
If you were correct and absorptivity was the sole determinate factor, snow would melt with an overcast sky.
Do you not agree with transition levels within molecules?
No, it wouldn’t. The effective temperature of a cloud layer is almost exactly the same as the surface. Most sunlight that penetrates the cloud layer will be reflected by the snow. Unless there is warm air coming from somewhere, or it starts to rain, there will be insufficient energy to melt snow.
L.J. Ryan,
So it’s not possible to understand your series of statements from February 14, 2012 at 7:17 pm.
I tried to help you out on February 9, 2012 at 9:01 pm by proposing an equation for your emission of thermal radiation.
Either absorptivity at atmospheric wavelengths (5-50 μm) = 0.0, or emission of thermal radiation has a different equation from what we find in textbooks.
I have already written down the relevant equations and people like yourself show up and say “blah blah blah” – but no equations.
You have produced an equation for the energy of a photon, which is a real equation. But that’s it.
Please write down your ideas as a series of equations, and provide graphs or values for relevant coefficients used within this series of equations.
Let me help you with a list:
Given DLR from the atmosphere, RL↓
1. Provide a graph, range of values or average value for absorptivity of the ocean for the range of wavelengths of RL↓ (as over 70% of the world’s surface is ocean this should be a good start).
2. Energy absorbed by the surface, Ea = ?
3. Energy radiated by the surface, Er = ?
Should be so simple. You have the floor.
LJ Ryan,
Your following two statements are in direct contradiction:
“I am not suggesting the earth’s surface has zero absorptivity.”
“It’s absorbed…and re-radiated. It does not however, increase the surface temperature beyond current brightness.”
If the effect of your theory is that radiation is absorbed then re-emitted at particular frequencies, then that is equivalent to stating that absorptivity is zero at those frequencies.
If you write these statements as equations, this becomes apparent.
You also comment
“That is, if SW radiation translates to 1 eV, a parallel input of .086 eV does not result in 1.086 eV,..parallel inputs differ to the higher potential.”
This suggests to me that your theory is that where there are two or more bodies radiating heat, the radiation absorbed at any given frequency (or summed over all all frequencies?) by a third body is represented by the largest from any one of the other bodies, rather than the total sum from all of them.
Is this correct? If it is, I suggest you consider applying reductio ad absurdum to help you see if it’s true or not.
It would really help if you could respond to Sod’s challenge and formulate as an equation as that would help elucidate your true intent.
Oh, and “poignant”. Indeed.
VeryTallGuy
Umm…correct? For a given frequency, surface absorptivity does equal surface emissivity.
α(λ) = ε(λ)
If one heating element in my oven radiates at 400 F and the other radiates 200 F, the cast iron pan on the rack will not reach 600F. Tell me VeryTallGuy, what’s the max temperature of the pan?
Ah, that explains it and it’s a great examples of why equations really are much better than “Blah Blah Blah”
Your *text* says that with an additional heat input from a third body, the same amount of energy will be remitted from the surface *without a corresponding increase in temperature*.
Whereas your equation says that absorptivity and emissivity are the same at the same wavelengths. Which I agree with.
If the surface was originally in equilibrim, both receiving and emitting Qo w/m2, at temperature To then
Qo=(emissivity)(sigma)To^4
If an additional Qe is added by radiation *at any wavelength whatsoever*, then the surface balance changes to
(Qo+Qe) = (emissivity)(sigma)Te^4
And we can see that Te must be larger than To, to compensate for the extra incoming radiation.
Well we haven’t yet seen the complete series of equations from L.J. Ryan.
We have only seen two equations from L.J. Ryan –
1. the energy of a photon
2. emissivity = absorptivity (at a given wavelength)
Probably we won’t a complete series.
So what about the collective might of all the blogs conceived in liberty and dedicated to the proposition that no energy from the atmosphere can affect the surface temperature?
[I could provide a list of these blogs but I’m sure readers already know them].
Can’t the many valiant upholders of the truth, defenders of science, protectors of the (imaginary) second law of thermodynamics, destroyers of the ridiculous claims of climate science – band together for this one simple task?
Write down a few equations as already described?
Surely it can be done. Just a few equations?
Returning to sanity now, as already predicted, no one will show up to answer this call.
More “blah blah blah”. But no equations.
I hope this outcome helps the many with inquiring minds who are not sure of the correct answer.
Not sure what the purpose of the pan analogy is – the pan cannot get above 400F. It might get above 200F, depending on geometry, insulation etc.
But all this tellls us is that the surface of the Earth can’t get higher than the hottest known object in the universe.
L.J. Ryan,
If you have three bodies.. then it is different from the two body problem.
The two body problem is simple – the temperature of the hotter body moves towards the colder body, and the temperature of the colder body moves towards the hotter body.
Everyone knows this and no one disputes it.
Advocates of the (imaginary) second law of thermodynamics tirelessly repeat the example that everyone agrees with in the manner of “ha, got ya”. Never wondering why it is that everyone already agrees with them.
Sadly missing the point that the elephant in the room is the third body.
With the sun, the earth & atmosphere.. (count them, three bodies), if the colder atmosphere cannot increase the temperature of the surface of the earth compared with a much colder 3K background radiation (no atmosphere) scenario – then it should be so easy to find a flaw in The Three Body Problem.
In this example the first law of thermodynamics and the second law of thermodynamics are shown to be preserved.
As I said in that article:
And in a very nice demonstration of my claim, over 170 comments followed. Many of these were from the “against greenhouse coalition” yet not a single person provided a calculation to show that the second law of thermodynamics was violated.
I had shown that entropy increases in all cases.
Why has no one done the calculation to prove me wrong?
Because readers, the “against greenhouse coalition” have a conceptual problem but no clue about the real second law of thermodynamics.
If entropy increases, the second law is not violated.
Can any “against greenhouse coalition” members actually do maths and calculate it? A scientific person would say “oh, I have reproduced the results and entropy increases, so therefore the second law of thermodynamics is not violated“.
A non-scientific person says “I don’t like the result, blah blah blah”.
Just like in this article.
– Prediction 1 – so far correct.
– Prediction 2 – so far correct.
The defence rests. (For now).
That’s easy!
since the oven has a thermostat… 400 degrees! if left on long enough, the pan should reach equilbrium with the heat source, and since the thermostat keeps the oven at 400 degrees…..so goes the pan…
will this work even if the oven leaks heat? NO! your badly manufactured oven will work and work but never cook at the proper temperature..
hmmm.. that’s like a metaphor.
DeWitt Payne February 10, 2012 at 9:43 pm and February 15, 2012 at 4:33 am
and
So if understand you correctly, when surface temperature equals overcast sky temperature, flux exchange is equal and opposite…as such the snow covered surface remains frozen.
This however, seem contrary to Idealized greenhouse model. That is, the model formulates a colder atmosphere warming a still warmer surface; while the cloudy sky, pyrgeometer calculated, DLR is greater, it provides no warmth.
SoD
Agreed. So a CO2 molecule energize via 750 cm^-1 photon stream can simultaneously be energized by a 650 cm^-1 photon steam? Do these energies combine ie .174 eV…then radiate like water ~ 1400 cm^-1?
L.J. Ryan,
We were discussing the solid/liquid surface absorptivity.
Onto your question about gases – what happens is that a CO2 molecule absorbs a photon and so its internal energy is increased by the energy of the photon, E=hv or E=hc/λ. Long before it can reemit a photon corresponding to this energy increase it collides with other air molecules and this energy is “thermalized”.
Here is a good explanation from Infrared Radiation and Planetary Temperatures by Pierrehumbert in Physics Today:
A photon is absorbed, increasing its energy.
The energy is shared with other molecules via collision which becomes translational energy which is temperature.
So absorbed photons increase the temperature of the gas.
Radiatively-active molecules in the gas emit photons according to their temperature and the specific allowable energy states (the spectral lines of absorption and emission).
So a 15 μm photon absorbed does NOT cause that molecule to reemit a 15 μm photon.
None of this is the slightest bit controversial – in the fields of radiation and spectroscopy.
Of course, in the blog world where people learn their physics from blog writers who haven’t read a textbook it is a different story. That’s not physics controversy.
SoD
Ok. So if CO2 does not reemit the15 μm photon absorbed , then how does CO2 radiate at said wavelength?
L.J. Ryan,
I’m not sure where to start.
Here you are confidently asserting all kinds of novel ideas about absorption and re-emission that aren’t found in textbooks and then.. this question.
Are you asking it because you think it is too tricky for me and then you will provide the real answer? Or you have no idea?
And here I was waiting for you to provide a series of equations for your claims.
Emission of radiation from an object follows the Planck law for a blackbody, which is a function of temperature and wavelength, modified by the emissivity, which is a function of wavelength.
The Planck law is an equation which describes the spectral intensity of a blackbody, B(λ,T) in units of W/(m2.sr.μm) – note this version is for wavelength λ, there is an alternative version for wavenumber.
So emission of radiation, E(λ) = ε(λ).B(λ,T).
That’s the mathematical description.
What do you mean “how”?
A CO2 molecule changes from one energy state to a lower energy state, where the difference is the energy of a 15 μm photon, and emits a 15 μm photon.
L.J. Ryan says
Ok. So if CO2 does not reemit the15 μm photon absorbed , then how does CO2 radiate at said wavelength?
————
Because the process by which an excited CO2 molecule gives up it’s energy to surrounding molecules acts both ways.
1. When a CO absorbs an IR photon it vibrates more vigorously. After a short time these vibrations give surrounding molecules a kick and the excess vibrational energy is transferred to it’s neighbors.
2. But a CO2 molecule just sitting there also receives kicks from its neighbors who are themselves, whizzing and spinning about. These kicks can sometimes cause the CO2 molecule to be sufficiently excited that it vibrates more vigorously. In that condition it can emit an IR photon of the same energy it may have absorbed in the past.
SoD
You missed the question regarding CO2…from February 16, 2012 at 5:55 am
I wasn’t asking about energy dissemination to other molecules. I was asking about an already, relatively old, energized CO2 molecule absorbing additional energy from a slightly longer photon stream. Does the CO2 further increase energy to reconcile newly absorbed photon?….a photon within α(λ) for CO2
L.J. Ryan,
Your questions are undoubtedly poignant.
Statistical thermodynamics is all about the properties of large numbers of molecules. Not about trying to track one molecule called Colin and one photon called Jane and say what happens.
If a molecule absorbs a photon of energy E, its internal energy increases by E. This is true regardless of what has happened on its journey before.
Whether it will absorb a photon of energy E depends on whether E corresponds exactly to the quantized energy involved in a rotational/vibrational change for that molecule.
If a molecule emits a photon of energy E, its internal energy reduces by E. Whether it will emit a photon of energy E depends on the same principle as for the absorption.
In a gas of sufficient pressure that collisions are common enough the energy in the gas is “spread out” such that the Maxwell-Boltzmann distribution applies. When this distribution applies lots of other equations become valid. When this distribution doesn’t apply lots of other equations are not valid. It’s statistics. Not “a day in the life of a photon and Colin”.
I am guessing from your strange question that you have some idea about tracking photon movements and applying statistical thermodynamics to one molecule to create some Reductio ad absurdum. But I might be way off base.
Your question is not clear.
From your “tone” you have a theory. Why not share it?
Using an equation for your theory will bring much joy.
Eli is rather more blunt than SoD. There are NO old energized CO2 molecules. Energized CO2 molecules loose their energy by collisions much faster than they can radiate. However, a small number of CO2 molecules have two quanta (or more) of excitation gained by high energy, low probability collisions with other molecules. Let’s start with a simplified spectroscopic picture.
CO2 has three vibrational modes, the bending mode at ~700 cm-1 being the principal one that we have to deal with when talking about absorption and emission of radiation in the atmosphere. This mode can have zero, one or two or more quanta of excitation and we can approximate the energy in that mode by
Ev = hn (v+1/2)
where h is Planck’s constant, n the frequency of the vibration and v an integer from 0 up. (There are anharmonic terms in the energy expression, and we will discuss them later)
There is what is called a selection rule for radiative transitions, that v can only change by one, +1 for absorption and -1 for emission. Of course, v can change by more than +/- one in a collision and anharmonicity makes +/- 2 radiative changes possible, but very weak, weak enough to ignore for our purposes, but they are handled in the radiative transfer codes
At 300K, about 6% of the CO2 molecules have v=1 and about 6% of that, or overall ~0.36% have v=2. The transitions we would see in emission are 1–> 0 and 2–> 1. 2–> 0 is essentially forbidden (very very weak, see anharmonicity above).
In both cases, as SoD says, the energy quickly is degraded to kinetic energy by collisions with nitrogen and oxygen
SoD and VeryTallGuy
My example and statements are consistent. SoD says those of us dubious of DLR are not recognizing the elephant in the room…the atmosphere. Well in my example, the two of you missed the precious third body.
Body1 = heating element at 400 F
Body2 = cast iron pan with ε= 1
Body3 = heating element a 200 F the elephant
Body2 is placed in the oven Body1 is powered on. When LTE is reached both Body1 and Body2 are radiating at 400 F. Body3 is now powered on.
Blah…blah…blah equations:
Qb2 = εσTb2^4 = 2950 W/m2 prior to Body3
Qb3 = εσTb3^4 = 1023 W/m2
(Qb3+Qb2) = εσTb2^4 …. as stated by VeryTallGuy
[(Qb3+Qb2)/εσ]^.25 = Tb2 = 415K = 465 F
“And we can see that (Tb2) must be larger than (Tb1), to compensate for the extra incoming radiation. “
Poignant indeed!
Now, can you convince yourselves the true, non-calculated, temperature is 465 F. Wait, true temperature relative to Body1.
LJ Ryan,
in your example, you have forgotten a 4th body, the walls of the oven, and not taken geometry into account.
The only way the pan can reach 400F with a maximum temperature heat source at 400F is if the oven is perfectly insulated, and it’s walls are therefore themselves at 400F. The pan receives radiation from both the heating element and the walls.
If you now introduce your 4th body at 200F it will actually *reduce* the temperature of the pan slightly (by shielding from the walls at 400F), until it too comes to equilibrium at 400K.
For the earth’s climate remember the surroundings are at a temperature close to zero K, *not* in equilibrium with the surface or atmosphere.
On the equations themselves, your most basic errors are to work in fluxes rather than flows and to omit geometry. Not *all* the heat emitted from any of these bodies impinges on the others (geometry) and the amount of energy emitted depends on the surface area.
All this is very well understood, and used routinely in the design of furnaces and the like. You really don’t need to invent new physics from scratch to understand it.
Good luck.
You are pouring energy into the heating elements. You have to account for that. You have not.
L.J. Ryan,
As VeryTallGuy points out, your confidence greatly outweighs your understanding of the very basics. Well, it’s clear you have never read a textbook on radiative heat transfer.
Pronouncing success via proving a point based on the premise of being ignorant of the basic theory – does this have a word?
It should. And it should rhyme with poignant. Hopefully any literate readers fascinated by watching someone blunder around the room knocking over various objects and breaking them can provide linguistic insight.
Let’s review this fascinating example.
Assumption A. The walls of the oven are perfectly insulated.
Assumption B. The walls of the oven have emissivity, ε=1 (we need something here)
Assumption C. At time t1 (prior to putting energy into body 3), the whole oven has reached 400F (204.4’C)
Assumption D. At time t1 you “turn on” the element, body 3.
Proposition i. Because the whole oven has reached 204.4’C at time t1, all parts of the oven are radiating 2949 W/m2.
Proposition ii. At the start of the experiment, time t0, body 1 is emitting 2949 W/m2 but this is NOT the power absorbed by body 2. You need to know the view factor – which is the proportion of all that radiation which leaves surface 1 and strikes surface 2. You can read about it (please read about it) in the wikipedia link provided.
Proposition iii. However, with our perfectly insulated oven and enough time eventually the whole oven must reach the temperature of body 1, the 400F (204.4’C) element.
This is because there is an external source of energy being continually provided to body 1 (and some automatic control to ensure the correct temperature is reached and not exceeded – or it is a very large external thermal reservoir at 400F connected into body 1 from outside).
Proposition iv. If instead, at time t0, we had body 1 at 400F with no external source of energy and the oven, body 4 at say 70F, then the final result at time t1 (prior to putting energy into body 3) would be the whole oven at some intermediate temperature between 70F and 400F.
Question 1. What exactly do you mean “turn on”? Body 3 is already at 400F. How can you turn it on? Are you sucking energy out of the oven, so it has a cooling capability? Or are you somehow adding more energy?
Proposition v. If body 3 (the now inappropriately-named “200F element”) adds additional energy into the oven then it can only do so because there is something hotter than 400F supplying it.
Proposition vi. If instead we imagine a very large thermal reservoir at 200F connected outside the oven, then “turning on” body 3 means that heat is transferred from our 400F reservoir (the oven) to the 200F reservoir (the source of body 3 called “the 200F element”). Otherwise the 2nd law of thermodynamics has been violated.
L.J. Ryan, please correct assumptions, answer the one question and challenge propositions as appropriate.
In summary, you have assumed the 2nd law of thermodynamics is violated (a 200F reservoir transfers heat to a 400F reservoir) and the end result in your proof is that the 2nd law of thermodynamics is violated.
This result is unsurprising.
Or you have assumed that the external source of the “200F element” is hotter than 400F (no second law violation, but a strange naming convention) and are now surprised to find that the oven ends up hotter than 400F (because you were confused by your own naming convention).
Poignant!
Try working through The Three Body Problem and check conservation of energy and increase in entropy. The calculations are there.
This would mean taking a huge step and wondering if you are wrong. Unlikely given the great prowess you have already demonstrated in this subject. But just humor everyone and do the calculations. And report back.
As a note, the sun and the earth are not in thermal equilibrium – this is very important – so if you want to do an oven example of the Three Body Problem you start with a non-closed system.
And you compare two examples, one with a “super cold” outside temperature and one with a “just chilly” outside temperature.
Surprisingly, the steady state temperature inside the oven will be warmer when the outside is “just chilly” than when the outside is “super cold”. (It is impossible for the steady state temperature to be the same in both cases unless the first law of thermodynamics is wrong, or the equations of conductive, convective and radiative heat transfer are all wrong).
VeryTallGuy & SoD
Agreed! Yes Body3(4) will reduce the temp and real world applications follow this know principle.
Yet the calculations, via the equation you provided, the same equations used to model “greenhouse” effect, say Body3(4) will reach 465 F. Oh yes, you wish to add a fourth body (walls) and include view factor. Ok.
Body1 = heating element at 400 F
Body2 = cast iron pan with ε= 1
Body3 = heating element a 200 F — the elephant
Body4 = oven walls with ε= 0 — the second elephant
oven dimensions .5m
oven shape cubic
Blah…blah…blah equations
Now we can go through the calculations using your equations, but the result is the same. When Body3 is powered on, additional flux is cast upon Body2…so according to your equation :
(Qb3+Qb2) = εσTb2^4
and since Qb3 is > zero Tb2 will be > 400 F.
Your equations confounds reality.
Note: I started typing this response before getting called away, so the posting was initially addressed to VeryTallGuy solely. Now that SoD has contributed a retort, I thought it necessary to include a time reference..everything henceforth come 20 minutes after reading SoD posts.
prop I. Ok
prop ii. As you stated in prop I. Body2 is already radiating 2949 W/m2 so view factor is irreverent.
prop iii. As stated above Body4, ε= 0. Body1 temperature has no control feedback but rather a fixed electrical input.
prop iv. Not relevant
Question 1. Good point. Again like Body1, Body 3 has no control feedback simply a fixed electrical input.
prop v. “it can only do so because there is something hotter than 400F supplying it.” wait a minute…sound as if your quoting the imaginary 2nd law.
prop vi. I completely agree! Though the equations, as I explain above, say otherwise.
You still haven’t grasped the basics of your mistake.
– What temperature is body 3 at time t1?
[And as a side note if the emissivity of body 4, the walls of the oven = 0 it changes some of the propositions slightly, but is not important at the moment]
SoD
“- What temperature is body 3 at time t1?”
400F.
And what temperature is body 3 after time t1? (Let’s ask for the steady state temperature)
Sod “And what temperature is body 3 after time t1? (Let’s ask for the steady state temperature)”
Well…the real world temperature 400 F. The calculated, power is power, equations rule despite reality temp, >400 F.
Sorry for not providing more clarity,but this is very much the problem I have with parallel input energies to the surface….reality vs. blah…blah…blah equations.
L.J. Ryan,
The problem you have is you are confused about your own problem.
I think you are saying it will stay at 400F in the real world, but you think that applying equations we find (incorrectly) that it gets hotter?
What is this magic device, body 3, the “200F heating element”?
Can you describe it?
You have probably misapplied equations to make the thought experiment hotter than 400F. But until you describe this body 3 it isn’t clear what the correct equation is, or what the right answer is.
(The correct equation always leads to the right answer, which is why heat transfer textbooks always agree and students of the field are able to design heat exchangers).
Body 3 was radiating at 2,949 W/m2 at time t1 (because you had externally heated it to 400F), and at time t1 you do something to it. What is it that you did?
Learning heat transfer, people start with conduction because it is simplest.
If you take a look at the worked examples in any heat transfer textbook they start with simple 1d cases where the boundary conditions are well defined.
And the student is taught how to turn a boundary condition in words into mathematical form – in fact it is drummed into you that you have to write down all assumptions and information provided in mathematical form.
Otherwise you can’t solve the problems.
This same practice is of course needed for radiative heat transfer.
Here’s an example of boundary condition definition from Incropera & DeWitt (2007):
The student who is unable to write an equation for boundary conditions will not pass. It is the language of physics and engineering.
And here is a typical worked example for conduction:
Here is the basic concept for solving radiative heat transfer problems, from A Heat Transfer Textbook by Lienhard (2008):
Room for another in the conversation?
Matter to matter application of the S-B equation gave the wrong answer for equilibrium temperature. The anomaly, it was claimed, would be rectified by taking geometry and view factors into consideration – a complicated business.
Far simpler to recognise the fifth element, another elephant in the oven, the electromagnetic field which fills it. And to deal with energy transfers between the field and the various material objects independently rather than directly between the objects.
The direction of the flow of energy across the boundary between the field and the body is determined by the energy density on either side of the boundary. At time t(-1), say, the field’s energy density is determined by the power-supplied body at 400F and the pan and the walls would gain energy from the field until at time t(0) the oven and its contents are in thermal equilibrium at a temperature of 400F.
Introduce the 200F body. It’s energy density is less than the field’s and energy flows from the field into it. It heats up until its energy density equals that of the field and once again the oven and its contents are in thermal equilibrium at 400F.
The reasoning is based on the experimental findings of Tyndall in 1865 and of Dulong and Petit earlier: the rate of cooling of a body is a function of the temperatures of both the body and its surroundings. And temperature and energy density are related in the S-B equation.
Heat transfer is a “complicated business”.
I’m happy when people imply all heat transfer textbooks are a waste of time because “there is a simpler way”.
It helps identify the competence of the person making the implication. And see my earlier comment.
The extract from the textbooks must have been posted as I was composing my comment.
Lienhard includes the medium as an influencing factor if it absorbs or emits radiation; and says that air can be ignored. He says nothing about the ubiquitous electromagnetic field medium which does absorb abd emit.
SOD, why is it unphysical to conceptualise the system, 2 bodies and the surrounding electromagnetic field, as comprising two simpler sub-systems, a body and the surrounding field, in which energy is exchanged?
And, also from A Heat Transfer Textbook by Lienhard (2008), here is a worked example of radiative heat transfer:
Following on from the earlier extracts from heat transfer textbooks.. examples of a closed system in thermal equilibrium (TE) aren’t very useful for heat transfer. By definition, once thermal equilibrium is reached there is no heat transfer taking place. So no useful result can be derived.
In fact the solution for TE is very simple and doesn’t usually need any of the complexity shown in the previous textbook extracts.
But, as soon as a change is made – e.g., a heating element is “turned on” (whatever that means for a boundary condition) – then the equations of heat transfer by conduction, convection and radiation have to be used to calculate the dynamic and steady state conditions.
Students of heat transfer must be able to turn language into equations.
So, “a heating element is turned on”, would be useless.
Instead something like this:
Inserted in the wall of the chamber (geometry of chamber defined), a thin conductive heating block of area A1 and thickness t1, emissivity ε1 has its outside surface kept at constant temperature source, T1 on the outside of the chamber.
And then the question would be asked, for example: Calculate the new steady state temperature at point X inside the chamber and the steady state heat flow through the heating block.
With this more precise definition it would be possible to write down some equations. The whole scenario would need to be defined in a similar way to create the set of equations that would allow the solution to be calculated.
SoD from February 18, 2012 at 6:26 am
“What is this magic device, body 3, the “200F heating element”?”
Umm…a resistor. Specifically, nichrome 80/20 (80% nickel, 20% chromium) wire, ribbon, or strip. Nichrome 80/20 is an ideal material, because it has relatively high resistance and forms an adherent layer of chromium oxide when it is heated for the first time. Material beneath this layer will not oxidize, preventing the wire from breaking or burning out.
L.J. Ryan,
Ok, you want to drag it out, you are “having a laugh”..
So if your heating element is defined as a resistor then you can’t “turn it on”.
You have heated this passive element, via external means, to 400F and when you “turn it on” – words without any meaning – it is still a passive element at 400F.
You called it “200F heating element” – that’s your choice of naming convention. You could have called it “Marilyn Monroe”. No skirt and no blonde hair, just a name for a resistor..
So no heat is added or taken away. So the oven, already in TE, stays in TE.
Unless you want to define what is connected to this resistor. A heat source perhaps? A thermal reservoir? Or just a plain resistor with no connection to anything?
SoD from February 18, 2012 at 7:12 am
I don’t have Incropera & DeWitt (2007) but do have A Heat Transfer Textbook by Lienhard (2008) & Thermal Physics by Schroder (2000) and Electromagnetic Wave by Inan (2000) and Physical Chemistry by Gordon (1988)….the most amazing aspect of all these texts, DeWitt 2007 aside maybe, the limited coverage of greenhouse effect. At most a three sentences.
Oh, and Engineering Electromagnetics by Inan (1999)
What’s amazing about that? Lienhard is about practical heat transfer.
These authors write nothing about stellar interiors so clearly the theory behind stellar interiors is made up..
Or so it seems from your implication..
What would be better would be for you to be able to solve heat transfer problems as a result of reading Lienhard (2008). Step 1 – Having it, Step 2 – Reading it, Step 3 – Solving the problems in it, Step 4 – Understanding heat transfer.
Thermal Physics, by Shroeder will explain statistical thermodynamics to you (if you read it and understand it), and is amazingly well written.
Seeing as you brought it up, here’s Lienhard, obviously bonkers and clearly knowing nothing about heat transfer (don’t even get me started with his chapters on radiative heat exchange where he gets delusional and starts saying that thermal radiation from colder bodies gets absorbed by hotter bodies):
And the fact that Lienhard didn’t write much means he didn’t really believe it, or it wasn’t true and anyway that fact that he is only a Professor of Mechanical Engineering at MIT means he doesn’t really understand the subject.
As your predecessor, Bryan, pointed out, these people are professors of “mechanical engineering” so clearly not competent:
Luckily I was redirected to Siegel and Howell, but we all know how that ended (they were professors of mechanical engineering as well and also agreed with the same fundamental points).
I write these historical points for entertainment value only.
SoD says
“Luckily I was redirected to Siegel and Howell,”
Who SoD implies agrees with SoD that heat can transfer spontaneously from a colder to a surface at a higher temperature.
Perhaps SoD can direct us to the page or pages where this is printed.
We can all then check if SoD can read!
The book is available as a free download!
SoD from February 18, 2012 at 10:00 am
I never said “turn on”…if that’s what bounds you. I’ve consistently said powered on.
Umm….a wall receptacle. A high current recep, but recep.
L.J. Ryan,
“Powered on”, “Turned on”, actually these are the same thing.
I’m confusing you no doubt with this continued request for detail. Why are details so important?
It is: “A high current receptacle”. [ update – my comment about ‘high current source’ corrected shortly afterwards].
So body 3, the confusingly named “200F heating element”, turns out to be a resistor in series with probably a fixed voltage source but high current capability. And some kind of temperature measuring device (bimetallic strip or thermocouple) to ensure that the temperature doesn’t go above 200F.
If it is already heated up to 400F and you connect it in series to this fixed voltage source, with a temperature measuring device, what do you think will happen?
I expect that the temperature measuring device will hold out the voltage source (break the electrical connection) because the temperature of the element is too high.
So nothing will happen.
Of course, depending on the physical connection, it might conduct heat away from the oven to this voltage source. In that case the heat flux out of the oven will depend on the thermal conductivity, cross sectional area, length of wire to the source – and temperature of the voltage source.
What makes you think heat is supplied externally through this device?
Bryan
“Who SoD implies agrees with SoD that heat can transfer spontaneously from a colder to a surface at a higher temperature.
Perhaps SoD can direct us to the page or pages where this is printed.
We can all then check if SoD can read! ”
could I suggest you read the page above from Lienhard posted by sod on February 18, 2012 at 7:12 am
It clearly shows energy flows between two bodies. There is flow in both directions, from hot to cold and cold to hot.
The DLR is a measured flow of exactly this sort.
Just because there is a net flow from hot to cold does not imply no flow from cold to hot.
VeryTallGuy
What do you understand by the word …HEAT?
Carnot, Clausius, Kelvin and other founders of thermodynamics were practical men who wanted to know how to get more work out of engines.
They found that only by operating a heat engine by extracting heat from a high temperature source, doing work and then dumping the unused thermal energy in a low temperature sink could they ever get the engine to do anything.
Thus Clausius framed the second law by saying for a complete cycle that heat will only move spontaneously from a higher to a lower temperature.
So for the nth plus one time
In the case of a purely radiative transfer;
Radiation can be transferred in both directions (highT to low T)
Energy can be transferred in both directions (highT to low T)
Heat which is the difference of the radiative fluxes can only transfer spontaneously from a higher to a lower temperature.
Bryan,
yes, the *ne*t heat transfer is from hot to cold.
Are you aware of anyone arguing otherwise?
VeryTallGuy says
“Bryan,
yes, the *ne*t heat transfer is from hot to cold. ”
There is no ‘net’ heat flow only heat flow.
VeryTallGuy
You VeryTallGuy, are arguing cold to hot heat flow. Remember….
If flux is additive, as you suppose, and temperature is a function of these added fluxes, then heat is transferred from cold to hot.
If you only look at part of a system, you can always make it appear as if some thermodynamic law is being violated. That’s what you’re doing.
If you have two parallel planes at different temperatures with constant energy flux density between them and you increase the temperature of the colder plane, the temperature of the hotter plane must also increase to maintain constant flux. But no net energy is transferred from the colder to the hotter plane and neither the first nor the second law is violated. Assuming the same emissivity for both planes, the solution to the problem is F=εσ(T1^4-T2^4). Not surprisingly, this is the difference between the energy radiated by each plane. Unless photons have additional properties that no one has noticed previously, that means that each plane must absorb all the energy emitted by the other plane at all wavelengths. But each plane only emits a spectrum consistent with its temperature as described by the Planck equation.
One could make the problem more complicated by having the emissivity/absorptivity of each plane be a complex function of wavelength. Then rather than using the Stefan-Boltzmann equation, one would have to integrate the product of the Planck function for the temperature of each plane times the emissivity at each wavelength over all wavelengths for each plane to get the energy emitted. Then one would have to also calculate absorption at each wavelength. If I remember correctly, the photon gas between the planes will have a spectrum equal to the sum of the blackbody spectra for each plane. The end result is the same, though. If you raise the temperature of the lower temperature plane, the temperature of the higher temperature plane must go up to maintain a constant flux.
VeryTallGuy,
Bryan believes there is one, and only one, definition for the term ‘heat’ in thermodynamics. To him, ‘net heat flow’ is doubly redundant.
This is because my university thermodynamics text book was
Heat and Thermodynamics by Zemansky.
Which has the distinction of being the only book recommended by Feynman in his 3 volume lectures.
Bryan has accepted the same equations as me.
The rest is just his cognitive dissonance. It must be painful.
The equations themselves can usually be accepted as a given.
Its the “Blah blah blah” behind the equations that requires scrutiny.
For instance you place a great emphasis on the radiative transfer equations for atmospheric calculations.
Yet people that I respect such as G&T and Joseph Postma think that their use is inappropriate for planetary calculations.
They think that these equations developed for understanding stars are miss applied by IPCC climate science.
I personally have not the time to devote to everything and so this aspect is not a priority.
Just as I feel that you have not studied the Carnot Cycle .
However I am still open to revise my priorities and will ask your outline of a solution using the radiative for my next post.
SoD
So here’s the substantive problem.
The DALR equation is g/Cp
Cp = heat capacity of air at constant pressure.
Now I think we are all in agreement that the radiative transfer equations are not required here.
But my question is why not ?
The CO2 is still radiating as usual!
The best answer I can come up with is that the radiative properties of CO2 are included in the bulk thermodynamic quantity Cp.
If we look at Cp for air there is very little variation between 250K and 350K
However for CO2 the variation is 13% because the rotational and vibrational modes of CO2 are now activated.
These correspond to the 15um and 4um emission/absorption wavelengths.
So if this was a problem posed to a climate science class
1. Outline the use the radiative transfer equations to solve the tropospheric transfer for dry air atmosphere
2. Outline the use the radiative transfer equations to solve the tropospheric transfer for pure CO2 atmosphere.
Does the value of Cp have to be reduced to account for the radiative component removed for radiative transfer.
In practice are there special reduced Cp tables for the use of such calculations.
To get the total heat transfer all methods(convection,conduction included) must be reconciled.
My worry is, if not, there is a large degree of double counting of energy going on.
Bryan
your “substantive” question
“But my question is why not ?
The CO2 is still radiating as usual!”
has, at least as I understand it, a trivial answer – the *rate* of emission from CO2 is small compared to the temperature changes from the work done as the gas rises, to it is ignored for the purposes of this calculation.
To check, you could write an equation comparing the two…
VeryTallGuy
The fraction of CO2, some 380ppm, is indeed small.
The DALR equation also holds for air with a limited amount of H2O also radiating.
So the question holds, at what point do we need to use the radiative transfer equations?
DeWitt Payne
Two points:
1. Your statement seems to question the theory of atmospheric forcing. I read you saying: Photons may in fact be absorbed by a surface with out increasing the surface temperature. Am I understanding you correctly?
2. The equations I used were offered by VeryTallGuy and vehemently defended by SoD. As of yet, SoD and VeryTallGuy have been unable to square calculated temperature with reality. So you won’t find me defending the equations…from the onset, I said power can not just be added together.
LJ Ryan,
I’ve tried to extract from you exactly what it is that you have believe in your thought experiment is “turned on” at t1.
This is because it is important to know the temperature of this device, body 3, before and after t1 – that is, the equation you are trying to use requires the temperature of this device.
And questions about the second law also depend critically on knowing what temperature reservoir is hooked up externally to this body 3.
Your equations suggested that the “200F element” radiated as if it was a 400F body with extra energy from a 200F body, with no explanation about the physical reality of this body.
Well, strictly speaking your equations were already completely wrong for post time t1 because we need the view factor for the various bodies in question as well as the temperatures for each body.
As you will find if you read Lienhard and see the worked examples and problems.
Sadly I don’t see any interest on your part in trying to understand the subject. You think you have a “gotcha” but myself, VeryTallGuy and Eli have all pointed out the same facts. These are basic points in heat transfer.
If, however, you can find in a heat transfer textbook that bodies can radiate energy according to the sum of their previous temperature and their new temperature please draw it to our attention.
I hope the series of comments is a useful record for other readers.
If anyone else has trouble understanding why a body can only radiate according to its current temperature and not according to the sum of previous temperatures it has been at, please ask and I will try and answer.
R ≠ εσ(T14 + T24 + .. + Tn4)
– where R= emission of thermal radiation, ε=emissivity, σ=5.67×10-8, T1..Tn = time series of temperatures for a body.
R = εσT4
– where T= current temperature
This latter equation is found in all good textbooks.
No, it doesn’t and you aren’t. In fact you have demonstrated and continue to demonstrate a total lack of understanding of the physics of heat transfer. You’ve created a strawman that has little to do with what I said by doing exactly what I pointed out was wrong with your previous argument. You’ve isolated a single part of a system in order to create an apparent contradiction. The temperature doesn’t change at steady state because energy in equals energy out. That’s the definition of steady state. If the temperature of one object in a system is changed, the other objects must also change their temperature until steady state is again achieved.
And that’s your problem.
SoD from February 18, 2012 at 10:47 am
As I said no feedback i.e. no bimetallic strip or thermocouple,..just restive heating element. Voltage is predetermined to deliver 200 F.
Ohm’s Law. V = IR P = IR^2 = IV = V/R^2
So where is my error? Perhaps the error is not mine, perhaps the error is with your blah blah blah equation.
So lets have it SoD. Is the equation (Qb3+Qb2) = εσTb2^4 correct and Body2 exceeds 400 F or OR is the equation wrong and therefore the very premise by which AGW is contrived is also wrong?
Your equation is wrong.
If the 200F body is at 200F it radiates less than a 400F body.
The sum of energy received at body 2 depends on the view factors, emissivities and temperatures of each body.
This is the premise of heat transfer for furnaces, boilers and heat exchangers. That’s why textbooks teach it.
AGW and climate science just uses this existing proven theory
Your inability to understand it and correctly use an equation doesn’t make it wrong.
I have trouble understanding how neutron stars can rotate so fast but that doesn’t make the theory of angular momentum wrong either.
Good luck in your journey.
OK, my final.
LJ Ryan,
your 200F device as described is in fact a constant power device. (I2R is the power).
It is *impossible* to state a constant power and constant temperature. If you deliver a constant power, then the temperature will come to a new equilibrium.
This new equilibrium will be above 400F. (in fact, because your assumptions imply a perfectly insulated oven, the temperature will increase forever)
Please read a textbook and work through the examples to understand.
Please.
Bryan
The DALR = dry adiabatic lapse rate.
Adiabatic = no exchange of heat with the environment. This is why the radiative transfer equations are not required to derive the DALR, not because the “radiative properties of CO2” are included in the heat capacity of air.
And the reason this (adiabatic) is a good approximation for rising air is because conduction is negligible in gases and for atmospheric air radiative cooling and heating are relatively slow processes.
SoD says
“no exchange of heat with the environment. This is why the radiative transfer equations are not required to derive the DALR, not because the “radiative properties of CO2″ are included in the heat capacity of air.”
The way you put it almost suggests that the CO2 has stopped radiating but I’m sure you don’t mean that.
I thought your answer would be that the radiative transfers would be equal and opposite and cancel.
My main point is that the radiative component of CO2 is already included in Cp and that the radiative calculations are superflous.
Bryan,
You should probably read some atmospheric thermodynamics or, more generally, some fluid mechanics.
An adiabatic process is an approximation. Like the ideal gas is an approximation.
Pretty much everything in physics relating to the real world is an approximation.
The derivation of the dry and moist adiabatic lapse rates depend on the following approximate relationships:
– ideal gas law
– hydrostatic equilibrium
– adiabatic process
Having followed your amazing logic for about two years I expect great things in your follow up.
But before you write, try and come up with an equation or two and include it in your idea.
If you really studied physics and understood it, writing a few equations to explain your ideas will be easy. If you can’t write equations for your next (or current) idea maybe your next (or current) idea is not physics.
SoD says
“But before you write, try and come up with an equation or two and include it in your idea.”
The molar heat capacity at constant pressure for permanent diatomic gases N2 and O2 is equal to 7R/2 and is nearly constant over atmospheric temperatures.
Polyatomic gases like CO2 and CH4 with active rotational and vibrational modes will not have Cp constant .
In the example of CO2 an increasing with temperature variation of 13% is found for the atmospheric range of temperatures.
This variation is because Cp now includes the radiative contributions.
So if radiative transfer is required then the value of Cp must be reduced.
Cp = (A) non radiative contribution + (B) radiative contribution
So if (B) is dealt with separately by radiative transfer.
Then for other non radiative contribution calculations a separate table of values of (A) must be established.
If this is not done then a large over calculation in energy transfer is inevitable.
I think you need a more extensive set of equations to overturn the consensus on atmospheric radiation and thermodynamics, but it’s nice to see half an equation as a gesture of good faith.
After thinking about it for 10 seconds, Cp must be calculated from the mix of gases in simple ratios according to concentration. I’m sure someone will let me know if I am wrong.
If so, then if you doubled or halved the Cp of CO2 it would have zero measureable effect on the Cp of air.
Cp = r1.Cp1 + r2.Cp2 + r3.Cp3.. + ri.Cpi
where ri is the ratio of gas i, and Cpi is the specific heat capacity of gas i.
r(co2) = 0.00036
Checking some apocryphal source on the web, Cp = 1005 at 300K and 1003 at 250K.
The lapse rate itself is way more inaccurate a tool than the minute changes in Cp with temperature or diabatic processes.
Steady on SoD!
You are liable to prove that there is no significant greenhouse effect.
Cp = r1.Cp1 + r2.Cp2 + r3.Cp3.. +
The fact that Cp is almost constant is because Cp1 is N2, Cp2 is O2 both making up 99% of air
The molar heat capacity at constant pressure for permanent diatomic gases N2 and O2 is equal to 7R/2 and is nearly constant over atmospheric temperatures.
As you say
” ri is the ratio of gas i, and Cpi is the specific heat capacity of gas i.
r(co2) = 0.00036″
Thus because the trace gas CO2 is such a small fraction that its radiative effect is so insignificant that the total heat capacity of air (Cp) is a constant.
However for a pure CO2 atmosphere Cp would vary by 13% for atmospheric temperature range to take full account of its radiative properties.
Now since the radiative effects are naturally included in Cp is there any point in the radiative transfer equations?
You say
“but it’s nice to see half an equation as a gesture of good faith.”
Half an equation like half a hole cannot exist.
Be assured I can write equations to a band playing.
But like the radiative transfer equations there might be a question of their link to reality.
No, they’re not. The heat capacity of a gas at constant pressure has nothing whatsoever to do with its radiative emission and absorption properties. It’s the degrees of freedom of movement of the atom or molecule that determine the heat capacity.
DeWitt Payne says
“No, they’re not. The heat capacity of a gas at constant pressure has nothing whatsoever to do with its radiative emission and absorption properties. It’s the degrees of freedom of movement of the atom or molecule that determine the heat capacity.”
What do you you think these extra degrees of freedom correspond to?
For CO2 for example it corresponds to rotational and vibrational modes.
These are the modes corresponding to among others to the 15um and 4um wavelengths .
N2 or the other hand has no significant rotational and vibrational modes.
Perhaps you can explain why CO2 has a 13% increase in Cp and N2 ha no increase between 250K and 350K?
Bryan,
Those would be the two bending vibrations at 15μm and the asymmetric stretch mode at 4μm. But those vibrations don’t contribute to the heat capacity at normal surface temperature because only a small fraction of the molecules are even in the first excited state. You’ve also left out the symmetric stretch mode which isn’t radiatively active. Only the two rotational modes (water, being asymmetric on all three rotational axes, has three) contribute degrees of freedom to the heat capacity at normal surface temperature. The rotational energy levels are in the microwave range, but since CO2 is symmetric, the rotational levels don’t emit significantly on their own.
Wrong again. Like CO2, the temperature doesn’t get high enough to populate higher levels of the stretch vibrational mode, but N2, like all diatomic molecules, has two rotational degrees of freedom. Those aren’t radiatively active because the molecule has no electric or magnetic dipole. Oxygen, however, is paramagnetic and it’s rotational modes are radiatively active. The oxygen 60 GHz band is used for satellite remote temperature sensing.
Because the bending modes of CO2 are relatively low energy, the levels are starting to be populated significantly between those temperatures. The fraction of molecules in the first excited state at 250K is 2.2% and 6.4% at 350K. The population of the second vibrational level goes from 0.2% to 1.0% and the third level goes from 0.01% to 0.2%. But the energy emitted by those transitions is irrelevant to the heat capacity because when measuring the heat capacity, the temperature is controlled, so any energy lost by radiative emission is returned by the walls of the container, which is probably opaque to IR anyway.
Again, the radiative properties of the gas have no bearing on the value of the heat capacity.
DeWitt Payne
Its very odd that I am the one left to explain the importance of the radiative properties of CO2 when yourself and SoD seem to be marginalising them.
You say
“Because the bending modes of CO2 are relatively low energy, the levels are starting to be populated significantly between those temperatures. The fraction of molecules in the first excited state at 250K is 2.2% and 6.4% at 350K. The population of the second vibrational level goes from 0.2% to 1.0% and the third level goes from 0.01% to 0.2%.”
So accepting your calculation and from memory
For bending mode1 increased energy = 4.2% X twice average translational KE
For second mode increased energy = 1% X twice average translational KE
For antisymetric stretch mode increased energy = 0.2% X four times average translational KE
Which gets us pretty near the 13% increase in Cp from tables
You say
“But the energy emitted by those transitions is irrelevant to the heat capacity because when measuring the heat capacity, the temperature is controlled, so any energy lost by radiative emission is returned by the walls of the container”
I do not accept that the laboratory measured Cp will be a different value for Cp measured in the free atmosphere or why wouldthey bother to measure it?
You say
“Again, the radiative properties of the gas have no bearing on the value of the heat capacity.”
The fact that these additional degrees of freedom correspond directly to the absorption/emission wavelengths proves that the above statement is wrong.
The frequency of the first vibrational level of N2 is 2359cm-1 so at 350K, only 0.006% of N2 molecules are in the first vibrational excited state, and 0.0001% at 250K.
DeWitt Payne says
“Those would be the two bending vibrations at 15μm”
Your focus on detail misses the main point.
What your previous post was trying to convey was that Cp for CO2 was unrelated to the radiative properties of CO2.
This is the big picture I was posting about.
I was contrasting Cp for air and Cp for CO2 which you choose to ignore.
If you like we can get down to the nitty gritty of each wavelength.
I feel that this will turn out to be a dead end for IPCC science and a vindication of traditional Natural Philosophy.
Bryan,
I have posts that apply directly to CO2 in moderation. Patience grasshopper.
Bryan,
The activation of those bending modes would increase the heat capacity of CO2 whether radiation was emitted or not. The fraction of excited molecules that actually emit is quite small. For LTE to exist, 99.9+% of excited molecules must lose their energy by collision before they radiate. But the 99.9+% is where the energy goes to increase the heat capacity. And the gas doesn’t have to be in a container. In a large volume of gas, the radiation will be isotropic at constant temperature with no energy lost from any smaller volume inside the larger volume because all emissions will be matched by absorptions.
I made a mistake calculating the population of the second and third excited states. The correct numbers are smaller. For the second excited state (J=2) the fraction of molecules at 350K is 0.4%, not 1.0% and for J=3 it’s 0.03% at 350K, not 0.2%.
DeWitt Payne
Remember that we are talking about a pure sample of CO2.
Assuming LTE there will be maintained fractions which will be vibrationally or rotationally excited or both.
The exact proportion of each depends on the temperature.
Although some may be emitting there will be an equal number absorbing to keep the population at the calculated level.
We usually assume that for each gas volume the neighbouring volumes are emitting and absorbing equally.
The definition of Cp.
Extra energy will be required to raise the temperature of the defined gas sample by one Kelvin (but not in a linear way as with N2).
The rotational and vibrational properties of CO2 and their corresponding wavelengths are inextricably linked
Constant Cp is true for a pure sample of N2 it is not for CO2.
Here we would have to be very careful and use changing values of Cp as the temperature changes for accurate calculations .
This was part of my original question to SoD who I had assumed to have considered lapse rates for a pure CO2 atmosphere but as yet no answer.
I did my own calculations
Between 250K and 350K there is an increase of 8% in 15um population
For 4um the increase is 0.15%.
I am off on a trip for 48hours so no need to rush a reply.
Bryan,
I wonder what equations they would suggest for the interaction of radiation with the atmosphere.
I have supplied the equations in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations.
I have also explained their derivation from first principles in that article.
And I have shown examples of theory and measurement matching up for the spectrum of atmospheric radiation at the top of atmosphere and at the surface. See Theory and Experiment – Atmospheric Radiation and The Amazing Case of “Back Radiation” – Part Two.
We will have to wonder what Postma, G&T and Bryan have developed as equations because my prediction is that we will never actually see an alternative equation from them for the absorption and emission of radiation by the atmosphere.
SoD form February 19, 2012 at 7:31 am
My equation! The equation was supplied by VeryTallGuy. To point, at t1 the oven has reached equilibrium and Body3 is powered on. Because Body3 is a resistive heating element, when attached to a potential difference current will flow and heat is produced. In the case of Body3 the temperature achieved via this current, is 200F.
Again, my equation! The whole point of this exercise is to disprove additive power…(Qb3+Qb2) =εσTb24.
Enough with the view factor nonsense. If F32 is > zero the Q32 is positive. And if Q32 is positive then Q32 +Q12 is > Q12, and since Q12=Qb2 at equilibrium, which translates to 400 F. Now turn on B3 and according to VeryTallGuy and yourself Qb2 = Q32 +Q12 and T2 temperature exceeds 400F.
SoD why not correct your equations, account for anything you deem necessary, let’s see if you can get Tb2< 400 F. If you are going to offer up a blah…blah…blah equation, defend it.
L.J. Ryan,
R12 = irradiation at body 2 from body 1 in J/second
R32 = irradiation at body 2 from body 3 in J/second
[Irradiation = energy received per second at the surface of the body, only a fraction of which is absorbed, dependent on absorptivity, α]
R12 = A1F12ε1σT14 …[1]
R32 = A3F32ε3σT34 …[2]
where A1 = area of body 1, F12 = view factor of body 1 to body 2, ε1 = emissivity of body 1 for this temperature, σ = Stefan-Boltzmann constant, T1 = temperature of body 1, and similarly for the subsequent equation.
If body 4 is reflecting or emitting radiation we need to consider this irradiation value as well.
And so irradiation at body 2, I2 = R12 + R32 + R42 …[3]
Then we have to ask about the value of T1 as VeryTallGuy has already pointed out. Is it held constant via a control mechanism?
Solving the equations depends on whether T1 is held constant or the power into body 1 (the “400F element”) is held constant. The boundary conditions are essential as already outlined.
And I have already asked about T3. L.J Ryan says that it becomes 200F after t1.
Mathematically minded readers will see immediately that the effect of the important view factors demonstrates that “the bit of the oven that is at 200F” is not at 400F it is at 200F and so the whole oven is not radiating at 400F. This is important.
Non-mathematically minded readers might image an oven almost uniformly at 400F (hot) with a chunk at 200F (cooler) and wonder whether the total irradiation experienced at body 2 will be something between that emitted by a body 400F and a body at 200F – and wonder what on earth L.J.Ryan is going on about.
L.J.Ryan will continue to insist that it’s “our equations” but we aren’t allowed to use view factors (that we keep pointing out are in “our equations”) and “therefore” adding together numbers from “our equations” proves that “our equations” are wrong.
It’s an Alice in Wonderland experience.
VeryTallGuy …February 19, 2012 at 9:29 am
What are you talking about…the IR catastrophe. Can discussion of such fantastical anomalies be found in textbooks? In fact, what you describe the exact opposite of Black Body radiation.
Not at all. If you put an energy source into a perfectly insulated container, the temperature in the container increases without limit because there’s nowhere else for the energy to go, perfect insulation, remember.
But let’s ignore the perfect insulation part. Take an insulated box and put a 40W light bulb in it and turn it on. Eventually the system will achieve a steady state with the average internal temperature higher than ambient. What you propose is to put another light bulb in the oven at an initial temperature below the temperature of the oven and turn it on. The transient behavior is complicated, but the final steady state will be an average oven temperature higher than the temperature with just one 40W bulb.
SoD…February 19, 2012 at 7:38 am
Hold the phone…did you actually say energy absorption is a function TEMPERATURE of each body…well view factor and emissivity, BUT TEMPERATURE!
Wait do the photons traveling from a cold source to a hot source stick a finger in the air, decide it’s too hot and turn around….sarcasm aside
This is exactly the point I’ve been making from the get go. That is, flux from a cooler lower energy source will not increase that of higher energy hotter source. And now some 186 post into comments and you suddenly agree with me…fantastic!
L.J.Ryan on February 20, 2012 at 7:56 am,
“Sum of energy received at body 2” = “irradiation”.
Irradiation = All the incident radiation arriving at the surface of a body (in this case body 2).
I try to combine a mix of technical language (that general readers might not understand) with a more English explanation where possible that explains the same concept.
The irradiation is a function of the emission of radiation of all the bodies radiating towards body 2 (and therefore their temperatures and emissivities), as well as a function of the view factors of these bodies.
I already reproduced the short, simple and technical explanation earlier (February 18, 2012 at 7:12 am), for the slightly simplified case of a black body (bodies with emissivity < 1.0 make the equation a little more complicated). Here it is again:
SoD February 20, 2012 at 9:31 am
I never defined T3 to be 200F after t1. I said it’s powered on. You have the flexibility define the T3 however you like.
Previously T2 was defined by following equation:
(Qb3+Qb2) =εσTb2^4.
You’ve offered:
R12 = A1F12ε1σT1^4 …[1]
R32 = A3F32ε3σT3^4 …[2]
How do you now define T2? Perhaps it will look like:
(R12 + R32) = εσTb2^4.
This get a bit tricky for you SoD. If R32>zero, T2 is > 400F.
My prediction: instead of providing an equation(s) you will continue to obfuscate with more blah blah blah.
If you put an additional energy source into, say, an oven, the final steady state temperature will be higher than it was before. That’s precisely what you’re doing. The temperature of the oven will drop initially while the 200F object warms up. But it’s powered, so pretty soon its temperature will exceed 400F and the whole system will be warmer. There is no contradiction or violation of any thermodynamic law.
You claim that if R32 > >0 then T2 > 400F – but you haven’t proved it.
I have provided equations. Let’s see your proof.
L.J.Ryan,
I note your earlier comment from February 20, 2012 at 7:50 am:
And now on February 20, 2012 at 3:59 pm:
More Alice in Wonderland stuff.
I repeat that if T3>400F then of course T2>400F. Correct and clear definition of boundary conditions is important in problem solving.
Don’t forget to state your boundary conditions in your upcoming proof.
L.J.Ryan,
Let’s go back to fundamentals and your original statement of the problem:
The problem as stated is grossly underspecified:
1. The initial conditions are far from steady state.
You can’t have two heating elements inside the oven at different temperatures at steady state by definition. If both heating elements are inside the oven, you can’t get around this by having the lower temperature element turn on later unless it is lower power than the higher temperature element and is turned on only slightly later. Otherwise, it will still be heated by the higher temperature element.
2. The initial temperature of the oven isn’t specified for either the air or the walls.
3. The power to the heating elements and their sizes isn’t specified.
4. The emissivities of the heating elements, the pan and the oven walls aren’t specified.
5. The thermal resistance between the oven and ambient isn’t specified.
6. Ambient temperature isn’t specified.
Therefore, any attempt to find a unique solution to this problem must fail. As a result, it is indeed possible to specify boundary conditions that would have the cast iron pan reach any temperature you want, including 600F.
A more reasonable problem would be if one wall were heated to 400F and the opposite wall was cooled to maintain it a temperature of 200F. Then the pan in between would have a temperature intermediate between 400F and 200F. But the temperature of the pan will depend on the temperatures of both walls. Raise either temperature and the temperature of the pan rises also.
DeWitt Payne
I agree. The real question is however, what limits the absolute max temp. If I read your posts correctly, you argue there is no limit…other then the number of bulbs in the box.
I argue, the max temperature is limited by the hottest bulb. So if temperature of the tungsten filament in first bulb is 3000 F and all additional bulbs have lower filament temperature, max ambient box temperature is 3000 F.
Nope. The temperature will be limited by the physical limits of the insulation, the filament or the bulb. At some point either the heat flow through the insulation will reach steady state or something will melt. As the oven temperature goes up, so does the filament temperature. This problem is different from focusing solar radiation where there is an upper limit on the temperature that can be achieved equal to the brightness temperature of the radiation, ~6,000K for sunlight.
SOD: Reading your debate over the basics of radiative heat transfer with LJ, Bryan and DeWitt, made me wonder if there isn’t a simple laboratory demonstration that will show that the cooler walls of a surrounding container can transfer energy to a warmer object inside. Ideally, a video of such a lab demonstration might already exist online, but I couldn’t find one. You seem to have lots of experience with how such problems should be approached wit pencil and paper, but a demonstration (that could be easily replicated elsewhere) might be more effective than words. A demonstration where all parties can propose hypotheses about the results will turn out before the experiment is run. If I have some thoughts, if you are interested.
Frank,
The textbooks are crystal clear. But they rely on old fashioned equations which are confusing and irrelevant.
So an idea for a new experiment will be interesting. More people will emerge to explain why the results cannot be correct.
DeWitt has already done an interesting experiment which supports the equations in heat transfer textbooks. So clearly some methodological error in there somewhere.
That’s not how it works, and you should know better. The container wall temperature influences the temperature of the warmer object at steady state if, and only if, there is a constant energy flow from the object to the surrounding container and the walls of the container are maintained at a constant temperature. If there is no constant flow and constant wall temperature, the object will cool to the wall temperature or both will reach an intermediate temperature depending on how well the container is insulated.
DeWitt: Thanks for the comment. As I wrote, I was contemplating how best to do an experiment under precisely the conditions you describe. However, I did say:
“the cooler walls of a surrounding container CAN transfer energy to a warmer object inside”
As best I can tell from the discussion, the doubters believe this CAN’T happen. A simple way to show that it DOES happen – which they can watch or repeat for themselves – might be value. The circumstances you describe are one way to demonstrate what does happen.
You said:
“If there is no constant flow and constant wall temperature, the object will cool to the wall temperature or both will reach an intermediate temperature depending on how well the container is insulated.”
Just because the object cools to the wall temperature or reaches an intermediate temperature doesn’t change the fact that “the cooler walls of a surrounding container DO transfer energy to a warmer object inside”. Changing temperature and equilibration simply make it harder to prove that a transfer from cold to hot does occur. There is, of course, always a larger transfer from hot to cold than cold to hot. Unless the emissivity or temperature of a surface is zero, it will emit radiation that other objects – warmer or colder – will absorb unless their absorptivity is zero.
Please let me know, if you still think I’ve got it wrong.
SoD February 20, 2012 at 6:38 pm
This is getting quite silly SoD. Instead of defending your position, you have resorted to misrepresenting my posts. I could list these distortions, but what’s the point.
Lets recall the initial argument as posed by VeryTallGuy:
…formatting error…see next post.
SoD February 20, 2012 at 6:38 pm
This is getting quite silly SoD. Instead of defending your position, you have resorted to misrepresenting my posts. I could list these distortions, but whats point.
Lets recall the initial argument as posed by VeryTallGuy:
I contend this is wrong, introduce the pan in the oven model as explanation, and we spend five days arguing boundary conditions.
And now you want me to disprove (Qo+Qe) = εσTe^4 by proving (Qo+Qe) = εσTe^4. This formula as related to the pan is (Qb3+Qb2) = εσTb2^4 and therefore Qb3 need be > 0 for Tb2 to exceed 400F…as laid out by VeryTallGuy.
My guess, if VeryTallGuy had an opportunity to retract or restate his post, he would. That is, apparently (Qo+Qe) = εσTe^4 only if unphysical boundary conditions are maintained. And thus can not be proven or unproven. Or as DeWitt Payne put it “Therefore, any attempt to find a unique solution to this problem must fail.”
If you agree (Qo+Qe) = εσTe^4, then perhaps we can test against a new model. A simple very conclusive model…with predetermined physical boundary conditions…one which any interested reader can duplicate.
How about making a partially energized tungsten bulb radiate visibly, via IR.
LJ Ryan
I quoted Q as a flux, ie the flux *reaching* one body from the other. You are attempting to use them as total heat flows.
Work through SODs kindly provided scanned textbook page.
Please.
VeryTallGuy
What are you talking about? Your contention:(Qo+Qe) = (emissivity)(sigma)Te^4
From my post…February 17, 2012 at 6:35 am
Qb2 = εσTb2^4 = 2950 W/m2 prior to Body3
Qb3 = εσTb3^4 = 1023 W/m2
(Qb3+Qb2) = εσTb2^4 …. as stated by VeryTallGuy
[(Qb3+Qb2)/εσ]^.25 = Tb2 = 415K = 465 F
You are assuming implicitly that all the radiation from body three impinges on body 2 (view factor unity)
You are also neglecting that you are reducing the view factor from the walls (think casting a shadow on body 2)
See the later posts for a much more comprehensive follow up.
Frank wrote:
“In an unpublished manuscript, VanAndel estimated by two methods that an additional 20 W/m2 of energy is required to raise tropical SST from 30 to 31 degC. That’s a local climate sensitivity of about 0.2 degC for 2XCO2.”
SOD replied:
The surface forcing is totally different from the TOA forcing – which is also known as “radiative forcing”.
More about this in Radiative Forcing and the Surface Energy Balance.
And interesting that Ramanathan 1981 also computed similar numbers to VanAndel (caveat, this is from memory). The surface forcing is very high compared with the TOA forcing. Important to understand that.
Frank replies:
I think surface forcings are smaller than TOA forcings. While trying to dig up information I once knew about this subject, I came across the following information at Pielke Sr’s blog that was published in a book chapter. (These number seem low compared with DLR from K&T possibly, because they are for clear skies and DLR is higher below clouds.)
“There are two tables that Norm Woods prepared that are insightful in terms of the effect of different atmospheric concentrations of CO2 and water vapor. For the tropical sounding, the downwelling longwave flux at the surface when the CO2 concentration changes from 360 ppm to 560 ppm is 0.09 Watts per meter squared, as contrasted with a change of 0.41 Watts per meter squared when the concentration changes to 360 ppm from 0 ppm. The reason for this relative insensitivity to added CO2 in the tropics is due to the high concentrations of water vapor which results in additional long wave flux changes due to CO2 being very muted.
For the subarctic summer sounding, the corresponding values are 2.94 Watts per meter squared when changing the CO2 concentrations to 360 ppm from 0, and 0.47 Watts per meter squared when changing the CO2 concentrations to 560 ppm from 360 ppm. For the subarctic winter sounding, the change is 14.43 Watts per meter squared when the CO2 concentrations are changed to 360 ppm from 0, and 1.09 Watts per meter squared when the CO2 concentrations are changed to 560 ppm from 360 ppm.
For water vapor, with the tropical sounding, the change of the concentration from zero to its current value, results in a 303.84 Watts per meter squared change in the downwelling longwave flux at the surface. Adding 5% more water vapor, results in a 3.88 Watts per meter squared increase in the downwelling longwave flux. In contrast, due to the much lower atmospheric concentrations of water vapor in the subarctic winter sounding, the change from a zero concentration to its current value results in an increase of 116.46 Watts per meter squared, while adding 5% to the current value results in a 0.70 Watts per meter squared increase.
This analysis shows that
1. The effect of even small increases in water vapor content of the atmosphere in the tropics has a much larger effect on the downwelling fluxes, than does a significant increase of the CO2 concentrations. Thus, the monitoring of multi-decadal water vapor trends in the tropics should be a high priority. While the increase in CO2 concentrations, and resulting increase in downwelling longwave flux can result in surface ocean warming, and thus increase evaporation into the atmosphere, it is the atmospheric water vapor signal that should be monitored for long term trends, as it is the dominant greenhouse gas that has the greater climate response.
2. The fractional contribution of the effect of added CO2, relative to a 5% increase of water vapor in the subarctic winter is significantly larger than in the tropical sounding. This is because the subarctic sounding is quite dry. An increase in absolute terms of water vapor similar to a 5% increase in the tropical sounding would, however, dominate the increase of downwelling longwave fluxes. This again indicates that the assessment of long term water vapor atmospheric concentrations needs to be a climate science priority.”
pielkeclimatesci.wordpress.com/2006/05/05/co2h2o/
vanAndel looked at the correlation between SST and wind speed in the tropics and calculated how evaporation would change with SST due to the combined effects of wind and temperature. The results showed that a temperature rise from 29 to 30 degC would result in an additional 20 W/m2 leaving the surface as latent heat. IF either vanAndel’s figure OR Pielke’s figures are correct, CO2 has negligible ability to change tropical SSTs. (That leaves a “minor” problem explaining the PETM and other paleoclimate events supposedly driven by CO2.)
(The physics of how temperature, wind and relative humidity control evaporation rate might be something interesting to write about. I think I read somewhere that evaporation from the ocean (averaging about 1.4 m per year) is a small percentage of what is possible.)
Judy’s Discussion with mean 2XCO2 surface forcing of 1 W/m2:
judithcurry.com/2010/12/11/co2-no-feedback-sensitivity/
Judy cited Ramanathan (FIgure 2), with roughly the same value:
http://journals.ametsoc.org/doi/pdf/10.1175/1520-0469%281981%29038%3C0918%3ATROOAI%3E2.0.CO%3B2
DeWitt reported some similar he obtained personally somewhere at SOD.
Frank,
I shouldn’t have cited from memory and without thinking enough. Expect a reply but it will take a few days so I can get some thinking time. (That means it’s a good question).
That doesn’t square with MODTRAN calculations. For clear sky tropical atmosphere, changing from 0 to 360 ppmv CO2 increases DLR by 7.2 W/m² from 341.004 to 348.226. Increasing from 360 to 560 adds an additional 0.9 W/m² to 349.168 W/m².
MODTRAN
subarctic summer:
CO2 DLR
0 250.258
360 269.789
560 271.327
subarctic winter
0 133.105
360 162.746
560 164.567
Removing water vapor can only get a change of 300 W/m² for a tropical atmosphere if the CO2 concentration is also zero. Otherwise, you see a lot of CO2.
Your conclusion is also flawed because that’s only the instantaneous change in DLR holding everything else constant. But if the decrease in outgoing radiation at the TOA causes the surface temperature to increase, surface DLR increases as well. In fact, the DLR increases much faster in the tropics with temperature than it does at high latitudes. Of course with polar amplification expected, the temperature at high latitudes will also increase faster than the temperature in the tropics.
CO2 forcing is higher in the tropics as well because the effective emission altitude for CO2 is higher and colder in the tropics than at high latitudes. OTOH, increasing CO2 should act to flatten the latitudinal emission profile. The deficit between incoming radiation absorbed in the tropics compared to radiation emitted to space should increase and the excess of radiation emitted to radiation absorbed at high latitudes should also increase.
There is are so many values available elsewhere on ‘radiative’ forcing, that I fid it frustrating and difficult to convert them to something useful, and end up calculating optical thicknesses from scratch.
Is it my understanding correct that these radiative forcing values (from Modtran, etc) are calculated by holding fixed a temperature and pressure profile in the atmosphere and then increasing the concentration of one of the component gases? (then looking at the change in transmitted flux)
If so, to derive a gas property (not dependent on the source flux) one would need to know the source flux, the final flux and not just the delta (forcing between them)
It would be good to have some sort of conversion between radiative forcing and absolute values (or even delta values) of optical depth for the atmosphere.
If forcing = dF = Gout – Gin
Gout = Gin * (1 – e) then
e = dF/Gin to get the emissivity or optical depth one would need to know the source flux Gin.
Why is pretty much everything in the literature reported as delta fluxes or radiative forcings?
I was somewhat suspicious of Pielke’s figures. You can’t get any warming in the tropics at all if his figures are right. Do you know what surface temperature and humidity were used to calculate your values?
I understand the TOA concept, but would prefer not to transfer warming to the surface with a fixed lapse rate. I think I understand the implications of the instantaneous change.
I’ve been thinking about surface forcing in the following way: Given X W/m2 of surface forcing (from any source), when equilibrium is re-established,what fraction of the new energy will leave the surface via increased convection and what fraction will leave via radiation? Loss by radiation requires surface warming. Loss by convection requires running the Hadley, Ferrel and polar circulations a little faster. There are frictional forces opposing these flows, but I don’t know how to account for the energy dissipated. (It becomes atmospheric heat anyway.) As long as enough heat is transferred to the characteristic emission level, this “bottom up” energy balance doesn’t contradict the “top down” approach. If models can’t accurately describe convection, how can they properly partition increased DLR into the upward convection and radiation channels?
LJ Ryan,
I’ll try and define a little nomenclature.
You have introduced a system with four bodies. I’ll number them thus:
Body 1. A heating element. Controlled power input to maintain a constant surface temperature at 400F. Unknown size and location, thermal properties
Body 2. A “pan”. Unknown size and location, thermal properties
Body 3. Another heating element. Defined both as constant power (I2R) and constant temperature (200F). *See problem at the end* Unknown size and location.
Body 4. An oven. This encloses all the other bodies. Unknown size, thermal properties.
My assumptions:
Assumption 1. The oven maintains a perfect vacuum.
Assumption 2. All the bodies are physically disconnected from each other.
Assumption 3. All the bodies have a very high thermal conductivity – so we can neglect temperature gradients within the bodies.
Because of assumptions 1 and 2 we can neglect conduction and convection meaning we need only consider radiative flows.
Your initial conditions
Initial temperature of bodies 1 and 2 are both 400F.
This implies several other properties of the system.
Firstly, the system is in equilibrium.
Secondly that body 4 is also therefore at 400F
Thirdly that body 4 is perfectly insulated – no heat can exit the oven (otherwise it would not be at equilibrium, but would be losing heat to its environment, and this would also prevent body 2 reaching 400F)
*problem*
Body 3 has been defined as having both constant power output and constant temperature. I’ll consider both cases, but it would be helpful for you to specify one or the other.
The equations that describe this are exactly those in the scanned textbook page from SOD.
I’ll follow up with posts which describe how the system will respond to the introduction of body three in the constant power and constant temperature scenarios.
Can you clarify if you disagree with any of my points above, or if I have misunderstood your scenario in any way.
Case 1. Body 3 at Constant temperature 200F
Body 3 is introduced. We know nothing about it’s size or location, but as the whole system is at 400F, it *must* reduce the view factor from at least one other body at 400F to body 2. The result is that the total energy reaching body 2 is reduced. It continues to emit energy according to the SB law, so the temperature reduces in line with the reduction in incident energy.
Note that in order to maintain the temperature of body 3 at 200F there must be some mechanism of removing heat from body 3. We can think of this as heat exchange with a constant temperature sink at 200F.
Body 2 will be between 200 and 400F in this case
Case 2. Body 3 at Constant Power (I2R)
Initially the same happens as in case 1. Then, the temperature of body 3 rises, rate being dependent on the heat capacity of body. As this happens, the temperature of all the other bodies will also rise. Once body 3 reaches 400F, body 1 will need a heat sink to remove heat to maintain it at 400F. Eventually the system will come to a new dynamic equilibrium where the heat removed to this sink equals the I2R being applied to body 3.
Body 2 will be between 200 and 400F in this case.
If, however, there is no heat sink for body 4 to remove heat, then the temperature of the system will rise without limit – it is perfectly insulated and there is a constant power input.
I’ll also put forward a third case which may be more meaningful.
Case 3 – no oven.
Finally, we’ll now consider the case where the oven does not exist, and the temperature of the surroundings is absolute zero. This is rather more meaningful to considering the type of problem posed by a planetary energy balance.
Initally, body 1 is at 400F as before. Body 2 can be at any temperature from 400F to approaching zero K dependent on the view factor.
Limiting geometries for this are:
400F – body 2 is enclosed within body 1 – view factor unity
approaching zero K – body 2 is at a very long distance from body 1 compared to the size of body 1 – view factor approaching zero.
We now introduce body 3, which we will only consider now to be at a controlled temperature of 200F
Body 2 now receives additional radiation from body 3. It’s temperature rises. It emits more radiation according to the SB law. A new dynamic equilibrium is established once it is emitting sufficient radiation to balance the new incident flux from body 3.
The new temperature for body 2 cannot, however be above 400F. This is because of the effect of the view factors in the calculation. Consider the limiting cases:
400F – enclosed within body 1 (view factor of unit for body 1, zero for body 3)
200F – enclosed within body 3(view factor of unit for body 3, zero for body 1)
approaching zero K – body 2 is at a very long distance from both bodies 1 and 3 compared to their sizes. Both view factors approach zero.
The temperature of body 2 will rise, potentially above 200K dependent on the view factors, but never above 400K
VeryTallGuy from February 22, 2012 at 9:31 pm
As I said in my post February 22, 2012 at 6:36 am…I contend this[(Qo+Qe) = εσTe^4] is wrong, introduce the pan in the oven model as explanation, and we spend five days arguing boundary conditions.
I did not neglect view factor, it’s irrelevant. Regardless of the geometry/ view factor B2 will never rise above 400F.
LJ Ryan,
I’ve explained above in great detail why the numbers you put in my equation are incorrect.
We agree on the temperatures.
The equations give the same temperatures.
The boundary conditions show why the numbers you put in the equations are inapplicable.
There’s no point using equations if you can’t justify the numbers you put into them.
VeryTallGuy
Timing clarification…my post February 22, 2012 at 10:10 pm was typed prior to reading your latest posts. I should remember to refresh prior to posting.
Thanks for providing the detailed case scenarios. In all three cases, I agree with your conclusion. That is, B2 will never rise above 400F.
So when is is Qo+Qe = εσTe^4 valid?
You said:
“There’s no point using equations if you can’t justify the numbers you put into them.”
I would add, there’s no point using an equation if you can’t justify the resultants.
LJ Ryan
“When is Qo+Qe = εσTe^4 valid?”
When Qe represents the increase in the average flux received at the surface of the body.
In your oven example the average flux received by body 1 when body 3 (the 200F body) is introduced actually *reduces*, rather than increases because the new body will shield the pan from radiant heat from the walls of the oven. The walls are at 400F because the boundary conditions you set imply thermal equilibrium has been attained.
The equation is valid, but Qe is negative.
Makes sense?
VeryTallGuy
Got it, I think. Though, the naming convention between your formula and it’s prescription to the oven model is inconsistent.
Qb2 = εσTb2^4 = 2950 W/m2 prior to Body3
Qb3 = εσTb3^4 = 1023 W/m2
(Qb3+Qb2) = εσTb2^4
So B3 at 200 F is initially a sink for the oven. Given sufficient time, however, oven temperature will rise without limit…assuming white walls or perfectly insulated.
Do I have this right?
That’s about right I think, yes
DeWitt Payne
You’re contradicting black body radiation. Specifically, Kirchhoff’s cavity theorization/experiment.
Radiation streams into a cavity through a small aperture…this radiation is continually absorbed and re-radiated by cavity walls…eventually the cavity will come to an equilibrium temperature.
So back to the bulb in the box, temperature can not increase above that of the filament.
LJ Ryan
your mistake is to ascribe a fixed temperature to the filament.
The temperature is not fixed – it is a function of the surroundings. Try a thought experiment where the light bulb before being switched on is put in a box where the walls are held at 3000C (or whatever a filament temperature is in a normal bulb) and allowed to come to equilibrium. Now turn on the bulb. What happens to the filament temperature?
In a perfectly insulated box, any power input will cause temperature to rise (1st law). It will rise forever.
In reality, either the insulation will be sufficiently imperfect to allow a dynamic equilibrium to be reached, or something will melt.
Not the same thing at all. There is no power source inside Kirchhoff’s cavity. Energy can only enter or exit through the hole. At steady state, energy in equals energy out. But you don’t have a hole and you do have a source of energy in the electric power that heats the lamp filament. There’s nowhere for that energy to go so the energy content, and thus the temperature of everything inside the sealed cavity with a light bulb in it increases until something breaks.
DeWitt Payne
Not true. The cavity acts to retain the the radiation thereby equating frequency to source temperature.
Cavity with a hole
A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation.[10] Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large.
But we need to check our ideas experimentally: so how do we construct a perfect absorber? OK, nothing’s perfect, but in 1859 Kirchhoff had a good idea: a small hole in the side of a large box is an excellent absorber, since any radiation that goes through the hole bounces around inside, a lot getting absorbed on each bounce, and has little chance of ever getting out again.
Since, by definition, the body absorbs (and, hence, emits) the maximum radiation corresponding to the given temperature, the characteristics of an enclosing system have no influence on the emission properties of a black body. Therefore, the total radiation energy of a black body is a function of its temperature only.
A physical realization of a black body is a cavity with a small hole (Figure 19.3). There are many reflections and absorptions. Very few entering photons (light rays) will get out. The inside of the cavity has radiation which is homogeneous and isotropic (the same in any direction, uniform everywhere).
Suppose we put a small black body inside the cavity as seen in Figure 19.4. The cavity and the black body are both at the same temperature.
The radiant energy absorbed by the black body per second and per m2 is , where is the irradiance, the radiant energy falling on any surface inside the cavity. The radiant energy emitted by the black body is . Since for a black body, . The irradiance within a cavity whose walls are at temperature is therefore equal to the radiant emittance of a black body at the same temperature and irradiance is a function of temperature only.
VeryTallGuy
Can your provide a real world application where Qo+Qe = εσTe^4 applies. An application wherein a lower energy, lower temperature surface increase energy of higher energy, hotter surface. Not a conceptual consideration but a very real example.
Good question.
How about
1) Night temperatures. The temperature of the ground falls more rapidly if there is no cloud. When there is a cloud layer, it’s temperature is lower than the ground. The cold cloud layer heats the warmer ground.
2) Campfire. Imagine a campfire giving out enough heat to keep you warm at night. Now put the same fire in a room. You feel (and are) warmer in the room, even though the walls of the room are colder than you. The cold walls heat the warm person.
VeryTallGuy
1. Cloud cover provides radiative insulation, not a radiative heat source. Currently, radiative barriers are available for the home. And although radiative losses will be reduced with foil barriers and/or clouds, it does not mean either provides energy and thereby heating. If Qo+Qe = εσTe^4 were true, I could make a geothermal furnace simply by foil insulating a dry well
2. Again, walls slow loss, they do not provide energy in excess of the fire. If Qo+Qe = εσTe^4 were true, there would be no maximum temperature of a wood fire. In actuality peak temperature tops out ~3500 F. Wood gasification boilers, which are specifically designed to advantage this maximum, can only achieve ~2500 F.
Well, I’m at a loss as to how to even start to help you think through the inconsistencies in your reply.
1) Can you tell me what the difference is between “radiative insulation” and “radiative heat source”. In order to provide “insulation” the cloud layer must be radiating back – there is no contact between the ground and cloud other than through radiation.
I wonder as I write this if you mean that the cloud reflects rather than emits. I think from reading around that clouds essentially do not reflect any longwave eg http://earthobservatory.nasa.gov/Features/Clouds/ but can’t give you a definitive answer on that. Perhaps someone else can help?
2) The maximum temperature of a flame is defined by the heat available from combustion divided by the specific heat of the gases. All the heat is then radiated or conducted away. The temperature can be increased, for instance
– By increasing the inlet temperature of the gases as in a regenerative thermal oxidiser http://www.anguil.com/oxidizers/regenerative-thermal.aspx
– by decreasing the heat capacity of the gases, for instance by using oxygen rather than air as in an oxy-acetylene torch.
But radiative heat transfer imposes no limit on flame temperature.
See http://en.wikipedia.org/wiki/Adiabatic_flame_temperature
In all honesty, you seem to really struggle with the absolute basics of heat transfer and thermodynamics. There are people on this site far better qualified than you (or I) – can you summon the humility to listen to them? You’d learn a lot if you could.
VeryTallGuy
Bulb radiance is a function of temperature…on that we agree. Bulb temperature is function of surroundings or electrical input, but not both. That is, if the surrounding temperature is 3000 F the bulb, according to tungsten filament radiation tables, will/may be dull red. If you then power on the bulb, which normally radiated 580 nm, it will not, WILL NOT now radiate with greater intensity at 580 nm, will not be brighter.
Actually it will. The energy radiated will be that initially plus the extra energy from the electrical current passing through.
VeryTallGuy
Well then…a test! I proposed to SoD, a couple days ago, a test to either confirm or put to rest additive power…(Qo+Qe) = εσTe^4. A simple very conclusive model…with predetermined physical boundary conditions…one in which any interested reader can duplicate. And in fact goes to this very bulb in a box argument.
How about making a partially energized tungsten bulb radiate visibly, via IR?
The premise:
Power on a standard light bulb. Pot back just until no visible light radiates. Take temperature and power input measurements. This will be To condition. Assuming To, the bulb will visibly illuminate when irradiated with sufficient IR…if (Qo+Qe) = εσTe^4 is true.
Possible sources of IR to test:
1. self radiation….bulb in a box
2. oven IR, say 400 F
3. outside, irradiated by the DLR
If you agree with the premise then we need only agree to the variables and run the test.
A good way to see if your proposal is a good one is to put some numbers into the equations.
Lets assume unity emissivity.
Light is first visible from a bulb at c. 480 degrees C (http://en.wikipedia.org/wiki/Thermal_radiation)
sigma = 5.67e-8 J/sm2K4
Flux emitted from a bulb at 480C therefore = 18,229W/m2
Oven at 400F
400F = 204C
The oven walls are emitting 2935 W/m2
This is added to the flux from the electrical current = 18229+2935 = 21164 W/m2
We’ll ignore changes in electrical resistance due to temperature.
The new temperature is 509 degrees C
Is this enough to see a difference?
I doubt it – according to the wiki reference going from 480 to 580 degrees is required to go from faint red to dark red. The oven door will make more difference to what you can see.
The radiative fluxes necessary to make a significant difference to visible light from a thermal source appear to be too large to measure qualitatively – a sensitive quantitative test is necessary. I’d suggest that doing such a test would be better in the IR than the visible to avoid the need for high temperatures.
Other followers of the blog might be able to suggest better tests.
Using your suggested test for DLR is even more difficult – I’ll leave it to you to go through why.
The various bodies in the oven emit an amount of Watts. You need to know the area of each body before you can calculate Watts from W/m2.
And view factor tells us what proportion of flux (radiation) from each body strikes each other body.
So you need to know the view factor of each body to each other body before you can calculate the total flux incident on each body.
As already explained on February 20, 2012 at 9:31 am.
I started doing a worked example of an oven but it’s boring (4 areas, 4 temperatures, 16 view factors, lots of simultaneous equations) and I didn’t expect that the result would help L.J.Ryan understand anything.
Well, the problem with physics is that one does not use equations to prove something doesn’t happen. We use equations as mathematical descriptions of physical laws. We can only apply equations when the correct conditions are present that we can actually apply the relevant physical law. We verify the validity of the equations by doing laboratory experiments to demonstrate we can make reliable and accurate predictions.
“Greenhouse theory” has no physical law. It has no validly applied equation. It has no laboratory experiments that quantify gaseous warming caused by radiation in a system where conduction, convection and radiation are operative.
blouis79,
You can write an equation of what does happen instead.
– How much radiation (flux) from the atmosphere.
– Value of flux that arrives at the surface
– Proportion of that flux that is absorbed by the surface
– Emission of thermal radiation from the surface
Over to you.
Something that doesn’t happen? Say, the atmosphere does not emit any radiation – as an example of something that might not happen.
It is easy to write that in an equation:
Radiation emitted by the atmosphere, Ra = 0
Radiation from the atmosphere reaching the surface, RRL↓ = 0
So it is quite possible to write equations around processes you don’t believe happen.
When you do write a few equations to explain your view of the climate system we will see whether you can string together a coherent physics idea.. or not. And we will be able to test it.
250+ comments, and still no one has provided an alternative equation of what happens to radiation from the atmosphere when it reaches the surface.
My predication is so far proven true.
DeWitt Payne on February 13, 2012 at 3:10 pm
“The calibration equations used provide results that agree with independent measurements using FT-IR spectrophotometers. Both are in agreement with spectra calculated using the radiative transfer equations”.
It’s the word “independent” that I find uncompelling.
Manufactured calibration data set.
Dome correction term ignored.
Two specifications of regression equations reflecting different theories:
A: 2-way matter-matter energy exchange; and
B: 1-way matter-field energy exchange.
Estimating constants and coefficients obtained:
A: Wbb = 185 + 2.49*V + 0.33*(S-B)c
B: Wbb = -120 + 2.49*V + (S-B)c
A, B give identical Wbb in the laboratory.
In the field, a V reading would be consistent with either A or B theory. It would meet a necessary condition but not a sufficient one to prove DLR.
A Fourier Transform Infrared Spectrophotometer (FT-IR) uses a completely different method to measure IR radiation than a pyrgeometer.
See http://www.arm.gov/instruments/aeri
That’s what I mean by independent confirmation.
I don’t see how your equations work in the real world. Say the detector and the calibration black body temperature is 300 K so V = 0, if V is the thermopile voltage. Wbb = 459.3 W/m². Equation A gives a value of (S-B)c = 831 W/m² while for equation B, (S-B)c = 579.3 W/m². If, OTOH, V in your equation is the actual output of the instrument, it already includes (S-B)c, which I assume is the blackbody emission of the instrument case, and the coefficient should be 0.249 if V is in μV.
Its unfortunate that the only way to get information about calibration uncertainties of this instrument is to contact by e-mail a man called Knutson.
An interferometer is capable of great accuracy in measuring wavelength but much less so of intensity.
Here the atmospheric readings are compared to a blackbody reference by an algorithm which is not produced for inspection.
Both the pyrgeometer and the FT-IR both appear to use the Stephan – Boltzmann equation and cavity theory.
(So in this respect they are not independent of each other.)
This is then applied to the atmosphere which has a filtered spectrum where a T^4 law is not appropriate.
Here is a much more realistic description of the use of the instrument.
Click to access ftir_spie.pdf
Relevant extract from Bryan’s reference:
Prediction of passive IR spectra is possible if the temperature, pressure, and concentration distribution for all layers are included in the radiation layer model. Calculations can be done by several computer programs like FASCODE14 and MODTRAN15. A certain atmospheric model can be confirmed (but not proved) by such calculations. The reverse procedure i.e. the evaluation of layer parameters from the open path spectra is not unambiguous, such that only semi quantitative results can be estimated.
Bryan,
Calibrating an FT-IR spectrophotometer is done using the Planck equation, not S-B. You can’t use the integrated form of the Planck equation when you’re not integrating. Are you saying that the Planck equation is wrong and that it does not accurately describe the radiation intensity of a blackbody as a function of wavelength or frequency? Talk about throwing out 100 years of physics! The reason you don’t see the algorithm is because it’s trivial. You obtain spectra at two black body temperatures so you have two intensities at each wavelength. The detector is linear so two points gives a calibration at each wavenumber. The process is described in the AERI handbook page 15. You can see the black body sources attached to the instrument. They’re the two cylinders on the end of the instrument.
John Millet,
Inverse problems are frequently difficult. But solutions are not impossible. Otherwise we wouldn’t be able to get crystal structures by x-ray diffraction.
DeWitt Payne
Perhaps reading your comment to John Millett above;
“Equation A gives a value of (S-B)c = 831 W/m²”
gave me the impression that the Stephan Boltzmann equation was being used.
John Millet also pointed out from my link that for intensity
“such that only semi quantitative results can be estimated.”
Would hardly be an improvement on the latest model Pyrgeometer uncertainty values of around 17W/m2
A full technical expositions of the instruments uncertainty factors can only be obtained by opening an e-mail correspondence with Mr Knuteson and so there is every reason to be cautious.
Bryan,
Your linked reference has almost nothing to do with measuring the clear sky atmospheric emission spectrum with the spectrometer pointed at the sky rather than some emitting background. If the spectrometer is pointed upwards so it sees nothing but sky, the background temperature is 3K so there is no absorption of radiation from the background. All the caveats about sensitivity in your linked article are largely irrelevant since they have to do with relatively short path remote sensing.
The comment to John Millet referred to his peculiar calibration equations for pyrgeometers, not FT_IR spectrophotometers. Pyrgeometer output is clearly dependent on the S-B equation, but it’s the emission level of the detecting surface that’s important. And that will be accurately described by the S-B equation.
For equations describing atmospheric thermodynamics, try reading Claes Johnson’s works. The equations are complex.
EG
Click to access climatethermoslayer.pdf
Click to access ambsblack.pdf
Check out the Etiquette:
Claes Johnson is warmly embraced by so many people who have no idea about physics. He is a smart guy no doubt.
Readers with a passing knowledge of physics realize he is in disagreement with many tens of thousands of physicists (nothing to do with climate science here) who have come before him, who are also very smart people.
As and when the physics world starts seriously questioning the last 100 years of physics fundamentals then this blog will open up discussion on whether or not quantum mechanics and statistical thermodynamics are just plain wrong.
Until that time we will stay with standard textbook physics.
I happily accept that IF standard textbook physics is wrong then climate science will need to be reviewed.
VeryTallGuy February 26, 2012 at 7:23 pm
1) For the purposes of your equation (Qo+Qe) = εσTe^4, the cause of Qo is irrelevant. That is, if the cloud layer is IR black then all IR radiation form the earth is absorbed then isotropically radiated. So Qo is via re-radiation. If the cloud layer were IR white, Qo would be the same though as a function of reflection. And IR gray would yield a smaller Qo then black or white, yet power would still be added.
The radiative barrier introduction, simply maximizes Qo…and yet with this maximum (Qo+Qe) = εσTe^4 demonstrable wrong.
2) Wood gasification is a process by which exhaust gases…never mind! My point, walls in the room do not make the fire burn hotter…they simply slow the loss.
LJ Ryan. Let’s forget (2)
For (1) I have to confess I’m utterly confused by what your position is.
You appear to state upthread that back radiation cannot affect the surface temperature (as the clouds are colder)
You also appear to state upthread that clouds do not radiate to the surface, rather they act as a “radiative insulator”
Yet here you state that the clouds do emit via “re-radiation”
To help me in my confusion could you please, using your own equations, write down equations explaining the energy flows between the surface and the clouds and vice-versa to help me understand?
VeryTallGuy from February 25, 2012 at 11:52 am
I did not suggest approximating slightly different shades of red…I suggested no visible to any visible. Is it possible to tell no visible radiation to faint red visible…even through an oven window?
However, assuming (Qo+Qe) = εσTe^4 is true, 509 C as a resultant temperature is generous. Emissivity of tungsten is .35 – .42… and view factor for a coiled wire centered in a cube, good luck.
I suppose it could be deduced by measuring temperature increase of a cold filament from the warm oven…backing out the known variables…but in the end view factor will be rather limiting. And I’m not just saying that to get on SoD’s good side…see watch: Atmospheric forcing is non-physical.
I still like the bulb in the box test for (Qo+Qe) = εσTe^4. Maybe instead of a standard bulb, we can reduce the view factor considerable by using a par bulb.
LJ Ryan,
I’ve been thinking a little more about this at a conceptual level to define a good experiment.
Let’s think about how to define a sensitive enough test
My nomenclature:
To is the initial temperature of the hot body
Te is the final temperature of the hot body
Qo is the corresponding thermal heat flux radiated = (Emissivity)(sigma)(To)^4 W/m2
Ah is the hot body area
Tc is the cold body temperature
Qc is the corresponding thermal heat flux radiated = (Emissivity)(sigma)(Tc)^4 W/m2
Ac is the cold body area
Pc is the power radiated by the cold body = QcAc
Fc-h is the view factor from cold to hot body
Qe is the extra heat flux received by the hot body as a result of introducing the cold body to the system.
Note that Qe is NOT equal to Qc
Qe=(Pc)(Fc-h)/(Ah) – power received by hot body divided by its area.
= Qc(Fc-h)(Ac/Ah)
=(emissivity)(sigma)(Tc^4)(Fc-h)(Ac/Ah)
As before, (Qe+Qo) = (emissivity)(sigma)(Te^4)
We’ll assume for simplicity that all bodies are black, or have the same emissivity, and cancel all the sigmas:
(Tc^4)(Fc-h)(Ac/Ah) + To^4 = Te^4
So for the effect to be significant, (Tc^4)(Fc-h)(Ac/Ah) must be a significant fraction of To^4. Note that the product (Fc-h)(Ac/Ah) cannot be greater than unity.
What this means in reality then is that:
1) Tc cannot be small compared to To. ie for a cold body to have a significant effect on the temperature of a hot body, it’s temperature cannot be MUCH lower.
2) (Fc-h)(Ac/Ah) cannot be small compared to unity. This is a measure of the geometry. Practically I think this means either the bodies must be very close (eg two parallel plates) or largely enclose each other (oven/contents or atmosphere/earth)
So if you want to observe an effect, your cold body must be close in temperature to the hot body. For the filament in oven example, if the filament is at 480 degrees C (just visible), the oven cannot be significantly below this – I’d guess 400 degrees C at least. That’s not possible with a domestic oven.
So, ruminating on this, I’d propose the following experiment.
For a hot body, choose a heating element, ideally embedded in a well conducting block. Suspend in the oven with the door open. Turn on and measure its surface temperature (eg with a contact thermocouple). If necessary adjust the current to ensure this is within the range of your oven. Once a steady temperature is reached, this is To.
Now, turn on the oven with a setpoint of say (To-20K). This is Tc and is high enough to measureably change the temperature of the heater but also for us to be confident that it is genuinely below the surface temperature of the heater.
Close the door and turn on the oven. The measured temperature will rise, due to absorption of radiation from the colder oven walls.
It really needs to be a vacuum oven so we can neglect convection. A fan oven would be worst of all. The higher the oven temperature the better, again as convection is relatively less significant for higher temperatures.
Prediction: in an oven at 180C, thermocouple at 200C initially, Te=277C
I’ve assumed that room temperature radiation is negligible in defining To, and that the factor (Fc-h)(Ac/Ah) is unity – I think this is correct for an enclosing body.
So radiation from our cold body at 180 degrees C will raise the hot body temperature from 200C to 277C.
This is likely an overestimate due to convection effects and neglecting room temperature radiation.
I lack the kit to do this. Perhaps you fancy an all expenses trip to Stockholm by doing the experiment and proving me wrong?
VeryTallGuy:
“So radiation from our cold body at 180 degrees C will raise the hot body temperature from 200C to 277C”.
The 200C hot body will fill the oven cavity with an energy wave field/photon gas with energy density consistent with that temperature. This would exceed the energy density of the cooler oven walls and energy would flow from the field to the walls which would heat up in response. Eventually the system (walls, cavity and hot body) would reach thermal equilibrium at 200C. With the thermostat set at 180C, turning the oven on would be met with nil response.
Oh, puhleeze. Obviously this won’t work if you use a thermostat to control the oven power. VTG is assuming, I think, that there is a constant power setting for the oven heating element that will produce a steady state temperature of 200 C, just like there is a constant power setting that will heat the cold body to a steady state temperature of 180 C.
I read VTG differently:
“Once a steady temperature is reached, this is To.
Now, turn on the oven with a setpoint of say (To-20K).”
Payne DeWitt and John Millett
Always good to get a response as it shows how unclear it’s possible to be – despite my trying to be really precise you’ve both misunderstood my intent. I need to try harder on clarity.
A reminder that LJ Ryan’s thesis is that it’s impossible for a “cold” body to radiate heat to a “hot” body and thereby raise the temperature of the “hot” body.
Now, you may feel this is so obviously in error it doesn’t need proof, either theoretical or experimental, but LJ Ryan feels otherwise. The theoretical is above.
Experimentally, I have proposed the following:
The “hot” body is an independent heating element or block, suspended in an oven. This has an electrical power source and it’s corresponding surface temperature is measured. We set the electrical current to give a temperature of this “hot” surface of 200C at ambient conditions. Ambient conditions are with the oven door open and the oven heating control set to off. This current is henceforth controlled to a constant level, thereby giving a constant power output.
The “cold” body is the walls of an oven. This is initially at ambient, but will then be controlled at 180C by the usual oven thermostat.
I propose that the temperature of the “hot” body will increase from 200C to around 277C as the “cold” oven rises from ambient to 180C, and that this is due to (mainly radiant) heat transfer from the relatively colder oven walls. The calculation is set out above.
This is, of course, entirely unsurprising
(John – I agree with your scenario. In mine the suspended “hot” element is constant power, not constant temperature. It needs to have a power output small compared to heat losses from the oven walls to the environment, otherwise the walls will rise above 180C. This will likely be the case for a small, say 50 – 100W source. However, the oven internal walls would always be *below* the surface temperature of the suspended “hot” surface regardless and still prove the theoretical point that a “cold” surface can raise the temperature of a “hot” surface)
A point of detail – I pondered about the relativities of convective and radiative heat transfer in this experiment.
Convective unforced heat transfer coefficients depend on geometry but are typically of the order of 5 W/m2K. We have ca 100K temperature difference from “hot” body to the “cold” oven air. This gives an order of magnitude convective heat flux of 500W/m2. The radiative flux of a black body at 277C is ca 5000W/m2. So I think it is legitimate to neglect convective heat transfer as a first approximation, even without using a vacuum oven for the experiment.
OK, that makes sense. I think it would be clearer, though, if you first adjusted the hot object outside the oven where the heat supplied by the object won’t change the ambient temperature. Then if you put it in a box or oven where the wall temperature at steady state will be 180C, the surface temperature of the heated object will indeed increase as the walls heat up.
This is actually a variation on the Wood experiment. If the oven walls were IR transparent, the temperature of the object would remain at 200C.
VeryTallGuy,
In fact, as soon as the part I ordered arrives, I can do an experiment almost identical to the one you described. Since I don’t have a pyrheliometer, a pyranometer and a pyrgeometer, I don’t know the exact amount of energy I’m receiving from the sun and the sky in my version of the Wood experiment. So I’m going to replace the sun with a heating pad running at constant power. But I can’t use an ordinary heating pad, so I’ve ordered one that can stand higher temperature. Then I can do a proper energy balance. But it’s on back order at the moment. I’m hoping to get it in early March.
Payne DeWitt
I did think about whether it was better to calibrate inside or outside the oven. My thinking was that to minimise changes from geometry causing convection, it’s worth doing it inside, notwithstanding the potential temperature increase of the oven.
If you’re really going to do this, it would be worthwhile calculating convection losses properly. Also, repeating at different Tc and To conditions.
I’m now on tenterhooks to see how close my prediction is!
Scienceofdoom:
“However, the sun does actually exist and the question is simply whether the presence of the (colder) atmosphere affects the surface temperature compared with if no atmosphere existed. It is The Three Body Problem.”
The “three body problem” article demonstrated compliance with conservation and entropy laws. While this constitutes a necessary condition for validating the matter-matter energy exchange model, it’s not a sufficient condition if similar compliance can be demonstrated in another model.
In the matter-field model, planet earth exists in solar and space radiation fields, on opposite hemispheres. The fields (at TOA) have temperatures of 394K and 3K, respectively, compared with the planet’s surface temperature of 288K. According to the Stephan-Boltzmann law, energy density (units: joules per cubic metre) is proportional to the fourth power of temperature. In accordance with entropy law, energy will flow from regions of higher energy density to regions of lower energy density, from the 394K solar field to the 288K planet and from the planet to 3K space.
A proportion (30%) of the solar energy flow in is reflected by the planet. The planet imports energy from the solar field over its disc area {pi*(radius)^2}
Energy in (per second) = 0.7*(3.14*10^6)*5.67*10^-8*{394^4 – 288^4} = 2.15*10^9 J
(Dimensional analysis: m2*J.s-1.m-2.K-4*K4*s = J)
The planet exports energy to space over a hemispherical surface {2*pi*(radius)^2} with emissivity “e” (less than 1).
Energy out (per second) = e* (0.63*10^7)*5.67*10^-8*{288^4 – 3^4} = e*2.46*10^9 J
Energy balance: Energy in = Energy out, when e = 0.87
Entropy: deltaS = deltaE/T
Solar field – planet : deltaS = -2.15*10^9 (1/394 – 1/288)
Planet – space: deltaS = -2.15*10^9 (1/288 – 1/3)
Total deltaS = -2.15*10^9{1/394 – 1/288 + 1/288 -1/3} which is greater than zero.
Conclusion: Both models of energy exchange – matter, matter and matter, field – comply with conservation and entropy laws. Compliance proves the validity of neither.
Raypierre,
It’s geometry isn’t it? X axis, temperature; Y axis, altitude; fixed lapse rate depicted as backward sloping line from the surface.
Trad (fixed): a vertical line from a point to the left of surface temperature intersecting the lapse rate.
Zrad: the point on the Y axis horizontally opposite the intersection noted above
Increase Z by dZ which raises the intersection point
DeWitt Payne,
Since you introduced gravity into the analysis, I would have thought that the forces on an element of rock below the surface would be of the same type as those on a parcel of air above it – gravity downwards and pressure differential upward, ignoring vertical shear.
“You don’t have a single lamp at a variable distance. The sources are all around you”.
True, an observation point within the atmosphere would be surrounded by a 3-D universe of radiating molecules, each separated from its nearest neighbour by about a thousand molecular diameters. Why would the observer, of molecular scale, sense the same intensity of radiation from the nearest molecule as from the farthest one? I suppose an answer might go along the lines that the observer wouldn’t be able to sense radiation from a discrete molecule at a particular distance; only universal radiation (akin to the CMB?). But the observer’s inability to distinguish different intensities from near or far radiators doesn’t rule such differences out.
My understanding of the relevant physical principles is: molecular radiation results from periodic acceleration of electrons in the atoms of an oscillating molecule; it is non-directional leaving the molecule; and it propagates on an expanding spherical surface. If this be true, the intensity must reduce as the surface area increases. For intensity to remain constant, wouldn’t radiation leaving the molecule have to be directional?
Scienceofdoom,
A good deal of comment relates to “observation” by pyrgeometers of longwave radiation from the sky of around 300 Wm-2 (DLR) providing incontrovertible evidence of atmospheric backradiation and the greenhouse effect. I find the evidence uncompelling for two reasons.
First, the instrument reading is in fact the arithmetical sum of an observed X flux and the computed S-B surface flux. KippZonen, an instrument maker, gives X values (negative) ranging from 5 to 90 Wm-2 for overcast and clear sky conditions, respectively. Stoffel reports pyrgeometer precision of +/- 15 Wm-2 or 30% of X for average sky conditions.
Second, the instrument is programmed to give an X observation consistent with DLR. This can be seen in the linear regression equation used in the calibration process which takes the form:
Wbb = K0 – K1*V – K2*(S-B)r – K3*{(S-B)d – (S-B)r}
where Wbb denotes the blackbody radiation from the calibrating radiating hemisphere;
V denotes the instrument’s thermopile output voltage;
(S-B) denotes the well-known equation relating energy flux and temperature;
the subscripts “r” and “d” denote the instrument’s receiver-detector plate and dome, respectively; and
K0 and Ki (1-3) are, respectively, the constant and coefficients to be derived from the regression.
That is, the sky is modeled in the pyrgeometer as a blackbody surface radiating according to its temperature; and the model output faithfully “observes” that to be the case.
Specifying the regression equation consistent with thermodynamic law, energy flowing in one direction only, from hot to cold, would produce a different set of coefficients in the laboratory calibration and, hence, a different reading in the field.
NREL Blackbody Calibration
The calibration is performed at 7 pyrgeometer case and blackbody temperature
combinations, then a linear regression is used to calculate the calibration coefficients.
The instrument outputs three electrical signals: thermopile voltage and two thermistor resistances which convert to temperatures of the dome and the case, from the latter of which the receiver temperature is derived and used in the regression equation. (Source: ARM Pyrgeometer Calibration and Field measurements; p24 Appendix. Tom Stoffel December 2005)
Testing the theory of radiative exchange is best attempted with a simpler model than the surface-atmosphere one – a body suspended in a vacuum within impervious walls. Entropy law says that, irrespective of the initial temperatures of the walls and the body, the system (walls, body and electromagnetic field) will come to thermal equilibrium. Then, the temperatures of the walls and body will be equal and constant. Radiative exchange theory posits accompanying dynamic radiative equilibrium – the body gaining as much energy from the walls as it loses to them. The theory holds for blackbody walls and body. It fails when different emissivities and absorptivities are assigned to the radiating surfaces.
Introducing the electromagnetic field into the analysis allows dynamic radiative equilibrium between the field and the walls and body, independently – a local closed-circuit energy flow. Why nature would trade energy in this nil-result way is not obvious. The more natural outcome, cessation of radiation at thermal equilibrium, has been attributed to Prevost:
“Pierre Prévost’s theory of heat and radiation exchange, stating that cold is the absence of heat, hot bodies radiate continually and that a lack of radiation indicates equilibrium with surroundings temperature. (Www.omega.math.albany.edu)
The apparent internal contradiction – “hot bodies radiate continually”…….”lack of radiation” disappears when “hot” is taken in the relative rather than the absolute sense – hotter than the surroundings.
SOD
The pyrgeometer’s algorithm takes the form: DLR = X + (S-B)s………[eqn 1]
where (S-B)s denotes the well-known equation relating energy density to temperature (assuming blackbody emissivity) and the subscript “s” denotes surface. One manufacturer gives typical values for X: 0 Wm-2 for an overcast sky; and -150 Wm-2 for clear sky.
From eqn 1, X = DLR – (S-B)s = 0 for overcast sky.
That is, DLR = (S-B)s which can be expressed: (e*S-B)a = (S-B)s ………[eqn 2]
Since in eqn 2, (S-B)a is less than (S-B)s, “e” must be greater than 1, an unphysical condition.
The regression equation takes the form:
In the field, the instrument records the three electrical signals, an algorithm converts two of these to temperatures, converts the temperatures to fluxes and, via the coefficients, outputs DLR, the equivalent of Wbb in the calibrating regression equation. That is, proof of the existence of DLR is built into the measuring technique, or a pyrgeometer doesn’t independently measure DLR.
The calibrating regression equation could be specified differently, say, to conform with the second law of thermodynamics
In a calibrating laboratory, X = (downward flux, Fd, from a radiator set above the pyrgeometer) – (upward flux, Fu, from the pyrgeometer’s receiving plate). These fluxes are calculated from the measured temperatures of the radiator and the receiver via S-B. That is, radiative exchange between the two bodies is assumed; and zero flux from the cooler of the radiator and receiver is precluded. In the field, therefore, the pyrgeometer must always find non-zero DLR. But that is not independent proof of its existence – rather, it is regurgitating the measuring instrument’s in-built proof.
An alternative assumption, one consistent with thermodynamic laws, could be incorporated into the calibration. Then X would be the energy lost by the warmer and gained by the cooler region. It would be measured by the rise in temperature
SOD wrote, in answer to Leonard Weinstein:
“The relationship between surface temperature, convection, lapse rate and emission of radiation to space from the troposphere is of course the most important determinant of the surface temperature”
Isn’t it necessary to distinguish between temperature level and variation? Climate system processes determine the variations (diurnal, seasonal and inter-glacial) in surface temperature, not its level (Ts) which reflects the internal energy of the whole planet. The internal energy of the climate system, a fraction of that of the whole, is reflected in its effective radiating temperature (Ta) which, therefore, must be less than Ts. Kramm and Dlugi’s endorsement of G&T’s finding, that the arithmetical excess of Ts over Ta is a “meaningless number” (and says nothing about the greenhouse effect), is warranted IMO.
The Open letter by 38 scientists led by Kevin Trenberth, including 5 Australians, 3 from Melbourne, 2 from Sydney:
We are the climate experts
Models tell us: Non-surface warming = deep ocean warming (which we can’t measure as yet)
(President Lincoln’s) National Academy of Science is with us.
97% of actively-publishing scientists are also with us.
The greenhouse effect
A typical graphical explanation of the greenhouse effect has the following features:
1. A downward sloping arrow depicting incoming solar radiation fixed in quantity after allowing for a constant reflected proportion or albedo.
2. A solid horizontal line depicting the surface from which a vertical upwards line depicts outgoing terrestrial radiation.
3. A dotted horizontal line above the surface depicting the atmosphere from which vertical lines extend up an down depicting atmospheric radiation of equal magnitude in both directions.
4. All radiation quantified by the S-B equation
5. All sources of radiation with equal emissivities and all equal to unity
6. A calculation of Te, the effective radiating temperature of the planet or the temperature of a blackbody required to balance solar irradiance = 255K which is 33K less than the surface temperature, expressing the magnitude of the greenhouse effect.
Comments:
Point 6:
Comparing the effective planetary radiating temperature with the observed surface temperature is comparing apples and oranges. The effective radiating temperature is notional and relates to the energy density of the planetary climate system. The surface temperature, by contrast, is real and relates to the total planetary energy density. Whole planet energy density exceeds that of a component of it. viz.,the climate system. Energy balances within the climate system affect surface temperature variability (diurnal, seasonal and inter-glacial), not its level, (Ts). The surface temperature therefore exceeds the other but the arithmetical difference between them is meaningless. A proper, though still meaningless, temperature difference would be that between the surface’s and the actual mean radiating temperature of the climate system. The latter temperature can be derived from the notional one by accounting for two properties governing radiation in the climate system: emissivity and reduced energy density with distance from source. Both adjustments lead to Ta>Te. The smaller difference between Ts and Ta, however, is still meaningless as a measure of the strength of the greenhouse effect.
The greenhouse effect is attributed to the presence in the atmosphere of radiatively-active molecules. Increasing the atmospheric concentration of such molecules by burning fossil fuels, mainstream climate science claims, warms the surface. Extracting and burning fossil fuels transfers mass from the planetary crust to its atmosphere. The process increases the energy density of the climate system but not of the planetary whole. That is, Ta would rise relative to Ts and Te which are unaffected. This implies a reduction in the rate at which temperature reduces with height above the surface. This rate, the dry adiabatic lapse rate, varies inversely with the specific heat (at constant pressure) of the atmosphere. Of the gases making up the atmosphere, CO2 has the lowest specific heat. A CO2-enriched atmosphere would have a higher lapse rate – temperature at a given height above the surface would be lower than in a normal atmosphere. ????
The greenhouse effect is better understood by thought-comparing atmospheres with and without radiatively-active gases. In both cases solar energy gained at the surface and thermalised is transported to the atmosphere mostly by mass transfer, cooling the surface and heating the atmosphere. An atmosphere lacking the capacity to cool by radiating to space would continue to warm until Ta = Ts. This would imply an isothermal climate system which, according to the Ideal Gas Law in a gaseous atmosphere bound by earth’s gravity, is unphysical. The existence of a radiatively-active component in the system gives it the necessary cooling mechanism. That is, the “greenhouse” effect is, perversely, a cooling one.
It might appear that enhancing the greenhouse effect, by increasing the atmospheric concentration of the radiatively-active component, would increase the effectiveness of the cooling mechanism, beneficially. However, radiative activity involves both emission and absorption. The radiatively-active molecules absorb both incoming solar energy and outgoing terrestrial energy. Atmospheric absorption of solar energy occurs mainly by H2O molecules in liquid phase in clouds. Thermalised, the absorbed energy warms the cloud relative to the surrounding air and the cloud cools by expanding The lower surface of the emits bestows a cooling effect on the surface by replacing direct short wave length irradiation with the long wave diffuse variety weakened according to the inverse square rule. ????????
A radiatively active atmosphere also plays a supporting role in transporting energy from the surface to the atmosphere. The contribution varies directly with the temperature difference between the surface and its atmospheric surroundings. Some of the contribution goes directly to space, bypassing the atmosphere through the “atmospheric window” within a known band of wavelengths. However, the radiatively-active component of the atmosphere gains energy, in descending order of magnitude, through: molecular collision with the much more prevalent non-radiative component; absorption of incoming short wave; and absorption of outgoing long wave. Molecular radiation, being isotropic or diffuse in nature, transports energy into the surrounding electromagnetic field on an expanding spherical front, the energy density on which diminishes with distance from the source. Having regard for the three spatial axes and the positive and negative directions along each, five-sixths of the energy from molecular radiation flows outwards to space, the remainder inwards towards the surface.
This “back-radiation” is said either to heat the surface or to slow its rate of cooling, ie, to make it warmer than it otherwise would be, and this, it is said, constitutes the greenhouse effect. Either proposition violates the second law of thermodynamics which prohibits spontaneous flow of heat from colder to warmer regions. Climate science argues that there is no conflict: the surface emits more energy than it receives and “net heat” flows properly thermodynamically from warm to cool. This requires dynamic radiative equilibrium, equal quantities of energy entering and leaving simultaneously, concomitant with static thermal equilibrium. While this condition is feasible with theoretical blackbodies, it is not generally so with real greybodies with different emissivities.
Think of a body
Prevost hypothesised radiative exchange in 1792 – all bodies radiate all of the time with strength increasing with temperature – in order to avoid the question: How would bodies in a vacuum, with no connecting medium, know to stop radiating on reaching thermal equilibrium? The hypothesis has yet to be demonstrated experimentally. Never, anywhere, is there nothingness : always, everywhere, is an electromagnetic field exhibiting properties of energy density, mass, momentum and pressure. The radiative exchange, therefore, would be between bodies and their surrounding electromagnetic field, rather than between bodies. A cooling body, by definition one with energy density exceeding that of the surrounding field, would lose energy to the field, which loss would be the field’s gain in accord with the first law of thermodynamics. As the body cooled, its rate of energy loss would slow, eventually to zero at thermal equilibrium, a condition accompanied by equality of energy density between body and field. This process in reverse would apply to a body with energy density less than that of the surrounding field. Energy would flow from the higher-density field to the body and warm it. In Prevost’s time scientists envisaged “cold flow” to explain a person’s sense of feeling colder standing next to a block of ice. The sense of temperature fall in fact reflects a flow of energy from the person into the field as its energy density reduces as the ice draws energy from it to increase its own energy density and melt. The ice would still melt in the absence of the person, demonstrating the field’s fundamental role in the process. The presence of the person, to create a 3-body problem, doesn’t displace the field’s role in the melting of the ice.
The earth’s atmosphere, a spherical shell of thickness 120km, say, is essentially an electromagnetic field populated by a small volumetric proportion of suspended matter in the form of gas molecules (and aerosols), a small fraction of which are radiatively active (the “greenhouse” gases), a minor fraction of which are CO2 molecules. The radiatively active molecules absorb energy from the field and emit energy into it, as does the surface. There is no radiation from the atmosphere to the surface. During the day the
The existence of a radiatively-active atmosphere, together with the lapse rate, ensures that the actual mean radiating temperature, Ta, is lower than the surface temperature. Ta can be derived from Te by accounting for: emissivity less than unity ie Ta>Te; and flux at TOA diminished by the inverse square rule.
Point 5: Emissivity is a property of the radiating surface and is a measure of radiating efficiency relative to the theoretical maximum, a blackbody with unit emissivity. Though according unit emissivity to the solar photosphere seems a reasonable approximation, extending the approximation to the planetary atmosphere and variegated surface seems questionable. That is, the S-B equations should include specific emissivities and the atmospheric energy balance would read: e*sigma Ta^4 = Te^4 and Ta>Te.
Point 3: Atmospheric radiation is diffuse or isotropic in nature but analytically it can be directed according to the 6 cardinal axes of 3-D space of which only one is directed away from outer space and towards the surface. That is the depicted atmospheric energy balance should be in the proportions 5 up and 1 down. Therefore 5/6 sigma Ta^4 = Te^4 and Ta>Te.
Radiation energy propagates on a spherical front centred on the source and the flux therefore diminishes with the square of distance from source. Therefore the atmospheric energy balance would read: 5/6 * (z/r)^-2 sigma Ta^4 = Te^4 where “z” is distance from source and “r” is the radius of the source.
1. The climate system comprises the atmosphere, the oceans’ thermocline (say to a depth of 700m) and the crust to a depth of plant root system. The energy content of the system is only a fraction (unknown) of the total planetary energy content. The planetary surface temperature reflects total energy content and therefore is not determined by the climate system, though it is influenced by it.
The atmosphere extends for about 120 km above the surface where ultra violet radiation from the sun dissociates N2 and O2 molecules creating the ionosphere and giving rise to temperatures exceeding that at the surface. This layer of the atmosphere, called the thermosphere, extends surfacewards to about 90km, the temperature falling to about 180K, the coldest region of the atmosphere. Temperatures rise to about 250K over the next approx 40km descent in the next layer called the mesosphere. Temperatures fall again in the next 30km descent to about 200K to the tropopause which separates the stratosphere from the troposphere which descends to the surface and is where most of the weather occurs. Absorption of solar radiation by ozone in the stratosphere causes the rise in temperature with height above the surface. The temperature decline with height above the surface is the result of a balance between convective heat transport from the surface and radiative cooling in the troposphere.
The height of the tropopause varies with latitude: it is highest in the tropics, lower at the poles. Accordingly, the tropical tropopause is the coldest region in the troposphere; and at higher latitudes temperatures above about 10km are relatively constant. Heat transported in the troposphere from the tropics to the poles, together with less efficient radiation from atmospheric gases than from the surface, results in the temperature inversion, particularly in the sun-less winter.
Temperature variation: seasonal by latitude; seasonal at 75N; annual mean by latitude
2. The volume of the spherical shell we call the atmosphere is occupied predominantly by electromagnetic fields which are extension of the sun’s field during the day and, during the night, of deep space’s. A small fraction of the volume is occupied by terrestrial matter in the form of gas molecules. A small fraction of these molecules are radiatively active i.e. they interact with the electromagnetic field.
Avogadro, 1811: atom, the smallest unit of a substance in a chemical reaction; molecule, the smallest stable stand-alone unit of a substance; equal volumes of gases at a given temperature and pressure contain equal numbers of molecules.
Bernoulli, 1739, explained Boyle’s law ( pV = 1/3Mv^2) or p = 1/3xdensity x speed squared, from which molecular speed can be estimated approximately – 5*10^2 m/s.
Consider a cylindrical enclosure with unit cross-sectional area and length numerically equal to the molecular speed, c, containing molecules at a density of n per unit volume. In the time taken by the farthest molecule to traverse the cylinder in one direction, 1/c seconds, one sixth of the number of contained molecules, nc/6, each with momentum mc, would rebound elastically from the other end of the cylinder with resultant momentum change per second per unit area = nc/6 . 2mc = force per unit area = pressure.
Therefore, p = 1/3 nm c^2 = 1/3 x density x speed squared.
Young and Laplace
Estimated approximately the molecular diameter (1.5*10^-8cm) by considering the work done in overcoming inter-molecular forces in the cases of latent heat and surface tension. Postulate a distance d between molecules less than which the inter-molecular attractive force is a constant f and above which it is zero. In order to escape f a molecule below the liquid surface must travel a distance 2d. Work done per unit mass is therefore 2fd/m = latent heat.
Surface tension: A molecule within a distance d of the surface will be pulled back into the body of the liquid by the force f. In creating unit area of new free surface, all of the molecules in volume d will move on average distance d/2. Work done per molecule = 1/2fd. Number of molecules to be migrated = mass/unit volume x volume / mass per molecule = density x d/m.
Therefore work done = ½ x density x fd^2/m = S
L = 2fd/m
S = 1/2fd^2/m x density
d = Lm/2f = S x 2m/(density x fd)
L = 4S x f / (density x fd) = 4S/(density x d)
Therefore dL = 4S/density From which d = 4S/Lxdensity
For liquid water: S = 75 ergs/cm2; L = 2*10^10 ergs/g; density = 1g/cm^3
d = 4*75/ 2*10^10 = 1.5*10^-8 ergs cm-2/(ergs g-1 gcm-3) = ergs cm-2 ergs-1 cm3 = cm OK
Clausius and Clerk Maxwell 1857-59
dropped Bernoulli’s constant speed assumption in favour of a distribution of speeds in which the most probable speed is a bit faster than the root mean square speed the equivalent of Bernoulli’s assumption. Maxwell found:
f(v) = constant x v^2 exp(-mv^2/2kT) where k is Boltzmann’s constant = 1.38*10^-16 ergs/K
= R/N = gas constant per mole/Avogadro’s number.
Zartmann 1931 and Ko 1934: A rotating cylinder with a glass plate on which a deposit of bismuth atoms evaporated in an oven, collimated and introduced into the cylinder once a revolution through a slit opposite the receiving plate. Faster molecules would deposit at the leading edge of the plate and slower ones at the trailing edge. Hence the deposit was analogous to the velocity spectrum.
Rainwater and Havens 1946: neutrons produced in a cyclotron, slowed down and brought, via collisions, into temperature equilibrium in a paraffin block from which they diffuse out and are collimated and fall upon a counter. The cyclotron and the counter, separated by distance l are activated for only a few microseconds at a time, the counter with a variable lag of time t. The system will record only to neutrons with speed l/t. A plot of the number of recorded pulses against time of flight t is the velocity distribution.
Mean free path
A cylinder of a fluid, of density n molecules per unit volume, of radius equal to the molecular diameter d and length equal to the molecular speed by an element of time dt contains
n pii d^2vdt molecules which is the number of collisions a single molecule would make traversing the cylinder in time dt. The mean free path, lamda, equals the length of the cylinder divided by the number of collisions = 1/n pii d^2, more correctly 1/Root2 n pii d^2 accounting for the Maxwellian distribution of molecular velocities.
The mean free path is a mean of a distribution of distances between successive collisions. The probability of no collision in distance x is p(x) and the probability of collision in the next dx is proportional to dx and = say, adx. The the probability of no collision in dx = (1-adx)
The probability of no collision in distance (x + dx) = probability of no collision in distance x and no collision in a further dx.
Therefore p(x + dx) = p(x) X (1-adx)
p(x) + dp/dx*dx = p(x) – a p(x)dx Using taylor’s expansion to two terms
whence p(x) = constant X e ^-ax = e^-ax ( for x=0, p(x)=1 ie the constant disappears)
The probability of collision in dx at x = probability of no collision in distance x X probability of collision in dx = p(x) a dx from which lamda = 1/a and finally p(x) = exp(-x/lamda)
magnitude of lamda
known: 1 g of liquid H2O ( 1/16 g molecule) occupies 1 cc from which d ~ 2*10^-8
volume occupied by one molecule ~ d^3 ~ 10^-23 cc
therefore number of molecules in 1 g ~ 10^23
therefore number of molecules in 1 g molecule ~ 16*10^23 ~ 2*10^24 = N
known: 1 mole (= 1 g molecule) of any gas or vapour occupies 22.4 litres (~ 2*10^4 cc) at NTP and contains the same number of molecules, N
hence n (number of molecules per cc) ~ 2*10^24/2*10^4 = 10^20
Therefore, lamda = 1/n pii d^2 = 1/(10^20 pii 4*10^-16) ~ 10^-5 cm at NTP
This is comparable to the wavelength of visible light making direct observation difficult.
Lamda is inversely proportional to the number of molecules which is directly proportional to pressure. At a pressure of 10^-3 mm mercury, lamda ~ 760/10^-3 times lamda NTP
~ 10^6 times lamda NTP ~ 10cm
Viscosity and diffusion
Maxwell shoed that viscosity of a gas is independent of its pressure (except at very low pressures).
The coefficient of viscosity = 1/3 nm vbar lamda = 1/3 density vbar lamda = 1/3 mvbar(nlamda)
The coefficient of diffusion = 1/3 vbar lamda = coefficient of viscosity/density
Units: viscosity – g cm-3 cm sec-1 cm = g cm-1 sec-1 = mass per distance per time
diffusion – distance squared per time
The actual distance between collisions
3. Owing to earth’s distance from the sources of these external fields, their waves propagate in uniform directions and are called direct radiation. Terrestrial radiation emanating from the surface and from the radiatively-active atmospheric molecules is continuous as opposed to the diurnal switching nature of the two external sources. It is also different in that it is diffuse i.e. it propagates on expanding hemispherical or spherical fronts centred on a small surface area or an atmospheric molecule, respectively, into the surrounding field in all directions, not in a particular direction. Distributing energy emitted along the six cardinal axes, five sixths would be directed outwards towards space beyond the atmosphere, only one sixth inwards towards the surface.
4. The radiatively-active molecules absorb energy from the electromagnetic field as well as emit into it. They absorb from the sun’s field and, to a greater extent, from the terrestrial field. They also receive energy from the predominant non-radiatively-active molecules through molecular collision. (
5. An electromagnetic field exerts a pressure which is proportional to its intensity. During the day, the greater intensity and pressure of the solar field would dominate the terrestrial one suppressing outwards oriented waves. At night, the situation is reversed, outward terrestrial waves dominating incoming ones from space. Thus the climate system warms during the day and cools at night.
6. The IPCC’s global mean energy budget shows the surface reflecting about 15% of the solar irradiation, absorbing the remainder. It also shows the surface losing energy mainly through mass transfer, and to a lesser extent by radiation, to the atmosphere. Atmospheric molecules are heated by contact with the surface and carried aloft by convection currents. This heats the atmosphere relative to the surface. Over the oceans, surface H2O molecules change phase from liquid to vapour (evaporation) extracting latent heat from the surface which is carried aloft by convection. In the formation of clouds, the reverse phase change, the latent heat converts to sensible heat warming the cloud
What a disaster!
Scienceofdoom:
“However, the sun does actually exist and the question is simply whether the presence of the (colder) atmosphere affects the surface temperature compared with if no atmosphere existed. It is The Three Body Problem.”
The “three body problem” article demonstrated compliance with conservation and entropy laws. While this constitutes a necessary condition for validating the matter-matter energy exchange model, it’s not a sufficient condition if similar compliance can be demonstrated in another model.
In the matter-field model, planet earth exists in solar and space radiation fields, on opposite hemispheres. The fields (at TOA) have temperatures of 394K and 3K, respectively, compared with the planet’s surface temperature of 288K. According to the Stephan-Boltzmann law, energy density (units: joules per cubic metre) is proportional to the fourth power of temperature. In accordance with entropy law, energy will flow from regions of higher energy density to regions of lower energy density, from the 394K solar field to the 288K planet and from the planet to 3K space.
A proportion (30%) of the solar energy flow in is reflected by the planet. The planet imports energy from the solar field over its disc area {pi*(radius)^2}
Energy in (per second) = 0.7*(3.14*10^6)*5.67*10^-8*{394^4 – 288^4} = 2.15*10^9 J
(Dimensional analysis: m2*J.s-1.m-2.K-4*K4*s = J)
The planet exports energy to space over a hemispherical surface {2*pi*(radius)^2} with emissivity “e” (less than 1).
Energy out (per second) = e* (0.63*10^7)*5.67*10^-8*{288^4 – 3^4} = e*2.46*10^9 J
Energy balance: Energy in = Energy out, when e = 0.87
Entropy: deltaS = deltaE/T
Solar field – planet : deltaS = -2.15*10^9 (1/394 – 1/288)
Planet – space: deltaS = -2.15*10^9 (1/288 – 1/3)
Total deltaS = -2.15*10^9{1/394 – 1/288 + 1/288 -1/3} which is greater than zero.
Conclusion: Both models of energy exchange – matter, matter and matter, field – comply with conservation and entropy laws. Compliance proves the validity of neither.
John Millet,
I’ll address one point. I doubt I have the patience to do more:
To answer your last question first, yes, it is directional. But the direction is random for an individual molecule.
Molecular radiation in the thermal IR has nothing to do with electron energy levels or electrons oscillating. A molecule isn’t equivalent to a radio antenna. A molecule that has an electric or magnetic dipole can vibrate and rotate. The rotational and vibrational energy levels are quantized. The rule is that you can only change an energy level quantum number by one for a given transition. The CO2 15 μm band results from the transition from the first bending vibrational level to the ground state. The band structure comes from the fact that a large number of rotational energy levels are populated and those can change by ±1 or not change too when the vibrational energy level changes.
Try asking questions rather than making uninformed assertions.
DeWitt Payne,
I raised this issue in Back-radiation Part 3. The question I put there was: Which physical principle transforms isotropic radiative flux from atmospheric molecules, which decays with distance from source, into a one-directional constant value flux?
With further consideration, the question has reduced to: Which physical principle supports the application of the S-B law to a horizontal atmospheric plane populated by CO2 molecules at a spatial concentration of 500 parts per million?
Workings: Assume a 1D atmospheric column, 1 metre square base, 20km high; and CO2 volume concentration (benign) = 280 parts per million parts of molecular matter.
Molecular matter exists in the atmosphere in the proportion 90 parts per million:
[Avogadro : 6 x 10^23 molecules (1.5 x 10^-8 cm diameter) occupy 22.4 litres:
6 x 10^23 x (1.5 x 10^-8)^3 / (22.4 x 10^3) = 0.9 x 10^(23 -24- 3) ]
CO2 molecules exist in the atmosphere in the proportion 280 parts per million parts of molecular matter.
Therefore, the spatial concentration of CO2 = 90*10^-6 X 280*10^-6
= 25.2 parts per billion.
The volume to cross section ratio in the 20km column is 2×10^4.
Therefore, the planar concentration of CO2 = 25.2*10^-9 x 2*10^4
= 500 parts per million.
Hence the question: What considerations allow S-B to be applied to a “surface” occupied by such a small proportion of matter?
Of course the matter is neither contiguous nor stationary. Does the incessant movement of very large numbers of individual molecules and the very high frequency of interactions with the surrounding energy field and non-radiative molecules generate a “virtual surface” to which S-B can be properly applied? If not, what?
That’s today’s question.
.
You’re drastically over complicating the situation. It’s very simple. You measure radiation flux. You convert it to a temperature by assuming that it was radiated by a black body. This is called the effective temperature or Teff. It’s also how an IR thermometer works. In no way does this mean that you have to believe that the radiation was actually emitted by a black body.
Also your calculations are irrelevant because your assumption that emission comes from a surface is wrong. It comes from the entire depth of the atmosphere. More precisely, the effective altitude of emission looking up is the altitude where the optical depth reaches a value of one. That varies with the wavelength of the radiation. At the peak of the CO2 band, the altitude is measured in centimeters. In the 12-14μm ‘window’ it may never reach a value of one on a clear day outside of the tropics.
Do you deny that there is a flux of radiation emitted from the atmosphere towards the surface? If there is such a flux, you can always calculate an effective temperature of that flux by using the S-B equation. That violates no known physical principles.
VeryTallGuy
So view factor and geometry are primary to actualizing cold to hot, thermal radiation… and delta T can not be too large…do I have this right?
Maintaining all the dimensioning and procedural conditions you set forward… and only change starting temperature: make Tc = 2 C and Th = 7C.
Are you telling me Te will actually radiated at 56 C?
LJ Ryan
It would be really good if you could honour the title of the post and use some *equations* rather than blah blah blah.
I have now put in quite a lot of time not only defining the *equations* for heat transfer in this system, but also solving them and using that solution to suggest an experimental validation, together with an actual prediction.
You have not indicated if you now agree with these *equations*. If you do, letting me know that my hard work has been appreciated would seem only polite.
If you do not, I would very much appreciate you putting in a similar effort to define your own *equations* for heat transfer in this system, solve them and let us know the result, together with your own prediction as to what would happen.
As to Tc=2C, Th=7. You have not defined To. I’ll assume you mean To = 7C.
Let’s define a new variable Tcalib, the initial calibration temperature at which the power Qo and corresponding current required to heat the hot body to To are defined. In my experiment this is ambient, say 20C. Ideally it would be 0K.
The experiment requires this calibration. The whole point is to demonstrate that walls warmer than the calibration (ie ambient) temperature, but still colder than the hot body, cause the temperature of the hot body to rise. Your temperatures are *below* ambient, so you need to think up a different calibration, either with an entirely different procedure, or somehow using temperatures significantly below 2C.
Again, using *equations*, we could characterise this by a further constraint on the experimental conditions: (Tc-Tcalib)/(To-Tc)>>1, which ensures that (Th-To) is significant and therefore readily measurable and distinguishable from other sources of variability. For my proposal this dimensionless quantity is 8.
Secondly:
We’ll now define Qcalib as radiative gain of the hot body during calibration from its surrounds.
I have assumed implicitly that during calibration, radiative heat gain from surroundings is small compared to the output from the electric heater. We can calculate the relative magnitudes: (Qo/Qcalib)=(To/Tcalib)^4 = 6.8 – which is reasonable I think. Your “calculation” of 56 degrees would be valid if Qcalib were small compared to Qo. If for your experiment we use the same ratio, you require a calibration temperature of -102C. If such an experiment were practical, 56C seems intuitively reasonable for Te.
Thirdly, one less obvious reason: Radiative heat falls as the 4th power of temperature. Very rapidly convection and conduction will take over at lower temperatures, so the higher the temperature the better. As I did in my previous post, we can use *equations* to calculate these effects. Put dimensionlessly, (sigmaTh^4)/(U(Th-Tc))>>1. where U is the overall convective heat transfer coefficient. This quantity is ca. 10 for my proposal. For yours….?
Finally I suspect your temperatures are too close to experimentally distinguish given likely temperature gradients across both the cold walls and hot body.
Your calculation of Te=56 is wrong for these reasons. Yet again, you have plugged in numbers to equations without attempting to understand them. Unsurprisingly, you get the wrong answer.
There’s a great similar worked example here:
http://moyhu.blogspot.com/2012/02/miracles-of-2lot.html
VeryTallGuy
Occasionally I reply without having sufficient time to allow an adequate response. I apologize curtness of my last post.
Regarding equations and my “blah blah blah”, as I said to SoD a month ago, your equations are no different then mine…I think.
The qualifier, “I think” is (Qo+Qe) = εσTe^4 . This equation is in direct conflict with black body radiation…specifically, Kirchhoff’s cavity theorization/experiment.
Radiation streams into a cavity through a small aperture…this radiation is continually absorbed and re-radiated by cavity walls…eventually the cavity will come to an equilibrium temperature.
If however, flux can be added as “I think” supposes, Q of source will not equal σT^4 but rather the sum of re-radiated flux between walls of the cavity. That is, σT^4 = Qn + Qn+1 + Qn+2 …. thus T will forever increase and thus black body is irrelevant.
To illiterate the absurdity of “I think”, I proposed the pan in the oven scenario. Both you and SoD and disagreed with the answer showing the pan exceeding oven temperature…both you and SoD went on for pages an pages with the how and why I was wrong. And now, you’ve detailed an example wherein a thermal mass, in an OVEN, betters oven temperature.
Ok, great! Does your oven and thermal mass example work at other design temperatures? Apparently not. See, although ambient temp. is irrelevant it needs to be considered . Convection at low temper…blah blah blah…..
My take on your model.
Tc = 275K
To = 280K
Te = 330K
Tcalib = 293K
Tc-Tcalib)/(To-Tc)>>1 but my take -3.6 >1 348/5U = 28 >>1
Unsurprisingly, my wrong answer is wrong, because the physical world does not subscribe to “I think”.
VeryTallGuy
A couple of my calculations didn’t copy over…
Tc = 275K
To = 280K
Te = 330K
Tcalib = 293K
Tc-Tcalib)/(To-Tc)>>1 but my take -3.6 >1 348/5U = 28 >>1
Unsurprisingly, my wrong answer is wrong, because the physical world does not subscribe to “I think”.
again:
Tc = 275K
To = 280K
Te = 330K
Tcalib = 293K
Tc-Tcalib)/(To-Tc)>>1 but my take -3.6 >1 348/5U = 28 >>1
Unsurprisingly, my wrong answer is wrong, because the physical world does not subscribe to “I think”.
fourth time:
(Tc-Tcalib)/(To-Tc) >> 1 but my take -3.6 > 1 348/5U = 28 >>1
VeryTallGuy
Fifth time…I’ll try to block quote my calculations:
Final time…just the answers
Your dimensionless quantity 8 is my -3.6. Does this mean Tcalib influence Tc…only to advantage your “I think”
Your secondly: 6.8 is my .83 What does this mean, I don’t know but apparently 6.8 is better.
Thirdly: Your U of 10 my 2.4 and therefore your (sigmaTh^4)/(U(Th-Tc))>>1 is 14 mine is 28.
LJ Ryan.
I take it from your repsonse that you do not agree that my equations are appropriate to the system.
Please set out your own – equations, not blah blah blah.
As to your numbers – your interpretation is wrong because you require a heat sink rather than source as your “oven” temperatures are below ambient. The equations will still work, although the experiment would be close to impossible.
DeWitt Payne March 5,
We have come some distance on this journey. Let me summarise:
The flux from molecular radiators in the atmosphere, individually and collectively, is subject to decay according to the inverse square law;
Your “Assume an infinite plane with 100W bulbs spaced at 1m intervals horizontally and vertically. No matter how far you get from the plane, the light intensity you observe will be constant. Strictly speaking, the plane should have a uniform flux density” led me into a cul de sac of over-complicatedness. Now I have to come to grips with the simple metric, optical depth.
Meanwhile, physics textbooks convey the impression that radiation is a surface phenomenon: “The surface of every body …….emits energy, in the form of thermal radiation, due to the motion of electric charges near the surface” (Fundamentals of Modern Pysics: Eisberg, Wiley, 1961).
As to your question, the holding answer is “neither deny nor confirm”, though I have expressed my reservations, as you will be aware from our conversation, upon which a separate comment will elaborate..
It’s a surface phenomenon if the body is perfectly opaque, which is sort of obvious on its face. It’s not a strictly surface phenomenon if the body has non-zero transmittance. Water is blue rather than black because it’s quite transparent in the visible. But it does absorb longer wavelengths more strongly so you see scattered blue light because the red end of the spectrum is more strongly absorbed. OTOH, it’s nearly perfectly opaque in the thermal IR so emission comes from very close to the surface.
And that would be continuum thermal radiation, not molecular emission. You don’t get much continuum emission from a gas because the molecules aren’t sharing electrons.
DeWitt Payne,
I offer the following argument:
1. The concept of back-radiation rests on Prevost’s 1791 theory of exchanges and on observation by instruments based on the physical principles of the thermocouple (pyrgeometer) or of interferomtry (FT-IR)
2. The theory of exchanges implies the co-existence of dynamic radiative equilibrium and static thermal equilibrium. For matter-matter exchange this condition applies only for blackbodies. Consider opposing surface elements each of area dA on infinite parallel planes of equal temperature. S-B gives the 2-way fluxes between them, equal in magnitude. Therefore, each is importing from and exporting to the other equal quantities of energy in a closed loop. Why would nature trade energy in this way?
3. For non-blackbodies, that is, all real bodies, the magnitude of the flux is modified by the emissivity “e” of the radiating surface. As well, the proportion of the flux imported is modified by the absorptivity “a” of the absorbing surface. For surface element 1:
Energy in = a1*e2*(S-B)2*dA
Energy out = e1*(S-B)1*dA
By Kirchoff’s law, e = a ; and at thermal equilibrium, (S-B)1 = (S-B)2
Therefore at thermal and radiative equilibria: e1*e2 = e1, or e2 = 1 = blackbody.
The argument being symmetrical, both bodies must be blackbodies, an analytical result contradicting its premise.
4. Matter- field energy exchange overcomes this limiting condition. Thermal and radiative equilibria would co-exist at each surface independently. Each matter surface would import from and export to the field equal quantities of energy, according to its particular emissivity and absorptivity, in a local closed loop. Again, why would nature trade energy in this way?
5. Pending an answer to the question raised in points 2 and 4, the interim conclusion is that surface radiation ceases at thermal equilibrium. This is consistent with experimental findings in 1817 (Dulong and Petit) and in 1865 (Tyndall) that the rate of cooling of a body is a function of the temperatures of itself and of its surroundings. The smaller the temperature difference the slower the body will cool (lose energy), until at zero difference it will no longer be losing energy, that is, no longer radiating – unless in the curious closed-loop manner.
6. The closed-loop energy exchange between matter and field ( matter-matter energy exchange is untenable – point 3) is a necessary corollary of the dictum that all bodies with temperatures above absolute zero radiate energy. Kelvin proposed an “absolute temperature scale in which a unit of heat descending from a body A at the temperature T° of this scale, to a body B at the temperature (T−1)°, would give out the same mechanical effect [work], whatever be the number T. Such a scale would be quite independent of the physical properties of any specific substance.[16] By employing such a “waterfall”, Thomson postulated that a point would be reached at which no further heat (caloric) could be transferred, the point of absolute zero about which Guillaume Amontons had speculated in 1702″. (Wikipedia)
It is not obvious from this account that Kelvin thought that all matter above absolute zero loses energy by radiation according to its temperature. On the contrary, the temperature difference between the body and surroundings, not the body’s temperature alone, determines energy loss. This is consistent with earlier experimental findings (point 5).
7. All of this can be related to the climate system through the global mean energy balance. In K&T’s version, the surface loses about 60 Wm-2 energy by radiation, a function of surface temperature and that of the atmosphere above it, accompanied by a redundant closed loop of some 300 Wm-2 between the surface and atmosphere.
8. If back-radiation is redundant, what do pyrgeometers and interferometers observe? A good question for further consideration.
You’re ignoring reflection. For parallel planes at the same temperature, the emissivity/absorptivity of each plane doesn’t matter as long as it isn’t identically zero. Assume the planes are opaque so transmissivity equals zero. Then if the absorptivity, a, is less than one, the reflectivity must be 1-a. From the viewpoint of each plane, the other plane has an effective emissivity of 1 because what isn’t being absorbed/emitted is reflected. What that amounts is that at equilibrium, the temperature and spectrum of the photon gas between the two planes is exactly (if the planes are indeed infinite) equal to the temperature it would be if the planes had unit absorptivity. That invalidates your reductio ad absurdum of your point 3.
That’s also why you can make a near perfect black body by cutting a small hole in a closed box with walls at constant temperature. The absorptivity of the interior walls of the box doesn’t matter as long as the size of the hole is much, much smaller than the area of the walls.
The simplest explanation of what pyrgeometers and IR spectrophotometers observe is that the standard theory is indeed correct and that emission does not stop at equilibrium, not that the atmosphere and the surface, for example, are at equilibrium.
John Millett: Twice above you ask: “Why would nature behave this way?” Nature doesn’t have any objectives or motivations. Nature isn’t even required to make sense. The following passage from p10 of Feynman’s QED (a small book based on a series of lectures on quantum mechanics) is illuminating:
“The next reason that you might think you do not understand what I am telling you is, when I am describing to you HOW Nature works, you won’t understand WHY Nature works that way. But you see, nobody understands that. I can’t explain why Nature behaves in this peculiar way.” [When Feynman accepts not understanding why things behave as they do, does it make sense for you to ask “Why would nature behave this way?”]
“Finally, there is this possibility: after I tell you something, you just can’t believe it. You can’t accept it. You don’t like it. A little screen comes down and you don’t listen anymore. I’m going to describe to you how Nature is – and if you don’t like it, that is going to get in the way of your understanding it. It’s a problem that physicists have learned to deal with: They’ve learned to realize that whether they like a theory is NOT the essential question. Rather, it is WHETHER OR NOT THE THEORY GIVES PREDICTIONS THAT AGREE WITH EXPERIMENT. It is not a question of whether a theory is philosophically delightful, or easy to understand, or perfectly reasonable from the point of view of common sense. The theory of quantum electrodynamics describes Nature as absurd from the point of view of common sense. And it agrees fully with experiment. So I hope you can accept Nature as She is – absurd.”
In the case of radiation, Nature seems to make a fair amount of sense to me, but clearly not to you. The radiation leaving an object depends only on the object itself (eoT^4), not its surroundings. The fraction of incoming radiation at a particular wavelength absorbed by an object depends only on its absorptivity (including angular dependence), not its temperature or anything else. Absorptivity = emissivity. Neither absorption nor emission is influenced by the presence or absence of other types of energy transfer such as conduction and convection. An object has no innate desire to be a particular temperature, its temperature remains the same when its total incoming and outgoing fluxes by all routes are equal and changes when they are not. Changing temperature changes the object’s internal energy (so we can have conservation of energy). If you analyze situations correctly, you will find two satisfying results:
1) NET flow of radiant energy is always from warmer to colder. (When it isn’t, you’ve made a mistake in your analysis).
2) The two objects inside a “perfectly reflecting” evacuated container will come to the same equilibrium temperature even when their surfaces have different optical properties. (When they don’t, you’ve made a mistake in your analysis, as in your item 3 above).
The old physicists whose names you drop were brilliant in their day, but they were working in the dark ages before we understood what temperature is (which turns out to be quite complicated), before we knew molecules existed, and before we could explain the behavior of macroscopic objects in terms of the behavior of their constituent molecules (which don’t follow Newtonian mechanics), etc. The only sensible place to begin is with equations found in modern physics textbooks – equations that have repeatedly been shown correctly predict how nature behaves (if you apply them correctly).
Frank,
Thank you for that Feynman insight. Does anyone understand Feynman?
He recommends accepting matching theory and experiment over doomed-to-fail understanding how or why. French’s textbook (you referred it to me an age ago) which is otherwise replete with descriptions of experiments confirming theory, lacks one relating to Prevost, the text using the verb “asserts” in stating his theory of exchanges.
“An object has no innate desire to be a particular temperature…”. I wonder about that – entropy law suggests that it desires to be at the same temperature as its surroundings; and it thus spontaneously imports from or exports to its surroundings sufficient energy to achieve that condition, vide, the cup of tea or glass of ice sitting on the table.
NET is a counting term made necessary in the subject context by the assumed universal truth of two-way matter-matter energy exchange. The question is: Does a colder body affect the temperature of a hotter one? Maybe, if it slowed its rate of cooling. Could this result from thermalisation in the hotter body of absorbed radiation emitted by the colder one? No, because that would entail the spontaneous flow of energy from colder to hotter regions, a violation of the second law of thermodynamics. Could radiation from the colder body increase the temperature of the other’s surroundings? No, for the same reason.
Do you agree that NET and related violation are avoidable under an alternative assumption of one-way matter-field energy exchange? Do you agree that this is how your two bodies with different optical properties could achieve the same temperature in the reflective-walled cavity – they equilibrate independently with the cavity-filling field generated by the wall.
“The old physicists … were brilliant in their day, but they were working in the dark ages…”
Kelvin included?
SOD assured us that recent developments in our understanding of the microscopic world confirmed our long-standing understanding of the macroscopic world, if I understood correctly at the time.
John: I may not always understand Feynman, but he understands YOU. The passages about not wanting to accept equations that accurately predict how Nature behaves were written for you. Consider reading it carefully five times.
John wrote: “The question is: Does a colder body affect the temperature of a hotter one? Maybe, if it slowed its rate of cooling.”
Even if an object is warming, it still absorbs radiation emitted by a cooler object. The object can’t know if any particular photon arriving at its surface came from a cooler or warmer object. You don’t need to be concerned about it either unless you are CALCULATING entropy change.
Frank wrote earlier: “An object has no innate desire to be a particular temperature…”.
John questioned: I wonder about that – entropy law suggests that it desires to be at the same temperature as its surroundings; and it thus spontaneously imports from or exports to its surroundings sufficient energy to achieve that condition, vide, the cup of tea or glass of ice sitting on the table.
The object “knows” nothing about its surroundings or so it can’t desire to be at the same temperature as its surrounding. YOU want it to behave certain way, but the object doesn’t care about you or the surroundings. It emits radiation according to eoT^4, absorbs radiation according to its absorptivity, and may receive or lose energy by other pathways. The Law of Entropy doesn’t want anything either; it simply says that if you PROPERLY sum all the entropy changes (dS = dq/T) associated with heat transfer to and from your object, entropy will increase or remain the same.
In contrast to SOD, I (a chemist by training) think it is much easier to correctly apply the laws of physics when you are aware of the microscopic world of molecules. In the microscopic world, a slower-moving molecule CAN collide with a faster-moving molecule and increase the kinetic energy of the faster-moving molecule (but most collisions decrease the kinetic energy of the faster-moving molecule). In the macroscopic world, the 2LoT requires heat to flow from hot to cold. In this case, we don’t need to resolve the potential contradiction because we normally can’t observe individual collisions that appear to violate the 2LoT. We know these “seemingly-forbidden” collisions occur because otherwise all molecules would end up with the same kinetic energy, not a Boltzmann distribution.
In the macroscopic world, a slower-moving GHG in the atmosphere can emit a photon that travels 1 kilometer before being absorbed by a faster-moving molecule on the surface of the earth (or a infrared photon detector) and increase the energy of the faster-moving molecule (but more photons travel in the opposite direction). Since we can detect the downward flux of photons, we appear to have a problem: Doesn’t this violate the 2LoT?
Physicists eventually resolved this dilemma through the development of statistical mechanics, which explains the behavior of the macroscopic world in terms of the behavior of molecules (which obey quantum mechanics). Although temperature is proportional to the average kinetic energy of molecules, physicists realized that no single molecule has a temperature because there is a Boltzmann distribution of kinetic energies associated a given temperature. So statistical mechanics says temperature is defined ONLY for a collection of molecules colliding frequently enough to maintain a Boltzmann distribution of kinetic energies (which physicists call “local thermodynamic equilibrium”). So above I’m forced to say a “slower-moving molecule” rather than a “colder molecule”, even though intuitively these words seem to mean the same thing. A single photon isn’t moving from cold to hot when it travels from the atmosphere to the surface because the emitting and absorbing molecules don’t HAVE a defined temperature. The 2LoT can’t be applied to a system where temperature is not defined. (SOD solves this problem by opening a textbook that says the 2LoT only applies to the NET flux of radiation; some readers chose to not believe him.)
Statistical mechanics also provided a molecular explanation for entropy; it is proportional to the natural logarithm of the number of states available or “disorder”. Unfortunately, statistical mechanics also demoted the 2LoT from a law of nature to a mere probability of nature – it is exceeding unlikely that you will see entropy decrease or heat flow from cold to hot in the real world.
Much of Lord Kelvin’s work took place before the development of statistical mechanics and quantum mechanics. Trust a modern textbook, not something some genius wrote while modern physics was taking shape.
Frank,
I’m a fan of Statistical Thermodynamics, although a recent convert, never liked it in the old days.
I thought it was harder to explain relevant physics to the advocates of the imaginary second law of thermodynamics using this principle.
Mind you, it’s difficult to even cite a textbook or state 4-3=1 and 4-3 doesn’t equal -1 to such folk.
So perhaps I should give up on the Illuminati and we should use more statistical thermodynamics..
Frank wrote quoting John Millett;
John wrote: “The question is: Does a colder body affect the temperature of a hotter one? Maybe, if it slowed its rate of cooling.”
Later on, correctly, Frank gave a particular example of ‘back conduction’ which happens despite being statistically unlikely.
“a slower-moving molecule CAN collide with a faster-moving molecule and increase the kinetic energy of the faster-moving molecule (but most collisions decrease the kinetic energy of the faster-moving molecule). In the macroscopic world, the 2LoT requires heat to flow from hot ”
Why is it then, that SoD (in common with IPCC climate science) elevate the unlikely and ignore the real world?
In the real world the presence of a colder object will most likely reduce the temperature of a neighbouring hotter object.
I think the lessons of this historic experiment have not been assimilated by some people.
Pictet
Click to access Pictet%27s%20experiment.pdf
Only if the colder object is colder than the ambient temperature. If, for example, you have a pan in an oven at 400F at steady state, and you add a pan at 100F to the oven, everything will cool. But suppose you had an insulated evacuated box containing block with a heater operated at constant power so the block wall temperature was 600F and the wall temperature of the box (it’s a big, poorly insulated box) was 200F. Then if you put another block with a temperature of 300F in the box, the temperature of the heated block would, in fact, go up. But for the planet, the ambient temperature is 2.725K. It’s a little difficult to find an object colder than that.
Actually, a simpler example would be to surround the heated block with a thin steel shell inside the outer box. The outer walls would still be at 200F because the total energy dissipation hasn’t changed, but the inner shell would be hotter than 200F but cooler than the heated block and the heated block would be higher than 600F. The actual magnitude would depend on the various view factors. This is a modification of Willis Eschenbach’s Steel Greenhouse thought experiment. So inserting a cooler object can indeed raise the temperature of a warmer object.
DeWitt Payne
“Only if the colder object is colder than the ambient temperature.”
Yes the surroundings must be included.
So there are really 3 temperatures to consider.
Th = Hotter object’s temperature
Tc = Colder object’s temperature
Ts =Temperature of surroundings
If Ts > Tc then Th will drop
If Ts < Tc then Th will drop more slowly
If Ts = Tc then Th will behave as if Tc did not exist.
Bryan,
that’s actually a really interesting paper you’ve linked to.
A genuine question – have you read it?
Frank,
“Consider reading it carefully five times”.
Once was enough to grasp the importance Feynman placed on experimental confirmation of theory. Approaching the issue less obliquely than in my earlier comment: What experimental evidence validates Prevost’s theory of exchanges?
On anthropomorphism: Does the object “know” itself – what its temperature is and how many photons to emit to satisfy S-B – with any better quotient than it knows its surroundings? I think not. Rather, spontaneously, unconsciously, unemotionally, energy flows between the body and its surroundings according to their relative energy densities until these equalise. Does the flow then stop, as “dark-age” experiment found; or does it continue in a closed loop as another “dark-ager” asserted?
“Since we can detect the downward flux of photons, we appear to have a problem: Doesn’t this violate the 2LoT? “
Do we detect a downward flux of photons; or do we detect a change in the temperature/ energy density of the (pyrgeometer) detector and from that infer a downward flux? The latter, I think. Couldn’t we equally infer an exchange of energy between the detector and its surroundings? The surroundings, after all, comprise a wave energy field (or photon gas/soup) populated by matter in a proportion less than 100 parts per million.
DeWitt Payne,
Thank you for pointing to that deficiency. To correct for it, body one’s E_ in includes the portion of E_out reflected by body 2 : e1*(S-B)1*(1-a2); and E_out includes the portion of body two’s E_out reflected by body 1 : e2*(S-B)2*(1-a1).
Restated (from body 1 perspective, and dealing with fluxes):
F_in = a1*e2*(S-B)2 + e1*(S-B)1*(1-a2)
F_out = e1*(S-B)1 + e2*(S-B)2*(1-a1)
e1 = a1; e2 = a2; (S-B)1 = (S-B)2 = (S-B) at temperature equilibrium. Therefore:
F_in = (S-B){e1*e2 + e1*(1-e2)}
F_out = (S-B){e1 + e2*(1-e1)}
F_in / F_out = {e1*(e2 + 1 – e2)} / {e1 + e2 – e1*e2} = e1 / {e1 + e2 – e1*e2}
This ratio is not generally equal to the unity required for temperature equilibrium. But it is, only if e1 = e2 = 1 or the bodies are blackbodies.
Perhaps accounting for repeated reflections might bring the ratio to unity?
I grow tired of this.
Of course it does. Or in a word: Duh! You could have determined this yourself. A photon can only be reflected, absorbed or transmitted. If it’s reflected, it still exists.
Suppose each plane has an emissivity of 0.1 and a reflectivity of 0.9. Now let each plane emit 10 photons per unit time per unit area. 9 will be reflected and 1 absorbed from the other plane so next time step the each plane sees 19 photons, etc., etc. until at steady state each plane will be absorbing 10 photons, emitting 10 photons and reflecting 90 photons. That’s 100 photons/unit time/unit area or exactly what each plane would emit/absorb if its emissivity were 1.0.
This is really basic stuff. A little knowledge is a dangerous thing and clearly you only have a little knowledge.
You should be most skeptical of your own ideas. If you think standard physics is somehow wrong because it doesn’t produce the results you think it should, you should think again.
Ouch!
Let’s see if I can restore your natural good humour. Lacking SOD’s facility in posting photocopies of extracts of text books, I have to do it the hard way:
“Consider a cavity with metallic walls at temperature T. The walls emit thermal electromagnetic radiation. In thermal equilibrium this radiation has a black body spectrum characteristic of the temperature T. Furthermore, as we shall show, in the steady state attained at equilibrium the electromagnetic radiation inside the cavity must exist in the form of standing waves with nodes at the metallic surfaces.” (Eisberg: Fundamentals of Modern Physics, Wiley 1961)
Surface node means purely reflecting surface – zero absorption,emission – radiation ceases at thermal equilibrium. No?
Bryan had some particularly illuminating questions and statements above:
1) “Why is it then, that SoD (in common with IPCC climate science) elevate the unlikely and ignore the real world?”
IMO, SOD doesn’t elevate the UNLIKELY, he elevates the LAWS OF PHYSICS, so we can see where they are conflict with our intuition about how the world actually works. Our intuition says that photons traveling from hot to cold violate the 2LoT. SOD presents experimental measurements of DLR, reviews which equations should be applied to this situation, and shows what their consequences will be in various circumstances. Overcoming intuition (which is similar to philosophy or religion) can be hard for those who don’t routinely make decisions based on scientific experiments and theories.
You, on the other hand, are an expert at taking irrelevant science experiments, (such as the above Pictet reference with disturbing phrases like “cold emanations”) and using them to cast doubt on settled physics – physics that you sometimes acknowledge is correct. These are the tactics of trial lawyers and politicians, not scientists. Society seeks for justice and public policy by these tactics, but ethical scientists do not seek scientific “truth” this way. See Cargo Cult Science.
IMO, the IPCC’s WG1 elevates science with large uncertainties and possibly systematic weaknesses (climate models, feedbacks, paleoclimatology) into “settled science” for political purposes. I can’t judge whether The IPCC’s conclusions are likely or unlikely. Science begins with well-designed experiments that that support a conclusion where the null hypothesis can be rejected with p<0.05. If you read 20 papers describing such experiments, one can optimistically hope that only one conclusion is wrong, but systematic flaws and bias add to the error rate. Two such well-designed experiments will allow the FDA to approve a new drug. Particle physicists want 5 sigma before officially proclaiming discovery of the Higgs boson. The IPCC's "more likely than not" and "likely" are political terms that magically convert uncertainty into settled science.
2) "In the real world the presence of a colder object will most likely reduce the temperature of a neighbouring hotter object."
No! No! NO! There is no "likely" about it. Nothing "should" happen. We use physics to calculate what WILL happen in a specific situation (or do experiments to determine what actually happens when we aren't sure what physics applies). An object's temperature WILL drop if the outgoing flux of energy is greater than incoming; and increase if the opposite is true. The emissivity and absorptivity of the objects are as critical as their temperatures. Internal sources of energy and objects doing work can complicate the analysis. What happens is determined by physics, not intuition or generalities.
Or as SOD so elegantly put it: "Blah-blah-blah vs. equations".
Frank says
“You, on the other hand, are an expert at taking irrelevant science experiments, (such as the above Pictet reference with disturbing phrases like “cold emanations”) and using them to cast doubt on settled physics”
You should not be so dismissive of the classic experiments and founders of thermodynamics.
The clear thinking of Prevost Carnot and Clausius is still very relevant.
Incidentally i am becoming ever more convinced that the thermodynamic content of a climate science degree is pretty truncated.
I asked Judith Curry over on Climate Etc if the Carnot Cycle was included was included in undergraduate studies.
She replied that only the thermodynamics relevant to climate studies was taught.
I took that as a no to my question.
Over on Skeptical Science Chris Colose is again insisting that heat can move spontaneously from a cold to a warmer object.
He has no idea of the difference between em radiation and heat.
Yet he is considered to be something of an expert in climate science.
Can you see why I’m not impressed?
If you get the basics all muddled up then what is the point of theories and equations based on nonsense.
Brian – And again… have you read the paper about Pictet you referenced?
VTB asks
“have you read the paper about Pictet you referenced?”
Why ask silly questions?
Because the paper argues the precise opposite of your case.
So I’m wondering why you cited it.
Very tall Man of very few words you will have to be more explicit!
Section IV
VTG
Criptic!!!!
[Apologies, this comment just retrieved from the spam queue]
Bryan: I never wrote that Carnot and Clausius are not relevant. I said your mention of experiments by Pictet with confusing terminology like “cold emanations” is intended to create doubt about a settle area of physics. If one looks closely, there is nothing in these experiments that couldn’t be predicted from the science discussed by SOD.
I have written elsewhere that modern physics textbooks are likely to be the best source of information about the discoveries of Carnot, Clausius and other pre-20th century physicists, because their contributions will be set in presented in light everything we currently know, including statistical mechanics and quantum mechanics. For example, the concept of temperature has evolved from something that causes liquids to expand in a thermometer, to expansion of gases according to the ideal gas law (which gives us our first look at absolute zero), to the kinetic theory of gases and to a temperature scale based on entropy. Today, we have a fairly good idea of why these different derivations of temperature are consistent with each other, but non-specialists have no idea of what Clausius knew about temperature when he was writing. So it’s easier to avoid mistakes if you stick to sources that aren’t less than 100 years old.
Do you to really expect anyone to believe your negative remarks about Chris and Judy without links support your contentions?
Frank says
“Do you to really expect anyone to believe your negative remarks about Chris and Judy without links support your contentions?
Here’s the quote from Chris
“So yes, colder objects can and do radiate toward (and heat!) warmer objects.”
The Planetary Greenhouse Engine Revisited
Posted on 15 June 2011 by Chris Colose on Skeptical Science.
Finding the Judith Curry reference is very difficult because of the nesting comments method used with very large postings.
My comment anyway was not negative.
Her reply was ambiguous in the sense that it was unclear that the Carnot Cycle topic was included.
I took it as a “no” but did not pursue the matter further at the time.
If you doubt that this exchange took place I will spend further time to convince you of its reality.
Your semantic nitpicking is beyond tiresome. You know perfectly well that Colose’s statement:
does not violate the Second Law and could easily be rephrased to avoid offending even your tender sensibilities. For example:
But that’s a very clumsy sentence. Any rational person not looking to pick a fight knows exactly what Colose meant. Words mean what you want them to mean, no more, no less, only when you say or write them and define what you mean by the word. Heat does, in fact, have multiple meanings. Textbooks on thermodynamics are not the controlling authority here either. Show me where the CGPM or the IUPAC has defined the term ‘heat’ to mean only what you think it means and why your definition is still consistent with other widely used terms like heat content, heat capacity and heat of reaction.
DeWitt Payne says
“Your semantic nitpicking is beyond tiresome. You know perfectly well that Colose’s statement:
“So yes, colder objects can and do radiate toward (and heat!) warmer objects.”
does not violate the Second Law and could easily be rephrased .
to avoid offending even your tender sensibilities.”
Well De Witt is the ulcer playing up again?
How do you know what Chris means?
Is he not an adult?
Do you need to rephrase his language for him?
I have no idea what Chris had in mind when he proposed a violation of the second law.
Did he fully intend to, or does he not really know what he was on about?
De Witt can mind read now apparently.
According to DeWitt’s new hippy interpretation of language we can say anything and leave others to guess what we really mean.
So a whale can now be said to be a fish because we know what the guy was on about.
Sloppy rubbish.
Bryan: “Sloppy rubbish.”
“Can and do” does not equal must always. So if you agree with DeWitt’s phrasing you agree with Chris’s. It does seem to me like you are nitpicking.
Bryan,
you referenced the paper, but without any explanation. I can only presume you believe it supports your case.
Do you think it supports you?
If so, why?
VTG
You seem to be under the impression that the Pictet paper contradicts something that I have said.
However you will not tell us what this contradiction is!
You have posted several times without explaining what you are on about.
One last try, point out the contradiction or I will just have to ignore you.
Bryan,
you posted the link without saying why.
Presumably you wanted others to read it.
I did.
I can find nothing in it which supports your position – in fact as well as an interesting history lesson, it provides an excellent explanation of how mainstream physics, as laid out here by SoD, predicts the results of the experiment.
Rather than just post a link without explanation, perhaps you’d be so good as to explain why you posted it, and what points are made in the paper which support you.
Otherwise, I’ll just have to assume you posted the link without actually reading the content.
VTG says
“you posted the link without saying why.”
Perhaps you failed to read
“In the real world the presence of a colder object will most likely reduce the temperature of a neighbouring hotter object.
I think the lessons of this historic experiment have not been assimilated by some people.”
So obviously I agree with the modern interpretation explaining with photons what Prevost explained by exchanges.
VTG goes on
” I can find nothing in it which supports your position ”
Yet he does not tell us what position of mine it fails to support.
One last chance to explain what you are rambling on about, otherwise I will consider this exchange as a waste of time.
Bryan,
OK, so you agree with the modern explanation. That’s good.
It is also precisely the same as SoDs position which you seem to disagree with.
So I’m bemused.
As to ““In the real world the presence of a colder object will most likely reduce the temperature of a neighbouring hotter object.” – the obvious follow on is “colder than what?”
In the case of the greenhouse effect, the atmosphere is colder than the ground, but it is NOT colder than the background of outer space. Which is why it heats the surface. In the case of the experiment, the cold object is colder than the background, which is why it cools the thermometer.
VTB….. I thought I covered all of that in my reply to
“DeWitt Payne
“Only if the colder object is colder than the ambient temperature.”
Yes the surroundings must be included.
So there are really 3 temperatures to consider.
Th = Hotter object’s temperature
Tc = Colder object’s temperature
Ts =Temperature of surroundings
If Ts > Tc then Th will drop
If Ts < Tc then Th will drop more slowly
If Ts = Tc then Th will behave as if Tc did not exist."
Sorry for being a bit narky in my previous posts.
Bryan,
Narky – likewise from me, it’s all too easy to get riled on blogs and it never helps anyone.
I’d assumed you had read and agreed with the Pictet stuff and not bothered to read to the end of the paper, so I’d like to extend you my apologies too.
I’ve now got no idea on what you disagree with SoD over.
VTG
VeryTallGuy
The fact that I do not agree with “I think” is irrelevant. The fact that the physical world does not agree with “I think” is very necessary.
My take on your “I think” produces fantastic results; you cry foul due to ambient temperature. Though Tcalib > To would aid your “I think”, helping to increase thermal mass temp. Ambient temperature exceeds To, so “I think” doesn’t apply…Why? What is the physical explanation for this exception?
About a month ago, SoD said radiative transfer “equations are true while the atmosphere is in LTE (local thermodynamic equilibrium)”.
Is your model is in LTE?
SoD and VTG
As Frank quite correctly stated, “In the microscopic world, a slower-moving molecule CAN collide with a faster-moving molecule and increase the kinetic energy of the faster-moving molecule (but most collisions decrease the kinetic energy of the faster-moving molecule).”
In other words, higher kinetic energy transfers energy to lower energy most of the time. In other words, most of the time “I think” ((Qo+Qe) = εσTe^4) is invalid. In other words, the “imaginary” 2LoT and the “real” 2LoT agree most of the time.
So where do the real and the imaginary diverge, the infrequent occasion when a low energy photon happens to increase a the vibrational oscillation of a higher energy surface. And since vibrational states are discrete, how does the low energy photon further energize the faster surface to higher frequency step?
BTW, my tangential question regarding CO2 IR absorption February 14, 2012 at 7:17 pm, was to this exact aim.
LJ Ryan.
You don’t believe my equations represent the system.
Fair enough – your turn to define your own.
Apropos to “blah blah blah” vs equations, linked below is 6000 words of blah blah blah and 0 equations of SoD-baiting. I would be disappointed if SoD rose to bite at the rotting piece of worm, but SoD might enjoy the read. It might also be useful as some kind of gold standard.
It is a thoroughly referenced work, mostly to articles by an author I’d never heard of, somebody named Wikipedia.
Click to access psi_radiated_energy.pdf
Re: conversation Bryan, DeWitt Payne, VeryTallGuy, Frank:
Bryan, March 10:
“So there are really 3 temperatures to consider.
Th = Hotter object’s temperature
Tc = Colder object’s temperature
Ts =Temperature of surroundings
If Ts > Tc then Th will drop
If Ts < Tc then Th will drop more slowly
If Ts = Tc then Th will behave as if Tc did not exist."
Since Th exceeds Tc & Ts, it will fall for all Tc, Ts
Th will fall slower when Tc exceeeds Ts, than otherwise. The question is: How is the rate of cooling slowed?
Is it, as SOD and others argue, because (at least some) photons emitted by the cold object will become incident on the hot object, be absorbed and thermalised, thus causing the hot body to cool more slowly than it otherwise would (not warming it in an absolute sense)? This process, of course, raises the issue of violation of the 2LoT, to which SOD responds by affixing the word "imaginary" to that understanding of the law and claiming that true understanding recognises only the net flow of photons into and out of the hot body. Call this process "matter-matter' energy exchange.
Or is it because, in a process we might call "matter-field" energy exchange and which avoids the 2Lot issue, the two bodies independently interact with their common surroundings, an ambient energy field whether in its wave or particle manifestation? The energy density/temperature of the hot body, by definition, exceeds that of the ambient field and energy would flow from higher to lower density at a rate determined by the difference between the densities. Introduce the second piece of matter at energy density/temperature,Tc, which will also interact with the field. If Tc exceeds that of the field, energy will flow from it into the field raising the field's energy density/temperature and reducing the difference between it and the hot body, thus slowing the latter's rate of cooling. Conversely, if the second body is colder than the ambient field, the hot body will cool faster, as was the case in the Pictet experiment.
Which physics laws/principles prohibit this process?
You keep talking about EM radiation as a field. I don’t think you understand the meaning of the term ‘field’ in physics. EM radiation, whether emitted by a solid material with a continuum spectrum or an atom or molecule with a line spectrum, has properties that cannot be described mathematically as a simple field like an electric, magnetic or gravitational field. I suspect you’ve been reading Claes Johnson or someone of his ilk. There are lots of good reasons why the concept of the photon and quantum mechanics was invented. The first reason is the photoelectric effect. The final reason is that it works and works very well. Things do behave as if they had both particle and wave properties. Electrons, for example diffract. But you don’t see anyone claiming that electrons don’t exist as individual particles.
I don’t have to cite a physical law that your theory violates. What you have to do is prove your theory describes all observations, not just radiative heat transfer, better than quantum mechanics. Good luck with that.
DeWitt Payne,
A wave (em radiation) looks like a particle when the width of the split in the experimental apparatus greatly exceeds its wavelength. A particle (an electron) looks like a wave if its (De Broglio) wavelength exceeds the width of the split. Is this a correct understanding?
We need to limit our ambitions. Rather than my proving that a theory describes all observations, let you (in the universal AGW sense, not the personal one) prove consistency between back-radiation and 2LoT in a way less underwhelming than the invention of a new physical property called “Net Heat”.
DeWitt & John: In his book, QED, Feynman is quite adamant that we consider photons to be particles, not waves or “wave-particle duality”. He says if the human eye were about 10X more sensitive, we would perceive dim light of a single wavelength as a random series of flashes (from individual photons) of equal intensity. Then everyone would understand why photons are particles, not waves. We know this because we have detectors more sensitive than our eyes that count individual photons and determine how much energy is delivered by each one. Photons and electrons are particles that have strange rules of behavior (amplitudes that are complex numbers) that account for what happens in a double-slit experiments. Interference in a double-slit experiment occurs when only one photon at a time is passing through a double-slit device, so waves are nonsensical even in this situation. (Claes Johnson doesn’t appear to care if his equations are capable of predicting all aspects of the known behavior of photons, like QM does.)
John: No 2LoT issue exists. Some collisions transfer kinetic energy from slower-moving to faster-moving molecules. More collisions do the opposite. These random collisions create the Boltzman distribution. Individual collisions don’t obey the 2LoT. When we have large numbers of molecules colliding, we can talk about temperature (a bulk property – mean kinetic energy – that has no meaning for individual molecules) and the fact that heat flows from hot to cold when large numbers of collisions are involved.
Copying, pasting, and changing a few words (capitalized) in the above paragraph gives: Some PHOTONS transfer energy from slower-moving to faster-moving molecules. More PHOTONS do the opposite. Individual PHOTONS don’t obey the 2LoT. When we have large numbers of PHOTONS, we can talk about temperature (a bulk property – mean kinetic energy – that has no meaning for individual molecules) and the fact that heat flows from hot to cold when large numbers of PHOTONS are EXCHANGED. The only difference between energy transfer by collision and radiation is that one can’t directly observe the individual collisions that appear to violate the 2LoT while one can detect the photons that appear to do so.
DeWitt Payne
Individual electrons diffract? Are they split into quarks the reassembled as electrons post aperture? Are electrons not elementary particles?
Electron diffraction is limited by the induced wavelength. So unless λ < the diameter of the electron, your not observing true diffraction of electrons. It is no more diffraction then is billiard balls bouncing down a channel then releasing through the open end. Length of oscillation between the channel wall and size of opening determine impact pattern. So are billiard balls waves?
I suppose one might say photon diffraction is also limited by λ. I suppose one might say photon diffraction is also dependent on photon diameter. So the real question is, what is the diameter of a photon?
DeWitt Payne
And since you brought it up: A PV cell is irradiated via a stream of photons with λ1 and a second stream of photons with λ2 . The resultant energy as claimed by SoD, VTG, DeWitt …etc. Et=E1 + E2 = hc/λ1 + hc/λ2 is Et= hc(1/λ1 +1/ λ2).
Using our summed energy Et, the maximum kinetic energy of ejected electrons is Km = hc(1/λ1 +1/ λ2 -1/ λo) where λo is the threshold wavelength.
Assume λ1= λ2 then Km = hc(2/λ1 -1/ λo)
now her comes the magic if λ1 = λo
Km = hc/λo electrons flow at threshold wavelength!
Simply by employing “I think” ((Qo+Qe) = εσTe^4) we halved the threshold wavelength.
“Threshold! AGW physics don’t need no stinkin threshold”
LJ Ryan
Great to have you back!
Wondering when you are going to set out the equations governing you theory of heat transfer for the oven example?
cheers
VTG
VTG
Do you agree with my application of E= hc/λ to your “I think”? Namely: Et=E1 + E2 = hc/λ1 + hc/λ2 is Et= hc(1/λ1 +1/ λ2).
First:
In order for me to offer an equation, we must agree upon a starting point. I have repeatedly stated parallel inputs differ to the higher potential. Do you agree?
Second:
Team GHG seems unwilling to square black body theory (Kirchhoff’s cavity theorization/experiment) and GHG physics “I think”. That is “I think” supposes, Q of source will not equal σT^4 but rather the sum of re-radiated flux between walls of the cavity…σT^4 = Qn + Qn+1 + Qn+2 …. thus T will forever increase and thus black body is irrelevant.
So if I offer an equation defining photon absorption in a presently excited molecule, team GHG will diffract (pun intended) the argument to impertinent replies.
VTG
take two
First:
In order for me to offer an equation, we must agree upon a starting point. I have repeatedly stated parallel inputs DEFER to the higher potential difference. Do you agree?
LJ Ryan.
We don’t need to agree on anything as a starting point. The field is open to you to offer a coherent set of equations which predict the outcomes.
I did this above; you feel that you have a superior theory to that of standard physics.
I put a set of equations together which predicted a specific outcome for a specific set of conditions.
Only once you’ve done likewise is it possible to judge your theory.
Equations, not blah blah blah – clue’s in the title…
DeWitt Payne,
Revisiting your day of boredom (March 8) and mine of pain (March 12).
My claim was: Prevost’s theory of exchanges (simultaneous thermal and dynamic radiative equilibria) applies only for blackbodies.
Your claim that, taking reflection into account, it is universally applicable raises the issue of time. Radiation, emitted and reflected, travels at 3×10^10 cm per sec. The lifetime of an energy state in the atoms of the radiating surfaces is of the order of 10^-9 sec. That is, the reflected radiation travels 30 cm before the next surface emission occurs. A system in which surface reflectivity is high or distance between radiating surfaces is greater than 30 cm is never going to reach Prevost’s joint equilibria.
Frank, March 24
Confusion: radiation is a particle not a wave; but it has a wavelength. Why doesn’t it have a diameter?
L.J.Ryan,
Electron diffraction is a well known and widely used phenomenon. It was the subject of the 1937 Nobel Prize in Physics. Apparently you didn’t even bother to look it up. Here’s the Wikipedia link: http://en.wikipedia.org/wiki/Electron_diffraction
Oh, and neutrons diffract too.
I suggest you take a freshman physics course at your local community college. But you’d probably fail because in any disagreement between what you were taught and what you think you know, you would think you were correct and your professor was wrong. Your arrogance despite the proven fact of your lack of knowledge boggles the mind.
DeWitt Payne,
You’re implying by omission, electrons do split and reassemble post aperture. You’re implying by omission, electrons are not elementary particles.
My contention, diffraction is a function of λ and width of aperture.
My contention, if width of aperture < diameter of particle, no diffraction.
And so do billiard balls…and photons.
Diameter of electron d = < 10^-16 m
Diameter of neutron d = < 10^-13 m
Diameter of billiard ball d = 5.7 x 10^-2 m
Diameter of photon d = ?
So tell me professor Payne, what is the diameter of a photon?
L.J.Ryan,
I am implying no such thing. It is your misapprehension that a particle needs to split and reassemble in order to diffract and cause an interference pattern in a two slit experiment that is the problem. Asking why an electron diffracts is a pointless question. It just does. As long as the paths are indistinguishable, i.e. you’re not checking to see if the electron goes through slit one or slit two, the math is the same as if the electron goes through both slits. In terms of physics, you’re still living in the 19th century.
As far as diameters, have you not heard of the uncertainty principle either? Obviously, if the probability of a particle passing through a slit is zero, there will be no diffraction. So what.
Frank,
“The only difference between energy transfer by collision and radiation is that one can’t directly observe the individual collisions that appear to violate the 2LoT while one can detect the photons that appear to do so”.
In the absence of observation of energy transfer from slower-moving molecules to faster-moving ones resulting from collision between them, how can you be confident that such transfers occur?
Your implied commonality of behaviour between molecules and photons invites interesting conjectures. The occupants of the spherical shell volume we call the atmosphere are predominantly photons, molecules being present in the ratio 90 parts per million (assuming 20km depth). Conjecture: molecules are far more likely to exchange energy with photons than with each other.
Both the atmosphere’s photon gas and molecular gas exhibit pressure which varies directly with temperature (we are dealing with entities in bulk, not individually). When gases at different pressures come together, entities flow from the higher-pressure gas to the lower until pressures are equalised(although I expect that quantum theory or statistical mechanics or QED would allow some individual aberrant movement of practical inconsequence). Solar photon gas temperature/pressure exceeds that of terrestrial photon gas which exceeds that of space photon gas. Conjecture: terrestrial radiation occurs daily only during the time between temperature maximum and minimum.
Wrong. If that were the case, then the molecules would not have a Boltzmann energy distribution. The mean free path of a photon is wavelength dependent, but even at the peak of the 15μm absorption band, it’s far longer than the mean free path of a CO2 molecule before colliding with another molecule. The probability of radiative energy transfer is three or more orders of magnitude smaller than for collisional energy transfer until you get above about 100 km altitude.
But the temperature of space is always lower than the temperature of the planet. Outgoing thermal radiation is 24/7. Are you implying that if a shield were placed between the sun and the Earth, the Earth wouldn’t continue to cool?
DeWitt Payne:
“The mean free path of a photon is …..s far longer than the mean free path of a CO2 molecule before colliding with another molecule”.
I don’t follow. What is of interest is the mean free path of a molecule in a photon gas relative to that in a molecular gas. In general the mean free path varies inversely with the concentration of the entity – number per unit volume. In the atmosphere the photon concentration exceeds the molecular. The molecule will collide with photons more frequently than with other molecules.
“Outgoing thermal radiation is 24/7”
True, the temperature of space is always lower than that of the planet. But the planet is not exposed to it 24/7. Half of the rotating planet is exposed to the temperature of the solar energy field which is higher than its own. Shielding the planet from this field would expose it 24/7 to space’s lower temperature and, hence, hasten its rate of cooling. Conversely limiting its exposure to space’s field to 12/7 also limits outgoing thermal radiation to 12/7.
The sun subtends an angle of ~0.5 degrees. The rest is space. And even for that 0.5%, there is radiation outward from the Earth to the Sun. It’s just overwhelmed by the incoming radiation from the Sun to the Earth. There is no solar energy ‘field’ that somehow blocks radiation to space when the sun is above the horizon.
That should have bee 0.5 degrees, not %.
You are under the misapprehension that every close encounter between any photon and any molecule results in an interaction between the two. You could not possibly be more wrong. Photons in the thermal IR effectively do not interact with N2 and O2 molecules at all. They aren’t absorbed and they aren’t even scattered. Even with molecules that can absorb and photons of the correct wavelength to be absorbed, the probability of interaction with an individual molecule is quite small.
Molecules, OTOH, bounce off each other all the time. Mostly the collisions are elastic with no kinetic energy transferred to rotational or vibrational modes.
That’s what I meant by the mean free path of a photon being very long compared to that for a molecule.
John wrote: “In the absence of observation of energy transfer from slower-moving molecules to faster-moving ones resulting from collision between them, how can you be confident that such transfers occur?”
Frank responds: If all collisions transfered energy only from faster-moving to slower-moving molecules, all molecules would be moving at the same speed. If you believe in the Boltzman distribution of molecular speeds, logically you should believe that the 2LoT doesn’t apply to INDIVIDUAL molecular collisions. If you believe that energy transfer from a slower-moving to a faster-moving molecule by collision is consistent with the 2LoT, there is no reason to postulate that a photon violates the 2LoT when it does the same thing.
Furthermore, it is easy to visualize how a slower-moving molecule can bump into the side (roughly perpendicularly) of a faster-moving molecule and increase the speed and kinetic energy of the faster-moving molecule.
John wrote: “Your implied commonality of behaviour between molecules and photons invites interesting conjectures.”
Frank replies: The commonality I cited involved different MECHANISMS of energy/heat transfer: molecular collision and radiation.
It’s dangerous to imply commonality between molecules and photons. Gas molecules have a mass and a radius of nearly 1 nm. They occupy a definite volume of space and collisions result when two molecules try to occupy the same volume. Photons have energy (and therefore mass via E=mc2), but their rest mass is believed to be zero or at least 10^25 times smaller than the mass of typical gas molecules. The radius of a photon appears to be unknown. Do photons collide with each other or even with molecules? I doubt it:
1) Pulses of light travel both directions in fiber optic cables in the Internet.
2) An interference pattern can be seen when only one photon at a time is passing through a double slit. Interference is not the result of collisions between photons
3) The interaction between photons and molecules aren’t collisions; instead we say there is a SMALL PROBABILITY of a photon being absorbed or scattered when it passes within a certain distance of a molecule. Since the distance can be in any direction, it is technically called an absorption cross-section. These cross-sections are mathematical constructs that are not directly related to physical size of the molecule. (According to Petty, most scattering of visible and infrared radiation in our atmosphere is due to particulate matter – large clumps of molecules – not individual gas molecules.)
John wrote: “Conjecture: molecules are far more likely to exchange energy with photons than with each other.”
Frank replies: The mean free path (distance traveled between collisions) of a gas molecule at atmospheric pressure is about 10-7 meters. About half of incoming SWR makes it through the whole atmosphere. Most LWR travels hundreds of meters before being absorbed.
http://www.uccs.edu/~tchriste/courses/PHYS549/549lectures/gasses.html.
John, your conjecture is incorrect by a factor of 10^10. Don’t you feel like checking even a little before posting wild ideas? Posing a question makes sense than proposing a conjecture and may prompt you to recognize that an answer may be easily be found at Wikipedia or by googling. This might keep you in better touch with known science and focus your attention to the real weaknesses in the theory of CAGW.
LJ Ryan
Rather than go off into neutron diffraction, perhaps you could help by sharing the equations that describe your novel theory of radiative heat transfer.
After all, you already have these (there’s no way you’d have convinced yourself that you understood the subject better than anyone else without already formulating your theory, right?)
The post is about the power of equations vs blah blah blah.
Let’s see your equations.
SOD, DeWitt, others: I tried reading Grant Petty’s A First Course in Atmospheric Radiation (p 31) to see how he handled the contradictions between “electromagnetic radiation” (the wave theory of light) and photons (the particle theory of light):
“Now that I have succeeded in indoctrinating you with the wave-based mental model of EM radiation … I will demolish your newly won confidence by asserting that you should view EM not as waves, but as particle! At least some of the time.”
After 17 pages of an incorrect “mental model” and numerous eqns culminating in Maxwell’s eqns, we get one page of “quantum mechanics” discussing the photoelectric effect, E = hv and a formula for calculating the number of photons for a given flux of radiation. If this is the best anyone does, it is not wonder there is alot of confusion.
“The amount of energy a photon has can cause it to behave more like a wave, or more like a particle. This is called the “wave-particle duality” of light. It is important to understand that we are not talking about a difference in what light is, but in how it behaves. Low energy photons (such as radio photons) behave more like waves, while higher energy photons (such as X-rays) behave more like particles”. (NASA; Imagine the universe)
Terrestrial radiation is closer to low-energy photons that high-energy ones and behaves likes waves, right?
I recollect reading (though not where) that photons as particle travel in a wave-like motion – the higher the energy, the tighter the wave motion.
DeWitt Payne
“The sun subtends an angle of ~0.5 degrees. The rest is space”.
The smallness of the subtended angle tells us how little of solar energy output our planet uses and allows us to consider solar radiance as parallel rays (as opposed to the diffuse nature of terrestrial radiation). Is this not so?
And surely the solar influence is felt outside that subtended angle? Polar GHG’s, as well as equatorial ones, would absorb some solar photons? The moon comes under solar influence?
DeWitt Payne:
“Even with molecules that can absorb and photons of the correct wavelength to be absorbed, the probability of interaction with an individual molecule is quite small”.
This seems to be saying that transmission of surface radiation through the atmosphere is more likely than absorption, the opposite of greenhouse hypothesis.
Percent transmission is a function of path length, number density of absorbers and molecular absorptivity (which varies strongly with wavelength). Paths in the atmosphere can be measured in kilometers. The mean free path of a molecule is measured in nanometers, 68 nm for surface pressure. About 15% of photons emitted upward at the surface for a tropical atmosphere are not absorbed by the atmosphere. Most of those are in the frequency range of 800-1200 cm-1 where transmissivity averages about 50% For sub-Arctic winter conditions, ~32% of photons are not absorbed. Photon-photon scattering can be ignored in the thermal IR.
Frank,
“Furthermore, it is easy to visualize how a slower-moving molecule can bump into the side (roughly perpendicularly) of a faster-moving molecule and increase the speed and kinetic energy of the faster-moving molecule”.
I visualise the faster particle being bumped onto a different path with a reduction in its original path speed and an increase in speed (from zero) on the path of the slower particle, with no overall change.
As to the other extreme case, head-on, (contact is possible only when the slower particle is moving generally in the opposite direction, to a limit at right angles, to the faster one). I find it difficult to imagine any increase in speed.
“there is a SMALL PROBABILITY of a photon being absorbed or scattered when it passes within a certain distance of a molecule”.
DeWitt Payne makes the same point. My question: Isn’t this another way of saying that transmission is more likely than absorption?
You are right; the focus should be on the real defects in AGW hypothesis. Back-radiation from atmospheric matter at a concentration of 100 parts per billion delivering twice as much energy to the earth’s surface as the sun is still a bit difficult for me to grasp, despite SOD’s (and others’) valiant attempts to educate me. That’s before the clear violation of 2LoT (in bulk – aberrant behaviour of individual photons is of no practical consequence). Add the lack of experimental validation of Prevost’s theory of exchanges on which back-radiation rests.
Prevost’s ‘theory’ isn’t a theory at all, it’s a definition of radiative equilibrium. As such it is not subject to confirmation by experiment. Or are you saying that there is no such thing as radiative equilibrium and that two objects inside a perfectly reflecting container can each have any arbitrary temperature after the passage of an infinite amount of time?
No, not that. I say that the two objects can each more simply reach thermal and radiative equilibria with their common surroundings, the energy field/photon gas (which you ignored, but which fills the container) than with each other. Further, that the radiative equilibrium is static, not dynamic – that is, at thermal equilibrium radiation stops rather than creating a useless loop between the body and its surroundings.
All I can say is: Wow! If radiation stops, there is no photon gas because all the photons will be absorbed. So constant radiation is hardly useless.
I really think you are beyond help. As I said above, you need to either take a course or two or read some physics textbooks with an open mind rather than rejecting any concept you deem useless. I don’t have the time or patience to hold your hand anymore.
Bye.
John: Experimental evidence provided by SOD proves that DLR exists, so the appropriate question is: “Has evidence of DLR proven that the 2LoT is wrong?” The 2LoT tells us heat must flow from higher temperature to lower temperature. DLR photons are emitted and absorbed by individual molecules that are faster- and slower-moving, but do not have defined temperatures. I showed that SOME collisions must transfer kinetic energy from slower-moving molecules to faster-moving molecules. I described one type of collision that does this. The Boltzman distribution demonstrates that this must happen. Therefore, the 2LoT doesn’t apply to one-way energy transfer between individual molecules. The 2LoT does apply to the net radiative exchange between the surface and the atmosphere and here observations show heat flowing in the correct direction.
100 parts per Billion is vastly incorrect for the amount of GHG in the atmosphere. CO2 today is almost 400 parts per Million. Water vapor (a more important GHG near the surface) averages about 1 part per HUNDRED (1%).
How much GHG do we need to change the atmosphere? The atmosphere is hard to visualize. Imagine the atmosphere condensed to a liquid with each gas forming a separate layer. The liquid would be about 10 meters deep, with almost 8 meters of liquid nitrogen and 2 meters of liquid oxygen. The water layer would be 0.1 m = 10 cm = 4 inches thick. The carbon dioxide layer would be 4 mm thick – about the thickness of the glass in your car that warms up to 150 degF in the sun because visible light passes easily through glass and IR does not. Do you use sunscreen? How thick is the layer of UV absorbing molecules that protects your skin from sunburn by absorbing UV radiation? The layers of minor GHGs are thicker than sunscreen. Don’t let the parts per million (ppm) or parts per billion (ppb) fool you into thinking something is unimportant. The sun is 6000 degC and 93 million miles away. 14.6 pounds of atmosphere radiating DLR is found above every square inch of the earth and half of the atmosphere is within a few miles of the surface. Our intuitions are completely worthless when considering these quantities. You need to trust solid science (which is what you usually find here at SOD). From your personal knowledge, you should recognize that the absorption due to 4 mm of glass or a few um of sunscreen can be extremely important. These precedents should convince your intuition that “too little” isn’t a good reason for rejecting CAGW. Neither is the 2LoT.
John: You apply perhaps 20 cc of sunscreen containing about 10% PABA over 2 m^2 of skin, a layer that is 0.001 mm thick. You understand that this thin layer absorbs >90% of UV radiation from the sun (SPF >10). The CO2 in the atmosphere – if condensed to a liquid – would form a layer 4 mm thick (400X thicker) over the surface of the planet and water would form a highly variable layer 10 cm thick on the average (10,000X thicker). Somehow you say that GHGs cover “only 2% of the planar surface” and question whether GHGs can absorb 90% of radiation emitted by the surface. Calculations with the measured absorption coefficients say they do, your personal experience with an 0.001 mm thick layer of sunscreen should tell you this isn’t unprecedented or unreasonable. The 4 mm thick glass in your car that lets visible light into your car and blocks infrared light from escaping provides another reasonable precedent at infrared wavelengths.
The earth’s surface is absorbing an average of about 160 W/m2 of SWR energy from the sun, emitting about 390 W/m2 of LWR from its surface and about 80 W/m2 of latent heat (water vapor which returns to the surface as 1 m of rainfall per year). The average of 333 W/m2 of DLR that we measure is needed to balance incoming and outgoing energy at the surface (along with a little sensible heat) can’t be explained as: a) the experimental error of pyrgeometers or b) heat transfer from a warmer atmosphere to a colder surface in Antarctica. Either the 2LoT permits radiation to flow in both directions (with net flux from hot to cold), or the surface of the earth is violating the first law of thermodynamics (energy is conserved), by losing much more energy than it receives (without cooling rapidly).
The simple physics you have been questioning will cause the temperature of the upper troposphere (where radiative equilibrium controls temperature) to warm about 1 degC each time CO2 is doubled. It doesn’t tell us what will happen at the surface, which loses more energy via convection than by net radiation. CAGW is predicted by GCM’s and supported dubious estimates of temperature and GHG change between now and the last ice age. The GCM’s predict that the surface will warm the same amount as the upper troposphere and that warming will be amplified by changes (feedbacks) in water vapor and clouds
Frank,
“100 parts per Billion is vastly incorrect for the amount of GHG in the atmosphere. CO2 today is almost 400 parts per Million. Water vapor (a more important GHG near the surface) averages about 1 part per HUNDRED (1%)”.
(for what it’s worth) the reasoning in my response to your statement has led me to think that the polemical tool – a system of two bodies at different temperatures in vacuo coming to thermal equilibrium by mutual exchange of radiant energy – is both too simple and not simple enough for its purpose: it is too simple by ignoring the energy field/gas which is an element in all thermodynamic systems; and it omits to reduce the system to two simpler ones – each body interacting independently with the common surrounding energy field/gas.
On your figures, matter occupies 10 metres of the depth of the spherical shell we call the atmosphere, a spatial concentration (assuming 20km depth) of 5×10^-4. Using Avogadro’s figures (6 x 10^23 molecules occupy 22.4 litres) and taking molecular diameter of 1.5 x 10^-8 cm, the spatial concentration of matter is 9×10^-5. The discrepancy in these estimates is unimportant in the current context. What is relevant is that what we call the atmosphere is predominantly quanta/photons, whether in wave or particle manifestation, everywhere surrounding very low concentrations of matter and GHG matter in particular. In their particle manifestation, the quanta could be likened to a photon gas. That is, the atmosphere comprises two gas species – energy and matter, photons and molecules. Molecules also exhibit an energy property, kinetic energy, different from the radiant energy of photons. Interaction between the species takes the form of energy transfer and transformation – to and from, kinetic to radiant. When a GHG molecule emits a photon, the stock of kinetic energy in the matter species decreases and that of radiant energy in the other species increases by equal amounts; and vice versa when it absorbs a photon. Intra-species interaction occurs only in matter, in the form of molecular collisions, study of which gave rise to Maxwell’s velocity distribution and Boltzmann’s energy distribution. Intra-matter interactions are much more frequent than inter-species ones. Consequently energy gained by a molecule from an inter-species interaction is quickly distributed to other molecules (creating a local thermal equilibrium and the basis for a bulk temperature which is non-physical for an individual molecule) before another inter-species interaction reverses the gain.
“Experimental evidence provided by SOD proves that DLR exists, so the appropriate question is: “Has evidence of DLR proven that the 2LoT is wrong?”
The evidence is too weak to disprove 2LoT. In the pyrgeometer output, DLR equals S-B_surface plus or minus “X” where X is a net radiative flux resulting from energy exchange between the surface of detector plate and its surroundings, the photon gas inside the dome. The wavelength filter tells us the range of wavelengths comprising that gas; but nothing about origins. Photons could originate from GHGs in the atmosphere. They could also originate from the surface. Photons emerge from the surface in all directions, implying that 4 of 5 do so laterally. These could be reflected or scattered from their original paths, multiple times, to new paths, including downwards, and enter the pyrgeometer dome. Moreover, photons could originate from GHGs in an atmosphere warmer than the surface (temperature inversions resulting from a dry surface cooling faster than the air aloft at night and as found at the South Pole in winter by Town et al 2005) well in accord with 2LoT.
“Do you use sunscreen?”
Yes, applied with 100% coverage, somewhat better than GHG’s 2% planar coverage. Low coverage together with wavelength-specific absorptivity would require very high mass absorption coefficients to account for 90% absorption of surface radiation.
Where are values for these coefficients published?
“The sun is 6000 degC and 93 million miles away”.
Nevertheless, its irradiance on our planet (a function of the fourth power of absolute temperature) has an effective temperature of 394K compared with the troposphere’s range from 288K at the surface, reducing by 6.5 degrees per kilometer of altitude. Moreover, whereas sun-shine propagates as parallel rays in a full spectrum with constant strength, atmosphere-shine spreads out in all directions in a partial spectrum and diminishes in strength with the square of distance travelled. On the other hand, atmosphere-shine impinges on an area 4 times that of sun-shine; 30% of sun-shine is reflected; and the atmosphere intercepts 20% of sun-shine (according to K&T’s global mean energy budget). On the third hand, polemical GHG models assume that atmosphere-shine propagates only up and down, equally; whereas it does so isotropically, implying that two-thirds propagates laterally and one-sixth downwards.
Before accounting for the qualitative differences between sun- and atmosphere-shine, that is, assuming blackbodies all round, the relative irradiances at the surface would be:
atmosphere/sun = (240 x 4 x 1/6)/(1367 x 0.7 x 0.8) = 0.2
“These precedents should convince your intuition that “too little” isn’t a good reason for rejecting CAGW. Neither is the 2LoT”.
What good reasons are there for rejecting CAGW?
“On the third hand, polemical GHG models assume that atmosphere-shine propagates only up and down, equally; whereas it does so isotropically, implying that two-thirds propagates laterally and one-sixth downwards.”
How about almost half somewhat up, almost half somewhat down, and very little exactly laterally?
Utahn,
The numbers are in accord with the six directions of the three orthogonal axes.
So that’s isotropic?
DeWitt Payne, March 31
“….you need to…….read some physics textbooks ……”
I do and this is what one says on the relevant subject:
“Consider a cavity with metallic walls at temperature T. The walls emit thermal electromagnetic radiation. In thermal equilibrium this radiation has a black body spectrum characteristic of the temperature T. Furthermore, as we shall show, in the steady state attained at equilibrium the electromagnetic radiation inside the cavity must exist in the form of standing waves with nodes at the metallic surfaces.” (page 51, Eisberg: Fundamentals of Modern Physics, Wiley 1961).
Eisberg explains that Planck’s genius was to make Rayleigh-Jeans’ spectral distribution of blackbody radiation conform with experiment by mathematical summing of discrete energy quantities rather than integrating over a continuous function as in classical physics. But Planck’s spectral distribution of blackbody radiation retains the core of R-J’s construction, which is that energy density in a wavelength interval is the product of the number density of standing waves in the interval and the average energy per wave.
Standing waves with nodes at the surfaces imply purely reflective surfaces – zero absorption, zero emission, radiation ceases at thermal equilibrium.
Complete rubbish. It implies no such thing. Nor does your quote support that conclusion.
There is no physical mechanism for the absorptivity of a surface to change at all, much less go to zero at thermal equilibrium. There are no tiny spectrophotometers in the surface or any other mechanism to determine that the surface is at thermal equilibrium with its surroundings. Thermal equilibrium means that absorption and emission are equal. There is no requirement that equal means identically zero.
To put it another way: Saying that the radiation is standing waves with nodes at the walls only says that the wavelengths of the radiation are quantized. It says nothing whatsoever about the intensity of the radiation at each of the allowed wavelengths or how the intensity can vary over time. It’s basically the particle in a box problem: http://en.wikipedia.org/wiki/Particle_in_a_box and the number of particles (photons, say) at a given wavelength in the box represents the intensity of the radiation. And we’re not talking about an empty box. The box contains at least one object with non-zero absorptivity so it can have a defined temperature.
DeWitt Payne,
Thanks for the particle_in_a_box reference. It contains the following statements:
“…..there are regions within the box for which P(x) = 0, indicating that spatial nodes exist at which the particle cannot be found”; and “The probability density does not go to zero if relativistic effects are taken into account”.
Eisberg (page 52): “….electromagnetic radiation is a transverse vibration……propagating perpendicular to the wall……(and is therefore) parallel to the wall. But a metallic wall cannot support an electric field parallel to its surface, as currents can always flow….to neutralise the electric field…….which therefore must always vanish at the wall”.
If the photon cannot be found at the wall how can it be absorbed by the wall?
Together these explanations support your argument:”Thermal equilibrium means that absorption and emission are equal. There is no requirement that equal means identically zero”. Conversely, they lend no support to the notion of equality of absorption and emission by the wall at S-B intensity at thermal equilibrium. Rather they convey a picture of reducing intensity of radiation as the system moves towards thermal equilibrium but never quite reaching zero. The circular flow of energy between the walls and the cavity all but stops, the consequently almost-stable stock of photons within the cavity behaving as standing waves exhibiting an energy density derivable from the Planck function.
“There are no tiny spectrophotometers in the surface or any other mechanism to determine that the surface is at thermal equilibrium with its surroundings”.
However, surface atoms are in physical contact with a photon gas. The most probable energy state of the atom is its ground state from which it has to be shifted to a higher energy state if absorption is to occur. The photon gas exhibits such inter-related properties as energy density, pressure and temperature. I can imagine an equilibrium relationship between the atom’s energy state and the photon gas pressure. Pressures above that equilibrium level are necessary to force absorption and the accompanying shift to a higher energy state. In this process the photon gas pressure reduces towards the equilibrium level at which it is no longer able to force the upward shift in the atom’s energy state and absorption ceases.
“There is no physical mechanism for the absorptivity of a surface to change”
This looks to be at odds with SOD’s post on emissivity centred on Wibur’s work. Wilbur obtained his emissivity values by measuring reflectivity and inferring emissivity from the relationship between reflectivity, absorptivity and emissivity. Reflectivity varies with wavelength and angle of incidence of radiation and so must absorptivity.
This is pointless. You’re going to believe your own nonsense regardless of what I say. Bye.
SoD says:
“1 W/m² absorbed from the atmosphere is identical to 1 W/m² absorbed from the sun.”
The implication here is that 1 W/m^2 of post albedo solar power and 1 W/m^2 of additional atmospheric absorption act to radiatively force the system equally. I don’t see how this could be, unless all the radiative power from the surface absorbed by the atmosphere is downward re-emitted, never leaves the system, and ultimately returns to the surface one way or another. Being that a huge portion of the LW flux exiting at the TOA must originate from the atmosphere (as opposed to the surface), and all the non-radiative flux from the surface to the atmosphere is in addition to the surface radiative flux (and must be conserved), I maintain this cannot be so.
Maintain away. I’ve long since given up trying to explain basic physics to you.
But to convince someone else reading this blog, write an equation. That is what this article is all about.
Or, novel approach – open a heat transfer textbook and read the equation for change in temperature as a result in change in energy. I’m just kidding of course, I don’t expect you to do something so ridiculous..
OK, here’s my equation:
F = 1/2*(Δa)
Where ‘F’ equals the post albedo solar equivalent radiative forcing and ‘a’ equals the surface radiation absorbed by the atmosphere.
BTW, I’ve made no such claim that the increase in thermal energy per 1 W/m^2 of radiative power absorbed from the surface or the Sun are not equal to one another. Of course they are. A watt is a watt, independent of where it last originates from. What I contend is that upon radiative re-emission, half of the absorbed power is emitted up, acting to the cool the system and ultimately the surface. In this specific circumstance a watt of increased atmospheric absorption is not the same as a watt of post albedo solar power all downward emitted into the system.
RW,
Apparently you have missed the details of how the atmospheric greenhouse effect actually works. An increase in CO2, for example, causes a decrease in emission from the top of the atmosphere to space. The calculations are quite straightforward and are confirmed by observation. It is true that increasing ghg concentration in the stratosphere will increase emission and cause cooling. But the stratosphere is optically thin. The troposphere isn’t. The observed spectrum of atmospheric emission to space shows a large dip at the CO2 band, not a peak. There is a small peak in the center of the band, but that is caused by emission from CO2 in the stratosphere, where your mental model of the atmosphere is more or less correct.
The claim, the very very simple claim, is that 1 W/m2 of solar radiation absorbed by the surface has exactly the same effect as 1 W/m2 of atmospheric radiation absorbed by the surface.
I have to break it down into these tiny portions so that all the people with the random ideas have to explain in specific points what is wrong with general climate science on each specific point. Rather than the “blah blah blah”..
SoD says
“The claim, the very very simple claim, is that 1 W/m2 of solar radiation absorbed by the surface has exactly the same effect as 1 W/m2 of atmospheric radiation absorbed by the surface.”
It depends on the surface to some extent, does it not?
SoD,
“The claim, the very very simple claim, is that 1 W/m2 of solar radiation absorbed by the surface has exactly the same effect as 1 W/m2 of atmospheric radiation absorbed by the surface.”
My apologies. I absolutely agree with this (of course). I thought you were saying that 1 W/m^2 of additional atmospheric absorption of surface radiation is equal to 1 W/m^2 of solar radiation entering the system.
Bryan,
“It depends on the surface to some extent, does it not?”
No. A watt is a watt, independent of where it last originates from.
Dewitt,
“Apparently you have missed the details of how the atmospheric greenhouse effect actually works. An increase in CO2, for example, causes a decrease in emission from the top of the atmosphere to space. The calculations are quite straightforward and are confirmed by observation.”
According to the RT simulations that calculate 3.7 W/m^2 per CO2 doubling, the physical meaning of this quantity is the instantaneous reduction in the direct surface radiation to space (I’ve confirmed this with multiple sources). The IPCC designates this entire amount as ‘forcing’ (i.e. all downward directed); however, the actual physical meaning itself says nothing about what happens after absorption, in particular any amount that finds its way emitted (up) out to space as part of the LW flux leaving at the TOA originating from the atmosphere.
The question that none of detractors of this ever seem to be able to answer is – if not about 50/50, then what fraction and based on what physics or data? Even if you can’t agree the split is about 50/50, surely the fraction of absorbed power ultimately emitted up and directed out to space cannot be acting to warm the surface the same as post albedo solar power all coming down in, right? The flow of this energy, even that which is still within (i.e. not leaving in present), is away from the surface and out of the system, is it not?
As I said, it seems to me the only way to reconcile this discrepancy is if all the radiation absorbed by the atmosphere is downward re-emitted, never leaves the system, and ultimately returns to the surface one way or another. Being that most of the LW flux exiting at the TOA must originate from the atmosphere (as opposed to the surface), and all the non-radiative flux from the surface to the atmosphere is in addition to the surface radiative flux (and must be conserved), I can’t accept this.
Please cite those sources. They are either wrong or you have misinterpreted them. Radiative forcing is the reduction in emission to space at the tropopause, not the surface. Only a small amount of radiation on the short wavelength wing of the CO2 band goes directly to space. The rest is absorbed by the CO2 or water vapor on the long wavelength wing of the CO2 band. It’s calculated at the tropopause because the stratosphere is allowed to cool by radiation before the forcing is calculated. The radiative equilibrium time constant for the stratosphere is weeks to months.
IPCC AR4 WG1 Chapter 2.2:
[my emphasis]
I don’t see how you could possibly manage to interpret that as a reduction in direct radiation to space from the surface.
Dewitt,
Recently I’ve confirmed with Myhre (regarding Myhre et. al. 1998), which is the standard reference for the figure, that the actual physical meaning of the cited 3.7 W/m^2 per CO2 doubling is the net absorption increase (i.e. the instantaneous reduction in direct surface radiation to space). In contrary to this, the IPCC arbitrarily claims the referenced 3.7 W/m^2 is ‘net (down minus up)’, but I don’t see how it could be, as this would imply that power absorbed by the atmosphere from the surface radiative flux is all downward re-emitted and never leaves the system, which is obviously cannot be correct.
It seems somewhere back many years ago someone misinterpreted a instantaneous reduction in direct surface radiation to space as being an equal and opposite downward directed change, which no one ever caught or thought much about.
Dewitt,
“Radiative forcing is the reduction in emission to space at the tropopause, not the surface.”
It’s the reduction in direct surface radiation to the tropopause. There is almost no difference betweeen that through to the tropopause and that all the way through the stratosphere (after ‘adjustment’ or whatever).
Dewitt,
I should say the ‘stratospheric adjustment’ is included in the 3.7 W/m^2, which means it’s equal to the reduction in direct surface radiation to space. The actual adjustment, BTW, is tiny – amounting to less than 0.1 W/m^2. Meaning even without doing it the difference is negligible.
RW,
No. You have misinterpreted Myhre. You keep talking about emission up as well as down, but you ignore the consequences. Emission from the lower atmosphere will be absorbed as well as emission from the surface. Let’s look at the actual numbers neglecting solar. At the tropopause, CO2 should have little effect on the intensity of incoming solar radiation. MODTRAN only calculates from 100-1500cm-1, but that includes essentially all the effect of CO2. Using the 1976 US standard atmosphere profile, looking from the tropopause downward (13km), the atmosphere absorbs 27.03% of radiation from the surface at 280 ppmv and 26.41% at 560 ppmv. At a surface temperature of 288.20K, the emission at a surface emissivity of 0.98 is 360.472 W/m² So 2.23 W/m² of direct emission to space from the surface is absorbed. But the difference in emission at 13km is:
264.576 – 261.185 = 3.391 W/m²
That’s why forcing is calculated at the tropopause. The actual forcing is larger than the absorption of surface emission only. One reason is that CO2 absorbs water vapor emission on the long wavelength side of the band because CO2 is well-mixed, but water vapor isn’t and is concentrated at lower altitudes. But that emission does not come from the surface because water vapor absorbs strongly at those wavelengths.
And by the definition of forcing, a change of 1 W/m² of incoming solar radiation is exactly equivalent to a change of 1 W/m² of upward emission.
And your arrogance in assuming that you have found something obvious that thousands of professional scientists that do this for a living have somehow missed is astonishing.
SoD says:
“1 W/m² absorbed from the atmosphere is identical to 1 W/m² absorbed from the sun.”
It is only identical with respect to the first law of thermodynamics which deals with quantity of energy..
The second law of thermodynamics deals with the quality of the energy and in this case the two energy sources are quite different.
A relevant equation is the energy of a photon E = hf.
For N photons being absorbed in an area of one square metre per second we can also write
P = Nhf (W/m2)
A look through any reference on the photoelectric effect will highlight the difference.
On this fine day in Scotland each watt of solar radiation makes possible photosynthesis.
One or more watts of radiation from the atmosphere will not assist photosynthesis.
Bryan, you have already agreed that the energy from the atmosphere is absorbed according to a formula which relies on a material property called “absorptivity”.
I explained it on February 2, 2012 at 9:22 am. And when you agreed I asked my next question of February 4, 2012 at 8:45 am. Of course you didn’t respond for obvious reasons.
Would you like to change your mind about your initial affirmation?
The question is what happens as a result of 1 W/m2 absorbed from solar radiation vs 1 W/m2 absorbed from atmospheric radiation?
What happens to the internal energy as a result of the absorbed energy?
What happens to the temperature as a result of change internal energy?
Please supply
1. your equation for absorption of radiation from different sources
2. your equation for change in internal energy as a result of absorption of radiation
3. your equation for temperature change as a result of change in internal energy
If you want to claim that the energy from the atmosphere is not absorbed then you need to revise your earlier agreement.
Just come out and say that you were wrong before and also of course, Kramm and Dlugi were wrong..
Equations from you – a complete set – would be wonderful, but very unlikely, for reasons that regular readers will completely understand. Instead random incoherent claims contradicting earlier random incoherent claims..
SoD says
“1 W/m² absorbed from the atmosphere is identical to 1 W/m² absorbed from the sun.”
I was just looking at this isolated sentence!
With qualification it could be correct but at other times it would be completely incorrect.
Correct would be where both absorptions were involved with say increasing the absorbers thermal energy by translational KE of the molecules of a colder surface.
Incorrect would be if photochemical changes were possible such as in photosynthesis.
Dewitt,
Let me elaborate in more detail what I’m talking about. In general, the 3.7 W/m^2 of ‘forcing’ from 2xCO2 is supposed to be equal to post albedo solar power entering the system (i.e. the same as an increase from about 240 W/m^2 to 243.7 W/m^2), right? This is the origin of the so-called ‘zero-feedback’ warming from 2xCO2 of about 1.1C (390/240 = 1.625; 3.7 W/m^2 x 1.625 = 6.0 W/m^2 = 1.1C from S-B), right?
Using some rough numbers, at 288K the surface emits a radiative flux of about 390 W/m^2, and about 90 W/m^2 of this passes directly into space and about 300 W/m^2 is therefore absorbed by the atmosphere. Of the 300 W/m^2 initially absorbed by the atmosphere, about 150 W/m^2 is ultimately emitted to to space as part of the flux leaving at TOA originating from the atmosphere (150 + 90 = 240 W/m^2 leaving at the TOA), and 150 W/m^2 of non-incident post albedo solar is ultimately returned or re-circulated back to the surface as part of the net flux of energy entering the surface boundary required to sustain a temperature of 288K (240 + 150 = 390 W/m^2). Or the requirement for equilibrium and COE is about half of what’s absorbed by the atmosphere from the surface radiative flux ends up emitted to space without ever being incident on the surface.
When CO2 doubles, the 90 W/m^2 direct surface radiation to space reduces to 86.3 W/m^2 and the atmosphere absorbs an additional 3.7 W/m^2 (an increase from about 300 W/m^2 to 303.7 W/m^2). How can the fraction (about half) of the 3.7 W/m^2 of incremental absorption that is emitted (up) out to space without ever being incident on the surface be considered the same as post albedo solar power all coming down into the system? It doesn’t seem to me like it can, as how can the fraction of absorbed power never ultimately received by the surface be acting to warm the surface?
In other words, what I’m saying the net input ‘forcing’ acting to the warm the system (and ultimately the surface) from the 3.7 W/m^2 of increased absorption from 2xCO2 is only equal to about half or about 1.85 W/m^2, and the so-called ‘zero-feedback’ warming per CO2 doubling is only about 0.55C instead of 1.1C.
Unless you can demonstrate that the net absorption increase per CO2 doubling is actually about 7.4 W/m^2 and/or the direct surface radiation to space is significantly greater than about 90 W/m^2, you really don’t have a case.
RW
SoD said
“The claim, the very very simple claim, is that 1 W/m2 of solar radiation absorbed by the surface has exactly the same effect as 1 W/m2 of atmospheric radiation absorbed by the surface.”
I said
“It depends on the surface to some extent, does it not?”
You said
“No. A watt is a watt, independent of where it last originates from.”
Did you notice the the part of SoD quote saying THE SAME EFFECT.
We are all agreeing with the trivial statement that one watt is one watt.
The absorbed one watt of radiation can be entirely thermalised increasing the translational KE of the surface molecules.
On the other hand part of the energy of the radiation may for instance induce electrons into a higher orbit or indeed completely ionise a molecule.
Part may produce a photochemical change such as photosynthesis.
The exact outcome of the absorption strongly depends on the frequency of the radiation and the nature of the surface.
So no, one watt of solar radiation is not always equivalent to one watt of atmospheric radiation
Dewitt,
You say:
“You have misinterpreted Myhre.”
I assure you I have not. I went out of my way to clarify and get absolute confirmation from him on this. That is the exact physical meaning of the 3.7 W/m^2 is the instantaneous reduction in direct surface radiation to space per CO2 doubling. In other words, this means that upon CO2 doubling the atmosphere will absorb an additional 3.7 W/m^2 of surface radiative power that was previously passing directly from the surface into space the same as if the atmosphere wasn’t even there.
As far as ‘net (down minus up)’, Myhre’s paper and RT calculation itself doesn’t actually say anything about this, as it is not its function or purpose to do so.
You say:
“You keep talking about emission up as well as down, but you ignore the consequences. Emission from the lower atmosphere will be absorbed as well as emission from the surface.”
But this doesn’t increase atmospheric opacity. The bottom line is this is not what the RT simulation calculates.
RW,
Myhre, et. al. 1998 nowhere states that the physical meaning of forcing is the instantaneous reduction in direct surface radiation. In fact it refers to Hansen, et.al. 1997.
Again, no mention of absorption of direct surface radiation only, only a change in total flux at a specific altitude (or pressure). If one allows the stratosphere to equilibrate, then the flux change can be measured at the top of the atmosphere. I challenge you to find a quote in Hansen1997 that supports your claim of increased absorption of direct radiation to space only rather than, say, an increase in the effective altitude of emission.
If you have a copy of Myhre saying something different, then you should post it.
The increased absorption occurs all the way through from the surface to the tropopause or after stratosphere adjustment from the surface through the TOA.
This is nothing revelatory, BTW, as all Myhre did was confirm what multiple other sources said the physical meaning of the 3.7 W/m^2 is, including George White the author of the referenced paper.
Send me an email at wetmorer ‘at’ hotmail.com if you want me to forward you Myhre’s confirmation of this. I don’t feel comfortable posting the email here. Or you can email him yourself.
RW,
Duh!
I have already demonstrated that absorption of surface radiation only from doubling CO2 is insufficient to obtain 3.7 W/m² of forcing at the tropopause. There must be additional absorption of radiation emitted by the atmosphere above the surface. That alone is sufficient to invalidate your conjecture. But your whole approach is wrong.
Emission in the atmosphere is indeed all directions with about 50% up and 50% down, but at low altitudes everywhere except the window region, most of the emitted radiation is absorbed by other molecules because the optical density is much greater than 1. Radiation is only emitted to space from a layer of the atmosphere centered where the optical density at that wavelength is equal to 1. That altitude is determined by the number density of the molecules. The number density is proportional to concentration and absolute pressure. Double the concentration and that altitude increases. Below the tropopause, the temperature decreases with altitude so emission to space, which at high optical density is equivalent to emission from a blackbody at the same temperature and wavelength, is lower.
A forcing of 3.7 W/m² at the tropopause, whether from an increase in incoming solar radiation or a decrease in emission upward, will eventually produce the same increase in surface temperature. The transient response will be different, but the new steady state will be the same. Try reading the Hansen paper I linked above.
Your conjecture that the IPCC definition of forcing was somehow changed from its original meaning is also not supported by Hansen’s paper, which predates and was cited by Myhre.
You don’t have to post the whole email, btw.
Dewitt,
You say:
“And by the definition of forcing, a change of 1 W/m² of incoming solar radiation is exactly equivalent to a change of 1 W/m² of upward emission.”
It depends what you mean by ‘the definition of forcing’. 1 W/m^2 of increased absorption from surface radiation is NOT equal to the ‘forcing’ of 1 W/m^2 post albedo solar radiation entering the system. This is because when the absorbed photons from the surface are re-emitted in the atmosphere they have a 50% of being emitted up instead of down, and this is the case on each subsequent emission until they either pass into space or return to the surface in some form. Only the downward re-emitted fraction of the absorbed power is being input into the system (i.e. acting to warm) the same as post albedo solar radiation all coming down in or all downward emitted in.
Now, technically all the 3.7 W/m^2 is ‘radiatively forced’, it’s just that about half is forced in the same direction it was already going – up towards space.
You say:
“And your arrogance in assuming that you have found something obvious that thousands of professional scientists that do this for a living have somehow missed is astonishing.”
Well I’m sorry, but I’ve spent nearly two years investigating this specific issue and it has indeed been missed, as embarassing as it may be. SoD dismissed this a couple years ago when I brought it up here, but I don’t think he really understood it.
Here is the original referenced paper:
http://www.palisad.com/co2/div2/div2.html
Most people do not understand what it is that is being depicted and claimed. They think it’s trying to say something about why the boundary fluxes are what they are or why the surface temperature is what it is. It isn’t.
Oh, please. Surely you can do better than that. That ‘paper’ is a bad joke. G&T make more sense. White completely neglects convection in his energy balance and the atmosphere isn’t a thin single slab at the same temperature. Not to mention that an average emissivity/absorptivity of 0.5 is way too low. We know for a fact that emission upward from the top of the atmosphere is lower than emission downward from the atmosphere just above the surface. It’s been measured many times in many places. The emitting region, especially for CO2, is much colder. 40% of the sky isn’t cloud covered and even clouds emit less upward than downward because the cloud top is colder than the cloud bottom. And some of that radiation is absorbed by the CO2 above the cloud top.
MODTRAN again:
US 1976 standard atmosphere with cumulus cloud cover, cloud base 0.66 km and cloud top 2.7 km, 375 ppmv CO2
surface looking up: 359.216 W/m²
70 km looking down: 222.218 W/m²
So even for clouds, it’s not 50% up and 50% down. If I set the CO2 concentration to zero, upward emission is only 240.084 W/m² and the effective cloud top temperature is about 265K compared to the surface temperature of 288.2K. For comparison, clear sky emission at 70 km looking down with 375 ppmv CO2 is 258.86 W/m².
Dewitt,
I wrote:
“It depends what you mean by ‘the definition of forcing’. 1 W/m^2 of increased absorption from surface radiation is NOT equal to the ‘forcing’ of 1 W/m^2 post albedo solar radiation entering the system.”
I should clarify what I mean by this: As far as its ability to ultimately act to warm the surface, 1 W/m^2 of increased atmospheric absorption of surface radiation is NOT equal to 1 W/m^2 of post albedo solar power entering the system, because unlike post albedo solar power which is all directed toward the surface, about half of the power absorbed by the atmosphere is directed away from the surface out into space. This makes it essentially the same as radiative power passing directly from the surface into space (i.e. all acting to cool the surface).
And that’s your problem in a nutshell.
Half the power absorbed by the atmosphere is not radiated upward. Initially, none of it is radiated upward. Apparently you don’t understand the concept of absorption. We’re talking instantaneous change here. The temperature profile of the troposphere is unchanged, which means that emission at each altitude is unchanged. But the effective altitude of emission increases so emission to space decreases. The net decrease is 3.7 W/m², not 3.7-1.85 W/m².
When the system reaches steady state again at a higher temperature, upward power at the TOA will be back to the status quo ante, but emission downward at the surface will be a lot higher. As far as absorption at the surface, 100% is radiated and convected upward. But most of that is absorbed by the atmosphere too, until the temperature increases enough to achieve approximate balance again.
Dewitt,
It’s hard to know what specifically of yours to respond to.
First of all, I’ve confirmed directly with Myhre and multiple other sources that the physical meaning of the 3.7 W/m^2 per CO2 doubling is exactly as I’ve defined it. As I said, I went out of my way to get absolute clarification from him on this, because many people such as yourself have claimed otherwise. I’m happy to forward you the email or you can ask him yourself if you want. Maybe it’s just me, but it doesn’t seem quite right to post a private email on a public forum like this.
Second of all, George White’s 50/50 atmospheric split model is not a model of the actual behavior, but instead a model of the net result equivalent of the actual behavior at the boundaries of the surface and the TOA. The purpose of the model is to strip the atmosphere down to net energy flow. In other words, the he has constructed a black box of the Earth-atmosphere system. The boundary conditions match those of the real and much more complex system in between the boundaries. It’s not attempting to say anything about why the boundary fluxes are what they are or why the surface temperature is what it is (a common misconception).
Also, in my experience there seems to be a fundamental terminology discrepancy where the author of that paper, George White, has a different meaning for the term ‘radiative balance’ than what it apparently means in traditional atmospheric physics. What he means by the term ‘radiative balance’, in particular at the surface, is just the net flux required to sustain the radiative flux emitted from surface whose ultimate origin can only be from downward emitted radiative effects (since radiation is the only significant source of energy entering the system). In other words, because the entire energy budget for the system is all EM radiation. Now, of course the net flux itself entering the surface boundary is a chaotic combination of SW, LW and non-radiative power. Moreover, the net power flux itself (about 385 W/m^2 to sustain 287K) is the net result of all of the effects and their complex interdependencies – both radiative and non-radiative (convection, conduction, evapotranspiration, clouds, precipitation, wind, etc.). In short, by the term ‘radiative balance’ in the steady-state, he’s not implying the actual surface is in pure radiative equilibrium with the atmosphere, as of course it isn’t.
I also agree that due to the lapse rate the total downward emitted LW entering the surface is not equal to the LW emitted from the atmosphere exiting at the TOA. I also agree that the total downward LW between any two particular layers of the atmosphere is not equal to the total upward LW. I also agree that in general, between any two particular layers, downward LW is larger than that emitted upward.
As I understand him, White is not making the contention that the atmosphere is isothermal or the split of LW between any two particular layers of the atmosphere is 50/50. Indeed, it is not. White is instead just claiming that on a photon by photon basis, all the radiative emission in the atmosphere is isotropic (be it from the heated atmosphere itself or directly from GHG molecules). Also, no doubt there are multiple absorptions and re-emissions along the way until the required emitted power from the atmosphere eventually passes into space at the TOA, but at each and every stage or level there is re-emission, on a photon by photon basis, it’s always isotropic. This is the fundamental physical basis behind the claim in White’s paper where he says “From the physics of black bodies (or grey bodies in this case), the atmosphere should behave as an isotropic radiator with half of it’s emitted power going up and half down”.
He is making no contention that between any two layers there is or should be radiative equilibrium, as indeed this is not the case because layers above other layers are emitting at decreasing rates with altitude, as temperature decreases with altitude.
Again, by the ‘radiative balance’ he just means the net energy flux entering the surface boundary required to sustain the radiative flux emitted from the surface, whose ulimate origin can only be from downward emitted radiative effects in the atmosphere. Of course, the net energy flux entering the surface is a chaotic, varying combination of both SW, LW and non-radiative flux; however, some of this energy flux originated non-radiatively from the surface in addition to the surface radiative flux, so any of this that returns to the surface (in the form of either direct radiative flux or non-radiative flux) is a net zero flux entering the surface boundary; and is more or less a closed loop in the steady-state (i.e. surface -> atmosphere -> surface, as opposed to Sun -> space -> atmosphere -> surface -> atmosphere -> space). The primary source of this non-radiative energy circulation loop is of course that of water (surface water -> water vapor -> clouds -> precipitation -> surface water). Now, some of the energy within this loop can end up radiated out to space and back to the surface, some can be replenished by post albedo solar energy absorbed in the atmosphere or by energy emitted from the surface – it doesn’t really matter as it all has to be conserved one way or another.
The key is non-radiative fluxes from the surface to the atmosphere, from the atmosphere to other parts of the atmosphere, and from the atmosphere back to the surface no doubt have an absolutely enormous influence on the whole energy balance of the system and the net resulting surface temperature, as huge portion of the roughly 300 W/m^2 of the surface LW flux absorbed by the atmosphere is from water vapor and clouds, which are moved non-radiatively from the surface into the atmosphere. And no doubt the surface is considerably cooler and subsequently radiates less as a result of convection in the atmosphere, which increases the rate at which the system can cool and/or ultimately emit energy back out to space (i.e. there is a net convective loss from the surface to the atmosphere). But power convected from the surface that ultimately ends up radiated out to space just offsets additional power that would otherwise have to be radiated from a warmer surface in order to achieve equilibrium at the TOA.
The ultimate point, according to White’s analysis, is all of the non-radiative fluxes from the surface are in addition to the surface radiative flux, all occur in between the surface and the TOA, and are more or less just moving energy around still within the thermal mass (which is part atmosphere) so the total atmospheric absorption from the surface LW flux is about 300 W/m^2 and the surface energy balance is what it is – about a net of 385 W/m^2 entering the surface from the atmosphere to sustain 287K.
The point of the exercise is to show that when only the radiative components are considered (the only significant source of energy entering the system), the 50/50 emerges from the basic constraints of Conservation of Energy (i.e. that the requirement for equilibrium is half of the surface radiative power absorbed by the atmosphere is directed away from the surface and out into space, and is essentially the same as power passing directly from the surface into space). This is demanded by the raw physics of BB radiation, which is always isotropic on a photon by photon basis, where the atmosphere compromises only an infinitesimal fraction of the total thermal energy in the system.
I meant to say here:
“where the atmosphere [b]is composed of[/b] only an infinitesimal fraction of the total thermal energy in the system.”
Dewitt,
I’d like to pose a few questions to you:
Do you agree that all the energy in the atmsophere is either on a path where it will be radiated out to space or returned to the surface in some form (in a relatively short period of time)?
Do you agree that photons emitted from the surface absorbed by the atmosphere, upon re-emission, have a 50% chance of being emitted up instead of down and the same is the case on each subsequent re-emission until they eventually either pass into space or return to the surface in some form (they don’t necessarily have to return as direct radiative flux)?
Do you agree that the power flux of about 150 W/m^2 leaving at the TOA originating from the atmosphere can only come from upward half of emitted radiation in the atmosphere?
Do you agree that all the radiation emitted upwards in the atmosphere that finds its way radiated out to space as part of the flux leaving is acting the cool the system instead of warm it? That is the flow of this energy, even that which is still within (i.e. not exiting at present), is away from the surface and out of the system?
How can the fraction of absorbed surface radiation in the atmosphere re-emitted up and eventually finding its way radiated out to space without ever returning to the surface, be acting to warm the system or be the same as post albedo solar power all coming down in?
Isn’t then only the downward re-emitted porton of absorbed surface radiation being input into the system (i.e. acting to warm) the same as post albedo solar power?
Also, do you understand what this graph is depicting?
RW,
Also, do you understand what this graph is depicting?
Yes, and it’s a trivial result and does not prove your conjecture. It’s well known that the energy radiated downward by low clouds is very nearly equal to the energy radiated upward by the surface. That is, the temperature of the cloud base is about the same as the temperature of the surface. But that tells you nothing about the temperature of the cloud top. Clouds do not radiate equal energies up and down because the cloud top is colder than the cloud base.
MODTRAN
1976 US standard atmosphere, cumulus cloud cover, base 0.66km, top 2.7 km
0.5 km looking up: 350.738 W/m² (100-1500 cm-1)
0 km looking down: 360.472 W/m²
3.5km looking down: 272.112 W/m²
0.66 km temperature: 283.91K
3 km temperature: 268.70
With an emissivity of 1, which is a good approximation for clouds, that’s 295.6 W/m² up and 368.4 W/m² down over the full wavelength range.
You think White is onto something with his analysis. But in fact, it’s nothing more than the standard single slab gray atmosphere toy model that is a fixture in every atmospheric radiation transfer textbook. For example it can be found starting at page 139 in A First Course in Atmospheric Radiation, 2nd edition, Grant Petty, Sundog Publishing, 2006. But since the atmosphere isn’t gray and isn’t isothermal and isotropic you would need to have 10,000-100,000 slabs at a given altitude to begin to properly model the wavelength response and 30-100 layers of these slabs at different altitudes to model the change in temperature and pressure with altitude. And if you’re going to do an energy balance, you can’t ignore convection as White does.
RW,
Your other questions are irrelevant. The answers to them do not lead to the proof of your conjecture. Quite the opposite, in fact.
In case newcomers think that RW is onto something, I recommend reading the similar lengthy and pointless exchange in an earlier article, starting somewhere around here.
There’s no benefit to RW in me responding (again) to his confusion over absolute basics.
But if others would like me to address specific points made by RW please go ahread and raise them.
SoD,
With all due respect, I’m telling you – you don’t understand what is being depicted and claimed. You think you do, but you really don’t. If you give me a chance to take you through it step by step, I think (like me) you will have no choice but to accept that it is at least basically correct.
RW,
Here’s an example of a 10 layer gray atmosphere. Each layer has an emissivity/absorptivity of 0.5 and emits the same amount of energy up as well as down, i.e. 50% up and 50% down. The system is constrained so each layer emits and absorbs the same amount of energy except for the surface layer (layer 0) which has an emissivity of 1 and is not constrained to have an energy balance, i.e. there is an additional source of energy to the surface that is not specified. Here is the resulting temperature profile:
layer temperature(K)
0 300
1 287.7289679
2 280.9541275
3 273.6503727
4 265.7100086
5 256.9862734
6 247.2710251
7 236.2533186
8 223.4345937
9 207.9293186
10 187.8853489
The surface emits 105.985 W/m² more than it receives and the emission from the top layer upward is also 105.985 W/m². That would make the effective emission temperature of the system 207.93 K. So an atmospheric greenhouse effect is not ruled out by the constraint that emission upward and downward at any point in the atmosphere must be equal.
If I set the layer emissivity to 0.11971224 with a surface temperature of 288.2 K and adjust the layer temperatures for radiative balance at each layer, the radiative imbalance at the surface is 239 W/m², direct transmission of surface radiation is 27.94% and total emission from the top layer is also 239 W/m², making Teff = 254.8 K. Look familiar?
Can you provide a few more details here, as I don’t quite see what you’re doing.
RW,
It should be obvious to anyone actually capable of understanding atmospheric radiative transfer.
Instead of a one layer toy model as White shows, I’m using a ten layer model. Each layer has the same emissivity/absorptivity that is constant over all wavelengths. So emission from each layer can be calculated from the Stefan-Boltzmann equation. The total emission from a layer is twice the calculated amount because each layer emits upward as well as downward. Absorption of incoming radiation = emissivity times the flux and total absorption is the sum of absorbed up and down and what isn’t absorbed is transmitted. So starting at the surface, which has an emissivity of one and a fixed temperature, transmission through the first layer is added to the emission upward from the first layer and this continues to the top layer. The process is repeated in the other direction with zero incoming radiation. The temperature of each layer is adjusted so that the sum of the absorbed radiation in that layer is equal to the sum of the emitted radiation from that layer (radiative balance) and so the net emitted radiation at the surface is equal to the net emitted radiation at the top layer. It’s trivial to do this in Excel using Solver to adjust the temperatures. The emissivity can be adjusted to produce a specific net outward total flux from the top layer.
If you increase the emissivity of the layers, the surface temperature must be raised to maintain the same outward radiative flux.
Here’s the whole matrix from the spreadsheet:
layer temp emission up total up emission down balance
0 288.2 391.1640777 391.1640777 -239
1 261.2330936 31.61072006 375.9476699 152.1640777 2.58382E-10
2 257.3854843 29.78912981 360.7312622 136.9476699 2.97916E-10
3 253.3571479 27.96753955 345.5148544 121.7312622 3.43412E-10
4 249.1269436 26.1459493 330.2984466 106.5148544 3.95836E-10
5 244.6695637 24.32435904 315.0820389 91.29844663 1.39685E-09
6 239.954327 22.50276879 299.8656311 76.08203886 5.35564E-10
7 234.9434908 20.68117853 284.6492233 60.86563109 6.25697E-10
8 229.5898309 18.85958828 269.4328155 45.64922332 7.28257E-10
9 223.8330627 17.03799803 254.2164078 30.43281555 8.45375E-10
10 217.5943582 15.21640778 239 15.21640778 -1.3599E-08
emissivity 0.11971224
Dewitt,
You say:
“Also, do you understand what this graph is depicting?
Yes, and it’s a trivial result and does not prove your conjecture. It’s well known that the energy radiated downward by low clouds is very nearly equal to the energy radiated upward by the surface. That is, the temperature of the cloud base is about the same as the temperature of the surface. But that tells you nothing about the temperature of the cloud top. Clouds do not radiate equal energies up and down because the cloud top is colder than the cloud base.”
Yes, I do understand what it is depicting. Apparently, you do not. The graph shows that even when most or all of the surface radiative power is absorbed by the atmosphere, at least half is still escapting to space, consistent with what’s depicted by the equivalent 50/50 model.
The ‘surface power out’ is the surface radiative power as a result of the surface temperature. The ‘cloud power out’ is the radiative power exiting at the TOA from the same parts of the surface covered by clouds.
You say:
“You think White is onto something with his analysis. But in fact, it’s nothing more than the standard single slab gray atmosphere toy model that is a fixture in every atmospheric radiation transfer textbook. For example it can be found starting at page 139 in A First Course in Atmospheric Radiation, 2nd edition, Grant Petty, Sundog Publishing, 2006. But since the atmosphere isn’t gray and isn’t isothermal and isotropic you would need to have 10,000-100,000 slabs at a given altitude to begin to properly model the wavelength response and 30-100 layers of these slabs at different altitudes to model the change in temperature and pressure with altitude. And if you’re going to do an energy balance, you can’t ignore convection as White does.”
Again, it’s not a model of the actual behavior, and he’s not ignoring convection. Convection contributes greatly to why the fluxes at the boundaries are what they are, but convection can only occur in between the boundaries of the surface and the TOA. Energy cannot be convected from the surface into space.
BTW, here is a blog post on JoNova by White himself that perhaps explains this more clearly than I have:
“It might help if I clarify what I’m trying to show here and why the approximations I’ve made are valid, even if they deviate from the specific internal processes in play. My goal was to quantify the required behavior of the atmosphere based on the boundary conditions between the atmosphere and space and between the atmosphere and the surface. Keep in mind that the behavior I derived at the surface boundary was a consequence of the behavior between the atmosphere and space, which by definition, is purely radiative.
Consider a hypothetical planet whose atmosphere has about the same amount of trace gas GHG absorption as the Earth, the same amount of N2 and O2, but has no water and all of the planets thermal mass is below the surface. In this case, my equivalent view of the energy balance is much closer to the actual physical mechanisms maintaining the balance. Where the current system gets complicated is with the movement of energy throughout the thermal mass. When contained within the oceans or atmosphere (i.e Hadley cell circulations), it is properly ignored. When the movement is between the oceans and clouds, where clouds comprise part of the thermal mass, the tendency is to count that movement as part of the energy balance, when it should more properly be ignored like the other circulation currents.
My equivalent view of the Earth is just as valid at quantifying the behavior dictated by the boundary conditions, but less accurate relative to representing the low level physical mechanisms establishing the balance, specifically between the surface and the atmosphere, once water is added and part of the active thermal mass of the planet is moved into the atmosphere. It’s also very important to recognize my simplified model is an equivalent model whose behavior at the boundaries matches the required behavior. That is, if the Earth’s actual atmosphere was replaced with an equivalent atmosphere with my specified behavior, the surface temperature would be exactly the same.”
Dewitt,
“Your other questions are irrelevant. The answers to them do not lead to the proof of your conjecture. Quite the opposite, in fact.”
Well, if you’re not willing to answer my questions then this is not going to be very productive.
Let me pose a few other questions that might be easier to answer:
Do you agree that, in the steady-state, simultaneously, about 240 W/m^2 exits at the TOA, about 240 W/m^2 enters the system post albedo and the surface receives a net of about 390 W/m^2 to sustain a temperature of 288K?
Do you agree that the only source of energy in the system, excluding an infinitesimal amount from geothermal, is that which enters post albedo from the Sun?
Do you agree that the 240 W/m^2 entering the system post albedo and the 240 W/m^2 exiting the system at the TOA is all EM radiation (i.e. that at the TOA only radiation enters and leaves)?
I should add:
Do you agree that the atmosphere cannot create any energy of its own? That all it can do is redirect the energy supplied from the Sun?
RW,
Take a closer look at the figure from White. If the emission is 146 W/m² and the emissivity is 0.759 (1-0.241). Then the temperature of the layer must be 241K. Doesn’t that seem a little unreasonable to you? It’s about right for clear sky winter conditions for the mid-latitudes but not for the tropics. As shown in his other diagram, cloud cover emission will also be a lot higher. Also, as I said above, there is no convective energy transfer from the surface to the atmosphere in the diagram so the energy balance is far removed from reality.
No it isn’t. The convective transfer from the surface to the atmosphere make the surface temperature a lot colder than it would be with a pure radiative transfer system, about 17 C colder on average. As I said, White isn’t even close to the level of G&T, he’s more like Nasif Nahle or Doug Cotton.
This is getting very repetitive so unless you can ask some questions that demonstrate that your mind isn’t completely closed, I’m signing off.
Dewitt,
You say:
“Take a closer look at the figure from White. If the emission is 146 W/m² and the emissivity is 0.759 (1-0.241). Then the temperature of the layer must be 241K. Doesn’t that seem a little unreasonable to you?”
Is there a part about not being a model of the actual behavior in betweeen the boundaries that you don’t understand? The point is 146 W/m^2 of outgoing flux originates from the atmosphere. The contribution is from any of the layers where some of the emission passes through into space. White’s equivalent model is saying absolutely nothing about the temperature profile of the atmosphere – his model is built for an entirely different purpose.
You say:
“Also, as I said above, there is no convective energy transfer from the surface to the atmosphere in the diagram so the energy balance is far removed from reality.
No it isn’t. The convective transfer from the surface to the atmosphere make the surface temperature a lot colder than it would be with a pure radiative transfer system, about 17 C colder on average.”
This is already embodied in the surface temperature, which is slaved to emitted power in W/m^2 by the Stefan-Boltzman law. The net incident flux on the surface of about 385 W/m^2 to sustain a temperature of 287K is itself the net result of all of the effects, including convection and everything else. The effect of convection cools the surface, requiring the surface to emit less radiation in order to achieve equilibrium with space. All that is happening is non-radiative flux from the surface is being traded off for radiative flux from the surface.
You say:
“As I said, White isn’t even close to the level of G&T, he’s more like Nasif Nahle or Doug Cotton. This is getting very repetitive so unless you can ask some questions that demonstrate that your mind isn’t completely closed, I’m signing off.”
Suit yourself, but how about answering my questions?
Dewitt,
You say:
“It should be obvious to anyone actually capable of understanding atmospheric radiative transfer.
Instead of a one layer toy model as White shows, I’m using a ten layer model. Each layer has the same emissivity/absorptivity that is constant over all wavelengths. So emission from each layer can be calculated from the Stefan-Boltzmann equation.”
OK, I appreciate all the details. This is what I thought you were doing, but I wanted to make sure. Your model is really only a hypothetical case and the physics are not the same as an atmosphere where the absorption of radiation is via GHGs and the atmosphere is composed of only a tiny fraction of the total thermal energy contained below the surface. The real atmosphere contains less than 0.001% of the total energy contained below the surface (primarily in the oceans). See here:
This makes for a fundamentally different dynamic, where the atmoshere is essentially just a fast acting radiative flux filter between the surface and space, where absorbed radiation is quickly re-radiated and soon thereafter finding its way radiated out to space or returned to the surface.
Can you, using your hypothetical model of any number multiple layers, derive an atmosphere with a surface temperature of 287K (385 W/m^2), a post albedo solar power of 239 W/m^2 and direct surface to space transmittance (the ‘T’ value) of 0.241? (Hint: The answer is ‘no’).
Dewitt,
I think you may also not be realizing that the amount of direct radiative flux from atmosphere to the surface is not the same as net power down to the surface. As I’m sure you know, the surface is not in pure radiative equilibrium with atmosphere – it’s convectively coupled and there is a large amount of latent heat transfer as well. White’s model is saying absolutely nothing about the amount of direct radiative flux that occurs from the atmosphere to the surface boundary in the real atmosphere, which is generally estimated to be about 300 W/m^2 or more.
At the surface boundary, White’s model is only depicting net power down, which in reality is a varying combination of SW, LW and non-radiative power.
Dewitt,
Is it clear that the full post albedo (239 W/m^2) from the Sun does not all go straight to the surface as SW radiation, as depicted in White’s model? Some of it is absorbed in the atmosphere (mostly by clouds). Some of this absorbed power is emitted down to the surface in the form of ‘forward’ LW radiation yet to reach the surface. Some can get to the surface in non-radiative form (as the temperature component of precipitation, for example). Some can even exit at the TOA without ever getting to the surface, but this just offsets power emitted from the surface absorbed by the atmosphere that would otherwise be leaving the planet, and subsequently getting back to the surface as a result. Since the Sun is the only source energy in the system, COE dictates that the 239 W/m^2 coming in from the Sun must ultimately get to the surface one way or another. So in terms of net energy flow, it’s the same as if it all went straight to the surface, as depicted in White’s model.
Again, these points get back to the fact that the model is not a model of the actual behavior that occurs in between the boundaries of the surface and the TOA.
Is it also clear that there is no way to trace photon paths, specifically those emitted from the surface absorbed by the atmosphere and those that arrive from the Sun?
The ultimate point is, in the steady-state, an amount equal to about half the surface radiative power absorbed by the atmosphere is continously exiting the system the same as radiative power passing directly from the surface into space is continuously exiting the system (i.e. acting to cool). At the same time, a net of about 385 W/m^2 is entering the surface boundary to sustain a temperature of about 287K. Both the radiative power emitted from the surface and the net power flux incident on the surface to sustain it, is itself the result of all the effects in the system – both radiative and non-radiative.
Dewitt,
I’ve boiled it down to this:
Post albedo solar power is continuously being emitted down into the system acting to warm it, right?
Where as, an amount equal to half the power absorbed by the atmosphere (about 150 W/m^2) is continuously exiting the system at the TOA acting to cool it, right?
And the surface radiative power that is passing directly into space is also continuously exiting the system at the TOA acting to cool it, right?
In both cases, the flow of the energy – even that which is still within (i.e. not leaving in present), is away from the surface and out of the system, is it not?
Only the downward re-emitted portion of the surface radiative power absorbed by the atmosphere is continuously being emitted down into the system the same as post albedo solar power.
As long as the power is constantly being emitted down into the system, it doesn’t really matter if it all goes directly to the surface as SW or not, as in the case of post albedo solar power, or if it’s just continuously emitted down into the system, as would be the case with the dowward re-emitted portion of the power absorbed by the atmosphere.
The actual ‘forcing’ effect on the system, and ultimately the surface, is the same.
In the end, this is all that George White’s equivalent 50/50 model diagram is depicting.
SoD,
“In case newcomers think that RW is onto something, I recommend reading the similar lengthy and pointless exchange in an earlier article, starting somewhere around here.”
I’ve spent some time reviewing the prior discussion. I admit that some of the things I said were perhaps a bit muddled and unclear.
However, it seems to me the crux of the matter comes down this from you:
“He writes the same confused reasons that you have for why convection = 0, in laymans terms “..if something that is not true was actually true then this other thing will be true”
He says “A further constraint of Conservation Of Energy is that the global net non radiative flux between the atmosphere and the surface must be zero in the steady state if the radiative flux is also zero.”
And yet if net radiative flux is not zero then non-radiative flux is also not zero. As I have already explained, numerous times.
Conservation of energy = “conservation of energy” ≠ “conservation of radiation”.
He says “if” and offers no proof.
Here are the correct equations, using his notation and adding the missing terms:
1. For TOA:
F0 = solar radiation absorbed by the climate system, therefore at TOA, radiation leaving must balance
F0 = 239 = 385.T + (1-F).A ….[eq 1]
so far so good.
2. Surface:
Energy out = energy in
⇒ 385 + K = 239(1-Fs) + F.A ….[eq 2]
where K is net convected flux from the surface
and Fs = fraction of solar radiation absorbed by the atmosphere.
3. Atmosphere:
Energy out = energy in
⇒ A = 385(1-T) + K + 239.Fs ….[eq 3]
To prove K = 0 requires proving it.
To prove Fs=0 requires proving it.”
Unless I’m missing something, this was specifically addressed by White in the paper where he says (in paragraph 5) “Implicit in this formulation is that the power entering the atmosphere is equal to the power leaving and that most of the planets thermal mass is contained within the surface radiator and not within the atmosphere.”
This is just a further extension of the following from White (in paragraph 4), where he says “A condition on the altitude of the lower atmospheric boundary is that it must separate the thermal mass from the atmosphere. Setting this boundary to be coincident with the surface is only approximately true, but none the less, the total heat capacity of the atmosphere is a tiny fraction of the heat capacity of the planet making this a reasonable approximation.”
This seems to be the piece that is being overlooked. Do you dispute the numbers in this link below?
You also said:
“The surface of the earth has a net convective loss to the atmosphere. This is returned via radiation.”
and
“Yes, the surface would be hotter if there was no convection. That is because convection is a net heat transfer from the surface to the atmosphere. If convection = 0, the surface would be hotter.
I don’t understand what you’re saying here. While I certainly agree that some of the power convected from the surface can return to the surface via direct radiative flux from the atmosphere, I don’t understand how a lack of convection would make the surface hotter if all the power convected away is returned via radiation. How is there even a net energy loss for cooling? Maybe you just mistated?
At any rate, I can see that you’re apparently not interested in discussing this any further. That’s fine I guess – it’s your blog. I suppose the readers can decide for themselves.
This is actually a legitimate question, so I’ll answer it.
It all goes back to the energy balances that you still don’t understand because you are hung up on the 50% up and down thing, which is true, but only locally, not globally. All the power convected away from the surface is not returned via radiation. In fact, none of it is. The net energy flux balance is 168 W/m² of incoming solar flux absorbed by the surface and 102 W/m² of convective energy transfer plus 66 W/m² net radiative transfer (390-324 W/m²) emitted from the surface. In the absence of convection, the surface would have to emit an additional 102 W/m² to achieve energy balance in and out. That could only happen if the surface were hotter, specifically, 17.2 K hotter.
Dewitt,
You say:
“It all goes back to the energy balances that you still don’t understand because you are hung up on the 50% up and down thing, which is true, but only locally, not globally.”
This graph of ISCCP data covers the entirety of both hemispheres (i.e. the whole globe):
The power emitted to space is virtually never less than 1/2 of the surface radiative power for nearly 3 decades of coverage.
You say:
“In fact, none of it is. The net energy flux balance is 168 W/m² of incoming solar flux absorbed by the surface and 102 W/m² of convective energy transfer plus 66 W/m² net radiative transfer (390-324 W/m²) emitted from the surface.”
I don’t see how this is possible with these numbers. The surface cannot be receiving a total of 168 W/m^2 + 324 W/m^2 and only emitting a radiative flux of 390 W/m^2 in the steady-state (235 W/m^2 in and out). If none the so-called convected power returns via direct radiative flux, using these numbers, where is the 324 W/m^2 coming from?
390 – 168 – 67 = 155 W/m^2 and 324 – 67 – 155 = 102 W/m^2 unaccounted for.
Whether correct or not, Trenberth returns an amount equal to the total non-radiative flux from the surface (102 W/m^2) as part of the 324 W/m^2 designated as ‘back radiation’. This is true in some sense since during its circulatory path (surface -> atmosphere -> surface), the latent heat of water is released as it condenses to form clouds, which then radiates some of this energy back down the surface.
The bottom line is the surface at 288K cannot be receiving a net power flux of more or less than 390 W/m^2 in the steady-state, for if it was, it would be either in the process of warming or cooling and thus not in the steady-state. This is the net result of everything that happens, known and unknown, radiative and non-radiative, in between the boundary of the surface and the TOA.
You say:
“In the absence of convection, the surface would have to emit an additional 102 W/m² to achieve energy balance in and out. That could only happen if the surface were hotter, specifically, 17.2 K hotter.”
Using these numbers (Trenberth ’97), I agree.
I meant to say:
“in between the boundaries of the surface and the TOA.
We’ve been over this more times than I care to count, but one more time because the concept of net power still seems to elude you. The surface gains 168 W/m² net power from incoming sunlight, not 390 W/m² and loses the same; 390-324=66 W/m² as radiation, and 102 W/m² as convection.
Incoming sunlight is the only source of power there is. If the sun went out, the surface would cool. But because the atmosphere also radiates. the surface is warmer than it would be if the atmosphere didn’t absorb and emit. But there is no net energy transfer by radiation from the atmosphere to the surface on a global average. There can’t be because the atmosphere is colder than the surface. The nettransfer must be the other way, and it is.
The gross power gained by the surface is 168+324 = 492 W/m² and it loses the same 390+102 W/m². The convective transfer is by definition a net transfer from the surface to the atmosphere. Again, the net convective transfer must be from the surface to the atmosphere and it can’t be zero (and can’t be neglected) because again, the surface is warmer than the atmosphere so heat must flow from warmer to colder. But it doesn’t have to all flow by radiation at the surface as it does at the top of the atmosphere.
And you’re missing the point of the ISCCP data. It shows beyond a doubt that the cloud tops are colder than the surface and emit less. Nothing in atmospheric radiative transfer theory says that clouds have to emit at half the rate of the surface. That’s your and White’s delusion. You can run the numbers in MODTRAN and probably produce a diagram very similar to your graph. The ISCCP data, in fact, proves that the atmosphere does not emit equally up and down.
Tropical atmosphere, 100km looking down:
clear sky: 287.812 W/m²
cumulus cloud cover: 260.84 W/m²
ratio: 0.906
Dewitt,
You say:
“We’ve been over this more times than I care to count, but one more time because the concept of net power still seems to elude you. The surface gains 168 W/m² net power from incoming sunlight, not 390 W/m² and loses the same; 390-324=66 W/m² as radiation, and 102 W/m² as convection.
Incoming sunlight is the only source of power there is. If the sun went out, the surface would cool. But because the atmosphere also radiates. the surface is warmer than it would be if the atmosphere didn’t absorb and emit. But there is no net energy transfer by radiation from the atmosphere to the surface on a global average. There can’t be because the atmosphere is colder than the surface. The nettransfer must be the other way, and it is.
The gross power gained by the surface is 168+324 = 492 W/m² and it loses the same 390+102 W/m². The convective transfer is by definition a net transfer from the surface to the atmosphere. Again, the net convective transfer must be from the surface to the atmosphere and it can’t be zero (and can’t be neglected) because again, the surface is warmer than the atmosphere so heat must flow from warmer to colder. But it doesn’t have to all flow by radiation at the surface as it does at the top of the atmosphere.”
Your playing a shell game with the various fluxes. In the steady-state, simultaneously, the boundary fluxes are a net of 390 W/m^2 entering the surface boundary, 235 W/m^2 entering post albedo from the Sun and 235 W/m^2 exiting at the TOA. All the energy in the atmosphere is on a path where it will be either radiated out to space as part of the 235 W/m^2 flux leaving or go to the surface as part of the net flux of 390 W/m^2 entering the surface boundary to sustain 288K. The is the net result of all the physical processes in the entire system (known and unknown).
Also, there has to be net energy transfer by radiation from the atmosphere to the surface boundary, because the only source of energy in the system, excluding and infinitesimal amount from geothermal, is all EM radiation (235 W/m^2 from the Sun). The GHE is radiatively induced effect. The difference of 155 W/m^2 (390 – 235 = 155) precisely quantifies the the whole of GHE. Your correct that the flow of radiation in total from the warmer surface has to be greater than the net amount from the colder atmosphere back to the surface, and it is.
You say:
“And you’re missing the point of the ISCCP data. It shows beyond a doubt that the cloud tops are colder than the surface and emit less. Nothing in atmospheric radiative transfer theory says that clouds have to emit at half the rate of the surface. That’s your and White’s delusion. You can run the numbers in MODTRAN and probably produce a diagram very similar to your graph. The ISCCP data, in fact, proves that the atmosphere does not emit equally up and down.
Tropical atmosphere, 100km looking down:
clear sky: 287.812 W/m²
cumulus cloud cover: 260.84 W/m²
ratio: 0.906”
I appreciate your willingness to continue to discuss this, but this is not what is depicted in that plot of ISCCP data. The ‘cloud power out’ is not the power emitted direct from the cloud tops, but rather the power exiting at the TOA originating from the corresponding parts of the atmosphere covered by clouds. Clouds are mostly opaque to surface emitted radiation – meaning very little is transmitted through clouds directly into space. What it shows is that even if most or all of the surface radiation is absorbed by clouds in the atmosphere, at least half is still being emitted to space, consistent with what is shown in the 50/50 split simplified model.
How is it that the meaning of the adjective ‘net’ continues to elude you and you keep misusing it? You’re the one playing the shell game by conflating gross and net fluxes.
net, adjective Miriam Webster:
Net flux means incoming flux minus outgoing flux. For the surface we can separate short wavelength, long wavelength and convective fluxes. There is no outgoing short wavelength flux to speak of so the SW flux is 168 W/m². The LW flux is 324 incoming from the atmosphere minus 390 out, equal to -66 W/m². The outgoing convective flux is -102 W/m² 168 – 66 – 102 = 0, net radiative balance. At the surface, the amount of incoming SW radiation absorbed by the atmosphere is irrelevant to the energy balance since it doesn’t get to the surface.
Your 390 W/m² isn’t even the correct gross balance. That’s 168 + 324 = 492 W/m², not 390 W/m². The gross outgoing flux is 390 + 102 = 492 W/m²
I never said it was. The MODTRAN calculation is for the TOA emission from a clear sky and a cloud covered surface. That’s what “100km looking down” means.
As for the 50% thing, if you do the single slab gray atmosphere correctly, you get the expected result of a temperature increase at steady state from a decrease in transmission through the atmosphere.
Let Ta be the temperature of the atmosphere slab in K, Ts be the surface temperature, A be the LW absorptivity of the atmosphere and σ be the Stefan-Boltzmann constant, 5.67E-08. The surface is assumed to be a blackbody with emissivity = absorptivity = 1. Incoming SW flux is 239 W/m². In the White article, A = 0.759 = 1-0.241. We can solve for Ta and Ts because we know the net incoming flux at the TOA and the surface is 239 W/m² and net outgoing flux must equal net incoming flux.
At the TOA the net outgoing flux is the sum of surface transmitted plus atmosphere emitted:
(1-A)*σ*Ts^4 + A*σ*Ta^4 = 239 W/m²
At the surface the net LW flux is surface emitted minus atmosphere emitted which, in the absence of convection must equal incoming SW flux:
σ*Ts^4 – A*σ*Ta^4 = 239 W/m²
Setting A = 0.759 and solving the two equations for Ts and Ta:
Ts = (478/(1.241*σ))^0.25 = 287.09 K
Ta = ((239-0.241*σ*287.09^4)/(0.759*σ))^0.25 = 241.41 K
Now let’s increase the absorptivity enough to decrease outgoing radiation by 3.7 W/m² while keeping Ts and Ta constant (instantaneous change):
(1-A)*σ*287.09^4 + A*σ*241.41^4 = 235.3
A = (385.17 – 235.3)/(385.17 – 192.575 ) = 0.778
Now we’ll solve for the steady state temperatures at the new absorptivity:
Ts = (478/(1.222*σ))^0.25 = 288.20 K
Ta = ((239 – 0.222*σ*288.20^4)/(0.778*σ))^0.25 = 242.34 K
So decreasing the absorptivity of the atmosphere does increase the surface temperature at steady state by 1.11 K, which you would have known if you had, for example, read Grant Petty’s book.
Dewitt,
You say:
“Net flux means incoming flux minus outgoing flux.”
Exactly.
You say:
“Your 390 W/m² isn’t even the correct gross balance.”
I know. It’s the net flux entering the surface boundary to sustain a temperature of 288K. You don’t seem to recognize or acknowledge that the surface being very close to a perfect black body is slaved to emitted radiative power by the Stefan-Boltzmann law. It cannot be receiving a net power flux of more or less than 390 W/m^2 in the steady-state, for it was, it would either be warming or cooling and thus not in the steady-state.
You also don’t seem to realize that all the energy in the atmsophere is on path where it will be radiated out to space or received by the surface. It doesn’t remain in the atmosphere or disappear into a black hole. Every bit of it has to be conserved one way or another.
And yes, as far as I’m concerned, you’re playing a shell game with the various fluxes. Excluding a tiny amount from geothermal, the only source of energy is that which enters post albedo from the Sun (about 235-240 W/m^2). This means that virtually all the energy in the climate system contained below the surface (primarily in the oceans) has to come from this source. One way or another COE dictates that it all gets to the surface, albeit not all directly as SW radiation.
You say:
“I never said it was. The MODTRAN calculation is for the TOA emission from a clear sky and a cloud covered surface. That’s what “100km looking down” means.”
I understand that. I thought you were referring to the graph of ISCCP data in White’s paper.
You say:
“As for the 50% thing, if you do the single slab gray atmosphere correctly, you get the expected result of a temperature increase at steady state from a decrease in transmission through the atmosphere.
Let Ta be the temperature of the atmosphere slab in K, Ts be the surface temperature, A be the LW absorptivity of the atmosphere and σ be the Stefan-Boltzmann constant, 5.67E-08. The surface is assumed to be a blackbody with emissivity = absorptivity = 1. Incoming SW flux is 239 W/m². In the White article, A = 0.759 = 1-0.241. We can solve for Ta and Ts because we know the net incoming flux at the TOA and the surface is 239 W/m² and net outgoing flux must equal net incoming flux.
At the TOA the net outgoing flux is the sum of surface transmitted plus atmosphere emitted:
(1-A)*σ*Ts^4 + A*σ*Ta^4 = 239 W/m²
At the surface the net LW flux is surface emitted minus atmosphere emitted which, in the absence of convection must equal incoming SW flux:
σ*Ts^4 – A*σ*Ta^4 = 239 W/m²
Setting A = 0.759 and solving the two equations for Ts and Ta:
Ts = (478/(1.241*σ))^0.25 = 287.09 K
Ta = ((239-0.241*σ*287.09^4)/(0.759*σ))^0.25 = 241.41 K
Now let’s increase the absorptivity enough to decrease outgoing radiation by 3.7 W/m² while keeping Ts and Ta constant (instantaneous change):
(1-A)*σ*287.09^4 + A*σ*241.41^4 = 235.3
A = (385.17 – 235.3)/(385.17 – 192.575 ) = 0.778
Now we’ll solve for the steady state temperatures at the new absorptivity:
Ts = (478/(1.222*σ))^0.25 = 288.20 K
Ta = ((239 – 0.222*σ*288.20^4)/(0.778*σ))^0.25 = 242.34 K
So decreasing the absorptivity of the atmosphere does increase the surface temperature at steady state by 1.11 K, which you would have known if you had, for example, read Grant Petty’s book.”
You appear to be using something like the Arrhenius formulation for calculing changes in surface temperature for changes in OLR using a one layer atmosphere. The problem is there is nothing implicit in this formulation or method that the OLR change inputed be an instantaneous change. All the formulation really does is apply the ratio of power densities (that at surface and the TOA) to the inputed OLR change and then adds it to the initial surface power baseline. If you multiply the 3.7 W/m^2 by the ratio of surface radiative power to post albedo incident solar power, using your same values, and then add it to the surface power baseline, you’ll get the exact same answer (about +1.11K).
What White’s analysis and 50/50 split model shows is that the actual OLR change is only half of the intantaneous change, albeit after a slight delay for the time it takes for the fraction of absorbed surface radiation re-emitted up to re-establish equilibrium with space.
Dewitt,
Do you (or can you) at least agree that the so-called ‘zero-feedback’ warming to +3.7 W/m^2 of post albedo solar power is about 1.1C?
When and where did I ever say it wasn’t? This whole conversation started with the comment that I agree with that a watt is a watt whether it’s from a decrease in atmospheric transmissivity or an increase in solar emission.
I wrote:
“What White’s analysis and 50/50 split model shows is that the actual OLR change is only half of the intantaneous change, albeit after a slight delay for the time it takes for the fraction of absorbed surface radiation re-emitted up to re-establish equilibrium with space.”
The ultimate point here is the flow of this energy is directed away from the surface out into space (i.e. acting to cool the system instead of warm it). In order for this outgoing energy flux at the TOA to be continuously supplied as required in the steady-state, an amount equal to it in the atmosphere has to be continuously flowing away from the surface towards space.
That’s technical gobbledegook worthy of a Star Trek show. White’s analysis shows no such thing because it’s wrong. Here’s the problem:
I must have left the slash out of the blockquote close again.
Dewitt,
You say:
“Holding the atmospheric emission constant at 146 W/m² while the absorptivity of the atmosphere changes is wrong. It says the atmosphere would emit 146 W/m² up and down even if it were completely transparent, which is obviously completely wrong. Atmospheric emission is, in fact, directly proportional to its absorptivity. The correct formula for the atmospheric emission when the transmissivity changes instantaneously from the values in White’s diagram with a surface emission of 385 and a transmissivity of 0.241 is (1-T)*192.5 which equals 146 when T=0.241. So now you have 1-T in the numerator and the denominator and F = 192.5/385 = 0.5 for any value of T.”
The whole point is with the known boundary fluxes, when ‘T’ equals 0.241, F equals 0.5. This says nothing about what the emission would be after the system’s response to a change, like if ‘T’ were to decrease, except that after equilibrium F would equal 0.5.
Here is what happens in that case:
When CO2 is instantaneously doubled, ‘T’ (and OLR) reduces by 3.7 W/m^2 (from 239 W/m^2 to 235.3 W/m^2). For so-called ‘zero-feedback’ sensitivity per George’s model, to re-establish equilibrium with space, the amount emitted to space from the atmosphere ultimately has to increase. The upward emitted half of the 3.7 W/m^2 absorbed by the atmosphere (1.85 W/m^2) re-establishes equilibrium with space fairly quickly, because this power upon re-emission is directed away from the surface toward space and the thermal time constants of the atmosphere are infinitesimal compared those below the surface. Once equilibrium is re-established, this power is essentially the same as that passing directly from the surface into space (i.e. like ‘T’). The downward re-emitted 1.85 W/m^2 is input into the system and ultimately reaches the surface acting to warm it, requiring the surface to warm further in response in order to re-emit the -1.85 W/m^2 at the TOA back out to re-establish full equilibrium with space (239 W/m^2 in and out). This requires the surface to emit an additional 1.15 W/m^2, because 62% of what’s emitted from the surface is ‘blocked’ by the atmosphere and returned or re-circulated back to the surface (239/385 = 0.62; 1.85 W/m^2 x 0.62 = 1.15 W/m^2 and 1.85 W/m^2 + 1.15 W/m^2 = 3.0 W/m^2 = 0.55C from S-B). Or it takes about 1.61 W/m^2 of surface radiative power to allow 1 W/m^2 at the TOA (385/239 = 1.61; 1.85 W/m^2 x 1.61 = 3.0 W/m^2 = 0.55C from S-B).
The new values after ‘zero-feedback’ equilibrium is re-established would be:
Post albedo solar power = 239 W/m^2
‘T’ = 90.0 W/m^2 = 0.232
‘A’ = 298 W/m^2
Amount of ‘A’ emitted to space = 149.0 W/m^2
Amount of ‘A’ returned to the surface = 149.0 W/m^2
Ts = 287.55K = 388 W/m^2
Again, it’s important to note that White’s model is an equivalent model whose behavior at the bounaries matches the required behavior.
By this I mean if you just assumed or inputed that the full 3.7 W/m^2 is equal to post albedo solar power entering the system, using White’s model and this basic method, you would get the same exact ‘zero-feedback’ sensitivity as you did above (about 1.1 C).
Or do you not want to know?
Wrong again. You still don’t get it. Did you even read what I wrote? Apparently not. Here it is again and this really is for the last time:
The instantaneous effect of increasing ghg concentration is to decrease transmission and increase emission because emissivity equals absorptivity. Total emission decreases because transmission decreases faster than emission increases because the surface is warmer than the atmosphere. Your calculation, like White, assumes that only transmission decreases. That violates Kirchhoff’s Law and amounts to a violation of the Second Law. If you decrease transmission from 93 by 3.7 to 89.3 W/m², emission increases from 146 to 147.85 W/m² so total emission at the TOA only decreases to 237.15 W/m², half of what you need. You have to decrease transmission by 7.4 W/m² to get a reduction of total emission of 3.7 W/m². Here are the correct values for different values of transmissivity, T.
T transmitted emitted total up Ts new
0.180 69.3 157.85 227.15 290.73
0.200 77.0 154.00 231.00 289.51
0.220 84.7 150.15 234.85 288.32
0.222 85.6 149.70 235.30 288.18
0.232 89.3 147.85 237.15 287.62
0.240 92.4 146.30 238.70 287.15
0.242 93.0 146.00 239.00 287.06
0.260 100.1 142.45 242.55 286.00
Note that to decrease the total TOA emission by 3.7 W/m², the value of T must be 0.222, not 0.232. But this is still a toy model, not the real atmosphere. As T → 0, Ts new → 303 K. In the real world, the Ts would increase exponentially.
Dewitt,
You say:
“The instantaneous effect of increasing ghg concentration is to decrease transmission and increase emission because emissivity equals absorptivity. Total emission decreases because transmission decreases faster than emission increases because the surface is warmer than the atmosphere. Your calculation, like White, assumes that only transmission decreases. That violates Kirchhoff’s Law and amounts to a violation of the Second Law. If you decrease transmission from 93 by 3.7 to 89.3 W/m², emission increases from 146 to 147.85 W/m² so total emission at the TOA only decreases to 237.15 W/m², half of what you need. You have to decrease transmission by 7.4 W/m² to get a reduction of total emission of 3.7 W/m².”
I’m afraid I really don’t quite understand what your talking about here. Can you elaborate in more detail? If you disagree that the 3.7 W/m^2 per CO2 doubling is the instananeous reduction in ‘T’ (the direct surface radiation to space) and this results in an instantaneous reduction at the TOA of 3.7 W/m^2, then this is where the problem between us lies. I have a few sources, including Myhre himself, that verifies the 3.7 W/m^2 is exactly as White says it is – the reduction in ‘T’.
Post your email address or send me an email and I’ll forward you the entire exchange between myself and Myhre.
Dewitt,
“When and where did I ever say it wasn’t?”
You didn’t, but I just wanted to clarify to be absolutely sure.
Might I ask, do you agree that post albedo solar power (ignorning diurnal fluctuations) is all continuously downward emitted into the system, acting to warm the system and ultimately the surface?
If yes, do you agree that an amount equal to about half of the surface radiative power absorbed by the atmosphere is continuously exiting the system, acting cool the system and ultimately the surface?
If no to one or both, can you explain your objection?
RW says
“If you disagree that the 3.7 W/m^2 per CO2 doubling is the instananeous reduction in ‘T’ (the direct surface radiation to space) and this results in an instantaneous reduction at the TOA of 3.7 W/m^2, then this is where the problem between us lies. I have a few sources, including Myhre himself, that verifies the 3.7 W/m^2 is exactly as White says it is – the reduction in ‘T’.”
The 3.7 W/m^2 is due the reduction in T from the effective change in radiating altitude… not surface cooling. But the fact that the average height of emission to space rises with an increase in opacity. So the higher altitude of effective emission from the troposphere to space is initially cooler, due to its raised altitude, from an increase in opacity(adding GHG’s)
So the incoming E would be greater than the out going E, leading to an increase of E in the system, until the T increases enough, at the new average height of emission that equilibrium is achieved. That what comes in goes out.
I think you were talking about the same stuff about six months to a year ago, on other threads here… i may be taking it out of context if this is a different argument?
In George White’s analysis, the ‘T’ variable is the direct surface radiation to space.
These are all very nice equations and maybe even some of them equate to the weather. It is not possible for them to equate to climate.
Climate is entirely controlled by external influences and what we get is weather, as the Earth tries to come to equilibrium with ever varying imputs.
Good luck with your weather analysis.
Didn’t read all the comments searching to see if you had and answer yet.
I have no source for this, so I think I realized it for myself but I have int he past found out I simply forgot where I learned/(was taught) something. It is I believe self evident like most things are, once you actually see it.
Conservation Angular & Linear momentum is trivially and obviously tied to newtons laws, when we put in the extra words that were too too obvious to be said.
For every force there is an equal and opposite force that …….
exists for exactly the same length of time as the other one and
it is also co-linear with the other one.
Change in momentum = Impulse = F t
As the forces are co – linear. The for every possible axis of rotation there is an equal and opposite force that produces by mere computation an equal and opposite torque, and thus an equal and opposite change in angular momentum about any axis you chose.
HTH. its part repayment for all the things you have cleared up for me
9,999+ to go.
Ta.