There’s a huge amount of attention paid to the air temperature 6ft off the ground all around the continents of the world. And there’s an army of bloggers busy re-analyzing the data.
It seems like one big accident of history. We had them, so we used them, then analyzed them, homogenized them, area-weighted them, re-analyzed them, wrote papers about them and in so doing gave them much more significance than they deserve. Consequently, many people are legitimately confused about whether the earth is warming up.
I didn’t say land surface temperatures should be abolished. Everyone’s fascinated by their local temperature. They should just be relegated to a place of less importance in climate science.
Problems with Air Surface Temperature over Land
If you’ve spent any time following debates about climate, then this one won’t be new. Questions over urban heat island, questions over “value-added” data, questions about which stations and why in each index. And in journal-land, some papers show no real UHI, others show real UHI..
One of the reasons I posted the UHI in Japan article was I hadn’t seen that paper discussed, and it’s interesting in so many ways.
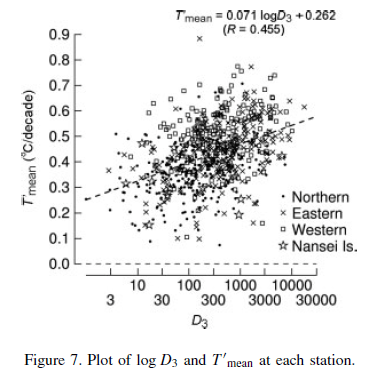
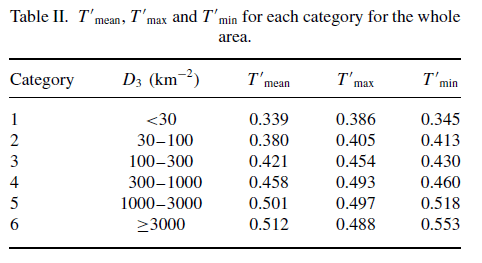
The large number of stations (561) with high quality data revealed a very interesting point. Even though there was a clear correlation between population density and “urban heat island” effect, the correlation was quite low – only 0.44.
Lots of scatter around the trend:

Estimate of actual UHI by referencing the closest rural stations - again categorized by population density
This doesn’t mean the “trend” wasn’t significant, as the result had a 99% confidence around it. What it meant was there was a lot of variability in the results.
The reason for the high variability was explained as micro-climate effects. The very local landscape, including trees, bushes, roads, new buildings, new vegetation, changing local wind patterns..
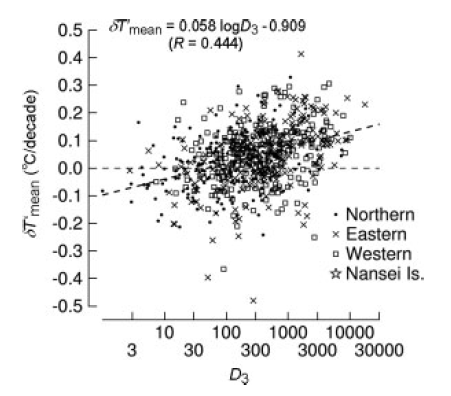
Interestingly, the main effect of UHI is on night-time temperatures:
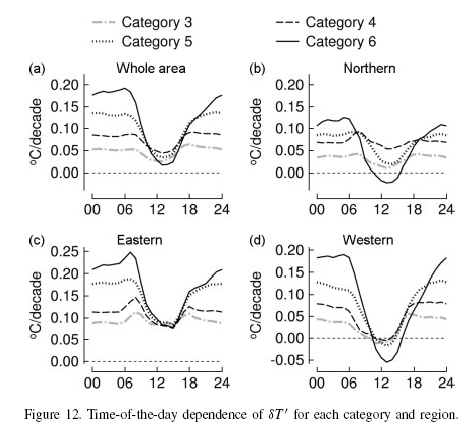
Temperature change per decade: time of day vs population density
Take a look at the top left graphic (the others are just the regional breakdown in Japan). Category 6 is the highest population density and category 3 the lowest.
What is it showing?
If we look at the midday to mid-afternoon temperatures then the average temperature change per decade is lowest and almost identical in the big cities and the countryside.
If we look at the late at night to early morning temperatures then average change per decade is very dependent on the population density. Rural areas have experienced very little change. And big cities have experienced much larger changes.
Night time temperatures have gone up a lot in cities.
A quick “digression” into some basic physics..
Why is the Bottom of the Atmosphere Warmer than the Top while the Oceans are Colder at the Bottom?
The ocean surface temperature somewhere on the planet is around 25°C, while the bottom of the ocean is perhaps 2°C.
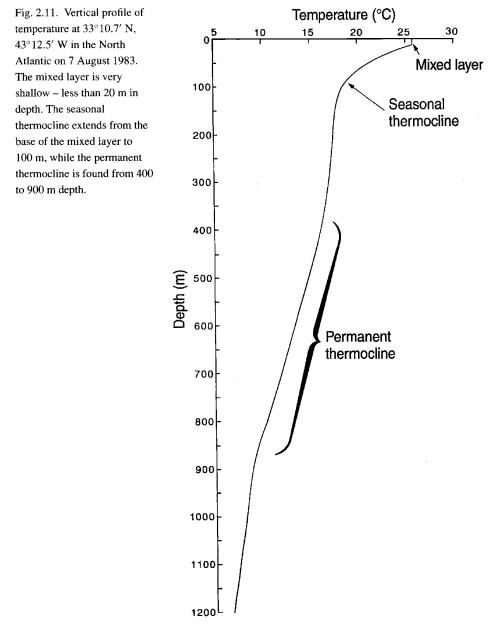
Ocean temperature vs depth, Grant Bigg, Oceans and Climate (2003)
The atmosphere at the land interface somewhere on the planet is around 25°C, while the top of the troposphere is around -60°C. (Ok, the stratosphere above the troposphere increases in temperature but there’s almost no atmosphere there and so little heat).
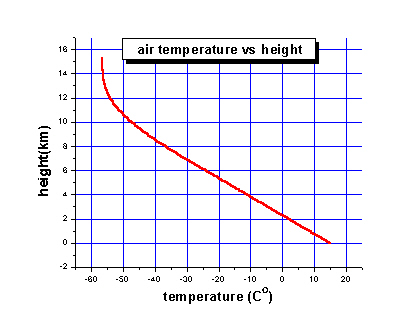
Typical temperature profile in the troposphere
The reason why it’s all upside down is to do with solar radiation.
Solar radiation, mostly between wavelengths of 100nm to 4μm, goes through most of the atmosphere as if it isn’t there (apart from O2-O3 absorption of ultraviolet). But the land and sea do absorb solar radiation and, therefore, heat up and radiate longwave energy back out.
See the CO2 series for a little more on this if you wonder why it’s longwave getting radiated out and not shortwave.
The top of the ocean absorbs the sun’s energy, heats up, expands, and floats.. but it was already at the top so nothing changes and that’s why the ocean is mostly “stratified” (although see Predictability? With a Pinch of Salt please.. for a little about the complexity of ocean currents in the global view)
The very bottom of the atmosphere gets warmed up by the ground and expands. So now it’s less dense. So it floats up. Convective turbulence.
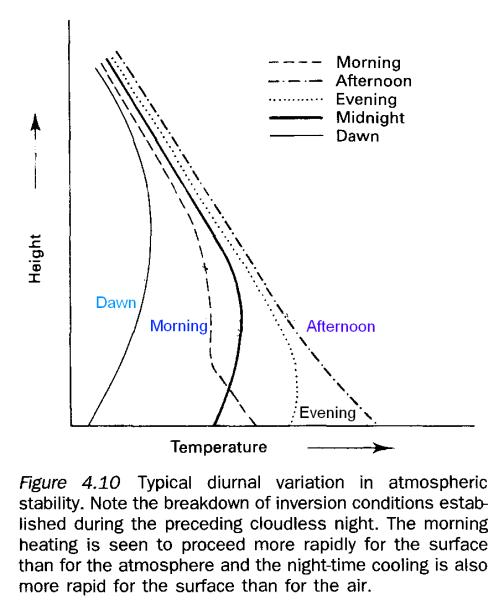
This means the troposphere is well-mixed during the day. Everything is all stirred up nicely and so there are more predictable temperatures – less affected by micro-climate. But at night, what happens?
At night, the sun doesn’t shine, the ground cools down very rapidly, the lowest level in the atmosphere absorbs no heat from the ground and it cools down fastest. So it doesn’t expand, and doesn’t rise. Therefore, at night the atmosphere is more stratified. The convective turbulence stops.
But if it’s windy because of larger scale effects in the atmosphere there is more “stirring up”. Consequently, the night-time temperature measured 6ft off the ground is very dependent on the larger scale effects in the atmosphere – quite apart from any tarmac, roads, buildings, air-conditioners – or urban heat island effects (apart from tall buildings preventing local windy conditions)
There’s a very interesting paper by Roger Pielke Sr (reference below) which covers this and other temperature measurement subjects in an accessible summary. (The paper used to be available free from his website but I can’t find it there now).
One of the fascinating observations is the high dependency of measured night temperatures on height above the ground, and on wind speed.
Micro-climate and Macro-climate
Perhaps the micro-climate explains much of the problems of temperature measurement.
But let’s turn to a thought experiment. No research in the thought experiment.. let’s take the decent-sized land mass of Australia. Let’s say large scale wind effects are mostly from the north to south – so the southern part of Australia is warmed up by the hot deserts.
Now we have a change in weather patterns. More wind blows from the south to the north. So now the southern part of Australia is cooled down by Antarctica.
This change will have a significant “weather” impact. And in terms of land-based air surface temperature we will have a significant change which will impact on average surface temperatures (GMST). And yet the energy in the climate system hasn’t changed.
Of course, we expect that these things average themselves out. But do they? Maybe our assumption is incorrect. At best, someone had better start doing a major re-analysis of changing wind patterns vs local temperature measurements. (Someone probably did it already, as it’s a thought experiment, there’s the luxury of making stuff up).
How much Energy is Stored in the Atmosphere?
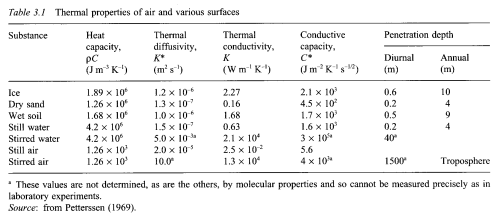
The atmosphere stores 1000x less energy than the oceans. The total heat capacity of the global atmosphere corresponds to that of only a 3.2 m layer of the ocean.
So if we want a good indicator – a global mean indicator – of climate change we should be measuring the energy stored in the oceans. This avoids all the problems of measuring the temperature in a highly, and inconsistently, mobile lightweight gaseous substance.
Right now the ocean heat content (OHC) is imperfectly measured. But it’s clearly a much more useful measure of how much the globe is warming up than the air temperature a few feet off the ground.
If the primary measure was OHC with the appropriately-sized error bars, then at least the focus would go into making that measurement more reliable. And no urban heat island effects to worry about.
How to Average
There’s another problem with the current “index” – averaging of temperatures, a mix of air over land and sea surface temperatures. There is a confusing recent paper by Essex (2007), see the reference below, just the journal title says it’s not for the faint-hearted, which says we can’t average global temperatures at all – however, this is a different point of view.
There is an issue of averaging land and sea surface temperatures (two different substances). But even if we put that to one side there is still a big question about how to average (which I think is part of the point of the confusing Essex paper..)
Here’s a thought experiment.
Suppose the globe is divided into 7 equal sized sections, equatorial region, 2 sub-tropics, 2 mid-latitude regions, 2 polar regions. (Someone with a calculator and a sense of spherical geometry would know where the dividing lines are.. and we might need to change the descriptions appropriately).
Now suppose that in 1999 the average annual temperatures are as follows:
- Equatorial region: 30°C
- Sub-tropics: 22°C, 22°C
- Mid-latitude regions: 12°C, 12°C
- Polar regions: 0°C, 0°C
So the “global mean surface temperature” = 14°C
Now in 2009 the new numbers are:
- Equatorial region: 26°C
- Sub-tropics: 20°C, 20°C
- Mid-latitude regions: 12°C, 12°C
- Polar regions: 5°C, 5°C
So the “global mean surface temperature” = 14.3°C – an increase of 0.3°C. The earth has heated up 0.3°C in 10 years!
After all, that’s how you average, right? Well, that’s how we are averaging now.
But if we look at it from more a thermodynamics point of view we could ask – how much energy is the earth radiating out? And how has the radiation changed?
After all, if we aren’t going to look at total heat, then maybe the next best thing is to use how much energy the earth is radiating to get a better feel for the energy balance and how it has changed.
Energy is radiated proportional to σT4, where T is absolute temperature (K). 0°C = 273K. And σ is a well-known constant.
Let’s reconsider the values above and average the amount of energy radiated and find out if it has gone up or down. After all, if temperature has gone up by 0.3°C the energy radiated must have gone up as well.
What we will do now is compare the old and new values of effective energy radiated. (And rather than work out exactly what it means in W/m2, we just calculate the σT4 value for each region and sum).
- 1999 value = 2714.78 (W/arbitrary area)
- 2009 value = 2714.41 (W/arbitrary area – but the same units)
Interesting? The “average” temperature went up. The energy radiated went down.
The more mathematically inclined will probably see why straight away. Once you have relationships that aren’t linear the results doesn’t usually change in proportion to the inputs.
Well, energy radiated out is more important in climate than some “arithmetic average of temperature”.
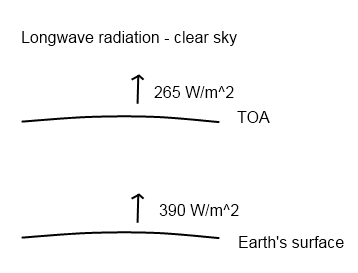
When Trenberth and Kiehl updated their excellent 1997 paper in 2008 the average energy radiated up from the earth’s surface was changed from 390W/m2 to 396W/m2. The reason? You can’t average the temperature and then work out the energy radiated from that one average (how they did it in 1997). Instead you have to work out the energy radiated all around the world and then average those numbers (how they did it in 2008).
Conclusion
Measuring the temperature of air to work out the temperature of the ground is problematic and expensive to get right. And requires lot of knowledge about changing wind patterns at night.
And even if we measure it accurately, how useful is it?
Oceans store heat, the atmosphere is an irrelevance as far as heat storage is concerned. If the oceans cool, the atmosphere will follow. If the oceans heat up, the atmosphere will follow.
And why take a lot of measurements and take an arithmetic average? If we want to get something useful from the surface temperatures all around the globe we should convert temperatures into energy radiated.
And I hope to cover ocean heat content in a follow up post..
Update – check out The Real Measure of Global Warming
References
Detection of urban warming in recent temperature trends in Japan, Fumiaki Fujibe, International Journal of Climatology (2009)
Unresolved issues with the assessment of multidecadal global land surface temperature trends, Roger A. Pielke Sr. et al, Journal of Geophysical Research (2007)
Does a Global Temperature Exist? C. Essex et al, Journal of Nonequilibrium Thermodynamics (2007)
Read Full Post »


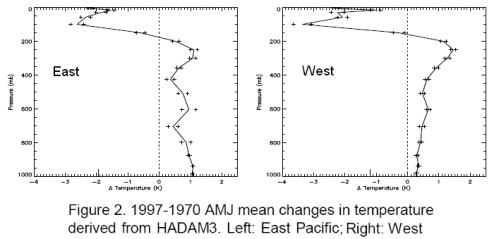
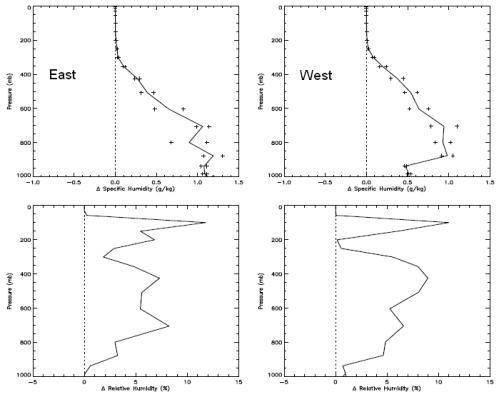
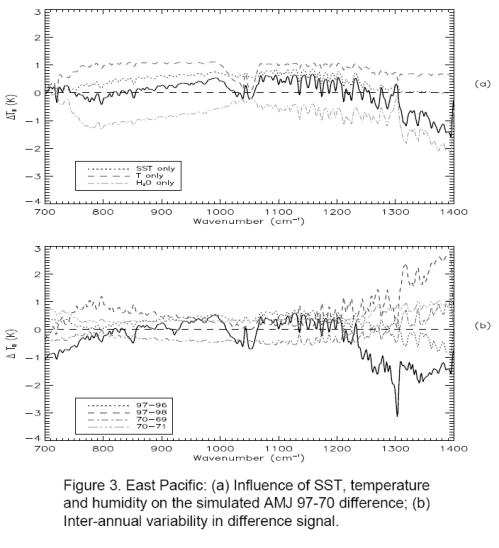
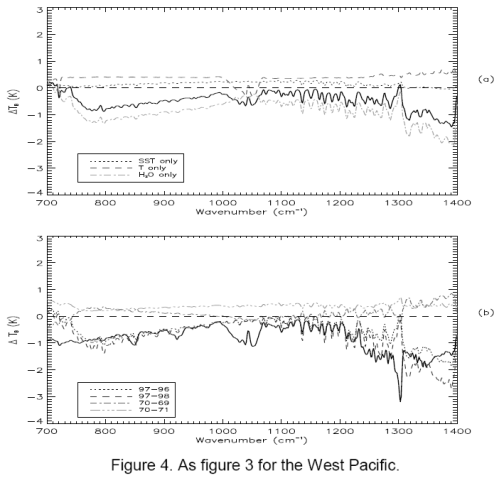







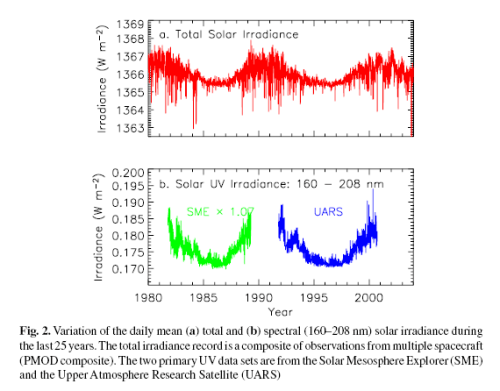

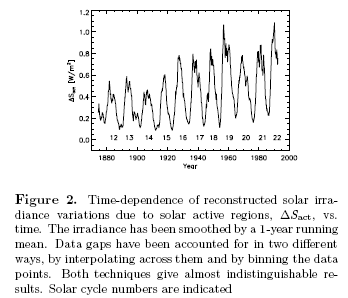
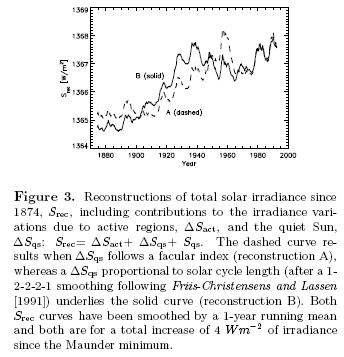
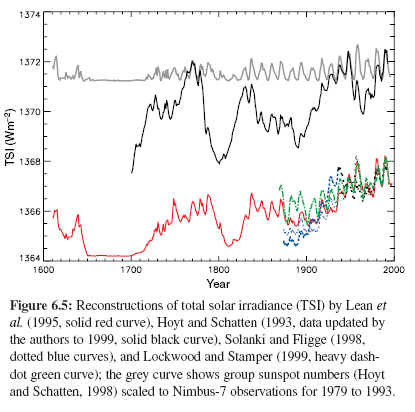







Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored
Posted in Commentary, Measurement on March 2, 2010| 49 Comments »
There’s a huge amount of attention paid to the air temperature 6ft off the ground all around the continents of the world. And there’s an army of bloggers busy re-analyzing the data.
It seems like one big accident of history. We had them, so we used them, then analyzed them, homogenized them, area-weighted them, re-analyzed them, wrote papers about them and in so doing gave them much more significance than they deserve. Consequently, many people are legitimately confused about whether the earth is warming up.
I didn’t say land surface temperatures should be abolished. Everyone’s fascinated by their local temperature. They should just be relegated to a place of less importance in climate science.
Problems with Air Surface Temperature over Land
If you’ve spent any time following debates about climate, then this one won’t be new. Questions over urban heat island, questions over “value-added” data, questions about which stations and why in each index. And in journal-land, some papers show no real UHI, others show real UHI..
One of the reasons I posted the UHI in Japan article was I hadn’t seen that paper discussed, and it’s interesting in so many ways.
The large number of stations (561) with high quality data revealed a very interesting point. Even though there was a clear correlation between population density and “urban heat island” effect, the correlation was quite low – only 0.44.
Lots of scatter around the trend:
Estimate of actual UHI by referencing the closest rural stations - again categorized by population density
This doesn’t mean the “trend” wasn’t significant, as the result had a 99% confidence around it. What it meant was there was a lot of variability in the results.
The reason for the high variability was explained as micro-climate effects. The very local landscape, including trees, bushes, roads, new buildings, new vegetation, changing local wind patterns..
Interestingly, the main effect of UHI is on night-time temperatures:
Temperature change per decade: time of day vs population density
Take a look at the top left graphic (the others are just the regional breakdown in Japan). Category 6 is the highest population density and category 3 the lowest.
What is it showing?
If we look at the midday to mid-afternoon temperatures then the average temperature change per decade is lowest and almost identical in the big cities and the countryside.
If we look at the late at night to early morning temperatures then average change per decade is very dependent on the population density. Rural areas have experienced very little change. And big cities have experienced much larger changes.
Night time temperatures have gone up a lot in cities.
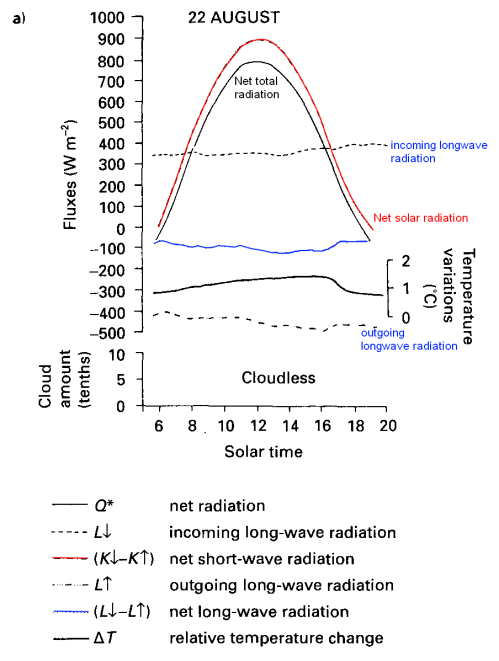
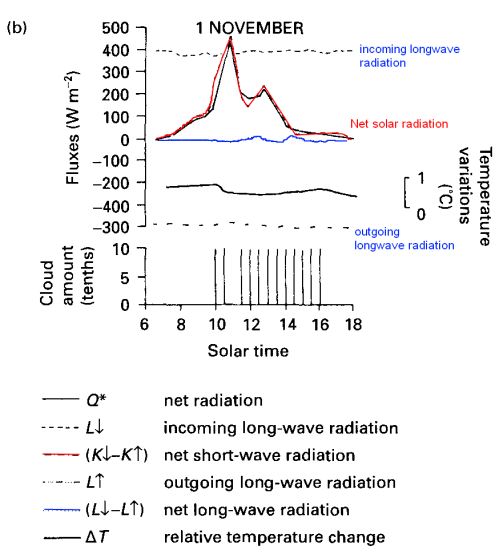
A quick “digression” into some basic physics..
Why is the Bottom of the Atmosphere Warmer than the Top while the Oceans are Colder at the Bottom?
The ocean surface temperature somewhere on the planet is around 25°C, while the bottom of the ocean is perhaps 2°C.
Ocean temperature vs depth, Grant Bigg, Oceans and Climate (2003)
The atmosphere at the land interface somewhere on the planet is around 25°C, while the top of the troposphere is around -60°C. (Ok, the stratosphere above the troposphere increases in temperature but there’s almost no atmosphere there and so little heat).
Typical temperature profile in the troposphere
The reason why it’s all upside down is to do with solar radiation.
Solar radiation, mostly between wavelengths of 100nm to 4μm, goes through most of the atmosphere as if it isn’t there (apart from O2-O3 absorption of ultraviolet). But the land and sea do absorb solar radiation and, therefore, heat up and radiate longwave energy back out.
See the CO2 series for a little more on this if you wonder why it’s longwave getting radiated out and not shortwave.
The top of the ocean absorbs the sun’s energy, heats up, expands, and floats.. but it was already at the top so nothing changes and that’s why the ocean is mostly “stratified” (although see Predictability? With a Pinch of Salt please.. for a little about the complexity of ocean currents in the global view)
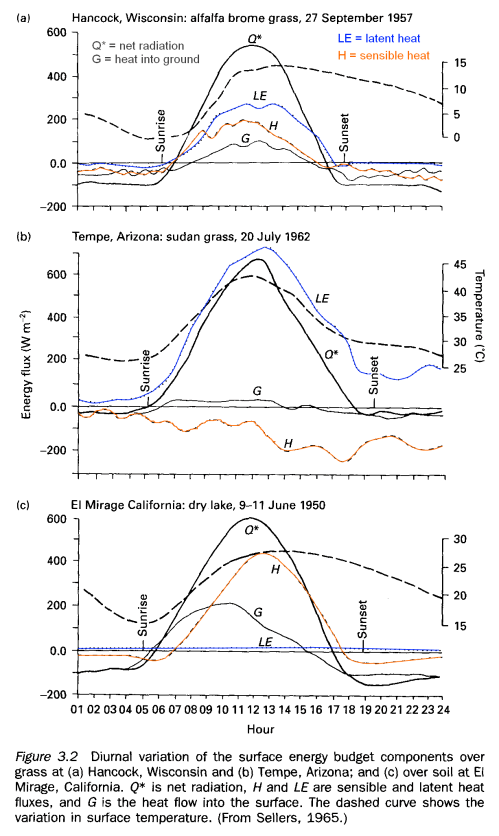
The very bottom of the atmosphere gets warmed up by the ground and expands. So now it’s less dense. So it floats up. Convective turbulence.
This means the troposphere is well-mixed during the day. Everything is all stirred up nicely and so there are more predictable temperatures – less affected by micro-climate. But at night, what happens?
At night, the sun doesn’t shine, the ground cools down very rapidly, the lowest level in the atmosphere absorbs no heat from the ground and it cools down fastest. So it doesn’t expand, and doesn’t rise. Therefore, at night the atmosphere is more stratified. The convective turbulence stops.
But if it’s windy because of larger scale effects in the atmosphere there is more “stirring up”. Consequently, the night-time temperature measured 6ft off the ground is very dependent on the larger scale effects in the atmosphere – quite apart from any tarmac, roads, buildings, air-conditioners – or urban heat island effects (apart from tall buildings preventing local windy conditions)
There’s a very interesting paper by Roger Pielke Sr (reference below) which covers this and other temperature measurement subjects in an accessible summary. (The paper used to be available free from his website but I can’t find it there now).
One of the fascinating observations is the high dependency of measured night temperatures on height above the ground, and on wind speed.
Micro-climate and Macro-climate
Perhaps the micro-climate explains much of the problems of temperature measurement.
But let’s turn to a thought experiment. No research in the thought experiment.. let’s take the decent-sized land mass of Australia. Let’s say large scale wind effects are mostly from the north to south – so the southern part of Australia is warmed up by the hot deserts.
Now we have a change in weather patterns. More wind blows from the south to the north. So now the southern part of Australia is cooled down by Antarctica.
This change will have a significant “weather” impact. And in terms of land-based air surface temperature we will have a significant change which will impact on average surface temperatures (GMST). And yet the energy in the climate system hasn’t changed.
Of course, we expect that these things average themselves out. But do they? Maybe our assumption is incorrect. At best, someone had better start doing a major re-analysis of changing wind patterns vs local temperature measurements. (Someone probably did it already, as it’s a thought experiment, there’s the luxury of making stuff up).
How much Energy is Stored in the Atmosphere?
The atmosphere stores 1000x less energy than the oceans. The total heat capacity of the global atmosphere corresponds to that of only a 3.2 m layer of the ocean.
So if we want a good indicator – a global mean indicator – of climate change we should be measuring the energy stored in the oceans. This avoids all the problems of measuring the temperature in a highly, and inconsistently, mobile lightweight gaseous substance.
Right now the ocean heat content (OHC) is imperfectly measured. But it’s clearly a much more useful measure of how much the globe is warming up than the air temperature a few feet off the ground.
If the primary measure was OHC with the appropriately-sized error bars, then at least the focus would go into making that measurement more reliable. And no urban heat island effects to worry about.
How to Average
There’s another problem with the current “index” – averaging of temperatures, a mix of air over land and sea surface temperatures. There is a confusing recent paper by Essex (2007), see the reference below, just the journal title says it’s not for the faint-hearted, which says we can’t average global temperatures at all – however, this is a different point of view.
There is an issue of averaging land and sea surface temperatures (two different substances). But even if we put that to one side there is still a big question about how to average (which I think is part of the point of the confusing Essex paper..)
Here’s a thought experiment.
Suppose the globe is divided into 7 equal sized sections, equatorial region, 2 sub-tropics, 2 mid-latitude regions, 2 polar regions. (Someone with a calculator and a sense of spherical geometry would know where the dividing lines are.. and we might need to change the descriptions appropriately).
Now suppose that in 1999 the average annual temperatures are as follows:
So the “global mean surface temperature” = 14°C
Now in 2009 the new numbers are:
So the “global mean surface temperature” = 14.3°C – an increase of 0.3°C. The earth has heated up 0.3°C in 10 years!
After all, that’s how you average, right? Well, that’s how we are averaging now.
But if we look at it from more a thermodynamics point of view we could ask – how much energy is the earth radiating out? And how has the radiation changed?
After all, if we aren’t going to look at total heat, then maybe the next best thing is to use how much energy the earth is radiating to get a better feel for the energy balance and how it has changed.
Energy is radiated proportional to σT4, where T is absolute temperature (K). 0°C = 273K. And σ is a well-known constant.
Let’s reconsider the values above and average the amount of energy radiated and find out if it has gone up or down. After all, if temperature has gone up by 0.3°C the energy radiated must have gone up as well.
What we will do now is compare the old and new values of effective energy radiated. (And rather than work out exactly what it means in W/m2, we just calculate the σT4 value for each region and sum).
The more mathematically inclined will probably see why straight away. Once you have relationships that aren’t linear the results doesn’t usually change in proportion to the inputs.
Well, energy radiated out is more important in climate than some “arithmetic average of temperature”.
When Trenberth and Kiehl updated their excellent 1997 paper in 2008 the average energy radiated up from the earth’s surface was changed from 390W/m2 to 396W/m2. The reason? You can’t average the temperature and then work out the energy radiated from that one average (how they did it in 1997). Instead you have to work out the energy radiated all around the world and then average those numbers (how they did it in 2008).
Conclusion
Measuring the temperature of air to work out the temperature of the ground is problematic and expensive to get right. And requires lot of knowledge about changing wind patterns at night.
And even if we measure it accurately, how useful is it?
Oceans store heat, the atmosphere is an irrelevance as far as heat storage is concerned. If the oceans cool, the atmosphere will follow. If the oceans heat up, the atmosphere will follow.
And why take a lot of measurements and take an arithmetic average? If we want to get something useful from the surface temperatures all around the globe we should convert temperatures into energy radiated.
And I hope to cover ocean heat content in a follow up post..
Update – check out The Real Measure of Global Warming
References
Detection of urban warming in recent temperature trends in Japan, Fumiaki Fujibe, International Journal of Climatology (2009)
Unresolved issues with the assessment of multidecadal global land surface temperature trends, Roger A. Pielke Sr. et al, Journal of Geophysical Research (2007)
Does a Global Temperature Exist? C. Essex et al, Journal of Nonequilibrium Thermodynamics (2007)
Read Full Post »