Recap
Part One of the series started with this statement:
If there’s one area that often seems to catch the imagination of many who call themselves “climate skeptics”, it’s the idea that CO2 at its low levels of concentration in the atmosphere can’t possibly cause the changes in temperature that have already occurred – and that are projected to occur in the future. Instead, the sun, that big bright hot thing in the sky (unless you live in England), is identified as the most likely cause of temperature changes.
And covered the “zero-dimensional” model of the sun and the earth. Also known as the “billiard ball” model. It was just a starting point to understand the very basics.
In Part Two we looked a little closer at why certain gases absorbed energy in certain bands and what the factors were that made them more, or less, effective “greenhouse” gases.
In this part, we are going to start looking at the “1-dimensional” model. I try and keep any maths as basic as possible and have separated out some maths for the keen students.
When you arrive at a new subject, the first time you see an analysis, or model, it can be confusing. After you’ve seen it and thought about it a few times it becomes more obvious and your acceptance of it grows – assuming it’s a good analysis.
So for people new to this, if at first it seems a bit daunting but you do want to understand it, don’t give up. Come back and take another look in a few days..
Models
If your background doesn’t include much science it’s worth understanding what a “model” is all about. Especially because many people have their doubts about GCM’s or “Global Climate Models”.
One of the ways that a model of a physics (or any science) problem is created is by starting from first principles, generating some equations and then finding out what the results of those equations are. Sometimes you can solve this set of equations “analytically” – which means the result is a formula that you can plot on a graph and analyze whichever way you like. Usually in the real world there isn’t an “analytical” solution to the problem and instead you have to resort to numerical analysis which means using some kind of computer package to calculate the answer.
The starting point of any real world problem is a basic model to get an understanding of the key “parameters” – or key “players” in the process. Then – whether you have an analytical solution or have to do a numerical analysis doesn’t really matter – you play around with the parameters and find out how the results change.
Additionally, you look at how closely the initial equations matched the actual situation you were modeling and that gives you an idea of whether the model will be a close fit or a very rudimentary one.
And you take some real-world measurements and see what kind of match you have.
Radiative Transfer
In the “zero dimensional” analysis we used a very important principle:
Energy into a system = Energy out of a system, unless the system is warming or cooling
The earth’s climate was considered like that for the simple model. And for the simple model we didn’t have to think about whether the earth was heating up, the actual temperature rise is so small year by year that it wouldn’t affect any of those results.
In looking at “radiative transfer” – or energy radiated through each layer of the atmosphere – this same important principle will be at the heart of it.
What we will do is break up the atmosphere into lots of very thin sections and analyze each section. The mathematical tools are there (calculus) to do that. The same kind of principles are applied, for example, when structural engineers work out forces in concrete beams – and in almost all physics and engineering problems.
And when we step back and try and re-analyze, again it will be on the basis of Energy in = Energy out
If you are new to ideas of radiation and absorption, go back and take a look at Part One – if you haven’t done so already.
In this first look I’ll keep the maths as light as possible and try and explain what it means. If following a little maths is what you want, there is some extra maths separated out.
First Step – Absorption
As we saw in part one, radiation absorbed by a gas is not constant across wavelengths. For example, here is CO2 and water vapor:
What we want to know is if we take radiation of a given wavelength which travels up through the atmosphere, how much of the radiation is absorbed?
We’ll define some parameters or “variables”.
I(λ) – The intensity, I, of radiation which is a function of wavelength, λ
I0(λ) – is the initial or starting condition (the intensity at the earth’s surface).
z – the vertical height through the atmosphere
n – how much of an absorbing gas is present
σ(λ) – absorption cross-section at wavelength λ (this parameter is dependent on the gas we are considering, and identifies how effective it is at capturing a photon of radiation at that wavelength)
The result of a simple mathematical analysis produces an equation that says that as you:
- increase the depth through the atmosphere that the radiation travels
- or the concentration of the gas
- or its “absorption cross-section”
Then more radiation is absorbed. Not too surprising!
When the concentration of the gas is independent of depth (or height) the mathematical result becomes:
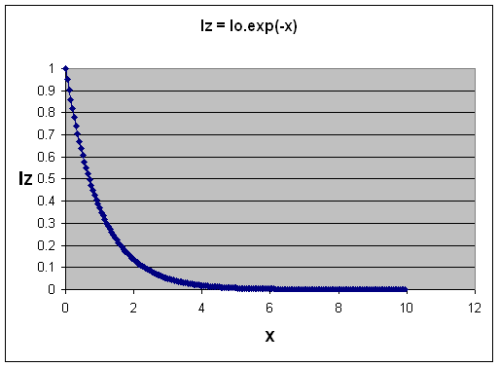
Iz = I0(λ).exp(-nσ(λ)z) also written as Iz = I0(λ).e-nσ(λ)z
This is the Beer-Lambert Law. The assumption that the number of gas molecules is independent of depth isn’t actually correct in the real world, but this first simple approximation gets us started. We could write n(z) in the equation above to show that n was a function of depth through the atmosphere.
[In the above equation, e is the natural log value of 2.781 that comes up everywhere in natural processes. To make complex equations easier to read, it is a convention to write “e to the power of x” as “exp(x)”]
Here’s what the function looks like as “nσ(λ)z” increases – I called this term “x” here in this graph.
It’s not too hard to imagine now. Iz is the amount of radiation making it through the gas. Iz=1 means all of it got through, and Iz=0 means none of it got through.
As you increase vertical height through the gas, or the amount of the gas, or the absorption of the gas, then the amount of radiation that gets through decreases. And it doesn’t decrease linearly. You see this kind of shape of curve everywhere in nature including the radiation decay of uranium..
This result is not too surprising to most people. But it’s knowing only this part which has many confused, because the question comes – about CO2 – doesn’t it saturate?
Isn’t it true that as CO2 increases eventually it has no effect? And haven’t we already reached that point?
Excellent questions. Skip the maths derivation of this section if you aren’t interested to find out about our Second Step – Radiation
First Step – Absorption – Skip this, it’s the Maths
You can skip this if you don’t like maths.
The intensity of light of wavelength λ is I(λ). This light passes through a depth dz (“thin slice”) of an absorber with number concentration n, and absorption cross-section σ(λ), and so is reduced by an amount dI(λ) given by:
dI(λ) = -I(λ)nσ(λ)dz = I(λ)dχ [equation 1]
where χ is defined as optical depth. It’s just a convenient new variable that encapsulates the complete effect of that depth of atmosphere at that wavelength for that gas.
We integrate equation 1 to obtain the intensity of light transmitted a distance z through the absorber Iz(λ):
Iz(λ) = I0(λ) exp{-∫nσ(λ)dz} [equation 2]
[note the integral is from 0 to z – not able to get the webpage to display what I want here]
In the case where the concentration of the absorbing gas is independent of the depth through the atmosphere the above equation is simplified to the Beer Lambert Law
Iz = I0(λ).exp(-nσ(λ)z) also written as Iz = I0(λ).e-nσ(λ)z
Note that this assumption is not strictly true of the atmosphere in general – the closer to the surface the higher the pressure and, therefore, there is more of absorbing gases like CO2.
Second Step – Radiation
Once the atmosphere is absorbing radiation something has to happen.
The conceptual mistake that most people make who haven’t really understood radiative transfer is they think of it something like torchlight trying to shine through sand – once you have enough sand nothing gets through and that’s it.
But energy absorbed has to go somewhere and and in this case the energy goes into increased heat of that section of the atmosphere, as we saw in Part Two of this series.
In general, and especially true in the troposphere (the lower part of the atmosphere up to around 10km), the increased energy of a molecule of CO2 (or water vapor, CH4, etc) heats up the molecules around it – and that section of the atmosphere then radiates out energy, both up and down.
Let’s introduce a new variable, B = intensity of emitted radiation
The relationship between I (radiation absorbed) – and B (radiation emitted) – integrated across all wavelengths, all directions and all surfaces is linked through conservation of energy.
But these two parameters are not otherwise related. Making it more difficult to conceptually understand the problem.
I depends on the radiation from the ground, which in turn is dependent on the energy received from the sun and longwave radiation re-emitted back to the ground.
Whereas B is a function of the temperature of that “slice” of the atmosphere.
The equation that includes absorption and emission for this thin “slice” through the atmosphere becomes:
dI = -Inσdz + Bnσdz = (I – B)dχ (where χ is defined as optical depth)
dI is “calculus” meaning the change in I, dz is the change in z and dχ is the change in χ, or optical thickness.
What does this mean? Well, if I could have just written down the “result” like I did in the section on absorption, I would have done, but because it has become more difficult, instead I have written down the equation linking B and I in the atmosphere..
What it does mean is that the more radiation that is absorbed in a given “slice” of the atmosphere, the more it heats up and consequently the more that “slice” then re-emits radiation across a spectrum of wavelengths.
Solving the Equation to Find out what’s Going on
There are two concepts introduced above:
- absorption, relatively easy to understand
- emission, a little harder but linked to absorption by the concept “energy in = energy out”
From here there are two main approaches..
- One approach is called the grey model of radiative transfer, and it uses a big simplification to show how radiation moves energy through the atmosphere.
- The other approach is to really solve the equations using numerical analysis via computers.
The problem is that we have some equations but they aren’t simple. We saw the Beer-Lambert law of absorption links to the emission in a given section of the atmosphere, but we know that the absorption is not constant across wavelengths.
So we have to integrate these equations across wavelengths and through the atmosphere (to link radiation flowing through each “slice” of the atmosphere)
To really find the solutions – how much longwave radiation gets re-radiated back down to the earth’s surface as a result of CO2, water vapor and methane – we need a powerful computer with all of the detailed absorption bands of every gas, along with the profile of how much of each gas at each level in the atmosphere.
The good news is that they exist. But the bad news is that you can’t grab the equation and put it in excel and draw a graph – and find out the answer to that burning question that you had.. what about the role of CO2? and how does that compare with the role of water vapor?
And I still haven’t spelt out the saturation issue..
Finding out that the subject is more complex that it originally appeared is the first step to understanding this subject!
The important concept to grasp before we move on is that it is not just about absorption, it’s also about re-emission.
The Gray Model
The “gray” model is very useful because it allows us to produce a simple mathematical model of the temperature profile through the atmosphere. We can do this because instead of thinking about the absorption bands, instead we assume that the absorption across wavelengths is constant.
What? But that’s not true!
Well, we do it to get a conceptual idea of how energy moves through the atmosphere when absorption and re-emission dominate the process. We obviously don’t expect to find out the exact effect of any given gas. The gray model uses the equations we have already derived and adds the fact that the absorber varies in concentration as a function of pressure.
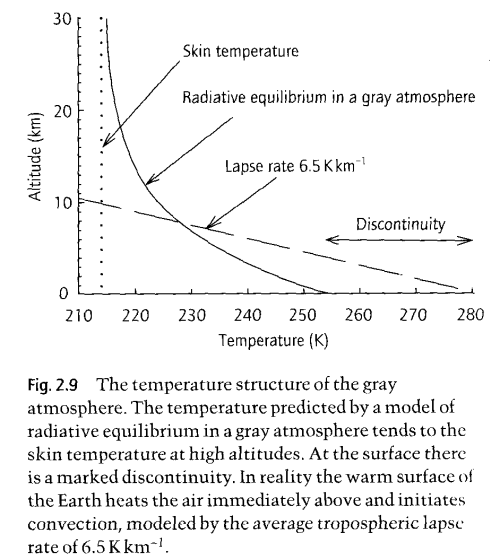
The Gray Model of Radiative Equilibrium, from "Handbook of Atmospheric Science" Hewitt and Jackson (2003)
The graph shown here is the result of developing the equations we have already seen, both for absorption and the link between absorption and re-emission.
The equations totally ignore convection! On the graph you can see the real “lapse rate”, which is the change in temperature with altitude. This is dominated by convection, not by radiation.
So how does the gray model help us?
It shows us how the temperature profile would look in an atmosphere with no convection and where there is significant and uniform absorption of longwave radiation.
Convection exists and is more significant than radiation in the troposphere – for moving energy around! Not for absorbing and re-emitting energy. The significance of the real “environmental lapse rate” of 6.5K/km is that it will change the re-emission profile. So it complicates the numerical analysis we need to do. It means that when the numerical analysis is done of the equations we have already derived, the real lapse rate is one more factor that has to be added to that 1-d analysis.
To get a conceptual feel for how that might change things – remember how the radiation spectrum changes with temperature – not a huge amount. So at each layer in the atmosphere the radiation spectrum using the real atmospheric temperature profile will be slightly different than using the “gray model”. But it can be taken into account.
Conclusion
This post has covered a lot of ground and not given you a nice tidy result. Sorry about that.
It’s an involved subject, and there’s no point jumping to the conclusion without explaining what the processes are. It is understanding the processes involved in radiative physics and the way in which the subject is approached that will help you understand the subject better.
And especially important, it will help you see the problems with a flawed approach. There are lots of these on the internet. There isn’t a nice tidy analytical expression which links radiative forcing to CO2 concentration, and which separates out CO2 from water vapor. But 1-d numerical models can generate reliable and believable results.
In Part Four, we will finally look at saturation, how it’s misunderstood, how much radiative forcing more CO2 will add (all other things being equal!) and how CO2 compares with water vapor.
So watch out for Part Four, and feel free to comment on this post or ask questions.
Update – Part Four is now online



[…] – Part Three is now online Possibly related posts: (automatically generated)CO2 Lags Temperature in the Ice-Core […]
[…] Part Three introduced Radiative Transfer Equations and finished up with a look at what is called the gray […]
[…] Three and Four got a little more technical – an unfortunate necessity. Part Three introduced Radiative Transfer Equations including the Beer-Lambert Law of absorption. It also […]
[…] (RTE) for that vertical profile through the atmosphere. Solving those equations, as you can see in CO2 – Part Three, Four and Five – requires knowledge of the temperature profile as well as the concentration […]
[…] re-radiation of this energy takes place according to an energy balance equation that you can see in CO2 – Part Three. The energy balance or radiative transfer equations rely on knowledge of the temperature profile in […]
[…] For more on these equations, see the CO2 – An Insignificant Trace Gas series, especially Part Three, Four and […]
[…] being absorbed, but we’ll stay away from maths in this post. You can see the equation in CO2 – An Insignificant Trace Gas? Part Three. And if you see any “analysis” of the effectiveness of CO2 or any trace gas which […]
You wrote
The relationship between I (radiation absorbed) – and B (radiation emitted) – integrated across all wavelengths, all directions and all surfaces is linked through conservation of energy.
But these two parameters are not otherwise related. Making it more difficult to conceptually understand the problem.
.
Ah but they are! They must be.
a)An absorption increases a quantum number (puts the molecule in a higher energy state)
b)an emission decreases a quantum number (puts the molecule in a lower energy state)
c)We normally know that the distribution of the quantum states (quantum numbers) must obey the Maxwell Boltzmann distribution
d)This distribution depends only on temperature
e) In equilibrium (what is what you suppose , right ?) temperature is constant.
If all that is correct , from a) through e) follows that for every 15µ photon (just an example , the same is valid for any other wavelength) absorbed in a small volume or slice in equilibrium there is one 15µ photon emitted .
So emission and absorption is also linked by the necessity for the molecules to have at all times an exactly constant proportion of 15µ excited states .
There can be neither net absorption of some wavelength nor net emission.
F.ex imagine a thick slice of CO2 in equilibrium illuminated by a 15µ beam of 100 W/m² . What LWR would come out ?
Actually it would be 100 W/m² and this is indeed only energy conservation.
But not just any 100 W/m² , most of it would be at or near 15 µ because of the reasons a) through e) above.
This is a bit more constraining than just energy conservation , don’t you think?
Philip:
These are good points.
If the atmosphere was only CO2 (or any one gas) then this would be mostly correct.
But still CO2 would radiate out at any wavelength where it had emissivity (=absorptivity) – such as 4.3um, 7.5 and the rest of the 15um band (in proportion to the planck function for that temperature)
But in the mixed atmosphere, CO2 absorbs energy and warms up the rest of the atmosphere. Then all gases emit radiation – again as they are able, so of course O2 and N2 won’t be really participating. Water vapor, CH4, O3 etc will all be at the same temperature and will emit at their characteristic wavelengths.
But still CO2 would radiate out at any wavelength where it had emissivity (=absorptivity) – such as 4.3um, 7.5 and the rest of the 15um band (in proportion to the planck function for that temperature)
That’s why I wrote mostly and not only.
However in my example where the incoming radiation was monochromatic (15µ beam) the emitted radiation would be also 15µ.
The reason for that is that this beam would excite only the 15µ energy level. As there can be no net absorption (or emission) in thermal equilibrium of an IR active gas , the molecules have no choice but to get the 15µ level back to the proportion dictated by the MB distribution for the equilibrium temperature (see points a) through e) in above post).
This happens massively by emitting 15 µ. A very small part happens by different cascades ( f.ex 15->4.3->ground) what explains a small proportion of non 15µ radiation in the emitted total .
But in the mixed atmosphere, CO2 absorbs energy and warms up the rest of the atmosphere. Then all gases emit radiation – again as they are able, so of course O2 and N2 won’t be really participating.
This is not clear .
CO2 in thermal equilibrium while absorbing and emitting IR , can’t “heat” the atmosphere in any usual sense of the word “heat”.
The only sense I could see is that the CO2 “heats” N2 and O2 (e.g increases their average velocity by collisions).
But this is also an equilibrium because it works both ways.
CO2 hits N2 , decreases its vibrationnal energy and increases the kinetic energy of N2 (e.g CO2 “heats” the N2).
Or.
CO2 hits N2 , increases its vibrationnal energy and decreases the kinetic energy of N2 (e.g CO2 “cools” the N2).
Both processes must exactly compensate (e.g are in equilibrium).
If they wouldn’t , there would be a NET energy transfer from one molecular species to another (f.ex CO2 towards N2).
That would mean that one of the species would cool and the other heat what is forbidden because they must stay at the same temperature if in equilibrium.
Or are you considering gases out of equilibrium like in the N2-CO2 laser ?
In this case , indeed , hot N2 is “pumping up” selectively the vibrationnal energy of cold CO2 what enables to obtain afterwards an emission of a monochromatic IR beam from CO2 molecules when they deexcite and the mixture finishes in equilibrium.
What you described seemed to me like an “inverse laser” :
I start with CO2 and N2 in equilibrium , send an IR beam in the mixture and finish with hot N2 and cold CO2.
This would of course violate the 2 LOT so you probably don’t mean that.
Philip:
Think of it another way..
In a steady state condition of CO2 receiving lots of 15um energy and let’s pick CH4 receiving very little 7um energy, if there was no net transfer of heat, CH4 would be cooling down and CO2 would be heating up.
As I can see you understand, this wouldn’t happen. Both gases would be at the same temperature, sharing their kinetic energy.
So in this case of lots of 15um incoming radiation, we would now have some outgoing 7um and 15um radiation as the mixed gas reached an equilibrium temperature.
That’s what the original comment was aimed at.
Energy incoming = energy outgoing if we are at equilibrium temperature but that doesn’t mean that 15um incoming = 15um outgoing. It might, but it depends on the mix of gases, their absorptivity and the radiation they receive.
This was not another way , just a variation on the same theme .
In your mixture example if the CO2 gets a lot 15µ , it will radiate a lot of 15 µ while CH4 receiving little 7 µ it will radiate little 7 µ .
Both will radiate exactly what is needed to have a constant proportion of their respective energy levels (15µ for CO2 and 7 µ for CH4) because as per your hypothesis they must stay at the same temperature .
Neither would cool or heat and both would stay at the same temperature .
But there will still be no net transfer between both species because the collisional energy exchanges are necessarily an equilibrium as I have said in the previous post .
So it seems that you are repeating exactly what I said only with 2 gases instead of 1 .
The difference being that for me it seems that on top of energy conservation , for 15 µ incoming there is (approximately) as much 15 µ outgoing as can be checked by illuminating CO2 with a 15µ laser .
As for you , are you saying that for 100 W of incoming 15µ in some CO2 containing mixture staying in equilibrium , you would observe f.ex 25 W of outgoing 15 µ ?
If yes then it can mean only one of 2 things :
– the MB distribution of the energy states is violated (e.g lasers can’t work)
– the gas is violently out of equilibrium (e.g it contradicts the hypothesis that we have equilibrium)
Were you going to answer by what you mean by “CO2 heats N2” later or didn’t you read this part of my previous post yet ?
Perhaps to make things clearer with some simple maths :
Let’s suppose that we have only 15µ beam with power P incoming on a CO2, N2 mixture .
Let’s neglect cascades and consider only 2 vibrational energy states of CO2 :
E0 ground and E1 (first 15µ excited) .
N1 is the number of excited states and N0 the number of ground states .
The gases are in equilibrium at temperature T for and N1/N0 = constant.
If all of the beam is absorbed then the number of 0->1 transitions per second is Y = P/(E1-E0) .
We don’t need to consider N2 and the N2 concentration for this purpose because it is IR inactive .
What power Pe will be emitted by the mixture ?
Pe = X.(E0-E1) where X is the number of 1->0 transitions per second .
But as N1/N0 must stay constant (equilibrium) we have necessarily X = Y = P / (E1-E0) .
Then Pe = [P / (E1-E0)] . (E0-E1) = – P .
So not only energy is conserved but the emitted power is exclusively in form of 15µ radiation .
One can make the same calculation with the same result for n different resonance radiations . This is only the simplest case with 1 frequency .
Of course in reality there are also cascades so the above is only approximately true . But for room temperatures (very low N1/N0) and strong lines there should be no big difference .
That’s what I have been saying since my first post .
Do you see any significant problem with the above ?
Philip:
There’s nothing really wrong with it.
Going back to my statement you queried:
..Perhaps we should say that there are many circumstances where absorption and emission are very similar under equilibrium conditions.
But we won’t know without solving the equations to find out?
I can’t solve the equation in my head. There are lots of emission possibilities for many gases.
I have no idea of the proportion of conditions in the real atmosphere that match your scenario.
If it was “nearly all” you could rewrite the radiative transfer equations.
I would say that in all cases the power of an emitted frequency is (necessarily) very near the power of absorbed frequency in equilibrium .
In one case the equality is strict and this is precisely the 15µ case for CO2 (no equation solving necessary) and that’s why I took this example .
Why is it so ?
Because the 15µ is the lowest vibrational energy level available for a CO2 molecule . There is nothing below but the ground state .
That’s why if you have an excess of 15µ excited states because you have a lot of 15µ radiation , the only way to get rid of it and go back to the constant N1/N0 is to go to ground . There are no indirect ways available . And going to ground emits the same amount of exactly 15 µ radiation that was absorbed .
That is also the reason why the 15µ emission line is the strongest one in a CO2 emission spectrum .
At room temperatures and below (that is what concerns us in the atmosphere) there are only the 3 lowest levels and especially the 15µ that are activated anyway and it is not SO complicated .
What stays still unexplained is the question of “N2 heated by CO2” as you called it . For explanation – I am not especially interested by climate questions (I study QM) but a friend told me that here was a blog deserving being read . The few what I heard about climate always contained a very irritating statement . And I found it here too .
Namely that IR “heats the atmosphere via CO2 absorption” . This is wrong and I explained why .
Do you agree that the “green house” effect has nothing to do with CO2 “heating the atmosphere in equilibrium” ?
Philip:
Re-reading the points you have made along the way, I am still not 100% sure I understand you. So if I’ve got it wrong, my apologies.
Clearing up something you asked a couple of times when you were testing my “theory”:
I didn’t respond on that because you are correct “I didn’t mean that”.
What I did mean was adding 15um radiation, only absorbed by CO2 would mean that CO2 and N2 were heated up. CO2 absorbs the 15um radiation and shares it thermally, through collisions with N2. So in the new equilibrium condition, whatever that is, both CO2 and N2 are at the same temperature, and this new temperature is higher than the starting temperature.
I can’t work out from all your comments above whether you agree or disagree with this.
I think you disagree and yet you agree that energy is shared through collisions. So there’s something I’m missing in getting to grips with your comment. Maybe you think energy can be shared under some conditions but isn’t in this case?
You said:
This is the point at issue. Obviously you think you have explained why it can’t be true/isn’t true, however, I don’t think you have. So perhaps you can comment on the question above.
Quoting “Handbook of Atmospheric Science” by Hewitt and Jackson (2003) –
Up until now this appeared to be an uncontroversial statement – as you find similar statements in every atmospheric physics book.
Thanks for the explanation so far. I’m looking forward to part 8 on saturation.
A question on the graph showing the Gray atmosphere. What is the skin temperature and why isn’t it closer to -18C (or was it -16C)? Also I seem to recall that the temperature drops to the top of the troposphere and then rises again. Is this correct and if so it seems to be a departure from the Gray atmosphere (which is an approximation)? I’m not sure if these are difficult or easy questions – hopefully they are easy.
BC
Good questions. The derivation of the skin temperature is slightly in depth, but is calculated from considering the emission from the top of the troposphere as being the effective energy emitter that balances the solar radiation absorbed.
So this emitting temperature at the top of the troposphere is 255K (which equates to 239W/m^2 or average solar energy absorbed).
And then considering the stratosphere as an optically thin “slab” and working out an energy balance equation for this “slab” – of energy absorbed (from the stratosphere) vs energy emitted in both directions.
The calculation comes out to T(stratosphere) = 255/(2^1/4). And therefore = 215K.
This might not make a lot of sense, but don’t worry, it might be something that gets covered properly on this blog, perhaps after an article explaining the convective profiles in the troposphere.
On the second question, you are correct, after the tropopause the temperature begins to rise again. This is because the gray model is only an approximation.
The reason the temperature rises to the top of the stratosphere is due to O2 and O3 absorbing solar energy and therefore heating. Without this effect, the stratosphere would be close to the gray model.
Thanks for the response. I can sleep easy now.
[…] You can see an introduction to absorption and re-emission in CO2 – An Insignificant Trace Gas? Part Three. […]
[…] So far, neither Dexter, nor his enthusiastic supporters at American Thinker have got around to updating the now defunct Wikipedia article on the Radiative Transfer Equations which describe the “old school” mathematics and are slightly more complicated.. (See also CO2- An Insignificant Trace Gas? Part Three.) […]
scienceofdoom, an excellent post.
I think that CO2 is an “insignificant trace gas” for a very different reason. I look, not at the proportion of gas in the atmosphere, but the proportion of forcing from a doubling of CO2.
I divide forcings into “first order”, “second order”, and “third order”
A first order forcing has an effect which is greater than ten percent of the total. Second order forcings have an effect of from one to ten percent of the total. And finally, a third order forcing is less than one percent of the total.
A doubling of CO2 is estimated to cause a TOA forcing of about 3.7 W/m2. The total TOA forcing is on the order of 160 W/m2. This means that a doubling of CO2 will change the TOA forcing by something on the order of 2%.
Or looking at it from the point of view of the ground, at the surface there is about 500 W/m2 striking the earth. Due to a variety of radiative processes, a 3.7 W/m2 change at the TOA gives a change on the order of 17 W/m2 at the ground. This is on the order of 3%, so the answer is the same.
Remember, it is quite unlikely that CO2 will double in the next century. On an annual or a decadal basis, therefore, the effect will only be a hundredth or a tenth of that.
This puts it at the small end of a second order forcing on a century-long basis, and makes it inconsequentially small on an annual or decadal basis.
A cloud coming between the surface and the sun, on the other hand, can cause a change in forcing of hundreds of watts per square metre. When the clouds build up on a tropical afternoon, it is a huge, first-order change in forcing.
Which is why I call CO2 an inconsequential trace gas … not because its actual amount in the atmosphere is so small, but because its effect is so small.
Excellent site, kudos for honesty, science, and lack of censorship.
Willis Eschenbach:
Ah, but it’s 3.7 W/m2 over the entire Earth. Your cloud comes and goes, but CO2 just keeps on heating.
But there are always a lot of clouds (66% coverage)
Is it realistic to treat cloud coverage as a constant value as far as radiation is concerned without considering the effect of its variability?
scienceofdoom
I like your goal. Good technical discussion of the CM issues is much needed. But your discussion of Co2 absorbtion got off in the weeds by getting involved too deeply in radiative equilibrium at the outset. I think that it is generally accepted that the temperature profile in the troposphere is set near the adiabatic lapse rate by convection+latency. This makes the radiation from the earth and from the atmosphere independent (we have a predetermined T, the same for all gas components. In that case saturation occurs when the absorption of up radiation is a few absorption lengths (alpha*z>>1). If (aplha*z <1) there is no saturation. This separation is possible because the temperature of the air is not determined by the radiation.
The stratosphere is a different issue. But to address that we need some numbers on the relative absorption in troposphere vs. stratosphere.
Robm:
I get onto this in Part Five with the radiative-convective model of Ramanathan and Coakley.
I wasn’t sure what you meant by this: This makes the radiation from the earth and from the atmosphere independent – independent from each other? or independent of the trace gas concentration?
In case you meant the latter.. strictly speaking the radiation from the atmosphere will depend on the concentrations of the various trace gases in two ways.
First, for a given temperature profile the radiation is dependent on the emissivity of those gases at various wavelengths, so the higher the concentration, the higher the radiation.
Second, with a given convective lapse rate, more absorbing gases will tend to increase the surface temperature – and therefore the temperature at each height in the atmosphere. The surface temperature is increased through an effect explained more fully in The Earth’s Energy Budget – Part Three.
Well, you might not have meant what I thought so feel free to clarify.
Scienceofdoom
I meant independent of each other. One is absorbed by a grey body at T(z) the other is radiated by that grey body. For example when alpha*z>>1. (maybe never happens, but for thought purposes) the outgoing radiation will be from high in the atmosphere (Cold). The lower atmosphere will be in radiation exchange up and down but down will be smaller than up because of the lapse rate.
The extra energy is carried up by convection. This general concept applies whether the absorbtion is total (saturated) or not but it is easier to see in the total absorbtion situation.
[…] the seven-part series on CO2 basics. Part One introduced the idea of CO2 with some basic concepts. Part Three opened up the radiative transfer equations, not solvable on the pocket calculator. Part Five showed […]
[…] of the CO2 atmosphere we have to solve the radiative transfer equations, which you can see in CO2 – An Insignificant Trace Gas? Part Three and Part Five (and the whole […]
[…] Part Three – the Beer Lambert model of absorption and the concept of re-emission of radiation […]
[…] can see the equations of radiative transfer in CO2 – An Insignificant Trace Gas? Part Three. In essence, the proportion of radiation absorbed in a small section of the atmosphere is […]
SOD
Your claiming co2 that H2O’s absorption band is around 6.2u. When I looked at a spectra diagram on Wikipedia and it showed water overshadowing most of CO2’s footprint, especially above 10u.
On the source page Wikipedia give these parameters of forcing:
Water Vapor H2O 36 ~ 72 %
Carbon Dioxide CO2 9 ~ 26 %
Methane CH4 4 ~ 9 %
Ozone O3 3 ~ 7 %
http://en.wikipedia.org/wiki/Green_house_gas
In your reference to wikipedia water vapor you neglected to give the rest of the comment which is Water vapor (H2O) ~0.40% over full atmosphere, typically ***1%~4% at surface.*** It’s the surface figure that is most significant as that’s where most of the greenhouse effect occurs.
Frankly, I think your presentation is rather contrived, something the IPCC would do to give CO2 a false significance.
When I look at the empirical evidence against the computer predictions, the MODTRAN just doesn’t hold a lot of panther piss.
As I mentioned before I don’t see how the conclusions can be reach from satellite temps alone as to what is actually doing the forcing.
If you have two air masses at 70 degrees but one has zero humidity and the other has relative humidity at 60%, what is the difference? Heat content of course and that has a strong effect on the Earth’s heat budget.
You might get a silver ring for presenting some science on the Green house effect but no gold ring, no cigar.
To get a real idea on whats really going on you should read:
http://objectivistindividualist.blogspot.com/2010/07/9-july-updated-version-do-ir-absorbing.html
And I doubt if CO2 has much more forcing past 250ppm.
[…] Understanding the theory of radiative transfer is quite daunting without a maths background, and as many readers don’t want to see lots of equations I will try and describe the approach non-mathematically. There is some simple maths for this subject in CO2 – An Insignificant Trace Gas? Part Three. […]
Science of Doom:
“the closer to the surface the higher the pressure and, therefore, there is more of absorbing gases like CO2”.
Is this right, SOD? I would have thought that the higher concentration of CO2 near the surface would reflect its specific gravity, not higher pressure which, at any altitude, is a measure of the mass above it.
However, CO2 is a “well-mixed” component of the atmosphere according to the IPCC. As well, I seem to remember one of your graphics showing constant concentration with altitude.
“The relationship between I (radiation absorbed) – and B (radiation emitted) – integrated across all wavelengths, all directions and all surfaces is linked through conservation of energy”.
Is this right, SOD? I would have thought that the energy conservation law in this context would equate the absorbed energy with the increase in emitted radiation resulting from the temperature increase induced by the absorption, that is, dI = dB. Doesn’t Stephan-Boltzmann come in here?
The exponential decay shape shows clearly how acutely calculations of optical thickness depend on the accuracy of measurements of the concentration of the absorber and of its effectiveness. SOD, do you have any data on these parameters?
Am I correct inferring that K&T’s energy budget implies atmospheric optical thickness of 0.8 for solar radiation and of 1 for terrestrial radiation in the atmospheric window and 0 elsewhere in the LW spectrum?
John Millett:
There’s more mass of atmosphere at the ground than at 10km up.
Therefore, as CO2 is well-mixed – in parts per million – the number of CO2 molecules per unit volume is much higher nearer the ground than 10km up.
On the 2nd question:
Take a slab of atmosphere:
— Energy in = Energy out – if the temperature of the slab of atmosphere is not changing.
— Energy in – Energy out = increase in energy absorbed by the slab of atmosphere.
These are both true of any body, not just a slab of atmosphere.
Your statement;
“I would have thought that the energy conservation law in this context would equate the absorbed energy with the increase in emitted radiation resulting from the temperature increase induced by the absorption, that is, dI = dB.”
– seems correct.
With the proviso that I’m not 100% certain that you mean what I think you mean.
So I would add that absorbed energy can equal emitted energy with no increase in temperature.
The Stefan-Boltzmann law is the total energy emitted from a surface across all directions and all wavelengths.
So you don’t actually need it to solve this problem. In fact, it’s not easy to use this law to find the solution to this problem. But the reasons why are a little complex – in a mathematical sense.
John Millett
I am currently writing an article (slowly) about Kiehl and Trenberth 1997. Watch this space.
Overall their energy budget doesn’t rely on these parameters. The “atmospheric window” is a “by the way” kind of point. Not a core part of their analysis.
“optical thickness of .. 1 for terrestrial radiation in the atmospheric window and 0 elsewhere in the LW spectrum?””
More the other way round.
Top of atmosphere values are measured.
Surface radiation values – downward – “the back radiation” are measured in places. Calculated via models to work out the global annual average – but vetted against the measurements.
Surface radiation values – upward – are almost all calculated – via the Stefan-Boltzmann law.
Latent heat is calculated with respect to rainfall (what goes up must go down).
Sensible heat is calculated as the “balancing item”.
I look forward to the forthcoming K&T piece. Meanwhile, the zero in my post should read “4” – I was simply relating the K&T values to your graphic.
“dI = -Inσdz + Bnσdz = (I – B)dχ (where χ is defined as optical depth)”
It’s the similar forms taken by the absorbing and emitting elements in this equation that puzzles me.
John Millett:
The equation:
“dI = -Inσdz + Bnσdz = (I – B)dχ (where χ is defined as optical depth)”
is true for a monochromatic wavelength
if we rewrite it in English:
i) if we shine a beam of monochromatic wavelength through a small distance,
ii) the change in intensity through this small distance is equal to the radiated value at this wavelength less the absorbed amount;
iii) the absorbed amount will be proportional to the intensity of the original beam AND the number of absorbers (n) and their effectiveness (σ);
iv) the emitted amount will be proportional to the Planck function at the temperature of the gas, the number of absorbers (n) and their effectiveness at emitting (σ)
This graphic from Theory and Experiment – Atmospheric Radiation shows it better:
And why is the form of the equation the same?
Well, it’s all to do with a gas that absorbs at one wavelength will also emit at that wavelength.
The amount of radiation absorbed is NOT EQUAL to the amount of radiation emitted at that wavelength.
It’s just that the proportion of INCIDENT radiation absorbed is equal to the proportion of the Planck curve radiated.
So if through a small slab of gas of temperature T, 0.01% of 15.015um radiation was absorbed, we would expect that the emission of 15.015um radiation would be 0.01% of the Planck function (for temperature T).
Scienceofdoom:
Thanks for that. Meanwhile, let’s see if I’m getting all this:
The formula from which we calculate CO2 forcing – 1.7 Wm-2 due to the increase in concentration from pre-industrial time to the present and 3.7 from a doubling of concentration since then – was derived from numerical solutions of RTE equations which combine absorption and emission by successive thin vertical atmospheric layers. Right?
CO2 is radiatively active at 2.7, 4.2 and 15 microns, the foremost being in the SW part of the spectrum, the hindmost in the LW part and 4.2 microns in both parts.
On my figuring (DANGER: first time solver of the Planck function manually or user of spectralcalc.com) CO2 prevents more energy getting to the surface than it prevents leaving it:
2.7 microns, T= 5780K, reduced by a factor of 215^2: 11.9 Wm-2
4.2 microns, T= 5780K, reduced by a factor of 215^2: 2.4 Wm-2
4.2 microns. T= 288K : 0.6 Wm-2
15 microns, T= 288K : 5.8 Wm-2
Question: Do the RTE equations include CO2 absorption in the SW as well as the LW? Is the 3.7 number net or a “warming only” one?
[…] The equation of absorption is known as the Beer-Lambert law – you can see more about it in CO2 – An Insignificant Trace Gas? Part Three. […]
SoD, great site as always! I would give allot to know what the DLR bands of CO2 looked like at night, when they act to cool the atmosphere, and no ULR is present. Do you know where such info can be found?
Considering applications of Beers Law, it occurred to me that, instead of guessing (however reasonably accurate the mathematical guess), maybe shining a CO2 laser at night through the atmosphere to a satellite would give us the atmosphere’s total absorption?
Mark O,
How about 75’S on May 1st at 22:30?
This can be seen in The Amazing Case of “Back Radiation” – Part Two and is taken from Measurements of the downward longwave radiation spectrum over the Antarctic plateau and comparisons with a line-by-line radiative transfer model for clear skies, Walden et al, Journal of Geophysical Research (1998).
Beautiful, I love it. Now what about my laser idea? Wouldn’t that be a simple test for total atmospheric absorption?
SoD;
I have spent some more time looking at your essays. I believe I have narrowed down what is bothering me about this presentation. Consider this;
“The conceptual mistake that most people make who haven’t really understood radiative transfer is they think of it something like torchlight trying to shine through sand – once you have enough sand nothing gets through and that’s it.”
Well, that’s true enough about light and sand. The thing is, it’s also true of radiative transfer. Terms like absorption, transmission, and attenuation are not unique to atmospheric physics. They are used very widely in scientific and engineering disciplines. And the phenomenon you are modeling is not what is usually meant by “attenuation”. The reality, if I may abuse that term, is that the radiation that goes in at the bottom (at the CO2 wavelength) is very quickly absorbed, while the radiation that comes out the top is thermal radiation from the upper layers of the atmosphere.
You may say that photons don’t have labels, and there is no way of determining the provenance of the outgoing radiation, but that is not true. Suppose that you modify your model by setting the Earth surface temperature to, say, 5 K. Then there will be almost zero radiation going in at the bottom, yet the same amount will be coming out at the top. When that happens in a Nd-YAG rod, or a radio transmitter, we call it “amplification”. But I don’t see you referring to your column of atmosphere as an amplifier. So why do you feel OK about describing it as an attenuator? If Bob goes into a store, and Alice comes out, would you say that Bob has been attenuated into Alice?
The terms you are employing are typically used in a context of linear systems, in which the output varies with the input. Using that terminology to describe decidedly non-linear phenomena leads very easily, indeed, predictably, to misunderstandings. As does the frequent use of the term “greenhouse” when referring to phenomena unrelated to greenhouses. Given that these extremely crude models are being described as “settled science”, and used to justify radical policy prescriptions, many people are beginning to suspect that this miscommunication is deliberate. Sometimes what is desired is heat, not light.
Jerome
And that’s precisely why there is an atmospheric greenhouse effect. The emission from the TOA is lower than emission from the surface in the spectral regions where absorption is high because the troposphere cools with altitude. Which means the surface temperature has to be higher to approximately balance energy in with energy out.
I also beg to differ about the effect in the atmosphere being unrelated to greenhouses. The optical properties of the covering of a greenhouse can make a difference. Low emissivity glass, for example, can cut heat loss from a greenhouse as well as it does in your house. It isn’t normally used, though, because it’s too expensive. Single or double layer polyethylene sheeting is a lot cheaper and is all that is needed most places.
We are discussing here phenomena that are not understood fully without fairly strong background in physics. Anyone attempting to explain such phenomena do to a wider audience tries to find simplifications and analogs that help in making at least part of the full picture more understandable. We have seen time after time that each of us has different views on, how that’s done best.
From his background Jerome does not to like all the choices made by SoD, and I’m sure he would not like all the approaches that I like most. There are no unique best solutions for explaining physical phenomena to non-physicists. It must be understood and accepted that every approach has it’s weaknesses, while many have also strengths.
Rather than immediately condemning some particular formulation a better approach is to propose, how the message could be made more understandable to those with less science background but with a willingness to learn. Many of us are trying to do that. We get some ideas and propose new approaches or formulations. They are not always real improvements but looking at the same issues in varying ways helps often someone.
Having so many approaches may also be confusing, at least for while, but I think that’s unavoidable and we should not worry too much about that.
Jerome wrote: “Terms like absorption, transmission, and attenuation are not unique to atmospheric physics.” Later: “The reality, if I may abuse that term, is that the radiation that goes in at the bottom (at the CO2 wavelength) is very quickly absorbed, while the radiation that comes out the top is thermal radiation from the upper layers of the atmosphere.”
It is easy to forget about emission, a term you didn’t mention. I might have written the same words before I painfully learned how to integrate emission with my understanding of absorption. I knew that the popular, but over-simplied, concept that CO2 traps heat in the atmosphere was wrong, but my practical experience with IR radiation came from a dual-beam IR spectrophotometer. There was no need to take into account the thermal emission from carbon dioxide and water vapor in the 300 degK air in surrounding the spectrophotometer when the filament in the lamp of the spectrophotometer was several thousand degK. The sample only attenuated that radiation and the photons emitted by the sample and air towards the detector could be ignored. Outside the lab, the surface of the earth (somewhat equivalent to the lamp) and the atmosphere (the sample) have similar temperatures, so emission from the atmosphere can’t be ignored. But how does one account for it? I never found SOD’s early posts satisfying until he introduced me to the Schwartzschild eqn:
dI/ds = – I_0*n*o + B(lamba,T)*n*o
Suddenly, everything was clear. Translated, the incremental change in radiation intensity at any wavelength lamba (dI) as it passes an incremental distance through the atmosphere (ds) is determined by the loss to absorption and the gain through emission; where I_0 is the incoming intensity, n is the number of absorbing/emitting molecules the radiation encounters, B(lamba,T) is the Planck function for that wavelength and temperature, and o is the absorption and emission cross-sections – which are equal. The number of molecules is given in weight or moles per unit volume (or calculated from density and mixing ratio) and the cross-section in area per weight or mole. DeWitt provided an integrated form of the Schwartzschild eqn for a homogeneous gas where tau is n*o*s.
If radiation at a particular wavelength (with a non-zero absorption cross-section) has passed far enough through a homogeneous gas (or other medium) so that absorption and emission have reached equilibrium (dI/ds = 0), the intensity of the radiation at that wavelength will be equal to that emitted by a blackbody. When it hasn’t gone far enough for emission and absorption to reach equilibrium, the intensity is gradually changing from the intensity which entered the gas to the intensity expected for blackbody radiation. These changes take place over shorter distances for more strongly absorbing (and emitting) the gases, but absorption never reduces the flux to zero – as it appears to do in a laboratory spectrophotometer. It takes only a few meters of atmosphere for the strongest absorption lines of carbon dioxide to change the intensity of radiation passing through it to the intensity of blackbody radiation at those wavelengths – but carbon dioxide never reduces the flux to zero. Since the air near the earth has approximately the same temperature as the surface, the intensity at strongly absorbed wavelengths doesn’t even change appreciably near the surface! However, changes in carbon dioxide do influence the emission altitude of photons successfully escaping to space. In general, the higher the altitude, the colder it is; reducing emission via the Planck term.
Jerome Berryhill
I’m just looking for words to explain complex phenomena. Many people have conceptual problems with radiation. A common one is that current levels of CO2 already “saturate” the atmosphere, and so more CO2 cannot have any effect. Another conceptual problem is that 300 ppm of CO2 cannot have any appreciable effect at all. Another problem again is that water vapour, being over 100x more prevalent than CO2, must be 100 times more effective as a greenhouse gas. And there are more..
I try to find a balance between “here are the equations of radiative transfer along with a numerical solution for some sample values” and “here’s why your problem written in words is not really capturing the essence of the problem”.
I’m sure others could find better words to capture, crystallize and diffuse the conceptual problems of the many people seeking to understand climate basics.
Also, when I wrote this series, on the subject of “saturation”, I was not able to separate out two competing effects in our real atmosphere:
a) the effect of emission of radiation from a column of gas with a lapse rate (reducing temperature with height)
b) the effect of the wings of the CO2 band
Now I’ve created a numeric model of the atmosphere and used the HITRAN database I have been able to understand this better myself.
The wings of the CO2 band are more important. This effect is highlighted more clearly in:
Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Nine
Visualizing Atmospheric Radiation – Part Seven – CO2 increases.
And as Pekka points out well in his latest comment, in the end we can provide physics in physics-language, or provide explanations in words (English only for me) to attempt to explain to equation-less people why the world is like it is.
I accept that my words are often flawed, and that they often present physics in an imperfect light. If they help a few climate-seekers understand climate better then the effort has been worthwhile.
Jerome Berryhill,
Can you please quote where SoD uses “attenuation” as the sole descriptor of the phenomenon he is modeling. The term that is used is “radiative transfer”. Attenuation or absorption is part of the radiative transfer function and, as far as I can tell, is always used correctly in these essays to mean I(λ) = Io(λ) * exp(-τ) where τ is the optical depth for a given path length and wavelength for that medium. The radiative transfer function for a homogeneous medium, however, is I(λ) = Io(λ)*exp(-τ) + B(λ,T) * (1-exp(-τ)) where B(λ,T) is the Planck function for the specified wavelength and temperature. It appears to me that you are reading something into these essays that simply isn’t there.
OK SOD, some facts and nuances.
> The 15 micron band BB emission undergoes total absorption within 10 meters of the Earth surface.
> The CO2 metastable energy state at .0825 ev has a long mean emission time, hundredths of a second due to the low energy.
> The first molecular air collision able to cause a virtual phonon transition to kinetic energy will occur in about .13 nano-seconds.
> Over 300 million collisions with virtual photon transition probability will occur before any natural re-emission of the 15 micron photon can occur.
> The only BB IR radiation that can escape from the troposphere is through the IR Window, That is a constant and unchanged by CO2 ppm levels.
> All 15 micron emissions for the past 65 million years have been totally blocked within a few meters of the Earth surface. During that time CO2 ppm has varied from 1500 ppm down to ~ 250 ppm and there has never been a climate catastrophe’ caused by CO2 ppm concentration in the atmosphere.
> Plant growth and plant health is optimized for a CO2 ppm level of ~ 800 ppm.
> At 331 ppm CO2 (1930’s) we were starving all plant life on Earth with insufficient CO2.
> Still not seeing how changing CO2 ppm from 300 to 400 can be a causal condition for warming of the Earth Surface. Show me what has been changed as the Stratosphere is cold, low pressure and has less than 100 ppm CO2 and that is the location of the non-IR Window IR emissions which is a very small amount of energy compared to the IR Window output.
> As the CO2 extinction distance is growing shorter as CO2 ppm rises, any emitted IR (15 micron) will undergo more immediate absorption and conversion back to thermal energy (kinetic energy). The kinetic energy conversion process in thousands of times more favorable than re-emission.
> Seems you are playing fast and loose with terms like re-emission and ignoring the scale of the absorption process in comparison to unimpressive re-emission claims.
> You do not even attempt to model conduction, convection and the cooling through the latent heat of vaporization of water. IR BB radiation is not the dominant cooling mechanism for the Earth’s Surface. Evaporation of water dominates that IR stuff in temperate and tropical climates.
> Show how you model the latent heat of vaporization into your optical only model. I don’t see that anywhere in your discussions.
PSG
Dr G,
Take a look at Visualizing Atmospheric Radiation – Part Seven – CO2 increases, for example:
– this graph shows the change in transmissivity outside of the central 667cm-1 = 15 μm region.
And this one:
– difference in transmissivity of layer 10 for 280 ppm – 560 ppm
I look forward to your comments now that you know that there is a substantial change in atmospheric absorption due to increases in CO2.
—
On other points, e.g., “..You do not even attempt to model conduction, convection and the cooling through the latent heat of vaporization of water. IR BB radiation is not the dominant cooling mechanism for the Earth’s Surface. Evaporation of water dominates that IR stuff in temperate and tropical climates..”
Of course, everyone in climate science knows this (of course apart from conduction). The point is that with a given temperature profile through the atmosphere – which is generated from convection, latent heat and radiation – when you increase CO2 you change the energy balance.
More in The “Greenhouse” Effect Explained in Simple Terms and the references within.
SOD,
So what is the source of IR to transmit through the atmosphere at 16.9 km (55,446.19 ft.)? It isn’t from the Earth surface because that is blocked by lower altitude H2O and CO2 molecular capture. See first reference.
> Yes, you can capture a small amount of Solar IR, but that would result in cooling not heating.
Even 25% or 5% transmittance doesn’t affect anything if there is no IR source.
Finally, any radiation or cooling flux is outward, not downward. That can’t change our near surface conditions.
> You can’t make T = 220K suddenly send energy to a T=300K system, All the flux is from high to low. If you argue for that the low sends energy to high, you are trying to prove ‘perpetual motion’ and getting ‘something from nothing’.
> Still not seeing the CO2 as a big problem.
Dr. G.
It’s simple.
The equation of radiative transfer.
Apply this with the absorption/emission lines of CO2, and other gases and you find the radiative forcing as a result of changes in CO2 concentrations.
You can see this equation derived at Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations.
You do know this equation, right?
If you double CO2 from pre-industrial concentrations you get a reduction in OLR of about 4W/m2.
As most of your comment is a random collection of scientific words, I’ll wait for you to demonstrate:
a) the equation of radiative transfer is wrong – or
b) applying increases in CO2 concentrations to this equation doesn’t result in a decrease in OLR – or, for bonus points
c) it’s impossible for OLR to reduce because “thermodynamics”
or, for even more bonus points
d) if OLR reduces then somehow “thermodynamics” won’t allow temperature to increase (somehow the first law of thermodynamics is violated but that’s ok, because.. stuff..)
Reblogged this on Climate- Science.