This first part considers some elementary points. In the next part we will consider more advanced aspects of this subject.
Since 1978 we have had satellites continuously measuring:
- incoming solar radiation
- reflected solar radiation
- outgoing terrestrial radiation
To see how we can differentiate the solar and terrestrial radiation, take a look at The Sun and Max Planck Agree – Part Two.
Top of Atmosphere Satellite Measurements
The top of atmosphere (TOA) radiation from the climate system is usually known as outgoing longwave radiation, or OLR. “Longwave” is a climate convention for wavelength >4μm.
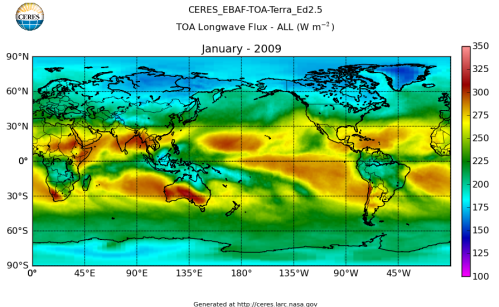
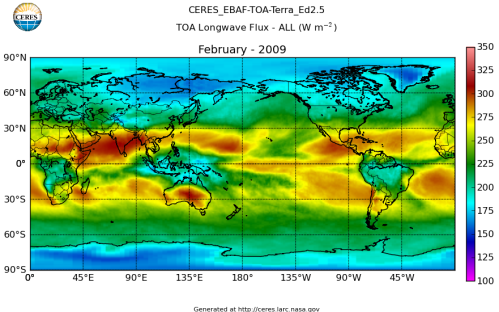
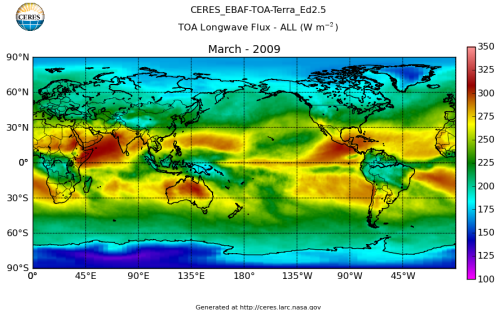
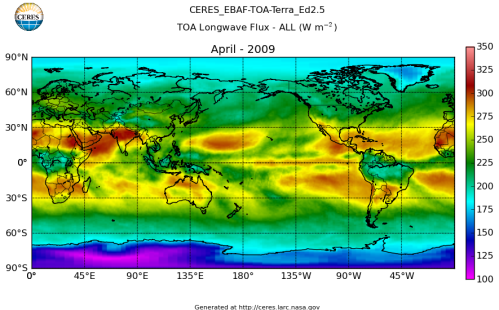
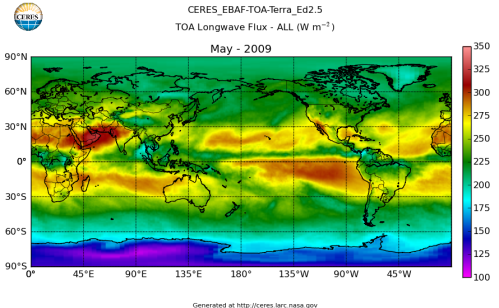
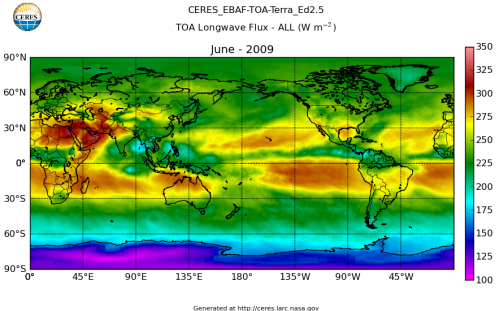
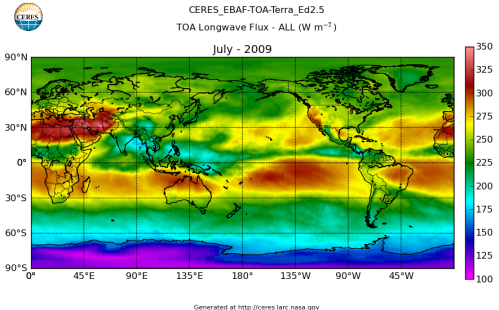
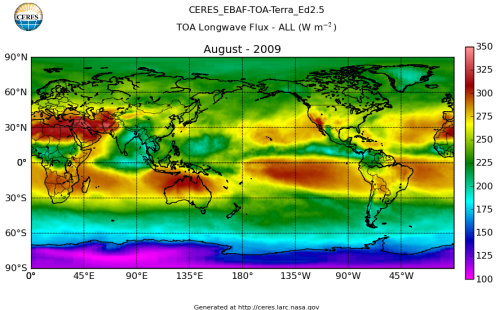
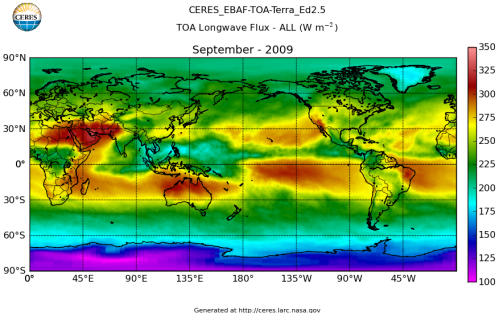
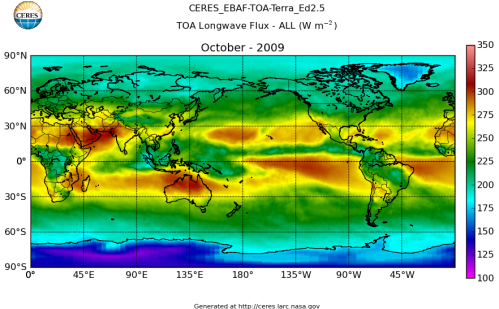
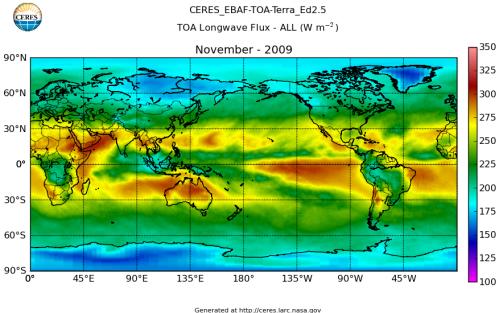
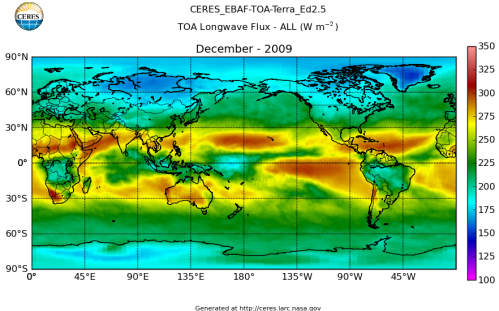
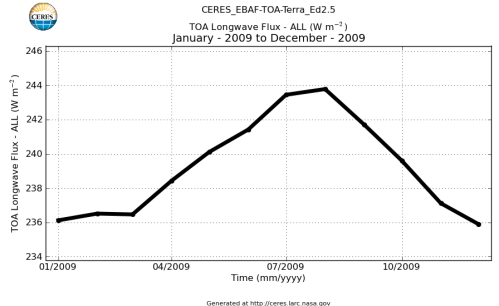
Here’s what the OLR looks like to the satellites. I thought it might be interesting for some people to see how the values change each month:
All of this data comes from CERES – Clouds and the Earth’s Radiant Energy System. You can review this data for yourself here. How accurate is the data?
The uncertainty of an individual top-of-atmosphere OLR measurement is 5 W/m², while the uncertainty of average OLR over a 1°-latitude x 1°-longitude box, which contains many viewing angles, is ≈1.5 W/m²
from Dessler et al (2007) writing about the CERES data.
If we summarize this data into monthly global averages:
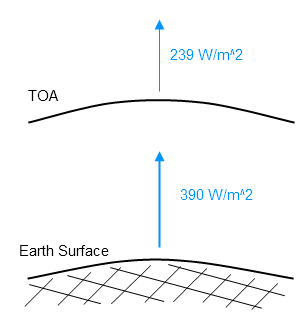
The average for 2009 is 239 W/m². This average includes days, nights and weekends. The average can be converted to the total energy emitted from the climate system over a year like this:
Total energy radiated by the climate system into space in one year = 239 x number of seconds in a year x area of the earth in meters squared
= 239 x 60 x 60 x 24 x 365 x 4 x 3.14 x (6.37 x 106 )²
= 239 x 3.15 x 107 x 5.10 x 1014
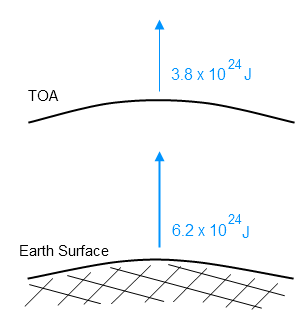
ETOA= 3.8 x 1024 J
The reason for calculating the total energy in 2009 is because many people have realized that there is a problem with average temperatures and imagine that this problem is carried over to average radiation. Not true. We can take average radiation and convert it into total energy with no problem.
What about the radiation from the surface?
Surface Radiation
What do the satellite measurements say about surface radiation?
Nothing.
Well strictly speaking – they say a lot, but only once certain theories of radiative transfer are embraced.
To be more accurate, what satellite measurements OF surface radiation do we have?
None.
That’s because the atmosphere interacts with the radiation emitted from the surface. So any top-of-atmosphere measurements by satellite are not “unsullied surface measurements”.
There are temperature stations all around the world – not enough for some people, and not as well-located as they could be – but what about stations for measuring radiation upwards from the earth (and ocean) surface?
Thin on the ground, extremely thin.
Luckily, there is a very simple formula for radiation emitted from the surface of the earth:
E = εσT4
where σ is a constant = 5.67 x 10-8, ε = emissivity, a property of surface material, and T = temperature in K (absolute temperature)
This equation is called the Stefan-Boltzmann equation. More about it in Planck, Stefan-Boltzmann, Kirchhoff and LTE. It is a well-proven equation with 150 years of evidence behind it – and from all areas of engineering and physics. It is used in calculations for heat-exchangers and boilers, for example.
Still, many people when they find out that the radiation from the surface of the earth is calculated not measured are very suspicious. It’s good to be skeptical. Ask questions. But don’t assume it’s made up just because it’s calculated. Why trust thermometers? They actually rely on material properties as well..
Anyway, back to the emission of radiation from the surface. What about this parameter emissivity, ε?
Emissivity is a function of wavelength. This means it varies as the wavelength of radiation varies. Some examples, not all of them materials from the surface of the earth:
Reflectivity vs wavelength for various surfaces, Incropera (2007)
Note that reflectivity = 1 – emissivity in the graph above.
Without going into a lot of detail, all it means is that the measurement of emissivity needs to be for the appropriate temperature. See note 1.
If we measure emissivity of water one day, we find it is the same the next day and also in 589 days time. It is a material property which means that once measured, the only questions we have are:
a) what is the temperature of the surface
b) what is the material of the surface (so we can look up the measured emissivity for this temperature)
Generally the emissivity of the earth’s surface is very close to 1 (for “longwave” measurements).
Oceans, which cover 71% of the earth’s surface, have an emissivity of about 0.98 – 0.99.
The average temperature of the earth’s surface (including days, nights and all locations) is around 15°C (288K). Average temperature is a problematic value because radiation is not linearly dependent on temperature – it is dependent on the 4th power of temperature. See The Dull Case of Emissivity and Average Temperatures for an example of the problems in using “average temperature”.
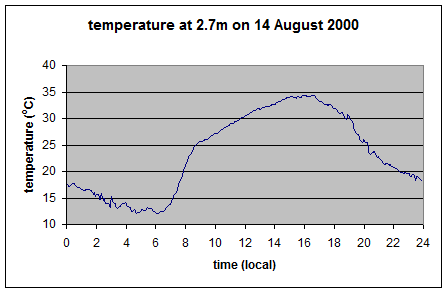
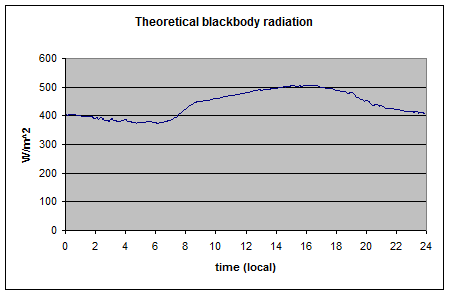
Here is an example of measurement of upward surface radiation:
Upward and downward radiation measurements, EBEX 2000, Kohsiek (2007)
The line with the x’s is the measured surface upward radiation.
Here is the actual temperature:
Temperature for 14 August 2000, from Wim Kohsiek, private communication
And calculated emitted radiation:
Calculated (theoretical) upward radiation, 14 August 2000
Note how it matches the measured value. You can see this in more detail in The Amazing Case of “Back Radiation” – Part Three.
The theory about emitted radiation
E = εσT4
– is a solid theory, backed up over the last 150 years.
If we calculate the average radiation from the surface, globally annually averaged, we get a value around 390 W/m².
If we calculate the total surface radiation over one year, we get Esurf = 6.2 x 1024 J.
The Inappropriately-Named “Greenhouse” Effect
The surface radiates around 390 W/m². The climate system radiates around 239 W/m² to space:
How does this happen?
As I found with previous articles, many people’s instinctive response is “you’ve made a mistake”.
Usually those that just aren’t happy with this diagram solve the “dissonance” by concluding that there is something wrong with the averaging, or Stefan-Boltzmann’s law, or the measurement of emissivity around the planet.
Here’s the total energy for one year radiated from top of atmosphere and from the surface:
Remember that the top of atmosphere number is measured. Remember that the surface radiation is calculated, and relies on measurements of temperature, the material property called emissivity and an equation backed up by 150 years of experimental work across many fields.
This effect which we see has come, inappropriately, to be called the “greenhouse” effect. We could convert the effect to a temperature but there are more important things to move onto.
Before examining how this amazing effect takes place and what happens to all this energy – “Does it just pile up and eventually explode, no – so obviously you made a mistake”, and so on – I’ll leave one thought for interested students..
We have looked at the average radiation from surface and top of atmosphere (and also totaled that up).
Instead, we could take a look at some individual ocean locations where the temperature is well known. We have the CERES monthly averages on a 1° x 1° grid above.
Take a few ocean locations and find the average temperatures for each month.
Then calculate the surface radiation using the known emissivity of 0.99. Compare that to the top of atmosphere radiation from the CERES charts at the start of the article. Also calculate what value of ocean emissivity would actually be needed for surface radiation to equal the top of atmosphere radiation (so as to make the “greenhouse” effect disappear). Please report back in the comments.
The reason I chose the ocean for this exercise is because the emissivity is well known and measured so many times, because ocean surfaces don’t change temperature very much from day to night (because of the high heat capacity of water) and because oceans cover 71% of the earth’s surface. If ocean data verifies the “greenhouse” effect to you, then it’s pretty hard to find emissivity values of other surface types that would make the “greenhouse” effect disappear.
Interaction of Matter with a Radiation Field
Huh? Let’s choose a different heading..
What Happens to Radiation as it Travels Through the Atmosphere
If longwave radiation (remember this is the radiation emitted by the earth and climate system) was transparent to the various gases in the atmosphere the surface radiation would not change on its journey to the top of atmosphere. See The Hoover Incident for more on this and the consequences.
Instead at each height in the atmosphere there is absorption of some radiation. The detail gets pretty complicated because each gas absorbs at very selective wavelengths (see note 2).
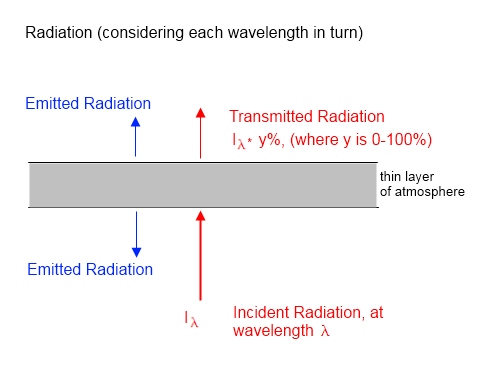
The very fact that radiation can be absorbed by gases shows that you shouldn’t expect the radiation going into a layer of atmosphere to be the same value when it emerges the other side. Here’s a simple diagram (which also can be found in Theory and Experiment – Atmospheric Radiation):
If a proportion of the upward radiation is absorbed by the atmosphere so that less radiation emerged than entered (the red text and arrows) then isn’t this a first law of thermodynamics problem?
Well, being specific:
Energy In – Energy Out = Energy Retained in Heating the Layer
So if the temperature of that layer was not increasing or decreasing then:
Energy in = Energy out.
So surely, absorption of radiation with no continuous heating is a problem for the first law of thermodynamics?
Of course, energy transfer can also take place via convection. So it is theoretically possible that energy could be absorbed as radiation and leave via convection. But that isn’t really possible all through the climate as convection would need to transfer energy from high up in the atmosphere to the surface, whereas in general, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.
So what happens and how does the first law of thermodynamics stay intact?
Very simple – every layer of atmosphere also radiates energy. This is shown as blue text and arrows in the diagram.
Each layer in the atmosphere does obey the first law of thermodynamics. But by the time we reach the top of atmosphere the upwards radiation has been significantly reduced – on average from 390 W/m² to 239 W/m².
Each layer in the atmosphere absorbs radiation from below (and above). The gases that absorb the energy share this energy via collisions with other gases (thermalization), so that all of the different gases are at the same temperature.
And the radiately-active gases (like water vapor and CO2) then radiate energy in all directions.
This last point is the key point. If the radiation was (somehow magically) only upwards then the “greenhouse” effect would not occur.
Digression – Up & Down or All Around?
You will often see explanations with “the layer then radiates both up and down” – and I think I have used this expression myself. Some people then respond:
Doesn’t it radiate in all directions? Looks like another climate science over-simplication..
This is a good point. Radiation from the atmosphere does go in all directions not just up and down.
In the radiative transfer equations this is taken into account. The simplified explanation just makes for an easier to understand point for beginners. See Vanishing Nets under Diffusivity Approximation for more about the calculation.
End of digression.
Radiation Through the Atmosphere
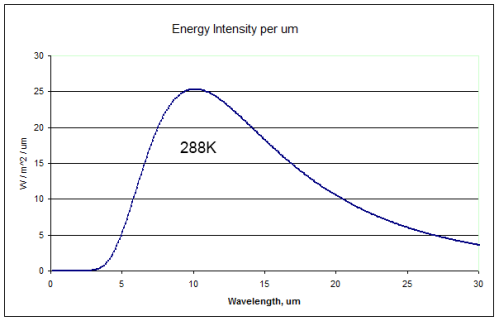
Solar radiation is mostly absorbed by the earth’s surface (because the atmosphere is mostly transparent to solar radiation). This heats the surface, which radiates upward. The typical radiation from the earth’s surface at 15°C measured just above it looks something like this:
The atmosphere absorbs this longwave radiation and consequently radiates in all directions. This is why, when we view the spectrum of the upward radiation at the top of atmosphere we see something like this:
From Atmospheric Radiation, Goody (1989)
Note the reversal of the x-axis direction.
The “missing bits” in the curve are the wavelengths where the radiatively active gases have absorbed and re-radiated. Some of the radiation is downward, which explains where the “missing radiation” goes.
At the surface we can measure this downward radiation from the atmosphere. See The Amazing Case of “Back Radiation” -Part One and the following two parts for more discussion of this.
But – as already stated – at each height in the atmosphere, energy fluxes are balanced:
Energy in = Energy out
Or – the difference between energy in and energy out results in increasing or decreasing temperature.
If you like, think of the atmosphere as a partial mirror reflecting a proportion of the radiation at a number of layers up through the atmosphere. It’s a mental picture that might help even though what actually happens is somewhat different.
Convection
No explanation of radiation would be complete without people saying that this argument is falsified by the fact that convection hasn’t been discussed. Just to forestall that: Convection moves heat from the surface up into the atmosphere very effectively and cools the surface compared with the case if convection didn’t occur.
But – emission and absorption of radiation still takes place. Convection doesn’t change the absorption of radiation (unless it changes the concentration of various gases). But convection, by changing the temperature profile, does change emission.
As we will see in Part Two, absorption is a function of concentration of each gas; while emission is a function of concentration of each gas plus the temperature of that portion of the atmosphere.
Conclusion
The atmosphere interacts with the radiation from the surface and that’s why the surface radiation has been reduced by the time it leaves the climate system.
The satellites measure the value at the top of atmosphere very comprehensively.
For those convinced that there is no “greenhouse” effect, I recommend focusing on the emissivity measurements used in the calculation of emission from the surface.
The ocean has been measured at 0.98-0.99 and covers 71% of the surface of the earth but perhaps the average surface emissivity at terrestrial temperatures is only 0.61.. A measurement snafu..
In the next part we will consider in more detail how the different effects cause changes in the OLR.
Other articles:
Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only
Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.
Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.
Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”
Part Six – The Equations – the equations of radiative transfer including the plane parallel assumption and it’s nothing to do with blackbodies
Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking
And Also –
Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.
References
An analysis of the dependence of clear-sky top-of-atmosphere outgoing longwave radiation on atmospheric temperature and water vapor, Dessler et al, Journal of Geophysical Research (2008).
Notes
Note 1: Radiation from a surface at 15°C (288K) will have a peak radiation at 10μm with radiation following the Planck curve. The average emissivity for 288K needs to be the wavelength-dependent emissivity weighted appropriately for the corresponding Planck curve. This will be very similar for the emissivity for the same surface type at 300K or 270K but is likely be totally different for the emissivity for the surface at 3000K – not a situation we find on earth.
Note 2: The most common gases in the atmosphere, Nitrogen and Oxygen, don’t interact with longwave radiation. They don’t absorb or emit – at least, any interaction is many orders of magnitude lower than the various trace gases like water vapor, CO2, methane, NO2, etc. This is after taking into account their much higher concentration. See CO2 – An Insignificant Trace Gas? Part Two
The Science of Doom 
I’m afraid that this is very off-topic but I don’t know where else to post it.
I need an expert to read, free of charge, an 8-pp. double spaced draft on the West Antarctica Ice Sheet (WAIS).
Any volunteers?
Best,
Hunt Janin
Vignoble
47270 St. Urcisse
France
You are quite right to indicate the importance of accuracy in measurements.
Also the focus on the emissivity of sea water as the most significant single value for surface radiation calculations.
You quote 0.98 to 0.99 value for sea water.
What value is used for global average surface emissivity by the IPCC.
Do they take the natural turbulence of sea water into account?
This article disputes the IPCC figures on which such estimates are based.
I tried to look up other figures for turbulent sea waters but although there are plenty citations unfortunately they are all behind pay walls.
Perhaps you can help?
Click to access 2006.06.17_Sea_Water_Emissivity_Volz.pdf
Dessler et al is available here.
Thanks Nick, I updated the article with the link.
The Dessler et al link says they used 0.97 for the Oceans emissivity.
So if someone uses 0.99 instead of 0.97 they introduce an error of 2.06% right at the very start of the process.
If this kind of sloppy work continues by say using an ARM pyrgeometer
Click to access ellingson2_rg.pdf
Then before very long the errors in the measuring process are bigger than the subtle proposed forcing outcome.
How reliable are the conclusions from such a process?
Bryan,
Oh, the irony. Did you not notice that Volz ignores convection? If the water surface disturbed by wind emits more or less energy, then convective transfer will vary to compensate. It’s the energy balance that’s important. While that varies daily and seasonally, the annual averages of energy in and out are very close to equal. The atmospheric transmissivity isn’t 0.65 for LW radiation from the surface either. It’s more like 0.1.
As I commented in the article, for those who believe the “greenhouse” effect doesn’t exist, the best focus of attention is emissivity.
When I present evidence for the emissivity measurement then the questions will probably focus on the measurement equipment.
For others, it probably seems strange that this particular parameter (emissivity) and this particular measurement device (pyrgeometer) is held up for questioning.
Why not pick on annenometers? Or hygrometers? Or expendable bathythermograph?
In fact, the idea that the simple pyrgeometer when used is out by a factor of almost 2 is quite entertaining.
For those who don’t believe in the “greenhouse” effect I notice that they are quite careful not to actually try to make a coherent set of claims themselves, only to “cast doubt” on the “accuracy” of the readings.
For the non-greenhouse brigade, holders and defenders of true science, why not put together a simple yet coherent explanation for the measurements? (The readers know why).
And why not come clean and admit that it isn’t that you think emissivity of the ocean might be perhaps 0.96 instead of 0.98 – 0.99 but you actually think it is 0.6 or 0.7.
Because if you believe there is no “greenhouse” effect then the surface radiation averaged globally annually can only be 239 W/m^2.
And if you don’t believe this low number for surface radiation is a supportable value then you already believe in the “greenhouse” effect.
scienceofdoom
Match your answer to the perfectly straight forward question I asked.
You are seriously off beam.
In your Axiom post you indicated an interest in the topic of accuracy of measurement.
In the post above you underlined this apparent interest in accuracy/
……”For those convinced that there is no “greenhouse” effect, I recommend focusing on the emissivity measurements used in the calculation of emission from the surface.”…..
I agree, the simplest starting figure I can think of is the Earth Surface Radiation.
You say it is calculated rather than measured.
The emissivity is the only quantity that varies apart from the temperature.
How confident are the orthodox greenhouse proponents in the figure they use?
What is the margin or error quoted?
The only reason I cited the source I supplied was when I googled the rest were behind pay walls.
Perhaps everyone else in the planet are quite happy to use unity and no questions asked.
Nick Stokes seemed to understand my question and supplied a link for which I am grateful.
I now have a basis to work on.
Reference to the inappropriately-named “greenhouse” effect and emphases on measurement accuracy and on emissivity are all welcome.
That the difference between OLR at the surface and at TOA is a whole-of-atmosphere effect and not only of its radiatively-active component is beyond question. The questions relate to the magnitude of the warming effect and whether increasing the concentration of that component increases the warming, as per AGW hypothesis.
Continuous satellite measurements, since 1978, of the climate system’s incoming and outgoing energy fluxes has not yet confirmed that hypothesis: the measured difference between fluxes falls within flux measurement tolerances.
Emissivities, being temperature-dependent properties of the radiating material, are likely to vary considerably within the climate system. Emissivity of the atmosphere, which accounts for the bulk of the climate system’s radiation to space, is arguably of more interest that that of the predominant watery surface. Whereas the latter largely determines OLR at the surface of known temperature; the former determines the system’s effective radiating temperature consistent with known OLR flux at TOA.
One source, (Swinbank 1963), posits that the emissivity of air varies with the square of temperature, setting up an equation for finding the effective radiating temperature and associated altitude and emissivity of OLR:
235 = (0.937*10^-5)*(5.667*10^-8)*T^6
From which T = 275K , altitude is 2km and emissivity = 0.7, (approx).
This implies a much smaller natural atmospheric effect than AGW calculates.
Amusingly, a surprisingly large number of things are mis-named. They were appropriately named hundreds of years ago, but time has changed any meaning.
Many people are in-appropriately named, having inherited their ancestors surname.
One can take literal interpretations far to far, to the point of policing naming conventions. The ‘greenhouse effect’ is absolutely appropriately named, because it follows the long human tradition of naming new things and keeping that name no matter what.
Any ‘conservative’ that likes keeping things as they are, should of course be defending the ‘greenhouse effect’ name to the hilt, because it is a part of a cultural tradition.
Scienceofdoom,
A well stated post. However, most scientific skeptics already agree with the model of the atmospheric greenhouse effect you show, so you are arguing against the small minority that will not be convinced no matter what you show.
Leonard Weinstein:
Thanks.
I know of course that most people with a science background understand that the greenhouse effect exists.
But I don’t think it’s fair to say that those who believe it doesn’t exist won’t be convinced no matter what.
For some that is true. For others – well, atmospheric physics can be a confusing subject – and presenting the basics in a different way can help crystallize the fact that this effect is real and easily measured.
I actually started the article with more advanced objectives, now delayed until part two.
[…] of our commenters asked what value the IPCC uses. The answer is they don’t use a value at all because they summarize […]
Once the ubiquitous but questionable black-body assumption is dropped, interesting things emerge.
Consider a body surrounded by a medium. In Doom’s model, heat flows to and from the body. For the body to be at constant temperature, the heat flowing into it must equal the heat flowing out of it. The heat flowing into the body equals the heat flowing out of the medium modified by the body’s absorptivity which, by Kirchoff’s law, is equal to its emissivity.
That is: e*T^4 (body) = e(body)*e(medium)*T^4 (medium) which simplifies to:
T^4 (body) = e*T^4 (medium)
In the general case (e T (body); that is, by radiative means, a body can reach temperature equilibrium only when surrounded by a warmer medium and the system (body and medium) can’t reach equilibrium -a contradiction of the 2nd law of thermodynamics. No such problem arises in an alternative model in which heat flows in just one direction. Doom’s model describes the special (and unreal) case of heat exchange between black bodies.
Switching focus to DLR in the K&T global energy balance – 278 Wm-2 for clear skies and 324 Wm-2 for cloudy ones – with 0.7 emissivity, atmospheric temperatures of 288K to 300K would be required, equal to or greater than the surface temperature. This temperature inversion, apparently not uncommon at night, implies that observed DLR represents heat transfer from a warmer region to a cooler one, in accordance with, not contrary to, the 2nd law of thermodynamics.
SOD, first-off, thanks for the awesome blog. For many months I drifted in despair across the internet hoping to find an island where classic physics still flourished. I thank you for preserving this island… you’ve made a grumpy old guy happy.
My question is this. I understand the upwelling radiation as viewed TOA should approximate a black body with notches for molecular vibrational absorption cut out of it. The figure you show from Goody supports this. However, the lamba max of the distribution indicates one is viewing a black body at something like -80degC, not the surface of the earth. Yes I’ve allowed for the fact the X axis is in wavenumbers not wavelength. Comments anybody?
However, the lamba max of the distribution indicates one is viewing a black body at something like -80degC, not the surface of the earth.
This is because it’s measured at the top of the atmosphere.
D.
David Reeve:
Thanks for the kind comments.
The first graph under “Radiation Through the Atmosphere” is of the earth’s surface and has the maximum energy at 10um. Wien’s law says that the maximum wavelength is at 2898/T = 2898/288 = 10.06um.
The second graph, as diessoli rightly says, is radiated by the atmosphere. In reality it is like a composition graph as different parts of the atmosphere have radiated from different heights.
This graph is a better one for illuminating it:
– and can be found in The Earth’s Energy Budget – Part Three.
The reason that the second graph is not just the first graph (under “Radiation Through the Atmosphere”) with “notches cut out” is because almost no surface radiation makes it to the top of atmosphere.
I’m OK with the fact we are viewing the TOA at some low temperature, but I’m not OK that a body of gas should look like a BB.
What does the radiative emission from a slab of atmosphere look like (forget for the moment what might or might not be behind the slab). I would have thought it would be dominated by the vibrational lines of CO2 and H20. The pressures and temperatures are too low for significant line broadening, so where does the apparent continuum component come from?
A further development of this argument is that given CO2 is a major radiative component, why is the approx. 15um band a notch in the emission envelope? Surely it should be a peak?
John Millett:
Not true.
Check out Planck, Stefan-Boltzmann, Kirchhoff and LTE.
Emissivity and absorptivity are wavelength dependent parameters. The energy the earth receives is from the sun with a central wavelength of 0.5μm. The energy absorbed is incident energy x absorptivity at 0.5μm.
(The absorptivity is 1-albedo).
The energy the earth radiates is with a central wavelength of 10μm. The energy the atmosphere radiates to space is with a central wavelength around 15μm.
Therefore, there is no reason for absorptivity (of energy received) to equal emissivity (of energy radiated). Because absorptivity at 0.5μm = emissivity at 0.5μm (Kirchhoff) but absorptivity at 0.5μm ≠ emissivity at 10μm.
At the moment I can’t make sense of the rest of your comment, but you might want to review it with this important point.
SoD
I may be reading too much into your remarks about the energy balance in an atmospheric layer but it does seem you are implying that the amount absorbed I(1-y) is equal to the sum of the amounts emitted by your two blue arrows.
This seems unlikely to me for two reasons. First the diagram does not show any incident radiation from above, a proportion of which will also be absorbed.
Secondly, I used Modtran to check the radiation into and out of an arbitary layer and found that it was actually showing a deficit rather than the surplus you initially mentioned.
Actually I did some calculations with Modtran to see if I could separate the absorbtion and emission within the layer but could only do so if I made two assumptions. One was that the upward emitted was equal to the downward emitted. I think this is reasonable for a thin layer. The other was that the percentage absorbed was the same for both up and down radiation. I suspect this is not so reasonable as the spectral composition is not the same.
Anyway, I look forward to the next installment.
Jorge:
You are correct there would be incident radiation from above. I am trying to keep the concept simple, but then of course, I make it too simple and confuse other readers like yourself.
The idea behind the “simplicity” was just to show that radiation in one direction would be absorbed but the layer must also emit radiation.
Here is the updated graphic:
Jorge:
I’m not clear on what exactly you found with Modtran.
Yes, because a “thin layer” will be isothermal (same temperature throughout).
The percentage absorbed at each wavelength for up and down radiation will be identical. But as you correctly point out, because the spectral composition is different the actual results will be different for upwards and downwards radiation.
John Millet,
That’s not how you calculate Teff.
So Teff for 278 W/m2 is 265 K and for 324 W/m2 is 275 K. Something like 90% of the radiation seen by the surface comes from within 500 m or less of the surface so the actual atmospheric temperature is very close to the surface temperature. The emissivity for the CO2 band and much of the water band is close to 1 as well. Total emission is lower because there are bands where emissivity is very low.
The 324 W/m2 is not for cloud covered sky. It’s the average for clear plus cloud covered sky. A completely cloud covered sky (ceiling 1 km or lower) emits almost exactly the same radiance as the surface because clouds have an emissivity in the thermal IR very close to 1 and a temperature very close to the surface temperature.
Thanks SoD
The simple thing I did with Modtran was to use a standard atmosphere and look at the layer between 5 km and 5.1 km.
Looking down from 5km gives the incident upward radiation and looking up from 5.1km gives the incident downward radiation. These are both entering the layer.
Looking up from 5km gives the remains of the downward incident radiation and part of the emitted radiation. Looking down from 5.1km shows the remains of the upward incident radiation and the rest of the emitted radiation. These are all leaving the layer.
The end result is that the amount leaving exceeds the amount entering by 0.754 W/m2. Effectively, this layer is emitting more energy than it is absorbing.
I really ought to check with more values for the thickness and at some extra levels to see how general this result is. In the meantime I´m going to speculate that this imbalance is made up by convection.
Jorge:
I think I see your problem and it is probably a common conceptual problem when someone starts thinking about atmospheric radiation. I have experienced it myself anyway.
The upward flux you see at 5km has no relationship to the downward flux at 5km. Well, “no relationship” is not strictly true but the relationship is only expressed as part of a massively complex equation..
Using Modtran the way you are will not tell you the difference between emitted and absorbed radiation.
What you need to do is look at the downward flux at 5km and at 5.1km and subtract the two, then look at the upward flux at 5km and 5.1km and subtract the two – the two numbers should be in balance.
Well, they would be if there were no convective flux, but that would be an unrealistic model and wouldn’t produce useful numbers.
In any case I used Modtran for a mid-latitude summer with the defaults:
Ground T, K = 294.20
Looking down 5.0km – Iout, W /m^2 = 333.782
Looking down 5.1km – Iout, W /m^2 = 332.526
Downward difference = 1.256
Looking up 5.0km – Iout, W /m^2 = 141.237
Looking up 5.1km – Iout, W /m^2 = 138.914
Upward difference = 2.323
So the radiation emerging at 100m above the 5km layer is reduced by 1.256 W/m^2, while the radiation emerging at the 5km layer has increased by 2.323 W/m^2 compared with the amount that entered 100m above.
The layer is not creating energy. Convection has brought energy into the layer from below.
In the interesting “thought experiment” of no convection the two values would be in balance, by definition (for steady state conditions). You can see the “grey atmosphere” solution in Vanishing Nets
David Reeve from December 28, 2010 at 9:59 am:
Take the 11μm wavelength. Not many absorbers at this wavelength. The earth’s surface emits radiation like this:
Radiation at 11μm has been emitted from the 288K surface and makes it (almost) unabsorbed out through the top of the atmosphere.
Now consider the 15μm wavelength. It is emitted from the 288K surface and almost immediately gets absorbed by the atmosphere. That layer of atmosphere also emits at 15μm but it is a little colder than the surface so the 15μm wavelength is at a slightly lower intensity. It keeps getting absorbed and re-emitted. Eventually the atmosphere is “optically thin” enough that the atmosphere emits 15μm radiation which actually escapes to space.
This 15μm radiation has been emitted from a very high level in the atmosphere which is very cold. So the intensity of the 15μm wavelength radiation is much lower than the 11μm radiation which was radiated from the surface and escapes almost unabsorbed.
Does this make sense?
If radiation is emitted from a 200K body it will be a lower intensity than from a 300K body. The more the atmosphere absorbs a given wavelength, the higher up the radiation which finally escapes to space has been emitted from – and so the lower the intensity.
Surely another interpretation of this graph is that the 15um wavelengths and any associated line broadening has been thermalised closer to the Earth surface and not reemitted.
Ah, that makes perfect sense. The apparent depth of “view” into the atmosphere, and thus temperature, is going to vary markedly with wavelength. I’ve spent too long looking at laboratory spectra :-).
However, this now makes me question the “fitting” of a BB emission curve to such an envelope. The exercise shown in Fig 2.9 above seems questionable when we have every reason to believe the temperature of the “body” is varying with wavelength on the X axis. Or am I getting this wrong…. certainly the lamda max of the curves don’t match the Wien Law.
David Reeve:
Take a look at The Amazing Case of “Back Radiation” – Part Two.
Here is a very dry cold atmosphere radiating:
This is the downward radiation from the atmosphere measured at the surface.
Here is a warm moist atmosphere radiating:
You can see in the first spectrum the various gases identified – CO2, O3, CH4, water vapor.
The second spectrum shows how water vapor emits (and absorbs) across almost the entire spectrum.
In any case, these are the measured atmospheric spectrum with no warm surface behind them.
Thanks for that. Fig 11 was what I was expecting, but I can see that if you looked down from the TOA, even the weakest emitters will be bolstered by the thickness of the sample and you are going to end up with a mass of lines, especially from H2O, right across the IR band.
I will read your “Amazing Case of ….” post and think for a while. Please keep up the good work.
SoD – Thanks again,
I think my way went straight to the total energy balance of the ins and outs from the layer. Your way separated the the up and down but the final result is the same. There is an energy deficit to be made up and it is nice to know my speculation about convection seems to be correct.
I don´t think it is really possible to calculate the values of absorptions within the layer and the emissions from the layer. The problem is that when looking down from 5.1km what you see is the remains (after absorption) of the upward incident radiation plus half the emitted radiation from the (thin) layer. When you do the subtraction there is no way to tell if there was a lot of absorption together with a lot of emission or less absorption and less emission. All we can view is the net effect.
I should make clear that I am sure Modtran knows what is going on as these details are part of its internal calculation but cannot be seen in the resulting look up/down values.
If one makes the assumptions that the up/down emissions from a thin layer are equal and both up and down are absorbed by the same percentage it is possible to find two simultaneous equations with emission and absorption as the two unknowns. Unfortunately if the up and down absorption factors are not equal we have three unknowns and, so far, I have been unable to find a third equation to resolve the quandary.
Jorge,
I think it’s pretty safe to assume that layer absorption does not depend on direction. However, I don’t think it’s safe to calculate a single value for the absorption for each layer. I think you have to do it separately for each frequency. The data are available by using the save text for later retrieval feature, but it would be a lot of work.
DeWitt Payne
I thought it would be interesting to attach some real numbers to the six arrows in the diagram that SoD provided. This would only have applied to a particular layer and would have shown values averaged over all wavelengths.
I tried the save text feature a while back. There was more information than I knew what to do with. I decided to wait until I was qualified to enter the extremely advanced Radiation 201 course!
Jorge,
You could do the calculations at SpectralCalc using a gas cell calculation with the pressure, temperature and composition for the altitude of interest specified by some atmospheric profile such as tropical or mid-latitude summer. But that would have even more information than MODTRAN because the resolution is much higher. You have to calculate emission at each frequency (cm-1), though, rather than trying to calculate an average absorptivity and plugging that into Stefan-Boltzmann. If you subscribe, SpectralCalc will do that for you, but you still have to split the spectral range into blocks because of limits on the total number of data points.
On further thought, I think you have to subscribe to get anything really useful out of SpectralCalc, but the subscription rates are quite reasonable.
DeWitt Payne,
My interest is with actual rather than effective temperature.
Your reference goes on to say “Effective temperature is often used as an estimate of a body’s temperature when the body’s emissivity curve (as a function of wavelength) is not known.”
My first comment introduced an emissivity curve for air, as a function of temperature, and calculated a radiating temperature and emissivity for the climate system of 275K and 0.7.
In the second part of the second comment, to which you kindly responded, I reasoned that with 0.7 emissivity, atmospheric temperatures exceeding the surface temperature would be necessary to generate the back-radiation in K&T’s energy budget. That offered the prospect of putting behind us the interminable argument about back-radiation violating the 2nd law of thermodynamics.
You point out that measured DLR comes predominantly from within 500 m of the surface where temperatures are not much less than at the surface, (and would likely be higher during night-time temperature inversion). This seems to me to offer the same prospect.
ScienceofDoom,
My abstruseness or your obfuscation? Whichever, I couldn’t discern in your response much of relevance to the issue I raised. I will recast it as a statement:
Your preferred model – two-way radiative energy exchange between, say, a body and its surrounding medium – holds true only for black-body radiation; it breaks down when emissivities less than unity are involved.
This can be seen at temperature equilibrium when the body’s energy gain must equal its energy loss. The gain is that part of the medium’s emission absorbed by the body; it is a function of the medium’s emissivity and the body’s absorptivity. At temperature equilibrium the two-way radiative exchange will exhibit a common wavelength spectrum and Kirchoff’s Law equating absorptivity and emissivity holds. Therefore, while the body’s energy gain is a function of its own emissivity and that of the medium, its energy loss is a function of just its own emissivity. Energy gain and loss do not cancel out and the body’s temperature is not stable, contrary to the stated condition.
The alternative model in which energy flows in just one direction, from hot to cold, doesn’t suffer this impediment. At equilibrium, energy gain = energy loss = 0.
“Of course, energy transfer can also take place via convection. So it is theoretically possible that energy could be absorbed as radiation and leave via convection. But that isn’t really possible all through the climate as convection would need to transfer energy from high up in the atmosphere to the surface, whereas in general, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.”
Evidence?
Evidence for which bit? That convection occurs? That convection doesn’t on average transfer energy downwards?
Evidence that it isn’t really possible for convection to transfer energy from high up in the atmosphere to the surface, because convection transfers energy in the other direction.
I split your statement into 3 parts:
1) But that isn’t really possible all through the climate
2) as convection would need to transfer energy from high up in the atmosphere to the surface,
3) whereas in general, convection transfers energy in the other direction
Your argument appears to be: 1 implies 2; 3 contradicts 2; therefore 1.
1 would only imply 2 if you interpret the statements locally. In some places energy must be transferred upwards, in other places downwards, so for convection to be a factor all through the climate it would sometimes have to locally transfer heat downwards.
3 only contradicts 2 if 3 is interpreted as a general principle, rather than a net “on average”. If it is impossible for convection to transfer a significant amount of heat downwards anywhere, then it contradicts the requirement in 2 for heat to transfer down in some places. But a statement about the average doesn’t obviously contradict a statement about the components that make it up.
That is at least how I interpreted your intention. But I don’t see why 3 interpreted as a general principle must be true. It’s certainly not true locally – fohn winds being one classic example of convection-driven winds conveying heat down the leeward slopes of mountains – but I accept that it might be true contingently in the Earth’s actual atmosphere on a larger scale. If so, what is the evidence?
Two obvious possibilities to investigate are the North African desert being hotter than the equator, and the polar winters. Do the Hadley and Polar cells carry heat from lower latitudes down to the surface, from which it is radiated?
Bryan from December 28, 2010 at 12:43 pm:
That is the process by which the absorption and re-emission takes place.
Suppose for example we only shone 15um wavelengths into a layer of atmosphere and all other wavelengths were blocked.
What would be emitted would be 15um, 10um (ozone), all of the water vapor lines, methane lines.
This is because CO2 absorbs the 15um radiation then shares this energy via collisions with the rest of the “local” atmosphere = thermalization. Then the various emitters radiate at their characteristic wavelengths.
Science of Doom
We appear to be almost in agreement here.
However if 15um radiation only, was incident on the colder atmosphere then Stephan Boltzmann statistics tell us that not much 15um radiation would be emitted after thermalisation.
Rather the radiation emitted would be predominantly of permitted wavelengths with longer wavelengths.
This is exactly in line with second law.
On each thermal interaction from higher to lower temperatures the radiation spectrum centre gets longer and longer in wavelength
John Millett:
Not true at all. Check out any heat transfer textbook which includes radiant heat transfer.
The blackbody radiation is simply the easiest example to begin with. All of the same maths applies when the emissivity is less than 1 as when the emissivity = 1. The results change but the method of calculation is the same.
I still don’t understand the rest of your comments.
Why don’t you provide a 2-body example in a closed system with two starting temperatures, the emissivity/absorptivity of each body (the same value across all wavelengths would make it easy to understand = grey body) – and explain what you think the final result is?
Or some other example which you think demonstrates the point you want to make.
David Reeve from December 29, 2010 at 11:11 am:
It’s just for illumination. It helps people see the temperature of the layer which is emitting at that wavelength. Well, strictly speaking it’s more of a “composite” of slightly different temperatures from different depths.
You are correct that “the temperature of the “body” is varying with wavelength on the X axis.”
Another term which causes confusion – the quoted “effective radiating temperature” of the atmosphere of 255K. This is simply the blackbody temperature that would emit 239W/m^2.
It’s more a shorthand – or convention. It doesn’t mean that the atmosphere is at 255K and radiating as a blackbody..
Nullius in Verba on December 29, 2010 at 8:58 pm:
That isn’t what I believe and I didn’t intend to imply that.
If, instead of “whereas in general, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.”
I say: “whereas on average, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.”
Does that clarify my viewpoint?
Surely, you agree?
The surface is hotter than the atmosphere – on average. Net heat moves from hotter to colder.
That clarifies part of it, but makes the logic of the rest of the statement more puzzling.
You said “So it is theoretically possible that energy could be absorbed as radiation and leave via convection.” This gives the impression of heat moving from surface to atmosphere – hotter to colder- by radiation, and then potentially from atmosphere to surface (and elsewhere in the atmosphere) by convection. You then disagree with this picture, saying it isn’t really possible because it would require heat to move downwards. But now you say that you meant it would have to move heat downwards on average. I don’t see how that implies the impossibility of heat moving from atmosphere to surface.
To put it another way, longwave radiation on average transfers heat upwards, but this does not prove it impossible that “energy could be absorbed as radiation and leave via [radiation]” to “transfer energy from high up in the atmosphere to the surface”. If you substitute “convection” for “radiation”, why does the average convective flow being upwards lead to a different conclusion to the average radiative flow being upwards?
Would it help if we called it advection instead?
On another site, someone asked:
The location is: the CERES website itself
Here is what the selection tool looks like:
Nullius in Verba
Yes.
Moist air rises in the tropics following (more or less) a moist adiabat with a relatively low lapse rate. The water condenses and precipitates. But air that goes up must come down somewhere else. When the dry air comes down, the lapse rate is higher so the temperature at the surface is higher, but not the heat content compared to moist air at the same temperature. The air flows along the surface and picks up moisture and goes around the cycle again But the system isn’t adiabatic. At high altitude, energy is lost by radiation so the air coming down isn’t as warm as it could have been and heat lost from the surface by evaporation is replaced by solar radiation.
This is similar to a katabatic wind like the Santa Ana in southern California. The foehn wind isn’t quite the same but has some similarity.
The dry air is also more transparent to LW IR so more radiation from the surface will be reach space directly.
Thanks. Yes, that’s helpful.
“When the dry air comes down, the lapse rate is higher so the temperature at the surface is higher, but not the heat content compared to moist air at the same temperature.”
Agreed. The way I would have interpreted it would be to say that the higher temperature at the surface was from the latent heat dumped into the atmosphere earlier when the water vapour condensed. If you count latent heat represented by the water vapour as part of the “heat content of moist air” then I agree.
But that’s a detail. It was the question of whether heat could ever be transported downwards that I was mainly interested in, and I think you’ve both answered/clarified that. Thank you.
It can if there’s a horizontal temperature gradient to provide the energy. Transporting energy against a temperature gradient requires doing work. It’s basically a heat pump. The driver for the atmospheric heat pump is the horizontal movement of air generated by the difference in temperature between low and high latitudes caused by the difference in insolation.
Nick Stokes has written about this at Moyhu:
http://moyhu.blogspot.com/2010/01/what-if-there-were-no-greenhouse-effect.html#more
http://moyhu.blogspot.com/2010/05/greenhouse-effect-and-adiabatic-lapse.html
http://moyhu.blogspot.com/2010/06/venus-models-and-adiabatic-pump.html
Then there were the Venus threads here…
Scienceofdoom December 29:
“Why don’t you provide a 2-body example in a closed system with two starting temperatures, the emissivity/absorptivity of each body (the same value across all wavelengths would make it easy to understand = grey body) – and explain what you think the final result is?”
Better late than never:
Apparatus: two gray bodies, at different temperatures and with different emissivities, in an enclosed vacuum.
The system moves energy from its initial “lumpy” distribution to a more even one at equilibrium, in a two-way radiation between hot and cold which doesn’t cease at equilibrium. The radiation exchange model is based on the Stefan-Boltzmann relation between energy flux and temperature:
F = rho.T^4 where
F = black-body energy flux Wm-2
T = absolute temperature K
rho = a constant
Let:
e = emissivity 0 < e < 1
a = absorptivity 0 < a < 1
and denote the cooler of the two bodies with the prime character (‘)
For the hotter of the two bodies:
Energy in = a* (e’F’)
Energy out = e* F
At equilibrium, Energy in = Energy out; Ts and Fs are equal all round; and, by Kirchoff’s Law, a = e.
Therefore: e* e’F = e*F which simplifies to e’ = 1.
Similarly, e = 1
That is, the model holds true only for black bodies.
I don’t think that answers the question.
If your bodies don’t have an internal energy source the equilibrium will be at T=0K (i.e. F=F’=0) , regardless of the starting point (assuming there is no cosmic background radiation). If at least one of them has one, the interesting point is what the equilibrium Temperatures will be, given the initial temperatures.
D.
[…] Part One I said: In the next part we will consider more advanced aspects of this […]
[…] […]
Diessoli January 23:
Thank you for your response; and apologies for the delay in mine.
T equil won’t be 0K. We need to consider how this system achieves radiative and thermal equilibrium simultaneously. My amateur reasoning goes as follows:
Energy balance (= energy in – energy out): for the warmer body = e*F (e’ – 1) < 0
That is, the body exports more energy than it imports; as, similarly, does the cooler body.
By design, no energy leaves the enclosed space. By the conservation law, energy balance within the system requires a photon gas to populate the enclosure. Or, said another way, the bodies generate radiative energy fields. This implies that the bodies are not engaged in mutual radiative exchange as modeled. Another implication is that the modeled vacuum is not a void: while matter can be withdrawn from the enclosed space, the energy field generated by the enclosing matter remains. This requires a modification to the model, recognising the temperature of the enclosing matter, T#, which it gives to the energy field it generates. By design, T# < T’.
So, what is the equilibrium temperature, T$?
Since both bodies export more energy than they import, they cool. Therefore, T$ T#; and T’ > T$ > T#.
That is, the equilibrium temperature lies between the initial temperatures of the enclosing matter and of the cooler of the two bodies.
Note that in this modified model, both bodies are energy sources and the energy field that surrounds them is the sink. What if, instead, we reverted to the mutual exchange model, substituting the enclosing matter for the cooler body? The original conclusion stands: the model holds only for black bodies. It seems that the ubiquitous energy field is an inherent element in a model of energy redistribution incorporating gray bodies.
What if, by design, T# > T’; the temperature of the enclosing matter and its generated energy field lies between those of the two bodies? Then the energy field is a sink for the warmer body and a source for the cooler one. As before, the warmer body exports more energy to the field than it imports from it and cools: T$ T’. The surrounding field imports from the warmer body and exports to the cooler one. Its energy balance and therefore temperature change is ambiguous in the absence of actual data. The best we can say is that
T > T$ > T’ , the equilibrium temperature lies between the initial temperatures of the two bodies.
Conclusion:
In a real world model, the enclosed space would contain both matter and an energy field, at a common temperature. Spontaneous energy redistribution within the system, from the designed initial “lumpy” state to uniform equilibrium state, would occur by all available means of energy transport: conduction, convection and radiation. Irrespective of the transport method, the direction of flow would be from the warmer region to the colder one, in accordance with the entropy law. If the body is warmer than the surrounding matter-and- energy medium it will export energy into the medium which will warm while the body cools; and vice versa. The notion of a spontaneous energy flow from cold to hot is tenable only in the idealised case of blackbodies.
What is the area under the curve for CO2 in your 288K graph? CO2 at 15 micro has small area I would think. So are you saying that a very small percent (area under the curve) of LW can cause the heating?
mkelly:
The area under the curve?
The value on the y-axis is W/m² per μm.
That means if we calculate the whole area under the curve (across all wavelengths) we get the total energy from a 288K surface.
I haven’t shown the whole curve but the summation (the integral) will be 390 W/m^2.
If we take the energy for 14.5-15.5μm? You can see on the graph that the value around 15μm is approx 18 W/m².μm so this means in a 1μm bandwidth we will have 18 W/m².
According to the excellent A First Course in Atmospheric Radiation by Grant Petty:
If we calculate the energy between 13.5-17μm from a 288K Planck curve it is 63 W/m².
Does this answer your question?
What would be the fraction of surface longwave emission that is reabsorbed by the CO2 in the atmosphere (ignoring other absorbers). Assume a temperature of 288 K
scienceofdoom said,
Isn’t the intensity of the absorption and emission of the 15 um CO2 band nearly independent of the amb_ient temperature? The energy absorbed or emitted is always exactly (or darn near) the same and the intensity would be a function of the molecule’s propensity (a time constant) to emit which is only loosely related to temperature – nothing near the temperature connection to Planck radiation.
Or maybe this is too far into the detailed mud for your article’s purpose, in which case I apologize. Or maybe this is addressed later, in which case I apologize again!
Rod B
The absorption is independent of temperature. Solution to this problem gives the Beer-Lambert law.
See under the heading Absorption of Radiation in Part Six.
The emission is not independent of temperature. Emission is given by Planck’s law multiplied by the emissivity.
Emissivity is wavelength dependent and the emissivity at a given wavelength is not a function of temperature.
But Planck’s law is very much a strong function of temperature.
See under the heading Emission in the same Part Six.
I would be interested in where you got the idea that emission is independent of temperature. It helps me to write better articles..
scienceofdoom, thanks for the reply.
I have to disagree — I think… A CO2 molecule emitting by relaxing a vibration energy mode will emit a photon at very near 15um or 2×10^13 Hz with 1.325×10^-20 joules of energy. That exact energy will be emitted every time a molecule relaxes no matter what the temperature of the CO2 bath is. The intensity, as in how many joules per second, of such emission will (I think…) be related to how often some CO2 molecule relaxes. (Though the intensity in watts per square meter raises some goofy questions…) That frequency of emission is loosely related to the temperature bath, but nowhere near a function of T^4 as with Planck.
I haven’t thought this through but it seems that a molecule with some charge distribution could release planck function energy of non-specific frequency by converting some of its unquantized translation energy. This would be more of a direct function of temperature. I suppose further that this might allow the discrete vibration energy to relax via internal energy transfer (ala equipartition), though not necessarily via photonic emission. Anything to this?
Something is amiss here; or I’m totally missing something.
Rod B:
Why do higher temperatures emit at a higher intensity and at shorter wavelengths?
It’s described by the Planck law but is what is observed in nature.
Following your explanation the observations are all wrong?
You are correct about the energy of a specific transition between 2 energy levels. But there is more to emission of radiation.
The specific energy levels are the reason why emissivity at a given wavelength does not change with temperature.
scienceofdoom, thanks again
Higher temperatures do emit at a higher intensity and at shorter wavelengths, though it might be helpful to be more precise in the wording: higher temperatures emit at a higher intensity over all wavelengths and emit peak intensity at shorter wavelengths per the Planck function. But this does not describe the process of photonic relaxation of internal energy levels of electrons, vibration or rotation. As I asserted in my previous post a relaxing vibration mode of CO2 emits at a wavelength of 15um no matter what the body temperature is. Double or halve the ambient temperature and the vibration emission of radiation energy will still be the same — 15um, whatever the equivalent Boltzmann distribution of molecular energy is.
A helpful example might be the spectral emission of Helium. Helium emits a strong spectral line at about 447nm whether it is from a bath of a five hundred degrees here in a lab or from a 5000 degree sun surface. Though it may be slightly stronger from the sun for other “propensity to emit” reasons, it won’t be any way near10^4 stronger and the wavelength won’t change a whit.
In general (ala Planck), I agree that the emissivity at a given wavelength does not change with temperature , but the emission does.
I’m just getting into your treatises and would still like to discuss this unless you think I’m getting ahead of myself and should wait a bit.
Great website and info.
One question (not a challenge, just looking for clarification). How much (if any) is the difference in total upward radiation due to the different total sperical surface areas at earth surface v. TOA? i.e. at TOA, the radius is slightly larger, so the surface area greater, and the total integral of W/m2 over the whole atmosphere will be greater than for the same W/m2 at the surface. I’d expect this is a small difference, but it would be good to know the magnitude. Many thanks.
Jim A:
The amount is tiny.
The radius of the earth = 6.36×106m.
Surface area = 4.pi.r2
So surface area of the earth = 5.08×1014m2.
The tropopause is about 10km above the surface of the earth, so the radius to the tropopause = 6.37×106m.
The surface area at the tropopause = 5.10×1014m2.
An increase of 0.3%.
And of course the earth isn’t a perfect sphere either but has no impact on the magnitude of the effect you are asking about.
Thanks. Makes perfect sense.
[…] […]
[…] reading – Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part One and New Theory Proves AGW […]
[…] – In Atmospheric Radiation and the “Greenhouse” Effect – Part One: […]
John Millet
If it is true that Methane is “23 times more active” than CO2 as a greenhouse gas in trapping the energy of radiation in the atmosphere, why is the notch on the blackbody curves shown so small in comparison to that of CO2?
The phrase “23 times more active” comes from the lexicon of scientivism. Take a look at “molar absorptivity” for something more scientific. Getting from there to the size of the notch in the black body curve is a solid piece of work, but nevertheless scientific. The “23 times more active” meme is hand-waving.
The effect of the CO2 15 μm band on atmospheric transmission to space of surface emission can be crudely approximated by assuming total opacity between 13.5 and 17μm, and total transparency outside these limits..
What would be the fraction of surface longwave emission that is reabsorbed by the CO2 in the atmosphere (ignoring other absorbers). Assume a temperature of 288 K
Anyone has the answer to that?
Sebastien,
Using your assumptions the answer is 16%.
The actual answer will be different because CO2 absorption across its band varies by several orders of magnitude – see Part Nine of this series, especially figure 13.
(That figure is drawn with wavenumber, for comparison, 13.5 μm = 740.7 cm-1 and 17 μm = 588.2 cm-1).
Thank you very much for your answer. However, how do you know it’s 16%.
I am actually getting asked to estimate the fraction of surface longwave emission on a graph that the max wavelength (T=288 K) is function of the fraction of total of blackbody emission.
Thanks again for your help!
It’s just an integral under the curve of the Planck function.
Integration across all wavenumbers and directions is the total flux (and = the Stefan Boltzmann equation).
Integration across the wavenumbers in question (and all directions) is the amount absorbed in your approximation.
The ratio is 16%. I did the integral numerically.
The calculation assumes that the emissivity of the earth’s surface is uniform with wavelength and direction. If we consider the ocean this is a very good assumption.
Sebastien: I hope that you realize that CO2 can’t “TRAP” energy in the atmosphere by absorbing all (or any fraction) of the radiation between 13.5 and 17 um. Yes, the excited state produced by absorbing a photon is collisional deactivated and becomes heat (thermalized). However, the reverse process – collisional excitation followed by emission of a 13.5 -17 um photon – also occurs. So the energy isn’t “trapped” anywhere, it is continuously absorbed and emitted. The amount of light absorbed depends on the intensity of the incoming radiation, while the amount of light emitted depends on the local temperature.
In FIgure 6.1 above, the depth of the trough between 13.5 and 17 um isn’t determined by absorption; it’s determined by the temperature where the atmosphere is thin enough for photons of this wavelength to escape to space. You can see a tiny spike in the center of the trough that arises from emission of photons by CO2 in the stratosphere (warmer than the tropopause) at the wavelength with the greatest cross-section.
Great Stuff if you are looking for atmospheric Check empireav.com
You are saying that at the TOA the energy emitted is measured as 239 wpsm and you calculate that at the surface it is 390 wpsm. TOA is 500 to 1000 km above the surface of the earth. The earth is 6,371 km in radius. The energy radiates out in all directions reducing in intensity inversely to the cube of the distance traveled. ie 6,371^3 / 7,371^3 = 0.65, 0.65 x 390 w/sqm = 251 w/sqm probably within Calculation + Measurement Error?
What height are they measuring the TOA energy levels?
For the purposes of radiation to space, the effective altitude is more like 5km. There is very, very little atmospheric radiation above 70km. According to MODTRAN, at 70km looking up, the downward radiation intensity is 0.051 W/m².
Inverse cube?? Since when? When you’re close enough that the emitter is a large fraction of the total solid angle viewed, it’s not even inverse square. At the limit of an infinite plane, the intensity does not vary at all with distance.
Regarding DeWitt
My apologies it is to the square, though at 70k looking straight at the sun I would doubt the 0.051 W/m²
So that makes the energy at TOA 291 wpsm Depends a lot on the height of the satellite measuring the outgoing energy. CERES was on Aqua (EOS PM-1) at an apogee of 702Km.
So if that is where the measurements came from then, the calculated intensity should be 316 wpsm and the loss is 77.4 wpsm, not 151 wpsm. That account for around 50% of the loss.
Cheers
Brian,
The so-called ‘effective’ radiating altitude doesn’t really matter. The bottom line is the whole combined surface/atmosphere system is passing about 240 W/m^2 into space. The total of the 240 W/m^2 has contributions from all levels, including the surface itself.
Brian the Engineer,
Sounds like you are assuming that the teams processing the satellite data are composed of idiots. I am pretty sure that assumption is wrong, I’m sue they understand that the flux per square meter depends on the radius of the surface in question and adjust to some conventional radius. Sounds like they use TOA, which they define as 20 km above the surface of the Earth. https://ceres.larc.nasa.gov/faq_main.php#ceres_toa
make that
So that makes the energy at TOA 316 wpsm
Brian the Engineer: Let’s consider the relative surface area of two spheres: 4*Pi*R^2 at the surface and 4*Pi*(R+h)^2 at a “TOA” with height h. The ratio of the larger area to the smaller area is 1+2h/R+(h/R)^2. The third term is negligible when h is a small fraction of R. R is 6371 km. So, if we assume the TOA is about 30 km, the increase in surface area due to the additional height is only about 1% (and the flux decrease due to the expanded surface area would also be about 1%). The flux decreases about 40% between the surface and the TOA. You would need to place the TOA about 40X further, for the expanded surface area to account for the drop in outgoing flux
So where is the TOA? One pragmatic definition might be above 99% of the atmosphere. Surface pressure is about 1000 m, so only 10% of the atmosphere is above 100 mb (16 km) and 1% of the atmosphere is above 10 mb (30 km). However, water vapor, a major GHG, is not evenly distributed. It’s saturation vapor pressure drops at higher altitudes where it is colder. So less than 10% and 1% of the GHGs in the atmosphere lie above 16 and 30 km.
You can calculate the drop in OLR with altitude using MODTRAN, a program that uses absorption coefficients for all of the GHGs in the atmosphere and temperature and humidity profiles for the atmosphere. Using the US Standard Atmosphere, OLR drops about 1 W/m2 (or 0.4%) between 30 km and 70 km. (Between those altitudes, we go from being above about 99% of the atmosphere to above about 99.99%. So OLR doesn’t change much above 30 km.
http://climatemodels.uchicago.edu/modtran/
You can try other altitudes, but you’ll find the situation is more complicated than implied above. OLR actually increases very slightly traveling upward through the stratosphere because the temperature (and therefore emission by GHGs) rises with altitude there. Nevertheless, most of the reduction in OLR occurs in the troposphere and the change above about 20 or 30 km is tiny.
Hi RW
The altitude matters 240 wpsm at a height of 2,000 m is four times the total energy if they measure 240 wpsm at a height of 1,000 m
Hi Mike M
I assume they are very smart and well credentialed but people make mistakes, you may remember the Hubble telescope. A simple conversion error to metric.
Apparently the level to calculate the outgoing energy from is 5 k above the surface. TOA is in other sources is 100 k above the surface, though perhaps the 20 k in the very interesting site you posted has its reasons and I like the ellipsoid description of the TOA. I shall do some more reading there.
Nevertheless the statement above is that CERES is measuring the energy and the orbit appears to be at 700 k above the surface. They mention that they calculate the surface temperature but don’t mention a correction to the CERES measurement.
Is there some reason they calculate the outgoing radiation at the surface rather than measure it directly? Put CERES in a balloon at a 5 k altitude perhaps. send it around the world and take an average as a check.
Hi Frank
I may have led you astray. My question is whether they adjusted the measurement of the outgoing radiation that was measured at +700k. Your calculation of 1% loss at 30k is correct but they are measuring it at 700 k and the loss there would be almost 19%
This is a passage from the dissertation above.
“The average for 2009 is 239 W/m². This average includes days, nights and weekends. The average can be converted to the total energy emitted from the climate system over a year like this:
Total energy radiated by the climate system into space in one year = 239 x number of seconds in a year x area of the earth in meters squared
= 239 x 60 x 60 x 24 x 365 x 4 x 3.14 x (6.37 x 10^6 )²
= 239 x 3.15 x 10^7 x 5.10 x 10^14
ETOA= 3.8 x 10^24 J”
WPSM x seconds in a non leap year x 4 x PI x Earths Radius squared.
Look closely and you see he is using the energy measured from
CERES =239 WPSM which is either at TOA +30 or 700k above the surface but he has used the radius at the Earth at the surface (6.37E6).
If WPSM is the measurement at +700 ETOA would be 4.74E+24 J including a quarter day for a leap year. So where it is measured is very important. I will keep checking.
I also agree that the systems are more complex than implied above, there is also convection sending hot air closer to TOA and the GHG’s also screen out some of the Sunlight EM on the way in as it is 50% + IR radiation.
Cheers
Brian the Engineer,
Sure, smart people make mistakes. They also cross check their work and catch their mistakes. Although these numbers are expressed as W/m^2, the fundamental quantity is total radiation out, integrated over the globe and averaged over time, since that must balance total radiation in, to within experimental uncertainty. If they did that calculation while making some silly error in the radius of the surface used, it would not balance and the error would have been caught. So we can be confident that any such error must be small enough to be lost in the measurement uncertainty. I think that uncertainty is less than 1%, so any error in radius must be no more than about 30 km. Given the fact that issues like the radius of the surface are integral to doing the calculations, I doubt that they have overlooked even such a small factor.
Mike M.,
“I think that uncertainty is less than 1%
Not that it’s of any major relevance, but I highly doubt that. Where are you getting this, BTW?
RW,
I should have checked. The number given by Stephens et al. is 239.7 +/- 3.3 W/m^2. That is a 90% confidence interval. It is 1.4%, so I stand corrected.
Reference: G. L. Stephens et al., “An update on Earth’s energy balance in light of the latest global observations”, Nature Geoscience, vol 5, 691-696, DOI: 10.1038/NGEO1580, 2012.
Is that based on the actual margin error of the measurement instruments themselves, or their aggregation of the values given by the measurements? That is an important distinction. Again, not that it’s of any major relevance, but I though the margin error of the measurements was like at least +/- 5% and probably more like 10%.
Do you have a link to the paper by chance?
RW wrote: “Is that based on the actual margin error of the measurement instruments themselves, or their aggregation of the values given by the measurements”
I don’t see why they would be different in this case. Some of the individual components have larger errors, but those come from uncertainties in disaggregating measurements of the total flux.
You should be able to find the paper just by putting the DOI into a search engine. One link I found just wants to start a download of the PDF.
Brian the Engineer,
Someone made a mistake once, somewhere, in another field (astronomy), therefore you are asking someone here to prove that no one in a different field (climate science) has made an elementary high school mistake in calculating the TOA outgoing longwave radiation (OLR) because they are unfamiliar with the inverse square law?
The actual measurement in the instrument is not some W/m2 value. That flux value is derived from the temperature of the detector. Maybe we need to prove to you that they measured that correctly, then calculated the correct value of flux from that? Maybe they had the wrong reference temperature? Maybe they pointed the satellite at the wrong planet? The list of possible mistakes is very long.
Consequently, the chances of someone doing everything right is vanishingly small. In fact, the only way they could possibly get the same value of OLR as the previous ERBE satellites, and the same value as the absorbed solar radiation is clearly that they fixed the answer to match..
Well, it’s been a long day. Forgive my random walk down assumption street.
Do you have some reason to pick on the lack of knowledge of the inverse square law in the field of satellite radiation measurements? There are lots of other formulas in this field, way more complicated.
You should comb through all the papers in the field, and the textbooks – and demonstrate the mistakes. Start with Clouds and Earths Radiant Energy System-CERES-An Earth Observing System Experiment, Wielicki et al (1998). Look up all the earlier papers referenced and all the subsequent papers that cite it. When you have finished present your results.
Of course, people always do make mistakes, just they are usually quite small in a field crowded with professionals. For example, check out Reexamination of the Observed Decadal Variability of the Earth Radiation Budget Using Altitude-Corrected ERBE/ERBS Nonscanner WFOV Data
Takmeng Wong et al (2006). One of the co-authors is Bruce Wielicki of the earlier paper.
Once you have read 10 papers in this specific field you will start to appreciate that they are professionals. Don’t take my word for it. We are skeptics here – test the ideas. But, alternatively, don’t arrive and confidently assume that the field of climate science is full of charlatans. Test your ideas.
If you don’t have access to these papers I will be happy to send them to you, just email me at scienceofdoom – you know what goes here – gmail.com.
A couple of books I recommend where you might appreciate that there are solid professionals in the field:
– Radiation & Climate, Vardavas & Taylor (2007) – F.W.Taylor is a professor of physics at Oxford University.
– A First Course in Atmospheric Radiation – Grant Petty (2006) – this is much much easier than Vardavas & Taylor and yet, you will see many pages explaining for novices, the inverse square law.
You can see the second reviewed in Find Stuff Out and Book Reviews along with some extracts of an earlier much cited work by Goody and Yung (Atmospheric Radiation: Theoretical Basis) that the excellent Vardavas and Taylor work improves on.
Brian the Engineer,
You can’t measure the outgoing radiation at the surface with a satellite.
The outgoing radiation is 4-100 μm (well we could write 4-50, there are diminishing returns as we go to longer wavelengths) but most of this radiation gets absorbed by the atmosphere.
So any satellite can only measure what the “climate system” radiates out. Of course lots of experiments have verified that the surface radiation follows the Stefan-Boltzmann equation, which is why we still find this equation in all heat transfer textbooks.
To calculate surface emitted radiation we only need to know the surface temperature and the emissivity (varies with temperature – it is a material property).
This is how it is easy to determine that the surface emitted radiation is around 390 W/m2 (globally, annually averaged)
And the OLR of the climate system is around 240 W/m2 (globally, annually averaged) – as measured by satellites.
And for surface emitted radiation, you can also read The Amazing Case of “Back Radiation” – Part Three, which shows some results (towards the end of the article) from The Energy Balance Experiment EBEX-2000. Part III: Behaviour and quality of the radiation measurements, Kohsiek et al, Boundary Layer Meteorology (2007).
Brian: Your question was confusing, so I spelled out the mathematics in a way that made it possible to quickly agree.
One explanation for this problem may lie in the definition of W/m^2 or WPSM as you call it. We might think of a “m^2” as the measure of solid angle extending from the center of the earth through an area 1 m^2 at the surface of the earth and continuing into space where the CERES and ERBE detectors orbit. If we think of a m^2 as a solid angle, the flux would not vary for geometric reasons involving height, but would change only because of absorption and emission. That would make 1 m^2 equal to 2.464E-14 steradian. The scientists working on this project are probably accustomed to analyzing everything in terms of solid angles and viewing angles.
That doesn’t mean scientists always get things right. IIRC, the raw satellite data shows the Earth emitting more energy than it receives. It should be cooling, not warming. The imbalance apparently is within the expected error of the instruments. The Earth’s radiative imbalance is assessed via the rate of ocean warming, not satellite data. One version of CERES data – EBAG? – has been corrected so that the imbalance agrees with ARGO (+0.5 W/m2).
Nic Lewis got his start on climate sensitivity by questioning Gregory Forster about some details in his papers. By the time the IPCC’s zeroeth order draft for AR5 reported a lower limit for the forcing from aerosols, Nic knew exactly what the implications were, including the smaller errors he found in Gregory’s papers and the re-analysis of Gregory’s work used in AR4. His name is now on two of the most important papers on climate sensitivity, Otto (2013) and Lewis and Curry (2014). However, I suspect Nic didn’t get his start by telling Forster that he was wrong!
On the other hand, I got my start here by trying to tell SOD how he was trying to mislead me. Now I find some of my early comments embarrassing. It is hard to be receptive if you aren’t listening. Fortunately, patient replies from SOD convinced me that we were both interested in exploring what was true (or not) about climate science.
So right now 390 W/m^2 is leaving the surface (~= the same as is entering the earth system?). And only 239 is leaving the earth system, the difference being retained.
I’m struggling to understand from the above why this would not result in indefinite warming even if GHGs were held constant. Contrary to the notion of an ECS.
Punksta,,
239 W/m2 is being absorbed by the climate system (see Earth’s Energy Budget), which matches the amount leaving the climate system. So the climate system is roughly in balance.
The reason why the upward radiation from the surface is higher than the outward radiation from the top of atmosphere is because terrestrial radiation gets absorbed in the atmosphere and emitted back to the surface.
The surface is also in balance, roughly speaking (globally annually averaged).
That is, as best as anyone can measure (and the earth is a big place), when you sum the upward radiation, sensible and latent heat (convection) it matches the downward radiation from the atmosphere. Really, it can’t be accurately measured as you can see when you look at papers like Earth’s Annual Global Mean Energy Budget, J. T. Kiehl and Kevin E. Trenberth, 1997 (or the updated version in 2009: Earth’s Global Energy Budget, Trenberth, John T. Fasullo, and Jeffrey Kiehl) – the sensible heat, which is the hardest to estimate, is calculated from the requirement for the conservation of energy at the surface.
Hope this helps. There are lots of article explaining this from different aspects.
I have a problem with the description of absorbed intensity of 239W and a surface emitting at a higher intensity, You (SOD) present a model that is basically saying that on planet earth 240W=390W without further explanation of how intensity can increase when the source intensity is constant.
Temperature doesn´t accumulate spontaneously over time, it is instantaneous. Energy stored in mass can accumulate according to heat capacity, but in that case temperature does not rise. It rises when the limit of heat capacity is reached. Or it is carried away, like water carries energy away from the surface when molecules break internal bonds and evaporate.
I´ve seen you use the equation for heat transfer, so you are familiar with it. But you seem unaware of the fact that a system like earth, that is heated by an external source of high intensity, and close to zero generation of heat internally, only subtract in all heat transfer happening within the system. Every transfer between molecules and atoms is a reduction of intensity in the process of transfer. I have seen that you use addition in the heat transfer equation within the system and that is unique for the energy balance you represent as explanation of surface temperature. There is no other model anywhere in litterature that does the same thing.Intensity only increase when received intensity increase. Nothing in the earth system has a higher intensity than the source of it´s own energy.
All systems displaying an increase in intensity in the process of heat transfer has an internal source of energy and a conductive shell, preventing all other modes of transfer but conduction leading to a temperature with following radiation of energy. If these parts are missing, increased intensity cannot happen. An atmosphere is not a conductive barrier and it does not limit the surface ability to radiate energy. A low density volume of mass at low temperature is an addition of radiating matter increasing the surface area that radiate to space. The difference in intensity cause energy to transfer from the warmer parts. A drop in intensity radiated from the atmosphere only cause more heat transfer without rising temperature.
And the most surprising misinterpretation of thermal energy transfer is seen in your description of how a cooler atmosphere forces the surface to heat up.
By only increasing absorption in the atmosphere when it gets heated by longwave radiation.A drop in intensity radiated from the atmosphere only cause more heat transfer without rising temperature. This is the most obvious part of heat transfer. High intensity in the absorber equals less transfer of heat.
Since you are familiar with heat transfer as a process happening at a rate equal to the difference in intensity, and you point to the fact that co2 increase absorption in the atmosphere, you should have noticed that a reduction of intensity in the atmosphere will result in an increased rate of transfer from the surface. In heat transfer, increased absorption when all other factors are constant, is equal to a reduction in temperature in the absorbing mass. And nothing more. When you say that the reduction in OLR is a mechanism forcing surface intensity to increase, you ignore the whole concept of heat transfer.
As absorption increase when reduction of intensity is observed in the colder receiving point of heat transfer as the single change in the relationship, that can only be caused by a reduction in temperature. The larger difference in temperature increase the rate of transfer in equal amount and the radiation to space is balanced instantaneously by more energy transfer to the atmosphere. If the emission of the troposphere decrease, an equal increase of transfer from the surface has already happened simultaneously.
The rate of transfer adds to the radiated energy from surface. So if the surface emits 400W/m^2, and the atmosphere emits 200W, there is 600W/m^2 of thermal energy flowing from the surface in total. But the energy in transfer doesn´t show until temperature rise in the atmosphere. And that doesn´t even have to happen if there is not enough input from the sun to cover a rising temperature. Which is exactly the situation we see.
Using the observed intensities, we see that the surface transfers energy to the atmosphere at a mean rate of ~150W/m^2. That is an addition of 150W to the radiated 390W. But it doesn´t show in any other way than the difference in intensity. If the surface use 390W itself to reach the observed intensity, and you add a layer of cool gas that is heated by surface emission to 240W, you need more energy. How can you have read any texts about heat transfer and still not grasp that an increase in volume or mass, or both, when the input of energy is constant, only can reduce the energy density as the same amount of energy is divided by increased mass and volume.? Increasing mass, even if it is a very small amount measured in ppm, is not adding energy available for heating, it does the opposite.
On top of that, you claim that adding mass in form of a molecule that is a powerful absorber of thermal energy, would increase temperature.
If something is absorbing at an increased rate, that means that available energy to heat something is lowered by an equal amount.
If you had paid attention to the litterature you refer to in relation to heat transfer, you would have noticed that temperature never increase when temperature drop. It is very simple, the reduction in intensity of OLR, is equal to increased absorption, increased absorption is equal to increased heat transfer into the absorber at the cost of thermal energy in it´s surroundings, and as the only change happening, it can only come from a reduction of temperature.
Where in the litterature do you find support for a claim that a reduction of intensity/temperature/energydensity can cause an increase in intensity/temperature/energydensity?
When clearing up the confused statements of how increased absorption leads to increased intensity without adding any energy to the system, the above is all that is left. Your argument boils down to nothing more than increased absorption in the part of the system with the lowest energydensity, and that can only be caused by a reduction of temperature in that exact part.
You cannot make a more precise contradiction of thermodynamic principles and the concept of heat transfer than claiming that a reduction of temperature cause an increase in temperature.
Your attitude towards objections trying to find support in the laws of thermodynamics for a model that use a dropping temperature as a cause of increasing temperature is an embarrasment that you have to live with, as it will stay on the internet forever.
For your own sake, try to find an example in experimental data or theory in the litterature describing heat transfer and thermal energy in general, where a cold gas heated by a source, increase intensity of it´s own source by being cold, and getting colder. If you want to be realistic, put the system in 3K vacuum, and don´t cheat with adding walls or insulation. Just a source of thermal energy with a skin of cold gas floating in vacuum of 3K. It is of course impossible to find that, but it is also impossible if the system sits on the surface of earth.
Good luck with that. Try to be open to the fact that your model lacks support in observation and is based only on a misunderstandning of effective temperature and a correlation with fluctuation of temperature which seems to be falling apart. This is all you have. I would never trust a model with so little support in data.
You know that effective temperature is a concept valid only for a blackbody with a totally even distribution of energy within, absorbing and emitting from an infinitely thin, perfectly black surface?
It is not valid for A surface. If used as a reference for surface temperature of a planet with an atmosphere it is of no use for understanding how the system is heated. Which you demonstrate very well when you claim that on earth the cold atmosphere can do this: 240W=390W.
The third,
You have written a long comment so I will start with the first point:
This is not correct.
Energy and temperature are related by heat capacity.
The formula, elementary and found in all physics and engineering textbooks (that cover the subject) –
ΔQ = cmΔT
where c = specific heat capacity, m = mass, ΔT = change in temperature and ΔQ = change in energy.
The only time energy can accumulate and not increase temperature is during a phase change (e.g. where the energy is being used to turn ice into water).
Are you disputing this formula? Or you have never seen it?
The third,
I picked up your first mistake (“Energy stored in mass can accumulate according to heat capacity, but in that case temperature does not rise”) – are you going to respond on that?
Is it a foundation?
Was it irrelevant?
I gave two links to read and respond to. Are you going to respond to those?
The third,
Other articles explain more about the basics of the inappropriately-named “greenhouse” effect for people having a conceptual issue with physics basics.
For example:
1. Do Trenberth and Kiehl understand the First Law of Thermodynamics? which gives a simple worked example of a source internally heated.
You can see from the comments all the conceptual problems commenters have with the result without ever being able to figure out what is wrong with that simple problem (there is nothing wrong with it).
Likewise, within the climate system, solar radiation is absorbed primarily at the earth’s surface because the atmosphere is mostly transparent to solar radiation. But the atmosphere is mostly opaque to terrestrial radiation, so the earth cools to space mostly from the atmosphere.
2. The Three Body Problem – a simple example with three bodies to demonstrate how a “with atmosphere” earth vs a “without atmosphere earth” will generate different equilibrium temperatures.
And many more under the heading: Confusion over the Basics.
I have read them all and I would not write this if there was an acceptable explanation of increasing intensity without adding energy. If we have an absorbed intensity of 240W/m^2, nothing inside the system have higher intensity without added work or a second source which must be above 240W/m^2. Every single watt above 240W has to come from a source with flux at least equal to the same intensity.flux cannot be piled on top of each other, If that was the case, enough rocks radiating at a temperature of 200K would equal the heat of the sun. But you know that regardles of the number of bodies radiating 200K the temperature will never rise above that intensity.
I ask very clearly that you present a reference to the mechanism behind circulation of energy in cold gas as the cause of increasing temperature.
While looking, a reference to circulation of energy in any form that is spontaneous would be of interest.
Opaque, that is a misleading way of describing how emitted heat decrease when propagating through air. What happens is that the energy loses potential when balancing high and low intensity. The gradient is showing how energy density is drained into lower density.
The term Opaque relates to how radiation dissapears from sight in varying degree. How can that be interpreted as anything else that the energy that is not observed in radiation, is not longer available?
A reference to a cold gas increasing the temperature of it´s heat source would also be nice.
A reference to the claim that absorption of radiation in co2 leads to emitted energy of equal intensity at the same temperature where energy is absorbed would be candy.
A reference to the claimed transfer of energy at intensity that is much higher than the observed temperature of the transferring gas would be very nice.
(like the energy budget where 300W or more is transferred from the atmosphere at a temperature mean -18C.)
A reference to the claim that photons independence of surrounding temperature when emitted can replace the equation of heat transfer when describing how energy transfers and heats a surface that is warmer would be awesome.
A reference to the logic of calculating effective temperature, and the difference to reality is cause of temperature rising without increase of energy.
Not a single one of all your sources include explanation of the above details that is of fundamental importance.
The assumption that observed absorption in a cold body is a cause of heating a warmer body is a big problem. Can you see why absorption in colder body cannot be assumed to cause an equal heating of a warmer body? And that absorption is a consequence of dropping temperature, not rising?
The third,
I think it would be helpful to conceptualize essentially three separate bodies involved: The Earth’s surface and below (but not including the heated core), the atmosphere, and the Sun (the main source of energy into the climate system). Nearly all of the absorbed stored solar energy in the system is located below the surface, primarily in the oceans. Only a tiny fraction (less than 0.1%) is contained within the atmosphere and almost all of that is in that of the linear kinetic energy of the N2 and O2 in the atmosphere, which have an emissivity near zero and by and large don’t even emit radiation.
The GHE is a *radiatively* induced effect, and the wavelength spectrum emitted by the surface is largely opaque through the atmosphere due to GHGs and is mostly ‘blocked’ from passing into space. The atmospheric absorbed surface emitted IR energy is henceforth re-radiated both up and down, i.e. some back towards the surface, where it’s re-absorbed at a lower point (with perhaps some passing all the way back to the surface) and subsequently re-radiated again and again, etc. This slows down the rate of radiative cooling by IR emission up towards space. The slow down of radiative cooling requires or forces the lower atmosphere and ultimately the surface to be emitting at higher rates than the 240 W/m^2 being passed into space, in order for the surface and the whole of the atmosphere to be ‘pushing through’ the required 240 W/m^2 of absorbed solar energy back out to space.
The fact that IR radiation is the dominant way energy flows downwards towards the surface should make this easy to conceptualize. In fact, as a rough approximation the atmosphere as a whole passes more radiation to the surface than is absorbed into the system by the Sun! So again, this should not be hard to see. There’s no net conductive flow of energy towards the surface, and thus no violation of basic physical laws or concepts.
So is the calculation of the PVC sphere correct or incorrect?
The third,
“Every single watt above 240W has to come from a source with flux at least equal to the same intensity.flux cannot be piled on top of each other,”
The proper way to think of COE is really just conservation of joules (radiant absorbed joules in this case), independent of manifested flux density at any one particular location, like at the surface of the Earth. There are not any joules created from nothing if the surface is gaining a net flux of about 390 W/m^2 while 240 W/m^2 is being passed, i.e. radiated back into space to offset the 240 W/m^2 absorbed radiation from the Sun. It just means that 390 W/m^2 is the rate of joule accumulation at the surface in conjunction with all of the physics, radiant and non-radiant, required to achieve that equilibrium.
“The percentage absorbed at each wavelength for up and down radiation will be identical. But as you correctly point out, because the spectral composition is different the actual results will be different for upwards and downwards radiation.”
“The spectral composition” is of unclear importance until observation says otherwise.
We can limit the process to intensity of thermal radiation. There is no reason to account for the smallest fluctuation in OLR, or how the cold of the atmosphere heats earth by dropping 1W of intensity, First we need relationship between intensities in real time.If we assume that regardless of instantaneous propagation of energy in relation to temperature in the same spot., Assuming the fluctuation of 1W is the expression of threatening increase of intensity, explained by circulation of energy without loss, is a bit hysterical.
That is an argument about how a perpetuum mobile acts as a big force. Energy emitted in the past has done all work possible at that point in spacetime. As soon as it is lost from the surface, it is compensated instantaneously on the side irradiated by the sun.
Do you know of any technology that has a low intensity input and a higher intensity output, without an extra source of energy and decreasing total energy emitted. . If the temperature increase intensity to the fourth power in watts, how can the atmospheres 240W added to the suns energy density, make the intensity increase?
When adding 240W of energy density to the same area as irradiated, the density gets lower.
If temperature is increased when combining the atmosphere and surface energydensity, it is not a correct model of the state of matter in relation to change in temperature.
A mean temperature of 390W/m^2 mixed with an 240W intensity at low frequency in the same surface, has a potential 1/3 less than the surface alone.
How can we inhabit the higher states needed to reach a fluxdensity of 390W, if atmosphere radiation added to sunlight result in lower total energy. Only higher intensity radiation provide the needed density of higher states for a temperature of 390W.
At all times we can be sure of the relationship between varying intensities in a field to always be a transfer of all relevant energy towards lower intensity. and receive from higher intensity. It is exclusively a one way process.
Give me just a single example of increasing temperature when adding radiation with a distribution of energy much less probable to have the same densiity of higher states needed at a certain temperature.
That is the mechanism behind the laws of thermodynamics. Energy density is a state of energy moving in direction of lower density.
That absence of transfer towards lower temperature can result in higher intensity of emission is a situation of “not cooling” compared to heating, and is not what is claimed in GHE, The opposite, increased absorption and rate of transfer is the proposed cause.Using absorption in the opposite way of how increased absorption otherwise only accounts for cooling of surroundings.
Again, show an example where absorption increase in relation to the source that is constant, and that it leads to increasing temperature in the whole system.
Show an example of anything with a trend of rising temperature, without adding a heat source of higher intensity. Focus on avoiding to think about blankets or insulated houses, or how to build a trap for radiation out of air, or how to slow down radiation from the surface with really cold air causing the speed of light to slow down.
Explain what happens when 240W/m^2 becomes 390W/m^2 at the surface by circulation of energy in cold air, that should convince me of it´s superior logic compared to being sceptic and assuming that the source of high intensity radiation is the only source of heat potential that can raise temperature.
It is truly the “ether” of science today. It is literally made of air instead of thermal energy as an explanation of temperature.
You can also read A Challenge for Bryan – where a fellow traveller like yourself was asked to make a basic energy calculation that relates to the “greenhouse” effect.
See what you think.
Most people with conceptual problems on the “greenhouse” effect are able to write long comments but unable to write a few equations.
As with the PVC sphere in Do Trenberth and Kiehl understand the First Law of Thermodynamics?, let’s see your answer.
Is the worked example correct or incorrect?
Students of cognitive dissonance will enjoy your explanation.
The third: One point you make repeatedly is summarized by this sentence you wrote:
“Intensity only increase[s] when received intensity increase[s]. Nothing in the earth system has a higher intensity than the source of it´s own energy.”
However, the dark side of the earth continues to radiate to space almost as much thermal infrared power during night as during the day – despite the fact that there is no incoming solar radiation. The north pole has been in total darkness for two months, but continues to radiate thermal infrared to space and will continue to do so for another four months of darkness. Averaged over a whole year, polar regions radiate more energy to space than they receive from the sun. Clearly your principle that “intensity out” depends on “intensity in” is fundamentally incorrect in some situations. Conservation of energy does not demand conservation of radiation.
The fundamental principle that does apply is that the energy radiated away by any object *usually* depends ONLY on its temperature – not how much radiation it receives. Both the dark and sunlit parts of the planet’s surface and atmosphere radiate thermal infrared at a rate that depends on their local temperature, not how much sunlight they receive. Temperature changes when ALL incoming energy (not just the radiative flux from a warmer source**) and ALL outgoing energy are not in balance.
How does a molecule on the surface or in the atmosphere (ie a GHG) know how often to emit thermal infrared photons? Many people mistakenly think that molecules only emit a photon after they absorb a photon. The truth is that few molecules on Earth emit a photon immediately after they have been excited by absorbing a photon. Excited states are usually “relaxed” (or thermalized) by molecular collisions much faster than they emit a photon. And vibrational excited states in GHGs are created much faster by collision than by absorbing a thermal infrared photon. Collisions transfer kinetic energy, which is related to temperature. When the number of excited states (and therefore emission of photons) is controlled by temperature (rather than the local radiation field), then we say that local thermodynamic equilibrium (LTE) exists. LTE exists in the troposphere and lower stratosphere and on the surface. See Grant Petty, A First Course in Atmospheric Radiation, p 126-7 (a paperback which is relatively cheap).
*Usually* has stars because a few devices – LEDs, fluorescent lights and lasers, for example – are not in LTE and emit far more radiation that expected for their temperature.
** Before you bring up the 2LoT, I’ll note that it only applies to heat flux between groups of colliding molecules large enough BE hot or cold – to have a mean kinetic energy that doesn’t fluctuate with each collision – to have a temperature. The 2LoT applies to the NET flux of photons (heat) exchanged between large groups of molecules, but doesn’t apply to individual photons traveling between two molecules. Individual molecules and photons obey the laws of quantum mechanics and large groups of such molecules obey the laws of thermodynamics.
Of course, energy transfer can also take place via convection. So it is theoretically possible that energy could be absorbed as radiation and leave via convection. But that isn’t really possible all through the climate as convection would need to transfer energy from high up in the atmosphere to the surface, whereas in general, convection transfers energy in the other direction – from the surface to higher up in the atmosphere.
That is from the introduction by the author.
Why does convection have to transfer energy from the top of the atmosphere to the surface?
Very interesting presentation. Could you tell me why the TOA longwave flux for 2009 shows 8 Watts per square meter higher values in August than in January? I looked up the perihelion (closest earth approach to the sun) occurred January 4 and the aphelion occurred July 4. TOA incoming solar average during perihelion is 24 Watts per square meter higher than during aphelion. Plus this is 6-7 months out of phase relative to the outgoing TOA longwave flux. If the difference is due to the increased land area in the northern hemisphere and summer land surfaces emit more IR than summer water surfaces, then the average TOA IR flux over water is 228 W/sq-m and the flux over land is 268 W/sq-m, but this doesn’t explain why it is out of phase with the incoming solar short wave flux. Any explanation?
The simple answer is heat capacity. An increase in incident radiation does not cause an immediate increase in surface temperature to the steady state value. It’s much like adding capacitance to an electronic circuit. It produces a phase shift in the response. For frequencies much higher than the cutoff frequency, the phase shift is 90 degrees or 3 months. The cutoff frequency for the oceans is probably measured in centuries^-1.
Terry: As DeWitt mentions, the heat capacity of the NH is about half of that of the SH (which has more ocean, strong winds and a deeper mixed layer). Thus the amplitude of seasonal warming in the NH is about twice that of seasonal warming in the SH. THe net result is that GMST (without anomalies) is 3.5 K warmer in July than in January. That produces the 8 W/m2 increase in OLR in July, something that occurs regularly every year.
That means that the LWR climate feedback parameter is 2.3 W/m2/K, consistent a combined WV+LR feedback of about 1 W/m2/K and no LWR cloud feedback. The seasonal change in LWR is very linear with GMST, but seasonal change in reflected SWR is less linear.
Isn’t the internet wonderful. Anybody can produce articles like this that look like science to the uneducated but are in fact complete rubbish. And this is just one page of seven.
For what it’s worth, there’s a numerical approximation to the problem of how much energy is radiated between zero and lambda, called “D,” and the fraction between two wavelengths is then D2 – D1. Here it is as a Fortran-95 function:
! DD finds the Planck radiation fraction from 0 to lambda.
real(dbl) function DD(lambda, T)
implicit none
real(dbl), parameter :: c2 = 14387.77d0
real(dbl), parameter :: pi = 3.141592653589793d0
real(dbl), parameter :: k = 15d0 / (pi * pi * pi * pi)
real(dbl), intent(in) :: lambda, T
integer :: m
real(dbl) :: f, q, sum, term1, term2
real(dbl) :: lastSum, eps
lastSum = -1d0
m = 0
q = c2 / (lambda * T)
sum = 1d-18
do
m = m + 1
f = m * q
term1 = exp(-f) / (m * m * m * m)
term2 = f * (f * (f + 3d0) + 6d0) + 6d0
sum = sum + term1 * term2
eps = abs(sum – lastSum) / sum
if (eps .lt. 1d-6) exit
lastSum = sum
end do
DD = k * sum
end function DD
-BPL