Introduction
This is the long-promised eighth part of the seven-part series on CO2 basics. Part One introduced the idea of CO2 with some basic concepts. Part Three opened up the radiative transfer equations, not solvable on the pocket calculator. Part Five showed two important solutions. And Part Seven showed the current best solutions along with what “radiative forcing” actually means, and where the IPCC logarithmic formula comes from.
The even numbers in the series shouldn’t be ignored either, especially Part Four which explained band models vs line by line (LBL) calculations.
Now the concept of “saturation” is one that everyone wants an answer to. Saturation, however, means different things to different people. Consider shining a torch through sand. Once you have a few millimeters thickness of sand, no light gets through. So adding a meter of sand won’t make any difference. That’s how most people are thinking about saturation and that is the perspective that we will look at in this article:
- For CO2 – will doubling CO2 (from pre-industrial) levels add any more warming?
- And will doubling it again add any more?
The answer already noted in earlier parts of this series is “yes”, but of course, everyone wants to know why, or what this means for the idea of “saturation”.
Boringly, we will first look at some results from the radiative transfer equations.
The RTE
The RTE were introduced in Part Three – these are the full solution to the problem of absorption and emission by each “layer” of the atmosphere. The equations are challenging to solve because every absorption line for each gas has to be calculated, and a similar process goes on for emission of radiation by each layer in the atmosphere. It’s not some kind of mystery, it’s just very computationally expensive, so big computers and plenty of time are required. See Part Six for an example of theory matched up with measurement.
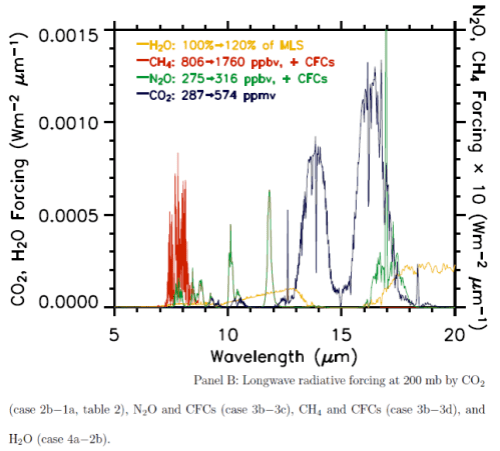
A fairly recent model inter-comparison effort was done which included the results from LBL (line by line spectra) for increases in CO2 and other trace gases. The inter-comparison focused on comparing the results from many GCM’s with the LBL results (see note 1). Although it wasn’t the focus of the paper, a graph of radiative forcing vs wavelength was included:
This is from W.D. Collins (2006), reference below. (Interested students will note that the vertical axis appears to have the wrong units, I have emailed Prof Collins to ask about this – update, he has confirmed that the vertical axis is incorrect).
The blue line is the “radiative forcing” vs wavelength for CO2.
The best way to explain why something called radiative forcing is used is that is a “standardization tool”. A simple explanation of radiative forcing is that it is the extra downward radiation at the tropopause before feedbacks from the surface and the lower atmosphere (the troposphere). You can see a little more on this concept in Part Seven.
Now that’s over with – check out the graph. Red is a methane increase from pre-industrial levels to current levels, green is a nitrous oxide increase and yellow is the effect of a possible increase in water vapor. The important point is that for the increases for CO2 (blue), most of the increase in energy is not in the center of the 15μm CO2 band.
It is interesting to see that the effect of the center of the CO2 band is not zero, although it is very low, but the main increase is in “the wings” of the band. This is the primary reason why doubling CO2 provides a significant increase in “radiative forcing” – or more heat into the surface and lower atmosphere.
To demonstrate this result wrong simply requires the interested student to prove the RTE (radiative transfer equations) wrong, or the line by line database of absorption for CO2 wrong, or the particular methods of solving the RTE in these models wrong. So it could all be over here.. but of course there’s more to think about.
By the way, the line by line method uses each individual absorption line stored in a huge database (like HITRANS), but the story is yet more complicated because each line has a definite width and a line shape, and these factors depend on the pressure and temperature. For example, each CO2 line is broader closer to the surface than it is high up in the troposphere. And the shape also changes. More on this at some later date, maybe..
Some Conceptual Ideas – Absorption and Re-emission and Planck Blackbody Radiation
Everyone likes to understand a subject conceptually. This is sometimes difficult but these mental models are very helpful if they can provide us with understanding. However, it is important to remember that just because something seems “conceptually right” doesn’t mean it is, and vice-versa. In the end, a theory stands or falls on the ability to falsify it and not on our ability to “picture it”. (The popularity of a theory on the other hand..)
The most important conceptual idea to understand is that the radiation from the surface which is absorbed by CO2 doesn’t just disappear. (The same applies to all “greenhouse” gases but I’ll stay with using CO2 as the prime example).
We will consider the atmosphere in a number of vertical “layers”, stacked one on top of the other. CO2 absorbs energy, shares it with other molecules in the atmosphere and therefore that layer of the atmosphere heats up (see note 2). Some molecules, like nitrogen and oxygen, have no ability to absorb or emit longwave radiation (see CO2 – Part Two), but by collision with molecules like CO2 and water vapor they will share energy and be at the same temperature.
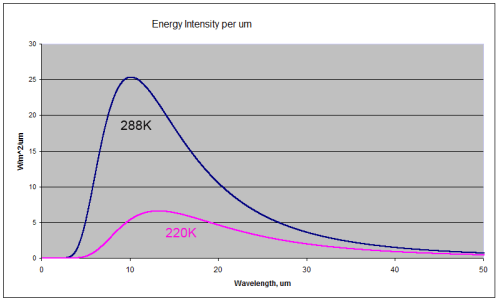
For those new to the basics of radiation, here are two comparison radiation curves for a blackbody at the typical temperature of the earth’s surface (288K or 15ºC) and at a typical temperature at the top of the troposphere
(220K or -53ºC).
You can see that the radiation emitted by a 288K body is a lot higher than the 220K body (the total integrated across all wavelengths is greater by a factor of 3). You can also see that for the colder body the energy has shifted to longer wavelengths (the wavelength of maximum radiance has moved from 10.1μm for 288K to 13.2μm for 220K).
A blackbody is a perfect radiator and absorber – so think of these curves as the ideal – the best that might be attained.
The surface of the earth is very close to a blackbody (the emissivity is close to 1) for longwave radiation – see The Dull Case of Emissivity and Average Temperatures. The atmosphere is not even close to being a blackbody. Atmospheric gases absorb and emit radiation at well-defined spectral lines. But the Planck function – as the curves above are called – tells us the “shape” that these spectral lines fit under.
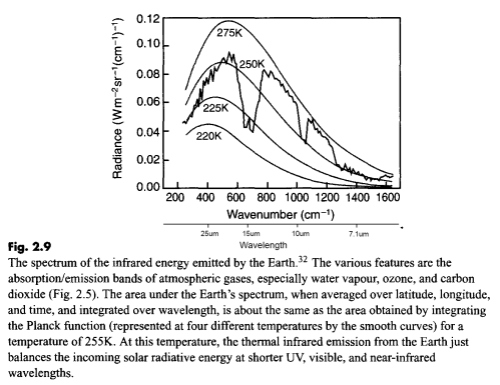
Here is a measurement of outgoing longwave radiation by satellite (the “upward” radiation) with the Planck function for different temperatures overlaid:
I’ve added “wavelength” under “wavenumber” on the horizontal axis for convenience.
What this shows is the effective temperature of radiation for each part of the longwave spectrum. Take a look at the spectrum between 10-13μm. The radiation between these wavelengths corresponds to around 270K. Now look at the spectrum between 14-16μm. The radiation here corresponds to around 223K.
That’s because there is not much absorption by the atmosphere in the 10-13μm spectrum, consequently most of the radiation from the surface goes straight out to space.
By comparison, absorption is very high between 14-16μm so almost no radiation from the surface goes straight out to space.
But – and here is the conceptual idea I want to get across – why is there any radiation between 14-16μm (measured by satellite)? Absorption by CO2 in the center of the 15um band is so strong that surely there should be no radiation – or nothing measurable..
This subject was covered in some detail in The Earth’s Energy Budget – Part Three, but essentially each layer of the atmosphere also radiates energy. If CO2 can absorb radiation at 15μm, it can also radiate at 15um. But it radiates according to its temperature. So when you see the measurement by satellite of the 15μm band reflecting a temperature of 223K you know that the bulk of the radiation was emitted by CO2 at a temperature of 223K (-50ºC).
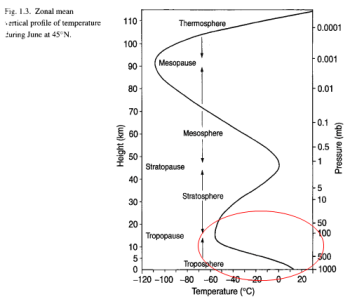
For the temperature of CO2 to be 223K (-50ºC) means that it must be located around the top of the troposphere:
How does all of this relate to “saturation”?
One Conceptual Saturation Idea – it Can’t Get any Colder
One way of thinking about the absorption and re-emission of 15μm radiation is like this – if the 15μm band is already radiating from the coldest part of the atmosphere, then increasing CO2 will have no effect on the earth’s energy balance because even if the 15μm band radiates from higher up, it won’t get any colder and, therefore, the amount of radiation at this wavelength won’t be decreased.
But this is just in the center of the 15μm band. As we saw from the detailed line by line calculation in the paper by Collins, the bulk of the reduction in outgoing radiation is from 13-14.5μm and from 15.5-17μm.
You can play around with these ideas by using the Modtran model. It uses band models (not line by line calculations) but band models give reasonable results. What is interesting is to increase the amount of CO2 and (looking down from 70km) see what effect takes place at 15μm – not much in the center of the band – for the reasons already explained: the atmosphere doesn’t get any colder.
However, you will notice that the width of this heavily saturated band increases – as with the more accurate treatment by Collins at the beginning of the article.
Another Conceptual Saturation Idea – the Two Slab Model
There is a simple model which is worth looking at by Barton Paul Levenson. What it demonstrates is that if you take a gas which absorbs across all longwave (>4μm) wavelengths, then even if this gas totally absorbs all radiation in the lower part of the atmosphere, adding more of this gas will still increase the surface temperature.
This is for the simple reason that the incoming solar energy at the top of the atmosphere must be balanced by energy leaving from the top of the atmosphere – otherwise temperature will increase (see The Earth’s Energy Budget – Part Two). And if one “layer” of the atmosphere totally absorbs it will still radiate energy to the atmosphere above. As the atmosphere gets thinner it will eventually be radiating out to space – and it’s at these levels (heights) in the atmosphere that adding more CO2 will reduce the outgoing radiation.
And if the outgoing radiation is reduced then there will be more incoming solar radiation than outgoing longwave radiation and the surface/atmosphere will heat up. Take a look at his model.
Fascinating as it is, I don’t think it answers the question of “saturation” or not by CO2 in the actual climate.
The reasons are complex, but read on if you are interested..
This is because the center of the CO2 band (15μm) is already radiating from the coldest part of the atmosphere. Therefore, increasing CO2 can’t reduce the radiation from the 15um band – unless more CO2 can change the temperature structure by lifting the height of the tropopause which will result in a colder tropopause.
In a climate with a “gray” absorber (one that absorbs equally across all wavelengths) an increase in this absorber would almost certainly change the tropopause height. Why? The tropopause is the point at which the atmosphere becomes optically thin and so radiation to space can take place from that point. Radiation is now more effective than convection at moving heat upwards through the atmosphere. So a climate model (even a more refined one with many layers) with a gray absorber will do as Levenson’s model predicts.
But a climate model with an almost transparent atmosphere in places will respond in less clear ways. Modeling the height and temperature of the tropopause is a difficult challenge and not something to get into here.
For those new to this topic, it probably doesn’t make a lot of sense. Think of this section as a “by the way an interesting idea about saturation..”
Conclusion
Most of the confusion about “saturation” of CO2 comes from a lack of understanding of how both absorption and re-emission are linked in the atmosphere.
The confusion also arises because atmospheric physics uses the term “saturation” to mean something more technically defined – that the atmosphere is “optically thick” at that wavelength. Two groups of people using the same word with a different (but related) meaning inevitably leads to confusion.
The radiative transfer equations are the basic and proven equations for the absorption and radiation of energy in the atmosphere. Solving these equations using line by line calculations shows that most of the additional effect from more CO2 occurs in the “wings” of the band and not in the band center.
Doubling CO2 from pre-industrial levels will lead to an increased “radiative forcing” of around 3.7 W/m2, and this part of climate science at least, is well understood.
Demonstrating that this result is wrong requires over-turning the radiative-convective model which currently calculates outgoing longwave radiation (at top of atmosphere) and downward longwave radiation (at the surface) quite accurately compared with measurements.
The mental models that many people have about saturation are not necessarily what is actually happening in the atmosphere.
Notes
Note 1 – The specific conditions for this inter-comparison (by Collins et al) were slightly different from the standardized method of “radiative forcing” in that they didn’t include stratospheric adjustment – allowing the stratospheric temperatures to achieve equilibrium after the changes in trace gases. This has a small but significant effect on the overall total values of radiative forcing, but the results are useful because the graph of radiative forcing against wavelength is given, whereas most results are simply given as a W/m2 value.
Note 2 – The subject of molecules of CO2 and water vapor absorbing energy and sharing this energy by collision with other molecules close by was covered to a limited extent in How Much Work Can One Molecule Do?
References
Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the IPCC AR4, W.D. Collins et al, Journal of Geophysical Research (2006)
Elementary Climate Physics, F.W. Taylor (2005) Oxford University Press


This posting will be given careful and detailed
attention when I can find the time. Clearly
considerable effort has gone into it and it
therefore deserves some real study time. On
my first reading, however, I have to comment that it seems to speak for the basic position that the IPCC has taken
on CO2, and to maybe be a bit weak in the understanding
of basic statistical thermodynamics and in the
understanding of complex system theory.
The author of this post seems to take the position,
prevalent in much of the climate debate,
that climate science starts from the bottom,
with such matters as the details of CO2 transmission curves,
and works up. The contrary position, that
climate science starts from the top, with the basics
of thermodynamics and complexity theory, and works
down, is increasingly well represented by recent papers.
Here is a good one:
Click to access miskolczi_extended_24-03-10.pdf
Note in particular the remarks that, as long as
there are sufficient degrees of freedom, the climate
will be constrained by fundamental thermodynamics
and complexity theory to satisfy
2 = t + ( exp (-t) )
where “t” stands for the average global optical depth of the
atmosphere. The details of how the atmosphere
reaches the correct entropy level which the above
equation bespeaks are not important.
In particular, the exact details of the transmission structure
of CO2 do not matter; the thermodynamic
balance, which both the math and more recent
data assert, requires that the atmosphere
compensates nearly fully for changes in CO2.
The paper which I referenced above is one of many
recent papers which assert that the climate is in a state of homeostasis.
The paper I have cited asserts that, because it has sufficient degrees of freedom to do so, the atmosphere adjusts itself via negative feedback loops so as to almost
totally neutralize CO2 changes. The more recent
experiments on atmospheric feedback loops,
showing negative feedback to CO2 changes,
also seem to agree.
I did a similar forcing graph using MODTRAN for 287-574 ppmv CO2 using the 1976 standard atmosphere and a viewing height of 12 km (as close to 200 hPa as I could get. MODTRAN has the short wavelength side of the CO2 band larger than the long wavelength side. Did the article note which atmospheric temperature profile and what surface temperature was used for the calculation? Is there a free copy on line somewhere? Archer MODTRAN is only version 3, so that may explain some or all of the difference.
My guess is that the units are W/m2 /nanometer, not micrometer
The MODTRAN units depend on which output file and which column of that file you use. . My version (4.0) outputs MODOUT1 in a ~human readable format with columns for both wavenumber and wavelength values.
Wavenumber in W/ cm^2-ster-cm^-1
Wavelength in W/ cm^2-ster-micron
The less human readable file MODOUT2 uses the wavenumber units.
So, don’t forget the pi associated with the steradians.
And, don’t forget to use the appropriate integration variables if you use the MODTRAN output and integrate in wavelengths. You need to divide the wavenumber based values by wavelength^2 to get the integrals correct.
Or, am I talking to the choir and choir masters here?
“Most of the confusion about “saturation” of CO2 ”
I think most of the ‘confusion’ about saturation comes from misuse of the word.
Wasn’t it already established in CO2 – a trace gas that the effects from CO2 are logarithmic , hence each succeed ppm has a smaller impact then the previous ppm.
The example used when I learned about logarithmic behavior in school –
If a young couple is sitting on opposite ends of a couch in her parents house and every 15 minutes move 1/2 the distance closer to each other, at what point do they actually touch?
The ‘technical’ answer is never.
Within 2 hours there is 1/4″ left between them.
As far as the over protective father is concerned, they are ‘touching’.
Am I wrong to conclude that ‘for all practical purposes at some point adding an additional few parts per million of CO2 makes no discernible difference?
280ppm to 560ppm = 1.2c rise
(on average each 100 ppm results in a .4 C rise)
560ppm to 1120 ppm = 1.2c rise
(on average each 100 ppm results in a .2 C rise)
1120 ppm to 2240 ppm = 1.2c rise.
(on average each 100 ppm results in a .1C rise)
ScienceOfDoom,
Very nice sequel to your series. On this one I got to understand where the lower limit of 220ºK comes from. A few questions:
Why is the tropopause origin of this limit, and not some higher level like the mesopause for instance?
Is the paper Taylor 2005 available online? I´d like to have a reference of that sattellite measurement. If not, could you please post the complete reference?
I understand Levenson´s model is more an illustrative one. Even if all radiation were to be absorbed in the lower atmospheric layer, warming would go on. Of course, the real world is far more complex. And I´m not a big fan of the “gray body” approximation either. It did not help much in my learning efforts.
DeWitt Payne:
The conditions are-
You can get an (unformatted) version of the paper at http://www.cgd.ucar.edu/cms/wcollins/papers/rtmip.pdf
harrywr2:
That’s correct.
“Saturated”, to some people, means that each increase in CO2 has no effect.
To others, it means that CO2 has a tiny effect.
To the climate science community it means the optical thickness is greater than 1, which means something quite different.
No one (?) believes it has a linear effect.
“Discernable” might be a judgement call, but an effect which is logarithmic always has diminishing returns.
It might be worth noting that harrywr2 makes a mistake in using an analogy with an asymptote and logarithms do not have asymptotes. It’s a mistake I’ve seen before.
Alexandre:
I should have put in the reference – which I will add to the text. It is from his book, Elementary Climate Physics, FW Taylor (2005).
Definitely recommended if you don’t mind seeing a fair amount of equations. The content and the explanation is very good and much can be learnt even without following the maths.
The “Elementary” in the title is very much from the perspective of a professor of physics rather than someone who wants to learn climate science.
You can buy it for just under $40 with free shipping worldwide from The Book Depository –
http://www.bookdepository.co.uk/search?searchTerm=elementary+climate+physics&search=search
Alexandre:
I missed a question, the best question:
At you go up through the atmosphere it gets thinner, much thinner. At the stratopause, 50km, (between the stratosphere and the mesosphere), the atmosphere is only 1/1000th as dense as at the surface. So even with 1000ppm of CO2 the stratopause would be the surface equivalent of only 1ppm of CO2.
Therefore, as the atmosphere gets thinner there is always a height (really a range of heights) where, at any given wavelength, the radiation from the atmosphere can escape to space.
It is at this height, or range of heights, where radiation is more effective at moving heat than convection. In a simplified model the atmosphere above the tropopause is a constant temperature. (It’s not in practice because of O2+O3 solar absorption in the stratosphere).
James Kennedy,
Miskolczi’s paper, though impressively written, is pseudoscience. He really doesn’t know what he’s talking about. Here’s a brief review:
http://BartonPaulLevenson.com/Miskolczi.html
In addition, a point I didn’t mention in the web page above–his equation 4 requires that the atmosphere be self-aware and have magical powers. There’s no other way it could distinguish heat from one source from heat from another, and exactly balance just one part of the input.
Miskolczi has actually been participating in a discussion at The Air Vent. I’m still less than impressed but there was a clarification to some extent of the 2:1 ratio of potential to kinetic energy. He gets that ratio by restricting the KE to motion in the z direction only. He claims to account for x, y, rotation and vibration elsewhere (which gives a ratio of 2:5 rather than 2:1). I suspect that for completeness you also have to include latent heat of vaporization of water as another degree of freedom, or maybe it’s potential energy.
The method of calculating tau seems to be questionable as well. Clouds are opaque to IR from the surface so I would think that tau should be calculated by averaging radiation to space from the cloud tops with that from the clear sky surface, not by just using radiation to space from the clear sky surface compared to total radiation from both cloud covered and clear sky surface.
But the real problem to me is the reduction to basically a 1D model, which is basically a toy. I don’t see how you can generalize from a toy model to the real world. Toy models are useful for illustration, not for making general conclusions
Oops, left out the link to The Air Vent thread:
James Kennedy writes: The paper which I referenced above is one of many
recent papers which assert that the climate is in a state of homeostasis.
Really? Then where does the Pleistocene glacial/interglacial cycle come from? Or the PETM and the other Eocene hyperthermal events?
James, please check out Barton’s comments about Miskolczi’s paper. I would not rely too heavily on Miskolczi if I were you.
scienceofdoom,
The issue of atmospheric greenhouse gas increasing surface temperature is being distorted on both sides of the issue. Your explanations of details of the physics of CO2 absorption and re-radiation, is well presented but several assumptions and statements along the way (and by your quoted authors) may confuse the underlying points. Surface temperature (assuming average equilibrium) is driven by the following facts:
1) The basic driving input of energy to the Earth is the Sun’s radiation level, which has a range of visible and near visible wavelengths (ignoring planetary internal energy here)
2) The effective planet albedo (including from the surface, atmospheric clouds, and aerosols) determines how much of the Sun’s radiation level is reflected without being absorbed. Any albedo change is the main feedback factor
3) The combination of absorbing gasses, clouds, and aerosols cause absorption of some of the input energy. The rest of any absorption of the Sun’s radiation occurs on the surface of the Earth
4) The heated surface and atmosphere re-radiate longer wave (thermal blackbody and molecular type) energy, which is re-absorbed and re-radiated by greenhouse gasses many times depending on the optical density of these greenhouse gasses
5) The mass of the atmosphere and gravity of Earth cause an average temperature drop with increasing altitude called the lapse rate. This is basically caused by adiabatic expansion of the atmosphere with altitude (or effectively losing kinetic energy due to gaining gravitational potential energy). Details can vary (as with water vapor evaporation and condensation), but the net overall effect is only dependent on the gas properties, mass, and gravity.
6) The absorption and re-radiation of thermal energy from the surface to most of the atmosphere (and back radiation) have only a very small and unimportant effect on the surface temperature. Almost all of the thermal energy from the heated surface is transported by convection including vaporization and convection of water (which condenses at intermediate altitudes).
7) The only place greenhouse gasses directly affects the surface temperature is in the upper atmosphere, where the radiation leaves the atmosphere to space. Their only effect is to increase the average altitude of the tropopause (due to more absorption in lower densities). Increasing the altitude of the tropopause increases the amount of the total atmosphere below it, and thus increases the mass of atmosphere the lapse rate acts on, and thus makes the surface hotter.
8) If the planet is not in equilibrium (using average values), the Solar flux in that is not reflected does not have to equal the long wave thermal radiation out at the outer edge of the atmosphere. This is only valid if there is increasing or decreasing energy storage (typically in the oceans), or continual changing surface temperature (also a storage effect). This is a transient condition, and careful measurements need to demonstrate it as being in effect.
9) The last decade of average Earth temperatures and ocean energy storage do not show a significant lack of constant average equilibrium, and thus no reason to expect sudden warming in the near future.
Regarding point 9:
Well, speaking statistically, it is more likely that warming has occurred in the last decade than not. The slope remains positive, unless you are very judicious in your choice of start and end years. Warming over that short time frame has not been statically significant using 95% confidence intervals, but the situation does not lend itself to saying that there hasn’t been any warming either.
In context, solar energy has been in a low over the same time frame; so, it seems a reasonable expectation that as the sun enters a more active phase, more warming should occur.
There is also a confusion in some of the comments on the need to have the tropopause cooler if the ground is hotter. This is only true while the ground is heating (or energy being stored continually as in the ocean). Once it reaches a new steady higher level, the tropopause temperature will go back to the same level as when the ground was at a steady lower level. Input has to equal output if there is no storage going on. The change would only be due to either a change in albedo, or increase in greenhouse gas, but would be caused by increasing the altitude of the tropopause – thus increasing the total lapse effect.
“6) The absorption and re-radiation of thermal energy from the surface to most of the atmosphere (and back radiation) have only a very small and unimportant effect on the surface temperature. Almost all of the thermal energy from the heated surface is transported by convection including vaporization and convection of water (which condenses at intermediate altitudes).”
I’m also convinced.
It’s worth the time to understand how things work. It is also good to place things in perspective.
When the effects of water vapor and precipitation are removed, the residuals are underwhelming and there is no signal of any specific cause seen in it.
In short, the principles described, while true, don’t signify – in real life they are not manifest because other things, such as latent heat of vaporization, are many orders of magnitude larger than any effect postulated for any non-phase change gas.
It is not a dry atmosphere. It is a heat pump and water is the working fluid.The lapse rate is not that of dry gas, it is that of a refrigerant gas – one that has a phase change.
All energy is moved with the flow of the working fluid to the condenser by convection. Radiation is of no consequence until it hits the condenser – and space is an infinite heat sink.
Radiation physics is cool in its own right, though. It’s useful for photography, downloading isos, cooking, keeping furniture from fading, burning ants, the high tech analogs of burning tiny things and even more fun, burning things far away – there’s no end of what you can use it for or just enjoy understanding for its own sake.
Breathes there a man with soul so dead he doesn’t love a radiometer?
The topic is fun, even though it happens to be a political football at the moment. The brilliant minds are still in the lab doing wonderful and useful things of relevance to our lives.
Mostly what you have said is true, but convection and phase state changes will not transport energy away from the earth. Ultimately, all energy leaving the earth is in the form of EM radiation. So, changes in the radiative properties of the atmosphere do matter.
Atmospheric radiation drives the heat engine. In the absence of LW emission/absorption from the atmosphere, the atmospheric temperature profile would be a lot closer to isothermal. The adiabatic lapse rate is an upper limit (using the meteorological convention of a decrease in temperature with altitude means the lapse rate is positive). Any lower lapse rate is stable because there is no driving force for vertical convection at a lapse rate less than the adiabatic rate. In the absence of convection, the lapse rate due to radiation only would be much higher than the adiabatic rate. So the actual lapse rate is driven up to the adiabatic rate by radiation. But at the adiabatic lapse rate, there is an excess of emission to space from the atmosphere compared to absorption from the surface so the difference must be made up by convection of latent and sensible heat from the surface.
In a transparent atmosphere with a meridional surface temperature gradient (it gets colder as you move away from the equator), there is a driving force for horizontal convection that may induce some vertical convection, but the heat transfer downward at high latitude has to be too slow, IMO, to cause the temperature profile at the equator to achieve the adiabatic rate.
Slightly confusing wording in the article,
“You can see that the radiation emitted by a 288K body is a lot higher than the 220K body (the total integrated across all wavelengths is greater by a factor of 3). You can also see that the energy has shifted to longer wavelengths (the wavelength of maximum radiance has moved from 10.1μm to 13.2μm).”
On first read, it sounded as though you were saying that the higher temperature body has peak emissions at a longer wavelength. It’s the opposite of course.
Chris G., Thanks, that’s a very good point, I have fixed up the wording.
DeWitt Payne
“In the absence of convection, the lapse rate due to radiation only would be much higher than the adiabatic rate. ”
Why would there be an absense of convection when the Earth surface is heated directly by 168W/m2 Solar Radiation?
Sorry, I didn’t make it clear that this was a thought experiment where we freeze the atmosphere in place and allow it to attain a new steady state temperature profile by transfer of energy by radiation only. Another way of doing the thought experiment would be to postulate a much lower heat capacity for air at constant pressure, Cp from its value of 1,004 J kg-1 K-1, which would increase the adiabatic lapse rate (g/Cp, where g is the acceleration due to gravity 9.81 m s-2) from 9.8 K/km to a value higher than the radiative only lapse rate.
DeWitt Payne
The temperature profile of the troposphere can be broadly explained by elementary Kinetic Theory in a Gravitational Field .
No reference whatsoever is made as to whether the air molecules have radiative properties or not.
It’s become obvious to me that Payne knows more about atmospheric mechanics than I remember, but I’ll attempt a response.
Energy coming off of the surface adds energy to the air; the closer, lower altitude air receives more. Outside of a phase change or chemical reaction, more energy means higher temperature. Higher temperature under the same pressure means less density; there is convection in the within the lower atmosphere. Convection shuts down at altitudes where the energy coming down from above is absorbed and is greater than or equal to the energy coming up from below.
Last, why would the lack of a reference to radiative properties mean that air molecules don’t have them?
You can see that the black body radiation of water vapor at 1C is the same as any other gas at 1C.
You can see that the blackbody radiation of water at -1C is the same as any other gas at 1C… except…
What’s the frequency, Kevin?
Dave,
I think missed the part where gases do not behave like black bodies.
FWIW, and I’m a long why from sure on this, but…
I’ve always imagined that the function that describes the chance that a photon goes upward and escapes the earth system is a probability function based on (1 – ). The probability that it continues an upward path increases as the density of the atmosphere decreases. (Or, is the sum of the partial pressures of GHGs + plus particulates + clouds a better concept for this?) Conversely, inbound radiation has to reach the surface in order to warm it; so, the same function works in reverse for inbound photons. Of course, you have to also consider (integrate over) all the radiative energy of photons that were re-emitted in approximately their original up or down direction. So, in this framework, the tropopause is the break-even point where it is just as likely that a photon traveling upward will eventually, after 0 or more absorb-emit cycles, leave the earth, as it is that a photon traveling downward will eventually reach the surface.
I don’t remember enough symbols to express this mathematically, but are there any comments as to whether is a reasonably accurate working model?
Considering the absorption as a probability function makes it easy to respond to arguments like:
A) CO2 is a trace gas and can’t possibly have a significant effect.
B) The atmosphere is already saturated with CO2; adding more will have a negligible effect.
At the top of the atmostphere, A is largely correct. Near the surface, B is largely correct. It is at some point in between top and bottom where increasing the partial pressure of CO2 relative to the other gases, like O2, matters. If this model has any validity, then an answer to an earlier question is, “Yes, changing the level of a GHG, CO2 included, changes the altitude of the tropopause.” From there down, PV = nRT rules, and if the tropopause temperature remains the same, which it should in order for energy-in to remain in balance with energy-out, a higher altitude for the tropopause implies a higher temperature for the surface.
Couple of minor points:
I’m more comfortable, conceptually, with thinking of atmospheric composition as overlapping, contiguous partial pressure curves than I using a layered model. I grant you, as your number of layers approaches infinite, it all adds up the same.
Regarding, “If CO2 can absorb radiation at 15μm, it can also radiate at 15um. But it radiates according to its temperature. ”
I was under the impression that gases absorb and and emit at specific wavelengths, irrespective of temperature. I suspect that when a satellite reads a temperature of 223 K, it is reading off all the gases, etc., not just CO2.
In hindsight, I see my post was way too long.
And, darn html interpreted my description at (1 – ) to be some kind of tag. It should read as (1 – the chance that it encounters something that redirects it).
I’ve also been thinking of the post by Dave McK and how the temperature within the troposphere really is closely tied to PV = nRT. So, it finally dawned on me, or I remembered, that convection is what keeps the troposphere mixed well enough so that this can be true. Convection still can’t remove energy from the earth; radiative probability curves still apply, but this also means that a dual layer model isn’t as bad a first order approximation as I was thinking either.
In his article Science of Doom made the common claim: “For the temperature of CO2 to be 223K (-50ºC) means that it must be located around the top of the troposphere”.
Alexandre then questioned why the level should not be in the Stratosphere or Mesosphere, to which Science of Doom responded (17May, 0853), with words to the effect that the high atmosphere is too thin to support the intensity of radiation observed.
I disagree.
1. Above the top of the Tropopause there is still around 5% of the atmosphere. Anywhere other than the tropics there is over 25% of the atmosphere above the lowest part of the Tropopause. Any radiation at 15um has to get through the overlying CO2 molecules and these are fierce consumers of radiation at that frequency (at ground level, for instance, over half the 15um radiation emitted from the surface is absorbed within the first 25m of atmosphere). It is highly unlikely for any photon emitted below the Tropopause to make it through the remaining 25% of atmosphere. The majority of emissions must be coming from higher than the bottom of the Tropopause.
2. Looking at the detailed emission spectra (see for example http://www.sundogpublishing.com/AtmosRad/Excerpts/AtmosRad217.pdf) it is noticeable that most of the CO2 band emissions are at a “temperature” of around 215DegK, but the centre of the band at 15um is around 15DegK HIGHER.
3. Because we know that absorption is strongest at 15um, it follows that the atmosphere is optically thicker at that frequency, and that the 15um emissions are coming from HIGHER in the atmosphere than the wings. A higher emission temperature at a higher altitude can only occur if both the wing and the centre frequencies are being emitted from the lower Stratosphere.
Your link to the spectrum is broken.
If you go to the MODTRAN page, pick the 1976 standard atmosphere and a viewing height of 20 km you get these spectra looking up and looking down from 20 km.
So most of the emission from CO2 comes from below 20 km. The CO2 (and ozone) emission in the stratosphere is at higher temperature because temperature increases with altitude in the stratosphere. But the lines are much narrower at high altitude. A 1 km path length spectrum of CO2 at 20 km has a lot of gaps between the very narrow absorption lines.
Why would a completely transparent atmosphere be nearly isothermal? Let’s restrict this to a 1 dimensional atmosphere with altitude only. Assume the surface is a blackbody at all wavelengths. Initial conditions are absolute zero with 10,000 kg/m2 frozen gas on the surface. Now turn on a sun with a solar constant at the surface of 390 W/m2. The surface warms, warming the gas above it. The warm gas at the surface is less dense than the gas above it and it rises and the cooler gas sinks. Over time, the surface will eventually reach a steady state temperature of 288 K. If the acceleration of gravity at the surface is 9.8 m s-2 and the heat capacity of the gas at 1,000 hPa is 1,000 J kg-1 K-1 then convection will continue until the temperature is decreasing at 9.8 K km-1. Since the gas is completely transparent, there will be no tropopause, which is caused by the absorption of UV radiation by oxygen and ozone.
But things won’t stop there. Conduction, which can normally be ignored because it’s so small compared to radiation and convection, will continue to transfer energy across the temperature gradient from the surface upward. Since there is no mechanism to lose heat above the surface, the temperature at altitude will continue to increase until the temperature gradient is zero and the atmosphere is isothermal.
Things will be much more complicated on a spherical, rotating planet. Some heat transfer from the equator to the poles will happen. But I don’t think its possible to transfer enough heat by advection (horizontal convection) to achieve an adiabatic lapse rate even at the equator and the lapse rate would have to be negative at high latitude for heat to be transferred from the atmosphere to the surface.
DeWitt Payne
…..temperature at altitude will continue to increase until the temperature gradient is zero and the atmosphere is isothermal…..
Any gas particle or group of particles moving down will accelerate this means that their temperature will increase.
Likewise Any gas particle or group of particles moving up will decelerate this means that their temperature will decrease.
Tides and rivers will still flow, katabatic winds will still be there, Earth surface absorption features will vary and a host of other features will continue to stir the atmospheric gases and maintain a vertical temperature drop through the atmosphere.
However on the positive side I take it that you think that in the absence of radiative gases in the air will
…..eventually reach a steady state temperature of 288 K. …
Quite reassuring!
“Any gas particle or group of particles moving down will accelerate this means that their temperature will increase.”
That’s true for an adiabatic process. You’re trading kinetic energy for gravitational potential energy with no change in total energy. But conduction makes the process diabatic. Heat will always flow from hot to cold. That energy will be proportioned over all degrees of freedom including gravitational potential energy and the temperature will go up until the temperature gradient goes to zero and conduction stops too.
I’ll repeat: meteorologists ignore conduction except at surfaces with a very high temperature gradient because conduction is small compared to convection and radiation. Radiation drives convection. If you eliminate radiation then convection will eventually slow to a crawl and conduction can no longer be ignored.
With a completely transparent atmosphere there can’t be a negative temperature gradient everywhere because then no heat would be transferred from the tropics to the poles. You can only transfer heat downward in the absence of radiation if the temperature gradient is positive and then only by conduction, possibly accelerated by eddy diffusion.
“However on the positive side I take it that you think that in the absence of radiative gases in the air will
…..eventually reach a steady state temperature of 288 K. …
Quite reassuring!”
Apparently you didn’t notice that I picked my incoming radiant flux to produce a surface temperature of 288 K. That flux, 390 W m-2, is much higher than we get from the sun even if the albedo were zero, which is 342 W m-2.
“Tides and rivers will still flow”
Nope, no water vapor or liquid water in the model. Completely transparent, remember
“katabatic winds will still be there,”
Nope.
“A katabatic wind originates from the cooling by radiationof air atop a plateau, a mountain, glacier, or even a hill. Since the density of air is inversely proportional to temperature, the air will flow downwards, warming adiabatically as it descends. ”
No radiative cooling, no katabatic wind.
The Collins, 2006 forcing plots (Panel B, radiative forcing vs. wavelength) confuse me. From my laser days I recall that CO2 is highly absorbent at 14.9 microns which I would have thought should result in a peak in the forcing plot rather than a minimum.
Maybe the plot is upside down or CO2 suddenly became transparent at wave number 670.
The mechanics of the plot are:
1. Calculate the atmospheric emission spectrum for 287 ppmv CO2
2. Calculate for 574 ppmv CO2
3 Subtract spectrum 2 from spectrum 1.
Since there will be less emission at higher CO2, the difference is positive.
gallopingcamel:
It’s the “change in radiative forcing” from current conditions to doubled CO2 conditions.
So it shows that the increase in CO2 has the most effect in the wings not in the center of the band.
If it was a graph of “radiative forcing” then it would be the graph you were expecting to see.
Apologies to Chris G and anyone else who found my comment merely obscure or silly.
All things radiate as blackbodies (or maybe a bit grayish) and noting that while water does not change temperature as it changes phase, it radiates many hundreds of times more energy in the process than any other gas.
Therefore, the blackbody spectrum may not change a whit, but …
There are a number of things that water gas does which are scarcely mentioned. It seems to be considered nothing but a handmaiden to CO2.
However there are many things that water does which define the atmosphere, the lapse rate and the thermal equilibrium.
In the first place, it evaporates. When it does, 3.7 teaspoons of liquid becomes one liter of gas, absorbing 0.462 kJ/kg. This happens without temperature change. No change occurs in the black body spectrum.
The expansion increases the local pressure above what a dry gas can under the same conditions.
At the same time, water is much lighter than any other gas in our atmosphere (except the traces of He and H), , massing a measly 18g/mole – so it rises straight up, shifted by coriolis effect as it billows wider and wider.
When it finally condenses, at the same temperature as the surrounding gas, it radiates the one spectrum throughout its phase change, indicating no higher temperature while it radiates 0.462 kJ/kg and changes back to 3.7 teaspoons from (a bit less than, now) a liter of gas, producing a local low pressure drop of that draws the atmosphere below up to fill it. (To get a 1% pressure drop by changing the temperature in a dry gas you need to do from 298 to 292.04 = 5.96 degrees instead of no temperature change with 1% water gas in it.)
If water is but one percent of the volume, (using a sample volume of 100 liters that started at STP) the constituents would radiate their share as well, depending on the specific heat-
um… well, the other gases don’t radiate any more than they gain from below or sideways, or the temperature would actually drop- but for a one degree drop:
N2 (89.3g = 78%) 1.039 kJ/kg = 92.J
O2 (13.1g= 20%) 0.915 kJ/kg = 12.0J
CO2 (0.02g = 500ppm) 0.189 = 0.008J
H2O (18g = 1%) 0.462 kJ/kg = 406.41367968J
Unless my math is horribly wrong, water does more work than everything else combined – without changing its blackbody spectrum.
Water powers the convection engine due to its mass, phase change and relative density. Everything else is just along for the ride. Radiative effects within the working fluid are high frequency transients in the resounding roar of the refrigeration cycle.
(Compared to the CO2, water moves 50,000 times more energy from surface to space.)
The remark ‘what’s the frequency, Kevin’, refers to ‘what’s the frequency, Kenneth’, in reference to an incident when Dan Rather was assaulted by a paranoid who was convinced he’d been taken control of by electromagnetic radiation – an original tin-foil hatter.
This was an oblique conceit regarding Kevin Trenbreth’s Travesty (sic) of the Missing Heat.
As I gaze at this wall of text, I can forgive myself the earlier but more cryptic expression because it’s not really random noise- it’s only compressed to remove redundancy. I understand the two are indistinguishable without the extraction algorithm, though. I hope I fixed that.
Phase change does the work in a cooling system and none of that work can be seen looking at blackbody spectra.
Degrees don’t measure heat.
[…] – CO2 – An Insignificant Trace Gas? Part Eight – Saturation is now […]
Science of Doom,
That was really helpful! Now I am emboldened to ask another question. While I am a physicist, my field is electro-optics and particle accelerators so “Climate Science” strikes me as a “Black Art”. To make things worse I failed “Thermodynamics” when I was in college and my brain has deteriorated since.
If I have correctly understood your excellent presentations, radiative forcing caused by CO2 appears to be ~ 4 Watts/sq. meter/doubling. In the absence of other effects this should cause a ~1 Kelvin increase in global temperatures owing to Stefan-Boltzmann’s radiation equation.
The current orbit of Earth relative to the sun is claimed to be an ellipse with an eccentricity of 0.0167. I ran the numbers and found that the corresponding range in Total Solar Irradiance to be ~90 Watts/sq. meter. Happily, my back of the envelope calculation appears to be within 1% of the official answer.
Given that a 4W/m2 forcing is expected (by many) to cause “Catastrophic” climate change, why does oscillating forcing with an amplitude of 90W/m2 have no noticeable effect?
gallopingcamel:
Funnily enough I was just looking for some equations relating to changes in TSI as a result of eccentricity.
I was looking for annual change in TSI as a function of e, and also some formula which provides max and min daily average insolation as a function of e.
Do you have these?
I think the way you ran the numbers might be a mistake.. 90W/m^2 out of 1367W/m^2 seems high unless it is the max daily value.
The annual TSI change should be quite small – for e=0.0167 vs a perfect circle – as the earth is closer at some periods and further away at others. But as the energy received is a function of r^2 it won’t quite net out to zero.
If you have the formulae I will take a look.
In any event the key issues are the total annual TSI and then daily changes, and also variations at particular latitudes.
If TSI varies throughout the year but nets out to zero for the whole year it will have only a small effect as the oceans act as big heatsinks.
And by the way, just for completeness, as you can see in Earth’s Energy Budget you do have to multiply the TSI by (1-A)/4, where A is albedo is a fraction (about 0.3), to convert to the same effect as CO2 forcing..
There is a whole big subject around eccentricity, precession and obliquity called “Milankovitch cycles” which I hope to write more about soon, to follow on from the first post – Ghosts of Climates Past.
Maybe this site: http://aom.giss.nasa.gov/solar4x3.html will help with the Milankovitch cycles.
Jonathan Levine has a Matlab program that calculates insolation at any point on the Earth’s surface for the last 3 My. It’s no longer available on line but he says he wil send a copy on request. See his page here: http://www.ssl.berkeley.edu/~jlevine/
Assuming that the average distance from Earth to the Sun is 149, 598 km and the orbit eccentricity is 0.0167:
Aphelion = r * (1+e) = 149,598 * 1.0167 = 152,096 km
Perihelion = r * (1-e) = 149,598 * 0.9833 = 147,100 km
Radiation intensity follows an inverse square law so assuming the annual mean TSI ~ 1,366 W/m2 we have:
TSI (Aphelion) = 1,321 W/m2 – (July 4)
TSI (Perihelion) = 1,413 W/m2 – (Jan 4)
See: http://en.wikipedia.org/wiki/Sunlight
TSI change = 92 * (1-a) = 64 W/m2
The change in radiative forcing is still rather large.
After further thought my question may belong in the “dumb” category. The TSI variations caused by Earth’s rotation, axial tilt and orbit eccentricity cause the huge temperature changes that we experience day to day and season to season. However, as long as the cycle exactly repeats itself, the temperature anomaly is zero.
Then I looked up Milankovitch cycles and found that the TSI oscillation can have an amplitude of ~100 W/m2 or 16 times the effect of a CO2 doubling (even after correcting for albedo).
Milankovitch cycles are calculated at latitude 65 N on July 1 on the theory that there is more land in the NH than the SH and land temperatures are more sensitive to changes in insolation. The annual average insolation to the entire planet changes very little over the course of Milankovitch cycles, far less than 100 W/m2. See the graph here: http://www.climatedata.info/Forcing/Forcing/milankovitchcycles.html
The dominance of land temperature fluctuation is evidenced by the peaking of the global average temperature during the NH summer even though peak insolation occurs during SH summer as a result of orbital eccentricity. See graph here: http://i165.photobucket.com/albums/u43/gplracerx/LowerTroposphereTemperature.png
When comparing ghg forcing to insolation change, one should compare apples to apples, that is either divide the insolation by 4 to get the daily surface average or multiply the ghg forcing by 4. Ghg forcing is averaged over the whole planet, so it’s at least an order of magnitude larger than the effect of Milankovitch cycles globally.
Delete ‘at least an order of magnitude’ in the last sentence . If you scroll the graphs down on the right side of the linked page there’s a graph of the global insolation fluctuation over the last 800,000 years and the range is less than 2.5 W/m2 compared the the current level of 340.5 and CO2 doubling of 3.7 W/m2 global average.
DeWitt Payne,
Many thanks for the information. It looks as if I got hold of the July, 65N information thinking it was the global average.
A little knowledge is a dangerous thing!
Science of Doom
I found that formula on Planetary albedo: E = (1-A)S/4
http://ceos.cnes.fr:8100/cdrom-98/ceos1/science/dg/dg12.htm
I see now that I should have divided by a factor of four to average the incoming solar irradiance over the entire surface of the Earth rather than its disk. Duh!
Thank you for your patience. I will try to be a little less dense in future.
Looks like we both wrote at the same time (see below).
There’s no problem with asking questions or trying ideas, often the answers are not so obvious. And if you have a question so do many people less willing to write them down.
gallopingcamel
The number you calculated:
Should be 92 * (1-a)/4 = 16 W/m^2 as the difference between aphelion and perihelion.
The reason is to convert incident radiation to the average over the whole surface area of the earth. Incident radiation is over a “disc area”=pi x r^2 and the surface area of the earth is over 4 x pi x r^2. (Longer explanation in the link I gave earlier). The definition of radiative forcing is expressed by surface area and is needed to match like for like with ghg forcing.
It would be handy to see the derivation for the annual average calculation in terms of eccentricity as eccentricity itself varies over 400,000 years cycles and 100,000 year cycles.
I have seen a few results quoted but not the maths and haven’t got around to tracking it down.
DeWitt Payne:
Thanks for the resources on Milankovitch.
You might want to look into Muller’s theory that orbital inclination is as or more important than eccentricity, precession and axial tilt.
See here: http://muller.lbl.gov/papers/scicorr.htm
He’s got a book out that goes into much more detail, Ice Ages and Astronomical Causes, but it’s $224.50 at Amazon. Too rich for my blood.
Orbital inclination peaked about 32,000 years ago and the lag between orbital inclination and its effect on climate is about 33,000 years.
I was interested to hear that a couple of “Warmists” who turned up at the recent ICCC meeting of “Skeptics”. While I don’t like sticking labels on people there is no denying that are two pretty well defined groups in “Climate Science”.
Scott Denning (Warmist) gave what I consider a pretty nifty review of radiative forcing and Ice Age cycles, aimed at non-experts.
http://www.heartland.org/events/2010Chicago/PowerPoints/Scott_Denning.ppt
I would be interested to hear your comments on this presentation if you have time.
There are a couple of questions I would have asked given the opportunity:
Q1. The effect of increased CO2 concentration makes sense in isolation but what if some other complex molecule (e.g. water vapor) has already absorbed 90% of the radiation available in the Long Wavelengths?
Q2. There is a good correlation between CO2 concentration and global temperature over the last 750,000 years but when one looks closer, temperature leads CO2 concentration by several hundreds of years in most cases. Are you asking us to abandon the idea that cause precedes effect?
Q1
Water vapor has a scale height (the altitude where the pressure is 1/e that of the surface pressure) of about 2 km compared to 8 km for non-condensable gases so even if there were enough water vapor in the lower atmosphere to make CO2 absorption insignificant, it would still have an effect at higher altitude. Also, the temperature required to get that much water vapor in the lower atmosphere is quite high.
Q2
CO2 doesn’t cause glacial/interglacial cycles so there is no reason for CO2 to increase before the temperature increases. But it should amplify the increase. I have a post on the subject here:
Jeff’s server has been slow lately, be patient. Clicking on refresh seems to help.
Q2. I am happy to hear that CO2 does not cause glacial cycles. When I asked a similar question on John Cook’s blog (Skeptical Science) the reaction was quite different; many of the denizens of that blog think that CO2 drives climate change on all time scales.
I read your guest post on the “Air Vent” with great interest and while there must be some amplifying of the warming as CO2 is evolved from the oceans, other effects are intertwined. Changes in cloud cover, changes in humidity and changes in albedo due to melting ice sheets come to mind. It can’t be easy to sort out the magnitude of these effects and the time constants associated with them. Analysis is seldom easy but synthesis can be really hard!
Q1
Given the variability of water vapor in the atmosphere it must be difficult to figure out how much of the available outgoing radiation it soaks up (averaged across the planet). If water vapor absorbs a significant fraction of the available outgoing radiant energy won’t that reduce the effect of CO2 pro rata?
My understanding is that the effective radiative temperature of our planet is ~255 kelvin (-18 Centigrade). While the vapor pressure of water is quite low at this temperature, it should still account for up to 1,250 ppmv or more than 3 times the concentration of CO2.
galloping camel,
Your experience at Skeptical Science doesn’t surprise me. The peanut galleries at places like that, and that includes WUWT and RC as well, are usually clueless. The posts may be interesting, but the signal to noise ratio in the comments is near zero.
As far as the relative contributions of CO2 and water vapor, I recommend you examine the results of different scenarios using the MODTRAN site:
http://geoflop.uchicago.edu/forecast/docs/Projects/modtran.orig.html
Look at the Iout number and the spectrum at the top of the atmosphere , 100 km looking down, and see how it changes when you change conditions. You can set any level of CO2 that you want, but you can only change water vapor in the lower troposphere using the Water Vapor Scale setting. But it does give you an idea of the relative level of effect. There’s more water vapor than CO2, but CO2 absorbs more strongly over a narrower range of frequency (the spectrum is in cm-1 referred to by spectroscopists as wavenumber which is equivalent to frequency) and that absorption is in a region where water vapor absorbs less strongly.
Example:
1976 standard atmosphere, 100 km looking down
375 ppmv CO2, WVS 1, Iout=287.812 W/m2
0 ppmv CO2, WVS 1, Iout=318.396
375 ppmv CO2, WVS 0, Iout=345.714
So to a first approximation, water vapor is about twice as effective as CO2 under these conditions. It’s somewhat more than that because there’s still water vapor in the stratosphere as well as nitrous oxide, chlorofluorocarbons and other minor ghg’s that are not adjustable.
There’s some other peculiarities of the MODTRAN calculations. The complete spectrum isn’t calculated and integrated so, for example, when looking at the surface, 0 km looking down, Iout will be less than that calculated by the Stefan-Boltzmann equation using an emissivity of 0.98. But the differences between conditions will be approximately correct.
Once again, many thanks. I will have a try at MODTRAN but am somewhat challenged by complex software.
This site strikes me as one of the few that is dedicated to understanding the science without trying to fit it to some kind of agenda. It puzzles me that WUWT lists “Science of Doom” as “Pro-AGW”.
I am reasonably comfortable with the scientific basis for the relationship between CO2 and radiative forcing. Probably the most important issue is now that of “Feedbacks”, so I look forward to posts on this site when (if?) Roy Spencer’s paper comes out, see:
“Strong Negative Feedback from the Latest CERES Radiation Budget Measurements Over the Global Oceans
Friday, May 7th, 2010”
In slides 15 & 16 of Scott Denning’s presentation at the recent ICCC he estimates 3.2 degrees Celsius per doubling of CO2 concentration. This corresponds to an amplifying effect of about three times compared to the expected forcing without feedbacks.
Denning’s estimate only makes sense if CO2 concentration is the “Cause” and global temperature is the “Effect”.
If I understood DeWitt Payne’s position correctly, he rejects this hypothesis.
What does “scienceofdoom” say?
GC,
My impression is a bit different from yours. To me, DeWitt is merely saying that the root cause, or trigger, for glacial cycles is not CO2. Nothing unexpected there, but I think you’ll find common agreement that the energy flux changes associated with Milankovitch cycles by themselves are not enough to account for the changes in temperature/climate. That leaves room for CO2 to do what physics predicts it will do, if an increase in temperature changes the balance, in favor of the atmosphere, of how much of it is stored in the air, ocean, and land. That’s also pretty much in agreement with most of the comments I see over at Skeptical Science.
Climate warming will occur regardless of if the trigger is something like albedo and CO2, water vapor, etc. are feedbacks, or if CO2 is a trigger and albedo, etc are feedbacks. To me, it’s like a multibody problem; you can’t change any factor without affecting other factors.
And, the feedbacks occur on different timescales and with different magnitudes. For instance, water vapor reacts quickly to temperature and achieves a new equilibrium quickly; CO2 has multiple storage locations, each with its own response time; ice sheets take a while to melt, etc. So, temperature response curves tend to be lumpy.
gallopingcamel
Watch this space. I am currently working on a new post, Clouds and Water Vapor, watch out for it..
ChrisG,
When it comes to triggering Ice Ages it looks as if the “Usual Suspects” have alibis.
Milankovitch cycles ……..variations are too small.
CO2 concentration………follows rather than leads.
Total Solar Irradiance…..variations are too small.
Cosmic rays……………….weird science?
Probably there are some more I am not aware of.
Is there anyone out there who has a plausible prediction as to when the next Ice Age will start?
gallopingcamel,
I think refreshing your understanding of the concept of an unstable equilibrium my help you work past some sticking points. In a system that is at an unstable equilibrium, a slight forcing can push it to a new equilibrium that isn’t closely related to the previous equilibrium or the force that caused it to leave the previous state. Looks to me that the earth system has some inherent instabilities. At least, that is how I reconcile the observations that show large changes associated with small forcings, and what I hear to the effect that feedbacks are everything.
David Archer, I believe, has put forth a reasonable argument that we’ve managed to put off the next ice age to far enough into the future that it’s not a concern to us, or rather, there are other, far more pressing concerns that will occur between now and then.
The interglacial/glacial cycle is something that is directly related to climate sensitivity obviously… As to the mechanisms, well they are highly contentious. The fact is that during the last interglacial the inferred temperatures were warmer than present when it shifted back towards glaciation.
This ice house period as a whole began some 2.5million years ago, but the initial trigger was continental drift some 50 odd mybp. With ice sheets forming on Antarctica 30mybp… And i believe 15mybp was when the first northern hemisphere ice sheets started forming…. I agree with yer that the earth at present shows an unstable equilibrium, which certainly appears at face value to be the case with the earth when ever its in a ice house phase(maybe as a result of low GHG levels)… But what the paleo reconstructions seem to hint at is that the current continental configuration weighs the climate more towards glaciation than “run away” warming. I dont believe enough is known to state with any confidence that the earth is free of its glacial cycles in the next 1ky for example. It may be that warming triggers glaciation(im not convinced) by shutting down the THC for example… It maybe that persistent GHG levels will avert glaciation.. But I dont think its cut n dried, not enough is known.
DeWitt Payne responded to my assertion that most 15u photons must be coming from the high atmosphere with:
“Your link to the spectrum is broken.
If you go to the MODTRAN page, pick the 1976 standard atmosphere and a viewing height of 20 km you get these spectra looking up and looking down from 20 km.
So most of the emission from CO2 comes from below 20 km. The CO2 (and ozone) emission in the stratosphere is at higher temperature because temperature increases with altitude in the stratosphere. But the lines are much narrower at high altitude. A 1 km path length spectrum of CO2 at 20 km has a lot of gaps between the very narrow absorption lines.” (1510, 21MAY)
I agree with DeWitt Payne that the lines are much narrower at higher altitudes. Roughly they will be about 100 times broader (30GHz, Barrett) at sea level than at 30km (300MHz). But this fall off in bandwidth with height is very small, compared with the fatal attraction that CO2 has for 15u photons. So I’m not sure that the argument is correct – though at some point (very unlikely at the surface) the leakage around the sides of the lines becomes important. I need to do some more research.
Consider a line with a width of zero. No matter how strong the line, there would be no absorption of energy. A narrow line necessarily absorbs less energy from a continuum source than a broad line even if the area under the line remains the same. Radiation from below is effectively continuum so the spaces between the narrow lines at high altitude and low temperature is going to be energy that can’t be absorbed.
[…] Now effective temperature at the top of atmosphere is 230K, so an opaque atmosphere has increased the surface temperature significantly – but not to 730K. (Barton Paul Levenson has a model like this, commented on in CO2 – An Insignificant Trace Gas? Part Eight – Saturation) […]
Gentlemen all: This thread and website is thoroughly enjoyable. I have question related to CO2. I know from what chemistry I remember and from my geology classes, that age dating for rocks and fossils can be done by looking at the C12/C14 ratios. I have have been told that man-made CO2 can be differentiated from natural CO2 by analyzing the C12/C13 ratios in the gas. The question is: do any of you know of any studies done that been done to give a quantitative result of how much “man-made” vs natrual CO2 is in the atmosphere and the oceans? I assume the ocean doesn’t care which CO2 molecule it absorbs.
[…] Part Eight – Saturation – explaining “saturation” in more detail […]
[…] Part Eight – Saturation – explaining “saturation” in more detail […]
[…] This graph is from W.D. Collins (2006) – see CO2 – An Insignificant Trace Gas? – Part Eight – Saturation. […]
[…] links to other informative articles. mdn, you are excused, wouldn't want you to hurt yourself. CO2 – An Insignificant Trace Gas? – Part Eight – Saturation The Science of Doom Introduction This is the long-promised eighth part of the seven-part series on CO2 basics. Part […]
[…] CO2 – An Insignificant Trace Gas? – Part Eight – Saturation […]
Dear Science of Doom,
I much enjoy your thorough discussion of radiative transfer and on the impact of CO2 in the radiation balance of the atmosphere. Illuminating the case from all possible angles is required, as you do, to gain real understanding. Being a (former) astronomer there are still many things in the climate business that I don’t understand or don’t agree with. I recently bought the book “Climate Change – observed impacts on the planet earth” , ed. Trevor M. Letcher, Elsevier, 2008 to get a feeling for real observations rather than model data. This book is written in a rather tough standard scientific jargon by different researchers – not about their own research but as a review with numerous references. The first chapter is written by R.P. Tuckett and is about the role of the atmospheric gases in global warming (note that the latter is presupposed).
In this article he shows a table with the relative radiative efficiency of various gases including CO2, CH4 etc. He shows the radiative efficiency in terms of a0/Wm-2 ppbv-1.Thus he assumes the radiative efficiency to be completely linear with gas concentration. This is amazing (there are quite a few more amazing statements in that article – including evident misunderstanding of the greenhouse effect)! You don’t really express yourself very clearly on this point except stating that linear relations (obviously!) are not to be expected in the general case. Also, Tuckett lacks a proper discussion of H2O as a greenhouse gas. You discuss the problem with H2O at considerable length but you don’t stress it as much as it should be, I think – if the troposphere has 2% or 3% water vapour makes a BIG difference. In addition, it varies very much from place to place – can it be meaningfully averaged? And how can the climate models put in the right number of this very important number when it is as poorly known as you state?
There is another problem about this that neither you nor Tuckett discuss. It is an obvious concept when you think of it. In astrophysics it is call the curve of growth and it is e.g. extensively treated online by J.B. Tatum here http://www.astro.uvic.ca/~tatum/stellatm/atm11.pdf. The idea is simply that when you have an optically thin line (few atoms) you expect the absorption (or emission) to grow (when adding additional atoms) quite differently than an optically thick line.
Both H2O and CO2 are obviously optically thick and, as you state, it is in the line wings that extra absorption occurs when you add atoms. But Tuckett goes on in his table with rare gases such as SF5CF3 and states radiative efficiency in the same way for all atoms. Ought not a rare gas such as SF5CF3, less than 10 to the -10 times as abundant as CO2, to be optically thin and thus have a radically different growth curve? Either I am missing something fundamental here or the entire treatment in the article is completely wrong which should be quite embarrassing for the climate lobby since this book seem to be endorsed by various tycoons.
Steven Jörsäter
PhD, Sweden
Steven Jörsäter:
You are correct about the “curve of growth”. This is covered via the result from band models in Part Four.
However, I do plan to cover it in more detail, probably in the current series: Understanding Atmospheric Radiation and the “Greenhouse” Effect. (Although I make many plans to cover subjects and some are still “in waiting”).
Water vapor is agreed by all to be the most important “greenhouse” gas. Water vapor concentration (in time and space) is a response to climate conditions and this response is one of the most challenging (and important) questions of current climate research.
You can read a little about water vapor in Clouds and Water Vapor.
Climate models calculate the amount of water vapor and you can see model results and errors in Models, On – and Off – the Catwalk – Part Two.
Lastly, I don’t know anything about the book so can’t comment. But there are many poor books on climate and many lightweight treatments of important subjects.
You will find the subject thoroughly treated in textbooks like “Radiation and Climate” by Vardavas & Taylor (2007).
It is very well known to everyone (almost everyone?) studying atmospheric radiation.
[…] run more detailed models under more exacting conditions – for example, the graph shown in CO2 – An Insignificant Trace Gas? – Part Eight – Saturation from Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the IPCC […]
I would like to know what concentration is required for the CO2 to reach saturation?
The approximately logarithmic dependence of forcing on CO2 concentration tells that gradual saturation is present over a very wide range of concentration. It starts at very low concentration like a few ppm and goes on to much higher concentrations than anybody considers possible in the Earth atmosphere.
Calculations at 25 times the present concentration, i.e. at 10000 ppm, tell that there may be actually a little less saturation at high concentration than the logarithmic formula would predict.
Rich,
What do you mean by saturation? Pekka answered your question using the meaning that is used by spectroscopists, that is basically when increasing absorption is no longer linear with number density and the absorptivity is very close to 1 at the line peak for the path length of interest. If you mean the concentration where increasing CO2 has no additional effect at all, then the answer is that there is no limit. Even if the atmosphere were pure CO2, adding more CO2 would still have an effect.
Dewitt, my understanding is that CO2 has its main absorption band at 15 microns, so isn’t possible to block all the energy in that band at some concentration level.
Taking a slightly different tack, what do you mean by concentration? Absorption is a function of density (partial density), and density changes with altitude, but concentration does not change with density. Even a pure CO2 atmosphere would become not saturated at some altitude less than top of atmosphere. More CO2 raises the altitude at which whatever level of absorption you select occurs.
Rich and Chris: If I_0 is the intensity of light entering a homogeneous solution or gas with a density of n absorbing molecules with an absorption coefficient of o, Beer’s Law tells us that the fraction of light (I_n/I_0) that passes through a distance s, is given by:
I_n/I_0 = exp(-nos) or -nos = ln(I_n/I_0)
If you are a chemist, you use log10 instead of ln, powers of 10 instead of the exponential function, and report the density of absorbing molecules in molarity. If you are a physicist studying the atmosphere, you often express the density of absorbing molecules as the product of a “mixing ratio” (0.0004 for CO2 today) and the density of the atmosphere at a particular altitude.
If we double the density of absorbing molecules to 2n, we find that the fraction of light passing through I_2n/I_0 is:
I_2n/I_0 = exp(-2nos) = [exp(-nos)]^2 = [I_n/I_0]^2
Since pressure drops with altitude, the real atmosphere is not homogeneous, but this answer is still correct. This result applies to one wavelength, but you can integrate over a range of wavelengths if you know all of the absorption coefficients.
Let’s calculate how much doubling the number of absorbing molecules will reduce transmittance at one wavelength:
I_n/I_0 I_2n/I_0 Reduction in Transmittance
99% 98% 1%
90% 81% 9%
75% 56% 19%
50% 25% 25%
25% 6.25% 19%
10% 1% 9%
1% 0.01% 0.99%
0.1% 0.0001% 0.0999%
If the fraction of light absorbed before doubling is too large OR too small, doubling reduces transmission modestly or negligibly. When the fraction of light absorbed before doubling is high and is changed negligibly by doubling, we say that absorption is “saturated”. Since doubling will always reduce transmittance to some extent, there is no unambiguous way to define a minimum concentration above which saturation “begins”.
If 50% of the light is transmitted before doubling, doubling can decrease this to 25%. Reduction in transmittance is maximal under these circumstances. The wavelengths where 10-90% of radiation passes through the atmosphere are those where doubling has the biggest impact on absorption and produce most radiative forcing. These wavelengths are on the SIDE of the major absorption bands as shown on the graph where saturation isn’t important.
Unfortunately, absorption is only half of the story! GHG emission also varies with density and is arguably MORE important than absorption. 90% of the LWR emitted by the planet comes from GHGs in the atmosphere. Doubling the concentration of a GHG has its main effect by raising the altitude (thus lowering the temperature) from which photons that escape to space are emitted. The troposphere LOSES more energy by emission than it gains by absorption – the difference is supplied by convection.
To understand the combined effect of absorption and emission and calculate radiative forcing, you need to numerically integrate the Schwarzschild equation found in part 3 of this series:
dI/ds = n*o*B(T) – n*o*I
B(T) is the Planck function (“blackbody intensity”) for a particular wavelength and causes emission to vary with temperature. (If you drop the n*o*B(T) emission term, integration gives Beer’s Law.) Doubling the density of absorbing molecules (n) doubles the rate of change in intensity of radiation with distance — but that change can be positive or negative depending on the temperature, wavelength and intensity of the incoming radiation (I). Some people make mistakes by assuming that n, I or B(T) are constants and move them outside the integral.
My intuition doesn’t extend to the results of calculating radiative forcing by numerically integrating of the Schwarzschild equation over all wavelengths and altitudes of the atmosphere. But such calculations DO include saturation. They also require that one specify the temperature and composition of the atmosphere at all altitudes; so those calculations can tell you about initial change in radiative flux caused by changes in GHGs, but not the change in temperature that will follow.
Phil B,
There are later articles that address your question in much more detail.
In brief, the absorption is very wavelength dependant.
So at 667.5 cm-1, or 14.98 μm, 95% of radiation will be absorbed in only 1m of the atmosphere at the surface.
But at 666 cm-1, or 15.015 μm, only 5% of radiation will be absorbed in this 1m path through the atmosphere.
Well, you are probably thinking, that’s not much practical difference because if 5% is absorbed in 1m then 99.4% will be absorbed in 100m (note: multiply transmissivities for each additional path length, so this result = 1 – 0.95100)
And you would be correct.
But let’s widen out a little bit more, and at 645 cm-1, or 15.50 μm, only 50% will be absorbed in 100m.
At 575 cm-1, or 17.39 μm, the whole troposphere absorbs only 20% of radiation due to CO2.
Here is a sample calculation from the surface to the tropopause:
And here is the difference between 280ppm and 560ppm (CO2 doubling from pre-industrial levels) across the whole CO2 absorption band:
Take a look at:
Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Eight
Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Nine
Thanks SoD, I will take a look at part 8 & 9. I do enjoy your site.
I hope it’s ok to ask a general question about modtran (http://forecast.uchicago.edu/modtran.html) in this thread.
When I am looking down from 0 km, the graph looks like a blackbody radiation, but the “Upward IR Heat Flux” is less than calculated by the Stefan–Boltzmann law.
The buttton “Show Raw Model Output” shows a file that says “BOUNDARY EMISSIVITY = 0.980” in one of the last lines. Is that the epsilon in the Stefan–Boltzmann law? It is not small enough to explain the difference.
Example: 1976 Standard Atmosphere, 288.2 K, 0 km, looking down.
Modtran says: 360.47 W/m2
Calculation: 288.2^4 * 5.67 * 0.98 / 100000000 = 383.34
kereng,
I haven’t noticed that before, but it seems that the calculation includes only the wavenumber range 100 – 1500 1/cm and that this range is fixed. Missing high and low tails make the difference.
Pekka is correct. I’ve actually done the calculation from 5-5000cm-1 using the Planck function and the MODTRAN curve from 100-1500cm-1 is the same. The Stefan-Boltzmann integration is from 0 to ∞ cm-1. The MODTRAN curves are not equal to zero at 100 and 1500cm-1 so you would expect that some of the emission is missed.
However, the atmosphere is completely opaque at frequencies <100cm-1 and >1500cm-1 so you’re not really missing any information.
Thank you both for your answers.
The difference will be no problem when MODTRAN is used to examine the impact of greenhouse gases. But I tried to calculate the blackbody radiation for some temperatures and thought “why not just use MODTRAN with 0 km?”
Now I see, that is not what it is made for.
kereng,
You might find that the series Visualizing Atmospheric Radiation is a help.
I wrote it sometime after this series, with the aid of a line-by-line model (in MATLAB) to calculate all kinds of interesting results.
Results include demonstrating how “saturation” is something that is so wavelength dependent – see Visualizing Atmospheric Radiation – Part Seven – CO2 increases, which includes graphs like this one:
Reading all the way to the bottom with nice graphs and the corresponding temperatures. I find the conclusion in Watts per Meter Squared, a unit not mentioned in all the the text above.
To wit:
“Doubling CO2 from pre-industrial levels will lead to an increased “radiative forcing” of around 3.7 W/m2, and this part of climate science at least, is well understood.”
Elsewhere, my favorite quote is from Dr. Hansen in chapter 8 of the IPCC’s AR4 page 631:
“In the idealised situation … the climate response to a doubling of atmospheric CO2 … would be around 1.2°C”
Is that about right, basic climate sensitivity of CO2 is about 1.2°C?
Steve,
Explained simply in Opinions and Perspectives – 7 – Global Temperature Change from Doubling CO2
The saturation argument has come stronger again after the paper of W. A. van Wijngaarden and W. Happer(2020): Dependence of Earth’s Thermal Radiation on Five Most Abundant Greenhouse Gases. I think most of the headlines they made are based om a misunderstanding of the paper, when it is claiming that more CO2 doesn`t give higher surface temperatures. And I think that basically the paper is in agreement with SoD. There may be some differences in the calculation of increase in radiative forcing with more CO2, but Wijngaarden and Happer use a doubling of CO2 from 400ppm to 800ppm. This gives a radiative forcing of 3,0 W/m2.
SoD: “Doubling CO2 from pre-industrial levels will lead to an increased “radiative forcing” of around 3.7 W/m2, and this part of climate science at least, is well understood.” This doubling is from 280 to 560 ppm CO2.
One interesting calculation in the Wijngaarden/Happer paper is the decreased radiative forcing in the middle of the broadest CO2 band: “An exception is the band of frequencies near the center of the exceptionally strong bending-mode band of CO2 at 667 cm−1 . Here doubling CO2 moves the emission heights to higher, warmer altitudes of the stratosphere, where molecules can more efficiently radiate heat to space.”
Link to paper Wijngaarden and Happer (2020), WH20: https://arxiv.org/pdf/2006.03098.pdf
NK: Climate sensitivity normally refers to a three-dimensional model of our planet with clouds and atmospheric temperature profiles and composition generated by the model. The authors of WH20 calculated climate sensitivity for three ONE-DIMENSIONAL MODELS of the atmosphere with NO CLOUDS (and no cloud feedback). In one model, there is no water vapor feedback (fixed absolute humidity) or lapse rate feedback (6.5 K/km fixed lapse rate). In the second model, water vapor feedback is added by changing to fixed relative humidity. In the third model, lapse rate feedback is added by using a pseudoadiabatic lapse rate. WH20 uses more sophisticated radiative transfer calculations than earlier groups: more weak lines, no water vapor continuum, 500 levels of atmosphere to a 85 km TOA, and improved line shape (?) further from the line center.
Similar radiation transfer calculations were performed with one-dimensional models nearly fifty years ago and in 2019 by Kluft et al (K19) using the Rapid Radiative Transfer Model for GCMs (RRTMG) being used by many AOGCMs. In a sense, radiative transfer calculations with such one-dimensional models serve as a benchmark for effect of changing methodology in radiative transfer calculations – or would be a benchmark, if there weren’t minor differences in the vertical profile of water vapor and temperature near the tropopause. (The K19 model may be slanted towards a 1D model for tropical oceans rather than the planet as a whole.)
K19: https://journals.ametsoc.org/view/journals/clim/32/23/jcli-d-18-0774.1.xml?tab_body=fulltext-display
Is there anything critically new in these papers or their [minor] disagreements? Probably not. However, from K19, I gained a greater appreciation for the fact that the forcing from 2XCO2 is not a fixed 3.7 W/m2/doubling. That value comes from radiative transfer calculations for change in the net LWR flux at the tropopause or at the TOA after the stratosphere adjusts. The forcing for 2XCO2 can also be calculated for these one dimensional models and forcing changes as water vapor feedback and lapse rate feedback can added to these one-dimensional models. When changes to the troposphere are allowed to influence forcing, we refer to effective radiative forcing. Every climate model has different effective radiative forcing for CO2 and other GHGs and agents. I thought these differences arose in some mysterious was from changes in clouds and other phenomena associated with climate change that models might not get right, since ERFs do differ substantially from model to model. However, the K19 one-dimensional model shows that the instantaneous forcing for 2XCO2 is 2.9 W/m2, but rises to 4.7 W/m2 when water vapor and lapse rate feedbacks are operating. So these differences between iRF and ERF are not necessarily the result of mysterious processes in AOGCMs. These differences can be the result of well understood changes in water vapor and lapse rate. K19 notes that the instantaneous forcing for 2XCO2 in the average CMIP5 model is down to 2.9 W/m2, while ERFs vary widely but average 3.45 W/m2.
Thank you for your comment Frank.
I think the work of Kluft et al is very important. It is climate science at its best.
It make me wonder why it has taken so long to get some reasonable research about forcing and feedback. Perhaps the politicization of science has lagged the development of climate knowledge by 10 to 20 years?
Or as Madame Curry says: Uncertainty is the enemy of established orthodoxy.
Myhre came up with a figure of 3.7 W/m2 for the forcing from 2XCO2 by considering a collection of 1D models that covered various latitudes and seasons. Both K19 and WH20 consider only a single 1D column (and not identical columns). Therefore neither study can be considered to provide a “global” forcing for 2XCO2. This is unfortunate, but may be fixed in follow on publications using a collection of 1D models
Of course, the ultimate collection of 1D models is an AOGCM. Those models given us a “global” Planck feedback of 3.2 W/m2 that takes into account the variation in surface temperature (and surface emissivity) everywhere on the at roughly 1,000,000 surface locations and radiative transfer from there to space. The 1D equivalent of this is a graybody model with Ts = 288 K, emissivity 0.615 and a Planck feedback (dW/dTs) = 3.3 W/m2. The 1D model works surprisingly well given that Ts varies from almost 100 degK over the planet.
However water vapor and lapse rate feedbacks in the output from climate models are now being analyzed in terms of the combined WV+LR feedback expected for a planet were relative humidity remains constant and the lapse rate is isentropic or pseudoadiabatic. (K19 uses the former term and WH20 the latter term. I would benefit from a review of this terminology, but I assume the two are equivalent.). So, if we think of AOGCMs being composed of a million or so 1D columns, current analysis can produce a global WV+LR feedback at constant RH and isentropic lapse rate (“CRH+ILR WV+LR”), and model-specific deviations in WV and LR feedbacks from this ideal. Next time I’m looking at a paper that analyzes feedbacks from models, I’ll need to study this more closely.
If I had my own climate model, at each time point I would artificially raise and lower the temperature by 1, 2, 3, 4, and 5 degC in each grid cell and use the radiation transfer model to calculate pdW/pdTs for every grid cell at that timepoints. Then I’d calculate dW/dTs for the same temperature steps after adjusting to constant relative humidity and isentropic lapse rate in each column of grid cells. Then I’d move on to as many time points over as many decades as needed. I’m fairly sure that the partial derivatives that come from “radiative kernels” are not calculated this way, but instead abstracted from the changes in temperature the model produces by a process I don’t fully understand.