While writing an article on Lapse Rates and Potential Temperature I realized, from questions on this blog and from comments on other blogs, that the subject of stability perhaps wasn’t so clear.
So in advance of that article, here are some basics on stability and density in fluids. Science, unlike for example most of history and politics, is one subject built on another. If we fail to grasp fundamental concepts clearly then the more difficult subjects, the next steps, will always be a mystery.
Therefore, if you reach the end of this article and don’t feel that the subject has been clearly explained, ask away.
Stability
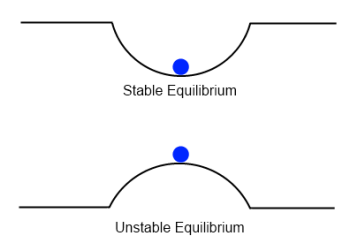
This can be an involved subject but we only want to consider a very simple aspect of stability. Take a look at the two cases below. In both cases the ball is not moving. It is in equilibrium:
Figure 1
Everyone can appreciate the difference between the two from common experience.
The first case is stable – push the ball a little to the left or right and it moves back to the center, overshoots, comes back, overshoots and so on.. and eventually ends up stationary at its starting point. It oscillates. Real world friction dissipates the energy injected into the system from the initial disturbance and causes the ball to finally return to rest.
The second case is unstable – push the ball a little to the left or right and it accelerates away and never returns to its starting point.
The reason for stating the apparent obvious is that both are in equilibrium. It is only with some kind of disturbance that the unstable situation “rearranges the energy of the system”. Without some kind of disturbance nothing happens. Of course, depending on the exact setup the disturbance needed might only be tiny.
Another way to think about stability is potential energy vs kinetic energy.
For newcomers to physics or mechanics, a non-technical description is:
- potential energy is the energy stored in a system
- kinetic energy is the energy from movement
Often with simple motion we can think about potential energy being converted into kinetic energy and vice-versa. Take a bouncy ball released from height so that it drops to the floor. It starts with zero kinetic energy and by the time the ball has hit the floor the potential energy (height) has been turned into kinetic energy (motion). Then the ball bounces up in the air, stops at a point and returns to the floor.
Energy is dissipated along the way by the friction due to air, and the energy lost in the impact so eventually the ball finishes at rest on the floor.
When a mass is moved higher in a gravitational field the potential energy is increased. When a mass is moved lower in a gravitational field the potential energy is reduced.
When potential energy is reduced, the change can be released as kinetic energy (like a falling ball). If however you increase the height of the mass then the increased potential energy can only consume kinetic energy (or it has to be supplied from elsewhere).
Take a look back at the two scenarios in figure 1. In the first scenario a disturbance increases potential energy so we have to do work to move it up the side of the container. Therefore, it is stable.
In the second scenario a disturbance reduces potential energy so we don’t need to do any work to create kinetic energy, or motion. (Only the small work needed to disturb the ball from its position). Therefore, it is unstable.
Hopefully, this is so clear that readers wonder why I am still explaining it..
Density in an Incompressible Fluid
Let’s look at the simple case of an incompressible fluid like water where density depends on temperature but not on pressure.
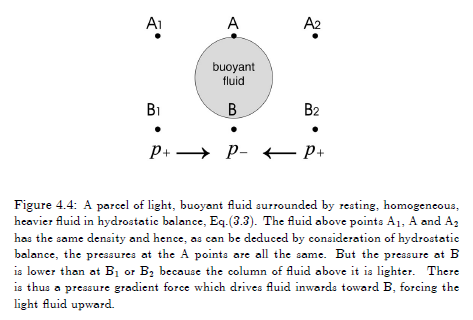
And let’s look at why it is that lighter fluids actually rise:
Figure 2
The description in the figure 2 caption is the best (i.e., simplest) explanation of why lighter fluids rise.
Displacement of a Parcel in An Incompressible Fluid
So consider a fluid parcel being displaced upwards. For now, it doesn’t matter why or how. Just that it is moved. If the movement is done quickly enough it will not lose or gain heat during its journey (because heat exchange can only take place by diffusion, which is a very slow process in most liquids).
We call this movement without exchange of heat (with the surroundings) an adiabatic process.
And because the fluid is incompressible it will do no work on its surroundings, so its internal energy will be conserved. As a result its temperature will stay the same and so its density will also stay the same.
If the density of the surrounding fluid increases with height then this parcel will accelerate upwards, because the parcel has a lower density than its environment and so (as in figure 2) the differential pressure will “push it” upwards.
If the density of the surrounding fluid reduces with height then the parcel will be slowed down and experience a restoring force back to where it came from.
Now usually density is related to temperature. In the case of water, as temperature is increased density is decreased.
So if the temperature of the surrounding fluid increases with height, the density decreases with height and displaced parcels of fluid have a restoring force back to their origin. So in this case (this normal case) the fluid is stable.
If the temperature of the surrounding fluid decreases with height, the density increases and displaced parcels accelerate in the direction in which they started moving. So in this case (this strange case) the fluid is unstable. Clearly the instability will result in fluid movement and therefore ultimately in stability.
So it’s all about the difference between the change in temperature of a displaced parcel vs the change in temperature with height of the environment. And the displacement can take place for many different reasons. Don’t think about the reason for the initial displacement – as with figure 1 just think about whether a displacement will result in a restoring force back to the starting point, or in an acceleration away from the starting point.
Here is a very educational example of convection as a result of heating a liquid from below. This example comes from the webpages accompanying the Marshall & Plumb (2008) textbook – I recommend the video link within that page (but read the text and diagrams first):
Figure 3 – Click for movie
And in the next article we will consider what happens with a compressible fluid like air. In that case when a parcel of air moves upwards, and expands because of lower pressure, its temperature drops. That makes the stability question slightly more complicated, but the same principles apply.
Further reading – new article: Potential Temperature



Nice read. It reminded me a lot of “Resilience Thinking” which was a text for my grad program. They take the physical system you described (a ball in a bowl) and translate that to complex systems such as ecosystems or even social systems. Interestingly, they do not discuss systems which are in equilibrium but inherently unstable, which I find to be interesting not just from a physical perspective but as you apply that concept as an analogy to other types of systems (like ecosystems or social systems).
Thanks again for your good work.
Fascinating demonstration. There was an interesting piece on the History Channel about boilover oil explosions. According to the expert a layer of heat travels (at one foot per hour) downward until it comes in contact with water on the bottom of the oil tank. kaboom. I’m not sure if you’d say the heat moving downward was convecting or conducting.
[…] Comments « Density, Stability and Motion in Fluids […]
[…] lapse rate has already been covered in Potential Temperature and for those new to the subject Density, Stability and Motion in Fluids is also worth a […]
[…] Density, Stability and Motion in Fluids « The Science of DoomDensity-Functional Theory for Complex Fluids. Jianzhong Wu and Zhidong Li. Department of Chemical and Environmental Engineering, University of California, … […]
[…] Convection moves heat if the atmosphere above is too cold (see Potential Temperature and Density, Stability and Motion in Fluids). Energy retained increases the temperature of the layer. Energy lost reduces the temperature of […]