The Science of Doom

Introduction

This is the long-promised eighth part of the seven-part series on CO2 basics. Part One introduced the idea of CO2 with some basic concepts. Part Three opened up the radiative transfer equations, not solvable on the pocket calculator. Part Five showed two important solutions. And Part Seven showed the current best solutions along with what “radiative forcing” actually means, and where the IPCC logarithmic formula comes from.

The even numbers in the series shouldn’t be ignored either, especially Part Four which explained band models vs line by line (LBL) calculations.

Now the concept of “saturation” is one that everyone wants an answer to. Saturation, however, means different things to different people. Consider shining a torch through sand. Once you have a few millimeters thickness of sand, no light gets through. So adding a meter of sand won’t make any difference. That’s how most people are thinking about saturation and that is the perspective that we will look at in this article:

• For CO2 – will doubling CO2 (from pre-industrial) levels add any more warming?
• And will doubling it again add any more?

The answer already noted in earlier parts of this series is “yes”, but of course, everyone wants to know why, or what this means for the idea of “saturation”.

Boringly, we will first look at some results from the radiative transfer equations.

The RTE

The RTE were introduced in Part Three – these are the full solution to the problem of absorption and emission by each “layer” of the atmosphere. The equations are challenging to solve because every absorption line for each gas has to be calculated, and a similar process goes on for emission of radiation by each layer in the atmosphere. It’s not some kind of mystery, it’s just very computationally expensive, so big computers and plenty of time are required. See Part Six for an example of theory matched up with measurement.

A fairly recent model inter-comparison effort was done which included the results from LBL (line by line spectra) for increases in CO2 and other trace gases. The inter-comparison focused on comparing the results from many GCM’s with the LBL results (see note 1). Although it wasn’t the focus of the paper, a graph of radiative forcing vs wavelength was included:

Longwave radiative forcing from increases in various "greenhouse" gases

This is from W.D. Collins (2006), reference below. (Interested students will note that the vertical axis appears to have the wrong units, I have emailed Prof Collins to ask about this – update, he has confirmed that the vertical axis is incorrect).

The blue line is the “radiative forcing” vs wavelength for CO2.

The best way to explain why something called radiative forcing is used is that is a “standardization tool”. A simple explanation of radiative forcing is that it is the extra downward radiation at the tropopause before feedbacks from the surface and the lower atmosphere (the troposphere). You can see a little more on this concept in Part Seven.

Now that’s over with – check out the graph. Red is a methane increase from pre-industrial levels to current levels, green is a nitrous oxide increase and yellow is the effect of a possible increase in water vapor. The important point is that for the increases for CO2 (blue), most of the increase in energy is not in the center of the 15μm CO2 band.

It is interesting to see that the effect of the center of the CO2 band is not zero, although it is very low, but the main increase is in “the wings” of the band.  This is the primary reason why doubling CO2 provides a significant increase in “radiative forcing” – or more heat into the surface and lower atmosphere.

To demonstrate this result wrong simply requires the interested student to prove the RTE (radiative transfer equations) wrong, or the line by line database of absorption for CO2 wrong, or the particular methods of solving the RTE in these models wrong. So it could all be over here.. but of course there’s more to think about.

By the way, the line by line method uses each individual absorption line stored in a huge database (like HITRANS), but the story is yet more complicated because each line has a definite width and a line shape, and these factors depend on the pressure and temperature. For example, each CO2 line is broader closer to the surface than it is high up in the troposphere. And the shape also changes. More on this at some later date, maybe..

Some Conceptual Ideas – Absorption and Re-emission and Planck Blackbody Radiation

Everyone likes to understand a subject conceptually. This is sometimes difficult but these mental models are very helpful if they can provide us with understanding. However, it is important to remember that just because something seems “conceptually right” doesn’t mean it is, and vice-versa. In the end, a theory stands or falls on the ability to falsify it and not on our ability to “picture it”. (The popularity of a theory on the other hand..)

The most important conceptual idea to understand is that the radiation from the surface which is absorbed by CO2 doesn’t just disappear. (The same applies to all “greenhouse” gases but I’ll stay with using CO2 as the prime example).

We will consider the atmosphere in a number of vertical “layers”, stacked one on top of the other. CO2 absorbs energy, shares it with other molecules in the atmosphere and therefore that layer of the atmosphere heats up (see note 2). Some molecules, like nitrogen and oxygen, have no ability to absorb or emit longwave radiation (see CO2 – Part Two), but by collision with molecules like CO2 and water vapor they will share energy and be at the same temperature.

For those new to the basics of radiation, here are two comparison radiation curves for a blackbody at the typical temperature of the earth’s surface (288K or 15ºC) and at a typical temperature at the top of the troposphere
(220K or -53ºC).

Blackbody radiation at 288K (15'C) and 220K (-53'C)

You can see that the radiation emitted by a 288K body is a lot higher than the 220K body (the total integrated across all wavelengths is greater by a factor of 3). You can also see that for the colder body the energy has shifted to longer wavelengths (the wavelength of maximum radiance has moved from 10.1μm for 288K to 13.2μm for 220K).

A blackbody is a perfect radiator and absorber – so think of these curves as the ideal – the best that might be attained.

The surface of the earth is very close to a blackbody (the emissivity is close to 1) for longwave radiation – see The Dull Case of Emissivity and Average Temperatures. The atmosphere is not even close to being a blackbody. Atmospheric gases absorb and emit radiation at well-defined spectral lines. But the Planck function – as the curves above are called – tells us the “shape” that these spectral lines fit under.

Here is a measurement of outgoing longwave radiation by satellite (the “upward” radiation) with the Planck function for different temperatures overlaid:

Outgoing longwave radiation at top of atmosphere, Taylor (2005)

I’ve added “wavelength” under “wavenumber” on the horizontal axis for convenience.

What this shows is the effective temperature of radiation for each part of the longwave spectrum. Take a look at the spectrum between 10-13μm. The radiation between these wavelengths corresponds to around 270K. Now look at the spectrum between 14-16μm. The radiation here corresponds to around 223K.

That’s because there is not much absorption by the atmosphere in the 10-13μm spectrum, consequently most of the radiation from the surface goes straight out to space.

By comparison, absorption is very high between 14-16μm so almost no radiation from the surface goes straight out to space.

But – and here is the conceptual idea I want to get across – why is there any radiation between 14-16μm (measured by satellite)? Absorption by CO2 in the center of the 15um band is so strong that surely there should be no radiation – or nothing measurable..

This subject was covered in some detail in The Earth’s Energy Budget – Part Three, but essentially each layer of the atmosphere also radiates energy. If CO2 can absorb radiation at 15μm, it can also radiate at 15um. But it radiates according to its temperature. So when you see the measurement by satellite of the 15μm band reflecting a temperature of 223K you know that the bulk of the radiation was emitted by CO2 at a temperature of 223K (-50ºC).

For the temperature of CO2 to be 223K (-50ºC) means that it must be located around the top of the troposphere:

Pressure and height vs temperature, Bigg 2005

How does all of this relate to “saturation”?

One Conceptual Saturation Idea – it Can’t Get any Colder

One way of thinking about the absorption and re-emission of 15μm radiation is like this – if the 15μm band is already radiating from the coldest part of the atmosphere, then increasing CO2 will have no effect on the earth’s energy balance because even if the 15μm band radiates from higher up, it won’t get any colder and, therefore, the amount of radiation at this wavelength won’t be decreased.

But this is just in the center of the 15μm band. As we saw from the detailed line by line calculation in the paper by Collins, the bulk of the reduction in outgoing radiation is from 13-14.5μm and from 15.5-17μm.

You can play around with these ideas by using the Modtran model. It uses band models (not line by line calculations) but band models give reasonable results. What is interesting is to increase the amount of CO2 and (looking down from 70km) see what effect takes place at 15μm – not much in the center of the band – for the reasons already explained: the atmosphere doesn’t get any colder.

However, you will notice that the width of this heavily saturated band increases – as with the more accurate treatment by Collins at the beginning of the article.

Another Conceptual Saturation Idea – the Two Slab Model

There is a simple model which is worth looking at by Barton Paul Levenson. What it demonstrates is that if you take a gas which absorbs across all longwave (>4μm) wavelengths, then even if this gas totally absorbs all radiation in the lower part of the atmosphere, adding more of this gas will still increase the surface temperature.

This is for the simple reason that the incoming solar energy at the top of the atmosphere must be balanced by energy leaving from the top of the atmosphere – otherwise temperature will increase (see The Earth’s Energy Budget – Part Two). And if one “layer” of the atmosphere totally absorbs it will still radiate energy to the atmosphere above. As the atmosphere gets thinner it will eventually be radiating out to space – and it’s at these levels (heights) in the atmosphere that adding more CO2 will reduce the outgoing radiation.

And if the outgoing radiation is reduced then there will be more incoming solar radiation than outgoing longwave radiation and the surface/atmosphere will heat up. Take a look at his model.

Fascinating as it is, I don’t think it answers the question of “saturation” or not by CO2 in the actual climate.

The reasons are complex, but read on if you are interested..

This is because the center of the CO2 band (15μm) is already radiating from the coldest part of the atmosphere. Therefore, increasing CO2 can’t reduce the radiation from the 15um band – unless more CO2 can change the temperature structure by lifting the height of the tropopause which will result in a colder tropopause.

In a climate with a “gray” absorber (one that absorbs equally across all wavelengths) an increase in this absorber would almost certainly change the tropopause height. Why? The tropopause is the point at which the atmosphere becomes optically thin and so radiation to space can take place from that point. Radiation is now more effective than convection at moving heat upwards through the atmosphere. So a climate model (even a more refined one with many layers) with a gray absorber will do as Levenson’s model predicts.

But a climate model with an almost transparent atmosphere in places will respond in less clear ways. Modeling the height and temperature of the tropopause is a difficult challenge and not something to get into here.

For those new to this topic, it probably doesn’t make a lot of sense. Think of this section as a “by the way an interesting idea about saturation..”

Conclusion

Most of the confusion about “saturation” of CO2 comes from a lack of understanding of how both absorption and re-emission are linked in the atmosphere.

The confusion also arises because atmospheric physics uses the term “saturation” to mean something more technically defined – that the atmosphere is “optically thick” at that wavelength. Two groups of people using the same word with a different (but related) meaning inevitably leads to confusion.

The radiative transfer equations are the basic and proven equations for the absorption and radiation of energy in the atmosphere. Solving these equations using line by line calculations shows that most of the additional effect from more CO2 occurs in the “wings” of the band and not in the band center.

Doubling CO2 from pre-industrial levels will lead to an increased “radiative forcing” of around 3.7 W/m², and this part of climate science at least, is well understood.

Demonstrating that this result is wrong requires over-turning the radiative-convective model which currently calculates outgoing longwave radiation (at top of atmosphere) and downward longwave radiation (at the surface) quite accurately compared with measurements.

The mental models that many people have about saturation are not necessarily what is actually happening in the atmosphere.

Notes

Note 1 – The specific conditions for this inter-comparison (by Collins et al) were slightly different from the standardized method of “radiative forcing” in that they didn’t include stratospheric adjustment – allowing the stratospheric temperatures to achieve equilibrium after the changes in trace gases. This has a small but significant effect on the overall total values of radiative forcing, but the results are useful because the graph of radiative forcing against wavelength is given, whereas most results are simply given as a W/m² value.

Note 2 – The subject of molecules of CO2 and water vapor absorbing energy and sharing this energy by collision with other molecules close by was covered to a limited extent in How Much Work Can One Molecule Do?

References

Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the IPCC AR4, W.D. Collins et al, Journal of Geophysical Research (2006)

Elementary Climate Physics, F.W. Taylor (2005) Oxford University Press

Read Full Post »

Redefining Physics

Dexter Wright re-defined the radiative transfer equations in his American Thinker article “Global Warming on Trial” with these immortal words:

Clearly, H2O absorbs more than ten times the amount of energy in the IR spectrum as does CO2. Furthermore, H2O is more than one hundred times more abundant in the atmosphere than CO2. The conclusion is that H2O is more than one thousand times as potent a greenhouse gas (GHG) as CO2.With such immutable facts facing the EPA, how will they explain their stance that CO2 is a greater danger to the public than water vapor?

So far, neither Dexter, nor his enthusiastic supporters at American Thinker have got around to updating the now defunct Wikipedia article on the Radiative Transfer Equations which describe the “old school” mathematics and are slightly more complicated.. (See also CO2- An Insignificant Trace Gas? Part Three.)

But in wondering why they hadn’t, it did occur to me that non-linearity is something that most people struggle with. Or don’t struggle with because they’ve never heard of it.

I think that the non-linear world we live in is not really understood because of the grocery factor..

(And it would be impolite of me to point out that Dexter didn’t know how to interpret the transmittance graphs he showed).

Groceries and Linearities

Dexter is in the supermarket. His car has broken down so he walked a mile to get here. He has collected a few groceries but his main buy is a lot of potatoes. He has a zucchini in his hand. He picks up a potato in the other hand and it weighs three times as much. He needs 100 potatoes – big cooking plan ahead – clearly 100 potatoes will weigh 300 times as much as one zucchini.

Carrying them home will be impossible, unless the shopping trolley can help him negotiate the trip..

Perhaps this is how most people are thinking of atmospheric physics.

In a book on Non-linear Differential Equations the author commented (my memory of what he stated):

The term “non-linear differential equations” is a strange one. In fact, books about linear differential equations should be called “linear differential equations” and books about everything else should just be called “differential equations” – after all, this subject describes almost all of the real-world problems

What is the author talking about?

Perhaps I can dive into some simple maths to explain. I usually try and avoid maths, knowing that it isn’t a crowd-puller. Stay with me..

If we had the weight of a zucchini = M_z, and the weight of a potato = M_p, then the weight of our shopping expedition would be:

Weight = M_z x 1 + M_p x 100, or more generally

Weight = M_z N_z + M_p N_p , where N_z = number of zucchinis and N_p = number of potatoes. (Maths convention is that AB means the same as AxB to make it easier to read equations)

Not so hard? This is a linear problem. If you change the weight (or number) of potatoes the change in total is easy to calculate because we can ignore the number and weight of zucchinis to calculate the change.

Suppose instead the equation was:

Weight = (M_z N_z) N_p² + (M_p N_p) N_z³

What happens when we halve the number of potatoes? It’s much harder to work out because the term on the left depends on the number of zucchinis and the number of potatoes (squared) and the term on the right depends on the number of potatoes and the number of zucchinis (cubed).

So the final result from a change in one variable could not be calculated without knowing the actual values of the other variables.

This is most real-world science/engineering problems in a nutshell. When we have a linear equation – like groceries but not engineering problems – we can nicely separate it into multiple parts and consider each one in turn. When we have a non-linear equation – real world engineering and not like groceries – we can’t do this.

It’s the grocery fallacy. Science and engineering does not usually work like groceries.

Stratospheric Water Vapor

In many blogs, the role of water vapor in the atmosphere (usually the troposphere) is “promoted” and CO2 is “diminished” because of the grocery effect. Doing the radiative transfer equations in your head is pretty difficult, no one can disagree. But that doesn’t mean we can just randomly multiply two numbers together and claim the result is reality.

A recent (2010) paper, Contributions of Stratospheric Water Vapor to Decadal Changes in the Rate of Global Warming by Solomon and her co-workers has already attracted quite a bit of attention.

This is mainly because they attribute a significant proportion of late 20th century warming to increased stratospheric water vapor, and the last decade of cooling/warming/pause in warming/statistically significant “stuff” (delete according to preferences as appropriate) to reduced water vapor in the stratosphere.

(If you are new to the subject of the stratosphere, there is more about it at Stratospheric Cooling and useful background at Tropospheric Basics ).

There is much that is interesting in this paper.

Stratospheric water vapor - SW and LW effect vs altitude, Solomon (2010)

Firstly, take a look at the basic physics. The graph on the left is the effect of 1ppmv change in water vapor in 1km “layers” at different altitudes (from solving the radiative transfer equations).

Notice the very non-linear effect of “radiative forcing” of stratospheric water vapor vs height. This is a tiny 1ppmv of water vapor. Higher up in the stratosphere, 1 ppmv change doesn’t have much effect, but in the lower stratosphere it does have a significant effect. Very non-grocery-like behavior..

Unfortunately, historical stratospheric water vapor measurements are very limited, and prior to 1990 are limited to one site above Boulder, Colorado. After 1990, especially the mid-1990’s, much better quality satellite data is available. Here is the Boulder data with the later satellite data for that latitude “grafted on”:

Stratospheric water vapor measured 40'N, 1980-2010, Solomon (2010)

And the global changes from post-2000 less pre-2000 from satellite data:

Stratospheric water vapor change, measured vs latitude, Solomon (2010)

It looks as though the major (recent) changes have occurred in the most sensitive region – the lower stratosphere.

The paper comments:

Because of a lack of global data, we have considered only the stratospheric changes, but if the drop in water vapor after 2000 were to extend downward by 1 km, Fig. 2 shows that this would significantly increase its effect on surface climate.

The calculations done by Solomon compare the increases in radiative forcing from changes in CO2 with the stratospheric water vapor changes.

Increases in CO2 have caused a radiative forcing change of:

• From 1980-1996, about +0.36 W/m²
• From 1996-2005, about +0.26 W/m²

Changes in stratospheric water vapor have caused a radiative forcing change of:

• From 1980-1996, between 0 and +0.24 W/m²
• From 1996-2005, about -0.10 W/m²

The range in the 1980-1996 number for stratospheric water vapor reflects the lack of available data. The upper end of the range comes from the assumption that the changes recorded at Boulder are reflected globally. The lower end that there has been no global change.

What Causes Stratospheric Water Vapor Changes?

There are two mechanisms:

• methane oxidation
• transport of water vapor across the tropopause (i.e., from the troposphere into the stratosphere)

Methane oxidation has a small contribution near the tropopause – the area of greatest effect – and the paper comments that studies which only consider this effect have, therefore, found a smaller radiative forcing than this new study.

Water transport across the tropopause – the coldest point in the lower atmosphere – has of course been studied but is not well-understood.

Is this All New?

Is this effect something just discovered in 2010?

From Stratospheric water vapour changes as a possible contributor to observed stratospheric cooling by Forster and Shine (1999):

This study shows how increases in stratospheric water vapour, inferred from available observations, may be capable of causing as much of the observed cooling as ozone loss does; as the reasons for the stratospheric water vapour increase are neither fully understood nor well characterized, it shows that it remains uncertain whether the cooling of the lower stratosphere can yet be fully attributable to human influences. In addition, the changes in stratospheric water vapour may have contributed, since 1980, a radiative forcing which enhances that due to carbon dioxide alone by 40%.

(Emphasis added)

From Radiative Forcing due to Trends in Stratospheric Water Vapour (2001):

A positive trend in stratospheric H2O was first observed in radiosonde data [Oltmans and Hofmann, 1995] and subsequently in Halogen Occultation Experiment (HALOE) data [Nedoluha et. al., 1998; Evans et. al., 1998; Randel et. al., 1999]. The magnitude of the trend is such that it cannot all be accounted for by the oxidation of methane in the stratosphere which also show increasing trends due to increased emissions in the troposphere. This leads to the hypothesis that the remaining increase in stratospheric H2O must originate from increased injection of tropospheric H2O across the tropical tropopause.

And back in 1967, Manabe and Wetherald said:

It should be useful to evaluate the effect of the variation of stratospheric water vapor upon the thermal equilibrium of the atmosphere, with a given distribution of relative humidity.. The larger the stratospheric mixing ratio, the warmer is the tropospheric temperature.. The larger the water vapor mixing ratio in the stratosphere, the colder is the stratospheric temperature..

Emphasis added – note that this paper was discussed a little in Stratospheric Cooling

Conclusion

The potential role of stratospheric water vapor on climate is not a new understanding – but finally there are some observations which can be used to calculate the effect on the radiative balance in the climate.

The paper does illustrate the non-linear effect of various climate mechanisms. It shows that small, almost unnoticed, influencers can have a large effect on climate.

And it demonstrates that important climate mechanisms are still not understood. The paper comments:

It is therefore not clear whether the stratospheric water vapor changes represent a feedback to global average climate change or a source of decadal variability. Current global climate models suggest that the stratospheric water vapor feedback to global warming due to carbon dioxide increases is weak, but these models do not fully resolve the tropopause or the cold point, nor do they completely represent the QBO, deep convective transport and its linkages to SSTs, or the impact of aerosol heating on water input to the stratosphere. This work highlights the importance of using observations to evaluate the effect of stratospheric water vapor on decadal rates of warming, and it also illuminates the need for further observations and a closer examination of the representation of stratospheric water vapor changes in climate models aimed at interpreting decadal changes and for future projections.

References

Contributions of Stratospheric Water Vapor to Decadal Changes in the Rate of Global Warming, by Solomon et al, Science (2010)

Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity, by Manabe and Wetherald, Journal of Atmospheric Sciences (1967)

Stratospheric water vapour changes as a possible contributor to observed stratospheric cooling, by Forster and Shine, Geophysical Research Letters (1999)

Radiative Forcing due to Trends in Stratospheric Water Vapour, Smith et al, Geophysical Research Letters (2001)

Read Full Post »

In 1967 Journal of Atmospheric Sciences published the paper: Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity by Manabe and Wetherald.

Here is one interesting model projection:

Model predictions 1967

The corresponding note says:

Stratospheric cooling from increasing CO2

Can this be true? How can “greenhouse” gases reduce temperature? Is this another “global warming causes more snow storms” type story?

First, a little about the stratosphere.

Stratospheric Basics

Atmospheric Pressure and Temperature, Bigg (2005)

The stratosphere is the region of the atmosphere from around 10km to 50km. In pressure terms it’s the pressure between about 200mbar and 1mbar.

Ultraviolet radiation is almost completely absorbed in the stratosphere. The high energy photons of wavelength less than 0.24μm can break up molecular oxygen, O2, into atomic oxygen, O+O.

O2 and O combine to create O3, or ozone, which is again broken up with absorption of more ultraviolet.

Ozone production is greatest at a height around 25km. At higher levels, there are too few oxygen molecules to intercept all of the photons. At lower levels, there are few high energy photons left.

Here’s an interesting way of seeing how the absorption of solar energy at different wavelengths changes as thicker sections of the atmosphere,  especially the stratosphere, are traversed:

Absorption effects of different “amounts” of the atmosphere, Taylor (2005)

The reason why the troposphere (lower atmosphere) warms from the bottom is that once the UV is absorbed the atmosphere is mostly transparent to the rest of the solar radiation. Therefore, the radiation passes straight through and is absorbed by the earth’s surface, which warms up and consequently warms the atmosphere from beneath.

Air that warms expands, and so rises, causing convection to dominate the temperature profile of the lower atmosphere.

By contrast, the stratosphere is warmer at the top because of the effect of solar absorption by O2 and O3. If there was no absorption by O2 or O3 the stratosphere would be cooler at the top (as it would only be heated from underneath by the troposphere).

Just about everyone has heard about ozone depletion in the stratosphere due to CFCs (and other chemicals). Less ozone must also cause cooling in the stratosphere. This is easier to understand than the model results at the beginning (from increased “greenhouse” gases). Less ozone means less ability to absorb solar radiation. If less energy is absorbed, then the equilibrium stratospheric temperature must be lower.

Stratospheric Temperature Trends

Temperature measurements of the stratosphere are limited. We have satellite data since 1979 which doesn’t provide as much vertical resolution as we need. We have radiosonde data since the 1940s which is limited geographically and also is primary below 30hPa (around 25km).

Lots of painful work has gone into recreating temperature trends by height/pressure and by latitude. For example, in the 2001 review paper by Ramaswamy and many co-workers (reference below), the analysis/re-analysis of the data took 23 of the 52 pages.

Here is one temperature profile reconstruction from Thompson and Solomon:

Stratospheric Temperature Trends 1979-2003, Thompson (2005)

From Thompson & Solomon (2005):

From 1979 to 1994, global-mean stratospheric temperatures dropped by 0.75 K / decade in the stratosphere below 35 km and 2.5 K / decade near 50 km

Stratospheric temperature trends by pressure, 1979-2007, Randel (2008)

Before explaining why more CO2 and other trace gases could cause “stratospheric cooling”, it’s worth looking at the model results to understand the expected temperature effects of less ozone – and more CO2.

Observations and Recent Model Results

Notice that in the 1967 paper the predicted temperature drop was larger the higher up in the stratosphere. The effects of ozone are more complex and also there is more uncertainty in the ozone trends because ozone depletion has been more localized.

Here are model results for ozone – the best estimate of the observed temperature changes are in brown but aren’t expected to match the models because ozone is only one of the factors affecting stratospheric temperature:

Stratospheric observations and models for ozone changes, Shine (2003)

Note that the effect of ozone depletion has a projected peak cooling around 1hPa (50km) and a second peak cooling around 80hPa.

Now the same paper reviews the latest model results for stratospheric temperature from changes in “greenhouse” gases:

 

Stratospheric observations and models for “greenhouse” gas changes, Shine (2003)

 

The same paper reviews the model results for changes in stratospheric water vapor. This is a subject which deserves a separate post (watch this space):

 

Stratospheric observations and models for water vapor, Shine (2003)

 

Finally, the model results when all of the effects are combined together:

 

Stratospheric observations and models for ozone, GHG and water vapor changes, Shine (2003)

 

The model results are a reasonable match with the observed trends – but a long way off perfect. By “reasonable match” I mean that they reproduce the general trends of decadal cooling vs height.

There are many uncertainties in the observations, and there are many uncertainties in the changes in concentration of stratospheric ozone and stratospheric water vapor (but not so much uncertainty about changes in the well-mixed “greenhouse” gases).

A couple of comments from A comparison of model-simulated trends in stratospheric temperatures, by Shine et al, first on the upper stratosphere, reviewing possible explanations of the discrepancies:

None of these potential explanations is compelling and so the possibility remains that the discrepancy is real, which would indicate that there is a temperature trend mechanism missing from the models.

and then on the 20-70hPa region:

Nonetheless, assuming that at least some part of this discrepancy is real, one possible explanation is stratospheric water vapour changes. Figure 3 indicates that an extra cooling of a few tenths of a K/decade would result if the Boulder sonde-based water vapour trends were used rather than the HALOE water vapour trends. If this were one explanation for the model–observation difference, water vapour could dominate over ozone as the main cause of temperature trends in this altitude region.

Why Is the Stratosphere Expected to Cool from Increases in “Greenhouse” Gases?

This is a difficult one to answer with a 30-second soundbite. You can find a few “explanations” on the web which don’t really explain it, and others which appear to get the explanation wrong.

The simplest approach to explaining it is to say that the physics of absorption and emission in the atmosphere – when calculated over a vertical section through the atmosphere and across all wavelengths – produces this result. That is – the maths produces this result..

You can see an introduction to absorption and re-emission in CO2 – An Insignificant Trace Gas? Part Three.

[Note added to this article much later, the series Visualizing Atmospheric Radiation has an article Part Eleven – Stratospheric Cooling – from January 2013 on why the stratosphere is expected to cool as CO2 increases. It is quite involved but shows the detailed mechanism behind stratospheric cooling].

After all, this approach is what led Manabe and Wetherald to their results in 1967. But of course, we all want to understand conceptually how an increase in CO2 – which causes surface and troposphere warming – can lead to stratospheric cooling.

The great Ramanathan in his 1998 review paper Trace-Gas Greenhouse Effect and Global Warming (thanks to Gary Thompson of American Thinker for recommending this paper) says this:

As we mentioned earlier, in our explanation of the greenhouse effect, OLR reduces (with an increase in CO2) because of the decrease in temperature with altitude.

In the stratosphere, however, temperature increases with altitude and as a result the cooling to space is larger than the absorption from layers below. This is the fundamental reason for the CO2 induced cooling.

In Ramaswamy (2001):

For carbon dioxide the main 15-um band is saturated over quite short distances. Hence the upwelling radiation reaching the lower stratosphere originates from the cold upper troposphere. When the CO2 concentration is increased, the increase in absorbed radiation is quite small and the effect of the increased emission dominates, leading to a cooling at all heights in the stratosphere.

Are they saying the same thing? Yes (probably).

If these explanations help – wonderful. If they don’t, refer to the maths. That is, the mathematical result provides this solution and overall “hand waving” explanations are only ever a second-best “guide”. Also check out The Earth’s Energy Budget – Part Three for explanations about emissions from various levels in the atmosphere.

Conclusion

Understanding stratospheric temperature trends is a difficult challenge. Understanding the mechanisms behind this changes is much more of a conceptual challenge.

But over 40 years ago, it was predicted that the upper stratosphere would cool significantly from increases in CO2.

The depletion of ozone is also predicted to have an effect on stratospheric temperatures – in the upper stratosphere (where CO2 increases will also have the most effect) and again in the lower stratosphere where ozone is the dominant factor.

Stratospheric water vapor also has an effect in the lower stratosphere (where more water vapor leads to more warming and vice-versa), but more on this in a later post.

For some, who feel/believe that CO2 can’t really significantly affect anything in climate – this post isn’t for you – check out the CO2 – An Insignificant Trace Gas? series.

There will be others who will say “Ozone is the reason the upper stratosphere has cooled“. True, but increases in CO2 are also an important factor. The same calculations (maths and physics) that lead to the conclusion that less ozone will cool also lead to the conclusion that more CO2 will cool the upper stratosphere.

This subject also has two other possible consequences. One is about attribution. Global temperatures have increased over the last 40 years and many people want to understand the cause.

If solar heating was the direct cause (see Here Comes the Sun) the stratosphere would not be cooling. However, other effects could possibly also cause stratospheric cooling at the same time as tropospheric and surface heating. It’s a complex subject. But something to question for those other potential causes – would they also cause stratospheric cooling?

The other consequence is about GCMs. Some say that stratospheric cooling is a “vindication” of GCMs. In so far as we have covered the subject in this post we couldn’t reach that conclusion. The modeling of tropospheric and stratospheric temperature profiles can be done (and was by Manabe and Wetherald) with 1D radiative-convective models. Certainly 3d GCMs have also been used to calculate the effect by latitude but these results have more issues – well, the whole subject is much more complex because the change of ozone with height and latitude are not well understood.

But it is important to understand the difference between a GCM solving the general climate problem and a more constrained mathematical model solving the temperature profile against height through the atmosphere.

However, stratospheric cooling while the surface and troposphere are warming does indicate that CO2 and other “greenhouse” gases are likely influencers.

References

Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity, Manabe and Wetherald, Journal of Atmospheric Sciences (1967)

Trace-Gas Greenhouse Effect and Global Warming, Ramanathan, Royal Swedish Academy of Sciences (1998)

Stratospheric Temperature Trends: Observations and Model Simulations, Ramaswamy et al, Review of Geophysics (2001)

A comparison of model-simulated trends in stratospheric temperatures, Shine et al, Q. J. R. Meteorol. Soc. (2003)

Recent Stratospheric Climate Trends as Evidenced in Radiosonde Data: Global Structure and Tropospheric Linkages, Thompson & Solomon, Journal of Climate (2005)

An update of observed stratospheric temperature trends, Randel, Journal of Geophysical Research (2008)

Read Full Post »

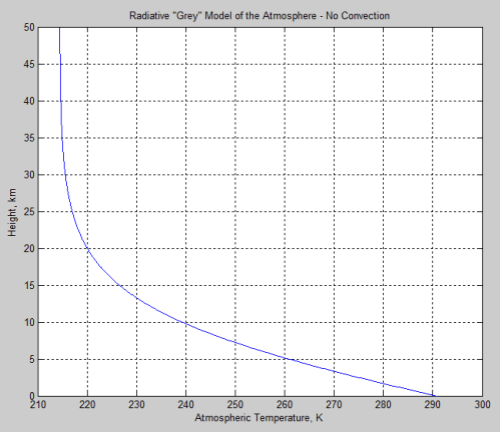
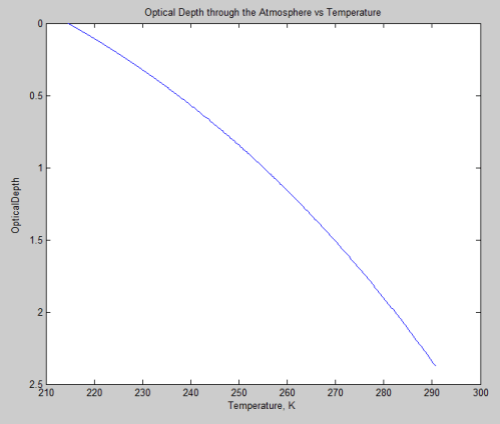
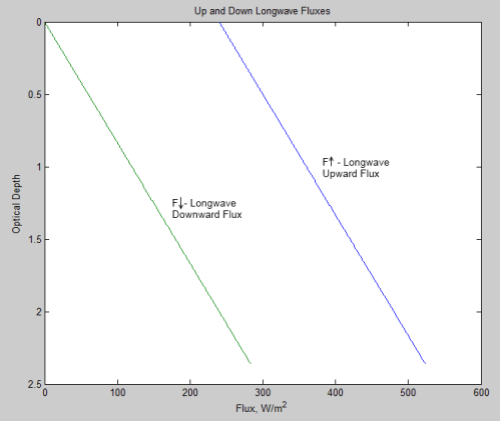
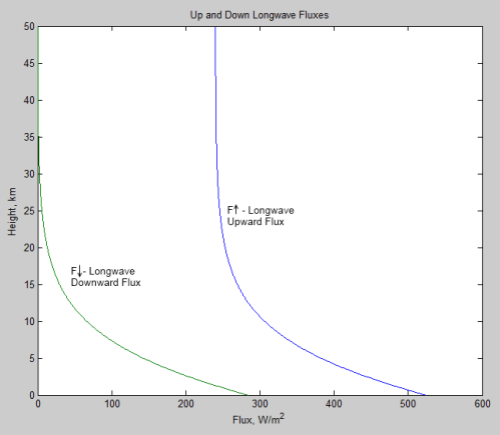
[Note: This article was significantly updated August 5th, 2010. Therefore, many comments became obsolete, or at least proved their worth, by encouraging an update]

If there’s one area that often seems to catch the imagination of many who call themselves “climate skeptics”, it’s the idea that CO₂ at its low levels of concentration in the atmosphere can’t possibly cause the changes in temperature that have already occurred – and that are projected to occur in the future. Instead, the sun, that big bright hot thing in the sky (unless you live in England), is identified as the most likely cause of temperature changes.

Argument from Inconceivability

I personally find it hard to believe that we are hurtling through space at 67,000 miles per hour on a big spinning rock. It doesn’t feel like it. (Actually that’s just the speed that we orbit the sun, and the sun is moving as well, so its more complicated..)

And is this table (you can’t see my table, but any table will do) really made of tiny atoms but science claims it’s mostly space between the little balls? What? Not likely.

Satire over.

For science, personal experience and imagination are not the deciding factors. They lead you astray. Instead, investigation of phenomena lead to hypotheses, experiments and eventually “theories” – as well-established science “facts” are known. Your intuition might be great for understanding people’s motivations, or whether a person can run 100m in 3 seconds, but not so great for the energy absorption characteristics of invisible molecules.

Let’s look at the science.

How do we analyze the Earth’s Climate?

It’s a tricky problem. And like most tricky science problems we start with some simplications. We analyze a simplified model and see where that gets us. Like, how does this simple model compare to reality? And how do we verify the results from the simplified model if the reality is so much more complicated?

Read on, it’s a journey.

Energy from the Sun

The sun is our source of heat. We are 150 million km from the sun, so how does that heat energy get here?

There are 3 mechanisms for heat transfer – conduction, convection and radiation. It’s a vacuum between the sun and the earth so energy from the sun can only arrive here through radiation. What does that radiation look like? A “body” emits radiation across a spread (a “spectrum”) of wavelengths, in a way that depends on that body’s temperature.

The fact that the wavelengths of the energy emitted vary with temperature is a key point, essential for understanding this aspect of climate science.

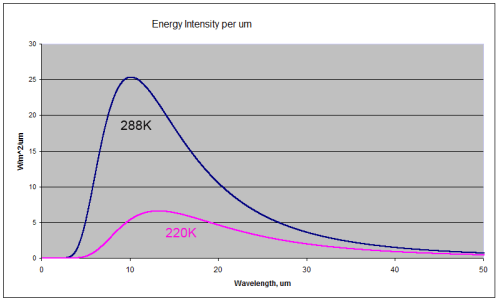
Here’s a few samples – each color represents a different temperature object. The blue line is a body at 5000K = 4727°C (8540°F).

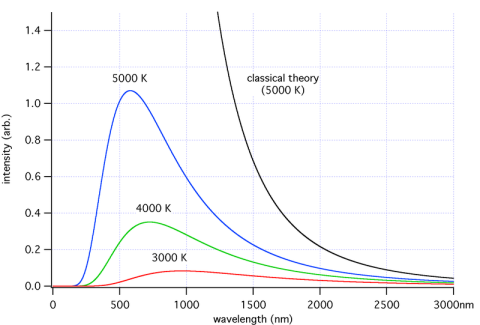
Energy intensity versus wavelength for different temperature objects

For those new to the subject, K (“Kelvin”) is absolute temperature. It tracks degree Centigrade/Celsius one for one, but whereas °C starts at the freezing point of water, K starts at, well, absolute zero.

So 0°C = 32°F = 273K;  and  -273°C = -459°F = 0K

There are reasons why this temperature scale exists, but let’s just leave it at that.

So if you look at the graph you can see that the higher the temperature, the higher the total energy (which everyone would expect) and the lower the wavelengths of the peak energy.

At the end of the post I’ll show some maths, but many people don’t want to see any equations. Just as a preview, total energy is proportional to the 4th power of absolute temperature. Double the temperature and the energy goes up by 16 times.

And it’s worth stating as well at this point, none of this is in question. It’s reproduceable, non-controversial thermodynamics – a branch of physics. You can reproduce it in the lab and measure it everywhere in the real world.

Energy from the Earth

Now the earth also emits radiation according to the same formula. If the earth isn’t heating up or cooling down the energy absorbed will be equal to the energy emitted. (And we’ll leave discussions about how we know whether the earth is heating up and exactly what that means for another day).

If you do the maths (see the end of the post), you find that the equations say that the earth should be about -18°C (255K) when in fact it is an average +15°C across the globe. What’s going on?

First let’s look at the energy from the earth and sun on the same graph. The sun has a surface temperature of 5780K:

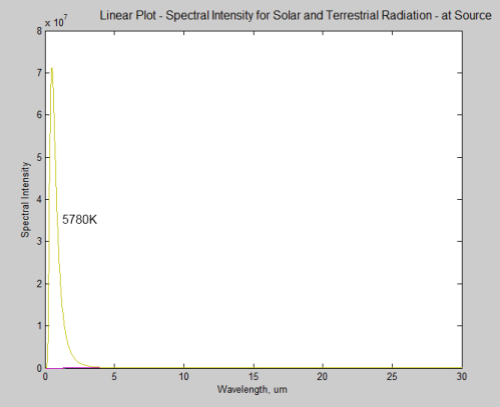
What’s happened to the earth’s radiation? It can barely be seen on a linear plot, it is so small in comparison. However, this is at source – picture a spaceship parked just off the surface of the sun taking the measurements.

By the time the solar radiation has reached the earth it has reduced in intensity by a factor of around 46,000 (see the Inverse Square Law or The Sun and Max Planck Agree – Part Two):

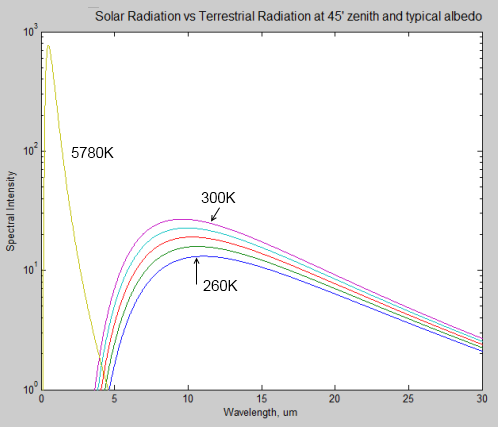
Here is a comparison of solar radiation (the 5780K curve) at the top of the atmosphere, compared with a few terrestrial radiation curves for 260K (-13°C) though to 300K (27°C). Note that it is a logarithmic plot.

Here is a linear plot of the same for comparison:

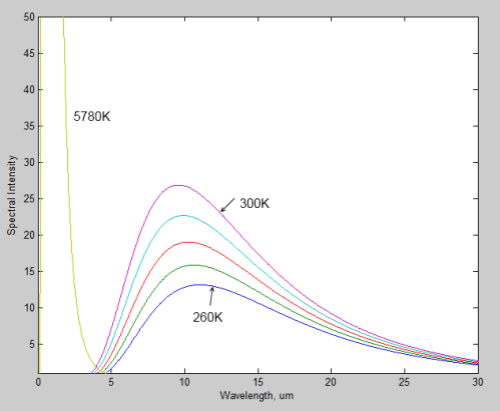
Notice how the wavelength of the peak value of radiation shifts to the right as the source of the radiation gets colder. The typical value for the earth is 10μm, while for the sun it is 0.5μm.

What’s great about the graph is you can see clearly how the radiation from the sun can be easily discriminated from the radiation from the earth. There’s no complicated deductive work, if you measure radiation below 4μm, you know it came from the sun, no matter how many things it bounced off in the meantime. If you measure radiation above 4μm, you know it’s generated by the terrestrial system.

Check out The Sun and Max Planck Agree and The Sun and Max Planck Agree – Part Two for more on this subject.

What does this mean? It means that we can confident of the amount of energy:

1. Arriving from the sun at the top of atmosphere and at the surface
2. From the sun that is reflected back into space by the atmosphere or the earth’s surface
3. Emitted by the earth

How do we work out 3)? We have satellites in space that look at the energy coming from the earth’s surface in the longer wavelengths that correspond to the lower temperatures of the earth’s surface.

And the climate science convention is to call the energy less than 4μm: short wave radiation and the energy greater than 4μm:  long wave radiation.

Note that “infrared” is radiation greater than 0.7μm – a different term than “longwave”.

Energy Absorbed by Gases in the Atmosphere

Let’s look at some more standard science.

Each gas in the atmosphere has different absorption characteristics, which vary according to the wavelength of the radiation. In detail it is very complex, but here is a broad overview of total absorption:

Absorption of different wavelength radiation in the earth’s atmosphere

Note that the horizontal axis is a logarithmic scale. The vertical axis shows “opacity” or what proportion of the energy is absorbed by the atmosphere. I picked this graph because you can easily see where the visible light fits in. What you should notice is how much radiation is actually absorbed by the atmosphere. This graphic is a bit too simplistic.

Here’s solar radiation at the top of atmosphere, and at the surface:

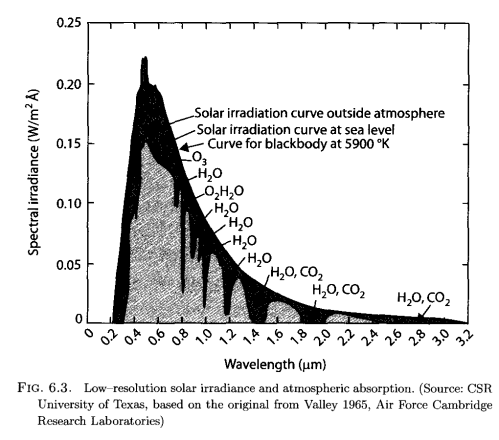
From Vardavas & Taylor (2007)

The lighter color is what we observe at the earth’s surface, while the darker surrounding is the observation of solar radiation by satellite. The difference is absorption by various molecules in the atmosphere and you can see from the annotation which gases absorb at which wavelength.

Here is a measurement of outgoing longwave radiation (terrestrial radiation) measured by satellite at the top of the atmosphere:

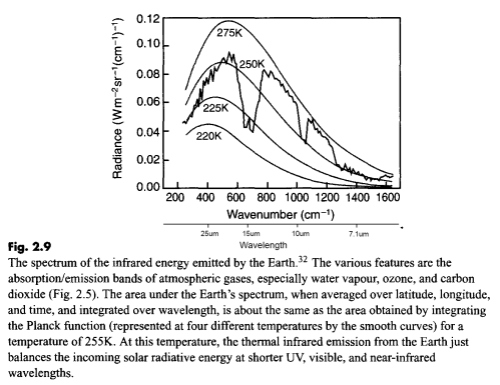
Outgoing longwave radiation at TOA, Taylor (2005)

For those new to this kind of graph, they are usually shown in “wavenumber” rather than wavelength. It’s not important at this stage except to note that the longer wavelengths are to the left and the shorter wavelengths are to the right.

The reason for picking this measurement to show is that the emission curves for typical temperatures of the earth’s surface are shown overlaid. The highest one is 275K or 2°C. The surface of the earth emits radiation very close to the blackbody shape (see The Dull Case of Emissivity and Average Temperatures) but by the time the radiation leaves the earth’s atmosphere that isn’t what we see.

Here is another example, this time with a theoretical calculation (overlaid and displaced for comparison) which is something covered much later in this series:

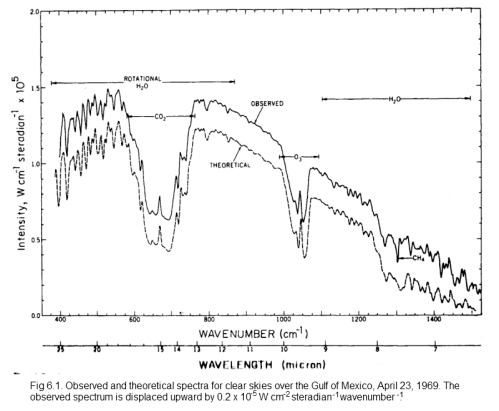
Measured and theoretical spectra, from Goody & Yung (1989)

Click for a larger view

On this spectrum, the authors have noted the reduced areas of outgoing radiation and marked CO2, H2O, O3 (ozone) and CH4 (methane).

How do they know these gases are the cause?

And what effect does it really have?

Measurements in the Lab

Scientists have been measuring the absorption characteristics of each gas in the atmosphere at different wavelengths for many decades.

Here is a good summary of the main absorption bands:

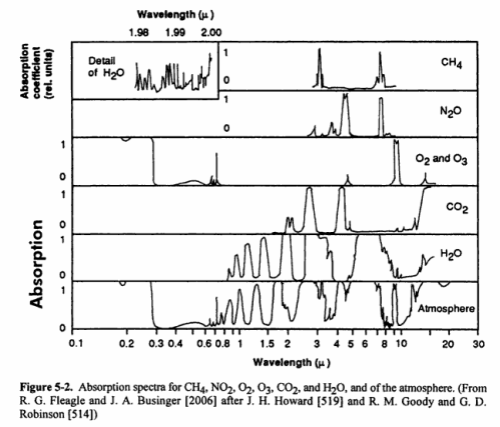
The last bottom line shows the total in the atmosphere. You might notice that N2 (nitrogen) doesn’t show up. Is climate science ignoring this important gas? No – nitrogen absorbs almost nothing, for reasons that are touched on in Part Two. We can say that nitrogen is transparent to solar and terrestrial radiation.

You will also notice that O2 and O3 (oxygen and ozone) are shown. There is a chemical cycle in the upper atmosphere called the Chapman cycle which is responsible for generating ozone. In the very short wavelengths – below 0.3μm – oxygen and ozone both absorb solar radiation. In the longer wavelengths, ozone absorbs around 9.6μm. Oxygen doesn’t absorb at all in longwave – it is also (like nitrogen) transparent to terrestrial radiation.

What you can’t tell from the chart above is how influential each of the gases is in terms of total energy absorbed. That is a much more complex challenge – covered in later articles (but it isn’t as simple as the ratio of each of the absorbing gases in the atmosphere).

Before we leave the subject of absorption, it’s worth showing some lab measurements – from the HITRANS database. This might help see the main characteristics of CO2 and water vapor as well as the complexity.

First the main characteristics on a linear graph:

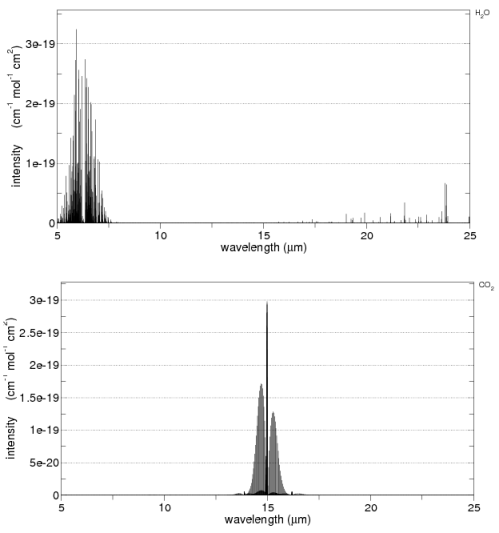
From the HITRANS 2008 database, via spectralcalc.com

You can see that CO2 has high absorption around 15μm and water vapor around 6.3μm.

Now on a log plot – this shows the complexity – but note that each horizontal line represents a factor of 100. O2 and N2 are included at the bottom for comparison:

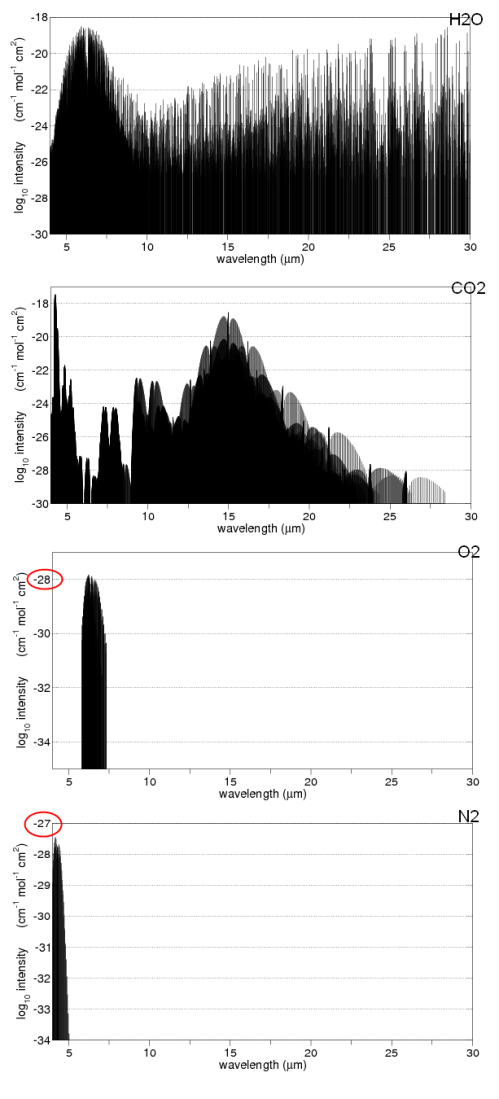
From the HITRANS 2008 database from spectralcalc.com

Note the vertical scale for N2 and O2 – even at their peak they absorb less than a billionth the radiation of CO2 and water vapor.

What Effect Does it Have?

Outside the world of atmospheric physics there is a lot of confusion about some thermodynamics basics. There are many articles on this blog that address those specific points (checkout the Roadmap) and there is no way to cover all of the misconceptions in this article – without it being 100 pages long..

As the surface of the earth heats up from the solar radiation absorbed, it in turn emits radiation – as shown in the 3rd and 4th graphs above.

If the atmosphere didn’t absorb any of this radiation then we would measure a spectrum like one of the Planck curves (as they are known). Instead we see large “chunks” (to use a non-technical term) of energy removed by the time the radiation leaves the atmosphere – “chunks” corresponding to water vapor, CO2 and ozone (as well as a number of other gases). And the larger the “chunk”, the more energy has been absorbed by the corresponding gas from the radiation.

When the atmosphere absorbs radiation it heats up. The absorbed energy is shared thermally via collisions with all other gas molecules, so the whole atmosphere in that region heats up. And the gases like CO2 and water vapor emit radiation – more emission as they increase in temperature.

The atmosphere, once heated up, radiates equally in all directions. Some of this is downward. Here is a measured spectrum at the earth’s surface:

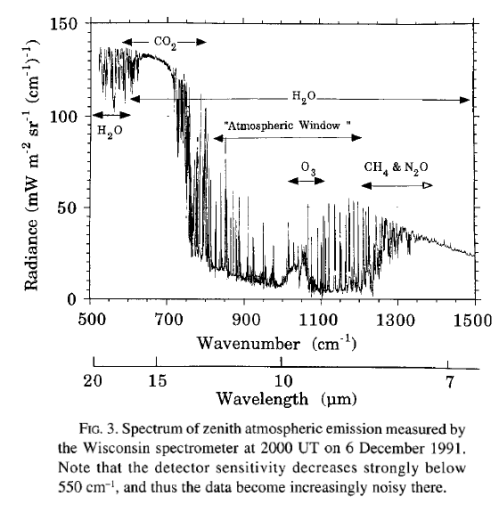
Wisconsin, Ellingson & Wiscombe (1996)

As you can see, the emission of radiation measured at the earth’s surface corresponds to the missing sections at the top of the atmosphere. See The Amazing Case of “Back-Radiation” and The Amazing Case of “Back Radiation” – Part Two.

Note: If a gas can absorb 15μm radiation it can also emit 15μm radiation. If a gas can’t absorb 15μm radiation it also can’t emit at that wavelength.

The energy radiated by the atmosphere which is received at the earth’s surface increases the temperature at the surface. (See The Amazing Case of “Back Radiation” – Part Three).

Although many people have become confused with imaginary second laws of thermodynamics to believe that this can’t happen, here is the easy way to understand the problem:

If we average the incoming solar radiation that is absorbed by the earth’s climate over the surface of the earth we get around 239 W/m². (See The Earth’s Energy Budget – Part One).

If we average the outgoing longwave radiation from the top of atmosphere we get the same value: 239 W/m².

If the atmosphere didn’t absorb any terrestrial radiation then the surface of the earth must also be emitting 239 W/m².

The only way that the surface of the earth could emit this amount is if the temperature of the earth was around 255K or -18°C.

And yet we measure an average surface temperature of around 15°C – an emission of radiation of 396 W/m². (See note 1).

If the atmosphere wasn’t absorbing and re-radiating longwave then the surface of the earth would be -18°C. This is the inappropriately-named “greenhouse” effect (and note that I haven’t used a greenhouse to demonstrate anything).

Conclusion

The question asked at the start was “Is CO₂ an insignificant trace gas?” and the answer is no.

CO₂ and water vapor are very significant in the earth’s climate, otherwise it would be a very cold place.

What else can we conclude? Nothing really, this is just the starting point. It’s not a sophisticated model of the earth’s climate, it’s a “zero dimensional model” or “billiard ball model” which takes a very basic viewpoint and tries to establish the effect of the sun and the atmosphere on surface temperature. It doesn’t look at feedback and it’s very simplistic.

Climate is a complex subject. Hopefully this explains some basics and we can start looking a little deeper in subsequent posts.

More in this series

Part Two – why different gases absorb different amounts of energy, why some gases absorb almost no longwave radiation

Part Three – the Beer Lambert model of absorption and the concept of re-emission of radiation

Part Four – band models and how transmittance of CO2 changes as the amount of CO2 increases under “weak” and “strong” conditions

Part Five – two results from solving the 1-d equations – and how CO2 compares to water vapor

Part Six – Visualization -what does the downwards longwave radiation look like at the earth’s surface

Part Seven – The Boring Numbers – the values of “radiative forcing” from CO2 for current levels and doubling of CO2.

Part Eight – Saturation – explaining “saturation” in more detail

CO2 Can’t have that Effect Because.. – common “problems” or responses to the theory and evidence presented

Other later series covering similar material

Visualizing Atmospheric Radiation – a lot more detail on how radiation travels through the atmosphere, and how it is absorbed and re-emitted by various “greenhouse” gases

Atmospheric Radiation and the “Greenhouse” Effect

The Maths

The Stefan-Boltzmann Law states:

j = εσT⁴

Where

j = total energy radiated per unit area per unit time
ε = emissivity, ranging from 0 to 1, where 1 is a perfect black body
σ = the Stefan Boltzmann constant, 5.67 x 10^-8
T = temperature in K

The effective temperature of the sun is 5780K, its emissivity is quite close to 1, and so it radiates 6.3 x 10⁷ W/m²

As the sun is a long way from the earth, its radiation by the time it reaches the earth is reduced according to Inverse Square Law.

The radius of the sun, rsun = 696 x 10⁶m

Distance from the sun to earth,  a_o = 1.5×10¹¹ m (150 million km)

Therefore the solar radiation is reduced by a factor of (1.5×10¹¹/(696 x 10⁶)² = (215)² = 46,225. Therefore, the solar radiation reaching the earth’s atmosphere = 6.3 x 10⁷ / 46,225 = 1360 W/m².

And from measurement by satellite we get 1367 W/m².

Now we have to note two important facts:

• Some of the solar radiation is reflected
• The sun isn’t directly above all points on the earth at the same time

So how much energy is actually absorbed by the climate system?

The measured proportion of reflected solar radiation is 30% – we call this the albedo.

To work out the effect of the day and night and different angles of solar radiation sounds tricky but it’s actually an easy problem. The solar radiation from a long way away hits a disc of area = πr². But the surface of a sphere is 4πr² – (see The Earth’s Energy Budget – Part One for a fuller explanation). Therefore, to calculate the energy absorbed by the climate system averaged over the surface of the earth we can just divide by 4:

E_solar = 1367 x (1 – 0.3) / 4 = 239 W/m²

If the earth is not heating up or cooling down then the earth’s climate system must also be emitting radiation at the same rate.  Note that these are global annual averages.

If there was no absorption of surface radiation by the atmosphere then the surface radiation would also be – on average – 239 W/m².

What temperature of the earth’s surface does this correspond to?

Remember the equation at the start of the maths section: j = εσT⁴
Rearranging to solve, T = (j/εσ)^1/4

The emissivity of the earth is very close to 1 (see The Dull Case of Emissivity and Average Temperatures), therefore:

T = 255K or -18°C

Given that we actually experience much higher temperatures on the surface of the earth, we need an explanation. This can be found in the inappropriately-named “greenhouse gases”, which include water vapor, CO2 and methane (CH4).

When the earth emits its longwave radiation, these gases absorb energy and then re-emit, so that the earth’s energy doesn’t just fly off into space but instead it’s absorbed and re-transmitted, some of it back down to earth.

The “greenhouse gases” heat the earth’s surface up approximately 33°C higher than it would be otherwise.

Note 1:

There is a lot of confusion about the use of average temperatures in this approach to explaining the role of CO2 and water vapor in the atmosphere.

Calculating an average temperature has a lot of issues, as explained in Why Global Mean Surface Temperature Should be Relegated, Or Mostly Ignored. However, the explanation above doesn’t rely in any way on the arbitrary construct of average temperatures.

I simply used average temperatures to help newcomers visualize the issue more clearly. If I say that the earth’s average temperature should be -18°C everyone knows that I am wrong. If I say that the emission of surface radiation should be 239 W/m² who would know?

The use of energy per m² also confuses – the poles are colder, the equator is hotter – maybe the averages have lost something important. Once again, the averages just make it easier to understand. However, for those readers convinced that there is a problem in comparing average values, we can calculate the total energy:

Total solar energy absorbed globally annually = solar “constant” x (1 – albedo) x surface area the solar radiation irradiates x number of seconds in a year

Total energy = 1367 W/m²  . (1 – 0.3) . πr_e² . 365.24.3600 = 3.8 x 10²⁴ J

where r_e = radius of the earth = 6.37 x 10⁶m.

How much energy does the surface of the earth radiate? Well, it can be calculated from the global temperature database and the Stefan-Boltzmann law.

This was done in Earth’s global energy budget, Trenberth and Kiehl, Bull. Amer. Meteor. Soc. (2009). They expressed the number as an global annual average – 396 W/m². We can simply multiply it back up the same way – using the surface area of the earth – to get

Total energy radiated from the surface = 396 x 4πr_e² . 365.24.3600 = 6.4 x 10²⁴ J

Now there are no averages and no temperatures involved, but the same fundamental issue – the incoming and outgoing radiation balance at the top of the atmosphere, but the energy leaving from the surface of the earth is much higher than the incoming solar energy.

The absorption and re-radiation by “greenhouse” gases in the atmosphere is responsible.

Read Full Post »