This could be considered as a continuation of the earlier series – Atmospheric Radiation and the “Greenhouse” Effect – but I’ve elected to start a new series.
It’s clear that many people have conceptual problems with the subject of what is, in technical terms called radiative transfer. That is, how radiation travels through the atmosphere and is affected by the atmosphere.
Radiation and Gas in a Box
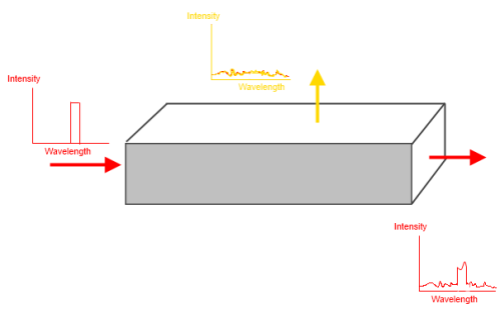
First, let’s consider what happens as we shine an intense beam of infrared radiation at a narrow range of wavelengths (let’s say somewhere in the region of 15μm) through a box of CO2 gas at room temperature:
Figure 1
The red arrow on the left is the incident radiation. The graph indicates the spectrum. The spectrum on the right is made up of two main parts:
- the transmitted radiation – the incident radiation attenuated by the absorbing gas
- the emitted radiation due to the temperature and emissivity of the gas at these wavelengths
The yellow spectrum shows what we would measure from one of the sides. Note that the transmitted radiation that goes from left to right has no effect on this yellow spectrum (except in so far as absorption of the incident radiation affects the temperature of the gas).
If we increase the length of the box (left to right) – and keep the density the same – the transmitted radiation from the right side would decrease in intensity. If we reduce the length of the box (again, same density) the transmitted radiation from the right would increase in intensity.
But the emitted radiation from the top is only dependent on the temperature of the gas and its emission/absorption lines.
And the temperature of the gas is of course affected by the balance between absorbed and emitted radiation as well as any heat transfer from the surroundings via convection and conduction.
Hopefully, this is clear. If anyone thinks this simple picture is wrong, now is the time to make a comment. Confusion over this part means that you can’t make any progress in understanding atmospheric radiation.
Scattering is insignificant for longwave radiation (4μm and up). Stimulated emission is insignificant for intensities seen in the atmosphere.
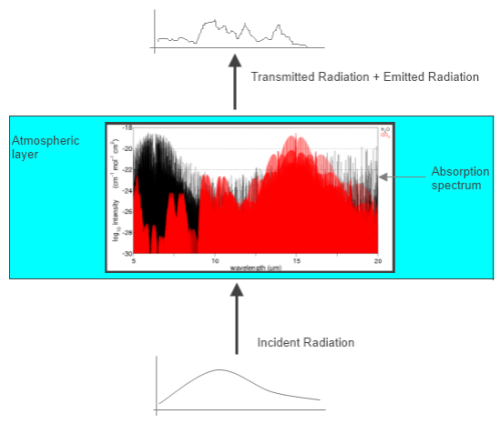
Radiation in the Atmosphere
How does radiation travel through the atmosphere?
Figure 1
The idea shown here is a spectrum of radiation at different wavelengths incident on a “layer” of the atmosphere (see note 1). The atmosphere has lots of absorption lines of many different strengths. As a result the transmitted radiation making it out of the other side is some proportion of the incident radiation. The proportion varies with the wavelength.
The atmosphere also emits radiation, and the emission lines are the same as the absorption lines. More about that in Planck, Stefan-Boltzmann, Kirchhoff and LTE.
However, the emission depends on the temperature of the gas in the layer (as well as the absorption/emission lines). But the absorption depends on the intensity of incident radiation (as well as the absorption/emission lines), which in turn depends on the temperature of the source of the radiation.
So in almost every case, the sum of transmitted plus emitted radiation is not equal to the incident radiation. By the way, the spectrum at the top is just a raggedy freehand drawing to signify that the outgoing spectrum is not like the incoming spectrum. It’s not meant to be representative of actual intensity vs wavelength.
And – it’s a two way street. I only showed one half of the story in figure 1. The same physics affects downward radiation in exactly the same way.
Considering One Wavelength at a Time
To calculate the actual transmission of radiation through the layer we simply work out the transmissivity, tλ, of the layer at each wavelength, λ (tλ simply indicates that t will vary for each value of λ we consider). We do that by looking up values calculated by spectroscopic professionals. These values are per molecule, or per kg of particular molecules so we need to find out how much of each absorbing gas is present.
1. The incident radiation making it through the layer = Iλ x tλ – for example, it could be 90% making it through, or 20%.
2. The “new” radiation emitted from each side of the layer equals the “Planck blackbody function at the temperature of the layer and the wavelength of interest” x Emissivity of the gas at that wavelength.
In case people are interested this can be written as Bλ(T).ελ, where ελ = emissivity at that wavelength, and Bλ(T) is the “Planck function” at that temperature and wavelength. Well, emissivity = absorptivity (at the same wavelength) and absorptivity = 1-transmissivity, so the same equation can be written as Bλ(T).(1-tλ).
Digression
Perhaps (the Planck function showing up in an equation) this is where many blogs (Parady blogs?) get the idea, and promote and endorse the idea, that climate science depends on the assumption that the atmosphere emits as a blackbody. There are some cases where the atmospheric emission is not far from the “blackbody assumption” (e.g., in clouds), but that is due to reality not assumption. There is no “blackbody assumption for the atmosphere” in climate science. But there is a movement of people who believe it to be true.
Misleadingly, they like to be known as “skeptics”.
End of digression..
Doing the Calculation
So it’s not really that hard to understand how radiation travels through the atmosphere. It is difficult to calculate it, mostly due to having to read a million absorption lines, figure out the correct units, get a model of the atmosphere (temperature profile + concentration of different “greenhouse” gases at each height), write a finite element program and work out a solution.
But that is just tedious details, it’s not as hard as having to understand general relativity or potential vorticity.
One important point – it is not possible to do this calculation in your head. If you think you have done it in your head, even to a close approximation, please go back and read this section again, then look up all of the absorption lines.
Still convinced – post your answer in a comment here.
In the next article I’ll explain radiative-convective models and show some results from the atmospheric model I built in MATLAB which uses the HITRAN database. Now that we have a model which calculates realistic values for emission, absorption and transmission we can slice and dice the results any way we want.
Does water vapor mask out the effects of CO2? What proportion of radiation is transmitted through the atmospheric window? What is the average emission height to space?
Related Articles
Part Two – some early results from a model with absorption and emission from basic physics and the HITRAN database
Part Three – Average Height of Emission – the complex subject of where the TOA radiation originated from, what is the “Average Height of Emission” and other questions
Part Four – Water Vapor – results of surface (downward) radiation and upward radiation at TOA as water vapor is changed
Part Five – The Code – code can be downloaded, includes some notes on each release
Part Six – Technical on Line Shapes – absorption lines get thineer as we move up through the atmosphere..
Part Seven – CO2 increases – changes to TOA in flux and spectrum as CO2 concentration is increased
Part Eight – CO2 Under Pressure – how the line width reduces (as we go up through the atmosphere) and what impact that has on CO2 increases
Part Nine – Reaching Equilibrium – when we start from some arbitrary point, how the climate model brings us back to equilibrium (for that case), and how the energy moves through the system
Part Ten – “Back Radiation” – calculations and expectations for surface radiation as CO2 is increased
Part Eleven – Stratospheric Cooling – why the stratosphere is expected to cool as CO2 increases
Part Twelve – Heating Rates – heating rate (‘C/day) for various levels in the atmosphere – especially useful for comparisons with other models.
Notes
Note 1 – What is a layer of atmosphere? Isn’t the thickness of this layer somewhat arbitrary? What if we change the thickness? And doesn’t radiation go in all directions, not just up?
These are all good questions.
In typical physics terms the actual equation of “radiative transfer” is a differential equation, which expresses continual change. In practical terms, solving a differential equation in most real world cases requires a numerical solution which has finite thicknesses for each layer.
People trying to solve these kind of problems usually check what happens to the solution as they go for more of thinner layers vs less of thicker layers. There is a trade-off between accuracy and speed.
Radiation does go in all directions. The plane parallel assumption has very strong justification and – in simple terms – mathematically resolves to a vertical solution with a correction factor. You can see the plane parallel assumption and the derivation of the equations of radiative transfer in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations.


Thanks for this.
I think it is just about possible to write your own radiative transfer code – at least for one gas CO2. My first attempt is described here. Ken Gregory even wrote an excell spreadsheet for it – which is much easier to understand and can be download here. By doing this first step I learnt a lot and have now improved things. Modtran is great as a tool – but it is still a bit of a black box.
I look forward to how you integrate convection !
Clive,
I applaud your efforts to get a better understanding by writing your own code. I found for myself that the bits I didn’t understand only became clearer as I turned them around, looked at them in different directions, tried to model them – and read different textbooks.
Playing around with your own model will give you much better understanding of how various gases affect heat transfer in the atmosphere.
One item that seems wrong in your description is:
Later in the comments in response to some questioning over this point you said:
I’ve explained why emission does not equal absorption in Part Two. In brief, it’s because absorption amount depends on the absorptivity and the intensity of the incident radiation, but emission depends on the emissivity (= absorptivity) and the temperature of the local gas.
And it’s even more true (emission ≠ absorption) for a specific gas, just as it is for a particular wavelength – or band of wavelengths.
From other comments you made it is possible you are confusing LTE (local thermodynamic equilibrium) with TE (thermodynamics equilibrium). They are easy to confuse because the names are almost the same. However, they are quite different animals.
TE is where Kirchhoff’s law applies – it’s not a very useful condition for the atmosphere.
LTE essentially means that there are lots of collisions so that normal energy states are distributed how you would expect and consequently the Planck law is correct.
More in Planck, Stefan-Boltzmann, Kirchhoff and LTE.
Anyway, I hope the more detailed explanation along with the accompanying diagrams of flux and spectra at different heights is clear – if not please comment here or in Part Two.
SoD,
Yes, probably one of my faults is that I use imprecise language, but I hope my physics is more precise.
I agree with that – emission is thermal but incident absorption/transmission is not !
So LTE applies to (thermal) emission of radiation by CO2 but not to absorption or transmission of incident radiation. However, I think it can be assumed that thermodynamics ( convection/latent heat + absorbed radiation) results in the measured lapse rate.
The transmitted radiation is the most interesting ( for me at least) because it increases with altitude. The net radiation to space for 13-17 microns is about half that radiated from the surface ( ~ 72 watts/m2) more or less in agreement with satellite data.
Once the atmosphere dominates radiation losses compared to direct radiation to space from the surface, then greenhouse gas dynamics seemingly also maximise cooling (maximum entropy).
For the Earth’s atmosphere today this coincides with current CO2 concentrations.
sorry!
link to Ken Gregory’s spreadsheet is http://members.shaw.ca/sch25/Ken/Clive_Radiation.xlsx
SoD,
There is one case where you can do the calculation in your head, because there’s no calculation. If the source radiation is from a black body at the same temperature as the gas temperature, there will be no change in the observed spectrum regardless of the cell length or gas composition.
SoD,
Are you sure your diagram is correct ? I reckon you would need to add H2O and water droplets to the box to get the broad wavelength spectrum you show. Surely pure CO2 would only emit IR in the main absorption lines. For a box of CO2 in LTE at room temperature I would also expect to see a CO2 line in the yellow graph. The incoming beam gets attenuated as you show, but its transmission is in addition to the thermal emissions of a box of CO2 at 293K.
Or am I wrong ?
clivebest,
You are kind of correct. I should have either specified some other gases as well, or drawn an accurate spectrum.
The yellow spectrum is just a random squiggle, not intended to be the spectrum of any gas, or combination of gases.
However, I didn’t specify the wavelength range on the x-axis or the intensity of the incident beam or the temperature of the gas. So it is quite possible for the diagram to be roughly correct – but I take your point.
SOD,
Thank you for this. Some questions/comments:
“But the emitted radiation from the top is only dependent on the temperature of the gas and its emission/absorption lines”.
This is true only because density of absorber/emitter is a given; in general however, and particularly in the real atmosphere where these are traces only, density is also a determinant of radiation intensity?
“There is a trade-off between accuracy and speed”.
Shouldn’t the trade-off in the choice of layer thickness be between constraints in physics before considerations of model performance: thick enough as to contain sufficient numbers of molecules for thermodynamic laws to apply; and thin enough as to justify isothermal and LTE assumptions? Has anyone determined what that thickness would be? I note that MODTRAN works on a thickness in the troposhere (1km) over which a temperature differential up to 3% would apply.
“Radiation does go in all directions. The plane parallel assumption has very strong justification and – in simple terms – mathematically resolves to a vertical solution with a correction factor”.
Your justification of the plane parrallel assumption is differential pressure gradients, vertically (large) and horizontally (small). Is it also to avoid the complication of spherical geometry? If so, it leads to the “half up, half down” directional apportionment of the energy flux, an approximation to the true “more up than down” apportionment.
“And – it’s a two way street. I only showed one half of the story in figure 1. The same physics affects downward radiation in exactly the same way”.
The same physics but differential transmissivities: the larger upward portion of the flux experiencing increasing transmissivity, the smaller downward portion, decreasing transmissivity. Intuitition (which I can’t explain in physics) suggests a net space-ward movement of the photons that make up the atmospheric electromagnetic energy stock to counter supply from the surface.
Finally, given that radiation in the atmosphere is generated isotropically by individual molecules, the intensity of which being subject to decay according to the inverse square law, how is this property incorporated/exempted in radiation transfer theory?
John Millett,
You are correct. The “optical thickness”, τ is directly proportional to the number of molecules of the absorber in the path. And the emissivity, ε = 1-exp(-τ).
The layer is massively larger than is necessary for thermodynamics laws to apply.
The layer doesn’t need to be isothermal for the numerical calculation to work. If you take any heat transfer problem and solve it via finite element analysis (making blocks or layers or squares instead of continuous) then you always have an approximation.
I ran my model of the atmosphere – soon to be seen in part two – with 10 layers (of equal pressure change) and got TOA OLR=237.9 W/m2 and DLR=282.7 W/m2. Then I ran with 20 layers and the same temperature and humidity conditions and got TOA OLR=239.5 W/m2 and DLR=282.8 W/m2. For me, the increase in accuracy is not enough for the extra time for a run. (There are plenty of other sources of error in this model).
Essentially, I use the temperature of the midpoint of the layer (midpoint defined in pressure terms) as the temperature that defines the emission of thermal radiation. The top part of the layer will be emitting a little less and the bottom part of the layer will be emitting a little more. This leads to a small error.
I can keep making the layer thinner to reduce the error but even if I had 1 cm thick layers the top and bottom would be actually emitting slightly different amounts from the middle of the layer. It isn’t a fundamental issue. Just a practical trade-off.
The plane parallel assumption only assumes that horizontal variations in values like pressure and absorber quantities are much smaller than vertical variations and can be neglected.
This assumption then allows us to sum all of the upward components over all angles to get the total upward flux- in a much easier fashion.
It then also allows us to sum all of the downward components over all angles to get the total downward flux – in a much easier fashion.
There is no assumption about equal up and down in the plane parallel approximation. The approximation is just about the mathematical approximation of a complex integral – as you can see in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. under the heading It’s Not Over Yet – Conversion from Intensity to Flux and the Diffusivity Approximation.
SOD,
From the Part Six link:
“we can produce an approximation which is known as the diffusivity approximation:
2 ∫ e-τ(z,0)/μ μ.dμ ≈ e-τ/μ’
Where μ’ is the “effective angle” which produces a close approximation to the actual answer without needing to integrate across all angles (for each wavelength). The best value of μ’ = 0.6”.
In my visualisation, the “effective angle” wouldn’t be (approx) 0.6 in both up and down directions. I visualise a larger apportionment of power, generated by individual molecules, space-wards than surface-wards as a consequence of Earth’s spherical geometry. And that seems to be contrary to what your model shows. Perhaps the second part will reveal my misunderstanding.
John Millett,
Your visualization is not the correct one.
This is what is going on:
All paths are integrated to get total spectral emissive power for the hemisphere.
Each path length is z/cos(θ). So, for example, the path vertically up is z, the path at 30' is 0.866z, the path at 60' is 0.5z and so on. So if the optical thickness vertically up is τ then the optical thickness at 30' is 0.866τ, the optical thickness at 60' is 0.5τ.
So to calculate transmission of radiation you use the formula for transmission, t=exp(-τ/cos(θ)). Integrate (sum up) over all solid angles and you end up with result being one that can be approximated by an optical thickness of τ*1.66.
It is just geometry.
With the technical note that the solution is over the hemisphere so spectral emissive power W/(m2.cm-1) rather than one “ray” which is spectral intensity at W/(m2.sr.cm-1). – that is, watts per square meter per steradian per wavenumber
John Millett,
..In case this is your issue..
At a given point on the earth’s surface the height of the troposphere is about 12km or so. The fact that the earth “drops away” over the horizon has zero impact on the geometry argument. By the time we get to 90′ from the zenith (the horizontal ray), the path length is so long that its contribution to the spectral emissive power is zero.
SoD,
I don’t think it’s correct to say that the spherical shape of the Earth is taken formally correctly into account in the approximation. The zenith angle is not in any way related to longitude and latitude, but the relationship between the zenith angle, path length and change in altitude duo depend also on the Earth radius.
The real justification is that the Earth radius is much larger than the thickness of the atmosphere and most path lengths still is much shorter. Therefore the additional errors made in forgetting the curvature are insignificant in comparison to the other errors made in performing approximate calculations.
It’s very common and well justified to neglect the shape of Earth in many atmospheric calculations. One must just be careful and remember to think when that can be done and when not. In most radiative calculations the error is easily seen to be small, while the shape of Earth and rotation are important for many rather small scale weather phenomena.
SoD,
This post gives some answers along the line I had in mind when I wrote that something more might be needed on the basics. Perhaps a part zero would also be useful, where something more would be written about micro level physical basis like interaction of radiation with gas molecules and perhaps also with condensed matter.
What I have more generally in mind is a collection of fundamental physical phenomena and laws that are most relevant to physics of Earth atmosphere. We see quite often comments which seem to originate from misconception of these basics. The collection could have the structure of questions and answers and it would be important to cross link related material when it’s divided in short sections written to answer specific points. I might try to help in putting such material together if you feel that would be worthwhile. I think this site could be a good place for that as the basic goal is the same: To explain science and help in figuring out what’s significant for understanding the atmosphere.
Pekka,
I would definitely appreciate your help in putting these basics you have in mind together.
SoD,
I try to make a rough sketch of my ideas and contact you first by email. At a later stage the approach could be brought to wider discussion here.
I state just he central idea. That’s to build a static but gradually improving and extending component for the site. It would have some similarities with that of Wiki but it should be kept concise or at least maintain a concise core. My idea is that it could not be directly edited by many but that proposals for improvement would be welcome and be implemented as far as possible. In contrast to posts that are usually not changed essentially later this would keep on improving.
The matter included should all be noncontroversial (within the science community at least) and be usable as reference when needed to support later posts as well as discussion. Presently the same issues must be explained time after time in the discussion threads. A permanent carefully formulated link would serve better that need.
Another related idea would be to improve on your present Roadmap and build a table of contents or (logically organized index) for this site that links in a structured way to the existing posts.
One technical point is whether WordPress allows implementing the ideas exactly as I would like. I have my own limited site based on WordPress software (not at WordPress.com) but I have not spent much effort to learn all the possibilities that WordPress offers.
I cannot promise that I’ll move fast. Having retired doesn’t mean that I would have enough time for everything i would like to do.
Pekka,
You have heard of Parkinson’s Law: “Work expands so as to fill the time available for its completion.”
I consider that to be a corollary, like Murphy’s Law, of my fundamental principle of human endeavor: Irony Increases
[…] « Visualizing Atmospheric Radiation – Part One […]
SOD,
“This is what is going on:…..”
Rather than a hemisphere centred on an infinitesimal surface element, I visualise a sphere centred on a radiating molecule. One-dimensionally, I visualise eqi-spaced rays radiating from the centre, more of the rays directed towards space than the surface. That’s equivalent to slicing the sphere below the equator and integrating over a larger theta upwards than downwards.
If I understand correctly, Pekka is saying that the difference can be approximated away (as one of a number of approximations necessary to solving the radiation transfer equation)?
I’m not sure I have understood your point, but I’ll have a stab at what it might be just in case.
The theory of radiant heat transfer is not with reference to one molecule. It is with reference to a surface or a body.
This makes the maths easy to understand and is practical.
So a body of the atmosphere – say a layer of atmosphere 100m thick – radiates at a certain spectral intensity (where the geometry is per meters squared per steradian). We can calculate this spectral intensity from Planck’s law, the number of each type of molecule and their set of absorption/emission lines.
Then we can use geometry to calculate what happens some distance away and the cumulative effect of many different paths, layers, locations, etc.
We don’t think in terms of one molecule radiating and if you try to start from that basis for your geometry and the inverse square law in reference to the diameter of a molecule you won’t get far. Because you will be using the wrong theory.
SOD,
“The theory of radiant heat transfer is not with reference to one molecule. It is with reference to a surface or a body”
A well executed stab – right to the heart of the matter. What you say, I know.
What I would like to know is how theory manages to transform energy generation by particles free floating within the volume of an air body into energy generation at the surface of a body made up mostly of radiatively-inactive particles.
John Millett
I’m not the right guy to explain this part of the theory. It’s fairly heavyweight.
We have experimental results. We have theory that matches. Ultimately we have long derivations from statistical thermodynamics and quantum mechanics that explain the “theory” from more fundamental principles.
The important bit (from my perspective) is to understand that the actual equation of emission of thermal radiation from a surface or a body of gas is:
a) well understood, and
b) is with reference to the geometry of the surface or the body of gas – not with respect to the geometry of, or location of, a molecule
John,
You refer to a “surface of a body made up mostly of radiatively-inactive particles”. That’s not correct. Solid and liquid matter is not radiatively inactive. Solid and liquid bodies are actually radiatively highly active. While gas molecules are far apart and can emit and absorb significantly only at a discrete set of levels, the atoms of solids and liquids interact with many neighboring atoms and can interact at all wavelengths over wide ranges. In particular most solid and liquid surfaces are almost black for LWIR, i.e. they absorb and emit almost as much as Planck’s law allows.
When radiation meets matter, there are three possibilities:
– it keeps on going, i.e. it’s transmitted
– it gets absorbed
– it gets scattered or reflected
(There’s one more complication that’s due to the average strength of interaction of radiation with matter, which leads to the fact that being transmitted does not mean maintaining the same direction. At solid and liquid surfaces we have refraction and in gases of varying density we have slight bending.)
In gases reflection does not occur and scattering is weak. Thus transmission and absorption are the two dominant possibilities. Most solid surfaces don’t allow for significant transmission leaving absorption and reflection as the main alternatives. That’s true also for water at LW. (There’s some transmission in solids and liquids as well, but when the penetration depth is very small it’s for most purposes correct to consider only what happens over larger distances, and then we have only reflection and absorption.)
In the above I have discussed what happens to arriving radiation. In addition we have the emission that occurs everywhere we have absorption, and typically with a strength that’s not very different of the strength of absorption when we consider LWIR.
You use the expression “energy generation”. I don’t know precisely what you have in mind. For the present consideration the only important place where energy is generated is the sun. In the Earth system energy is moved around and it’s changing form, but not generated at a scale that’s nearly as important as what happens for the energy received from the sun.
Convective heat transfer is one-sided as it transfers energy almost exclusively upwards due to its connection to gravitation. Both conduction and radiative energy transfer go always on the net from warmer to colder, but on micro level of molecules and photons both involve energy transfer in all directions. For conduction the microscopic level is unobservable but in case of radiative energy transfer it’s easy to observe photons coming from all directions. That the net transfer is always from warmer to colder is a statistical phenomenon, and a very certain and predictable one due to the huge number of individual events involved.
I will make two comments.
1. The length of the box should be a variable and to understand anything, I need to see the graph of the output versus the length of the box.
2. Next I would like to see the output graph as a function of the “size” of the input stimulus at the particular wavelengths you have chosen.
Before I can understand what you are delivering I think you must explain #1 and #2 above. If not, I think you are only speaking to the elite, and not,to the public.
Ed Bradford
Pflugerville,TX
Ed Bradford,
In simple terms:
2. The output intensity is directly proportional to the input intensity.
1. The output intensity falls as a function of e-L (“2.72 to the power of -L”) where L is the length of the box (assuming the density stays the same). This is the Beer Lambert law.
So if you double the intensity of the incoming radiation, the output intensity doubles.
If you halve the intensity of the incoming radiation, the output intensity halves.
If you double the length of the box, the intensity falls to 37% of its original value. If you halve the length of the box the intensity increases to 2.72x its original value.
This graph below shows the relationship. It shows transmittance (proportion of incident radiation transmitted) as a function of optical thickness. Optical thickness is directly proportional to length. See technical bit below the graph.
In more technical terms:
The optical thickness at any given wavelength, τv=σvNd
where σv is a material property of the gas – the capture cross section (the absorption ability at that wavelength), N = number of molecules per m3, d = path length
And the intensity of any given wavelength I = I0e-τv
where I0 = incident radiation at start of path.
And just to be complete, the gas also emits radiation as a function of its own temperature. So the measurement of I at a wavelength will be the formula above plus some emission. We can take the case where the intensity of emission is negligible compared with the incident beam and then the above formula will be correct.
SOD,
“We have experimental results. We have theory that matches”.
Trouble is, the experimental results are not independent of the theory and can provide only ambivalent verification of it. In the case of DLR, the pyrgeometer reading is composed predominantly of a flux derived from a precise calculation based on the theory it supposedly verifies.
John Millet,
Why the concentration on pyrgeometers. That’s not the only instrument used to determine DLR. How about Fourier Transform Infrared Spectrophotometers? They measure spectra, i.e. flux vs. frequency (cm-1) and the observed spectra match the calculated spectra. I guess you don’t own an IR thermometer either as you couldn’t possibly believe it was accurate since it works exactly like a pyrgeometer except with a much more limited field of view.
John,
All measurement devices rely on a theory. People do lots of experiments that isolate different components to prove theories. In the end, we get instruments that rely on various physics theories. Thermometers rely on the theory of heat. But how we do ascertain the theory of heat? With thermometers! It’s circular, there is no heat, it’s all wrong!
The theory of thermal emission of radiation has been established for over 100 years. I have Max Planck’s 1914 The Theory of Heat Radiation with him citing references for experiments from the 1870s to the early 1900s.
The kind of experiments people did was to put a heated object in a vacuum chamber and measure how the object’s temperature changed. And how the temperature of the wall of the chamber changed.
This established that heat transfer takes place according to a formula that was empirically derived to begin with. Then followed decades of experiments measuring spectra and emissivities and everything else.
My interest level in demonstrating to you that a body radiates according to standard theory is extremely low. It involves digging through lots of really really old stuff and that means finding it in the first place.
If you believe Planck, Kirchhoff, Stefan, and thousands of physicists that followed were all wrong or didn’t bother to check, then I applaud your..
I’ve already spent too much time on this subject.
Everyone has their special research interest. Good luck with yours.
But can we please just accept for the sake of this blog that here we are accepting of 100 year old uncontroversial physics?
SoD,
For things like temperature, it’s even worse. Temperature is state function of the system, not a property of the components of the system. And the only thermodynamic measure of temperature, a monatomic ideal gas thermometer, can never be realized in practice. So all our definitions are more than somewhat arbitrary. We measure temperature between fixed points like the triple point of water and the freezing point of zinc using a specified interpolation device such as the standard platinum resistance thermometer. I’ve used one. It’s a chore.
SOD,
“But can we please just accept for the sake of this blog that here we are accepting of 100 year old uncontroversial physics?”
Yes, we can. We can also on occasion question its application in climate science. Planck, Kirchoff and Stefan were physicists whose work was unconnected to climate.
Can even century old theory lacking experimental validation ever be truly uncontroversial? Or is quantum theory inaccessible to experimental validation, too difficult to be explained except by exceptional talents and generally has to be taken on trust?
In the teacher-student space, teacher frustration (and the student variety, as well) come with the job – an occupational hazard.
John Millett,
All things can be questioned. However, every blog needs a niche, a focus and a perspective. This blog accepts the fundamentals as found in standard physics textbooks.
After all, when it comes to AGW / the “greenhouse” effect / climate change / global warming / global cooling what many people believe they are questioning is not whether elementary basic physics is true (the foundation building blocks), but whether climate science uses these building blocks to create something valid – and what are the limits of knowledge from the physics basics and observations.
Some basic questions on the foundations are good – and often essential – as readers need to establish how strong the foundations are for each topic under consideration.
But I just don’t want main threads to end up continually debating whether statistical thermodynamics is correct, or equations for heat transfer might be all just plain wrong.
Pekka Pirila,
“You refer to a “surface of a body made up mostly of radiatively-inactive particles”. That’s not correct”.
Implicit in my statement, which was a response to SOD’s, is that the “body” is a gas. The “gas body” is indeed made up mostly of radiatively-inactive particles.
“You use the expression “energy generation”. I don’t know precisely what you have in mind”.
I should have written “emission”, a change in the form of energy not generation of it.
“…but on micro level of molecules and photons both involve energy transfer in all directions”.
Would I be correct in mentally adding ” the strength of the emission decaying with the square of distance from its molecular source” ?
“…in case of radiative energy transfer it’s easy to observe photons coming from all directions”.
Would I be correct in mentally adding “though it is impossible to see photons coming into and going from a body simultaneously, as required by the theory of radiative exchange”?
John Millet:
No. You would be wrong. An emitted photon doesn’t change frequency in its travel so it doesn’t change energy (unless it gets red-shifted by the expansion of the universe). Emission intensity decreases as the inverse square of the distance from a small source because the area that the emission is spread over increases as the square of the distance. If the source is an infinite plane, the intensity doesn’t decrease with distance at all. This is, in fact, the same reason that a solar furnace cannot possibly exceed a temperature of ~6,000K.
Somehow this all seems familiar. I have the nasty suspicion we’ve been over this before.
John Millett,
You extend your comments to a very wide range of issues. Comparing to an university syllabus finding answers to all of them would require material from several courses or textbooks. Trying to answer to all the questions you have asked – and that you may well ask in the future given your approach – is beyond the possibilities of any blob. That’s even more true because the questions are seldom clear enough to be answered directly. When SoD, DeWitt, me, or anyone else tries to answer a question that leads usually to the observation that you didn’t want ask exactly what the answer was about.
One basic issue is the nature of scientific knowledge and the development of physical theories. Every good physical theory is applicable to many different problems and capable of making very many predictions. It should not contradict any well confirmed empirical observation within its limits of applicability. Stating the limits of applicability is part of a good theory.
Within the limits of applicability it can be used in calculation of many things that are difficult or even impossible to study empirically. When these calculation fall safely within the limits, we may have great trust in the correctness of these calculation in cases where the same results have been observed independently by several people. This is the way physics is all the time used in engineering and other fields of application as well as a tool in other sciences.
The typical timeline of good physical theory is as follows:
First there are empirical observations of some related phenomena.
Next some ad hoc models are presented to describe these phenomena. Each of the models has a very limited applicability and the models are not fully based on known theories.
At this stage someone presents an hypothesis that can explain at once the observed validity of the ad hoc models and also some other empirical observations that have lacked even simple models as explanation.
The new hypothesis makes additional predictions and scientists start to look for experiments that could show that the theory is wrong. That may lead to some changes in the theory, and finally a formulation that doesn’t contradict any confirmed observations.
At this point a good theory has been formulated.
Assuming that the theory is in an area of practical significance it starts to be put in practical use. Every successful practical use of the theory provides additional confirmation for it, but nobody tries anymore to keep track on the number of ways it has been confirmed as it has already reached the status of a good theory. It’s still true, however, that clear failures are noticed and lead often to further research in attempt to understand the source of failure. Thus stringent testing goes on forever.
Often the most stringent examples of the above paragraph are related to the application of the theory in other fields of science or in collecting large databases related to the theory.
The theory of interaction of radiation with matter has gone trough all these stages. It’s empirical tests must by now count in at least tens of thousands more probably in millions. In many cases the tests have been extremely accurate. Collecting the HITRAN database is a strong empirical confirmation of many parts of the theory as thousands of lines have been both calculated and observed and found to be in agreement. Many different empirical methods have been used and their agreement gives evidence that the theory used in developing and interpreting these methods is also valid.
This is the reason scientists don’t have much doubt on the theory of interaction of radiation with matter. Similarly scientists have little doubt on the validity of thermodynamics or quantum mechanics within the limits given for each of these theories.
[…] Visualizing Atmospheric Radiation – Part One with a few basic concepts […]
SOD: I find Figure 1 questionable because it appropriate for a laboratory experiment with a spectrophotometer and someone misleading the real atmosphere. With a spectrophotometer, one uses a radiation source that is many orders of magnitude more intense than the emission that comes from the sample of gas. Such experiments are appropriate for recording the absorption spectrum of a sample of sample – without having to worry about any photons emitted by the gas.
In the atmosphere, the intensity of the radiation entering and passing through a slice of the atmosphere (let’s make it 1 km thick) is comparable to the intensity of the emission FROM that slab at many (or most) infrared wavelengths. The earth is emitting about 390 W/m2 upward and most of the 333 W/m2 coming back down was emitted from 1 km or below. Between 1 and 5-10? km, most of the photons traveling through the atmosphere were emitted by the atmosphere and will be absorbed by the atmosphere before they escape to space. This is because the gases in the atmosphere most frequently emit the wavelengths they absorb best.
I’ve struggled to change my thinking from the laboratory situation where emission is negligible to the atmosphere, but I still don’t have a good mental picture of what is happening. Consider a slab of atmosphere at 2.5-3.5 km*. Where did most of the upwards and downwards traveling photons in that slab originate? What fraction will be adsorbed? How does the total power absorbed compare with the total power emitted? For the emitted photons, how far on the average will they travel upward or downward before they are absorbed? What fraction will reach space or the surface of the earth? (A quick glance at Parts 2 and 3 suggest that I may not find definitive answers in them.)
* I’d prefer to consider the 1% (by weight) of the atmosphere centered at 3 km and contrast it to 1% of the atmosphere centered at 1 km and 10 km. In other words, the same mass of atmosphere in slabs of different thickness.
[…] radiation. If a gas molecule absorbs at one wavelength, it can also emit at that wavelength. See Part One and Part Two for the […]
[…] radiation then the result is not so different. This is something I might try to demonstrate in the Visualizing Atmospheric Radiation […]
[…] Part One – some background and basics […]
[…] Part One – some background and basics […]
[…] Part One – some background and basics […]
[…] Part One – some background and basics […]
What happens to incident radiation that does not match the absorption spectrum? Does it just pass straight through unaffected, as if the gas was not there at all?
And what is reflection all about ? A joint absorption-emission behavior?
Thanks.
Montalbano,
Radiation that doesn’t get absorbed passes trough a gas almost unaffected. Scattering is usually a minor factor. Another minor factor is bending from the same basic mechanism that causes refraction at the surface of water or glass.
Several different phenomena cause scattering. In some cases the deviation from the original direction is mostly rather small, in others scattering occurs to all directions with comparable strength. Scattering is due to interaction of the photon with a molecule or a larger aerosol droplet/particle. Scattering is not equally dependent on the wavelength as absorption by gas molecules as it’s not restricted to certain specific wavelengths by the quantization of molecular energy levels.
All electromagnetic radiation can be considered both in terms of photons and in terms of waves. Reflection, refraction, and bending are phenomena that are best understood in terms of waves. That is true also for scattering of short wavelength radiation (X-rays) from crystals.
The so called “wave-particle duality” of Quantum Mechanics tells that the two very different points of view (particles and waves) can be true simultaneously.
[…] those interested, here's the long and technical 10-part series on how atmospheric radiation works. Visualizing Atmospheric Radiation ? Part One | The Science of Doom It's not light reading. Naturally, the cultists will scream that it's liberal propaganda and they […]
[…] Det här är i verkligheten betydligt mer invecklat än beskrivet ovan, läs mer t ex här. […]
Thanks for the excellent illustration. I wonder when the radiation on the right (part of the incident + emitted due to the gas temperature) could be larger or smaller than the incident radiation. If the box is warmer than the surroundings, could the radiation on the right be larger than the incident one?