I created some simulations of different CO2 concentrations using the atmospheric radiation model described (briefly) in Part Two and in detail in Visualizing Atmospheric Radiation – Part Five – The Code.
- surface temperature = 300 K
- lapse rate = 6.5 K/km
- 10 layers (of roughly equal pressure change to keep similar number of molecules in each layer)
- top layer, layer 10, centered at 16.9 km or 98 hPa and 7.0 km thick
- temperature of layer 10 = 220K
- Water vapor RH=80% in boundary layer, 40% in free troposphere
- CH4 at 1775 ppmv, N2O at 319 ppbv, no ozone
- Line width resolution = 0.1 cm-1
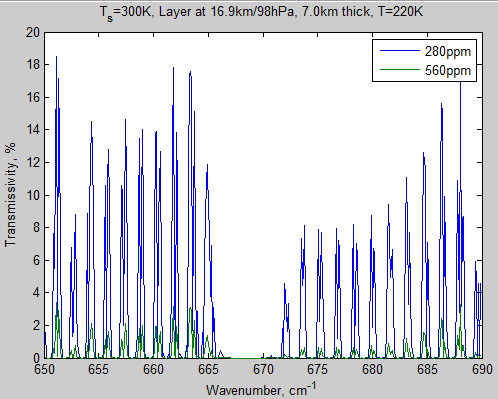
Here’s the transmissivity of the atmosphere with CO2 at pre-industrial levels of 280 ppm compared with doubled at 560 ppm. Transmissivity just means “what proportion of incident radiation makes it through”:
Figure 1 – Transmissivity of layer 10 from 666.6-667.6 cm-1
Wavenumber 667 cm-1 = 15 μm. (Wavenumber in cm-1 = 10000/wavelength in μm).
So we see that at 280 ppm a miniscule fraction of 666.6 cm-1 makes it through and at 560 ppm that’s gone to zero. But 0.05% down to 0% in just one small part of the spectrum is not much of an issue.
The equivalent graph for the surface layer is just plain 0.00000% making it through.
So it’s pretty clear that CO2 is already saturated and increasing CO2 has no effect.. well.. not in this 1 cm-1 range of the peak absorption of CO2.
Here’s another graph of this high up layer, across a wider wavenumber range:
Figure 2 – Transmissivity of layer 10 from 650-690 cm-1
We can see that there’s quite a difference as a result of doubling CO2.
Let’s take a look at the same graph for the bottom layer of atmosphere in this model. The center of this layer is at 420 m and it is 840 m thick at an average temperature of 297K:
Figure 3 – Transmissivity of bottom layer from 650 – 690 cm-1
Notice that the transmissivity scale has been dropped considerably from that of the top layer and still the transmissivity is zero – in both cases. So going from 280 ppm to 560 ppm has absolutely no effect on this layer.
Before we move on.. how can a layer with a similar number of molecules have such different characteristics?
The difference is the pressure. The line width of a typical CO2 absorption line is 0.07 cm-1 at the surface. At 100 hPa (17km) its line width will be about 0.008 cm-1(see note 1). The peak gets higher but the line gets thinner. Add lots of lines together at the surface and nothing gets through. Add lots of lines together at 100 hPa and quite a bit gets through.
Wait a bit.. if we consider all the layers together don’t we get back to zero transmissity?
Good point. (On a technical note we multiply transmissivities together, so if 10% gets through one layer and 5% through the next layer the total effect is only 0.5% getting through – and anything x 0 = 0).
So that’s clear then. If we take the entire spectrum from 650 – 690 cm-1 (15.4 – 14.5 μm) and look at the surface emitted radiation, nothing gets through to the top of atmosphere (TOA) regardless of whether we are at pre-industrial levels of CO2 or the future potential doubled CO2.
Right?
Let’s take a look at outgoing radiation at the top of the atmosphere:
Figure 4 – TOA Radiation from 650 – 690 cm-1
Why is there any radiation at all? Because the atmosphere emits radiation as well as absorbs radiation. If a gas molecule absorbs at one wavelength, it can also emit at that wavelength. See Part One and Part Two for the basics.
So, even though the total transmissivity through the atmosphere at these wavenumbers is zero, there is emitted radiation at these wavenumbers. And, there appears to be some small change in TOA radiation. If you reduce outgoing terrestrial radiation (called outgoing longwave radiation or OLR) and still absorb the same amount of solar radiation then the climate must warm.
Let’s look at the magnitude of this change – the calculation in the top right is the sum (the integral) of the curve. The change is less than 0.001 W/m²!! I knew it!
Figure 5 - Difference in TOA Radiation for 280 ppm – 560 ppm CO2 from 650 – 690 cm-1
So doubling CO2 wil cause a tiny tiny reduction in outgoing radiation at TOA in this band (all other things being equal). Except it doesn’t look like much - and it’s not.
If you have grasped why figure 5 is like it is even though total atmospheric transmissivity is zero then you have understood some important points.
Now let’s look at the whole picture. Here’s the top layer again, with the same conditions, but over a wider wavenumber range:
Figure 6 - Transmissivity of layer 10 from 650-690 cm-1 – Click to enlarge
It’s worth clicking on the graph to expand the scale.
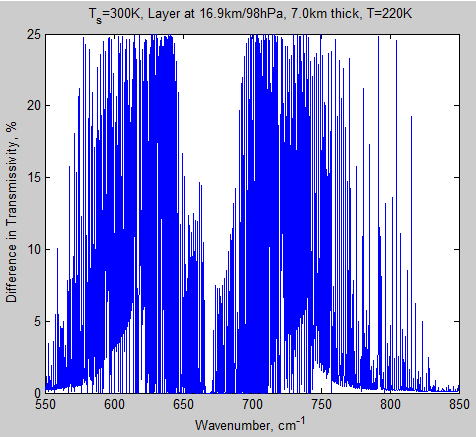
Here’s the transmissivity difference between the two cases for this top layer:
Figure 7 – Difference in transmissivity of layer 10 for 280 ppm – 560 ppm - Click to enlarge
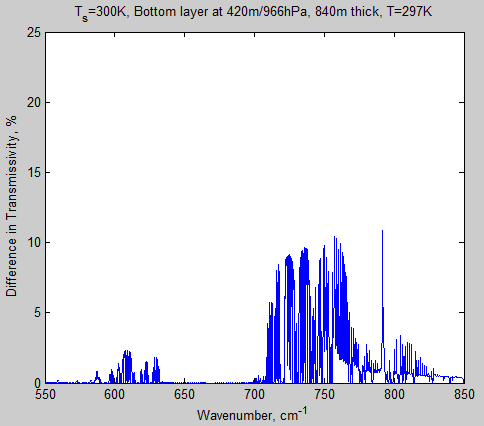
And, as before, let’s compare with the bottom layer – and with the same scale of transmissivity as figure 6:
Figure 8 - Transmissivity of layer 10 from 650-690 cm-1 - Click to enlarge
Let’s see the difference, on the same transmissivity scale as figure 7:
Figure 9 – Difference in transmissivity of layer 10 for 280 ppm – 560 ppm - Click to enlarge
Why is figure 9 so different from figure 7? There are two reasons:
- first, as before, the CO2 lines are narrower high up in the atmosphere meaning that there are more gaps in the spectrum
- second, water vapor absorption is very high around the 550 cm-1 region
The mixing ratio of water vapor molecules in the surface layer is more than 100 times greater than the top layer we are considering (in this scenario). So water vapor absorption is considerable near the surface, and very small in the top layer. (I might do a simulation with zero water vapor to see what the water vapor impact is around 800 cm-1 - as the water vapor continuum may be playing a role here).
As before, let’s consider total atmospheric transmissivity. From the graphs above of top and bottom layer of the atmosphere we might expect some wavenumber regions to be close to zero and others possibly not.
That’s what we find:
Figure 10 - Transmissivity of total atmosphere from 650-690 cm-1 - Click to enlarge
And the difference between 280 ppm – 560 ppm:
Figure 11 – Difference in transmissivity of total atmosphere from 650-690 cm-1- Click to enlarge
Now let’s look at the TOA spectrum.
As before when we considered a much narrower bandwidth, the value of TOA is not zero, and there is also a significant difference between the cases at 280 ppm and 560 ppm, even where the total atmospheric transmissivity is zero (compare with fig. 11):
Figure 12 – TOA radiation from 650-690 cm-1 - Click to enlarge
The reason should be clear – the atmosphere emits radiation. The radiation that escapes to space is NOT surface radiation attentuated by the transmissivity of the whole atmosphere. It is a sum of radiation from the surface and from all different levels in the atmosphere, all very dependent on wavelength. In the wavelengths where the atmosphere absorbs strongly the emission to space is from higher levels.
Take a look at Part Three – Average Height of Emission and Part Four – Water Vapor for more insight.
Here is the difference in TOA radiation for 280 ppm – 560 ppm. The total flux difference between the two cases in this wavelength region = 4.3 W/m².
Figure 12 – Difference in TOA radiation for 280 ppm – 560 ppm - Click to enlarge
Conclusion
Simple considerations of transmissivity of radiation in the most absorbing wavelengths of CO2 have led many people in the blog world to conclude that increases in CO2 will have no impact on outgoing radiation and that CO2 is “already saturated”.
Others have stated that water vapor totally overwhelms the effect of CO2.
We can see that these both misunderstand the actual, more complex, situation.
The data for the model comes from the HITRAN database (reference below) compiled over decades by spectroscopy professionals. The formula for absorption is the Beer-Lambert law. The formula for emission is the Planck emission law, modified by the emissivity at the wavelength in question. The formula for line width changes under atmospheric conditions have been known for 50 years or more and published in hundreds of papers.
I created this model from scratch using these equations. The equations can be seen in the Matlab model in Part Five.
The results look very similar to those published by atmospheric physicists who have run more detailed models under more exacting conditions – for example, the graph shown in CO2 – An Insignificant Trace Gas? – Part Eight – Saturation from Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the IPCC AR4, W.D. Collins et al, Journal of Geophysical Research (2006).
Hopefully, the data presented here helps to verify the approximate magnitude of the net change in absorbed radiation due to CO2 doubling (see note 2).
Much more important – the aim to to help the reader see more clearly how radiation interacts with the atmosphere under different conditions.
Related Articles
Part One - some background and basics
Part Two - some early results from a model with absorption and emission from basic physics and the HITRAN database
Part Three – Average Height of Emission - the complex subject of where the TOA radiation originated from, what is the “Average Height of Emission” and other questions
Part Four – Water Vapor - results of surface (downward) radiation and upward radiation at TOA as water vapor is changed
Part Five – The Code - code can be downloaded, includes some notes on each release
Part Six – Technical on Line Shapes - absorption lines get thineer as we move up through the atmosphere..
Part Eight – CO2 Under Pressure - how the line width reduces (as we go up through the atmosphere) and what impact that has on CO2 increases
Part Nine – Reaching Equilibrium - when we start from some arbitrary point, how the climate model brings us back to equilibrium (for that case), and how the energy moves through the system
Part Ten – “Back Radiation” - calculations and expectations for surface radiation as CO2 is increased
Part Eleven – Stratospheric Cooling - why the stratosphere is expected to cool as CO2 increases
Part Twelve – Heating Rates - heating rate (‘C/day) for various levels in the atmosphere – especially useful for comparisons with other models.
References
The data used to create these graphs comes from the HITRAN database.
The HITRAN 2008 molecular spectroscopic database, by L.S. Rothman et al, Journal of Quantitative Spectroscopy & Radiative Transfer (2009)
The HITRAN 2004 molecular spectroscopic database, by L.S. Rothman et al., Journal of Quantitative Spectroscopy & Radiative Transfer (2005)
Notes
Note 1: The formula for line half-width in the troposphere is basically bl0.(p/p0).(T0/T)0.5
where bl0 is the value measured at p0 & T0 (usually 1013 hPa and 296K) and p, T describe the pressure and temperature where we want to know the new line half-width. For in depth material on this see Part Six – Technical on Line Shapes
Note 2: This is often known as radiative forcing. That term has some more restrictive conditions around it – primarily it is the case before any response from the lower atmosphere (i.e., the surface and atmospheric temperature are held constant) but after allowing for the stratosphere to return to radiative equilibrium, which takes a few months.
This Matlab model does not have a proper treatment of the stratosphere, and stratospheric radiation change does have an impact on the tropospheric radiation balance. The intent of this model is not to redo what atmospheric physicists have done, but to provide a reasonably realistic tropospheric model which allows us to look behind the scenes.
The model has the basic mistake, that the greenhouse effect is not considered. The assumptions used for 280 ppm can be made – but doubling the concentration to 560 ppm has an impact on the greenhouse effect. The surface temperature can be assumed with 303 K, the temperature of the layer 10 is then 211 K and the average pressure of layer 10 is reduced (for example 97 Pa), because the rises of height of tropopause.
These changes result from the higher disability rating of radiation propagation through more CO2 while maintaining the total radiation of all wavelengths. The cumulative curve is beginning with a higher performance by level 0 and larger slope at the upper end.
I think the calculation with the transmission is counterproductive, because where is strongly absorbed, is also emitted strong. A calculation with intensities that are much higher than the intensity of thermal emission, says nothing: The absorption onto the Beer-Lambert law neglected the thermal emission – only the radiative transfer equation is considered for the thermal emission, only by neglecting of the thermal emission in the radiative transfer equation is the Beer-Lambert law correct, ie the intensity change by the use of Beer-Lambert law requires intensities that are far above the actual intensities and therefore unrealistic.
Sincerely
The results are deliberately shown with the same surface and atmospheric conditions.
As I stated in the conclusion to Part Four – Water Vapor (but for slightly different reasons):
So the intent here is to show how the same atmospheric conditions but different concentrations of CO2 cause a change in outgoing radiation.
For people familiar with the basic physics this is, of course, very obvious and not so interesting.
For people getting to grips with the physics of radiative transfer this is essential knowledge. What wavelengths cause what changes and so on.
Comparing with fig 12, we can see the fine difference in atmospheric radiation at TOA when the simulation (for 280 vs 560 ppm) is run at Δv = 0.01 cm-1 vs Δv = 0.1 cm-1. The view zooms in on one wavelength region of 580 – 590 cm-1.
Click for expanded view
In terms of total upward flux at TOA, the calculated value is the same whether the atmosphere is evaluated at 0.1 or 0.01 cm-1.
SoD,
What’s the change in downward flux to the surface. That would answer almost directly some of the recent questions presented in other threads as far as this model is considered representative for the whole atmosphere.
Pekka,
Do you mean the DLR for the difference of Δv of 0.1 cm-1 vs 0.01 cm-1? If so, the answer is also 0.0 W/m2.
Or the change as a result of introducing the diffusivity factor to the continuum?
I plan to do a separate article on the downward flux.
I meant the effect of doubling CO2.
I did my own calculation with slightly different input (and a little modified model with 10 azimuthal segments). That gave an decrease of 5.05 W/m^2 in the flux up at TOA, 3.24 W/m^2 in flux down at surface and thus a net rate of 1.81 W/m^2 was left to warm the atmosphere.
This simple clear atmosphere model gives a high value for the forcing, but what I had in mind was the point that about 64% of the warming goes initially to the surface and 36% stays in the atmosphere.
Due to the smaller heat capacity the atmosphere warms at that point much faster but that will soon affect convection, and at that stage the energy the atmosphere takes in further warming is very little. What’s initially 64% is soon almost 100%.
Pekka,
That sentence reads flux down at the surface decreases. That must be an increase or the net wouldn’t be smaller. That’s a rather large increase in flux down for doubling CO2. That’s what I would expect to see for very low humidity, like the sub-Arctic winter atmosphere.
DeWitt,
You’re right. The flux down to surface increases. Words “.. and an increase ..” were missing from my previous message.
In this calculation the boundary layer humidity is 80% and the top of the boundary layer at 920 hPa / 400 m. Above that altitude the humidity is 40%. I haven’t paid much attention to the parameters. Thus the values are perhaps the most appropriate ones.
However well the model is made to calculate the radiative transfer, it’s still based on one clear sky profile only and therefore not quantitatively right for global averages of the real Earth system.
Pekka,
That profile would give very low total column precipitable water for a surface temperature that high. Looking at the different profiles, only the US 1976 standard atmosphere likely has total column water that low. At 300 K, you get ~+2.5 W/m² increase in DLR for doubling CO2 and a reduction of 4 W/m² at the tropopause looking down.
It makes me suspect that there might be a problem with the water vapor pressure calculation.
DeWitt,
I haven’t studied any part of the code related to water vapor, just used the code as SoD has written it. The moisture levels are also the same he has been using.
My implementation differs in two ways:
- I read the HITRAN data from text files downloaded from SpectralCalc rather than HITRAN-files directly.
- I have added the possibility of separating segments of different azimuthal angles. In many runs I use ten segments as the program runs fast enough even with those (the most time consuming step need not be modified for that). It turns out that this added complexity makes little difference for the results. (The up and down fluxes change by +0.4 and -0.5 W/m^2, when 10 segments are taken into use rather than one with diffusion factor 1.66).
When I use more closely his parameter values the changes from doubling CO2 are -4.2 W/m^2 up and +2.8 W/m^2 down.
Pekka,
Can I see the code for the different azimuthal angles?
Did you do this rather than use the Zhao & Shi method, because it’s potentially more accurate?
DeWitt,
The code for water vapor is:
————————————-
function [ es ] = satvaph2o( T )
% Saturation vapor pressure in Pa at temperature T in K
% Using wiki formula
% T can be a vector
Tc=T-273.15; % temperature in ‘C
es=610.94.*exp(17.625.*Tc./(Tc+243.04));
end
—————————————-
In the main function this is called like this:
for i=1:numz-1
% now calc mixing ratio in molecules for water vapor at prescribed RH
% = RH * es / p
% currently satvaph2o() gives es=610.94.*exp(17.625.*Tc./(Tc+243.04)); where Tc in ‘C
if i==1
mixh2o(i)=BLH*satvaph2o(Tinit(i))/p(i);
else
mixh2o(i)=FTH*satvaph2o(Tinit(i))/p(i);
end
end
————————————–
And the number of molecules is worked out via:
na=(Na*rho(i)/mair)/1e6; % number of air molecules per cm^3
….
if mol(m)==1 % if water vapor, special case
mix(m)=mixh2o(i); % precalculated for each layer using prescribed RH
….
nummol=isoprop(m,iso(im(j)))*mix(m)*na;
….
At the end the function returns the vector mixh2o() so the mixing ratio by volume can be seen for each layer.
SoD,
I just sent it to you (before I read this message).
Here are the mixing ratio values (%) for a 10 layer model with a surface temperature = 288K, BLH = 80% and FTH = 40%.
Height= 0.4 km, Pressure= 966.1588 hPa, Mixing Ratio= 1.1785%
Height= 1.26 km, Pressure= 870.9433 hPa, Mixing Ratio= 0.44898%
Height= 2.21 km, Pressure= 774.2521 hPa, Mixing Ratio= 0.3269%
Height= 3.27 km, Pressure= 677.3866 hPa, Mixing Ratio= 0.22389%
Height= 4.45 km, Pressure= 580.6494 hPa, Mixing Ratio= 0.14243%
Height= 5.81 km, Pressure= 483.9863 hPa, Mixing Ratio= 0.080612%
Height= 7.41 km, Pressure= 387.3887 hPa, Mixing Ratio= 0.03837%
Height= 9.36 km, Pressure= 290.8015 hPa, Mixing Ratio= 0.01374%
Height= 11.95 km, Pressure= 194.1372 hPa, Mixing Ratio= 0.0031486%
Height= 16.2 km, Pressure= 97.5971 hPa, Mixing Ratio= 0.006263%
SoD,
You asked also for the preference of this over Zhao and Shi.
When I realized that the extra computational work is not too heavy, this approach seems clearly preferable. Using this approach the whole diffusion approximation can be dropped as the path-lengths are real path-lengths, not parametrizations. The need of using some “fudge factor” like 1.66 is not there any more.
The Zhao and Shi approach is likely to give results that depend a little on the selected layer thickness while this other method is approximate only in the same sense as using a finite number of layers is approximate. (Using a discrete set of frequencies is on still better basis as that does not introduce bias, but only effectively random errors.)
From practical point it’s nice to see that the simple diffusion factor of 1.66 works so well, while it’s a little disappointing that the theoretically better method is so little better in practice. Differences are so small that they can be ignored for most purposes. There are certainly again some detail results where the difference is larger.
One example is the spectrum of radiation that escapes directly from surface to space. That’s a quantity for which I get quite different results from some early calculations and from my present version. I’m not quite certain on the reason. There may be an error in either one calculation. That’s anyway just one of those “curiosity values” as it’s not possible to tell in reality what’s the point of emission of each photon. The diffusion factor is certainly important for that, but in this case we know by definition that the photons must traverse the whole atmosphere. Thus the angular dependence of the optical thickness is also known exactly and can be used in a separate calculation as I have done.
There’s certainly a risk that my code has errors, but the results are, in general, in good agreement with expectations. In particular it gives exactly the same results as your code, when the 1/cos(theta) factor is replaced by 1.66 for all angles.
As I expected, your atmosphere is really dry. Here’s a comparison of water vapor mixing ratios with pressure for your atmosphere and the US 1976 standard atmosphere with humidity corrected to a surface temperature of 300 K. If I did my sums correctly, the total water vapor content in atm cm for your atmosphere is 2597 compared to 3855 for the US 1976 standard atmosphere relative humidity profile at the same surface temperature.
SoD,
I went here: http://www.humidity-calculator.com/index.php
I plugged in the numbers for the boundary layer, 80% RH, 297.4 K and 96616 Pa, the calculated water vapor mixing ratio was 1.6076% w/w or 2.5847% v/v. Something’s wrong somewhere.
SoD,
I somehow missed that the surface temperature in your table was 288 K. The web site calculated volumetric mixing ratio for 285.4 K and 966.16mbar is 1.19945% compared to your 1.1785%. That’s not far off. So your atmosphere is wetter in the boundary layer and dryer at higher altitude with ~2 cm precipitable water compared to ~1.4cm for the US 1976 atmosphere.
DeWitt,
Quite high on my list of things to do with this model is to run it with some US standard atmospheres.
Do you have the data (atmospheric temp & water vapor mixing ratio or RH) available in a convenient table, at the tropospheric resolutions I’d need (at least 10 layers in the troposphere)?
I haven’t looked very hard but when I did look some time ago I found the data up to 100km but not at all good resolution for the troposphere.
SoD,
MODTRAN will give you 1 km resolution up to 25 km and then 5 km to 50 km. Just click on the ‘view the whole output file’ link at the bottom of the right hand pane after you submit the calculation for a particular atmosphere. All the spectral data are there too. The spectral data, however, are only for the selected observation height and direction. Also, the atmosphere data are for the specified surface temperature. If you change the surface temperature, you really need to change the atmosphere pressure profile too which will change the number densities of the various molecules. MODTRAN only changes the temperature up to 13km when you change the surface temperature offset. It probably doesn’t make much difference for small changes in temperature.
[...] 2013/01/13: TSoD: Visualizing Atmospheric Radiation – Part Seven – CO2 increases [...]
[...] « Visualizing Atmospheric Radiation – Part Seven – CO2 increases [...]
scienceofdoom on January 14, 2013 at 9:08 am
“The results are deliberately shown with the same surface and atmospheric conditions.”
This allowed for calculations. But then you have to point out that the energy balance is violated in any height. This violation of the energy balance is stored in the atmosphere – and leads to temperature changes at the new temperatures lead back to the energy balance.
Pekka Pirilä on January 14, 2013 at 8:20 pm
“I have added The Possibility of separating segments of different azimuthal angles.”
The integration over all angles is not spread as Beer-Lambert law, but the Exponential integral function.
Sincerely
The exponential integral is obtained from a calculation of transmission trough a single layer of given thickness. It cannot be applied exactly to the succession of several layers because it cannot describe properly the probability of photons passing trough several layers. The approach of handling the azimuthal angle as an extra parameter does this as well. Therefore this approach is fundamentally correct while the use of exponential integrals remains an approximation in the multilayer case.
Doing the calculation of transmission trough one layer having the azimuthal angle as one variable leads exactly to the exponential integral when integrated over azimuthal angles. The numerical method based on a few discrete values for the azimuthal angle is naturally an approximation but it’s accuracy can be improved by increasing the number of these discrete values. It’s easy to find out empirically, how many values are needed for accurate enough results. That number seems to be rather small.
Pekka,
If I remember correctly, Miskolczi used either seven or nine azimuthal angles in his LBL program. As far as I know, there’s nothing wrong with his LBL program. It’s the rest of his theory that leaves something to be desired.
DeWitt,
Miskolczi has 9 azimuthal angles. I have also got the impression that his radiative calculation is correct, or at least I haven’t found anything wrong in it. Concerning his 2010 paper it’s a bit strange that he gets so far essentially correctly and then just misses the opportunity of reaching reasonable results on GHE by doing one more very simple step correctly.
[...] But the effect of increasing CO2 on the TOA radiation balance is completely different. High surface humidities have little or no effect on this TOA balance. And there, doubling CO2 has a significant impact (all other things being equal) as shown in figure 12 of Part Seven – CO2 increases. [...]
[...] Visualizing Atmospheric Radiation – Part Five – The Code Visualizing Atmospheric Radiation – Part Seven – CO2 increases [...]
[...] Part Seven – CO2 increases - changes to TOA in flux and spectrum as CO2 concentration is increased [...]
[...] Part Seven – CO2 increases - changes to TOA in flux and spectrum as CO2 concentration is increased [...]
[...] Part Seven – CO2 increases - changes to TOA in flux and spectrum as CO2 concentration is increased [...]
[...] Part Seven – CO2 increases - changes to TOA in flux and spectrum as CO2 concentration is increased [...]
Out of interest, what’s the corresponding figures for the next sets of doubling? eg, 1120, 2240, 4480ppm?
I think it’s about 4 W/m^2 of increased absorption per incremental doubling.
I checked using my version of SoD’s model what repeated doubling does for the TOA OLR intensity for three standard profiles: tropical, mid-latitude summer, and subarctic summer. On linear scale the results look like this, and with logarithmic concentration axis like this. Highest curve is from tropics and lowest from subarctic.
We can see clear saturation on linear scale as expected, but the plot with logarithmic scale tells that the saturation is not as strong as what a logarithmic dependence on concentration would predict. That’s not really surprising as the logarithmic law is not derived from accurate theory but has been described as a qualitatively good fit to some model results. Results from models can be presented in many different ways. Some other quantities might behave more linearly as function of the logarithm of the concentration.
Pekka,
I think there’s something fundamentally wrong with your model. It seems to wildly overstate the forcing and curvature at high levels of CO2. Compare these numbers from MODTRAN, 20 km, looking down:
CO2 tropical mid-lat summer sub-arctic winter
100 295.4 285.9 266.7
200 291.4 282.4 263.9
500 285.8 277.7 260.1
1000 281.5 273.9 257
2000 276.8 269.9 253.8
5000 270.1 264.1 249.2
10000 264.3 259.2 245.3
Plotting on a log10(CO2) scale gives a nearly straight lines (R² = 0.996) with slopes of -15.4, -13.2 and -10.6 W/m²/decade.
DeWitt,
Do you know, what’s the width of the frequency bands in that UChicago MODTRAN implementation. MODTRAN5 allows for highly different bandwidths from 0.1 to 15 1/cm and the broader ones might not be good for this kind of calculations.
SoD’s model is not a band model but a sampling line-by-line model. Band models may produce systematically biased results while a sampling line-by-line model has larger random errors without bias.
I did my earlier calculation with a 1 1/cm grid. Then I redid some of the calculations with a 0.1 1/cm grid. The results changed a little, but not enough to make any difference for the present discussion.
I*m still wondering, whether I have missed something, but haven’t found anything.
Pekka,
Here’s the header from the data file:
***** MODTRAN3 Version 1.3 12/1/95 *****
0 CARD 1 *****T 1 3 1 0 0 0 0 0 0 0 0 0 -1 0.000 -1.00
0 CARD 2 ***** 2 0 0 0 0 0 0.000 0.000 0.000 0.000 0.000
0 CARD 3 ***** 70.000 0.000 180.000 0.000 0.000 0.000 0
0 CARD 4 ***** 100 1500 2 2
0 PROGRAM WILL COMPUTE RADIANCE
0 ATMOSPHERIC MODEL
TEMPERATURE = 1 TROPICAL MODEL
WATER VAPOR = 1 TROPICAL MODEL
OZONE = 1 TROPICAL MODEL
M4 = 1 M5 = 1 M6 = 1 MDEF = 1
0 AEROSOL MODEL
REGIME AEROSOL TYPE PROFILE SEASON
BOUNDARY LAYER (0-2 KM) RURAL 5.0 KM VIS AT SEA LEVEL
TROPOSPHERE (2-10KM) TROPOSPHERIC TROPOSPHERIC SPRING-SUMMER
STRATOSPHERE (10-30KM) BACKGROUND STRATO BACKGROUND STRATO SPRING-SUMMER
UPPER ATMOS (30-100KM) METEORIC DUST NORMAL
0 SLANT PATH TO SPACE
H1 = 70.000 KM
HMIN = 0.000 KM
ANGLE = 180.000 DEG
0 FREQUENCY RANGE
IV1 = 100 CM-1 ( 100.00 MICROMETERS)
IV2 = 1500 CM-1 ( 6.67 MICROMETERS)
IDV = 2 CM-1
IFWHM = 2 CM-1
I created two pictures from the model output that tell, how complex the effect is. All this is based on the AFGL mid-latitude summer profile.
The first graph shows the flux up at 20.5 km calculated with a resolution of 0.1 1/cm over the range 600-700 1/cm. The red line corresponds to 100 ppm, green to 1000 ppm and blue to 10000 ppm.
We see that the blue line is very smooth. The concentration is high enough to lead to high opacity over the whole range. A little off from the line center the 100 ppm case does already deviate significantly while 1000 ppm leads still to high opacity. Below 630 1/cm also the 1000 ppm case starts to differ significantly from the 10000 ppm case. The general conclusion from the range 600-700 1/cm is that the saturation is stronger than logarithmic, i.e. the red curve differs from the green more than the green curve from the blue.
Another very important point is that the peaks are so narrow that averaging in the calculation over 1 1/cm bands would lead to totally different results. The UChicago implementation of MODTRAN 3 uses 1 1/cm bands, and is therefore incapable of calculating this correctly.
The second graph is over the range 700-900 1/cm. Here we see that the situation is reversed above 750 1/cm. The green curve is now closer to the red one than the blue one. Over this range we don’t have strong saturation at all but this range is very important in the continuing influence of more CO2 at concentration above 1000 ppm in the model calculation.
One may wonder, what’s the origin of this smooth difference that contributes so much to the overall result. We see few individual absorption lines in this range. Thus it must come from the relatively fat tails of the main absorption peak around 667 1/cm according to the Lorentz profile. I’m not at all sure that the Lorentz profile can be used so far from the peak as it’s an idealization based on time between collisions of molecules, whose structure is not taken into account. Some cutoff should be applied to the Lorentz profile, and the proper scale for the cutoff could be a few tens of 1/cm. Thus this result may, indeed, be spurious, but I don’t know quantitatively what would be the right way of introducing a cutoff to the Lorentz profile.
This problem with the tails of the Lorentz profile has little effect at present concentration (it’s still small at 1000 ppm), but affects strongly the results above 1000 ppm.
Rechecking DeWitt’s message, the bandwidth of the MODTRAN3 calculation is 2 1/cm, which makes it even more suspect for this kind of calculations. I cannot say that the results are finally wrong, but neither would I trust the results in calculations in a range where their correctness has not been verified by comparisons with a more accurate model.
In this paper Takagi et al compare several profiles that add cutoff to the Lorentz profile in calculations of Venus atmosphere.
Their conclusion is that a cutoff is needed, but also that the strongest proposed forms of the cutoff (or sub Lorentzian profile) seem to be too strong.
Pekka,
The problem is that your emission decreases much more rapidly above 800 cm-1 than is calculated by MODTRAN. That has nothing to do with model resolution as it’s pretty much continuum at those frequencies. For example, Tropical Atmosphere 20.5 km looking down:
cm-1 100ppmv 1000 10000
860 0.341 0.361 0.358 W/(m² cm-1)
The bottom of the dip is lower in MODTRAN as well, ~0.10 compared to your 0.15. I’m betting it does the same below 600 cm-1 as well because emission in MODTRAN starts increasing below about 630 cm-1 at 10000 ppmv CO2 while you have a flat line from 600-700.
DeWitt,
That’s exactly what I said about that issue. As far as the correct cutoff is not known, neither the MODTRAN results nor my results are correct on that point. We just don’t know the correct behavior at high concentration.
My other and separate point is that one cannot trust the MODTRAN band model at high CO2 concentration even in the range closer to the absorption peaks unless it’s validity has been verified also at high concentration. The band model is a biased approximation. The bias may be small, but that must be checked separately by a comparison with a line-by-line model.
As I tried to make clear, my results are not correct, but most probably the MODTRAN results are not any more trustworthy beyond the range, where they have been explicitly validated.
Both models calculate correctly according to their specifications, neither is developed to perform well at 10000 ppm.
As the Takagi et all paper tells, the issue of cutoff becomes important in the case of Venus atmosphere, but the correct line shape is not known.
Pekka,
I went to Spectralcalc ( http://www.spectralcalc.com ) and calculated what I could for free. I used an 8 km path length, 1013.25 mbar total pressure and 296K, sort of worst case. The transmittance at 860 cm-1 is greater than 90% for a VMR of 0.01 or 10,000 ppmv. If there were significant contribution from the wings of distant lines at that frequency, it certainly would have been noticed when the weak lines between 800 and 900 cm-1 were measured using techniques like cavity ringdown. If your program disagrees with MODTRAN and Spectralcalc, it’s vastly more likely that your program is wrong.
Your results are therefore not evidence that the effect of higher levels of CO2 isn’t logarithmic. A result that far out of line would prompt me to try to fix it rather than wave my hands and say that the other programs are probably wrong too.
Certainly well known models like MODTRAN are likely to perform better than a “toy model” or educational model built on the most simplistic line shape for the tails. I did also write in an above comment that a cutoff is to be expected roughly on the scale of tens of 1/cm as such a cutoff corresponds to the size of the molecules.
The present MODTRAN5 has been improved very much since MODTRAN3. Thus it’s likely to be better verified also on results that depend on far tails.
The original question was, what does SoD’s model predict. I believe that I have now answered that question ans also explained why it differs from MODTRAN results.
Even so I have still some doubts on the accuracy of MODTRAN as well at high CO2 concentration. Tools like MODTRAN are developed to work well over the range where they are needed in practice. Whether that has led to validation of it over the range of interest here is not that obvious.
I would certainly like to see direct information on research focused on the line shape of CO2 peaks far from their center. The Takagi et al paper seems to tell that the uncertainties have not been resolved.
I found some further information on the CO2 line shape. There are several papers on the accurate line-by-line model LBLRTM, where this issue is discussed.
This poster by Shephard et al has a picture and comments on Chi Factor, which is the cutoff multiplier. The factor chosen for the use in the model is shown in red. The cutoff starts to have a sizable influence a few 1/cm of the peak, somewhat earlier than I expected based on rough semi-quantitative estimates.
The strength of the resulting CO2 continuum is greatly suppressed by the introduction of the chi factor.
It’s likely that MODTRAN development has taken advantage of more accurate models like LBLRTM on this point, how far that’s true for the old MODTRAN3 is less certain.
Some interesting LBLRTM model results on radiative forcing are presented in a 2008 paper by Ianoco et al.. There they report that the broadband models of the same group (AER) reproduce well the results of the LBL models over the range relevant for global warming studies.
Pekka,
I have Spectralcalc results. The datafiles are large and the program doesn’t produce overlays. Suffice it to say, however, that the results look a lot more like MODTRAN3 than yours. For short, here are the calculated in-band radiances in W/(m² sr) for Spectralcalc and MODTRAN for 100, 1000 and 10000 ppmv CO2 (scale factors 0.303, 3.03 and 30.3)
600-700 cm-1 20.5 km nadir angle 0 surface 299.7 K emissivity 0.98
MODTRAN Spectralcalc
5.87 5.96
4.28 4.41
3.68 3.78
700-900 cm-1
21.99 21.95
19.86 19.54
17.35 16.36
So a more up to date calculation shows radiance falling off a little faster than MODTRAN3, but not that much. So a log plot would be curved, but nothing like as drastic as yours. As expected, the radiance at frequencies greater than 840 cm-1 doesn’t change with CO2 concentration. I can load the files and graphs into a public folder in Dropbox if you want them. I can do different nadir angles too.
DeWitt,
I have stated repeatedly that my results are not valid for real atmosphere. They tell the outcome of SoD’s model, because I use his model (with some additions that were not activated in these calculations).
There’s no point in arguing on that.
What I did say in addition is that even the best known and most reliable tools are reliable only within the limits they have been built to be reliable and validated. It’s not at all obvious that the UChicago implementation of MODTRAN3 is reliable in these calculations, although it surely is more correct than SoD’s model.
My calculation with SoD’s model was interesting in showing, how sensitive the near logarithmic dependence on CO2 concentration is on some details that might very well differ from the real case. The logarithmic dependence is not forced by fundamentals but is only observed to apply fairly well over a wide range of concentration. At some point the deviations will start to grow both going down and going up in concentration.
Sam,
Good question.
I haven’t had a spare minute for the Science of Doom blog for the last few months – sorry to everyone !!!! – but should be able to check out this point on the weekend.
DeWitt,
The reason might be in the handling of the stratosphere. I didn’t check the values at 20 km, but at the top of the whole AFGL profile that extends to 120 km.
At high CO2 concentration the role of the stratosphere may get important. Thus neither excluding the stratosphere nor including it as simply as I did is likely to give really meaningful results. I didn’t even include the Voigt profile although I have that in my version of the model.
Pekka,
If you included the stratosphere but didn’t change the temperature profile, forcing would be even less because emission from the stratosphere would increase. That’s why I used an observation height of 20 km. The keeps the bottom of the CO2 dip flat.
70 km looking down, tropical atmosphere, 10,000 ppmv CO2: 271.5 W/mN
I don’t think it has anything to do with the Voigt profile either. Perhaps you should plot some of your emission spectra and compare them to MODTRAN. The MODTRAN data can be obtained by clicking on the ‘view the whole output file’ link below the graphs. As far as I can tell, it always saves the text.
DeWitt,
My code is essentially that of SoD. At various points I have made some additions like calculating the azimuthal distribution of direction of radiation explicitly or adding the Voigt profile.
The data is from HITRAN and other sources listed by SoD. I’m pretty sure the code does these calculations correctly, but I may have done something wrong, when I did the calculations that gave those results. I haven’t used the model since January, and it’s not very user friendly. Therefore I picked one earlier set of parameters and used it as starting point. I may have missed some exceptional values among the parameters, and that may affect the outcome.
Sod wrote that he might also do the calculation. It’s interesting to see, what he gets out of his model.
SoD,
The recent discussion here has brought up that using the Lorentz line shape without some form of cutoff (or chi factor) may be largest source of error in your model.
In case of water vapor the continuum contribution may largely represent double counting of the Lorentzian tails, but it’s also possible that the added continuum is so much stronger that the double counting issue is moot. The water vapor continuum is so strong because water molecules stick together and this effect is not included in the Lorentzian line shape.
The very strong effects seen in my calculations have rather little influence as long as the CO2 concentration is well below 1000 ppm, but there may be some significant effects from closer to the main absorption peaks at smaller concentrations as well.
I added a cutoff to the Lorentz line shape multiplying with a secondary Lorentz shape of half width 6 1/cm. This value is taken from the the poster of Shephard et al that I linked in a comment above. The curve they present in the poster agrees fairly well with Lorentz shape and a product of two Lorentz functions has a strong enough cutoff to make details of the tail irrelevant.
So far I have calculated three fluxes up at 20.5 km to compare with DeWitt’s MODTRAN results. The results for the mid latitude summer are (in parenthesis DeWitt’s results:
100 ppm 282.9 (285.9)
1000 ppm 268.0 (273.9)
10000 ppm 249.7 (259.2)
They do still differ but much less than before. My results are also now much closer to the logarithmic dependence on concentration as the differences are 14.9 and 18.3 (DeWitt’s MODTRAN results have differences 12.0 and 14.7).
My results at the top of the whole range (82.5 km for this profile) are actually closer to MODTRAN results (for 20 km) being 282.0, 270,3, and 258.2. They follow furthermore almost perfectly the logarithmic dependence.
Pekka,
Spectralcalc uses the following line shape correction factor for far wing effects on the line profile:
(ν/ν_c)*tanh(hcν/2kT)/tanh(hcν_c/2kT)
where ν_c is the central frequency of the line.
Apparently this is part of the LinePak™ algorithms of Gordley, et. al. (1994)
DeWitt,
That factor does not lead to any cutoff. It’s effect is to make the peak slightly asymmetrical. It’s influence on the results is very small, may be too small to see at all.
Gordley et al paper on LinePak is available from SpectralCalc
From the paper we can read:
Thus there’s no cutoff function in LinPak, just a crude procedure of full cutoff with user adjustable parameters.
Search with words “modtran far tail cutoff” finds several papers. The impression that I get from those papers is that a cutoff is applied at 25 1/cm off the peak, but I’m not fully certain that I have understood correctly, what the papers tell.
One more interesting comment is presented in Pierrehumbert’s course material. He is discussing an educational model Pytran stating (emhasis mine)
Interesting discussion and unfortunate that I haven’t had any time to engage recently on this.
My take on it – the MATLAB model may have some flaws, I’m sure it has some. It is quite faithful to the professionally produced heating and cooling curves for current GHG concentrations. It produces spectral results for doubling CO2 similar to professional calculations.
Pekka has got further than I have with azimuth calcs and the Voigt line shape. So far neither of them appear to have a big impact so far.
But once we get to much higher concentrations of CO2 the MATLAB model needs validation.
The aim of the model for me was to:
a) see how closely we could replicate existing professional models
b) break out the different components and perform sensitivity analyses to help readers (and me) understand the impact of the various factors
Whether MODTRAN or our model is better at very high concentrations of CO2 is hard to determine without some professional opinion. It’s easy for me to expect MODTRAN to be better but it is a parameterized model and our MATLAB model is a first principles model. So who can tell? We would need to compare results with a professional LBL model.
SoD,
I’m pretty certain that your model without any cutoff for far tails reproduces spurious results at concentration over 1000 ppm. I’m less certain on the relative accuracy, when the cutoff is introduced by a Chi Factor that follows closely enough the curve presented in the poster of Shephard et al.
With that function is plausible that the modification of your model is more correct on the cutoff than typical MODTRAN runs. There may be some additional points not considered by either of us, where MODTRAN is better even at high concentrations.
I introduced the following lines in the function optical
if cutoff > 0
dt1=1./(((vt-v(im(j))).^2+ga^2).*(1+((vt-v(im(j)))/cutoff).^2));
% line shape across all wavenumbers
else
dt1=1./((vt-v(im(j))).^2+ga^2); % line shape across all wavenumbers
end
and gave the value 6 for the cutoff parameter.