Many blogs write about over-simplifications of the radiative effects in climate. Many of these blog articles review simple explanations of how it is possible for atmospheric radiative effects to increase the surface temperature – e.g. the “blackbody shell” model.
As a result many people are confused and imagine that climate science hasn’t got past “first base” with how radiation interacts with atmospheric gases.
In any field the “over-simplified analysis” is designed to help the beginner to gain conceptual understanding of the field. Not to present the complete field of scientific endeavor.
This article will try to “bridge the gap” between the over-simplified models and the very detailed theory.
Note – it isn’t possible to cover the whole subject in one blog article and a decent treatment of radiative transfer consumes many chapters of a textbook.
There will be some maths. But I will also try to provide a non-mathematical explanation of “the maths” – or “the process”.
If you find maths daunting or incomprehensible that is understandable, but there is a lot that can be learned by trying to grasp some of the basic concepts.
Monochromatic Radiation
This means we need to treat each wavelength separately. Why? Because absorption and emission is a wavelength dependent process.
For example, here is the absorption spectrum of one part of NO2:
From Vardavas & Taylor (2007)
Figure 1
So when we consider radiation “zooming” through the atmosphere we have to take it “one wavelength” at a time.
There isn’t really any such thing as monochromatic radiation or being able to take “one wavelength at a time” – but that doesn’t stop us analyzing the problem..
A Digression on “Calculus”
How does the world of science and engineering deal with continuous change?
If a force, or a ray of radiation, or a movement of the atmosphere is a continuously changing value, how do we define it? How do we deal with it?
Calculus is the answer. This branch of mathematics allows us to deal with small changes and continuous changes and provide theorems, answers and equations.
For example, if we know something about the variable distance, s, with respect to time, t, then an equation defines the relationship between velocity, v, and these other variables:
v = ds/dt
where the “d”s at the beginning means: “the rate of change of”, so the formula means – in English:
Velocity = the rate of change of Distance with respect to Time
Generally when you see something like “da/db” it means “the rate of change of variable a with respect to variable b“.
It is also common to see Δx and δx – meaning “a small change in x”. This is different from “the continuous change of x”, but the specific rationale behind when we use “dx” and “Δx” isn’t so important for this article.
The other important area of calculus is “summing” results when again there is continuous change. If someone travels at 10 km/hr for 1 hour and then at 20km /hr for 1 hr they will have traveled 10km + 20km = 30km. That’s an easy calculation. But if velocity has continuously changed with time – how do we calculate the total distance traveled?
This means, in (harder to understand) English:
Distance = the integral of Velocity with respect to Time, between the limits of time = t1 and time = t2.
The integral is like the summation of each of the tiny distances covered in each very small time period (between t1 and t2). The integral is also often referred to as “the area under the curve”.
..end of digression
Absorption of Radiation
Let’s define a monochromatic beam of radiation, Iλ, travelling through the atmosphere:
Figure 2
We have some information we can use:
The rate of absorption of the beam of radiation as it travels through the atmosphere is proportional to the amount of absorbers at that wavelength and the ability of that absorber to absorb radiation of that wavelength
This is known as the Beer-Lambert law, and is written like this (note 1):
dIλ = -nσIλ .ds [1]
which means the same thing in mathematical terms, with n=number of absorbing molecules per unit volume (corrected), and σ=capture cross-section (or effectiveness at absorbing at that wavelength), and the subscript λ indicates that this equation is only true for the radiation at this wavelength
The value σ is a material property and so constant for one gas at one wavelength at one temperature and one pressure, but varies with the temperature and pressure of the gas (see comment). The value n will depend on location in the atmosphere. If we solve this equation between two arbitrary points, s1 and s2, we get:
Iλ(s2) = Iλ(s1). exp [ -∫σn(s).ds ] [2]
where the integral is between the limits s1 and s2
What it means in English:
The intensity of radiation at wavelength λ is reduced as it travels through the atmosphere according to the total amount of the absorber along the path. “exp” is e, or 2.718, to the power of the value in the square brackets.
If the concentration of the gas doesn’t change along the path the equation becomes a simpler version:
Iλ(s2) = Iλ(s1). exp [ -σn.(s2 - s1) ] [3]
Optical Thickness & Transmittance
These are some important properties to understand.
Optical thickness, usually written as τ, is the property inside the exponential in equation [1].
τ = ∫σn(s).ds [4]
where the integral is between the limits s1 and s2
Transmittance, usually written with a weird T symbol not available in WordPress, but with “t” here, is the amount of radiation “getting through” along the path we are interested in.
t(s1,s2) = exp [-τ(s1,s2)] [5]
also written as:
t(s1,s2) = e-τ(s1,s2)
The optical thickness is “dimensionless” as is the transmittance.
So we can rewrite equation [1] as:
Iλ(s2) = Iλ(s1).t(s1,s2) [6]
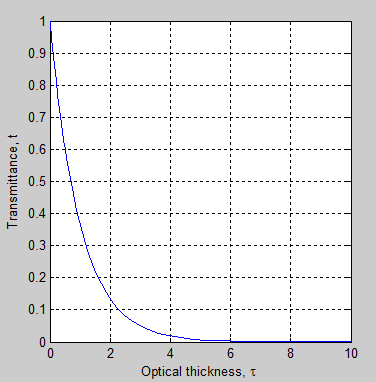
The transmittance can be a minimum of zero – although it can never actually get to zero – and a maximum of 1. So it is simply the proportion of radiation at that wavelength which emerges through the section of atmosphere in question:
Figure 3
With optical thickness, τ = 1, transmittance, t = 0.37 – which means that 63% of the radiation is absorbed along the path and 37% is transmitted.
With optical thickness, τ = 10, t=4.5×10-5 – that is, 45 ppm will be transmitted through the path.
A note on definitions – optical thickness is usually defined as = 0 at the top of atmosphere, where z is a maximum and a maximum at the surface, where z = 0:
Figure 4
So τ increases while z decreases, and z increases while τ decreases.
Absorptance
In the absence of scattering (note 2), absorptance, a = 1 -t.
That is, whatever doesn’t get transmitted gets absorbed.
Plane Parallel Assumption
If you refer back to Figure 2, you see that the radiation is not travelling vertically upwards, but at an angle θ to the vertical.
Using simple trigonometry, ds = dz / cos θ [7]
It’s always an advantage if we can simplify a problem and relating everything to only the vertical height through the atmosphere helps to solve the equations.
Atmospheric properties vary much more in the vertical direction than in the horizontal direction. For example, go up 10 km and the pressure drops by a factor of 5 – from 1000 mbar to 200 mbar. But travel 10 km horizontally and the pressure will have changed by less than 1 mb. Temperature typically changes 100 times faster in the vertical direction than in the horizontal direction.
And as air density is determined by pressure and absolute temperature we can make a reasonable assumption that the density at a given height, z directly above is the same as the density at the same height when we look at an angle of 45°.
Of course, by the time we are considering an angle close to 90° – i.e., horizontal – the assumption is likely to be invalid. However, the transmissivity of the atmosphere at angles very close to the horizon is extremely low anyway, as we will see.
Therefore, making the assumption of a plane parallel atmosphere is a good approximation.
Let’s review the earlier equations using a mathematical identity that reduces “equation clutter”:
μ = cos θ [8]
And rewrite equation [5]:
t(z1,z2) = exp [-τ(z1,z2)/μ] [9]
Notice that the equations are now rewritten in terms of the optical thickness between two vertical heights and the angle of the radiation.
It might help to see it in graphical form – and note here that the optical thickness, τ, is for the vertical direction (otherwise the graph would make no sense):
Figure 5
This simply demonstrates that as the angle increases the radiation has to travel through more atmosphere.
So suppose the optical thickness vertically through the atmosphere, τ = 1, then for:
- a vertically travelling ray the transmittance = 0.37
- for a ray at 45° the transmittance = 0.24
- for a ray at 70° the transmittance = 0.05
- for a ray at 80° the transmittance = 0.003
Emission
Using Kirchhoff’s law, absorptivity of a material = emissivity of a material for the same wavelength and direction. For diffuse surfaces – and for gases – direction does not affect these material properties, so they are only a function of wavelength. (And for all intents and purposes, absorptance is the same term as absorptivity, and transmittance is the same term as transmissivity-see comment).
Emission of radiation at any given wavelength for a blackbody (a perfect emitter) is given by Planck’s law, which is usually annotated as Bλ(T), where T = temperature.
The absorptivity of a gas, aλ = 1-tλ =emissivity of a gas, ελ. (Corrected)
For a very small change in monochromatic radiation due to emission:
dIλ = ελBλ(T) .ds [10a]
Therefore:
dIλ = nσBλ(T) .ds [10b]
So if now combine emission and absorption, equations 1 & 10:
dI/ds = nσ.(Bλ(T) – Iλ) [11]
If we combine this with our definition of optical thickness, from equation [4]:
dIλ/dτ = Iλ – Bλ(T) [12]
which is also known as Schwarzschild’s Equation – and is the fundamental description of changes in radiation as it passes through an absorbing (and non-scattering) atmosphere.
It says, in not so easy to understand English:
The change in monochromatic radiation with respect to optical density is equal to the difference between the intensity of the radiation and the Planck (blackbody) function at the atmospheric temperature
Sorry it’s not clearer in English.
In more vernacular and less precise terms:
As radiation travels through the atmosphere, the intensity increases if the Planck blackbody emission is greater than the incoming radiation and reduces if the Planck blackbody emission is less than the incoming radiation
Solving Schwarzschild’s Equation
Notice that this important equation contains the Planck term, which is for blackbody radiation (i.e., radiation from a perfect emitter), yet the atmosphere is not a perfect emitter. We definitely haven’t assumed that the atmosphere is a blackbody and yet the Planck terms appears in the equation. It’s just how the equation “pans out”..
I mention this only because so many people have come to believe that there is some “big blackbody assumption” in climate science and they might be concerned by this term. Nothing to worry about, this has not been assumed.
Let’s find a solution to the equation if we are measuring the TOA (top of atmosphere) radiation. Refer to Figure 4:
- at TOA, z=zm and τ=0
- at the surface, z=0 and τ = τm
Now some maths manipulation – skip to the end people who don’t like maths..
First we note a handy party piece:
d/dτ [Ie-τ] = e-τ. dI/dτ – Ie-τ [13]
Now we multiply both sides of equation [12] by e-τ:
e-τ.dIλ/dτ = e-τ.Iλ – e-τ.Bλ(T) [14]
Re-arranging:
e-τ.dIλ/dτ – e-τ.Iλ = – e-τ.Bλ(T) [14a]
And substituting “handy party piece” [13] into [14a]:
d/dτ [Iλe-τ] = – e-τ.Bλ(T) [15]
Now we integrate [15] between τ=0 and τ=τm:
Iλ(τm)e-τm – Iλ(0) = – ∫ Bλ(T)e-τ dτ [16]
where the integral is between the limits of 0 and τm
And re-arranging we get:
..end of maths manipulation
Iλ(0) = Iλ(τm)e-τm + ∫ Bλ(T)e-τ dτ [16]
Which – for those who haven’t followed the intense maths:
Iλ(0) = Iλ(τm)e-τm + ∫ Bλ(T)e-τ dτ [16]
The intensity at the top of atmosphere equals..
The surface radiation attenuated by the transmittance of the atmosphere, plus..
The sum of all the contributions of atmospheric radiation – each contribution attenuated by the transmittance from that location to the top of atmosphere
Don’t worry about the maths, but it is definitely worth spending some time thinking about the words in colors – to get a conceptual understanding of how atmospheric radiation “works”.
It’s Not Over Yet – Conversion from Intensity to Flux and the Diffusivity Approximation
Remember the note about the Plane Parallel Assumption ?
Getting equations into WordPress is painful and time-consuming so a quick explanation followed by the result, especially as maths fatigue will have set in among most readers, if any made it this far.
Equation [16] is for spectral intensity. That is, one direction rather than the complete hemispherical power (flux).
To calculate spectral emissive power (flux per unit wavelength) we need to integrate the equation over one hemisphere of solid angle. We re-write equation [16] in the form of equation [9] so that the optical thickness references vertical height, z and μ, which is the cosine of the angle from the vertical. Then we integrate from μ=0 (θ=0°) to μ=1 (θ=90°).
Transmittance, t(z,0) = 2 ∫ e-τ(z,0)/μ μ.dμ
where the integral is from 0 to 1
This equation doesn’t have an “analytical” solution, meaning we can’t rewrite it in a nice equation form without the integral. But with some clever maths that I haven’t tried to follow – but have checked – we can produce an approximation which is known as the diffusivity approximation:
2 ∫ e-τ(z,0)/μ μ.dμ ≈ e-τ/μ’
Where μ’ is the “effective angle” which produces a close approximation to the actual answer without needing to integrate across all angles (for each wavelength). The best value of μ’ = 0.6.
Here is the calculated integral (left side of the equation) vs the approximation with μ’ = 0.6, as a function of optical thickness, τ, demonstrating the usefulness of the approximation:
Figure 6
There are some other refinements needed, for example, the reflection of atmospheric radiation for a surface emissivity < 1, which is then attenuated by the absorptance of the atmosphere before contributing the TOA measurement. But these factors can all be introduced into the equations.
Full Color Solution
What we have produced so far is a solution for each monochromatic wavelength, λ.
Also, we haven’t explicitly stated the fact that the optical thickness depends on the concentration and “capture cross section” of each absorber for that wavelength. So the optical thickness, and transmittance, for each height requires combining the effects of each active molecule.
The solution for flux, W/m², requires integrating the equations across all wavelengths.
Wow. Conceptually straightforward. But computationally very expensive – check out Figure 1 – the absorption characteristics of each radiatively-active gas vary significantly with wavelength.
Conclusion
The equation for radiative transfer is commonly known, (in differential form) as Schwarzschild’s Equation. It relies on fundamental physics.
To solve the equation requires some maths.
To solve the equation in practical terms the plane parallel assumption is used. This relies on the fact that variations in temperature and pressure (and therefore density) are negligible in the horizontal direction compared with the vertical direction.
The equation could be solved without this plane parallel assumption, but the variations horizontally in pressure and temperature are so slight that the same result would be obtained, unless extremely high quality data on temperature, pressure, density and concentration of absorbers was available.
To solve the equation in practical terms we need to know:
- the temperature (vs height) in the atmosphere
- the concentration of each absorber vs height
- the absorption characteristics of each absorber vs wavelength
In any practical field, the “proof of the pudding is in the eating”, and so take a look at Theory and Experiment – Atmospheric Radiation – where theoretical and practical results are compared.
And lastly, the Stefan-Boltzmann equation, correct and accurate though it is (check out Planck, Stefan-Boltzmann, Kirchhoff and LTE) is not used in the actual equations of radiative transfer in the atmosphere. Nor is any assumption of “unrealistic blackbodies”.
I only note these last points due to the high quantity (but not high quality), of blog articles and comments demonstrating the writers haven’t actually read a textbook on the subject, but still feel qualified to pass judgement on this field of scientific endeavor.
Other articles:
Part One – a bit of a re-introduction to the subject
Part Two – introducing a simple model, with molecules pH2O and pCO2 to demonstrate some basic effects in the atmosphere. This part – absorption only
Part Three – the simple model extended to emission and absorption, showing what a difference an emitting atmosphere makes. Also very easy to see that the “IPCC logarithmic graph” is not at odds with the Beer-Lambert law.
Part Four – the effect of changing lapse rates (atmospheric temperature profile) and of overlapping the pH2O and pCO2 bands. Why surface radiation is not a mirror image of top of atmosphere radiation.
Part Five – a bit of a wrap up so far as well as an explanation of how the stratospheric temperature profile can affect “saturation”
Part Seven – changing the shape of the pCO2 band to see how it affects “saturation” – the wings of the band pick up the slack, in a manner of speaking
And Also -
Theory and Experiment – Atmospheric Radiation – real values of total flux and spectra compared with the theory.
Notes
Note 1: There are many formulations of the Beer-Lambert law and even much dispute about who exactly the law should be attributed to.
Other formulations include using the density of the gas and a matching coefficient for the effectiveness of the gas at absorbing.
Note 2: When considering solar radiation (shortwave), scattering is important. When considering terrestrial radiation (longwave), scattering can be neglected. In this article, we will ignore scattering, so the results will be appropriate for longwave but not correct for shortwave.
[...] This post was mentioned on Twitter by diyana, Margie. Margie said: Understanding Atmospheric Radiation and the “Greenhouse” Effect … http://bit.ly/dT3kne [...]
Just thanks for your efforts, though I’m not good with maths, I know people that are more skeptical of the details of the greenhouse effect and more skilled in maths than me, and I’ve occasionally directed them to your blog.
One of the important consequences of The Equation is that it describes what we will “see” when looking at a given object. For instance, the temperature of the core of the Sun is around 13.6 million K but what we see is the object of temperature approximately 5778K.
Thus, we are not able to see the hotter part of the object if radiation from that part is absorbed on its way to the outer parts of the object. The radiation leaving the top of the atmosphere gives thus mainly the information about the temperature of the deepest part of the object that can be seen as well as about the absorption properties of the matter from this area and up to the outer part of the object.
To the contrary, if we are inside the object then we will not be able to see the colder, outer parts of the object. The only thing we will see, here feel, is the temperature of the closest to us part of the object. The changes in the temperature of the outer parts (for example due to the change in their composition) will, however, influence the rate of heat exchange between the inner and outer parts of the object, which will affect the temperature (and its variations) of the closest to us part of the object.
In order to estimate the temperature of the parts that we are not able to see, we have to perform a lot of thinking and calculations, which “science of doom” is showing us in a very pedagogical manner. Thanks for that.
With optical thickness, τ = 1, transmittance, t = 0.37 – which means that 63% of the radiation is absorbed along the path and 37% is transmitted.
With optical thickness, τ = 10, t=4.5×10-5 – that is, 45 ppm will be transmitted through the path.
Can you please explain this better. How can you use the same formula with different inputs,1 vs 10, and go from a percent to a ppm?
mkelly:
They are different ways of writing the same number. A lot of people less familiar with maths have trouble “seeing” what 4.5×10-5 actually is.
So 0.000045 = 4.5×10-5 = 0.0045% = 45 parts per million.
That is what I thought. I just wanted to make sure. Also please don’t be quite so condesending. I have a degree in mechanical engineering so I follow what you say. I use my J.P Holman “Heat Transfer” text book for light reading as followup to reading here.
But I think you should keep the same units when explaining things.
I enjoy this blog.
Sorry, it wasn’t intended that way.
I was attempting to explain that the reason that at times I write non-standard descriptions is because many people can’t visualize a number like 4.5×10-5. It wasn’t aimed at you.
SOD: Very nice. My only complaint is that you used Kirchhoff’s Law and emissivity in this derivation. There should be no need to invoke Kirckhoff’s law or any of the “old-fashioned” physics of bulk materials that was developed in the Dark Ages before we knew that molecules existed and developed quantum mechanics to explain their behavior. The absorption coefficient or cross-section, σ – more properly written as σ(λ) – is the probability from quantum mechanics that applies to absorption and emission. These two processes are the “time reverse” of each other so the same probability, σ or more properly σ(λ), should apply to both:
1) a molecule in a high energy state emitting photon of a given wavelength and lowering its energy by hc/λ.
2) a same molecule in a lower energy state absorbing a passing photon and increasing its energy by hc/λ.
Another problem with Kirchhoff’s Law is that it was meant to describe absorption and emission from bodies or surfaces in thermal equilibrium. For surfaces – the material for which Kirchhoff developed his law – radiation that isn’t absorbed is reflected (or scattered?). For gases, radiation that isn’t absorbed is transmitted (or scattered). For liquids, all of these processes may apply.
Above you say: “The absorptance of a gas, aλ = 1-tλ =emittance of a gas, ελ.” Then you equate the “emittance” (which appears to really be “transmission” and should have nothing to do with emission of photons) with “emissivity”, which opens the door for introducing Planck’s function into Equation 10a. If this hand waving isn’t correct and if σ is the constant that applies to the quantum mechanics for both absorption and emission, how does B(λ,T) get into the equation for emission?
If there are N molecules in a state capable of absorbing a photon and n molecules in the higher energy state produced by absorption, then n could equal to N*B(λ,T). If this were the case, we might expect Maxwell-Boltzmann statistics to apply to the situation. The Planck function, however, is derived for photons in otherwise empty space from Bose-Einstein statistics. Including the photon gives two states: State1, a molecule with photon near enough to be absorbed. State2, a molecule in a higher energy state. Then B(λ,T) would be the relative populations of these two states. Perhaps I should withdraw my comments about “old-fashioned physics”, “Dark Ages” and “hand waving”, because it is becoming clear that I don’t understand the situation. All my attempts to find a QM explanation for why Planck’s function appears in Schwartzschild’s equation on the web have failed. (I did see derivations similar to SOD’s) Can anyone help?
Frank:
Kirchhoff’s law proves that bodies in Thermodynamic Equilibrium have emissivity equal to absorptivity.
Experimental work subsequently proves that the material properties of bodies don’t change when they are out of Thermodynamic Equilibrium, as explained in Planck, Stefan-Boltzmann, Kirchhoff and LTE.
Kirchhoff’s law is true and can be applied, so why not use the simple explanation?
SOD (and DeWitt): I have now resolved my conceptual problems equating the behavior of solid surfaces and gases. For other skeptics, Kirchhoff’s Law was originally devised to explain the behavior of a surface at thermal equilibrium inside an enclosure. If absorption didn’t equal emission, the surface would warm or cool compared to the surroundings. If the surface is replaced with a volume of gas in a transparent vessel inside the same enclosure (and the other air is removed), the same reasoning appears to be true – even though the non-adsorbed radiation is reflected in the first case and transmitted in the second. In both cases, however, Kirchhoff’s “Law” is derived from common sense and should be verified. (My comments about your confusing transmissivity and emissivity don’t make sense on further review.)
However, I hate (perhaps irrationally*) the idea of treating absorption and emission as two fundamentally different physical processes, when they are simply the time-reverse of each other. At a microscopic level, why is Planck’s function (which has been derived by QM) the right factor for joining absorption to emission? The semi-classical derivation of Planck’s function begins with a box of oscillators at a given temperature and seems (if I understand correctly) to derive the energy flux (per unit volume per solid angle, if my dimensional analysis is correct) emitted in all directions from that volume – without reference to the nature of the oscillators. More fundamentally, Planck’s function is derived from Bose-Einstein statistics, wherein the relative number of particles in a higher energy state E = hv is proportional to (exp(E/kT-1))/exp(E/kT). Compared with Planck’s function, I see an extra exp(E/kT) term to cancel Maxwell distribution of energy between the two states of the GHG. Though I don’t really understand this physics, some of the right mathematical terms needed to derive Schwartzschild’s equation seem to be present and “begging” to be joined. Do we really have to go to a macroscopic scale – and invoke Kirchhoff’s Law – to derive Schwartzchild’s equation? (It seems clear that this is what some textbooks do, so I’m not criticizing anyone.) Or is Kirchhoff’s Law, like so many other macroscopic “laws”, a consequence of more fundamental physics?
*My aversion to the macroscopic descriptions is that they often get misapplied: Slabs of atmosphere don’t always emit black- or gray-body radiation. Emissivity is not a constant for gases. DLR isn’t contrary to the 2LoT. In my dreams, we would: Derive the correct laws from the microscopic scale, then show in which situations these fundamental laws do and do not produce the “laws” used to describe macroscopic behavior. This doesn’t mean I don’t appreciate SOD’s (generally heroic) efforts and the useful comments of others.
Frank.
I interpret the appearing of the Planck function in the Schwarzschild equation as the ”background” radiation, which, if one so desires, might be put to zero. In such a case, we will get the pure Beer law.
But generally, we have a background radiation from the object A of temperature T and the irradiation from the object B. If both objects are at the same temperature then the irradiation from B will not contribute to the change of the intensity of radiation from the object A when being measured by a detector in some given direction. A and B will only exchange the same power density (W/m^2) with each other which does not affect the outgoing radiation in the direction to the detector.
If the temperature of B is higher than that of A then we will have an excess of power density from B to A and it is this excess (which might be called signal) that is denoted by I. The intensity of the signal I is diminishing exponentially along it way of propagation through the object A in the direction to the detector until it drops to the level of the background radiation. After that, the signal will not be detectable.
On the molecular level we have the molecular excitations due to the collisions between the molecules in the sample. The incoming signal increases the fraction of the excited molecules within the given volume from n to n+dn. A part of the extra excited molecules, dn, will re-emit photons while a part will lose the energy in collisions, which will increase the kinetic energy of the molecules, instead (the absorption and thermalizing process). The process of thermalizing is associated to the absorptivity of the medium in respect to the given wavelength (photon energy). The absorptivity is thus a function both of absorption properties of the molecules and of the rate of molecular collisions. Thus the absorption coefficient of molecules is not the same as the absorption properties of the sample, these different absorptions should be not confused with each other. But it is correct that the absorption coefficient of the molecules is equal to their emission coefficient for the given wavelength (in accordance to Einstein theory of interaction of matter with radiation), and that you can describe this formally as the reversion of the absorption process in time.
There will be less and less photons in the signal. The propagation of the signal (photons above the background level) creates thus the temperature gradient along the direction of propagation of the signal. Conduction, convection and radiation processes will then strive to zero thus induced gradient.
In this interpretation, the background radiation given by the Planck function plays the similar role as mc^2 plays in the special theory of relativity, m being the rest mass of the object. In the classical physics, mc^2 is put to zero as the Planck function is put to zero in the Beer law.
Frank,
The derivation of the Planck function in Appendix A of Introduction to Atmospheric Radiation by K-N Liou starts with this phrase:
In accordance with Boltzmann statistics,…
Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics at high temperature or at low concentration. Low concentration means densities much less than a white dwarf. I suspect high temperature means anything well above absolute zero. IOW, a gas or a solid object on the Earth’s surface at 300 K is going to follow Maxwell-Boltzmann statistics.
[...] will eventually point out that I didn’t make use of the diffusivity approximation from Part Six in my [...]
Now we can understand where the “old-fashioned” physics of bulk materials – especially black- and grey-body radiation – comes from and how it gets MISAPPLIED to GHGs. In equation 11 above, if light has been passing through a homogeneous material (gas, liquid, or solid) for long enough that emission and absorption have reached equilibrium, we get
dI/ds = nσ[B(λ,T) – I] = 0 [11a]
(I, σ and ε vary with λ.) In this case, either σ is zero or I = B(λ,T). For materials where σ is not zero at any wavelength, emitted radiation follows Planck’s Law, I = B(λ,T) and the emission integrated over all wavelengths follows the Stefan-Boltzmann Law, W = oT^4. (o is the Stefan-Boltzmann constant and σ is still the absorption coefficient.) When σ is zero at some wavelengths, there is no light absorbed or emitted at this wavelength and any light coming through the material was emitted from behind. In this case, when we integrate over all wavelengths (the intensity is either B(λ,T) or zero), we come with a modified form of the Stefan-Boltzmann Law, W = εoT^4, where ε, emissivity, is a constant between 0 and 1 that corrects for all of those wavelengths where σ is zero.
For solids and liquids, radiation traveling through the material usually has passed by enough molecules so that emission and absorption have reached equilibrium. When radiation leaves their surfaces, we say the material emits “blackbody” or “graybody” radiation. This behavior is just Schwatzschild’s equation applied to a particular situation, not a fundamental “law” of physics.
This “law” is not true for gases. Many people (not SOD) like to pretend that we can discuss the radiation leaving a “slab of atmosphere” in terms of blackbody radiation. Those who wish to be technically correct will call it an “optically thick” slab, meaning that the slab is thick enough so that equilibrium between absorption and emission has been reached. “Optically thick” doesn’t apply to the Earth’s atmosphere, especially above the tropopause, where radiative equilibrium determines temperature. There are some wavelengths, such as the 15 um CO2 band, where the Earth’s atmosphere is acts optically thick, but radiative forcing comes from the flanks of these strong bands – which are not optically thick! No wonder there is so much confusion.
Worst of all, these same people like to say that the energy emitted by a slab of atmosphere is oT^4 or εoT^4, thereby allowing us to believe that emission doesn’t depend on the number of GHG molecules in the slab. As everyone recognizes, absorption does depends on the number of GHG molecules in the slab. Thus we create the widespread illusion that GHGs TRAP energy trying to the leave the atmosphere and don’t emit it. Perhaps SOD will want to discuss this illusion some day.
Frank,
Then there’s the people that want it both ways. Well one person anyway. The essence of the argument as near as I can tell is that the integrated emissivity over all wavelengths for CO2 for a 1 m length path through the atmosphere is small, but increasing the path length doesn’t change the emissivity. In other words, the slab is optically thin and thick at the same time.
If I’m the “one person” you are referring to above, I’d really like to have it one way – the scientifically correct way – assuming I can see passed my prejudices clearly enough to recognize it. From what I’ve learned, the enhanced greenhouse effect exists, but “trapping” is an extremely poor description of the mechanism.
I appreciate your help and SOD’s when I do get off-track.
I’m guessing that DeWitt Payne is referring to his amazingly patient debate in Lunar Madness and Physics Basics.
SoD,
That would be it. I didn’t want to mention the name as names have power and might attract unwanted attention (and I was too lazy to look up a link).
That actually proved to be useful as it gave me a better understanding of the mechanics of the Hottel/Leckner approach to calculating radiant heat transfer in gases.
make that two people
Frank on February 9, 2011 at 10:36 pm:
Perhaps I have misunderstood what you are getting at..
Let’s just consider vertically travelling radiation to simplify things (otherwise I have to amend my drawing I’m about to show and add some integrals).
The height of the thin layer = dz.
dI/dz ≠ 0 (upward radiation through the layer)
dI’/dz ≠ 0 (downward radiation through the layer)
Even in equilibrium.
If there is no convection then in equilibrium:
dI/dz – dI’/dz = 0 (with appropriate clarification of directions of I and I’).
With convection then we have to add in a convection term and sum to zero.
Even more important is that the I in this conservation of energy equation is not Iλ. It is the integral over all wavelengths.
For misapplication of blackbody radiation, try Figure 6.8 of FW Taylor’s book (which you recommended to me). Of course, he doesn’t say that this multi-slab model applies to the earth. You could add Figure 3.5, but this refers to an optically thin slab, which he says it emits oT^4. It needs an emissivity term that varies with the concentration of GHG. For me (at least), this drawing suggests that absorption depends on GHG concentration and emission does not.
I do believe that misapplication of blackbody radiation leads to the myth that the mechanism of the enhanced greenhouse effect is that GHGs “trap” energy in the atmosphere. Emission is constant; absorption increase. GHGs both emit and absorb – they are the means of getting rid of the energy extra energy they absorb. More GHGs speed up the transfer of energy, but reduce the distance over which the transfer is made. Whether more GHGs at a location causes warming or cooling is a complicated function of the temperatures at the multiple locations between which energy is being transfered.
The comments of David Reeves to part 5 are illustrative: Why doesn’t more CO2 increase DLR (since we all know CO2 traps energy)?
If CO2 traps energy, why does radiative forcing occur mostly in the wings of the 15 um band?
I should make it clear that I have no doubt about the existence of the enhanced greenhouse effect – just how it is explained. This series of posts is explaining it the right way. “Trapping” does not.
A more simple form of (16) is
I = Io[exp(-krz)] + B[1-exp(-krz)] (16a)
representing intensity of the transmitted radiation of a particular wavelength after the passage of the distance z through the absorbing medium.
Io = intensity of the incoming radiation at this particular wavelength
k = absorption coefficient
r = density of the absorbing/emitting gas
B = Planck function defining the intensity of the thermal radiation at the given wavelength.
You can regroup this equation to the form
I = (Io-B)exp(-krz) + B (16b)
or, if introducing Is = Io – B. where Is is the intensity of the signal
I = Is*exp(-krz) + B (16c)
In this form, it is easier to discuss the transmission properties of the medium. It should be observed that B might represent either black body or the gray body.
To avoid confusion by changing symbols, you can copy and paste Greek symbols (but not sub- or superscripting) from SOD’s post into your comments.
Optical thickness τ is probably not the same thing as krz because it is the result of an integration in equation 4. If the atmosphere were homogeneous, τ would be krz, but n decreases with z. My guess is that your simpler equation only applies to a homogeneous atmosphere whose pressure doesn’t decrease with height.
Optical thickness is a confusing concept for me, but dimensional analysis and equation 4 makes it appear to be a quantity of GHG – the number of molecules in a long, thin cylinder with a circular base of area σ (the absorption cross-section) long enough to absorb 1/e of the radiation passing through its length. It doesn’t matter whether the GHGs are distributed evenly or decrease as you move from one end of the cylinder to the other. Using the term “optical thickness” also suggests a length for this cylinder, but it doesn’t have units of length. When I think of τ as a quantity or length, I have trouble with the concept of integrating from one τ to another. SOD’s explanation of the terms in Equation 16 in red, blue and green is elegant.
τ also describes a cylinder extending from space down into the earth’s atmosphere that contains enough GHG to absorb 1/e the radiation passing through its length. This cylinder extends to infinity at one end, but the other end defines an altitude from which 1-1/e of the emitted photons escape to space – called the characteristic emission level.
Correction to above: τ is a dimensionless quantity. σ has units of area/molecule. τ can’t be an exponent with units.
Frank.
Thank you for a tip about copying Greek symbols from SOD’s text, I was afraid that this would not work.
In the case when there is a temperature or density gradient (or both) then the Schwarzschild equation for the transmission of radiation at the particular wavelength is given by
I = Io[exp(-σns)] + B(Te)[1 - exp(-σn’s)] (16)
where n’ and (Te) refer to the density of the absorbing molecules and temperature, respectively, at the end of the air layer, compare http://www.barrettbellamyclimate.com/page45.htm
This gives
I = [Io - B(Te)]exp(-σns) + B(Te)[exp(-σns) - exp(-σn’s)] + B(Te) (16a)
or
I = Is*exp(-σns) + B(Te)[exp(-σns) - exp(-σn’s)] + B(Te) (16b)
where
Is = Io – B(Te)
is the intensity of radiation (ie intensity of the “signal”) above the background thermal radiation (ie above the “noise”).
The extra term B(Te)[exp(-σnz) - exp(-σn’z)] describes the decrease of the “noise” along the way of propagation of the “signal”.
SOD: There appears to be a QM derivation of Schwartzschild’s equation on a microscopic scale that parallels the macroscopic derivation that you provided. (The derivation below originates with me, so there is no guarantee what follows is all or even partially right.) The derivation of Planck’s Law tells us the (energy) density of photons of a given wavelength, λ, present around one or more GHG’s inside an enclosure at a given temperature, T is given by: u(λ,T) = 4Pi*B(λ,T). The rate of absorption of photons is determined by to the number of GHGs (n), the density of photons and a QM probability of absorption (r). Absorption (per unit volume) = rn*4Pi*B(λ,T). At equilibrium inside the enclosure, the rate of absorption must be equal to the rate of emission, so emission must also be rn*4PI*B(λ,T). (The QM term r is required to be the same in both directions). When we remove the enclosure and allow the photons to escape, the density of photons can take on any value, but emission will continue at a rate of nr*4Pi*B(λ,T).
Taking the derivative of these equations with respect to position, s, gives dr/ds = σ, the cross-section for absorption. The density of photons becomes the flux of photons (per unit area) and the 4Pi term is eliminated when radiance in all direction is converted to flux in one direction. Kirchhoff’s Law would then be a consequence of the QM requirement that r be the same in both directions. There would be no need for separate bulk properties, ε and σ.
Frank,
I think your derivation is overly simplistic. I don’t think you can use a derivation that depends on the presence of a black body in a perfectly reflecting container to derive the radiation field for a collection of molecules which may only approximate a black body at certain wavelengths depending on the size of the box and the partial pressure of the gas. Your r is going to be a function of temperature and pressure as well as wavelength as you have both line strength and line shape to deal with as well as the superposition of multiple lines. I seriously doubt that u(λ,T) = 4πB(λ,T) at a wavelength where r is much much less than 1.
Dewitt: I’m sure my derivation is overly simplistic. However, all of your caveats about r varying apply to both macroscopic scale and quantum scale.
I simply tried to use the density of a photon gas (u(λ,T)) inside an enclosure to calculate an absorption rate (which must be equal to an emission rate at equilibrium). With the assistance of Kirchhoff, SOD uses the flux from such a photon gas on a macroscopic scale to demonstrate the ε must be nσ in Equation 10.
The standard model for radiative transfer breaks down when the distance traveled (and the size of the enclosure used to derive Planck’s Law) isn’t bigger than wavelength. http://web.mit.edu/press/2009/heat-0729.html
Frank:
I’m glad you got the book.
I returned my copy to the library, but for reference I did scan a few pages, luckily this includes Chapter 3.
I have Figure 3.5.
There is indeed a mistake in the diagram. But if you read the text and equations that is clear:
eσTE4 = 2eσTS4
Where TS is the temperature of the stratosphere and e is the emissivity of the stratosphere.
The optically thin stratosphere is not radiating like a blackbody.
I don’t have chapter 6.
However, I do remember reading the book and much of Taylor’s excellent explanations are helping the reader to develop a conceptual understanding, which means starting from overly simplistic models and gradually making them more realistic.
I recall a number of simplified “greenhouse” models where he says things like ‘..and so this gives us a surface temperature of 320K..” clearly out by a factor of … not bad for such a simplistic model..” and so on.
If you want formal and complete derivations with consequently much more work for the student, try the expensive “Radiation and Climate” by Vardavas and Taylor, Oxford Science Publications (2007).
SOD: Taylor solves your equation (eσTE4 = 2eσTS4) to find that the stratosphere is 215 degK by assuming e is the same for both layers – even though one layer is the surface of the earth combined with the troposphere. Since e varies with the density of GHGs and is very different for the surface of the earth, this appears to be incorrect.
Ignoring the fact that emissivity for a gas, unlike traditional surfaces, varies with the composition of the gas is the cause of much confusion in climate physics. Picture a photon at the tropopause trying to escape to space through 1X or 2X GHG. The photon is more likely to “trapped” in the atmosphere, so the earth will warm. Now remember that there are 2X GHG’s emitting photons at the tropopause. The earth doesn’t warm. Memo to all proCAGWers: Avoid reminding anyone that emissivity depends on GHG concentration. (The proper physics is too hard to explain.)
Even worse (I hadn’t noticed before), Taylor goes on to calculated a no-feedbacks climate sensitivity of 18 degK in Table 7.3 and implies that the current absence of such a large temperature rise could be explained by a massive change in albedo! Improper treatment of emissivity appears to be the cause.
Frank on February 11, 2011 at 10:21 pm:
You are not correct about this assumption.
Note the added red text to correct the diagram.
What is the energy absorbed by the layer? It is the earth’s surface/tropospheric radiation x absorptivity of the layer
Ein = eσTE4, where e = emissivity = absorptivity of the layer
What is the energy radiated by the layer? It radiates from two “surfaces”, so:
Eout = 2eσTS4
Therefore, in equilibrium, Ein = Eout and so:
TS = TE/21/4
There is no assumption that the emissivity of the stratosphere is equal to the emissivity of the earth’s surface + troposphere.
Once you start working on the assumption that most of the content of books by Professors of Physics is correct – even, amazingly, those involved in climate science – you will probably find that you learn more from their books.
Frank:
Can you scan and post somewhere? Or email to me, scienceofdoom – you know what goes here – gmail.com.
I doubt that your criticisms will survive review. Maybe even your own review.
SOD: You are correct that I should start out with the assumption that the mathematics and physics of most books by physics professors is correct. You are completely correct (as usual) that emissivity is not misused on p47 as written. The “error” on this page is that emissivity is assumed to be 1 for the earth+troposphere layer used in the model, but this error is compensated for by choosing a “surface temperature” of 255 degK.
When I wrote my comment, I had been spending my time looking at why emissivity seems to be absent from many of the equations in chapter 6 (radiative transfer) and chapter 7 (the greenhouse effect). I saw the equation concerning the stratosphere in your post from chapter 3 and, to save time, mistakenly used this as an example. (A poor excuse for carelessness. Since I don’t have the time to master every detail, I often use words like “appears to” or “seems to”, but sure didn’t in this case.)
With regard to Table 7.3 (which I have just emailed), Professor Taylor certainly doesn’t use the phrase “no-feedbacks climate sensitivity”. He calls it “Model results for surface temperature corresponding to different values of Earth’s albedo, A, and different atmospheric CO2 mixing ratios”. The model results are surface temperatures, so one has to subtract to come up with climate sensitivity. So I think I fairly characterized his results. I have no reason to think that Taylor’s math will be found to incorrect for the model he presents, but the final answer is absurdly wrong: a no-feedbacks climate sensitivity of 18 degK with 1/3 of this rise predicted for the “current” value of 367 ppm of CO2. He goes on to explain that some of the difference (20-50%) is due to thermal inertia of the ocean. Then he suggests that changing albedo could account for some of the discrepancy, using albedos of 0.25, 0.30 and 0.35! Albedo may be changing, but I’ve never seen changes this large.
As best I can tell, a significant amount of confusion and distortion in climate physics arises from models that treat emissivity as a constant that doesn’t vary with GHG concentration. This leads to the idea that increasing GHG absorb, but don’t emit, more outgoing radiation and thereby “trap” heat in the atmosphere. However, I’m no longer sure that this is the fundamental cause of Taylor’s misleading results.
Although we can usually count on professors of physics to get their mathematics correct, we apparently can’t count on them to be fully candid about the limitations of their work. In this case, the professor seems to be obscuring the limitations of his model with unreasonably? large changes in albedo and misdirection about climate sensitivity with and without feedbacks. I was unable to find what I understand to be the truth in his book – that the no-feedbacks climate sensitivity for 2X CO2 from our best models is about 1.2 degK, not 18 degK. Taylor does say that his result is six times to larger than the IPCC’s value, but the IPCC’s value includes feedbacks (a concept Taylor introduces later).
Steven Schneider, a pioneering climate scientist, once said: “as scientists, we are ethically bound to the scientific method, in effect promising to tell the truth, the whole truth, and nothing but — which means that we must include all the doubts, the caveats, the ifs, ands, and buts”. Then he went on to explain what type of activities were appropriate when talking to the public in order to “make the world a better place”, which includes “telling scary stories”. Is Table 7.3 presented in a manner appropriate for “science” or is it a “scary story”?
Frank is annoyed by the usage of “heat-trapping gases”. I googled for the term and found it being used by the EPA, the NYT and on Scott Mandia’s blog (i could go on.). And here by Dessler, North et.al.:
http://www.chron.com/disp/story.mpl/editorial/outlook/6900556.html
(from March 6, 2010)
“Heat-trapping gases are very likely responsible for most of the warming observed over the past half century”
Draw your own conclusions.
I don’t find that any more misleading than the term greenhouse effect. It’s an analogy. All analogies fail when examined closely. It’s like trying to explain all of quantum mechanics using only English. You can’t.
Frank,
Kirchhoff’s Law and Planck’s derivation of his own function also breaks down if there isn’t an actual black body in a perfectly reflective cavity.
See: http://www.ptep-online.com/index_files/2009/PP-19-01.PDF
Absent a hole, which acts as a source of radiation, or the presence of a black body, it’s not clear that a photon gas with Planck properties exists in a perfectly reflective cavity. Since a molecular gas is very far from being black or even gray, it would be surprising to me if the photon gas in a sealed reflective cavity containing only a molecular gas had a black body spectral distribution.
Science of doom
In my opinion, the use of the plane geometry, Figures 2 and 4 above, when studying the outgoing radiation is an unnecessary complication as compared to the spherical geometry representing the actual form of the atmosphere.
The plane geometry might be useful when studying the incoming radiation from the Sun, but in such a case one must take additionally into consideration the tilting of the absorbing surface in relation to the direction of propagation of irradiation and not only the increase of the path of propagation related to 1/μ, μ being given by [8].
In such an interpretation, Figure 2 would indicate that the radiation from the Sun is falling on the area dA*μ along the path s = z/μ (the arrow Iλ being directed down). The incoming radiation is absorbed, thermalized and emitted upward. It is sufficient to regard the propagation of the upward (long wave) radiation along the axis z, which is due to the spherical form of the surface of the Earth. This is similar as when studying the radiation from the Sun.
However, the calculation presented by “science of doom” are still valuable if assuming that the parameter τ(z1,z2)/μ in [9] relates to n/μ where μ is not necessary a cos function (but nothing prohibits us to treat μ as a cos function, either). n/μ represents the change of n, as, for example, when enriching the atmosphere by a given kind of absorbing molecules as the result of the human industrial activity.
In particular, the doubling of concentration of the absorbing molecules from the level n corresponding to τ(z1,z2) = 0.1 to the level 2n = n/cos(60) corresponding now to τ(z1,z2) = 0.2 will change the transmittance of the layer (z1,z2) from about t = 0.9 to about t = 0.82, see Figure 5. Certainly, when n goes to infinity, which corresponds to cos(90), the slab (z1,z2) will become completely opaque to the given wavelength.
One can relate the optical thickness to the distance (z1,z2) at which the transmittance drops by i/e, as Frank had mentioned. In my opinion, the optical thickness should be related to the distance (z1,z2) at which the intensity of the signal drops to zero, which corresponds to the case when the intensity of the incoming radiation drops to the level B(λ,T).
Frank:
Thanks for sending me the relevant chapter from Taylor’s book.
Why don’t I write an article explaining many aspects? And then more people can learn and ask questions and, of course, criticize.
SOD: A separate post on how Taylor arrives at the results in Table 7.3 would be more useful than a discussion here. I initially grabbed his book to find an example of a misleading model with an optically thick slab atmosphere, but I don’t fully understand why his calculations appear to be so far off.
How about another post on the theme “GHGs redirect, but do not trap, infrared radiation”? Stratospheric cooling proves that “trapping” is not a general property of GHGs. With more GHG’s, there are more photons traveling shorter distances. It is easy to see why this cools the stratosphere, but less obvious why it warms the troposphere.
SOD wrote:
The absorptance of a gas, aλ = 1-tλ =emittance of a gas, ελ.
For a very small change in monochromatic radiation due to emission:
dIλ = ελBλ(T) .ds [10a]
Therefore:
dIλ = nσBλ(T) .ds [10b]
In equations 10a and 10b, you equate ελ and nσ. Emissivity often a dimensionless number between 0 and 1. nσ appears to have units of inverse distance and the potential to be >1. What am I missing?
I think you missed
nσ = τ
For very small τ a = ε = τ
DeWitt:
τ = ∫σn(s).ds [4]
So τ is not equal to nσ, dτ/ds = nσ. This affords the correct units (1/distance). The slope of a function is not equal to the value of the function, but when we are dealing with an exponential function like n(s), the slope is proportional to the value of the function. So we could say τ = knσ, but with no obvious reason to say that k=1. Am I being obtuse?
I went back to Petty on the derivation of the Schwarzchild equation. I think the confusion arises because SoD is using ελ and ε is usually emissivity. In fact, the emissivity in SoD’s notation is actually ελds. so ελ in SoD’s notation isn’t dimensionless, it also has dimension (1/distance) Petty avoids this confusion by using βa as the extinction coefficient. The absorptivity a is then βa ds The extinction and emission coefficients are equal.
Which means ελ in SoD’s notation is the emission coefficient, not the emissivity.
Frank:
DeWitt Payne is spot on.
There are many ways to write some parts of the equations and I have generated confusion by a lack of clarity and especially by an incorrect definition at the start.
Many others might also be confused for different reasons.
Let me review and explain a few steps, including questions not asked – for others. Repeated content from the article in italics.
1. Early on:
..with n=number of absorbing molecules per unit distance, and σ=capture cross-section..
INCORRECT definition for n:
n = number of absorbing molecules per unit volume, so the units are 1/m3.
σ = units are m2.
** Article will be updated **
2. Therefore considering this first equation:
dIλ = -nσIλ .ds [1]
nσ .ds has units of 1/m3 . m2 . m = dimensionless
Of course, we need this to be dimensionless (ask if it isn’t clear why).
3.
The absorptance of a gas, aλ = 1-tλ =emittance of a gas, ελ.
Note the subscript λ is explaining that the relationship is ONLY true for monochromatic radiation (radiation at one wavelength). Often, in derivations, the λ subscript is dropped just to make the equations clearer (less clutter). I don’t do that here because it’s very easy for newcomers to think that an identity is true across all wavelengths.
So ελ = aλ = 1-tλ
Let’s calculate ελ across a very small distance, ds:
ελ = 1 – exp(-nσ.ds)
How do we manipulate this equation?
4.
Using the Taylor expansion – a mathematical manipulation method – we find that
exp(x) ≈ 1-x, for very small x
And so ελ = 1 – exp(-nσ.ds) = 1 – (1 – nσ.ds) = nσ.ds
This expression is dimensionless, as already demonstrated, which is what we want.
5. Therefore:
For a very small change in monochromatic radiation due to emission:
dIλ = ελBλ(T) .ds [10a]
Therefore:
dIλ = nσBλ(T) .ds [10b]
SOD and DeWitt: Isn’t ε dimensionless in this reply everywhere but equation 10a, suggesting something is wrong somewhere? There could be a problem with infinitesimals in step 3; one side of the equation is an infinitesimal and the other side isn’t. (If we limit the discussion to a single wavelength, the λs can be omitted for clarity.)
ε =? 1 – exp(-nσ.ds) (dubious from SOD above )
dε =? 1 – exp(-nσ.ds) (this isn’t right either)
a = 1 – exp(-nσs) (homogeneous only)
ε = 1 – exp(-nσs) (Kirchhoff)
dε/ds = nσ*exp(-nσs)
dε = nσ*exp(-nσs) .ds
I = ε * B(T,λ). B(T,λ) is constant with position. If there is a dI with respect to position, there must be a dε. Therefore
dI = nσ*exp(-nσs) * B(T,λ) .ds (homogeneous only)
dI = nσ * B(T,λ) .ds (when s =0)
Before this reply, Equation 10a (with apparent units of 1/distance for ε) seemed to appear out of nowhere. In a previous (possibly erroneous*) comment, I made the assumption that Equation 10a was equivalent to a definition of emissivity written in differential form.
I = ε * B(T,λ) definition of emissivity
dI = ε * B(T,λ) .ds Eqn 10a
However,
dI/ds = dε/ds * B(T,λ) + ε * dB(T,λ)/ds
dI/ds = dε/ds * B(T,λ) + 0
dI = dε/ds * B(T,λ) .ds
Not: dI = ε * B(T,λ) .ds [Equation 10a]
When DeWitt tells me that SOD and I are using different meanings for ε, the second meaning could be dε/ds. For exponential functions like ε, dε/ds is proportional to ε, but not equal to ε. The units are also different. However, as best I can tell, SOD and I use the same ε everywhere.
*In my earlier comment, I assumed SOD had gotten Equation 10a by treating ε as a constant when writing a differential form of I = ε*B(T,λ). If he had properly differentiated both sides of this equation with respect to s and ε were constant, both dε/ds and dI/ds would have been zero.
Equation 10a appears to be wrong. I = ε*B(T,λ), but this equation can’t be differentiated with respect to s because ε = a and absorptivity/absorbance is certainly a function of s. (Yet another example demonstrating that “all” problems with climate physics originate with the assumption that emissivity is a constant for gases.
)
I = a * B(T,λ) = [1 - exp(-τ)] * B(T,λ)
Differentiating with respect to s:
dI/ds = B(T,λ) * exp(-τ) * dτ/ds *
For an infinitesimal path ds, τ approaches 0 and exp(-τ) approaches 1. τ = Int[n(s)σ.ds], so dτ/ds = nσ
dI/ds = B(T,λ) * nσ
dI = nσB(T,λ) .ds (I = emission) [10b]
But your ε is not the same as SoD’s. You’re using ε to mean emissivity. SoD isn’t. The integrated form of 10a in SoD’s terminology assuming n is constant in the layer and the layer thickness is s:
I =[1 - exp(-ελs)]Bλ(T)
I don’t know of anyone other than he who shall not be named and his followers that think that emissivity isn’t a function of path length.
Above, I tried to offer a derivation of Equation 10b without going through Equation 10a. Unfortunately, I may have made the explanation too short when editing. Expressing Kirchhoff’s Law for a volume of gas gives:
a = ε
a = 1- I/I_0 = 1 – exp(-τ) I = transmitted light
ε = I / B(T,λ) I = emitted light
1 – exp(-τ) = I / B(T,λ) I = emitted from here on
I = a*B(T,λ) = [1-exp(-τ)]*B(T,λ) “Kirchhoff’s Law”
Differentiating with respect to s:
dI/ds = B(T,λ) * exp(-τ) * dτ/ds *
For an infinitesimal path ds, τ approaches 0 and exp(-τ) approaches 1. τ = Int[n(s)σ.ds], so dτ/ds = nσ
dI/ds = B(T,λ) * nσ
dI = nσB(T,λ) .ds (I = emission) [10b]
Frank,
On further consideration, you’re right and 10a is wrong. ελ is defined as emittance which is a function of path length and is dimensionless, so its appearance undifferentiated in 10a is wrong.
In fact ελ is emissivity rather than emittance. Emittance is equal to:
ελBλ(T)
and has units of W/m2.
A convert! Your comments drove me to make a cheat sheet with all of the terms, defining equations and units. If logic prevailed, emittance would be a synonym for emissivity.
I’ve always thought of absorption cross-section in units of m2/molecule rather than SOD’s m2 and density in terms of molecules/m3 rather than 1/m3. “Molecule(s)” could be individual molecules, moles, grams, mixing ratio*density, etc. Are SOD’s units the traditional ones for this field.
Absorptance and Transmittance are ratios, so they’re equivalent to absorptivity and transmissivity. Emittance isn’t a ratio. So SoD’s statement that:
“The absorptance of a gas, aλ = 1-tλ =emittance of a gas, ελ.”
is wrong. It’s absorptivity equals emissivity. So 10a is wrong and unnecessary. It should be eliminated and 10b renamed 10.
Petty doesn’t use absorptivity and emissivity when he derives the Schwarzchild equation. He uses the extinction coefficient. Emittance isn’t even in the index, just emission and emissivity
Just went back and read that thread, DeWitt Payne. Nyarlathotep’s balls, He Who Shall Not Be Named was a ===== (moderator’s note, please observe the Etiquette, painful though that might be).
A certain regular commenter took him seriously, too.
What happened to Mark? Would be sad if he gave up reading this blog.
SoD,
You say:
“The value σ is a material property and so constant for one gas at one wavelength.”
and:
“The intensity of radiation at wavelength λ is reduced as it travels through the atmosphere according to the total amount of the absorber along the path.”
The period at the end of your statements suggests that this is the full explanation. But I think you should say a word about the fact that σ = σ (T, p).
Therefore I think the full (I mean, the correct) statements would be these:
“The value σ is a material property and so constant for one gas at one wavelength at one temperature and one pressure, but varies with the temperature and pressure of the gas.”
and:
“The intensity of radiation at wavelength λ is reduced as it travels through the atmosphere according to the total amount of the absorber along the path, and according to the temperature and pressure distribution of the gas along the path.”
Miklos Zagoni:
You are correct and I have added this note to the article.
I am working on another article to explain this subject more fully.
Frank on February 16, 2011 at 7:14 pm (and also DeWitt Payne on his followup).
Sorry it has taken a few days to respond. Unfortunately it has been a very busy week and some questions need mental energy that has been in short supply.
For some reason I started using the term emittance instead of emissivity.
I have no idea why – except that I was focused on the maths. Emittance is definitely the wrong term.
I will update the article soon and also address your maths points at the same time.
[...] as transmittance decreases. Check out the heading Optical Thickness & Transmittance in Part Six if this isn’t [...]
[...] previous articles in this series I created two fictitious molecules, pCO2 and pH20, and solved the radiative transfer equations for a variety of conditions for these two molecules through the [...]
On another blog I have said that I will provide evidence that the article writer has made false claims.
Here is an extract from Grant Petty, A First Course in Atmospheric Radiation, demonstrating that the atmosphere is not considered as a “blackbody” with an emissivity = 1:
Referencing my comment above, here is an extract from Radiation & Climate, Vardavas & Taylor (2007):
Note the highlighted equation.
The term S is the “source function” – which, when the atmosphere is in local thermodynamic equilibrium (LTE), is equal to the Planck function.
So if the emissivity was assumed to be 1 – a blackbody – then this would NOT be multiplied by the emissivity term, exp (-(t2λ-t1λ)/μ.
And by the way, this equation is the solution at one wavelength.
Finally following up on the earlier comments (e.g. February 20, 2011 at 3:18 am) about the correct terms..
Having consulted 5 textbooks covering a period of 4 decades it appears that the term emittance is a problem term and used differently by different authors.
There is no confusion in the basics of heat transfer in these books, as they define their terms.
Emittance – if consistency was observed – would relate to emissivity the same way that transmittance relates to transmissivity.
Essentially, transmittance is the ratio of transmitted radiation, as is transmissivity. The first is the extensive term, the second is the intensive term.
Following this convention – as some have tried to do including Lienhard (2008) – emittance would be the fraction of radiation from a real surface as a proportion of blackbody radiation.
However, most people have come to use emittance as the actual emitted flux.
Therefore, I will use emissivity and am correcting the text accordingly.
So as a result we have “Absorptance = Emissivity” which I have changed to “Absorptivity = Emissivity” so as not to confuse readers more than necessary(?).
[...] Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations - the actual equations of radiative transfer (no blackbodies or Stefan-Boltzmann equations to be seen) [...]
[...] Note 1: Optical thickness is proportional to the number of absorbers (molecules that absorb radiation) in the path. So as the atmosphere thins out the density reduces and, therefore, the optical thickness must also reduce. You can read more about the equations of optical thickness in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations [...]
RSS feed request to Before It’s News
Hi,
My name is Ben Chasteen and I’m the Science editor at Before It’s News http://www.beforeitsnews.com. Our site is a People Powered news platform with over 2,500,000 visits a month and growing fast.
We would be honored if we could republish your blog RSS feed in our Science category. Our readers need to read what your Science of Doom blog has to say.
Syndicating to Before It’s News is a terrific way spread the word and grow your audience. Many other organizations are using Before It’s News to do just that. We can have your feed up and running in 24 hours. I just need you to reply with your permission to do so. Please include the full name and email of the person who will be attached to the account, and let me know the name you want on the account (most people have their name or their blog name).
You can also have any text and/or links you wish appended to the end or prepended to the beginning of each of your posts on Before It’s News. Just email me the text and links that you want at the beginning and/or ending of each post. If you know html you can send me that. If not, just send me the text and a link to your site. It should be around 200 characters or less (not including links).
You can, if you like, create a custom feed for Before It’s News that includes multiple links back to your blog or web site. We only require that RSS feeds include full stories, not partial stories. We don’t censor or edit work.
Thank you,
Ben Chasteen
Editor, Before It’s News
http://www.beforeitsnews.com
[...] The only way to answer these questions is to solve the Schwarzschild equation – see Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. [...]
[...] can find a more complete explanation of optical thickness in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations, which I definitely recommend reading even though it has many equations. (Actually, because it has [...]
[...] calculate this value, you need to solve the radiative transfer equations, shown in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. These equations have no “analytic” solution but are readily solvable using numerical [...]
[...] simple – and is not used to really calculate anything of significant for our climate. See Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations for the real [...]
I think the Greenhouse effect is much simpler than this explanation.
The essential simplified model to understand ‘global’ warming of Greenhosue effect is that of a ‘filtered blackbody’ (fBB).
Imagine a theoretical blackbody (BB) at 255K. It is emitting power right across the theoretical BB spectrum.
Now what happens if if you wrap the BB with a filter that covers the 600-700 wavenumber range?
The fBB quickly changes to a new dynamic thermal equalibrium: it emits more radiation over the non-filtered wavenumbers but overall emits the same total power as before.
So it ‘looks’ to an outside observer like a BB at 295K but with a chunk of the spectrum missing. And at the macro (global) leve this is fairly much what would happened.
You would be able to say that the ‘Greenhouse’ effect results in a global temperature rise of 40K.
Now look at an emissions spectrum for Earth.
http://lasp.colorado.edu/~bagenal/1010/graphics/earth_ir_emission.gif
This looks fairly much like an fBB to me. Visually you can see that it looks like something at about 295K with some ‘chunks’ missing and has the equivalent power output of a true BB at 255K.
Next question is what would be the impact on the above graph of doubling CO2 concentation in the atmosphere?
I haven’t been able to find an answer, but what I have seen so far indicates, well, not much would happen. Absorption at CO2 and H2O wavenumbers is near satured and while there might be an effect in the ‘wings’ of the CO2 absorption spectrum this would be very minimal.
Apparently some radiance might be filtered out round about wn740 … but how much would the power output across the rest of spectrum need to increase to compensation?
We would be talking about a very minor impact indeed on the total Greenhouse effect.
Flash:
It depends on what you mean by “not much”.
The answer is given in CO2 – An Insignificant Trace Gas? Part Seven – The Boring Numbers.
An insight into the effect of CO2 across its spectrum is shown (along with the calculations) in Part Nine – you can see that absorption is not “saturated” along with the calculation of transmittance through the atmosphere with a doubling of CO2.
And you can find explanation about the question of “saturation” in CO2 – An Insignificant Trace Gas? – Part Eight – Saturation.
There’s some complex theory on ‘wings’ and ‘shoulders’ and stuff. A bit over my head, but the general gist seems to be a widening of the potential absorption band by a little bit (we’re talking 2-15 wavenumbers here depending on source and only in one direction because the other way we’re into the already saturated H2O spectrum).
In paractice, there are some observations of the change in the ‘filtered’ spectrum between 1970 and 1997. Some of that was due to inreased H2O absoroption but some apparently due to the CO2 ‘wing’ effect in wavenumbers ~735 (so it would appear to be a real and observable phenomenon). But not by a lot (a change in intensity over a narrow band of wavenumbers by no more that 1.5Teff). This was from a ‘warmists’ site so I assume is the worst case … reality might be less. Dunno, needs more observational data.
I took the suggested extra absorptions over the 27 years (1970 -1997) and then multiplied them by 10(!) to represent the standard CO2 doubling and then factored them in to a new Greenhouse Effect as per my filtered Blackbody (fBB) model. Net impact was about 0.2oC.
Does anyone have a model of the emissions spectrum they think that Earth will have if CO2 doubles? That will tell us all we need to know.
Yes, see the above link in my earlier comment: CO2 – An Insignificant Trace Gas? – Part Eight – Saturation.
See Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Twelve – Curve of Growth
And also: Part Nine.
Hi SoD,
Lots of (probably interesting) but not overly relevant stuff.
My question is … can you show me what the models say the emissions spectrum of Earth looks like with double 1970′s CO2?
Take this as a reference point …
http://lasp.colorado.edu/~bagenal/1010/graphics/earth_ir_emission.gif
I want something that shows how this changes. How does this change if there is 2*70′s CO2?
This is the ONLY thing that tells me what the impact of CO2 is on the Greenhouse Effect.
Thanks,
Andrew
Hi SoD,
Yeah. So, okay, the ‘Doppler’ effect as the recipient moves forward and backward smears the absorbable quantum wavenumber out a bit. It still does not open up much of a ‘wing’ in the filtered spectrum.Doesn’t this just affect absorption in neighbouring wavenumbers?
As per my fBB model Greenhouse warming is a factor of the total absorbed spectrum ‘v’ the unabsorbed ‘window’.
Flash:
This was in the link of “not overly relevant stuff”.
It is relevant because it directly answers your question.
Strictly speaking it doesn’t actually answer the question you asked – because you asked about doubling 1970′s CO2. Whereas the answer everyone else poses and considers (for consistency) is what happens when we double CO2 from pre-industrial levels.
I picked 1970 as a base year because we seem to have some records from then!
No point starting with a point we cannot measure reliably.
Pre-industrial we don’t have any records of what Earths transmission spectrum looked like.
The diagrams above are not an Earth’s emission spectrum … which is what I am looking for.
Does anyone have a model emissions spectrum of what they think it will look like if CO2 levels go up?
If the answer to this is NO, no-one has ever done this that would be interesting too.
A.
[...] of 289K. The diffusivity approximation was used to estimate total hemispherical transmittance (see Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations). The wavenumber step, Δν = 1 cm-1. The calculations were done from 100 cm to 2500 cm (4μm [...]
[...] the atmosphere is not gray so this is not a simple problem, but it can be solved using the radiative transfer equations with numerical [...]
[...] Radiation does go in all directions. The plane parallel assumption has very strong justification and – in simple terms – mathematically resolves to a vertical solution with a correction factor. You can see the plane parallel assumption and the derivation of the equations of radiative transfer in Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The Equations. [...]
[...] What’s the Palaver? – Kiehl and Trenberth 1997 Do Trenberth and Kiehl understand the First Law of Thermodynamics? Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Six – The… [...]