The Science of Doom

In Atmospheric Circulation – Part One we saw how the pressure “slopes down” from the tropics to the poles creating S→N winds in the northern hemisphere.

In The Coriolis Effect and Geostrophic Motion we saw that on a rotating planet winds get deflected off to the side  (from the point of view of someone on the rotating planet). This means that winds flowing from the tropics to the north pole will get deflected “to the right”.

Taylor Columns

Strange things happen to fluids in rotating frames. To illustrate let’s take a look at Taylor columns.

From Marshall & Plumb (2008)

Figure 1

The static image is quite beautiful, but the video illustrates it better. Compare the video of the non-rotating tank with the rotating tank.

Now to stretch the mind we have a rotating tank with an obstacle on the base – in this case a hockey puck. The height of the puck is small compared with the depth of the fluid. The fluid flow has come into equilibrium with the tank rotation.

We slow down the rotation slightly. We sprinkle paper dots on the surface of the water. Amazingly the dots show that the surface of the fluid is acting as if the puck extended right up to the surface – the flow moves around the obstacle at the base (of course) and the flow moves “around” the obstacle at the surface. Even though the obstacle doesn’t exist at the surface!

Take a look at the video, but here are a few snapshots:

Figure 2

This occurs when:

• the flow is slow and steady
• friction is negligible
• there is no temperature gradient (barotropic)

Under the first two conditions the flow is geostrophic which was covered with examples in The Coriolis Effect and Geostrophic Motion.

And under the final condition, with  no temperature gradient the density is uniform (only a function of pressure).

“Thermal Wind”

Now let’s look at an experiment with a “cold pole” and “warm tropics”:

From Marshall & Plumb (2008)

Figure 3

The result:

Figure 4

Even better – take a look at the video.

This experiment shows that once there is a N-S temperature gradient the E-W winds increase with altitude.

Which is kind of what we find in the real atmosphere:

From Marshall & Plumb (2008)

Figure 5

Why does this happen? I found it hard to understand conceptually for a while, but it’s actually really simple:

From Stull (1999)

Figure 6

So the ever increasing pressure gradient with height (due to the temperature gradient) induces a stronger geostrophic wind with height.

Here is an instantaneous measurement of E-W winds, along with temperature in a N-S section:

From Marshall & Plumb (2008)

Figure 8

The measurement demonstrates that the change in E-W wind vs height depends on the variation in N-S temperature.

The equation for this effect for the E-W winds can be written a few different ways, here is the easiest to understand:

∂u/∂z = (αg/f) . ∂T/∂y

where ∂u/∂z = change in E-W wind with height, α = thermal coefficient of expansion of air, g = acceleration due to gravity, f = coriolis parameter at that latitude, T = temperature, y = N-S direction

It can also be written in vector calculus notation:

∂u/∂z = (αg/f)z x ∇T

where u = wind velocity (u, v, w), z = unit vector in vertical

In the next article we will look at why the maximum effect in the average, the jet stream, occurs in the subtropics rather than at the poles.

References

Meteorology for Scientists and Engineers, Ronald Stull, 2nd edition – Free (partial) resource

Atmosphere, Ocean and Climate Dynamics – An Introductory Text, Marshall & Plumb, Academic Press (2008)

This is a tricky but essential subject and it’s hard to know where to begin.

Geopotential Height – The Height of a Given Atmospheric Pressure

Let’s start with something called the geopotential height. This is the height above the earth’s surface of a particular atmospheric pressure. In the example below we are looking at the 500 mbar surface. For reference, the surface of the earth is at about 1000 mbar and the top of the troposphere is at 200 mbar.

From Marshall & Plumb (2008)

Figure 1

At the pole the 500 mbar height is just under 5 km, and in the topics it is almost 6 km.

Why is this?

Here is another view of the same subject, this time the annual average latitudinal value (expressed as difference from the global average):

From Marshall & Plumb (2008)

Figure 2

See how the geopotential height increases in the tropics compared with the poles. And see how the difference increases with height.

The tropics are warmer than the poles – warm air expands and cool air contracts.

There is a mathematical equation which results from the ideal gas law and the hydrostatic equation:

z(p) = R/g ∫(T/p)dp

where z(p) = height of pressure p, R = gas constant, g = acceleration due to gravity, T = temperature

This is (oversimplified) like saying that the height of a “geopotential surface” is proportional to the sum of the temperatures of each layer between the surface and that pressure.

At 500 mbar, a 40ºC change in temperature leads to a height difference of just over 800 m.

North-South Winds

Because of the pressure gradient at altitude between the tropics and the poles, there is a force (at altitude) pushing air from the tropics to the poles.

From Goody (1972)

If the earth was rotating extremely slowly, the result might look something like this:

From Marshall & Plumb (2008)

Figure 3

However, the climate is not so simple. Here are 3 samples of the north-south circulation for annual, winter and summer:

From Marshall & Plumb (2008)

Figure 4

So instead of a circulation extending all the way to the poles we see a circulation from the tropics into the subtropics (note especially the DJF & JJA averages).

Here is an experiment shown in Goody (1972) to help understand the processes we see in the atmosphere:

Figure 5

Note that the first example is with slow rotation and the second example is with fast rotation.

And here is a similar experiment shown in Marshall & Plumb, but they come with videos, which help immensely. First the slow rotation experiment:

Figure 6

And second, the fast rotation experiment:

Figure 7

In both of the above links, make sure to watch the videos.

The reason the circulation breaks down from a large equator-polar cell to the actual climate with an equator-subtropical cell plus eddies is complex. We’ll explore more in the next article.

As a starter, take a look at the west-east winds:

From Marshall & Plumb (2008)

Figure 8

In the next article we will look at the thermal wind and try and make sense out of our observations.

Update – now published:

Atmospheric Circulation – Part Two – Thermal Wind

References

Atmosphere, Ocean and Climate Dynamics – An Introductory Text, Marshall & Plumb, Academic Press (2008)

Atmospheres, Goody & Walker, Prentice Hall (1972)

Here is an article from Leonard Weinstein. (It has also been posted in slightly different form at The Air Vent).

Readers who have been around for a while will remember the interesting discussion Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion in which myself, Arthur Smith and Leonard all put forward a point of view on a challenging topic.

With this article, first I post Leonard’s article (plus some graphics I added for illustration), then my comments and finally Leonard’s response to my comments.

Why Back-Radiation is not a Source of Surface Heating

Leonard Weinstein, July 18, 2012

The argument is frequently made that back radiation from optically absorbing gases heats a surface more than it would be heated without back radiation, and this is the basis of the so-called Greenhouse Effect on Earth.

The first thing that has to be made clear is that a suitably radiation absorbing and radiating atmosphere does radiate energy out based on its temperature, and some of this radiation does go downward, where it is absorbed by the surface (i.e., there is back radiation, and it does transfer energy to the surface). However, heat (which is the net transfer of energy, not the individual transfers) is only transferred down if the ground is cooler than the atmosphere, and this applies to all forms of heat transfer.

While it is true that the atmosphere containing suitably optically absorbing gases is warmer than the local surface in some special cases, on average the surface is warmer than the integrated atmosphere effect contributing to back radiation, and so average heat transfer is from the surface up. The misunderstanding of the distinction between energy transfer, and heat transfer (net energy transfer) seems to be the cause of much of the confusion about back radiation effects.

Simplest Model

Before going on with the back radiation argument, first examine a few ideal heat transfer examples, which emphasize what is trying to be shown. These include an internally uniformly heated ball with either a thermally insulated surface or a radiation-shielded surface. The ball is placed in space, with distant temperatures near absolute zero, and zero gravity. Assume all emissivity and absorption coefficients for the following examples are 1 for simplicity.

The bare ball surface temperature at equilibrium is found from the balance of input energy into the ball and radiated energy to the external wall:

T_o = (P/σ)^0.25 ….(1)

Where T_o (K) is absolute temperature, P (Wm^-2) is input power per area of the ball, and σ = 5.67×10^-8 (Wm^-2T^-4) is the Stefan-Boltzmann constant.

Ball with Insulation Layer

Now consider the same case with a relatively thin layer (compared to the size of the ball) of thermally insulating material coated directly onto the surface of the ball. Assume the insulator material is opaque to radiation, so that the only heat transfer is by conduction. The energy generated by input power heats the surface of the ball, and this energy is conducted to the external surface of the insulator, where the energy is radiated away from the surface. The assumption of a thin insulation layer implies the total surface area is about the same as the initial ball area.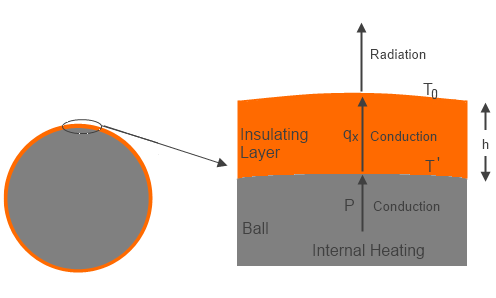

Figure 1 – Ball with Insulation

The temperature of the external surface then has to be the same (=T_o ) as the bare ball was, to balance power in and radiated energy out. However, in order to transmit the energy from the surface of the ball to the external surface of the insulator there had to be a temperature gradient through the insulation layer based on the conductivity of the insulator and thickness of the insulation layer.

For the simplified case described, Fourier’s conduction law gives:

q_x=-k(dT/dx) ….(2)

where q_x (Wm^-2) is the local heat transfer, k (Wm^-1T^-1) is the conductivity, and x is distance outward of the insulator from the surface of the ball. The equilibrium case is a linear temperature variation, so we can substitute ΔT/h for dT/dx, where h is the insulator thickness, and ΔT is the temperature difference between outer surface of insulator and surface of ball (temperature decreasing outward).

Now qx has to be the same as P, so from (2):

ΔT = (T_o-T’) = -Ph/k ….(3)

Where T’ is the ball surface temperature under the insulation, and thus we get:

T’ = (Ph/k)+T_o ….(4)

The new ball surface temperature is now found by combining (1) + (4):

T’ = (Ph/k)+(P/σ)^0.25 ….(5)

The point to all of the above is that the surface of the ball was made hotter for the same input energy to the ball by adding the insulation layer. The increased temperature did not come from the insulation heating the surface, it came from the reduced rate of surface energy removal at the initial temperature (thermal resistance), and thus the internal surface temperature had to increase to transmit the required power.

There was no added heat and no back heat transfer!

Ball with Shell & Conducting Gas

An alternate version of the insulated surface can be found by adding a thin conducting enclosing shell spaced a small distance from the wall of the ball, and filling the gap with a highly optically absorbing dense gas. Assume the gas is completely opaque to the thermal wavelengths at very short distances, so that he heat transfer would be totally dominated by diffusion (no convection, since zero gravity).

The result would be exactly the same as the solid insulation case with the correct thermal conductivity, k, used (derived from the diffusion equations).

It should be noted that the gas molecules have a range of speeds, even at a specific temperature (Maxwell distribution). The heat is transferred only by molecular collisions with the wall for this case. Now the variation in speed of the molecules, even at a single temperature, assures that some of the molecules hitting the ball wall will have higher energy going in that leaving the wall. Likewise, some of the molecules hitting the outer shell will have lower speeds than when they leave inward. That is, some energy is transmitted from the colder outer wall to the gas, and some energy is transmitted from the gas to the hotter ball wall. However, when all collisions are included, the net effect is that the ball transfers heat (=P) to the outer shell, which then radiates P to space.

Again, the gas layer did not result in the ball surface heating any more than for the solid insulation case. It resulted in heating due to the resistance to heat transfer at the lower temperature, and thus resulted in the temperature of the ball increasing. The fact that energy transferred both ways is not a cause of the heating.

Ball with Shell & Vacuum

Next we look at the bare ball, but with an enclosure of a very small thickness conductor placed a small distance above the entire surface of the ball (so the surface area of the enclosure is still essentially the same as for the bare ball), but with a high vacuum between the surface of the ball and the enclosed layer.

Now only radiation heat transfer can occur in the system. The ball is heated with the same power as before, and radiates, but the enclosure layer absorbs all of the emitted radiation from the ball. The absorbed energy heats the enclosure wall up until it radiated outward the full input power P.

The final temperature of the enclosure wall now is T_o, the same as the value in equation (1).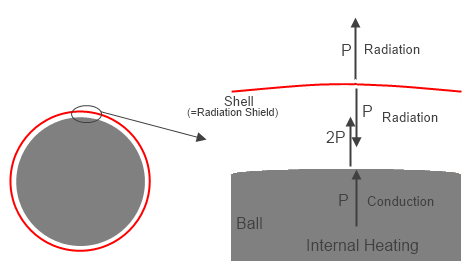

Figure 2 – Ball with Radiation Shield separated by vacuum

However, it is also radiating inward at the same power P. Since the only energy absorbed by the enclosure is that radiated by the ball, the ball has to radiate 2P to get the net transmitted power out to equal P. Since the only input power is P, the other P was absorbed energy from the enclosure. Does this mean the enclosure is heating the ball with back radiation? NO. Heat transfer is NET energy transfer, and the ball is radiating 2P, but absorbing P, so is radiating a NET radiation heat transfer of P. This type of effect is shown in radiation equations by:

P_net = σ(T_hot⁴-T_cold⁴) ….(6)

That is, the net radiation heat transfer is determined by both the emitting and absorbing surfaces. There is radiation energy both ways, but the radiation heat transfer is one way.

This is not heating by back radiation, but is commonly also considered a radiation resistance effect.

There is initially a decrease in net radiation heat transfer forcing the temperature to adjust to a new level for a given power transfer level. This is directly analogous to the thermal insulation effect on the ball, where radiation is not even a factor between the ball and insulator, or the opaque gas in the enclosed layer, where there is no radiation transfer, but some energy is transmitted both ways, and net energy (heat transfer) is only outward. The hotter surface of the ball is due to a resistance to direct radiation to space in all of these cases.

Ball with Multiple Shells

If a large number of concentric radiation enclosures were used (still assuming the total exit area is close to the same for simplicity), the ball temperature would get even hotter. In fact, each layer inward would have to radiate a net P outward to transfer the power from the ball to the external final radiator. For N layers, this means that the ball surface would have to radiate:

P’ = (N+1)P_o ….(7)

Now from (1), this means the relative ball surface temperature would increase by:

T’/T_o = (N+1)^0.25 ….(8)

Some example are shown to give an idea how the number of layers changes relative absolute temperature:

N       T’/T_o

——————-
1       1.19
10      1.82
100    3.16

Change in N clearly has a large effect, but the relationship is a semi-log like effect.

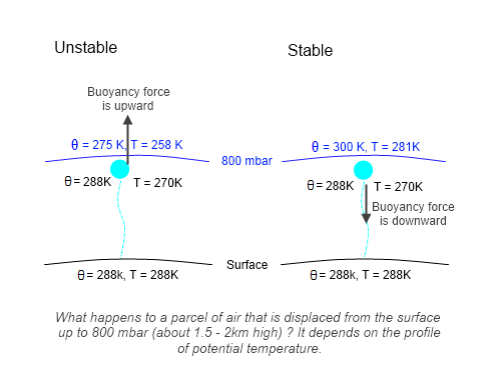
Lapse Rate Effect

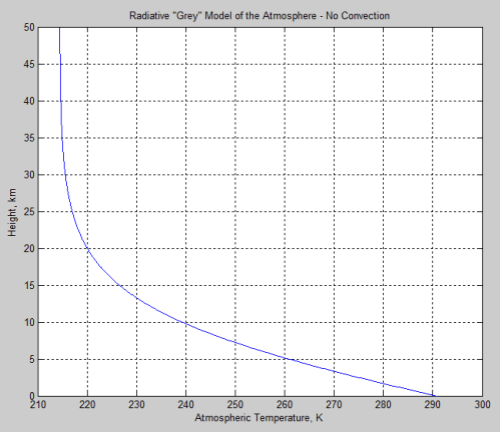
Planetary atmospheres are much more complex than either a simple conduction insulating layer or radiation insulation layer or multiple layers. This is due to the presence of several mechanisms to transport energy that was absorbed from the Sun, either at the surface or directly in the atmosphere, up through the atmosphere, and also due to the effect called the lapse rate.

The lapse rate results from the convective mixing of the atmosphere combined with the adiabatic cooling due to expansion at decreasing pressure with increasing altitude. The lapse rate depends on the specific heat of the atmospheric gases, gravity, and by any latent heat release, and may be affected by local temperature variations due to radiation from the surface directly to space. The simple theoretical value of that variation in a dry adiabatic atmosphere is about -9.8 C per km altitude on Earth. The effect of water evaporation and partial condensation at altitude, drops the size of this average to about -6.5 C per km, which is the called the environmental lapse rate.

The absorbed solar energy is carried up in the atmosphere by a combination of evapotransporation followed by condensation, thermal convection and radiation (including direct radiation to space, and absorbed and emitted atmospheric radiation). Eventually the conducted, convected, and radiated energy reaches high enough in the atmosphere where it radiates directly to space. This does require absorbing and radiating gases and/or clouds. The sum of all the energy radiated to space from the different altitudes has to equal the absorbed solar energy for the equilibrium case.

The key point is that the outgoing radiation average location is raised significantly above the surface. A single average altitude for outgoing radiation generally is used to replace the outgoing radiation altitude range. The temperature of the atmosphere at this average altitude then is calculated by matching the outgoing radiation to the absorbed solar radiation. The environmental lapse rate, combined with the temperature at the average altitude required to balance incoming and outgoing energy, allows the surface temperature to be then calculated.

The equation for the effect is:

T’ = T_o -ΓH ….(9)

Where T_o is the average surface temperature for the non-absorbing atmospheric gases case, with all radiation to space directly from the surface, Γ is the lapse rate (negative as shown), and H is the effective average altitude of outgoing radiation to space. The combined methods that transport energy up so that it radiated to space, are variations of energy transport resistance compared to direct radiation from the surface. In the end, the only factors that raise ground temperature to be higher than the case with no greenhouse gas is the increase in average altitude of outgoing radiation and the lapse rate. That is all there is to the so-called greenhouse effect. If the lapse rate or albedo is changed by addition of specific gases, this is a separate effect, and is not included here.

The case of Venus is a clear example of this effect. The average altitude where radiation to space occurs is about 50 km. The average lapse rate on Venus is about 9 C per km. The surface temperature increase over the case with the same albedo and absorbed insolation but no absorbing or cloud blocking gases, would be about 450 C, so the lapse rate fully explains the increase in temperature.

It is not directly due to the pressure or density alone of the atmosphere, but the resulting increase in altitude of outgoing radiation to space. Changing CO2 concentration (or other absorbing gases) might change the outgoing altitude, but that altitude change would be the only cause of a change in surface temperature, with the lapse rate times the new altitude as the increase in temperature over the case with no absorbing gases.

One point to note is that the net energy transfer (from combined radiation and other transport means) from the surface or from a location in the atmosphere where solar energy was absorbed is always exactly the same whatever the local temperature. For example, the hot surface of Venus radiated up (a very short distance) over 16 kWm^-2. However, the total energy transfer up is just the order of absorbed solar energy, or about 17 Wm^-2, and some of the energy carried up is by conduction and convection. Thus the net radiation heat transfer is <17 Wm^-2, and thus back radiation has to be almost exactly the same as radiation up. The back radiation is not heating the surface; the thermal heat transfer resistance from all causes, including that resulting from back radiation reducing net radiation, results in the excess heating.

In the end, it does not matter what the cause of resistance to heat transfer is. The total energy balance and thermal heat transfer resistance defines the process. For planets with enough atmosphere, the lapse rate defines the lower atmosphere temperature gradient, and if the lapse rate is not changed, the distance the location of outgoing radiation is moved up by addition of absorbing gases determines the increase in temperature effect. It should be clear the back radiation did not do the heating; it is a result of the effect, not the cause.

—— End of section 1 ——

My Response

I agree with Leonard. Now for his rebuttal..

Ok, a few words of clarification. I agree with Leonard about the greenhouse mechanism, the physics and the maths but see a semantic issue about back radiation. It’s always possible it’s a point of substance disguised as a semantic issue but I think that is unlikely.

A large number of people are unhappy about climate science basics but are unencumbered by any knowledge of radiative heat transfer theory as taught in heat transfer textbooks. This group of people claim that back radiation has no effect on the surface temperature. I’ll call them Group Zero. Because of this entertaining and passionate group of people I have spent much time explaining back radiation and physics basics. Perhaps this has led others to the idea that I have a different idea about the mechanism of the inappropriately-named “greenhouse” effect.

Group Zero are saying something completely different from Leonard. Here’s my graphic of Leonard’s explanation from one of his simplified scenarios:

Figure 2 – again

From the maths it is clear that the downward radiation from the shell (shield) is absorbed by the surface and re-emitted. Here the usual graphic presented by the Group Zero position, replete with all necessary equations:

Figure 3 – how can you argue with this?

And here’s an interpretation of a Group Zero concept, pieced together by me from many happy hours of fruitless discussion:

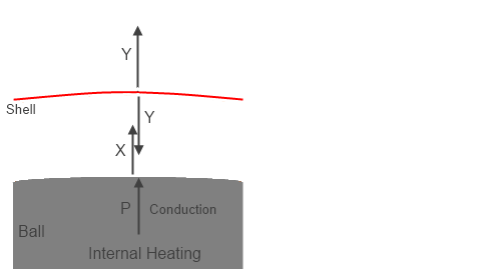
Figure 4 – Group Z?

In this case P, the internal heating, is still a known value. But Y and X are unknown, which is why I have changed them from the solution values shown in figure 2.

Now we have to figure out what they are. Let’s make the assumption that the shell radiates equally inwards and outwards, which is true if it is thin (and so upper and lower surfaces will be at the same temperature) and has the same emissivity both sides. That is why we see the upward flux and the downward flux from the shell both = Y.

Because, according to Group Zero, the downward radiation from a colder atmosphere cannot “have any effect on” the surface, I’m going to assume their same approach to the radiation shield (the “shell”). So the surface only has the energy source P. Group Zero never really explain what happens to Y when it “reaches the ground” but that’s another story. (Although it would be quite interesting to find out along with an equation).

So at the surface, energy in = energy out.

P=X ….(10)

And at the shell, energy in = energy out.

X = 2Y ….(11)

In figure 2, by using real physics we see that the surface emission of radiation by the ball = 2P. This means the surface temperature, T’ = (2P/σ)^0.25.

In figure 4, by using invented physics we see that the surface emission of radiation by the ball = P. This means the surface temperature, T'(invented) = (P/σ)^0.25.

So the real surface temperature, T’ is 1.19 times larger than T'(invented). Because 2^0.25 = 1.19.

And back to the important point about the “greenhouse” effect. Because the atmosphere is quite opaque to radiation due to radiatively-active gases like water vapor and CO2 the emission of radiation to space from the climate system is from some altitude. And because temperature reduces with height due to other physics the surface must be warmer than the effective radiating point of the atmosphere. This means the surface temperature of the earth is higher than it would be if there were no radiatively-active gases. (The actual maths of the complete explanation takes up a lot more room than this paragraph). This means I completely agree with Leonard about the “greenhouse” effect.

If back radiation were not absorbed by the surface lots of climate effects would be different because the laws of physics would be different. I’m pretty sure that Leonard completely agrees with me on this.

—— End of section 2 ——

Leonard’s Final Comment

I think we are getting very close to agreement on most of the discussion, but I still sense a bit of disagreement to my basic point. However, this seems to be mainly based on difference in semantics, not the logic of the physics. The frequent use of the statement of heat being transferred from the cold to hot surface (like in back radiation), is the main source of the misuse of a term. Energy can be transferred both ways, but heat transfer has a specific meaning. An example of a version of the second law of thermodynamics, which defines limitations in heat transfer, is from the German scientist Rudolf Clausius, who laid the foundation for the second law of thermodynamics in 1850 by examining the relation between heat transfer and work. His formulation of the second law, which was published in German in 1854, may be stated as: “No process is possible whose sole result is the transfer of heat from a body of lower temperature to a body of higher temperature.”

The specific fact of back radiation and resulting energy transfer does result in the lower surface of the cases with radiation resistance going to a higher temperature. However, this is not due to heat being transferred by back radiation, but by the internal supplied power driving the wall to a higher temperature to transfer the same power. The examples of the solid insulation and opaque gas do exactly the same thing, and back heat transfer or even back energy transport is not the cause of the wall going to the higher temperature for those cases. There is no need to invoke a different effect that heat transfer resistance for the radiation case.

An example can give some insight on how small radiation heat transfer can be even in the presence of huge forward and back radiation effects. For this example we use an example with surface temperature like that found on Venus.

Choose a ball with a small gap with a vacuum, followed by an insulation layer large enough to cause a large temperature variation. The internal surface power to be radiated then conducted out is 17 Wm^-2 (similar to absorbed solar surface heating on Venus). The insulation layer is selected thick enough and low enough thermal conductivity so that the bottom of the insulation the wall is 723K (similar to the surface temperature on Venus). The outside insulation surface would only be at 131.6K for this case.

The question is: what is the surface temperature of the ball under the gap?

From my equation (6), the surface of the ball would be 723.2K. The radiation gap caused an increase in surface temperature of 0.2K, which is only 0.033% of the temperature increase. The radiation from the surface of the ball had increased from 17 Wm^-2 (for no insulation) to 15,510 Wm^-2 due to the combined radiation gap and insulation, and back radiation to the ball is 15,503 Wm^-2. This resulted in the net 17 Wm^-2 heat transfer. However, the only source of the net energy causing the final wall temperature was the resistance to heat transfer causing the supplied 17 Wm^-2 to continually raise the wall temperature until the net out was 17 Wm^-2. Nowhere did the back radiation add net energy to the ball wall, even though the back radiation absorbed was huge.

This post is intended to help readers better understand how changes in temperature and water vapor at different locations affect the radiation balance of the planet, primarily outgoing longwave radiation (OLR).

A lot of questions on this blog come about because people have trouble visualizing the process of radiative transfer. This is not surprising – it’s not an intuitive subject.

Basic energy balance for the planet is covered in The Earth’s Energy Budget – Part One and Part Two. If some change to the climate causes more energy to be radiated into space then the climate system will cool. Likewise, if some change causes less energy to be radiated into space then the climate system will warm (assuming constant absorbed solar radiation). We use the term OLR (outgoing longwave radiation) for the radiation from the climate system into space.

Heating the Atmosphere and the Surface

Here is a calculation of how changing temperature in the atmosphere affects OLR at different latitudes and different pressures (1000mbar at the bottom of the graph is the surface):

From Soden et al (2008)

Figure 1 – Italic text is added

Understanding the Terminology

The top two graphs show the same effect under two different conditions. The top one is “All Sky” which is all conditions. And the second one is “Clear Sky”, i.e., the subset of conditions when clouds are not present. From left to right we have latitude and from bottom to top we have pressure. 1000mbar is the surface pressure = zero altitude, and 200mbar is the pressure at the top of the troposphere, and is around 14km (it varies depending on the latitude).

The units (the values are shown as colors) are in W/m².K.100hPa. (See Note 1). Already some readers are lost?

The important part is W/m² – this is flux (radiation in less technical language) or watts per square meter. We can call it power per unit area.

W/m².K is watts per square meter per 1K temperature change. So this asks – how much does the power per unit area increase (or decrease) for each 1K of temperature change?

If we asked, how much does the OLR increase for 1K increase in the whole atmosphere we would use the units of W/m².K. But when we want to look at how different layers in the atmosphere affect the OLR we are considering just once “slice”. So we have to have watts per meter squared per Kelvin per slice. In this case we are considering 100mbar (=100hPa) slices so this is how we get W/(m².K.100hPa).

Understanding the Results

So now the basics are out of the way, what do the graphs show us?

At the simplest level if the whole atmosphere heats up by 1K, the graphs show us the relative contribution of different latitudes and altitudes to OLR.

Let’s suppose we increase the temperature of the atmosphere at the equator between 1000 and 900 mbar by 1°C (=1K). This means we have taken a “layer” of the atmosphere and somehow just increased its temperature. What is the effect on the OLR? All bodies, including gases, emit according to their temperature and their emissivity.

Increase the temperature and the radiation (flux) increases. In our graph, at that location, for 1°C the flux increases by about 0.3 W/(m².100hPa).

Of course this means the climate cools which should be totally unsurprising. Increase the temperature of the atmosphere and it radiates more energy away into space. This is negative feedback. You can see from the graph that no matter where you heat the atmosphere it increases the flux into space – cooling the climate back down.

The bottom graph shows the result of heating the earth’s surface for clear sky and for all sky conditions. Note the difference. Under clear skies the increased flux emitted by the surface more easily escapes to space. When clouds are present the increased surface radiation is absorbed by clouds and the clouds emit at the cloud top temperature. (The cloud top temperature is high up in the atmosphere, is cooler than the surface, and so the emission to space is reduced by the presence of clouds).

At this point let’s make it clear what the graphs are not showing. They are not showing the ultimate result of heating the surface or a slice of the atmosphere after the whole climate has come into a new “equilibrium”. They are simply showing what happens directly to radiation balance as a result of a change in temperature of a “portion” of the climate.

If you’ve understood why the all sky/clear sky results in the surface graph are different then the difference between the first and second graph might be clear. The first graph is under all sky conditions (including clouds) and so the cloud tops are the region where a 1K increase has the greatest effect on OLR. Lower down in the atmosphere an increase in flux (due to hotter conditions) can be masked by clouds.

In contrast, under clear sky conditions changes in the lower atmosphere have a similar effect to changes in the upper atmosphere.

The authors say:

Under total-sky conditions the longwave fluxes are most sensitive to temperatures at the level of cloud tops that are exposed to space. This results in an obvious maximum just beneath the tropopause, where convectively detrained cirrus anvils are common, and along the top of the cloud topped boundary layer. By masking the surface, clouds also diminish the surface contribution to K^T

Adding Water Vapor to the Atmosphere

More water vapor in the atmosphere generally reduces the outgoing longwave radiation which has a heating effect on the atmosphere. (The opposite of higher atmospheric temperatures).

The reason for this is with more water vapor the atmosphere becomes more opaque to longwave radiation. So, for example, with more water vapor in the upper atmosphere, radiation from the surface or the lower atmosphere is absorbed by the water vapor higher up.

Another way of looking at the problem is to say that the more opaque the atmosphere the higher up the effective radiation to space. And higher altitudes have colder temperatures. This is the essence of the inappropriately-named “greenhouse” effect. For more on this see The Earth’s Energy Budget – Part Three.

From Soden et al (2008)

Figure 2 – Italic text is added

Any calculation / visualization of the climate effect of increased water vapor has a choice – do you show the effect from absolute or relative changes in water vapor? As water vapor concentration reduces by more than 1000 times as you go up through the atmosphere showing relative change is generally preferred over showing absolute change.

The authors of this paper have chosen relative changes and calculated the change in OLR if temperature changes by 1K and relative humidity stays constant.

Some of the readers might be tempted to jump in here thinking that some unproven claim is being used as a premise for a climate calculation. But this is not so. It is simply a convenient way of illustrating OLR changes with water vapor changes.

Reviewing the graphs, we can see that under clear skies the deep tropics have the dominant water vapor response. This is not surprising as the tropics have so much more water vapor than the rest of the globe. See Clouds and Water Vapor – Part Two for discussion on this.

Under all sky conditions the effects of clouds are seen. The subtropics become more important than the tropics because the subtropics are mostly cloud-free. In the deep tropics the clouds “mask” the effects of lower levels in the atmosphere.

The authors comment:

By masking underlying water vapor perturbations, clouds reduce the sensitivity of OLR to water vapor changes and increase the relative importance of upper-tropospheric moistening to the total feedback.

Water vapor also absorbs solar radiation. If there was no water vapor wouldn’t the surface absorb all the solar radiation anyway? Does it make a difference? The surface doesn’t absorb all the solar (shortwave) radiation, and especially over snow/ice covered areas the proportion of reflected solar radiation is high. Therefore, solar absorption by water vapor (as water vapor increases) has a relatively larger impact at the poles.

From Soden et al (2008)

Figure 3 – Italic text is added

And Out of Interest..

This graph below wasn’t the intent of the article, but is in the Soden et al paper and is quite interesting.

This article is aimed at showing how the net radiative climate balance changes when atmospheric temperature and water vapor changes under clear and cloudy skies.

But once a climate model is used to compute changes in temperature we can see what different climate models show for the difference between the feedbacks:

Soden et al (2008)

This graph shows the results of various climate models.

As an example, Lapse rate feedback is the feedback from changes in the atmospheric temperature profile.

Final results from climate models are much more complex than determining how changes in water vapor or atmospheric temperature affect the emission of thermal radiation into space.

Conclusion

This article is aimed at increasing understanding of how changes in temperature and water vapor change the net radiation balance of the climate before any feedback.

The whole paper is well worth reading.

Further reading

        Understanding Atmospheric Radiation and the “Greenhouse” Effect – Part Ten

References

Quantifying Climate Feedbacks Using Radiative Kernels, Soden et al, Journal of Climate (2008) – Free Link

Notes

Note 1 – The units in figure 1 are Wm^-2K^-1. To non-mathematicians this notation can be difficult to understand. Most people know what m² means – it means meters squared. m^-2 means per meter squared. So we can write Wm^-2 or W/m². Both mean the same thing.

The mathematical convention of Wm^-2K^-1 is better because it is more precise (when I write W/m²K does it mean watts per meter squared per Kelvin, or Watts per meter squared times Kelvin?)

But I write the slightly less mathematically precise way to provide better readability for the non-mathematicians.

Here is the annual mean temperature as a function of pressure (=height) and latitude:

From Marshall & Plumb (2008)

Figure 1 – Click for a larger image

We see that the equator is warmer than the poles and the surface is warmer than the upper troposphere (“troposphere” = lower atmosphere). No surprises.

Here is “potential temperature”, whatever that is..

From Marshall & Plumb (2008)

Figure 2 – Click for a larger image

We see that – whatever “potential temperature” is – the equator is warmer than the poles, but this version of temperature increases with height.

Why does temperature decrease with height? What is potential temperature? And why does it increase with height?

The Lapse Rate

Atmospheric pressure decreases with height. This is because as you go higher up there is less air above you, and therefore less downward force due to the weight of this air.

Because pressure decreases – and because air is a compressible fluid – air that rises expands (and air that sinks contracts).

Air that expands does “work” against its surroundings and because of the first law of thermodynamics (conservation of energy) this work needs to be paid for. So internal energy is consumed in expanding the parcel of air outwards against the atmosphere. And a reduction in internal energy means a reduction in temperature.

• Air that rises expands
• Expanding air cools

A little bit more technically.. adiabatic expansion is what we are talking about. An adiabatic process is one where no heat is exchanged with the surroundings. This is a reasonable approximation for typical rising air. It is reasonable because conduction is an extremely slow process (= negligible) in the atmosphere and radiative heat transfer is quite slow.

So if heat can’t be exchanged between a “parcel of air” and its surroundings it is relatively simple to calculate how the temperature changes. An example which contains way too much detail (because it is debunking a “debunking”) at Paradigm Shifts in Convection and Water Vapor?

The essence of the calculation is to equate internal energy changes with work done on the environment.

Textbooks usually start off with the simplest version, the dry adiabatic lapse rate, or DALR. (The “lapse rate” is the change in temperature with height of a parcel of air).

The DALR is for air without any water vapor. Now water vapor is very influential in our climate. The reason for neglecting it and starting off with this simplification is:

• the calculation is easy and everyone (almost) can understand it
• it represents one extreme of the atmosphere (polar climates and upper troposphere)

The result from this simplification:

Change in temperature with height = -g/c_p ≈ -10 °C/km, where g = acceleration due to gravity = 9.8 m/s² and c_p = heat capacity of air at constant pressure ≈ 1 J/kg.K

So for every km we displace air upwards it cools by about 10°C – so long as we displace it reasonably quickly. Well, this is true if it is dry.

A note on conventions – dry parcels of air moved upwards cool by 10°C per km, but the lapse rate is usually written as a positive number. So a cooling of 10 °C/km =  -10 °C/km, but by convention, equals a “lapse rate” of +10 °C/km. This makes it very confusing when people say things like “the environmental lapse rate must be less than the adiabatic lapse rate“. Are we talking about the number with the minus sign in front? Or not?

It’s not easy to think about negative numbers being less than other negative numbers when the “less than” test is applied after they have been made into positive numbers. Not for me anyway. I have to write it down each time.

The Saturated Lapse Rate

If a parcel of air contains water vapor and it cools sufficiently then the water vapor condenses. This releases latent heat.

As a result, moist rising air cools slower than dry rising air

So the saturated adiabatic lapse rate is “less than” the dry adiabatic lapse rate.

E.g. the change in temperature with height of a dry parcel of air ≈ -10 °C/km, while the change in temperature with height of a moist parcel of air in the tropics near the surface ≈ -4 °C/km.

Conventionally we say that the saturated adiabatic lapse rate is less than the dry adiabatic lapse rate. Because we write them as positive numbers.

Now note the caveats around the value for the moist parcel of air rising. I said “..in the tropics near the surface..”, but for the DALR there are no caveats. That’s because once we consider moisture we have to consider how much water vapor and the amount varies hugely depending on temperature (and also on other factors – see Clouds and Water Vapor – Part Three).

The maths is somewhat harder for the saturated adiabatic lapse rate but it’s not conceptually more difficult, there is just an addition of energy (from condensing water vapor) to offset the work done.

Potential Temperature

Potential temperature is usually written with the Greek letter θ.

θ = T.(p₀/p)^k

where T = (real) temperature, p = pressure, p₀ = reference pressure (usually at 1000 mbar) and k = R/c_p = 2/7 for our atmosphere (more on this in a later article)

With a bit of tedious maths we can prove that θ stays constant under adiabatic conditions (for dry air).

Let’s look at what that means.

Suppose the surface (1000 mbar) temperature = 288 K (15°C) so also θ = 288K.

Now the air is moved (adiabatically) to 800 mbar, so T = 270 K. That’s what you expect – temperature falls with height. And no change to potential temperature, so θ = 288 K.

Now we move the air to 600 mbar, and T = 249 K. More reduction of temperature. And still θ = 288 K.

So is this a useful parameter – move the air (adiabatically) and the potential temperature stays the same?

The parameter is mathematically sound, but whether it is useful remains to be seen. As an artificial construct no doubt many people will be shaking their heads..

Stability and Potential Temperature Profile

In Density, Stability and Motion in Fluids we saw that for a fluid to be stable, lighter fluid must be above heavier fluid. No surprise to anyone.

And we saw that in mechanical terms equilibrium is different from stability.

An unstable equilibrium can exist, but a slight displacement will turn the instability into motion. Whereas with a stable equilibrium a slight displacement (or a large displacement) will result in a restoring force back to its original position. For the simplest case – an incompressible fluid – this means that the temperature must increase with height.

If you watched the accompanying video of a tank of water being heated from below you would have seen that the instability caused turbulent motion until finally the tank was well-mixed.

We left the more complex case of compressible fluids (like air) until today. What we will find is that with a compressible fluid potential temperature is effectively the same as “real” temperature for an incompressible fluid.

So if potential temperature increases with height the fluid is stable, but if potential temperature decreases with height the fluid is unstable.

Let’s look at two examples:

Figure 3

On the left hand side we see an example where potential temperature decreases with height. At the surface, θ = 288 K but at 800 mbar, θ = 275 K. A parcel of air displaced adiabatically from the surface to 800 mbar will keep its potential temperature of 288 K. Now we convert that to real temperatures. The environmental temperature at 800 mbar is 258 K, but the parcel of air cools to only 270 K. This means the displaced parcel is warmer than the surroundings, so it is less dense – and therefore it keeps rising.

This case is unstable – clearly any air that starts rising or falling (perhaps due to atmospheric winds, pressure differentials, etc) will keep rising or falling.

On the right hand side we see potential temperature decreasing with height. The parcel of air displaced from the surface to 800 mbar reaches the same temperature as on the left – 270 K. But here the environmental temperature is 281 K. So the parcel of air is cooler than the surrounding air, so it is more dense – and so it falls.

This case is stable – any air that starts rising or falling experiences a restoring force.

So the potential temperature profile with height tells us whether the atmosphere is stable, neutral or unstable. If potential temperature increases with height the atmosphere is stable, and if potential temperature decreases with height the atmosphere is unstable.

This is exactly the same as comparing the actual temperature change with the lapse rate.

Both answer the same question about atmospheric stability.

Moist Potential Temperature

The previous section slightly over-simplified things because potential temperature is with reference to dry air and yet moisture changes the way in which temperature decreases with height.

So here is the real deal – moist potential temperature. This is also known as equivalent potential temperature:

From Marshall & Plumb (2008)

Figure 4 – Click for a larger image

Here we see the “real potential temperature” and notice that especially in the tropics moist potential temperature is almost constant with height – up to the tropopause at 200 mbar. This is due to convection creating a well-mixed atmosphere. In the polar regions we see that the atmosphere is still quite stratified, which is due to the lack of convective mixing.

Conclusion

Potential temperature is very useful. It is a method of comparing the temperature of air at two different heights.

And if potential temperature is constant or increasing with height then the atmosphere is stable.

The atmosphere is mostly stable for dry air. If you refer back to figure 2 you see that (dry) potential temperature is quite stratified which means any displaced air experiences a restoring force. So it is moisture in the air that is the enabler for most of the convection that takes place. Figure 4 shows us that the atmosphere is “finely” balanced as far as moist convection is concerned.

(Remember of course that these graphs are annual mean values. It doesn’t mean that dry convection does not occur).

Potential temperature is also a useful metric because the change of potential temperature with height can be used to calculate the strength of the restoring force on displaced air. The result is the buoyancy frequency and the period of internal gravity waves.