The Science of Doom

In recent articles we have looked at rainfall and there is still more to discuss. This article changes tack to look at tropical cyclones, prompted by the recent US landfall of Harvey and Irma along with questions from readers about attribution and the future.

It might be surprising to find the following statement from leading climate scientists (Kevin Walsh and many co-authors in 2015):

At present, there is no climate theory that can predict the formation rate of tropical cyclones from the mean climate state.

The subject gets a little involved so let’s dig into a few papers. First from Gabriel Vecchi and some co-authors in 2008 in the journal Science. The paper is very brief and essentially raises one question – has the recent rise in total Atlantic cyclone intensity been a result of increases in absolute sea surface temperature (SST) or relative sea surface temperature:

From Vecchi et al 2008

Figure 1

The top graph (above) shows a correlation of 0.79 between SST and PDI (power dissipation index). The bottom graph shows a correlation of 0.79 between relative SST (local sea surface temperature minus the average tropical sea surface temperature) and PDI.

With more CO2 in the atmosphere from burning fossil fuels we expect a warmer SST in the tropical Atlantic in 2100 than today. But we don’t expect the tropical Atlantic to warm faster than the tropics in general.

If cyclone intensity is dependent on local SST we expect more cyclones, or more powerful cyclones. If cyclone intensity is dependent on relative SST we expect no increase in cyclones. This is because climate models predict warmer SSTs in the future but not warmer Atlantic SSTs than the tropics. The paper also shows a few high resolution models – green symbols – sitting close to the zero change line.

Now predicting tropical cyclones with GCMs has a fundamental issue – the scale of a modern high resolution GCM is around 100km. But cyclone prediction requires a higher resolution due to their relatively small size.

Thomas Knutson and co-authors (including the great Isaac Held) produced a 2007 paper with an interesting method (of course, the idea is not at all new). They input actual meteorological data (i.e. real history from NCEP reanalysis) into a high resolution model which covered just the Atlantic region. Their aim was to see how well this model could reproduce tropical storms. There are some technicalities to the model – the output is constantly “nudged” back towards the actual climatology and out at the boundaries of the model we can’t expect good simulation results. The model resolution is 18km.

The main question addressed here is the following: Assuming one has essentially perfect knowledge of large-scale atmospheric conditions in the Atlantic over time, how well can one then simulate past variations in Atlantic hurricane activity using a dynamical model?

They comment that the cause of the recent (at that time) upswing in hurricane activity “remains unresolved”. (Of course, fast forward to 2016, prior to the recent two large landfall hurricanes, and the overall activity is at a 1970 low. In early 2018, this may be revised again..).

Two interesting graphs emerge. First an excellent match between model and observations for overall frequency year on year:

From Knutson et al 2007

Figure 2

Second, an inability to predict the most intense hurricanes. The black dots are observations, the red dots are simulations from the model. The vertical axis, a little difficult to read, is SLP, or sea level pressure:

From Knutson et al 2007

Figure 3

These results are a common theme of many papers – inputting the historical climatological data into a model we can get some decent results on year to year variation in tropical cyclones. But models under-predict the most intense cyclones (hurricanes).

Here is Morris Bender and co-authors (including Thomas Knutson, Gabriel Vecchi – a frequent author or co-author in this genre, and of course Isaac Held) from 2010:

Some statistical analyses suggest a link between warmer Atlantic SSTs and increased hurricane activity, although other studies contend that the spatial structure of the SST change may be a more important control on tropical cyclone frequency and intensity. A few studies suggest that greenhouse warming has already produced a substantial rise in Atlantic tropical cyclone activity, but others question that conclusion.

This is a very typical introduction in papers on this topic. I note in passing this is a huge blow to the idea that climate scientists only ever introduce more certainty and alarm on the harm from future CO2 emissions. They don’t. However, it is also true that some climate scientists believe that recent events have been accentuated due to the last century of fossil fuel burning and these perspectives might be reported in the media. I try to ignore the media and that is my recommendation to readers on just about all subjects except essential ones like the weather and celebrity news.

This paper used a weather prediction model starting a few days before each storm to predict the outcome. If you understand the idea behind Knutson 2007 then this is just one step further – a few days prior to the emergence of an intense storm, input the actual climate data into a high resolution model and see how well the high res model predicts the observations. They also used projected future climates from CMIP3 models (note 1).

In the set of graphs below there are three points I want to highlight – and you probably need to click on the graph to enlarge it.

First, in graph B, “Zetac” is the model used by Knutson et al 2007, whereas GFDL is the weather prediction model getting better results in this paper – you can see that observations and the GFDL are pretty close in the maximum wind speed distribution. Second, the climate change predictions in E show that predictions of the future show an overall reduction in frequency of tropical storms, but an increase in the frequency of storms with the highest wind speeds – this is a common theme in papers from this genre. Third, in graph F, the results (from the weather prediction model) fed by different GCMs for future climate show quite different distributions. For example, the UKMO model produces a distribution of future wind speeds that is lower than current values.

From Bender et al 2010

Figure 4 – Click to enlarge

In this graph (S3 from the Supplementary data) we see graphs of the difference between future projected climatologies and current climatologies for three relevant parameters for each of the four different models shown in graph F in the figure above:

From Bender et al 2010

Figure 5 – Click to enlarge

This illustrates that different projected future climatologies, which all show increased SST in the Atlantic region, generate quite different hurricane intensities. The paper suggests that the reduction in wind shear in the UKMO model produces a lower frequency of higher intensity hurricanes.

Conclusion

This article illustrates that feeding higher resolution models with current data can generate realistic cyclone data in some aspects, but less so in other aspects. As we increase the model resolution we can get even better results – but this is dependent on inputting the correct climate data. As we look towards 2100 the questions are – How realistic is the future climate data? How does that affect projections of hurricane frequencies and intensities?

Articles in this Series

Impacts – I – Introduction

Impacts – II – GHG Emissions Projections: SRES and RCP

Impacts – III – Population in 2100

Impacts – IV – Temperature Projections and Probabilities

Impacts – V – Climate change is already causing worsening storms, floods and droughts

Impacts – VI – Sea Level Rise 1

Impacts – VII – Sea Level 2 – Uncertainty

Impacts – VIII – Sea level 3 – USA

Impacts – IX – Sea Level 4 – Sinking Megacities

Impacts – X – Sea Level Rise 5 – Bangladesh

Impacts XI – Rainfall 1

Impacts – XII – Rainfall 2

Impacts – XIII – Rainfall 3

References

Hurricanes and climate: the US CLIVAR working group on hurricanes, American Meteorological Society, Kevin Walsh et al (2015) – free paper

Whither Hurricane Activity? Gabriel A Vecchi, Kyle L Swanson & Brian J. Soden, Science (2008) – free paper

Modeled Impact of Anthropogenic Warming on the Frequency of Intense Atlantic Hurricanes, Morris A Bender et al, Science (2010) – free paper

Notes

Note 1: The scenario is A1B, which is similar to RCP6 – that is, an approximate doubling of CO2 by the end of the century. The simulations came from the CMIP3 suite of model results.

Read Full Post »

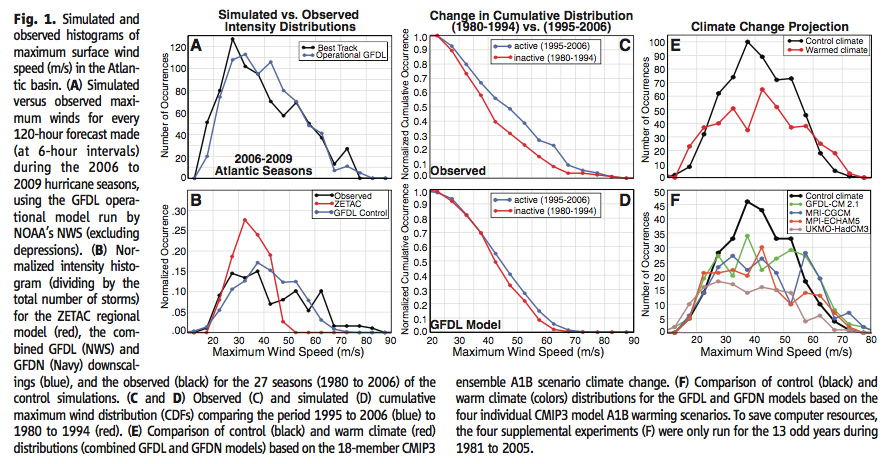
In XII – Rainfall 2 we saw the results of many models on rainfall as GHGs increase. They project wetter tropics, drier subtropics and wetter higher latitude regions. We also saw an expectation that rainfall will increase globally, with something like 2-3% per ºC of warming.

Here is a (too small) graph from Allen & Ingram (2002) showing the model response of rainfall under temperature changes from GHG increases. The dashed line marked “C-C” is the famous (in climate physics) Clausius–Clapeyron relation which, at current temperatures, shows a 7% change in water vapor per ºC of warming. The red triangles are the precipitation changes from model simulations showing about half of that.

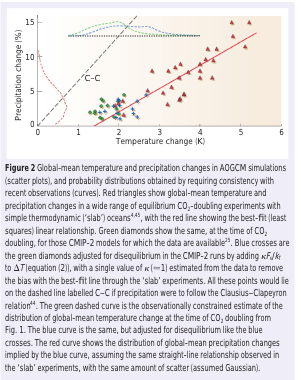
From Allen & Ingram (2002)

Figure 1

Here is another graph from the same paper showing global mean temperature change (top) and rainfall over land (bottom):

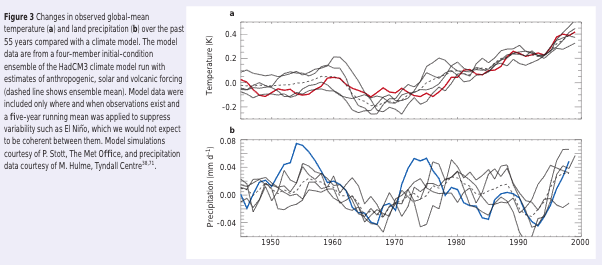
From Allen & Ingram (2002)

Figure 2

The temperature has increased over the last 50 years, and models and observations show that the precipitation has.. oh, it’s not changed. What is going on?

First, the authors explain some important background:

The distribution of moisture in the troposphere (the part of the atmosphere that is strongly coupled to the surface) is complex, but there is one clear and strong control: moisture condenses out of supersaturated air.

This constraint broadly accounts for the humidity of tropospheric air parcels above the boundary layer, because almost all such parcels will have reached saturation at some point in their recent history. Physically, therefore, it has long seemed plausible that the distribution of relative humidity would remain roughly constant under climate change, in which case the Clausius-Clapeyron relation implies that specific humidity would increase roughly exponentially with temperature.

This reasoning is strongest at higher latitudes where air is usually closer to saturation, and where relative humidity is indeed roughly constant through the substantial temperature changes of the seasonal cycle. For lower latitudes it has been argued that the real-world response might be different. But relative humidity seems to change little at low latitudes under a global warming scenario, even in models of very high vertical resolution, suggesting this may be a robust ’emergent constraint’ on which models have already converged.

They continue:

If tropospheric moisture loading is controlled by the constraints of (approximately) unchanged relative humidity and the Clausius-Clapeyron relation, should we expect a corresponding exponential increase in global precipitation and the overall intensity of the hydrological cycle as global temperatures rise?

This is certainly not what is observed in models.

To clarify, the point in the last sentence is that models do show an increase in precipitation, but not at the same rate as the expected increase in specific humidity (see note 1 for new readers).

They describe their figure 2 (our figure 1 above) and explain:

The explanation for these model results is that changes in the overall intensity of the hydrological cycle are controlled not by the availability of moisture, but by the availability of energy: specifically, the ability of the troposphere to radiate away latent heat released by precipitation.

At the simplest level, the energy budgets of the surface and troposphere can be summed up as a net radiative heating of the surface (from solar radiation, partly offset by radiative cooling) and a net radiative cooling of the troposphere to the surface and to space (R) being balanced by an upward latent heat flux (LP, where L is the latent heat of evaporation and P is global-mean precipitation): evaporation cools the surface and precipitation heats the troposphere.

[Emphasis added].

Basics Digression

Picture the atmosphere over a long period of time (like a decade), and for the whole globe. If it hasn’t heated up or cooled down we know that the energy in must equal energy out (or if it has only done so only marginally then energy in is almost equal to energy out). This is the first law of thermodynamics – energy is conserved.

What energy comes into the atmosphere?

1. Solar radiation is partly absorbed by the atmosphere (most is transmitted through and heats the surface of the earth)
2. Radiation emitted from the earth’s surface (we’ll call this terrestrial radiation) is mostly absorbed by the atmosphere (some is transmitted straight through to space)
3. Warm air is convected up from the surface
4. Heat stored in evaporated water vapor (latent heat) is convected up from the surface and the water vapor condenses out, releasing heat into the atmosphere when this happens

How does the atmosphere lose energy?

1. It radiates downwards to the surface
2. It radiates out to space

..end of digression

Changing Energy Budget

In a warmer world, if we have more evaporation we have more latent heat transfer from the surface into the troposphere. But the atmosphere has to be able to radiate this heat away. If it can’t, then the atmosphere becomes warmer, and this reduces convection. So with a warmer surface we may have a plentiful potential supply of latent heat (via water vapor) but the atmosphere needs a mechanism to radiate away this heat.

Allen & Ingram put forward a simple conceptual equation:

ΔR_c + ΔR_T = LΔP

where the change in radiative cooling ΔR, is split into two components: ΔR_c that is independent of the change in atmospheric temperature; and ΔR_T that depends only on the temperature

L = latent heat of water vapor (a constant), ΔP = change in rainfall (= change in evaporation, as evaporation is balanced by rainfall)

LΔP is about 1W/m² per 1% increase in global precipitation.

Now, if we double CO2, then before any temperature changes we decrease the outgoing longwave radiation through the tropopause (the top of the troposphere) by about 3-4W/m² and we increase atmospheric radiation to the surface by about 1W/m².

So doubling CO2, ΔR_c = -2 to -3W/m²; prior to a temperature change ΔR_T = 0; and so ΔP reduces.

The authors comment that increasing CO2 before any temperature change takes place reduces the intensity of the hydrological cycle and this effect was seen in early modeling experiments using prescribed sea surface temperatures.

Now, of course, the idea of doubling CO2 without any temperature change is just a thought experiment. But it’s an important thought experiment because it lets us isolate different factors.

The authors then consider their factor ΔR_T:

The enhanced radiative cooling due to tropospheric warming, ΔR_T, is approximately proportional to ΔT: tropospheric temperatures scale with the surface temperature change and warmer air radiates more energy, so ΔR_T = kΔT, with k=3W/(m²K)..

All this is saying is that as the surface warms, the atmosphere warms at about the same rate, and the atmosphere then emits more radiation. This is why the model results of rainfall in our figure 2 above show no trend in rainfall over 50 years, and also match the observations – the constraint on rainfall is the changing radiative balance in the troposphere.

And so they point out:

Thus, although there is clearly usable information in fig. 3 [our figure 2], it would be physically unjustified to estimate ΔP/ΔT directly from 20th century observations and assume that the same quantity will apply in the future, when the balance between climate drivers will be very different.

There is a lot of other interesting commentary in their paper, although the paper itself is now quite dated (and unfortunately behind a paywall). In essence they discuss the difficulties of modeling precipitation changes, especially for a given region, and are looking for “emergent constraints” from more fundamental physics that might help constrain forecasts.

A forecasting system that rules out some currently conceivable futures as unlikely could be far more useful for long-range planning than a small number of ultra-high-resolution forecasts that simply rule in some (very detailed futures as possibilities).

This is a very important point when considering impacts.

Conclusion

Increasing the surface temperature by 1ºC is expected to increase the humidity over the ocean by about 7%. This is simply the basic physics of saturation. However, climate models predict an increase in mean rainfall of maybe 2-3% per ºC. The fundamental reason is that the movement of latent heat from the surface to the atmosphere has to be radiated away by the atmosphere, and so the constraint is the ability of the atmosphere to do this. And so the limiting factor in increasing rainfall is not the humidity increase, it is the radiative cooling of the atmosphere.

We also see that despite 50 years of warming, mean rainfall hasn’t changed. Models also predict this. This is believed to be a transient state, for reasons explained in the article.

References

Constraints on future changes in climate and the hydrologic cycle, MR Allen & WJ Ingram, Nature (2002)  – freely available [thanks, Robert]

Notes

1 Relative humidity is measured as a percentage. If the relative humidity = 100% it means the air is saturated with water vapor – it can’t hold any more water vapor. If the relative humidity = 0% it means the air is completely dry. As temperature increases the ability of air to hold water vapor increases non-linearly.

For example, at 0ºC, 1kg of air can carry around 4g of water vapor, at 10ºC that has doubled to 8g, and at 20ºC it has doubled again to 15g (I’m using approximate values).

So now imagine saturated air over the ocean at 20ºC rising up and therefore cooling (it is cooler higher up in the atmosphere). By the time the air parcel has cooled down to 0ºC (this might be anything from 2km to 5km altitude) it is still saturated but is only carrying 4g of water vapor, having condensed out 11g into water droplets.

Read Full Post »